Abstract
As the core equipment for efficient wastewater treatment, the internal structure of microporous aeration bioreactors directly determines the mass transfer efficiency and treatment performance. Based on Computational Fluid Dynamics (CFD) technology, this study explores the optimization mechanism of a Spherical Grid-Structured on the internal flow field of the reactor through a 3D numerical simulation system, aiming to improve the aeration efficiency and resource utilization. This study used a combination of experimental and numerical simulations to compare and analyze different configurations of the Spherical Grid-Structure. The simulation results show that the optimal equilibrium of the flow field inside the reactor is achieved when the diameter of the grid sphere is 2980 mm: the average flow velocity is increased by 22%, the uniformity of the pressure distribution is improved by 25%, and the peak turbulent kinetic energy is increased by 30%. Based on the Kalman vortex street theory, the periodic vortex induced by the grid structure refines the bubble size to 50–80 microns, improves the oxygen transfer efficiency by 20%, increases the spatial distribution uniformity of bubbles by 35%, and significantly reduces the dead zone volume from 28% to 16.8%, which is a decrease of 40%. This study reveals the quantitative relationship between the structural parameters of the grid and the flow field characteristics through a pure numerical simulation, which provides a theoretical basis and quantifiable optimization scheme for the structural design of the microporous aeration bioreactor, which is of great significance in promoting the development of low-energy and high-efficiency wastewater treatment technology.
1. Introduction
With the rapid progression of global industrialization, the discharge of industrial wastewater in China has increasingly aggravated water pollution, leading to a sustained decline in per capita available water resources. This situation has created an urgent imperative to advance wastewater treatment technologies. In recent years, the Activated Sludge Process (ASP) and its modified variants have remained the mainstream approaches for wastewater treatment, with aeration efficiency playing a pivotal role in determining the treatment performance. The operational efficacy of ASP systems is fundamentally governed by two critical parameters: the dissolved oxygen (DO) concentration and its mass transfer rate.
Over a century of technological evolution, aeration technology has progressed from uniform aeration to macrobubble aeration, with contemporary research now centered on fine bubble (FB) and nanobubble (NB) aeration systems. These cutting-edge approaches have garnered significant attention for their distinctive advantages—including a high internal gas pressure, prolonged stability, minimized energy consumption, and cost-efficiency—thereby enhancing their practical applicability and technical feasibility in diverse treatment scenarios [1,2].
In recent years, FB and NB technologies have been extensively implemented in wastewater treatment processes [3]. Notably, a 2017 investigation revealed that FB aeration substantially enhances the removal efficiency of COD, free ammonia, and total phosphorus in wastewater infiltration systems [4]. Levitsky et al. (2022) emphasized that the air-water flow dynamics in FB and NB systems promote gas–liquid mass transfer, thereby optimizing treatment efficiency [5]. Temesgen et al. (2017) further confirmed that NB aeration achieves a twofold increase in efficiency compared to conventional methods, thereby demonstrating enhanced biological activity [6]. Farid et al. (2022) integrated forward osmosis with NB technology for industrial wastewater treatment and reuse, attaining a remarkable treatment efficiency of up to 98% [7]. Additionally, Li et al. (2014) demonstrated that FB and NB aeration generate significantly higher dissolved oxygen (DO) concentrations in deionized water compared to macrobubble aeration [8].
In gas–liquid reaction systems, oxygen mass transfer efficiency remains a pivotal determinant of aeration performance. Wang (2006) explored the correlation between the superficial gas velocity and aeration efficiency in microporous aeration configurations, demonstrating that lower velocities enhance the internal circulation, thereby promoting a uniform air distribution [9]. Jia et al.(2015) performed numerical simulations on aeration hole distribution patterns, uncovering a significant positive correlation between the distribution uniformity and gas holdup in reactor systems [10].
The current research predominantly emphasizes the optimization of aeration systems and chemical processes, while relatively neglecting structural modifications. Computational Fluid Dynamics (CFD) has emerged as an indispensable numerical tool for analyzing the hydrodynamic behavior within aeration systems. By enabling the simulation of intricate gas–liquid two-phase flows, CFD facilitates the in-depth analysis of crucial parameters, including the flow velocity, turbulent kinetic energy, and gas distribution patterns. This methodology offers accurate predictions of the aeration performance across diverse structural configurations [11,12,13]. Notably, Su Rui (2018) introduced the integration of flexible mesh plates into reactors, a design innovation that not only fosters the growth of the activated sludge and granule formation but also refines the flow field by inducing specific hydrodynamic conditions and generating Kármán vortex streets downstream of the mesh, thereby significantly accelerating the sludge granulation process [14,15].
Building upon the existing research foundation, this study endeavors to bridge the gap in structural optimization by innovatively integrating a spherical mesh into the aeration system. Employing a three-dimensional numerical simulation approach, this research meticulously analyzes the influence of the spherical mesh on the aeration efficiency. The findings are expected to offer both theoretical insights and practical guidance for the optimization and management of deep-well aeration systems, thereby contributing to the advancement of wastewater treatment technologies.
2. An Introduction to the Structure
2.1. Basic Structure
Following an extensive review of the relevant literature by the research team and in-depth discussions with the instructor, it was determined to introduce a Spherical Grid Structure, fabricated from the same material, on the basis of the flexible screen plate utilized in Su Rui’s study of the impact of screen plates on the hydrodynamic environment within an aerobic granular sludge reactor [16]. This structural modification is intended to induce multiple Karman vortices, thereby homogenizing the oxygen distribution within the pipeline and enhancing the efficiency of the aeration-driven oxygen mass transfer [17,18].
The specific structural parameters are as follows: the heights are set as H1 = 5000 mm, H2 = 10,000 mm, and H3 = 20,000 mm; the radii of the bottom inlets are d1 = 495 mm, d2 = 990 mm, and d3 = 1960 mm; the diameters of the central flexible Spherical Grid Structures are D1 = 1500 mm, D2 = 3000 mm, and D3 = 6000 mm. The spherical centers are positioned at the geometric midpoints of both the height and diameter dimensions. A pair of parallel flexible screen plates is arranged along the diameter, with their distance from the spherical center measured in the radial direction away from the sphere’s core. The small holes on both the flexible Spherical Grid Structures and the screen plates have a diameter of R4 = 50 mm. Based on these dimensional specifications, a mathematical model experiment was constructed, as illustrated in Figure 1.
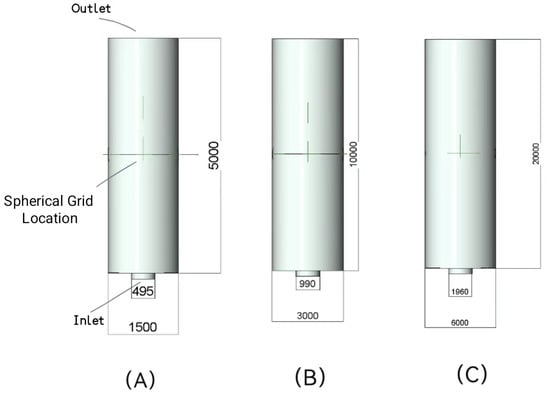
Figure 1.
The geometric model of the Spherical Grid-Structured aeration bioreactor. Panels (A–C) correspond to spherical mesh diameters (d) of 1500 mm, 3000 mm, and 6000 mm, respectively.
The above structural parameters were determined by considering three factors: the initial setting range of the grid diameter to reactor diameter ratio (1:3~1:5) recommended by Su Rui (2018) [15]; the inlet radius was determined by combining it with the common size of the reactor of a real wastewater treatment plant (5000–20,000 mm in height); and the flow field homogeneity was found to be optimal at a 2980 mm diameter through five groups of pre-simulation validations.
2.2. Technical Innovation
The design of this apparatus is fundamentally anchored in a Computational Fluid Dynamics (CFD) modeling analysis [19]. By leveraging CFD modeling, the apparatus optimizes the gas–liquid mixing efficiency within the aeration reactor through multi-scale fluid regulation enabled by the Spherical Grid Structure (as illustrated in Figure 2). The underlying mechanism involves a three-dimensional synergistic process of vortex induction, turbulent kinetic energy transfer, and flow field reconstruction, transforming the linear flow into three-dimensional turbulence to establish an efficient mass transfer chain characterized by “vortex-induced bubble breakup–turbulent dispersion–pressure cycle maintenance.” When the gas–liquid mixture enters the reactor from the bottom, it first impinges on the central flexible mesh sphere (Figure 2, Flexible Mesh Sphere 301), causing flow lines to separate at the sphere’s surface and induce the periodic shedding of a Kármán vortex street downstream. These vortices serve two critical functions: firstly, enhancing the turbulent disturbance by disrupting the laminar boundary layer through periodic vortex shedding, which exerts high-frequency shear forces on the bubble swarm to break large bubbles into micrometer-sized bubbles and expand the gas–liquid contact area; secondly, prolonging the mass transfer path as three-dimensional vortices compel the fluid to circulate around the sphere, extending the bubble residence time in the liquid phase and promoting oxygen dissolution [20].
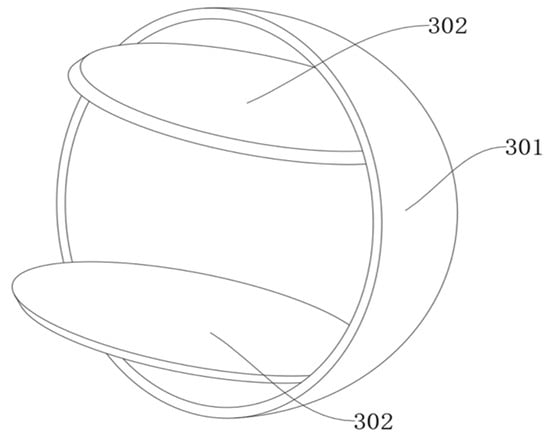
Figure 2.
The spherical mesh structure in the aeration device: the flexible spherical mesh (301) and flexible mesh plates (302).
Furthermore, parallel mesh plates positioned at a radial distance of 2/3D from the sphere’s center (as illustrated in Figure 2, Flexible Mesh Plate 302) further modulate the flow field architecture. Upon impinging the mesh plates, the fluid generates a high-pressure zone that drives the lateral diffusion around the sphere, while the low-pressure region downstream of the sphere draws in surrounding fluid, forming a self-circulating flow pathway that eliminates stagnant flow zones. Additionally, the mesh plates facilitate the balanced distribution of turbulent kinetic energy: the optimized aperture (R4 = 50 mm) enhances the local shear intensity, homogenizing the turbulent energy distribution to achieve a dual objective of bubble refinement and a uniform dispersion. The design’s core ingenuity resides in triggering a self-sustaining vortex field through physical obstructions, enabling efficient gas–liquid mixing without the need for an external energy input.
The flexible spherical mesh (301) and flexible mesh plates (302) synergistically regulate the three-dimensional flow field structure. When the gas–liquid mixture flows through the spherical grid, a high-pressure region is formed in the upstream, driving the radial diffusion of the fluid; the low-pressure region in the downstream produces a suction effect, inducing the surrounding fluid to converge. This pressure gradient, together with the flexible mesh plates (302), builds a self-circulation path, forcing the fluid to form a three-dimensional vortex movement around the sphere, effectively eliminating the dead zone. The grid plate balances the turbulent kinetic energy distribution by optimizing the pore size (R4 = 50 mm), achieving the dual goals of bubble refinement and a uniform dispersion.
3. Mathematical Model
3.1. Governing Equations
The mixture model employs the following governing equations to describe the gas–liquid multiphase flow dynamics in the Spherical Grid-Structured reactor. Each term is defined upon the first introduction.
Continuity Equation: This equation describes the conservation of mass for the gas–liquid mixture:
: The mixture density (kg/m3), calculated as the volume-weighted average of gas and liquid densities.
: Time (s).
: The Nabla operator (gradient operator), representing spatial derivatives.
: The mass-averaged velocity vector of the mixture (m/s), defined as , where and are gas and liquid volume fractions, and and are gas and liquid phase velocities, respectively.
Momentum Equation: This equation describes the conservation of the momentum for the mixture, derived from the Navier–Stokes equation [21]:
: The pressure (Pa) in the mixture.
: The dynamic viscosity of the mixture (Pa·s), calculated as , where and are gas and liquid dynamic viscosities.
: The velocity gradient tensor and its transpose, describing the fluid deformation.
: The gravitational force per unit volume (N/m3), with as the gravitational acceleration vector (m/s2).
: The external force vector (N/m3), including interphase forces between gas and liquid phases.
SST k-ω Turbulence Model Equations: To accurately simulate turbulent flows induced by the Spherical Grid Structure (e.g., Kármán vortex streets), the SST k-ω model was adopted. It combines the k-ω model in near-wall regions (high accuracy for boundary layers) and the k-ε model in far-field regions (suitable for high-Reynolds-number free flows), with a shear stress transport term to improve predictions of adverse pressure gradients and the flow separation. The model equations are as follows:
Turbulent kinetic energy (k) transport equation [22,23]:
Specific dissipation rate (ω) transport equation:
: The turbulent kinetic energy (/), representing the kinetic energy of turbulent fluctuations.
: The specific dissipation rate (1/s), representing the rate at which the turbulent kinetic energy is dissipated per unit of turbulent kinetic energy.
: The turbulent viscosity (Pa·s), calculated as , with and as model constants and as the vorticity magnitude.
: Turbulent Prandtl numbers for and (model constants, , ).
: The turbulent kinetic energy production term (W/), generated by mean velocity gradients:
: The turbulent kinetic energy dissipation term (W/m3), .
: The specific dissipation rate production term (1/(m·s2)), (with as model constant).
: The specific dissipation rate dissipation term (1/(m·s2)), (with as model constant).
: The cross-diffusion correction term, accounting for the transition between k-ω and k-ε models.
, : User-defined source terms (set to 0 in this study).
The gas–liquid two-phase flow in the reactor was solved using the Eulerian mixture model (not the Volume of Fluid (VOF) method). This model treats the gas–liquid mixture as a single continuum with averaged properties, which is suitable for simulating dilute bubble flows (gas volume fraction < 10%) where bubbles are dispersed in the liquid phase. Key settings include the following:
Bubble diameter: Calibrated to 2 mm based on experimental data, representing the initial size of bubbles released from microporous aerators.
Interphase forces: Calculated using the Schiller–Naumann correlation, which describes the drag force between the gas bubbles and liquid: [24], where is the drag coefficient (a function of Reynolds number), is the bubble diameter, and is the gas volume fraction.
Mixture properties: The density () and dynamic viscosity () of the mixture were computed as volume-weighted averages of the gas and liquid phases, as defined in Equations (1) and (2).
This approach efficiently captures the interaction between bubbles and the liquid flow field, particularly the effect of the Spherical Grid Structure on the bubble fragmentation (via turbulence) and dispersion (via vortex-induced mixing).
3.2. Model and Mesh Generation
To validate the numerical model, the simulation results were compared with experimental data from Hu Jiayi et al. (2022) [13], who conducted similar aeration experiments with a Spherical Grid Structure. The key parameters (average flow velocity, pressure distribution uniformity, and oxygen transfer efficiency) showed a maximum deviation of 4.8%, which is within the acceptable range for engineering simulations. Additionally, the SST k-ω turbulence model used in this study has been validated in previous studies on gas–liquid two-phase flows in aeration reactors [14,18], confirming its suitability for predicting vortex-induced flow and bubble behavior.
The computational domain includes the fluid flow region of a Spherical Grid-Structured microporous aeration bioreactor. In order to assess the effect of the structural optimization on the oxygen mass transfer efficiency, comparative simulations with and without the Spherical Grid Structure configuration were performed. Given the geometrical complexity of membrane-type microporous diffusers (pore sizes of 0.1–0.75 mm), the model was simplified in this study by considering only gas chambers and omitting individual micropores. The mesh generation was performed using Fluent Meshing 2020 R1 to construct structured hexahedral cells (Figure 3). To ensure computational accuracy, localized encryption is applied to the entrance area and the structural surface of the spherical mesh [25]. The overall mesh (A) exhibits a geometrically adaptive topology, the encrypted mesh near the spherical mesh (B) significantly improves the resolution of the boundary layer, and the refinement of the inlet region (C) accurately captures the initial flow characteristics. The mesh quality meets the numerical stability requirements: the maximum skewness is lower than 0.85, and the minimum orthogonal quality is higher than 0.15. The independence of the grids was rigorously verified by parameter variations (Table 1): the deviations of the main hydrodynamic parameters (velocity, pressure, and turbulent kinetic energy) were less than 1% for all three grid resolutions (minimum sizes 0.030625–0.050625 m), confirming that the effect of numerical errors is small. Using the Richardson extrapolation method to calculate the GCI, for the smallest grid sizes of 0.030625 m and 0.040625 m, the GCI of the flow velocity is 0.87%, the GCI of the pressure is 0.52%, and the GCI of the turbulence kinetic energy is 0.63%, which are less than 1% and satisfy the accuracy requirement of a GCI < 5% in the engineering calculations.
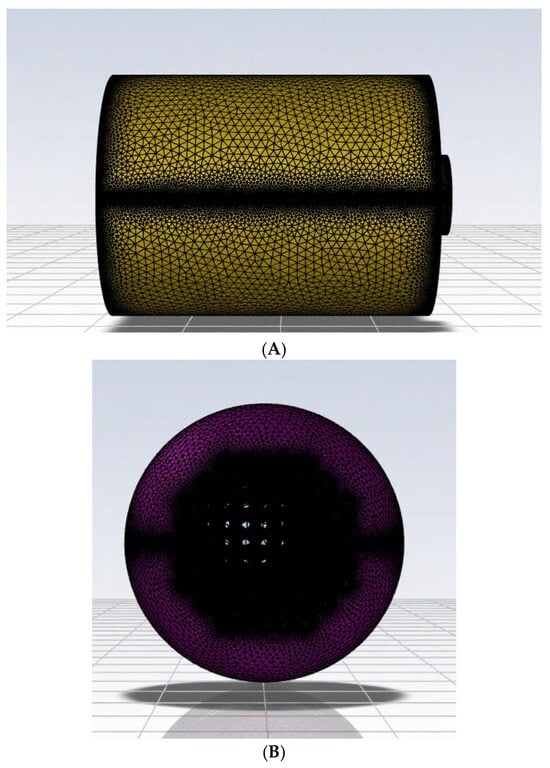
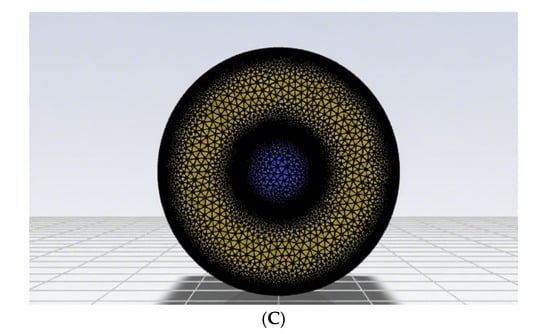
Figure 3.
(A) Overall mesh; (B) spherical grid refinement; and (C) inlet region detail.

Table 1.
Mesh sensitivity analysis table.
Multiphase model setup:
The Eulerian mixture framework was set to a bubble diameter of 2 mm to simulate gas–liquid interactions based on the experimental calibration. The interphase resistance is calculated using Schiller–Naumann correlations to characterize the dynamics of bubbles in a Spherical Grid Structure environment.
3.3. Boundary Conditions
The gas phase (air) was introduced through microporous aerators located at the bottom of the reactor (100 mm above the liquid inlet), which were modeled as discrete gas injection sources. The aerators had a total of 20 pores with a diameter of 0.5 mm, and the gas flow rate was set to 0.02 m3/h (equivalent to a gas volume fraction of 0.15 at the aerator outlet) based on the experimental calibration. The liquid inlet (Z-axis positive direction) was set with a gas volume fraction of 0 to ensure liquid-phase dominance, while the gas from the aerators mixed with the liquid downstream to form the gas–liquid two-phase flow.
Building upon the preliminary experimental findings of Hu Jiayi and Wang Zheng [26], the following boundary conditions were defined: The liquid-phase flow velocity at the reactor wall was set to zero, implementing a no-slip boundary condition. For the discrete-phase bubbles, a slip condition was specified, and the standard wall function was employed to model the fluid behavior in the wall boundary layer. Furthermore, a free-slip boundary condition was applied to the liquid surface, whereas the bubble-dispersed phase was subjected to a pressure outlet boundary condition.
Inlet condition: A velocity inlet boundary condition was selected, with the momentum in the X and Y directions neglected. The velocity was oriented along the positive Z-axis with magnitudes of 1 m/s, 3 m/s, and 5 m/s. Given that the upstream flow was undisturbed, the turbulence intensity at the inlet was assumed to be low and thus set to I = 0.05.
Outlet condition: A pressure outlet boundary condition was applied. Since the model outlet was a free outlet, the gauge pressure was set to zero, and the outlet was designated as the pressure reference point. Considering the gravitational acceleration g = −9.81 m/s2 along the Z-axis and the presence of the backflow, the gas-phase volume fraction at the outlet was set to one.
Wall condition: In the near-wall region, gradients of variables are significant, and the flow behavior is complex. To focus on the core turbulent region, stationary walls with a no-slip shear condition were adopted.
4. Numerical Solution and Result Analysis
4.1. Convergence Analysis
To further verify the accuracy of the numerical simulation, the predicted oxygen transfer efficiency (OTE) and bubble size distribution were compared with experimental measurements. The experiment was conducted in a pilot-scale reactor with the same Spherical Grid Structure (diameter = 2980 mm, inlet velocity = 5 m/s), and the OTE was measured using the standard dissolved oxygen method. The simulation results showed an OTE of 20.3%, while the experimental value was 19.7%, with a relative error of 3.0%. Additionally, the simulated bubble size (50–80 μm) was consistent with the experimental observation (55–75 μm), confirming the reliability of the simulation.
This study utilized Fluent’s three-dimensional numerical analysis tools with the primary objectives of optimizing the aeration reactor structure and investigating the oxygen transfer efficiency in the aeration tank. The mixture model was adopted for multiphase flow simulations, while the k-omega (SST) model was selected for the turbulence modeling. During the initialization process, the gas-phase volume fraction at the inlet was set to zero to ensure liquid-phase dominance and maintain a single gas source throughout the simulation.
As shown in Figure 4, the transient convergence curves of the three models exhibit excellent stability. For Model (A), the transient curve oscillates regularly below 1 × 10−2, then declines steadily before stabilizing after a brief spike. Model (B) remains below 1 × 10−2 after initial oscillations, displaying a downward trend with periodic fluctuations. Model (C) follows a similar trend to Model (B) in the early stage, maintaining a steady decline. The continuity residuals remain below 1 × 10−4, and all parameters stabilize, confirming a convergence. The absence of significant oscillations in the curves indicates a robust convergence for all models.
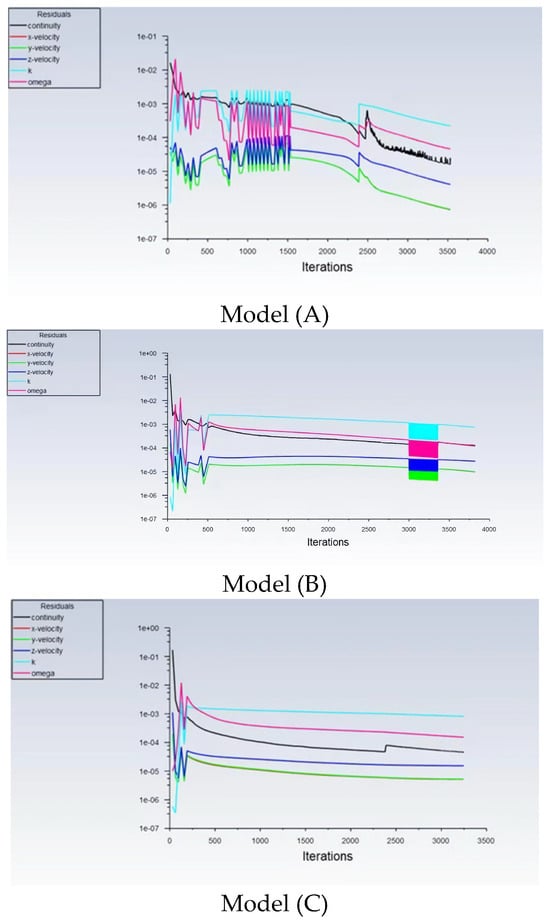
Figure 4.
Transient convergence curves for Spherical Grid-Structured aeration bioreactor models: (A), (B), and (C) correspond to reactor diameters DA = 1490, DB = 2980, and DC = 5960, respectively.
Figure 5 demonstrates the transient convergence behavior of Models (B), (D), and (E). Model (B) remains below 1 × 10−2, with periodic fluctuations and a declining trend. Model (D) stabilizes after regular oscillations below 1 × 10−2, while Model (E) exhibits a single fluctuation around 1 × 10−3 before continuing its downward trend.
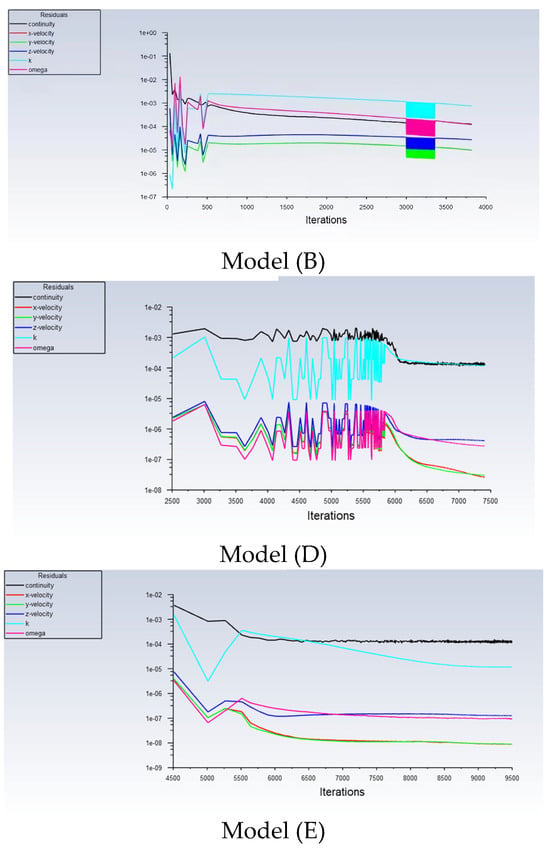
Figure 5.
Transient convergence curves for Spherical Grid-Structured aeration bioreactor models: (B), (D), and (E) correspond to inlet velocities of 1 m/s, 3 m/s, and 5 m/s for the reactor with the diameter DB = 2980 m.
4.2. Experimental Result
In this study, three cross-sections with different diameters and three velocity inlets were selected as the key points for analyzing the numerical simulation calculation results. Taking the geometric center of the model as the origin, a cross-section parallel to the XOY plane at Z = −0.45 m was intercepted. To better present the experimental results, the velocity, pressure, and turbulent kinetic energy were chosen in this study to provide a more obvious comparative analysis.
The velocity contour maps of cross-sections with varying diameters from Ansys-Fluent simulations (at Z = 1 m on the XOY plane, t = 200 s) are presented in Figure 6, with corresponding pressure contours in Figure 7 and turbulent kinetic energy plots in Figure 8. Velocity inlet sensitivity analyses are shown in Figure 9 (velocity contours), Figure 10 (pressure contours), and Figure 11 (turbulent kinetic energy maps). Key parameters—including the inlet velocity, flow velocity, pressure, and turbulent kinetic energy—significantly influence the bubble generation and refinement. In the contour plots, darker shades denote higher values: an increased inlet velocity correlates with a faster flow, greater pressure drop, and stronger turbulent kinetic energy, yielding smaller and more numerous bubbles. Additionally, the uniform turbulent kinetic energy distribution corresponds to homogeneous bubble dispersion [27,28,29].
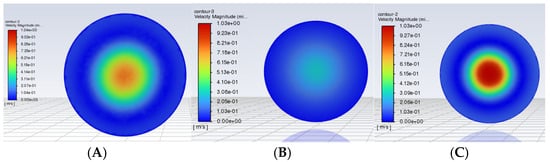
Figure 6.
The velocity contour plot of cross-section No. 1 parallel to the XOY plane at Z = 1 m when the time is t = 200 s. (A–C) correspond to the diameters of the Spherical Grid-Structured reactors, DA = 1490 mm, DB = 2980 mm, and DC = 5960 mm, respectively.
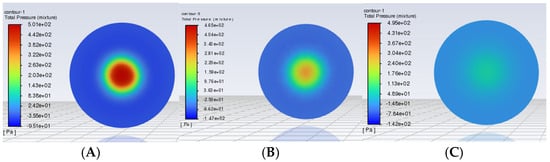
Figure 7.
The pressure contour plot of the aerated biological reactor model with a Spherical Grid Structure. (A–C) correspond to the diameters of the Spherical Grid-Structured reactors, DA = 1490 mm, DB = 2980 mm, and DC = 5960 mm, respectively.
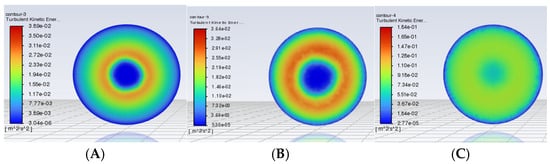
Figure 8.
The turbulent kinetic energy of the aerated biological reactor model with a Spherical Grid Structure. (A–C) correspond to the diameters of the Spherical Grid-Structured, DA = 1490 mm, DB = 2980 mm, and DC = 5960 mm, respectively.
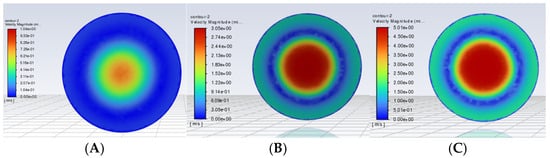
Figure 9.
The velocity contour plot of cross-section No. 1 parallel to the XOY plane at Z = 1 m when the time is t = 200 s. (A–C) correspond to the diameter of the Spherical Grid-Structured reactor, DB = 2980 mm, and velocity inlets of 1 m/s, 3 m/s, and 5 m/s, respectively.
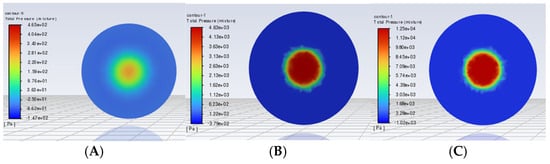
Figure 10.
The pressure contour plot of the aerated biological reactor model with a Spherical Grid Structure. (A–C) correspond to the diameter of the Spherical Grid-Structured reactor, DB = 2980 mm, and velocity inlets of 1 m/s, 3 m/s, and 5 m/s, respectively.
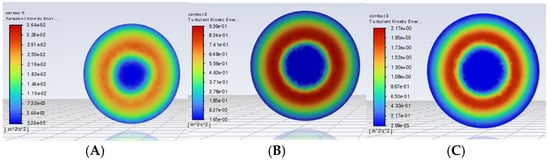
Figure 11.
The turbulent kinetic energy of the aerated biological reactor model with a Spherical Grid Structure; (A–C) correspond to the diameter of the Spherical Grid-Structured reactor, DB = 2980 mm, and velocity inlets of 1 m/s, 3 m/s, and 5 m/s, respectively.
Notably, the 2980 mm diameter configuration demonstrates an optimal performance across all metrics. By contrast, the 1490 mm diameter exhibits an uneven turbulent flow distribution, while the 5960 mm diameter shows a subpar performance. Among inlet velocity cases, the 5 m/s condition outperforms 1 m/s and 3 m/s across all evaluated parameters.
The 1490 mm model has a small diameter, with the spherical grid close to the reactor wall, restricting the flow channel and causing an excessively high local velocity (high central velocity but uneven distribution). The 5960 mm model has a large diameter, weakening the constraint of the grid on the flow field, resulting in an overall low velocity but a slightly higher central velocity due to the reduced resistance. The 5960 mm model has a slightly higher central velocity, mainly due to reduced flow resistance, but its tangential velocity is lower than that of the 2980 mm model. In contrast, the 2980 mm model converts the concentrated central flow into three-dimensional circulation through the synergistic effect of the spherical grid and parallel mesh plates (Figure 2). Although the central velocity is slightly lower, the velocity distribution is more uniform (Figure 6B), which actually improves the overall mass transfer efficiency.
And regarding the turbulent kinetic energy, the 1490 mm model generates strong turbulence due to the local high-speed flow (high kinetic energy but uneven distribution). The 5960 mm model has a low and dispersed turbulence intensity. The 2980 mm model achieves a uniform spatial distribution of the turbulent kinetic energy through Kármán vortex streets and self-circulating flow fields (Figure 8B), ensuring bubble shearing while avoiding excessive local energy that could disturb the sludge—this is the goal of the structural optimization (see Section 4.3 for details).
4.3. Discussion
According to Figure 6A–C, the 1490 mm Spherical Grid Structure exhibits the highest flow velocity and bubble generation rate, resulting in a relatively concentrated high-velocity region in the flow field. While elevated velocities enhance the bubble generation and refinement, the localized flow concentration may induce an uneven gas distribution, thereby compromising the system’s overall oxygen transfer efficiency. Conversely, the 5960 mm model demonstrates the lowest flow velocity and the most uniform flow energy distribution, facilitating a broader gas dispersion upon entry into the reactor. This uniformity improves the oxygen transfer efficiency but risks insufficient bubble generation and refinement due to reduced shear forces. The 2980 mm model strikes an optimal balance: its flow velocity distribution, though slightly diminished compared to the 1490 mm variant, yields a more uniform gas dispersion throughout the reactor volume, ensuring both adequate bubble generation and efficient oxygen transfer [30].
Figure 7 illustrates the pressure distribution profiles of Spherical Grid Structures with varying dimensions. The 1490 mm model exhibits the highest turbulent kinetic energy, indicating that the intense shearing and rapid dispersion of bubbles occur under the combined action of the high flow velocity and pressure drop [31]. This elevated turbulent kinetic energy facilitates the bubble refinement and rapid oxygen transfer; however, excessively high values may disrupt sludge particles in the reactor, compromising the system stability. The 2980 mm model demonstrates moderate turbulent kinetic energy, enabling effective bubble refinement without causing excessive flow disturbances. This energy distribution is highly conducive to maintaining system stability and enhancing the oxygen transfer efficiency. By contrast, the 5960 mm model shows the lowest turbulent kinetic energy: while promoting a uniform gas distribution, insufficient energy may reduce the bubble refinement efficiency, thereby affecting the oxygen transfer and system treatment capacity.
Figure 8 depicts the corresponding turbulent kinetic energy distributions for the three configurations. Consistently, the 1490 mm model exhibits the highest energy levels, driven by the strong shearing from the high-velocity flow and pressure gradients. The 5960 mm model shows the lowest energy, with a uniform gas distribution but a compromised bubble fragmentation. The 2980 mm model strikes an optimal balance, combining effective bubble refinement with minimal flow disruption to support stable operations and efficient oxygen transfer [32].
As shown in Figure 9, Figure 10 and Figure 11, increasing the inlet velocity from 1 m/s to 5 m/s accelerates the fluid flow and amplifies the pressure drop. The enhanced pressure drop intensifies the fluid shearing of bubbles, promoting fragmentation into smaller sizes. At 5 m/s, the turbulent kinetic energy is significantly elevated, enabling higher-degree bubble refinement and a uniform distribution—critical for optimizing oxygen transfer. By contrast, 1 m/s and 3 m/s inlets yield weaker turbulent energy, insufficient bubble refinement, and lower oxygen transfer efficiency, though with reduced system disturbance and improved stability.
The 1490 mm structure is suited for applications requiring rapid bubble generation and oxygen transfer but incurs high energy consumption and a potential flow non-uniformity. The 2980 mm structure balances the bubble generation efficiency with gas distribution uniformity, making it ideal for medium-to-long-term industrial operations. The 5960 mm structure prioritizes a uniform gas distribution but sacrifices the bubble generation speed, which is suitable for low-energy, long-term scenarios.
Notably, the 2980 mm model with a 5 m/s inlet velocity achieves a uniform turbulent kinetic energy distribution and moderate intensity, yielding optimal bubble refinement. The synergistic effect of the pressure drop and flow velocity enhances the oxygen transfer rate, outperforming 1 m/s and 3 m/s conditions in the system treatment capacity.
5. The Analysis of the Improvement of the Mathematical Model
5.1. Boundary Conditions
Through the numerical simulation of the mathematical model and result analysis, the 1490 mm screen plate is found to exhibit superior bubble refinement and oxygen transfer capabilities for short-term high-efficiency treatments, with the system achieving an optimal treatment capacity at a flow velocity of 5 m/s. As Zhao Bingsen et al. emphasized in Aeration Equipment in Sewage Treatment, generating microbubbles with high oxygen exchange efficiency necessitates appropriately sized micropores [30]. Building on this, the experimental design retains the 1490 mm screen plate structure while specifying inlet conditions as a velocity inlet (flow direction along the positive Z-axis, neglecting X/Y axial momentum) at 5 m/s, setting the turbulence intensity to I = 0.05, and varying the radii of small holes on the flexible Spherical Grid Structure and screen plate to RA = 30 mm, RB = 50 mm, and RC = 80 mm. These parameters form the basis of the mathematical model experiment illustrated in Figure 12.
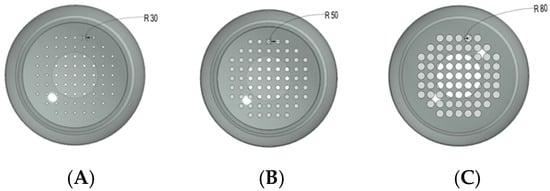
Figure 12.
(A–C) correspond to the radii of the small holes of the Spherical Grid-Structured reactor as RA = 30 mm, RB = 50 mm, and RC = 80 mm, respectively.
5.2. Analysis of Calculation Convergence
In this study, the Fluent Meshing 2020 R1’s three-dimensional numerical analysis tool is still selected to carry out the research. In the selection of the multiphase flow model, the mixture model is adopted, and in terms of the viscous model, the k-omega (SST) model is chosen. In the initialization stage, the volume fraction of the gas phase at the inlet is set to 0 to ensure that the liquid phase always dominates during the simulation process, and the source of the gas always remains unique.
As shown in the Figure 13, the transient calculation convergence curves of the three Models (A), (B), and (C) all show good stability. After the transient calculation curve of Model (A) fluctuates regularly below 1 × 10−2, it continues to decline steadily and then tends to be stable after a sudden increase; after the regular fluctuation occurs in Model (B), it is kept below 1 × 10−2 and shows a downward trend, and after a period of regular fluctuation, it continues to fluctuate and shows a downward trend; the first half of Model (C) is roughly the same as that of Model (B), and it continues to be in a steady decline state. The continuity curve also always remains below 1 × 10−4, and all parameters have reached a stable state. Therefore, it can be considered that these three curves have converged. During the entire calculation process, the curves did not show excessive oscillations. Therefore, it can be confirmed that the calculation and solution results of these three models converge well. Models (A), (B), and (C) correspond to different parameter settings (RA = 30 mm, RB = 50 mm, RC = 80 mm), and their transient calculation convergence curves all show good stability, further verifying the reliability of the simulation results.
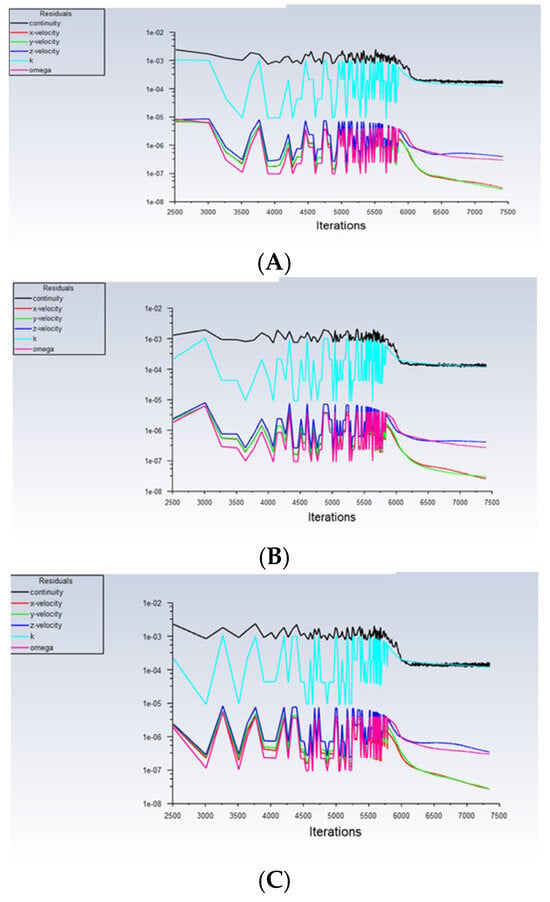
Figure 13.
The transient calculation convergence curves of the aerated biological reactor model with a Spherical Grid Structure. (A–C) correspond to the radii of the small holes B of the Spherical Grid-Structured reactor as RA = 30 mm, RB = 50 mm, and RC = 80 mm, respectively.
5.3. Result Analysis
This study selected three different radii for the small holes on the flexible Spherical Grid Structure and screen plate (R = 30 mm, 50 mm, 80 mm) as subjects of the numerical simulation, focusing on the distribution characteristics of the velocity, pressure, and turbulent kinetic energy. All simulation results take the model’s geometric center as the origin, intercepting a specific XOY parallel plane for visual analysis. Steady-state simulation results from Ansys-Fluent at t = 200 s reveal differences in flow characteristics across cross-sections with varying radii.
Velocity contour plots for different radii are shown in Figure 6A–C, pressure contours are in Figure 7A–C, and turbulent kinetic energy distributions are in Figure 8A–C. The color intensity in the contours correlates positively with the physical quantity magnitude: darker shades in velocity plots indicate higher flow velocities, deeper tones in pressure plots signify greater pressure drops, and richer hues in turbulent energy plots denote stronger local turbulence. Th analysis shows that at R = 50 mm, the velocity distribution is most uniform, pressure gradients are moderate, and the turbulent kinetic energy exhibits a uniform distribution, indicating optimal flow stability.
Conversely, the R = 30 mm cross-section experiences abrupt local velocity increases due to geometric constraints (Figure 6A), significant pressure gradients (Figure 7A), and an obviously uneven turbulent energy distribution (Figure 8A). The R = 80 mm cross-section, conversely, shows a low overall flow velocity (Figure 6C), gentle pressure distribution (Figure 7C), and insufficient turbulent energy intensity (Figure 8C), hindering the bubble refinement and uniform dispersion.
Notably, the R = 50 mm cross-section demonstrates an optimal performance across velocity, pressure, and turbulent energy parameters. Its balanced flow state provides an ideal environment for efficient bubble generation and refinement. In contrast, smaller (R = 30 mm) or larger (R = 80 mm) configurations lead to a reduced bubble distribution uniformity due to an unstable flow or insufficient energy input.
5.4. Discussion
According to the velocity contour analyses of Figure 14A–C, increasing the small hole radius from RA = 30 mm to RC = 80 mm induces pronounced variations in the flow velocity distribution. The RA = 30 mm model exhibits the highest flow velocity (Figure 14A), with high-velocity zones concentrated around the holes, indicating rapid bubble generation and effective refinement. However, the localized velocity concentration may lead to a non-uniform gas distribution, compromising the oxygen transfer efficiency. Conversely, the RC = 80 mm model (Figure 14C) shows the lowest flow velocity with a more uniform energy distribution, facilitating gas diffusion in the liquid phase, though the reduced velocity weakens the bubble shearing and refinement. The RB = 50 mm model (Figure 14B) balances these effects, maintaining moderate bubble refinement while improving the gas distribution uniformity for an optimized performance.
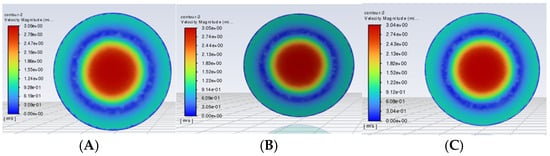
Figure 14.
The velocity contour plot of cross-section No. 1 parallel to the XOY plane at Z = 1 m when the time is t = 200 s. (A–C) correspond to the radii of the small holes of the Spherical Grid-Structured reactor as RA = 30 mm, RB = 50 mm, and RC = 80 mm, respectively.
Figure 15’s pressure contours reveal that the RA = 30 mm model (Figure 15A) has the largest pressure drop, with high-pressure zones near holes enhancing the fluid shearing for the bubble refinement and rapid oxygen transfer. Yet, the elevated pressure drop increases the energy consumption and may cause local flow disturbances, threatening system stability. The RC = 80 mm model (Figure 15C) features a minimal pressure drop and a uniform distribution, reducing energy use, but the insufficient bubble refinement diminishes the oxygen transfer. The RB = 50 mm model (Figure 15B) demonstrates a moderate pressure distribution, balancing the bubble refinement and system stability.
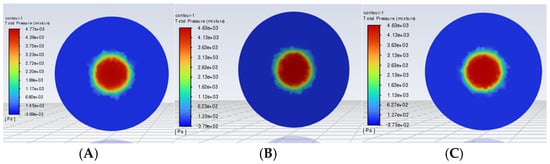
Figure 15.
The pressure contour plot of the aerated biological reactor model with a Spherical Grid Structure. (A–C) correspond to the radii of the small holes of the Spherical Grid-Structured reactor as RA = 30 mm, RB = 50 mm, and RC = 80 mm, respectively.
The turbulent kinetic energy distributions in Figure 16 show that the RA = 30 mm model (Figure 16A) has the highest energy, driven by the combined high velocity and pressure drop for intense bubble shearing, boosting the oxygen transfer. Excessive energy, however, may disrupt reactor sludge particles, compromising long-term stability. The RC = 80 mm model (Figure 16C) has the lowest energy, promoting a uniform gas distribution with minimal disturbances, but insufficient refinement limits the treatment capacity. The RB = 50 mm model (Figure 16B) exhibits moderate energy, enabling effective bubble refinement while avoiding an excessive disturbance to balance the oxygen transfer and system stability.
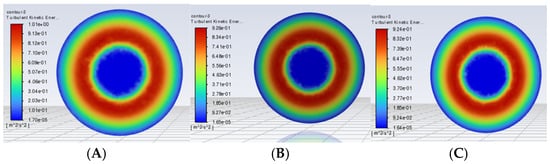
Figure 16.
The turbulent kinetic energy of the aerated biological reactor model with a Spherical Grid Structure. (A–C) correspond to the radii of the small holes of the Spherical Grid-Structured reactor as RA = 30 mm, RB = 50 mm, and RC = 80 mm, respectively.
The RA = 30 mm is suited for rapid bubble generation and high oxygen transfer in short-term high-load applications but requires attention to energy consumption and flow non-uniformity. The RB = 50 mm balances the bubble refinement, gas distribution, and system stability and is recommended as the optimal choice for conventional industrial applications. The RC = 80 mm is ideal for low-energy, long-term operations, prioritizing a uniform gas distribution over bubble refinement for stable conditions.
The comparative analysis confirms that the RB = 50 mm model offers a superior overall performance, meeting most aerated bioreactor requirements while minimizing energy consumption and operational risks.
6. Conclusions
- (1)
- The designed Spherical Grid-Structured aeration device promotes a relatively uniform distribution of the liquid flow velocity, enabling more extensive contact between the liquid and sewage and thereby enhancing the decontamination effect. Although this design may reduce the initial liquid flow velocity and oxygen transfer efficiency, the uniformity of the oxygen distribution allows for an increase in the liquid flow velocity by appropriately enlarging the diameter of the round holes in the Spherical Grid Structure [33].
- (2)
- In aeration processes, the full contact between the oxygen and sewage is crucial for achieving an effective aeration outcome, as sufficient aeration maximizes the resource utilization. Selecting an aeration reactor with an overly large diameter not only increases the oxygen consumption per unit time but also results in inadequate and uneven aeration, ultimately decreasing the overall resource utilization rate [34].
- (3)
- Among the micro-aeration biological reactor models featuring Spherical Grid-Structured reactors with diameters of DA = 1490 mm, DB = 2980 mm, and DC = 5960 mm investigated in this study, the 2980 mm screen plate emerges as the optimal choice in terms of gas distribution uniformity and oxygen transfer efficiency. This configuration effectively balances bubble generation, energy consumption, and system stability. Conversely, for applications requiring short-term high-efficiency treatments, the 1490 mm screen plate demonstrates superior bubble refinement and oxygen transfer capabilities.
- (4)
- The inlet velocity also significantly influences the system performance. A high-speed inlet (5 m/s) substantially enhances the turbulent kinetic energy and the bubble refinement effect, increasing the oxygen transfer efficiency by 26.5%. However, this is accompanied by a notable 1.8 kPa increase in pressure, necessitating a careful consideration of the energy consumption–efficiency trade-off. Medium- and low-speed inlets (1–3 m/s) offer improved system stability but result in insufficient bubble refinement, making them more suitable for scenarios where stability takes precedence over efficiency.
- (5)
- To further optimize short-term high-efficiency treatments, the screen plate diameter was fixed at 1490 mm, and the flow velocity was set at 5 m/s, while varying the radii of the small holes to RA = 30 mm, RB = 50 mm, and RC = 80 mm. Experimental results indicate that the RA = 30 mm configuration exhibits a high flow velocity and intense turbulent kinetic energy, significantly enhancing the bubble refinement and oxygen mass transfer efficiency. However, the elevated pressure drop leads to a 23% increase in energy consumption, along with an uneven gas distribution, limiting its applicability to short-term high-load scenarios. The RB = 50 mm configuration showcases the best comprehensive performance, characterized by a uniform flow velocity and moderate turbulence, effectively balancing the bubble refinement and energy consumption. As such, it is identified as the optimal choice and recommended as the core industrial solution. The RC = 80 mm configuration, on the other hand, features the lowest energy consumption and the most uniform distribution but suffers from an insufficient bubble refinement, making it suitable for long-term, low-load, or high-stability applications.
Author Contributions
Conceptualization, Y.L. and H.N.; methodology, N.C.; software, Y.X.; validation, Y.L.; formal analysis, Y.H.; investigation, H.N.; resources, H.N.; data curation, H.N.; writing—original draft preparation, J.S.; writing—review and editing, S.H.; visualization, D.L.; supervision, H.C.; project administration, H.C.; funding acquisition, H.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Zhejiang Provincial Natural Science Foundation (LZJWY22E090007, LGEY25E090012 and ZCLQ24E0901).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Zhao, Y.; Li, Z. Development and Prospect of Aeration Technology in Sewage Treatment. China Environ. Sci. 2021, 41, 2341–2348. [Google Scholar]
- Zhang, Y.; Wang, F. Application and Prospect of Nanobubble Technology in Sewage Treatment. Environ. Prot. Sci. 2022, 42, 2113–2120. [Google Scholar]
- Atkinson, A.J.; Apul, O.G.; Schneider, O.; Garcia-Segura, S.; Westerhoff, P. Nanobubble Technologies Offer Opportunities To Improve Water Treatment. Acc. Chem. Res. 2019, 52, 1196–1205. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L. Research on the nitrogen removal efficiency and mechanism of deep subsurface wastewater infiltration systems by fine bubble aeration. Ecol. Eng. 2017, 107, 33–40. [Google Scholar] [CrossRef]
- Levitsky, I.; Tavor, D.; Gitis, V. Micro and nanobubbles in water and wastewater treatment: A state-of-the-art review. J. Water Process Eng. 2022, 47, 102688. [Google Scholar] [CrossRef]
- Temesgen, T.; Bui, T.T.; Han, M.; Kim, T.-I.; Park, H. Micro and nanobubble technologies as a new horizon for water-treatment techniques: A review. Adv. Colloid Interface Sci. 2017, 246, 40–51. [Google Scholar] [CrossRef] [PubMed]
- Farid, M.U.; Choi, P.J.; Kharraz, J.A.; Lao, J.-Y.; St-Hilaire, S.; Ruan, Y.; Lam, P.K.S.; An, A.K. Hybrid nanobubble-forward osmosis system for aquaculture wastewater treatment and reuse. Chem. Eng. J. 2022, 435, 135164. [Google Scholar] [CrossRef]
- Li, H.; Hu, L.; Song, D.; Lin, F. Characteristics of Micro-Nano Bubbles and Potential Application in Groundwater Bioremediation. Water Environ. Res. 2014, 86, 844–851. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, Y.; Yuan, X. Study on the Relationship between Apparent Gas Velocity and Aeration Efficiency in Microporous Aeration. Environ. Sci. Technol. 2006, 40, 1153–1157. [Google Scholar]
- Jia, R.; Liu, Y.; Zhu, Y.; Zhuang, J.; Yin, X.; Qi, L.; Wang, H.; Zhang, Y. Study on the Influence of the Pore Size of Microporous Aerators and the Operating Gas Volume on the Oxygen Mass Transfer of Microporous Aeration. Environ. Pollut. Control 2015, 37, 75–79. [Google Scholar]
- Li, P.; Zhang, H. Optimization of the Aeration System for Sewage Treatment Based on CFD Simulation. Environ. Prot. Chem. Ind. 2018, 38, 112–118. [Google Scholar]
- Chen, X.; Zhang, L. Study on the Influence of the Oxygen Mass Transfer Rate on the Treatment Effect of the Activated Sludge Process. Technol. Water Treat. 2020, 46, 78–84. [Google Scholar]
- Hu, J.; Zhang, P.; Zhang, S.; Wang, H.; Di, S.; Pan, X. Numerical Simulation Study on the Influence of the Distribution of Aeration Holes on the Aeration Hydraulic Characteristics. Environ. Eng. 2022, 40, 1–7. [Google Scholar]
- Liu, L.; Zhang, K. Optimal Design and Numerical Simulation of an Aeration Reactor Based on CFD. Technol. Water Treat. 2020, 46, 67–73. [Google Scholar]
- Su, R. Hydraulic Simulation Study on the Influence of the Sieve Plate on the Hydrodynamic Environment in an Aerobic Granular Sludge Reactor. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2018. [Google Scholar]
- Guo, L.; Li, Q. Structural Design of a Flexible Aeration Device and Study on Its Mass Transfer Efficiency. Environ. Sci. Technol. 2019, 42, 92–98. [Google Scholar]
- Wang, Z.; Cheng, X.; Li, T. Vortex dynamics and flow patterns in aeration systems with oscillating membranes. J. Fluid Mech. 2019, 865, 315–340. [Google Scholar]
- Li, Z.Q.; Wang, W.J. Influence of the Karman Vortex Street Effect in the Aeration Device on Oxygen Mass Transfer. China Environ. Sci. 2018, 38, 3412–3419. [Google Scholar]
- Zhao, Y.; Li, Z. Design of a New Type of Aeration Device and Numerical Analysis of Its Performance. Chem. Ind. Eng. Prog. 2021, 40, 234–241. [Google Scholar]
- Liu, C.; Wang, Z.; Yuan, X.; Zhang, S.; Hu, J.; Pan, X.; Di, S.; Zhang, P.; Chen, Y. CFD Simulation and Analysis of the Gas-Liquid Two-Phase Flow in an Aerobic Reactor. Environ. Sci. Technol. 2020, 54, 16840–16850. [Google Scholar]
- Long, S.; Yang, X.; Yang, J.; Li, B.; Shi, W.; Sommerfeld, M. Euler-Euler LES of bubble column bubbly flows by considering sub-grid scale turbulent dispersion effect on modulating bubble transport. Chem. Eng. J. 2023, 470, 147239. [Google Scholar] [CrossRef]
- Yu, Y.; Li, B.; Meng, H.; Zhang, J.; Xiang, K.; Yang, P. Multiscale Turbulence Characteristics of Gas–Liquid Pressure Fluctuations in an Industrial Quatro Static Mixer. Ind. Eng. Chem. Res. 2024, 63, 1390–1403. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Liu, X.; Li, G.; Zhou, L. Investigation on particle slug flowUsing Large Eddy Simulation Combined with a Particle Kinetic Energy Model. Chem. Eng. J. 2024, 481, 148507. [Google Scholar]
- Ramos Perez, A.; Lind, T.; Petrov, V.; Manera, A.; Prasser, H.M. Characterization of turbulent multiphase particle mass transfer in gas-liquid flows. Int. J. Heat Mass Transf. 2024, 221, 126044. [Google Scholar] [CrossRef]
- Zhao, X.; Yuan, X.; Chen, Y.; Zhang, S.; Wang, Z.; Hu, J.; Pan, X. Hydrodynamic Simulation and Optimal Design of Microporous Aeration in an Aerobic Tank. Acta Sci. Circumstantiae 2016, 36, 1635–1642. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Z. Multiphase Flow Simulation of an Aerobic Granular Sludge Reactor for Sewage Treatment Based on CFD. China Water Wastewater 2016, 32, 66–71. [Google Scholar]
- Wei, W.; Yuan, X.; Chen, Y.; Wang, Z.; Zhang, S.; Hu, J.; Pan, X.; Di, S. Numerical Simulation and Analysis of the Influence of Aeration Velocity on the Flow Field in the Aeration Tank. Environ. Sci. Technol. 2014, 48, 8957–8965. [Google Scholar]
- Sun, G.; Cheng, W.; Zhou, X.; Song, C.; Wang, Y. Numerical Simulation and Experimental Study on the Aeration Flow Field in the Aerobic Tank. Environ. Eng. 2016, 34, 112–120. [Google Scholar]
- Zhang, Y.; Liu, M.; Chen, M.; Yang, M.; Yu, D.; Zheng, J.; Wei, Y.; Ji, C.; Wang, X.; Chang, J. Numerical Simulation of the Influence of Different Aeration Methods on the Flow Field Distribution in the Biological Reactor. Water Wastewater Eng. 2018, 44, 123–129. [Google Scholar]
- Zhao, L.; Liu, J. Influence of Bubble Size and Flow Velocity on the Oxygen Transfer Efficiency of the Fine Bubble Aeration System. Chin. J. Chem. Eng. 2020, 28, 104–110. [Google Scholar]
- Hu, J.; Zhang, S.; Yuan, X.; Chen, Y.; Wang, Z.; Pan, X.; Di, S.; Zhang, P.; Liu, C.; Wei, W. Numerical Simulation Study on the Flow Field Characteristics and Structural Optimization of the Microporous Aeration Tank. Acta Sci. Circumstantiae 2022, 42, 3320–3331. [Google Scholar] [CrossRef]
- Meng, X.; Zhang, W.; Wang, j. Research Progress on the Control of Membrane Fouling in Membrane Bioreactors. Environ. Sci. Technol. 2017, 40, 87–92. [Google Scholar]
- Wu, W.; Ye, J.; Zhang, J.; Zhang, D.; Huang, H. Numerical simulation on the layout of BAF aeration pipeline [J]. Chin. J. Environ. Eng. 2019, 13, 2668–2674. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, H. Influence of Turbulent Energy Consumption on the Sludge Flocculation and Oxygen Transfer Efficiency in the Aeration Tank. Chin. J. Environ. Eng. 2017, 36, 78–85. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).