Abstract
Urbanization always leads to increasing challenges to the groundwater resources in karst regions due to intensive land use, infrastructure development, and the rapid transmission potential of pollutants. This study proposed an improved groundwater vulnerability assessment (GVA) framework by modifying the widely used COP (Concentration of flow, Overlying layers, and Precipitation) model, through the integration of three additional indicators: urban underground rail transportation (UURT), land use and cover (LULC), and karst development (K). Guiyang, a typical urbanized karst city in southwest China, was selected as the case study. The improved COP model, namely the COPK model, showed stronger spatial differentiation and a higher Pearson correlation coefficient () with nitrate concentrations ( = 0.4388) compared to the original COP model (R = 0.3689), which validates the effectiveness of the newly introduced indicators. However, both R values remained below 0.5, even after model modification, suggesting that intensive human activities play a role in influencing nitrate distribution. The pollution load index (PI) was developed based on seven types of pollution sources, and it was integrated with the COPK vulnerability index using a risk matrix approach, producing a groundwater risk map classified into five levels. Global Moran’s I analysis (0.9171 for COP model and 0.8739 for COPK model) confirmed strong and significant spatial clustering patterns for the two models. The inclusion of UURT and LULC improved the model’s sensitivity to urban-related pressures and enhanced its capacity to detect local risk zones. It is a scalable tool for groundwater risk assessment in urbanized karst areas and offers practical insights for land use planning and sustainable groundwater management.
1. Introduction
Karst aquifer systems (KASs) constitute a critical component of the global freshwater resources, which provide potable water for approximately 25% of the global population [1,2]. Due to their unique geological structures, such as complex networks of fissures and caves, KASs are highly sensitive to external changes in the water cycle, including rainfall events, seasonal fluctuations in recharge, land use alterations, and engineering disturbances [3,4,5,6]. Also, KASs are particularly vulnerable to pollution, where contamination events often result in extended and difficult recovery efforts [7,8,9]. In recent years, human activities such as excessive extraction [10], urban expansion [11], poor management practices [12], industrial discharges [13], and agricultural runoff [14] have increasingly threatened both the quantity and quality of groundwater in KASs. These pressures compromise the sustainability of groundwater, leading to risks to public health and ecosystem stability [15,16,17,18]. Therefore, employing advanced technologies such as remote sensing (RS), geographic information systems (GISs), and predictive modeling has become a crucial pursuit for global scholars aiming to achieve sustainable groundwater management [19,20].
Groundwater vulnerability assessment (GVA) serves as an essential management tool for identifying areas where pollutants from the surface are more likely to reach the groundwater system [21,22,23]. It is a critical initial step in hydrogeological studies and lays the foundation for future sustainable groundwater management [24,25]. Groundwater vulnerability (GV) can be categorized into intrinsic vulnerability, which considers the aquifer’s physical characteristics such as geology and hydrology, and specific vulnerability, which assesses the impact of specific contaminants and their interaction with the aquifer [26,27,28,29]. In karst regions, a range of GVA models have been specifically developed or adapted for KASs, including EPIK [30], REKS [31], RISKE [32], PI [33], KARSTIC [34], COP [35], PaPRIKa [36], IZDAN [37], PRESK [38], DRISTPi [39], LEPT [40], and IVAKY [41]. These models incorporate, either fully or partially, key geological, hydrological, and climatic features such as soil properties, surface conditions, karst development, characteristics of the saturated and unsaturated zones, and precipitation patterns to construct karst GVA models. In these models, the COP model is one of the most commonly used GVA models, focusing on three key factors: concentration of flow (C), overlying layers (O), and precipitation (P) [42,43,44,45], making it a practical and widely adopted framework for assessing intrinsic vulnerability in KASs.
Beyond direct applications, recent studies have frequently modified COP models to enhance their applicability and accuracy. For example, Li et al. [46] enhanced the COP model by incorporating sinkhole density, land use and cover (LULC), and karst network development, significantly improving GVA in karst regions. Cao et al. [47] and Qiu et al. [48] modified the COP method into the COPK approach by considering karst development to assess GV in northern China’s karst areas, notably improving model accuracy. Ghezelayagh et al. [49] introduced the COPKAT model, which enhances the traditional COP model by incorporating karstification, atmospheric conditions, and tectonics using the fuzzy logic method. Although these improvements to the traditional COP model enhance its performance by introducing new indicators, they still do not sufficiently address the changing surface conditions and hydrological dynamics under rapid urbanization. In particular, LULC such as impervious surfaces can significantly alter infiltration and runoff behavior. Also, urban underground rail transportation (UURT) introduces subsurface disturbances and concentrated drainage structures [50,51,52,53]. However, the two factors are rarely considered in existing models. In the context of urbanization, particularly in China, UURT and the increase in impervious surfaces are important aspects of city development [54]. Effectively integrating the impacts of UURT and LULC on groundwater into GVA models is crucial for more accurately identifying pollution-prone areas.
The aim of this study is to modify the traditional COP model by incorporating the impacts of UURT and LULC in Guiyang, a typical karst region, to accurately construct a GVA model. Additionally, the regional groundwater risk distributions are calculated, taking into account seven potential pollution sources (PPSs), including industrial, agricultural, mining activities, hazardous waste disposal sites, landfills, gas stations, and golf courses. This study is the first to incorporate UURT into GVA in karst areas, while also systematically integrating LULC. Combined with regional groundwater risk mapping, this constitutes the main innovation of the work. Nitrate (NO3−), a commonly used groundwater quality parameter for validating GV models, is employed to compare the performances of the modified model before and after its improvement. The objectives of this study are twofold: first, to establish a GVA model for karst regions that takes into account the impacts of UURT and LULC within an urbanized context in Guiyang City; and second, to assess regional groundwater risks, considering multiple PPSs.
2. Study Area
Guizhou Province, located in the Yunnan–Guizhou Plateau, is one of the three largest karst regions in the world, with carbonate rocks accounting for 71.7% of its total area. The study area, Guiyang City, is located in the center of Guizhou Province, covering an area of 2527.32 km2, with exposed carbonate rocks making up 74.68% (Figure 1). The study area has a subtropical humid and temperate climate, with an average temperature of 15.3 °C, extreme highs of 39.5 °C, and lows of −9.5 °C. It has an annual average of 1148.3 h of sunshine and records minimal snowfall. This area has an unevenly distributed annual precipitation averaging 1136.96 mm, peaking during the rainy season from April to October, while the dry season spans from December to March. The terrain is varied, being higher in the north and south, with elevations ranging from 800 m to 1600 m. Geologically, the study area is characterized by significant uplift during the Early and Middle Paleozoic, resulting in the widespread absence of the Devonian, Silurian, and parts of the Carboniferous and Ordovician strata across most of the region. In several locations, the Lower Carboniferous or Permian strata are in direct contact with underlying Cambrian or Ordovician rocks. The widespread distribution of carbonate rocks fosters active karst features like sinkholes and underground rivers, increasing the region’s susceptibility to surface pollution. As urbanization progresses, exemplified by three operational urban rail transit lines as of March 2024, the risks of groundwater contamination have heightened, highlighting the need for focused studies on GV in this karst-rich municipal area.
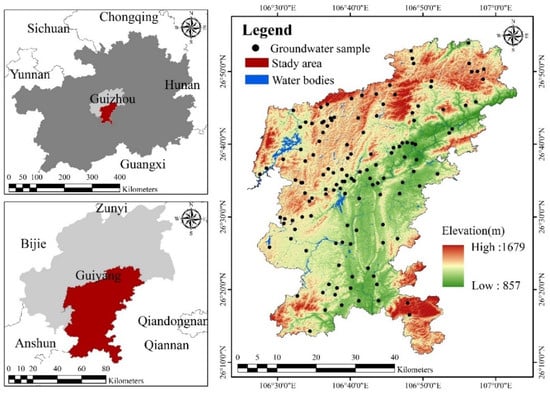
Figure 1.
Study area (Guiyang City).
3. Methodology
Figure 2 illustrates the methodological framework of this study. Based on the traditional COP model, we introduced three additional factors: distance to UURT, LULC, and karst development (K). They were integrated into the vulnerability index calculation to formulate the improved COPK model. Nitrate (NO3−), as a commonly used groundwater quality parameter, was employed to validate and compare the performance of the modified COPK model against the COP model. Finally, by combining the COPK results with various PPSs, regional groundwater risk was assessed, resulting in a spatial risk zoning map.
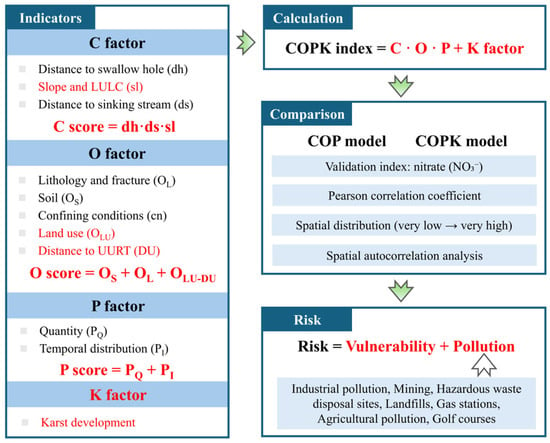
Figure 2.
Methodology framework.
3.1. Data Source and Pre-Processing
Table 1 presents the data sources used in this study. The dataset includes vector, raster, and csv formats. All vector data, such as lithology, LULC, and distance to UURT, were converted into raster format with a spatial resolution of 30 m using vector-to-raster transformation in ArcGIS 10.8. For raster datasets such as normalized difference vegetation index (NDVI, 1 km), digital elevation model (DEM, 30 m), and soil (1 km), resampling techniques were applied to standardize them to a uniform resolution of 30 m. This process can facilitate the following overlay analysis and spatial calculations for GV map generations [46,55,56].

Table 1.
Data sources.
3.2. COP Model
The baseline COP model assesses GV by individually scoring the C, O, and P factors and then calculating their product (Equation (1)). A higher COP index indicates a stronger protective effect against contamination, corresponding to the lower GV of the KAS [23,35]. In this study, the calculation of the COP model was conducted in strict accordance with the methodology proposed by Vías et al. [35]. and the detailed scoring criteria for each factor are provided in Appendix A.
where C score, O score, and P score represent the degree of flow concentration (C), the protective capacity of the overlying geological layers (O), and the precipitation intensity and distribution (P), respectively.
3.2.1. C Factor
The C factor (concentration of flow) in the COP model considers four elements: sinkholes, sinking streams, slope, and vegetation cover (Figure 3). According to the existing literature, areas that are close to sinkholes and sinking streams and have low vegetation cover and steep slopes tend to have lower scores, which indicates the weaker natural protection and higher GV of the KSA [45,48]. Figure 3e presents the spatial distribution of the C factor as calculated in the traditional COP model (Equation (2)).
where , , and represent the distance to sinkholes, the distance to sinking streams, and the harmonized score of slope and vegetation cover, respectively.
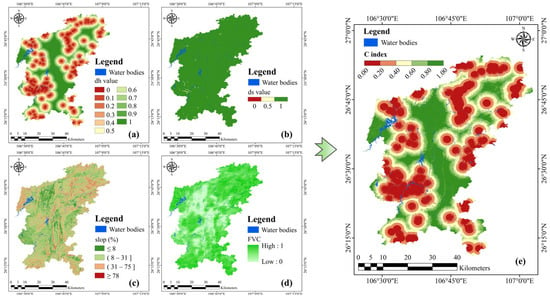
Figure 3.
C factor and corresponding indicator distribution. (a) Distance to sinkholes (); (b) distance to sinking stream (); (c) slope; (d) vegetation; (e) C factor distribution.
3.2.2. O Factor
The O factor in the traditional COP model includes four key components: soil type, soil thickness, lithology, and confining conditions. In general, compact soil or lithologies, greater soil thickness, and confined aquifer conditions provide stronger protection against contamination [57,58]. The calculation for the O score is provided in Equation (3). The spatial distribution of the O factor and its four contributing indicators are shown in Figure 4.
where represents the protective capacity of the soil layer, and is the protective capacity of the unsaturated lithological layer beneath the soil.
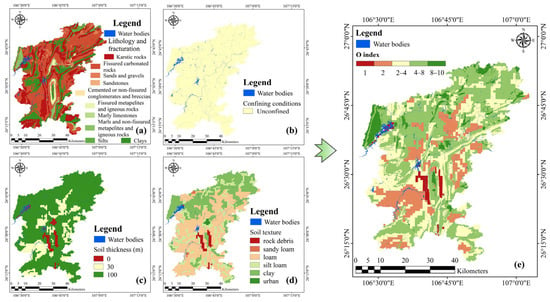
Figure 4.
O factor and corresponding indicator distribution. (a) Lithology; (b) confining conditions; (c) soil thickness; (d) soil texture; (e) O factor distribution.
3.2.3. P Factor
The P factor in the COP model typically considers two main components: annual average rainfall and temporal distribution [45]. Precipitation can significantly affect the migration of contaminants in the subsurface environment [59]. The temporal distribution of precipitation affects the timing and duration of recharge events, which in turn influences the potential for surface pollutants to reach the aquifer. P score is calculated by Equation (4) and Figure 5 shows the distribution of P factor and two indicators. Table 2 presents the information of all monitoring stations in the study area from 2009 to 2023. According to the COP model standard criteria outlined in Appendix A, all stations have PQ values within 800–1200 mm (assigned a weight of 0.2) and PI values below 10 mm/day (assigned a weight of 0.6). Therefore, there is a uniform p-value (0.8) throughout the study area.
where and represent the quantity and temporal distribution of precipitation, respectively.
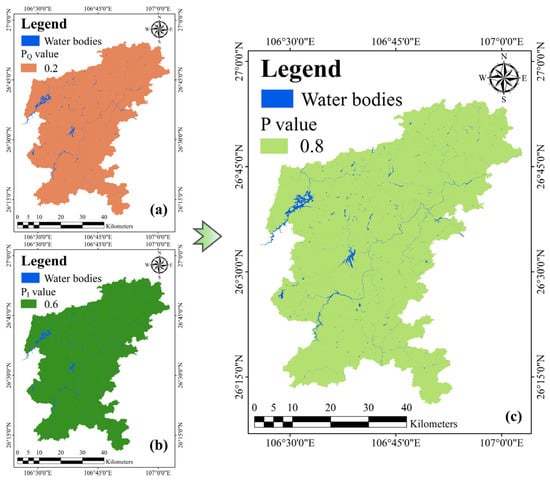
Figure 5.
P factor and corresponding indicator distribution. (a) Annual average rainfall; (b) temporal distribution of precipitation; (c) P factor distribution.

Table 2.
Precipitation information in Guiyang City.
3.3. Modified COPK Model
To enhance the applicability of the COP model under urbanization, particularly in karst regions influenced by UURT and LULC, three additional indicators were introduced in this study: distance to UURT (DU), LULC, and karst development (K). The modified COPK model is calculated by Equation (5).
where sl refers to the composite score of slopes and LULC, presents the composite score of LULC and distance to UURT, and K is the karst development. The meanings of the other variables are consistent with those defined previously.
In particular, is defined as follows:
where is the score based on the distance to UURT at location , where lower values indicate higher GV due to proximity. is the LULC score at location , and is a binary spatial mask function, equal to 1 if the location is within the UURT influence zone, and 0 otherwise.
3.3.1. Modified C Factor
In the modified C factor, LULC replaces the NDVI component in the traditional COP model. The original binary classification of vegetation as simply “high” or “low” was considered insufficient to represent real surface conditions. Instead, LULC was integrated with a slope to form a composite variable (sl), with scoring criteria provided in Table 3.

Table 3.
The score of slopes and LULC (sl) in the C factor.
From the aspect of flow concentrations, areas categorized as construction land, cultivated land, or bare land are more likely to promote surface runoff and increase the concentration of flow, thus receiving lower scores in the C factor assessment [11,60]. These LULC types reduce surface infiltration and enhance the potential for rapid pollutant transport toward KASs. In contrast, areas covered by shrubland, forest, or grassland tend to enhance surface infiltration and reduce concentrated flow [61,62]. Figure 6 shows the sl indicator and spatial distribution of the modified C factor.
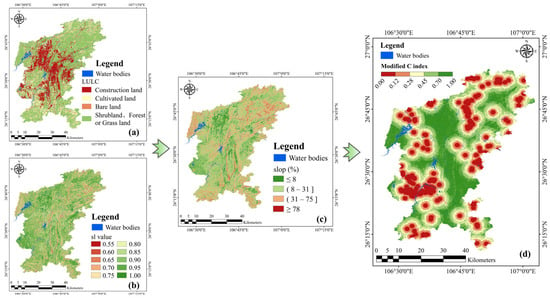
Figure 6.
Modified indicators for new C factors. (a) LULC; (b) slope; (c) score of sl indicator; (d) modified C factor distribution.
3.3.2. Modified O Factor
For the improvement of the O factor, the effects of UURT and LULC were integrated to better represent the protective capacity of the overlying layers. A composite indicator () was developed and the corresponding scores are shown in Table 4. The areas closer to UURT lines were assigned lower scores, indicating a higher GV because of the increased disturbance of the natural hydrological system. Notably, construction land, as an impervious surface, has the highest protective capacity in terms of preventing vertical infiltration, and thus receives the highest scores in this component. In OLU-DU, the influence of UURT is given priority over LULC when determining the overlaying layers. Specifically, scores from UURT are assigned to areas within its influence zone, replacing the original land use scores, while land use values are retained elsewhere. The modification process is shown in Figure 7.

Table 4.
The scores of UURT and LULC (OLU-DU) for the O factor.
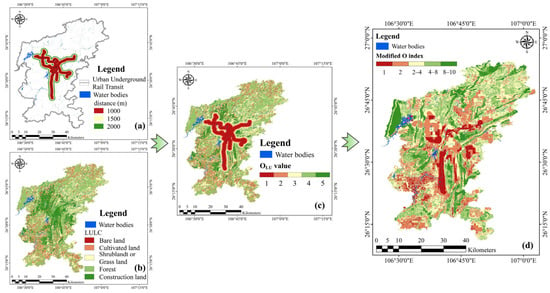
Figure 7.
Modified indicators for new O factors (a) UURT; (b) LULC; (c) ; (d) modified O factor distribution.
3.3.3. K Factor
The K factor was introduced as an additional factor to represent the degree of karstification, which directly influences GV due to variations in conduit connectivity [63]. In this study, karst development was classified based on the Chinese standard (Code for Geotechnical Investigations of Urban Rail Transit of Guizhou Province, DBJ52/T099-2020 [64]). This classification standard integrates carbonate rock formations, karst development features, hydrogeological characteristics, and representative lithologies of Guizhou to categorize the K factor into three levels: strong, moderate, and poor [46]. These categories are assigned scores from 1 to 3, respectively, and other areas outside the classified karst zones are assigned a score of 4. The detailed classification method is provided in Appendix B, and Figure 8 shows the spatial distribution of the K factor.
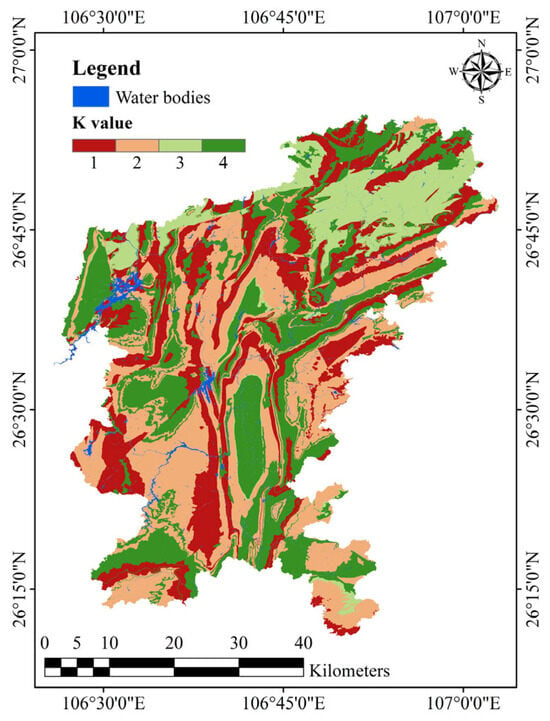
Figure 8.
K factor.
3.4. Model Validation
To assess the performance of the two GV models, nitrate (NO3−) was selected as the groundwater quality parameter for validation, given its widespread use as a tracer for anthropogenic pollution in KASs [65,66,67]. In this study, the Pearson Correlation Coefficient () was used to validate the performance of the original COP and modified COPK models [67,68,69]. This correlation was calculated for two models to quantify the correlation between the predicted GV scores and the measured nitrate levels, and it has been widely used for the validation of GV models [48,70]. Generally, a higher indicates a higher model performance for the GV model. The equation for r calculation is as follows:
where is the GV index at the sampling point ; is the corresponding nitrate concentration; and are the mean values of GV and NO3−, respectively; and is the total number of samples.
A total of 133 groundwater samples were used to assess the correlation between NO3− and the GV scores. Since the vulnerability indices generated by the COP and COPK model represented the protective capacity of the aquifer (i.e., higher values indicate lower GV), an inverse transformation of NO3− concentration was applied prior to validation. Specifically, the adjusted NO3− value for each groundwater sample was calculated as follows:
where is the original NO3− of sample , and is the maximum NO3− concentration among all samples. This transformation ensures that higher adjusted NO3− corresponds to a higher GV, aligning with the model’s output logic.
3.5. Spatial Autocorrelation
Spatial autocorrelation was applied to examine the spatial structure and clustering characteristics of GV maps. It quantifies the degree of similarity between attribute values at neighboring spatial units [71,72]. In this study, both global and local spatial autocorrelation methods were employed. The global Moran’s I index was used to assess the overall spatial correlation across the study area, and local spatial autocorrelation analysis was further used to detect local spatial clusters. A positive Moran’s I value suggests spatial clustering of similar values, a negative value implies spatial dispersion, and a value near zero indicates a random spatial pattern [73,74]. The global spatial autocorrelation index is calculated as follows:
where is the total number of spatial units; and are the attribute values at cells and , respectively; is the mean of all values; and is the spatial weight between units and .
3.6. Groundwater Risk Calculation
To assess groundwater risk in the study area, seven categories of PPSs were identified, including industrial pollution sources, mining areas, hazardous waste disposal sites, landfills, gas stations, agricultural pollution sources, and golf courses. The identification of PPSs’ categories and their calculation was based on previous studies [75,76,77]. The pollution load risk index for an individual groundwater pollution source was calculated using Equation 10. The details of the calculation are shown in Appendix C.
where is the pollution load risk index for pollution source ; is the toxicity of pollutants associated with source ; is the likelihood of release from source ; and is the quantity of pollutants potentially released.
The final pollution source load index map was generated by overlaying the calculated pollution loads of all PPS categories. The comprehensive PI was calculated using the following equation:
where represents the comprehensive pollution load index at a given location, and is the weight assigned to the category of pollution source (Table 5).

Table 5.
Weights for seven categories of PPSs.
The final groundwater risk was assessed by integrating the results of the GV index and the PI. A matrix-based approach was employed to combine the five classes of GV with the five classes of pollution load, resulting in five levels of groundwater risk. The risk levels were classified as follows: very high, high, moderate, low, and very low.
4. Results
4.1. GV Map
Figure 9 shows the GV mapping results derived from the COP and COPK models, respectively. The COP model was classified based on the method proposed by Vías et al. [35], while the COPK model was classified using the natural breaks method. Overall, the COPK model had a large proportion of very high (27.73%) and high (27.52%) GV zones compared to the COP model, while the proportions of low (15.03%) and very low (6.33%) zones were significantly smaller than those in the COP model. Also, NO3− sampling points were shown on both GV maps. A general consistency was observed between the spatial distribution of high NO3− concentrations and the areas classified as highly vulnerable, supporting the validity of the model outputs.
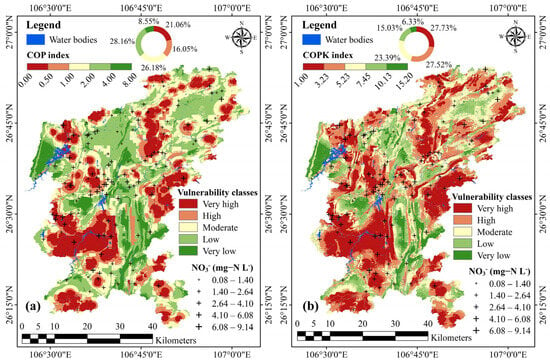
Figure 9.
GV maps. (a) COP model; (b) modified COPK model.
4.2. Model Validation Results
To evaluate the performance of the GV models, both the COP and the modified COPK models were compared against transformed NO3− concentrations. As shown in Figure 10, scatter plots with linear regression fits were generated for each model, and PCCs were calculated to quantify the correlations. The results indicate a positive correlation between the two models and NO3− concentrations, which confirms the reasonability of model construction. The very small p-value (p < 0.001) implies that the result is robust and unlikely to result from random noise. Notably, the improved from 0.3689 in the COP model to 0.4388 in the COPK model, which suggests that the newly introduced indicators and scoring processes such as distance to UURT, LULC, and karst development significantly enhanced the model’s accuracy in urbanized karst areas. The modified COPK model is considered more suitable for this study area and can serve as a reliable basis for future groundwater risk assessments. However, it should be noted that even after these improvements, the value remains below 0.5, which may indicate the significant influences of human activities in the study area.
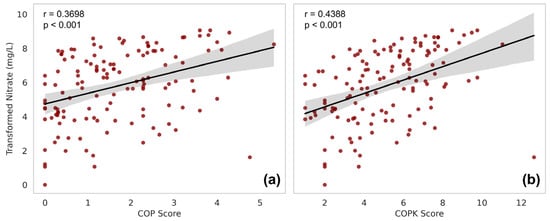
Figure 10.
Model validation results with transformed NO3− concentrations with 95% confidence interval. (a) COP model (r = 0.3698); (b) COPK model (r = 0.4388).
4.3. Spatial Autocorrelation Results
Table 6 shows the results of global Moran’s I for the COP and COPK models. The two models have strong and statistically significant positive spatial autocorrelation, which indicates the obvious and robust spatial clustering of the GV index (p-value < 0.001). The COP model yielded a Moran’s I value of 0.9171, while the COPK model resulted in a slightly lower value of 0.8739. Although the spatial autocorrelation of COPK is marginally weaker, it remains high and significant. The slight reduction in spatial autocorrelation may be attributed to the increased heterogeneity introduced by UURT, LULC, and karst development, which better differentiates localized vulnerability.

Table 6.
Global Moran’s I calculation.
Figure 11 shows the results of local Moran’s I analysis for the COP model and the COPK model. Both models display significant spatial clustering, dominated by High–High (HH) and Low–Low (LL) types. Compared to the COP model, the COPK model exhibits a more dispersed pattern, reflecting the impact of UURT and LULC on local spatial structure. Additionally, HH clusters account for over 50% of the area in both models, confirming strong local spatial autocorrelation.
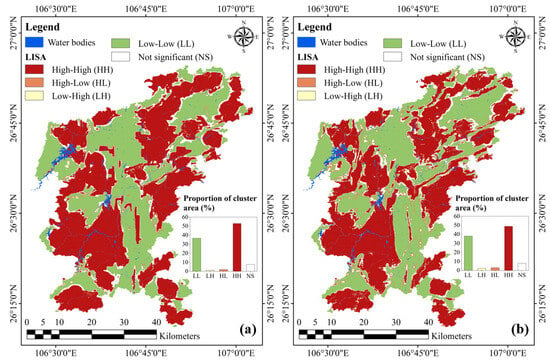
Figure 11.
LISA mapping and spatial agglomeration: (a) COP model; (b) COPK model.
4.4. Groundwater Risk
Figure 12 presents the spatial distribution of groundwater risk across the study area, based on the integration of GV and pollution load. Figure 12a shows the spatial distribution of the PI. Overall, PI in Guiyang is relatively low and is scattered across the region in a fragmented pattern. The PI layer and the COPK vulnerability index were combined using the risk matrix approach, as shown in Figure 12c. Finally, a groundwater risk map was created in Figure 12d, including five levels: very low, low, moderate, high, and very high, classified by the natural breakpoint method. Overall, the groundwater risk in Guiyang is relatively low. Moderate- to high-risk areas are primarily concentrated in the central part of Guiyang City, and a closer comparison reveals a notable spatial correspondence with the distribution of the buffers of UURT. This alignment strongly supports the effectiveness of the UURT as an important indicator in capturing the impact of urban infrastructure on GVA.
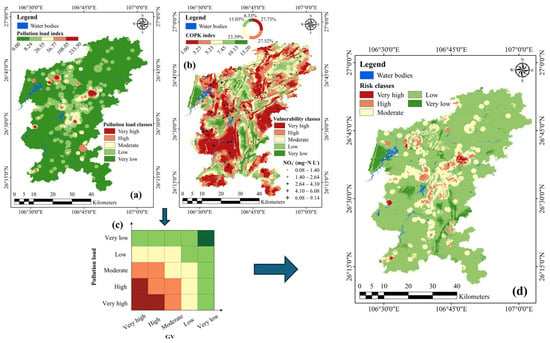
Figure 12.
Groundwater risk calculation. (a) Pollution load; (b) COPK; (c) a matrix approach for risk assessment; (d) groundwater risk map.
5. Discussion
5.1. Effectiveness of the Modified COPK Model Under the Urbanization Context
In this study, the traditional COP model was modified and enhanced by introducing three additional indicators: UURT, LULC, and K. Specifically, UURT and LULC were integrated into the C and O factors with differentiated scoring approaches, allowing for a more precise assessment of anthropogenic impacts. Compared with existing modifications that primarily focus on improving the K factor [46,47,48], the modified COPK model offers a novel and comprehensive improvement, confirming that UURT, LULC, and K are essential for GVA in karst regions. Previous studies have pointed out that UURT can disrupt the natural surface cover and facilitate the rapid infiltration of pollutants into aquifers through construction-related fractures and subsurface disturbances [51,52,78]. Although modern UURTs are typically equipped with engineered drainage facilities, it is nearly impossible to completely avoid surface and subsurface disturbances [79,80]. Thus, incorporating UURT into GVA models provides a more realistic representation of urbanization impacts on groundwater conditions. Likewise, LULC has been widely recognized as a key factor in GVA under urbanization [81]. While in porous media settings, models such as DRASTICL have proven the value of the model improvement with the involvement of LULC [82,83,84,85], its application in karst GV assessments remains limited. Li et al. [46] incorporated the LULC indicator into the COP model to assess GV across karst regions in Guizhou Province, which was a valuable attempt. Building upon this, this study considers LULC in both the C (flow concentration) and O (overlying protective layer) factors, which proved to be highly effective in enhancing GV model accuracy. Additionally, we also noticed that the values of two models were both below 0.5, which was consistent with the relatively low in many previous studies [22,86,87,88]. This outcome highlights the substantial impact of anthropogenic activities, particularly the clustered pollution sources in the study area, which can obscure or weaken the statistical relationship between vulnerability and observed nitrate contamination [89,90]. Therefore, three major recommendations are derived from this work. Firstly, UURT and LULC should be systematically incorporated into the karst GVAs under the urbanization context. Secondly, urban rail development should prioritize the preservation of surface integrity and hydrological function to minimize the risk of contaminant migration, especially in vulnerable KASs. Finally, taking into account the impact of more complete human activities on GVA models remains a worthy direction for future research.
5.2. Analysis of Groundwater Risk Assessment
The groundwater risk assessment conducted in this study effectively integrated GVA and pollution loads, and the use of a risk matrix approach allowed for a structured classification of risk levels, which aligns with widely accepted practices in sustainable groundwater management. In recent years, such integrated approaches have been widely adopted in vulnerability risk modeling, as demonstrated in the works of Li et al. [91], Zhang et al. [92], and Li et al. [93], all of which successfully combined GV with pollution loading to derive spatial risk distributions. Compared to these studies, the present work offers a more comprehensive consideration of PPS categories. Specifically, seven major PPSs were considered in PI evaluation, including industrial pollution, mining activity location, hazardous waste disposal site, landfill, gas station, agricultural pollution, and golf courses. For each PPS category, three factors (pollutant toxicity, release probability, and expected contaminant quantity) were independently evaluated and integrated to generate the composite PI, as shown in Appendix C. This evaluation process was guided by the existing literature [75,76,77]; however, a standardized framework for PI calculation has yet to be established. Therefore, we recommend that future research should formalize the PI evaluation process and promote the application of the risk matrix approach used in this study. Also, from a management perspective, areas identified as high risk should be prioritized for monitoring, pollution source control, and infrastructure planning. The findings reinforce the importance of integrated risk assessment models in supporting proactive and spatially targeted groundwater protection strategies.
5.3. Urban Planning and Infrastructure Development for Sustainable Groundwater Management
This study presents a case-specific demonstration of how urban infrastructure (specifically, UURT) can be effectively incorporated into GVA to better reflect real-world anthropogenic pressures. While UURT represents one major component of urban development, it is important to recognize that a wide range of infrastructure projects, including road networks [94], land reclamation [95], and drainage systems [96], can also significantly alter hydrological conditions and increase risks to groundwater systems. The integration of UURT into the COP vulnerability framework in this study serves as a good example, illustrating the potential to incorporate other urbanization-related indicators into GV models. In the context of urbanization, GV should be viewed as a core constraint in spatial planning, particularly in ecologically sensitive areas such as karst regions where the aquifer system is highly vulnerable to disturbance. From a broader perspective, sustainable groundwater management requires a proactive and spatially informed planning approach, where vulnerability maps are used not only as scientific outputs, but as decision-support tools for urban planners, environmental regulators, and infrastructure designers. By identifying high-risk zones before construction, cities can implement preventive measures such as impermeable zone control, buffer zone planning, enhanced drainage designs, and pollution source zoning.
5.4. Limitations and Future Research
While this study presents an improved COP-based framework by incorporating UURT, LULC, and K to assess GV and risk in urbanized karst regions, several limitations should be acknowledged. First, the scoring and classification of the newly introduced indicators (particularly in UURT and LULC) still rely partly on expert judgment and semi-quantitative methods. Although spatial accuracy has been improved, the subjectivity in scoring may lead to uncertainty. Second, the model currently assumes static conditions for LULC and PPSs, which may not fully capture the temporal dynamics of urban development and contamination processes. Future studies should consider incorporating time-series data, such as changes in LULC, urban expansion stages, or seasonal nitrate variability, for more accurate GV model construction. Third, although the study area represents a typical urbanized karst region, the transferability of the model to other karst systems with different conditions requires further validation. In particular, more comparative applications across varying urbanization gradients and karst morphologies could enhance the generalizability of the approach. Fourth, this study focuses on nitrates as the primary validation parameter. While nitrate is widely accepted as a representative pollutant in vulnerability assessments, future research should expand validation efforts to include multi-contaminant indicators, such as heavy metals, organics, or microbial risks, to provide a more comprehensive evaluation of model performance under diverse pollution scenarios. Finally, future research should also explore coupling vulnerability risk models with decision-making systems, integrating them into urban planning platforms or environmental early-warning mechanisms, to facilitate real-time responses to emerging groundwater threats.
6. Conclusions
This study proposed an improved GV risk assessment framework designed for urbanized karst regions, using Guiyang City as a case study. The traditional COP model was enhanced by incorporating three critical indicators (UURT, LULC, and K), which were combined into the C and O factors to form the modified COPK model. This modification significantly improved the model’s performance and its correlation with observed transformed NO3− concentrations ( = 0.4388) was higher than the COP model ( = 0.3698). A comprehensive PI was constructed by integrating seven types of PPSs, including industrial, mining, hazardous waste disposal, landfills, gas stations, agricultural land, and golf courses. The COPK-based GV map and the pollution load map were combined using a risk matrix approach, resulting in a detailed spatial classification of groundwater risk into five levels. Moderate- to high-risk areas were primarily concentrated in the central part of Guiyang City, and a closer comparison revealed a notable spatial correspondence with the distribution of the buffers of UURT.
Overall, this work highlights the importance of integrating infrastructure-related indicators into GV models under urbanization contexts. The case of UURT reflects how surface disruption and subsurface alteration can exacerbate GV. Meanwhile, LULC proves to be a critical dual-role factor that influences both runoff concentration and protective-layer characteristics. This framework not only improves the scientific basis for groundwater risk assessment in karst regions, but also provides operational tools for urban planning, land use zoning, and environmental decision-making. The proposed approach offers high applicability and can be extended to other rapidly urbanizing karst areas worldwide.
Author Contributions
Conceptualization, Q.Z. and X.S.; methodology, Q.Z., Y.W., Y.L. and H.X.; software, Q.Z., Y.L. and W.Z.; validation, Q.Z., C.M., Y.C. and X.S.; formal analysis, Y.W.; investigation, Q.Z., Y.L. and H.X.; resources, X.S.; data curation, Y.W.; writing—original draft preparation, Q.Z.; writing—review and editing, Y.W., Y.L., H.X., C.M., W.Z., Y.C. and X.S.; visualization, Q.Z.; supervision, X.S.; project administration, X.S.; funding acquisition, X.S. and W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by the project of the impact of urban rail transit construction on groundwater environment in karst areas and the research and application of key protection technologies, Qiankehe Support [2022] General 210; Pintang Karst Peak-cluster Depression Ecosystem Observation and Research Station of Guizhou Province, Qiankehe Platform, YWZ[2024]002.
Data Availability Statement
Data will be made available on request.
Acknowledgments
We gratefully acknowledge the support provided by the Research Project of the 111 Geological Brigade, Guizhou Geological and Mineral Exploration and Development Bureau.
Conflicts of Interest
Authors Xiaoqing Song and Ying Wang were employed by the company Guizhou Geological Engineering Investigation, Design and Research Institute Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A. The Scoring Process of the Traditional COP Model
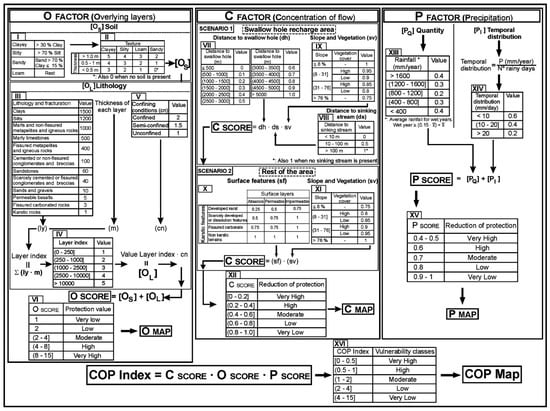
Figure A1.
The scoring system of the traditional COP model [35].
Appendix B. Karst Development Classification in DBJ52/T 099-2020
This section describes the classification of karst development (K) used in this study. The classification is primarily based on the carbonate formation types, karst development features, karst groundwater features, and representative lithologies in Guizhou Province. Table A1, Table A2, Table A3 and Table A4, respectively, present the four classification criteria under the three levels of K.

Table A1.
Carbonate formation types for three K levels.
Table A1.
Carbonate formation types for three K levels.
| K Levels | Carbonate Formation Types |
|---|---|
| Strong | Pure carbonate formations with wide exposure and substantial continuous thickness. |
| Moderate | Sub-pure carbonate formations, in which carbonate rocks are distributed in a banded pattern with a certain degree of continuity in thickness. |
| Low | Carbonate-poor formations which are characterized by interbedded carbonate layers with limited lateral continuity and thin single-layer thickness. |

Table A2.
Karst development features for three K levels.
Table A2.
Karst development features for three K levels.
| K Levels | Karst Development Features |
|---|---|
| Strong | Surface karst features such as depressions, sinkholes, and dolines are commonly observed, with dense distributions of solution grooves, solution troughs, and limestone pinnacles, and occasional occurrences of karst collapses. Subsurface soil cavities and solution caves are well developed. |
| Moderate | Surface karst features such as depressions, sinkholes, dolines, solution grooves, solution troughs, and limestone pinnacles are well developed, with occasional occurrences of small-scale karst collapses. Subsurface features such as soil cavities and solution caves are also relatively well developed |
| Low | Surface karst features are sparsely developed and mainly consist of solution grooves and solution troughs. Subsurface karst features are dominated by solution pores, crystal pores, and corrosion pitting, with no development of soil cavities |

Table A3.
Karst groundwater features.
Table A3.
Karst groundwater features.
| K Levels | Karst Development Features |
|---|---|
| Strong | Subsurface karst conduits or underground rivers are present, and springs are relatively abundant |
| Moderate | Small-scale subsurface karst conduits are present, and spring outcrops are relatively scarce |
| Low | Karst fractures are mostly filled, and spring outcrops are sparse or absent |

Table A4.
Representative lithologies in Guizhou.
Table A4.
Representative lithologies in Guizhou.
| K Levels | Karst Development Features |
|---|---|
| Strong |
|
| Moderate |
|
| Low |
|
Appendix C. Pollution Load Risk Index Calculation and Scoring Process
This section describes the PI calculation and scoring process, which includes seven categories of potential pollution sources: industrial pollution, mining activities, hazardous waste disposal sites, landfills, gas stations, agricultural pollution, and golf courses. The evaluation is based on three key components: pollutant toxicity, likelihood of release, and quantity of PPSs. The classification and scoring criteria for each of these components are presented in Table A5, Table A6 and Table A7.

Table A5.
Scores of pollutant toxicity.
Table A5.
Scores of pollutant toxicity.
| Pollution Types | Toxicity Category | Scores | Buffer (km) | |
|---|---|---|---|---|
| Industrial pollution | Petroleum processing, coking, and nuclear fuel processing industries | 2.5 | 1.5 | |
| Non-ferrous metal smelting and rolling processing industry | 3 | 1 | ||
| Ferrous metal smelting and rolling processing industry | 2 | 1 | ||
| Manufacturing of chemical raw materials and chemical products | 2.5 | 2 | ||
| Textile industry | 1 | 2 | ||
| Leather, fur, feather (down), and related products industry | 1 | 2 | ||
| Metal products industry | 1.5 | 1 | ||
| Other industries | 0.2 | 1 | ||
| Mining activities | Coal mining and washing industry, and oil and natural gas extraction industry | 1.5 | 1.5 | |
| Ferrous metal mining and dressing industry | 2 | 1 | ||
| Non-ferrous metal mining and dressing industry | 3 | 1 | ||
| Non-metallic mineral mining and dressing industry | 1 | 1 | ||
| Hazardous waste disposal sites | Mainly industrial hazardous waste and hazardous chemicals | 2 | 1 | |
| Landfills | Mainly domestic waste | 1.5 | 2 | |
| Gas stations | Petroleum hydrocarbons and polycyclic aromatic hydrocarbons (PAHs) | 2.5 | 1.5 | |
| Agricultural pollution | Cultivation | Chemical fertilizers, pesticides, and heavy metals | 1.5 | 1.5 |
| Farming | Antibiotics | 1 | 1 | |
| Golf courses | Pesticides | Industrial, domestic, and agricultural wastewater discharges | 1.5 | 1.5 |

Table A6.
Scores of pollutant release likelihood.
Table A6.
Scores of pollutant release likelihood.
| Pollution Types | Release Probability | Scores | |
|---|---|---|---|
| Industrial pollution | Commissioned after 2011 | 0.2 | |
| Commissioned between 1998 and 2011 | 0.6 | ||
| Commissioned before 1998 or without protective measures | 1 | ||
| Mining activities | Closed, with mine shafts backfilled | 0.5 | |
| Closed, with mine shafts not backfilled | 0.7 | ||
| In operation | 0.3 | ||
| Tailings pond or transfer stations equipped with anti-seepage measures | 0.5 | ||
| Tailings ponds or transfer stations without anti-seepage measures | 1 | ||
| Landfills | ≤5 years, harmless rating AAA | 0.1 | |
| >5 years, harmless rating AAA | 0.2 | ||
| ≤5 years, harmless rating AA | 0.2 | ||
| >5 years, harmless rating AA | 0.4 | ||
| ≤5 years, harmless rating A | 0.4 | ||
| >5 years, harmless rating A | 0.5 | ||
| Basic protection, harmless rating B | 0.6 | ||
| No protection, harmless rating B | 1 | ||
| Hazardous waste disposal sites | Regulated | 0.1 | |
| Without protective measures | 1 | ||
| Gas stations | ≤5 years, with double-layer tanks or anti-seepage basins | 0.1 | |
| (5, 15] years, with double-layer tanks or anti-seepage basins | 0.2 | ||
| >15 years, with double-layer tanks or anti-seepage basins | 0.5 | ||
| ≤5 years, with single-layer tanks and without anti-seepage basins | 0.2 | ||
| (5, 15] years, with single-layer tanks and without anti-seepage basins | 0.6 | ||
| >15 years, with single-layer tanks and without anti-seepage basins | 1 | ||
| Agricultural pollution | Agricultural cultivation | Paddy field | 0.3 |
| Dry land | 0.7 | ||
| Large-scale livestock farms | With protective measures | 0.3 | |
| Without protective measures | 1 | ||
| Golf courses | ≤18 holes | 0.1 | |
| (18, 36] holes | 0.2 | ||
| >18 holes | 0.5 | ||

Table A7.
Scores of quantities of PPSs.
Table A7.
Scores of quantities of PPSs.
| Pollution Types | Type | Scores | |
|---|---|---|---|
| Industrial pollution (Wastewater discharge volume, unit: ×103 t/a) | ≤1 | 1 | |
| (1, 5] | 2 | ||
| (5, 10] | 4 | ||
| (10, 50] | 6 | ||
| (50, 100] | 8 | ||
| (100, 500] | 9 | ||
| (500, 1000] | 10 | ||
| >1000 | 12 | ||
| Mining activities (Scale, unit: dimensionless) | Small scale | 3 | |
| Medium scale | 6 | ||
| Large scale | 9 | ||
| Landfills (Filling volume, unit: ×103 m3) | ≤1000 | 4 | |
| (1000, 5000] | 7 | ||
| >5000 | 9 | ||
| Hazardous waste disposal sites (Landfilled volume, unit: ×103 m3) | ≤10 | 4 | |
| (10, 50] | 7 | ||
| >50 | 9 | ||
| Gas stations (Number of 30 m3 fuel tanks, unit: units) | 1 | 1 | |
| Agricultural pollution | Cultivation (Fertilizer application, unit: kg/ha) | ≤180 | 1 |
| (180, 225] | 3 | ||
| (225, 400] | 5 | ||
| >400 | 7 | ||
| Large-scale livestock farms (COD discharge, unit: t/a) | ≤2 | 1 | |
| (2, 10] | 2 | ||
| (10, 50] | 4 | ||
| (50, 100] | 6 | ||
| (100, 150] | 8 | ||
| (150, 200] | 9 | ||
| >200 | 10 | ||
| Golf courses (Area occupied, unit: hm2) | ≤100 | 1 | |
| (100, 1000] | 3 | ||
| (1000, 5000] | 5 | ||
| (5000, 10,000] | 7 | ||
| >10,000 | 9 | ||
References
- Çallı, K.Ö.; Chiogna, G.; Bittner, D.; Sivelle, V.; Labat, D.; Richieri, B.; Çalli, S.S.; Hartmann, A. Karst water resources in a changing world: Review of solute transport modelling approaches. Rev. Geophys. 2025, 63, e2023RG000811. [Google Scholar] [CrossRef]
- Reberski, J.L.; Terzić, J.; Maurice, L.D.; Lapworth, D.J. Emerging organic contaminants in karst groundwater: A global level assessment. J. Hydrol. 2022, 604, 127242. [Google Scholar] [CrossRef]
- Guo, F.; Yang, J.; Li, H.; Li, G.; Zhang, Z. A convLSTM conjunction model for groundwater level forecasting in a karst aquifer considering connectivity characteristics. Water 2021, 13, 2759. [Google Scholar] [CrossRef]
- Jiang, X.; Lei, M.; Zhao, H. Review of the advanced monitoring technology of groundwater–air pressure (enclosed potentiometric) for karst collapse studies. Environ. Earth Sci. 2019, 78, 701. [Google Scholar] [CrossRef]
- Wang, Z.-J.; Yue, F.-J.; Lu, J.; Wang, Y.-C.; Qin, C.-Q.; Ding, H.; Xue, L.-L.; Li, S.-L. New insight into the response and transport of nitrate in karst groundwater to rainfall events. Sci. Total Environ. 2022, 818, 151727. [Google Scholar] [CrossRef]
- Jiang, C.; Jourde, H.; Aliouache, M.; Wang, X. The effect of seasonal variation of precipitation/recharge on karst genesis behaviors in different climatic contexts. J. Hydrol. 2023, 626, 130385. [Google Scholar] [CrossRef]
- Siarkos, I.; Sevastas, S.; Mallios, Z.; Theodossiou, N.; Ifadis, I. Investigating groundwater vulnerability variation under future abstraction scenarios to estimate optimal pumping reduction rates. J. Hydrol. 2021, 598, 126297. [Google Scholar] [CrossRef]
- Xiong, H.; Wang, Y.; Guo, X.; Han, J.; Ma, C.; Zhang, X. Current status and future challenges of groundwater vulnerability assessment: A bibliometric analysis. J. Hydrol. 2022, 615, 128694. [Google Scholar] [CrossRef]
- Agossou, A.; Yang, J.S. Comparative study of groundwater vulnerability to contamination assessment methods applied to the southern coastal sedimentary basin of Benin. J. Hydrol. Reg. Stud. 2021, 35, 100803. [Google Scholar] [CrossRef]
- Orhan, O. Monitoring of land subsidence due to excessive groundwater extraction using small baseline subset technique in Konya, Turkey. Environ. Monit. Assess. 2021, 193, 174. [Google Scholar] [CrossRef]
- Xiong, H.; Sun, Y.; Ren, X. Comprehensive assessment of water sensitive urban design practices based on multi-criteria decision analysis via a case study of the University of Melbourne, Australia. Water 2020, 12, 2885. [Google Scholar] [CrossRef]
- Gaye, C.B.; Tindimugaya, C. Review: Challenges and opportunities for sustainable groundwater management in Africa. Hydrogeol. J. 2019, 27, 1099–1110. [Google Scholar] [CrossRef]
- Jain, R.; Thakur, A.; Garg, N.; Devi, P. Impact of industrial effluents on groundwater. In Groundwater Geochemistry: Pollution and Remediation Methods; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2021; pp. 193–211. [Google Scholar]
- Juncal, M.J.L.; Masino, P.; Bertone, E.; Stewart, R.A. Towards nutrient neutrality: A review of agricultural runoff mitigation strategies and the development of a decision-making framework. Sci. Total Environ. 2023, 874, 162408. [Google Scholar] [CrossRef]
- Ravindiran, G.; Rajamanickam, S.; Sivarethinamohan, S.; Karupaiya Sathaiah, B.; Ravindran, G.; Muniasamy, S.K.; Hayder, G. A review of the status, effects, prevention, and remediation of groundwater contamination for sustainable environment. Water 2023, 15, 3662. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, S.; Shi, J.; Ma, T.; Xie, X.; Deng, Y.; Du, Y.; Gan, Y.; Guo, Z.; Dong, Y.; et al. Groundwater quality and health: Making the invisible visible. Environ. Sci. Technol. 2023, 57, 5125–5136. [Google Scholar] [CrossRef]
- Li, P.; Wu, J. Drinking water quality and public health. Expo. Health 2019, 11, 73–79. [Google Scholar] [CrossRef]
- Hancock, P.J.; Boulton, A.J.; Humphreys, W.F. Aquifers and hyporheic zones: Towards an ecological understanding of groundwater. Hydrogeol. J. 2005, 13, 98–111. [Google Scholar] [CrossRef]
- Shaikh, M.; Birajdar, F. Advancements in remote sensing and GIS for sustainable groundwater monitoring: Applications, challenges, and future directions. Int. J. Res. Eng. Sci. Manag. 2024, 7, 16–24. [Google Scholar]
- Abdelkareem, M.; Mansour, A.M.; Akawy, A. Securing water for arid regions: Rainwater harvesting and sustainable groundwater management using remote sensing and GIS techniques. Remote Sens. Appl. Soc. Environ. 2024, 36, 101300. [Google Scholar] [CrossRef]
- Machiwal, D.; Jha, M.K.; Singh, V.P.; Mohan, C. Assessment and mapping of groundwater vulnerability to pollution: Current status and challenges. Earth-Sci. Rev. 2018, 185, 901–927. [Google Scholar] [CrossRef]
- Guo, X.; Yang, Z.; Li, C.; Xiong, H.; Ma, C. Combining the classic vulnerability index and affinity propagation clustering algorithm to assess the intrinsic aquifer vulnerability of coastal aquifers on an integrated scale. Environ. Res. 2023, 217, 114877. [Google Scholar] [CrossRef]
- Taghavi, N.; Niven, R.K.; Paull, D.J.; Kramer, M. Groundwater vulnerability assessment: A review including new statistical and hybrid methods. Sci. Total Environ. 2022, 822, 153486. [Google Scholar] [CrossRef]
- Kang, J.; Zhao, L.; Li, R.; Mo, H.; Li, Y. Groundwater vulnerability assessment based on modified DRASTIC model: A case study in Changli County, China. Geocarto Int. 2017, 32, 749–758. [Google Scholar] [CrossRef]
- Foster, S.; Hirata, R.; Andreo, B. The aquifer pollution vulnerability concept: Aid or impediment in promoting groundwater protection? Hydrogeol. J. 2013, 21, 1389. [Google Scholar] [CrossRef]
- Douglas, S.H.; Dixon, B.; Griffin, D. Assessing the abilities of intrinsic and specific vulnerability models to indicate groundwater vulnerability to groups of similar pesticides: A comparative study. Phys. Geogr. 2018, 39, 487–505. [Google Scholar] [CrossRef]
- Martínez-Bastida, J.J.; Arauzo, M.; Valladolid, M. Intrinsic and specific vulnerability of groundwater in central Spain: The risk of nitrate pollution. Hydrogeol. J. 2010, 18, 681–698. [Google Scholar] [CrossRef]
- Wu, Q.; Ye, S.; Wu, X.; Chen, P. Risk assessment of earth fractures by constructing an intrinsic vulnerability map, a specific vulnerability map, and a hazard map, using Yuci City, Shanxi, China as an example. Environ. Geol. 2004, 46, 104–112. [Google Scholar] [CrossRef]
- Mimi, Z.A.; Assi, A. Intrinsic vulnerability, hazard and risk mapping for karst aquifers: A case study. J. Hydrol. 2009, 364, 298–310. [Google Scholar] [CrossRef]
- Doerfliger, N.; Jeannin, P.-Y.; Zwahlen, F. Water vulnerability assessment in karst environments: A new method of defining protection areas using a multi-attribute approach and GIS tools (EPIK method). Environ. Geol. 1999, 39, 165–176. [Google Scholar] [CrossRef]
- Marín, A.; Dörfliger, N.; Andreo, B. Comparative application of two methods (COP and PaPRIKa) for groundwater vulnerability mapping in Mediterranean karst aquifers (France and Spain). Environ. Earth Sci. 2012, 65, 2407–2421. [Google Scholar] [CrossRef]
- Petelet-Giraud, E.; Doerfliger, N.; Crochet, P. RISKE: Multicriteria assessment of karstic aquifer vulnerability mapping. Application to the Fontanilles and Cent-Fonts karstic aquifers (Herault, S. France). Hydrogéologie 2000, 4, 71–88. [Google Scholar]
- Goldscheider, N.; Klute, M.; Sturm, S.; Hötzl, H. The PI method–a GIS-based approach to mapping groundwater vulnerability with special consideration of karst aquifers. Z. Angew. Geol. 2000, 46, 157–166. [Google Scholar]
- Davis, A.; Long, A.; Wireman, M. KARSTIC: A sensitivity method for carbonate aquifers in karst terrain. Environ. Geol. 2002, 42, 65–72. [Google Scholar] [CrossRef]
- Vías, J.; Andreo, B.; Perles, M.; Carrasco, F.; Vadillo, I.; Jiménez, P. Proposed method for groundwater vulnerability mapping in carbonate (karstic) aquifers: The COP method: Application in two pilot sites in southern Spain. Hydrogeol. J. 2006, 14, 912–925. [Google Scholar] [CrossRef]
- Plagnes, V.; Kavouri, K.; Huneau, F.; Fournier, M.; Jaunat, J.; Pinto-Ferreira, C.; Leroy, B.; Marchet, P.; Dörfliger, N. PaPRIKa, the French multicriteria method for mapping the intrinsic vulnerability of karst water resource and source–two examples (Pyrenees, Normandy). In Advances in Research in Karst Media; Springer: Berlin/Heidelberg, Germany, 2010; pp. 323–328. [Google Scholar]
- Milanovic, S.; Stevanovic, Z.; Djuric, D.; Petrovic, T.; Milovanovic, M. Regional approach in creating groundwater vulnerability map of Serbia–A new “IZDAN” method. In Proceedings of the 15th Congress of Geologists of Serbia, Belgrade, Serbia, 26–29 May 2010; pp. 26–29. [Google Scholar]
- Lambrakis, N.; Stournaras, G.K.; Katsanou, K. Advances in the Research of Aquatic Environment; Springer: Berlin/Heidelberg, Germany, 2011; Volume 2. [Google Scholar]
- Jiménez-Madrid, A.; Gogu, R.; Martinez-Navarrete, C.; Carrasco, F. Groundwater for human consumption in karst environment: Vulnerability, protection, and management. In Karst Water Environment: Advances in Research, Management and Policy; Springer: Cham, Switzerland, 2019; pp. 45–63. [Google Scholar]
- Taheri, K.; Taheri, M.; Mohsenipour, F. LEPT, a simplified approach for assessing karst vulnerability in regions by sparse data: A case in Kermanshah province, Iran. In Proceedings of the 14th Sinkhole Conference, NCKRI Symposium. Rochester, MN, USA, 5–9 October 2015; pp. 483–492. [Google Scholar]
- Aguilar-Duarte, Y.; Bautista, F.; Mendoza, M.; Frausto, O.; Ihl, T.; Delgado, C. IVAKY: Índice de la vulnerabilidad del acuífero kárstico yucateco a la contaminación. Rev. Mex. De Ing. Química 2016, 15, 913–933. [Google Scholar] [CrossRef]
- Hamdan, I.; Margane, A.; Ptak, T.; Wiegand, B.; Sauter, M. Groundwater vulnerability assessment for the karst aquifer of Tanour and Rasoun springs catchment area (NW-Jordan) using COP and EPIK intrinsic methods. Environ. Earth Sci. 2016, 75, 1474. [Google Scholar] [CrossRef]
- Khazaa’lah, M.; Talozi, S.; Hamdan, I. Assessment of groundwater vulnerability using GIS-based COP model in the northern governorates of Jordan. Model. Earth Syst. Environ. 2023, 9, 19–40. [Google Scholar] [CrossRef]
- Tayer, T.d.C.; Velásques, L.N.M. Assessment of intrinsic vulnerability to the contamination of karst aquifer using the COP method in the Carste Lagoa Santa Environmental Protection Unit, Brazil. Environ. Earth Sci. 2017, 76, 445. [Google Scholar] [CrossRef]
- Vías, J.; Andreo, B.; Ravbar, N.; Hötzl, H. Mapping the vulnerability of groundwater to the contamination of four carbonate aquifers in Europe. J. Environ. Manag. 2010, 91, 1500–1510. [Google Scholar] [CrossRef]
- Li, Y.; Li, M.; Song, X.; Hu, X.; Guo, X.; Qiu, Y.; Xiong, H.; Cui, H.; Ma, C. An integrated approach combining LISA, BI-LISA, and the modified COPK method to improve groundwater management in large-scale karst areas. J. Hydrol. 2023, 625, 130111. [Google Scholar] [CrossRef]
- Cao, H.; Dong, W.; Chen, H.; Wang, R. Groundwater vulnerability assessment of typical covered karst areas in northern China based on an improved COPK method. J. Hydrol. 2023, 624, 129904. [Google Scholar] [CrossRef]
- Qiu, Y.; Ma, C.; Qian, J.; Wang, X. Comparison of different groundwater vulnerability evaluation models of typical karst areas in north China: A case of Hebi City. Environ. Sci. Pollut. Res. 2021, 28, 30821–30840. [Google Scholar] [CrossRef] [PubMed]
- Ghezelayagh, P.; Javadi, S.; Kavousi, A. COP* KAT: A modified COP vulnerability mapping method for karst terrains using KARSTLOP factors and fuzzy logic. Environ. Earth Sci. 2021, 80, 592. [Google Scholar] [CrossRef]
- Attard, G.; Winiarski, T.; Rossier, Y.; Eisenlohr, L. Review: Impact of underground structures on the flow of urban groundwater. Hydrogeol. J. 2016, 24, 5–19. [Google Scholar] [CrossRef]
- Chae, G.-T.; Yun, S.-T.; Choi, B.-Y.; Yu, S.-Y.; Jo, H.-Y.; Mayer, B.; Kim, Y.-J.; Lee, J.-Y. Hydrochemistry of urban groundwater, Seoul, Korea: The impact of subway tunnels on groundwater quality. J. Contam. Hydrol. 2008, 101, 42–52. [Google Scholar] [CrossRef]
- Vo, P.T.; Ngo, H.H.; Guo, W.; Zhou, J.L.; Listowski, A.; Du, B.; Wei, Q.; Bui, X.T. Stormwater quality management in rail transportation—Past, present and future. Sci. Total Environ. 2015, 512, 353–363. [Google Scholar] [CrossRef]
- Fiener, P.; Auerswald, K.; Van Oost, K. Spatio-temporal patterns in land use and management affecting surface runoff response of agricultural catchments—A review. Earth-Sci. Rev. 2011, 106, 92–104. [Google Scholar] [CrossRef]
- Qihu, Q. Present state, problems and development trends of urban underground space in China. Tunn. Undergr. Space Technol. 2016, 55, 280–289. [Google Scholar] [CrossRef]
- Barzegar, R.; Razzagh, S.; Quilty, J.; Adamowski, J.; Pour, H.K.; Booij, M.J. Improving GALDIT-based groundwater vulnerability predictive mapping using coupled resampling algorithms and machine learning models. J. Hydrol. 2021, 598, 126370. [Google Scholar] [CrossRef]
- Luo, D.; Ma, C.; Qiu, Y.; Zhang, Z.; Wang, L. Groundwater vulnerability assessment using AHP-DRASTIC-GALDIT comprehensive model: A case study of Binhai New Area, Tianjin, China. Environ. Monit. Assess. 2023, 195, 268. [Google Scholar] [CrossRef]
- Jones, N.A.; Hansen, J.; Springer, A.E.; Valle, C.; Tobin, B.W. Modeling intrinsic vulnerability of complex karst aquifers: Modifying the COP method to account for sinkhole density and fault location. Hydrogeol. J. 2019, 27, 2857–2868. [Google Scholar] [CrossRef]
- Yin, L.; Xu, B.; Cai, W.; Zhou, P.; Yang, L. Intrinsic vulnerability assessment of the qingduo Karst system, Henan province. Water 2023, 15, 3425. [Google Scholar] [CrossRef]
- Wang, P.; Quinlan, P.; Tartakovsky, D.M. Effects of spatio-temporal variability of precipitation on contaminant migration in the vadose zone. Geophys. Res. Lett. 2009, 36, L12404. [Google Scholar] [CrossRef]
- Guzha, A.C.; Rufino, M.C.; Okoth, S.; Jacobs, S.; Nóbrega, R.L. Impacts of land use and land cover change on surface runoff, discharge and low flows: Evidence from East Africa. J. Hydrol. Reg. Stud. 2018, 15, 49–67. [Google Scholar] [CrossRef]
- Dosskey, M.G.; Helmers, M.J.; Eisenhauer, D.E.; Franti, T.G.; Hoagland, K.D. Assessment of concentrated flow through riparian buffers. J. Soil Water Conserv. 2002, 57, 336–343. [Google Scholar] [CrossRef]
- Liu, Y.-J.; Hu, J.-M.; Wang, T.-W.; Cai, C.-F.; Li, Z.-X.; Zhang, Y. Effects of vegetation cover and road-concentrated flow on hillslope erosion in rainfall and scouring simulation tests in the Three Gorges Reservoir Area, China. Catena 2016, 136, 108–117. [Google Scholar] [CrossRef]
- Bakalowicz, M. Karst groundwater: A challenge for new resources. Hydrogeol. J. 2005, 13, 148–160. [Google Scholar] [CrossRef]
- DBJ52/T099-2020; Code for Geotechnical Investigations of Urban Rail Transit of Guizhou Province. Guizhou Provincial Department of Housing and Urban-Rural Development: Guiyang, China, 2020.
- Busico, G.; Kazakis, N.; Colombani, N.; Mastrocicco, M.; Voudouris, K.; Tedesco, D. A modified SINTACS method for groundwater vulnerability and pollution risk assessment in highly anthropized regions based on NO3− and SO42− concentrations. Sci. Total Environ. 2017, 609, 1512–1523. [Google Scholar] [CrossRef]
- Elzain, H.E.; Chung, S.Y.; Senapathi, V.; Sekar, S.; Lee, S.Y.; Roy, P.D.; Hassan, A.; Sabarathinam, C. Comparative study of machine learning models for evaluating groundwater vulnerability to nitrate contamination. Ecotoxicol. Environ. Saf. 2022, 229, 113061. [Google Scholar] [CrossRef]
- Kazakis, N.; Voudouris, K.S. Groundwater vulnerability and pollution risk assessment of porous aquifers to nitrate: Modifying the DRASTIC method using quantitative parameters. J. Hydrol. 2015, 525, 13–25. [Google Scholar] [CrossRef]
- Lasagna, M.; De Luca, D.A.; Franchino, E. Intrinsic groundwater vulnerability assessment: Issues, comparison of different methodologies and correlation with nitrate concentrations in NW Italy. Environ. Earth Sci. 2018, 77, 277. [Google Scholar] [CrossRef]
- Jaydhar, A.K.; Pal, S.C.; Saha, A.; Islam, A.R.M.T.; Ruidas, D. Hydrogeochemical evaluation and corresponding health risk from elevated arsenic and fluoride contamination in recurrent coastal multi-aquifers of eastern India. J. Clean. Prod. 2022, 369, 133150. [Google Scholar] [CrossRef]
- Arauzo, M. Vulnerability of groundwater resources to nitrate pollution: A simple and effective procedure for delimiting Nitrate Vulnerable Zones. Sci. Total Environ. 2017, 575, 799–812. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Xiong, H.; Zhang, F.; Qiu, Y.; Ma, C. Sustainable development assessment of ecological vulnerability in arid areas under the influence of multiple indicators. J. Clean. Prod. 2024, 436, 140629. [Google Scholar] [CrossRef]
- Xiong, H.; Yang, S.; Tan, J.; Wang, Y.; Guo, X.; Ma, C. Effects of DEM resolution and application of solely DEM-derived indicators on groundwater potential mapping in the mountainous area. J. Hydrol. 2024, 636, 131349. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, L.; Xu, W.; Ledwith, V. Use of local Moran’s I and GIS to identify pollution hotspots of Pb in urban soils of Galway, Ireland. Sci. Total Environ. 2008, 398, 212–221. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lv, W.; Wang, M.; Chen, X.; Li, Y. Application of improved Moran’s I in the evaluation of urban spatial development. Spat. Stat. 2023, 54, 100736. [Google Scholar] [CrossRef]
- Liu, J.; Wu, J.; Rong, S.; Xiong, Y.; Teng, Y. Groundwater vulnerability and groundwater contamination risk in Karst area of Southwest China. Sustainability 2022, 14, 14483. [Google Scholar] [CrossRef]
- Liu, M.; Huan, H.; Li, H.; Liu, W.; Li, J.; Zhao, X.; Zhou, A.; Xie, X. Quantitative Assessment and Validation of Groundwater Pollution Risk in Southwest Karst Area. Expo. Health 2025, 17, 81–96. [Google Scholar] [CrossRef]
- Xiong, Y.; Liu, J.; Yuan, W.; Liu, W.; Ma, S.; Wang, Z.; Li, T.; Wang, Y.; Wu, J. Groundwater contamination risk assessment based on groundwater vulnerability and pollution loading: A case study of typical karst areas in China. Sustainability 2022, 14, 9898. [Google Scholar] [CrossRef]
- Sartirana, D.; Rotiroti, M.; Bonomi, T.; De Amicis, M.; Nava, V.; Fumagalli, L.; Zanotti, C. Data-driven decision management of urban underground infrastructure through groundwater-level time-series cluster analysis: The case of Milan (Italy). Hydrogeol. J. 2022, 30, 1157–1177. [Google Scholar] [CrossRef]
- Sun, J.; Wu, X.; Wang, G.; He, J.; Li, W. The governance and optimization of urban flooding in dense urban areas utilizing deep tunnel drainage systems: A case study of Guangzhou, China. Water 2024, 16, 2429. [Google Scholar] [CrossRef]
- Ziv, N.; Kindinis, A.; Simon, J.; Gobin, C. Application of systems engineering for development of multifunctional metro systems: Case study on the fifth metro line of the Lyon metro, France. Undergr. Space 2021, 6, 24–34. [Google Scholar] [CrossRef]
- Jesudhas, C.J.; Chinnasamy, A.; Muniraj, K.; Sundaram, A. Assessment of vulnerability in the aquifers of rapidly growing sub-urban: A case study with special reference to land use. Arab. J. Geosci. 2021, 14, 60. [Google Scholar] [CrossRef]
- Jia, Z.; Bian, J.; Wang, Y.; Wan, H.; Sun, X.; Li, Q. Assessment and validation of groundwater vulnerability to nitrate in porous aquifers based on a DRASTIC method modified by projection pursuit dynamic clustering model. J. Contam. Hydrol. 2019, 226, 103522. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, Z.; Xiong, Y.; Yuan, W.; Wang, Y.; Tang, H.; Zheng, J.; Liu, Z. A critical application of different methods for the vulnerability assessment of shallow aquifers in Zhengzhou City. Environ. Sci. Pollut. Res. 2023, 30, 97078–97091. [Google Scholar] [CrossRef] [PubMed]
- Taghavi, N.; Niven, R.K.; Kramer, M.; Paull, D.J. Comparison of DRASTIC and DRASTICL groundwater vulnerability assessments of the Burdekin Basin, Queensland, Australia. Sci. Total Environ. 2023, 858, 159945. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Xiong, H.; Zhang, F.; Ma, C. Integrated assessment of groundwater vulnerability in arid areas combining classical vulnerability index and AHP model. Environ. Sci. Pollut. Res. 2024, 31, 43822–43834. [Google Scholar] [CrossRef]
- Hasan, M.; Islam, M.A.; Hasan, M.A.; Alam, M.J.; Peas, M.H. Groundwater vulnerability assessment in Savar upazila of Dhaka district, Bangladesh—A GIS-based DRASTIC modeling. Groundw. Sustain. Dev. 2019, 9, 100220. [Google Scholar] [CrossRef]
- Jahromi, M.N.; Gomeh, Z.; Busico, G.; Barzegar, R.; Samany, N.N.; Aalami, M.T.; Tedesco, D.; Mastrocicco, M.; Kazakis, N. Developing a SINTACS-based method to map groundwater multi-pollutant vulnerability using evolutionary algorithms. Environ. Sci. Pollut. Res. 2021, 28, 7854–7869. [Google Scholar] [CrossRef]
- Rajput, H.; Goyal, R.; Brighu, U. Modification and optimization of DRASTIC model for groundwater vulnerability and contamination risk assessment for Bhiwadi region of Rajasthan, India. Environ. Earth Sci. 2020, 79, 136. [Google Scholar] [CrossRef]
- Yang, S.; Luo, D.; Tan, J.; Li, S.; Song, X.; Xiong, R.; Wang, J.; Ma, C.; Xiong, H. Spatial mapping and prediction of groundwater quality using ensemble learning models and shapley additive explanations with spatial uncertainty analysis. Water 2024, 16, 2375. [Google Scholar] [CrossRef]
- Guo, X.; Xiong, H.; Li, H.; Gui, X.; Hu, X.; Li, Y.; Cui, H.; Qiu, Y.; Zhang, F.; Ma, C. Designing dynamic groundwater management strategies through a composite groundwater vulnerability model: Integrating human-related parameters into the DRASTIC model using LightGBM regression and SHAP analysis. Environ. Res. 2023, 236, 116871. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wu, H.; Qian, H. Groundwater contamination risk assessment using intrinsic vulnerability, pollution loading and groundwater value: A case study in Yinchuan plain, China. Environ. Sci. Pollut. Res. 2020, 27, 45591–45604. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, P.; Lyu, Q.; Ren, X.; He, S. Groundwater contamination risk assessment using a modified DRATICL model and pollution loading: A case study in the Guanzhong Basin of China. Chemosphere 2022, 291, 132695. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Gao, Y.; Qian, H.; Wu, H. Groundwater vulnerability and contamination risk assessment of the Weining Plain, using a modified DRASTIC model and quantized pollution loading method. Arab. J. Geosci. 2017, 10, 469. [Google Scholar] [CrossRef]
- Uliasz-Misiak, B.; Winid, B.; Lewandowska-Śmierzchalska, J.; Matuła, R. Impact of road transport on groundwater quality. Sci. Total Environ. 2022, 824, 153804. [Google Scholar] [CrossRef]
- Hu, L.; Jiao, J.J. Modeling the influences of land reclamation on groundwater systems: A case study in Shekou peninsula, Shenzhen, China. Eng. Geol. 2010, 114, 144–153. [Google Scholar] [CrossRef]
- Sojka, M.; Kozłowski, M.; Stasik, R.; Napierała, M.; Kęsicka, B.; Wróżyński, R.; Jaskuła, J.; Liberacki, D.; Bykowski, J. Sustainable water management in agriculture—The impact of drainage water management on groundwater table dynamics and subsurface outflow. Sustainability 2019, 11, 4201. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).