Abstract
To overcome the difficulty that existing hydrological models cannot accurately simulate hydrological processes with limited information in irrigated paddy areas in southern China, this paper presents a prediction model combining the Ensemble Empirical Mode Decomposition (EEMD) method and the Long Short-Term Memory (LSTM) network. Meteorological factors were set as the multivariate input to the model. Rainfall, regarded as the main variable affecting runoff, was decomposed and reconstructed into a combination of new series with stronger regularity by using the EEMD and K-means algorithm. The LSTM was used to explore the data laws and then to simulate and predict the runoff of the irrigated paddy areas. The Yangshudang (YSD) watershed of the Zhanghe Irrigation System (ZIS) in Hubei Province, China was taken as the study area. Compared with the other models, the results show that the EEMD-LSTM multivariate model had better simulation performance, with an above 0.85. Among them, the , , and of the EEMD-LSTM model were the best, and they were 0.85, 0.86, 1.106 and 0.35, respectively. The prediction accuracy of peak flows was better than other models, as well as the performance of runoff prediction in rainfall and nonrainfall events, while improving the by 0.05, 0.24 and 0.24, respectively, compared with the EEMD-LSTM model. Overall, the EEMD-LSTM multivariations model is suited for simulating and predicting the daily-scale rainfall–runoff process of irrigated paddy areas in southern China. It can provide technical support and help decision making for efficient utilization and management of water resources.
1. Introduction
Runoff simulation and prediction is a fundamental problem in water resource allocation, management and planning. Accurate and reliable runoff simulation and prediction are significant for water management in irrigated paddy areas and agricultural non-point-source pollution prevention and control. However, the runoff formation process is relatively complex and can be influenced by many factors, such as rainfall and topography, which gives the runoff series the characteristics of nonlinearity and nonstationarity [1]. The runoff yield and concentration of irrigated paddy areas are affected by human activities, especially by agricultural management measures. In addition, there are also few stations and incomplete data in irrigated paddy areas, making runoff simulation and prediction in agricultural irrigated areas more difficult to realize.
At present, process-driven models (conceptual and physically based) and data-driven models (statistical-science-based) have made certain progress in the field of runoff simulation and prediction. Ajmal [2] conceptualized a CN-based ensembled approach by amending the previously suggested formulation for enhanced watershed runoff prediction. Kim [3] found rainfall spatial distribution has a significant effect on accurate runoff prediction under midsize real field conditions. Among them, the distributed hydrological model that can describe the temporal and spatial change process of the water cycle has been widely used in the simulation of runoff yield and concentration in worldwide basins since it was proposed. However, most traditional hydrological models are developed based on natural basins, which are unsuitable for irrigated paddy areas with intense human activities [4]. Moreover, constructing a relative integrity process-driven model requires a large amount of input data, such as climate, topography, land use, etc. The computational complexity and parameters of uncertainty present the hydrological models with a significant challenge in practical applications [5].
With the improvement of computational power and data availability, the development of data-driven models has become more appealing. Artificial Intelligence algorithms have been extensively used in recent years in the development of hydrological prediction models [6,7]. Demirel et al. [8] found that an Artificial Neural Network (ANN) model could predict peak discharge more efficiently than the soil and water assessment tool (SWAT) model. Additionally, the data-driven model requires only a few time series, which directly excavates the complex relationship between the predicted object and the observed data through the black box model, reducing the difficulty of hydrological simulation and prediction in data-deficient areas [9]. At present, data-driven models are mainly divided into two categories. One is the traditional single-variation model based on the law of runoff series itself [10]. The other is multivariations models of regression analysis and machine learning through excavating the potential laws of hydrological and meteorological data and considering hydrological, meteorological and other multivariate variables as predictors. The latter has more knowledge of the physical mechanisms due to consideration of the meteorological factors, and it could fully capture the complex correlation characteristics between time series to obtain relatively high accuracy.
Furthermore, in recent years, in order to improve the prediction accuracy of ML algorithms, research has been directed toward the development of deep learning models (e.g., one-dimensional Convolutional Neural Networks and Long Short-Term Memory networks [11,12]) and ensemble or hybrid models [13,14]. Fu et al. [15] proposed a LSTM-based deep learning model to simulate streamflow in the Kelantan River, Malaysia. They found that the LSTM-based model showed high accuracy both in the prediction of smooth streamflow in the dry season and rapidly fluctuant streamflow in the rainy season, outperforming traditional neural networks. Kidoo et al. [16] created a multivariations input GRU model for the accurate prediction of water level by selecting meteorological data related to water level height at Hangang Bridge Station. Recent research has tried to propose some hybrid models to improve the accuracy and generalization of a model, such as LSTM-ALO [17], LSTM-GA [18], LSTM-INFO [19] and so on.
However, the drawback of data-driven models is overfitting, in which noise within the data negatively impacts the predictive performance of the model due to the lack of understanding of physical hydrological processes when handling new data [20]. Moreover, the decomposition method has shown that through the decomposition process, each subsequence of the original signal can reveal the signal’s distinct intrinsic features and obtain more features for the predicted signals. The empirical mode decomposition (EMD) technique has widely been used for decomposing original signals into their intrinsic multiscale features [21]. Tan [22] and Elias [23] each proposed a prediction model combining the EEMD method and the ML algorithms. They decomposed the runoff signal or water quality parameter datasets into more regular subseries and used them as input data for the model, which effectively improved the model prediction accuracy. Zhang et al. [24] proposed a depth prediction method of nonstationary time series based on multivariate decomposition to solve the prediction problem of multivariate, nonlinear complex time series and multiple factors affecting photovoltaic power generation. Ikram et al. [19] found that optimization algorithms can be utilized to model other hydrological variables. They can also be used with decomposition techniques to capture noise in data to improve the further prediction accuracy of the models.
It can be seen that, currently, there are few types of research about the combination of the decomposition method with multivariations models considering meteorological factors. Additionally, the current related research is mainly focused on natural watersheds. Additional study needs to verify whether such models can be applied to the irrigated paddy areas with limited data and that are severely affected by human activities. Therefore, this paper proposes a runoff prediction model based on EEMD and LSTM in an attempt to enhance existing prediction models. Firstly, we attempt to reconstruct the meteorological data by using three methods (Pearson correlation coefficient method, EEMD and K-means). Secondly, we attempt to use the meteorological data as multivariate input to the model to predict runoff in irrigated paddy areas. This study can give a better solution for daily runoff prediction in irrigated paddy areas with limited data and provide decision-making support for the efficient utilization and management of water resources in irrigated paddy areas by a runoff simulation and prediction method with higher accuracy.
2. Methods
2.1. Ensemble Empirical Mode Decomposition
The Ensemble Empirical Mode Decomposition (EEMD) was proposed by Wu and Huang in 2004. The EEMD method is an improved method based on Empirical Mode Decomposition (EMD) which can improve the efficiency of the signal decomposition process and overcome the inherent shortcomings of mode mixing [25]. The specific steps of the EEMD method are as follows:
- 1
- Add N groups of standard normal white noise sequences with mean 0 to the original signal and obtain a new signal sequence :
- 2
- The finite Intrinsic Mode Functions (IMFs) and a trend item (R) were obtained by using the conventional EMD method:where represents the jth IMF which is obtained by the ith decomposition; is the trend item by the ith decomposition; and n is the number of IMF components.
- 3
- The EEMD decomposition results are obtained by calculating the average value of N groups of IMF and trend item:where represents the jth IMF, and w denotes the number of times white noise is added.
2.2. Long Short-Term Memory Network
The Long Short-Term Memory (LSTM) neural network was proposed by Hochereiter and Schmidhuber [26] in 1997, and it is a special kind of Recurrent Neural Network (RNN). The LSTM model can decide which pieces of new information to store in the current state and what information to discard from the previous state through the setting of input gate, output gate and forge gate. Thus, it solves the problems of gradient explosion and gradient disappearance in the RNN model calculation process [27]. The specific operation method and calculation formula of the LSTM model can be found in the literature [26].
2.3. EEMD-LSTM Multivariations Model
The runoff of the irrigated paddy areas can be regarded as a typical nonlinear and nonstationary signal. Therefore, the combination of the EEMD and LSTM models was constructed to predict the runoff of the irrigated paddy areas in this study. With the novel hybrid model, the input data were decomposed through the EEMD method into different components to increase the prediction accuracy of the new model with a minimized error margin. The detailed step-by-step procedures demonstrated in Figure 1 show the three important key stages that precede the development of the novel hybrid EEMD-LSTM model.
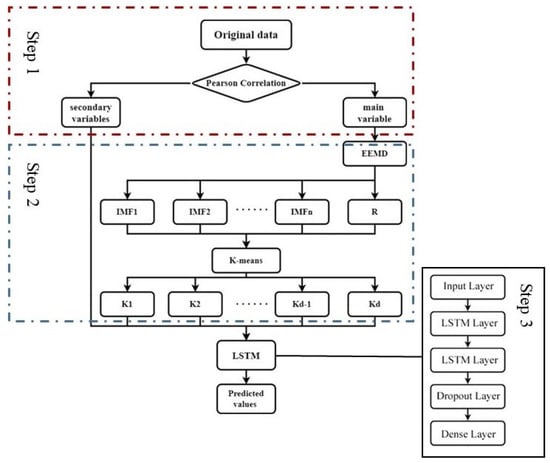
Figure 1.
The flowchart of the EEMD-LSTM model.
Step 1. The Pearson correlation coefficient method was used to select the most correlated variable with runoff. Then, the original time series data of the main variable were decomposed into several IMFs and R under different frequencies by applying the EEMD algorithm. Therefore, the different-scale fluctuations or trends were decomposed hierarchically from the original signal.
Step 2. To simplify the calculation volume of the subsequent model, the dimensionality of the decomposed data was reduced by using the K-means clustering method. Based on the clustering results, a new time series was reconstructed by superimposing the decomposed IMFs and R, which reduced the computational complexity of the model. In the meantime, by analyzing the prediction effect of different clustering numbers, the optimal clustering tag along with other meteorological data and historical runoff data were normalized and transferred into the LSTM network.
Step 3. The internal relationship and periodic rule between historical meteorological data and runoff volume were established through LSTM. Lastly, a reverse normalization operation was performed on the prediction values of the LSTM model to obtain the final predicted values. The LSTM neural network included two layers of the LSTM and one layer of Dropout. The LSTM layers were used to learn from the input dataset. Because most of the components after decomposition by the EEMD method had strong regularity, two layers of the LSTM were chosen to ensure better prediction performance in a shorter training time. The purpose of adding the Dropout layer later was to prevent overfitting of the model. Finally, the predicted value of the runoff volume was calculated from the output value of the Dropout layer by using a fully connected layer.
2.4. Predictive Evaluation Index
To quantify the performance of the EEMD-LSTM, four performance evaluation metrics were introduced to evaluate prediction accuracy. The coefficient of determination was used to evaluate the model’s accuracy, which ranges from 0 to 1 ( closer to 1 represents high model reliability). The Nash coefficient () is a widely used model evaluation criterion for hydrological models. is a dimensionless metric and a scaled version of , offering better physical interpretation [28]. The value range of the was . The closer the value is to 1, the higher the degree of fit between the simulated and measured values. Root mean square error () was used to assess the stability of the model outcomes. It provides the mean prediction error that is rather more sensitive, especially to extreme original measured values. The Relative Absolute Error () is a way to measure the performance of a predictive model. The corresponding formulas are as follows:
where , , , and n are the observed discharge, computed discharge, mean observed discharge, mean computed discharge and number of observations, respectively.
3. Example Analysis
3.1. Study Area
The YSD watershed (30°50′ N, 112°11′ E) in ZIS of the Hubei Province in China was selected as the study area. It is a relatively closed area of about 43.3 km within the ZIS. The research area and station distribution are shown in Figure 2. The meteorological data from Tuanlin meteorological station in Jingmen City (annually from May 20 to September 10 during the 2000–2010 and 2016–2017 periods) was set as the input data of the model, including daily precipitation, maximum temperature, minimum temperature, relative humidity, wind speed and solar radiation. Flow monitoring data were obtained from the YSD reservoir (annually from May 20 to September 10 during the 2000–2010 and 2016–2017 periods). The characteristics of the variables are shown in Table 1, and the runoff time series is shown in the Figure 3. This violin plot shows that the most runoff was in the range from 0 to 1 m/s.
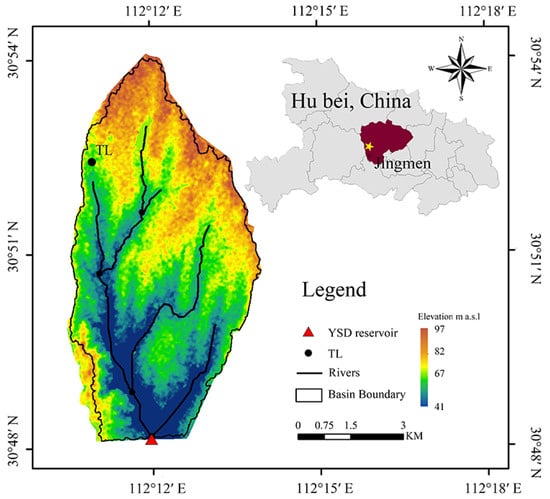
Figure 2.
The location of the Yangshudang watershed of the Zhanghe Irrigation System in Hubei Province (where TL is the Tuanlin meteorological station and YSD reservoir is the Yangshudang reservoir).

Table 1.
Characteristics of the meteorological and runoff time series datasets.
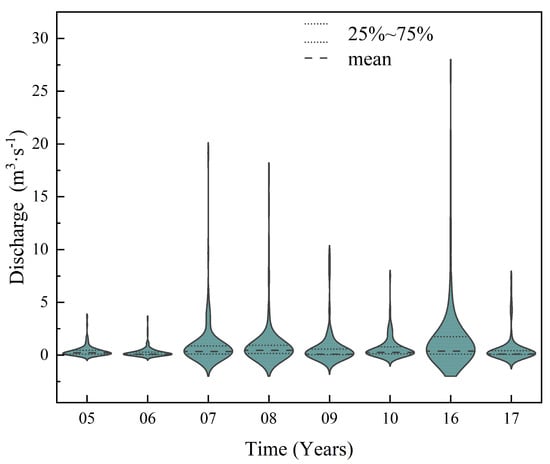
Figure 3.
Violin plot of the observed runoff times series.
3.2. Data Preprocessing
The existing correlations between each meteorological factor and runoff were analyzed by Pearson’s correlation coefficient method. It showed that rainfall and runoff had the best correlation in Table 2, so rainfall was selected as the main variable. The remaining meteorological factors were input into the model as secondary variables.

Table 2.
Correlation coefficient between runoff and meteorological factors.
Rainfall data were decomposed by EEMD mode to 9 IMF components and a trend term R. To reduce the amount of calculation in the subsequent model, the K-means algorithm was used to cluster the 9 IMF components and a trend item R by selecting different clustering numbers d. The decomposed 10 subsequences were classified into d groups according to the clustering labels, and the subsequences within each group were superimposed to obtain a new reconstructed sequence, denoted as –. The simulation evaluation metrics for various cluster numbers were shown in Table 3. According to Table 3, the model operation efficiency and all evaluation indexes had the best results when the number of clusters was 6.

Table 3.
Prediction error and time required of different cluster numbers.
The input and output data of the neural network were constructed by –, which were reconstructed by clustering labels and subvariables in the way of a sliding window. As shown in Figure 4, the relationship between the input and output was established to predict output values, which were based on the input of the given prediction set. The frequency of the – of rainfall data, which were decomposed and clustered, was more stable and had more obvious periodicity than the original rainfall data, and the phenomenon of modal mixing did not appear.
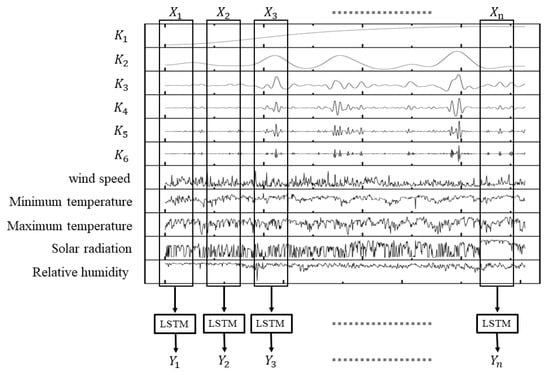
Figure 4.
Relationship between input variables and output variables based on EEMD.
3.3. Model Parameter Setting
Window sliding was used to process the time series after the integration process of clustering. The time step was chosen as 2 d. The meteorological data of the first two days of the week were used as the input features for constructing the neural network (meteorological data within the time period T-2 d to <T), and the runoff data of the day were used as the output labels of the neural network (i.e., runoff data at the time of T). The total dataset of the model was updimensioned from [908, 7] to [908, 12] based on the six new time series, which were obtained by decomposition and reconstruction of the filtered main variables. The 2005–2010 data were used as the training set of the model (the size of the model feature subdataset for the training period was [682, 11], and the size of the label subdataset was [682, 1]) to the projected runoff data for a total of 226 points from 2016–2017. In order to obtain the optimal model parameters and ensure prediction accuracy, the Grid Search optimizer was selected to optimize the LSTM model parameters.
4. Results and Discussion
4.1. Suitability Analysis of the EEMD-LSTM Multivariations Model
In order to verify the accuracy of the multivariations LSTM model more over the traditional single-variation LSTM model, the single-variation LSTM [15] model (using the runoff volume of the previous time period to predict the runoff volume of the next moment) and the multivariations LSTM [29], model (using the rainfall of the previous time period to predict the runoff volume of the next moment) were selected as comparison models. Moreover, the single-variation EEMD-LSTM [16] model and the EEMD-LSTM multivariations model (the EEMD-LSTM model, which is a multivariations LSTM model with the main variables reconstructed by EEMD decomposition, and the EEMD-LSTM model, which has the model input variables added to the remaining meteorological factors as secondary variables for runoff prediction) were selected as comparison models to verify the effectiveness of the EEMD method. The input and output settings of each model are shown in Table 4. The observed and predicted runoff hydrographs are presented in Figure 5 and Figure 6, and the prediction accuracy is shown in Table 5 and Table 6.

Table 4.
Comparison model input and output settings for differences.
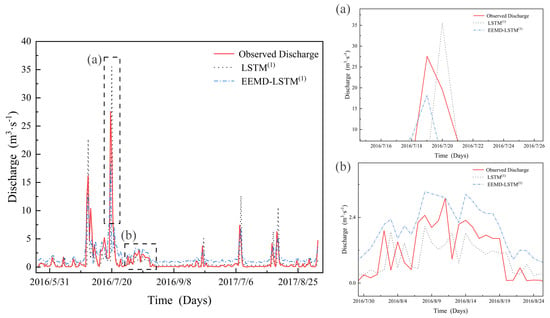
Figure 5.
Performance of runoff simulations of single–variation models, (a) high–flow periods, (b) low–flow periods.
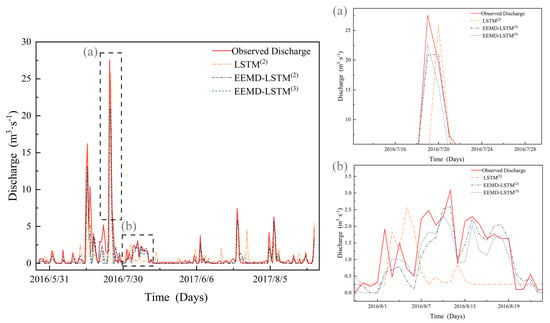
Figure 6.
Performance of runoff simulations of multi–variations models, (a) high–flow periods, (b) low–flow periods.

Table 5.
Comparison of simulation results of various models.

Table 6.
Comparison of simulation results of various models.
From Figure 5 and Table 5, the runoff series which were simulated by the LSTM model show significant lags compared with the measured runoff, and all evaluation indexes fail to meet the requirements. This indicates that the single-variation LSTM model could not achieve effective prediction of complex and nonlinear daily runoff in irrigated paddy areas based on a small number of training samples. The evaluation indexes which were simulated by the EEMD-LSTM model significantly improved compared with the single-variation LSTM model: the increased from 0.17 to 0.61. However, it still failed to meet the fitting requirements of the model [30]; the and were 1.86 and 0.19, respectively, which proved that there was a significant deviation between the predicted discharge and the observed discharge of the model.
According to Table 6 and Figure 7, the multivariate prediction models provided a better fit between predicted and observed values than the single-variable models. The and of the EEMD-LSTM model were improved by 0.26 and 0.25, respectively, to 0.85 and 0.86, while the and decreased by 0.76 and 0.48, respectively, compared with the EEMD-LSTM model. By comparing the simulation effects of each model during low-flow periods in Figure 5b and Figure 6b, the predicted runoff trend of the EEMD- LSTM multivariations model was better than other models, but it has the same problem of underestimating the peak flow, as shown in Figure 5a and Figure 6a. In addition, the difference of each evaluation index, which between the EEMD-LSTM and EEMD-LSTM models is within 0.02, indicates that the rainfall was determined as the main variable and the decomposed one. The addition of other secondary variables did not improve the overall simulation accuracy of the model.
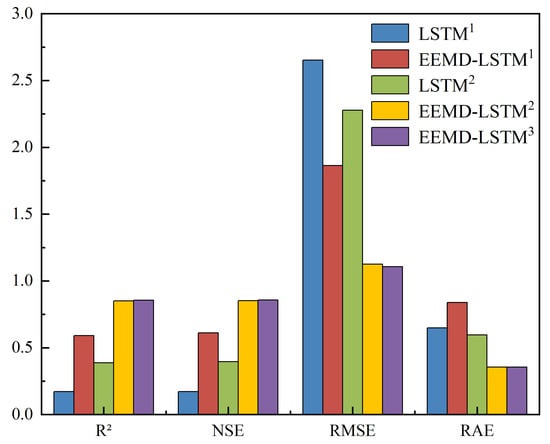
Figure 7.
Comparison of evaluation indicators.
According to the Taylor diagram in Figure 8, it can be seen that the simulation performance of the EEMD-LSTM multivariations models, namely the EEMD-LSTM and EEMD-LSTM models, was significantly better than other models, where the EEMD-LSTM model is slightly better than the EEMD-LSTM model in terms of correlation coefficient R. The results indicate that the EEMD-LSTM model is closer to the observed data. The EEMD-LSTM model was closer to 1 in than the EEMD-LSTM model, indicating that the EEMD-LSTM model is more concentrated than the EEMD-LSTM model in terms of overall dispersion.
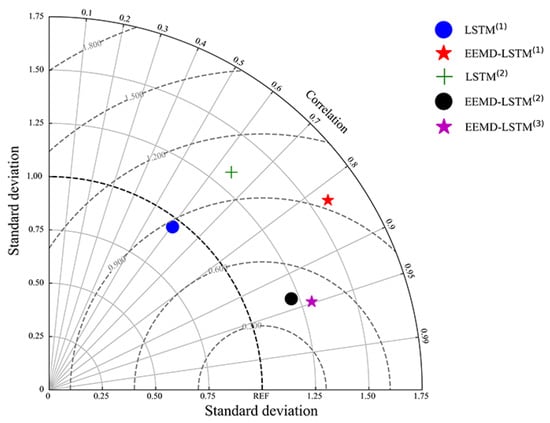
Figure 8.
Taylor diagram of various models.
In conclusion, the EEMD-LSTM model had a better ability for runoff prediction than the traditional LSTM model. The and of the EEMD-LSTM model were the best at 0.85 and 0.86, respectively, compared with the other models. The LSTM, EEMD-LSTM and LSTM models were unable to achieve effective prediction of the daily runoff in the irrigated paddy areas with a small number of training samples. Additionally, the LSTM model had a lag phenomenon of the predicted values relative to the measured values due to the low fitting degree. The LSTM model failed to correctly establish the complex rainfall–runoff relationship in the irrigated paddy areas with few training samples, so the simulated peak was significantly different from the observed one. This further indicated that the model does not have proper prediction ability without data preprocessing techniques [31], while the decomposition method could significantly improve prediction accuracy.
4.2. Peak Performance Evaluation
The accurate prediction of peaks was usually a challenge in data-driven models. Given the importance of peak flows in flood management, the peak data from two years of the validation period were extracted, as well as the prediction accuracy of peak flow values using the EEMD-LSTM, EEMD-LSTM and EEMD-LSTM models. Results are shown in Figure 9 and Table 7.
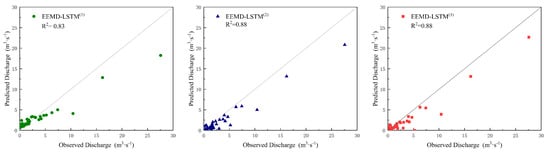
Figure 9.
Predicting peak discharges of various models.

Table 7.
Comparison of simulation results of various models.
As seen in Figure 9 and Table 7, three models could simulate the peak well, among which the EEMD-LSTM model had the best simulation effect. Still, the difference in the evaluation indexes between the EEMD-LSTM model and the EEMD-LSTM model was minute, and both and can reach 0.88. Moreover, combined with Figure 6a, it can be seen that at the maximum peak formed by torrential rain, with the addition of other meteorological factors, the EEMD -LSTM model can predict the flood flow more accurately than the EEMD-LSTM model.
4.3. Runoff Prediction in Rainfall and Nonrainfall Events
In the event of rainfall, because the ridges of paddy fields have the function of storage, even though rainfall is present during the growth stage of paddy fields, runoff yield and concentration are low or none. In the event of nonrainfall, due to the requirements of rice growth and irrigation systems, the paddy field maintains a certain depth of water layer. When rice does not need water, such as during the ripening stage, all the water in the field will be drained, thus creating a special phenomenon of “produce runoff without any rainfall”, which is different from the natural watershed. Therefore, in order to investigate the fit of the model for rainfall and nonrainfall events, runoff data were extracted for rainfall and nonrainfall dates, respectively, which were used to evaluate the accuracy of the models. Results are shown in Figure 10 and Figure 11 and Table 8 and Table 9.
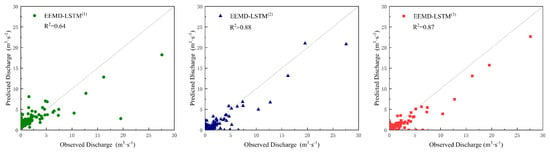
Figure 10.
Runoff prediction of various models in rainfall events.
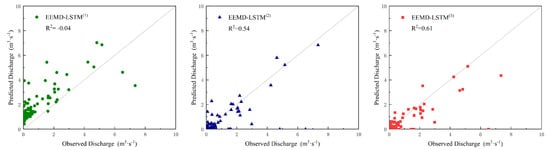
Figure 11.
Runoff prediction of various models in non–rainy events.

Table 8.
Comparison of simulation results of various models.

Table 9.
Comparison of simulation results of various models.
According to Table 8, the and of the EEMD-LSTMand EEMD-LSTM models were both improved by more than 0.2 compared with the EEMD-LSTM model. Among them, the EEMD-LSTM model had the best result, with an of 0.88, but its improvement over the EEMD-LSTM model was not significant. As shown in Figure 10, the prediction values of the EEMD-LSTM model were scattered at any level of rainfall, which indicates that it was difficult to make accurate predictions of the daily-scale runoff by relying on the regularity of runoff itself under the condition of a small number of training samples. With the input of rainfall data, EEMD-LSTM and EEMD-LSTM multivariations models have more physical significance and can better simulate the rainfall–runoff process. Moreover, because the EEMD-LSTM model was fully driven by rainfall data, its performance of simulation under the condition of rainfall events was better than the EEMD-LSTM model.
As shown in Figure 11, most of the predicted values which were simulated by the EEMD-LSTM model deviated significantly from the observed data in the nonrainfall events, which was an essential reason for the poor overall performance of the EEMD-LSTM model. Due to the minimal training samples and the high nonlinearity and nonstationarity of the runoff, the EEMD-LSTM model was unable to accurately predict IMF1. stationary The runoff subseries IMF1, which is based on the EEMD decomposition, represents the most unsystematic and disordered part of the daily flow data. The value of IMF1 was very small but significantly affected the accuracy of the prediction [32,33]. As can be seen from Table 9, the EEMD-LSTM multivariate models were all better than the EEMD-LSTM model in the nonrainfall events, among which the EEMD-LSTM model had the best simulation effect. The of the EEMD-LSTM model was improved by 0.65 and 0.07, the was improved by 0.24 and 0.07, the was reduced by 0.47 and 0.06 and the was reduced by 1.04 and 0.13, respectively, compared with the EEMD-LSTM and EEMD-LSTM models. This shows that adding other meteorological factors could give the model data support and constrain calculations by the physical mechanism of the nonrainfall event, which could effectively improve the ability to the prediction of daily runoff in irrigated paddy areas. This is also in line with the recent results by Kratzert [9], which show adding physical constraints to LSTM models might improve simulations.
5. Discussion
A clear understanding of the future state of any runoff, through accurate predictive modeling, is critical to the efficient utilization and management of water resources in irrigated paddy areas, which is also a critical element for sustainable water use and improved agricultural practices, or making a risk assessment [34] to reduce the potential risk of flooding [35]. These tasks have largely been accomplished through significant research aiming to develop statistical, physical, and more recently, dependable deep learning predictive methods to help policymakers in their day-to-day decision making. The current research integrates a predictive method (i.e., LSTM and GRU models) with a data analysis algorithm (i.e., EEMD and Variational Mode Decomposition, VMD) for improved performance accuracy. A comparison of the efficiency of the new hybrid EEMD-LSTM prediction model was performed against other similar hybrid models, such as the conventional LSTM model and EEMD-LSTM single-variation models. The result indicates a higher prediction accuracy of our proposed model. The performance gain is due to the application of the EEMD algorithm by our proposed novel hybrid EEMD-LSTM prediction model to effectively perform the decomposition of the original signals to obtain its constituent separate essential subsequences. The study was capable of predicting runoff to an acceptable degree of testing accuracy. The results achieved demonstrate that the EEMD algorithm is a strong data analysis tool that can identify the significant features within predictor variables, which is required to model the hydrological state of a river system. This notion is consistent with the quality of the hydrological datasets that could potentially influence the predictive merits of any hydrological model [35].
In this study, it was noted that the incorporation of meteorological data derived improved hybrid deep learning approaches developed for runoff prediction, and this performance was better than the conventional machine learning models. The performance of the models in this study also concurs with that of previous research. Madonia [15] proposed a multivariate and multistage medium- and long-term streamflow prediction model that achieved good application (the = 19.249 and = 0.985) in the Swat River Watershed, Pakistan. Ahmed [36] aggregates the significant antecedent lag memory of climate mode indices, rainfall and the monthly factor based on the periodicity as the predictor variables to attain significantly accurate stream water level forecasts with relatively low relative errors ( = 0.882%).
6. Conclusions
- 1
- This study proposed a prediction model of the daily runoff in irrigated paddy areas based on the EEMD-LSTM. Meteorological factors were used as the multivariations inputs, and the relationship between meteorological factors and runoff data was learned through LSTM, which solved the problem that traditional prediction methods have difficulty predicting the daily runoff in irrigated paddy areas accurately.
- 2
- By comparing the single-variation and multivariations prediction models with input data, whether decomposed by the EEMD method or not, the results show that the EEMD-LSTM multivariations model performed better than other models in simulating and predicting the daily-scale rainfall–runoff process in the irrigated paddy areas. Among them, the EEMD-LSTM model had the best simulation effect, with an of 0.86. The results demonstrate that the prediction results of the input data decomposed by the EEMD method exhibited better statistical performance than those of the original data, and the multivariations models could better solve the problem of having too little data to predict the daily runoff.
- 3
- The EEMD-LSTMand EEMD-LSTM models performed well in predicting peak flow and rainfall events. Among them, the EEMD-LSTM model significantly outperformed the other models in predicting nonrainfall events. It demonstrated that adding adequate meteorological factor data as the input could give the LSTM model certain constraints, making it more physically meaningful and effectively improving the prediction accuracy.
The effects of climate change, which make both floods and low-flow periods more frequent and severe, increase the need for reliable forecasting models [9,37]. Darianne et al. [38] proposed a model with a substantial seasonality index, which improved the test to 0.51 and provided more accurate results than the basic model. However, the observations collected in this paper are mainly from the summer season, and the time series collected are short. At a later stage, we will extend the runoff time series to expand the time frame for annual observations and then explore the importance and uncertainty of hydrological prediction under climate change. In addition, the model is not trained in stages for the different growth stages of rice, which can be used to improve the accuracy of the model in future studies.
Author Contributions
Conceptualization, S.H.; methodology, S.H.; software, S.H. and J.C.; validation, S.H., H.P. and W.L.; formal analysis, L.Y.; investigation, S.H., L.Y. and W.W.; resources, W.L.; data curation, S.H. and W.W.; writing—original draft preparation, S.H.; writing—review and editing, Z.Z.; visualization, S.H.; project administration, L.Y. and W.L.; funding acquisition, Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [NSFC-MWR-CTGC Joint Yangtze River Water Science Research Project] grant number [U2040213], and [the Fundamental Research Funds for Central Public Welfare Research Institutes] grant number [Grant No. CKSF2019251/NY, CKSF2021299/NY].
Data Availability Statement
Not applicable.
Acknowledgments
The authors thank the Agricultural Water Conservancy Department, Yangtze River Scientific Research Institute for providing the research fund.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chang, N.B.; Yang, Y.J.; Imen, S.; Mullon, L. Multi-scale quantitative precipitation forecasting using nonlinear and nonstationary teleconnection signals and artificial neural network models. J. Hydrol. 2017, 548, 305–321. [Google Scholar] [CrossRef]
- Ajmal, M.; Khan, T.A.; Kim, T.W. A CN-Based Ensembled Hydrological Model for Enhanced Watershed Runoff Prediction. Water 2016, 8, 20. [Google Scholar] [CrossRef]
- Kim, C.; Kim, D.H. Effects of Rainfall Spatial Distribution on the Relationship between Rainfall Spatiotemporal Resolution and Runoff Prediction Accuracy. Water 2020, 12, 846. [Google Scholar] [CrossRef]
- Gassman, P.W.; Jeong, J.; Boulange, J.; Narasimhan, B.; Kato, T.; Somura, H.; Watanabe, H.; Eguchi, S.; Cui, Y.; Sakaguchi, A.; et al. Simulation of rice paddy systems in SWAT: A review of previous applications and proposed SWAT+ rice paddy module. Int. J. Agric. Biol. Eng. 2022, 15, 1–24. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Pham, Q.B.; Kumar, M.; Di Nunno, F.; Elbeltagi, A.; Granata, F.; Islam, A.R.M.T.; Talukdar, S.; Nguyen, X.C.; Ahmed, A.N.; Anh, D.T. Groundwater level prediction using machine learning algorithms in a drought-prone area. Neural Comput. Appl. 2022, 34, 10751–10773. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Artificial Intelligence models for prediction of the tide level in Venice. Stoch. Environ. Res. Risk Assess. 2021, 35, 2537–2548. [Google Scholar] [CrossRef]
- Demirel, M.C.; Venancio, A.; Kahya, E. Flow forecast by SWAT model and ANN in Pracana basin, Portugal. Adv. Eng. Softw. 2009, 40, 467–473. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Herrnegger, M.; Sampson, A.K.; Hochreiter, S.; Nearing, G.S. Toward improved predictions in ungauged basins: Exploiting the power of machine learning. Water Resour. Res. 2019, 55, 11344–11354. [Google Scholar] [CrossRef]
- Ravansalar, M.; Rajaee, T.; Kisi, O. Wavelet-linear genetic programming: A new approach for modeling monthly streamflow. J. Hydrol. 2017, 549, 461–475. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F. Future trends of reference evapotranspiration in Sicily based on CORDEX data and Machine Learning algorithms. Agric. Water Manag. 2023, 280, 108232. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F.; de Marinis, G. Stacked machine learning algorithms and bidirectional long short-term memory networks for multi-step ahead streamflow forecasting: A comparative study. J. Hydrol. 2022, 613, 128431. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, S.; Qiao, H.; Liu, L.; Tian, F. Mid-long term forecasting of reservoir inflow using the coupling of time-varying filter-based empirical mode decomposition and gated recurrent unit. Environ. Sci. Pollut. Res. 2022, 29, 87200–87217. [Google Scholar] [CrossRef] [PubMed]
- Sibtain, M.; Li, X.; Saleem, S. A multivariate and multistage medium-and long-term streamflow prediction based on an ensemble of signal decomposition techniques with a deep learning network. Adv. Meteorol. 2020, 2020, 8828664. [Google Scholar] [CrossRef]
- Fu, M.; Fan, T.; Ding, Z.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. Deep learning data-intelligence model based on adjusted forecasting window scale: Application in daily streamflow simulation. IEEE Access 2020, 8, 32632–32651. [Google Scholar] [CrossRef]
- Park, K.; Jung, Y.; Seong, Y.; Lee, S. Development of deep learning models to improve the accuracy of water levels time series prediction through multivariate hydrological data. Water 2022, 14, 469. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y.; Muhammad Adnan, R. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Kilinc, H.C.; Haznedar, B. A hybrid model for streamflow forecasting in the Basin of Euphrates. Water 2022, 14, 80. [Google Scholar] [CrossRef]
- Ikram, R.M.A.; Mostafa, R.R.; Chen, Z.; Parmar, K.S.; Kisi, O.; Zounemat-Kermani, M. Water temperature prediction using improved deep learning methods through reptile search algorithm and weighted mean of vectors optimizer. J. Mar. Sci. Eng. 2023, 11, 259. [Google Scholar] [CrossRef]
- Ghaith, M.; Siam, A.; Li, Z.; El-Dakhakhni, W. Hybrid hydrological data-driven approach for daily streamflow forecasting. J. Hydrol. Eng. 2020, 25, 04019063. [Google Scholar] [CrossRef]
- Yao, H.; Tan, Y.; Hou, J.; Liu, Y.; Zhao, X.; Wang, X. Short-Term Wind Speed Forecasting Based on the EEMD-GS-GRU Model. Atmosphere 2023, 14, 697. [Google Scholar] [CrossRef]
- Tan, Q.F.; Lei, X.H.; Wang, X.; Wang, H.; Wen, X.; Ji, Y.; Kang, A.Q. An adaptive middle and long-term runoff forecast model using EEMD-ANN hybrid approach. J. Hydrol. 2018, 567, 767–780. [Google Scholar] [CrossRef]
- Eze, E.; Halse, S.; Ajmal, T. Developing a novel water quality prediction model for a South African aquaculture farm. Water 2021, 13, 1782. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Cheng, Q.Z.; Jiang, W.J.; Liu, X.F.; Shen, L.; Chen, Z.H. Photovoltaic Power Perdiction model based on EMD-PCA-LSTM. Acta Energiae Solaris Sin. 2021, 42, 62. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 1994, 5, 157–166. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. A refined index of model performance: A rejoinder. Int. J. Climatol. 2013, 33, 1053–1056. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Ritter, A.; Munoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Johnson, N.E.; Ianiuk, O.; Cazap, D.; Liu, L.; Starobin, D.; Dobler, G.; Ghandehari, M. Patterns of waste generation: A gradient boosting model for short-term waste prediction in New York City. Waste Manag. 2017, 62, 3–11. [Google Scholar] [CrossRef] [PubMed]
- Guo, Z.; Zhao, W.; Lu, H.; Wang, J. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model. Renew. Energy 2012, 37, 241–249. [Google Scholar] [CrossRef]
- Huang, S.; Chang, J.; Huang, Q.; Chen, Y. Monthly streamflow prediction using modified EMD-based support vector machine. J. Hydrol. 2014, 511, 764–775. [Google Scholar] [CrossRef]
- Rak, J.R.; Tchórzewska-Cieślak, B.; Pietrucha-Urbanik, K. A hazard assessment method for waterworks systems operating in self-government units. Int. J. Environ. Res. Public Health 2019, 16, 767. [Google Scholar] [CrossRef] [PubMed]
- Yaseen, Z.M.; Awadh, S.M.; Sharafati, A.; Shahid, S. Complementary data-intelligence model for river flow simulation. J. Hydrol. 2018, 567, 180–190. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Deo, R.C.; Feng, Q.; Ghahramani, A.; Raj, N.; Yin, Z.; Yang, L. Deep learning hybrid model with Boruta-Random forest optimiser algorithm for streamflow forecasting with climate mode indices, rainfall, and periodicity. J. Hydrol. 2021, 599, 126350. [Google Scholar] [CrossRef]
- Yin, J.; Gentine, P.; Slater, L.; Gu, L.; Pokhrel, Y.; Hanasaki, N.; Guo, S.; Xiong, L.; Schlenker, W. Future socio-ecosystem productivity threatened by compound drought–heatwave events. Nat. Sustain. 2023, 6, 259–272. [Google Scholar] [CrossRef]
- Dariane, A.; Farhani, M.; Azimi, S. Long term streamflow forecasting using a hybrid entropy model. Water Resour. Manag. 2018, 32, 1439–1451. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).