Abstract
Emptying processes are typical maneuvers that should be performed by water distribution companies for operation purposes. These processes involve a complex numerical analysis, since a set of algebraic and ordinary differential equations needs to be solved for the intricacy of hydraulic and thermodynamic formulations for two analyzed phases (liquid and gas). This research provides an implicit equation to compute exactly the final conditions in water emptying operations in single pipelines without an air valve (or admitted air). The implicit expression was developed by considering that for all final conditions, the water velocity is null, and thus, the water column length and air pocket pressure can be computed. The friction factor, internal pipe diameter, and opening maneuvers of drain valves do not disturb the final conditions in draining processes. The developed implicit formulation was validated using experimental measurements in a pipeline with a total length of 4.36 m. The equation is of utmost importance, since it can be utilized for engineers to easily plan for future conditions in water distribution networks.
1. Introduction
Emptying processes are common operations that should be performed in water distribution networks, since pipelines need to be maintained, repaired, and/or cleaned [1,2]. These processes are complex for simulating, because they involve the analysis of two fluids (water and air), where thermodynamic and hydraulic equations need to be formulated for knowing the behavior of the variables that describe these phenomena [2]. The implementation of mathematical models can vary depending on the installation or absence of vacuum air valves [3]. When vacuum air valves are installed, the water installation can be completely drained, and down-surge pulses can be less risky in comparison to when these devices have not been installed [2].
Mathematical models for analyzing emptying processes in water pipelines have been studied by the authors in recent years, both numerically and experimentally [4,5,6] considering and neglecting air valves. Experimental tests have been conducted at Hydraulic Laboratories of the University of Lisbon, Portugal, and Polytechnic University of Valencia, Spain, which were used to validate mathematical models proposed by the authors [4,5,6]. Experimental measurements in emptying pipelines by pressurized air have been conducted by some authors [7,8].
Different kinds of approaches have been implemented for studying emptying operations. In this sense, 1D mathematical models have been developed for predicting the evolution of the hydraulic and thermodynamic variables [4,5,6]. Afterwards, 2D and 3D computational fluid dynamics were used to study not only the behavior of variables, but also the backflow air phenomena [9,10,11]. The implementation of 1D mathematical models can be complex for engineers, since they must formulate a system composed by algebraic and ordinary differential equations. On the other hand, 2D and 3D CFD mathematical models have a high computing time.
This research focused on emptying processes without vacuum air valves. Under this consideration, the phenomenon can be modeled using three formulations for a one-dimensional (1D) approach: (i) the mass oscillation approach for describing the water column movement along a pipeline [12,13]; (ii) the polytropic law that describes the evolution of an entrapped air pocket [14,15]; and (iii) the piston flow model that simulates the air–water interface, which assumes a perpendicular separation of these two fluids regarding the main direction of a pipeline [16,17]. The numerical resolution of the system, composed by a set of algebraic and ordinary differential equations, is carried out using numerical methods [18,19,20]. Air pocket pressure, water velocity, and air–water interface position need to be computed to describe emptying processes in water pipelines. Currently, the mathematical model developed by the authors [4] is the unique formulation based on physical equations that can be used to simulate emptying operations with entrapped air pockets in water pipelines.
The purpose of this research was to calculate the final conditions of emptying processes without solving the set of algebraic and ordinary differential equations. An implicit equation was obtained to compute the final conditions of emptying processes in single pipelines. The new formulation was applied to a case study in order to know the final conditions during emptying maneuvers, for both the hydraulic and thermodynamic variables. The current research establishes an initial step for developing implicit formulations for water pipelines of irregular profiles [21,22] with entrapped air pockets as well as various air valves.
2. Numerical Approach
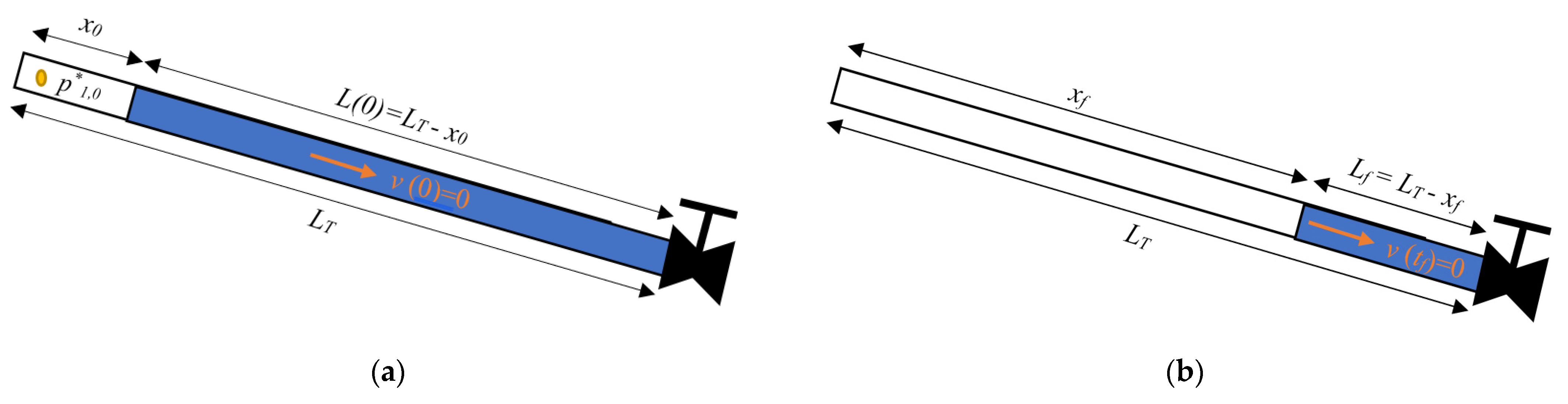
A mathematical model for simulating air pocket pressure (p*1), water velocity (v), and water column length (L) during drainage maneuvers in pressurized water installations was developed by the authors in previous publications [4]. A system of 3 × 3 algebraic and ordinary differential equations needs to be solved to obtain the responses of the aforementioned variables. Figure 1 describes the hydraulic and thermodynamic variables for the initial and final conditions during an emptying process without admitted air. Air pocket size is represented by x. The subscript 0 indicates the initial condition of an analyzed variable, and the subscript f is used to represent the final condition. Figure 1a shows the situation when a system is at rest, while Figure 1b presents the final position of an emptying process.
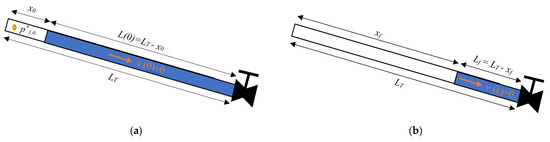
Figure 1.
Schematic of an emptying process with a trapped air pocket in a single water pipeline: (a) initial condition and (b) final condition.
A drainage maneuver in a single water pipeline with a total length of LT and an internal pipe diameter D can be analyzed using the formulations as follows:
where v = water velocity, L = water column length, p*1 = air pocket pressure, patm* = atmospheric pressure, r = water density, g = gravity acceleration, f = the Darcy–Weisbach friction factor, θ = pipe slope (rad), A = cross-sectional area of pipe, Rv = resistance coefficient, and k = polytropic coefficient.
The initial conditions of the system are: v(0) = 0, L(0) = LT-x0, and p1*(0) = patm* = 101,325 Pa.
The numerical resolution of Equations (1)–(3) provides the behavior of the variables of the emptying process (v, L, and p1*). Commonly, mathematical packages (e.g., Matlab, Scilab, or Octave) are utilized to compute the aforementioned variables. Equations (1)–(3) correspond with the mathematical model developed by the authors in previous works [4,23].
To demonstrate an implicit formulation that can be used to compute final conditions of draining processes, the following steps were developed in this research.
Equations (1)–(3) may be written in a simple form in a nonlinear differential equations system (NDES) composed by two formulations and two variables (L and v). The new system is transformed by plugging Equation (3) into Equation (2). Now, Equations (1) and (4) give the system responses.
The functions P and Q are defined by:
Then, the nonlinear differential equations system (NDES) can be written as:
Bear in mind, the functions P and Q do not explicitly depend on time (t). Therefore, the NDES is a nonlinear autonomous system, so it can be presented in a vector form. Thus, the variables L and v are placed in a vector, X, and the functions P and Q are also included in vector V, as follows:
Thus, both X and V are functions of t, so it can then be deduced that:
In this sense, V defines a vector field in a region in the plane (L, v) and the solution of the ordinary differential. Equation (10) describes the trajectory of a particle moving in a region with velocity V, passing through the initial point X(0) = (LT-x0, 0) at time t = 0.
Because X(t) is a vector function of t, then the points (L(t), v(t)), where (such that) X′ (L(t), v(t)) = (0, 0), are critical points of X. In order to find critical points, it is necessary to calculate V(L(t), v(t)) = (0, 0), which implies that: ⟨P(L, v), Q(L, v)⟩ = (0, 0). Then, the NDES (see Equation (4)) is reduced to:
where = water column length at the end of an emptying process.
Since there is not an algebraic method to solve Equation (11) because it has a decimal power k (polytropic coefficient), the Newton–Raphson method was used to find at the end of the transient event at . Otherwise, to begin the root search, it is important to have a good seed or initial value to guarantee the convergence of the algorithm. In this sense, the condition of a polytropic evolution (k = 1.0) was considered, because with it, an explicit equation is obtained. Thus, considering k = 1.0, Equation (11) can be reduced as:
By organizing terms:
By solving the quadratic equation for an Lf value, the initial value of is found for the method,
By using the Newton–Raphson method, the final value of Lf can be found with few iterations. The definition of is given by:
By deriving the last equation:
This application guarantees obtaining the correct values, since j′(Lf,i) is not null, when considering seed values ranging from 0 to LT-x0. The value Li+1 can be computed by considering the following formulation:
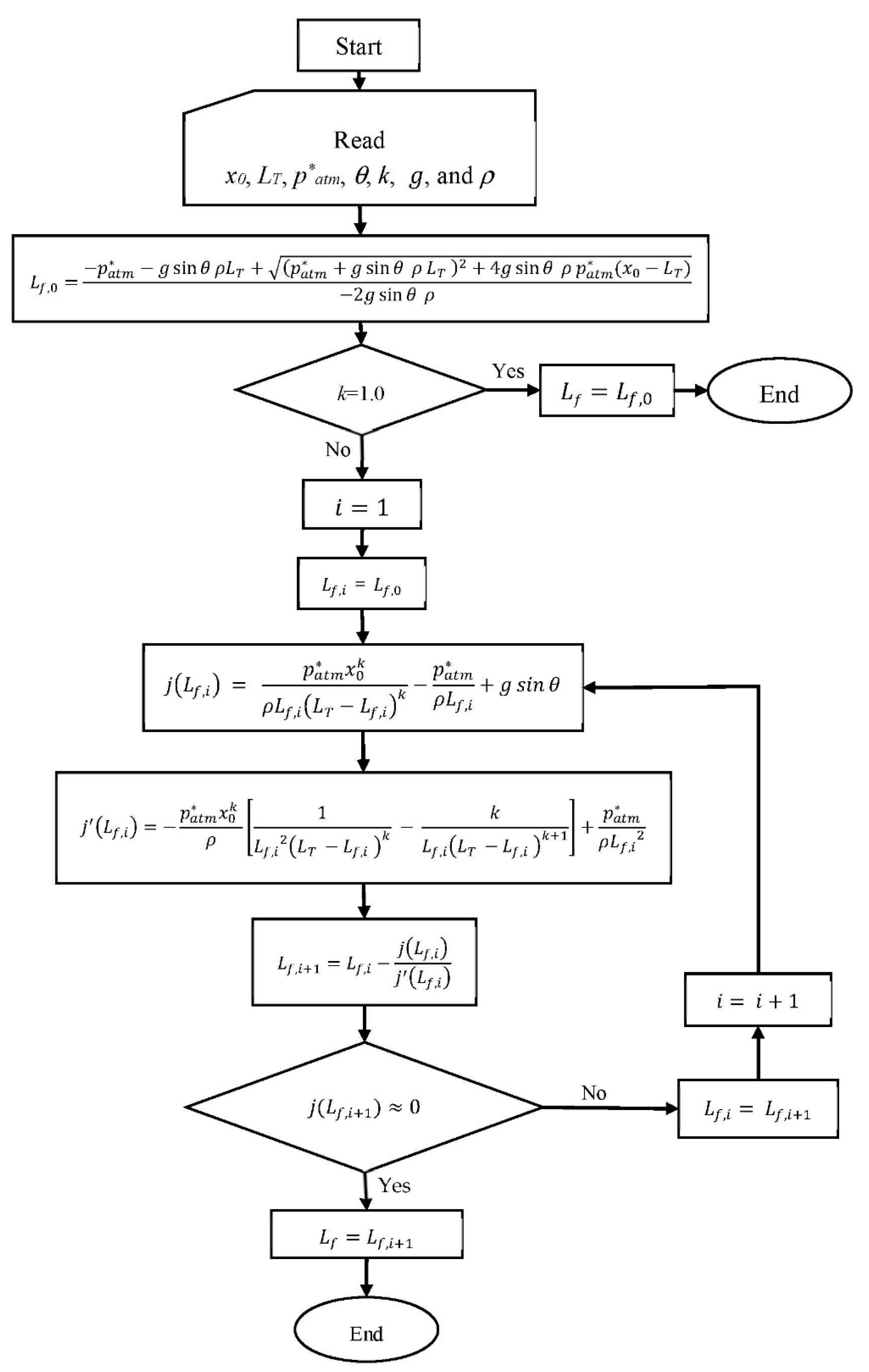
Figure 2 shows a flowchart to use the obtained implicit formulation.
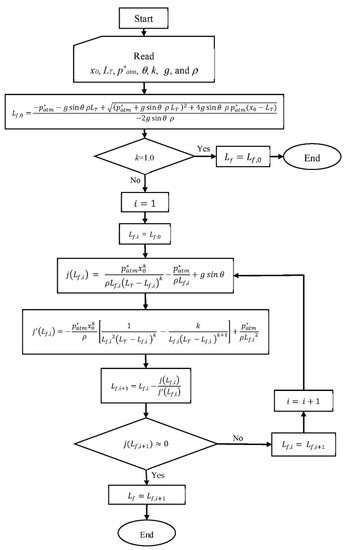
Figure 2.
Flowchart for computing final conditions in a single water emptying pipeline.
3. Analysis of Results
3.1. Practical Application
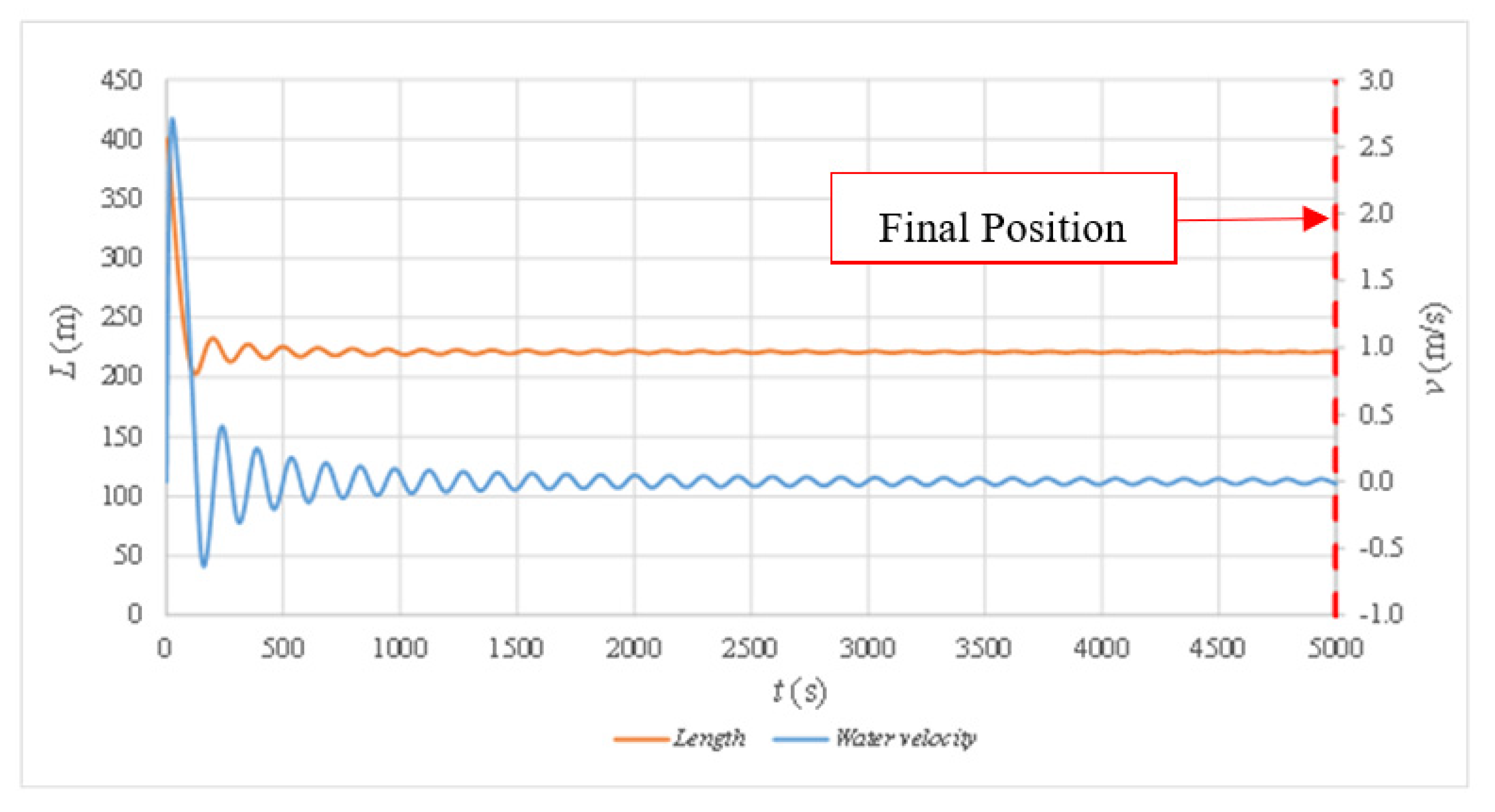
This section presents the application of these formulas to a case study. In this sense, the objective was to follow the presented flowchart (see Figure 2) to know the final position of a water column without applying the system composed by the three differential ordinary equations (see Equations (1) to (3)). To note the order of magnitude of the hydraulic and thermodynamic variables, the case study had the following data: LT = 600 m, f = 0.018, D = 0.35 m, Rv = 0.06 ms2 m−6, x0 = 200 m, k = 1.2, g = 9.81 ms−2, r = 1000 kg/m−3, p*atm = 101,325 Pa, and θ = 0.025 rad. Figure 3 presents the evolution of length and water velocity for the case study, which was obtained by solving the differential ordinary system composed by Equations (1)–(3). The numerical resolution of these equations was implemented by the authors in previous publications. At the beginning of the transient event, a maximum water velocity value of 2.66 m/s was attained at 25 s. A minimum value of −0.62 m/s was found at 160 s. After that, water velocity pulses were observed. From 3000 to 5000 s, the water velocity tended to be null (v = 0), which corresponded to the final water position during the transient event. The length of the water column rapidly decreased, passing from 400.0 m (at 0 s) to 202.9 m (at 124 s), which implied that almost half of the water column was drained. Then, some oscillations were detected, tending to a final value of 221.2 m (from 3000 to 5000 s).
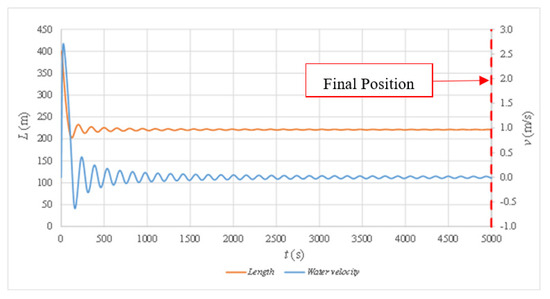
Figure 3.
Evolution of length and water velocity for the case study.
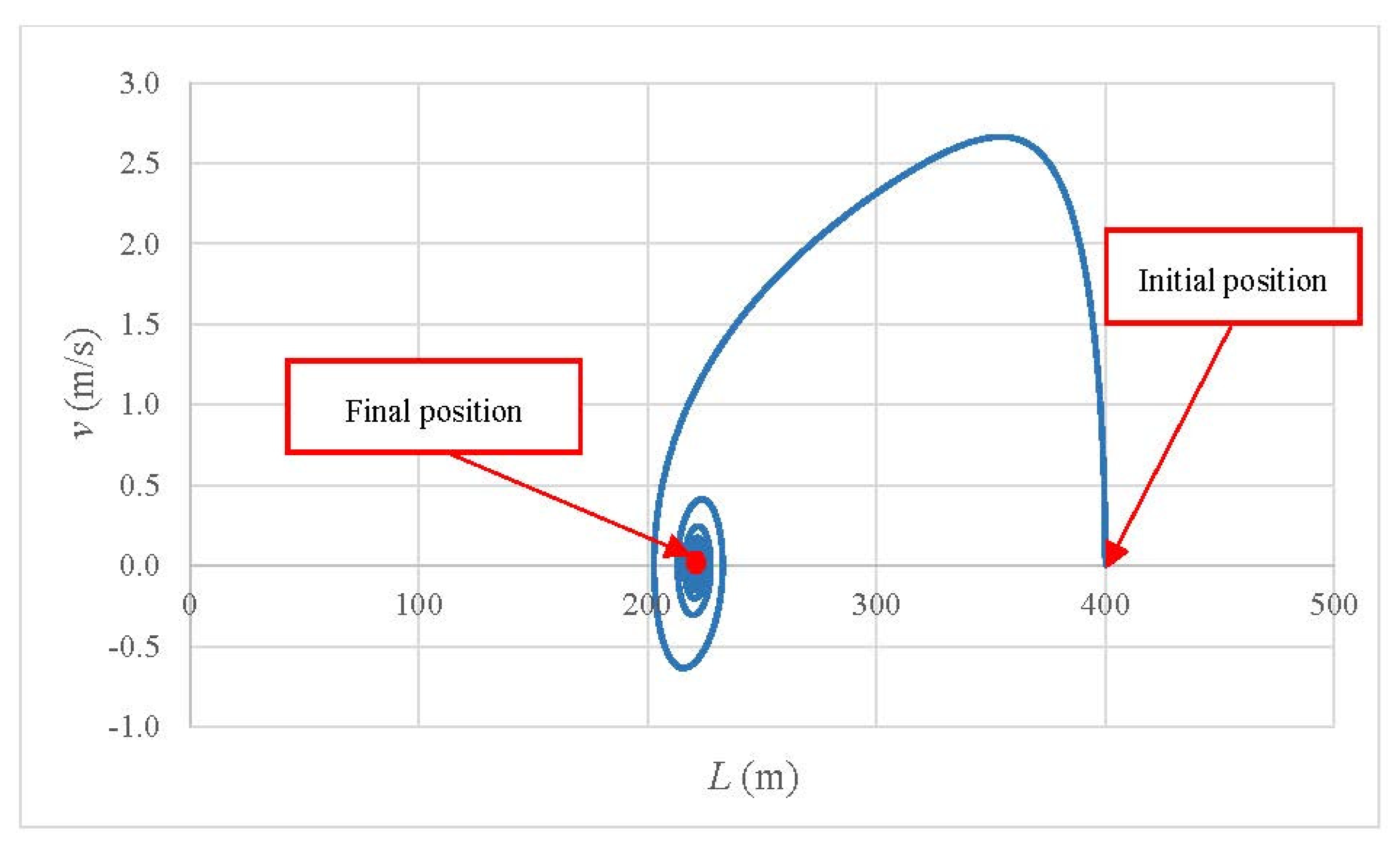
The final water column position is shown in a diagram of length versus water velocity (see Figure 4). The system starts at rest (v(0) = 0, and L(0) = 400 m). The maximum value of water velocity (2.66 m/s) is related to a water column length of 354.3 m. A spiral curve is presented towards the final position of the water column, reaching a water column length of 221.2 m.
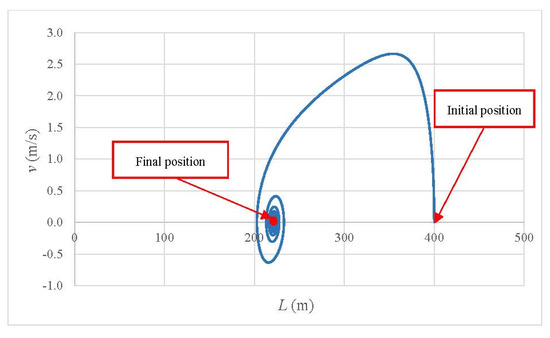
Figure 4.
Length versus water velocity for the case study.
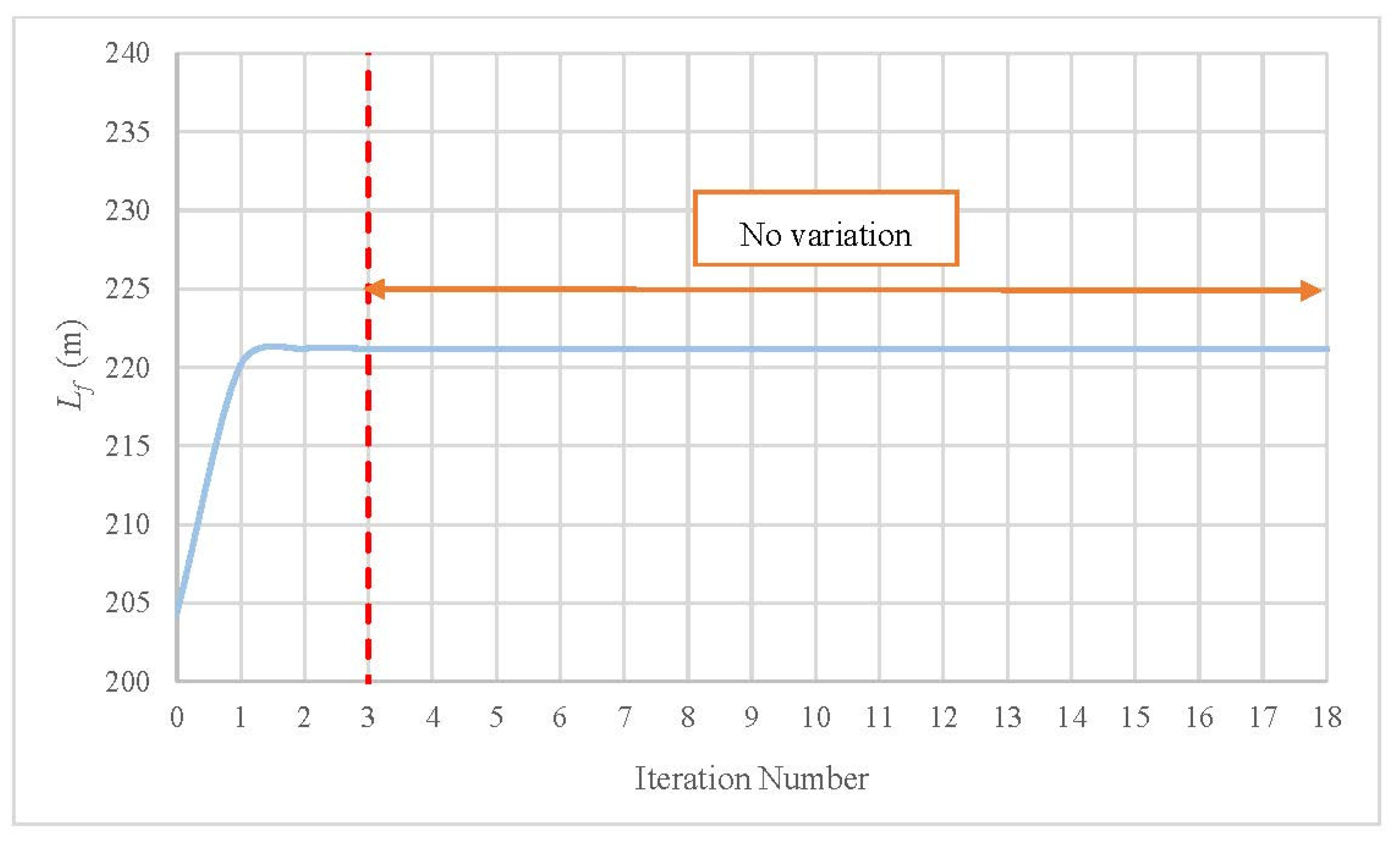
Based on the application of the flowchart (see Figure 2), it is possible to determine the final water column position without running the mathematical model composed by Equations (1)–(3). At the end of the transient flow, the water velocity was zero (v = 0), and the final water column position was 221.20 m (see Figure 2). Table 1 presents a scheme for computing the final water column position based on Figure 2, with a tolerance of 2.2204 × 10−17, which is practically null). According to the results, the Newton–Raphson method can converge rapidly (within four iterations) to find the required value. In this sense, the first iteration provided a value of 220.16 m, the second one found a value of 221.19 m, and from the third iteration, the value remained practically constant (221.20 m). The remaining iterations provided the same value. Figure 5 shows the results of the application of the Newton–Raphson method, which confirms how the convergence process is rapidly carried out. It shows how, from iteration three, there was no variation in the computation of Lf.

Table 1.
Newton–Raphson method.
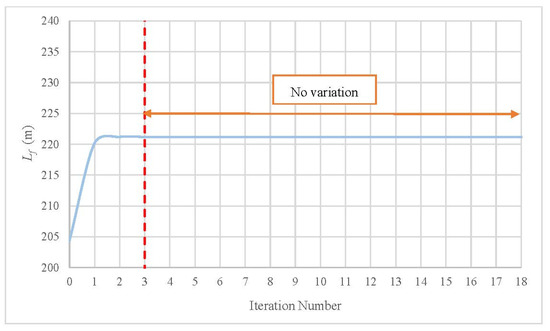
Figure 5.
Final water column length versus iteration number.
3.2. Validation
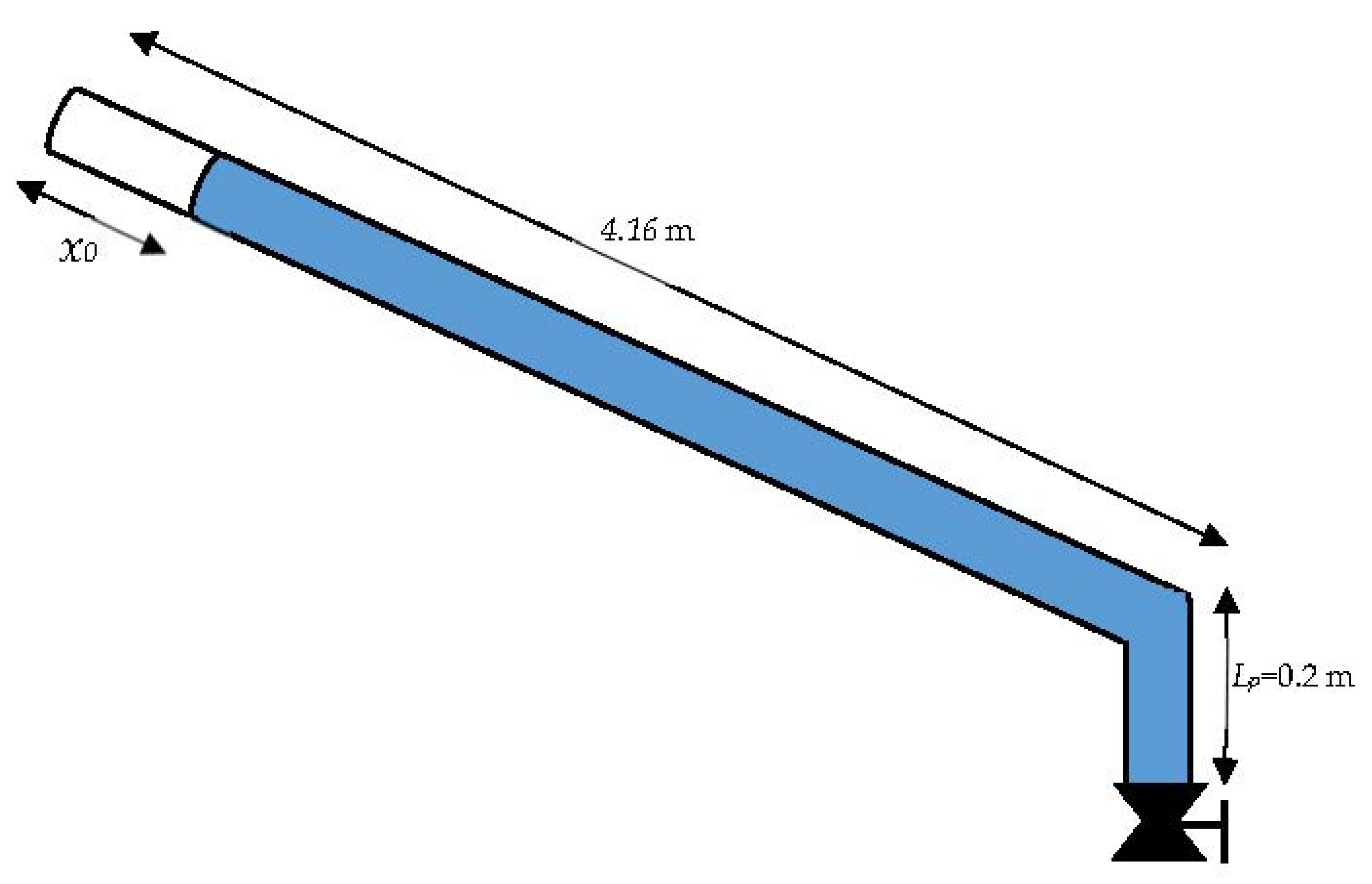
The experimental results were used to validate the developed implicit formulation. Data were obtained from Fuertes-Miquel et al. (2018) [23]. The experimental facility consisted of a PVC pipe that was 4.36 m long, with an internal pipe diameter of 42 mm. Figure 6 shows the used experimental facility. The total length was composed of two branches: an inclined pipe branch (4.16 m) and a vertical pipe branch (Lp = 0.2 m). A pressure transducer was installed at the upstream end, and a scour valve (ball valve) was installed at the downstream end to control the variation of water flow.
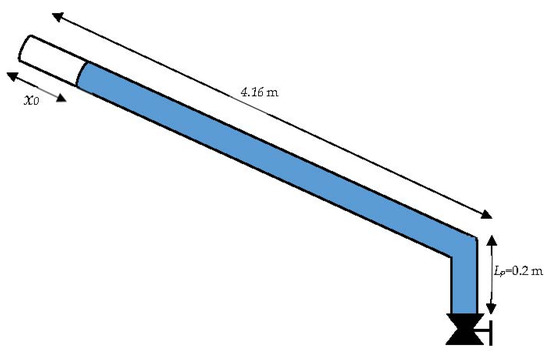
Figure 6.
Experimental facility.
Details of the experimental facility and experimental tests can be found in Fuertes-Miquel et al. (2018) [23]. When an inclined pipe is analyzed, the gravity is , while for the analyzed pipe system, the gravity term is:
Then, for the analyzed pipeline, the critical point can be found using the formulation as follows:
where Lp represents the vertical pipe length (0.2 m).
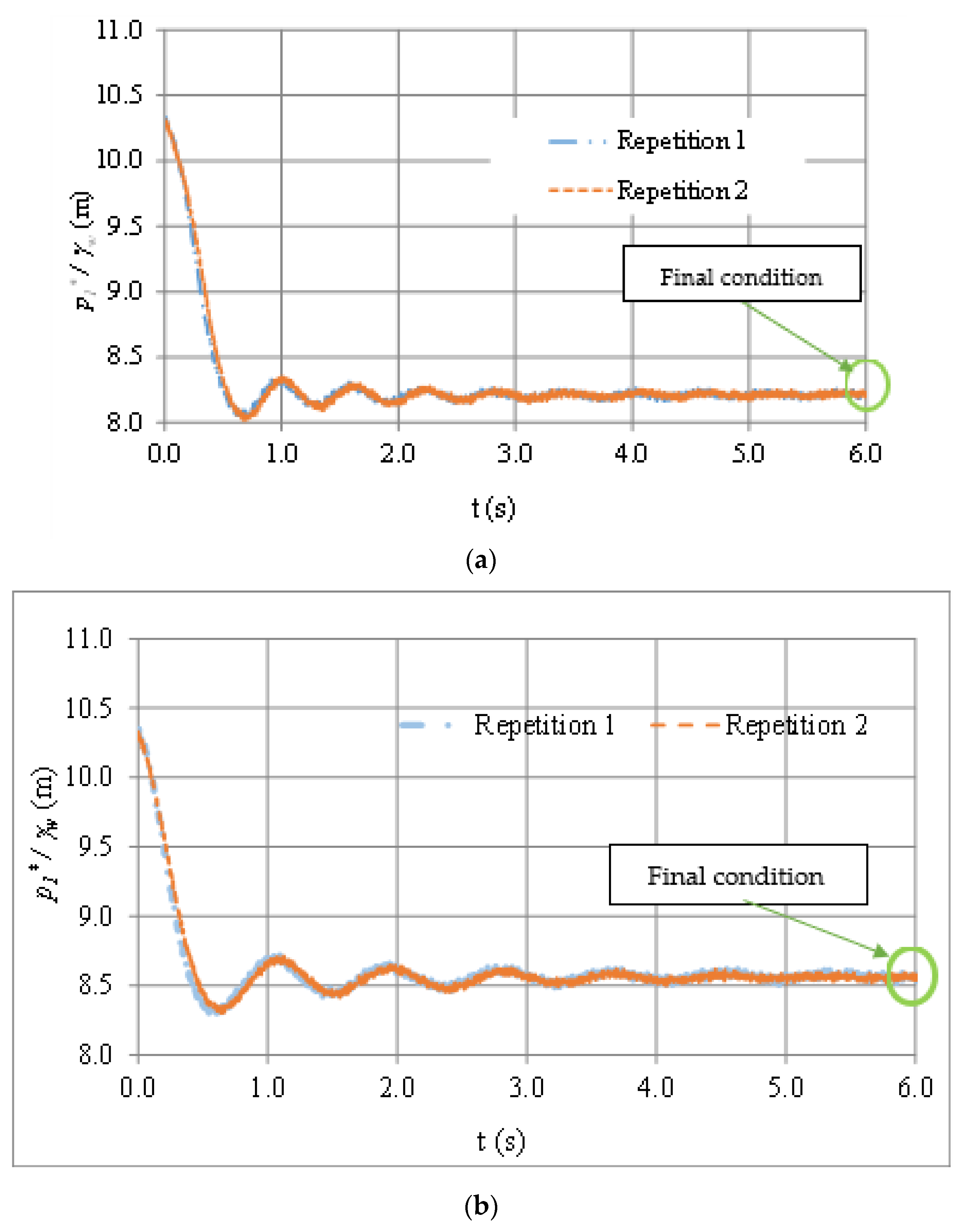
The experimental tests were conducted at the Polytechnic University of Valencia, Spain. A total of 12 experiments were performed as shown in the reference published by Fuertes-Miquel et al. (2018) [23]. For validation purposes, two experiments were used: (i) Test No. 1, which corresponds to an air pocket size (x0) of 0.205 m and a pipe slope (θ) of 0.515 rad; and (ii) Test No. 2, where an x0 value of 0.45 m and an θ value of 0.457 rad were considered. Programmed maneuvers were used with maximum resistance coefficients (Rv) of 30.86 × 106 and 14.79 × 106 ms2m−6 for Tests No. 1 and No. 2, respectively, in the ball valve. Each test was repeated twice to confirm the measurements. Figure 7 shows the results of the mathematical model (see Equations (1)–(3)). The final air pocket pressure was computed by considering both Equations (3) and (19). The measurements and the implicit formulation provided air pocket pressure heads of 8.22 and 8.54 m for Test No. 1 and No. 2, respectively, at the end of the transient event (at 6 s). This shows that the implicit formulation is suitable for computing final conditions, since it is based on a physical equation.
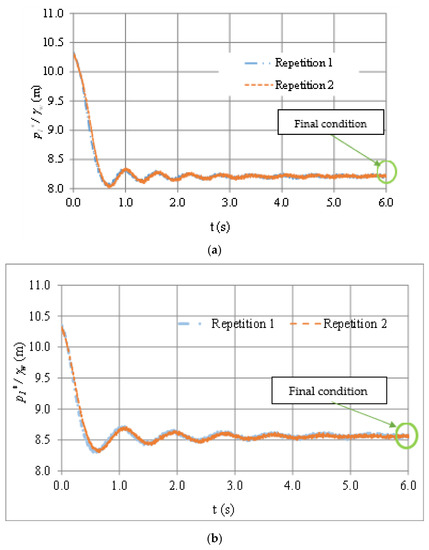
Figure 7.
Comparison between measured and computed (final condition) air pocket pressure: (a) Test No. 1 and (b) Test No. 2.
4. Sensitivity Analysis
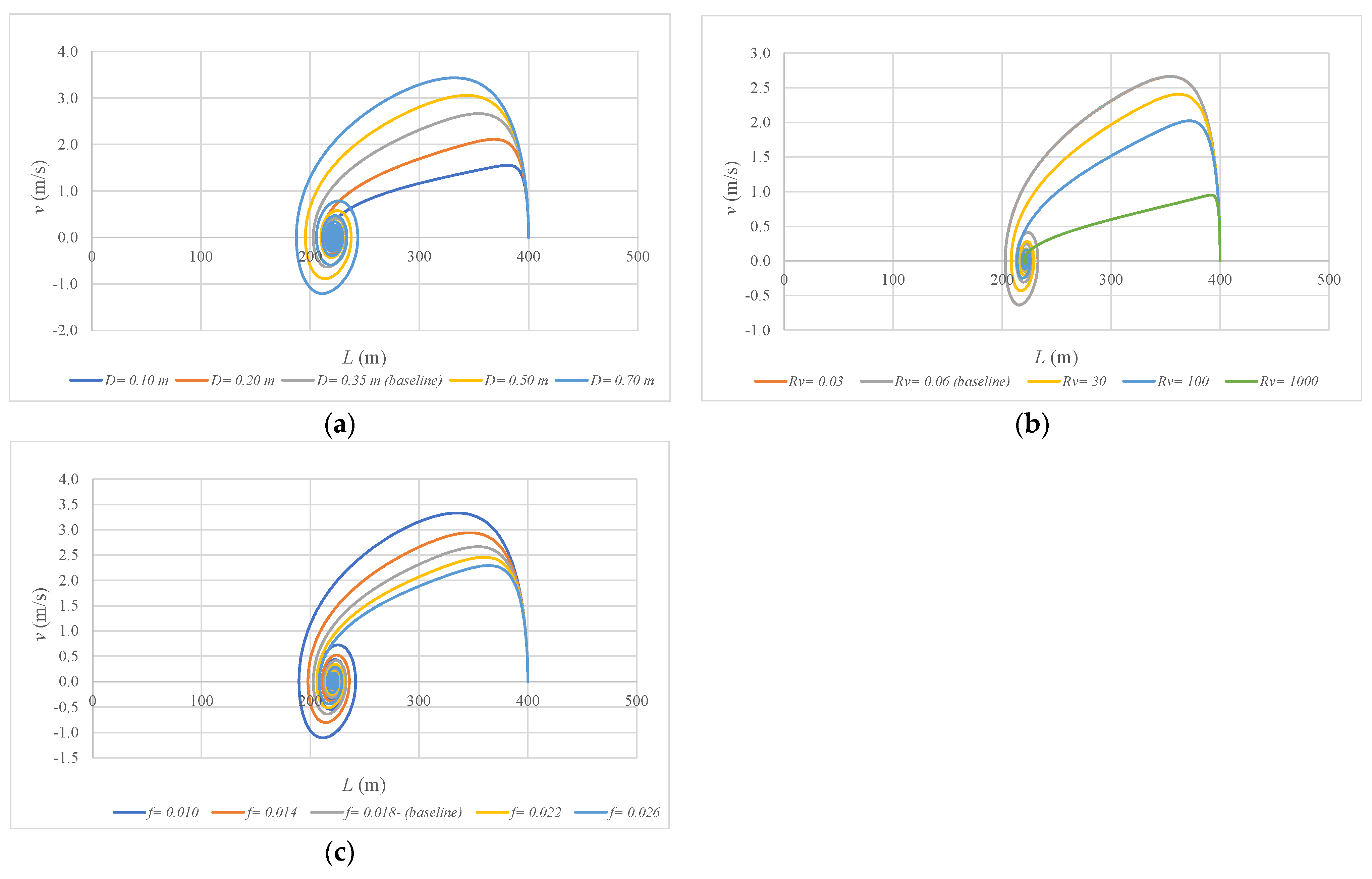
The final position during emptying processes does not depend on the internal pipe diameter (D), the drain valve maneuver (resistance coefficient (Rv)), or the friction factor (f), as shown in Equation (11). In this sense, a sensitivity analysis was performed based on the case study of Section 3. For the analysis, the internal pipe diameter varied from 0.10 to 0.70 m; the resistance coefficient ranged between 0.03 and 1000 ms2 m−6; and the friction factor varied from 0.010 to 0.026. Figure 6 presents the results of emptying simulations considering the variation of the mentioned parameters. Figure 8a–c shows that the final position of the water column length had no variation, independently of the used initial values of D, Rv, and f. For all cases, a final value of 221.20 m was found.
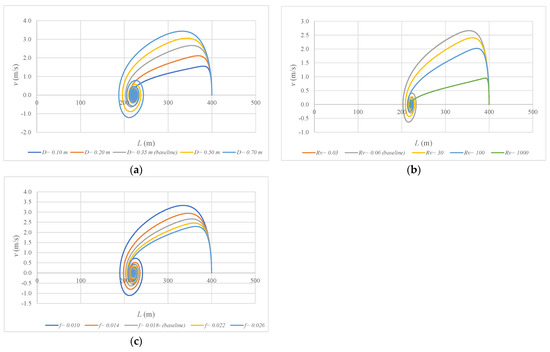
Figure 8.
Sensitivity analysis for non-dependent parameters: (a) internal pipe diameter; (b) resistance coefficient; and (c) friction factor.
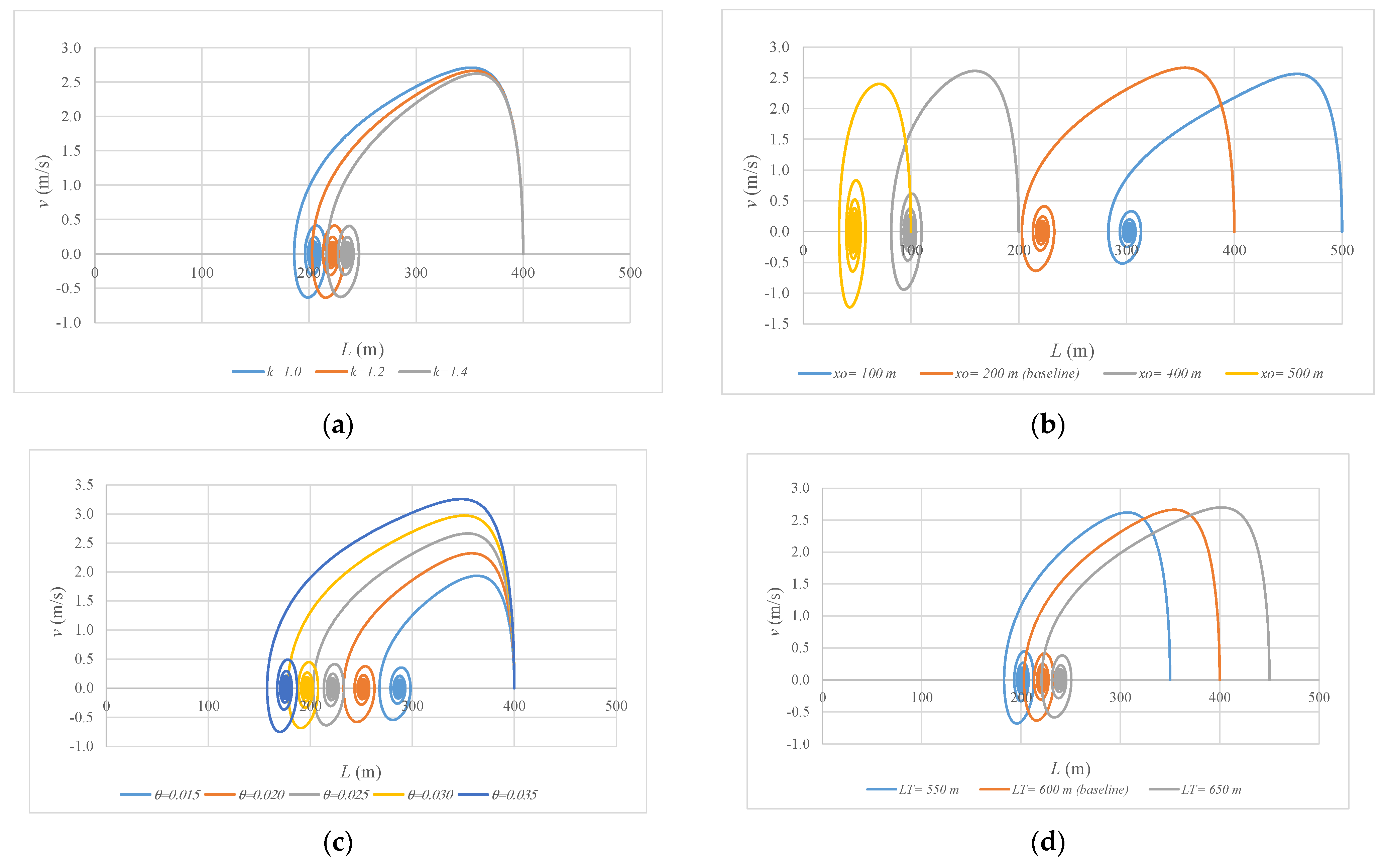
On the other hand, the final position of the length of a water column is related to the parameters of k, x0, θ, and LT according to Equation (11). Figure 9 presents the results for the mentioned parameters. Polytropic coefficients from isothermal (k = 1.0) to adiabatic (k = 1.4) were considered for simulations. The greater the polytropic coefficient, the lower the obtained value of the length of the water column (see Figure 9a). Adiabatic behavior always provides lower values of water column length compared to an isothermal evolution. The initial value of air pocket size (x0) influences the final position of water column length, as shown in Figure 9b. In this sense, considering an initial air pocket size of 100 m, a final value of 302.1 m for the water column length was computed; while, for an initial air pocket size of 500 m, the final position of the water column length was 47.1 m. The pipe slope (θ) is another parameter that is important to analyze for detecting changes regarding the final position of the water column length. The higher the pipe slope, the lower the attained values of the water column length. The total length (LT) of the pipeline was analyzed considering values between 550 and 650 m. The greater the value of the total length, the greater the reached values of the final water column length.
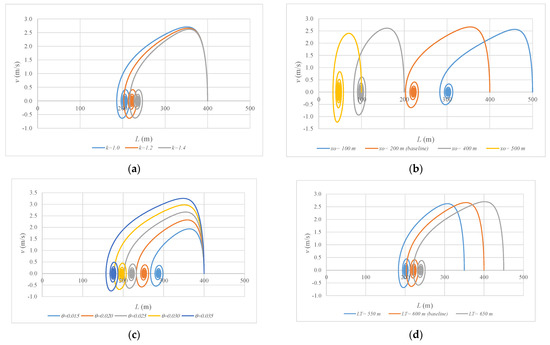
Figure 9.
Sensitivity analysis for dependent parameters: (a) polytropic coefficient (k); (b) initial air pocket size (x0); (c) slope pipe (θ); and (d) total pipe length (LT).
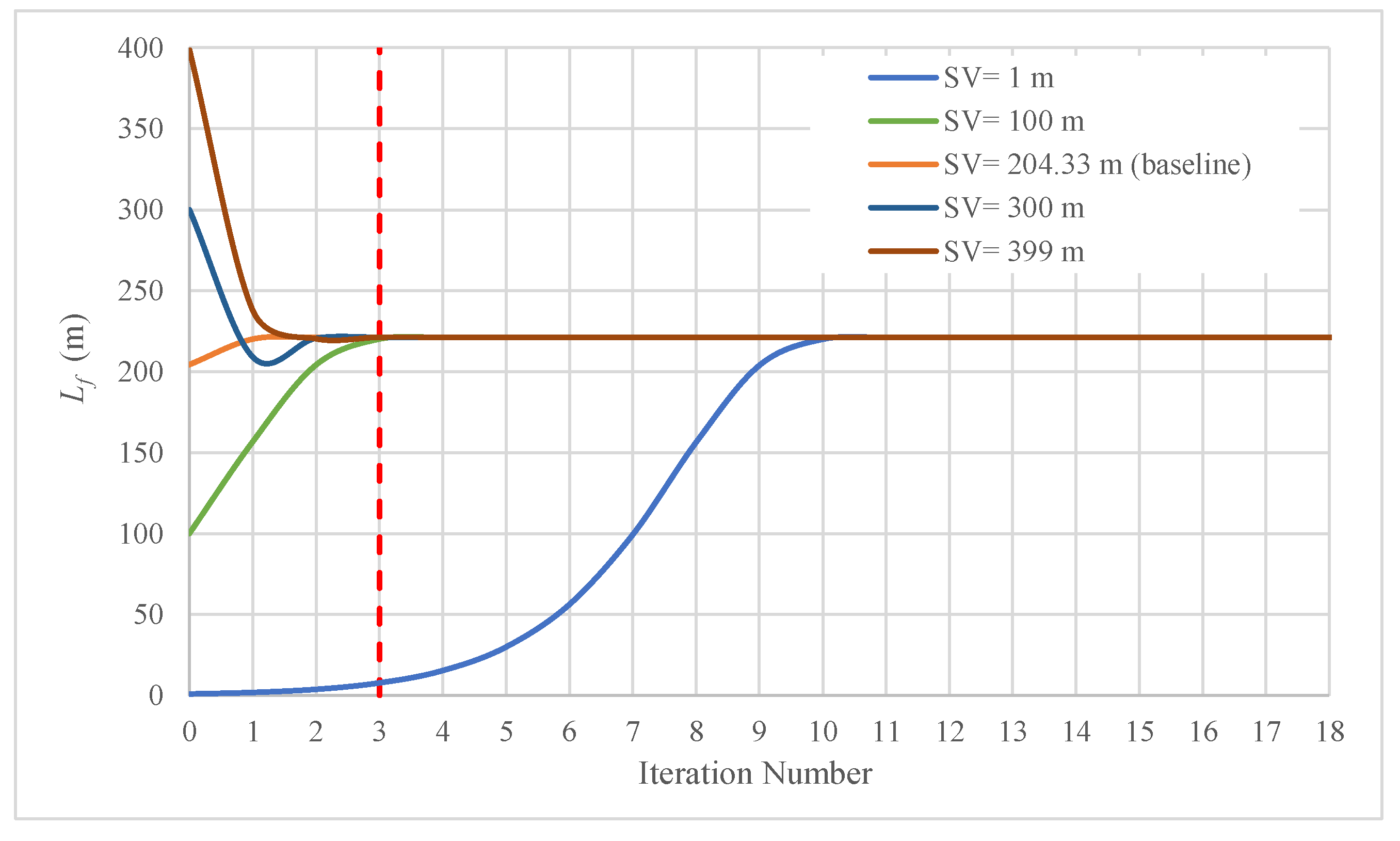
The Newton–Raphson method should be applied when considering seed values (SVs) varying from 0 to LT-x0 (0 to 400 m). If an isothermal evolution (k = 1.0) is presented, then the final position of the water column length can be computed using Equation (14). For other polytropic coefficients (, Equation (14) can be used for a seed value. A sensitivity analysis was performed using seed values from 0 to 400 m (see Figure 10). For all seed values, the Newton–Raphson method is suitable to compute the final position of the water column length (221.20 m). The seed value computed with Equation (14) (SV = 204.33 m) was the best starting point to calculate the final position of the water column length.
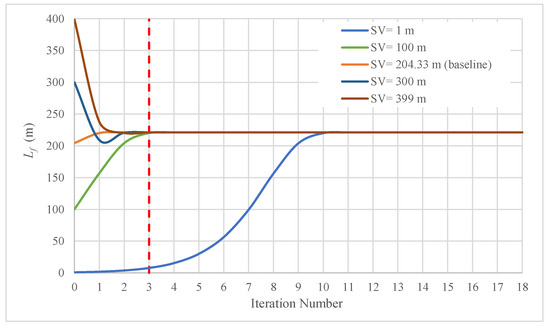
Figure 10.
Sensitivity analysis of iteration number using the Newton–Raphson method.
5. Conclusions
In this research, an implicit equation was developed (see Equation (11)) to compute final conditions in emptying processes without admitted air (no air valves) in single pipelines, which was derived by considering that water velocity tends to be null. Thus, the water column length can be directly obtained. The final air pocket pressure can be computed using the polytropic law.
The implicit equation was solved using the Newton–Raphson method, since the function derivative is not null for seed values ranging from 0 to LT-x0. For the case study, the Newton–Raphson method provided excellent results, independently of a selected seed value. Seed values varying from 0 to 400 m were used, obtaining the searched root with a maximum of four iterations.
Both the implicit equation (see Equation (11)) and the algebraic differential equations (see Equations (1) to (3)) show that the final conditions in water emptying pipelines do not depend on the friction factor, internal pipe diameter, or resistance coefficient of a discharge valve. On other hand, the remaining parameters (pipe slope, air pocket size, total length of a pipeline, and polytropic coefficient) affect the final conditions in emptying processes. In addition, the implicit formulation was validated by considering experimental measurements in an experimental facility that was 4.36 m long.
The implicit formulation can be used for engineers and designers for knowing final conditions in emptying operations without solving the algebraic differential equations.
Author Contributions
Conceptualization, O.E.C.-H. and D.M.B.-C.; methodology, A.L., V.S.F.-M., G.G., R.L. and J.R.C.-H.; formal analysis, O.E.C.-H. and D.M.B.-C.; writing—original draft preparation, O.E.C.-H. and D.M.B.-C.; supervision, A.L, V.S.F.-M., G.G., R.L. and J.R.C.-H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Escuela Naval de Cadetes “Almirante Padilla”—Armada de Colombia with the financial support of the ARC-Minciencias for the project entitled “Console Prototype of engineering in virtual reality and simulation in the training of crew members in emergency procedures” with grant number 75926.
Data Availability Statement
Data is contained within the article.
Acknowledgments
The authors are thankful to the Escuela Naval de Cadetes “Almirante Padilla” – Armada de Colombia, since the obtained implicit formulation in draining maneuvers can be considered as an additional criteria in simulated practices of the virtual reality tool in the Console Prototype of engineering in virtual reality and simulation in the training of crew members in emergency procedures (engineering plant) for type units of the Naval Fleet of the Armada de Colombia for making decisions in problems related to draining maneuvers in water distribution networks of ships.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations were used in this research:
| A | Cross-sectional area of pipe (m2) |
| D | Internal pipe diameter (m) |
| f | Friction factor (-) |
| g | Gravity acceleration (m s−2) |
| k | Polytropic coefficient (-) |
| j | Used function in the Newton–Raphson equation |
| L | Water column length (m) |
| LT | Pipe length (m) |
| P | Function based on piston flow model |
| patm* | Atmospheric pressure (101,325 Pa) |
| p*1 | Air pocket pressure (Pa) |
| Q | Function based on both mass oscillation equation and polytropic law |
| Rv | Resistance coefficient (ms2 m−6) |
| t | Time (s) |
| v | Water velocity (m s−1) |
| V | Vector field on a region in the plane (L, v) |
| x | Air pocket size (m) |
| X | Vector function of t |
| r | Water density (kg m−3) |
| θ | Pipe slope (rad) |
| γw | Water unit weight (N m−3) |
| Subscripts | |
| 0 | Refers to an initial condition |
| f | Refers to a final condition |
| i | Iteration number |
| Superscripts | |
| ′ | Derivative |
References
- Ramezani, L.; Karney, B.; Malekpour, A. The Challenge of Air Valves: A Selective Critical Literature Review. J. Water Resour. Plan. Manag. 2016, 141, 04015017. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, Ó.E.; Mora-Melia, D.; Iglesias-Rey, P.L. Hydraulic Modeling during Filling and Emptying Processes in Pressurized Pipelines: A Literature Review. Urban Water J. 2019, 16, 299–311. [Google Scholar] [CrossRef]
- AWWA (American Water Works Association). Manual of Water Supply Practices M51—Air Valves: Air Release, Air/Vacuum and Combination; AWWA: Denver, CO, USA, 2016. [Google Scholar]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Subatmospheric Pressure in a Water Draining Pipeline with an Air Pocket. Urban Water J. 2018, 15, 346–352. [Google Scholar] [CrossRef]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Iglesias-Rey, P.L.; Martínez-Solano, F.J. Rigid Water Column Model for Simulating the Emptying Process in a Pipeline Using Pressurized Air. J. Hydraul. Eng. 2018, 144, 06018004. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Quiñones-Bolaños, E.E.; Gatica, G.; Coronado-Hernández, J.R. Simplified Mathematical Model for Computing Draining Operations in Pipelines of Undulating Profiles with Vacuum Air Valves. Water 2020, 12, 2544. [Google Scholar] [CrossRef]
- Laanearu, J.; Annus, I.; Koppel, T.; Bergant, A.; Vučkovič, S.; Hou, Q.; van’t Westende, J.M.C. Emptying of Large-Scale Pipeline by Pressurized Air. J. Hydraul. Eng. 2012, 138, 1090–1100. [Google Scholar] [CrossRef]
- Tijsseling, A.; Hou, Q.; Bozku¸s, Z.; Laanearu, J. Improved One-Dimensional Models for Rapid Emptying and Filling of Pipelines. J. Press. Vessel Technol. 2016, 138, 031301. [Google Scholar] [CrossRef]
- Besharat, M.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Viseu, M.T.; Ramos, H.M. Backflow Air and Pressure Analysis in Emptying Pipeline Containing Entrapped Air Pocket. Urban Water J. 2018, 15, 769–779. [Google Scholar] [CrossRef]
- Hurtado-Misal, A.D.; Hernández-Sanjuan, D.; Coronado-Hernández, O.E.; Espinoza-Román, H.; Fuertes-Miquel, V.S. Analysis of Sub-Atmospheric Pressures during Emptying of an Irregular Pipeline without an Air Valve Using a 2D CFD Model. Water 2021, 13, 2526. [Google Scholar] [CrossRef]
- Besharat, M.; Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Viseu, M.T.; Ramos, H.M. Computational fluid dynamics for sub-atmospheric pressure analysis in pipe drainage. J. Hydraul. Res. 2020, 58, 553–565. [Google Scholar] [CrossRef]
- Liou, C.P.; Hunt, W.A. Filling of pipelines with undulating elevation profiles. J. Hydraul. Eng. 1996, 122, 534–539. [Google Scholar] [CrossRef]
- Izquierdo, J.; Fuertes, V.; Cabrera, E.; Iglesias, P.; Garcia-Serra, J. Pipeline start-up with entrapped air. J. Hydraul. Res. 1999, 37, 579–590. [Google Scholar] [CrossRef]
- Martins, N.M.; Delgado, J.N.; Ramos, H.M.; Covas, D.I. Maximum transient pressures in a rapidly filling pipeline with entrapped air using a CFD model. J. Hydraul. Res. 2017, 55, 506–519. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D. Experimental Investigation of Entrapped Air Pocket in a Partially Full Water Pipe. J. Hydraul. Res. 2013, 51, 469–474. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D.; Karney, B. Investigation of hydraulic transients of two entrapped air pockets in a water pipeline. J. Hydraul. Eng. 2013, 139, 949–959. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; López-Jiménez, P.A.; Martínez-Solano, F.J.; López-Patiño, G. Numerical modelling of pipelines with air pockets and air valves. Can. J. Civ. Eng. 2016, 43, 1052–1061. [Google Scholar] [CrossRef]
- Chapra, S.; Canale, R. Numerical Methods for Engineers, 7th ed.; Mcgraw-Hill Education, Cop: New York, NY, USA, 2015. [Google Scholar]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis; Springer: New York, NY, USA; London, UK, 2011. [Google Scholar]
- Zill, D. Differential Equations with Boundary-Value Problems; Cengage Learning: Melbourne, Australia, 2016. [Google Scholar]
- Suribabu, C.R. Location and Sizing of Scour Valves in Water Distribution Network. J. Hydraul. Eng. 2009, 15, 118–130. [Google Scholar] [CrossRef]
- Suribabu, C.R. Optimal locations and sizing of scour valves in water distribution networks. J. Pipeline Syst. Eng. 2020, 11, 04019056. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, Ó.E.; Mora-Melia, D.; Iglesias-Rey, P.L. Transient phenomena during the emptying process of a single pipe with water–air interaction. J. Hydraul. Res. 2018, 57, 3. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).