Abstract
Precipitation is a key variable in the hydrological cycle and essential input data in rainfall-runoff modeling. Rain gauge data are considered as one of the best data sources of precipitation but before further use, the data must be spatially interpolated. The process of interpolation is particularly challenging over mountainous areas due to complex orography and a usually sparse network of rain gauges. This paper investigates two deterministic interpolation methods (inverse distance weighting (IDW), and first-degree polynomial) and their impact on the outputs of semi-distributed rainfall-runoff modeling in a mountainous catchment. The performed analysis considers the aspect of interpolation grid size, which is often neglected in other than fully-distributed modeling. The impact of the inverse distance power (IDP) value in the IDW interpolation was also analyzed. It has been found that the best simulation results were obtained using a grid size smaller or equal to 750 m and the first-degree polynomial as an interpolation method. The results indicate that the IDP value in the IDW method has more impact on the simulation results than the grid size. Evaluation of the results was done using the Kling-Gupta efficiency (KGE), which is considered to be an alternative to the Nash-Sutcliffe efficiency (NSE). It was found that KGE generally tends to provide higher and less varied values than NSE which makes it less useful for the evaluation of the results.
1. Introduction
Precipitation is one of the major driving forces in the hydrological cycle that affects hydrological processes [1,2]. Nowadays, precipitation data are mainly acquired from rain gauges, weather radars, and satellites, while the first two are considered as the best data sources for catchment modeling [3]. Even though there are measurement alternatives to rain gauges, the data acquired at in-situ measurements are still frequently used in many hydrological applications as they provide reliable and measured (not estimated) point information on the precipitation. However, before further use, the rain gauge data must be spatially interpolated, which might significantly affect the accuracy of the spatial precipitation field [4]. The process of obtaining a reliable interpolated precipitation field is particularly challenging in mountainous environments. The spatial patterns of precipitation over these areas are mainly affected by the topography of the area and wind direction, which significantly affects runoff modeling in the catchment [5]. Moreover, mountainous areas often face the problem of sparse rain gauge networks, which limits the accessibility of the data and affects the interpolation accuracy [6].
The amount of precipitation measured by the rain gauge provides local information on the precipitation, not its areal variability [7]. In hydrological applications, it is necessary to acquire the areal height of precipitation. Therefore, the rain gauge data is subject to spatial interpolation to reproduce its spatial variability. One of the main problems with spatial interpolation of rain gauge data is the small number of measurement points [8], which is often insufficient to correctly reproduce areal precipitation, although the rainfall values measured at a given point are correct [7]. An equal measurement of the precipitation height is expected within a distance of a few meters from each other, while at several hundred meters, this convergence is significantly reduced [9].
Gridded datasets based on in-situ observations are mainly affected by station density and interpolation methodology [10]. As for interpolation methodology, two aspects are crucial: the choice of the method and the resolution of the interpolation grid. Spatial interpolation techniques can be divided into deterministic and probabilistic methods. The first ones are based on deterministic interpolation algorithms, as a result of which a continuous or discontinuous precipitation field is created. The latter are based on algorithms in which it is assumed that the point information from measurement has a deterministic and a spatially correlated random component. Among the deterministic methods, the most commonly used techniques include inverse distance weighting (IDW), polynomial interpolation, and Thiessen polygons [2,11,12]. As for the geostatistical methods that are the most used, the techniques are ordinary kriging and co-kriging [13]. When the amount of available rain gauges is very limited, the geostatistical methods will not be effective [14].
In many previous studies (e.g., [6,10,15,16]) assessments of interpolation methods were done in terms of statistical analysis like cross-validation or minimization of mean absolute error (MAE) or root mean square error (RMSE). However, when it comes to hydrological modeling, these statistical aspects of precipitation data are important, but their reliable values do not guarantee accurate discharge simulations using the rainfall-runoff model.
It’s frequently assumed that fully-distributed models are the best for investigation of the spatial variables (like precipitation) as they allow to provide input data in the grid cells and do not average values over larger areas like lumped and semi-distributed models do [2]. However, the semi-distributed hydrological models are also sensitive to the spatial distribution of variables. That was the subject of an investigation by Cheng et al. [1], where the authors analyzed the impact of three interpolation methods (Thiessen polygons, IDW, and co-kriging) and applied it to a semi-distributed model. Nonetheless, they omitted the aspects of grid resolution impact on interpolation outputs, as well as the impact of inverse distance power (IDP) value for IDW method. In another paper by Chen et al. [4], three interpolation methods were also analyzed (regression-based scheme, IDW, and multiple linear method) and applied to a semi-distributed model. However, in their study, the authors set up the grid resolution to 500 × 500 m without any investigation. The impact of the IDP value in the IDW method for the purpose of hydrological modeling is also not sufficiently analyzed. There are some papers (e.g., [17,18,19]) that investigated the effect of the IDP value on precipitation of the interpolation outputs, but the data were not applied to the hydrological model. Most frequently, the IDP value is set as equal to two, which seems to be a fine potency for hydrogeology applications [20,21]. As for hydrological applications, the IDP is also often assumed as two, but there is no strong evidence that it is the most optimal value.
For hydrological modeling, there is a great need to interpolate precipitation data even when the number of measuring stations is too small to prevent the use of any geostatistical method. Taking into account that the grid size aspects are mostly neglected when interpolating precipitation, the main objective of this paper is to investigate both the impact of grid resolution and deterministic interpolation technique and evaluate them via rainfall-runoff simulations using the Hydrologic Engineering Center-Hydrologic Modelling System (HEC-HMS) semi-distributed hydrological model over a sparsely gauged mountainous catchment. Also, for the inverse distance weighting method, the impact of the IDP value on the hydrological simulation results was investigated. The simulations were performed using two interpolation methods (inverse distance weighting and first-degree polynomial interpolation) and 6 grid sizes (ranging from 250 m to 5000 m). The impact of IDP value in IDW interpolation and its impact on discharge simulation was also subject to investigation. As the study area, a sparsely rain-gauged mountainous catchment in southern Poland was chosen which frequently faces flooding events. The simulation results were evaluated using Nash-Sutcliffe efficiency (NSE), Kling-Gupta efficiency (KGE), and percent bias metrics. The KGE criterion is often considered as an alternative to NSE, and this paper tries to judge which of these two allows for better evaluation of the modeling results.
2. Materials and Methods
2.1. Description of Study Area
The Skawa catchment is located in southern Poland and borders with the Czech Republic. Its area is equal to 1600 km2 and is entirely located in the Outer Carpathians. The catchment can be divided into two parts, upper- and lower-one [22], where the upper part is more exposed to the risk of flooding. Within the river basin, the elevation varies from 435 to 1038 m a.s.l. To the southwest of the catchment is the Babia Góra massif—the highest peak of the Polish part of the Carpathian Mountains. The highest rainfall is observed in the Babia Góra region and the lowest in the lower part of the catchment. Most of the catchment area is dominated by a warm temperate (up to approx. 700 m a.s.l.) or a cold temperate cold (at altitudes 700–1100 m a.s.l.). There are four rain gauges in the catchment area, of which one is directly located in the investigated study area. The rain gauges are not well distributed over the entire study area, which makes the areal estimation of precipitation based on them more challenging.
In this study, all analyses were limited to the upper part of the Skawa River (area of 240.4 km2), which is particularly at risk of flooding [23]. This part of the catchment consists of 6 sub-catchments. The upper Skawa catchment area is characterized by a dense water network with dominant short streams with large slopes, resulting from the mountainous nature of the Skawa river [22]. The area of the catchment is dominated by low permeable soils, which is one of the most major factors contributing to the formation of flash floods caused by excessive rainfall [24,25]. Discharge data for the catchment are available at the gauging station in Osielec, which is located downstream.
Figure 1 presents major characteristics of the area in terms of elevation, locations of rain gauges, and gauging station, as well as division into sub-catchments.
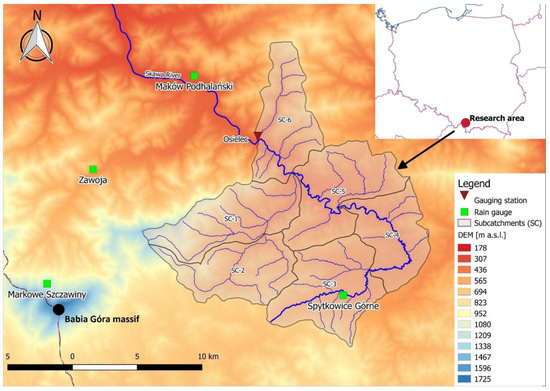
Figure 1.
Characteristics of the Upper Skawa River catchment in reference to digital elevation model (DEM).
The Upper Skawa catchment can be classified as a relatively small mountainous catchment with a quick time of response. The average of the time to peak of the catchment is around 2.5 h [26].
2.2. Data Collection and Processing
The precipitation data measured with rain gauges were obtained from the telemetric rain gauge network which is operated by the national hydrological and meteorological service—the Institute of Meteorology and Water Management National Research Institute. Precipitation on the rain gauges was measured in 10-min time-step intervals and for the purpose of this work was aggregated to 1-h intervals. All of the measurements undergo quality control by verifying their range according to climatological values, as well as spatio-temporal consistency [27]. There were four rain gauges located on-site or close to the study area (Table 1).

Table 1.
Characteristics of the rainfall stations used in the study.
The discharge data, at hourly time-step, came from the gauging station in Osielec (Figure 1) and were also provided by the Institute of Meteorology and Water Management National Research Institute.
Both precipitation and discharge data were obtained for the years between 2014 and 2019. During this period, there were several flash flood events resulting from excessive rainfall and they were subject to further investigation. Four events from 2014–2016 were selected for calibration of the hydrological model and another four events from 2017–2019 were chosen for its validation. That was the maximum of available precipitation events over the analyzed period.
Slope information, which was required in the hydrological model, was acquired from the Digital Elevation Model (DEM) of 100 m resolution that was provided by the Head Office of Geodesy and Cartography in Poland. As for the land-use data, the CORINE Land Cover Project CLC2012 v.18.5.1 was used. Complex information on the land-cover delimitation over the study area can be found in the paper by Gilewski and Nawalany [28].
All the data processing and statistical analysis were performed using R software.
2.3. Hydrological Modeling and Assesment
2.3.1. Selection of the Model
The increasing computer power enables the creation of more and more complex hydrological models considering a range of processes related to the dynamics of water movement and its accumulation in the catchment area. Fully distributed models allow to incorporate information on the spatial variability of input data, such as, e.g., rainfall or land-use. They usually require the availability of input data characterized by a high degree of quality (reliability), which, given the high resolution of the described variables and hydrological parameters, is a serious scientific and technical challenge. The computational time and calibration process of models with distributed parameters are longer and more complicated than for lumped or semi-distributed models [29].
In parallel to the development of models of high complexity, there are many works and research on the simpler models (lumped or semi-distributed) [30,31]. Simplified models are often used for preliminary analyses since they do not require high computing power and are characterized by a significantly shorter simulation time. One of the frequently discussed topics in the literature is an attempt to answer the question: are models with distributed parameters better than simplified models since they allow for more detailed modeling of hydrological processes in the catchment area? Answers that can be found in the literature (e.g., [32,33,34]) indicate that simulations performed with semi- and fully-distributed models give similar results.
For the purpose of this study, hydrological rainfall-runoff modeling was performed using the HEC-HMS (Hydrologic Engineering Center-Hydrologic Modelling System) version 4.2.1. This is a freeware software developed by the US Army Corps of Engineers. It enables modelling continuous and even-based outflows. Depending on the adopted parameters, the model can be either lumped or semi-distributed. Precipitation and discharge data were acquired into the hydrological model via HEC-DSSVue version 2.0 software.
The main components of the HEC-HMS software are the catchment model and meteorological model. Table 2 presents the parameters and methods used for modeling in this paper. They were selected in such a way as to be adequate for the event-based simulations in the model with semi-distributed parameters.

Table 2.
Methods applied in the Hydrologic Engineering Center-Hydrologic Modelling System (HEC-HMS) hydrological model.
As for the meteorological component, in total, 14 different data sources of precipitation were used:
- precipitation fields interpolated using the IDW interpolation method (IDP = 2.0) for 6 different grid sizes (250, 500, 750, 1000, 2500, and 5000 m);
- precipitation fields interpolated using the IDW interpolation method and different IDP values (0.5, 2.0 and 5.0) for 2 grid sizes (250 and 2500 m);
- precipitation fields interpolated using the first-degree polynomial interpolation method for 6 different grid sizes (250, 500, 750, 1000, 2500, and 5000 m).
2.3.2. Model Assessment
Assessments of the calibration and validation results from the hydrological model were conducted separately for each of the meteorological models, as the spatial distribution of precipitation has a significant impact on the estimation of model parameters. During the calibration process, the parameters for the rainfall loss method (initial abstraction and curve number) and transformation of effective precipitation (standard lag and peaking coefficient) were calibrated. The simulated model flow, at hourly time-steps, was compared to the observed flow at the gauging station Osielec. As an objective function during the calibration process, the peak-weighted RMSE metric was applied.
The assessment criteria were chosen based on the literature to perform a multi-aspect analysis of the model simulation results. It must be noticed that a comprehensive analysis of the results includes not only evaluation of the performance metrics, but also graphical evaluation of the results. For the purpose of this study, the following metrics were used to assess the performance of the modeled discharge in relation to the observed flow:
- Nash-Sutcliffe efficiency (NSE)—frequently used metric to determine the relative magnitude of the residual variance in relation to the measured data variance [35]. The NSE values range from −1 to 1. The closer to 1, the more accurate the model is. If NSE value = 0, it means that the model predictions are as accurate as the mean value from the observed data. Values < 0 indicate that the mean value from observed data is a better predictor than the model results. The NSE is defined as:where Qsim and Qobs are consecutively simulated and observed river discharge, represents the mean of observed values, and n stands for the number of observations.
- Kling-Gupta efficiency (KGE)—developed by Gupta et al. [36] is one of the alternatives to the NSE criterion [37], which is based on its decomposition (correlation, variability, and mean bias). Similarly, like NSE, the KGE value equal to 1 indicates a perfect agreement between model results and observation data, and values <0 means that the mean of observation data serves as a better predictor than the model outputs. The KGE is expressed as follows:where r is the linear correlation between the observed and simulated river flow, α is a measure of the flow variability error, and β represents a bias.
- Percent bias (PBIAS)—this metric is used to assess the model performance regarding the tendency of the simulated flow to be over- or underestimated [26]. If the value of PBIAS is greater than 20%, then it is considered to be unacceptable [38]. The formula for PBIAS is expressed as follows:where Qsim and Qobs are consecutively simulated and observed river discharge.
2.4. Spatial Interpolation of Precipitation
2.4.1. Interpolation Grid Resolutions
The spatial resolution of the precipitation field is one of the most important sources of uncertainty in the gridded data [10]. However, when it comes to semi-distributed hydrological modeling, this aspect is often neglected. Most of the time, only the interpolation method is investigated, but grid resolution is treated as fixed, like in the paper by Tobin et al. [39] where the authors were using 500 m resolution grid and investigated three interpolation methods (Inverse Distance Weighting, Ordinary Kriging and Kriging with External Drift). In this paper, six different grid sizes were analyzed (Figure 2).

Figure 2.
Comparison of the interpolation grids investigated in the study (a) 250 m, (b) 500 m, (c) 750, (d) 1000 m, (e) 2500 m. (f) 5000 m.
Considering the complex topography of the study area, it was decided that the initial resolution of the grid size would be set to 250 m. Such resolution is fair enough to represent the spatial variability of precipitation. Then, the grid sizes were gradually increased up to 5000 m, which, after investigation, seems to be the lowest acceptable resolution that could still be enough to represent spatial variability. These grids were used to create precipitation fields using the inverse distance weighting and polynomial interpolation methods.
2.4.2. Inverse Distance Weighting
The Inverse Distance Weighting (IDW) interpolation method was developed by Shepard in 1968 [40]. This method has been used for decades, and despite the passage of time and the development of more sophisticated interpolation methods, it is still widely used for spatial interpolation of point precipitation data [1,41]. The main advantage of this method is its simplicity in implementation and satisfactory interpolation results confirmed over the years in various works. The general concept behind this method is to attribute the value over an unsampled location as a weighted average of the known values located around [42]. In the case of the IDW method, the functions of the inverse distance are used where the weights are defined by the inverse of the distance and normalized, so their sum equals one [12].
The amount of precipitation at a location not covered by the measurement () is determined according to the formula [4,21]:
where Pi—rainfall amount measured at the rain gauge, D0i—distance between the location of the estimated part of the precipitation field and the rain gauge i, n—number of rain gauges used to estimate the precipitation amount at the location 0, p—power exponent responsible for assigning significance weights to individual rain gauges.
The outputs of IDW interpolation depend on two factors: density of the rain gauges network, which impacts the distance between the rain gauges and the estimated part of the precipitation field, and also the assumed value of the power parameter (p). To minimize the errors related to the distance problem, the density of the rain gauge network should be as high as possible. However, most researchers acquire the data from already existing measuring networks and have no real impact on the station’s density. The IDW method assumes that the mapped variable decreases in influence with increasing distance from the sampling locations. The influence depends on the power parameter (p), which is always a positive, real number, and usually assumed as equal to 2 [43] without further investigation. The general indication for mountainous areas is to assume the p-value as either 1, 2, or 3 [44]. After investigation of different values of the p parameter for the study area for further analysis, three values were chosen 0.5, 2, and 5.
The mentioned-above values represent a wide enough range to verify its impact on the precipitation estimates. From the conducted analysis, it turned out that the values greater than 5 seem to over-generalize the interpolation results when using them over an area of a small catchment.
Some studies show that by including the elevation weighting in the IDW method, better results can be obtained in the regions where the topographic impact on the precipitation is significant [45]. On the other hand, there are studies that indicate that the appropriate choice of the power parameter value is more important than including the elevation as explanatory data [11]. Therefore, when applying the rainfall data into a semi-distributed model, it was decided not to include this parameter, as it would be more reliable to investigate it in a fully-distributed model that takes into account spatially distributed information on the elevation.
2.4.3. Polynomial Interpolation
Spatial interpolation with the use of polynomial interpolation consists of matching the equation coefficients describing the spatial variability of precipitation so that the approximation error is as low as possible [46]. The most commonly used are first- and second-degree polynomials expressed successively as [14,46]:
where: —location not covered by the measurement, X and Y—geographical coordinates of locations with unknown precipitation height, a1–a6—regression function coefficients.
The least-square method is commonly used to determine the regression coefficients found in Equations (5) and (6). Polynomial interpolation allows accurate estimation of values at nodal points, whereas between them it can lead to the generation of values that have no physical justification [46]. Examples of the use of precipitation fields created by the means of polynomial interpolation can be found in numerous works [47,48]. When the number of rain gauge location is small, like in the case of the study area, the second-degree polynomial interpolation leads to large errors and unrealistic results [14]. Therefore, the first-degree interpolation was used in this work.
3. Results and Discussion
3.1. Impact of the Grid Resolution on the IDW Method
Figure 3 presents the comparison of observed and simulated discharge for the calibration events from 2014–2016. All of the simulations were performed at hourly time steps. The results of the evaluation criteria are shown in Table 3.
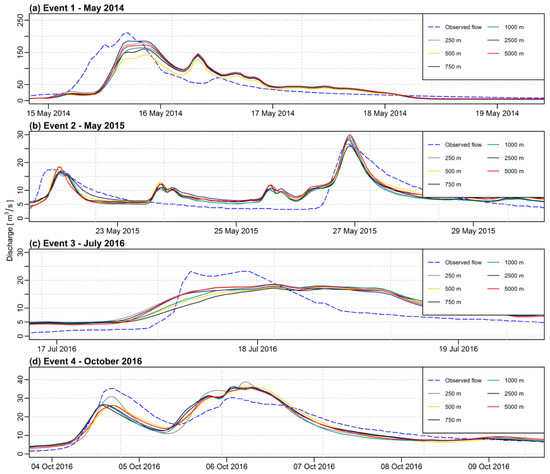
Figure 3.
Comparison of observed and simulated hydrographs using different grid sizes and inverse distance weighting (IDW) (inverse distance power (IDP) = 2.0) as an interpolation method for the calibration events (a) Event 1: May 2014, (b) Event 2: May 2015, (c) Event 3: July 2016, (d) Event 4: October 2016.

Table 3.
The results of the evaluation criteria for the calibration events using different grids sizes and IDW (IDP = 2.0) as an interpolation method.
Figure 4 shows the comparison of observed and simulated discharge for the validation events from 2017–2019. All of the simulations were performed at hourly time steps. The results of the evaluation criteria are presented in Table 4.
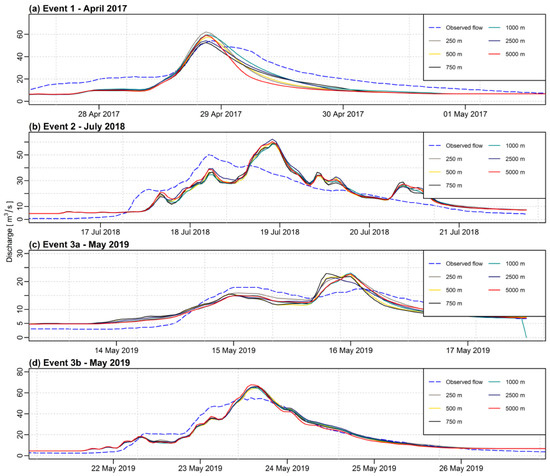
Figure 4.
Comparison of observed and simulated hydrographs using different grid sizes and IDW (IDP = 2.0) as an interpolation method for the validation events (a) Event 1: April 2017, (b) Event 2: July 2018, (c) Event 3a: May 2019, (d) Event 3b: May 2019.

Table 4.
The results of the evaluation criteria for the validation events using different grids sizes and IDW (IDP = 2.0) as an interpolation method.
Considering both the calibration and validation results, it can be noticed that in most of the cases the least satisfactory results were obtained when using 750 m and 1000 m interpolation grid. Results for the grids 250 m and 500 m are similar. Very good results were observed when using 2500 m resolution grid, and in most of the cases, they are much better than the grid of lower resolution—5000 m. Taking into consideration the following results, only the grids of 250 m and 2500 m were chosen for further investigation regarding the impact of IDP value on interpolation results.
Figure A1, presented in Appendix A, provides exemplary visualizations of precipitation fields applied in the shown above hydrological modeling.
3.2. Impact of the IDP Value on the IDW Method
The next step, after analyzing the impact of grid size on the interpolation outputs, was an investigation of the impact of the value of IDP on the IDW interpolation results. As mentioned in Section 2.4.2, three values of the p parameter were chosen for the analysis 0.5, 2, and 5. All simulations were performed at hourly time-steps. Figure 5 presents the comparison of observed and simulated discharge for the calibration events from 2014–2016. All of the simulations were performed at hourly time steps. The results of evaluation criteria for the calibration events are shown in Table 5.
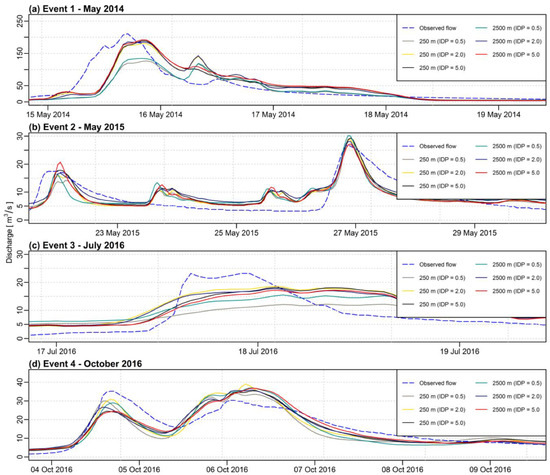
Figure 5.
Comparison of observed and simulated hydrographs using two grid sizes (250 m and 2500 m) and three IDW (IDP = 0.5, 2.0, 5.0) as an interpolation method for the calibration events (a) Event 1: May 2014, (b) Event 2: May 2015, (c) Event 3: July 2016, (d) Event 4: October 2016.

Table 5.
The results of the evaluation criteria for the calibration events using two grid sizes (250 m and 2500 m) and three IDW (IDP = 0.5, 2.0, 5.0) as an interpolation method.
Figure 6 shows the comparison of observed and simulated discharge for the validation events from 2017–2019. All of the simulations were performed at hourly time steps. The results of the evaluation criteria are presented in Table 6.
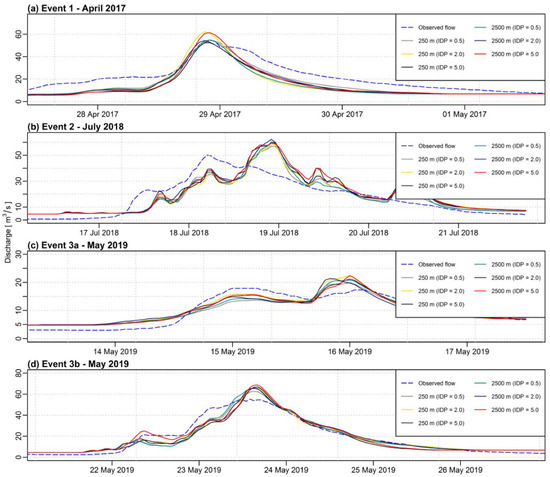
Figure 6.
Comparison of observed and simulated hydrographs using two grid sizes (250 m and 2500 m) and three IDW (IDP = 0.5, 2.0, 5.0) as an interpolation method for the validation events (a) Event 1: April 2017, (b) Event 2: July 2018, (c) Event 3a: May 2019, (d) Event 3b: May 2019.

Table 6.
The results of the evaluation criteria for the validation events using two grid sizes (250 m and 2500 m) and three IDW (IDP = 0.5, 2.0, 5.0) as an interpolation method.
Analyzing the calibration results we can observe that the best results were obtained for the highest value of IDP (equal to 5.0) and the worst for the smallest one (equal to 0.5). The results for traditionally applied IDP value, equal to 2.0, are somewhere in between the other two. As for the validation, the best results were obtained when using precipitation field interpolated with IDP equal to 0.5, but it must be highlighted that the differences in comparison with the other two investigated IDP values are not significant. In two cases out of two, different values of IDP than 2.0 generated better results.
Figure A2, presented in Appendix A, provides exemplary visualizations of precipitation fields applied in the shown above hydrological modeling.
3.3. Impact of the Grid Resolution on the Polynomial Interpolation
As argued in Section 2.4.3, the first-degree polynomial interpolation was performed to produce precipitation fields. Similarly, like for the IDW method, the impact of grid resolution in the interpolation results was investigated. All simulations were performed at hourly time-steps. Figure 7 presents the comparison of observed and simulated discharge for the calibration events from 2014–2016. The results of evaluation criteria for the calibration events are shown in Table 7.
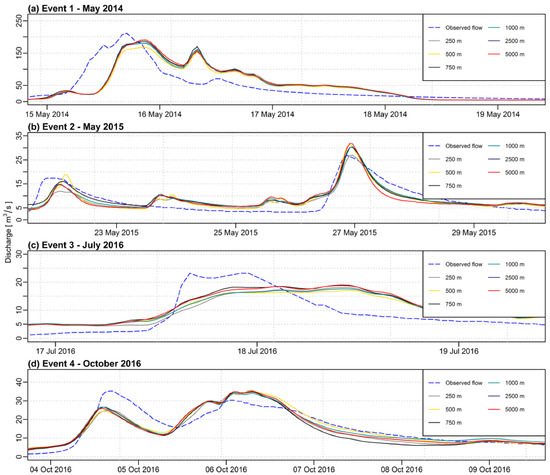
Figure 7.
Comparison of observed and simulated hydrographs using different grid sizes and first-degree polynomial as an interpolation method for the calibration events (a) Event 1: May 2014, (b) Event 2: May 2015, (c) Event 3: July 2016, (d) Event 4: October 2016.

Table 7.
The results of the evaluation criteria for the validation events using different grids sizes and first-degree polynomial as an interpolation method.
Figure 8 Reference source not found. shows the comparison of observed and simulated discharge for the validation events from 2017–2019. All of the simulations were performed at hourly time steps. The results of evaluation criteria are presented in Table 8.
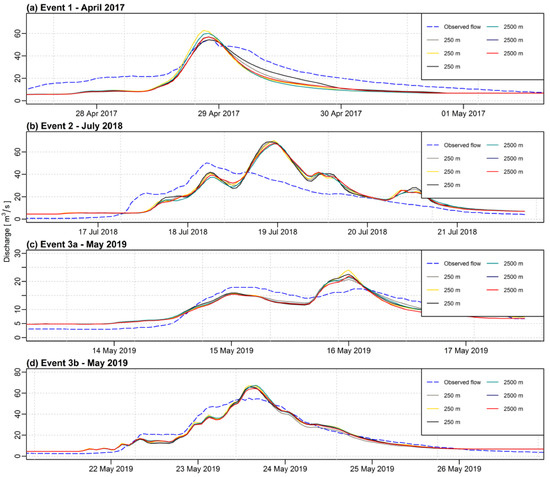
Figure 8.
Comparison of observed and simulated hydrographs using different grid sizes and first-degree polynomial as an interpolation method for the validation events (a) Event 1: April 2017, (b) Event 2: July 2018, (c) Event 3a: May 2019, (d) Event 3b: May 2019.

Table 8.
The results of the evaluation criteria for the validation events using different grids sizes and first-degree polynomial as an interpolation method.
The results for the calibration phase are similar between the different interpolation grids. However, it can be noticed that higher grid resolutions (500 m and 750 m) slightly outperform the lower ones (1000 m, 2500 m, and 5000 m). The same pattern can be found for the validation of the hydrological model. For this phase in most of the cases, the best results were obtained when the grid resolution ranged from 250 m to 750 m.
Figure A3, presented in Appendix A, provides exemplary visualizations of precipitation fields applied in the shown above hydrological modeling.
4. Summary and Conclusions
This paper presents a comprehensive investigation of the impact of deterministic interpolation methods of precipitation on rainfall-runoff modeling in a small mountainous catchment characterized by a quick time of response. When the number of rainfall stations is limited and too small to prevent the use of any geostatistical method, the deterministic methods are the only option. However, spatial interpolation of precipitation over a sparsely gauged mountainous catchment is particularly challenging. The performance of spatial interpolation of precipitation obtained using the inverse distance weighting and first-degree polynomial interpolation method was evaluated via the semi-distributed rainfall-runoff model. Furthermore, the impact of the grid resolution during the interpolation process was investigated for 6 grid sizes (ranging from 250 m to 5000 m). The impact of the IDP value in the IDW interpolation was also analyzed.
When using a semi-distributed hydrological model, the aspect of the grid resolution used for the preparation of precipitation data is often neglected. This study shows that for different interpolation methods, the grid resolutions have a significant impact on the outputs of hydrological modeling.
The following conclusions can be drawn from the analysis outcomes:
- When analyzing Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, it must be noticed that the curves for various sizes of the grid and different IDP values for the IDW method are very correlated when compared to the curve of the observed flow. Therefore, the choice of a different grid size (or IDP for the IDW method) does not change much the picture with respect to the observed discharge. However, when looking at the data more precisely with statistical analysis, some differences can be detected.
- The impact of the grid resolution is more visible for the IDW method than for the first-degree polynomial interpolation. As for the IDW method, the maximum difference for the NSE criterion is 0.26 for both, calibration, and validation phases. For the first-degree polynomial method, the maximum differences for the NSE are 0.12 and 0.16, respectively. As the IDW method is frequently used in hydrological applications, the appropriate choice of the interpolation grid is of particular importance.
- Among the analyzed grid resolutions, the best results for the IDW method were obtained for the grids of 250 m and 2500 m (average values of the NSE were 0.62 and 0.65 for the calibration and 0.74 and 0.76 for the validation respectively). For the first-degree polynomial method, higher grid resolutions (smaller or equal to 750 m) outperformed the lower ones (greater or equal to 1000 m). The mean value of the NSE for the calibration phase for grids up to 750 m was 0.63 and 0.67 for validation. As for the lower resolution grids, the results were 0.60 and 0.65 consecutively.
- The applied value of the IDP in the IDW method has a significant impact on the outputs of hydrological modeling. In most of the cases, more accurate results were obtained using different values of IDP than traditionally applied value equal to 2.0. Therefore, the choice of the appropriate IDP value when using a semi-distributed hydrological model cannot be neglected and should be taken into account.
- The IDP value in the IDW interpolation method has more impact on the simulation results than the grid size. That can be clearly seen when comparing the results presented in Table 6.
- Within the analyzed deterministic interpolation methods, slightly better results were obtained for the first-degree interpolation method than for the IDW interpolation considering the results of the evaluation criteria presented in Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8. Tobin et al. [39] reported that the IDW method tends to significantly underestimate rainfall volume, but this study shows that when using the right grid size and appropriate IDP value, this method can also be effective. It should also be noted (Figure A3) that the first-degree polynomial method can lead to significant underestimation of precipitation over relatively large areas (horizontal), especially when using low-resolution grids.
- For small mountainous catchments, the best data source on the precipitation field would be rain gauge data interpolated using the first-degree interpolation method and grid size smaller or equal to 750 m. This method, unlike the IDW, is more straightforward in application, and does not require subjective investigation of the method’s parameters (the IDP value in the IDW interpolation method).
- Kling-Gupta efficiency (KGE), which is considered as one of the alternatives to the Nash-Sutcliffe efficiency (NSE), generally tends to provide higher and less varied values, which makes it less useful for the evaluation of the results.
For future works, it will be interesting to investigate whether incorporating other environmental variables or covariates into the precipitation modeling process will lead to better simulation results when using a semi-distributed hydrological model. Apart from that, it would be worth considering other factors during the interpolation process, such as the density of meteorological stations or drainage area. Better simulation results might be obtained when performing validation of the precipitation field before its application into the hydrological model.
Author Contributions
Conceptualization, P.G. and P.G.; methodology, P.G.; software, P.G.; validation, P.G., P.G. and P.G.; formal analysis, P.G.; investigation, P.G.; resources, P.G.; data curation, P.G.; writing—original draft preparation, P.G.; writing—review and editing, P.G.; visualization, P.G.; supervision, P.G.; project administration, P.G.; funding acquisition, P.G. The author have read and agreed to the published version of the manuscript.
Funding
This research was paid via discount vouchers for reviews provided by the author for Multidisciplinary Digital Publishing Institute.
Data Availability Statement
Data available on request due to privacy restrictions when using the data provided by the Institute of Meteorology and Water Management National Research Institute.
Acknowledgments
In memory of my PhD supervisor, Professor Marek Nawalany, who passed away in May 2020 just a few weeks before I have finished the PhD thesis.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The appendix contains visualizations of the precipitation fields obtained using the investigated interpolation methods (inverse distance weighting, and first-degree polynomial). The data used for the visualizations are the 1-h precipitation accumulation for 4 July 2014, 18:00. At that time, all of the rain gauges available close to the study area registered measurement of precipitation greater than 0 mm. Figure A1 refers to Section 3.1, Figure A2 refers to Section 3.2, and Figure A3 refers to Section 3.3.
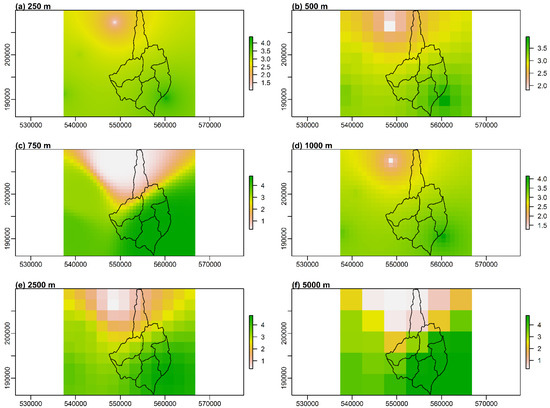
Figure A1.
Comparison of precipitation fields obtained using the Inverse Distance Weighting interpolation method (IDP = 2.0) for different grid sizes: (a) 250 m, (b) 500 m, (c) 750 m, (d) 1000 m, (e) 2500 m, (f) 5000 m.
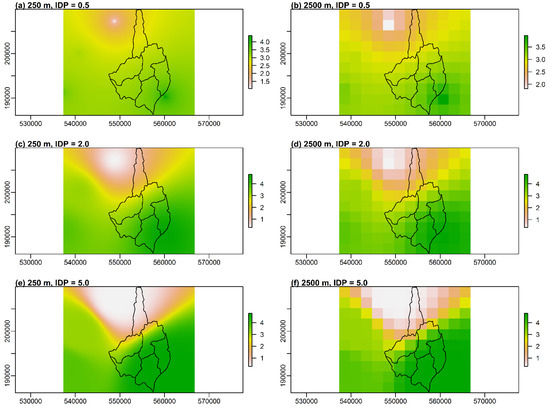
Figure A2.
Comparison of precipitation fields obtained using the Inverse Distance Weighting interpolation method and a grid size of 250 m: (a,c,e) and 2500 m: (b,d,f) for the IDP values of 0.5, 2.0, and 5.0 consecutively.
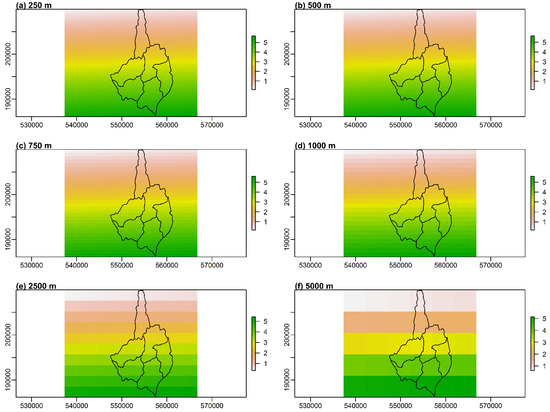
Figure A3.
Comparison of precipitation fields obtained using the first-degree polynomial as an interpolation method for different grid sizes: (a) 250 m, (b) 500 m, (c) 750 m, (d) 1000 m, (e) 2500 m, (f) 5000 m.
References
- Cheng, M.; Wang, Y.; Engel, B.; Zhang, W.; Peng, H.; Chen, X.; Xia, H.; Cheng, M.; Wang, Y.; Engel, B.; et al. Performance Assessment of Spatial Interpolation of Precipitation for Hydrological Process Simulation in the Three Gorges Basin. Water 2017, 9, 838. [Google Scholar] [CrossRef]
- Caracciolo, D.; Arnone, E.; Noto, L.V. Influence of Spatial Precipitation Sampling on Hydrological Response at the Catchment Scale. J. Hydrol. Eng. 2014, 19, 544–553. [Google Scholar] [CrossRef]
- Price, K.; Purucker, S.T.; Kraemer, S.R.; Babendreier, J.E.; Knightes, C.D. Comparison of radar and gauge precipitation data in watershed models across varying spatial and temporal scales. Hydrol. Process. 2014, 28, 3505–3520. [Google Scholar] [CrossRef]
- Chen, T.; Ren, L.; Yuan, F.; Yang, X.; Jiang, S.; Tang, T.; Liu, Y.; Zhao, C.; Zhang, L. Comparison of spatial interpolation schemes for rainfall data and application in hydrological modeling. Water 2017, 9, 342. [Google Scholar] [CrossRef]
- Bell, V.A.; Moore, R.J. The sensitivity of catchment runoff models to rainfall data at different spatial scales. Hydrol. Earth Syst. Sci. 2000, 4, 653–667. [Google Scholar] [CrossRef]
- Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inform. 2011, 6, 228–241. [Google Scholar] [CrossRef]
- Gabella, M.; Speirs, P.; Hamann, U.; Germann, U.; Berne, A. Measurement of precipitation in the alps using dual-polarization C-Band ground-based radars, the GPMSpaceborne Ku-Band Radar, and rain gauges. Remote Sens. 2017, 9, 1147. [Google Scholar] [CrossRef]
- Kitchen, M.; Blackall, R.M. Representativeness errors in comparisons between radar and gauge measurements of rainfall. J. Hydrol. 1992. [Google Scholar] [CrossRef]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Herrera, S.; Kotlarski, S.; Soares, P.M.M.; Cardoso, R.M.; Jaczewski, A.; Gutiérrez, J.M.; Maraun, D. Uncertainty in gridded precipitation products: Influence of station density, interpolation method and grid resolution. Int. J. Climatol. 2019, 39, 3717–3729. [Google Scholar] [CrossRef]
- Kurtzman, D.; Navon, S.; Morin, E. Improving interpolation of daily precipitation for hydrologic modelling: Spatial patterns of preferred interpolators. Hydrol. Process. 2009, 23, 3281–3291. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degré, A. Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: A review. Biotechnol. Agron. Soc. Environ. 2013, 17, 392–406. [Google Scholar]
- Zareian, M.J.; Eslamian, S.; Safavi, H.R. A modified regionalization weighting approach for climate change impact assessment at watershed scale. Theor. Appl. Climatol. 2015, 122, 497–516. [Google Scholar] [CrossRef]
- Gilewski, P. Sensitivity of the Catchment Outflow in a Mountainous Region Modeled with the Rainfall-Runoff Hydrological 529 Model to the Spatial-Temporal Distribution of Precipitation. Ph.D. Thesis, Warsaw University of Technology, Warsaw, Poland, 2020. (In Polish). [Google Scholar]
- Wang, S.; Huang, G.H.; Lin, Q.G.; Li, Z.; Zhang, H.; Fan, Y.R. Comparison of interpolation methods for estimating spatial distribution of precipitation in Ontario, Canada. Int. J. Climatol. 2014, 34, 3745–3751. [Google Scholar] [CrossRef]
- Foehn, A.; García Hernández, J.; Schaefli, B.; De Cesare, G. Spatial interpolation of precipitation from multiple rain gauge networks and weather radar data for operational applications in Alpine catchments. J. Hydrol. 2018. [Google Scholar] [CrossRef]
- Simanton, J.; Osborn, H. Reciprocal-Distance Estimate of Point Rainfall. J. Hydraul. Div. 1980, 106, 1242–1246. [Google Scholar]
- Tung, Y. Point Rainfall Estimation for a Mountainous Region. J. Hydraul. Eng. 1983. [Google Scholar] [CrossRef]
- Chen, F.-W.; Liu, C.-W. Estimation of the spatial rainfall distribution using inverse distance weighting (IDW) in the middle of Taiwan. Paddy Water Environ. 2012, 10, 209–222. [Google Scholar] [CrossRef]
- Wu, J.; Zheng, C.; Chien, C.C. Cost-effective sampling network design for contaminant plume monitoring under general hydrogeological conditions. J. Contam. Hydrol. 2005, 77, 41–65. [Google Scholar] [CrossRef]
- Malvić, T.; Ivšinović, J.; Velić, J.; Rajić, R. Interpolation of small datasets in the sandstone hydrocarbon reservoirs, case study of the sava depression, Croatia. Geosciences 2019, 9, 201. [Google Scholar] [CrossRef]
- Punzet, J. Hydrology of the Skawa river basin. Wiad. Sluz. Hydr. Meteo. 1994, 3–4, 29–40. [Google Scholar]
- Franczak, P. Rola wielkich wezbrań powodziowych w kształtowaniu życia ludności w zlewni górnej Skawy od XV wieku The role of major floods in shaping the life of the population in the catchment area of the upper Skawa River since the 15 th century. Wspolczesne Probl. Kierun. Badaw. Geogr. 2014, 2, 117–129. [Google Scholar]
- Bronstert, A. Rainfall-runoff modelling for assessing impacts of climate and land-use change. Hydrol. Process. 2004, 18, 567–570. [Google Scholar] [CrossRef]
- Witkowski, K. Evolution of the lower Skawa river bed in regard to hydrotechnical buildings. Acta Sci. Pol. Form. Circumiectus 2015, 14. [Google Scholar] [CrossRef]
- Gilewski, P.; Nawalany, M. Inter-Comparison of Rain-Gauge, Radar, and Satellite (IMERG GPM) Precipitation Estimates Performance for Rainfall-Runoff Modeling in a Mountainous Catchment in Poland. Water 2018, 10, 1665. [Google Scholar] [CrossRef]
- Szturc, J.; Jurczyk, A.; Ośródka, K.; Wyszogrodzki, A.; Giszterowicz, M. Precipitation estimation and nowcasting at IMGW-PIB ( SEiNO system ). Meteorol. Hydrol. Water Manag. Res. Oper. Appl. 2017, 6, 1–10. [Google Scholar] [CrossRef]
- Gilewski, P.; Węglarz, A. Impact of land-cover change related urbanization on surface runoff estimation. In Proceedings of the MATEC Web of Conferences, Lille, France, 8–10 October 2018; Volume 196, pp. 1–6. [Google Scholar]
- Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M.; et al. The Community Climate System Model Version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
- Kirchner, J.W. Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resour. Res. 2009, 45, 1–34. [Google Scholar] [CrossRef]
- Koster, R.D.; Mahanama, S.P.; Koster, R.D.; Mahanama, S.P.P. Land Surface Controls on Hydroclimatic Means and Variability. J. Hydrometeorol. 2012, 13, 1604–1620. [Google Scholar] [CrossRef]
- Orth, R.; Staudinger, M.; Seneviratne, S.I.; Seibert, J.; Zappa, M. Does model performance improve with complexity? A case study with three hydrological models. J. Hydrol. 2015, 523, 147–159. [Google Scholar] [CrossRef]
- Pina, R.D.; Ochoa-Rodriguez, S.; Simões, N.E.; Mijic, A.; Marques, A.S.; Maksimović, Č. Semi- vs. Fully-distributed urban stormwater models: Model set up and comparison with two real case studies. Water 2016, 8, 58. [Google Scholar] [CrossRef]
- Zhang, H.L.; Wang, Y.J.; Wang, Y.Q.; Li, D.X.; Wang, X.K. Quantitative comparison of semi- and fully-distributed hydrologic models in simulating flood hydrographs on a mountain watershed in southwest China. J. Hydrodyn. 2013, 25, 877–885. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.; Kling, H.; Yilmaz, K.; Martinez, G. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Knoben, W.; Freer, J.; Woods, R. Technical note: Inherent benchmark or not? Comparing Nash—Sutcliffe and Kling—Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Fang, G.; Yuan, Y.; Gao, Y.; Huang, X.; Guo, Y. Assessing the Effects of Urbanization on Flood Events with Urban Agglomeration Polders Type of Flood Control Pattern Using the HEC-HMS Model in the Qinhuai River Basin, China. Water 2018, 10, 1003. [Google Scholar] [CrossRef]
- Tobin, C.; Nicotina, L.; Parlange, M.B.; Berne, A.; Rinaldo, A. Improved interpolation of meteorological forcings for hydrologic applications in a Swiss Alpine region. J. Hydrol. 2011, 401, 77–89. [Google Scholar] [CrossRef]
- Shepard, D. Two-dimensional interpolation function for irregularly-spaced data. In Proceedings of the 1968 23rd ACM national Conference, New York, NY, USA, 27–29 August 1968; pp. 517–524. [Google Scholar]
- Garcia, M.; Peters-Lidard, C.D.; Goodrich, D.C. Spatial interpolation of precipitation in a dense gauge network for monsoon storm events in the southwestern United States. Water Resour. Res. 2008, 44, 1–14. [Google Scholar] [CrossRef]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008. [Google Scholar] [CrossRef]
- Ruelland, D.; Ardoin-Bardin, S.; Billen, G.; Servat, E. Sensitivity of a lumped and semi-distributed hydrological model to several methods of rainfall interpolation on a large basin in West Africa. J. Hydrol. 2008, 361, 96–117. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, L.; Liao, Q.; Liu, R.; Hong, Q. Impact of spatial rainfall variability on hydrology and nonpoint source pollution modeling. J. Hydrol. 2012, 472, 205–215. [Google Scholar] [CrossRef]
- Masih, I.; Maskey, S.; Uhlenbrook, S.; Smakhtin, V. Assessing the Impact of Areal Precipitation Input on Streamflow Simulations Using the SWAT Model. J. Am. Water Resour. Assoc. 2011. [Google Scholar] [CrossRef]
- Szczepanek, R. Spatio-Temporal Structre of Precipitation in Mountainous Catchment. Ph.D. Thesis, Cracow 592 University of Technology, Kraków, Poland, 2003. (In Polish). [Google Scholar]
- Basistha, A.; Arya, D.S.; Goel, N.K. Spatial Distribution of Rainfall in Indian Himalayas—A Case Study of Uttarakhand Region. Water Resour. Manag. 2008, 22, 1325–1346. [Google Scholar] [CrossRef]
- Gentilucci, M.; Bisci, C.; Burt, P.; Fazzini, M.; Vaccaro, C. Interpolation of Rainfall Through Polynomial Regression in the Marche Region (Central Italy). In Proceedings of the Annual International Conference on Geographic Information Science, Lund, Sweden, 12–15 June 2018; Springer: Cham, Swizerland, 2018; pp. 55–73. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).