Abstract
We confirm that energy dissipation weighting provides the most accurate approach to determining the effective hydraulic conductivity (Keff) of a binary K grid. A deep learning algorithm (UNET) can infer Keff with extremely high accuracy (R2 > 0.99). The UNET architecture could be trained to infer the energy dissipation weighting pattern from an image of the K distribution, although it was less accurate for cases with highly localized structures that controlled flow. Furthermore, the UNET architecture learned to infer the energy dissipation weighting even if it was not trained directly on this information. However, the weights were represented within the UNET in a way that was not immediately interpretable by a human user. This reiterates the idea that even if ML/DL algorithms are trained to make some hydrologic predictions accurately, they must be designed and trained to provide each user-required output if their results are to be used to improve our understanding of hydrologic systems.
1. Introduction
Numerical modeling is fundamental to understanding hydrologic systems and to predicting outcomes to be used for water resources management and groundwater contaminant remediation [1,2,3,4,5]. Water movement through the subsurface is controlled largely by the hydraulic conductivity distribution, which can vary over orders of magnitude across multiple scales [5].
Recent advances in hydrogeophysics increasingly suggest that the spatial pattern of hydraulic conductivity can be mapped effectively [6,7,8,9]. Coupled with carefully selected point measurements of hydraulic conductivity, these methods offer the promise of real improvements in our ability to accurately model water flow and associated solute transport in the subsurface. One remaining fundamental challenge is how to translate an image of a spatially heterogeneous K field to an upscaled, effective K for use in a flow model. The challenge of upscaling is critical to understanding how heterogeneous systems respond to applied stress, incorporating point measurements in relatively coarsely discretized models, and understanding whether the inherent spatial averaging of geophysical methods can provide useful estimates of upscaled hydrologic properties. In this study, we examine whether machine learning tools can provide insight into the problem of hydraulic conductivity upscaling.
There is a rich body of literature on the upscaling of hydraulic conductivity. Wen and Hernandez [10] categorized upscaling techniques as being either local or non-local. Local techniques, which include simple averaging, power averaging, renormalization, and percolation theory, are based on the assumption that effective upscaled conductivity depends only on the statistical distribution of media of different conductivities contained within the medium. Non-local techniques, which include inverse modeling and energy dissipation, also consider how boundary conditions and the local and larger structures of the K field affect flow.
Local methods based on simple or power averaging [11,12,13,14,15,16] typically represent the domain in terms of fractions, each having a single conductivity, and exponentially weigh the conductivity of each fraction by the percent area or volume that it occupies. The extreme cases of arithmetic weighting (exponent of 1, conceptually representing flow in parallel) and harmonic weighting (exponent of −1, conceptually representing flow in series) bound these approaches [17]. In general, local approaches work well provided that the spatial distributions of the fractions are not organized into patterns, giving rise to structure [18]. For any specific case, the value of the exponent can be estimated by running a flow model [19,20], but this requires the extra step of running the flow model to determine the effective conductivity, which is often counter to the intended purpose of the upscaling effort.
The renormalization method to compute block conductivity (Keff) is based on upscaling by a recursive calculation whereby the extent of each grid unit is doubled along each direction at each step [21,22]. This approach essentially allows for the use of arithmetic and harmonic averaging at the local scale, thereby simplifying the computation of effective conductivity. However, while the method is very fast and efficient, severe errors can occur in the final estimates at the scale of the largest blocks due to unrealistic boundary representations during the recursive upscaling process [23]. Further, as with the exponential approach, the renormalization method is only applicable to statistically isotropic, lognormal conductivity fields having no clear structure [19,24].
A significant advancement in the upscaling of K for binary media was achieved by the introduction of percolation theory, proposed by Vinay Ambegaokar et al. [25] to model electron hopping in semiconductors. The percolation concept was applied to hydrogeology to compute the Keff of a medium characterized by a strong contrast between low and high conductivities, with the assumption that the upscaled value of conductivity is primarily a consequence of flows through connected high permeability pathways, when they exist [6,25,26]. Subsequent studies in which percolation theory was used to assess Keff [27,28,29] have generally found that percolation theory is appropriate when the proportion of the high conductivity medium is close to the percolation transition threshold [20].
Non-local methods can be used to infer effective values for system parameters via inverse modeling, wherein the parameter field is constrained to be homogenous, and the corresponding best-fit equivalent upscaled parameter value is determined. Several recent studies [30,31,32,33] have used this technique for vadose zone parameter estimation. However, this approach requires solving the flow problem for specified boundary conditions. In many cases, this is counter to the objective of upscaling, which is aimed at producing effective parameters for use in a coarsely gridded flow model without requiring solution of the flow problem for a highly resolved grid. As a result, these approaches can be very computationally demanding [34]. Further, Lai and Ren [35] have shown that this approach can provide imperfect results; e.g., they showed that three different inverse approaches applied to a one-dimensional problem resulted in models that were unable to reproduce the average soil water content profile.
The most direct approach to determining how spatially variable averaging of hydraulic conductivities occurs during flow is through energy dissipation analysis. This inverse approach is largely limited to steady-state problems and requires solving the flow problem to determine the effective upscaled parameter value. In essence, the energy dissipation approach defines the energy required to force the fluid through each block of the porous medium; this value is normalized for the shape of the domain and the boundary conditions, and then can be used to define the spatial distribution of weights to be applied to the local conductivity values when upscaling to determine Keff. In this regard, Knight [36] and Indelman and Dagan [37] suggested that Keff can be determined from a grid of cells by assuming that dissipated energy must be preserved during the equivalent block conductivity computation.
Although the energy dissipation approach is computationally demanding and requires that the flow problem be solved for both the homogeneous and heterogeneous case, it has been found to be the most accurate and mathematically rigorous way to upscale conductivity for steady-state problems [20]. Further, it can provide significant insight into the specific locations that contribute most to the upscaled value of Keff. That is, the local K values in those areas within which most energy is dissipated contribute most to Keff. This approach is general, not limited to hydrologic problems. For example, Ferre et al. [38] used energy dissipation to define the sample area of time domain reflectometry probes, showing that relatively small areas of the domain contribute disproportionately to TDR-measured water content.
Recently, emergence of data-driven approaches has shown promising results in hydrogeology. Reviews of several studies in the context of estimating effective parameter values (e.g., [39,40,41,42]) indicate that data-driven approaches are efficient and can even outperform stochastic modeling or local (i.e., structure-based) techniques. For example, the architecture underlying convolutional neural networks (CNNs) allows for the preservation of spatial structure and correlation information, and we might therefore expect that the CNN approach may be particularly suitable for problems involving gridded inputs, such as hydraulic conductivity fields [2,40,43,44]. In the context of effective subsurface parameter estimation, the accuracy of CNN-based approaches can be attributed to the fact that, unlike classic stochastic approaches that only consider the first and second statistical moments of a highly spatially variant media, machine learning approaches can account for spatial patterns that are not explicitly characterized by those statistical moments or by classical structure-based models. Some recent examples include: Zhou et al. [44], who used a CNN to map conductivity fields to macro-dispersivity; Wu et al. [45] combined images of porous media with integral quantities of porosity and specific surface area to estimate pore-scale permeability, and Mo et al. [40] parameterized a non-Gaussian conductivity field using a convolutional adversarial autoencoder as well as proposing a deep residual dense CNN to map spatially distributed conductivity to head and solute concentration for 2D and 3D media.
Despite their impressive predictive power, DL-based models can suffer from a lack of interpretability [46,47]. Most studies have mapped from measured inputs to outputs without consideration of the underlying physical processes involved [44,45,48,49]. Consequently, several studies have attempted to incorporate physical constraints into DL algorithms. For example, Wang et al. [41] used a knowledge-based neural network to estimate head distribution by taking into consideration the residuals of the governing equations, boundary conditions, and expert knowledge when formulating the loss function used to train the model. Tartakovsky et al. [42] incorporated governing flow partial differential equation constraints (the Darcy and Richards equations) along with training data into a DL algorithm to infer the hydraulic conductivity map based on sparse observations of head and conductivity during saturated flow through a heterogeneous medium and to infer the constitutive pressure-conductivity relationship from observations of capillary pressures during unsaturated flow. Previous hydrology-relevant investigations of DL represent clear advances in the inclusion of expert knowledge in loss function design of a DL algorithm. However, to date, little attention has been paid to the design of the underlying ML/DL architecture as an alternative to, or complement for, including physical process constraints in loss function. In particular, we found no publications addressing the problem of how the ML/DL approach extracts and uses information from the heterogeneous field in the process of inferring Keff. Here, we make use of recently developed approaches that facilitate comparing the activation patterns of different DL models [50] to examine how these DL tools extract and use the knowledge that is relevant to the process of upscaling (i.e., energy dissipation weighting). To our knowledge, this is a first attempt to include knowledge about the system to design a DL architecture for hydrogeologic upscaling.
In summary, this study has two primary objectives. The first is to examine the potential for a specific type of CNN, an image-to-image translation algorithm known as UNET, to infer the effective hydraulic conductivities of two-dimensional binary conductivity fields. Conceptually, these binary fields can be viewed as simplifications of bimodal K fields that can result from coastal or riverine depositional processes or fracturing in low permeability media [51]. Often [20,52], the spatial distribution of conductivity is modeled as a random field with a given statistical distribution and a known covariance function. While these assumptions and simplifications can be useful for stochastic modeling efforts, we chose to examine a more general case: a random binary field without any assumptions regarding structure. This approach includes fields with spatial correlation, but is not limited to them. We then used DL to infer Keff in two modes: with and without energy dissipation weighting information provided. The second objective is to understand whether UNET learns to use energy dissipation weighting as an intermediate step for inferring Keff if those weights are not provided. That is, we first compared the ability of a UNET to infer Keff from a binary K grid when trained on both the K grid and the energy dissipation weighting, and when trained only on the K grid. Then, we examined the trained weights within the UNET trained only on the K grid to examine how it processes information. Based on this examination, we drew conclusions on whether the UNET is learning the energy dissipation weighting independently.
2. Methodology
We examined the effect of the structure of a binary medium on the effective hydraulic conductivity, Keff, using MODFLOW, a well-known finite difference numerical groundwater flow model. MODFLOW was used to produce the steady-state head distribution over a square grid with a 1-D applied gradient. That is, the left and right boundaries each had applied constant head values (Type I, Dirichlet) and the top and bottom boundaries were no flow (Type II, Neumann). We computed the steady-state flow and then calculated Keff as the homogeneous K necessary to achieve that flow for the same boundary conditions in a 1D flow system. The local head gradient was used to define the energy dissipation weighting in each cell, which can be combined with the local K values to determine Keff.
2.1. Flow through Heterogeneous Binary Grids (Dataset Generation)
We defined 25 by 25 grid domains with no flow boundaries at the top and bottom and constant head boundaries of 2 m and 1 m on the left and right boundaries, respectively. Each cell has a length of 1 m on a side. Two media populated the grid, one had a high K (1 cm/s) and the other had a low K of 0.001 cm/s. Note that the calculations were repeated for multiple high/low conductivity values with no appreciable difference in the results. Different percentages of the high K material were considered, ranging from 1% to 99%. For each high K percent, 3,000 random distributions of the media were modeled. Figure 1 shows one example of a grid with 50% high K material.
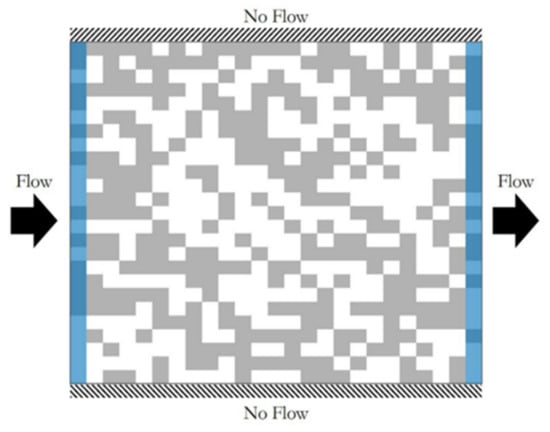
Figure 1.
Sample 25 × 25 cell grid with 50% high K (white) and 50% low K (gray) cells, constant head boundaries (blue), and no flow boundaries (diagonal hash marks). The left boundary has a constant head of 2 m and the right boundary has a constant head of 1 m, with flow occurring from left to right.
For each grid, the effective hydraulic conductivity was computed based on Darcy’s Law, Equation (1), the global gradient applied over the domain, and the calculated steady-state flow through the system. In Equation (1), Q is the flow rate [L3/T], A is cross section area [L2], and is hydraulic gradient [-]:
The convergence criterion on the head used in MODFLOW was 0.01 m. To account for small errors that persisted when the convergence criterion was met, the value of Keff was calculated based on the flow into the left boundary and the flow out of the right boundary. The resulting Keff values calculated with both of these flow rates always agreed within 1%, and the average value was used for all analyses.
2.2. Energy Dissipation Weighting Method
Conceptually, energy dissipation is defined as the energy per unit time necessary to force a fluid through a porous medium [37]. The value of Keff can be thought of as a weighted average of the spatially distributed values of K, in which the weight at each point is equal to the normalized energy dissipation of the field at that point:
In Equation (2), E is the local energy density [-] and is the total energy of field for the same boundary conditions with a homogeneous K. Note that the value of the homogeneous K does not affect the energy dissipation; this step accounts for the influence of the system geometry and boundary conditions on the energy dissipation distribution. Additionally, energy dissipations in the above equation is expressed by the following equation, in which is the gradient of potential (hydraulic head):
Therefore, energy dissipation can be used to define the spatial distribution of weighting factors at (x, y) based on the square of the gradient of the potential at that location, normalized by the sum of the square of the gradient of the potential for the same boundary conditions for a domain filled with a homogeneous medium [36]. The weighting factor at a point at (x, y) can be expressed as:
where w (x, y) is the weighting factor at point (x, y), (x, y) is the potential at each location, and is the potential distribution for the equivalent homogenous field. Combining Equations (2) and (4), Knight [36] showed that spatially variable properties (e.g., K) can be weighted to determine an upscaled property (here, Keff) as the sum of the local K weighted by the energy dissipation weighting factor over the domain, as:
In this study, the steady-state head values obtained from MODFLOW simulations were used to compute the energy dissipation distribution. As MODFLOW determines head values at the nodes and the K values are defined over the cells, the gradient and K values are not aligned. There are two approaches to compute Keff with the energy dissipation approach for these conditions. First, the gradient can be computed at each cell edge and the value of Keff at the edge can be determined based on the K value in the two neighboring cells. Second, the head values can be interpolated to the edges, allowing for gradients to be computed at the nodes, matching the locations of the K grid. Both of these approaches were tested and were found to agree within 1%; accordingly, the average of these two estimates of Keff was used for each grid for further analyses. Hereafter, the energy dissipation weights are referred to as ED weights, or simply as weights.
2.3. Estimating Keff with and without ED Weights
For a given percent of high K material, the energy dissipation distribution depends on the structure and arrangement of high K and low K cells in the domain. As a result, the K distribution and the ED weight distribution are related (but not identical) sources of information for inferring Keff. In particular, given that knowledge of energy dissipation has been shown [36,37,38] to provide valuable information regarding the weighting required to define Keff, the problem of estimating Keff from a grid of K values can be seen as a problem that has two stages. The first step is to estimate the energy dissipation weighting at each cell, and the second is to use the estimates of the spatially distributed ED weights to estimate Keff.
The power of ML and DL methods lies in their ability to learn more complex functions while providing enhanced generalization capabilities. The standard machine learning structure cannot map grids to Keff or resolve energy dissipation weightings of a grid because of their input and output formats. In contrast, DL methods, containing multiple hidden layers, provide us with both flexible input and output formats and the power to model a complex process. Hidden layers are layers of DL architecture that are located between inputs and outputs and are responsible for nonlinear transformation of the inputs. Each layer consists of several processing units (neurons). Each neuron is connected to adjacent layers with an individual weight assigned to each interlayer link. All inputs into a neuron are multiplied by their associated weight and summed to form a single output. Finally, each of these outputs is subject to a nonlinear transformation referred to as the activation function.
Recent advances in image processing have led to the development of powerful deep learning (DL) architectures. In particular, the UNET architecture [53] was developed to address problems that require consideration at multiple scales by including skip connections, which recombine information from earlier hidden layers, thereby preserving some structural information that might be lost during processing by intervening layers. UNET models are a variation of encoder-decoder algorithms, which include a contracting path (like a vanilla CNN) followed by an expanding path. The contracting path (i.e., the encoder) is responsible for capturing the context while the expanding path (i.e., the decoder) enables localization. Using encoder-decoder paths, the UNET can provide an output that has the same dimensions as the input. In our application, this property is necessary to obtain ED weights on a grid having the same size as the K grid.
To build the model, we modified and extended the UNET architecture such that it works for two tasks: inferring energy dissipation weighting and retrieving Keff from an image of the binary conductivity field. Figure 2 illustrates our proposed model. The model is composed of two sub-models, named “Energy Dissipation” and “Keff”. In this study, we proposed a modified UNET model. The architecture of the model is inspired by our physical domain knowledge, which suggests that knowledge of the energy dissipation weightings will result in improved estimation of Keff.
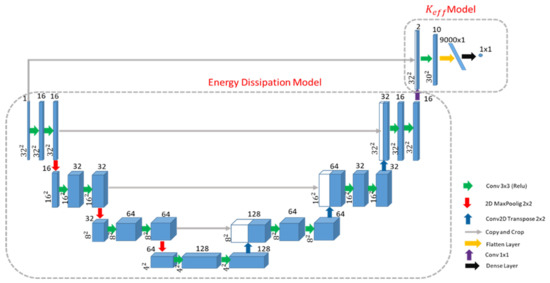
Figure 2.
Proposed U-net architecture. The architecture is composed of two sub-models. The energy dissipation model has a UNET-shaped structure followed by a CNN model to map output of the UNET to Keff. Blue boxes correspond to a multi-channel feature map. The number of channels is denoted on top of the box. The x-y size is provided at the lower left edge of the box. White boxes represent skipped connection. The arrows are operations performed on feature maps described in the legend.
We applied the UNET in two different ways to understand if and how ED weighting is used in the estimation of Keff. In the first implementation, referred to as ‘informed’, the model is trained using the freeze-training technique [54,55], in which the lower branch of the model (labeled “Energy Dissipation” on Figure 2) is first trained to estimate the spatially distributed ED weights. This is achieved by providing the K grids and the associated ED weights to the intermediate layers during training. Once partially trained, the weights of the lower branch were frozen and training was then continued by feeding only the K grid into the UNET. The trained algorithm was provided with only the K grid and it would first estimate the ED weights and then concatenate those with the K grid as input to the final fully connected layer to estimate Keff.
The second implementation of UNET is referred to as ‘uninformed’. The model structure was identical to the informed UNET, but the initial partial training step is removed. That is, the UNET was only provided the K grid information during training; it was not trained using any information about the actual ED weights. All weights in the model were fitted simultaneously during training to fit Keff.
The details of our UNET structure are provided in Appendix A (Table A1). Briefly, the contracting path is comprised of repeated blocks of two consecutive 3 × 3 convolutional kernels with rectified linear activation functions (ReLU) followed by a 2 × 2 max-pooling layer with a stride of 2 to reduce the number of parameters and diminish the next layer’s input size. On the contracting path, multilevel decomposition is applied to each layer, doubling the number of feature maps (i.e., filters) at each step. The expanding path consists of repeated blocks of transposed convolution layers with a kernel size of 2 × 2 and a stride of 2. In each block, the output of the transposed convolution layer is concatenated with the cropped feature map of the corresponding step from the encoding procedure (a skip connection). The concatenated values are subjected to two consecutive 3 × 3 convolutional kernels with ReLU activation functions. The skip connections help to recover information that may be lost by down-sampling during decoding. The cropping procedure in the concatenation ensures that the tensor extracted from the encoder will have the same size as the corresponding layer in the decoder. During decoding, the convolutional layer halves the number of channels. A final convolution layer with a kernel size of 1 x 1 and linear activation, maps the current number of channels to a single layer. A skip connection was introduced to recover information of the original grid, like the percent of high K, that may be lost when inferring the ED weights. Specifically, the inferred ED weights were concatenated with the K grid and fed through a convolutional layer and a dense, fully connected layer to estimate Keff. It should be noted that as part of preprocessing, we padded the input image to 32 × 32 to make the final output of the UNET the same as the original image.
2.4. Model Evaluation
Identical data were provided to both UNET implementations; specifically, the K grids (3000 realizations for each of 99 different percent high K values), MODFLOW-determined Keff values, and (for the informed UNETs) ED weights. The inputs and targets were divided into training, validation, and testing subsets. A random selection of 65% of the input cases were used for training and 15% were used as a validation dataset for hyperparameter tuning. The same training/validation/testing sets were used for all of the analyses reported herein. Model performance is reported using the testing data set, comprising the remaining 20% of the data. Before training, the inputs were standardized by subtracting the mean value and dividing by the standard deviation. All hyper-parameters were tuned using a grid search approach. The root mean squared error (RMSE) between the observed and model-calculated values (of Keff or ED weight) is used to assess the prediction quality of each model. The R2 value was also calculated, but it was only used to further illustrate the quality of the predictions.
2.5. Deep Learning Implementation
The deep learning architecture was implemented in Python 3.6.9 with TensorFlow V. 2.2.0 and CUDA version 10.1. Training and predictions were done on a P100 NVIDIA GPU. For both the informed and uninformed models, we used Adamax with a learning rate of 5 × 10−4 as the optimizer. Training was stopped when performance on the validation dataset stopped improving within a patience value equal to 50.
2.6. CKA and Similarity Analysis
In addition to investigating whether machine learning algorithms can be trained to predict Keff using gridded binary K information, we also wanted to determine whether these tools can infer the underlying pattern of energy dissipation in the process of inferring Keff. If it can be shown that the deep learning procedure naturally infers the spatial distribution of energy dissipation, then it would provide an example of how DL tools can learn underlying concepts. Further, because the distribution of energy dissipation indicates which parts of the medium have the largest impact on steady-state flow, the ability to make inferences regarding these patterns would also enable an understanding of the relationship between Keff and the structure of the K distribution. Such knowledge would also be valuable for understanding soil property distributions that may impact dispersion, colloid trapping/mobilization, and erosion/piping.
To investigate the ability of deep learning tools to make inferences regarding the underlying pattern of energy dissipation, we applied the UNET methodology in both informed and uninformed modes, as described above. To compare how information flowed through the UNET in the informed and uninformed modes, we examined the intermediate representations (i.e., hidden layer outputs) of each trained model. Specifically, the hidden layer outputs, known as hidden representations, characterize the “features” learned by a hidden layer of a neural network from an input (i.e., K grid), represented in a machine-readable format. Similarity measurements can be used to compare these intermediate representations between networks.
Kornblith et al. [50] showed that for a similarity index to be suitable, it should be invariant to orthogonal transformation and isotropic scaling, and not be an invertible linear transformation. We used the Hilbert–Schmidt independence criterion (HSIC) [56], which is a kernel-based statistical measure of the independence between two sets of variables:
where:
in which H is the centering matrix , 1 is the identity matrix, and are positive semidefinite kernel functions. For linear kernels, . An HSIC value of 0 implies independence. Other researchers [50,57,58] showed that HSIC can be made to be invariant to isotropic scaling by normalization. This normalized HSIC index is known as centered kernel alignment (CKA):
In this study, we used the centered kernel alignment (CKA) metric proposed by Kornblith et al. [50] with linear kernels to evaluate the similarities of layer representations in our trained networks. Specifically, we calculated the CKA between corresponding intermediate representations of the informed and uninformed networks. To assess the similarity between corresponding intermediate representations of any two models, referred to here generically as model 1 and model 2, at layer i and j, we flattened the representations and let and be the matrix of intermediate representations of model 1 and model 2 with m1 and m2 neurons for n examples. Then, we constructed the linear kernel matrices: and . Finally, we used Equation (7) to compute the CKA metric. We compared similarities for all paired combinations of layers to explore how information flowed through both networks. From this similarity, we can determine if the energy dissipation arm of the uninformed UNET was independently learning the energy dissipation weighting information without being required or instructed to do so.
3. Results
The main goal of this study was to investigate the impact that “structure” has on the effective value of hydraulic conductivity (Keff) of a binary heterogeneous medium. We examined this for multiple realizations of random fields that contain different percentages of the higher K material.
A key insight regarding this was presented by Knight [36] and Indelman and Dagan [37] who showed that the spatial distribution of energy dissipation during steady-state flow can be used to define spatially distributed weights on K that can be used to compute Keff. We first confirmed this finding for the set of binary grids examined. Then, we examined whether deep learning algorithms can predict Keff with and without information regarding the ED weights. By comparing DL algorithms trained with and without access to energy dissipation weightings’ information, we sought to understand the mechanism by which Keff is inferred by the DL.
3.1. Analysis of the Effective Hydraulic Conductivity (Keff) and High K Percentage
The steady-state flow problem, as shown in Figure 1, was solved for 3000 random realizations of a binary flow field for each high conductivity mixture ranging from 1 to 99%, for a total of 297,000 simulations. Keff was computed from the overall gradient applied over the domain and the steady-state flow through the domain. Figure 3 indicates how Keff varies as a function of the percent high K material present in the realization. The parallel (layers in the direction of flow) and series’ (layers perpendicular to flow) arrangements for each percent high K realization were calculated analytically and are shown by blue and orange color lines to place limits on the ranges that Keff values can take. The mean value of Keff for each high K percentage is shown as a solid red line.
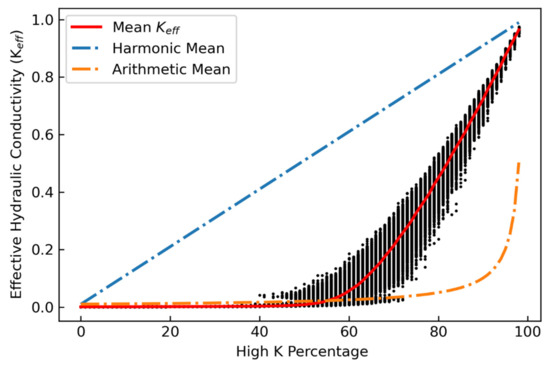
Figure 3.
Keff distribution as a function of percent high K for medium K contrast condition.
Figure 3 demonstrates the nonlinear dependence of Keff on percent high conductivity. At low percentages of high conductivity, Keff is only minimally affected by the addition of higher K material and remains approximately equal to the conductivity of the lower K material. A nonlinear transition zone is seen to occur at approximately 40 to 70% high K, and the relationship becomes approximately linear above 70%. For a given percentage of high K, the maximum variance of Keff occurs in the transition zone. These results illustrate the two related but different challenges for inferring Keff from a binary grid: predicting mean Keff as a function of the percent high K material, and predicting Keff for a specific grid given knowledge regarding the percentage of high K material present—especially in the transition zone of percent high K material.
3.2. Analysis of the Energy-Dissipation Weighting Method to Explain the Keff
Knight [36] showed that the pattern of energy dissipation weightings, calculated from the square of the gradient of the potential, can be used to determine an upscaled property like Keff. This fact is confirmed by our study (Figure 4). The energy dissipation approach can be thought of as computing a weighted average of the local K values on the grid that perfectly recovers the flow-based Keff.
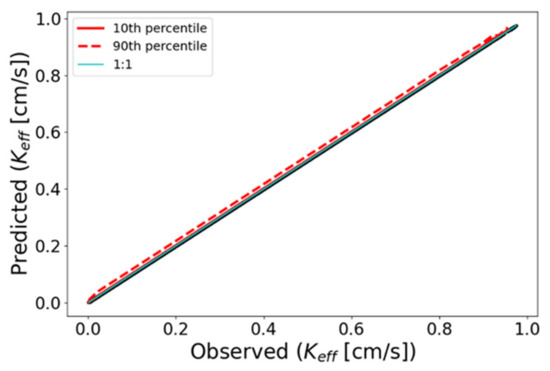
Figure 4.
Keff estimation using the energy dissipation method.
Despite the power of the energy dissipation approach, the weights are very difficult to identify visually. For example, the two grids that are shown in Figure 5A,B both have 80% high conductivity material but have strikingly different Keff values (0.53 and 0.24 cm/s, respectively). The corresponding maps of the ED weights are shown in Figure 5C,D, illustrating that the grid with the lower Keff has a much more localized pattern of ED weighting. While it might be tempting to attribute this localized weighting to the connected pattern of low K cells running vertically through Figure 5B, beyond this qualitative assessment, it is essentially impossible to visually infer the values of the ED weights from the knowledge of the spatial organization of K. Of course, both the pattern of ED weights and their values can be computed readily by solving the steady-state flow problem, but then the value of Keff can be determined directly, and knowledge of the ED weights is superfluous. Accordingly, the ED weighting approach is best seen as a method for understanding spatial organization [38] rather than a practical approach for inferring Keff from a K grid.
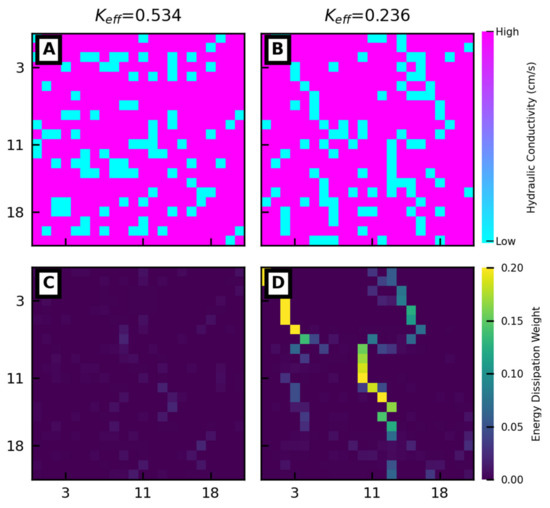
Figure 5.
Effects of structure on Keff for the structures with the same percent high conductivity: (A,B) Grid samples with percent high conductivity values of 80; (C,D) Corresponding energy dissipation weightings.
By classifying the domain into high and low weight areas, we can see that the spatial structure of high-weight areas varies systematically with the percent high conductivity material. The paired images in Figure 6A show how the fractions of high energy cells relate to the corresponding ED maps for several K grids with different percentages of high K material. Figure 6B shows the expected fraction of high energy cells as a function of the threshold used to define high weight areas. Specifically, to label the high ED weight cells in a grid, we followed the procedure of [38]. We first calculated the energy distribution after solving the steady-state head distribution with MODFLOW. The weights were sorted in descending order and a running sum was calculated from the highest local weight toward the lowest. Those cells that contributed a defined percent of total weight (shown in the legend on Figure 6B as a threshold) were identified as high energy cells. Then, the fraction of the total area of the domain that is located within these cells is determined. Following this approach, a low value of the expected fraction of high dissipation cells would indicate that most of the energy dissipation occurs in a very limited area. As shown on Figure 6B, the high energy area is restricted in a relatively small area when the high conductivity cells occupy between approximately 50 and 80% of the domain. In contrast, and as expected, if the domain is nearly homogeneous (containing >90% of either high or low K material), the areas of relatively high energy dissipation are distributed throughout the entire domain. The results are not highly sensitive to the choice of threshold, meaning that the structural interpretation of this high dissipation area is robust. Finally, Figure 6C indicates a strong relationship between Keff and the fraction of high energy dissipation cells (defined with a threshold of 95%), but with some interesting complications to that relationship in the range of 50 to 60% high conductivity material. These results suggest that information regarding the fraction of high energy cells may be informative for inferring Keff for most percent high conductivity material fractions, but this relationship varies in the nature and quality of the correlation as a function of the fraction of high dissipation cells and percent of high conductivity material.
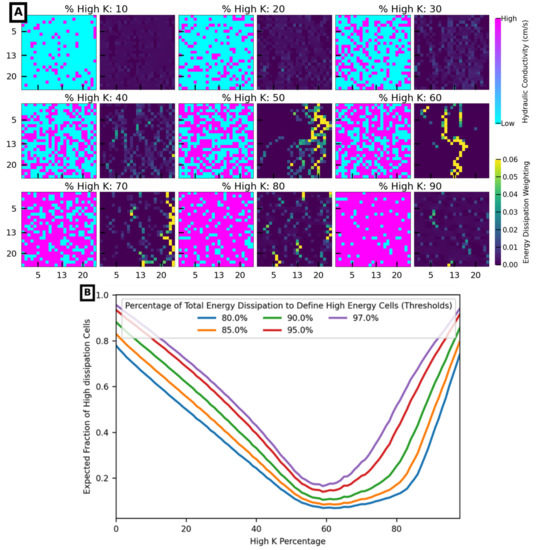
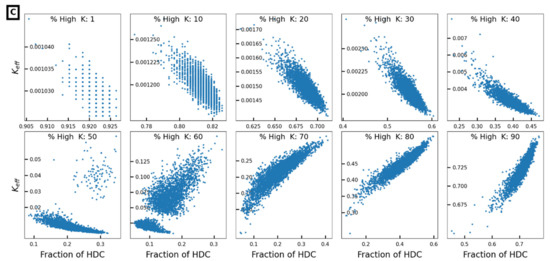
Figure 6.
The energy dissipation pattern for different percent of high K materials: (A) Grid samples and their corresponding energy dissipation weightings as a function of percent of high K material; (B) Average fraction of high energy dissipation cells as a function of the percent high K for different thresholds; (C) Correlation between observed Keff and fraction of high energy dissipation cells (HDC) as a function of percent of high K material. A threshold of 95% was used to define high energy cells.
3.3. Inferring Keff with UNET with and without ED Weights
The uninformed UNET achieved an RMSE = 0.0113 and R2 = 0.9984 when evaluated on the testing data (Figure 7A). Interestingly, the informed UNET (Figure 7B) offered only marginal improvement over the uninformed UNET with an RMSE = 0.0106 and an R2 = 0.9986. It is important to note that, although the informed UNET was provided information regarding the ED weights during training, its predictions of Keff are made based solely on the K grid. In other words, the uninformed UNET independently determined weights that are as good as the ED-informed. This leads to the question: Is the uninformed UNET discovering the ED weights, or has it found some other weighting scheme that is as effective as ED weighting? Regardless of the outcome, it is a contribution that the uninformed UNET has achieved this performance without requiring that a flow model be run. However, it would be even more interesting if it could be shown that the UNET was discovering ED weighting without being given the physical insight that underpins this approach.
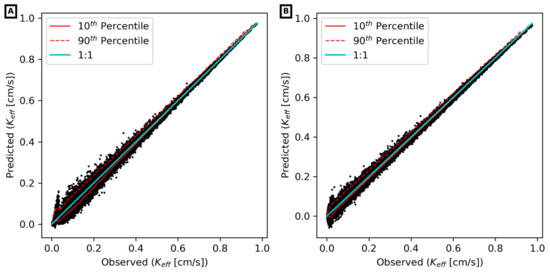
Figure 7.
The testing performance of Keff estimation using different methods: (A) Keff estimation using the energy dissipation uninformed UNET model; (B) Keff estimation using informed UNET model with pre-training on energy dissipation.
3.4. Inferring ED Weights with an Informed UNET
The performance of the informed UNET for inferring ED is illustrated for some example grids in Figure 8. The correspondence between the ED weights predicted by the informed UNET and the value calculated directly from the flow model shows low RMSE (0.0069) and high R2 (0.9549). This can also be aggregated to infer the fraction of high energy cells, showing similarly good results (RMSE = 0.04876 and R2 = 0.9832). However, considering all 625 cells in all 297,000 simulations, there are cases that show significant mismatch (Figure 9A). In particular, UNET consistently under-predicts the ED weights for cells that have very high actual weight (top right quadrant of Figure 9A). This leads to an over-prediction of the fraction of high energy cells for cases with intermediate percent high K (Figure 9B). From Figure 6B, these are the conditions that give rise to the most concentrated ED weighting. Taken together, these results suggest that the UNET has difficulty in inferring the ED weights when they are concentrated in highly localized areas (e.g., 60–75% high K material in Figure 6B).
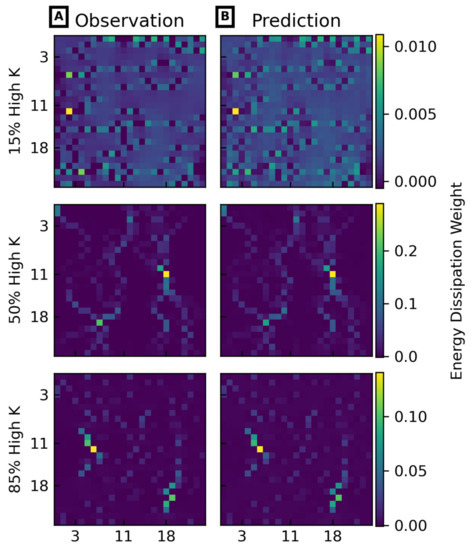
Figure 8.
Samples of energy dissipation weight distributions’ prediction for different ranges of percent of high K material: (A) Observation; (B) Predicted values.
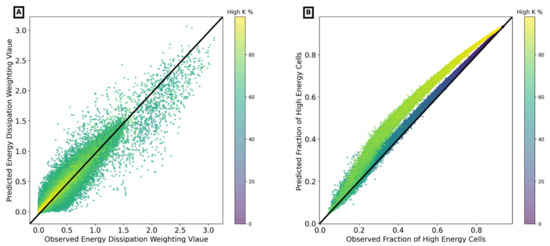
Figure 9.
Performance of informed UNET model in energy dissipation estimation: (A) Energy dissipation weighting prediction for all grids; (B) Fraction of high energy dissipation cells’ prediction performance as function of percent of high K material. With reference to Figure 6B, a threshold of 95% was used to define high energy cells.
4. Discussion
There were two primary objectives of this work. First, we aimed to investigate whether DL can predict Keff from a binary K grid, with or without ED weighting information being provided. Second, if an uninformed UNET can predict Keff, then does the weighting on the intermediate layers represent the DL independent learning of the ED weighting?
4.1. Dependence of the ED Weighting Distribution on the K Field
The Keff associated with binary grids showed a highly nonlinear dependence on the percentage of high K material (Figure 3). Specifically, Keff is closer to the arithmetic mean for materials with low to medium percentage of high K, while being approximately halfway between the arithmetic and harmonic means for materials with a higher percentage of high K. The variation in this trend is due to the influence of specific structural patterns in the spatial distribution of high and low K cells among grid realizations. The maximum degree of variability occurs for materials with intermediate percentages of high K values. In general, both the trend and the specific variations in Keff are very well explained by ED-weighted averaging (Figure 4).
Given that the energy dissipation weights carry information regarding the impact of structure on the effective conductivity of a binary K field, we examined the nature of this weighting as a function of the percentage of high K material present in the medium. Specifically, we defined the minimum area (i.e., threshold) that contains 95% of all of the ED weight, and classified the cells within this region as being ‘high energy cells’. At high and low percent high K conditions, the medium is nearly homogeneous, but the energy is distributed over ~75% of the domain (Figure 6B). The ED weighting is more highly constricted, residing in a smaller number of high energy cells for 60% high K material grids. The restricted high K areas centered around 60% high K material tend to form localized regions within which most of the energy dissipation occurs, indicating the influence of structures that force the flow to occur through regions of relatively low K, leading to high energy loss. However, as the percentage of high K increases to 80%, the high weight areas become concentrated in a small number of unconnected regions, suggesting a different structural mechanism whereby flow is forced through a small number of low K cells, rather than being channeled through a continuous structure.
4.2. Comparison of Performance
The UNET performance improves when ED information is provided during training (Table 1). However, the improvement is minimal: in terms of RMSE and R2, both informed and uninformed UNET performed extremely well.

Table 1.
Training, validation, and testing performance of all models.
The performance was poorest when Keff values were low (Figure 7). The performance was also relatively poor for intermediate percentage levels of high K material (Figure 10). That is, the UNET algorithms had the most difficulty when localized structures acted to impede flow, leading to a low Keff.
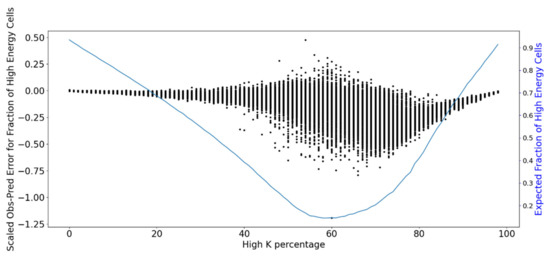
Figure 10.
Difference between inferred and actual fraction of high K cells for each grid. To compare the errors of grids at each high k percentage, the values of the left y-axis is scaled by average of actual number of high k cells at each k percentage. The fraction of high K cells for a 95% threshold is presented by a blue line.
4.3. Hidden Layer Representation Analysis
The superior performance of the informed UNET is notable because it does not require that the flow problem be solved to make predictions for the testing set. Specifically, once trained with ED weight information (requiring solving the flow problem during training and validation), the UNET algorithm uses the learned relationships to infer the values of the ED weights for the test samples and combines this with the K grid to infer Keff without having to solve the flow equation. In contrast, direct use of ED weighting requires the flow problem to be solved for every Keff inference.
The performance of the uninformed UNET, for which ED weight information was never presented, is comparable to that of the trained UNET. Again, this approach requires solution of the flow problem to determine the Keff during training and validation, but the ED weights are not determined. Given that the ED weights are thought to represent a key mechanism linking the K grid to the value of Keff, this raises the question of whether the uninformed UNET is somehow inferring information regarding the distribution of ED without being explicitly provided with such information during training.
For the informed UNET, the output layer of the lower branch, which is concatenated with the K grid before the final step of inferring Keff, represents the ED weight distribution. That is, as in the direct use of ED weights, this matrix is combined with the K grid matrix to infer Keff. Examining the corresponding layer of the uninformed UNET shows no correlation with the true ED weights. However, a more advanced analysis, based on computing the centered kernel alignment similarity (CKA) [50], provides a more complete picture of the information flows through the informed and uninformed UNETs. These results are visualized as a similarity matrix (Figure 11). The output of each layer of the informed model is compared to other layers of the uninformed model to examine the degree of similarity between them while accounting for the presence of invertible linear transformations. A similarity value of zero between two layers indicates that their representations are not invertible linear transformations of each other, while a similarity value of 1 indicates that the two layers are equivalent up to a linear transformation.
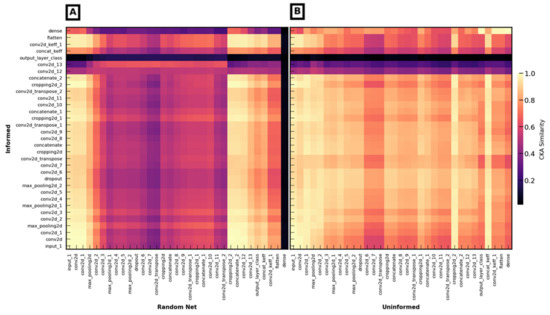
Figure 11.
CKA similarity matrix between: (A) Informed UNET and untrained UNET (Random net); (B) Informed UNET and uninformed UNET.
We first compared the results for the informed UNET with that of an untrained network with random initial weights, named as Random net, and the same architecture (Figure 11A). The values on the diagonal (representing the same layer in the two networks) have high CKA similarity for the first three layers; this makes sense given that both networks are being fed the same inputs. However, the similarity begins to diminish beyond that point; they show very strong dissimilarity at the output layer, where the informed UNET is constrained to predict values that correspond to the ED weights whereas Random net has no such constraint. They also differ strongly at the final dense layer, meaning that the untrained network did a poor job of inferring Keff.
The results are strikingly different when comparing the informed and uninformed UNETs (Figure 11B). Namely, layer similarity remains high for all layers except the output layer, where the informed UNET is required to predict values that correspond to the ED weights whereas the uninformed UNET is not. Unlike the comparison with the untrained network with random weights, the final dense layer is also highly similar, reflecting the near-identical skill in predicting Keff achieved by the informed and uninformed UNETs.
The similarity results (Figure 11) are consistent with the findings of Kornblith et al. [50] and Thompson et al. [59]. They show that there can be many possible intermediate architectural solutions to achieve the same task, but that representations learned for the layers closer to the inputs and the outputs tended to be similar. Further, we interpret the consistent similarity for almost all levels to mean that the untrained UNET is “learning” some useful information that is related to the ED weights directly from the K grids without any physical process constraints. However, the dissimilarity in the ED output layer indicates that the information is not a direct map of actual ED weights. Rather, when required to produce such a map (training under informed conditions), the UNET learns an intermediate relationship that can provide the ED map to the user. It then uses the ED distribution to infer Keff. However, when not required to produce an ED map (training under uninformed conditions), the UNET does not develop a layer to translate the information to a user-readable ED map. Rather, the latent information about the ED weights propagates through the UNET, with an associated change in the final dense layer to produce high-quality inferences of Keff.
The CKA analysis cannot uncover relationships between networks in the presence of invertible nonlinear transformations. To examine this, we sequentially swapped the weights of the uninformed UNET with those of the informed UNET. Specifically, at each step of this analysis (i.e., for each layer), we used the weights of the uninformed model for the preceding layers while maintaining the informed UNET weights for the succeeding layers. The results (Figure 12) are presented with the deepest layer at the top left, progressing along each row and then downward to the final layer, toward output and final dense layer, at the bottom right. There are strong linear correlations between the observed Keff and these predicted with the ‘swapped’ network until the substitutions reached the conv2d_12 layer. This is consistent with the high CKA representation’s similarity to this layer (Figure 11). There is a strongly nonlinear relationship for conv2d_13, which corresponds with a low CKA value at this layer. In the final layer (i.e., the output layer), we see a strong negative linear correlation between the output of the mixed structure model and that of the informed model. This pattern is consistent with the high CKA value observed in Figure 11, and suggests that an orthogonal transformation between the weights was necessary to overcome the changes applied in the deeper layers to recover the correct Keff values. This analysis suggests that both the informed and uninformed UNET are implementing similar computational processes, ostensibly extracting information corresponding to the ED distribution from the K grid, but representing it differently in n-d dimensional space. Further, the user-imposed requirement to produce a readable ED map results in a nonlinear transformation that must be compensated in later layers to produce accurate inferred Keff values.
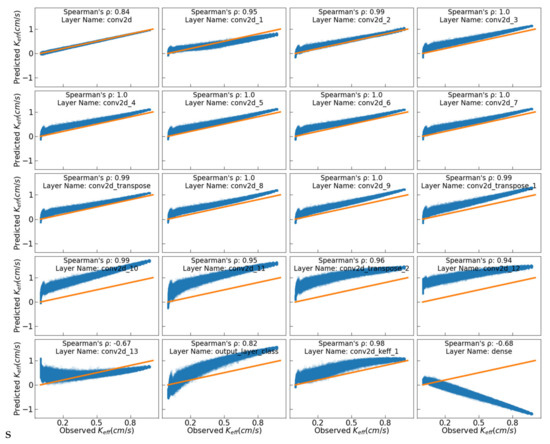
Figure 12.
Correlation between true Keff and the output of UNET model built up by sequential substitution of informed model weights with uninformed UNET collectively. Each subplot labeled with the corresponding layer name in DL model.
5. Conclusions
We have investigated the ability of DL algorithms to infer the effective hydraulic conductivity of binary K grids. Upon training, DL methods were able to infer Keff with extremely high accuracy (R2 > 0.99) when provided with only the binary grid.
Relying on previous work that showed the value of energy dissipation weighting for understanding and inferring Keff, we examined whether providing such information improved the DL performance. While adding information derived from the ED distribution improved the performance of each algorithm, the improvement was marginal.
The UNET architecture could be trained to infer the ED weighting from the K grid. This finding was supported by a similarity analysis of the hidden layers of UNETs with and without ED information provided. The accuracy of the inferred ED weights was lower when the energy dissipation weights were concentrated into small areas, i.e., the UNET was better able to infer the impacts of diffuse structures than highly localized structures. This finding may be due to the relatively small number of realizations that showed strong structural control in our sample set: highly localized structures are statistically less likely to occur in random grids. Future work should examine this possibility as well as extending the findings of this investigation to structured and geostatistically-constrained conditions.
While the UNET extracted the relevant ED weight information from the K grids, it only translated this information to a user-readable map if required to do so. This may have other implications for the use of ML/DL techniques in subsurface hydrology. For example, ML/DL algorithms may be able to implicitly infer head distribution information ‘naturally’ if they are trained to predict streamflow; however, the head distributions may not be available to the user unless the algorithms are specifically designed to produce them. This may be an important consideration if ML/DL algorithms are applied to models with multiple calibration data types or if the models will be used for multi-objective decision support.
Author Contributions
Conceptualization, P.A.T.F., M.A.M., and H.V.G.; Data curation, M.A.M. and J.K.; Formal analysis, M.A.M.; Investigation, J.K.; Methodology, M.A.M. and P.A.T.F.; Software, M.A.M. and M.R.E.; Supervision, P.A.T.F. and H.V.G.; Visualization, M.A.M. and M.R.E.; Writing—original draft, M.A.M.; Writing—review and editing, P.A.T.F., H.V.G., and M.R.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that supports the findings of this study are openly available in the University of Arizona Data Repository at 10.25422/azu.data.14399315, and can be obtained upon your request. Additionally, other relevant data will be provided on request from the corresponding author.
Conflicts of Interest
There is no conflict of interest in this research paper.
Appendix A

Table A1.
Deep learning structure parameters. UNET model structure.
Table A1.
Deep learning structure parameters. UNET model structure.
| MODIFIED UNET MODEL |
|---|
| 3 × 3 CONV. 16-SAME PADDING-STRIDE 1-RELU ×2 2 × 2 MAXPOOLING STRIDE 2 |
| 3 × 3 CONV. 32-SAME PADDING-STRIDE 1-RELU ×2 2 × 2 MAXPOOLING STRIDE 2 |
| 3 × 3 CONV. 64-SAME PADDING-STRIDE 1-RELU ×2 2 × 2 MAXPOOLING STRIDE 2 DROPOUT 0.64 |
| 3 × 3 CONV. 128-SAME PADDING-STRIDE1-RELU ×2 |
| 2 × 2 CONV2DTRANSPOSE. 64-SAME PADDING-STRIDE 2-NO ACTIVATION ×1 CROPPING CONCATENATION 3 × 3 CONV. 64-SAME PADDING-STRIDE 1-RELU ×2 |
| 2 × 2 CONV2DTRANSPOSE. 32-SAME PADDING-STRIDE 2-NO ACTIVATION ×1 CROPPING CONCATENATION 3 × 3 CONV. 32-SAME PADDING-STRIDE 1-RELU ×2 |
| 2 × 2 CONV2DTRANSPOSE. 16-SAME PADDING-STRIDE 2-NO ACTIVATION ×1 CROPPING CONCATENATION 3 × 3 CONV. 16-SAME PADDING-STRIDE 1-RELU ×2 |
| 1 × 1 CONV. 1-SAME PADDING-STRIDE 1-NO ACTIVATION ×1 |
| CONCATENATION 3 × 3 CONV. 10-SAME PADDING-STRIDE 1-TANH ×1 FLATTEN 1 DENSE-LINEAR |
References
- Ahuja, L.R.; Ma, L.; Green, T.R. Effective Soil Properties of Heterogeneous Areas for Modeling Infiltration and Redistribution. Soil Sci. Soc. Am. J. 2010, 74, 1469–1482. [Google Scholar] [CrossRef]
- Chan, S.; Elsheikh, A.H. Parametrization and generation of geological models with generative adversarial networks. arXiv 2017, arXiv:1708.01810. [Google Scholar]
- Aliyari, F.; Bailey, R.T.; Tasdighi, A.; Dozier, A.; Arabi, M.; Zeiler, K. Coupled SWAT-MODFLOW Model for Large-Scale Mixed Agro-Urban River Basins. Environ. Model. Softw. 2019, 115, 200–210. [Google Scholar] [CrossRef]
- Shamsudduha, M.; Zahid, A.; Burgess, W.G. Security of Deep Groundwater against Arsenic Contamination in the Bengal Aquifer System: A Numerical Modeling Study in Southeast Bangladesh. Sustain. Water Resour. Manag. 2019, 5, 1073–1087. [Google Scholar] [CrossRef]
- Adhikari, A.; Ehsani, M.R.; Song, Y.; Behrangi, A. Comparative Assessment of Snowfall Retrieval from Microwave Humidity Sounders Using Machine Learning Methods. Earth Sp. Sci. 2020, 7. [Google Scholar] [CrossRef]
- Slater, L. Near Surface Electrical Characterization of Hydraulic Conductivity: From Petrophysical Properties to Aquifer Geometries—A. Review. Surv. Geophys. 2007, 28, 169–197. [Google Scholar] [CrossRef]
- Hertrich, M. Imaging of Groundwater with Nuclear Magnetic Resonance. Prog. Nucl. Magn. Reson. Spectrosc. 2008, 53, 227–248. [Google Scholar] [CrossRef]
- Dlubac, K.; Knight, R.; Song, Y.-Q.; Bachman, N.; Grau, B.; Cannia, J.; Williams, J. Use of NMR Logging to Obtain Estimates of Hydraulic Conductivity in the High Plains Aquifer, Nebraska, USA. Water Resour. Res. 2013, 49, 1871–1886. [Google Scholar] [CrossRef]
- Ehsani, M.R.; Behrangi, A.; Adhikari, A.; Song, Y.; Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. Assessment of the Advanced Very High Resolution Radiometer (AVHRR) for Snowfall Retrieval in High Latitudes Using ClouSat and Machine Learning. J. Hydrometeorol. 2021, 22, 1591–1608. Available online: https://journals.ametsoc.org/view/journals/hydr/22/6/JHM-D-20-0240.1.xml (accessed on 11 June 2021).
- Wen, X.-H.; Gómez-Hernández, J.J. Upscaling Hydraulic Conductivities in Heterogeneous Media: An Overview. J. Hydrol. 1996, 183, ix–xxxii. [Google Scholar] [CrossRef]
- Journel, A.G.; Deutsch, C.; Desbarats, A.J. Power Averaging for Block Effective Permeability. In Proceedings of the SPE California Regional Meeting, Oakland, CA, USA, 2–4 April 1986. Paper Number: SPE-15128-MS. [Google Scholar]
- Matheron, G. Matheron’s Theory of Regionalised Variables; Pawlowsky-Glahn, V., Serra, J., Eds.; Oxford Scholarship Online: Oxford, UK, 2019; pp. 48–70. [Google Scholar]
- Desbarats, A.J.; Srivastava, R.M. Geostatistical Characterization of Groundwater Flow Parameters in a Simulated Aquifer. Water Resour. Res. 1992, 27, 687–698. [Google Scholar] [CrossRef]
- Zhu, J.; Mohanty, B.P. Upscaling of Soil Hydraulic Properties for Steady State Evaporation and Infiltration. Water Resour. Res. 2002, 38, 17-1–17-13. [Google Scholar] [CrossRef]
- Masihi, M.; Gago, P.A.; King, P.R. Estimation of the Effective Permeability of Heterogeneous Porous Media by Using Percolation Concepts. Transp. Porous Media 2016, 114, 169–199. [Google Scholar] [CrossRef]
- Arabzadeh, A.; Ehsani, M.R.; Guan, B.; Heflin, S.; Behrangi, A. Global Intercomparison of Atmospheric Rivers Precipitation in Remote Sensing and Reanalysis Products. J. Geophys. Res. Atmos. 2020, 125. [Google Scholar] [CrossRef]
- Cardwell, W.; Parsons, R. Average Permeability of Heterogeneous Oil Sands. Trans. AIME 1945, 160, 34–42. [Google Scholar] [CrossRef]
- Durlofsky, L.J. Representation of Grid Block Permeability in Coarse Scale Models of Randomly Heterogeneous Porous Media. Water Resour. Res. 1992, 28, 1791–1800. [Google Scholar] [CrossRef]
- Wen, X.-H.; Gómez-Hernández, J.J. Selective upscaling of hydraulic conductivities. In Geostatistics Wollongong ’96; Baafi, E., Schofield, N., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996; Volume 2, pp. 1112–1123. [Google Scholar]
- Colecchio, I.; Boschan, A.; Otero, A.D.; Noetinger, B. On the Multiscale Characterization of Effective Hydraulic Conductivity in Random Heterogeneous Media: A Historical Survey and Some New Perspectives. Adv. Water Resour. 2020, 140, 4. [Google Scholar] [CrossRef]
- King, P.R.; Neuwelier, I. Probability Upscaling. Comput. Geosci. 2002, 6, 101–114. [Google Scholar] [CrossRef]
- King, P.R. The Use of Renormalization for Calculating Effective Permeability. Transp. Porous Media 1989, 4, 37–58. [Google Scholar] [CrossRef]
- Malick, K. Boundary effects in the successive upscaling of absolute permeability. Master’s Thesis, Stanford University, Stanford, CA, USA, June 1995. [Google Scholar]
- Sánchez-Vila, X.; Girardi, J.P.; Carrera, J. A Synthesis of Approaches to Upscaling of Hydraulic Conductivities. Water Resour. Res. 1995, 31, 867–882. [Google Scholar] [CrossRef]
- Ambegaokar, V.; Halperin, B.I.; Langer, J.S. Hopping Conductivity in Disordered Systems. Phys. Rev. B. 1971, 4, 2612–2620. [Google Scholar] [CrossRef]
- Ehsani, M.R.; Arevalo, J.; Risanto, C.B.; Javadian, M.; Devine, C.J.; Arabzadeh, A.; Venegas-Quiñones, H.L.; Dell’Oro, A.P.; Behrangi, A. 2019–2020 Australia Fire and Its Relationship to Hydroclimatological and Vegetation Variabilities. Water 2020, 12, 3067. [Google Scholar] [CrossRef]
- Berkowitz, B.; Balberg, I. Percolation Theory and Its Application to Groundwater Hydrology. Water Resour. Res. 1993, 29, 775–794. [Google Scholar] [CrossRef]
- Hunt, A.G.; Sahimi, M. Flow, Transport, and Reaction in Porous Media: Percolation Scaling, Critical-Path Analysis, and Effective Medium Approximation. Rev. Geophys. 2017, 55, 993–1078. [Google Scholar] [CrossRef]
- Hunt, A.; Ewing, R.; Ghanbarian, B. Percolation Theory for Flow in Porous Media; Springer International Publishing: Cham, Switzerland, 2014; Volume 880. [Google Scholar]
- Hassanzadegan, A.; Cacace, M.; Sippel, J.; Scheck-Wenderoth, M. The Application of Inverse Modeling in Characterizing Hydraulic Conductivity beneath the City of Berlin, Germany. Environ. Earth Sci. 2016, 75, 1–17. [Google Scholar] [CrossRef]
- Kotlar, A.M.; Varvaris, I.; van Lier, Q.J.; de Jonge, L.W.; Møldrup, P.; Iversen, B.V. Soil Hydraulic Properties Determined by Inverse Modeling of Drip Infiltrometer Experiments Extended with Pedotransfer Functions. Vadose Zone J. 2019, 18, 1–11. [Google Scholar] [CrossRef]
- Cheng, Q.; Qiang, X.; Xianglin, C.; Song, Y.; Zhongyi, W.; Yurui, S.; Xiaofei, Y.; Jones, S.B. In-Situ Estimation of Unsaturated Hydraulic Conductivity in Freezing Soil Using Improved Field Data and Inverse Numerical Modeling. Agric. For. Meteorol. 2019, 279, 6. [Google Scholar] [CrossRef]
- De Oliveira, L.F.C.; de Souza, G.R.; Corrêa, F.V.; E Silva, J.R.M. Parameter Estimation of Soil Hydraulic Characteristics by Inverse Modeling of the Analytical Equation for Unsaturated Subsurface Water Flow. J. Hydroinform. 2020, 22, 1270–1282. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Stauffer, P.H.; Wöhling, T.; Robinson, B.A.; Vesselinov, V.V. Inverse Modeling of Subsurface Flow and Transport Properties: A Review with New Developments. Vadose Zone J. 2008, 7, 843–864. [Google Scholar] [CrossRef]
- Lai, J.; Ren, L. Estimation of Effective Hydraulic Parameters in Heterogeneous Soils at Field Scale. Geoderma 2016, 264, 28–41. [Google Scholar] [CrossRef]
- Knight, J.H. Sensitivity of Time Domain Reflectometry Measurements to Lateral Variations in Soil Water Content. Water Resour. Res. 1992, 28, 2345–2352. [Google Scholar] [CrossRef]
- Indelman, P.; Dagan, G. Upscaling of Permeability of Anisotropic Heterogeneous Formations: 2. General Structure and Small Perturbation Analysis. Water Resour. Res. 1993, 29, 925–933. [Google Scholar] [CrossRef]
- Ferré, P.A.; Knight, J.H.; Rudolph, D.L.; Kachanoski, R.G. The Sample Areas of Conventional and Alternative Time Domain Reflectometry Probes. Water Resour. Res. 1998, 34, 2971–2979. [Google Scholar] [CrossRef]
- Afzaal, H.; Farooque, A.A.; Abbas, F.; Acharya, B.; Esau, T. Groundwater Estimation from Major Physical Hydrology Components Using Artificial Neural Networks and Deep Learning. Water 2020, 12, 5. [Google Scholar] [CrossRef]
- Mo, S.; Zabaras, N.; Shi, X.; Wu, J. Integration of Adversarial Autoencoders with Residual Dense Convolutional Networks for Estimation of Non-Gaussian Hydraulic Conductivities. Water Resour. Res. 2020, 56, 1–24. [Google Scholar] [CrossRef]
- Wang, N.; Zhang, D.; Chang, H.; Li, H. Deep Learning of Subsurface Flow Via Theory-Guided Neural Network. J. Hydrol. 2020, 584, 124700. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Marrero, C.O.; Perdikaris, P.; Tartakovsky, G.D.; Barajas-Solano, D. Physics-Informed Deep Neural Networks for Learning Parameters and Constitutive Relationships in Subsurface Flow Problems. Water Resour. Res. 2020, 56, 1–16. [Google Scholar] [CrossRef]
- Canchumuni, S.W.A.; Emerick, A.A.; Pacheco, M.A.C. Towards a Robust Parameterization for Conditioning Facies Models Using Deep Variational Autoencoders and Ensemble Smoother. Comput. Geosci. 2018, 128, 87–102. [Google Scholar] [CrossRef]
- Zhou, Z.; Shi, L.; Zha, Y. Seeing Macro-Dispersivity from Hydraulic Conductivity Field with Convolutional Neural Network. Adv. Water Resour. 2020, 138, 103545. [Google Scholar] [CrossRef]
- Wu, J.; Yin, X.; Xiao, H. Seeing Permeability from Images: Fast Prediction with Convolutional Neural Networks. Sci. Bull. 2018, 63, 1215–1222. [Google Scholar] [CrossRef]
- Apley, D.W.; Zhu, J. Visualizing the effects of predictor variables in black box supervised learning models. J. R. Stat. Soc. Ser. B 2020, 82, 1059–1086. [Google Scholar] [CrossRef]
- Chakraborty, S.; Tomsett, R.; Raghavendra, R.; Harborne, D.; Alzantot, M.; Cerutti, F.; Srivastava, M.; Preece, A.; Julier, S.; Rao, R.M.; et al. Interpretability of deep learning models: A survey of results. In Proceedings of the 2017 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computed, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation, San Francisco, CA, USA, 4–8 August 2017. [Google Scholar] [CrossRef]
- Mosser, L.; Dubrule, O.; Martin, J.B. Reconstruction of three-dimensional porous media using generative adversarial neural networks. Phys. Rev. E 2017, 96, 43309. [Google Scholar] [CrossRef]
- Srisutthiyakorn, N. Deep Learning Methods for Predicting Permeability from 2-D/3-D Binary Segmented Images. SEG Tech. Progr. Expand. Abstr. 2016, 35, 3042–3046. [Google Scholar] [CrossRef]
- Kornblith, S.; Norouzi, M.; Lee, H.; Hinton, G. Similarity of Neural Network Representations Revisited. arXiv 2019, arXiv:1905.004142019, 6156–6175. [Google Scholar]
- Knudby, C.; Carrera, J.; Bumgardner, J.D.; Fogg, G.E. Binary Upscaling—The Role of Connectivity and a New Formula. Adv. Water Resour. 2006, 29, 590–604. [Google Scholar] [CrossRef]
- Pozdniakov, S.; Tsang, C.-F. A Self-Consistent Approach for Calculating the Effective Hydraulic Conductivity of a Binary, Heterogeneous Medium. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional Networks for Biomedical Image Segmentation. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. [Google Scholar] [CrossRef]
- Zoph, B.; Yuret, D.; May, J.; Knight, K. Transfer Learning for Low-Resource Neural Machine Translation. arXIv 2016, arXiv:1604.02201, 1568–1575. [Google Scholar]
- Brock, A.; Lim, T.; Ritchie, J.M.; Weston, N. FreezeOut: Accelerate Training by Progressively Freezing Layers. arXiv 2017, arXiv:1706.04983. [Google Scholar]
- Gretton, A.; Bousquet, O.; Smola, A.; Scḧlkopf, B. Measuring Statistical Dependence with Hilbert-Schmidt Norms. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3734, pp. 63–77. [Google Scholar] [CrossRef]
- Cristianini, N.; Kandola, J.; Elisseeff, A.; Shawe-Taylor, J. On Kernel Target Alignment BT—Innovations in Machine Learning: Theory and Applications. In On Kernel Target Alignment; Holmes, E., Jain, L.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 205–256. [Google Scholar]
- Cortes, C.; Mohri, M.; Rostamizadeh, A. Algorithms for Learning Kernels Based on Centered Alignment. J. Mach. Learn. Res. 2012, 13, 795–828. [Google Scholar] [CrossRef]
- Thompson, J.; Bengio, Y.; Schoenwiesner, M. The Effect of Task and Training on Intermediate Representations in Convolutional Neural Networks Revealed with Modified RV Similarity Analysis. arXiv 2019, arXiv:1912.02260. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).