Abstract
Hydro-floating ship lifts are a milestone in the field of high dam navigation. In order to ensure the running safety of a hydro-floating ship lift, the effective integration of a numerical simulation method and cloud model theory was carried out to deal with the hydrodynamic risks presented by water surface deviations from the shafts in the filling–emptying system such as a lock. In this study, the average values of water surface deviation from the shafts were 0.2, 0.22 and 0.24 m, through numerical simulation on a similar hydro-floating ship lift at the lifting heights of 80, 100 and 120 m, respectively. An increase in the lifting height causes the water surface deviation from the shafts to increase, and the hydrodynamic risk is greatly increased in the equal inertial pipeline filling–emptying system. In addition, the water surface deviations from the shafts of the equal inertial pipeline and longitudinal culvert filling–emptying system like a lock were compared. The longitudinal culvert was better at optimizing running safety in the filling–emptying system and dealing with the uncertainty of water surface deviation from the shafts. The results show that the numerical simulation method and cloud model theory can effectively control the risk of water surface deviation from the shafts and can be used to aid in decision-making for risk prevention in relation to hydro-floating ship lifts.
1. Introduction
A ship lift is a navigation building that raises and lowers ships to assist them in passing across dams in water conservancy projects [1,2,3]. Ship lifts are gradually developing towards the mega-scale with a 100 m lifting height in order to meet the predicted increase in waterway traffic [4]. A large number of traditional-type ship lifts have now been built and put into action throughout the world (e.g., the Three Gorges ship lift, China; Niederfinow ship lift, Germany; Luneburg ship lift, Germany, etc.) [5,6,7,8]. The running of these traditional ship lifts is driven by electric motors. The construction of hydro-floating ship lifts integrates the technical advantages of ship lock filling–emptying systems and traditional electrical-drive ship lifts. The new driving mode of hydraulic power is employed instead of electric power in the hydro-floating ship lift. Compared with an electrical-drive ship lift, a hydro-floating ship lift using a water driver has the advantages of a simple structure, low investment cost and advanced technology, allowing it to save construction, operation and maintenance costs [9,10]. The remarkable superiority of hydro-floating ship lifts can be attributed to their filling–emptying system, which was developed from ship locks. However, the long-term running of hydro-floating ship lifts under complex hydrodynamic conditions increases the risk of accidents, particularly the risk caused by water surface deviation from the shafts in the filling–emptying system [11,12]. Although the design of safety mechanisms in hydro-floating ship lifts has profited from the success of electrical-drive ship lifts, ship lock filling–emptying systems and other developments, it is necessary to analyze the potential hydrodynamic risk posed by filling–emptying systems.
Filling and emptying processes are common maneuvers while operating, controlling and managing water pipeline systems. The filling–emptying system is used to drive hydro-floating ship lifts. It is very important for this system to run safely, considering the intricacy of the calculations and configurations of the water pipeline system. The current layout types of filling–emptying systems mainly involve equal inertial pipelines and longitudinal culvert models [13,14]. The most common filling–emptying designs used by the U. S. Army Corps of Engineers have culverts within the lock walls that transfer water into and out of the lock chamber successfully. Unfortunately, as with the ship lock filling–emptying system, in the running process of a hydro-floating ship lift filling–emptying system, water surface deviation from the shafts occurs [15,16]. The hydrodynamic risk to equal inertial pipeline filling–emptying systems is caused by water surface deviations from the shafts in most cases. In addition, with an increase in the ship lift lifting height, the running of the filling–emptying system under the conditions of large flow and high velocity will result in more serious hydrodynamic risk. To achieve the safe running of mega-scale ship lifts with a 100 m lifting height, the layout of longitudinal culvert filling–emptying systems has been designed based on ship locks. Therefore, it is useful to analyze hydrodynamic risk by comparing equal inertial pipelines and longitudinal culvert filling–emptying systems.
Risk analysis methods applied in the context of water conservancy engineering focus on dam safety [17,18,19,20] or the early warning of flood risk [21,22,23], but there have been few studies on the running risk of ship lifts in the past years. In addition, there is an urgent need for feasible risk analysis methods for the filling–emptying systems of hydro-floating ship lifts to ensure running safety. The hydrodynamic risk of the filling–emptying system is mainly caused by the uncertainty and randomness of water surface deviation from the shafts. The original risk assessment methods (e.g., genetic algorithm [24,25,26,27] and Bayesian algorithm [28,29]) can solve complex problems, such as information processing and pattern recognition. However, these methods are mainly employed for identifying and predicting risk and thus cannot be used for practical, accurate assessment.
An artificial intelligence cloud model can convert qualitative concepts into quantitative data [30,31,32]. The digital characteristics of clouds can fully reflect the fuzziness and randomness of water surface deviation from the shafts. Furthermore, a cloud generator can realize indefinite membership degree representation, which can be applied to classify hydrodynamic risk in a filling–emptying system. Therefore, it is meaningful to develop a risk analysis method with a cloud model to solve the fuzziness and randomness of water surface deviation from the shafts.
In view of the above considerations, to ensure the running safety of a hydro-floating ship lift, the hydrodynamic risk of the filling–emptying system was analyzed. The objectives of this study were (1) to achieve layout optimization of the filling–emptying system by comparing the equal inertial pipeline with the longitudinal culvert; (2) to build an effective integration of the numerical simulation method and cloud model theory to deal with the fuzziness and randomness of water surface deviation from the shafts and solve the hydrodynamic risk of the filling–emptying system; and (3) to use the Jinghong hydro-floating ship lift as an example to analyze the hydrodynamic risk of the filling–emptying system at the mega-scale of a 150 m lifting height.
2. Materials
2.1. Study Area
To date, the only hydro-floating ship lift that has been built and put into operation is in the Jinghong hydropower station, China (Figure 1). It is the largest navigation building in the Lancang-Mekong River basin and represents a new driving mode of hydro-floating ship lifts originally developed in China. The running up or down of the ship chamber is driven by the buoyancy of the water, using an equal inertial pipeline filling–emptying system to fill and empty water from the shafts. The design parameters of the Jinghong hydro-floating ship lift are presented in Table 1. The passing ship tonnage of the lift is about 300–500 tons, the maximum lifting height is 66.86 m, the maximum lifting weight is 3140 tons and the single running time of the ship chamber is about 17 min.
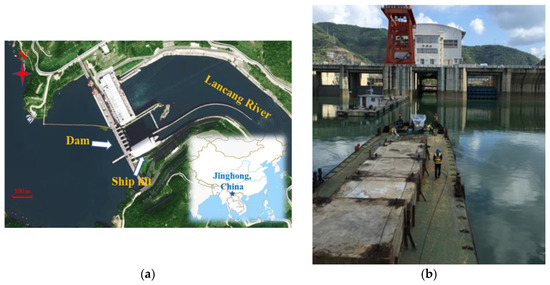
Figure 1.
Jinghong conservancy project: (a) top view and (b) upstream view of ship lift.

Table 1.
Design parameters of Jinghong hydro-floating ship lift.
The detailed layout of the equal inertial pipeline filling–emptying system is shown in Figure 2. Filling or emptying water from the shaft drive hydro-floating ship lift running by using filling and emptying valve controlled. The first (L1) and second (L2) diversions are arranged on a horizontal flat surface, and the third (L3) and fourth (L4) diversions are carried out on a vertical facade. After these four divergences, water flow from the upstream is distributed to each individual shaft along the pipeline. The geometric structure of the filling–emptying system with equal inertia is designed in a symmetrical way, and so the branch pipeline is completely symmetrical. According to theoretical calculation analysis, water flow from the upstream could be distributed to each individual shaft evenly and equally. The water level in each shaft rises and falls synchronously. It is helpful for the safe operation of hydro-floating ship lifts to ensure the synchronous rising and falling of the water level among the shafts.
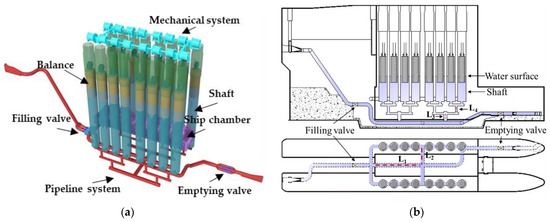
Figure 2.
Schematic diagram of equal inertial pipeline filling–emptying system: (a) three-dimensional and (b) plane mode.
However, in practical operation, it is very difficult to ensure the synchronous rising and falling of the water level among the shafts due to their complicated construction. In particular, with an increase in lifting height, the flow turbulence intensity in the pipeline is relatively large under the condition of a high flow rate and speed. A complex flow field structure and unsteady turbulence are generated in the filling–emptying system. Complex hydrodynamic conditions have a negative impact on the synchronous rising and falling of the water level among the shafts, which aggravates water surface deviation from the shafts. In addition, the connectivity of flow among the shafts is extremely poor and further results in the operational risk of hydro-floating ship lifts. Water surface deviation (Δhi) from the shafts causes torque (T) to be generated by the roller among drums (Figure 3). The larger the water surface deviation from the shafts, the larger the D-value of tension (Fi ≠ Fi′) among wire ropes, which leads to the corresponding increase of the torque (T) to be generated by the roller among drums and threatens the safe operation of the ship lift. Thus, reasonable measures must be taken to reduce the water surface deviation from the shafts.
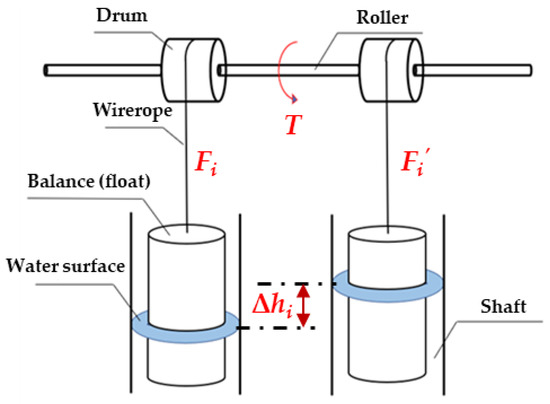
Figure 3.
Water surface deviation from the shafts causes torque to be generated by the roller among drums.
2.2. Optimization of Layout
In an equal inertial pipeline filling–emptying system, water surface deviation from the shafts leads to an operational risk to hydro-floating ship lifts. A longitudinal culvert filling–emptying system was therefore proposed (Figure 4). It is hoped that this may be able to reduce the hydrodynamic risk of filling–emptying systems in engineering applications. Compared to the equal inertial pipeline filling–emptying system, the shaft of the longitudinal culvert is arranged in the form of an entirely connected cuboid. There is plenty of buffer space to reduce water level changes. Therefore, the longitudinal culvert may be better at reducing the operational risk of hydro-floating ship lifts caused by the hydrodynamic characteristics of the filling–emptying system.
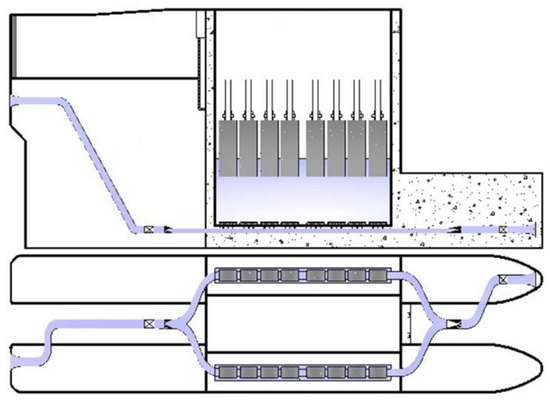
Figure 4.
Schematic diagram of the longitudinal culvert filling–emptying system.
3. Methodology
A new risk analysis method, based on a numerical simulation and cloud model theory, was applied to analyze the hydrodynamic risk of the filling–emptying system of a hydro-floating ship lift, as presented in Figure 5. First, a complete evaluation system and evaluation criteria for water surface deviation from the shafts were developed. Second, the numerical characteristics of water surface deviation from the shafts were computed and calculated by numerical simulation and cloud model theory. Third, the water surface deviation from the shafts was considered as a comparison analysis for the equal inertial pipeline filling–emptying system at the mega-scale of 80, 100 and 120 m lifting heights. Finally, the water surface deviation from the shafts in the filling–emptying system was optimized by comparing the longitudinal culvert with the equal inertial pipeline. Then, the risk analysis and optimization of water surface deviation from the shafts could be carried out.
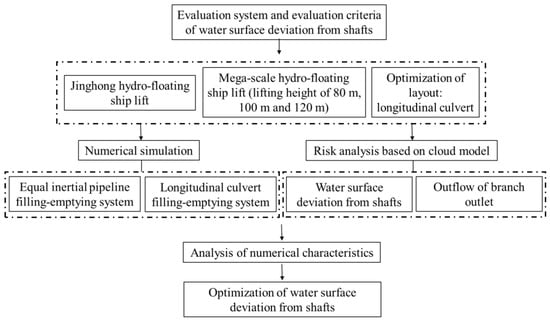
Figure 5.
Risk analysis and optimization process of water surface deviation from the shafts.
3.1. Numerical Simulation
The three-dimensional numerical model was established to simulate the process of water surface deviation from the shafts. The process of the water flow sequence passing through the filling–emptying system into the shafts was simulated by fluent. With respect to the similar hydro-floating ship (Jinghong), hydraulic parameters of the equal inertial pipeline and longitudinal culvert filling–emptying systems were designed and compared as shown in Table 2. The flow coefficient of the equal inertial pipeline and longitudinal culvert filling–emptying system were 0.297 and 0.318, respectively. The resistance coefficient of the equal inertial pipeline and longitudinal culvert filling–emptying system were 0.321 and 0.334, respectively.

Table 2.
Characteristic parameters of the filling–emptying system.
The running of one side’s shafts and pipes was researched by building a three-dimensional numerical model. The three-dimensional numerical model was established as presented in Figure 6 and Figure 7. The boundary conditions of the model included a wall boundary, velocity boundary and pressure boundary. The direction of flow velocity was perpendicular to the inlet section. The liquid level in the shaft was the interface of water and gas, which was set as the boundary of atmospheric pressure. In this paper, the calculation conditions of 80 m, 100 m, 120 m and 150 m lifting heights were designed to analyze the equal inertial pipeline filling–emptying system. The calculation condition of a 150 m lifting height was designed to analyze the longitudinal culvert filling–emptying system.
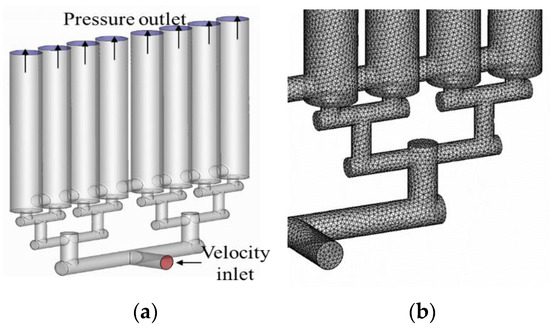
Figure 6.
Numerical simulation of the equal inertial pipeline filling–emptying system: (a) modeling and (b) meshing.
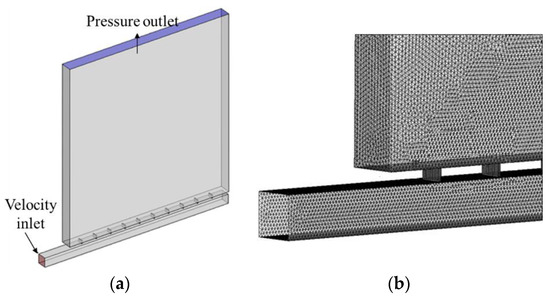
Figure 7.
Numerical simulation of the longitudinal culvert filling–emptying system: (a) modeling and (b) meshing.
We calculated the change process of the filling water flow in the filling–emptying system under the condition of 80 m, 100 m, 120 m and 150 m lifting heights (Figure 8). With this as the velocity inlet, the change of the shaft flow field structure in the process of filling water was simulated. Maximum flow of the filling–emptying system under the lifting heights of 80 m, 100 m, 120 m and 150 m were 60, 67, 74 and 82 m3/s, respectively.
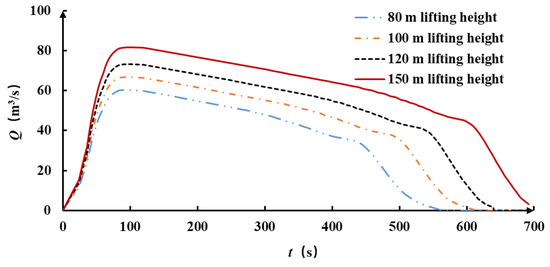
Figure 8.
The change process of the filling water flow in the filling–emptying system under the condition of 80 m, 100 m, 120 m and 150 m lifting heights.
3.2. Risk Analysis
Cloud models are applied widely to uncertainty analysis in different fields, such as computing with words, data mining, intelligent control, evaluations of complex big data systems and the prevention and control of disasters, etc. In this paper, a cloud model is applied to analyze the hydrodynamic risk of the filling–emptying system of a hydro-floating ship lift.
3.2.1. Cloud Model Definition
The cloud model derived from information science was proposed by Li to analyze uncertainty problems [33]. Li defined the cloud model in detail. Let U be a quantitative universe of discourse, which can be described by precise numerical values, and A is a qualitative concept of U. Assume that there is a quantitative number x ∈ U, and x is a random realization of concept A. For an arbitrary element x, there is a random variable with a stabilization tendency, called the certainty degree μ(x). The parameter μ(x) can be estimated as
where the distribution of x on U is called a cloud, and each (x, μ(x)) is a cloud drop.
In the original literature, Li introduced the digital characteristics of the cloud concept, digital cloud-features and the cloud generator implementation process and developed the cloud generator using a mathematical mode. According to the definition of clouds, a cloud is composed of numerous cloud drops, and it can transform a qualitative concept into a quantitative value. Each cloud drop is a quantitative representation of a qualitative concept in the U space. The certainty degree of a cloud drop reflects the fuzziness and randomness of a concept. The cloud model contains three parameters: expected value (Ex), entropy (En) and hyper entropy (He). The model can be expressed as (Ex, En, He). The implications of the three parameters are described below:
- Ex refers to the expectation of the cloud droplets, which is the central value in the universe of the qualitative concept. In this paper, the expected value (Ex) reflects the average variation degree of water surface deviation from the shafts in the filling–emptying system.
- En is the uncertainty measurement of the qualitative concept, which is codetermined by the randomness and fuzziness of the concept. In this paper, entropy (En) can reflect the uncertainty degree of the water surface deviation from the shafts.
- He is the uncertainty measurement of En; i.e., the entropy of En. It reflects the discrete degree of the cloud droplets. A larger He value represents a higher cloud dispersion. In this paper, if the value of hyper entropy (He) is larger, the uncertainty of water surface deviation from the shafts is more discrete.
3.2.2. Cloud Generator
A cloud generator is a tool used to implement the conversion between the qualitative index and the quantitative index. The cloud generator is divided into a forward cloud generator (FCG) and backward cloud generator (BCG), as shown in Figure 9.
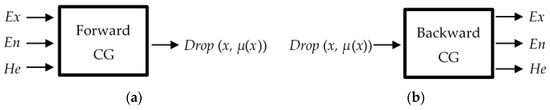
Figure 9.
Two different types of cloud generator (CG): (a) forward CG and (b) backward CG.
The FCG involves qualitative to quantitative mapping, which generates a number of cloud droplets based on (Ex, En, He). It is a direct forward process. If a variable x ∈ A is a random realization of the concept A and obeys the Gaussian distribution x~n (Ex, λ2), and λ obeys the Gaussian distribution λ~n (En, He2), the certainty degree of x to A, μ(x), satisfies
where λ is a normally distributed random number; the distribution of x in U is called a normal cloud.
The FCG is used in the following context, and its algorithm is described as follows:
| Algorithm 1. Algorithm of forward cloud generator (FCG). |
| Input: Parameters Ex, En and He and the number of cloud droplets to be generated, n. Output: Quantitative values of n cloud droplets xi and their corresponding certainty degrees μ(xi) (i = 1,2,…,n). Algorithm steps: Step 1: Generate a normally distributed random number λ with expectation En and variance He: λ~n (En, He2); Step 2: Generate a normally distributed random number xi with expectation Ex and variance λ: xi~n (Ex, λ2); Step 3: Calculate the certainty degree of xi, ; Step 4: Generate a cloud drop (xi, μ(xi)), and repeat steps 1 to 3 until n cloud drops are generated. |
Conversely, the BCG transforms the data from quantitative to qualitative. It can convert precise data into a qualitative concept as represented by (Ex, En, He). The specific algorithm of the BCG is as follows:
| Algorithm 2. Algorithm of backward cloud generator (BCG). |
| Input: Sample point data value xi (i = 1,2,…,n). Output: Parameters Ex, En, and He. Algorithm steps: Step 1: Calculate the sample mean of these data xi (i = 1,2,…,n), , and sample variance, ; Step 2: Calculate the expected value , ; Step 3: Calculate the entropy value, ; Step 4: Calculate the hyper-entropy value, . |
In summary, FCG and BCG were used to deal with the measured data of water surface deviation from the shafts. Three parameters (Ex, En, He) were used to measure the degree of change of the risk of water surface deviation from the shafts in the filling–emptying system.
3.2.3. Cloud Model for the Filling–Emptying System
Learning from the rate of contribution of cloud droplets Δx to the qualitative concept ΔA, the risk rate of the hydrodynamic risk factor to the risk phenomenon of the filling–emptying system was defined. The qualitative concept ΔA and total qualitative concept A can be estimated as [34]
The total qualitative concept A calculation results show that . Most cloud droplet values fell within the range [Ex − 3En, Ex + 3En], and the proportion outside this interval was only 0.26%.
To ensure long-term running safety, a risk analysis interval of hydrodynamic factors was proposed. Considering the rate of contribution of cloud droplets to the qualitative concept, the hydrodynamic risk factor was divided into risk intervals. The intervals were as follows:
- (1)
- “Security”: The data regarding the hydrodynamic risk factor for the filling–emptying system fall in the cloud droplet group of the [0, Ex + En] interval. The [0, Ex + En] interval accounts for 84.13% of the total area. If the measured data of the hydrodynamic factors fall in this range, this indicates the running safety of the filling–emptying system.
- (2)
- “Weak security”: The data regarding the hydrodynamic risk factor for the filling–emptying system fall in the cloud droplet group of the [Ex + En, Ex + 2En] interval. The [Ex + En, Ex + 2En] interval accounts for 13.59% of the total area. If the measured data of the hydrodynamic factors fall in this range, this indicates the weak running safety of the filling–emptying system. The operator should pay attention to changes in the measured data.
- (3)
- “Weak risk”: The data regarding the hydrodynamic risk factor for the filling–emptying system fall in the cloud droplet group of the [Ex + 2En, Ex + 3En] interval. The [Ex + 2En, Ex + 3En] interval accounts for 2.15% of the total area. If the measured data of the hydrodynamic factors are concentrated in this interval, this indicates that the filling–emptying system of the hydro-floating ship lift is in a state of “weak risk”. The operator should report the “weak risk” of the filling–emptying system and look up possible problems.
- (4)
- “Risk”: The data regarding the hydrodynamic risk factor for the filling–emptying system fall in the cloud droplet group of the [Ex + 3En, +∞] interval. The [Ex + 3En, +∞] interval accounts for 0.13% of the total area. If the measured data for the hydrodynamic factors fall in this range, the filling–emptying system exhibits a risk state. The operator should report the “risk” state of the filling–emptying system and stop the running of the hydro-floating ship lift according to the corresponding operation process and deal with the risk-causing fault.
4. Results and Discussion
4.1. Water Surface Deviation from the Shafts of an Equal Inertial Pipeline
4.1.1. Jinghong Hydro-Floating Ship lift
Taking the engineering project of the Jinghong hydro-floating ship lift as an example, our cloud model method was applied to evaluate the uncertainty of water surface deviation from the shafts. In the running of the Jinghong hydro-floating ship lift, fluctuations h of the water surface from the shafts and the rate of flow Q were measured three times (1#, 2#, 3#) and the measured data are shown in Figure 10. Under normal operating conditions, the typical measured data for water surface deviation from the shafts of the Jinghong hydro-floating ship lift were collected and analyzed as shown in Figure 11. The maximum water surface deviation from the shafts was less than 0.2 m, which was lower than the designed warning value (≤0.4 m). At present, this filling–emptying system can achieve the safe operation requirements of ship lifts.
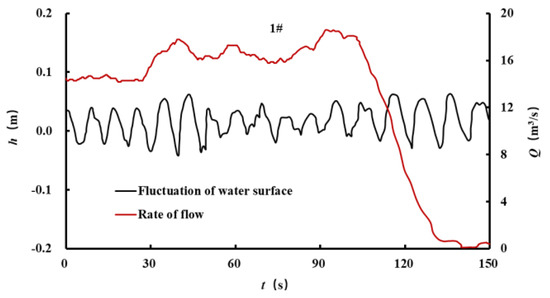
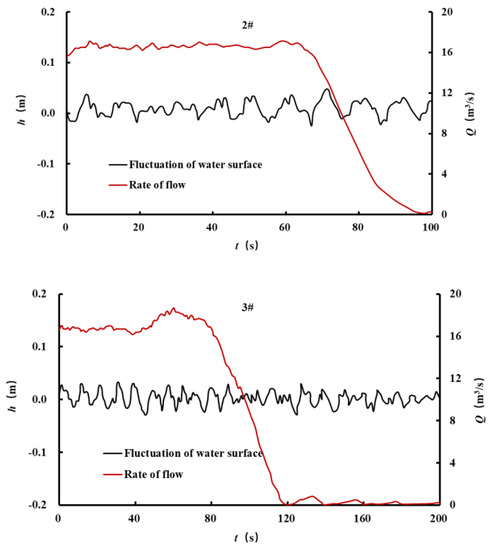
Figure 10.
Fluctuation of the water surface from the shafts and rate of flow.
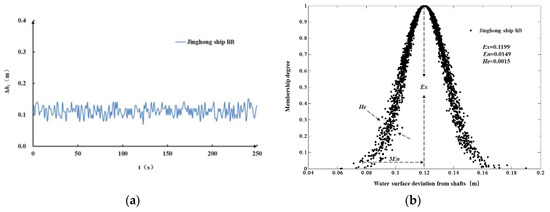
Figure 11.
Water surface deviation from the shafts in Jinghong ship lift: (a) the diagram of water surface deviation from the shafts and (b) the cloud model expression.
To deal with the uncertainty of water surface deviation from the shafts quantitatively, the typical measured data from the Jinghong hydro-floating ship lift were analyzed. Cloud generators were adopted to generate a qualitative conceptual model for the Jinghong ship lift, as shown in Figure 11b. The parameters (Ex = 0.1199, En = 0.0149 and He = 0.0015) of the cloud model were adopted to show the risk degree of water surface deviation from the shafts. The results show that the dispersion degree of water surface deviation from the shafts in the Jinghong ship lift is low and the operation of the filling–emptying system to date is in a safe range without risks.
According to the rate of contribution of water surface deviation from the shafts to the risk, the distribution rank of water surface deviation from the shafts was categorized. The risk warning threshold of water surface deviation from the shafts in the Jinghong hydro-floating ship lift was determined. The threshold intervals were security [0, 0.13], weak security (0.13, 0.15], weak risk (0.15, 0.17] and risk (0.17, +∞).
4.1.2. Numerical Simulation of 100 m Lifting Height
To fit the future development trend of a super-high lifting height, the water surface deviation from the shafts at the lifting heights of 80, 100 and 120 m was obtained through the numerical simulation of a similar hydro-floating ship lift, as shown in Figure 12. Using a number of cloud droplets, n, of 3000, the cloud figure of water surface deviation from the shafts was obtained, as shown in Figure 12b. The average values of water surface deviation from the shafts under the lifting heights of 80, 100 and 120 m were 0.2, 0.22 and 0.24 m, respectively. With an increase in lifting height, the uniformity of the diverging flow and synchronicity of the water level among the shafts shows a chaotic trend.
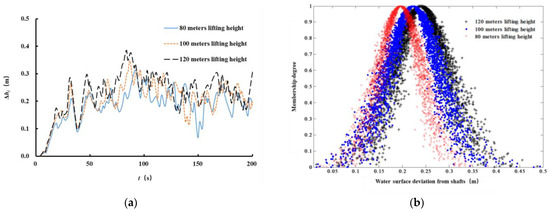
Figure 12.
Water surface deviation from the shafts in the filling–emptying system with an equal inertial pipeline under 100 m lifting height: (a) the diagram of water surface deviation from the shafts and (b) the cloud model expression.
In addition, the risk warning thresholds of water surface deviation from the shafts under the lifting heights of 80 m, 100 m and 120 m were predicted and statistically analyzed. The threshold of risk warning was computed by the numerical simulation of a similar hydro-floating ship lift, as shown in Table 3. Therefore, the increase in lifting height forces the water surface deviation from the shafts to increase, and the hydrodynamic risk was greatly increased in the equal inertial pipeline filling–emptying system.

Table 3.
Early warning threshold of water surface deviation from the shafts under different lifting heights in the filling–emptying system with an equal inertial pipeline.
4.2. Risk Analysis of Water Surface Deviation from the shafts in the Longitudinal Culvert
Taking the lifting height of 150 m as an example, two kinds of filling–emptying system (equal inertial pipeline and longitudinal culvert) were compared, as shown in Figure 13 and Figure 14. The flow uniformity of the branch outlet and water surface deviation from the shafts in the two kinds of filling–emptying systems were analyzed, respectively. A three-dimensional numerical model was applied to analyze the running process of the equal inertial pipeline and longitudinal culvert filling–emptying system at the lifting height of 150 m.
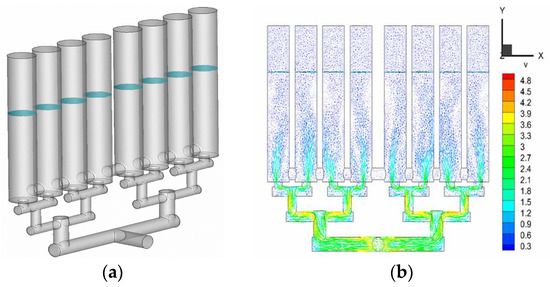
Figure 13.
Hydrodynamic characteristics of the equal inertial pipeline filling–emptying system under the condition of a 150 m lifting height: (a) the diagram of the vertical shaft water level and (b) longitudinal profile velocity.
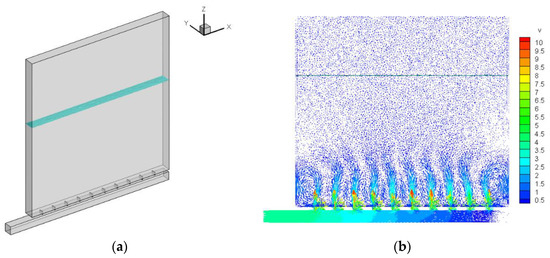
Figure 14.
Hydrodynamic characteristics of the longitudinal culvert filling–emptying system under the condition of a 150 m lifting height: (a) the diagram of the vertical shaft water level and (b) longitudinal profile velocity.
- (1)
- Flow of branch outlet
The change process of each branch outlet flow qi within the first 200 s at the lifting height of 150 m is shown in Figure 15. In the filling–emptying system, the flow rate deviation of each branch outlet became larger with the gradual increase of the flow rate of branch outlet.
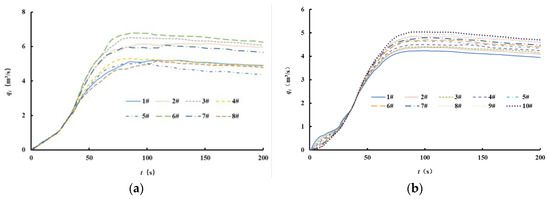
Figure 15.
The change process of each branch outlet flow in the filling–emptying system under the condition of a 150 m lifting height: (a) the diagram of an equal inertial pipeline and (b) the longitudinal culvert.
Furthermore, the Dq between the flow rate of each branch outlet and the average flow rate was calculated as shown in Figure 16. In the running of the equal inertial pipeline filling–emptying system, the maximum Dq of each branch outlet flow rate exceeded 1.0 m3/s. However, the maximum Dq of each branch outlet flow rate was less than 0.4 m3/s in the longitudinal culvert filling–emptying system. Therefore, the longitudinal culvert filling–emptying system performed better than the equal inertial pipeline from the perspective of the branch outflow.
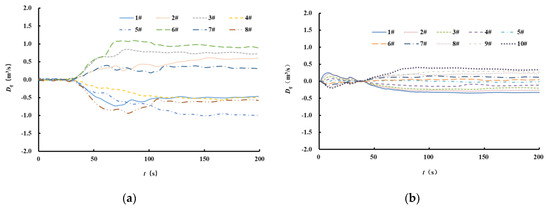
Figure 16.
The Dq process of each branch outlet flow in the filling–emptying system under the condition of a 150 m lifting height: (a) the diagram of the equal inertial pipeline and (b) the longitudinal culvert.
- (2)
- Water surface deviation from the shafts
The change process of water surface deviation from the shafts in the first 200 s under the condition of a 150 m lifting height is shown in Figure 17. The water surface deviation from the shafts between the equal inertial pipeline and longitudinal culvert filling–emptying systems was compared and analyzed. In the equal inertial pipeline filling–emptying system, the maximum value of water surface deviation from the shafts exceeded 0.8 m. However, the maximum value of water surface deviation from the shafts was less than 0.35 m in the longitudinal culvert filling–emptying system. Thus, the longitudinal culvert filling–emptying system was better able to solve the accumulation problem of water surface deviation from the shafts.
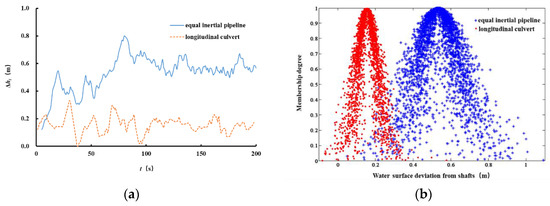
Figure 17.
The change process of water surface deviation from the shafts in the filling–emptying system under the condition of a 150 m lifting height: (a) the diagram of the equal inertial pipeline and (b) the longitudinal culvert.
4.3. Optimization of Water Surface Deviation from the Shafts
Three parameters (Ex, En, He) were used to represent the risk uncertainty of water surface deviation from the shafts. According to the analysis of the cloud model, three parameters of the filling–emptying system are presented in Table 4.

Table 4.
Three parameters of water surface deviation from the shafts in the filling–emptying system under the condition of a 150 m lifting height.
As shown in Table 4, with the increase in lifting height (from 66.86 m to 150 m), the values of the three parameters (Ex, En and He) increased from (0.1199, 0.0149 and 0.0015) to (0.5334, 0.1131 and 0.0494), respectively, in the equal inertia pipeline filling–emptying system. The three parameters showed that the expected value of water surface deviation from the shafts increased gradually and the uncertainty of water surface deviation from the shafts was more discrete in the equal inertial pipeline filling–emptying system. Therefore, there was an obvious uncertainty in water surface deviation from the shafts in the equal inertia pipeline filling–emptying system, which would increase the running risk of hydro-floating ship lifts. The reasons for the risk uncertainty are as follows: (1) due to space limitations of structural design, the straight pipe in front of the diversion port is short, and the flow is not smooth before diversion, which affects the next stage diversion of the flow; (2) the unsteady turbulence intensity in the pipeline is large and the flow field is complex, which has an adverse effect on the uniformity of the diversion; (3) each shaft is independent of others, and water surface deviation from the shafts cannot be adjusted and balanced quickly, which inevitably leads to the more discrete uncertainty of water surface deviation from the shafts; and (4) the uneven discharge outflow of the branch holes and the independence between the shafts leads to water surface deviation from the shafts, and water surface deviation from the shafts cannot be eliminated quickly.
Fortunately, the layout of a longitudinal culvert was applied for the optimization of running safety in the filling–emptying system, which significantly reduced the uncertainty of water surface deviation from the shafts. The values of the three parameters (Ex, En and He) in the longitudinal culvert filling–emptying system under the condition of a 150 m lifting height were 0.1545, 0.0531 and 0.0198, respectively, which were smaller than the values (0.5334, 0.1131 and 0.0494) of the equal inertial pipeline. The shaft of the longitudinal culvert filling–emptying system was arranged in the layout type of connected cuboids. The advantage of this design is that the water area is connected; even if there is water surface deviation from the upstream and downstream, water surface deviation from the shafts can be adjusted and balanced quickly, and the uncertainty problem of water surface deviation from the shafts can be eliminated. The water area of the shaft is completely connected to save space, the thickness of the water cushion is greatly increased, and the disturbance of the branch outlet flow is reduced. This can better achieve the synchronous lifting of the water surface among the shafts. Under the condition of a 150 m lifting height, the maximum longitudinal culvert in the longitudinal culvert filling–emptying system was 0.33 m, which was far less than the 0.82 m of the equal inertia pipeline. The results show that the optimized layout of a filling–emptying system (longitudinal culvert) has better outlet uniformity and synchronization of the water surface among the shafts. Thus, the longitudinal culvert filling–emptying system can better solve the uncertainty problem of water surface deviation from the shafts compared with the equal inertia pipeline filling–emptying system, which can reduce the running risks of the filling–emptying system and has greater application value in a hydro-floating ship lift.
5. Conclusions
Aiming at solving the hydrodynamic risk of water surface deviation from the shafts in the filling–emptying system of a mega-scale hydro-floating ship lifts, a complete evaluation system and an optimization method for water surface deviation from the shafts were established.
- (1)
- A layout optimization method for the longitudinal culvert filling–emptying system was put forward to be applied in a hydro-floating ship lift. Two kinds of filling–emptying system were compared and analyzed by using a numerical simulation method and cloud model theory.
- (2)
- Taking the engineering project of the Jinghong hydro-floating ship lift as an example, the uniformity of the diverging flow and synchronicity of the water level among the shafts showed a chaotic trend in the equal inertial pipeline filling–emptying system under the condition of a 100 m scale lifting height. The lifting height forces the water surface deviation from the shafts to increase, and the hydrodynamic risk will therefore be greatly increased.
- (3)
- To analyze the hydrodynamic risk of water surface deviation from the shafts, two kinds of filling–emptying systems (equal inertial pipeline and longitudinal culvert) were compared with each other under the condition of a 150 m lifting height. The longitudinal culvert filling–emptying system was better than the equal inertial pipeline in the branch outflow and better able to solve the risk problem of water surface deviation from the shafts.
- (4)
- A longitudinal culvert was applied for the optimization of running safety in the filling–emptying system. Three parameters (Ex, En, He) showed that the layout of the longitudinal culvert significantly reduced the uncertainty of water surface deviation from the shafts.
This approach provides a new guideline for the risk management of water surface deviation from the shafts and could effectively control the hydrodynamic risk of water surface deviation from the shafts. As an effective integration of the numerical simulation method and cloud model theory, this will have broad prospects in the decision-making process for risk prevention for hydro-floating ship lifts and even other water conservancy projects.
Author Contributions
Conceptualization, J.L. and Y.H.; methodology, J.L.; software, Z.L.; validation, Y.H., Z.L., S.X. and J.L.; formal analysis, J.L.; investigation, J.L.; resources, Y.H.; data curation, S.X.; writing—original draft preparation, J.L.; writing—review and editing, J.L.; visualization, J.L.; supervision, Y.H.; project administration, Y.H.; funding acquisition, Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was jointly funded by the National Key Research and Development Program of China (2016YFC0402007), China Huaneng Headquarters Science and Technology Project (HNKJ17-H19), and Research Projects of Nanjing Hydraulic Research Institute (LB21902).
Acknowledgments
The authors sincerely thank the reviewers who contributed their expertise and time on reviewing this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hu, Y.; Li, Z.; Li, Y.; Xuan, G. Research developments in the field of major ship lift in China. Port Waterw. Eng. 2016, 12, 10–19. (In Chinese) [Google Scholar] [CrossRef]
- Li, K.; Yi, Z.; Ling, C.; Yuan, Z.; Jiang, X. Weight minimization of ship chamber structure in vertical ship lift design based on multi-level structural optimization method. J. Mar. Sci. Technol. 2018, 26, 562–574. [Google Scholar] [CrossRef]
- Zhong, Y.; Tu, J.; Que, G.; Tu, B.; Xu, J. Analysis and control of the coupled vibration between the ship lift and ship chamber. Int. J. Civ. Eng. 2016, 14, 307–324. [Google Scholar] [CrossRef]
- Liu, J.; Hu, Y.; Xue, S. Risk assessment of water conveyance system in hydraulic ship lift based on cloud model. Port Waterw. Eng. 2020, 9, 14–18. (In Chinese) [Google Scholar] [CrossRef]
- Shi, D.; Cai, D.; Wu, Z. Finite element analysis on nut post structure of Three Gorges Project ship lift. J. Cent. South Univ. Technol. 2009, 16, 0614–0620. [Google Scholar] [CrossRef]
- Wang, J.; Wang, M.; Zhou, J.; Zuo, Q.; Shi, X. Simulation based optimal evacuation plan in vertical ship lift: A case study. Eng. Comput. 2020, 37, 1757–1786. [Google Scholar] [CrossRef]
- Zhou, Y. Fuzzy semi-active control and analysis of wind-induced vibration of a ship lift. Mater. Struct. 2015, 48, 3307–3316. [Google Scholar] [CrossRef]
- Shi, D.; Wang, Y.; Peng, H.; Zhao, T.; Cheng, S. Finite element and experimental analysis of pinion bracket-assembly of three gorges project ship lift. J. Cent. South Univ. 2015, 22, 1307–1314. [Google Scholar] [CrossRef]
- Ma, H.; Cao, X. Research on the key technologies of hydraulic new type ship lift. J. Hydraul. Eng. 2018, 49, 446–455. (In Chinese) [Google Scholar] [CrossRef]
- Liu, J.; Hu, Y.; Xue, S.; Li, Z. Risk analysis of important risk sources for running safety of hydraulic ship lift. Port Waterw. Eng. 2020, 12, 27–32. (In Chinese) [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, O.E.; Mora-Meliá, D.; Iglesias-Rey, P.L. Hydraulic modeling during filling and emptying processes in pressurized pipelines: A literature review. Urban Water J. 2019, 16, 299–311. [Google Scholar] [CrossRef]
- Schindfessel, L.; Mulder, T.; Creelle, S.; Schohl, G. On analytical formulae for navigation lock filling–emptying and overtravel. J. Hydraul. Res. 2015, 53, 134–148. [Google Scholar] [CrossRef][Green Version]
- Hite, J.E.; Stockstill, R.L. Hydraulic design of a longitudinal culvert for lock filling and emptying systems. J. Hydraul. Eng. 2004, 130, 381–388. [Google Scholar] [CrossRef]
- Gobbetti, L. Design of the filling and emptying system of the new Panama Canal locks. J. Appl. Water Eng. Res. 2013, 1, 28–38. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, J.; Wu, Y.; Cao, Y. Numerical simulation of water conveyance system in hydraulic floating shiplift. J. Hydraul. Eng. 2007, 38, 624–629. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, R.; Wu, Y.; Zhang, J.; Zhang, D.; Gao, J. Numerical simulation on synchronous characteristic of the shafts’ water levels in Jinghong hydraulic floating ship lift. J. Hydrodyn. 2007, 22, 31–39. (In Chinese) [Google Scholar] [CrossRef]
- Li, S.; Zhou, X.; Wang, Y.; Zhou, J.; Du, X.; Chen, Z. Study of risk acceptance criteria for dams. Sci. China Technol. Sci. 2015, 58, 1263–1271. [Google Scholar] [CrossRef]
- Morales-Torres, A.; Escuder-Bueno, I.; Serrano-Lombillo, A.; Castillo Rodríguez, J. Dealing with epistemic uncertainty in risk-informed decision making for dam safety management. Reliab. Eng. Syst. Saf. 2019, 191, 106562. [Google Scholar] [CrossRef]
- Morales-Torres, A.; Serrano-Lombillo, A.; Escuder-Bueno, I.; Altarejos-García, L. The suitability of risk reduction indicators to inform dam safety management. Struct. Infrastruct. Eng. 2016, 12, 1465–1476. [Google Scholar] [CrossRef]
- Serrano-Lombillo, A.; Morales-Torres, A.; Escuder-Bueno, I.; Altarejos-García, L. A new risk reduction indicator for dam safety management combining efficiency and equity principles. Struct. Infrastruct. Eng. 2017, 13, 1157–1166. [Google Scholar] [CrossRef]
- Delenne, C.; Cappelaere, B.; Guinot, V. Uncertainty analysis of river flooding and dam failure risks using local sensitivity computations. Reliab. Eng. Syst. Saf. 2012, 107, 171–183. [Google Scholar] [CrossRef]
- Chen, H.; Mehrabani, M. Reliability analysis and optimum maintenance of coastal flood defences using probabilistic deterioration modelling. Reliab. Eng. Syst. Saf. 2019, 185, 163–174. [Google Scholar] [CrossRef]
- Gersonius, B.; Morselt, T.; Nieuwenhuijzen, L.; Ashley, R.; Zevenbergen, C. How the failure to account for flexibility in the economic analysis of flood risk and coastal management strategies can result in maladaptive decisions. J. Waterw. Port Coast. Ocean Eng. 2012, 138, 386–393. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, W.; Chen, Y.; Hu, R.; Wei, K. Inverse modeling of leakage through a rockfill dam foundation during its construction stage using transient flow model, neural network and genetic algorithm. Eng. Geol. 2015, 187, 183–195. [Google Scholar] [CrossRef]
- Chang, L. Guiding rational reservoir flood operation using penalty-type genetic algorithm. J. Hydrol. 2008, 354, 65–74. [Google Scholar] [CrossRef]
- Lei, X.; Zhang, J.; Wang, H.; Wang, M.; Khu, S.; Li, Z.; Tan, Q. Deriving mixed reservoir operating rules for flood control based on weighted non-dominated sorting genetic algorithm II. J. Hydrol. 2018, 564, 967–983. [Google Scholar] [CrossRef]
- Park, C.; Joo, J.; Kim, J. Integrated washland optimization model for flood mitigation using multi-objective genetic algorithm. J. Hydro-Environ. Res. 2012, 6, 119–126. [Google Scholar] [CrossRef]
- Kalinina, A.; Spada, M.; Burgherr, P. Application of a Bayesian hierarchical modeling for risk assessment of accidents at hydropower dams. Saf. Sci. 2018, 110, 164–177. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.; An, R.; Zhu, F.; Xu, B. Risk analysis for real-time flood control operation of a multi-reservoir system using a dynamic Bayesian network. Environ. Modell. Softw. 2019, 111, 409–420. [Google Scholar] [CrossRef]
- Xiang, M.; Lin, X.; Yang, X.; Zhang, S. Ecological environment evaluation of forest ecosystem nature reserves using an unweighted cloud model. Water 2020, 12, 1905. [Google Scholar] [CrossRef]
- Wang, X.; Shi, K.; Shi, Q.; Dong, H.; Chen, M. A Normal Cloud Model-Based Method for Risk Assessment of Water Inrush and Its Application in a Super-Long Tunnel Constructed by a Tunnel Boring Machine in the Arid Area of Northwest China. Water 2020, 12, 644. [Google Scholar] [CrossRef]
- Yang, S.; Han, X.; Cao, B.; Li, B.; Yan, F. Cloud-model-based method for risk assessment of mountain torrent disasters. Water 2018, 10, 830. [Google Scholar] [CrossRef]
- Li, D.; Meng, H.; Shi, X. Membership clouds and membership cloud generators. J. Comput. Res. Dev. 1995, 6, 15–20. (In Chinese) [Google Scholar]
- Li, D.; Liu, C.; Gan, W. A new cognitive model: Cloud model. Int. J. Intell. Syst. 2009, 24, 357–375. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).