Abstract
The flood travel time (FTT) along the Longmen-Tongguan Reach, part of the stem channel of the Middle Yellow River, is shorter than 30 h, and estimating the FTT of different discharges propagating from Wubu Hydrology Station to Tongguan Hydrology Station is necessary. However, the propagation of floods in this river network, the main channel of the Wubu-Tongguan Reach and related tributaries, has rarely been analyzed due to the lack of geometry data. Thus, a one-dimensional (1D) dynamic model was selected to simulate the FTT along the WT reach. Firstly, the 1986 flood event was selected to calibrate the physical parameters in the hydraulic model. Secondly, the FTT with different discharges (500–9000 m3/s) were estimated with calibrated parameters. Thirdly, an empirical formula based on simulated results was fitted. This empirical formula could be used to describe the relation between discharges, distances to Tongguan Hydrology Station, and the FTT. Analyses showed that the discharges with minimum FTT were different for different tributaries. For the river reach between Wubu Hydrology Station and the Wuding River, the discharge and corresponding minimum FTT were 6000 m3/s and approximately 30.4–34 h, respectively. For the river reach between the Zhouchuan and Qingjian Rivers, the discharge and FTT were 3000–3500 m3/s and 21–26.8 h, respectively. The formula can be used to estimate the FTT of flood events, which would be cost-saving and time-saving for river management. Sensitivity analyses indicated that the FTT were sensitive to the Tongguan elevation and Manning’s roughness coefficient in the main channel.
1. Introduction
The flood travel time (FTT) of floods in river channel and reservoir is a subject of interest for the civil engineers, as it relates to forecasting floods in river channel and the operation of related reservoir, such as the compound operation of the Sanmenxia and Xiaolangdi Reservoir [1,2,3,4]. There are two ways to estimate the FTT, simulating the flood routing and estimate the FTT based on historical data. The simulation method includes the hydrologic model [2,5,6,7,8] or hydraulic model. Qiao et al. [4] developed a new automated computation system based on a vector-based river routing model. Yan et al. [2] developed the discrete generalized Nash model, and compared with the Muskingum method and dynamic wave model. Rong et al. [9] investigated the hydraulic characteristics of the dam discharge flow with a three-dimensional numerical model. Wang et al. [1] simulated and analyzed the FTT of flood along the Tarim River with a one-dimensional hydraulic model. Based on the hydraulic model of MIKE11, Cheng et al. [10] analyzed the FTT of surge wave along the upper Jingjiang Reach as influenced by the operation of the Three Gorges Dam. Li et al. [11] simulated the FTT along the lower Yellow River with MIKE11. They concluded that the FTT along the Lower Yellow River has been shortened [11]. The second category of methods for estimating FTT is based on historical data [12,13,14,15]. Based on historical data, Yang [12] estimated the relationship between discharge and FTT in unit channel length, and it improved the forecasting precision of FTT. Li and Cui [15] analyzed the average FTT along the Longmen-Tongguan Reach (LT Reach) with measured data of flood events.
The FTT along the Middle Yellow River (YR), which is important for river management, flood control and disaster reduction, is influenced by channel boundary conditions and the characteristics of floods. The estimation of FTT along the YR is relatively rare, especially the estimation of floods at Tongguan Hydrology Station [11,15]. With measured flood data of 50 floods occurred in 1960–2015, Li and Cui [15] pointed out that the average FTT with discharge larger than 6000 m3/s along the LT reach is 15.2 h, and it increases after 1986 and reaches its maximum value in 2003. Then, the average FTT is shortened to 20 h in recent year [15]. The forecasting requirement of the Tongguan Hydrology Station proposed by the River Management Institute is 30 h. As the FTT along the LT reach has is shorter than 30 h, the investigation of FTT along an extended river reach than the LT reach, namely the reach of Wubu-Tongguan (WT Reach), is necessary [16,17]. As the FTT is related to the magnitude of flood, it would be necessary to establish a relationship between discharge and FTT.
More than 70% of the water runoff observed at Tongguan Station comes from the Longmen Hydrology Station (data from 1950–2015), while floods in the Longmen Hydrology Station mainly consist of floods from the main channel (Wubu Hydrology Station) and tributaries of the middle YR such as the Wuding, Quchan, and Yanshui Rivers [5,18,19]. There are hydrology stations situated on most of the tributaries in the middle YR basin, and the area where water runoff and sediment load could not be measured only counts for about 2.2% of that of the Longmen Hydrology Station [20]. In total, runoff and sediment load at the Tongguan Hydrology Station concerns a river network with a large drainage area where water and sediment load could be measured at numbers of hydrology stations situated on the stem channel and tributaries, and forecasting requirement is a question of estimating the FTT of floods from hydrology stations for both the main channel and tributaries.
For a certain discharge, the FTT of floods from different tributaries varies due to its different distances to the Tongguan Station. The FTT of floods from different tributaries of the middle YR should be identified differently. In order to meet the demand of up to a 30 h-forecast in advance at Tongguan Hydrology Station by the Yellow River Conservancy Commission (YRCC, for the compound operation of the Sanmenxia and Xiaolangdi Reservoirs), the main purpose of this paper was to find an experimental formula based on simulated results by a dynamic model. Firstly, the physical parameters of this river network were calibrated by simulating the 1986 flood event with an established dynamic model. Secondly, based on the calibrated parameters, the FTT of floods with different discharges along the WT Reach were estimated. Thirdly, the relationship between discharges, distances to Tongguan, and FTTs were drawn by line fitting. Finally, the sensitivities of physical parameters are further discussed.
2. Drainage Area
The reach between the Wubu and Tongguan Hydrology Stations, namely the WT Reach, is part of the middle YR (Figure 1a). There are two sub-reaches, the sub-reach between Wubu and Longmen Hydrology Stations (WL Reach) and the reach between Longmen and Tongguan Hydrology Stations (LT Reach), as shown in Figure 1b.
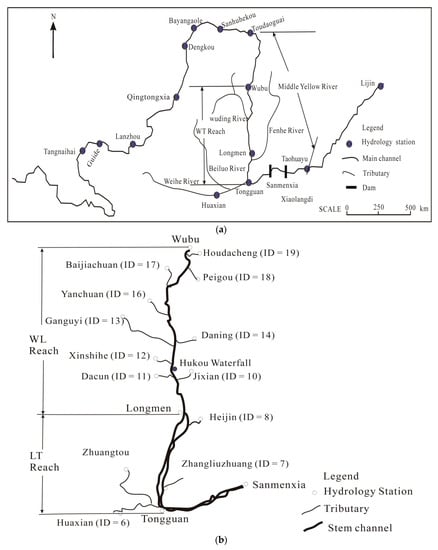
Figure 1.
The Yellow River (YR) basin (a); and sketch map of tributaries of the Wubu-Tongguan (WT) Reach (b).
The main channel of the WL Reach is part of the Jin-Shaan gorges, and the Hukou Waterfall is located in this reach [21]. The drainage area between these two stations is part of the Loess Plateau, which leads to high-sediment-contained floods.
There are various tributaries flowing into the main channel of the WL Reach [22]. Water runoff and sediment load originating from more than 97% of tributaries’ drainage area between the Wubu and Longmen Hydrology Stations can be measured by hydrology stations located on tributaries [20]. All of these tributaries are numbered with a specific number (ID) [20] (Figure 1b and Table 1). Tributaries that flow into the WL Reach are tributaries with IDs of 10 to 19. These tributaries are characterized with a high sediment modus, and hyper-concentrated floods can usually be detected. Moreover, sediments eroded from these tributaries are relatively coarse. In order to make it more readable, the tributaries mentioned below have also been termed with ID numbers. The ID number helps to identify the relative sequence where the tributary flows into the main channel as the ID values decrease from upstream to downstream.

Table 1.
Summation of tributaries along the Wubu-Longmen (WL) Reach.
The two major tributaries flowing into the LT Reach are the Weihe (ID = 6) and Fenhe Rivers (ID = 8), as shown in Figure 1b. The LT Reach is a wandering one, and cross sections in this reach are compound ones, which lead to serious deposition. Another tributary flowing into the LT Reach is the Beiluo River, which flows into the Weihe River near the Tongguan Hydrology Station (Figure 1b), and can be viewed as a tributary directly flowing into the YR. The tributary of Sushuihe River (ID = 7) was not considered as its small floods. The same applies to tributaries with the IDs of 15 and 9.
3. Methodology and Data
One-dimensional (1D) hydraulic model is widely adopted in hydraulics due to their low computational cost [23,24,25,26]. There are several additional problems needing further calibration for the WT Reach. First, the measured geometry data for only two cross-sections (namely the Wubu and Longmen Stations) are available in the WL Reach in yearbooks, while the distance between these two cross-sections is about 273 km. Secondly, in order to identify the FTT of floods from different tributaries in the WL Reach, the location of these tributaries and the corresponding channel geometry are important factors. Thirdly, the traveling of floods along the Hukou Waterfall should be calibrated.
Thus, a historical flood event was simulated with a dynamic model to calibrate the related physical parameters by comparing with measured data. After calibration, parameters were adopted in the model to estimate the FTT of floods with different discharges.
3.1. Hydraulic Models
Controlling equations for the hydraulic model are composed of mass and momentum conservation equations, and equations of sediment convection-diffusion and bed deformation. These equations have also been used in models by He et al. [27,28]:
where and are the time and longitudinal distance, respectively, and are the elevation and discharge, respectively, and are the flow area and mobile bed area, respectively, is the width of the wetted area, is flow depth at centroid of a cross section, and it is calculated as , in which is flow depth, is vertical distance from bed, and is width of cross-section at distance from bed, and is the hydraulic radius. The density of the sediment-laden flow can be estimated as , where , , and are the densities of water, suspended sediment, and bed material, respectively. is the gravitational acceleration, is Manning’s roughness coefficient, and is the recovery coefficient (1.0 for erosion, 0.25 for deposition). Volumetric concentration can be estimated as , where is the volumetric concentration of th-sized group of suspended sediment load. and are the inflow discharge per distance (m3/(s × m)) and velocity of tributary, respectively, and are the volumetric suspended sediment concentration and density of the tributary, respectively, and are the volumetric carrying capacity and settling velocity of the th-sized sediment group, respectively, and are the entrainment rate and deposition rate at the interface between the bed load and suspended load, respectively, and , . , , and are summations of all sized sediment groups and denotes the porosity of the bed material.
As a wandering river reach, previous research has mainly focused on describing the channel sedimentation along the LT Reach [29]. However, the WL Reach is a canyon one, and research has rarely focused on simulating the WL Reach or the WT Reach [30,31]. The finite volume method was adopted to simulate the FTT along the WT Reach [27,28]. A non-equilibrium sediment transport algorithm was adopted for the channels downstream of the Longmen Hydrology Station [27,28]. The necessary equations, including formulas for sediment carrying capacity and settling velocity, are the same as in reference [27].
3.2. FTT of Floods with Different Peak Discharges
In order to make a comparison, two different methods were adopted to estimate the wave speed. The wave speed of floods were estimated with dynamic wave (Method 1) and kinematic wave (Method 2):
where is the wave speed, u is the cross-sectional averaged velocity, is the cross-sectional water depth, and is a coefficient ().
The FTT of flood routing along a specific reach is related to the wave speed and its length [32]:
where is the FTT between sections and (s) and is the distance between the two cross-sections ( and ) (m). After the calibration of related parameters, the FTT of floods with different peak discharges can be estimated.
3.3. Data
Huaxian Hydrology Station is a station located on the lower stem channel of the Weihe River (ID = 6). As a tributary of the Weihe River, the Beiluo River flows into the Weihe River at a cross-section down the Huaxian Hydrology Station (as shown in Figure 1a). It means that discharge and sediment load from the Beiluo River are not counted at the Huaxian Hydrology Station. Thus, the Beiluo River was also considered in the simulation [33]. The three tributaries with IDs of 7, 9, and 15 were not considered as mentioned before.
3.3.1. Geometry Data of the Main Channel
The geometry data of the WL and LT Reaches were treated separately. For the WL Reach, the geometry data of only two cross-sections are available from the YRCC, namely the Wubu and Longmen Hydrology Stations. The channel slope of the WL Reach is approximately 0.03%–0.06%, and the length is approximately 723 km. The width of the WL Reach, except for the Hukou Waterfall, is approximately 400–600 m [22,34]. For convenience when estimating the FTT of floods from tributaries, two cross-sections on the main channel were interpolated for each tributary, which represent the cross-sections upstream and downstream the inflow of the tributary, respectively. There were nine tributaries (ID = 10–14, and ID = 16–19), and 18 interpolated cross-sections on the main channel of the WL Reach. The geometries of the 18 interpolated cross-sections are supposed to be similar with the measured cross-section at the Wubu Hydrology Station, with its elevation being interpolated according to the slope of the WL Reach and their distances from the Wubu Hydrology Station. It means that the geometry of the 18 interpolated cross sections has a similar shape with Figure 2a, but the elevation changes, as shown in Figure 2d.
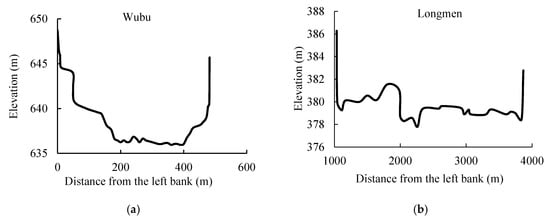
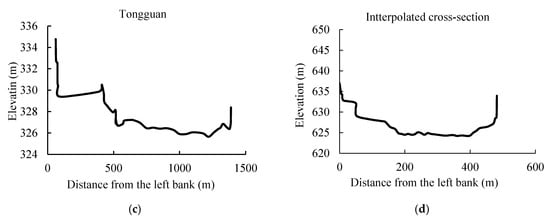
Figure 2.
Cross sections of the Wubu (a); Longmen (b); and Tongguan (c) Hydrology Stations; and one typical interpolated cross-section in the WL Reach (d).
The Hukou Waterfall is located in the WL Reach (Figure 1b), and two cross-sections were additionally interpolated. According to the geometry of the river reach around the Hukou Waterfall, these two interpolated cross-sections representing the upstream and downstream boundaries of the Hukou Waterfall were simplified as rectangular [21]. The width of the sections upstream of the Hukou Waterfall is approximately 300 m, and the drop of the fall is approximately 30 m [35]. The interpolated section upstream of the Hukou Waterfall was supposed to be 300 m upstream of the Hukou Waterfall. The interpolated section downstream the Hukou Waterfall was assumed to be 4.5 km downstream of the Hukou Waterfall, and the width and depth are approximately 50 m and 30 m, respectively. The 4.5-km long reach down the Hukou Waterfall is known as Shili Longcao. With these two additional interpolated sections, the FTT along the reach around the Hukou Waterfall can be described.
Finally, there are 22 cross-sections in the WL reach. The geometry data of the Wubu and Longmen Stations were measured in 1991 (Figure 2a,b). The WL Reach is a relatively balanced river reach as to erosion and deposition occurred, and these geometry data can be used to represent the up-to-date geometry.
Geometry data of the cross-sections in the LT Reach were measured in 2010 (typical cross-section as shown in Figure 3c). There are 29 cross-sections, and the average distance between two adjacent cross-sections is approximately 4.7 km, with a minimum value of 1.42 km. These geometry data were measured and published by the YRCC before the flood season.
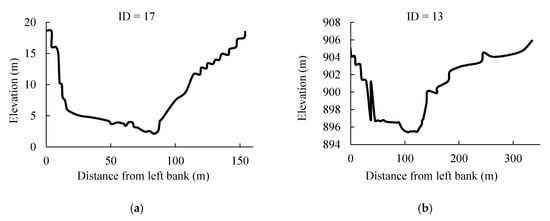
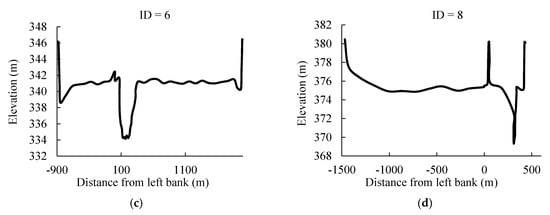
Figure 3.
Cross sections of hydrology stations of typical tributaries, (a) tributary with ID = 17, the Wuding River; (b) tributary with ID = 13, the Yanshui River; (c) tributary with ID = 6, the Lower Weihe River; and (d) tributary with ID = 8, the Fenhe River.
Manning’s roughness coefficient needs to be specified empirically. Manning’s roughness coefficient is approximately 0.035–0.04 (m−1/3 × s) in the floodplain of the YR [27,36]. According to the measured water stage () and discharge () at each hydrology station, the stage-versus-discharge curves at hydrology stations could be determined. Adding the geometry data of each hydrology station, the Manning’s roughness coefficients () of the main channel were back-calculated with , where hydraulic radius and is the measured slope [27]. According to these estimated Manning’s roughness coefficients at hydrology stations, the coefficients at sections between two adjacent hydrology stations were linearly interpolated [27]. For example, the Manning’s roughness coefficients at Wubu, Longmen and Tongguan Hydrology Stations were back-calculated, while coefficients at the other cross-sections were linearly interpolated.
3.3.2. Geometry Data of Tributaries
For each tributary, the FTT of floods running from its hydrology station to the stem channel was also considered. Distances between the hydrology stations and the stem channel were summarized in Table 1, with a range of 0–112 km. It also indicates that the drainage areas upper these hydrology stations were different from that of the corresponding tributaries. The drainage area where water runoff and sediment load originating from were not measured is approximately 1.083 × 104 km2, and it accounts for approximately 2.2% of the area of the Longmen Hydrology Station [20].
The topography data of the hydrology stations of all of these tributaries are also necessary for numerically simulating its FTT. Topography data of the hydrology stations of the tributaries were collected, which were measured in 2007 (Figure 3). The topography data of the hydrology station of the Beiluo River were measured in 1986. With the geometry data of the hydrology stations, the relationship between the sectional average velocities and discharges could be estimated. Adding the information of the river length from its hydrology station to the stem channel, the FTT of floods with different discharges could be estimated by the numerical model and Equations (5)–(7).
3.3.3. Boundary Condition
Boundary conditions include upstream and downstream boundary conditions.
For calibration, the upstream boundary conditions were hydrographs of discharge and sediment concentration measured at the inlet sections including cross sections of the stem channel and tributaries. These data were measured in 1986 and published by the YRCC. The LT Reach has experienced deposition since 1986. Thus, the geometry data of the channel used in calibration, as described in Section 3.3.1 and Section 3.3.2, may be different with that measured in 1986. The corresponding inaccuracies of estimated FTT were discussed in Section 4.4. For estimating the FTT, the upstream boundary conditions are floods with different discharges.
The downstream boundary condition is the water elevation of the outlet section at Tongguan Hydrology Station. For parameter calibration, the downstream boundary conditions were estimated with the measured stage and discharge in 1986 at Tongguan. For application in estimating the FTT, the back-calculated water stage using the measured stage-versus-discharge rating curve at the Tongguan Hydrology Station may lead to some uncertainties, which were discussed in Section 4.4.
4. Results and Discussion
Analyses of the measured data showed that the FTT of flood events could hardly be identified merely with the peak discharges, as there were phase lags between the peak discharges in tributaries and that of the main channel. Thus, the numerical simulated results were analyzed herein.
4.1. Calibration of Physical Parameters by Selected Flood Event
The 1986 flood event was adopted to calibrate the physical parameters by numerically simulating the measured flood event. The simulated reach was the WT Reach; flood traveling along the lower Weihe River (ID = 6) was also simulated. The Beiluo and Fenhe (ID = 8) Rivers were treated as lateral inflows during simulation. This means that the flood traveling in these two tributaries were not simulated. The simulated results are shown in Figure 4. Comparisons between the simulated and measured hydrographs of the discharge and sediment concentration showed that both the flood peak and its occurrence time at Longmen could be simulated properly.
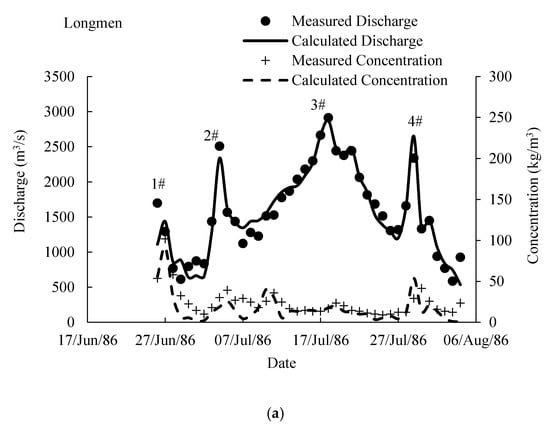
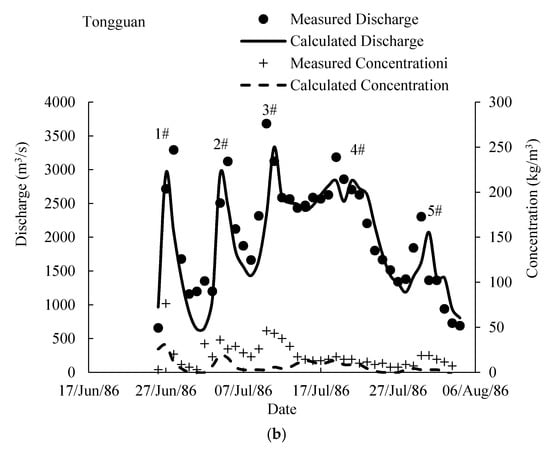
Figure 4.
Measured and simulated hydrographs of the discharge and concentration of the flood event that occurred in 1986 at the Longmen (a) and Tongguan (b) Hydrology Stations.
Four indicators were adopted to evaluate the simulated results: (i) the Nash-Sutcliffe efficiency coefficient (), (ii) the mean absolute relative error (), (iii) the percent error in peak (), and (iv) the error in time to peak flow () [37,38,39,40,41]:
where is the observed value at time step , is the simulated value at time step ; is the mean of the observed values, is the total length of the flow data, is the observed peak flood values at time , is the simulated peak value at time step , is the observed occurrence time of the peak floods, is the simulated occurrence time of the peak floods, and is the total number of flood events.
Figure 4 displays the comparison of the daily hydrographs of discharge and concentration, which may lead to large values of (as the unit is 24 h). Thus, the measured and simulated daily data were evaluated with and , and detailed simulated results (hourly) were compared with the measured flood data by and . According to Figure 4, there were four and five flood events at the Longmen and Tongguan Stations, respectively. The performance evaluations are listed in Table 2 and indicate that the peak values of measured sediment concentration were not simulated very well. The discrepancies of the occurrence time of peak discharge at Tongguan were relatively large. In total, calibrated parameters (including the geometry data of the WL Reach and the Hukou Waterfall) could be adopted to estimate FTT with different discharges along the WT Reach.

Table 2.
Mean values of evaluation indicators of the performance of simulated results.
The average values of Manning’s roughness coefficients in the main channel, the lower floodplain, and the higher floodplain were 0.009 m−1/3 × s, 0.035 m−1/3 × s, and 0.04 m−1/3 × s, respectively. Manning’s roughness coefficients of the main channel used in simulating the 1977 flood event, 2007 flood event, and 2009 flood event varied between 0.009–0.011 [16,28]. Thus, the Manning’s roughness coefficients in this model are reasonable.
Then, the calibration of FTTs with measured data was conducted by comparing with measured data. In Method 2, three different -values ( = 1, 1.5, and 2) were adopted to make a comparison. The hydrograph data used were measured in 1986, and the measured FTTs were collected based on flood data in 1986. Comparison with measure data were shown in Figure 5. The FTTs estimated by the Method 1 are relatively smaller, while the FTTs estimated by the Method 2 with varies between 1 and 1.5 are close to the measured data.
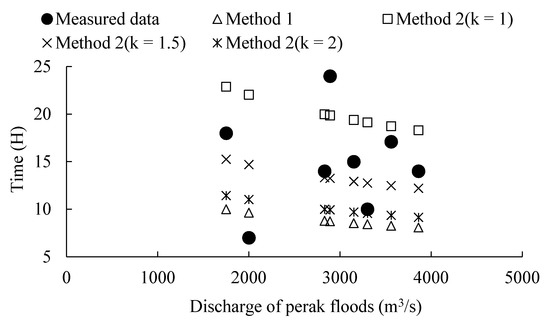
Figure 5.
Comparison between estimated and measured flood travel times (FTTs) of floods in 1986 along the Wubu-Longmen (WL) reach.
4.2. FTT of Floods with Different Discharges
To estimate the FTT of floods with different discharges, calibrated parameters (Manning’s roughness coefficient along the river reach) in the WT Reach were adopted in the model. The analyzed peak discharges were 500–9000 m3/s, with an interval of 500 m3/s. The geometry data of the LT Reach were measured in 2010, and could represent the up-to-date geometry of this river reach. The concentration and related geometry changes were not considered during the estimation of the FTT.
Firstly, the appropriate -value was calibrated with data by floods occurred in 2009 and 2017. As shown in Figure 6, = 1 is adopted in the following analyses.
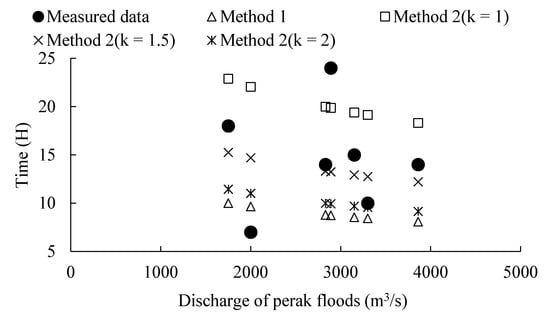
Figure 6.
Comparison between estimated and measured flood travel times (FTTs) of floods along the Wubu-Longmen (WL) Reach, based on geometry data measured in 2010.
Figure 7 shows the relationship between the FTT, discharge, and the longitudinal distance from the Tongguan Hydrology Station. The FTT means the time of floods with different discharges traveling from the local cross-section to the Tongguan Hydrology Station.
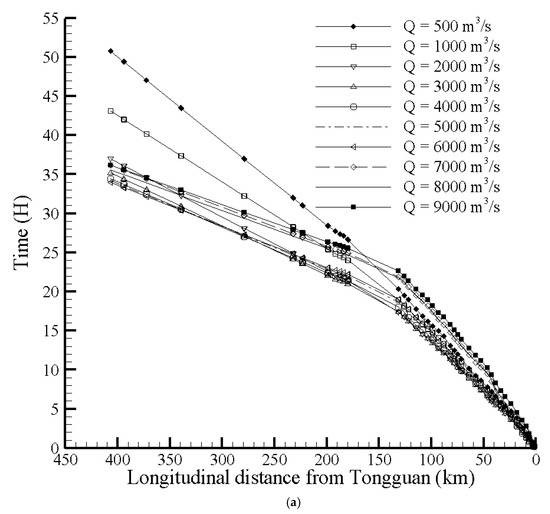
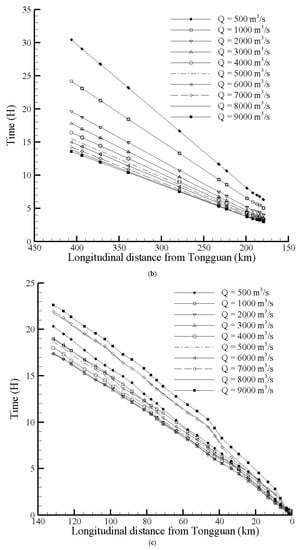
Figure 7.
FTT of floods with different discharges along the Wubu-Tongguan (WT) reach. (a) The Wubu-Tongguan (WT) Reach; (b) The Wubu-Longmen (WL) Reach; (c) The Longmen-Tongguan (LT) Reach.
For the WL Reach (Figure 7b), the FTT was positively related with the distance from Tongguan, and the relationship between the FTT and discharge was negative.
For the LT Reach, the FTT and distance from Tongguan was positively correlated (Figure 7c). However, the relationship between the discharge and FTT was more complex. When the flood discharges range from 500–3000 m3/s, the FTT may decrease with the increased discharge. When discharges are larger than 3000 m3/s, the FTT may increase with the increased discharge.
Coupling the non-linear relation in the LT Reach and the negative relation in the WL Reach, the relationship between the FTT and discharge in the WT reach was much more complex, as shown in Figure 7a.
The discharge with minimum FTT could be detected for each river reach, as shown in Figure 8. In total, the discharge with minimum FTT increased with the longer distance from the Longmen Hydrology Station. For the river reach between Wubu and tributary 17 (this being the conjunction cross-section of this tributary with the main channel, the same below), the discharge with minimum FTT was approximately 6000 m3/s, and the corresponding FTT of floods running to Tongguan was approximately 30.4–34 h. For the river reach of tributaries with IDs of 13 (Yanshui River) and 16 (Qinjian River), the discharge with minimum FTT was approximately 3500 m3/s, and the corresponding FTT of floods running to Tongguan was approximately 23.4–26.8 h. For the river reach of tributaries with IDs of 10 (Zhouchuan River) and 12 (Fenchuan River), the discharge with minimum FTT was approximately 3000–3500 m3/s, and the corresponding FTT of floods running to Tongguan was approximately 21–22 h. The FTT of floods running through the LT Reach was approximately 17.4 h, and the discharge was approximately 3000 m3/s. The bankfull discharge of the LT Reach was approximately 2600 m3/s [42]. Thus, the larger FTT of a larger discharge may be affected by over-flooding in the LT Reach. One important item that should be pointed out is that the minimum FTT and the corresponding discharge may have some inaccuracies, as the interval of the analyzed discharge was 500 m3/s.
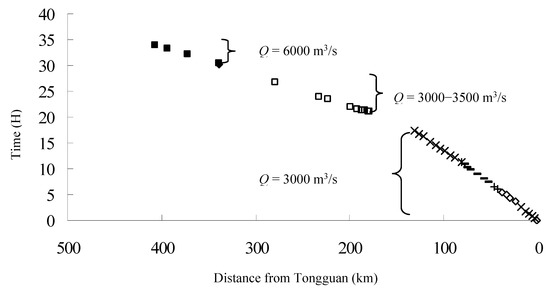
Figure 8.
FTT of floods running through the Wubu-Tongguan (WT) reach.
4.3. Fitted Formula for FTT
Based on the estimated results, the relationship between the FTT and distance from Tongguan Hydrology Station could be fitted for each given discharge.
For different discharges, the FTT of floods along the WL Reach (denoted as ) was linearly correlated with the distance from Tongguan (denoted as ), with . The gradients of the linear relations were highly correlated with the discharges, and could be expressed as (). The intercepts of the linear relations were also correlated with the discharges, and could be expressed as ().
The FTT of floods running through the LT Reach (denoted as ) was linearly correlated with distance from Tongguan (denoted as ), with . The gradients of the linear relations were highly correlated with the discharges, and could be expressed as (). The intercepts of the linear relations were also correlated with the discharges, and could be expressed as ().
In total, the FTT of different discharges could be estimated as:
where is the FTT of floods occurring in the WL Reach running to Longmen (H), is the FTT of floods occurring in the LT Reach running to Tongguan (H), is the distance of sections from Tongguan (km), and is the discharge (m3/s). The coefficients are listed in Table 3.

Table 3.
Coefficients of Equations (12) and (13).
According to Equations (12) and (13), the FTT of flood events or hydrographs of discharge could be estimated. Moreover, the relationship between the discharge and distance from Tongguan can also be determined, as shown in Figure 9, with the parameter of FTT. For tributary 16, the FTT of discharges ranging from 1500–8500 m3/s was less than 30 h, and the FTT of discharges ranging from 4500–7800 m3/s was longer than 30 h. The FTT was approximately 30–35 h for discharges ranging from 3300–9000 m3/s. Thus, real-time measured hydrographs in tributaries with ID ≥ 18 (Quchan River) and forecasting of tributaries with ID ≤ 17 (Wuding River) are necessary for the forecasting requirements of Tongguan Hydrology Station.
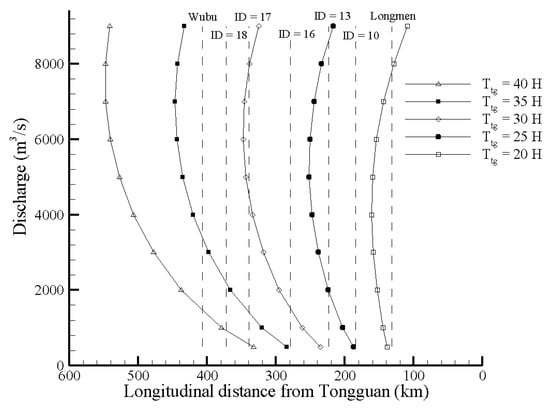
Figure 9.
FTT of floods from tributaries in the Wubu-Tongguan (WT) Reach (based on Equations (12) and (13)).
Measured flood data show that the average FTT in recent year in the LT Reach has shortened to 20 h [15]. It can also be observed in Figure 9. In Figure 9, if the flood peak discharge is larger than 8000 m3/s, the FTT of flood events along the LT Reach may be longer than 20 h. Otherwise, the FTT of flood events along the LT Reach is shorter than 20 h. The FTT for floods with peak discharge larger than 6000 m3/s is almost the maximum one.
4.4. Sensitivity Analysis of Model Parameters
The sensitivity of the estimated results can be evaluated by the generalized likelihood uncertainty estimation (GLUE) [27]. However, the observed FTT of the measured flood events is relatively difficult to identify, as its discharges varied. Thus, the criterion of MARE in Equation (9) was adopted. Here, is the simulated results with calibrated parameters at cross-section , and is the simulated results obtained using varied parameters at cross-section .
Three scenarios were simulated by selecting different drops of the Hukou Waterfall. In the Scenarios “D5,” “D10,” and “D20” Scenarios, the drops of the Hukou Waterfall were 5 m, 10 m, and 20 m, respectively. The calibrated value of the drop was 30 m.
Scenario “W477” was simulated by changing the width of the interpolated cross-sections upstream and downstream of the Hukou Waterfall. In the “W477” Scenario, the widths of these two adjacent cross-sections were the same as that of the Wubu Hydrology Station. The calibrated values of the widths of these two interpolated cross-sections were 300 m and 50 m, respectively.
The Tongguan elevation (water stage of a flood discharge at 1000 m3/s) changed dramatically during 1960–1974 due to the impoundment of the Sanmenxia Reservoir [43]. After 1975, the Tongguan elevation increased at an almost constant rate, and the annual changed elevation was approximately 0.086 m/yr [43]. Two scenarios (TE1 and TE2) were simulated to explore the effect of increased Tongguan elevation.
Another two scenarios were simulated by selecting different Manning’s roughness coefficients in the main channel. In the Scenario “W1,” the Manning’s roughness coefficient in the main channel increased by half, whereas in the Scenario “W2,” it increased to twice that of the calibrated value. Those values are still smaller than the recommended value for floodplain [27,36,44]. Table 4 summarizes the calibration parameters for different scenarios used for sensitivity analyses.

Table 4.
Selected physical variables and scenarios for sensitivity study.
Figure 10 shows the simulated results under those scenarios. The modeling results were very sensitive to the Tongguan elevation and Manning’s roughness coefficient in the main channel. The modeling results were not sensitive to the geometry of the reach around the Hukou Waterfall. On the basis of these results, it can be concluded that the modeled FTT was sensitive to the Tongguan elevation and roughness in the main channel. Fortunately, the Tongguan elevation can be measured every year, and the Manning’s roughness coefficient in the main channel could be back-calculated by up-to-date rating curves. The inaccuracies of the estimated occurring time concerning Tongguan in Table 2 could be partially modified by the newly measured data.
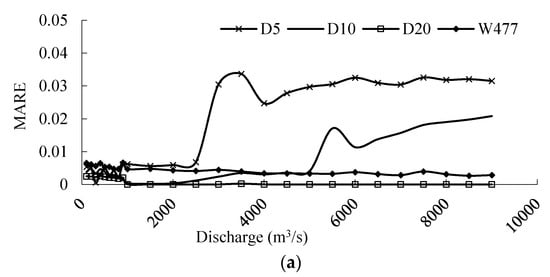
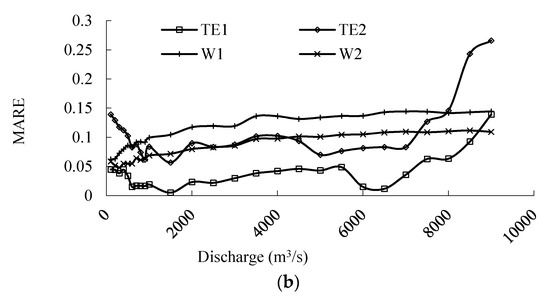
Figure 10.
Sensitivity index values of FTT, (a) and (b) for different physical variables.
It also indicates that more attention should be paid to the largest tributary of the YR, the Weihe River. The Weihe River is characterized with large discharge. Furthermore, floods in the Weihe River flow into the YR at a section near the Tongguan Hydrology Station, which will influence the water stage at Tongguan and the corresponding FTT. Thus, real-time forecasting of inflows from the Weihe River is necessary for the forecasting requirement.
5. Conclusions
The FTT of floods along the Longmen-Tongguan (LT) Reach is shorter than 30 h. Considering the requirements of river management, estimating FTT is necessary. The FTT to the Tongguan Hydrology Station was analyzed in this paper. The conclusions could be drawn as:
- (1)
- The selected dynamic model can be used to simulate the traveling of flood along the Wubu-Tongguan (WT) Reach. This dynamic model could also be used to simulate the flood propagation and estimate the FTT in other drainage areas.
- (2)
- For different river reaches, discharges with minimum FTT are different. For the river reach between Wubu and tributary 17 (Wuding River), the discharge with minimum FTT was approximately 6000 m3/s, and the corresponding FTT was approximately 30.4–34 h. For the river reach between tributaries 10 (Zhouchuan River) and 16 (Qingjian River), the discharge with minimum FTT and the corresponding FTT were 3000–3500 m3/s and 21–26.8 h, respectively. For the Longmen-Tongguan (LT) Reach, the discharge with minimum FTT and the corresponding FTT were 3000 m3/s and 17.4 h, respectively.
- (3)
- The sensitivity analyses indicate that the FTT simulated by the numerical model are sensitive to the Tongguan elevation, roughness in the main channel, and the Weihe River.
Application of this research may simplify the forecasting of discharge in the Tongguan Hydrology Station and help the compounded operation of the Sanmenxia and Xiaolangdi Reservoir.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 51979264 and 51579230.
Conflicts of Interest
The author declare no conflict of interest.
References
- Wang, Y.J.; Dong, Q.H.; Zhou, H.Y. Analysis and numerical simulation of flood routing of upper reaches of the mainstream of Tarim River. Arid Land Geogr. 2018, 41, 1143–1150, (In Chinese with English abstract). [Google Scholar]
- Yan, B.W.; Huo, L.; Liang, J.; Yang, W.F. Discretization of the generalized Nash Model for flood routing. J. Hydrol. Eng. 2019, 24. [Google Scholar] [CrossRef]
- Hernandez-Andrade, J.A.; Martinez-Martinez, S.I. Flood routing on a reservoir: Hydrologic or hydraulic? Tecnol. Y Cienc. Del Agua 2019, 10, 147–177. [Google Scholar] [CrossRef]
- Qiao, X.; Nelson, E.J.; Ames, D.P.; Li, Z.; David, C.H.; Williams, G.P.; Roberts, W.; Lozano, J.L.S.; Edwards, C.; Souffront, M.; et al. A systems approach to routing global gridded runoff through local high-resolution stream networks for flood early warning systems. Environ. Model. Softw. 2019, 120. [Google Scholar] [CrossRef]
- Bozog-Haddad, O.; Abdi-Dehkordi, M.; Hamedi, F.; Pazoki, M.; Loaiciga, H.A. Generalized storage equations for flood routing with nonlinear Muskingum models. Water Resour. Manag. 2019, 33, 2677–2691. [Google Scholar] [CrossRef]
- Yang, W.L.; Wang, J.; Sui, J.Y.; Zhang, F.X.; Zhang, B.S. A modified Muskingum flow routing model for flood wave propagation during river ice thawing-breakup period. Water Resour. Manag. 2019, 33, 4865–4878. [Google Scholar] [CrossRef]
- Lee, E.H.; Lee, H.M.; Kim, J.H. Development and application of advanced Muskingum flood routing model considering continuous flow. Water 2018, 10, 760. [Google Scholar] [CrossRef]
- Hu, P.; Chen, B.; Shi, P.J.; Chen, X.H. A method of calculating travel time based on county center. J. Beijing Norm. Univ. (Nat. Sci.) 2018, 54, 781–789, (In Chinese with English abstract). [Google Scholar]
- Rong, Y.T.; Zhang, T.; Peng, L.; Feng, P. Three-dimensional numerical simulation of dam discharge and flood routing in Wudu Reservoir. Water 2019, 11, 2157. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Chen, L.; Xu, Y.S. Surge wave and its propagation in upper Jingjiang Reach. Yangtze River 2016, 47, 30–47, (In Chinese with English abstract). [Google Scholar]
- Li, W.Y.; Yang, J.; Meng, X.L.; He, B.L. Characteristics of flood routing in the narrow reaches of the Lower Yellow River. Yellow River 2018, 40, 27–39, (In Chinese with English abstract). [Google Scholar]
- Yang, R.H. Prediction method of river course flood propagation time. Water Sci. Eng. Technol. 2012, 6, 16–19, (In Chinese with English abstract). [Google Scholar]
- Liu, C.J.; Liu, J. Application of modified method to estimate flood propagation time in the Middle Liaoning. Water Conserv. Tech. Superv. 2016, 24, 58. (In Chinese) [Google Scholar]
- Li, Q.; Shang, Z.R.; Guo, H.C. Propagation time of flood wave. Water Conserv. Hydropower Northeast China 2003, 21, 41. (In Chinese) [Google Scholar]
- Li, B.G.; Cui, Z.H. Variations in flood routing rules in Xiaobeiganliu Reach of the Yellow River. Yellow River 2018, 40, 12–16, (In Chinese with English abstract). [Google Scholar]
- He, L.; Wang, Y.B.; Fu, X.D.; Ji, Y.Q. Unsteady flow and sediment transport model in the Wubu-Tongguan reach of Yellow River. South North Water Divers. Water Sci. Technol. 2012, 10, 27–31, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- He, L.; Wang, G.Q.; Zhang, C. Application of loosely coupled watershed model and channel model in Yellow River. J. Environ. Inf. 2012, 19, 30–37. [Google Scholar] [CrossRef]
- Ma, W.J.; Cai, W.Y.; Cao, S.L.; Bai, Y.H.; Rui, J.F. Analysis on discharge and sediment laden in the Middle Yellow River. In Proceedings of the 7th Symposium Proceedings of the Professional Committee of China Hydropower Engineering Society Hydrology and Sediment, Hangzhou, China, 1 October 2007; pp. 54–58. (In Chinese). [Google Scholar]
- Liu, D.X.; Zhao, J.Y.; Cui, D.H.; Ma, W.J. Analysis on discharge and sediment laden in the Middle Yellow River. Water Resour. Hydropower Northeast China 2011, 6, 40–41, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- He, L.; Wang, G.Q.; Li, T.J. Catchment division of the water and sediment yield system and drainage network codification of the key region in the middle Yellow River basin. J. Sediment Res. 2009, 2, 39–45, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- He, L.; Fu, X.D. Distribution of flood travel time along the Wubu-Tongguan Reach of Yellow River. South North Water Divers. Water Sci. Technol. 2012, 10, 18–21; 26, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Fan, L.J.; Huang, C.C.; Pan, J.L.; Zha, X.C.; Zhou, Y.L.; Li, X.G.; Liu, T. Sedimentary records of palaeofloods in the Wubu Reach along the Jin-Shaan gorges of the Middle Yellow River, China. Quat. Int. 2015, 380–381, 368–376. [Google Scholar] [CrossRef]
- Cimorelli, L.; Cozzolino, L.; Morte, R.D.; Poanese, D.; Singh, V.P. A new frequency domain analytical solution of a cascade of diffusive channels for flood routing. Water Resour. Res. 2015, 51, 2393. [Google Scholar] [CrossRef]
- Serrano, S.E. Propagation of nonlinear flood waves in rivers. J. Hydrol. Eng. 2016, 21, 04015053. [Google Scholar] [CrossRef]
- Rak, G.; Kozelj, D.; Steinman, F. The impact of floodplain land use on flood wave propagation. Nat. Hazards 2016, 83, 425–443. [Google Scholar] [CrossRef]
- Hoch, J.M.; Haag, A.V.; Dam, A.V.; Winsemius, H.C.; Van Beek, L.P.H.; Bierkens, M.F.P. Assessing the impact of hydrodynamics on larger-scale flood wave propagation–a case study for the Amazon Basin. Hydrol. Earth Syst. Sci. 2017, 21, 117–132. [Google Scholar] [CrossRef]
- He, L.; Duan, J.; Wang, G.Q.; Fu, X.D. Case study: Numerical simulation of unsteady hyper-concentrated sediment-laden flow in the Lower Yellow River. J. Hydraul. Eng. 2012, 138, 958–969. [Google Scholar] [CrossRef]
- He, L. Application of 1D Finite Volume Model of Unsteady Flow in Wubu-Tongguan Reach, Middle Yellow River; CRC Press: Tokyo, Japan, 2013; ISSI2013. [Google Scholar]
- Liu, L.Q.; Jiang, X.H.; Tao, X.; Sun, W.J. Analysis of “03.7” flood characteristics in the middle reach of Yellow River. J. Water Resour. Water Eng. 2004, 15, 63–66, (In Chinese with English abstract). [Google Scholar]
- Cheng, W.; Cao, R.X.; Qian, Q.S.; Wang, X.H. A mathematical model for silt discharge of unconstant and unbalance about Xiaobeigan River. J. Hydrodyn Ser. A 1999, 14, 395–400, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Liang, G.T.; Gao, Y.T.; Liang, Y.P.; Gong, J. Establishing of unsteady simulation model and its application. J. Sediment Res. 1999, 4, 24–29, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- He, L.; Xia, J.Q.; Wang, G.Q. Estimating methods and application of flood propagation time and channel storage capacity in the Lower Yellow River. In Proceedings of the 6th National Symposium on Basic Theory of Sediment (V ii), Zhengzhou, China, 22–25 November 2005; pp. 744–749. (In Chinese). [Google Scholar]
- Cheng, L.Y.; Guo, X.Q.; Zhang, S.L.; Zheng, Y.F.; Liu, Y.E.; Ma, X.M. Effect of flood synthesis at Tongguan Station on the Weihe River and the Beiluohe River. J. Sediment Res. 2004, 6, 31–35, (In Chinese with English abstract). [Google Scholar] [CrossRef]
- Jiao, E.Z.; Zhang, C.P. Sediment transportation and deposit in North Main Reaches of Yellow River. Yellow River 1995, 11, 1–5. (In Chinese) [Google Scholar]
- Liu, Z.H. Paleohydrologic analysis of the Yellow River Hukou Waterfall and reconstructing the runoff rime series. Adv. Water Sci. 1995, 6, 218–223. (In Chinese) [Google Scholar]
- Zhang, H.W.; Huang, Y.D.; Zhao, L.J. A mathematical model for unsteady sediment transport in the lower Yellow River. Int. J. Sediment Res. 2001, 16, 150–158. [Google Scholar]
- Zhang, X.J.; Liu, P.; Cheng, L.; Liu, Z.J.; Zhao, Y. A back-fitting algorithm to improve real-time flood forecasting. J. Hydrol. 2018, 562, 140–150. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Khalil, M.; Panu, U.S.; Lennox, W.C. Groups and neural networks based streamflow data infilling procedures. J. Hydrol. 2001, 241, 153–176. [Google Scholar] [CrossRef]
- Green, I.R.A.; Stephenson, D. Criteria for comparison of single event models. Hydrol. Sci. J. Des Sci. Hydrol. 1986, 31, 395–411. [Google Scholar] [CrossRef]
- Lin, G.F.; Chen, L.H. A non-linear rainfall-runoff model using radial basis function network. J. Hydrol. 2014, 289, 1–8. [Google Scholar]
- Zheng, Y.F.; Shi, Y.M.; Ding, X.B.; Li, G.Y.; Wen, J.; Zhang, Y.H.; Liu, H.X. Shrinkage by sedimentation in the Longmen-Tongguan Reach and the lower Weihe River. Water Resour. Hydropower Northeast 2008, 26, 45–47. (In Chinese) [Google Scholar] [CrossRef]
- Wu, B.S.; Wang, G.Q.; Wang, Z.Y.; Xia, J.Q. Effect of changes in flow runoff on the elevation of Tongguan in Sanmenxia Reservoir. Chin. Sci. Bull. 2004, 49, 1658–1664. [Google Scholar] [CrossRef]
- Zhang, L.H. Analysis of the present situation of open channels roughness. Shuili Xuebao 2012, 43, 1154–1162, (In Chinese with English abstract). [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).