Abstract
An accurate analysis of the entire flooding process is critical to assess the damaged stability when a ship encounters distressed accidents such as collision, stranding, or grounding. Among many factors affecting the flooding process and damaged stability, the complex effect of air compression is significant and worthy of further research. In this paper, through establishing scenarios of the damage flooding for a cruise ship, the commercial software CD Adapco STARCCM+ is applied to perform time domain simulation of flooding processes under different ventilation levels. The basic mathematical models about air compression and specific simulation settings of computational fluid dynamics (CFD) are presented in detail. The simulation results show that water ingression results in an increase of air pressure and density inside the flooded compartment. The corresponding air compression can significantly delay the flooding process if the ventilation level is limited to a certain ratio. Finally, the stability of the damaged ship is affected.
1. Introduction
Ship survivability is a measure of a ship’s ability to withstand unplanned incidents, such as structural damage, fire, and flooding induced by accident or man-made hostilities, with minimum impact on ship system operations [1]. Based on the class of ship and its purpose, ship survivability involves three factors: Susceptibility, vulnerability, and recoverability. The main risk to handle here is flooding, which is closely related to recoverability. For the last 30 years, almost every ship has had a fire display in the command room, which is able to indicate where a fire is located and whether it is expanding. However, most serious ship incidents, from 1912 to the present day, have not been caused by the spread of fire through a vessel, but by the spread of flooding water. So, it is essential to perform relative studies about damaged flooding and its effect on a damaged ship. In addition to the damage stability requirements of the safety of life at sea (SOLAS) convention, the International Maritime Organization (IMO) has established new regulations for safe return to port (SRTP). In the design perspective, mainly requirements for the redundancy of systems are defined. Conventionally, the calculation of the stability of a ship after damaged flooding assumes that the damaged compartment is filled with flooding water very rapidly or with a few intermediate flooding stages. The crew determine the severity of the situation based on the righting lever curve (GZ). However, the traditionally applied method is unable to meet the current user requirements [2]. Because this method can only calculate the final equilibrium state of the damaged ship, it cannot predict how the situation will evolve and it is thus impossible to give a time line of when the damaged ship may be dangerous or even capsize or sink. Thus, the time-domain simulation method is an advanced approach that has been proposed to give more details about the flooding process. The physical behavior of the ship during flooding has been a research focus as summarized by the last several ITTC Stability in Waves Committee Reports [3,4,5].
During the flooding process, a ship’s motion impacts water flooding and sloshing in its compartment. Simultaneously, the liquid loads acting on the compartment also influence the motion response of the damaged ship [6]. Numerical simulation methods on this coupled motion have been conducted by various studies. A fundamental, but more sophisticated, time-domain simulation method of investigating the damage flooding has been developed in the European Commission Seventh Framework Programme (EU FP7), FLOODSTAND. The developed flooding simulation method is now included in the current software release of the NAPA ship design software. However, one important limitation of the NAPA flooding simulation model is that the impact of the seaway is only marginally considered [7]. In recent years, Gao et al. [8] applied an integrated method to study the interaction between the dynamics of the floodwater and the damaged ship in waves, which couples a sea-keeping solver and Navier-Stokes solvers. Hamid Sadai-Hosseini et al. [9] assessed CFD capability for the prediction of damaged ship motions. The Unsteady Reynolds-averaged Navier-Stokes (URANS) simulations predicted quite well the motions for all cases in calm water and regular beam waves. However, due to the very long computational time and the large number of simulations required for sea-keeping and damage stability studies in seaways, it is expected that hybrid methods combining simplified approaches will still be used in the near future [5]. In addition, a time domain theoretical model was proposed to predict the behavior of a damaged ship subject to progressing flooding. The model provides information in each stage of flooding concerning the ship motions, amount of water, shear forces, and bending moments acting on the ship [10]. Through the comprehensive analysis of the above simulation results, it can be found that the transient response of a ship to an abrupt flooding is dangerous. A numerical non-linear time domain simulation based on the lumped mass method [11] and an enhanced smoothed particle hydrodynamics (SPH) model were developed to investigate the response of a damaged ship under the condition of transient flooding water [12,13,14,15]. These numerical simulation methods have been proven to provide convenience and reliability for flooding research.
In the ship design stage, in order to enhance the survivability performance, several watertight compartments are distributed inside the ship. However, due to the existence of cables or small ventilation holes in the watertight compartment, this results in non-air tightness. Therefore, it is necessary to simulate the process of water ingress into watertight compartments and compartments with different ventilation levels. Previously, both the model test and explicit simulation methods were conducted to study the air compression of a flooded compartment. The dynamics between the air, water, and compartment were analyzed and the applied methods estimated accuracy well [7,16,17,18,19], while a new model was proposed for vented compartments, an accumulator model, which can adjust the inner pressure automatically, was proposed for use even in systems with many compartments and openings, and especially for fully flooded compartments [20]. In this paper, a comprehensive time domain simulation of damage flooding is performed on the basis of the CD Adapco STARCCM+. The analysis mainly focuses on the compression characteristics of air and the motion response of the damaged ship under different ventilation levels. The aim is to further validate whether air compression has a non-negligible effect on the flooding process and damaged stability.
2. Time Domain Simulation with Air Compression
In general, time domain flooding simulations are performed by iterating the combinations of hydrostatic and air pressure in all damaged compartments on the basis of the compressible Bernoulli equation and conservation of mass. In the following, the description of air compression in the damaged compartment and the application of the Bernoulli equation and conservation of mass for air flow are presented in detail. In addition, the state equation of ideal gas is required to derive the relation between pressure and density.
2.1. Air Description
In the simulation, air is considered to be an ideal gas. In this case, the relation between pressure and density can be obtained as follows:
where P is the absolute pressure of the air, V is the volume under consideration, is the ratio of specific heats, n is the mass of air, R is the universal gas constant, and T is the temperature of the air. The simulated cases in this paper are assumed as isothermal processes, so the value of is 1.0 [4]. The initial conditions of the air phase, denoted by the index, atm, for the environment, are summarized in Table 1. All other quantities in the time domain process can be derived from these constants.

Table 1.
Initial conditions of the air phase.
Since the temperature is taken as being constant, Boyle’s law can be applied. Consequently, the density of the compressed air depends linearly on the pressure multiplied by the constant ratio of the air density, , at ambient pressure, :
If the compressed air is totally trapped and only the increase of pressure in the flooded compartment is described, the mass is assumed to be constant as well, yielding in Boyle’s law:
where and are the initial pressure and volume, respectively.
In the entire flooding simulations, each damaged compartment is considered as a computational cell. The equation of continuity is checked for these control volumes. The conservation of mass for air can be expressed as:
where t is time, is the velocity vector, and is the surface that bounds the control volume, .
2.2. Flow of Compressed Air
In order to illustrate the basic equations and the physical properties of compressed air flow, three generic cases are investigated as shown in Figure 1. These three cases basically cover different ventilation scenarios.
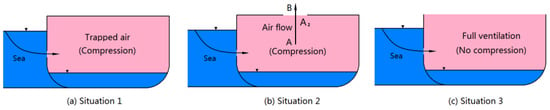
Figure 1.
Generic cases with air compression and air escape.
For realistic damage scenarios, due to complex compartment layouts, completely air-tight (Situation 1) and full ventilation (Situation 3) environments do not frequently occur. So, much emphasis is placed on the analysis of compartments with a certain ventilation capability. In general, the escape of compressed air is also possible through damaged openings, which are not submerged completely at a certain moment; however, escape occurs mainly through ventilation holes or ventilation pipes. In this section, the typical situation (Situation 2) is used as the research object to derive the basic equations of air flow in a flooded compartment. In this flooding case, the escape of air mass from the damaged compartment will cause a pressure decrease, while the air volume reduction caused by the water ingress will lead to a pressure increase. The mass flux balance between the air flux through the ventilation hole, , and the compartment air flux, , is derived using the following equations [7]:
Consequently, Equation (5) can be presented as:
Let us consider a streamline between the two points illustrated in Situation 2. A is in the damaged compartment and B is in the middle of the ventilation hole. The flow velocity through the ventilation hole can be derived by the compressible Bernoulli equation [17]:
It can be assumed that the velocity of air flow in the damaged compartment is zero, thus Equation (8) will be:
On the basis of the flow velocity, , the air flux through the ventilation hole, , can be obtained:
where is the area of the ventilation hole. The equations described above explain the continuity in the process of compressed air flow, which are commonly applied to CFD calculation. For the other two generic cases, the derivation processes are similar. It is notable that the situation considered here is about the ventilation hole. In the event that the escape of the compressed air is through the ventilation pipes, it is necessary to add a semi-empirical pressure loss coefficient to take the friction, bends, and valves into consideration. Especially in the flooding simulation, the pressure loss is represented as the discharge coefficient [21].
3. Simulation Study
3.1. Model Arrangement
Several flooding cases were performed to study the effect of air compression on a damaged buoy tender. The utilized model is drawn on the basis of the existing lines plan with a full scale. Because the ship is a River buoy tender (WLR), the size is relatively small. The main particulars of the ship are given in Table 2, while the views of the body plan and the damaged model are respectively shown in Figure 2 and Figure 3.

Table 2.
Main particulars of the damaged ship.
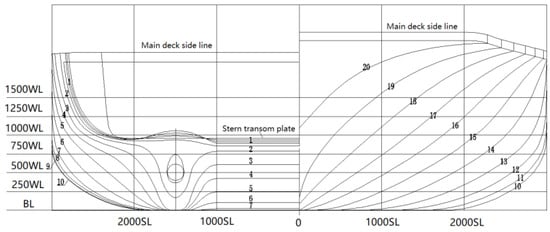
Figure 2.
Body plan (Unit: mm).
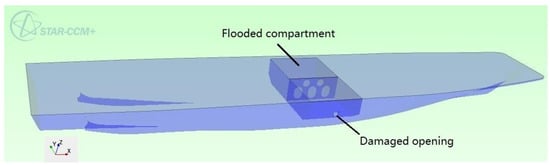
Figure 3.
3-D model of the damaged ship in STAR CCM+.
As illustrated in Figure 4, the damaged ship is placed in quasi-static water, ignoring the effect of wind and waves. The flooded compartment is placed in the middle of the ship. The damaged opening occurs on the starboard side of the flooded compartment, and the center point of the opening is at the midpoint of the ship length. The calculating displacement is set at 130 tons, allowing the initial free surface to completely submerge the damaged opening. As illustrated in Figure 5, the flooded compartment is separated by a longitudinal bulkhead with openings. The diameter of the circular opening is 400 mm, and the size of the manhole is 500 mm × 700 mm, which are set according to the latest rules for the classification of seagoing steel ships. On the one hand, the compressed air flowed through bulkhead openings to the other side. On the other hand, the flooding water flowed to undamaged side, forming the symmetric flooding. It can also be seen from Figure 4 that there are two ventilation holes on the upper deck of the flooded compartment. The small ventilation hole is on the port side with a diameter of 84 mm. The big ventilation hole is on the starboard side with a diameter of 120 mm. The size design of the ventilation holes is to verify a simplified assumption [22] that the flooded compartment can be considered as fully ventilated if the total area of the ventilation holes is more than 10% of the damaged opening area. In this matter, there is no need to consider the effect of air compression on the flooding. The area of the small ventilation hole is 6% of the area of the damaged opening and the ratio for the big ventilation hole is 12%. The obtained simulation results are applied to validate the simplified assumption.
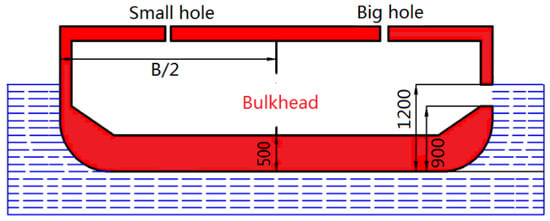
Figure 4.
Environment conditions of the time simulation.
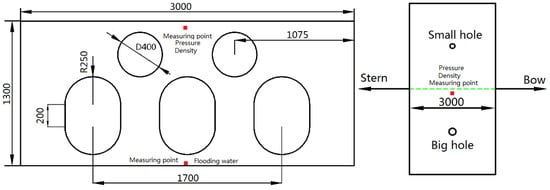
Figure 5.
Sketch of the longitudinal bulkhead (left) and the upper deck (right).
As shown in Table 3, five comparative flooding cases with different ventilation ratios are simulated separately. If the upper deck of the damaged compartment is closed (Case 1), the remaining compressed air inside the flooded compartment will be trapped. There will be final changes in the air pressure and density in the flooded compartment. In the event that there is a ventilation hole or several ventilation holes (Case 2, 3, and 4), compressed air will escape from the hole. The state of the air can be defined as vented air. In addition, Case 5 is the study of the situation of being fully ventilated, which is used to investigate the condition of no air compression.

Table 3.
Simulation cases.
3.2. Numerical Set Up
In the simulation process, the hull is considered to be a non-deformable rigid body, ignoring the longitudinal bending generated by uneven force. The computational model of the Euler multiphase flow under implicit unsteady is applied. The Euler multiphase flow model solves conservation equations for mass, momentum, and energy for each phase (air and water). Phase interaction models are provided to define the influence that one phase exerts upon another across the interfacial area between them. An implicit unsteady solver has been used to find the field of all hydrodynamic unknown quantities, in conjunction with an iterative solver to solve each time step. These inner iterations can be accomplished using implicit spatial integration or explicit spatial integration schemes. The integration scheme marches inner iterations using optimal pseudo-time steps that are determined from the Courant number. The simulation cases in this paper applied a constant physical time-step of 0.001 s, involving 10 inner iterations. In addition, the Reynolds stress is solved by means of the k-ε turbulence model. It is a two-equation model in which transport equations are solved for the turbulent kinetic energy and its dissipation rate. In Begovic et al. [23], it was reported that the numerical results from simulations with k-ω- and k-ε turbulence models are within 1.0% difference and it is not necessary to appreciate the difference between the two numerical curves.
After comprehensive consideration of previous research results [23,24] and the case of the KRISO Container Ship (KCS) with a rudder [25], the appropriate boundary types and solver settings in this paper are concluded in Table 4. By default, prism layers are not created for inlet, outlet, and symmetry boundaries. The entire computing region is arranged as shown in Figure 6 with the bow pointing towards the inlet. Because the physical model of quasi-static water is applied, the magnitude of the flow velocity specified on the velocity inlet is zero and the setting of the inlet and outlet does not affect the simulation results. In order to simulate the flooding response of the ship in infinite water, the boundaries on the left and right sides are set to be symmetry planes, which can reduce the interference from the coupled motion of the ship and water. The free surface is modelled with the two phase VOF (Volume of Fluid) approach with a high-resolution interface capture scheme (HRIC) scheme based on the compressive interface capture scheme for arbitrary meshes introduced by Ubbink [26] and developed by Muzeferija and Peric [27]. This VOF approach is provided for systems containing two or more immiscible fluid phases, where each phase constitutes a large structure within the system (such as typical free surface flows). This approach captures the movement of the interface between air and water, and is often used for marine applications [25]. Considering the movement of the ship, the ship’s 6-DOF (Degree of Freedom) are constrained to allow the ship to move vertically along the Z-axis and rotate around the X-axis. The sinking response due to additional flooding water was simulated by allowing the damaged ship to move along the Z-axis, while the heel angle was recorded by monitoring the rotation around X-axis. The specific coordinate axis is illustrated in Figure 3.

Table 4.
Boundary types and solver setting.
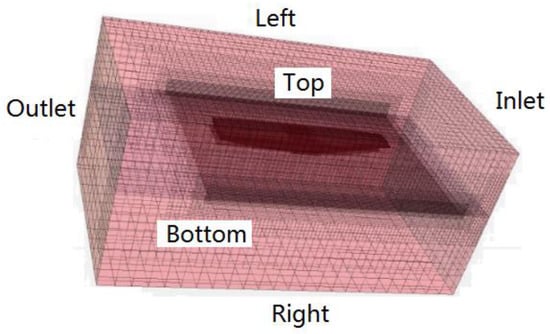
Figure 6.
Sketch of the computational region.
For the mesh generation, a trimmed mesh of hexahedral type is used, as shown in Figure 7. The relevant sensitivity analysis was detailed in Begovic et al. [23]. Generally, the meshing generation is an important factor in determining the accuracy of the calculation. It should ensure that the surface shape of the hull cannot be distorted, especially for some locations where the curvature changes greatly or the surface has openings. For the simulations in this paper, there is a damaged opening on the starboard side of the ship, ventilation holes on the deck, and openings on the longitudinal bulkhead. If the same mesh size is applied as the hull, the shapes of theses openings will be distorted, so the mesh sizes in these places should be locally refined. As shown in Figure 8, the shapes of the refined openings are almost the same as the original, thus the calculation results are reliable. In addition, the local volume mesh should be refined, which is also essential for improving the final accuracy. Here, the volume mesh of the free surface and the area of flooding are refined, which makes the mesh transition smoother and ensures convergence of the results. The specific mesh sizes in this paper are summarized as shown in Table 5. The entire meshing process is based on the base size, which is about 1.0% to 1.5% of the ship’s length. The mesh sizes of other parts or regions are determined by taking the ratio relative to the base size.

Figure 7.
Hexahedral trimmed mesh.
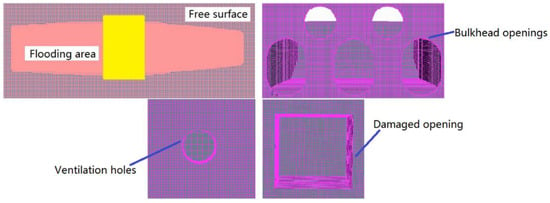
Figure 8.
Local mesh refinement.

Table 5.
Mesh sizes in different parts.
During the simulations, several physical quantities in the damaged compartment are monitored, including: The gauge pressure relative to the environment pressure, the density, the height of flooding water, and the stability parameters (heel angle and heave displacement). In the applied numerical procedures, the air pressure, density, and flooding water are accounted for by measuring points in the damaged compartment. The specific coordinates are shown in Table 2.
3.3. Simulation Results
3.3.1. Effect of the Ventilation Level
Four comparative cases are performed in order to assess the effect of the ventilation level on the air pressure in the flooded compartment. The monitored pressure, P, inside a flooded compartment is always taken as a gauge pressure relative to the environment pressure (101,325 Pa), because only the pressure differences are of importance to determine the air flux in the flooded compartment. This is determined by the algorithms built into the CFD software. As illustrated in Figure 9, when the flooded compartment is closed, the air compression effect is significant, and the maximum gauge pressure is over 2 kPa. When only the small ventilation hole is open, the maximum gauge pressure is 850 Pa. When only the big ventilation hole is open, the maximum gauge pressure is reduced to only 280 Pa. When both ventilation holes are open, it is very similar to the full ventilation scenario, and the maximum gauge pressure is only 130 Pa. This fully demonstrates the conclusion that a limited ventilation level impedes the flow of compressed air, resulting in an increase of pressure. This compression phenomenon becomes more obvious as the area of the ventilation hole becomes smaller.
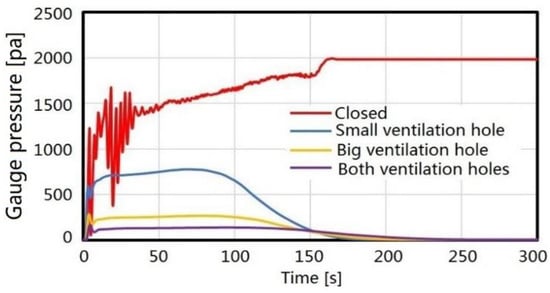
Figure 9.
Pressure with different ventilation levels.
It can be found from the trend of the curves that the changing processes of the gauge pressure is affected by the flooding stages. The beginning of the damage flooding is called the transient stage. In this stage, there may be a significant fluctuation in the gauge pressure, which is related to the transient response of the ship. Especially for the closed case, when the ship rolls due to flooding water, part of the compressed air overflows from the damaged opening. This explains why the overpressure fluctuates even though there are no ventilation holes in the closed case. The damaged scenarios studied in this paper are like a collision. Even if the flooded compartment is closed, compressed air still has a limited overflow path. This is different from bottom stranding. When the flooding water enters the compartment from the bottom and the dissolution of air is ignored, there is no overflow path for the compressed air. All the compressed air is trapped.
With the increase of flooding water, the motion of the ship tends to be stable, and the gauge pressure increases gradually until it reaches equilibrium status. This process can be understood as a process from the progressing stage to a steady stage. For the closed case, some air is trapped, and the gauge pressure is maintained at a constant value. However, in the ventilation cases, compressed air always escapes. When the gauge pressure increases to its maximum, the value continuously decreases until it reaches zero.
3.3.2. Variation of Density
In order to clearly describe the air compression, Figure 10 presents the changing processes of density. Four comparative cases were utilized to analyze the extent of air compression under different ventilation levels. For the ideal gas, if there is no air overflow during compression, the density is proportional to the pressure. As the pressure increases, so does the density. In the ventilation cases, the compressed air can escape from the ventilation hole, so the final density value stabilizes around the initial density. Considering the closed case, the compressed air is trapped in the remaining volume of the flooded compartment, and the final density is maintained at a constant value greater than the initial density. Although some compressed air escapes from the damaged opening, there is still a similar relationship between pressure and density. As shown in Figure 9, for the closed case, the final gauge pressure stabilized at 2 kPa. Calculated by Equation (2), the final density should be as follows: ρ = (101,325 + 2000)·1.1765/101,325 = 1.1997 kg/m3. The theoretical calculation values fit the finally simulated density value of 1.20 kg/m3 in the Figure 10. For other cases with better ventilation levels, the extent of compression is much smaller than the small ventilation case, and the variation processes of the corresponding density are similar. In general, the changing processes satisfy the state equation of the ideal gas. Simultaneously, the consistency between the theoretical density value and the simulated density value validates the reliability of the CFD simulation and the convergence of the calculated results in this paper.
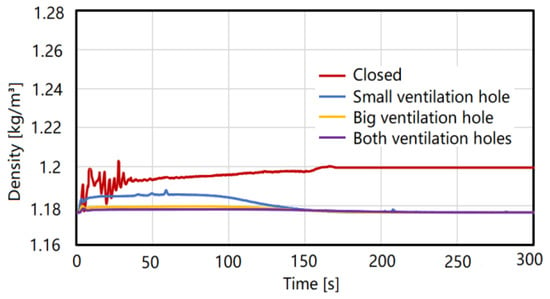
Figure 10.
Density with different ventilation levels.
After analyzing the pressure and density, Figure 11 shows the differences of flooding processes under different ventilation levels. For the entire flooding process, as the ventilation levels improve, the flooding progress becomes faster. It can also be seen that for the closed case, although there are no ventilation holes, there is still compressed air that overflows from the damaged opening. This explains why the final flooding height is only slightly different from other ventilation cases. Moreover, the compressed air in the closed compartment has a tendency to flow out, which causes the compressed air to impede the inflow of water and form a U-shape phenomenon near the opening. For the other two ventilation conditions, except for the flooding rate, the overall flooding process and the final flooding height are basically the same.
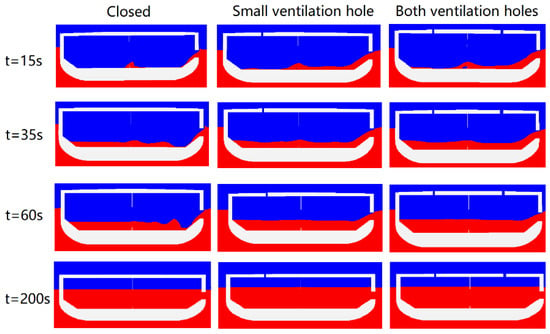
Figure 11.
The flooding differences between various ventilation cases.
3.3.3. The Height of the Flooding Water
The water heights were converted by measuring the hydrostatic pressure at the same point. As shown Figure 12, time domain comparisons were made for the water heights under different ventilation levels. The water heights are also affected by the flooding stage. Especially in the transient stage (about the first 50 s), the motion response of the ship is very complicated. The free surface in the flooded compartment is usually accompanied with sloshing, resulting in fluctuations of the height curves. With the ship motion tending to stabilize, the water height rises smoothly until it reaches equilibrium status, which can also be considered as a gradual process from the progressing stage to the steady stage. The specific ship motion response is described in Section 3.3.4.
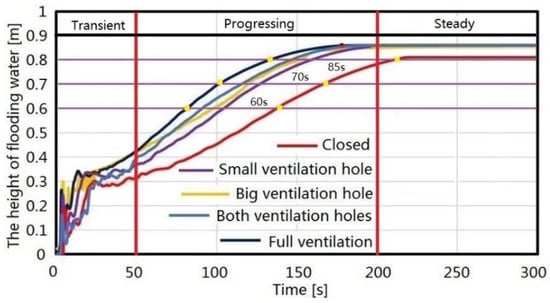
Figure 12.
Water heights with different ventilation levels.
By analyzing the five different ventilation cases in Figure 12, it can be found that the required time to reach the same flooding height is different. Also, as the ventilation level improves, the required time is less. Here, the effect of air compression on the flooding time is further investigated by comparing the closed case with the full ventilation case. As shown in Figure 12, three water heights (0.6 m, 0.7 m, and 0.8 m) were selected for the analysis of the flooding time. When the water height of 0.6 m is reached, the closed case takes an additional 60 s longer than the full ventilation case. When the water height 0.7 m and 0.8 m, the extra time gradually increases (70 s, 85 s). This directly causes the different times to complete the flooding. These results fully demonstrate the delaying effect of air compression on flooding. In addition, the results obtained can be applied to validate the assumption made by IMO about complete ventilation. For the large ventilation levels and both ventilation levels, the ventilation ratios are 12% and 18%, respectively. Their flooding heights and flooding times are basically the same as the full ventilation scenario. At this time, the air compression in the flooded compartment has little effect on the flooding. In the small ventilation case, the ventilation ratio is only 6%. The final flooding time is about 30 s longer than the other ventilation cases. In this matter, the effect of air compression on the flooding cannot be ignored. In general, the comparison results satisfy the IMO assumption. In addition, some emphasis was placed on the final water height. In the ventilation cases, although the flooding time is different, the final water heights are consistent. However, due to the influence of some trapped air, the water height of the closed case is a little smaller than the ventilation cases. To a certain extent, a reduction of the flooding volume can improve the anti-sinking ability of ships.
Here, the estimation of the flooding time considering air compression was only studied through two connected compartments. The extra time between the closed case and full ventilation case was only dozens of seconds. If damage involves multiple compartments, the effect of air compression on flooding time is more significant. The extra time can even be several minutes. IMO under SOLAS Chapter III Regulation 21.1.4 requires that all survival craft are capable of being launched with their full complement of persons within a period of 30 min from the time the abandon ship signal is given. For a damaged ship, the available rescue time from the 30 min period is small due to the panic of the crew. So, the influence of air compression on the flooding time must be properly considered by obtaining a precise time estimation to ensure successful rescue operation.
3.3.4. Motion Responses of the Damaged Ship
Through the above analysis, the characteristics of air compression and its influence on flooding were explained. However, the most significant point is to consider the effect of air compression on ship stability. In the simulations, the heel angle and heave displacement were monitored, reflecting the ship’s rolling damping and sinking status with different ventilation levels. In Figure 13, the first 50 s of heel curves and heave curves after 50 s are illustrated. Through the overall analysis, it was found that the heel angles of all calculating cases were stable after the flooding continued for 50 s. However, it can be seen from the curves of the water heights that the flooding is in progress after 50 s. This is related to the form of flooding. The flooding form in this paper was a symmetric flooding, in which the flooding water can flow from the bulkhead holes to the other side. After the ship experienced the transient stage, the influence of the flooding water on the heel angle was very small. Therefore, in the primary design of the ship, the cross-flooding structures should be designed as much as possible to ensure that the damaged ship can maintain a balanced state in a short time.
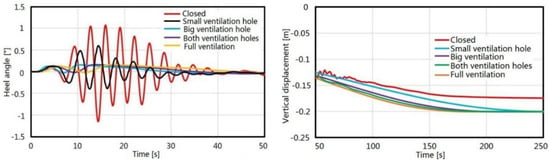
Figure 13.
Heel (left) and heave (right) curves with different ventilation levels.
Considering the magnitude of the heel angle, it can be seen that the closed ventilation case has a larger heel angle than the other ventilation cases. In the closed case, the maximum heel angle is 1.2°, which is twice the angle of the small ventilation case (0.6°) and six times the angles of the other ventilation cases (0.2°). For the large and both ventilation cases, the effect of air compression on the heel angle is small, almost the same as the full ventilation case. Similar comparisons were also made in the flooding height analysis. Although air compression causes a larger heel angle, the maximum heel angle of the closed case was only about one degree. This is because the symmetric flooding improves the stability of the damaged ship. If the flooding is asymmetric, even if the damaged compartment has a good ventilation level, the larger heel angle due to uneven force will pose a great threat to the safety of the ship. Pekka Ruponen et al. [17] presented a series of full-scale experimental tests for the asymmetric flooding of a tank with a restricted ventilation level. The final value of the heel angle was about 2.5°, which is twice the maximum value (1.2°) of the symmetric flooding in this paper. After comparing the heel angle curves under different ventilation levels, it was found that when flooding occurs, the better the ventilation level, the smaller the heel angle, and the higher the stability. From this perspective, a symmetric flooding form with proper ventilation is critical to improving the stability of a damaged ship. This is because when the ventilation levels are adequate, the compression characteristics of the air will not adversely affect the flooding and the response of the ship, while due to the symmetric flooding, a damaged ship can gradually stabilize with a small heel amplitude.
Because the ship’s heel angle tends to be stable at about 50 s, the curves after 50 s are more representative for the analysis of vertical displacement. From the vertical displacement curves, it can be seen that the final vertical positions of the ship are the same for different ventilation cases. Because compressed air in the damaged compartment can escape through ventilation holes, different ventilation levels will affect the flooding time, but it has no effect on the final flooding volume and stable vertical displacement. In the closed case, the trapped air in the damaged compartment results in a certain reduction in the volume of the flooding water. This is similar to the analysis of the water heights. It can be seen clearly from Figure 13 that the vertical displacement of the damaged ship in the closed case is smaller than the other cases. This also validates the basic conclusion that airtight compartments can improve the ship’s resistance to sinking. The obtained simulation results are satisfactory with the conclusion.
The described curves explain the damaged stability from two aspects, including the roll stability and heave motion. Especially for the closed case, it illustrates well the main influence of air compression. The relevant characteristics about the closed case are summarized as follows: First, due to the dynamics of compressed air, the ship’s heel angle is relatively larger than the ventilation cases. This is not recommended to improve ship stability; second, a closed compartment can reduce the volume of flooding water, which can effectively increase the ship’s anti-sinking ability. Combining these two characteristics, the suggestion given is that compartments with proper ventilation levels should be arranged inside the ship as much as possible, which can reduce the effect of air compression and slow down a ship’s sinking to a certain extent. However, the analysis and recommendations made are based on the assumption that the damaged ship will not capsize or sink due to damaged flooding. When damage occurs in more compartments, the ship will sink even if it is following the above suggestions of proper ventilation. In this case, no ventilation gives the possibility of floating, and the sinking time will take a long time even for the case of a sunk ship. Therefore, in future research, it is necessary that intelligent ventilation equipment is developed. If damage flooding occurs, the crew should firstly determine whether the ship may possibly sink. If the possibility of the ship sinking exists, the ventilation equipment can be used try to ensure that the compartments are airtight. Although it can cause a bad motion response, it can extend the floating time of the damaged ship and provide more convenience for rescue operations. Conversely, if the ship will not capsize, the ventilation ratio can be adjusted automatically to ensure a smooth motion response. The ventilation ratio is preferably controlled at around 10% based on the simulated results, which can greatly reduce the effect of air compression on the motion response. This is also satisfactory with the IMO assumption about complete ventilation.
4. Conclusions
The development of tools and methods for the analysis of damage flooding is an important aspect of improving ship stability in practice. This paper focused on the application of the commercial software, CD Adapco STARCCM+ RANS solver, for the analysis of the effect of air compression on the flooding process and damaged stability. The simulation results showed that air compression characteristics must be considered reasonably, which is critical to accurately estimate the flooding time to ensure the reliability of rescue. By analyzing the motion response of a damaged ship under different ventilation ratios, equipment that can automatically adjust the ventilation ratios was proposed. When the damaged ship has the possibility of capsizing, the equipment should try to ensure the airtightness of the compartment. This will help to extend the flooding time and guarantee rescue operations. If the damaged ship can remain in a floating state, the appropriate ventilation ratio can be automatically adjusted to ensure a stable motion response of the ship.
The serious challenge for the application of the CFD method for flooding simulation and stability analysis lies in the extremely high time consumption. All the simulations in this paper were processed on a 64-processor computer server with a high performance system (AMD Opteron 6200 series, 3.0 GHZ). The number of grids was about 1.4 million, and the calculation time took about 42 h. Therefore, how to set the appropriate solver conditions and generate the optimal mesh are the most influencing factors when applying CFD simulation to ship design in the future.
Author Contributions
X.L.Z. performed the numerical simulation and wrote the paper. Z.L. provided the detailed model information and proposed the research idea. P.L. collected references and summarized the research background. Y.D. derived and analyzed CFD theoretical formula. F.L. modeled the ship and post-processed the simulation results.
Funding
This research was funded by National Natural Science Foundation of China (NSFC Grants 51709063).
Acknowledgments
The authors thank Jiuyang Cang, Liang Wang for their assistance in the simulation setting. We also thank three anonymous reviewers for their valuable comments and suggestions that help us improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shafiepour, R.; Waltham-Sajdak, J. Total Ship Survivability System. 2015. Available online: https://pdfs.semanticscholar.org/5521/d27816202520bc50abbbd0c993c64bfcb42b.pdf (accessed on 20 February 2019).
- Pennanen, P.; Manderbacka, T.; Ruponen, P. Implications of different alternatives for damage stability analysis in decision support. In Proceedings of the 16th International Ship Stability Workshop, Belgrade, Serbia, 5–7 June 2017. [Google Scholar]
- ITTC. The specialist committee on prediction of extreme ship motions and capsizing. In Proceedings of the 23rd International Towing Tank Conference, Venice, Italy, 8–14 September 2002. [Google Scholar]
- ITTC. Stability in Waves Committee, Final Report and Recommendation. In Proceedings of the 27rd International Towing Tank Conference, Copenhagen, Denmark, 31 August–5 September 2014. [Google Scholar]
- ITTC. Stability in Waves Committee, Final Report and Recommendation. In Proceedings of the 28rd International Towing Tank Conference, Wuxi, China, 17–23 September 2017. [Google Scholar]
- Gao, Z.; Gao, Q.; Vassalos, D. Numerical simulation of flooding of a damaged ship. Ocean Eng. 2011, 38, 1649–1662. [Google Scholar] [CrossRef]
- Dankowski, H. A Fast and Explicit Method for Simulating Flooding and Sinkage Scenarios of Ships. Ph.D. Thesis, Technical University of Hamburg-Harburg, Hamburg, Germany, 2013. [Google Scholar]
- Gao, Z.; Vassalos, D. The dynamics of the floodwater and the damaged ship in waves. J. Hydrodyn. 2015, 27, 689–695. [Google Scholar] [CrossRef]
- Sadat-Hosseini, H.; Kim, Do.; Carrica, P.M.; Rhee, S.H.; Stern, F. URANS simulations for a flooded ship in calm water and regular beam waves. Ocean Eng. 2016, 120, 318–330. [Google Scholar] [CrossRef]
- Santos, T.A.; Guedes Soares, C. Time domain simulation of ship global loads due to progressive flooding. In Proceedings of the 1st International Conference on Marine Structures, Glasgow, UK, 12–14 March 2007; pp. 79–88. [Google Scholar]
- Manderbacka, T.; Mikkola, T.; Ruponen, P.; Matusiak, J. Transient response of a ship to an abrupt flooding accounting for the momentum flux. J. Fluid Struct. 2015, 57, 108–126. [Google Scholar] [CrossRef]
- Le Touzé, D.; Marsh, A.; Oger, G.; Guilcher, P.-M.; Khaddaj-Mallat, C.; Alessandrini, B.; Ferranta, P. SPH simulation of green water and ship flooding scenarios. J. Hydrodyn. 2010, 22, 231–236. [Google Scholar]
- Ming, F.R.; Zhang, A.M.; Cheng, H.; Sun, P.N. Numerical simulation of a damaged ship cabin flooding in transversal waves with Smoothed Particle Hydrodynamics method. Ocean Eng. 2018, 165, 336–352. [Google Scholar] [CrossRef]
- Guo, K.; Sun, P.; Cao, X.; Xiao, H. A 3-D SPH model for simulating water flooding of a damaged floating structure. J. Hydrodyn. 2017, 29, 831–844. [Google Scholar] [CrossRef]
- Cao, X.Y.; Ming, F.R.; Zhang, A.M. Multi-phase SPH modelling of air effect on the dynamic flooding of a damaged cabin. Comput. Fluids 2018, 163, 7–19. [Google Scholar] [CrossRef]
- Palazzi, L.; de Kat, J.O. Model experiments and simulations of a damaged ship with air-flow taken into account. Mar. Technol. 2004, 41, 38–44. [Google Scholar]
- Ruponen, P.; Kurvinen, P.; Saisto, I.; Harras, J. Air compression in a flooded tank of a damaged ship. Ocean Eng. 2013, 57, 64–71. [Google Scholar] [CrossRef]
- Ruponen, P. Progressive Flooding of a Damaged Passenger Ship. Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland, 2007. [Google Scholar]
- Gao, Z.; Wang, Y.; Su, Y. Numerical study of damaged ship’s compartment sinking with air compression effect. Ocean Eng. 2018, 147, 68–76. [Google Scholar] [CrossRef]
- Lee, G.J. Dynamic orifice flow model and compartment models for flooding simulation of a damaged ship. Ocean Eng. 2015, 109, 635–653. [Google Scholar] [CrossRef]
- Ruponen, P.; Pulkkinen, A.; Laaksonen, J. A method for breach assessment onboard a damaged passenger ship. Appl. Ocean Res. 2017, 64, 236–248. [Google Scholar] [CrossRef]
- IMO. Resolution MSC.245 (83): Recommendation on a Standard Method for Evaluating Cross-Flooding Arrangements; IMO: London, UK, 2007. [Google Scholar]
- Begovic, E.; Day, A.H.; Incecik, A.; Mancini, S.; Pizzirusso, D. Roll damping assessment of intact and damaged ship by CFD and EFD methods. In Proceedings of the 12th International Conference on Stability of Ships and Ocean Vehicles, Glasgow, UK, 14–19 June 2015. [Google Scholar]
- Mancini, S.; Begovic, E.; Day, A.H.; Incecik, A. Verification and validation of numerical modelling of DTMB 5415 roll decay. Ocean Eng. 2018, 162, 209–223. [Google Scholar] [CrossRef]
- CD-adapco STAR CCM+; Computational Dynamics-Analysis & Design Application Company Ltd.: Melville, NY, USA.
- Ubbink, O. Numerical Prediction of Two Fluid Systems with Sharp Interfaces. Ph.D. Thesis, Department of Mechanical Engineering, Imperial College of Science. Technology & Medicine, London, UK, 1997. [Google Scholar]
- Muzaferija, S.; Peric, M. Computational of Free Surface Flows Using Interface Tracking and Interface Capturing Methods”, Nonlinear Water Wave Interaction; WIT Press: Southampton, UK, 1999. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).