Abstract
Integrated environmental modelling requires coupling sub-models at different spatial and temporal scales, thus accounting for change of support procedures (aggregation and disaggregation). We introduce the R-package spatio-temporal Uncertainty Propagation across multiple scales, stUPscales, which constitutes a contribution to state-of-the-art open source tools that support uncertainty propagation analysis in temporal and spatio-temporal domains. We illustrate the tool with an uncertainty propagation example in environmental modelling, specifically in the urban water domain. The functionalities of the class setup and the methods and functions MC.setup, MC.sim, MC.analysis and Agg.t are explained, which are used for setting up, running and analysing Monte Carlo uncertainty propagation simulations, and for spatio-temporal aggregation. We also show how the package can be used to model and predict variables that vary in space and time by using a spatio-temporal variogram model and space-time ordinary kriging. stUPscales takes uncertainty characterisation and propagation a step further by including temporal and spatio-temporal auto- and cross-correlation, resulting in more realistic (spatio-)temporal series of environmental variables. Due to its modularity, the package allows the implementation of additional methods and functions for spatio-temporal disaggregation of model inputs and outputs, when linking models across multiple space-time scales.
1. Introduction
Integrated environmental modelling (IEM) often requires coupling models at multiple spatial and temporal scales. This is challenging due to the complexity of the models and differences in input and output supports between models. Leopold et al. [1] address the need for aggregation and disaggregation when coupling models. In addition, Bastin et al. [2] point out that spatio-temporal aggregation and disaggregation are common procedures in modelling chains. This challenge becomes more difficult if uncertainty propagation (UP) is analysed because uncertainty is support-dependent. Change of support procedures (i.e., aggregation and disaggregation) are also required when dealing with integration between models. Accounting for spatio-temporal uncertainty when coupling models in an integrated layout and when addressing change of support is a key component in the data—model—simulation—uncertainty quantification—decision-making chain. There is no software that can do all that is needed for UP analysis in such a complex case. Although important contributions have been made, e.g., the UncertWeb framework [2] and the R-package spup [3], there still is a need for tools for temporal, spatial and spatio-temporal UP accounting for change of support across multiple scales.
In the environmental and geospatial fields, modelling complex processes accounting for uncertainties exhibits specific issues. Bastin et al. [2] identified six main challenges. We summarise and relate these to the availability of tools accounting for uncertainty analysis in specific applications:
- (1)
- Lack of tools accounting for reliable uncertainty information of observational and other data.
- (2)
- Lack of tools for reliable information on model structural uncertainty.
- (3)
- Development of tools accounting for spatial, temporal and spatio-temporal uncertainty is still a challenge because many environmental variables are measured at diverse spatial and temporal scales and because there are strong correlations between variables.
- (4)
- Large computational budgets are required when modelling spatio-temporal distributed systems, due to the large number of variables and the correct characterisation of uncertainties and correlations.
- (5)
- Models commonly exhibit complex probability distributions in model output response due to nonlinear responses to model input, even for simple parametric input probability distributions.
- (6)
- The default mechanism to propagate uncertainties is the Monte Carlo method, which is highly computationally demanding. Therefore, large computational resources and implementations of computationally efficient tools are required.
Generally, in environmental and geospatial modelling, there are three main sources of uncertainty [4,5]: (1) Model input uncertainty; (2) Model parameter uncertainty; and (3) Model structural uncertainty. Proper characterisation and quantification of all three uncertainty sources are fundamental in the analysis of the propagation of uncertainties through environmental models. It is also important that practical tools are available to address the characterisation and propagation of uncertainties through models.
Spatial uncertainty propagation has been addressed in several fields, such as in hydrological and water quality modelling [6,7,8], in scenario analysis [9], and in soil pollution and nutrient modelling [1,10,11]. However, it is recognised that there is not a universal software tool for performing uncertainty propagation tasks [3].
Regarding software tools developed for uncertainty propagation analysis, Sawicka et al. [3] list different tools available for spatial and non-spatial uncertainty propagation and uncertainty assessment. Among the listed tools, there is free software, such as OpenTURNS [12], DACOTA [13], and DUE [14], commercial software, such as COSSAN [15], and free software written for licensed software, e.g., SAFE [16] and UQLab [17] toolboxes for MATLAB (MathWorks, Natick, MA, USA). An extensive review of available UP software tools is presented in [2]. Regarding existing R packages, there are few that deal with uncertainty propagation explicitly: propagate and errors. However, neither of these two packages provides functionality for spatial uncertainty analysis.
Widely used techniques for uncertainty assessment in stormwater quality modelling are the classical Bayesian approach based on Markov Chain Monte Carlo (MCMC) sampling and the Metropolis Sampler [18], Generalized Likelihood Uncertainty Estimation (GLUE) [19], the Multi-algorithm Genetically Adaptive Multi-objective method [20], and the Shuffled Complex Evolution Metropolis algorithm [21]. However, these approaches usually do not take all uncertainty sources into account [22,23]. Dotto et al. [5] found that the definition of different subjective criteria, such as user-defined likelihood measures and prior knowledge required in Bayesian techniques, are important issues that limit the application of these techniques. Wijesiri et al. [23] pointed out that these limitations could have a significant influence on management and planning decisions for mitigation of stormwater pollution. In stormwater quality modelling, a poor characterisation of the source uncertainty (process variability) is the main limitation in accounting for uncertainty [23]. Therefore, provided these uncertainty sources can be captured adequately by probability distributions, the use of Monte Carlo (MC) methods for uncertainty propagation is still a suitable option that can overcome most of these limitations.
The literature review above indicates that there are still gaps in research and development of tools for temporal, spatial and spatio-temporal UP accounting for change of support across multiple scales in environmental and geospatial domains. We present the spatio-temporal and Uncertainty Propagation across multiple scales R-package, “stUPscales”, which provides several R methods and functions for spatio-temporal uncertainty propagation through MC simulation in environmental models, while taking space-time aggregation and disaggregation procedures into account.
We recognise that spup [3] addresses spatial UP as well, both for continuous and categorical variables. Although there are similarities between spup and stUPscales, there are meaningful differences too. The main difference is that stUPscales can also handle UP in the temporal and spatio-temporal domain. In addition, in stUPscales, besides sampling from uniform, normal, log-normal, and normal truncated probability distribution functions (pdfs), it is also possible to simulate environmental variables as uni- and multi-variate autoregressive models of order one. Moreover, stUPscales has explicit functionality for spatio-temporal change of support. Additionally, another important difference between the two packages is the handling of data structure and objects. In stUPscales, the temporal dimension is handled as xts (eXtensible Time Series) objects from the xts package [24], while space-time objects are handled by the classes ST (Spatio Temporal) from the spacetime package [25], especially the class STFDF (Spatio Temporal Full Data Frame) for regular grids. The spup package makes use of the objects RasterStack from the Raster package [26].
We illustrate the package for temporal aggregation of time series as precipitation and pollutants of Urban Drainage Models (UDMs). In addition, we illustrate the methods and functions for uncertainty propagation in an example of a lumped UDM, EmiStatR, via MC simulation to evaluate water quantity and quality in emissions of Combined Sewer Overflows (CSOs). The example serves for testing the hypothesis that when characterisation of sewage quality indicators as chemical oxygen demand (COD) and ammonium (NH) is considered with the appropriate process variability, uncertainty can be quantified as an integral part of the total uncertainty in the modelling procedure.
Regarding the spatio-temporal uncertainty propagation domain, we show how the package can be used to model and predict variables that vary in space and time by using a spatio-temporal variogram model and space-time ordinary kriging. We emphasize that the spatio-temporal functionality developed in stUPscales for performing uncertainty propagation studies is an important contribution to the scientific and practitioner communities by making this open source tool accessible and illustrating its applicability in the water domain. However, it should be noted that the tool may also be applied to other domains in environmental modelling.
The objectives of this study are to: (1) Develop a tool for characterising uncertainty in spatial, temporal and spatio-temporal environmental variables (model inputs) as pdfs and as uni- and multi-variate autoregressive models; (2) Develop a tool for sampling from these pdfs (to support MC UP analysis) and to generate realisations of autoregressive models for environmental variables; (3) Develop functions for aggregation of realisations of environmental variables in space and time; (4) Illustrate the tool with a few simple examples; (5) Develop a method to propagate model input uncertainty through environmental models; (6) Develop a function to analyse results of a MC UP.
2. Materials and Methods
This section describes the R-package stUPscales, its main class, methods and functions.
2.1. The R-Package stUPscales
An overview of the conceptual framework is presented in Figure 1. Three steps are distinguished:
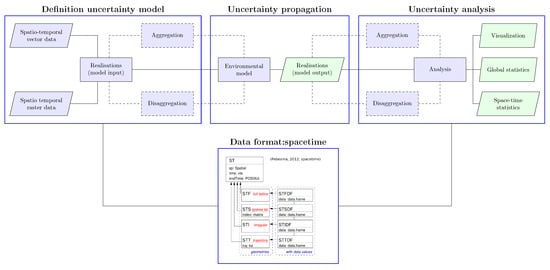
Figure 1.
Conceptual framework for uncertainty propagation across multiple scales with the stUPscales package. Blue rectangular node = process; blue trapezoidal node = input; green trapezoidal node = output; solid line = path; dashed line = optional path.
- (1)
- Definition of the uncertainty model (class setup and method MC.setup). Data in raster or vector format are retrieved and the uncertainty model defined. This characterises the input uncertainty in order to generate realisations from the pdfs or, in the case of time series, from uni- or multi-variate autoregressive models;
- (2)
- Uncertainty propagation (method MC.sim). A routine for automation of the chain model input—simulation—model output is defined. This routine is model-dependent and the model input format should match the specific format required by the model. The output format should match the format required by stUpscales. MC simulation is used for propagating model input uncertainty through the environmental model;
- (3)
- Uncertainty analysis (function MC.analysis). Summary statistics such as the mean, variance, and quantiles from the ensemble of MC simulations are computed. In addition, several plots summarising the outcome of the analysis are made.
The main class, methods and functions of stUPscales (version 1.0.3) are presented below. We describe the class setup and the methods and functions MC.setup, MC.sim and MC.analysis.
2.1.1. The Setup Class
The class setup is used to create objects of signature setup for further use in the Monte Carlo method. The created object contains eight slots (for more details, see the online user manual available at https://CRAN.R-project.org/package=stUPscales):
- id: Object of class “character” to identify the current MC simulation.
- nsim: Object of class “numeric” to specify the number of MC runs.
- seed: Object of class “numeric” to specify the seed of the random number generator.
- mcCores: Object of class “numeric” to specify the number of cores (CPUs) to be used in the MC simulation.
- st.input: Object of class “character” that defines the name of the file or url of the web service to retrieve the spatio-temporal input data.
- rng: Object of class “list” that contains the names and values of the variables to be used in the MC simulation. Five modes are available: (1) constant value; (2) a variable sampled from a uniform (uni) probability distribution function (pdf); (3) a variable sampled from a normal (nor) pdf; (4) a variable sampled from an autoregressive (AR) model and normal (nor) pdf; (5) a variable sampled from a vector autoregressive (VAR) model and normal (nor) pdf; (6) a variable sampled from discrete values (dis); and (7) a variable sampled from a truncated normal (tnor) pdf.
- ar.model: Object of class “list” containing the coefficients of the AR model as vectors, the name of which is the variable to be modelled and the length of which refers to the order of the model as required by function arima.sim from the base package stats.
- var.model: Object of class “list” containing the vector of intercept terms w, the matrix of AR coefficients A, and the noise covariance matrix C of the VAR model, the name of which is the variable to be modelled and the length of which refers to the order of the model as required by function mAr.sim from the package mAr. For mathematical details, see [27].
2.1.2. The MC.setup Method
Given an object of class setup, the method can be invoked for setting-up the MC simulation. The variables are sampled according to their parameters specified in the slot rng of the setup object. If ar.model is defined in slot ar.model, then the specified variables are sampled from the pdf or as an autoregressive (AR) model via the function arima.sim. If var.model is defined in slot var.model, then the specified variables are sampled from the pdf or as a vector autoregressive (VAR) model via the function mAr.sim (see [27,28] for details).
There are seven different cases considered in stUPscales (for more details see the online user manual available at https://CRAN.R-project.org/package=stUPscales). We developed specific cases accounting for autocorrelation of variables. An extract from the method MC.setup for selecting the sampling probability distribution function, case 2 of the method MC.setup, i.e., a normally distributed autocorrelated time series (AR1 model), is presented in Appendix A. Additionally, case 5 of the method, a normally distributed auto- and cross-correlated time series (var.model) in parallel code, is also presented in Appendix A.
2.1.3. The MC.sim Method
The method MC.sim is used to invoke a MC simulation. This method can be modified to work with another simulator. The method has two arguments:
- x: Object of class “list” as defined by method MC.setup.
- EmiStatR.cores: a numeric value for specifying the number of cores (CPUs) to be used in the EmiStatR method. Use zero for no use of parallel computation.
The value of the method is a list of length two. The first element of the list, mc, is a list that contains the MC.setup, timing and lap objects. The second element of the list, sim1, is a list that contains the Monte Carlo matrices of the simulator output.
2.1.4. The MC.analysis Function
The MC.analysis function is available for performing the statistical analysis of the MC simulation results. This function requires nine arguments:
- x: A list from the output of the method MC.sim.
- delta: A numeric value that specifies the level of temporal aggregation required in minutes.
- qUpper: A character string that defines the upper percentile to plot the prediction band of the results. Several options are possible: “q999” the 99.9th percentile, “q995” the 99.5th percentile, “q99” the 99th percentile, “q95” the 95th percentile, and “q50” the 50th percentile. The lower boundary of the prediction band (shown in grey in the output plots) is the 5th percentile in all cases.
- p1.det: A data.frame that contains the time series of the main driving force of the system to be simulated deterministically, e.g., precipitation. This data.frame should have only two columns: the first containing Time [y-m-d h:m:s], the second containing the (numeric) value of the environmental variable.
- sim.det: A list that contains the results of the deterministic simulation, here the output of EmiStatR given p1.det. See the method EmiStatR from the homonym package for details.
- event.ini: A time-date string in POSIXct format that defines the initial time for the event analysis.
- event.end: A time-date string in POSIXct format that defines the final time for the event analysis.
- ntick: A numeric value to specify the number of ticks in the x-axis for the event time-window plots.
- summ: A list provided as MC.analysis output, by default NULL. If provided, the list should contain an output of a previous MC.analysis function, so that the analysis is done again without the calculation of some of the internal variables, thus reducing computation time.
2.1.5. The Agg.t Function
The Agg.t function is used for temporal aggregation of environmental variables. Agg.t is a wrapper function of aggregate from the stats package. It requires five arguments:
- data: A data.frame that contains the time series of the environmental variable to be aggregated, e.g., precipitation. This data.frame should have two columns: the first is Time [y-m-d h:m:s]; the second the value of the environmental variable. If the environmental variable is different from precipitation, then the column name of the values can be any character string.
- nameData: A character string that defines the name of the environmental variable to be aggregated or an empty string (“ ”).
- delta: A numeric value that specifies the aggregation level required in minutes.
- func: The name of the aggregation function, e.g., mean, sum.
- namePlot: A character string that defines the title of the plot generated.
3. Example 1: Application of stUPscales to Temporal Uncertainty Propagation and Aggregation with the EmiStatR Model
We present a UP example using an environmental model with application in urban water modelling, the EmiStatR model, coded as R-package. Its input class and main method EmiStatR are presented as well.
The example is an application in temporal UP for simulation of the water volume and water quality dynamics in combined sewer systems (CSSs). CSSs are designed to convey wastewater during precipitation events and also directly to the wastewater treatment facility in dry weather flow conditions. In CSSs, two types of discharge are distinguished: (1) the pass forward flow, which transports the sewage discharge directly to the wastewater treatment facility [29]; (2) the combined sewer overflow (CSO), which is the sewage diverted from the treatment facility and discharged, untreated, into a local receiving water body during heavy precipitation events [30]. CSOs, when released to the environment, can have an important damaging impact on the water quality status of receiving waters (streams, rivers, ponds, lakes, wetlands, and oceans). About 50% of pollutants in stormwater are metals, nutrients, organic toxins, and bacteria, and are associated with particulate matter. The other 50% are soluble [30], and therefore these pollutants can be more persistent in the water and the environment itself. Minimisation of the CSO spill volume is therefore important for the preservation of good water quality status of receiving waters. The goal of this example is to quantify model output uncertainty when model input uncertainties are propagated through a simplified lumped urban drainage model.
3.1. The Model EmiStatR
The R-package EmiStatR version 1.2.0.4 is used to perform the simulations and to propagate model input uncertainty in the example with the R-package stUPscales. Details regarding the EmiStatR model are found in [31].
The main components of the EmiStatR model are: (1) Dry Weather Flow (DWF) including Infiltration Flow (IF); (2) Pollution of DWF; (3) Rain Weather Flow (RWF); (4) Pollution of RWF; (5) Combined Sewer Flow (CSF) and pollution; and (6) Combined Sewer Overflow (CSO) and pollution.
Basically, the total dry weather flow, is calculated as:
where is the dry weather flow estimated as the flow of the residential wastewater in the catchment, calculated as 86,400 (where 86,400 is a measurement unit conversion factor), with [PE] the population equivalents of the connected CSO structure, and the individual water consumption of households. is the infiltration flow that enters the pipes from groundwater flow through cracks and joints, calculated as , where [ha] is the impervious area of the catchment, and is the infiltration water inflow flux (specific infiltration discharge from groundwater flow). Variables and are dynamic and can be defined as time series with daily, weekly and seasonal patterns.
The contribution of rain water to the combined sewage volume is given by [m]. This is a vector whose length is equal to that of the input precipitation time series. is computed as:
where is a time series of rainfall depth ; is the impervious area of the catchment [ha]; is the total area of the catchment [ha]; is the run-off coefficient for impervious areas [-]; and is the run-off coefficient for pervious areas [-].
The load, [kg], of a specific water quality variable x (e.g., Chemical Oxygen Demand, COD, or Ammonium, NH) in the overflow is calculated as a function of the CSO spill volume, , a combined sewer mixing ratio, [-], the mean dry weather pollutant concentration, , and the concentration due to rainwater pollution, .
where refers to dry weather flow and to rainwater. , and are vectors of length equal to the input precipitation time series, . can be a vector of length equal to or a unique value constant in time. Two indicators of water pollution are simulated: COD and NH. Table 1 presents the main components and input variables of the EmiStatR model. The main model outputs are listed in Table 2.

Table 1.
General input data and combined sewer overflow (CSO) data to be defined by the input object.

Table 2.
Output variables of the EmiStatR method.
An object of class input can be defined to contain all required input data for running the model in deterministic mode. An object of class input can be created by invoking the command input() or new(“input”). The content details of an object of class input can be found in the user manual of the EmiStatR package available in CRAN (https://cran.r-project.org/web/packages/EmiStatR/). This object has 20 slots. For this example, the model input variables considered in the simulations and used to compute the output uncertainty are presented in Table 1.
If calibration data are available, EmiStatR parameters may be calibrated prior to simulation. If calibration is not feasible, the model can be run using parameter values taken from the reference literature and guidelines. Table 3 provides reference values and calibration ranges for the most important EmiStatR parameters.

Table 3.
Default values for input data of EmiStatR.
The output value of the EmiStatR method is described in the manual. Here, we are interested in propagating model input uncertainties through the simplified lumped urban drainage model.
3.2. Temporal Aggregation and Model Input Uncertainty Propagation
We used the Agg.t function, described in Section 2.1.5, to perform a temporal aggregation of the model input data to the time step required. The model input uncertainty propagation is done in a two-step process. First, a model input uncertainty definition is done by setting up the MC simulation. For this, we apply the setup class and the MC.setup method. Second, the MC simulation is performed by applying the MC.sim method, after which the UP analysis is done through the application of the MC.analysis function.
3.3. Results
In this section, we first present the input time series as the main driving force of the system modelled. This input is important because the other input time series definition depends on it to achieve the same model input support. Second, the results of input time series aggregation are shown. Finally, the results of the model input uncertainty propagation with stUPscales are presented.
3.3.1. Model Input
EmiStatR includes an example of a precipitation dataset called P1, used as main input data. This dataset is a list that contains a data.frame with two columns: “Time [y-m-d h:m:s]” and precipitation depth in millimetres “P [mm]”. The rain gauge station where the measurements were recorded (in this case Dahl) is located close to the catchment of the combined sewer overflow chamber at Goesdorf, Grand-Duchy of Luxembourg. The dataset contains records from 1 January until 2 February 2016. The recording time step is 10 min. We used this dataset as precipitation input.
3.3.2. Temporal Aggregation and Model Input Uncertainty Propagation
As an illustration of the Agg.t function, we aggregated the time series of precipitation P1 from 10 to 30 min. We took the sum as aggregation function. Following the two-step process, we performed the model input uncertainty propagation. First, an illustration of the model input uncertainty definition is presented by setting up the MC simulation. Second, the MC simulation is executed followed by its respective analysis.
3.3.3. Model Input Uncertainty and Monte Carlo Simulation Set-Up
For setting up the MC simulation, we applied the setup class and the MC.setup method. Appendix A.6.4 shows the R-code for the settings of the setup class. Upon the definition of the setup object, we proceeded to invoke the MC.setup to create the sampled variables from their corresponding probability distributions.
The water quantity input variables chosen for the uncertainty propagation analysis are water consumption (), infiltration inflow water (), run-off coefficient for impervious area (), run-off coefficient for pervious area (), population equivalents (), orifice coefficient of discharge () and the initial water level in the chamber ().
The precipitation input time series and the water quality input variables chosen for the uncertainty propagation analysis are plotted in Figure 2. A time window was chosen for illustration purposes. The sewage COD pollution per capita [PE] load per day () was modelled as an autoregressive order one (AR1) model with autoregressive coefficient equal to 0.7 (Figure 2). The sewage NH pollution per capita [PE] load per day () was also modelled as an AR1 model with autoregressive coefficient equal to 0.7 (Figure 2).
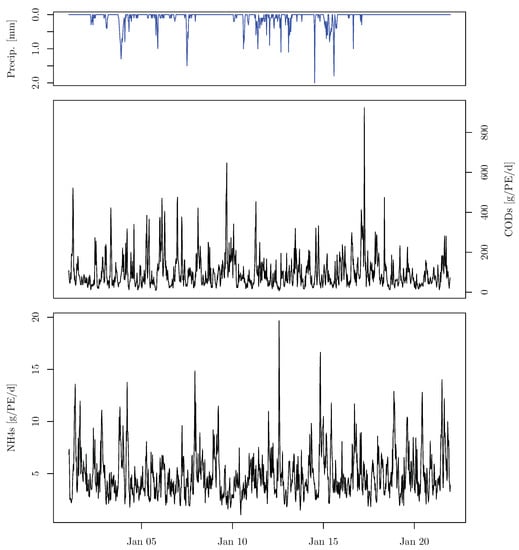
Figure 2.
Series of precipitation, sewage COD pollution and sewage NH pollution for the time window.
3.3.4. Monte Carlo Simulation and Analysis
The MC simulation was performed by invoking the MC.sim method. The analysis of the MC simulations was done by invoking the MC.analysis function. In order to proceed with the MC analysis, a deterministic simulation was defined and computed. First, we defined structure 1, named “E1”. Second, the input.user object of class input was defined. Next, we invoked the method EmiStatR with the deterministic input (input.user) defined before. Finally, the additional arguments of the MC.analysis function were defined. Upon definition of the additional arguments, the function MC.analysis was invoked. Appendix A.6.5 presents the R-code of the MC.sim method and the MC.analysis function.
Only part of the outputs of the analysis are presented here. Figure 3 presents the time series of the deterministic simulation, as well as the mean and 95% prediction band of the MC simulations at a 30-min time step, for simulation and analysis of the water volume. Figure 4 shows the time series window for COD load and concentration in spill water volume in the CSO and NH load concentration in spill water volume in the CSO, at a 30-min time step.
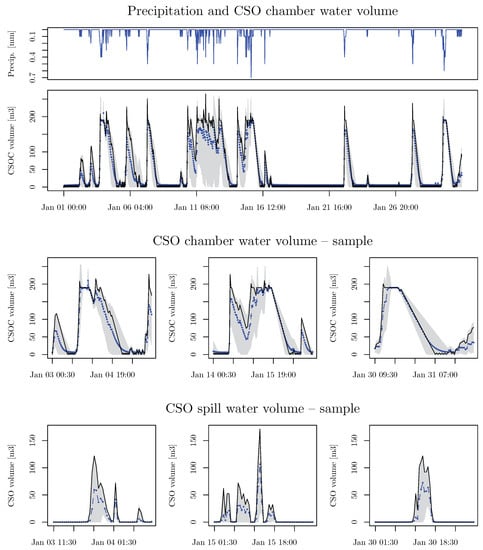
Figure 3.
January 2016 time series of deterministic simulation (continuous black line), mean (dotted blue line), and 95% prediction band (grey band) of the Monte Carlo simulation at 30-min time step for simulation and analysis of water volume. Time series window for precipitation (top), water volume in the combined sewer overflow (CSO) chamber (second), detailed snapshots for water volume in the CSO chamber (third), and spill water volume of CSO (bottom).
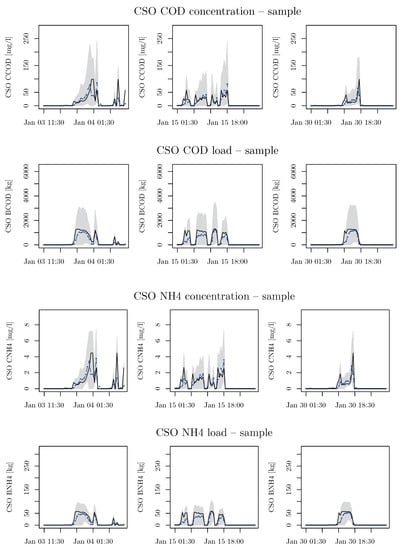
Figure 4.
Time series for chemical oxygen demand (COD) load and concentration in spill water volume in the combined sewer overflow (CSO) and ammonium (NH) load concentration in spill water volume in the CSO at 30-min time step for simulation and analysis of Monte Carlo simulation. Deterministic simulation (continuous black line), mean (dotted blue line), and 95% prediction band (grey band) of the Monte Carlo simulation.
4. Example 2: Application of stUPscales to Spatio-Temporal Uncertainty Characterisation of Precipitation for the Grand-Duchy of Luxembourg
This example illustrates the capability of stUPscales to address UP in the spatio-temporal domain. We illustrate how to characterise the spatio-temporal uncertainty of precipitation for the entire country of the Grand-Duchy of Luxembourg. We use observations of a precipitation time series measured at 25 rain gauges for the period January 2010 to December 2011, recorded at 10-min time steps. The set of time series was provided by the Luxemburgish Administration des Services Techniques de l’Agriculture (ASTA), and verified for consistency by the Observatory for Climate and Environment (OCE) of the Luxembourg Institute of Science and Technology (LIST).
We prepared the data to predict space-time precipitation fields at 500 m and 10-min time step. This space-time uncertainty information can, for instance, be used to feed a distributed rainfall–runoff model coupled with an urban drainage model. We only demonstrate the precipitation uncertainty characterisation, since an entire UP study of a rainfall–runoff model is out of the scope of this paper and will be addressed in subsequent papers.
4.1. Selection of Event
We selected a 10-h period where the cumulative precipitation of the time series is maximal, assuring to retrieve a precipitation event in all stations. The selected period of the event was 16 December 2011 from 12:00 a.m. to 10:00 a.m. A total of 32 stations were available. Seven stations were not taken into account because of no measurement in the selected period. For illustration purpose, Figure 5 presents eight out of the 25 selected time series, and Figure 6 illustrates 18 snapshots of the event every 30 min and shows how this event is distributed in space. It also shows the precipitation magnitude in the 25 rain gauges.
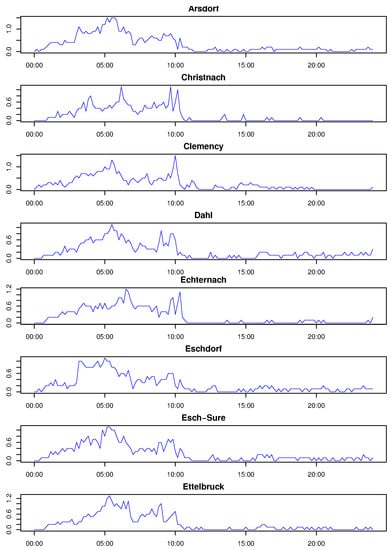
Figure 5.
Observed time series for event 16 December 2011, eight out of 25 stations. The experimental variogram was calculated in the interval from 12:00 a.m. to 10:00 a.m. including the 25 stations.
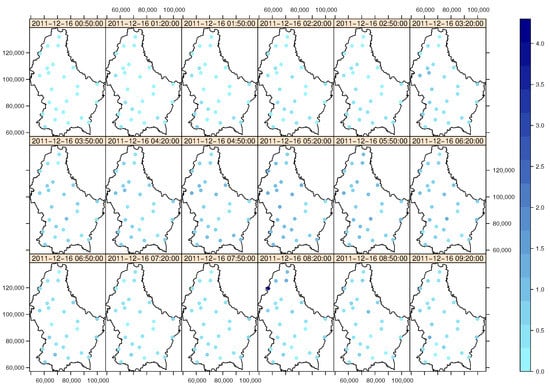
Figure 6.
Distribution of observations for event 16 December 2011 over the country of the Grand-Duchy of Luxembourg, 18 snapshots for illustration purpose only. Every dot represents a rain gauge observation. The units of the x and y scales are meters. The scale bar represents precipitation in millimeters.
4.2. Ordinary Kriging in the Space-Time Domain
To model precipitation fields in the spatio-temporal domain, we used the concept of the spatio-temporal variogram for spatio-temporal ordinary Kriging [36]. Following Snepvangers et al. [37], the aim of space-time geostatistical modelling is to predict or simulate an attribute z given by:
where refers to space, to time. The prediction or simulation of z is made at a space–time point , where z was not measured.
A space-time random function model Z can be defined to predict [37]:
where m is the trend component of the model and is a zero-mean stochastic residual component. The prediction is based at measurements in n space-time points . In space-time ordinary kriging (ST-OK), the trend component is assumed to be an unknown constant mean. The stochastic residual component is characterised by a space-time variogram, that, under second-order stationarity, can be computed from the measurements [37]:
where and are the space and time lags, and is the number of pairs in the space-time lag.
To fit a model to the space-time experimental variogram (Equation 6), we need to overcome some additional problems as we have space and time variation. In this example, we used a model that considers the definition of one covariance model (or variogram) for the space domain and one covariance model (or variogram) for the time domain, including an anisotropy parameter , as described by Bilonick [38] and revisited by Snepvangers et al. [37] and Graeler et al. [36]. This is the sum-metric covariance model:
The variogram is derived similar to the covariance [36,37] as:
stUPscales implements routines of the R package gstat [39] for representing the spatio-temporal covariance models. Besides the sum-metric model, four additional models are available in gstat: Separable; Product-sum; Metric; and Simplified sum-metric.
4.3. Results
The commands used to produce the results explained next are presented in Appendix A.7.
4.3.1. Events Selected and Space-Time Full Grid Object
stUPscales has a dataset with the selected events per station as an xts object in space-wide format for easy visualisation of the 25 stations in the object event.subset.xts. The spatial locations of the 25 rain gauge stations are provided as a dataset in SpatialPointsDataFrame format from the sp package [40]. The boundary of the country of the Grand-Duchy of Luxembourg is given as a dataset in sp format SpatialPolygonsDataFrame. The data were converted to a space-time full data.frame (STFDF) of the package spacetime [25], through the function stConstruct from the same package. The object is visualised in Figure 6.
4.3.2. Space-Time Variograms
Once the observation period was defined, we computed the experimental spatio-temporal variogram according to Equation (6) using the function variogramST of the gstat package, with time lags of 50 min and space lags of 5000 m. The spatio-temporal anisotropy was estimated by the estiStAni function (gstat). Before proceeding to the fit of the parameters, the experimental variogram and the anisotropy were scaled to have distances in kilometers.
The sum-metric variogram model (Equations (7) and (8)) was defined in gstat by using the vgmST function. The model was fitted using the fit.StVariogram gstat function with the L-BFGS-B optimisation algorithm described in Byrd et al. [41], which allows box constraints with lower and upper bounds. All space-time variogram parameters (spatial, temporal and joint nugget, range and partial sill) were estimated by minimising the mean squared error (MSE). The MSE of the best model fitted is 0.00013. Figure 7 shows the experimental spatio-temporal variogram (a), the fitted spatio-temporal variogram (b) and the residuals of the spatio-temporal variogram model for the sum-metric model (c). The fitted parameters of the sum-metric model are given in Table 4.
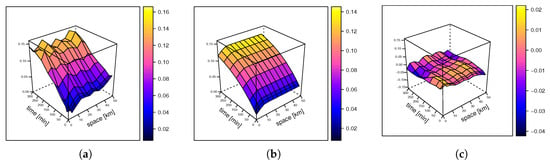
Figure 7.
Spatio-temporal variograms. (a) empirical (sample) variogram; (b) theoretical sum-metric model; (c) difference between sample and best fitting theoretical sum-metric model.

Table 4.
Space-time variogram model.
4.3.3. Space-Time Ordinary Kriging
Upon definition of the space-time variogram, we proceeded to create prediction maps using space-time ordinary kriging. For this, a prediction grid over Luxembourg was created and predictions were made by the function krigeST from gstat. The prediction maps are shown in Figure 8. Finally, we computed the lower and upper boundary of the 90 percent prediction interval as shown in Figure 9 and Figure 10.
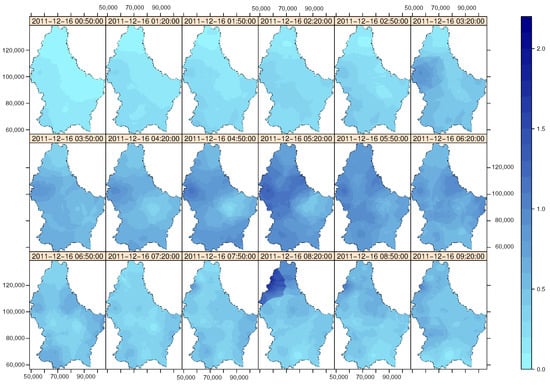
Figure 8.
Prediction maps obtained with the spatio-temporal sum-metric model.
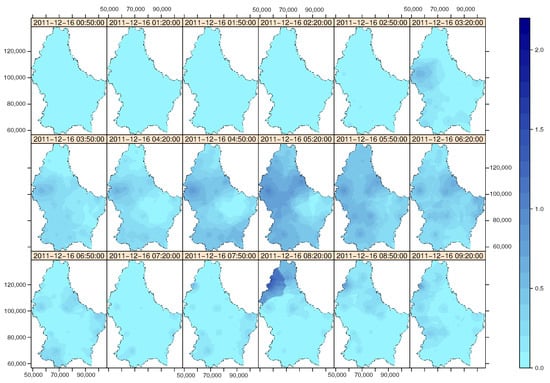
Figure 9.
Predictions obtained with the spatio-temporal sum-metric model (lower boundary of the 90 percent prediction interval).
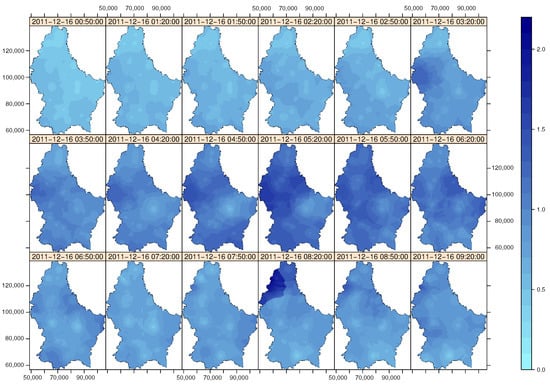
Figure 10.
Predictions obtained with the spatio-temporal sum-metric model (upper boundary of the 90 percent prediction interval).
With this, the stUPscales package is ready to characterise space-time uncertainties of environmental variables. The next steps for subsequent work are to simulate realisations of such variables and analyse the uncertainty propagation.
5. Discussion
We developed the stUPscales R package as a contribution to state-of-the-art software tools designed to perform spatio-temporal uncertainty characterisation and uncertainty propagation analysis of environmental models across different scales. We applied the tool in two examples where the class, methods and functions were tested satisfactorily as an illustration of the capabilities of the package. In this section, we highlight and discuss the main results obtained and put these in perspective with other studies.
5.1. Temporal and Spatio-Temporal Model Inputs
In Example 1, we used a simplified urban drainage model, EmiStatR, for testing purposes. We used this model because of its simplification and parallel computing coding, allowing a seamless uncertainty propagation in the R environment.
The main input variable of the modelling framework developed in the example corresponded to a time series of precipitation included as a dataset into the R-package EmiStatR. This time series includes records from 1 January to 2 February 2016 (4462 observations). The total precipitation in the time series is 89.6 mm, with a mean value for non-zero data of 0.18 mm and maximum value of 0.90 mm. While the recording time step is 10 min, we aggregated the precipitation to 30 min to illustrate the aggregation capabilities of stUPscales. We characterised the uncertainty of the temporal input by invoking the temporal autocorrelation function.
For Example 2, we used time series of precipitation for 25 rain gauges distributed over the country of Luxembourg as an input dataset. The event selected was a period of 10 h from 12:00 a.m. to 10:00 a.m. on 16 December 2011. Next, we characterised the spatio-temporal uncertainty by inferring the experimental space-time variogram from the observations for the entire spatial domain and time period.
5.2. Temporal Aggregation of Model Input
In Example 1, we illustrated the temporal aggregation function Agg.t of the stUPscales package. The level of aggregation was a 30-min time step. The resulting time series is composed of 1488 observations, summing up to a total precipitation of 89.6 mm, with a mean value for non-zero data of 0.33 mm and maximum value of 2.00 mm. This level of aggregation is useful when a large time series is used as input in the uncertainty propagation procedure, reducing the computational burden required for the MC simulation.
5.3. Model Input Uncertainty Propagation
In Example 1, we used the MC method for model input uncertainty propagation through the environmental model. In so doing, we accounted for temporal and cross-correlations when defining model input uncertainty and performing uncertainty propagation.
5.3.1. Model Input Uncertainty and Monte Carlo Simulation Set-Up
Moret at al. [42] present a literature review about characterisation of input uncertainties in strategic energy planning models. They found that, in the context of strategic design problems, Tock and Maréchal [43] use normal, uniform and beta distributions to define uncertainty of economic parameters with lower and upper limits defined from institutional reports. In addition, in the context of energy systems design under uncertainty, Dubuis [44] proposes a methodology based on statistical theory, i.e., on definition of probability distribution functions. However, uncertainty characterisation using pdfs is not always possible when data are unavailable. In the absence of data for defining future uncertainties in the UK energy transition pathways, Pye et al. [45] propose using triangular distributions for representing uncertainty between upper and lower limits, defined from the literature. To account for uncertainty in the assessment of biomass-to-fuel strategies in wastewater treatment applications, Sin et al. [46] assign different levels of cost uncertainty (low, medium, high), taking into account maturity and complexity. In addition, upper and lower limits to all model parameters were defined by expert knowledge and establishing uniform distributions. In the design of flexible multi-generation systems, Lythcke-Jorgensen et al. [47] assume variations of ±25% and uniform distributions for parameters of investment and operating cost.
In the urban drainage modelling domain, Wijesiri et al. [23] quantified uncertainty by uncertainty limits associated with predicted build-up and wash-off processes. Zoppou [48] states that “providing the uncertainty associated with model outcomes in terms of uncertainty limits is an effective way to enhance management and planning decisions".
Most of the reviewed literature highlighted that, regarding parameter uncertainty characterisation, there is a difficulty to define pdfs based on data at proper quantity and quality. In this sense, Moret et al. [42] present a method to characterise input uncertainty for strategic energy planning models. This method proposes the definition of a set of criteria for the establishment of variation ranges for uncertain parameters, instead of the definition of pdfs. For some techniques, such as robust optimization, full pdfs are not needed and specification of uncertainty ranges is enough [49].
The stUPscales package includes both pdf and range characterisations for input uncertainty quantification. The pdf option allows the definition of normal, log-normal and truncated normal pdfs. The range option consists of the definition of a uniform pdf where the lower bound (minimum value) and the upper bound (maximum value) are defined as function arguments. Additionally, two more options are available for the characterisation of model input uncertainty: (1) discrete, where a uniform discrete sampling is defined; and (2) constant, where a unique constant value is defined in time and space, i.e., suitable for representing model inputs that are not uncertain. With all these possibilities, we cover an important range of characterisations for model input uncertainty used in practice.
5.3.2. Monte Carlo Simulation and Analysis
In Example 1, the selected water quantity input variables for the uncertainty propagation analysis (water consumption, , infiltration inflow water, , impervious area, , run-off coefficient for impervious area, , run-off coefficient for pervious area, , population equivalents, , orifice coefficient of discharge, and the initial water level in the chamber, ), had been defined to quantify input uncertainty and analyse how it propagates through the environmental model, EmiStatR, to the different model outputs related to water quantity (‘CSO summary’ in Table 2, and Figure 3).
Regarding the selected water quality input variables for the uncertainty propagation analysis (sewage COD pollution per capita [PE] load per day, , sewage NH pollution per capita [PE] load per day, , and rain COD pollution, ), these reflect how the variability in the input uncertainty definition is translated to the model output (‘COD in spill volume’ and ‘NH in spill volume’, as shown in Table 2 and Figure 4).
In the case of total concentration of COD (CCOD) in the spill volume, a mean value of 145 mg·L and a maximum value of 190 mg·L were simulated in the deterministic run. In the Monte Carlo simulation, a mean value of 255 mg·L and a maximum value of 511 mg·L in the 95 percentile band were obtained. These large differences indicate a large uncertainty in this variable. The relative increase of the mean and maximum are 1.8 and 2.7, respectively.
In the case of total concentration of NH (CNH4) in the spill volume, a mean value of 4.1 mg·L and a maximum value of 6.5 mg·L were simulated in the deterministic run. In the Monte Carlo simulation, a mean value of 5.5 mg·L and a maximum value of 12.6 mg·L in the 95 percentile band were obtained. While the means are similar, the large increase in the maximum indicates that uncertainty in this variable is also substantial, as already indicated by the wide prediction bands (grey area) shown in Figure 4.
These results demonstrate the usefulness of performing model input uncertainty propagation through the environmental model, which is an important goal in the evaluation and communication of uncertainties in environmental modelling.
In order to further validate model accuracy, a complete uncertainty propagation analysis would have to involve (cross-)validation using independent observations. This was beyond the scope of the paper and is currently done in a subsequent paper on a full uncertainty propagation analysis of the EmiStatR model, including a stochastic sensitivity analysis to analyse the contribution of each source of uncertainty to the overall uncertainty of the model results.
5.4. Space-Time Characterisation of Model Input Uncertainty
In Example 2, we showed how space-time model input uncertainty is modelled in stUPscales. We used space-time ordinary kriging, with a space-time unknown constant mean of the process and a space-time stochastic residual for which the literature proposes different covariance models [36]. However, in the space-time domain, the fitting of the covariance model is not trivial compared to that in spatial kriging. We used the sum-metric model [36,37], which gave satisfactory results. We showed space-time prediction maps of the precipitation for a 10 h time period on 16 December 2011 for the Grand-Duchy of Luxembourg.
5.5. Data Format for Uncertainties
We have coded stUPscales to be compatible with standard spatio-temporal data concepts and formats in R, such as the spatio-temporal classes ST of the spacetime package [50]. This allows for seamless linkage of geospatial and spatio-temporal models and sub-models across multiple scales.
In addition, despite an attempt to create the Uncertainty Markup Language (UncertML) [51] as an Open Geospatial Consortium (OGC) standard to store metadata for uncertainty propagation applications [6], there is still an open question about the suitability of this data format to hold, visualise and communicate uncertainties together with the space-time ST classes in R. Furthermore, there is a potential to develop a new class or extend the ST classes to embed the uncertainty information regarding data uncertainty, input uncertainty characterisation, output uncertainty and summary statistics.
6. Conclusions and Future Research
We presented the R package spatio-temporal and Uncertainty Propagation across multiple scales, stUPscales. This package constitutes a contribution to the state-of-the-art of open source tools that aim to support uncertainty propagation in the spatio-temporal domain. The main class, methods and functions of the package were presented and illustrated with an example of temporal model input uncertainty propagation through a simplified lumped urban drainage model accounting for water quality modelling. We also showed how the package can be used to model and predict environmental variables that vary in time and space. Using simulations of these types of variables in MC uncertainty propagation will be done in subsequent work.
The main contribution of stUPscales compared to existing uncertainty propagation tools is that it is not restricted to uncertainty analysis of purely spatial applications but can also handle uncertain temporal and spatio-temporal variables. In addition, it is designed to handle aggregation and disaggregation of uncertain temporal, spatial and spatio-temporal variables. Through two examples, we demonstrated that stUPscales is suitable for characterising uncertainty in spatial, temporal and spatio-temporal environmental variables (model inputs) as probability distribution functions (pdfs) and as uni- and multi-variate autoregressive models. Moreover, it is possible to sample from these pdfs (to support MC UP analysis) and to generate realisations of autoregressive models. We illustrated the aggregation functionality of stUPscales by averaging realisations of precipitation in time. We propagated model input uncertainty through a simplified urban water model and analysed the results of an MC UP. Finally, we showed how space-time geostatistical interpolation is done in stUPscales.
It is worthwhile to explore the development of a new class or to extend the ST classes so that these incorporate uncertainty information regarding data uncertainty, input uncertainty characterisation, output uncertainty and summary statistics. We recommend that future implementations take this matter into account.
Further extension of the package will allow for implementing new methods and functions for spatio-temporal disaggregation of model inputs and outputs, giving more flexibility to the proposed workflow when linking models with different spatio-temporal support or across multiple space-time scales.
Author Contributions
J.A.T.M. is the main developer of stUPscales and the author of the text in this article. U.L. and G.B.M.H. are co-authors of stUPscales, they contributed to this article with their statistical, geostatistical and programming knowledge, reviewed and edited the text, and contributed to the stUPscales concept and development.
Acknowledgments
The authors thank the Luxemburgish Administration des Services Techniques de l’Agriculture (ASTA) for the time series of precipitation, and the Observatory for Climate and Environment (OCE) of LIST for its technical support. This study is part of the QUICS project and has received funding from the European Union’s Seventh Framework Programme under Grant No. 607000, and from LIST.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Appendix A.1. The setup Class
A default setup object can be created and checked as follows:
> library(stUPscales)
> new_setup <- setup()
> str(new_setup)
Formal class 'setup' [package "stUPscales"] with 8 slots
..@ id : chr "MCsim1"
..@ nsim : num 1
..@ seed : num 0.701
..@ mcCores : num 1
..@ st.input : NULL
..@ rng : NULL
..@ ar.model :List of 1
.. ..$ : NULL
..@ var.model :List of 1
.. ..$ : NULL
Appendix A.2. The MC.setup Method
An extract from the method MC.setup for selecting the sampling probability distribution function, in case 2 of the method MC.setup:
# case 2: normal autocorrelated time series (AR1 model)
requireNamespace("lmom")
r <- matrix(NA, nrow=nsim, ncol = nrow(st.input))
j <- 1
for(j in 1:nsim){
# r[j,] <- quanor(runif(nrow(st.input)), c(as.numeric(rng[[i]]["mu"]),
as.numeric(rng[[i]]["sigma"])))
y1 <- arima.sim(n = nrow(st.input) , list(order=c(1,0,0),
ar=ar.model[[names(rng)[[i]]]])) # ar =.5
m1 <- mean(y1); s1 <- sd(y1)
m2 <- as.numeric(rng[[i]]["mu"])
s2 <- as.numeric(rng[[i]]["sigma"])
y2 <- m2 +(y1-m1)*s2/s1
r[j,] <- y2
}
par[[i]] <- r
npar <- npar+1
}
Similar as above but now for case 5 of the method MC.setup:
# case 5: normal auto- and cross-correlated time series (var.model), parallel code
{
var1 <- (matrix(NA, nrow=1, ncol = nrow(st.input)) )
var2 <- (matrix(NA, nrow=1, ncol = nrow(st.input)) )
obj1 <- 1:nsim
requireNamespace("parallel")
requireNamespace("doParallel")
requireNamespace("foreach")
cl <- makeCluster(mcCores, outfile="")
registerDoParallel(cl, cores=mcCores)
numCores <- detectCores()
rp <- foreach(obj1 = obj1, .packages = c("lmom", "mAr", "parallel", "doParallel",
"foreach"), .export=c("obj1"), .errorhandling = "pass", .verbose=TRUE,
.combine = "rbind") %dopar% {
j <- obj1
print(paste(j, ", ", mcCores, " of ", numCores, " cores for creating
VAR model", sep=""))
y1 <- mAr.sim(w = var.model[["w"]], A = var.model[["A"]],
C = var.model[["C"]], N = nrow(st.input))
# code for only bivariate case
m1 <- mean(y1[,1]); s1 <- sd(y1[,1])
m2 <- as.numeric(rng[[indexVAR[1]]]["mu"])
s2 <- as.numeric(rng[[indexVAR[1]]]["sigma"])
y2 <- m2 +(y1[,1]-m1)*s2/s1
var1[1,] <- y2
m1 <- mean(y1[,2]); s1 <- sd(y1[,2])
m2 <- as.numeric(rng[[indexVAR[2]]]["mu"])
s2 <- as.numeric(rng[[indexVAR[2]]]["sigma"])
y2 <- t(as.data.frame(m2 +(y1[,2]-m1)*s2/s1))
var2[1,] <- y2
return(c(var1, var2))
}
stopCluster(cl)
# closeAllConnections()
# asignation only for bivariate case:
par[[indexVAR[1]]] <- rp[,1:nrow(st.input)]
par[[indexVAR[2]]] <- rp[,(nrow(st.input)+1):(nrow(st.input)*2)]
npar <- npar+2
}
The method is invoked as follows:
> new_mc_setup <- MC.setup(new_setup)
Appendix A.3. The MC.sim Method
The method MC.sim is invoked as follows:
> new_sim <- MC.sim(new_mc_setup)
Appendix A.4. The MC.Analysis Function
The function MC.Analysis is invoked as follows:
> new_analysis <- MC.analysis(new_sim, delta, qUpper, P1.det, sim.det,
+ event.ini, event.end, ntick)
Appendix A.5. The Agg.t Function
The function Agg.t is invoked as follows:
> library(stUPscales)
> new_aggregated <- Agg.t(data, nameData, delta, func, namePlot)
Appendix A.6. Example 1: Temporal uNcertainty Propagation and Aggregation
Appendix A.6.1. The Model EmiStatR
An object of class input can be created by invoking the command input() or new("input") as follows:
> library(EmiStatR)
> new_input <- input()
> str(new_input)
A deterministic simulation can be obtained by directly invoking EmiStatR as follows:
> sim_deterministic <- EmiStatR(new_input)
Appendix A.6.2. Model Input
EmiStatR includes an example of a precipitation dataset called P1, used as main input data. The rain gauge station where the measurements were recorded (in this case Dahl), is located close to the catchment of the combined sewer overflow chamber at Goesdorf, Grand-Duchy of Luxembourg. The dataset contains records from 1st January until 2nd February 2016. The recording time step is 10 min.
> library(EmiStatR)
> data("P1")
> summary(P1)
time P [mm]
Min. :2016-01-01 01:00:00 Min. :0.00000
1st Qu.:2016-01-08 18:57:30 1st Qu.:0.00000
Median :2016-01-16 12:55:00 Median :0.00000
Mean :2016-01-16 12:55:00 Mean :0.02007
3rd Qu.:2016-01-24 06:52:30 3rd Qu.:0.00000
Max. :2016-02-01 00:50:00 Max. :0.90000
> sum(P1[,"P [mm]"])
[1] 89.6
Appendix A.6.3. Temporal Aggregation of Model Input
As an illustration of the Agg function, we aggregated time series of precipitation P1 from 10 to 30 min. We took the sum as aggregation function. We proceed and visualise the results as follows:
> library(stUPscales)
> P1_30min <- Agg(P1, "P1", 30, sum, "")
> summary(P1_30min)
time Rainfall
Min. :2016-01-01 01:00:00 Min. :0.00000
1st Qu.:2016-01-08 18:52:30 1st Qu. :0.00000
Median :2016-01-16 12:45:00 Median :0.00000
Mean :2016-01-16 12:45:00 Mean :0.06022
3rd Qu.:2016-01-24 06:37:30 3rd Qu. :0.00000
Max. :2016-02-01 00:30:00 Max. :2.00000
> head(P1_30min,3)
time Rainfall
1 2016-01-01 01:00:00 0
2 2016-01-01 01:30:00 0
3 2016-01-01 02:00:00 0
Appendix A.6.4. Model Input Uncertainty and Monte Carlo Simulation Set-Up
For setting up the Monte Carlo simulation we applied the setup class and the MC.setup method. The following code illustrates the settings of the setup class.
> # defining curve level to volume of the storage chamber
> lev2vol <- list(lev = c(.06, 1.10, 1.30, 3.30), vol = c(0, 31, 45, 190))
> new_setup <- setup(id = "MC_1",
+ nsim = 16,
+ seed = 123,
+ mcCores = 8,
+ ts.input = P1_30min,
+ rng = rng <- list(
+ qs = c(pdf = "uni", min = 130, max = 170), # [l/PE/d]
+ CODs = c(pdf = "nor", mu = 4.378, sigma = 0.751), # log[g/PE/d]
+ NH4s = c(pdf = "nor", mu = 1.473, sigma = 0.410), # log[g/PE/d]
+ qf = c(pdf = "uni", min = 0.001, max = 0.1), # [l/s/ha]
+ CODf = 0, # [g/PE/d]
+ NH4f = 0, # [g/PE/d]
+ CODr = 0, # [mg/l]
+ NH4r = 2, # [mg/l]
+ nameCSO = "E1", # [-]
+ id = 1, # [-]
+ ns = "FBH Goesdorf", # [-]
+ nm = "Goesdorf", # [-]
+ nc = "Obersauer", # [-]
+ numc = 1, # [-]
+ use = "R/I", # [-]
+ Atotal = 46, # [ha]
+ Aimp = 25.2, # [ha]
+ Cimp = c(pdf = "uni", min = 0.25, max = 0.95), # [-]
+ Cper = c(pdf = "uni", min = 0.05, max = 0.60), # [-]
+ tfS = 0, # [time steps]
+ pe = c(pdf = "uni", min = 500, max = 800), # [PE]
+ Qd = 6.5, # [l/s]
+ Dd = .150, # [m]
+ Cd = c(pdf = "uni", min = 0.01, max = 2), # [-]
+ V = 190, # [m3] # 1100
+ lev.ini = c(pdf = "uni", min = 0.1, max = 3.5), # [m]
+ lev2vol = lev2vol), # [m] - [m3]
+ ar.model = ar.model <- list(
+ CODs = 0.7, # [-]
+ NH4s = 0.7), # [-]
+ var.model = var.model <- list(inp = c("", "")))
Upon definition of the setup object, we proceeded to invoke the MC.setup to create sampled variables from their corresponding probability distributions.
> new_mc_setup <- MC.setup(new_setup)
Appendix A.6.5. Monte Carlo Simulation and Analysis
The Monte Carlo simulation is performed by invoking the MC.sim method:
> new_sim <- MC.sim(newmcsetup, EmiStatR.cores = 0)
The deterministic simulation is defined and computed. First, we define structure 1, named "E1" :
> E1 <- list(id = 1, ns = "FBH Goesdorf", nm = "Goesdorf",
+ nc = "Obersauer", numc = 1, use = "R/I",
+ Atotal = 46, Aimp = 25.2, Cimp = 0.86, Cper = 0.55,
+ tfS = -1, pe = 650, Qd = 6.5,
+ Dd = 0.15, Cd = 1.25,
+ V = 190,
+ lev.ini = 0.89,
+ lev2vol = lev2vol)
Second, the input.user object of class input is defined:
> input.user <- input(spatial = 0, zero = 1e-5,
+ folder = system.file("shiny", package = "EmiStatR"),
+ cores = 0,
+ ww = list(qs = 150, CODs = 104, NH4s = 4.7),
+ inf = list(qf= 0.05, CODf = 0, NH4f = 0),
+ rw = list(CODr = 0, NH4r = 0, stat = "Dahl"),
+ P1 = P130min, st = list(E1=E1),
+ export = 1)
Next, we invoke the method EmiStatR with the deterministic input (input.user) defined before:
> sim.det <- EmiStatR(input.user)
Finally, the additional arguments of the MC.analysis function are defined:
> delta <- 30 # minutes
> qUpper <- "q95"
> event.ini <- as.POSIXct("2016-01-12 12:00:00")
> event.end <- as.POSIXct("2016-01-16 05:00:00")
Upon definition of the additional arguments, the function MC.analysis is invoked:
> analysis <- MC.analysis(new_sim, delta, qUpper, P1_30min, sim.det,
+ event.ini, event.end, ntick = 25)
Appendix A.7. Example 2: Spatio-Temporal Uncertainty Characterisation
Appendix A.7.1. Events Selected
stUPscales has a dataset with the selected events per station as an xts object in space-wide format. We can load the dataset by:
> library(stUPscales)
> data("Lux_precipitation")
and visualise the summary for five out of 25 stations in the loaded object event.subset.xts:
> summary(event.subset.xts[,1:5])
Index Dahl Echternach
Min. :2011-12-16 00:00:00 Min. :0.0000 Min. :0.000
1st Qu. :2011-12-16 02:30:00 1st Qu. :0.2000 1st Qu. :0.300
Median :2011-12-16 05:00:00 Median :0.4000 Median :0.500
Mean :2011-12-16 05:00:00 Mean :0.4361 Mean :0.482
3rd Qu. :2011-12-16 07:30:00 3rd Qu. :0.6000 3rd Qu. :0.600
Max. :2011-12-16 10:00:00 Max. :1.1000 Max. :1.200
Esch-Sure Eschdorf Ettelbruck
Min. :0.0000 Min. :0.0000 Min. :0.0000
1st Qu. :0.3000 1st Qu.:0.2000 1st Qu.:0.3000
Median :0.4000 Median :0.4000 Median :0.5000
Mean :0.4721 Mean :0.4787 Mean :0.5148
3rd Qu. :0.6000 3rd Qu.:0.8000 3rd Qu.:0.7000
Max. :1.1000 Max. :1.1000 Max. :1.3000
The summary for all stations can be computed as well:
> summary(as.vector(coredata(event.subset.xts)))
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000 0.2000 0.4000 0.4616 0.6000 4.3000
Appendix A.7.2. Space-Time Full Grid Object
The spatial location of the 25 rain gauge stations are provided in stUPscales as a dataset in SpatialPointsDataFrame format from the sp package [40], and the boundary of the country of Luxembourg as a dataset in sp format SpatialPolygonsDataFrame:
> data("Lux_stations")
> data("Lux_boundary")
The data were converted to an STFDF space-time full data.frame of the spacetime package [25], through the function stConstruct from the same package:
> library(spacetime)
> stfdf <- stConstruct(x = coredata(event.subset.xts),
+ space = list(values=1:ncol(event.subset.xts)),
+ time = index(event.subset.xts),
+ SpatialObj = stations, interval = TRUE)
The object can be visualised through:
> library(RColorBrewer)
> sample <- seq.default(from = 6, to = 57, by = 3)
> stplot(stfdf[, sample],
+ col.regions=colorRampPalette(c("cadetblue1","darkblue"))(60),
+ sp.layout = list("sp.polygons", boundary.Lux), scales=list(draw=T),
+ key.space="right", colorkey=T, par.strip.text=list(cex=1),
+ main="Sample from event for prediction",
+ xlim=c(boundary.Lux@bbox[1,]), ylim=c(boundary.Lux@bbox[2,]), cex=1)
Appendix A.7.3. Space-Time Variograms
The experimental spatio-temporal variogram is computed using:
> library(gstat)
> expVgm <- variogramST(values~1, stfdf, tlags = c(0,1,2,5,10,15,20,25,30),
+ cutoff = 50000, width = 5000)
The spatio-temporal anisotropy is estimated by the estiStAni (gstat) by defining:
> linStAni <- estiStAni(expVgm, c(100,50000))
The experimental variogram and the anisotropy are scaled to have distances in kilometers:
> expVgm$dist <- expVgm$dist/1000
> expVgm$avgDist <- expVgm$avgDist/1000
> expVgm$spacelag <- expVgm$spacelag/1000
> linStAni <- linStAni/1000
The sum-metric variogram model is defined in gstat by:
> smModel <- vgmST("sumMetric",
+ space = vgm(20, "Sph", 15, 1),
+ time = vgm(10, "Exp", 200, 0),
+ joint = vgm(80, "Sph", 1500, 2.5),
+ stAni = linStAni
+ )
> fitSmModel <- fit.StVariogram(expVgm, smModel, fit.method = 7, stAni=linStAni,
+ method = "L-BFGS-B",
+ lower = c(sill.s = 0, range.s = 0, nugget.s = 0,
+ sill.t = 0, range.t = 0, nugget.t = 0,
+ sill.st= 0, range.st = 10, nugget.st = 0,
+ anis = 40),
+ upper = c(sill.s = 300, range.s = 10, nugget.s = 20,
+ sill.t = 300, range.t = 300, nugget.t = 20,
+ sill.st= 300, range.st = 5E3, nugget.st = 20,
+ anis = 500)
+ )
The mean squared error (MSE) of the best model fitted is shown by:
> attr(fitSmModel, "optim.output")["value"]
\$value
[1] 0.0001309329
The fitted sum-metric model leads to the following parameters:
> fitSmModel
space component:
model psill range
1 Nug 0.00000000 0
2 Sph 0.02091874 10
time component:
model psill range
1 Nug 0.0000000 0.0000
2 Exp 0.1292266 201.8652
joint component:
model psill range
1 Nug 0.01587417 0.000
2 Sph 0.00000000 1506.002
stAni: 40
Appendix A.7.4. Space-Time Ordinary Kriging
To create prediction maps through space-time ordinary kriging, a prediction grid over Luxembourg is created:
> library(sp)
> grid.scale <- 500
> gridLUX <- SpatialGrid(GridTopology(boundary.Lux@bbox[,1]%/%grid.scale*grid.scale,
+ c(grid.scale,grid.scale),
+ cells.dim=ceiling(apply(boundary.Lux@bbox,1,diff)/grid.scale)))
> proj4string(gridLUX) <- stfdf@sp@proj4string
> fullgrid(gridLUX) <- F
> ind <- over(gridLUX, as(boundary.Lux,"SpatialPolygons"))
> gridLUX <- gridLUX[!is.na(ind)]
The parameters are rescaled to meters for prediction:
> fitSmModel$space$range <- fitSmModel$space$range*1000
> fitSmModel$joint$range <- fitSmModel$joint$range*1000
> fitSmModel$stAni <- fitSmModel$stAni*1000
The prediction is made by the function krigeST from gstat:
> LUX_pred <- STF(gridLUX, stfdf@time[sample])
> tIDS <- unique(pmax(1,pmin(as.numeric(outer(-5:5, sample, "+")), nrow(slot(stfdf, "time")))))
> SmPred <- krigeST(values~1, data=stfdf[,tIDS],
+ newdata=LUX_pred, fitSmModel, nmax=50,
+ stAni=fitSmModel[["stAni"]]/10/60,
+ computeVar = T)
Prediction maps are produced by:
> stplot(SmPred, col.regions=colorRampPalette(c("cadetblue1","darkblue"))(60),
+ scales=list(draw=T), main="spatio-temporal sum-metric model",
+ par.strip.text=list(cex=1),
+ sp.layout=list(list(boundary.Lux, fill="transparent")))
Similarly, the prediction error variance maps are produced by:
> SmPred.var <- SmPred
> SmPred.var[["var1.pred"]] <- SmPred.var[["var1.var"]]
> stplot(SmPred.var, col.regions=colorRampPalette(c("cadetblue1","darkblue"))(60),
+ scales=list(draw=T), main="spatio-temporal sum-metric model (variance)",
+ par.strip.text=list(cex=1),
+ sp.layout=list(list(boundary.Lux, fill="transparent")))
References
- Leopold, U.; Heuvelink, G.B.M.; Tiktak, A.; Finke, P.A.; Schoumans, O. Accounting for change of support in spatial accuracy assessment of modelled soil mineral phosphorous concentration. Geoderma 2006, 130, 368–386. [Google Scholar] [CrossRef]
- Bastin, L.; Cornford, D.; Jones, R.; Heuvelink, G.B.M.; Pebesma, E.; Stasch, C.; Nativi, S.; Mazzetti, P.; Williams, M. Managing uncertainty in integrated environmental modelling: The UncertWeb framework. Environ. Model. Softw. 2013, 39, 116–134. [Google Scholar] [CrossRef]
- Sawicka, K.; Heuvelink, G.B.M.; Walvoort, D. Spatial Uncertainty Propagation Analysis with the spup Package. R J. 2018. under review. [Google Scholar]
- Brown, J.D.; Heuvelink, G.B.M. Assessing Uncertainty Propagation Through Physically based Models of Soil Water Flow and Solute Transport. Encycl. Hydrol. Sci. 2005, 1181–1195. [Google Scholar] [CrossRef]
- Dotto, C.B.S.; Mannina, G.; Kleidorfer, M.; Vezzaro, L.; Henrichs, M.; Mccarthy, D.T.; Freni, G.; Rauch, W.; Deletic, A. Comparison of different uncertainty techniques in urban stormwater quantity and quality modelling. Water Res. 2012, 46, 2545–2558. [Google Scholar] [CrossRef] [PubMed]
- Hengl, T.; Heuvelink, G.B.M.; Van Loon, E.E. On the uncertainty of stream networks derived from elevation data: The error propagation approach. Hydrol. Earth Syst. Sci. 2010, 14, 1153–1165. [Google Scholar] [CrossRef]
- Hamel, P.; Guswa, A.J. Uncertainty analysis of a spatially explicit annual water-balance model: Case study of the Cape Fear basin, North Carolina. Hydrol. Earth Syst. Sci. 2015, 19, 839–853. [Google Scholar] [CrossRef]
- Muthusamy, M.; Schellart, A.; Tait, S.; Heuvelink, G.B.M. Geostatistical upscaling of rain gauge data to support uncertainty analysis of lumped urban hydrological models. Hydrol. Earth Syst. Sci. 2017, 21, 1077–1091. [Google Scholar] [CrossRef]
- Rauch, W.; Bach, P.M.; Brown, R.; Deletic, A.; de Haan, F.; Mair, M.; Kleidorfer, M.; Rogers, B.; Sitzenfrei, R.; Urich, C. Modelling transition in urban water systems. Water Res. 2017, 126, 501–514. [Google Scholar] [CrossRef] [PubMed]
- Nol, L.; Heuvelink, G.B.M.; Veldkamp, A.; de Vries, W.; Kros, J. Uncertainty propagation analysis of an N2O emission model at the plot and landscape scale. Geoderma 2010, 159, 9–23. [Google Scholar] [CrossRef]
- Vanguelova, E.I.; Bonifacio, E.; De Vos, B.; Hoosbeek, M.R.; Berger, T.W.; Vesterdal, L.; Armolaitis, K.; Celi, L.; Dinca, L.; Kjønaas, O.J.; et al. Sources of errors and uncertainties in the assessment of forest soil carbon stocks at different scales—Review and recommendations. Environ. Monit. Assess. 2016, 188, 630. [Google Scholar] [CrossRef] [PubMed]
- Andrianov, G.; Burriel, S.; Cambier, S.; Dutfoy, A.; Dutka-Malen, I.; de Rocquigny, E.; Sudret, B.; Benjamin, P.; Lebrun, R.; Mangeant, F.; et al. Openturns, an open source initiative to treat uncertainties, risks’n statistics in 520 a structured industrial approach. In Proceedings of the ESREL’2007 Safety and Reliability Conference, Stavenger, Norway, 25–27 June 2007. [Google Scholar]
- Adams, B.; Bauman, L.; Bohnhoff, W.; Dalbey, K.; Ebeida, M.; Eddy, J.; Eldred, M.; Hough, P.; Hu, K.; Jakeman, J.; et al. Dakota, a Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis: Version 5.4 User’S Manual; Report Sandia Technical Report SAND2010-2183; Sandia National Laboratories: Albuquerque, NM, USA, 2009.
- Brown, J.D.; Heuvelink, G.B.M. The data uncertainty engine (due): A software tool for assessing and simulating uncertain environmental variables. Comput. Geosci. 2007, 33, 172–190. [Google Scholar] [CrossRef]
- Schueller, G.I.; Pradlwarter, H.J. Computational stochastic structural analysis (COSSAN)—A software tool. Struct. Saf. 2006, 28, 68–82. [Google Scholar] [CrossRef]
- Pianosia, F.; Sarrazin, F.; Wagener, T. A matlab toolbox for global sensitivity analysis. Environ. Model. Softw. 2015, 70, 80–85. [Google Scholar] [CrossRef]
- Marelli, S.; Sudret, B. UQLab: A Framework for Uncertainty Quantification in Matlab; American Society of Civil Engineers: Reston, VA, USA, 2014; pp. 2554–2563. ISBN 978-0-7844-1360-9. [Google Scholar]
- Kuczera, G.; Parent, E. Monte Carlo assessment of parameter uncertainty in conceptual catchment models: The Metropolis algorithm. J. Hydrol. 1998, 211, 69–85. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Improved evolutionary optimization from genetically adaptive multimethod search. Proc. Natil. Acad. Sci. USA 2007, 104, 708–711. [Google Scholar] [CrossRef] [PubMed]
- Vrugt, J.A.; Gupta, H.V.; Bouten, W.; Sorooshian, S. A Shuffled Complex Evolution Metropolis algorithm for optimization and uncertainty assessment of hydrologic model parameters. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Rauch, W.; Harremoës, P. On the potential of genetic algorithms in urban drainage modeling. Urban Water 1999, 1, 79–89. [Google Scholar] [CrossRef]
- Wijesiri, B.; Egodawatta, P.; McGree, J.; Goonetilleke, A. Assessing uncertainty in pollutant build-up and wash-off processes. Environ. Pollut. 2016, 212, 48–58. [Google Scholar] [CrossRef] [PubMed]
- Ryan, J.A.; Ulrich, J.M. xts: eXtensible Time Series. The Comprehensive R Archive Network, CRAN; R Package Version 0.10-1. 2017. Available online: https://CRAN.R-project.org/package=xts (accessed on 22 June 2018).
- Pebesma, E. Spacetime: Spatio-Temporal Data in R. J. Stat. Softw. 2012, 51, 1–30. [Google Scholar] [CrossRef]
- Hijmans, R.J. Package “Raster”: Geographic Data Analysis and Modeling. The Comprehensive R Archive Network, CRAN. 2014. Available online: https://CRAN.R-project.org/package=raster (accessed on 22 June 2018).
- Luetkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Berlin, Germany, 2005. [Google Scholar]
- Barbosa, S.M. Package “mAr”: Multivariate AutoRegressive Analysis. The Comprehensive R Archive Network, CRAN. 2015. Available online: https://CRAN.R-project.org/package=mAr (accessed on 22 June 2018).
- Hager, W.H. Wastewater Hydraulics, 2nd ed.; Springer: Berlin, Germany, 2010; p. 652. [Google Scholar]
- Baker, L.A. (Ed.) The Water Environment of Cities; Springer: Berlin, Germany, 2009. [Google Scholar]
- Torres-Matallana, J.A.; Klepiszewski, K.; Leopold, U.; Heuvelink, G.B.M. EmiStatR: A simplified and scalable urban water quality model for simulation of combined sewer overflows. Water 2018, 10, 782. [Google Scholar] [CrossRef]
- Fan, L.; Liu, G.; Wang, F.; Geissen, V.; Ritsema, C.J.; Tong, Y. Water use patterns and conservation in households of Wei River Basin, China. Resour. Conserv. Recycl. 2013, 74, 45–53. [Google Scholar] [CrossRef]
- DWA. Arbeitsblatt DWA-A 131: Bemessung von Einstufigen Belebungsanlagen; DWA-Regelwerk: Hennef, Germany, 2002. [Google Scholar]
- DWA. ATV-DVWK-A 118: Hydraulische Bemessung und Nachweis von Entwässerungssystemen; DWA-Regelwerk: Hennef, Germany, 2006. [Google Scholar]
- Rawls, W.; Long, S.; McCuen, R. Comparison of Urban Flood Frequency Procedures. Preliminary Draft Report Prepared for the Soil Conservation Service; Soil Conservation Service: Beltsville, MD, USA, 1981.
- Gräler, B.; Pebesma, E.; Heuvelink, G.B.M. Spatio-Temporal Interpolation using {gstat}. R J. 2016, 8, 204–218. [Google Scholar]
- Snepvangers, J.J.J.C.; Heuvelink, G.B.M.; Huisman, J.A. Soil water content interpolation using spatio-temporal kriging with external drift. Geoderma 2003, 112, 253–271. [Google Scholar] [CrossRef]
- Bilonick, R.A. Monthly hydrogen ion deposition maps for the northeastern U.S. from July 1982 to September 1984. Atmos. Environ. 1988, 22, 1909–1924. [Google Scholar] [CrossRef]
- Pebesma, E.J. Multivariable geostatistics in S: The “gstat” package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Pebesma, E.; Bivand, R. Package “sp”: Classes and Methods for Spatial Data. The Comprehensive R Archive Network, CRAN. 2005. Available online: https://CRAN.R-project.org/package=sp (accessed on 22 June 2018).
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Moret, S.; Codina Gironès, V.; Bierlaire, M.; Maréchal, F. Characterization of input uncertainties in strategic energy planning models. Appl. Energy 2017, 202, 597–617. [Google Scholar] [CrossRef]
- Tock, L.; Maréchal, F. Decision support for ranking Pareto optimal process designs under uncertain market conditions. Comput. Chem. Eng. 2015, 83, 165–175. [Google Scholar] [CrossRef]
- Dubuis, M. Energy System Design Under Uncertainty. Ph.D. Thesis, École Polytechnique Fédérale De Lausanne, Lausanne, Switzerland, 2012. [Google Scholar]
- Pye, S.; Sabio, N.; Strachan, N. An integrated systematic analysis of uncertainties in UK energy transition pathways. Energy Policy 2015, 87, 673–684. [Google Scholar] [CrossRef]
- Sin, G.; Gernaey, K.V.; Neumann, M.B.; van Loosdrecht, M.C.M.; Gujer, W. Uncertainty analysis in WWTP model applications: A critical discussion using an example from design. Water Res. 2009, 43, 2894–2906. [Google Scholar] [CrossRef] [PubMed]
- Lythcke-Jørgensen, C.; Ensinas, A.V.; Münster, M.; Haglind, F. A methodology for designing flexible multi-generation systems. Energy 2016, 110, 34–54. [Google Scholar] [CrossRef]
- Zoppou, C. Review of urban storm water models. Environ. Model. Softw. 2001, 16, 195–231. [Google Scholar] [CrossRef]
- Bertsimas, D.; Sim, M. The Price of Robustness. Oper. Res. 2004, 52, 35–53. [Google Scholar] [CrossRef]
- Pebesma, E. Package gstat: Spatial and Spatio-Temporal Geostatistical Modelling, Prediction and Simulation. The Comprehensive R Archive Network, CRAN. 2012. Available online: https://CRAN.R-project.org/package=gstat (accessed on 22 June 2018).
- Williams, M.; Cornford, D.; Bastin, L.; Pebesma, E. Uncertainty Markup Language (UnCertML); Technical Report; The Open Geospatial Consortium Inc.: Wayland, MA, USA, 2009. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).