Abstract
Seawater intrusion in coastal aquifers is a worldwide problem exacerbated by aquifer overexploitation and climate changes. To limit the deterioration of water quality caused by saline intrusion, research studies are needed to identify and assess the performance of possible countermeasures, e.g., underground barriers. Within this context, numerical models are fundamental to fully understand the process and for evaluating the effectiveness of the proposed solutions to contain the saltwater wedge; on the other hand, they are typically affected by uncertainty on hydrogeological parameters, as well as initial and boundary conditions. Data assimilation methods such as the ensemble Kalman filter (EnKF) represent promising tools that can reduce such uncertainties. Here, we present an application of the EnKF to the numerical modeling of a laboratory experiment where seawater intrusion was reproduced in a specifically designed sandbox and continuously monitored with electrical resistivity tomography (ERT). Combining EnKF and the SUTRA model for the simulation of density-dependent flow and transport in porous media, we assimilated the collected ERT data by means of joint and sequential assimilation approaches. In the joint approach, raw ERT data (electrical resistances) are assimilated to update both salt concentration and soil parameters, without the need for an electrical inversion. In the sequential approach, we assimilated electrical conductivities computed from a previously performed electrical inversion. Within both approaches, we suggest dual-step update strategies to minimize the effects of spurious correlations in parameter estimation. The results show that, in both cases, ERT data assimilation can reduce the uncertainty not only on the system state in terms of salt concentration, but also on the most relevant soil parameters, i.e., saturated hydraulic conductivity and longitudinal dispersivity. However, the sequential approach is more prone to filter inbreeding due to the large number of observations assimilated compared to the ensemble size.
1. Introduction
It is generally accepted that climate change will increase saltwater intrusion in coastal aquifers due to sea-level rise as well as a decrease in groundwater recharge [1]. Anthropogenic demand of coastal groundwater through pumping also has the potential of increasing saltwater intrusion [2,3,4]. However, the effect of these phenomena on the intrusion depends on many hydrogeological parameters [5,6,7] and will therefore vary from one aquifer to another. In order to predict the dynamic evolution of the saltwater wedge in the groundwater and thus better manage water resources and their vulnerability in the mid and long terms, a careful and quantitative characterization of the aquifer is necessary. Traditionally, this characterization has been done using water testing in wells. However, even though this technique is efficient in measuring the salt concentration in groundwater, it does not permit the prediction of salt water intrusion before it reaches a bore and it does not allow for an accurate representation of the aquifer spatial complexity either, due to the typically low spatial coverage. Therefore, this method represents a detection tool, rather than a management tool.
For many years, electrical resistivity tomography (ERT) has been used to characterize saline tracers or contaminations [8] and, more recently, ERT has been increasingly used to monitor the saltwater wedge in coastal aquifers (e.g., [9,10,11,12,13,14,15,16]). Recent developments include the use of geophysical data to quantitatively characterize aquifers through hydrogeophysical inversions. ERT data have often been used to improve the spatial resolution of tracer tests (e.g., [17,18,19]) and to characterize aquifer hydraulic parameters through saltwater intrusion monitoring [20,21].
However, techniques based solely on the electrical model usually fail to infer maximas of hydrogeological parameters that drive the transport and neglect the physics and dynamics of groundwater flow and transport (e.g., [22] and references therein). In order to address these limitations, approaches based on data assimilation, such as the ensemble Kalman filter (EnKF), have been increasingly used by the hydrogeological community to condition aquifer parameters with time-dependent observations such as hydraulic heads [23,24,25] or concentrations [26,27,28]. To date, most of these studies have been conducted on synthetic test cases, with only a few applications to real-world field experiments (e.g., [29,30]) and, to the best of our knowledge, none to problems of seawater intrusion. All previous studies have led to different conclusions on the type of workflow to use or on the capability of data assimilation to infer hydrogeological parameters. Furthermore, while synthetic studies are useful but not always realistic, real-world experiments are often characterized by large uncertainties.
The present study aims to test the capability of ERT data assimilation to estimate the hydraulic parameters (permeability and dispersivity) in a highly controlled laboratory experiment of saltwater intrusion. The laboratory setting allows us to test our data assimilation approach with real-world data, but without the large uncertainties typical of field experiments. Both joint and sequential data assimilation approaches, based on the EnKF, are considered. In the joint approach, raw electrical resistances are assimilated into SUTRA [31] a density-dependent model of groundwater flow and transport, while in the sequential one, we assimilate inverted electrical resistivities. To the best of our knowledge, this is the first time the EnKF is applied to a real density-dependent problem of flow and transport in porous media.
2. Material and Methods
2.1. Saltwater Intrusion Experiment
A sandbox experiment was set up to reproduce the process of saltwater intrusion in coastal aquifers. The sandbox (Figure 1) is made of plexiglass and measures 5 m long, 0.3 m wide, and 0.6 m high. It was filled up to a height of 0.48 cm with glass beads, characterized by a nominal size ranging from 400 to 800 m, in order to mimic a homogeneous porous medium. This is in contact with two independent tanks that can be filled with fluids of different densities. The upstream tank, filled with freshwater, has a maximum capacity of 0.414 m, while the downstream tank, containing salt water, has a capacity of 2.097 m. The latter is much larger than the former, in order to minimize possible effects of dilution due to the incoming flux of freshwater. A sluice gate can be used to separate the sandbox from the downstream tank.
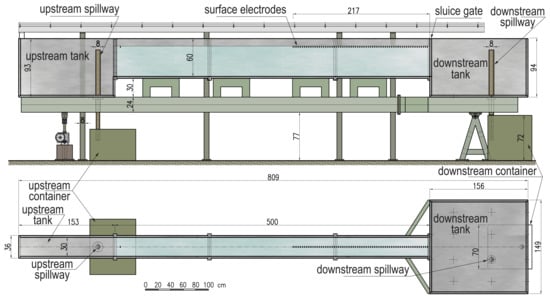
Figure 1.
Schematic (top) lateral and (bottom) plan views of the sandbox (all distances are in cm).
The saltwater intrusion experiment was carried out by imposing a hydraulic gradient of about 4.0 × 10 m/m. The hydraulic head in both tanks was maintained constant throughout the experiment by means of adjustable spillways. A small pump was used in the upstream tank to recirculate the freshwater, while an auxiliary small container below the saltwater tank was used to continuously monitor the outflow discharge. The electrical conductivity in the downstream tank was also continuously monitored, to check for the absence of significant dilution. The porous medium was preliminarily saturated with freshwater. Following this, freshwater in the downstream tank was replaced by salt water while keeping the sluice gate shut. Finally, the gate was open to let the saltwater wedge evolve in the porous medium. Overall, the experiment lasted 24 h without interruptions. The evolution of the saltwater wedge was visualized by coloring the salt water with red dye and monitored by taking photographs at regular time intervals. More details about the experimental facility and procedures can be found in Bertorelle [32], Costantini [33], Crestani et al. [34].
An ad hoc ERT system was designed to monitor the dynamic evolution of the saltwater wedge during the experiment. The ERT setup consists of three segments of 24, 1 cm-long, golden pin electrodes, for a total of 72, planted on the surface of the porous medium and placed parallel to the groundwater flow, exactly halfway between the lateral plexiglass walls. The electrodes are spaced 3 cm apart, with the line starting at 2.83 m ( m, Figure 1) from the upstream tank. The measurements were collected through a pole–dipole configuration, with the remote electrode located at 0.06 m from the upstream tank, i.e., 2.77 m from the closest electrode of the line. Raw data were collected every 20 min with an IRIS Syscal Pro 72 Switch system. The system was programmed to carry out high-speed sequences, with each measurement taken with a 200 ms current pulse, for a total acquisition time of 11 min for each ERT survey. Forward and reverse measurements were carried out to remove possible artifacts due to asymmetry.
2.2. Data Assimilation Approaches
Following Camporese et al. [35], two assimilation approaches based on the EnKF were tested, in order to investigate their pros and cons in the case of seawater intrusion in a freshwater aquifer. The first assimilation approach is here defined “joint”, as groundwater, petrophysical, and electrical models are used jointly to predict the electrical resistances at the electrode locations. A set of observed electrical resistances are then assimilated to update concentrations and hydraulic parameters via a dual-step approach. In the case of the joint approach, only an electrical forward model is necessary to predict the electrical resistance at the electrode locations.
In the second approach, which we define as “sequential”, the groundwater and petrophysical models are used to predict the soil electrical resistivities. The set of observed electrical resistances is then inverted to obtain estimated soil electrical resistivities. These inverted electrical resistivities and their corresponding inversion errors are used to update the concentrations and the hydraulic parameters via the same dual-step approach as in the joint method.
A simplified flow chart for both approaches is reported in Figure 2, while the details of the groundwater, petrophysical, and electrical models are described in the following sections.
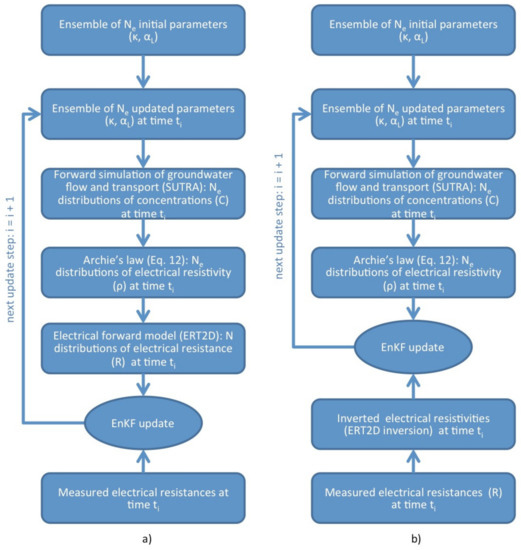
Figure 2.
Flow chart of (a) the joint and (b) sequential data assimilation approaches.
2.3. Groundwater Flow and Transport Modeling
Saltwater intrusion is modeled for both approaches using SUTRA, a well established model for saturated–unsaturated variable-density groundwater flow and transport developed by the United States Geological Survey [31]. SUTRA solves the following two-dimensional density-dependent flow and transport equations by means of the finite element method [31]:
In Equation (1), is water saturation, is fluid density, is specific pressure storativity, n is porosity, p is fluid pressure, C is solute concentration (salt in this case), is the permeability tensor, is an isotropic relative permeability for unsaturated flow, is fluid viscosity, is the gravity vector, and represents sources or sinks. The specific pressure storativity is a function of the fluid compressibility, , and bulk porous matrix compressibility, , through the expression:
In the transport Equation (2), is the molecular diffusivity, I is the identity matrix, and is the dispersion tensor, defined for two-dimensional flow and transport as
with
and
where v, and are the total magnitude of the velocity vector, , and its components along the x and y directions, respectively.
The longitudinal and transversal dispersion coefficients, and , are calculated from the longitudinal and transversal dispersivities, and , and the total magnitude of the velocity, v:
2.4. Electrical Modeling
The open source software ERT2D [37] was used for the electrical forward modeling and the nonlinear least-squares regularized inversion. The choice of this code was guided by its speed and flexibility; nevertheless, any other software could have been implemented within the methodology proposed in this study, as long as the equations solved do not change.
2.4.1. Forward Modeling
ERT modeling requires the definition of a petrophysical link between salt concentration in water and soil bulk conductivity (or resistivity). We use a conventional petrophysical relation where water electrical conductivity, , is linearly dependent on salt concentration, C [38]:
where is the electrical conductivity of freshwater and is a proportionality constant. Equation (11) is complemented by Archie’s law, which defines the relation between the bulk electrical conductivity of a porous medium, , water electrical conductivity, and saturation [38]:
where is the bulk electrical resistivity, n is soil porosity, m is the cementation index, and d is the saturation index. Equation (12) is sometimes expressed as a function of the parameter , which is known as formation factor and is often assumed to be an indicator of the hydraulic tortuosity.
The spatial distribution of electric potential, , follows the Poisson equation:
where is a vector of Cartesian coordinates, I is a source electrical current located in , and is the Dirac delta function.
Under the so-called 2.5D hypothesis, whereby the electrical conductivity distribution is assumed two-dimensional, i.e., constant across y, but the current is three-dimensional, the solution of Equation (13) is obtained transforming V from the 3D space into a 2D space by means of the Fourier transform and then integrating by finite differences (e.g., [39]).
Although Equation (13) is expressed for a point-current source, different protocol configurations, such as the pole–dipole used here, can be represented by appropriate superpositions.
2.4.2. Inverse Modeling
The goal of inverse modeling is to obtain a spatial distribution of from the voltage data collected during the ERT survey. The inversion is obtained by minimizing a regularized least-squares objective function (e.g., [40]):
where is a weighing matrix of the apparent resistivity data, , is the log-resistivity model, f denotes the forward operator, is a regularization matrix, is the regularization weight, and is the prior or first-guess log-resistivity model. Using log-transformed values of apparent resistivity and model resistivity () allows us to scale both observed data and model parameters, improving the stability of the inverse solution and ensuring the positiveness of model resistivity.
It can be shown that the error covariance of the final estimate of the log-resistivity model, , when neglecting the variance of the starting model, , is given by [41]:
where the generalized inverse, , depends on , i.e., the Jacobian matrix of at the last iteration.
2.5. Ensemble Kalman Filter with Nonlinear Observations and Dual-Step Update
The EnKF was developed as an extension of the original Kalman filter (KF) for non-linear dynamic models [42]. The EnKF, as the traditional KF, is a two-step approach. Both filters assume a state vector, , that evolves in time following a Markov chain stochastic process. The size of is , i.e., the number of computational nodes or cells in which the domain is discretized plus the number of parameters to be updated. In the EnKF, the state is represented by an ensemble of size , , which in the first step, i.e., the prediction step, is propagated forward in time by the physical model operator g:
In Equation (16), subscript t denotes the time discretization and is the model error, which is usually neglected in groundwater modeling applications (e.g., [24,26,28]), where all the uncertainty is typically assigned to the boundary conditions, initial conditions, and, most importantly, the parameters. The same approach is used in the present study.
The second step is the assimilation step, where the state is updated based on the observations , which are related to the system state through the observation function h:
where is the measurement error, assumed as normally distributed, , with mean zero and covariance .
The ensemble of predicted observations, , can be computed through the observation function, h:
The ensemble of perturbations (or anomalies) is defined as
where is a row vector of size with all elements equal to one and is the ensemble mean of . Analogously, the ensemble of perturbations of the predicted observations can be calculated as
where is the ensemble mean of the predicted observations.
The predicted (prior) ensemble can then be updated to get the posterior ensemble, :
where is the ensemble of perturbed observations (e.g., [43]).
In the present implementation of the EnKF, the state is augmented with the observations, in order to linearize the observation function. Therefore, the augmented system state reads
and the ensemble of predicted observations is related to the augmented state through
where is an identity matrix of size , with the latter being the number of observations, and is a matrix of size with all elements equal to zero.
Differently from previous studies, where soil hydraulic parameters were estimated through ERT data assimilation by directly augmenting the system state vector with the parameters (e.g., [29,35,44]), here we opted for a dual-step state-parameter update, whereby the system state in terms of concentrations is first updated by assimilating the ERT observations, and the soil hydraulic parameters, permeability () and longitudinal dispersivity (), are then updated by assimilating these new updated concentrations as observations, as reported in Table 1.

Table 1.
Variables of the EnKF in the dual-step update.
The main advantages of the proposed dual-step approach are that (i) it can remove potential spurious correlations between resistance or resistivity data and soil hydraulic parameters and that (ii) it allows for the use of a selected subset of concentration data.
After each assimilation at the time level , the concentrations are forecasted by running the saltwater intrusion model presented in Section 2.3 restarting from the beginning, i.e., from to , using the soil hydraulic parameters updated at time . Restarting the saltwater intrusion model from time ensures mass conservation and that the concentration values are always consistent with the parameters [24,45].
3. Modeling and Data Assimilation Setup
3.1. Fine- and Coarse-Resolution Groundwater Model
Two configurations of the numerical groundwater solver SUTRA were used in this study, the difference between the two model configurations being the discretization of the finite element grid. A fine grid was used to preliminarily calibrate the longitudinal and transversal dispersivities of the porous medium, all the other parameters being estimated from the experiment. This fine-resolution calibrated model served as the reference model. A coarser grid was then used in the data assimilation scenarios, where a large number of forward model realizations must be run.
In both cases, the model domain has the size of the porous medium in the sandbox, i.e., 5 m long and 0.48 m deep. The boundary conditions were assigned as follows: no flow across the top and bottom of the domain as well as the unsaturated upper parts of the lateral boundaries, while pressure values were imposed at the upstream and downstream boundaries, calculated consistently with water levels and densities in the freshwater and saltwater tanks, respectively, during the laboratory experiment. The density of the salt water is considered constant in the downstream tank, due to its larger size compared to the freshwater tank. Moreover, the uppermost four centimeters of the downstream boundary were assigned pressure values computed with freshwater density, to take into account the effect of freshwater discharge as observed during the experiment [33,34].
The transport equation boundary conditions were assigned according with those for the flow equation: no flow across the top and bottom of the domain and Dirichlet at the lateral boundaries, with values consistent with measured salt concentrations, i.e., 0 g/L for freshwater and 46 g/L for salt water (Table 2).

Table 2.
Groundwater model properties.
Proper initial conditions are needed for both the flow and transport Equations (1) and (2). Initial pressure conditions were obtained by a preliminary simulation of the flow model at steady state. The initial concentrations were set to zero across the entire domain.
The fine-grid model domain was divided in two sections. The upstream half of the domain (2.5 m by 0.48 m), which is not affected by the saltwater wedge, is discretized by quadrilateral elements of size 0.01 m by 0.0025 m. The second section, which represents the downstream half of the model, is more finely discretized with cells of 0.0025 m by 0.0025 m. This discretization agrees with the Peclet number criterion as suggested by Voss and Provost [31] for the downstream section, where the saltwater intrusion occurs, with respect to the calibrated dispersivities. This criterion states that the size of the elements parallel to the flow should be less than four times the longitudinal dispersivity, and the size of the elements perpendicular to the flow should be less than ten times the transversal dispersivity.
The dispersivities were calibrated by comparing the time evolution of the simulated saltwater wedge to the experimental saltwater wedge visualized in the photographs. The resulting longitudinal and transversal dispersivities are 1 and 1 m, respectively. In all of the following analyses, the relation between the two dispersivities will be always kept to . The simulated saltwater wedge resulting from the model calibration is presented in Figure 3, together with observations from the laboratory experiment.
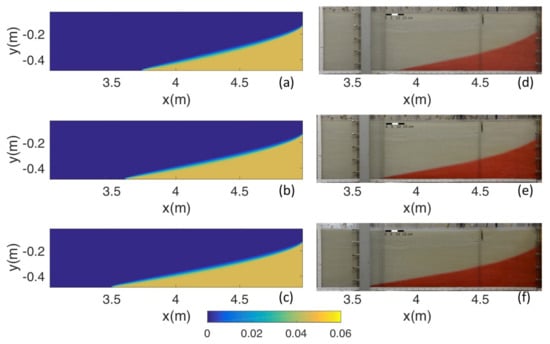
Figure 3.
(a–c) Simulated salt concentrations and (d–f) observed saltwater wedge at (a,d) 14 h, (b,e) 18 h, and (c,f) 22 h from the beginning of the experiment. The colorbar indicates simulated concentrations in kg of solute per kg of solution.
All the model parameters are presented in Table 2 and, except for the dispersivities, were estimated from the experimental data [32,34].
A model configuration with a coarser grid was defined to be used as the forward model in the data assimilation scheme. The coarse grid is a regular grid with quadrilateral elements measuring 0.01 by 0.01 m. This model grid no longer complies with the Peclet number criterion as described previously. However, the resolution of the measured electrical resistances (see Section 3.2) and the need for a decreased computation time justify the use of the coarse grid for the data assimilation, as the EnKF requires multiple runs of the groundwater model at each prediction step.
3.2. Setup and Calibration of the Electrical Model
The electrical forward model was first applied to the soil resistivities obtained by converting the concentrations resulting from the calibrated groundwater model. As mentioned in Section 2.1, forward and reverse measurements were taken during the experiment. The forward measurements were taken with the current injection pole located at various positions between the remote electrode and the electrical potential dipole in a configuration similar to a dipole–dipole configuration, whereas the reverse measurements were taken with the electrical potential dipole located at various positions between the current injection pole and the remote electrode, in a configuration similar to a Wenner–Schlumberger array. Therefore, the presence of the remote electrode at a finite distance from the current-injection electrode caused discrepancies between the forward and reverse measurements. This was confirmed by the observations and warranted the inclusion of the remote electrode in the electrical model.
The boundary conditions of the 2.5D finite difference electrical model of the saltwater intrusion experiment were initially implemented to represent a simple half-space. However, the plexiglass panes at the bottom of the sandbox and water tanks as well as the lateral walls of the freshwater and saltwater tanks would be better described as no-flow boundaries. In order to represent these boundaries appropriately, very high resistivity padding was added in the model (Figure 4). The resistivity of the padding was fixed at 2 m to effectively reproduce no flow conditions across the tank walls and sandbox bottom. The complete zonation of the electrical model with the padding is presented in Figure 4, while all the other properties are reported in Table 3.
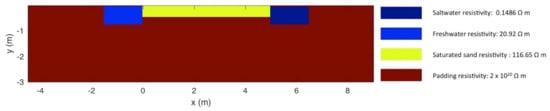
Figure 4.
Setup of the electrical model for the saltwater intrusion experiment, including very large electrical resistivity padding to reproduce the geometry of the sandbox and tanks.

Table 3.
Electrical model properties.
The salt concentration distribution obtained by the calibrated groundwater model was first converted to water electrical resistivity through Equation (11). This resistivity was then used to calculate the bulk soil electrical resistivity via Archie’s law (12), which depends also on water saturation, . However, the numerical groundwater flow model results in values ranging between 98 and 100%, with only a few centimeters at the top of the porous medium being partially saturated. Therefore, water saturation was fixed to 100% in Equation (12), for simplicity.
Figure 5 shows the reverse and forward pseudo-sections of the modeled electrical apparent resistivity (proportional to resistance through a geomagnetic factor) and measured apparent resistivity. It is worth noting that the asymmetries in the pseudo-sections are due to the choice of the protocol, which was optimized for speed and therefore neglected to probe some areas. The resistances resulting from the application of the electrical model to the calibrated groundwater model were orders of magnitude higher than the observed electrical resistances. This difference is probably due to the presence of the lateral plexiglass panes, while the model assumes an infinite extension along the third dimension [37]. Electrical potentials measured by a dipole become more sensitive to structures that are far away from the dipole (such as the lateral plexiglass panes) as the distance between the dipole and the current-injection pole increases. The formation factor that is used to convert the salt concentrations to electrical resistivity values may also be uncertain and contribute to the differences between observed and modeled electrical resistances. In order to compensate for the resistance overestimation in the subsequent data assimilation experiments, at each assimilation step we applied a linear correction to the measured resistances, based on the estimated linear relation between the modeled (calibrated with fine resolution) and measured resistances. These relations are presented for the first assimilation step, 14 h after the beginning of the intrusion, in Figure 6. The regression coefficients for each of the five data assimilation steps and each of the evaluated separation distances were larger than 0.80, and the slope coefficients varied between 4 and 5 depending on the separation distance and the time since the beginning of the intrusion.
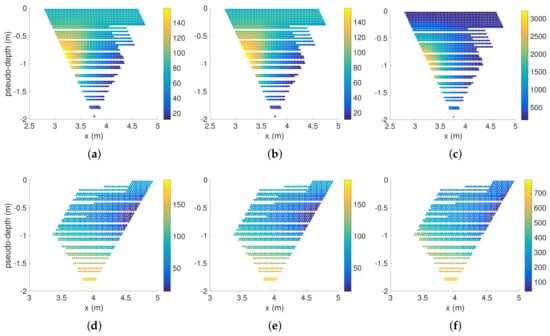
Figure 5.
ERT pseudo-sections 14 h after the beginning of the experiment for the (a–c) reverse and (d–f) forward pole–dipole configurations: (a,d) apparent resistivities modeled with the fine groundwater grid; (b,e) apparent resistivities modeled with the coarse groundwater grid; (c,f) observed apparent resistivities. Colorbars indicate resistivity in m.
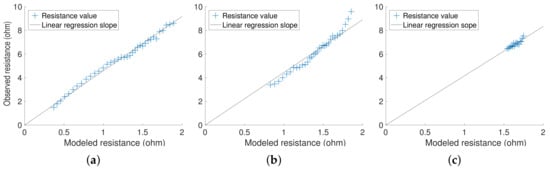
Figure 6.
Observed versus modeled resistances 14 h after the beginning of the experiment for a pole–dipole separation distance of (a) 0.81 m, (b) 1.08 m, and (c) 1.50 m.
Figure 5a,b,d,e also show the comparison between apparent resistivities simulated with the fine and coarse grids. It is clear that resistances modeled from concentrations simulated by the coarse grid are not significantly different from resistances modeled with concentrations simulated by the fine grid. Therefore, the use of a coarse grid for the groundwater model in the data assimilation scenario is fully justified.
The electrical inversion was carried out on the entire set of measurements (forward and reverse) with the software ERT2D [37]. The inversion procedure is applied on log-transformed resistances to avoid negative resistivity values. The minimization algorithm was repeated for a maximum of 15 iterations for each inversion, allowing the root mean square of the objective function to converge to a stable solution. The regularization weight ( in Equation (14)) was set to 0.1. The measurement errors are considered independent from each other. Therefore, the covariance matrix of the data error is assumed as a diagonal matrix in which the diagonal values correspond to the variance of each measurement error. The square root of these variances are proportional to the measured resistance, following
where is the error standard-deviation and R is the measured resistance. The minimum resistance that can be measured by the device is 0.022 . A proportionality value of 0.5735, i.e., higher than 50%, was chosen because of the discrepancies that had been noted between the modeled and measured resistances.
The results of the inversion at 14, 18, and 22 h are shown in Figure 7. The progression of the saltwater intrusion can be observed as a low resistivity zone starting at the saltwater tank boundary and advancing from right to left. However, a low resistivity layer at the top of the profile can also be observed. This low resistivity layer corresponds approximately to the surface electrode line, from 2.83 to 4.96 m and is probably due to the disturbance of the metallic grid separating the saltwater tank from the sandbox [32,33]. We do not expect this artifact, which is basically constant in time, to significantly affect the data assimilation results, as those should mainly depend on the temporal dynamics of the data.
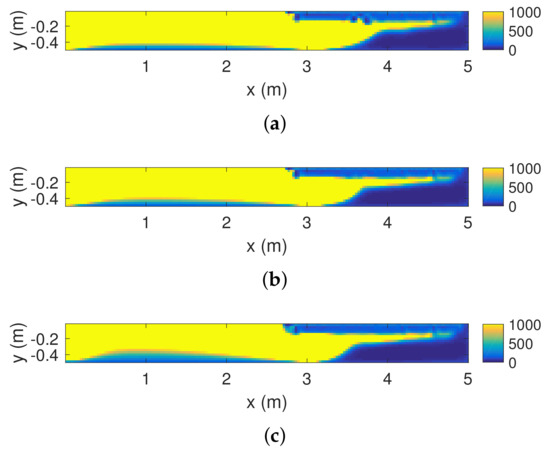
Figure 7.
Inverted electrical resistivity distributions at (a) 14 h, (b) 18 h, and (c) 22 h from the beginning of the experiment. Colorbars indicate bulk electrical resistivity in m.
As all the electrodes (pole current injection electrode and electrical potential dipole electrodes) are placed at a distance larger or equal of 2.83 m downstream of the freshwater tank, only the salt concentrations and electrical resistivities from 3 to 5 m will be taken into account in the assimilation scenarios. This will also prevent the low resistivity inversion artifact at the bottom of the electrical model from 0 to 3 m to affect the assimilation.
3.3. Setup of the Data Assimilation Scenarios
Dealing with a controlled laboratory experiment, where the hydraulic parameters for the groundwater model have been determined experimentally, except for the dispersivity, which has been calibrated, makes this a valuable test case to assess the capabilities of ERT data assimilation to estimate such groundwater parameters. The joint and sequential data assimilation approaches described previously are compared in two scenarios: in Scenario 1, defined as “unbiased”, the prior ensembles of longitudinal dispersivity and hydraulic permeability are centered on the known (calibrated or experimental) values; in Scenario 2, denoted here as “biased”, the prior ensemble of dispersivity is as in Scenario 1, but the prior ensemble of hydraulic permeability is biased towards values smaller than the experimental one.
In both scenarios, the prior ensembles are generated from a bivariate uniform distribution in which both variables are independent of each other. The uniform distribution maximizes the entropy, i.e., heuristically represents the minimal knowledge, of a bounded distribution [46]. The parameters are log-transformed, with the variance of set to 1.33, resulting in an initial permeability ensemble spanning four orders of magnitude, while the variance of is set to 0.33, whereby the initial ensemble of longitudinal dispersivity spans two orders of magnitude (Figure 8 and Figure 9). All of the simulations were run with an ensemble size of 225, a good compromise between required computational effort and statistical accuracy.
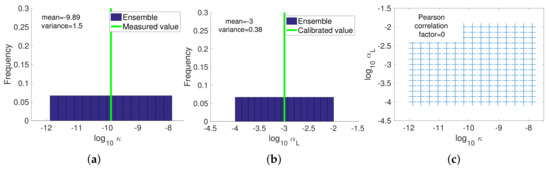
Figure 8.
Scenario 1: initial ensemble of (a) and (b) . (c) Cross-plot of the prior joint distribution.
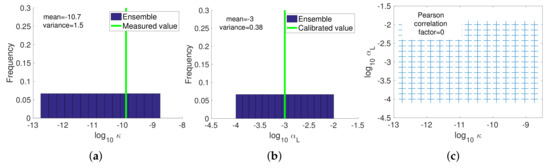
Figure 9.
Scenario 2: initial ensemble of (a) and (b) . (c) Cross-plot of the prior joint distribution.
The transversal dispersivity, , was set to , as in the calibrated model, and all other hydraulic parameters were considered known and equal to the values reported in Table 2.
Although electrical resistances were measured every 20 min from the beginning of the experiment, only data starting at 14 h were assimilated, in order to use only the ERT measurements that are more informative on the saltwater intrusion. Data assimilation frequency was one update every two hours, to ensure sufficient variations of the ERT data between two consecutive assimilations, resulting in a total of five assimilation steps.
3.3.1. Joint Assimilation Method
In the joint assimilation method, the measured electrical resistances are directly assimilated to update the salt concentrations, which are then used to update the permeability and longitudinal dispersivity. Only the forward measurements are used to update the concentrations, as their configuration is such that the electrical potential dipole better samples the saltwater wedge and, therefore, they are more informative than the reverse measurements.
A proportionality factor, F, is necessary to take into account the bias between the modeled and observed resistances. The predicted resistances, , will therefore become
where is the resistance resulting from the groundwater and electrical models, as described in Section 3.1 and Section 3.2.
As the slope of the regression between modeled and observed resistances depends on the pole–dipole separation distance (Figure 6), the proportionality factor will vary accordingly. Therefore, data taken by dipoles at different separation distances of 0.81, 1.08, and 1.50 m are assimilated sequentially, updating also the respective proportionality factor. The first of the two-step assimilation approach is therefore further subdivided in three sequential assimilation substeps. The state vector for the first assimilation substep is given by , where is the proportionality constant for the first spacing, 0.81 m, is the vector of predicted resistances resulting from Equation (25), and is the concentration vector. For the assimilation of resistance data of the second spacing, 1.08 m, the state vector is given by , where this time the predicted concentrations, , are given by the concentrations updated at the previous substep and the predicted resistances are computed by multiplying by the resistances calculated by the electrical forward model with . After the third substep, performed analogously, the final updated concentrations are used in the second step of the assimilation to update the hydraulic parameters. It should be noted that only predicted concentrations larger than zero are assimilated.
The initial ensemble of the proportionality factor was chosen based on the regression analysis presented in Section 3.2. Accordingly, the ensemble was initialized as a uniform distribution bounded between 3 and 6, in order to encompass all regression coefficients previously calculated for varying electrode spacings and times. Moreover, the ensemble of F was re-initialized after every assimilation step, to avoid propagation of possible errors from the previous step and reduction of ensemble variance as more assimilations are performed.
3.3.2. Sequential Assimilation Method
As a result of the biased electrical resistances, the inverted resistivities are also on average much higher than the resistivities resulting from the calibrated groundwater model. An additive factor, A, will enable us to take this difference into account while assimilating the inverted log-transformed resistivities. In a similar fashion to the proportionality factor applied in the joint assimilation method:
where are the electrical resistivities resulting from the application of the groundwater model and subsequent conversion of concentrations to electrical resistivities by Equations (11) and (12).
The state vector at the first step of each update is defined as . As in the joint approach, only updated concentrations larger than zero are then used in the second step to update the hydraulic parameters. The prior ensemble of additive factors is extracted from a uniform distribution bounded between 0.3 and 4.3. As for the proportionality factor, it is re-initialized after every assimilation step.
3.3.3. Evaluation Metrics
Two metrics are used to evaluate the hydraulic parameters and concentrations estimated through the assimilation of ERT data. The average absolute bias, , which measures the accuracy of the estimation, is defined as
and the ensemble spread (), which measures the uncertainty of the estimation, is defined as
where is the number of grid cells, is the number of ensemble members, is the value of the parameter at the grid cell r, for ensemble i, at assimilation step t, and is the ensemble variance of the parameter at the grid cell r at assimilation step t. Concentrations simulated with the fine-grid calibrated model are used as reference values to evaluate the various data assimilation schemes.
4. Results and Discussion
4.1. Data Assimilation Performance for System State
As previously noted, data assimilation in this study is carried out in two steps: in the first step, the electrical data, either observed electrical resistances or inverted resistivities, are assimilated to update the system state in terms of saltwater concentrations, while in the second step the updated saltwater concentrations are assimilated to estimate the hydraulic parameters (permeability and dispersivity). We analyze here the capability of the proposed assimilation approaches to estimate the system state, i.e, the evolution of the saltwater wedge, while the results in terms of parameter estimation are discussed in Section 4.2.
4.1.1. Unbiased Initial Ensemble (Scenario 1): Joint Assimilation
The proportionality factor ensembles for all electrode spacings and assimilation steps, before and after assimilation, are represented as box plots in Figure 10. It can be observed that the ensembles always encompass the calculated regression coefficient. The ensembles pre- and post-assimilation show a similar span. However, the ratio between the length of the boxes and the length of the whiskers is higher before the assimilation than after. This is due to the fact that the ensembles before the assimilation represent uniform distributions, while the assimilation with EnKF tends to normalize the distribution.
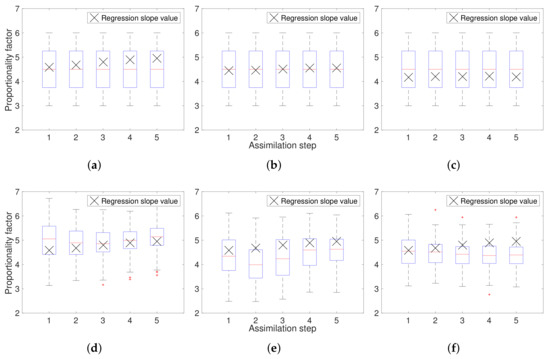
Figure 10.
Box plots of the proportionality factor ensembles: (a) before assimilation of measurements with 0.81 m electrode spacing; (b) before assimilation of measurements with 1.08 m electrode spacing; (c) before assimilation of measurements with 1.50 m electrode spacing; (d) after assimilation of measurements with 0.81 m electrode spacing; (e) after assimilation of measurements with 1.08 m electrode spacing; (f) after assimilation of measurements with 1.50 m electrode spacing.
The use of proportionality factors contributes to improve the estimation of concentrations through the substep assimilation of the observed electrical resistances at given electrode spacings. Indeed, the accuracy of the assimilation improves after each assimilation substep, as can be observed in Figure 11a, which shows the concentration over time. The second assimilation substep (data with electrode spacing of 1.08 m) seems to be the most informative for the concentration estimation, as it leads to the most significant decrease of . This is also confirmed by visual observation of Figure 12c,e,g,i, which show the evolution of the concentration distribution after each assimilation substep for the first assimilation step, whereby the biggest update of the saltwater wedge appears after the assimilation of resistances with an electrode spacing of 1.08 m. As assimilation steps progress, the variations in the saltwater wedge before and after the assimilation substeps decrease. After the first assimilation step, the predicted saltwater wedge and resistances are already very close to observations. As the difference between the predicted and measured resistances decreases, so does the effect of the assimilation of new data. At the last assimilation step (Figure 12d,f,h,j), the effect of assimilating electrical resistances on the updated saltwater wedge is hardly visible. However, the accuracy of the concentration estimation, in terms of , still mildly improved.
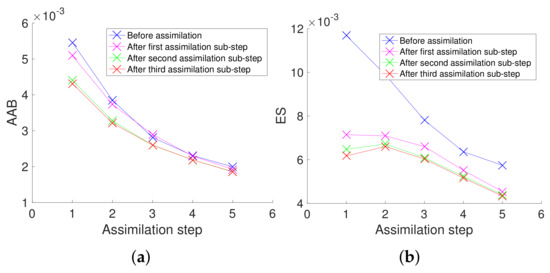
Figure 11.
Evaluation metrics for concentration estimations by assimilating electrical resistance measurements: (a) average absolute bias and (b) ensemble spread. The first, second, and third assimilation substeps correspond to assimilations of data collected with 0.81 m, 1.08 m, and 1.50 m electrode spacing, respectively.
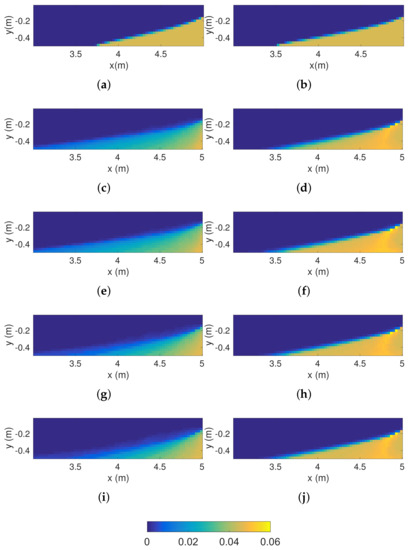
Figure 12.
Concentration distributions at the (a,c,e,g,i) first and (b,d,f,h,j) last assimilation steps: (a,b) reference values; (c,d) before assimilation; (e,f) after assimilation of measurements with 0.81 m electrode spacing; (g,h) after assimilation of measurements with 1.08 m electrode spacing; (i,j) after assimilation of measurements with 1.50 m electrode spacing. The colorbar indicates concentration in kg of solute per kg of solution.
A numerical artifact on the predicted saltwater wedge at the last assimilation step (Figure 12d,f,h,j) close to the saltwater tank (between 4.5 and 5 m) can also be noted. This is due to fluctuations of the groundwater flow and transport model solution for permeabilities around 1.30 m or higher and dispersivities of about 1 or lower, because of the coarseness of the grid. This artifact persists even after the assimilation of electrical resistances, which are not very sensitive to these small oscillations in concentration, as discussed in Section 3.1.
4.1.2. Unbiased Initial Ensemble (Scenario 1): Sequential Assimilation
The assimilation of inverted resistivity data caused the ensemble spread to decrease significantly, as can be observed in Figure 13, which shows the box plots of the additive factor ensembles before and after assimilation. This did not occur when observed resistances were assimilated and could be explained by the fact that the number of assimilated resistivity data (1139) is much larger than the observed resistance data assimilated in the joint approach (85). Moreover, the nature of the correction factor (additive versus multiplicative) is also different and may play a role in the decrease of the ensemble spread. Note also that the additive factor calculated with the calibrated model is not encompassed by the ensemble after assimilation.
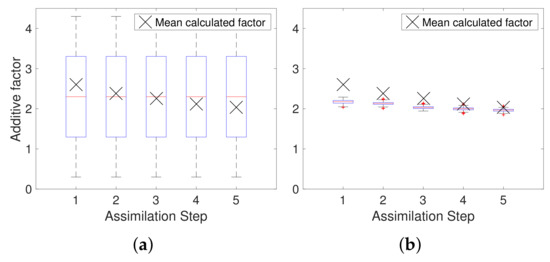
Figure 13.
Additive factor box plots for the sequential approach in Scenario 1 (a) before assimilation and (b) after assimilation of inverted resistivities.
The first assimilation of inverted resistivities significantly improved the accuracy of the concentration ensemble (Figure 14), but created artifacts in the saltwater wedge (Figure 15). However, after the second assimilation step, the accuracy of the concentration ensemble decreased (Figure 14a) and the overestimation of the distance of the saltwater wedge toe was greater after the assimilation (Figure 15h) than before the assimilation (Figure 15e). The subsequent assimilation steps brought negligible improvements, as can be seen in Figure 14a. Indeed, no significant changes can be detected in the post- versus pre-assimilation saltwater wedge at the last assimilation step (Figure 15f,i), even if the predicted wedge toe distance is still longer than the true one. This is a symptom of a phenomenon called “filter divergence” [24,42], caused by an excessive variance reduction, which leads to overconfidence in the model predictions and hence makes it impossible for the assimilation algorithm to exploit the information from the observation data. In this case, the occurrence of filter divergence is probably due to a combination of a relatively small ensemble size compared with the large number of assimilated data. This is likely to cause some spurious correlations that lead to exceedingly large updates in the first assimilation steps and thus to variance underestimation.
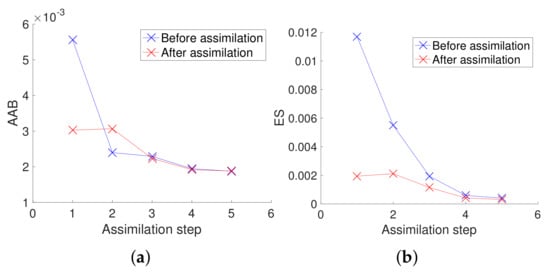
Figure 14.
Evaluation metrics for concentration estimations by assimilating inverted electrical resistivity data: (a) average absolute bias and (b) ensemble spread.
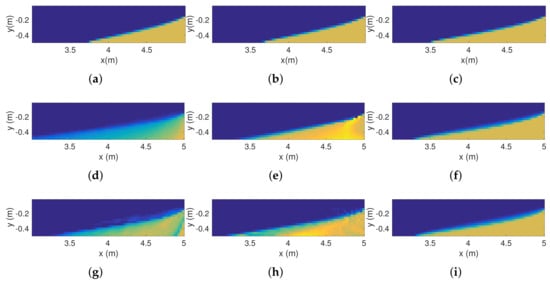
Figure 15.
Reference concentration distributions at times (a) 14 h, (b) 16 h, and (c) 22 h, corresponding to the first, second, and last assimilation steps, respectively. Concentration distributions in Scenario 1 with assimilation of inverted resistivities: (d) before and (g) after the first assimilation step; (e) before and (h) after the second assimilation step; (f) before and (i) after the last assimilation step.
4.2. Parameter Estimation: Joint Versus Sequential Assimilation
4.2.1. Unbiased Initial Ensemble: Scenario 1
In the second step of the proposed data assimilation approaches, a subset of the updated concentrations was used to update the hydraulic permeability and longitudinal dispersivity at each assimilation. The final distribution for each of these properties, as well as a scatter plot of their values, are presented in Figure 16 for both the joint (i.e., with electrical resistances) and sequential (i.e., with inverted resistivities) approaches in Scenario 1, when starting with an unbiased prior ensemble (see Figure 8). It can be noted that, for both properties, the spread of the ensemble resulting from the assimilation is much smaller in the sequential approach, when the inverted resistivities are assimilated. This is consistent with the reduced ensemble spread of the updated concentration values and is again due to the filter divergence.
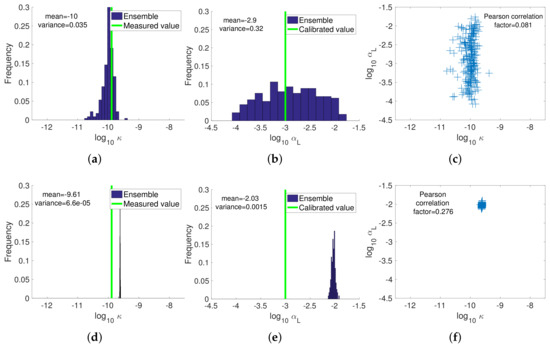
Figure 16.
Scenario 1 (unbiased prior permeability): final distribution after last assimilation step of (a) permeability and (b) longitudinal dispersivity with the (a,b) joint approach and (d,e) sequential approach. Panels (c,f) show the corresponding scatter plots.
The final distribution of the permeability in the joint approach matches the experimental value, while in the sequential approach we can observe a small bias between the EnKF estimate and the measured value. This can also be explained by the filter divergence.
It is also interesting to note that the updated dispersivity ensemble resulting from the assimilation of observed resistances has similar spread and mean compared to the initial ensemble. This would indicate that the observed resistances are not well correlated to the dispersivity. This is not surprising, as the effect of the dispersivity can be observed mainly in the transition zone of the saltwater wedge, but the resolution of the electrical measurements is too low to accurately resolve the transition zone. Therefore, the assimilation of raw electrical resistance data does not affect the estimation of the dispersivity. On the other hand, the final ensemble of dispersivities in the sequential approach is characterized by a significantly smaller spread and the mean is overestimated compared to the model calibrated value. This might be due to (i) some correlations between inverted resistivities and the dispersivities, even though such correlations could be spurious and again related to the filter divergence, or (ii) increased numerical dispersion, caused by the use of a coarser grid compared to the calibrated reference model.
4.2.2. Biased Initial Ensemble (Scenario 2)
In the second scenario, the ensemble of the initial permeability was negatively biased with respect to the measured permeability. Figure 17 shows that the permeability and dispersivity ensembles resulting from the assimilation of the observed electrical resistances were very similar to the results of the assimilation when the initial ensemble was unbiased (Scenario 1). This was not the case for the assimilation of the electrical resistivities. The dispersivity ensemble was still positively biased, whereas the updated permeability ensemble showed a negative bias, contrary to what previously observed in Scenario 1.
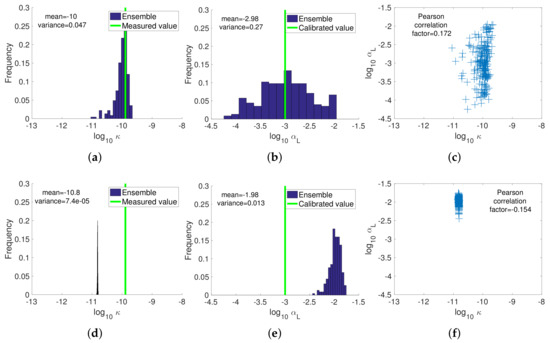
Figure 17.
Scenario 2 (biased prior permeability): final distribution after last assimilation step of (a) permeability and (b) longitudinal dispersivity with the (a,b) joint approach and (d,e) sequential approach. Panels (c,f) show the corresponding scatter plots.
The negative bias in the final updated permeability ensemble by assimilation of inverted electrical resistivities can be explained by the collapse of the ensemble spread resulting from the first assimilation. The ensemble of updated permeabilities after the first assimilation step does not encompass the actual permeability, all members of the updated permeability ensemble being smaller than the actual permeability (Figure 18a). Thus, the predicted saltwater wedge toe distance (Figure 18c) is shorter than the true one (Figure 18b). This also means that the concentration in a large part of the domain is zero and when this occurs for every member of the prediction ensemble in a grid cell, no effective update can be computed for those grid cells (the variance being zero and the covariance with electrical resistivities being also zero). Consequently, the assimilation of inverted resistivities does not improve the estimation of the saltwater wedge (Figure 18d).
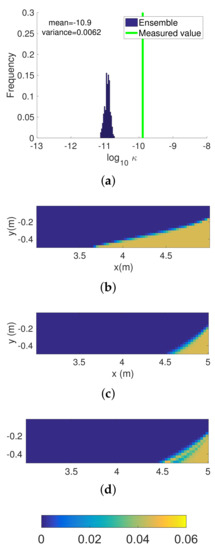
Figure 18.
(a) Predicted permeability ensemble, (b) reference concentration distribution, (c) predicted concentration distribution, and (d) updated concentration distribution at the second assimilation step in Scenario 2 for the sequential approach.
The collapse of the ensemble when hydraulic parameters are updated by assimilating inverted electrical resistivities can also be observed in Figure 19 and Figure 20, which report the evaluation metrics, and , of permeability and longitudinal dispersivity estimations for all the data assimilation scenarios analyzed. The ensemble spread of the hydraulic parameters is generally smaller when the inverted resistivities are assimilated than when the resistances are assimilated and the average absolute bias is larger. A strong decrease of the spread that is not accompanied by a more accurate estimation is confirmation of the ensemble collapsing. This occurs for both Scenarios 1 and 2.
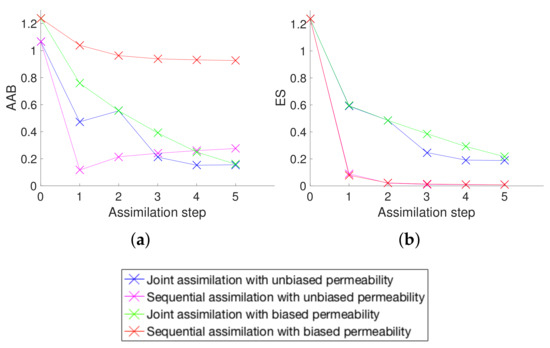
Figure 19.
Evaluation metrics for the estimation of the permeability: (a) average absolute bias and (b) ensemble spread.
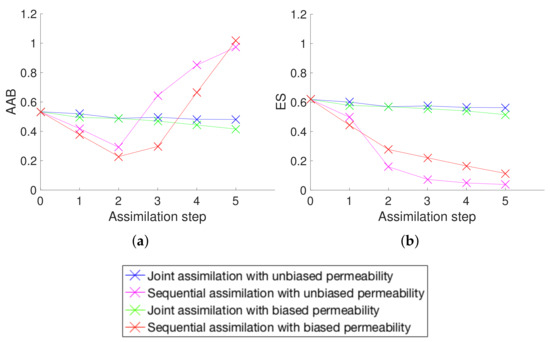
Figure 20.
Evaluation metrics for the estimation of the dispersivity: (a) average absolute bias and (b) ensemble spread.
On the other hand, the assimilation of measured electrical resistances is characterized by values of and that are generally similar to each other, a clear indication that the uncertainty is not underestimated [23]. This holds not only for the ensemble of hydraulic permeability but also for the dispersivity, even though the accuracy of the dispersivity ensemble does not improve much with the assimilation of electrical resistances, which confirms that the assimilated data are not sensitive to the dispersivity.
5. Conclusions
We presented here a research study aimed at evaluating the potential of electrical resistivity tomography (ERT) data assimilation for automatic update of groundwater states and parameters in coastal aquifers affected by seawater intrusion. The study was carried out by applying the EnKF to a numerical density-dependent groundwater model simulating a real laboratory experiment, where the saltwater wedge was monitored by ERT. Assimilation of electrical data was performed according to a joint approach, whereby raw electrical resistance data were assimilated, and a sequential approach, whereby inverted resistivities were used. In both cases, dual-step update strategies were proposed to obtain parameter estimates limitedly affected by spurious correlations and consistent with system states.
We proved that both joint and sequential EnKF assimilation schemes have the potential to infer hydraulic parameters, i.e., permeability and dispersivity. However, permeability was estimated much more accurately than dispersivity, probably due to the low resolution of the ERT measurements that did not allow for an accurate resolution of the transition zone of the saltwater wedge. Finally, we found that the sequential approach in our test case was heavily affected by the filter divergence, contrary to previous studies [35], probably due to the limited ensemble size compared to the amount of resistivity data assimilated.
Overall, we can confirm that the EnKF is a potentially powerful data assimilation tool that can reduce the uncertainty on system states and parameters in a wide range of groundwater processes, although further studies are needed to fully explore its capabilities in problems of seawater intrusion. In the future, the proposed approach will be applied to more complex experimental settings, including heterogeneous porous media and dynamic (i.e., time-variable) boundary conditions. Then, additional studies will be needed in real-world and full-scale test cases.
Acknowledgments
This study was funded by the PRIN 2010-11 project 20104J2Y8M_005 and the University of Padova project CPDR135701/13. We gratefully acknowledge Erika Bertorelle and Federico Costantini for helping with the experiments, in fulfillment of their MSc Thesis, as well as Enrica Belluco, who was instrumental in the setup of the physical model. We also thank Barbara Chiozzotto and Marco Giada for the collection of the ERT data, Maxime Claprood for his comments on an early version of the manuscript, and three anonymous reviewers whose comments helped to improve the paper.
Author Contributions
V.B. carried out the numerical simulations and wrote the first draft of the manuscript. E.C. and P.S. contributed to the laboratory experiment. E.G. and M.C. conceived and supervised the study and edited the manuscript. All authors reviewed the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kundzewicz, Z.W.; Mata, L.J.; Arnell, N.W.; Doll, P.; Kabat, P.; Jimenez, B.; Miller, K.; Oki, T.; Zekai, S.; Shiklomanov, I. Freshwater Resources and Their Management; Cambridge University Press: Cambridge, UK, 2007; pp. 173–210. [Google Scholar]
- Bobba, A.G. Numerical modelling of salt-water intrusion due to human activities and sea-level change in the Godavari Delta, India. Hydrol. Sci. J. 2002, 47, S67–S80. [Google Scholar] [CrossRef]
- Masterson, J.P. Simulated Interaction between Freshwater and Saltwater and Effects of Ground-Water Pumping and Sea-Level Change, Lower Cape Cod Aquifer System, Massachusetts; US Department of the Interior, US Geological Survey: Reston, VA, USA, 2004.
- Liu, J.; Rich, K.; Zheng, C. Sustainability analysis of groundwater resources in a coastal aquifer, Alabama. Environ. Geol. 2008, 54, 43–52. [Google Scholar] [CrossRef]
- Werner, A.D.; Simmons, C.T. Impact of Sea-Level Rise on Sea Water Intrusion in Coastal Aquifers. Ground Water 2009, 47, 197–204. [Google Scholar] [CrossRef] [PubMed]
- Barlow, P.M.; Reichard, E.G. Saltwater intrusion in coastal regions of North America. Hydrogeol. J. 2010, 18, 247–260. [Google Scholar] [CrossRef]
- Chang, S.W.; Clement, T.P.; Simpson, M.J.; Lee, K.K. Does sea-level rise have an impact on saltwater intrusion? Adv. Water Resour. 2011, 34, 1283–1291. [Google Scholar] [CrossRef]
- SIngha, K.; Day-Lewis, F.D.; Johnson, T.; Slater, L.D. Advances in interpretation of subsurface processes with time-lapse electrical imaging. Hydrol. Process. 2015, 29, 1549–1576. [Google Scholar] [CrossRef]
- Comte, J.C.; Banton, O. Cross-validation of geo-electrical and hydrogeological models to evaluate seawater intrusion in coastal aquifers. Geophys. Res. Lett. 2007, 34, L10402. [Google Scholar] [CrossRef]
- Zarroca, M.; Bach, J.; Linares, R.; Pellicer, X.M. Electrical methods (VES and ERT) for identifying, mapping and monitoring different saline domains in a coastal plain region (Alt Empordà, Northern Spain). J. Hydrol. 2011, 409, 407–422. [Google Scholar] [CrossRef]
- Ogilvy, R.; Meldrum, P.; Kuras, O.; Wilkinson, P.; Chambers, J.; Sen, M.; Pulido-Bosch, A.; Gisbert, J.; Jorreto, S.; Frances, I.; et al. Automated monitoring of coastal aquifers with electrical resistivity tomography. Near Surf. Geophys. 2009, 7, 367–375. [Google Scholar] [CrossRef]
- Satriani, A.; Loperte, A.; Imbrenda, V.; Lapenna, V. Geoelectrical surveys for characterization of the coastal saltwater intrusion in Metapontum forest reserve (Southern Italy). Int. J. Geophys. 2012, 2012. [Google Scholar] [CrossRef]
- Hermans, T.; Vandenbohede, A.; Lebbe, L.; Martin, R.; Kemna, A.; Beaujean, J.; Nguyen, F. Imaging artificial salt water infiltration using electrical resistivity tomography constrained by geostatistical data. J. Hydrol. 2012, 438–439, 168–180. [Google Scholar] [CrossRef]
- Rey, J.; Martínez, J.; Barberá, G.G.; García-Aróstegui, J.L.; García-Pintado, J.; Martínez-Vicente, D. Geophysical characterization of the complex dynamics of groundwater and seawater exchange in a highly stressed aquifer system linked to a coastal lagoon (SE Spain). Environ. Earth Sci. 2013, 70, 2271–2282. [Google Scholar] [CrossRef]
- Kazakis, N.; Pavlou, A.; Vargemezis, G.; Voudouris, K.; Soulios, G.; Pliakas, F.; Tsokas, G. Seawater intrusion mapping using electrical resistivity tomography and hydrochemical data. An application in the coastal area of eastern Thermaikos Gulf, Greece. Sci. Total Environ. 2016, 543, 373–387. [Google Scholar] [CrossRef] [PubMed]
- De Franco, R.; Biella, G.; Tosi, L.; Teatini, P.; Lozej, A.; Chiozzotto, B.; Giada, M.; Rizzetto, F.; Claude, C.; Mayer, A.; et al. Monitoring the saltwater intrusion by time lapse electrical resistivity tomography: The Chioggia test site (Venice Lagoon, Italy). J. Appl. Geophys. 2009, 69, 117–130. [Google Scholar] [CrossRef]
- Binley, A.; Cassiani, G.; Middleton, R.; Winship, P. Vadose zone flow model parameterisation using cross-borehole radar and resistivity imaging. J. Hydrol. 2002, 267, 147–159. [Google Scholar] [CrossRef]
- Pollock, D.; Cirpka, O.A. Fully coupled hydrogeophysical inversion of a laboratory salt tracer experiment monitored by electrical resistivity tomography. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Jardani, A.; Revil, A.; Dupont, J. Stochastic joint inversion of hydrogeophysical data for salt tracer test monitoring and hydraulic conductivity imaging. Adv. Water Resour. 2013, 52, 62–77. [Google Scholar] [CrossRef]
- Steklova, K.; Haber, E. Joint hydrogeophysical inversion: state estimation for seawater intrusion models in 3D. Comput. Geosci. 2017, 21, 75–94. [Google Scholar] [CrossRef]
- Beaujean, J.; Nguyen, F.; Kemna, A.; Antonsson, A.; Engesgaard, P. Calibration of seawater intrusion models: Inverse parameter estimation using surface electrical resistivity tomography and borehole data. Water Resour. Res. 2014, 50, 6828–6849. [Google Scholar] [CrossRef]
- Binley, A.; Hubbard, S.S.; Huisman, J.A.; Revil, A.; Robinson, D.A.; Singha, K.; Slater, L.D. The emergence of hydrogeophysics for improved understanding of subsurface processes over multiple scales. Water Resour. Res. 2015, 51, 3837–3866. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhang, D. Data assimilation for transient flow in geologic formations via ensemble Kalman filter. Adv. Water Resour. 2006, 29, 1107–1122. [Google Scholar] [CrossRef]
- Hendricks Franssen, H.J.; Kinzelbach, W. Ensemble Kalman filtering versus sequential self-calibration for inverse modelling of dynamic groundwater flow systems. J. Hydrol. 2009, 365, 261–274. [Google Scholar] [CrossRef]
- Zhou, H.; Gomez-Hernandez, J.J.; Franssen, H.J.H.; Li, L. An approach to handling non-Gaussianity of parameters and state variables in ensemble Kalman filtering. Adv. Water Resour. 2011, 34, 844–864. [Google Scholar] [CrossRef]
- Schöniger, A.; Nowak, W.; Hendricks Franssen, H.J. Parameter estimation by ensemble Kalman filters with transformed data: Approach and application to hydraulic tomography. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Crestani, E.; Camporese, M.; Bau, D.; Salandin, P. Ensemble Kalman Filter versus ensemble smoother for assessing hydraulic conductivity via tracer test data assimilation. Hydrol. Earth Syst. Sci. 2013, 17, 1517–1531. [Google Scholar] [CrossRef]
- Li, L.; Zhou, H.; Gomez-Hernandez, J.J.; Franssen, H.J.H. Jointly mapping hydraulic conductivity and porosity by assimilating concentration data via ensemble Kalman filter. J. Hydrol. 2012, 429, 152–169. [Google Scholar] [CrossRef]
- Crestani, E.; Camporese, M.; Salandin, P. Assessment of hydraulic conductivity distributions through assimilation of travel time data from ERT-monitored tracer tests. Adv. Water Resour. 2015, 84, 23–36. [Google Scholar] [CrossRef]
- Zovi, F.; Camporese, M.; Franssen, H.J.H.; Huisman, J.A.; Salandin, P. Identification of high-permeability subsurface structures with multiple point geostatistics and normal score ensemble Kalman filter. J. Hydrol. 2017, 548, 208–224. [Google Scholar] [CrossRef]
- Voss, C.I.; Provost, A.M. SUTRA: A Model for Saturated-Unsaturated, Variable-Density Ground-Water Flow with Solute or Energy Transport; Technical Report 02-4231; U.S. Geological Survey: Reston, VA, USA, 2010.
- Bertorelle, E. Laboratory Experiments on the Saltwater Intrusion Process. Master’s Thesis, University of Padova, Padova, Italy, 2014. [Google Scholar]
- Costantini, F.M. Un Caso Test Per L’intrusione Salina: Evidenze di Laboratorio e Numeriche. Master’s Thesis, University of Padova, Padova, Italy, 2015. [Google Scholar]
- Crestani, E.; Camporese, M.; Salandin, P. Physical and numerical modeling of seawater intrusion in coastal aquifers. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 7–22 April 2016; Volume 18. [Google Scholar]
- Camporese, M.; Cassiani, G.; Deiana, R.; Salandin, P.; Binley, A. Coupled and uncoupled hydrogeophysical inversions using ensemble Kalman filter assimilation of ERT-monitored tracer test data. Water Resour. Res. 2015, 51. [Google Scholar] [CrossRef]
- Voss, C.I. Seawater Intrusion in Coastal Aquifers—Concepts, Methods and Practices. In Theory and Appications of Transport in Porous Media; Chapter 9 USGS SUTRA Code—History, Pratical Use and Application in Hawaii; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; Volume 14, pp. 249–313. [Google Scholar]
- Bouchedda, A. Inversion Conjointe des Données Électriques et de Radar en Forage. Ph.D. Thesis, Ecole Polytechnique de Montréal, Montréal, QC, Canada, 2010. [Google Scholar]
- Lesmes, D.P.; Friedman, S.P. Hydrogeophysics; Springer: Dordrecht, The Netherlands, 2005; Chapter 4; pp. 87–128. [Google Scholar]
- Cardarelli, E.; Fischanger, F. 2D data modelling by electrical resistivity tomography for complex subsurface geology. Geophys. Prospect. 2006, 54, 121–133. [Google Scholar] [CrossRef]
- Binley, A.; Kemna, A. DC Resistivity and Induced Polarization Methods. In Hydrogeophysics; Springer: Dordrecht, The Netherlands, 2005; pp. 129–156. [Google Scholar]
- Gunther, T. Inversion Methods and Resolution Analysis for the 2D/3D Reconstruction of Resistivity Structures from DC Measurements. Ph.D. Thesis, TU Bergakademie Freiberg, Freiberg, Germany, 2004. [Google Scholar]
- Evensen, G. The ensemble Kalman filter for combined state and parameter estimation: Monte Carlo techniques for data assimilation in large systems. IEEE Control Syst. 2009, 29, 83–104. [Google Scholar] [CrossRef]
- Burgers, G.; Jan van Leeuwen, P.; Evensen, G. Analysis Scheme in the Ensemble Kalman Filter. Mon. Weather Rev. 1998, 126, 1719–1724. [Google Scholar] [CrossRef]
- Manoli, G.; Rossi, M.; Pasetto, D.; Deiana, R.; Ferraris, S.; Cassiani, G.; Putti, M. An iterative particle filter approach for coupled hydro-geophysical inversion of a controlled infiltration experiment. J. Comput. Phys. 2015, 283, 37–51. [Google Scholar] [CrossRef]
- Camporese, M.; Cassiani, G.; Deiana, R.; Salandin, P. Assessment of local hydraulic properties from electrical resistivity tomography monitoring of a three-dimensional synthetic tracer test experiment. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Kapur, J.N.; Kesavan, H.K. Entropy and Energy Dissipation in Water Resources; Chapter Entropy Optimization Principles and Their Applications; Water Science and Technology Library, Springer: Dordrecht, The Netherlands, 1992; Volume 9. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).