Abstract
This study aimed to assess the suitability of the parameters of a physically based, distributed, grid-based rainfall-runoff model. We analyzed parameter sensitivity with a dataset of eight rainfall events that occurred in two catchments of South Korea, using the Sobol’ method. Parameters identified as sensitive responded adequately to the scale of the rainfall events and the objective functions employed. Parameter sensitivity varied depending on rainfall scale, even in the same catchment. Interestingly, for a rainfall event causing considerable runoff, parameters related to initial soil saturation and soil water movement played a significant role in low flow calculation and high flow calculation, respectively. The larger and steeper catchment exhibited a greater difference in parameter sensitivity between rainfall events. Finally, we found that setting an incorrect parameter range that is physically impossible can have a large impact on runoff simulation, leading to substantial uncertainty in the simulation results. The proposed analysis method and the results from our study can help researchers using a distributed rainfall-runoff model produce more reliable analysis results.
1. Introduction
The distributed rainfall-runoff model simulates runoff on a grid, taking into account the spatial variability in physical properties of a catchment using geographic information system (GIS) techniques and the spatiotemporal variability of rainfall. Because of these advantages, this model is suitable for simulating rainfall-runoff from the common view [1] and aim to improve the simulation of hydrological process in the catchment [2]. For this reason, the distributed rainfall-runoff model is becoming increasingly popular in water resource planning and management [3,4], as well as in various other research fields [5,6,7,8,9,10,11,12,13]. In particular, Soil and Water Assessment Tool (SWAT) [14] and Topography based hydrological Model (TOPMODEL) [15] are widely used, because the former has the advantage of simulating hydrology, plant growth, sediments, nutrients, and pesticides in watersheds, and the latter has the advantage of simulating the catchment’s observed flow more appropriately, by simulating the dynamically variable slope of the catchment.
The grid-based rainfall-runoff model (GRM) [16] is a physically based, distributed rainfall-runoff model for simulating short-term flood events. This model uses GIS techniques such as a digital extraction model (DEM), soil map, and land use cover. This model has been used for various studies [16,17,18], and is used as an important model for flood simulation in Korean catchments.
The parameters of the distributed rainfall-runoff model simulate catchment runoff through calibration. However, estimated parameter values may not be true values that completely represent the hydrological process in the catchment, and are inevitably uncertain [19]. It is noteworthy that the parameters of the physically based distributed rainfall-runoff model can theoretically be estimated using observation data; thus, it does not require manual or automatic parameter calibration. However, parameters are generally calibrated because of errors in the observation data, missing data required for parameter estimation, and problems arising from the difference in grid scales between observation data and the rainfall-runoff model [20,21,22,23,24,25,26]. Uncertainty in parameters can be caused by extreme interaction between parameters or parameter non-uniqueness [27]; such uncertainty can cause an equifinality problem [28,29]. Parameter uncertainty is one of the most important uncertainty factors in hydrologic modeling; therefore, it is hard to construct accurate hydrologic predictions without parameter uncertainty assessment [30].
Parameter sensitivity analysis (SA) is a valuable tool for assessing important parameters [31], and is particularly important in distributed rainfall-runoff model assessment [32] and hydrological research [19]. Parameter sensitivity analysis has the following goals: (1) understand parameter characteristics that simulate the hydrologic system of catchments; (2) estimate appropriate parameter ranges and values; (3) improve the rainfall-runoff model; and (4) reduce uncertainties in the model and simulation results [33,34,35]. Sobol’ [36], Morris [37], and Regional Sensitivity Analysis [38] methods are widely used SA methods.
This study aimed to analyze sensitivity of parameters of the GRM, in order to investigate the reliability of simulation results. Parameter sensitivity was analyzed using the Sobol’ method, which is a global sensitivity analysis method [36], and data of eight rainfall events that occurred in Danseong and Seonsan catchments in South Korea. In the Sobol’ method, the parameter sensitivity index considers the interaction between parameters and allows direct interpretation. These benefits have made this method increasingly popular in recent hydrological studies [39]. The purpose of this study was: (1) to analyze the characteristics of GRM parameters and assess their suitability for different rainfall event scales and objective functions; (2) to analyze the effect of catchment characteristics on the sensitivity of parameters; and (3) to analyze the effect of GRM parameter range on parameter sensitivity, where it may affect the uncertainty of the simulation results.
2. Catchment and Data
The study sites were the Danseong and Seonsan catchments in South Korea (Figure 1). These catchments are based in major tributaries of the Nakdong river, which flows through southeast South Korea. The Danseong catchment is the first catchment in Korea to have a sudden flood forecasting system, due to frequent floods. Therefore, this catchment is an area where flood modeling is important. The Seonsan catchment is a small catchment about half the size of the Danseong catchment, but flood defenses are important because it includes urban areas. Therefore, the Danseong and Seonsan catchments are areas where various studies are needed. The Danseong and Seonsan catchment have different catchment characteristics. The areas of Danseong and Seonsan catchments are 1709 km2 and 977 km2, respectively. Approximately 73% of the Danseong catchment comprises steep mountains (mean slope 16.2%, maximum elevation 1834 m, minimum elevation 47 m), and 21% of the area near the river is farmland. The Seonsan catchment is gentler than Danseong catchment (mean slope 12.8 %, maximum elevation 1292 m, minimum elevation 38 m). Approximately 65% of the Seonsan catchment area is low mountains, 28% is farmland, and 4% is urban.
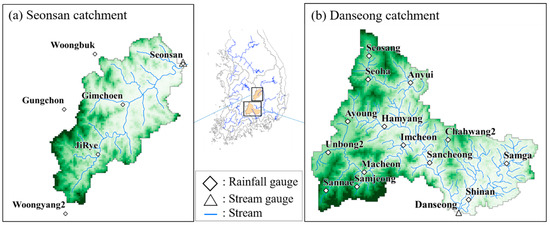
Figure 1.
Maps of the study areas: (a) Seonsan catchment and (b) Danseong catchment in South Korea.
The rainfall data used in this study are eight rainfall events that occurred in Danseong and Seonsan catchments (Table 1). The average rainfall data for each catchment were generated by the Thiessen Polygon method, using the observed rainfall of the rainfall stations (Figure 1). The rainfall stations are operated by the Ministry of Land, Infrastructure and Transport (http://www.molit.go.kr). The time interval of the data was 10 min, and the precipitation amounts varied from 43 mm to 225 mm. The precipitation time distribution of the rainfall events, and resulting hydrographs, show substantial variation (Figure 2).

Table 1.
Storm events for each catchment.
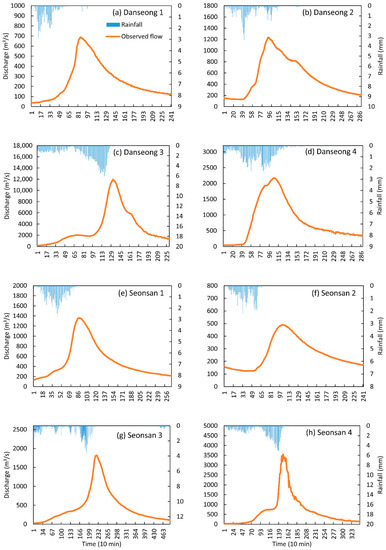
Figure 2.
Rainfall time series and observed hydrographs for the eight rainfall events in Danseong and Seonsan catchments. (a) Danseong 1; (b) Danseong 2; (c) Danseong 3; (d) Danseong 4; (e) Seonsan 1; (f) Seonsan 2; (g) Seonsan 3; (h) Seonsan 4.
3. Material and Sensitivity Analysis Method
3.1. Grid-Based Rainfall-Runoff Model
The GRM is an event based rainfall-runoff model. It simulates overland flow, channel flow, infiltration, subsurface flow, percolation, and baseflow (Figure 3). Runoff is calculated using the kinematic wave equation, and infiltration is calculated using the Green-Ampt model. The GRM can properly simulate short-term flood events using a short simulation time interval, such as a 10 min time interval (e.g., in References [17,18]). The governing equations of GRM are as follows.
where h is flow depth, q is flow rate per unit width, r is rainfall intensity, f is infiltration rate, qr is return flow into the overland flow, ∆y is the width of control volume, A is channel cross-sectional area, Q is discharge in the channel, qL is lateral flow from overland flow, qss is subsurface flow, qb is baseflow, S0 is surface slope, and Sf is friction slope. Input data for the GRM include hydrological topographic factors (slope of each grid and flow direction) extracted by a digital elevation model (DEM), and soil and land cover data. These data are inputted in raster file format. In this study, we converted the 30 m × 30 m DEM provided by the National Geographic Information Institute (http://www.ngii.go.kr) into 500 m × 500 m data to generate input topographic data of the target catchments. For land cover data, the upper-category land cover map of the Ministry of Environment (http://www.me.go.kr) was used. Soil texture and soil depth maps were produced using the high-precision soil map provided by the National Academy of Agricultural Science (http://www.naas.go.kr), in order to apply the Green-Ampt infiltration model. Table 2 shows the parameters used in the GRM. Note that all grids had different attribute/parameter values extracted from GIS data. The parameters related to land cover and soil of the GRM collectively adjusted the attribute/parameter values of these grids using ratios.
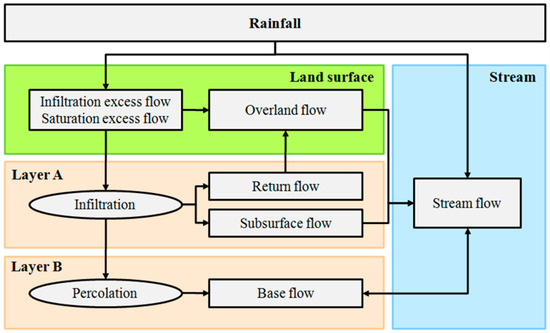
Figure 3.
Schematic of grid-based rainfall-runoff method (GRM) [40].

Table 2.
Parameters of the GRM model.
3.2. The Sobol’ Method
The Sobol’ method is a variance-based global sensitivity analysis method, which is currently widely used across various research fields [2,41,42,43,44,45,46,47]. This approach quantifies the relative effect of a parameter and its interaction with other parameters on model output variance, using the decomposition of model output variance.
This method calculates the first-order sensitivity index (FSI) and total sensitivity index (TSI). The FSI indicates the sensitivity of each parameter in relation to the model output, and the TSI is the sum of a parameter’s FSI and the sensitivity of the parameter’s interaction with other parameters influencing the model output [48]. Therefore, if there is no interaction between parameters, the sum of all parameters’ FSIs becomes 1. The FSI and TSI of parameters range between 0 and 1. In this study, we analyzed GRM parameter sensitivity using the latter, because TSI produces more suitable results than FSI when analyzing the general effect of each parameter on the model output [48]. The TSI is defined below [49].
where Xi is the ith parameter X~i represents the vector of all parameters not including Xi, and Y is the scalar objective function value. The inner variance of the numerator means that the variance of Y is considered over all possible values of Xi while maintaining X~i fixed. The outer expectation of the numerator is considered over all possible values of X~i. Thus, the numerator of TSI represents the expected variance that would be left if all parameters were fixed, not including Xi [49]. The variance of Y in the denominator indicates total unconditioned variance.
Saltelli’s scheme [50] was used for parameter sampling. This scheme shortens the time required for sensitivity calculation by reducing the number of samples from n × (2k + 2) to n × (k + 2). Here, n represents the initial sample size (10,000 in this study), and k is the number of parameters in the model. Therefore, the total number of samples used for a single sensitivity analysis of the GRM with nine parameters is 110,000. Latin Hypercube sampling was employed for the initial sampling, further details of which can be found in Shin et al. [51]. The R ‘sensitivity’ package [52] was used for the sensitivity analysis.
Three objective functions were used to analyze parameter sensitivity for high flow, medium flow, and low flow (low flow is baseflow of the recession curve during an event). First, the Nash-Sutcliffe efficiency (NSE) [53] was modified to analyze parameter sensitivity for high flow. The NSE function is expressed as:
where Qobs,i is the observed flow with time interval i (10 min in this study), is the mean value of observed flow, Qsim,i is the simulated flow, and n is the number of time steps. NSE ranges from −∞ to 1, where 1 indicates a perfect match between observed flow and simulated flow. NSE squares the difference between observed flow and simulation flow values; thus, a relatively greater weight is given to high flow fitting on the hydrograph [54,55,56]. However, the TSI value can turn into a bias due to a large negative NSE value, because NSE values range from −∞ to 1. For this reason, we employed NSE* [57], modified from NSE. The NSE* objective function is expressed as:
NSE* values range from −1 to 1. The NSE* objective function reduces the effect of a large negative NSE value on sensitivity without modifying the analysis of NSE values. When calculating NSE through a log transformation of observed and simulated data (NSElog), low flow fitting is given more weight [54,56]. Thus, NSElog*, modified from NSElog, was used for parameter sensitivity analysis of low flow. Finally, 0.5(NSE* + NSElog*), which gives equivalent weights to NSE* and NSElog*, was used to analyze parameter sensitivity for medium flow. These three objective functions were previously employed in the study of Shin et al. [51].
We first analyzed the effects of rainfall events on the sensitivity of parameters, using the various rainfall events and catchments mentioned above. We then analyzed whether the parameters reacted appropriately for various objective functions. Third, we analyzed the influence of the characteristics of the catchment on the sensitivity of the parameters. Finally, we analyzed the effect of the range of parameters on the sensitivity of parameters. The sensitivity analysis of the parameters was analyzed using the parameter values generated by the Latin Hypercube sampling method, so calibration and validation of the parameters for sensitivity analysis of the parameters was not performed.
4. Results and Discussion
4.1. Parameter Sensitivity Analysis Reflecting the Scale of Rainfall Events
Figure 4 and Figure 5 show parameter TSI values for four rainfall events in Danseong and Seonsan catchments for the three objective functions. Parameter sensitivity varied depending on the scale of rainfall events, even in the same catchment. The rainfall events of Danseong catchment showed greater parameter sensitivity differences than those of Seonsan catchment. Considering the fact that the precipitation amount during events was similar in both catchments (Table 1), the parameter sensitivity was likely affected by the runoff difference caused by different catchment characteristics (see Section 2).
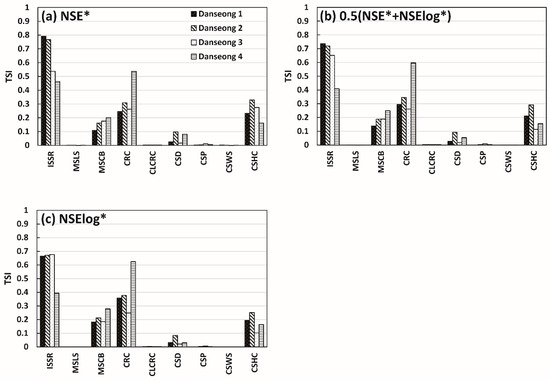
Figure 4.
Parameter sensitivity of rainfall events in Danseong catchment, calculated for three objective functions: (a) NSE*; (b) 0.5(NSE* + NSElog*); (c) NSElog*.
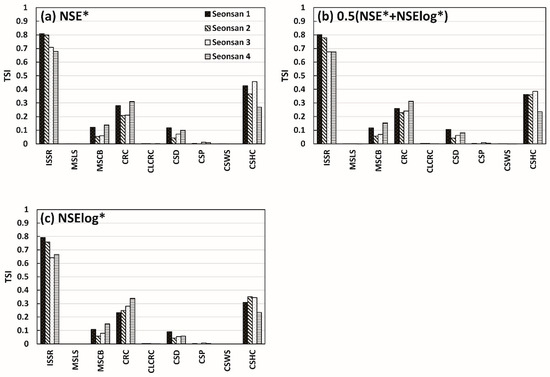
Figure 5.
Parameter sensitivity of rainfall events in Seonsan catchment, calculated for three objective functions: (a) NSE*; (b) 0.5(NSE* + NSElog*); (c) NSElog*.
In Danseong catchment, the TSIs of ISSR and CSHC (parameters related to soil water content, Table 2) of the fourth rainfall event (Danseong 4) were lower than those of the first (Danseong 1) and second (Danseong 2) rainfall events. Therefore, the fourth and largest rainfall event in Danseong catchment (Danseong 4) exhibited relatively low sensitivity of soil water content-related parameters. This means that the surface runoff of a river had a greater impact on total runoff than runoff from the soil in larger-scale rainfall events. This phenomenon is physically reasonable, and indicates that these parameters reacted appropriately to the different scales of rainfall events. This result is also supported by the fact that the TSIs of MSCB and CRC (river channel-related parameters, Table 2) in the Danseong 4 rainfall event were greater than those of Danseong 1 and Danseong 2. This phenomenon was also observed in Seonsan catchment; thus, the GRM effectively simulates the runoff of various catchments and rainfall events.
It is notable that Danseong 3 had a greater TSI of ISSR for initial soil saturation than Danseong 4, although the runoff volume of Danseong 3 was far greater than that of Danseong 4 (Figure 2). This phenomenon was observed with all objective functions, and the TSI of ISSR was higher using the low flow objective function (NSElog*) than when using that for high flow (NSE*). This suggests that the initial soil saturation is particularly important when calculating low flow during large rainfall events with very high runoff. In NSE*, Danseong 3 had a greater TSI of CSHC for soil water movement than Danseong 4, which indicates that this parameter plays an important role in high flow calculations of large rainfall events with very high runoff. As for MSCB and CRC, Danseong 3 had smaller TSI values than Danseong 4. This is probably because total runoff simulations consider the interaction between ISSR, MSCB, and CRC. For example, the TSI of river runoff-related MSCB and CRC decreases when the TSI of ISSR related to initial soil saturation increases.
4.2. Parameter Sensitivity Analysis Reflecting Different Objective Functions
Figure 6 and Figure 7 show the TSI of parameters for Danseong and Seonsan catchments, calculated for the three objective functions. The two soil-related parameters (ISSR and CSHC) and the two river-related parameters (MSCB and CRC) were highly sensitive in both catchments. Therefore, these four parameters must be estimated more carefully when estimating optimum parameter values. However, CSD was less sensitive and the remaining parameters (MSLS, CLCRC, CSP, and CSWS) exhibited minimal sensitivity. These insensitive parameters were not sensitive to all objective functions; thus, they can be fixed to specific values for Danseong and Seonsan catchments, as suggested by Shin et al. [51]. However, these parameters may be sensitive in other catchments with different characteristics and rainfall events. A preliminary sensitivity analysis is indispensable when applying the GRM to other catchments.
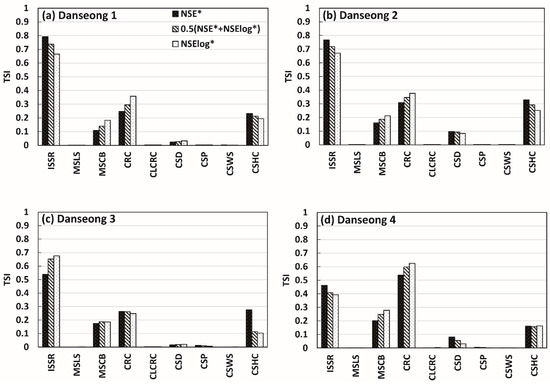
Figure 6.
Parameter sensitivity of the four rainfall events in Danseong catchment, calculated for the three objective functions: (a) Danseong 1; (b) Danseong 2; (c) Danseong 3; (d) Danseong 4.
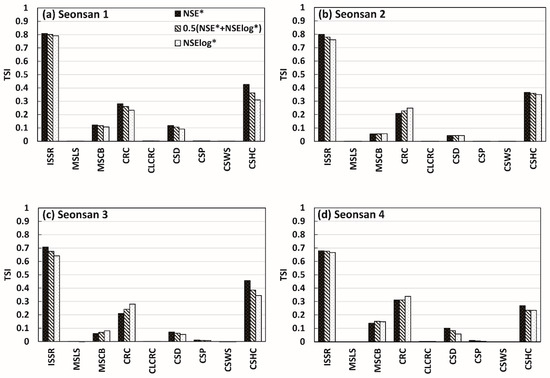
Figure 7.
Parameter sensitivity of the four rainfall events in Seonsan catchment, calculated for the three objective functions: (a) Seonsan 1; (b) Seonsan 2; (c) Seonsan 3; (d) Seonsan 4.
The soil-related ISSR and CSHC parameters were more sensitive to high flow than to low flow in Danseong and Seonsan catchments. This is reasonable because the range of change of the hydrograph due to the variation of soil water content is greater during high flow than low flow for normal rainfall events. However, for a large rainfall event with very high runoff (Danseong 3), the parameter for initial soil saturation (ISSR) had a greater effect on low flow simulation. Conversely, the river-related MSCB and CRC parameters were typically more sensitive to low flow than high flow. This is reasonable because low flow is more sensitive to friction due to river roughness than high flow. In summary, it was concluded that these parameters functioned appropriately according to the objective functions.
4.3. Parameter Sensitivity Analysis Reflecting Different Catchment Characteristics
The sensitivity of the parameters may vary depending on the catchment characteristics. In this section, we analyzed the effect of catchment characteristics on the sensitivity of parameters. Figure 8 shows the maximum and minimum TSI values of parameters among the four rainfall events in Danseong and Seonsan catchments. When the TSI values of parameters lie closer to the diagonal line, the maximum and minimum TSIs have similar values. TSI values of the parameters for Danseong catchment, calculated for all three objective functions, were farther from the reference line than those for Seonsan catchment. Danseong catchment is approximately twice as large as Seonsan catchment and has steeper mountains. Although there was a slight gap between the rainfall volumes in the two catchments (Table 1), the GRM parameter sensitivity changes were greater in the larger and steeper catchment than in the smaller, gentler catchment.
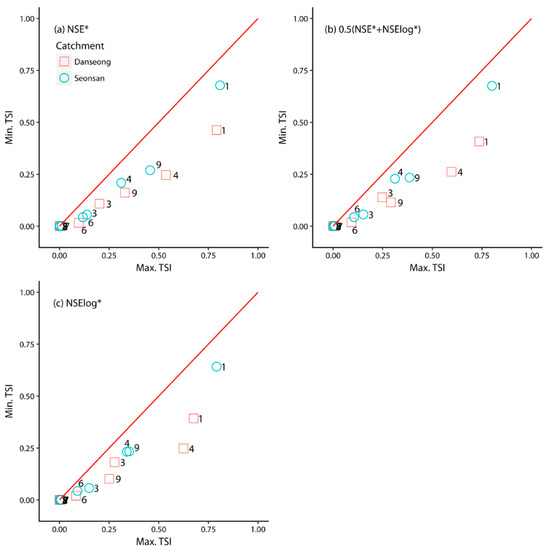
Figure 8.
Differences in parameter sensitivity of Danseong and Seonsan catchments, calculated for the three objective functions. Numbers in symbols indicate parameter numbers in Table 2. (a) NSE*; (b) 0.5(NSE* + NSElog*); (c) NSElog*.
4.4. Effect of Parameter Range on Sensitivity
Figure 9 and Figure 10 show the sensitivity results of the parameters for NSE*, using the parameter range suggested in Table 2 (original range), except for the parameters of MSLS and MSCB, which used a modified range with both MSLS and MSCB upper limits changed to 1 (45°) (wide range) (i.e., parameter ranges of MSLS and MSCB were all 0.0001–1). In the kinematic wave model used in the GRM, surface slope was used for the hydraulic gradient. These two parameters were employed to solve calculation errors caused by no transmission of the flood wave, due to extremely low land surface and channel bed slopes in the catchments. The reason for modifying the range of these two parameters was to test the effect of an artificially fixed slope value within the parameter range through pre-treatment of the DEM (fill sinks and remove flat areas) used to establish GRM input data on the simulation results.
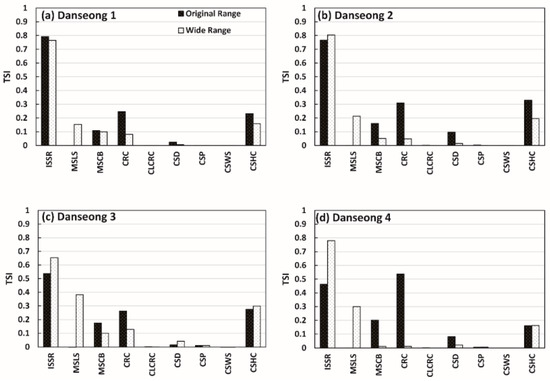
Figure 9.
Sensitivity changes of parameters for different parameter ranges for the Danseong catchment (using NSE* objective function): (a) Danseong 1; (b) Danseong 2; (c) Danseong 3; (d) Danseong 4.
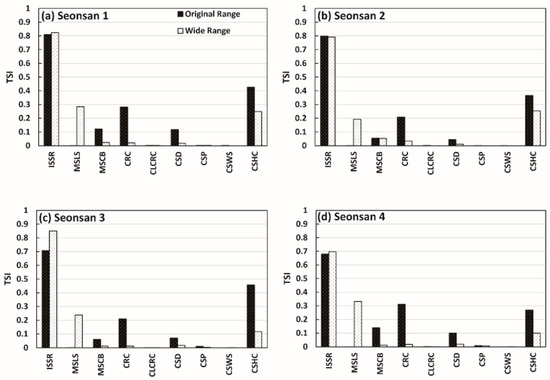
Figure 10.
Sensitivity changes of parameters for different parameter ranges for the Seonsan catchment (using NSE* objective function): (a) Seonsan 1; (b) Seonsan 2; (c) Seonsan 3; (d) Seonsan 4.
As a result, the TSI of MSLS was closer to 0 in the original range, but mostly over 0.2 in the modified range. This is because MSLS was a parameter for setting the minimum gradient for overland flow in most areas of the catchment. When this value becomes unrealistically large, it will have a considerable impact on runoff simulation in the catchment. Conversely, the TSI values of the other parameters typically decreased, except for ISSR, which is likely because the effect of the other parameters on runoff decreased as the sensitivity of MSLS increased.
Interestingly, the TSI value of MSCB decreased although the range of the MSCB parameter increased. The river grid influenced by MSCB accounted for 29% and 36% of the total grids of Seonsan and Danseong catchments, respectively. This was probably because it accounted for a smaller ratio than the catchment surface grid affected by MSLS; thus, the effect of MSCB on runoff decreased. However, setting 45° as the upper limit of MSLS and MSCB was not physically valid. Setting a physically invalid range for even one or two GRM parameters can not only substantially change the sensitivity of the parameter in question, but also that of other parameters, and can produce erroneous runoff simulation results. Therefore, the parameter range should be carefully determined by hydrology specialists to ensure physical validity.
5. Conclusions
In this study, we analyzed parameter sensitivity using the Sobol method in order to assess the suitability of the parameters of the GRM, which is a physically based, distributed rainfall-runoff model. Eight rainfall events in two different sized catchments in South Korea were used to analyze parameter sensitivity according to their different catchment and rainfall characteristics, and to determine parameter suitability.
As a result, parameter sensitivity varied depending on the scale of rainfall events, even in the same catchment. The size and characteristics of the catchment also had an effect on parameter sensitivity in different rainfall events. This result supports the results of van Griensven et al. [35], that the sensitivity of the parameters varies between catchments. Sensitive parameters adequately responded to the different scales of rainfall events and the objective functions in both catchments; thus, we concluded that the GRM model can produce reliable simulation results. The parameter ISSR, which is related to the initial soil saturation, was the most sensitive parameter for most catchments and rainfall events. River runoff-related parameters, MSCB and CRC, and the subsurface runoff-related parameter, CSHC, were identified as sensitive. These four sensitive parameters are important parameters for parameter estimation. The remaining parameters (CSD, MSLS, CLCRC, CSP, and CSWS) had less sensitivity for all objective functions; therefore, they can be fixed to specific values, at least for these study catchments, as suggested by Shin et al. [51]. However, the sensitivity of the parameters depends on catchment characteristics and rainfall events, so a preliminary sensitivity analysis is indispensable when applying the GRM to other catchments. Interestingly, parameters related to initial soil saturation and soil water movement played an important role in low flow simulation and high flow simulation respectively, in rainfall events with very high runoff. It was also found that the difference of parameter sensitivity for various rainfall events increased for the larger, steeper catchment. Finally, a physically impossible parameter ranges for the two parameters, related to catchment and river slopes, greatly influenced runoff simulation results. This implies that an incorrect parameter range can increase the probability of errors in runoff simulation results or uncertainties when analyzing runoff results. Therefore, it is important to set the parameter range based on physical validity.
In this study, it was important to evaluate the sensitivity of all the parameters used in the GRM, unlike previous studies (e.g., references [16,17]) that used only a few parameters of the GRM to calibrate the parameters. The results of this study can be used as an important guideline for researchers who use the GRM as to which parameters should be most carefully calibrated. In addition, the methods and results in this study can be an important precedent study for researchers who want to evaluate the sensitivity of parameters of distributed rainfall-runoff models other than the GRM. We analyzed parameter sensitivity for eight rainfall events in two South Korean catchments. In order to analyze parameters identified as not sensitive in this study, it is necessary to analyze the sensitivity of more catchments and rainfall events. However, the sensitivity analysis methods and results presented in this study can help researchers using the physically based distributed rainfall-runoff model to produce more reliable results.
Author Contributions
Conceptualization, M.-J.S.; Methodology, M.-J.S.; Software, M.-J.S. and Y.S.C.; Validation, M.-J.S. and Y.S.C.; Formal Analysis, M.-J.S. and Y.S.C.; Investigation, M.-J.S. and Y.S.C.; Resources, M.-J.S. and Y.S.C.; Data Curation, Y.S.C.; Writing-Original Draft Preparation, M.-J.S.; Writing-Review & Editing, Y.S.C.; Visualization, M.-J.S. and Y.S.C.; Supervision, M.-J.S.; Project Administration, Y.S.C.; Funding Acquisition, Y.S.C.
Funding
This research was funded by Ministry of Land, Infrastructure and Transport of Korean government (grant number 18AWMP-B127555-02).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Al-Qurashi, A.; McIntyre, N.; Wheater, H.; Unkrich, C. Application of the Kineros2 rainfall-runoff model to an arid catchment in Oman. J. Hydrol. 2008, 355, 91–105. [Google Scholar] [CrossRef]
- Herman, J.D.; Kollat, J.B.; Reed, P.M.; Wagener, T. Technical note: Method of morris effectively reduces the computational demands of global sensitivity analysis for distributed watershed models. Hydrol. Earth Syst. Sci. 2013, 17, 2893–2903. [Google Scholar] [CrossRef]
- Kannan, N.; White, S.M.; Worrall, F.; Whelan, M.J. Sensitivity analysis and identification of the best evapotranspiration and runoff options for hydrological modelling in SWAT-2000. J. Hydrol. 2007, 332, 456–466. [Google Scholar] [CrossRef]
- Wagener, T.; Van Werkhoven, K.; Reed, P.; Tang, Y. Multiobjective sensitivity analysis to understand the information content in streamflow observations for distributed watershed modeling. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Chaubey, I.; Haan, C.T.; Grunwald, S.; Salisbury, J.M. Uncertainty in the model parameters due to spatial variability of rainfall. J. Hydrol. 1999, 220, 48–61. [Google Scholar] [CrossRef]
- Du, J.; Xie, S.; Xu, Y.; Xu, C.Y.; Singh, V.P. Development and testing of a simple physically-based distributed rainfall-runoff model for storm runoff simulation in humid forested basins. J. Hydrol. 2007, 336, 334–346. [Google Scholar] [CrossRef]
- Emmanuel, I.; Payrastre, O.; Andrieu, H.; Zuber, F. A method for assessing the influence of rainfall spatial variability on hydrograph modeling. First case study in the Cevennes Region, southern France. J. Hydrol. 2017, 555, 314–322. [Google Scholar] [CrossRef]
- Foglia, L.; Hill, M.C.; Mehl, S.W.; Burlando, P. Sensitivity analysis, calibration, and testing of a distributed hydrological model using error-based weighting and one objective function. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Grayson, R.B.; Moore, I.D.; McMahon, T.A. Physically based hydrologic modeling: 1. A terrain-based model for investigative purposes. Water Resour. Res. 1992, 28, 2639–2658. [Google Scholar] [CrossRef]
- Jain, M.K.; Kothyari, U.C.; Raju, K.G.R. A GIS based distributed rainfall-runoff model. J. Hydrol. 2004, 299, 107–135. [Google Scholar] [CrossRef]
- Shah, S.M.S.; O’connell, P.E.; Hosking, J.R.M. Modelling the effects of spatial variability in rainfall on catchment response: 2. Experiments with distributed and lumped models. J. Hydrol. 1996, 175, 89–111. [Google Scholar] [CrossRef]
- Vansteenkiste, T.; Tavakoli, M.; Van Steenbergen, N.; De Smedt, F.; Batelaan, O.; Pereira, F.; Willems, P. Intercomparison of five lumped and distributed models for catchment runoff and extreme flow simulation. J. Hydrol. 2014, 511, 335–349. [Google Scholar] [CrossRef]
- Zhang, L.; Nan, Z.; Liang, X.; Xu, Y.; Hernández, F.; Li, L. Application of the MacCormack scheme to overland flow routing for high-spatial resolution distributed hydrological model. J. Hydrol. 2018, 558, 421–431. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. A dynamic top model. Hydrol. Process. 2001, 15, 1993–2011. [Google Scholar] [CrossRef]
- Choi, Y.S.; Choi, C.K.; Kim, H.S.; Kim, K.T.; Kim, S. Multi-site calibration using a grid-based event rainfallrunoff model: A case study of the upstream areas of the Nakdong River basin in Korea. Hydrol. Process. 2015, 29, 2089–2099. [Google Scholar] [CrossRef]
- Choi, Y.; Shin, M.-J.; Kim, K. Preliminary study of computational time steps in a physically based distributed rainfall-runoff model. Water 2018, 10, 1269. [Google Scholar] [CrossRef]
- Shin, M.-J.; Choi, Y. Combining an r-based evolutionary algorithm and hydrological model for effective parameter calibration. Water 2018, 10, 1339. [Google Scholar] [CrossRef]
- Abebe, N.A.; Ogden, F.L.; Pradhan, N.R. Sensitivity and uncertainty analysis of the conceptual HBV rainfall-runoff model: Implications for parameter estimation. J. Hydrol. 2010, 389, 301–310. [Google Scholar] [CrossRef]
- Abbott, M.B.; Bathurst, J.C.; Cunge, J.A.; O’Connell, P.E.; Rasmussen, J. An introduction to the European hydrological system—Systeme hydrologique Europeen, “SHE”, 1: History and philosophy of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 45–59. [Google Scholar] [CrossRef]
- Bagarello, V.; Ferro, V.; Keesstra, S.; Comino, J.R.; Pulido, M.; Cerdà, A. Testing simple scaling in soil erosion processes at plot scale. Catena 2018, 167, 171–180. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modeling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Storm, B. Construction, Calibration and Validation of Hydrological Models. In Distributed Hydrological Modeling; Abbott, M.B., Refsgaard, J.C., Eds.; Kluwer Academic Publishers: Dordrecht, the Netherlands, 1996; pp. 41–54. [Google Scholar]
- Sahoo, G.B.; Ray, C.; De Carlo, E.H. Calibration and validation of a physically distributed hydrological model, MIKE SHE, to predict streamflow at high frequency in a flashy mountainous Hawaii stream. J. Hydrol. 2006, 327, 94–109. [Google Scholar] [CrossRef]
- Vieux, B.E. Distributed Hydrologic Modeling Using GIS; Kluwer Academic Publishers: Dordrecht, the Netherlands, 2004; pp. 197–215. [Google Scholar]
- Shin, M.-J.; Guillaume, J.H.A.; Croke, B.F.W.; Jakeman, A.J. A review of foundational methods for checking the structural identifiability of models: Results for rainfall-runoff. J. Hydrol. 2015, 520, 1–16. [Google Scholar] [CrossRef]
- Beven, K. Prophecy, reality and uncertainty in distributed hydrological modelling. Adv. Water Resour. 1993, 16, 41–51. [Google Scholar] [CrossRef]
- Beven, K. A manifesto for the equifinality thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef]
- Li, Z.; Shao, Q.; Xu, Z.; Cai, X. Analysis of parameter uncertainty in semi-distributed hydrological models using bootstrap method: A case study of SWAT model applied to Yingluoxia watershed in northwest China. J. Hydrol. 2010, 385, 76–83. [Google Scholar] [CrossRef]
- Sieber, A.; Uhlenbrook, S. Sensitivity analyses of a distributed catchment model to verify the model structure. J. Hydrol. 2005, 310, 216–235. [Google Scholar] [CrossRef]
- Tang, Y.; Reed, P.; Van Werkhoven, K.; Wagener, T. Advancing the identification and evaluation of distributed rainfall-runoff models using global sensitivity analysis. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Hamby, D.M. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef]
- Lenhart, T.; Eckhardt, K.; Fohrer, N.; Frede, H.G. Comparison of two different approaches of sensitivity analysis. Phys. Chem. Earth. Pts. A/B/C 2002, 27, 645–654. [Google Scholar] [CrossRef]
- Van Griensven, A.; Meixner, T.; Grunwald, S.; Bishop, T.; Diluzio, M.; Srinivasan, R. A global sensitivity analysis tool for the parameters of multi-variable catchment models. J. Hydrol. 2006, 324, 10–23. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity analysis for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Spear, R.C.; Hornberger, G.M. Eutrophication in Peel Inlet-II. Identification of critical uncertainties via generalized sensitivity analysis. Water Res. 1980, 14, 43–49. [Google Scholar] [CrossRef]
- Zhang, C.; Chu, J.; Fu, G. Sobol’s sensitivity analysis for a distributed hydrological model of Yichun River Basin, China. J. Hydrol. 2013, 480, 58–68. [Google Scholar] [CrossRef]
- Choi, Y.S.; Kim, K.T. Grid based rainfall-runoff model user’s manual. Korea Inst. Civ. Eng. Build. Technol. Gyeonggi-do, Korea, 2017; pp. 1–21. Available online: https://github.com/floodmodel/GRM (accessed on 20 April 2018).
- Cuntz, M.; Mai, J.; Zink, M.; Thober, S.; Kumar, R.; Schäfer, D.; Schron, M.; Craven, J.; Rakovec, O.; Spieler, D.; et al. Computationally inexpensive identification of noninformative model parameters by sequential screening. Water Resour. Res. 2015, 51, 6417–6441. [Google Scholar] [CrossRef]
- Jepsen, S.M.; Harmon, T.C.; Ficklin, D.L.; Molotch, N.P.; Guan, B. Evapotranspiration sensitivity to air temperature across a snow-influenced watershed: Space-for-time substitution versus integrated watershed modeling. J. Hydrol. 2018, 556, 645–659. [Google Scholar] [CrossRef]
- Massmann, C.; Holzmann, H. Analysis of the behavior of a rainfall-runoff model using three global sensitivity analysis methods evaluated at different temporal scales. J. Hydrol. 2012, 475, 97–110. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ sensitivity analysis of a complex environmental model. Environ. Modell. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]
- Rakovec, O.; Hill, M.C.; Clark, M.P.; Weerts, A.H.; Teuling, A.J.; Uijlenhoet, R. Distributed evaluation of local sensitivity analysis (DELSA), with application to hydrologic models. Water Resour. Res. 2014, 50, 409–426. [Google Scholar] [CrossRef]
- Sarrazin, F.; Pianosi, F.; Wagener, T. Global sensitivity analysis of environmental models: Convergence and validation. Environ. Modell. Softw. 2016, 79, 135–152. [Google Scholar] [CrossRef]
- Shin, M.-J.; Kim, C.S. Assessment of the suitability of rainfall-runoff models by coupling performance statistics and sensitivity analysis. Hydrol. Res. 2017, 48, 1192–1213. [Google Scholar] [CrossRef]
- Saltelli, A.; Chan, K.; Scott, E.M. Sensitivity Analysis; Wiley: New York, NJ, USA, 2008. [Google Scholar]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis? Environ. Modell. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Shin, M.-J.; Guillaume, J.H.A.; Croke, B.F.W.; Jakeman, A.J. Addressing ten questions about conceptual rainfall-runoff models with global sensitivity analyses in R. J. Hydrol. 2013, 503, 135–152. [Google Scholar] [CrossRef]
- Pujol, G.; Iooss, B.; Janon, A. Package ‘sensitivity’: Sensitivity Analysis. R package version 1.15.2. 2018. Available online: http://cran.r-project.org/package=sensitivity (accessed on 2 September 2018).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I––A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Oudin, L.; Andr-assian, V.; Mathevet, T.; Perrin, C.; Michel, C. Dynamic averaging of rainfall-runoff model simulations from complementary model parameterizations. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Mathevet, T.; Michel, C.; Andréassian, V.; Perrin, C. A Bounded Version of the Nash-Sutcliffe Criterion for Better Model Assessment on Large Sets of Basins. In Large Sample Basin Experiments for Hydrological Model Parameterization: Results of the Model Parameter Experiment—MOPEX; IAHS (International Association of Hydrological Sciences) Publications: London, UK, 2006; Volume 307, pp. 211–219. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).