Sensitivity of Model-Based Water Balance to Low Impact Development Parameters
Abstract
1. Introduction
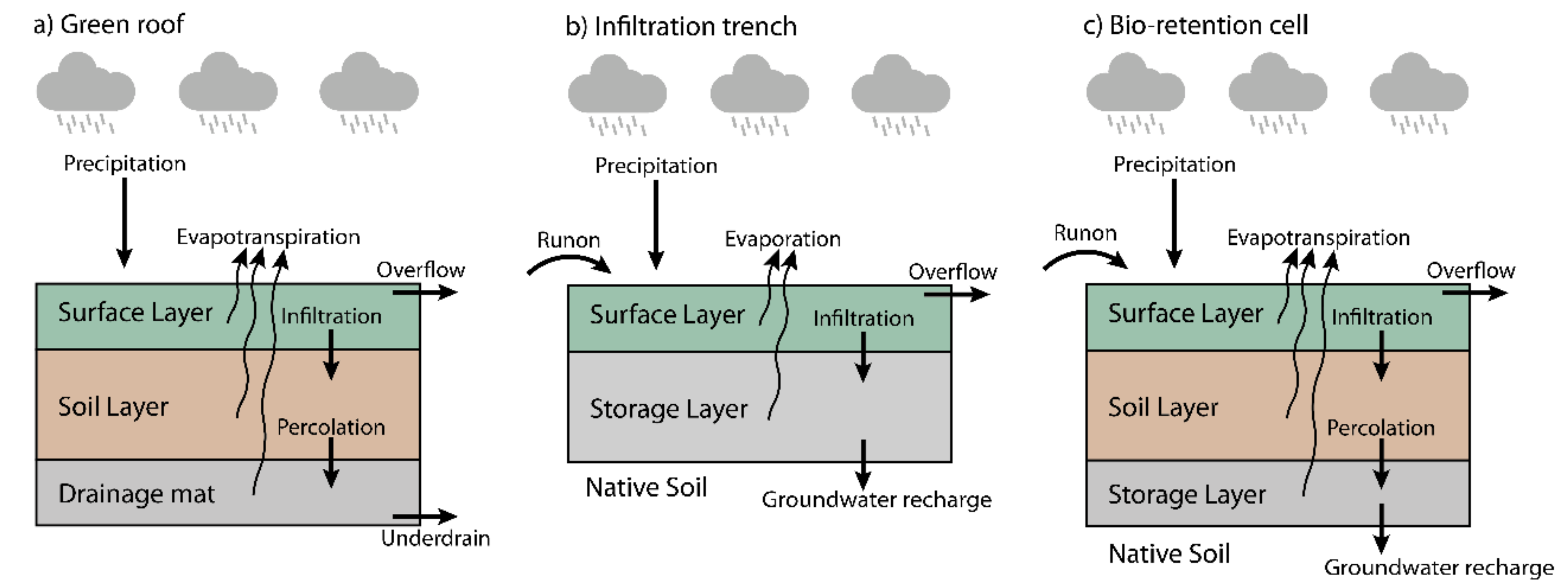
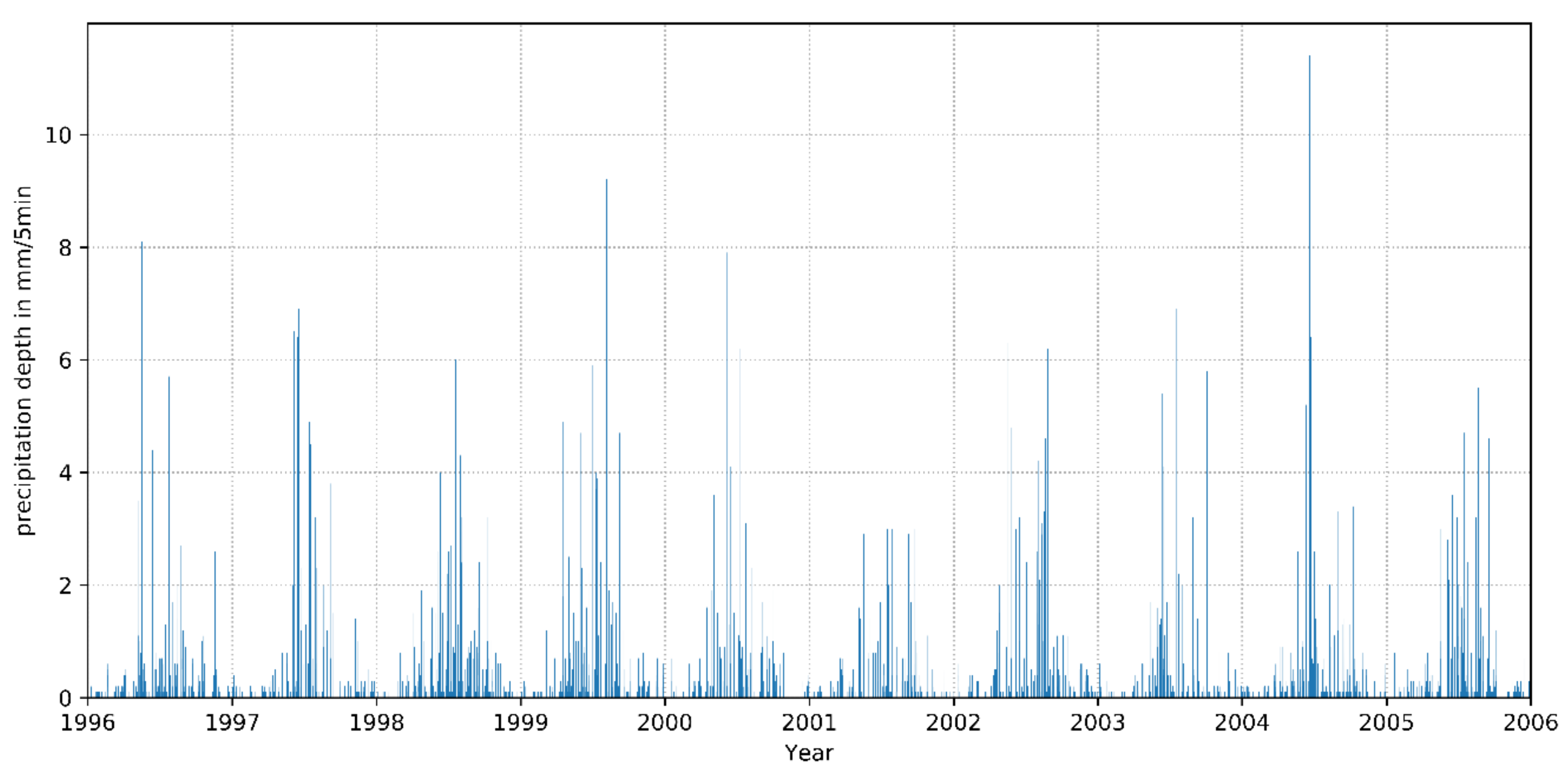
2. Materials and Methods
3. Results and Discussion
3.1. Long-Term Results
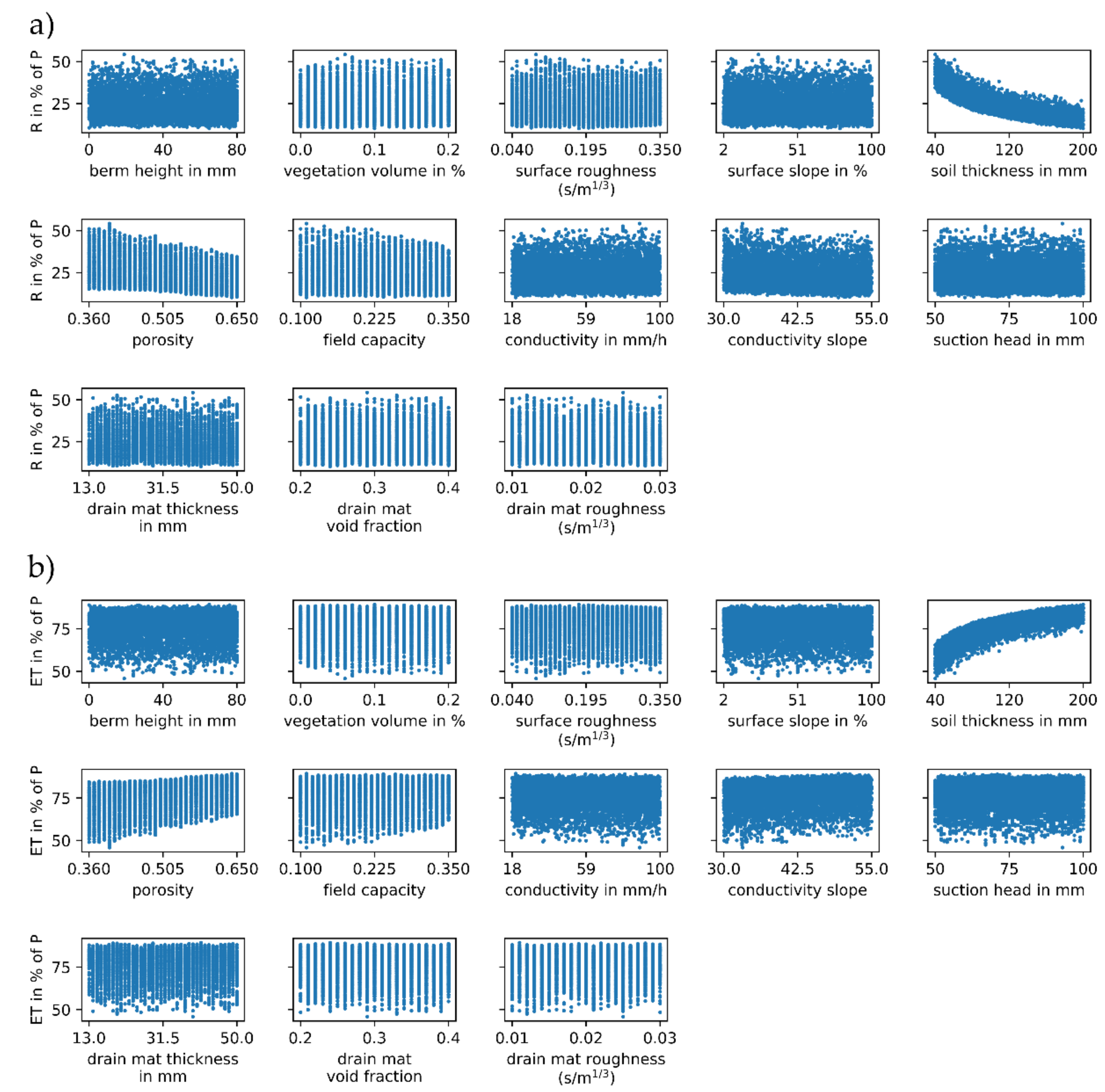
3.1.1. Green Roof
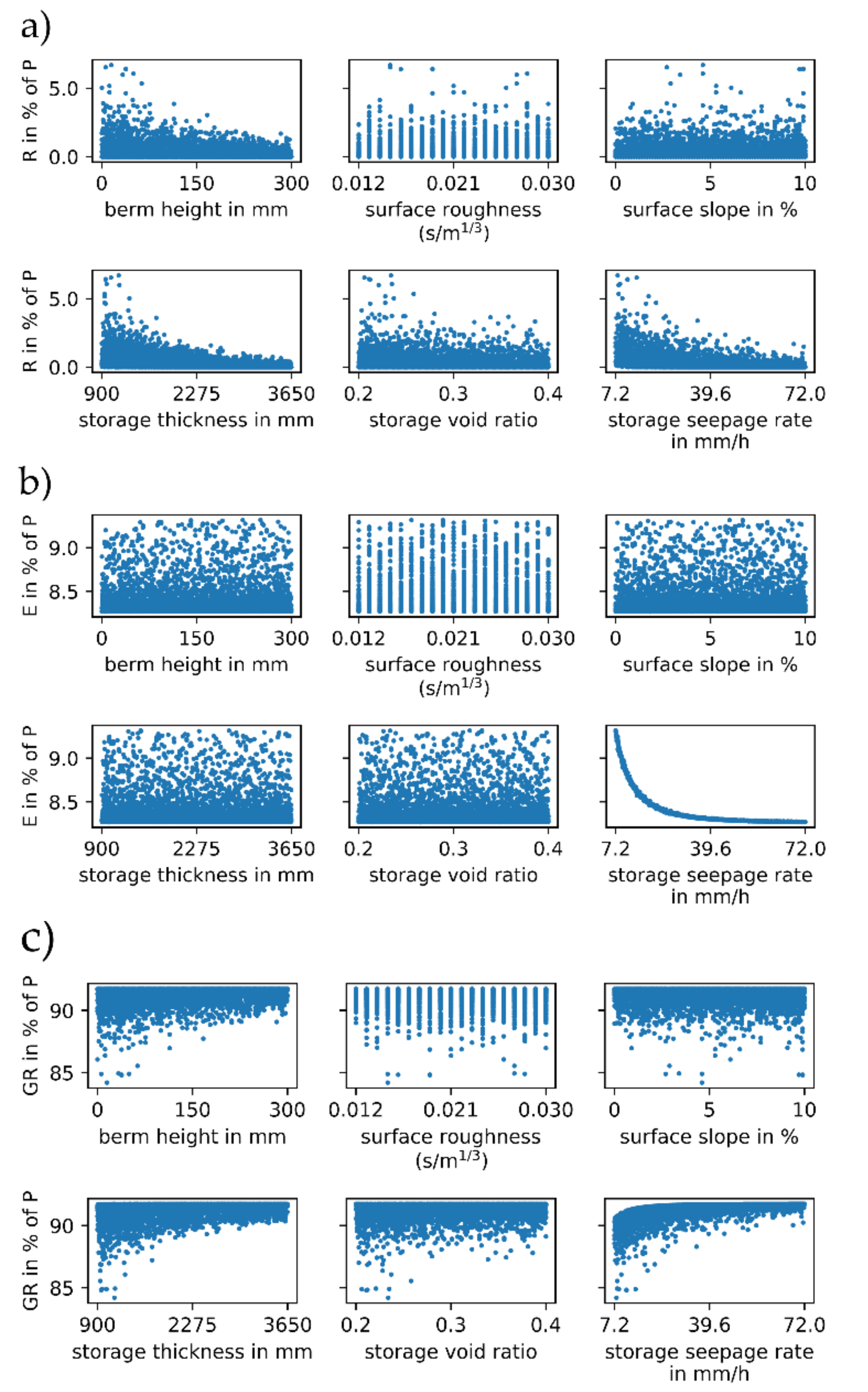
3.1.2. Infiltration Trench
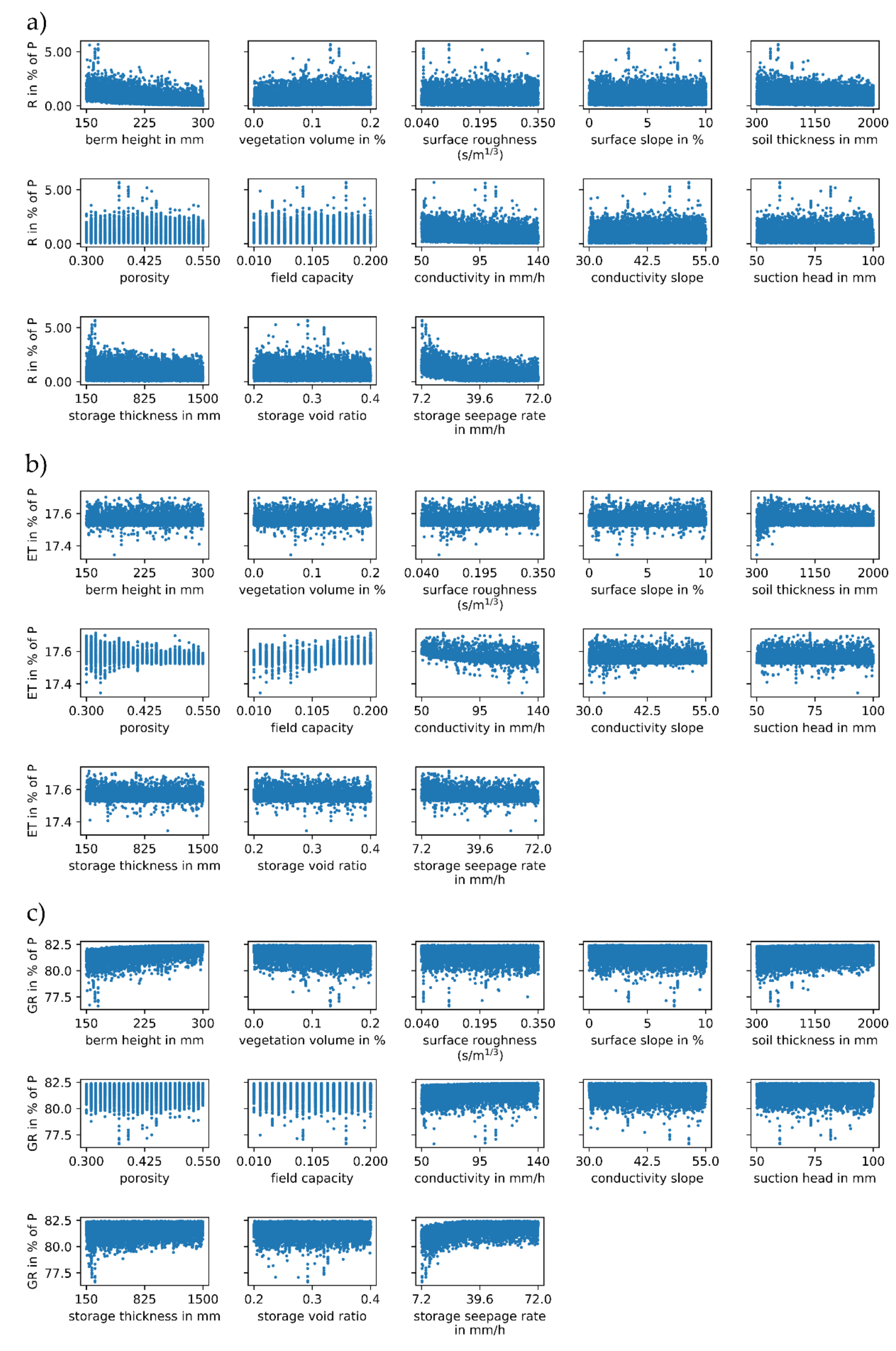
3.1.3. Bio-Retention Cell
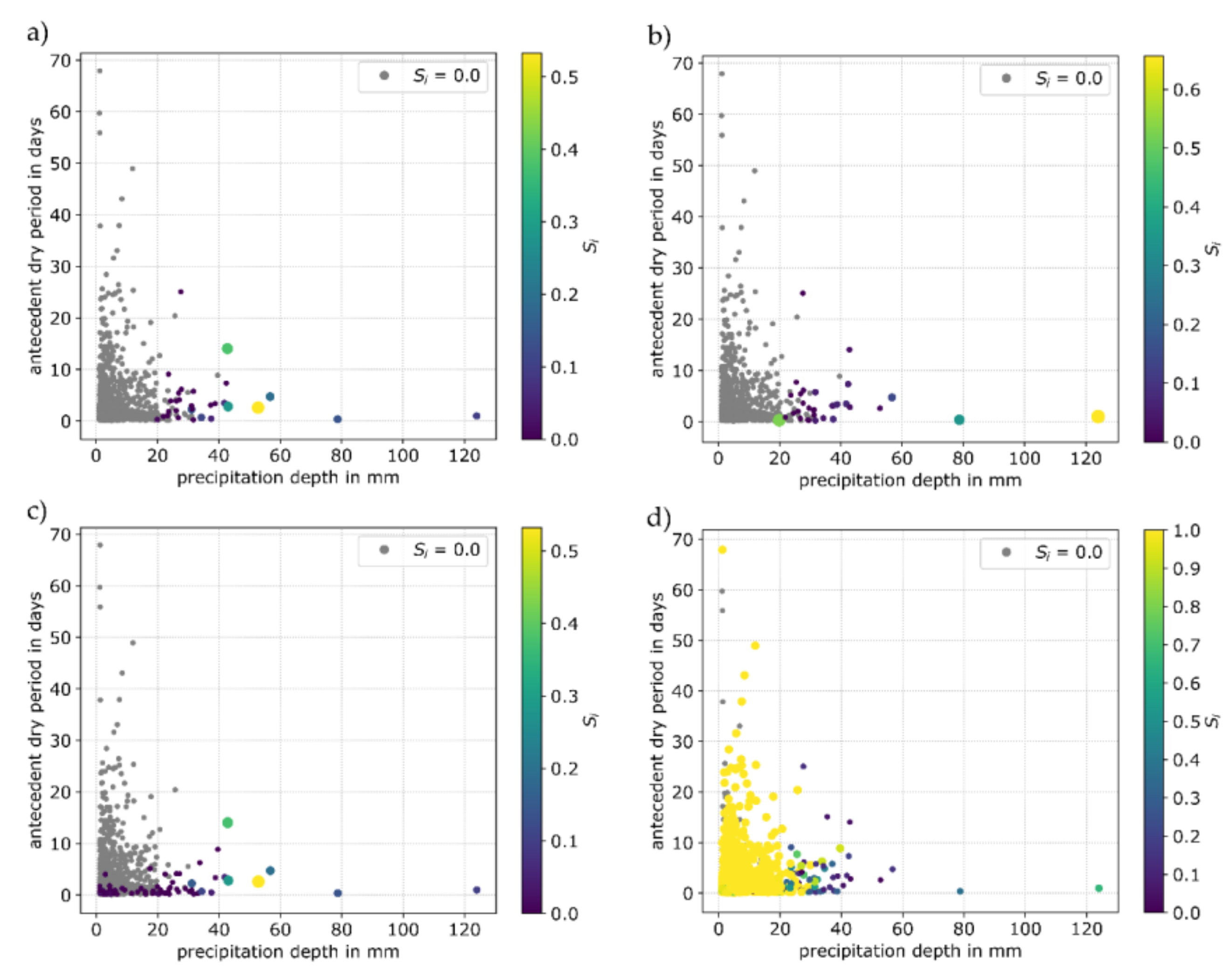
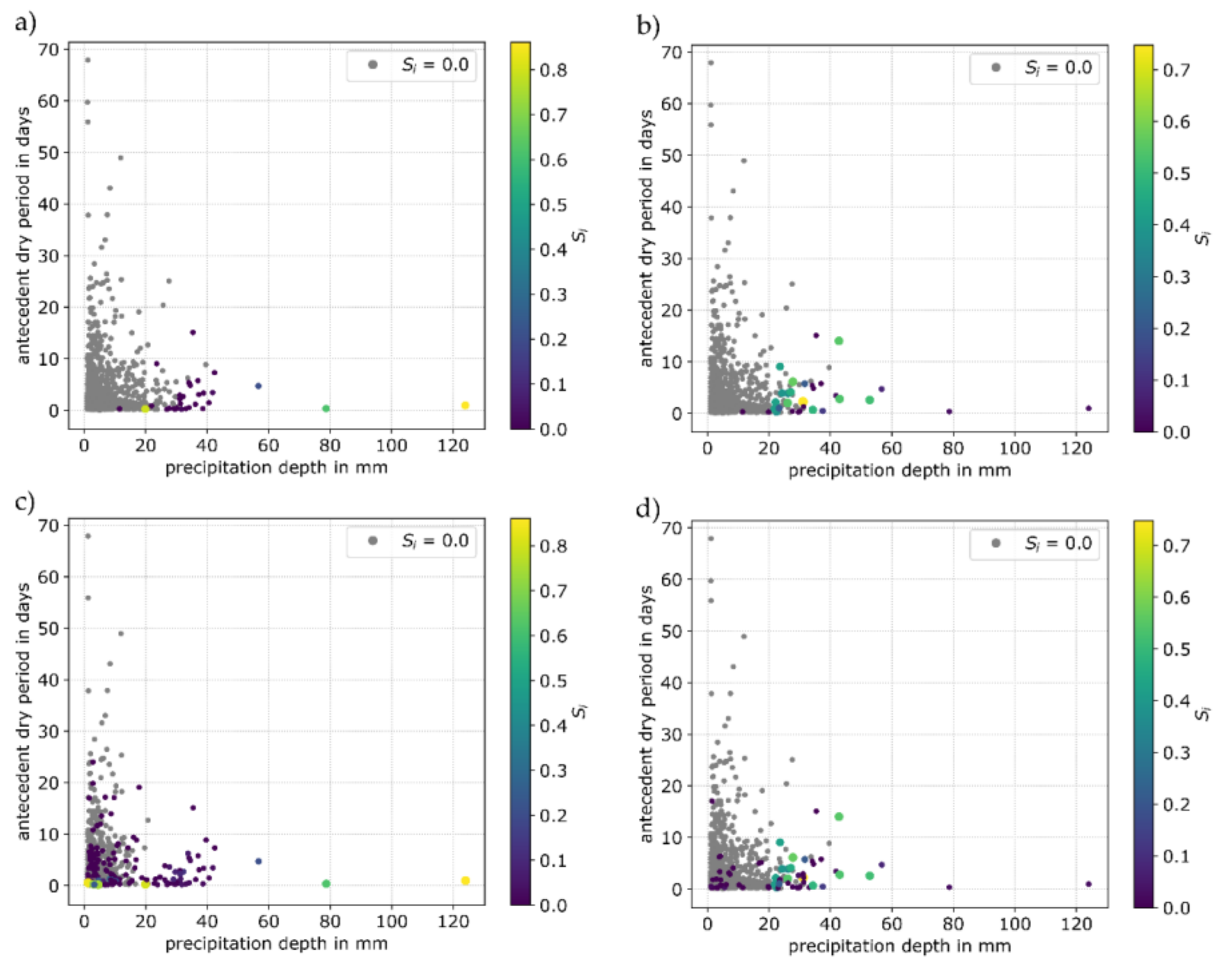
3.2. Storm Event-Based Results
3.2.1. Green Roof
3.2.2. Infiltration Trench
3.2.3. Bio-Retention Cell
3.3. General Discussion
4. Conclusions
- There were nine parameters for the green roof (berm height, vegetation volume, surface roughness, surface slope, conductivity, suction head, drainage mat thickness, drainage mat void fraction, drainage mat roughness),
- There were two parameters for the infiltration trench (surface roughness, surface slope), and
- There were three parameters for the bio-retention cell (surface roughness, surface slope, suction head).
- Soil thickness for green roof volume and evapotranspiration,
- Storage seepage rate for the complete water balance of the infiltration trench as well as for the bio-retention cell runoff volume and groundwater recharge, and
- Conductivity for bio-retention cell evapotranspiration.
Author Contributions
Funding
Conflicts of Interest
References
- Shuster, W.D.; Bonta, J.; Thurston, H.; Warnemuende, E.; Smith, D.R. Impacts of impervious surface on watershed hydrology: A review. Urban Water J. 2005, 2, 263–275. [Google Scholar] [CrossRef]
- Cheng, S.J.; Wang, R.Y. An approach for evaluating the hydrological effects of urbanization and its application. Hydrol. Process. 2002, 16, 1403–1418. [Google Scholar] [CrossRef]
- Haase, D. Effects of urbanisation on the water balance—A long-term trajectory. Environ. Impact Assess. Rev. 2009, 29, 211–219. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters: A state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- US EPA. Low Impact Development (LID)—A Literature Review; US EPA Office of Water (4203): Washington, DC, USA, 2000.
- Eckart, K.; McPhee, Z.; Bolisetti, T. Performance and implementation of low impact development—A review. Sci. Total Environ. 2017, 607, 413–432. [Google Scholar] [CrossRef] [PubMed]
- Ahiablame, L.M.; Engel, B.A.; Chaubey, I. Effectiveness of low impact development practices: Literature review and suggestions for future research. Water Air Soil Pollut. 2012, 223, 4253–4273. [Google Scholar] [CrossRef]
- Coffman, L. Low-Impact Development Design Strategies, an Integrated Design Approach; Department of Environmental Resources, Programs and Planning Division: Prince George’s County, MD, USA, 2000.
- DWA. Arbeitsblatt DWA-A 138—Planung, Bau und Betrieb von Anlagen zur Versickerung von Niederschlagswasser; Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall e.V.: Hennef, Germany, 2005. [Google Scholar]
- Austrian Standards Institute. ÖNORM B 2506-1: Regenwasser-Sickeranlagen für Abläufe von Dachflächen und Befestigten Flächen—Teil 1: Anwendung, Hydraulische Bemessung, Bau und Betrieb; ON: Vienna, Austria, 2013. [Google Scholar]
- Goebel, P.; Coldewey, W.G.; Dierkes, C.; Kories, H.; Meßer, J.; Meißner, E. Impacts of green roofs and rain water use on the water balance and groundwater levels in urban areas. Grundwasser 2007, 12, 189–200. [Google Scholar] [CrossRef]
- Henrichs, M.; Langner, J.; Uhl, M. Development of a simplified urban water balance model (WABILA). Water Sci. Technol. 2016, 73, 1785–1795. [Google Scholar] [CrossRef]
- Eger, C.G.; Chandler, D.G.; Driscoll, C.T. Hydrologic processes that govern stormwater infrastructure behaviour. Hydrol. Process. 2017, 31, 4492–4506. [Google Scholar] [CrossRef]
- Feng, Y.; Burian, S.; Pomeroy, C. Potential of green infrastructure to restore predevelopment water budget of a semi-arid urban catchment. J. Hydrol. 2016, 542, 744–755. [Google Scholar] [CrossRef]
- Jayasooriya, V.M.; Ng, A.W.M. Tools for Modeling of Stormwater Management and Economics of Green Infrastructure Practices: A Review. Water Air Soil Pollut. 2014, 225, 2055. [Google Scholar] [CrossRef]
- Rossman, L. Storm Water Management Model—User’s Manual Version 5.1; US EPA National Risk Management Research Laboratory: Cincinnati, OH, USA, 2015. [Google Scholar]
- Yang, J.; Wang, Z.-H. Physical parameterization and sensitivity of urban hydrological models: Application to green roof systems. Build. Environ. 2014, 75, 250–263. [Google Scholar] [CrossRef]
- Krebs, G.; Kuoppamäki, K.; Kokkonen, T.; Koivusalo, H. Simulation of green roof test bed runoff. Hydrol. Process. 2016, 30, 250–262. [Google Scholar] [CrossRef]
- Palermo, S.A.; Zischg, J.; Sitzenfrei, R.; Rauch, W.; Piro, P. Parameter Sensitivity of a Microscale Hydrodynamic Model. Green Energy Technol. 2018. [Google Scholar] [CrossRef]
- Song, J.-Y.; Chung, E.-S.; Kim, S.H. Decision Support System for the Design and Planning of Low-Impact Development Practices: The Case of Seoul. Water 2018, 10, 146. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P. How to avoid perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
- Rossman, L.A.; Huber, W.C. Storm Water Management Model Reference Manual Volume III—Water Quality; US EPA National Risk Management Research Laboratory: Cincinnati, OH, USA, 2016.
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis. The Primer; John Wiley & Sons, Ltd.: Chichester, UK, 2007; ISBN 978-0-470-72518-4. [Google Scholar]
- Saltelli, A.; Ratto, M.; Tarantola, S.; Campolongo, F. Sensitivity Analysis for Chemical Models. Chem. Rev. 2005, 105, 2811–2827. [Google Scholar] [CrossRef]
- Sobol, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Herman, J.; Usher, W. SALib: An open-source Python library for Sensitivity Analysis. Available online: http://joss.theoj.org (accessed on 1 March 2018).
- Saltelli, A. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Sobol, I.M. Uniformly distributed sequences with an additional uniform property. USSR Comput. Math. Math. Phys. 1976, 16, 236–242. [Google Scholar] [CrossRef]
- OEWAV. ÖWAV—Leitfaden—Niederschlagsdaten zur Anwendung der ÖWAV-Regelblätter 11 und 19; Österreichischer Wasser- und Abfallwirtschaftsverband: Vienna, Austria, 2007. [Google Scholar]
- ZAMG Jahrbuch—ZAMG. Available online: https://www.zamg.ac.at/cms/de/klima/klimauebersichten/jahrbuch (accessed on 28 November 2017).
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Leimgruber, J.; Steffelbauer, D.B.; Krebs, G.; Tscheikner-Gratl, F.; Muschalla, D. Selecting a series of storm events for a model-based assessment of combined sewer overflows. Urban Water J. 2018, 15, 453–460. [Google Scholar] [CrossRef]
- Rossman, L.A.; Huber, W.C. Storm Water Management Model Reference Manual Volume I—Hydrology; US EPA National Risk Management Research Laboratory: Cincinnati, OH, USA, 2016.
- FLL. Dachbegrünungsrichtlinie—Richtlinie für die Planung Ausführung und Pflege von Dachbegrünungen; Forschungsgesellschaft Landschaftsentwicklung und Landschaftsbau e.V.: Bonn, Germany, 2008. [Google Scholar]
- Sieker, F.; Adams, R.; Huhn, V.; Stecker, A. Naturnahe Regenwasserbewirtschaftung in Siedlungsgebieten—Grundlagen, Leitfaden und Anwendungsbeispiele; Expert Verlag: Renningen, Malmsheim, 1996. [Google Scholar]
- Feng, Y.; Burian, S. Improving Evapotranspiration Mechanisms in the U.S. Environmental Protection Agency’s Storm Water Management Model. J. Hydrol. Eng. 2016, 21, 06016007. [Google Scholar] [CrossRef]
- Palla, A.; Lanza, L.G.; La Barbera, P. A Green Roof Experimental Site in the Mediterranean Climate. In Proceedings of the 11th International Conference on Urban Drainage (ICUD), Edinburgh, UK, 31 August–5 September 2008; pp. 1–10. [Google Scholar]
- Kasmin, H.; Stovin, V.R.; Hathway, E.A. Towards a generic rainfall-runoff model for green roofs. Water Sci. Technol. 2010, 62, 898–905. [Google Scholar] [CrossRef] [PubMed]
- Stovin, V.; Poë, S.; Berretta, C. A modelling study of long term green roof retention performance. J. Environ. Manag. 2013, 131, 206–215. [Google Scholar] [CrossRef] [PubMed]

| Green Roof | |||||
|---|---|---|---|---|---|
| Layer | Parameter | min | max | Unit | Reference |
| Surface | Berm height | 0 | 80 | mm | [22] |
| Vegetation volume | 0 | 0.2 | % | [22] | |
| Surface roughness | 0.04 | 0.35 | s/m1/3 | [33] | |
| Surface slope | 2 | 100 | % | ||
| Soil | Soil thickness (for extensive green roof) | 40 | 200 | mm | [22] |
| Porosity | 0.36 | 0.65 | - | [22,34], adapted | |
| Field capacity | 0.1 | 0.35 | - | [22,34], adapted | |
| Wilting point | 0 | - | |||
| Conductivity | 18 | 100 | mm/h | [34], adapted | |
| Conductivity slope | 30 | 55 | - | [22] | |
| Suction head | 50 | 100 | mm | [22] | |
| Drainage mat | Drainage mat thickness | 13 | 50 | mm | [22] |
| Drainage mat void fraction | 0.2 | 0.4 | - | [22] | |
| Drainage mat roughness | 0.01 | 0.03 | s/m1/3 | [22] | |
| Infiltration Trench | |||||
| Layer | Parameter | min | max | Unit | Reference |
| Surface | Berm height | 0 | 300 | mm | [22] |
| Vegetation volume | 0 | ||||
| Surface roughness | 0.012 | 0.03 | s/m1/3 | [22] | |
| Surface slope | 0 | 10 | % | ||
| Storage | Storage thickness | 900 | 3650 | mm | [22] |
| Storage void ratio | 0.2 | 0.4 | - | [22] | |
| Storage seepage rate | 7.2 | 72 | mm/h | [35] | |
| Bio-Retention Cell | |||||
| Layer | Parameter | min | max | Unit | Reference |
| Surface | Berm height | 150 | 300 | mm | [22] |
| Vegetation volume | 0 | 0.2 | fraction | [22] | |
| Surface roughness | 0.04 | 0.35 | s/m1/3 | [33] | |
| Surface slope | 0 | 10 | % | ||
| Soil | Soil thickness | 300 | 2000 | mm | [33] |
| Porosity | 0.3 | 0.55 | - | [33] | |
| Field capacity | 0.01 | 0.2 | - | [33] | |
| Wilting point | 0 | - | |||
| Conductivity | 50 | 140 | mm/h | [33] | |
| Conductivity slope | 30 | 55 | - | [33] | |
| Suction head | 50 | 100 | mm | [33] | |
| Storage | Storage thickness | 150 | 1500 | mm | [33] |
| Storage void fraction | 0.2 | 0.4 | - | [33] | |
| Storage seepage rate | 7.2 | 72 | mm/h | [35] | |
| Runoff Volume | Evapotranspiration | |||
|---|---|---|---|---|
| Parameter | Si | STi | Si | STi |
| Berm height | 0.000 | 0.000 | 0.000 | 0.000 |
| Vegetation volume | 0.000 | 0.000 | 0.000 | 0.000 |
| Surface roughness | 0.000 | 0.000 | 0.000 | 0.000 |
| Surface slope | 0.000 | 0.000 | 0.000 | 0.000 |
| Soil thickness | 0.795 | 0.804 | 0.798 | 0.807 |
| Porosity | 0.168 | 0.188 | 0.166 | 0.186 |
| Field capacity | 0.003 | 0.030 | 0.003 | 0.030 |
| Conductivity | 0.001 | 0.004 | 0.001 | 0.004 |
| Conductivity slope | 0.022 | 0.024 | 0.021 | 0.023 |
| Suction head | 0.000 | 0.000 | 0.000 | 0.000 |
| Drainage mat thickness | 0.000 | 0.000 | 0.000 | 0.000 |
| Drainage mat void fraction | 0.000 | 0.000 | 0.000 | 0.000 |
| Drainage mat roughness | 0.000 | 0.000 | 0.000 | 0.000 |
| Runoff Volume | Evaporation | Groundwater Recharge | ||||
|---|---|---|---|---|---|---|
| Parameter | Si | STi | Si | STi | Si | STi |
| Berm height | 0.039 | 0.248 | 0.001 | 0.000 | 0.015 | 0.161 |
| Surface roughness | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Surface slope | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Storage thickness | 0.216 | 0.552 | 0.001 | 0.000 | 0.137 | 0.369 |
| Storage void ratio | 0.022 | 0.094 | 0.000 | 0.000 | 0.013 | 0.063 |
| Storage seepage rate | 0.285 | 0.465 | 0.999 | 1.000 | 0.533 | 0.642 |
| Runoff Volume | Evapo-Transpiration | Groundwater Recharge | ||||
|---|---|---|---|---|---|---|
| Parameter | Si | STi | Si | STi | Si | STi |
| Berm height | 0.296 | 0.336 | 0.000 | 0.000 | 0.282 | 0.319 |
| Vegetation volume | 0.026 | 0.032 | 0.000 | 0.000 | 0.025 | 0.030 |
| Surface roughness | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Surface slope | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Soil thickness | 0.052 | 0.081 | 0.009 | 0.134 | 0.051 | 0.083 |
| Porosity | 0.005 | 0.006 | 0.079 | 0.334 | 0.005 | 0.008 |
| Field capacity | 0.000 | 0.000 | 0.090 | 0.312 | 0.002 | 0.001 |
| Conductivity | 0.128 | 0.160 | 0.356 | 0.378 | 0.141 | 0.173 |
| Conductivity slope | 0.003 | 0.008 | 0.016 | 0.096 | 0.003 | 0.008 |
| Suction head | 0.002 | 0.001 | 0.005 | 0.004 | 0.003 | 0.001 |
| Storage thickness | 0.024 | 0.084 | 0.026 | 0.072 | 0.026 | 0.087 |
| Storage void ratio | 0.000 | 0.006 | 0.004 | 0.004 | 0.001 | 0.006 |
| Storage seepage rate | 0.348 | 0.420 | 0.055 | 0.111 | 0.345 | 0.419 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leimgruber, J.; Krebs, G.; Camhy, D.; Muschalla, D. Sensitivity of Model-Based Water Balance to Low Impact Development Parameters. Water 2018, 10, 1838. https://doi.org/10.3390/w10121838
Leimgruber J, Krebs G, Camhy D, Muschalla D. Sensitivity of Model-Based Water Balance to Low Impact Development Parameters. Water. 2018; 10(12):1838. https://doi.org/10.3390/w10121838
Chicago/Turabian StyleLeimgruber, Johannes, Gerald Krebs, David Camhy, and Dirk Muschalla. 2018. "Sensitivity of Model-Based Water Balance to Low Impact Development Parameters" Water 10, no. 12: 1838. https://doi.org/10.3390/w10121838
APA StyleLeimgruber, J., Krebs, G., Camhy, D., & Muschalla, D. (2018). Sensitivity of Model-Based Water Balance to Low Impact Development Parameters. Water, 10(12), 1838. https://doi.org/10.3390/w10121838






