Abstract
Coastal and hydraulic structures, such as revetments, embankments and levees—as well as their underlying soil—may experience piping when exposed to outward pressure gradients. The aim of the present study is twofold: (1) to derive the force-balance equation for soils with a sloping surface exposed to a steady hydraulic gradient (relevant to hydraulic structures) and to seek a criterion for piping, including the friction terms; (2) to study the case of unsteady hydraulic gradient forcing (relevant to coastal structures) by means of a series of experiments. The derived force-balance equation is compared with the available experimental and numerical model data from the literature and extended to soils protected by a filter/armour layer or rip rap. The experiments conducted to study the mechanism of piping under unsteady hydraulic gradients involved two types of loadings; sudden and oscillatory. The results show that although the mechanism of steady and unsteady piping has some similar aspects, the soil is generally more prone to piping in the unsteady hydraulic loading compared to the steady case, attributed to the inertia terms. The hydraulic conductivity of the soil becomes more distinctive for the unsteady piping case. Finally, remarks are made about practical applications.
1. Introduction
Coastal and hydraulic structures continuously experience static and dynamic fluid forces. One of the most common and significant forms of hydraulic loadings for coastal and hydraulic structures is the steady or unsteady pressure gradient (hydraulic slope) acting normal to the structure boundary (if the structure is porous), as well as the foundation soil. Hydraulic structures with an earth-fill core such as embankments, levees or dams are subjected to steady hydraulic slopes due to the water level differences between their sides. When the hydraulic slope reaches above a critical value, water forces its way through the soil such that a mixture of water and soil grains drains away in the form of capillary streamtubes. This phenomenon, known as piping, causes the loss of fines from the soil and eventually the failure of the structure. Many such failures of hydraulic structures are reported in the literature. Richards and Reddy [1] compiled more than 250 cases of piping (or related) failures of hydraulic structures.
Piping can be defined as a form of concentrated migration of fine granular material through very small canals caused by pore water flow or seepage driven by a hydraulic slope [2]. Tomlinson and Vaid [3] defines piping as the free movement of soil base particles through a granular filter, if such a filter layer exists. As stated above, not only structures exposed to steady hydraulic slopes (i.e., water-retaining structures such as a cofferdam, dyke or dam) but also structures exposed to unsteady (oscillatory, sudden, rapidly-increasing, etc.) pressure gradients due to wave or tide action may experience piping failure if proper filtering measures are not taken. Filter layer, which is responsible for prevention of fine material to be lost out through the larger units of the outer (filter) layer, must be designed in compliance with the gradation of the base material. The so-called “filter criteria” ensure two things: (1) drainage of pore-water through pores of filter layer must be easy so that pressure can be dissipated easily; (2) the gradation of the filter layer must be in proportion with the gradation of the base material so that sufficient amount of friction is generated; and (3) the pore sizes of filter layer must not be too large, not to let fine base material to pass through. The following relations institute these criteria [2]:
Here is the grain size which is 15% finer than the entire gradation. The subscript b represents base material and subscript f represents the filter material. The given set of filter criteria in Equations (1)–(4) is usually attributed to Terzaghi [4]. Although these criteria are very helpful for designing filter layers, they may not always be sufficient to ensure a well-performing filter layer. De Graauw et al. [5] performed an extensive set of experiments and parametrically tested the performance of different filter layer configurations under different magnitudes of hydraulic slopes parallel and perpendicular to filter layer-base material interface. They conducted the experiments for horizontally-laid filters under steady and oscillatory pore-water pressure gradients (hydraulic slopes). They enlisted a set of additional criteria for gradation, particle size and porosity of filter material, which has been very insightful for those designing filter layers for hydraulic and coastal structures such as rubble-mound structures, revetment slopes, rip-rap protection or scour protection of monopile foundations [6]. However, de Graauw et al. [5] did not set any specific criteria for the minimum necessary thickness of filter layers. In fact, although the first studies of piping in hydraulic structures date back to 1910 [1], very few studies so far directly dealt with the determination of the minimum thickness of the filter or cover layers so that no piping occurs. The seminal study of Tomlinson and Vaid [3] investigated the effect of filter thickness under constant confining pressure and showed that piping occurred under a much lower critical hydraulic slope (pressure gradient) in the case of a thin filter. Ojha et al. [7] carried out a theoretical analysis to suggest a criterion for piping that includes particle size, porosity and hydraulic conductivity, without the presence of a granular filter. Shamy and Aydin [8] numerically modelled the piping phenomenon under a river levee. Later on, Abdelhamid and Shamy [9] extended this model to simulate the migration of base material (piping) through a granular filter. More recently, Ko and Kang [10] experimentally tested the use of biopolymers for soil reinforcement against piping.
Piping against gravity (upward piping) is mostly the critical case for hydraulic structures, since the seepage force acts to decrease the effective stresses. Sterpi [11], Jacobsen [12] and Fleshman and Rice [13] conducted piping experiments under upward-directed pressure gradients without any filter layer or confining pressure. Likewise, Tao and Tao [14] modelled upward piping under zero confining pressure and no granular filter by means of a numerical model. Recently, Kirca et al. [15] carried out an experimental research on the effect of mechanical characteristics of steel slag for resisting against piping in a breakwater core under the action of oscillatory pressure gradients and waves. In these studies, where particles were only free to move upwards, the critical hydraulic slope for piping was found to be in the range of 0.6 to 3.
Wang et al. [16,17] conducted detailed experiments to study piping behaviour of block-in-matrix type of soils (gravel and silty clay mixtures). Their setup constituted samples which underwent piping under downward directed pressure gradient. They showed that even under zero confining pressure, the critical hydraulic slope for piping was at the order of 60 to 140. The results of Tomlinson and Vaid [3] also showed that for downward piping with proper filtering the critical gradient was in the range of 10 to 70.
As can be seen, base material is generally more resistant against piping in the case of downward hydraulic slope compared to the case of upward directed hydraulic slope. The reasons for this higher resistance are; (1) the self-weight of soil column as well as the seepage force acts to increase the effective stresses and shear resistance and enhances the bridging [5]; and (2) a certain amount of base material infiltrates into the filter layer/exit pores and forms filtration zones [3,18,19]. These can be termed as the secondary resistive processes against piping failure.
When it comes to coastal structures, waves usually generate the most significant design loads. Especially for sloped structures protected by an armour layer, such as coastal slopes protected by revetments/cover layers, the continuous wave action sequence of run-up and run-down potentially invokes a number of instabilities, one of which is piping [2]. Figure 1 schematically describes such a case of hydraulic loading. The unsteady pressure gradient, which is outward-directed during the run-down stage of the wave, is known to generate critical conditions in terms of piping (Figure 1b). Piping has a chain effect since it triggers other modes of failure. Yet, piping mode of failure received relatively less attention in the literature compared to other failure modes as far as coastal structures are concerned. Sumer and Nielsen [6] and Nielsen et al. [20] studied the necessary filter layer thickness for preventing or limiting the sinking of scour protection layers of monopile foundations exposed to current and/or wave action. Their approach mostly involved the horizontal migration of base material from underneath the filter, however vertical pressure gradients were also seen to be effective in the case of waves. On the other hand, Sumer et al. [21,22] conducted experiments on sand slopes exposed to breaking solitary and plunging regular waves, in which they measured the pore-water pressure variation within the base soil during the runup and rundown stages of wave action. Their results showed that the slope is exposed to strong outward directed pore-water pressure gradients (hydraulic slopes). These gradients may reach as high as (or very close to) the submerged weight of sand which renders the sand very mobile or may even drive piping. Jensen et al. [23] conducted laboratory measurements on an idealized rubble-mound breakwater model exposed to regular waves. They investigated the outward pressure gradients generated in the core material during the wave rundown stage and showed that these pressure gradients reach to magnitudes that may affect the overall instability of the structures. Recently, Alcérreca-Huerta and Oumeraci [24] conducted a soil stability analysis beneath a slope protected by a revetment layer under breaking wave attack. They assessed the total dislocation of the soil together with the filter/protection layer (total failure of the entire soil column) and termed the phenomenon as momentary liquefaction.
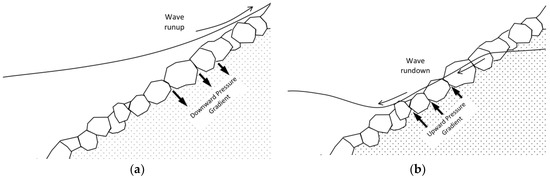
Figure 1.
The unsteady pressure gradient generated by wave action on a slope (only one layer of filter is shown to keep the figure simple): (a) Run-up stage; (b) Run-down stage (vulnerable to piping).
The purpose of the present study is to investigate the mechanism of piping under steady and unsteady hydraulic gradients. First, it is aimed at setting a physically-consistent criterion for a given soil with sloped face for determination of the critical hydraulic gradient against piping under steady conditions. For this purpose, the force-balance on the soil is derived by formulating the disturbing forces (hydraulic gradient/seepage force) and the resisting forces (self-weight and friction). The analysis is initially conducted for a sloped-face soil parcel with no filter layer and it is compared with the previous formulations. Then, it is extended to the case of base soil with sloped face protected by a granular filter layer. The performance of the formulation is tested with the available experimental and numerical data in the literature. Secondly, a series of experiments were conducted to study the mechanism of piping under unsteady hydraulic gradient, which is a relevant case especially for coastal structures. Two types of unsteady hydraulic loading were considered, sudden and oscillatory. The results are interpreted for understanding the mechanism of piping under unsteady hydraulic gradient. Finally, the results are discussed to state the similarities and differences between the steady and unsteady cases and remarks are made for practical application under the light of the present findings.
2. Unsteady Piping Experiments
2.1. Experimental Setup
The experiments were conducted in the Hydraulics Laboratory of Istanbul Technical University. A setup specially manufactured for large scale unsteady piping tests is used. The piping setup, shown in Figure 2, is composed of a fixed tank, a container tank for soil samples and a movable tank. These three plexiglas cylindrical tanks with 30 cm diameter are connected with hard plastic pipes as shown in Figure 2a. Two valves are placed on these connections as shown in the figure. The length of the container tank is 1 m and it is hinged to a support so that its tilt angle, , can be adjusted. The movable tank is controlled by a pneumatic piston and can be moved up and down along two guide rails for simulating an oscillatory pressure gradient. The head difference between the fixed tank and the movable tank is shown as on the figure.
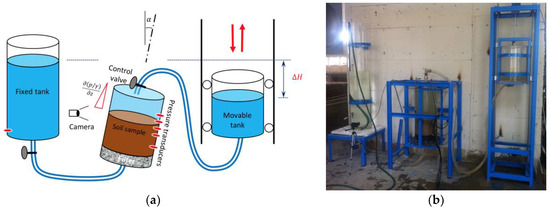
Figure 2.
The experimental setup used for in the study: (a) Sketch; (b) Photo.
Underneath the soil sample in the container tank, a 10 cm thick crushed stone filter composed of stones with size 1–2 cm is placed for facilitating even distribution of the seepage flow and the pressure gradient. Between the stone filter and the soil sample a two-layer steel grid with 40 microns openings is placed. Another steel grid with 100 microns opening is placed at the bottom of the container tank (beneath the crushed stone filter).
Five pressure transducers (Keller 0–0.2 Bar piezoelectric sensors) were placed at the side of the container tank as shown in Figure 2. The coordinates of the transducers were , , , and cm. Note that is measured downwards from the top level of the soil (as in Figure 3a). A sixth pressure transducer is placed at the bottom of the fixed tank for measuring the change in the water level when needed. The data is recorded with an NI-6210 data acquisition card with 100 Hz sampling rate per channel. A camera was placed next to the container tank which kept recording the process during the piping tests through the transparent walls of the container tank. The synchronization of the camera and the pressure measurements were made by means of a LED light connected to a battery in parallel with the data acquisition card. When the battery is triggered the LED light blinked simultaneously with a spike in one of the data channels. Three to five such blinks (or spikes) facilitated accurate synchronization of the data with the video recordings.
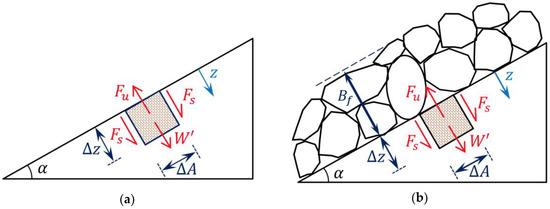
Figure 3.
Definition sketch of force-balance during piping: (a) Soil parcel without a granular filter; (b) Soil parcel underlying a granular filter with thickness .
2.2. Soil Characteristics
Three different soil types were tested against piping during the experiments. The soil parameters are given in Table 1. As seen, the soil characteristics correspond to silty fine sand, medium sand and gravel. The hydraulic conductivity values of the soils were obtained via the falling head permeameter. The angle of friction of the soils used were obtained by shear box tests for the first two type and angle of repose was measured and taken as the friction angle for the third type (gravel).

Table 1.
Characteristics of soils used in piping experiments.
2.3. Experimental Procedure
The conducted experiments, a total of 64, is listed in Table 2 below. The soil is placed in the container tank with minimum disturbance, initially with a cm thickness. During the soil placement in the container tank for the first time, the dry material is weighed for measurement of the porosity during and after the tests. Once the soil is placed, the material is very slowly saturated from bottom to top, by gradually opening the valve at the exit of the fixed tank. The saturation process took about two-three hours for the finest soil type. It was observed that the porosity of the placed soil did not change more than after the saturation, or after the tests.

Table 2.
List of unsteady piping experiments conducted.
Once the soil is fully saturated, the valve at the exit of the fixed tank is closed and the water is continued to be filled from top of the container tank via a by-pass entrance connected to the control valve. When the water in the moving tank is roughly levelled with the water in the fixed tank, the valve is gradually opened in order not to disturb the soil sample by causing premature piping. After waiting sufficiently long time to make sure that the fixed and moving tanks have exactly the same water levels, the valve at the exit of the container tank is closed.
As can be seen from Table 2, two kinds of tests are conducted: (1) sudden hydraulic loading tests; and (2) oscillatory hydraulic loading tests.
For conducting the sudden hydraulic loading tests, first the inclination of the container tank is adjusted. The head difference between the fixed tank and the movable tank, , is adjusted by lowering the head of the moving tank. The camera and the data acquisition are started and the valve at the exit of the container tank is suddenly opened. This sudden action causes a sharp upward-directed pressure gradient to take place through the soil sample, simulating a sudden hydraulic loading such as run-down phase of a wave on a slope. Observations as well as pressure measurements synchronized with the video recordings are performed to see if piping took place or not.
For conducting the oscillatory hydraulic loading test, first the valve at the exit of the container tank is opened when the fixed and movable tanks have equal water level. The distance is pre-designated on the pneumatic piston and the guide rails before the oscillatory hydraulic loading test, such that the movable tank is sinusoidally displaced between − and + with regard to the level of the fixed tank. The period of the sinusoidal motion, is also assigned. In order to simulate the storm waves on a slope, period is chosen in accord with the storm waves, such as , and s. This is an important advantage of the present experimental setup compared to the wave flume experiments, because it is not possible to scale the hydraulics of porous media by Froude modelling in standard hydraulic scale tests in flumes, which would have geometric scales generally less than 1:30, except large scale facilities which may have geometric scales go up 1:10 or more.
3. Force-Balance Equation on a Soil Element
In this section, the force-balance equation for a soil parcel (soil element composed of sediment grains and water) placed flush with the bed level is formulated under the effect of an outward directed pressure gradient. The definition sketch of the problem is given in Figure 3. To generalize the formulation for sloping faces, the surface is taken to make an angle with the horizontal. As demonstrated in Figure 3, the formulation will be derived for the two cases: (1) the slope is not protected by a filter layer; and (2) the slope is protected by a filter layer with a thickness . The former case was previously discussed in Kirca et al. [15], whereas the latter was handled in Kilci and Kirca [25].
3.1. Force-Balance Equation for a Sloped-Face Soil Parcel Without a Filter Layer
With reference to Figure 3a, the thickness of the soil element is and the cross-sectional area is , both shall be determined later. Considering the axisymmetric nature of the problem, the shape of the soil parcel is taken as cylindrical. The coordinate is downwards from the bed level and the surface has a slope of . Soil is submerged in water and fully saturated. The force-balance equation shall be derived along axis: is the bed-normal component of the submerged weight of soil, is the piping (or seepage) force generated by an upward directed pressure gradient and is the friction force between the soil element and the surrounding soil that resists against piping. For the piping failure to take place, force-balance necessitates that:
The piping force can be calculated as the volume of the soil parcel multiplied by the pressure gradient:
The submerged weight of the soil along shall be:
where is the specific gravity of sediment grains, is the specific weight of water and is the porosity of the soil parcel. Substituting Equations (6) and (7) into Equation (5) and rearranging the terms, one gets the following equation for critical hydraulic gradient for piping, , as:
Equation (8) was previously given by Kirca et al. [15]. When the friction force is zero, Equation (8) will be reduced to:
This equation becomes the well-known piping criterion for horizontal surface, , which was first introduced by Terzaghi and Peck [26].
The friction force, , can be formulated as the shear stress in the soil, , integrated over the contact surface area (lateral area) of the soil element with the surrounding soil:
in which is the perimeter of the cylindrical soil element.
The shear stress around the soil element is generated due to the normal effective stress perpendicular to the contact surface of soil element with the surrounding soil. This term can be formulated by use of the principle of shear resistance in cohesionless soil:
where is the friction angle of the soil, and are the vertical and horizontal effective stresses, respectively. The term in brackets in Equation (11) is the effective stress normal to the lateral area of soil parcel. Employing lateral coefficient of earth pressure, , , Equation (11) can be re-written as:
Note that Equation (12) will simplify to vertical friction equation for a horizontal surface where . The value of within the surrounding soil around the soil parcel marked in Figure 3a shall become the weight of overlying soil as a function of ;
whereas within the soil parcel, will be equal to the weight of the soil minus the pressure gradient force.
As the pressure gradient increases towards the instant of piping, the effective stress within the soil parcel (cf. Equation (13b)) is expected to vanish. Therefore, the friction force will be due to the effective stress within surrounding soil and the lateral earth pressure will act as an active case, . Substituting Equations (12) and (13a) into Equation (10) and integrating gives:
Finally, when Equation (15) is substituted into Equation (8), the critical hydraulic gradient for piping can be found as:
For a cylindrical soil element with height and diameter , the term will become:
It should be noted that Tao and Tao [14] derived a similar equation to Equation (17) for a flat bed, where . However, there were three distinct differences in their formulation compared to the present derivation. First, they had an extra term, , as a multiplier of the in the friction force, on the grounds that the friction is only between soil particles. However, this approach contradicts with the assumptions of soil mechanics since the angle of friction readily covers the influence of porosity [27]. Secondly, they took the lateral earth pressure coefficient in their equation as the “at rest” value () instead of the active case. The third difference was another extra term they have introduced as a multiplier to the right-hand side of Equation (17), named as the shape factor, taken from Fair et al. [28]. However, Fair et al.’s [28] approach was simply setting a hydrodynamic equation that was formulated through the seepage path in between the soil particles. Their equation was actually aimed at formulating the relation between the filtration velocity and the hydraulic gradient (or head loss). Thus, the shape factor cannot be directly used in a force-balance equation such as the present case. The shape of the grains is, again, accounted for within the internal friction angle and the porosity.
By use of the Coulomb theory [27], the active lateral earth pressure coefficient can be written for the present case as follows:
At this juncture, the dimensions of the cylindrical soil parcel that is subjected to piping, , must be discussed. The effect of ratio on critical hydraulic gradient can be demonstrated by the following numerical example. Assume a soil is given with an effective friction angle of , specific gravity of , porosity of and face slope of . For such a soil condition the variation of critical hydraulic gradient as a function of ratio is plotted in Figure 4. When , the friction force becomes zero. As can be seen from Figure 4, friction force becomes more effective when the face slope (i.e., inclination) increases. This is somewhat expected since the earth pressure acting on the lateral surfaces of the soil parcel in Figure 3a increases with the slope. This can readily be seen with the multiplier in Equation (17), which increase with .
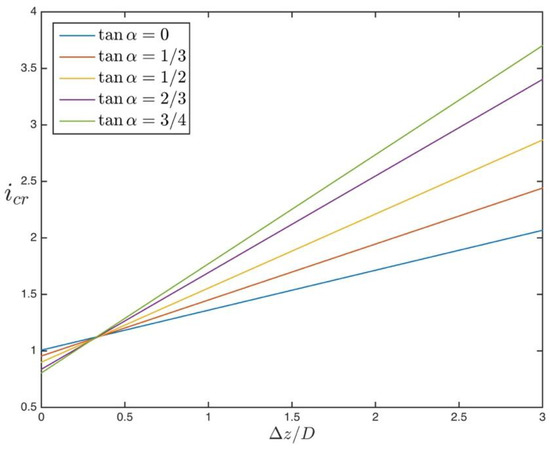
Figure 4.
Variation of the critical hydraulic gradient for piping () as a function of for different values of face slopes, cf. Equation (17). The soil parameters are , and .
3.2. Force-Balance Equation for a Sloped-Face Soil Parcel Protected by a Filter Layer
When the soil parcel is protected by a filter layer (Figure 3b), the filter layer will generate an extra overburden on the soil surface as much as = . However, we arrange the size of the soil parcel, , such that it fits the size of the intergranular pore space of the filter layer, , at the interface of contact as shown in Figure 3b. Apparently, this is the most critical case in terms of piping. As such, overburden due to the filter does not act on the soil parcel but on the neighbouring soil. Then, the effective vertical stress immediately outside the soil parcel shall be:
Since the maximum surface area of soil element exposed to piping force is dictated by the size of the pores within the grains of the filter layer, the diameter of the soil parcel will be set to the intergranular pore size of the filter layer in order to facilitate the force-balance equation against piping. Equation (5) will also be valid for the case with the filter layer, provided that Equation (19) is used instead of Equation (13) for effective stress. As a result, the critical hydraulic gradient can be found as follows:
It is particularly difficult to estimate the pore size distribution of a given granular material whose grain size distribution is known. However, a first approximation is presented here to estimate . If uniform grain size is assumed, one can reason that the number of grains per unit volume, , should be approximately equal to the number of pores in the same volume. The number of grains per unit volume of the filter layer would be
in which is the nominal spherical diameter of grains in the filter layer and is the nominal spherical diameter of the pores. From Equation (21), the nominal pore diameter in the filter grains can be approximated in terms of grain size as follows:
Yet, the approximation of uniform grain size may be misleading and the characteristic pore size must be truly dependent on the grain size distribution. As an alternative approach, Uno et al. [29] experimentally determined the mean diameter of the pores in a granular material as:
If the analysis presented in this subsection is to be repeated for a soil parcel covering a much larger area () beneath the filter, then the force balance should be formulated for the entire soil column, including not only the base soil but also the filter layer. Failure in such a situation means that the entire soil column is sucked out by the pressure gradient. Neglecting the friction forces, the critical hydraulic gradient for failure of entire soil column can be formulated as weight of the soil column counter-balanced by the hydraulic gradient:
The criterion given in Equation (24) is previously defined by Alcérreca-Huerta and Oumeraci [24]. One can see that the criterion defined in Equation (20) is more critical than the failure mechanism formulated in Equation (24), that is, .
Last but not the least, it should be emphasized that when the grain size ratio of filter to base material is smaller than a certain value (cf. Equations (2) and (3)), the resistance against piping increases very sharply due to the forming of filtration zones within the pores of filter and bridging phenomenon [3,5]. Although these effects have not been accounted for here, the filter criteria depending on the grain size ratio should not be overlooked.
4. Results
4.1. Comparison of the Steady Piping Criterion with the Available Data
In this section, the derived criterion for piping under a steady hydraulic gradient (without a filter layer, cf. Equation (17)) will be compared with the values from the literature. In order to see the performance of this criterion in estimating the critical steady hydraulic gradient for piping, two datasets are used for comparison. The first dataset is the experimental findings of Fleshman and Rice [13], whereas the second one is the numerical modelling results of Tao and Tao [14].
Fleshman and Rice [13] employed a cylindrical container with a diameter of cm and a length of cm. They have put the soil into the container in layers and compacted each layer. Once their sample is saturated they gradually increased the hydraulic gradient such that steady conditions prevail. They described piping process in a successive four stages: (1) first visible movement; (2) heave progression; (3) boil formation; and (4) total heave. Their experimental data is summarized in Table 3.

Table 3.
Summary of available data from [13,14], which shows the critical hydraulic gradient for piping in steady case.
Tao and Tao [14] conducted a numerical modelling study following a similar setup to [13] in their numerical container with spherical grains. They applied parametric changes in soil characteristics to see the sensitivity of the critical hydraulic gradient for piping. Their computational fluid dynamics numerical model was using a discrete element method (CFD-DEM) to model the behaviour of each particle. They have showed that their algorithm was capable of capturing the physics of the process. Tao and Tao [14] considered the same four stages that has been described above [13] and regarded the fourth stage (total heave) as piping. Their dataset is also enlisted in Table 3.
Figure 5 shows the comparison of the results found from Equation (17) with available data. It should be noted that the data points no. 12 and no. 16 from [14] are not included in Figure 5 since the angle of friction of those points are given as zero.
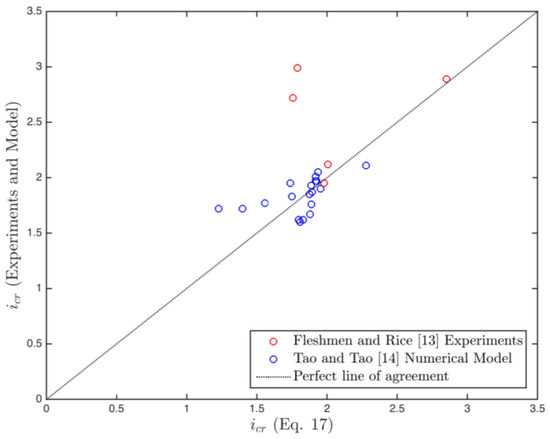
Figure 5.
Cross-plot of critical hydraulic gradient for steady flow piping; comparison of Equation (17) with experimental data from [13] and numerical model data from [14]. See Table 3 for details.
As can be seen from Figure 5, there is a fair agreement between the critical gradients predicted by Equation (17) and the data points. The discrepancy between the predicted values and the data from [14] tends to increase for small values of the angle of friction. The formulation derived tends to slightly underestimate these values. Although the reason is not clear, the secondary resistive processes (bridging, etc.) may be responsible for the discrepancy. The two data points from [13] that are the farthest from the line of agreement are data no. 3 and 4, both of which are angular grains. This point also suggests that angular grains may be more enhancing in terms of secondary resistive processes.
4.2. Experimental Findings on Unsteady Piping
Figure 6a shows the pressure time series recorded during Test No. 103, where the soil (medium sand) experienced piping under sudden hydraulic loading. This picture is typical for the sudden loading tests. Figure 6b shows the pressure profile with respect to depth at the instant when the maximum hydraulic gradient attained ( s). The hydraulic gradient is calculated from pressure measurements such as . As such the pressure gradient time series is calculated between depths 0–2 cm, 0–5 cm and 0–25 cm. This sort of a hydraulic gradient is consistent with the force balance approach defined in Section 3 above.
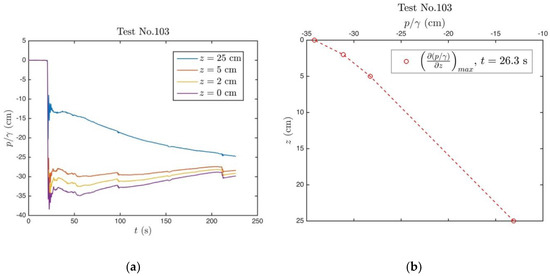
Figure 6.
(a) Pressure time series recorded at Test No. 103, sudden hydraulic loading; (b) Pressure profile with depth at the instant of maximum pressure gradient () measured, s.
The hydraulic gradient time series of Test No. 103 is presented in Figure 7. As can be seen the steepest hydraulic gradient is at the closest location to soil surface and its value is . The critical hydraulic gradient calculated with respect to Equation (17) is . Thus, piping is expected. It should be mentioned that that the friction angle between the Plexiglas side walls of the container tank and the soil inside it was taken as [27]. On the other hand, the driving pressure gradient of the sudden hydraulic loading was , where is the thickness of the soil layer. This value is incidentally larger than the measured maximum hydraulic gradient. This point shall be discussed below.
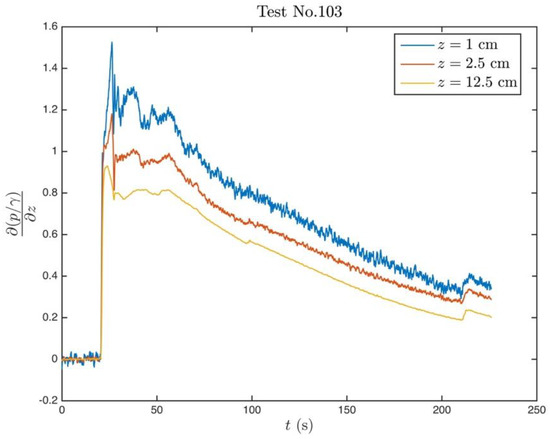
Figure 7.
Hydraulic gradient time series recorded at Test No. 103. The maximum pressure gradient is attained at s.
Figure 8a presents the pressure time series at Test No. 1003, where the soil experienced piping. As can be seen, the period of the oscillatory loading is s, a value that matches with the period of storm waves. In Figure 8b, pressure profiles at two different instants are given. When the hydraulic gradient is maximum (upward peak) and when it is minimum (downward peak). It is seen that the downward peak value of the hydraulic gradient that the soil experiences during the oscillatory loading is significantly sharper, especially close to the surface of the soil sample. Figure 9 presents the time series of the hydraulic gradient measured during Test No. 1003. The imbalance between the upward and downward peak pressure gradients are also evident from this figure. The maximum value of the upward hydraulic gradient value is , whereas the driving hydraulic gradient of the oscillatory motion was . The critical hydraulic gradient calculated with respect to Equation (17) is , whereas it is with respect to Equation (9) (when friction forces are disregarded). It is interesting to see that the soil underwent piping although the driving pressure gradient is significantly lower than the critical steady state value. It should be stressed out that this soil is silty fine sand, which has the lowest hydraulic conductivity value among the tested soils (cf. Table 1).
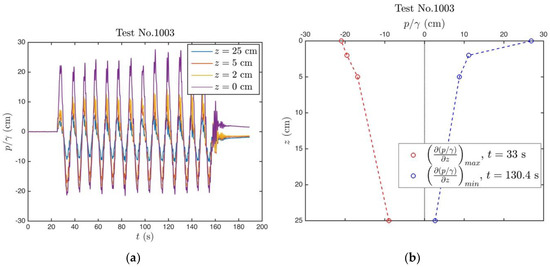
Figure 8.
(a) Pressure time series recorded at Test No. 1003, oscillatory hydraulic loading; (b) Pressure profile with depth at the instant of maximum and minimum pressure gradient () measured, s and s, respectively.
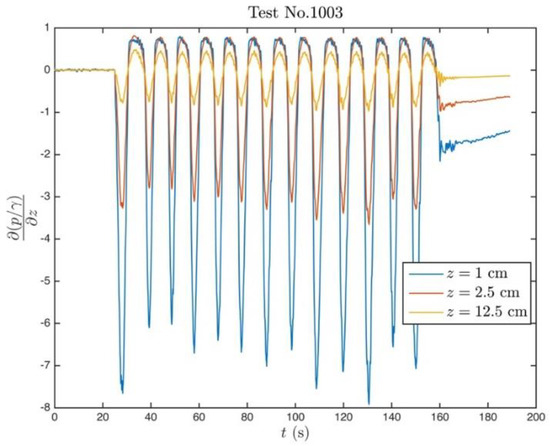
Figure 9.
Hydraulic gradient time series recorded at Test No. 1003. The maximum pressure gradient is attained at s.
Figure 10 shows the pressure and hydraulic gradient time series data from Test No. 307, sudden hydraulic loading of the gravel. As can be seen the resulting maximum hydraulic gradient is around although the driving pressure gradient was . This significant difference is due to the high hydraulic conductivity of the gravel which dissipates the driving pressure gradient very quickly. Thus, the soil is not subjected to a sufficiently high pressure gradient to initiate piping. As can be seen from Table 2, it was not possible to initiate piping in gravel, neither in sudden loading nor the oscillatory loading cases.
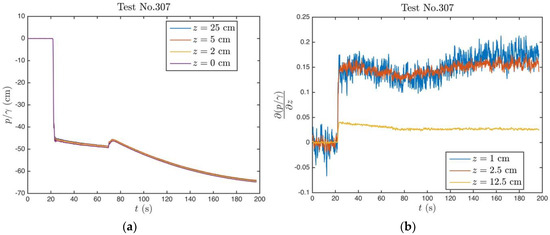
Figure 10.
Data from Test No. 307 (a) Pressure time series; (b) Hydraulic gradient time series.
In order to observe the relationship between the driving hydraulic gradient and the hydraulic gradient experienced by the soil, these two values are cross-plotted for each set of data. Figure 11 presents the data for medium sand with and silty fine sand with . On these figures, the critical hydraulic gradient for steady piping estimated by Equations (9) and (17) are also shown on both axes. The data points where piping is encountered are plotted with red markers. With respect to Figure 11a, the piping criterion estimated with Equation (17) seems to capture the piping limit but this does not hold for silty fine sand data in Figure 11b. The general behaviour is that the data points in Figure 11 align close to the line of agreement for small values, in other words the pressure gradient generated within the soil is close to the value of the driving pressure gradient for low hydraulic gradient loadings. As the driving hydraulic gradient increases, the pressure dissipation within the soil increases and the hydraulic gradient experienced by the soil decreases. Generally speaking, the fine soil tested comes out to be more prone to unsteady piping, as expected. Since the hydraulic conductivity of the soil in Figure 11b is very low, the pore water cannot easily react to the driving pressure gradient by flowing through the soil grains. Consequently, the inertia of the pore water triggers piping. This is one of the main differences between steady and unsteady piping, such that the inertia terms become effective in the unsteady case. It is also interesting to observe from both Figure 11a,b that the difference between sudden hydraulic loading and oscillatory hydraulic loading seems not to be too distinct in terms of their effect on the soil.
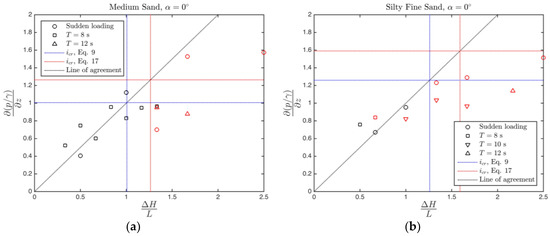
Figure 11.
Driving pressure gradient () vs. experienced maximum pressure gradient . Data points corresponding to piping are shown with red markers. (a) Tests with medium sand ; (b) Tests with silty fine sand .
Figure 12 presents the unsteady piping test data of silty fine sand for inclination angles of and . As can be seen the behavior is generally the same with the horizontal soil surface () case. Comparing the Figure 11b and Figure 12a,b it can be seen that the higher the face slope is, the more prone to piping the soil is. As the soil face gets inclined, the self-weight of the soil that resist against piping decreases. In the case given in Figure 12b, the soil experienced piping for hydraulic gradients as low as 0.5.
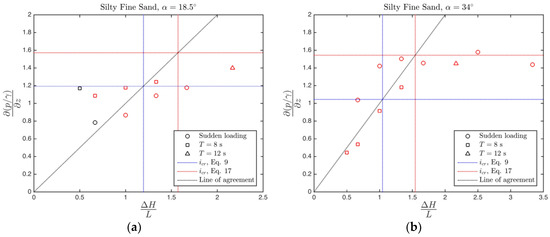
Figure 12.
Driving pressure gradient () vs. experienced maximum pressure gradient . Data points corresponding to piping are shown with red markers. Tests with silty fine sand (a) ; (b) .
The data obtained in the case of gravel is given in Figure 13a,b for inclination angles of and , respectively. As stated above, it was not possible to generate piping in the case of gravel, which has a very high hydraulic conductivity. From Figure 13, once again it is evident that sudden hydraulic loading and oscillatory hydraulic loading have almost the same effect on the soil.
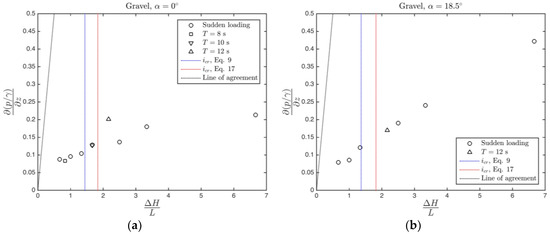
Figure 13.
Driving pressure gradient () vs. experienced maximum pressure gradient . Tests with gravel (a) ; (b) .
In Figure 13b, where the soil face is inclined, the maximum hydraulic gradient attained by the soil is almost two times larger compared to Figure 13a, the horizontal soil face. The two data points of gravel for will not be given for reasons of space but in those tests the hydraulic gradient experienced by the soil was slightly higher than the case, supporting the above statement.
5. Discussion and Remarks for Practical Applications
It has been shown that the piping behaviour of soil under steady hydraulic gradient and unsteady hydraulic gradient is quite different. In the case of steady hydraulic gradient, where the driving hydraulic gradient is constant or very gradually increasing, no inertia terms are present. But in unsteady hydraulic loading, the pore water is forced to be accelerated. Then, the hydraulic conductivity of the soil (drainage condition) becomes important for deciding how fast the pore water would react to the pressure gradient. In the latter case, a simple force balance approach would not be sufficient to come up with a correct piping criterion but a more general solution of the porous media flow equations, including the inertia terms, is needed [30].
Another mechanism that makes the soil more vulnerable to piping under unsteady hydraulic gradient is the lack of secondary resistive effects in the soil, such as bridging and filtration zones [3,4,5]. In the case of a granular filter layer that protects the soil against piping, these mechanisms become effective when a certain amount of base soil infiltrates into the filter layer. But when an unsteady (instantly increasing) hydraulic gradient is applied, the development of such secondary resistive mechanisms may not be possible before piping.
In practical applications, it is of great concern to design a proper filter layer as a countermeasure against piping. The design requirements can be enlisted as follows:
- The grain size ratio of the filter layer to the base soil must comply with the filter criteria given in Equations (1)–(4). This would ensure that the base soil will not be able to move through the grains of the filter layer without clogging the pores but the pore water can be drained easily through the filter. Hence, piping resistance would be enhanced.
- It was seen that the hydraulic conductivity is an important parameter in piping, especially when the hydraulic gradient acts unsteadily. Therefore, the selection of low hydraulic conductivity base soils (especially for coastal structures) must be omitted if possible (see also [2]).
- The thickness of the filter layer must be carefully determined. To this end, the criterion given with Equation (20) can be used to define the minimum filter layer thickness . The thickness of the base soil parcel, , can be taken as zero to omit the uncertainties and to stay on the safe side. Equations (18) and (22) can be used to determine the active lateral earth pressure coefficient () and the filter pore size (), respectively. It should be noted that the criterion for the total failure of the entire soil column given by [24] and defined in Equation (24) comes out to be less critical than the piping criterion ().
Still, there are many points yet to be enlightened by future research. Further experimental work and/or numerical modelling studies are necessary to fully reveal the mechanism of unsteady piping and to test the effect of filter layer characteristics on piping under unsteady hydraulic loading conditions.
6. Conclusions
In this study the mechanism of piping in hydraulic and coastal structures in the case of steady and unsteady hydraulic gradient was investigated. For the steady hydraulic gradient case, a force-balance equation that includes the friction terms and the inclination of soil surface is derived and the results obtained from this equation were compared with the available experimental and numerical model data from literature. To investigate the piping in the case of unsteady pressure gradient, experiments were conducted utilizing a novel experimental setup. With this setup, piping of three different kinds of soil was investigated under two different kinds of unsteady hydraulic loading; sudden loading and oscillatory loading. In order to minimize the scale effects, the value of the driving pressure gradient and the period of oscillatory hydraulic loading was chosen to reflect the field values for coastal structures, thanks to the experimental setup. The following conclusions can be drawn from this study:
- In the case of steady hydraulic loading, the comparison of the force-balance equation (Equation (17)) and the available data from the literature shows that friction forces are effective in resisting against piping. However, there are quite many uncertainties in estimating the friction forces. Therefore, it may be safer to resort to the force balance equation with zero friction (Equation (9)) for design purposes when there is no filter layer. The effect of filter layer on increasing the friction forces is formulated (Equation (20)) in terms of the filter layer thickness.
- The mechanisms of piping under steady and unsteady hydraulic loadings are quite different since the inertia terms become effective in the unsteady loading case. Generally speaking, soil is more prone to piping in the case of unsteady hydraulic loading. This was also shown by Tomlinson and Vaid [3] when they increased the hydraulic gradient in a rapid manner and got piping under a much lower hydraulic gradient compared to the gradually increasing case.
- Experimental findings showed that the period of oscillatory hydraulic loading did not have a significant effect on the results for the tested periods of loading ( s). Additionally, the sudden hydraulic loading did not generate a distinctly different effect on the soil compared to the oscillatory.
- The hydraulic conductivity of the soil becomes very important for piping vulnerability under unsteady hydraulic gradients, such that low conductivity soil was seen to be much more susceptible to piping. As the hydraulic conductivity gets higher, the soil becomes more resistant to piping under unsteady hydraulic loading. Therefore, the usage of low hydraulic conductivity soils in coastal structures must be omitted, as also suggested by the design guidelines [2].
Author Contributions
Conceptualization, formal analysis, writing V.S.O.K.; contribution to formal analysis, data curation, review & editing R.E.K.
Funding
This research received no external funding.
Acknowledgments
The support of Taylan Bagci in the execution of the experiments is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Richards, K.S.; Reddy, K.R. Critical appraisal of piping phenomena in earth dams. Bull. Eng. Geol. Environ. 2007, 66, 381–402. [Google Scholar] [CrossRef]
- CIRIA (Construction Industry Research, Information Association). The Rock Manual: The Use of Rock in Hydraulic Engineering; CIRIA Report; CIRIA: London, UK, 2007. [Google Scholar]
- Tomlinson, S.S.; Vaid, Y.P. Seepage forces and confining pressure effects on piping erosion. Can. Geotech. J. 2000, 37, 1–13. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons: New York, NY, USA, 1943; p. 510. [Google Scholar]
- de Graauw, A.F.; van der Meulen, T.; van der Does de Bye, M.R. Granular filters: Design criteria. J. Waterw. Port Coast. Ocean Eng. ASCE 1984, 110, 80–96. [Google Scholar] [CrossRef]
- Sumer, B.M.; Nielsen, A.W. Sinking failure of scour protection at wind turbine foundation. Proc. ICE-Energy 2013, 166, 170–188. [Google Scholar] [CrossRef]
- Ojha, C.S.P.; Singh, V.P.; Adrian, D.H. Determination of Critical Head in Soil Piping. J. Hydraul. Eng. 2003, 129, 511–518. [Google Scholar] [CrossRef]
- El Shamy, U.; Aydin, F. Multiscale modeling of flood-induced piping in river levees. J. Geotech. Geoenviron. Eng. 2008, 134, 1385–1398. [Google Scholar] [CrossRef]
- Abdelhamid, Y.; El Shamy, U. Pore-scale modeling of fine-particle migration in granular filters. Int. J. Geomech. 2015, 16, 04015086. [Google Scholar] [CrossRef]
- Ko, D.; Kang, J. Experimental Studies on the Stability Assessment of a Levee Using Reinforced Soil Based on a Biopolymer. Water 2018, 10, 1059. [Google Scholar] [CrossRef]
- Sterpi, D. Effects of the erosion and transport of fine particles due to seepage flow. Int. J. Geomech. 2008, 3, 111–122. [Google Scholar] [CrossRef]
- Jacobson, T. An Analysis on Soil Properties on Predicting Critical Hydraulic Gradients for Piping Progression in Sandy Soils. Master’s Thesis, Utah State University, Logan, UT, USA, 2013. [Google Scholar]
- Fleshman, M.; Rice, J. Laboratory modeling of the mechanisms of piping erosion initiation. J. Geotech. Geoenviron. Eng. 2014, 04014017. [Google Scholar] [CrossRef]
- Tao, J.; Tao, H. Factors Affecting Piping Erosion Resistance: Revisited with a Numerical Modeling Approach. Int. J. Geomech. 2017, 17, 04017097. [Google Scholar] [CrossRef]
- Kirca, V.S.O.; Caglar, B.; Bagci, T.; Kilci, E.; Kabdasli, M.S. Use of Steel Slag in Rubble-Mound Marine Structures. In Proceedings of the 3rd Iron and Steel Symposium (UDCS’17), Karabuk, Turkey, 3–5 April 2017; pp. 307–313. [Google Scholar]
- Wang, Y.; Li, C.; Zhou, X.; Wei, X. Seepage Piping Evolution Characteristics in Bimsoils-An Experimental Study. Water 2017, 9, 458. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Hu, Y.; Xiao, Y. Optimization of Multiple Seepage Piping Parameters to Maximize the Critical Hydraulic Gradient in Bimsoils. Water 2017, 9, 787. [Google Scholar] [CrossRef]
- Honjo, Y.; Veneziano, D. Improved filter criterion for cohesionless soils. J. Geotech. Eng. ASCE 1989, 115, 75–94. [Google Scholar] [CrossRef]
- Okita, Y.; Nikigaki, M. Filtration processes observed with g-ray density meter. In Filters in Geotechnical and Hydraulic Engineering; Brauns, J., Heibaum, M., Schuler, U., Eds.; A.A. Balkema: Rotterdam, The Netherlands, 1992. [Google Scholar]
- Nielsen, A.W.; Probst, T.; Petersen, T.U.; Sumer, B.M. Sinking of armour layer around a vertical cylinder exposed to waves and current. Coast. Eng. 2015, 100, 58–66. [Google Scholar] [CrossRef]
- Sumer, B.M.; Sen, M.B.; Karagali, I.; Ceren, B.; Fredsøe, J.; Sottile, M.; Zillioli, L.; Fuhrman, D.R. Flow and sediment transport induced by a plunging solitary wave. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef]
- Sumer, B.M.; Guner, H.A.; Hansen, N.M.; Fuhrman, D.R.; Fredsøe, J. Laboratory observations of flow and sediment transport induced by plunging regular waves. J. Geophys. Res. Oceans 2013, 118, 6161–6182. [Google Scholar] [CrossRef]
- Jensen, B.; Christensen, E.D.; Sumer, B.M. Pressure-induced forces and shear stresses on rubble mound breakwater armour layers in regular waves. Coast. Eng. 2014, 91, 60–75. [Google Scholar] [CrossRef]
- Alcérreca-Huerta, J.C.; Oumeraci, H. Soil stability analysis for wave-induced momentary liquefaction beneath porous bonded revetments. Coast. Eng. 2018, 138, 22–35. [Google Scholar] [CrossRef]
- Kilci, E.; Kirca, V.S.O. A Modified Piping Criterion for Determination of Effective Filter Thickness under Revetment Slopes. In Proceedings of the 13th Advances in Civil Engineering Congress, Izmir, Turkey, 12–14 September 2018. [Google Scholar]
- Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice; John Wiley & Sons: New York, NY, USA, 1948. [Google Scholar]
- Lambe, T.W.; Whitman, R.V. Soil Mechanics (SI Version); John Wiley & Sons: New York, NY, USA, 1979. [Google Scholar]
- Fair, G.M.; Hatch, L.P.; Hudson, H.E. Fundamental factors governing the streamline flow of water through sand [with discussion]. J. (Am. Water Works Assoc.) 1933, 25, 1551–1565. [Google Scholar] [CrossRef]
- Uno, T.; Kamiya, K.; Matsushima, T. The relationship between particle size and void diameter. In Proceedings of the Geofilters’96 Conference, Montreal, QC, Canada, 29–31 May 1996; pp. 67–74. [Google Scholar]
- Burcharth, H.F.; Andersen, O.K. On the one-dimensional steady and unsteady porous flow equations. Coast. Eng. 1995, 24, 233–257. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).