Using a Distributed Hydrologic Model to Improve the Green Infrastructure Parameterization Used in a Lumped Model
Abstract
1. Introduction
- Compare solutions to observations.
2. Materials and Methods
2.1. Description of Models
2.1.1. GSSHA
2.1.2. EPA-SWMM
2.2. Urban Benchmark Case Study: Green Infrastructure
2.3. Idealized Benchmark Test Cases
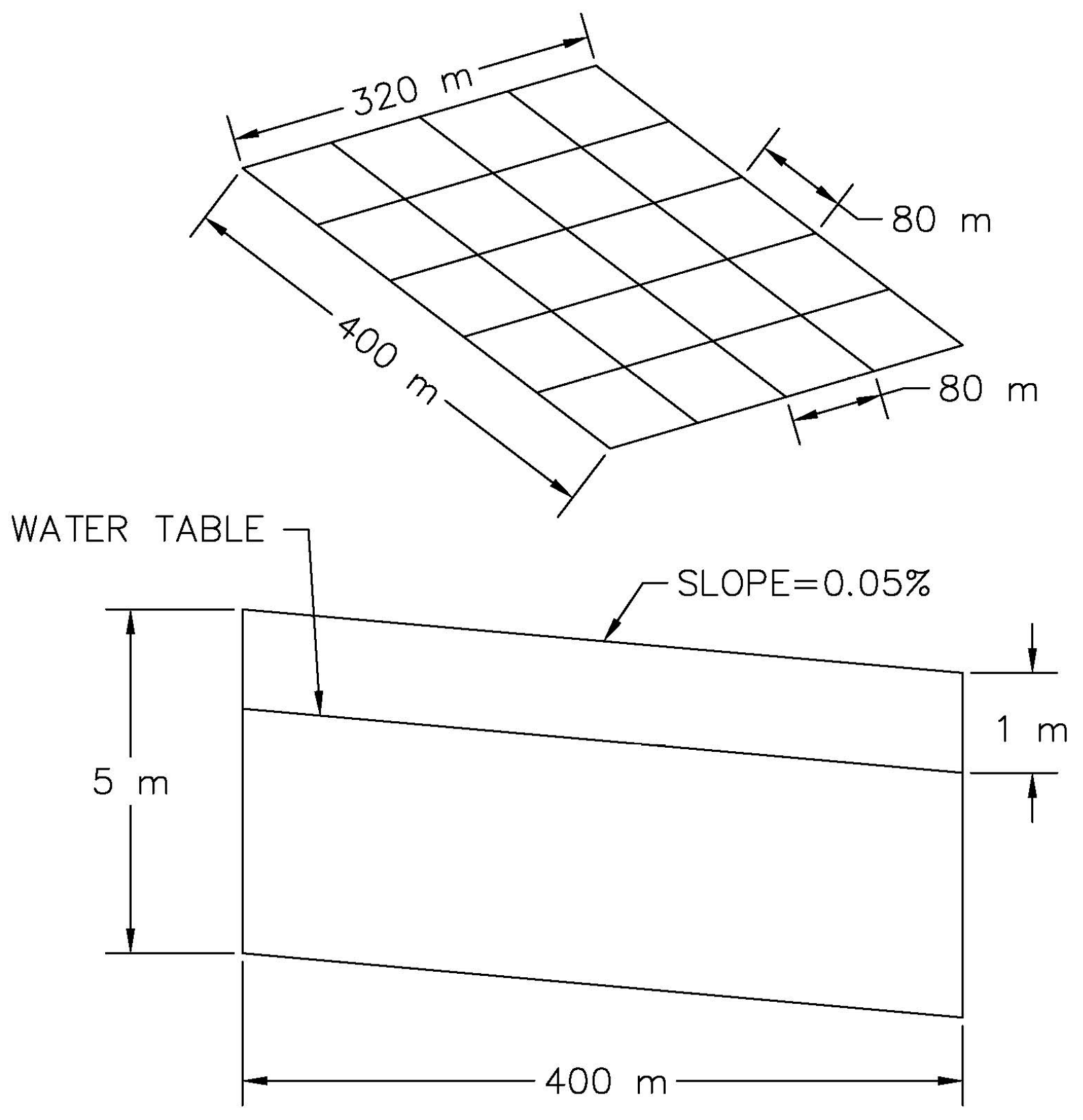
2.3.1. Infiltration Excess
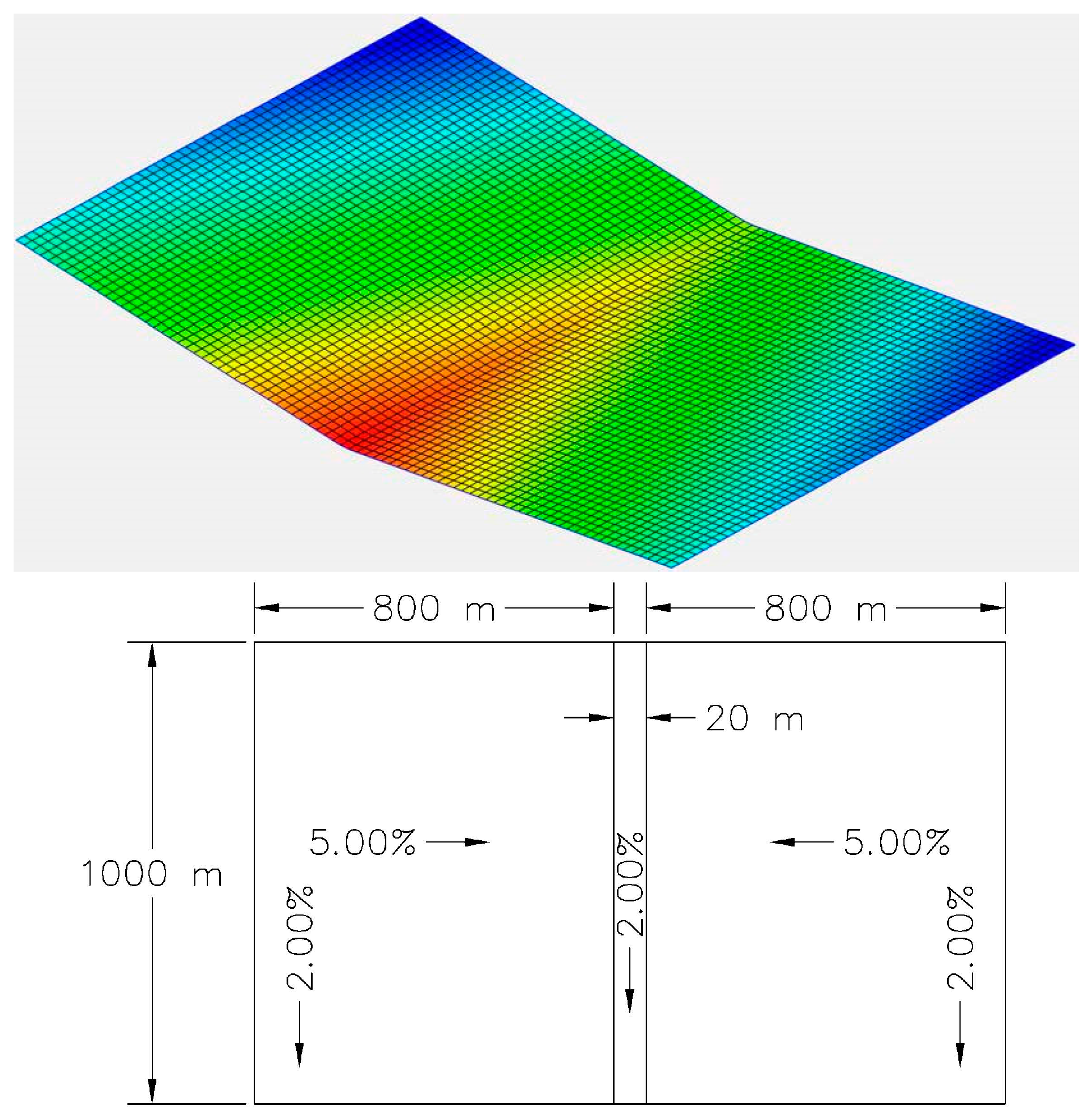
2.3.2. Tilted V-Catchment
3. Results
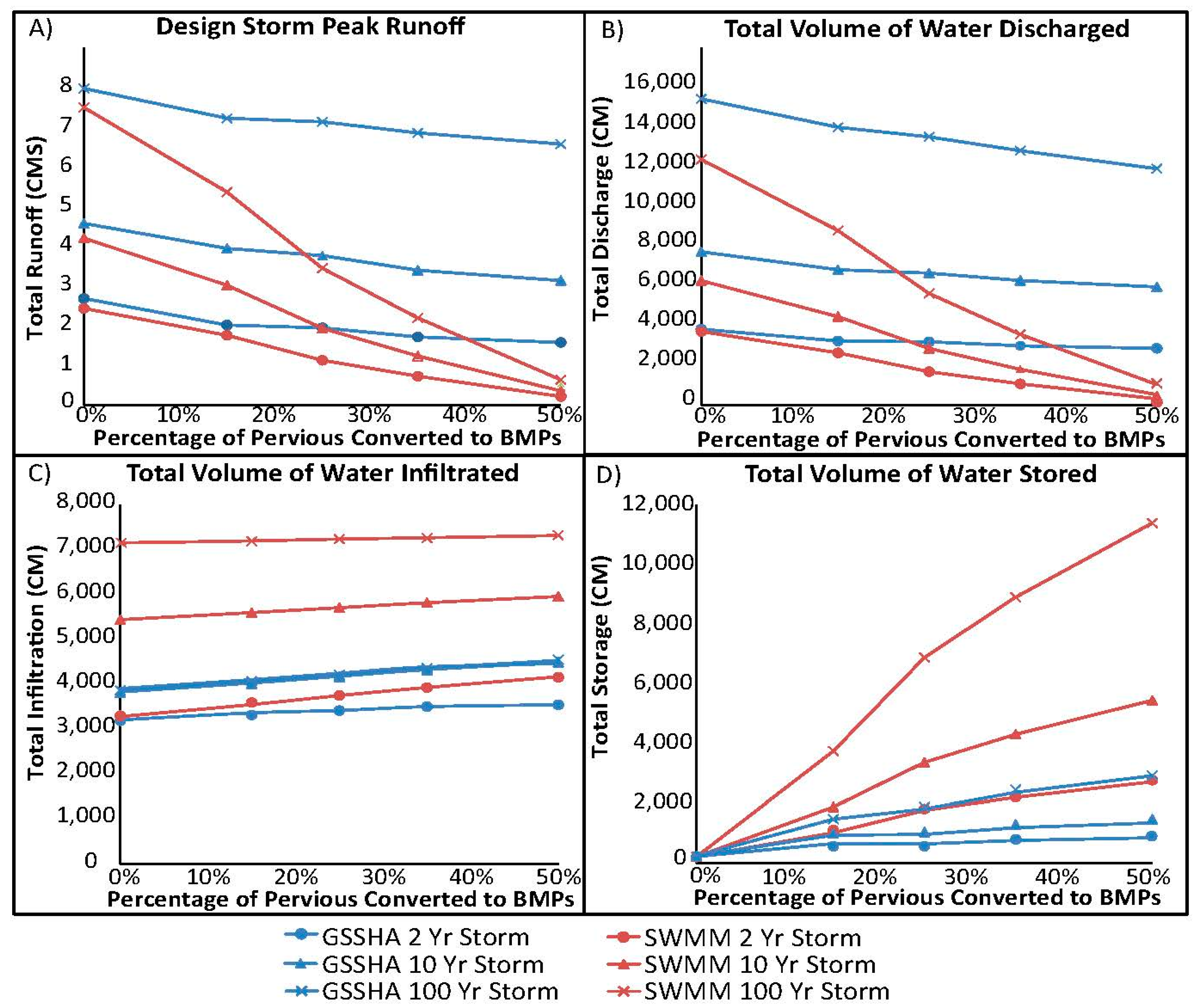
3.1. Urban Benchmark Case Study: Green Infrastructure
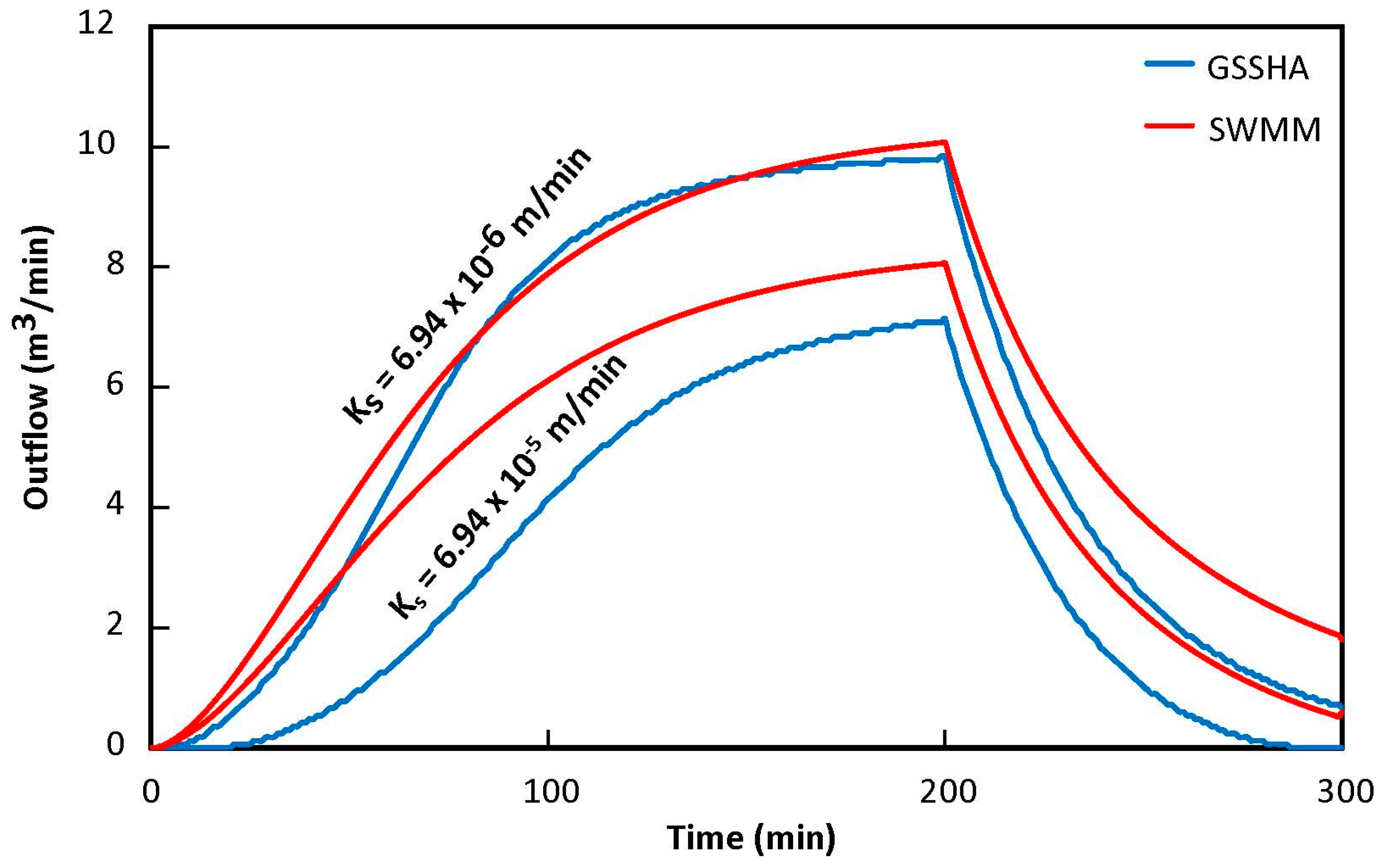
3.2. Infiltration Excess
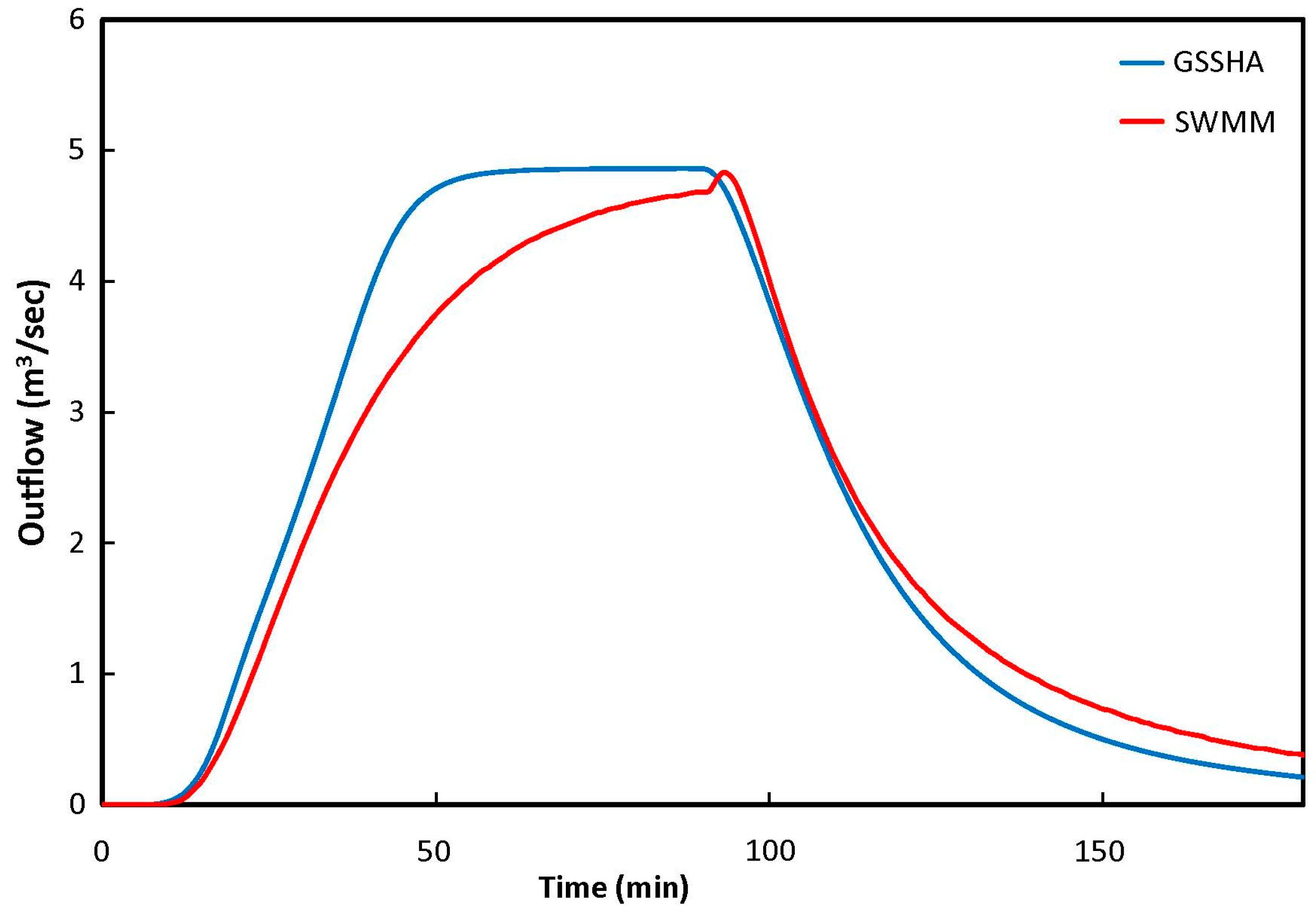
3.3. Tilted V-Catchment
4. Discussion
5. Conclusions
- A more complex simulation comparing existing urban conditions to proposed GI implementation was completed (Urban Case Study). This simulation compared a distributed model to a lumped model. The results showed a divergence in the model predictions of GI effectiveness. This divergence was the result of significant differences between how each type of model represents and solves the dynamic system. These results highlight the challenges of using lumped models to represent complex systems for future scenarios.
- The models showed consistent agreement for the simple test cases focused on infiltration (infiltration excess for the low Ks value). Simple test cases can serve to build model confidence as they cover a large range of runoff generating mechanisms often encountered in catchment hydrology [4].
- The models showed significant differences when comparing infiltration excess (high Ks value), and overland flow (Tilted-V). The different solution techniques used by each model and the increased complexity of the modeled system led to differences between the models.
- We incorporated BMP Effectiveness Ratios [7] from the distributed model that account for the dynamics of the environment and physics of flow based on storm intensity to a lumped model to improve GI modeling accuracy. Applying the distributed model BMP Effectiveness Ratios to the lumped model produced results consistent with the distributed model. This method provides a framework with which modelers can inform and improve GI modeling within lumped models.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barbosa, A.E.; Fernandes, J.N.; David, L.M. Key issues for sustainable urban stormwater management. Water Res. 2012, 46, 6787–6798. [Google Scholar] [CrossRef] [PubMed]
- Burns, M.J.; Fletcher, T.D.; Walsh, C.J.; Ladson, A.R.; Hatt, B.E. Hydrologic shortcomings of conventional urban stormwater management and opportunities for reform. Landsc. Urban Plan. 2012, 105, 230–240. [Google Scholar] [CrossRef]
- Jefferson, A.J.; Bhaskar, A.S.; Hopkins, K.G.; Fanelli, R.; Avellaneda, P.M. Stormwater management network effectiveness and implications for urban watershed function: A critical review. Hydrol. Process. 2017, 31, 4056–4080. [Google Scholar] [CrossRef]
- Maxwell, R.M. Surface-Subsurface model intercomparison: A first set of benchmark results to diagnose integrated hydrology and feedbacks. Water Resour. Res. 2014, 50, 1531–1549. [Google Scholar] [CrossRef]
- Bell, C.D.; McMillan, S.K.; Clinton, S.M.; Jefferson, A.J. Hydrologic response to stormwater control measures in urban watersheds. J. Hydrol. 2016, 541, 1488–1500. [Google Scholar] [CrossRef]
- Bhaskar, A.S.; Jantz, C.; Welty, C.; Drzyzga, S.A.; Miller, A.J. Coupling of the Water Cycle with Patterns of Urban Growth in the Baltimore Metropolitan Region, United States. J. Am. Water Resour. Assoc. 2016, 52, 1509–1523. [Google Scholar] [CrossRef]
- Fry, T.J.; Maxwell, R.M. Evaluation of Distributed BMPs in an Urban Watershed–High resolution modeling for Storm Water Management. J. Hydrol. Process. 2017. [Google Scholar] [CrossRef]
- Lim, T.C.; Welty, C. Effects of spatial configuration of imperviousness and green infrastructure networks on hydrologic response in a residential sewershed. Water Resour. Res. 2017, 53, 8084–8104. [Google Scholar] [CrossRef]
- Bosley, E.K. Hydrologic Evaluation of Low Impact Development Using a Continuous, Spatially-Distributed Model. Master’s Thesis, Virginal Polytechnic Institute and State University, Blacksburg, VA, USA, 2008. [Google Scholar]
- Miller, J.D.; Kim, H.; Kjeldsen, T.R.; Packman, J.; Grebby, S.; Dearden, R. Assessing the impact of urbanization on storm runoff in a peri-urban catchment using historical change in impervious cover. J. Hydrol. 2014, 15, 59–70. [Google Scholar] [CrossRef]
- Parlange, J.Y.; Rose, C.W.; Sander, G. Kinematic flow approximation of runoff on a plane: An exact analytical solution. J. Hydrol. 1981, 52, 171–176. [Google Scholar] [CrossRef]
- Panday, S.; Huyakorn, P.S. A fully coupled physically-based spatially-distributed model for evaluating surface/subsurface flow. Adv. Water Resour. 2004, 27, 361–382. [Google Scholar] [CrossRef]
- Kollet, S.J.; Maxwell, R.M. Integrated surface-groundwater flow modeling: A free-surface overland flow boundary condition in a parallel groundwater flow model. Adv. Water Resour. 2006, 29, 945–958. [Google Scholar] [CrossRef]
- Shen, C.; Phanikumar, M.S. A process-based, distributed hydrologic model based on a large-scale method for surface–subsurface coupling. Adv. Water Resour. 2010, 33, 1524–1541. [Google Scholar] [CrossRef]
- Sulis, M.; Meyerhoff, S.B.; Paniconi, C.; Maxwell, R.M.; Putti, M.; Kollet, S.J. A comparison of two physics-based numerical models for simulating surface water–groundwater interactions. Adv. Water Resour. 2010, 33, 456–467. [Google Scholar] [CrossRef]
- Sebben, M.L.; Werner, A.D.; Liggett, J.E.; Partington, D.; Simmons, C.T. On the testing of fully integrated surface–subsurface hydrological models. Hydrol. Process. 2013, 27, 1276–1285. [Google Scholar] [CrossRef]
- Kollet, S. The integrated hydrologic model intercomparison project, IH-MIP2: A second set of benchmark results to diagnose integrated hydrology and feedbacks. Water Resour. Res. 2017, 53, 867–890. [Google Scholar] [CrossRef]
- Bhaduri, B.; Harbor, J.; Engel, B.; Grove, M. Assessing watershed-scale long-term hydrologic impacts of land-use change using GIS-NPS model. Environ. Manag. 2000, 26, 643–658. [Google Scholar] [CrossRef] [PubMed]
- Khader, O.; Montalto, F.A. Development and calibration of a high resolution SWMM model for simulating the effects of LID retrofits on the outflow hydrograph of a dense urban watershed. Int. Low Impact Dev. Conf. 2008. [Google Scholar] [CrossRef]
- Lee, G.L.; Heaney, J.P. Estimation of urban imperviousness and its impacts on stormwater system. J. Water Resour. Plan. Manag. 2003, 129, 419–428. [Google Scholar] [CrossRef]
- Krebs, G.; Kokkonen, T.; Valtanen, M.; Setala, H.; Koivusalo, H. Spatial resolution considerations for urban hydrological modelling. J. Hydrol. 2014, 512, 482–497. [Google Scholar] [CrossRef]
- Elliott, A.H.; Trowsdale, S.A. A review of models for low impact urban stormwater drainage. Environ. Model. Softw. 2007, 22, 394–405. [Google Scholar] [CrossRef]
- Henderson-Sellers, A.; Pitman, A.J.; Love, P.K.; Irannejad, P.; Chen, T.H. The Project for Intercomparison of Land Surface Parameterization Schemes (PILPS): Phase 2 and 3. Bull. Am. Meteorol. Soc. 1995, 76, 489–503. [Google Scholar] [CrossRef]
- Yang, Z.L.; Dickinson, R.E.; Henderson-Sellers, A.; Pitman, A.J. Preliminary study of spin-up processes in land-surface models with the first stage data of Project for Intercomparison of Land Surface Parameterization Schemes Phase 1(a). J. Geophys. Res. 1995, 100, 16553–16578. [Google Scholar] [CrossRef]
- Chen, T.H. Cabauw experimental results from the Project for Intercomparison of land-surface parameterizations schemes. J. Clim. 1997, 10, 1194–1215. [Google Scholar] [CrossRef]
- Qu, W. Sensitivity of latent heat flux from PILPS land-surface schemes to perturbations of surface air temperature. J. Atmos. Sci. 1998, 55, 1909–1927. [Google Scholar] [CrossRef]
- Wood, E. The Project for Intercomparison of Land-surface Parameterization Schemes PILPS/phase 2c/Red-Arkansas River basin experiment. 1: Experiment description and summary intercomparisons. Glob. Planet. Chang. 1998, 19, 115–135. [Google Scholar] [CrossRef]
- Luo, L.; Robock, A. Effects of frozen soil on soil temperature, spring infiltration, and runoff: Results from the PILPS 2(d) Experiment at Valdai, Russia. J. Hydrometeorol. 2003, 4, 334–351. [Google Scholar] [CrossRef]
- Reed, S.; Koren, V.; Smith, M.; Zhang, Z.; Moreda, F.; Seo, D.J.; DMIP Participants. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Smith, M.B.; Seo, D.J.; Koren, V.I.; Reed, S.M.; Zhang, Z.; Duan, Q.Y.; Moreda, F.; Cong, S. The distributed model intercomparison project (DMIP): Motivation and experiment design. J. Hydrol. 2004, 298, 4–26. [Google Scholar] [CrossRef]
- Downer, C.W.; Ogden, F.L.; U.S. Army Corps of Engineers. Gridded Surface Subsurface Hydrologic Analysis (GSSHA) User’s Manual, Version 11,43 for Watershed Modeling System 6.1; Engineer Research and Development Center: Vicksburg, MS, USA, 2006; p. 207.
- Green, W.H.; Ampt, G.A. Studies on soil physics, part I: The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Ogden, F.L.; Saghafian, B. Green and Ampt infiltration with redistribution. J. Irrig. Drain. Eng. 1997, 123, 386–393. [Google Scholar] [CrossRef]
- Downer, C.W.; Ogden, F.L. Prediction of runoff and soil moistures at the watershed scale: Effects of model complexity and parameter assignment. Water Resour. Res. 2003, 39, 1045. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model Reference Manual Volume I–Hydrology (Revised); U.S. EPA Office of Research and Development: Cincinnati, OH, USA, 2016.
- Rossman, L.A. Stormwater Management Model User Manual Version 5.1; U.S. Environmental Protection Agency Office of Research and Development: Cincinnati, OH, USA, 2015.
- Gironas, J.; Roesner, L.A.; Davis, J. Storm Water Management Model Applications Manual; National Risk Management Research Laboratory Office of Research and Development, U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2009.
- Yao, L.; Chen, L.; Wei, W. Assessing the effectiveness of imperviousness on stormwater runoff in micro urban catchments by model simulation. Hydrol. Process. 2015. [Google Scholar] [CrossRef]
- Yao, L.; Wei, W.; Chen, L. How does imperviousness impact the urban rainfall-runoff process under various storm cases? Ecol. Indic. 2016, 60, 893–905. [Google Scholar] [CrossRef]
- Urban Drainage and Flood Control District. Urban Drainage and Flood Control District Criteria Manual 1; Urban Drainage and Flood Control District: Denver, CO, USA, 2016.
- City and County of Denver. Geographic Information System; City and County of Denver: Denver, CO, USA, 2014. [Google Scholar]
- Engman, T. Roughness Coefficients for Routing Surface Runoff. J. Irrig. Drain. Eng. 1986, 112, 39–53. [Google Scholar] [CrossRef]
- McCuen, R.; Johnson, P.; Ragan, R. Hydrology; Federal Highway Administration: Washington, DC, USA, 1996.
- McCuen, R.; Johnson, P.; Ragen, R. Highway Hydrology, 2nd ed.; Hydraulic Design Series No. 2; US Department of Transportation: Washington, DC, USA, 2002; Chapter 5; pp. 24–28.
- Rawls, W.J.; Brakensiek, D.L. A Procedure to Predict Green and Ampt Infiltration Parameters. In Proceedings of the ASAE Conference on Advances in Infiltration, Chicago, IL, USA, 12–13 December 1983; pp. 102–112. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L. Prediction of soil water properties for hydrologic modeling. In Symposium on Watershed Management in the Eighties; Jones, E.B., Ward, T.J., Eds.; American Society of Cicil Engineers: New York, NY, USA, 1985; pp. 293–399. [Google Scholar]
- Natural Resources Conservation Service. Soil Survey Data; US Department of Agriculture: Washington, DC, USA, 2014.
- City and County of Denver. Ultra-Urban Green Infrastructure Guidelines; City and County of Denver Public Works: Denver, CO, USA, 2016. [Google Scholar]
- Urban Drainage and Flood Control District. Urban Drainage and Flood Control District Criteria Manual 3; Urban Drainage and Flood Control District: Denver, CO, USA, 2016.
- Gottardi, G.; Venutelli, M. A control-volume finite-element model for two-dimensional overland flow. Adv. Water Resour. 1993, 16, 277–284. [Google Scholar] [CrossRef]
- Kumar, M.; Duffy, C.J.; Salvage, K.M. A second order accurate, finite volume based, integrated hydrologic modeling (FIHM) framework for simulation of surface and subsurface flow. Vadose Zone J. 2009, 8, 873–890. [Google Scholar] [CrossRef]
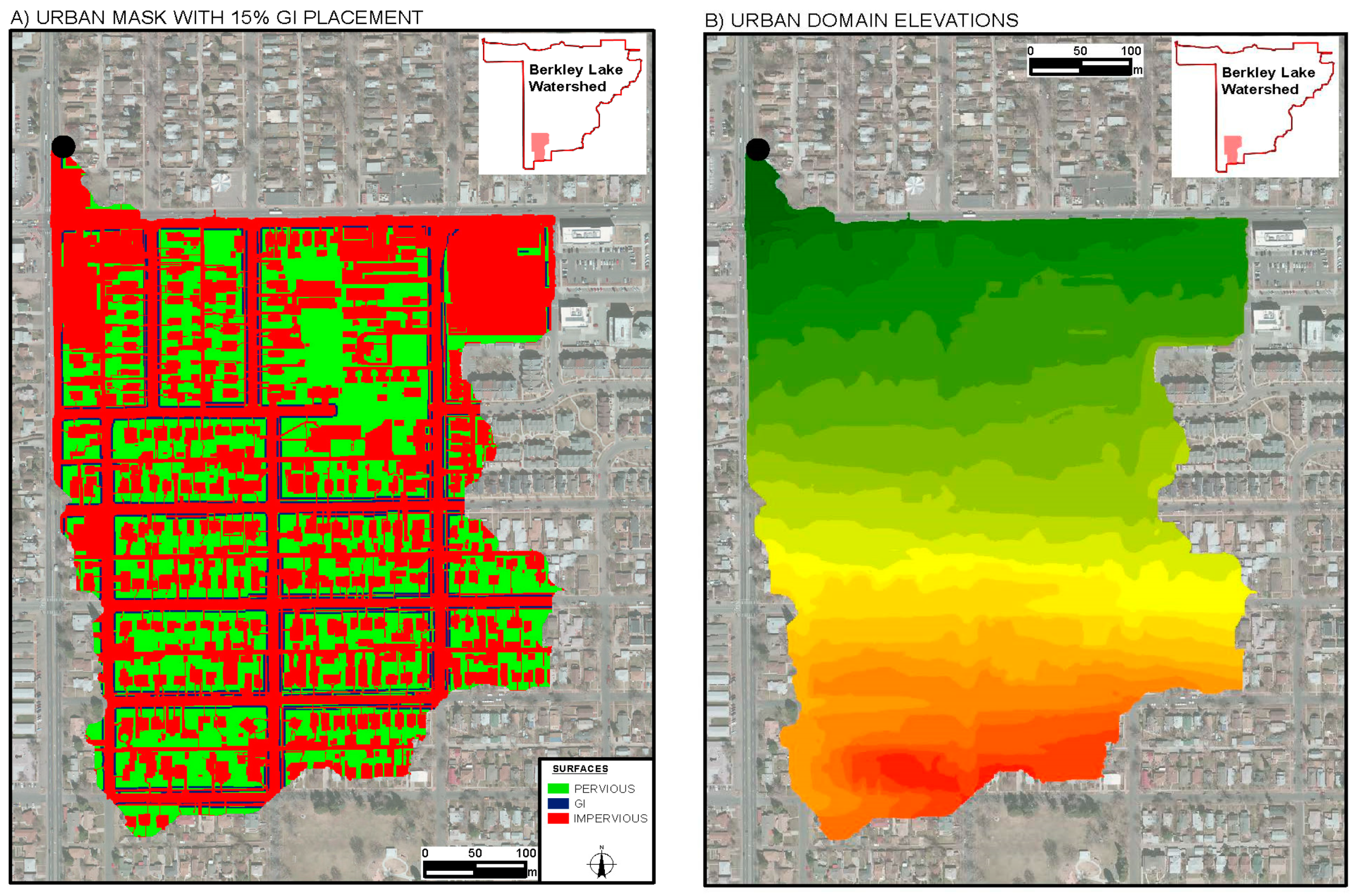

| Neighborhood Subset Characteristics | Value | Units | Source |
|---|---|---|---|
| Total Area | 261,422 | m2 | City and County of Denver Geographic Information system (GIS) (2014) [41] |
| Impervious Areas | 137,427 | m2 | |
| Pervious Areas | 123,995 | m2 | |
| Native Soil Properties | |||
| Hydraulic Conductivity | 0.06 | cm/h | Engman (1986) [42]; McCuen et al. (1996 and 2002) [43,44]; |
| Capillary Head | 32 | cm | Rawls and Brakensiek (1983 and 1985) [45,46]; US Natural Resources Conservation Service (NRCS) |
| Porosity | 0.4 | cm3/cm3 | Soil Survey Data (soils.usda.gov/survey) [47] |
| Residual Saturation | 0.165 | cm3/cm3 | |
| Field Capacity | 0.09 | cm3/cm3 | |
| Wilting Point | 0.4 | cm3/cm3 | |
| Initial Moisture | 0.27 | % | |
| Surface Roughness Values | |||
| Impervious Areas | 0.015 | Engman (1986) [42]; McCuen et al. (1996 and 2002) [43,44] | |
| Pervious Areas | 0.04 | ||
| GI Soil Properties | |||
| Hydraulic Conductivity | 1.09 | cm/h | City of Denver Ultra Urban Manual |
| Capillary Head | 11.01 | cm | (2016) [48]; Urban Drainage and Flood Control District (UDFCD) Vol. III (2016) [49] |
| Porosity | 0.412 | cm3/c3 | |
| Residual Saturation | 0.041 | cm3/cm3 | |
| Field Capacity | 0.207 | cm3/cm3 | |
| Wilting Point | 0.095 | cm3/cm3 | |
| Initial Moisture | 0.358 | % | |
| GI Characteristics | |||
| Surface Storage Depth | 304.8 | mm | UDFCD Vol. III (2016) [49] |
| Parameter Values for Benchmark Cases | ||||
|---|---|---|---|---|
| Units | 1. Infiltration Excess | 2. Tilted V-Catchment | ||
| Saturated Hydraulic Conductivity | Ks | m/min | 6.94 × 10−5 (High K) | a |
| m/min | 6.94 × 10−6 (Low K) | a | ||
| Manning’s Roughness | n | 0.01986 | 0.015 (Hillslope) | |
| 0.15 (Channel) | ||||
| Rainfall Rate | i | m/min | 3.30 × 10−4 | 1.80 × 10−4 |
| Specific Storage | Ss | 1/m | 5 × 10−4 | 5 × 10−4 |
| Porosity | Φ | 0.4 | 0.4 | |
| van Genuchten Parameters | ||||
| Alpha | α | 1/cm | 1.0 | 1.0 |
| Pore-size distributions | n | - | 2.0 | 2.0 |
| Residual water content | Sres | - | 0.2 | 0.2 |
| Saturated water content | Ssat | - | 1.0 | 1.0 |
| Green Ampt Parameters | ||||
| Capillary Head | Ψ | cm | 16.7 | 16.7 |
| Pore Distribution Index | λ | - | 2.0 | 2.0 |
| Residual Saturation | θr | - | 0.2 | 0.2 |
| Field Capacity | θf | - | 0.4 | 0.4 |
| Wilting Point | θwp | - | 0.15 | 0.15 |
| Infiltration Excess Ks = 0.01 | Infiltration Excess Ks = 0.1 | Tilted V-Catchment | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Qpeak | tpeak | Volume | Qpeak | tpeak | Volume | Qpeak | tpeak | Volume | |
| GSSHA | 0.164 | 199.80 | 1622 | 0.119 | 200.00 | 924 | 4.860 | 85.00 | 25,417 |
| SWMM | 0.170 | 199.80 | 1777 | 0.134 | 200.00 | 1325 | 4.830 | 93.00 | 24,065 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fry, T.J.; Maxwell, R.M. Using a Distributed Hydrologic Model to Improve the Green Infrastructure Parameterization Used in a Lumped Model. Water 2018, 10, 1756. https://doi.org/10.3390/w10121756
Fry TJ, Maxwell RM. Using a Distributed Hydrologic Model to Improve the Green Infrastructure Parameterization Used in a Lumped Model. Water. 2018; 10(12):1756. https://doi.org/10.3390/w10121756
Chicago/Turabian StyleFry, Timothy J., and Reed M. Maxwell. 2018. "Using a Distributed Hydrologic Model to Improve the Green Infrastructure Parameterization Used in a Lumped Model" Water 10, no. 12: 1756. https://doi.org/10.3390/w10121756
APA StyleFry, T. J., & Maxwell, R. M. (2018). Using a Distributed Hydrologic Model to Improve the Green Infrastructure Parameterization Used in a Lumped Model. Water, 10(12), 1756. https://doi.org/10.3390/w10121756