High-Resolution Discharge Forecasting for Snowmelt and Rainfall Mixed Events
Abstract
1. Introduction
2. Methods
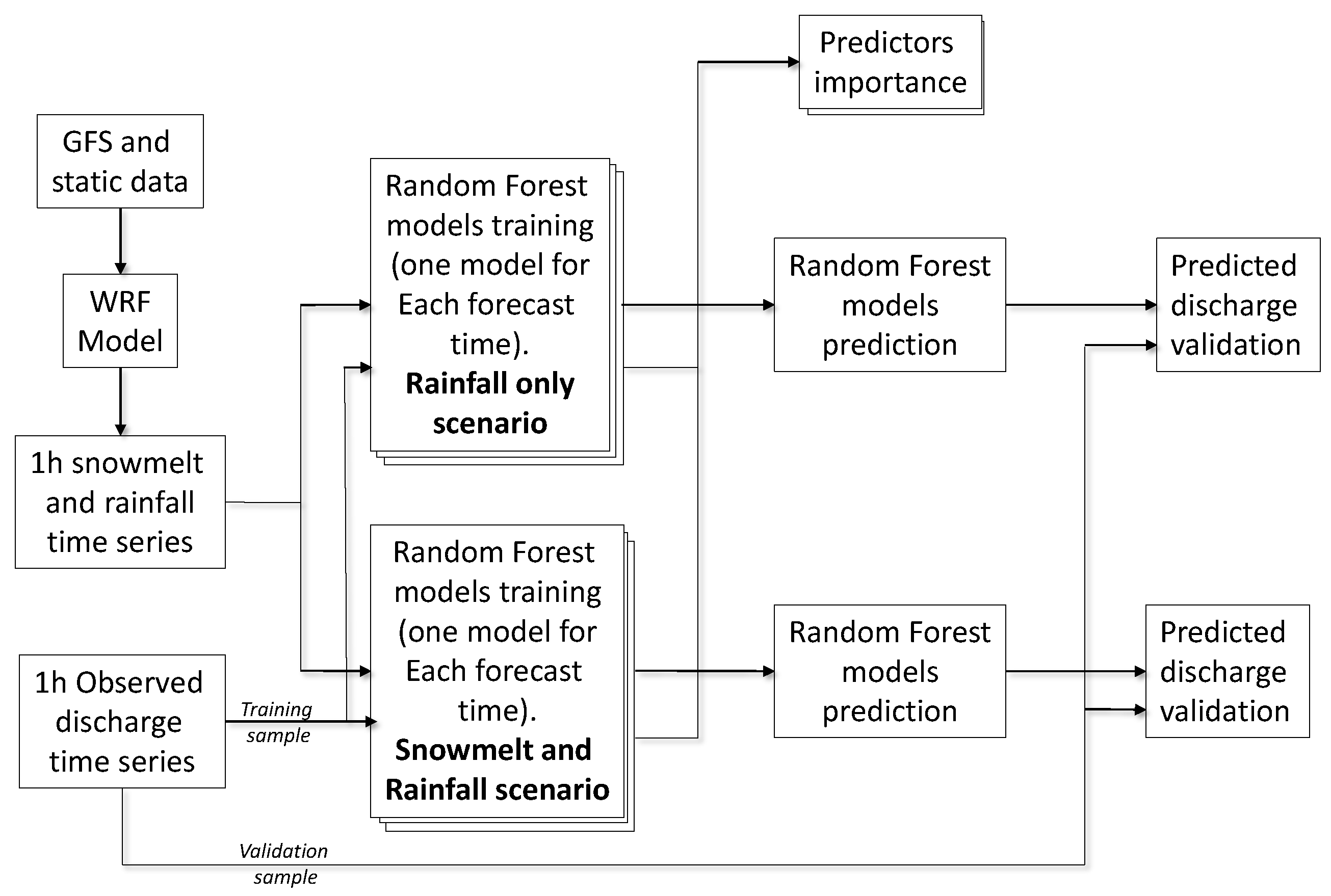
2.1. Discharge Forecasting
- A catchment response, expressed in discharge, to meteorological and climatological forcing is nonlinear. Hence, a nonlinear model is required to represent this system.
- Our approach uses big models, with multiple predictors that may vary in their significance for the forecast output. Hence, a multiple model resistive to overfitting is required to regress the variables.
- Our aim was also to gain insight into the forecasting model behaviour, for which a predictor’s importance estimation feature of Random Forests can be used.
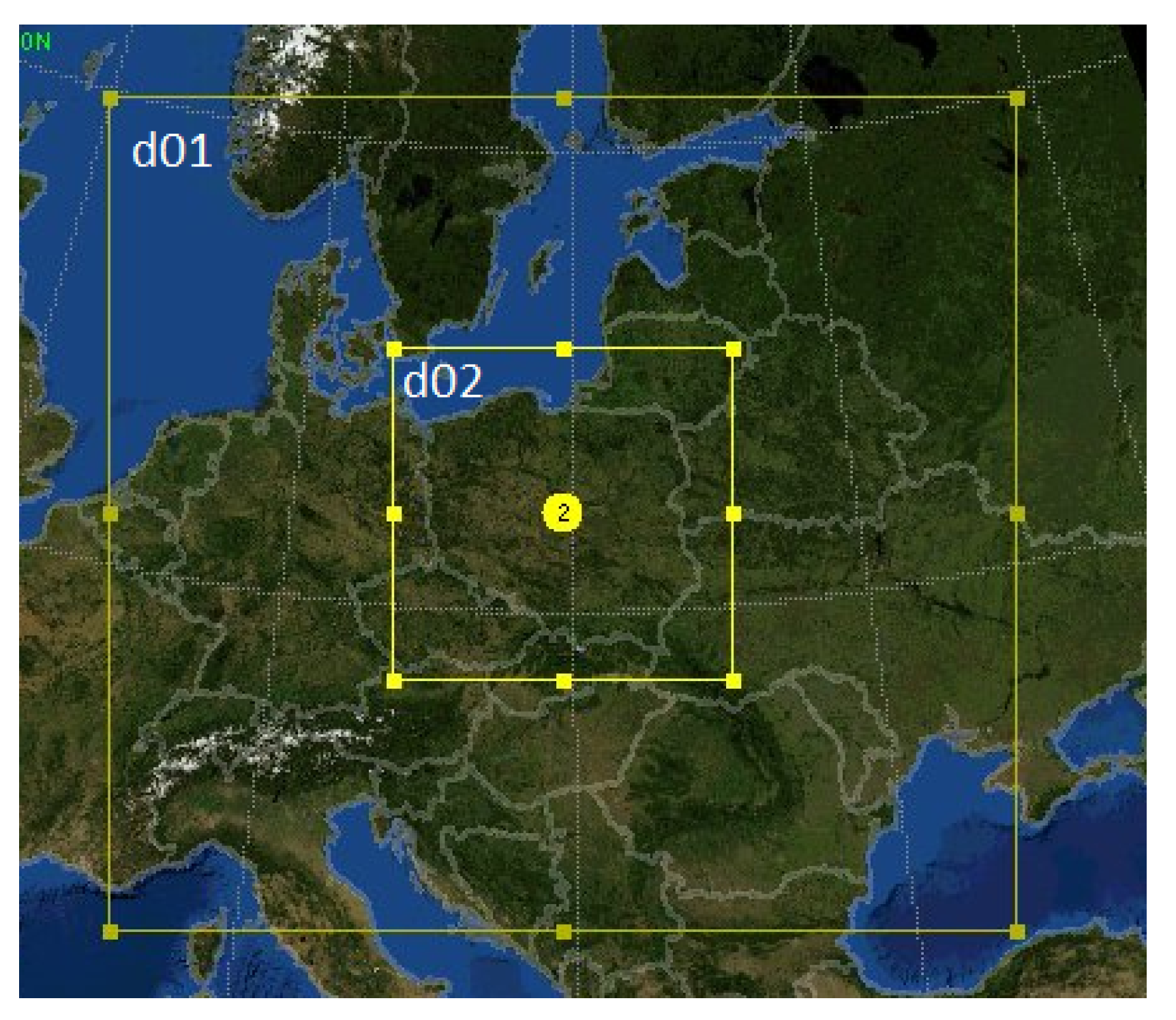
2.2. The WRF Model Setup and Output
2.3. Experimental Setup
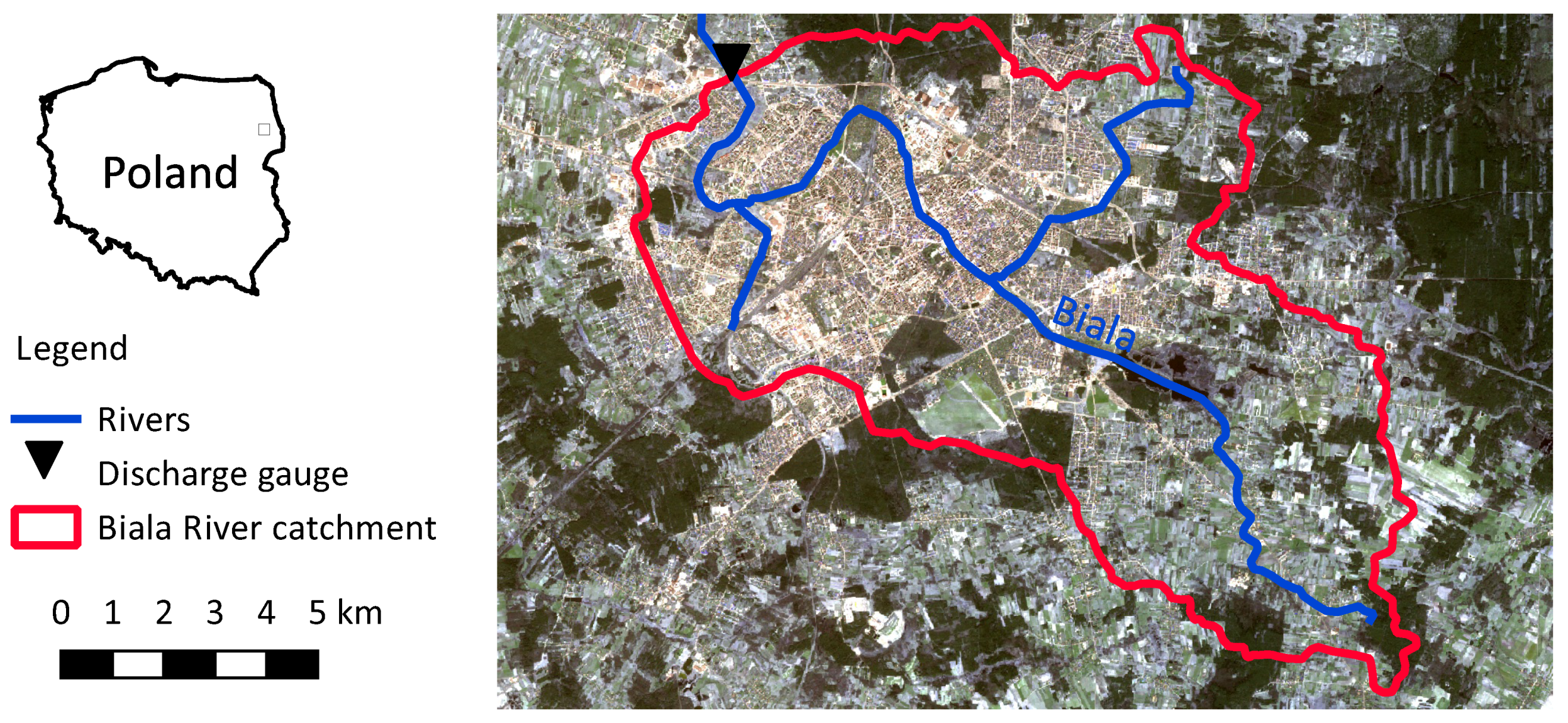
2.4. Study Area
3. Results
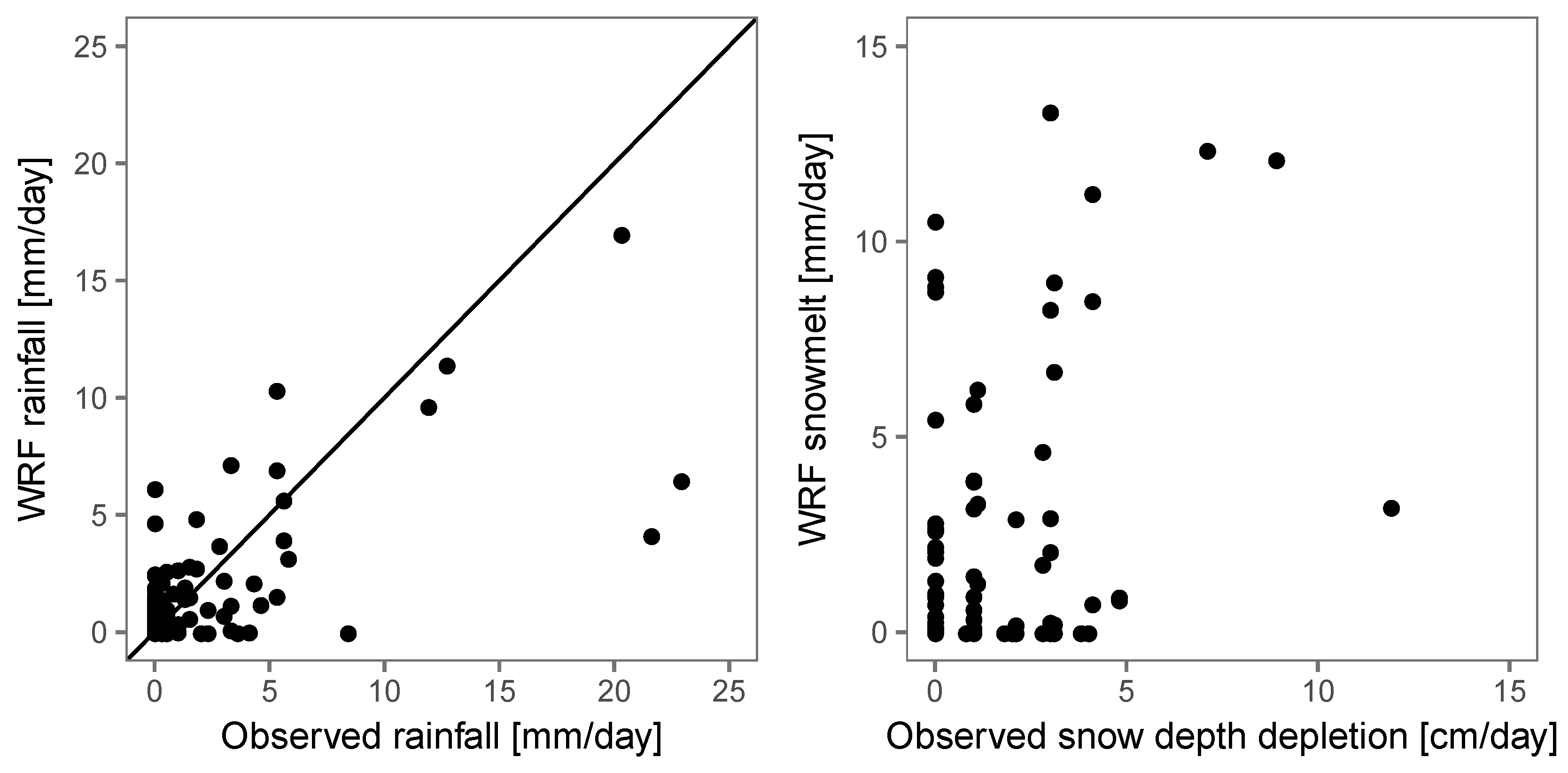
3.1. WRF Results
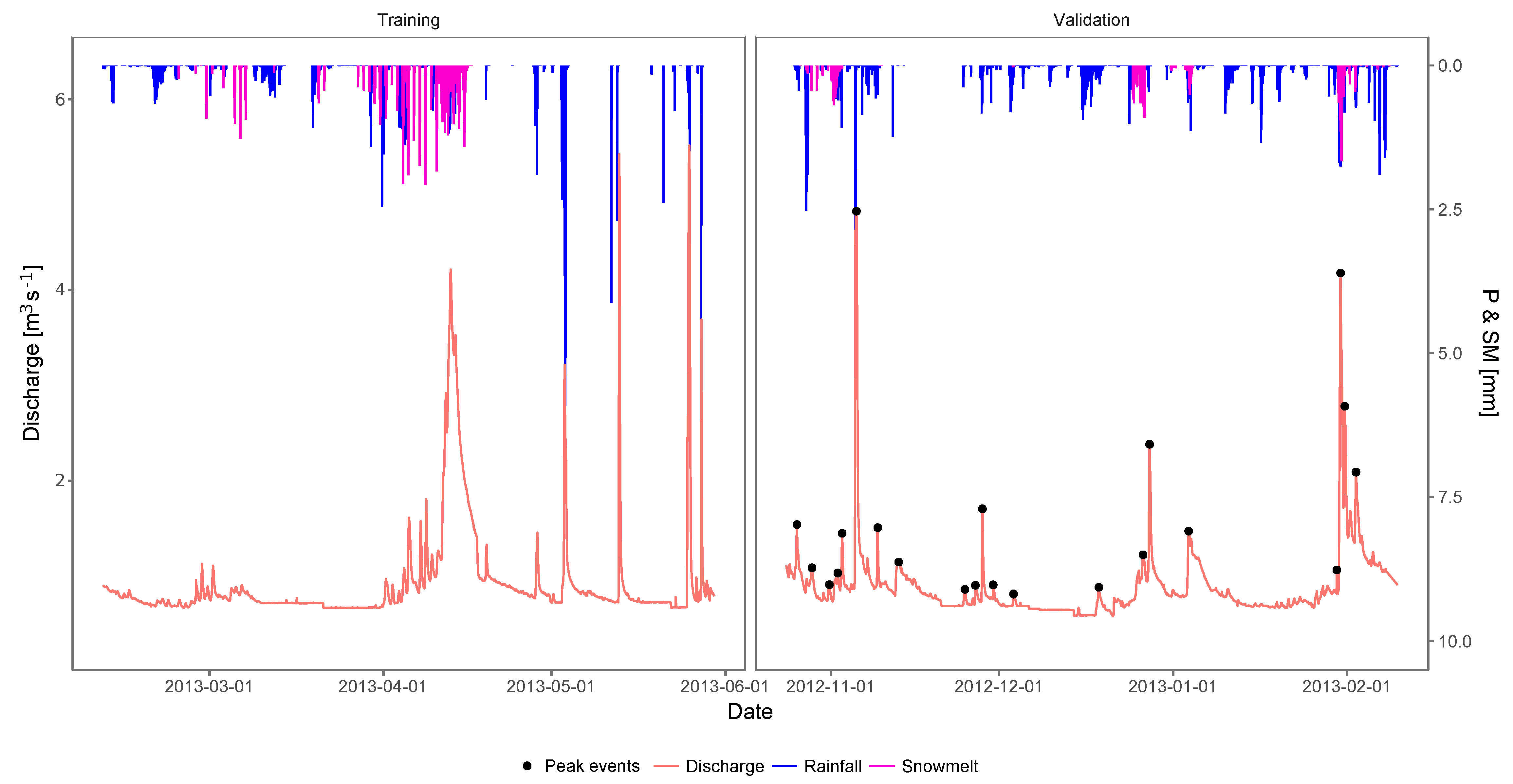
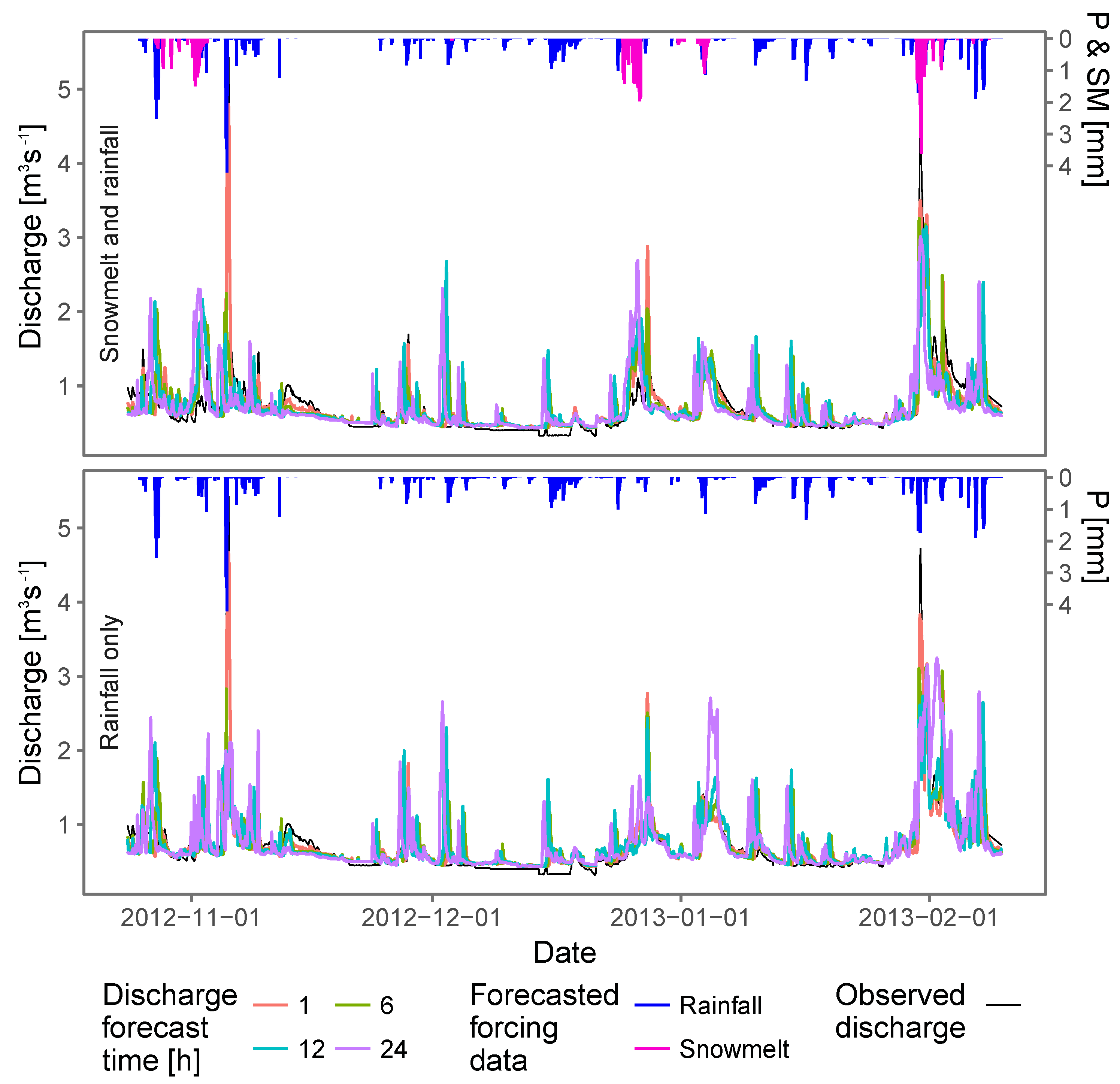
3.2. Discharge Forecasting
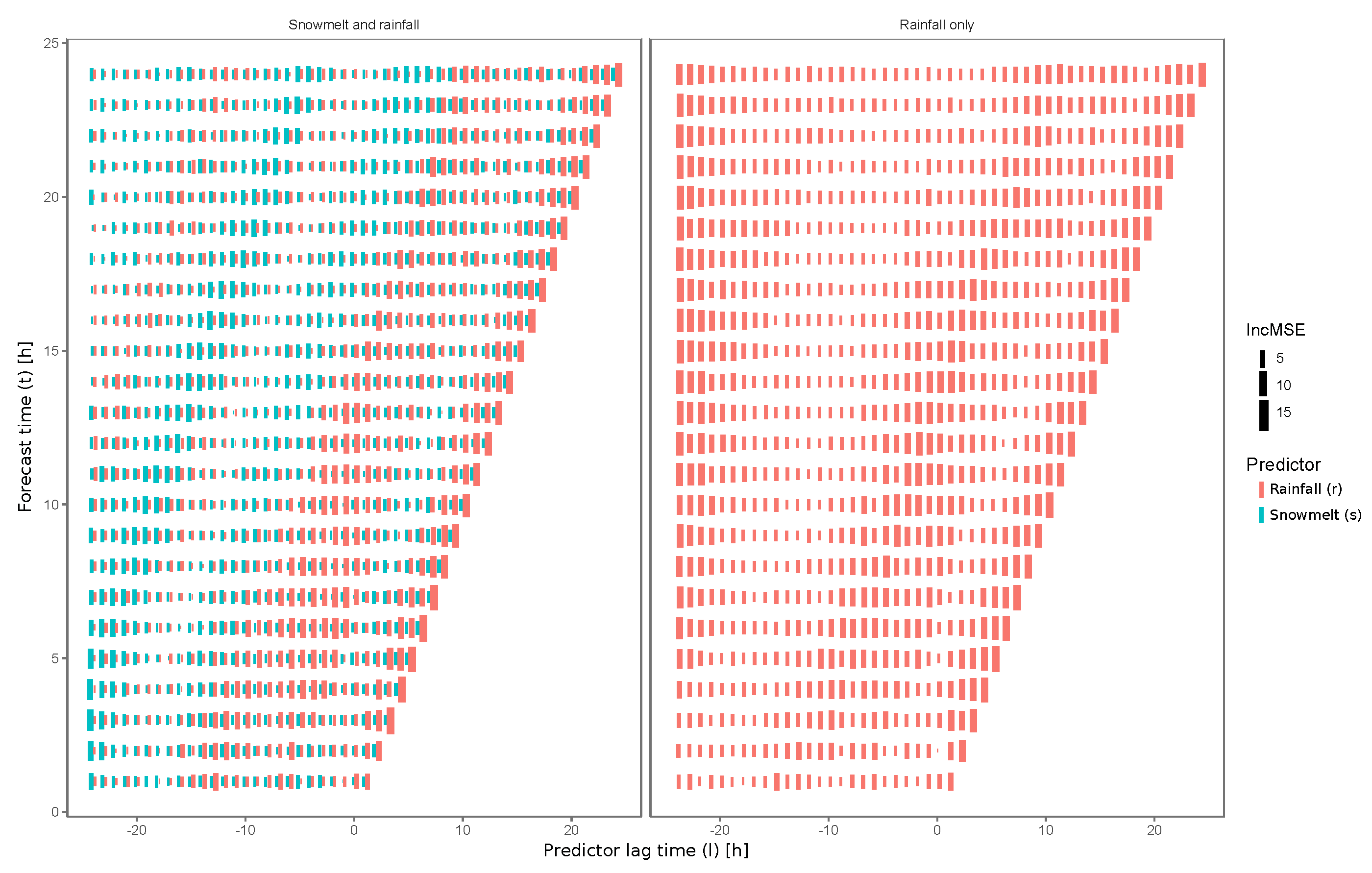
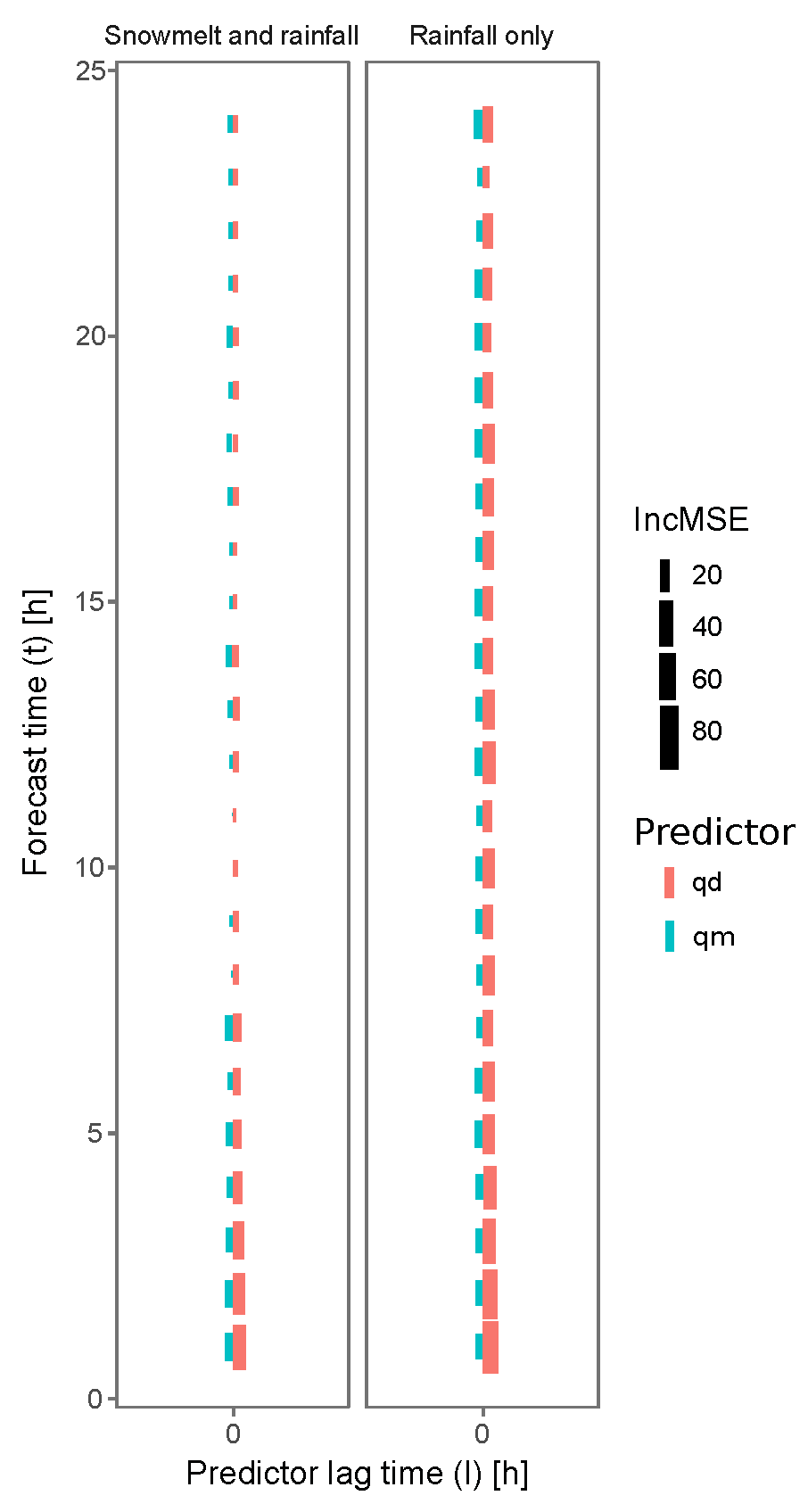
3.3. The Forecasting Models Structure
4. Discussion
4.1. WRF Forecasts
4.2. Random Forests Models
4.3. Discharge Forecast and Predictors Importance
4.4. Snowmelt in Discharge Forecasting
4.5. Outlook and Applicability
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Buttle, J.M.; Xu, F. Snowmelt Runoff in Suburban Environments. Hydrol. Res. 1988, 19, 19–40. [Google Scholar]
- Surfleet, C.G.; Tullos, D. Variability in effect of climate change on rain-on-snow peak flow events in a temperate climate. J. Hydrol. 2013, 479, 24–34. [Google Scholar] [CrossRef]
- Wever, N.; Jonas, T.; Fierz, C.; Lehning, M. Model simulations of the modulating effect of the snow cover in a rain-on-snow event. Hydrol. Earth Syst. Sci. 2014, 18, 4657–4669. [Google Scholar] [CrossRef]
- Cohen, J.; Ye, H.; Jones, J. Trends and variability in rain-on-snow events. Geophys. Res. Lett. 2015, 42, 7115–7122. [Google Scholar] [CrossRef]
- Langhammer, J.; Česák, J. Applicability of a Nu-Support Vector Regression Model for the Completion of Missing Data in Hydrological Time Series. Water 2016, 8, 560. [Google Scholar] [CrossRef]
- Rogelis, M.C.; Werner, M. Streamflow forecasts from WRF precipitation for flood early warning in mountain tropical areas. Hydrol. Earth Syst. Sci. Discuss. 2017, 2017, 1–32. [Google Scholar] [CrossRef]
- Li, J.; Chen, Y.; Wang, H.; Qin, J.; Li, J.; Chiao, S. Extending flood forecasting lead time in a large watershed by coupling WRF QPF with a distributed hydrological model. Hydrol. Earth Syst. Sci. 2017, 21, 1279–1294. [Google Scholar] [CrossRef]
- Tao, J.; Wu, D.; Gourley, J.; Zhang, S.Q.; Crow, W.; Peters-Lidard, C.; Barros, A.P. Operational hydrological forecasting during the IPHEx-IOP campaign—Meet the challenge. J. Hydrol. 2016, 541, 434–456. [Google Scholar] [CrossRef]
- Bauer-Gottwein, P.; Jensen, I.H.; Guzinski, R.; Bredtoft, G.K.T.; Hansen, S.; Michailovsky, C.I. Operational river discharge forecasting in poorly gauged basins: The Kavango River basin case study. Hydrol. Earth Syst. Sci. 2015, 19, 1469–1485. [Google Scholar] [CrossRef]
- De Lima, G.R.T.; Santos, L.B.L.; de Carvalho, T.J.; Carvalho, A.R.; Cortivo, F.D.; Scofield, G.B.; Negri, R.G. An operational dynamical neuro-forecasting model for hydrological disasters. Model. Earth Syst. Environ. 2016, 2, 1–9. [Google Scholar] [CrossRef]
- Oleson, K.W.; Lawrence, D.M.; Gordon, B.; Flanner, M.G.; Kluzek, E.; Peter, J.; Levis, S.; Swenson, S.C.; Thornton, E.; Feddema, J.; et al. Technical Description of Version 4.0 of the Community Land Model (CLM); National Center for Atmospheric Research: Boulder, CO, USA, 2010. [Google Scholar]
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.; Yang, Z.L.; Levis, S.; Sakaguchi, K.; et al. Parameterization improvements and functional and structural advances in Version 4 of the Community Land Model. J. Adv. Model. Earth Syst. 2011, 3. [Google Scholar] [CrossRef]
- Benjamin, S.G.; Grell, G.A.; Brown, J.M.; Smirnova, T.G.; Bleck, R. Mesoscale Weather Prediction with the RUC Hybrid Isentropic-Terrain-Following Coordinate Model. Mon. Weather Rev. 2004, 132, 473–494. [Google Scholar] [CrossRef]
- Niu, G.Y.; Yang, Z.L.; Mitchell, K.E.; Chen, F.; Ek, M.B.; Barlage, M.; Kumar, A.; Manning, K.; Niyogi, D.; Rosero, E.; et al. The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, X.; Decker, M. Improving snow processes in the Noah land model. J. Geophys. Res. 2010, 115, D20108. [Google Scholar] [CrossRef]
- Jin, J.; Wen, L. Evaluation of snowmelt simulation in the Weather Research and Forecasting model. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Förster, K.; Meon, G.; Marke, T.; Strasser, U. Effect of meteorological forcing and snow model complexity on hydrological simulations in the Sieber catchment (Harz Mountains, Germany). Hydrol. Earth Syst. Sci. 2014, 18, 4703–4720. [Google Scholar] [CrossRef]
- Wu, X.; Shen, Y.; Wang, N.; Pan, X.; Zhang, W.; He, J.; Wang, G. Coupling the WRF model with a temperature index model based on remote sensing for snowmelt simulations in a river basin in the Altay Mountains, north-west China. Hydrol. Process. 2016, 30, 3967–3977. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, Z.; Ye, B.; Qin, Y.; Wei, Z.; Fang, S. A snowmelt runoff forecasting model coupling WRF and DHSVM. Hydrol. Earth Syst. Sci. 2009, 13, 1897–1906. [Google Scholar] [CrossRef]
- Buttle, J.M. Effects of suburbanization upon snowmelt runoff. Hydrol. Sci. J. 1990, 35, 285–302. [Google Scholar] [CrossRef]
- Valtanen, M.; Sillanpaa, N.; Setala, H. Effects of land use intensity on stormwater runoff and its temporal occurrence in cold climates. Hydrol. Process. 2013, 28, 2639–2650. [Google Scholar] [CrossRef]
- Valeo, C.; Ho, C. Modelling urban snowmelt runoff. J. Hydrol. 2004, 299, 237–251. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Instytut Meteorologii i Gospodarki Wodnej—Państwowy Instytut Badawczy (IMGW-PIB). 1 h Discharge Time Series for Zawady (ID: 153230060) Gauging Station at Biała River (ID: 26168) for the Period 2010–2016; IMGW-PIB: Warsaw, Poland, 2017. [Google Scholar]
- Nakanishi, M.; Niino, H. Development of an Improved Turbulence Closure Model for the Atmospheric Boundary Layer. J. Meteorol. Soc. Jpn. 2009, 87, 895–912. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical Study of Convection Observed during the Winter Monsoon Experiment Using a Mesoscale Two-Dimensional Model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- National Centers for Environmental Information-National Oceanic and Atmospheric Administration (NOAA-NCEI). Daily Precipitation, Temperature and Snow Depth Time Series for the Bialystok, PL Station (ID: PLM00012295) 2010–2014; NOAA-NCEI: Washington, DC, USA, 2017.
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorologische Zeitschrift 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Berezowski, T.; Chormański, J.; Batelaan, O.; Canters, F.; Van de Voorde, T. Impact of remotely sensed land-cover proportions on urban runoff prediction. Int. J. Appl. Earth Obs. Geoinf. 2012, 16, 54–65. [Google Scholar] [CrossRef]
- Kioutsioukis, I.; de Meij, A.; Jakobs, H.; Katragkou, E.; Vinuesa, J.F.; Kazantzidis, A. High resolution WRF ensemble forecasting for irrigation: Multi-variable evaluation. Atmos. Res. 2016, 167, 156–174. [Google Scholar] [CrossRef]
- Yu, W.; Nakakita, E.; Kim, S.; Yamaguchi, K. Impact Assessment of Uncertainty Propagation of Ensemble NWP Rainfall to Flood Forecasting with Catchment Scale. Adv. Meteorol. 2016, 2016, 1384302. [Google Scholar] [CrossRef]
- García-Díez, M.; Fernández, J.; Fita, L.; Yagüe, C. Seasonal dependence of WRF model biases and sensitivity to PBL schemes over Europe. Q. J. R. Meteorol. Soc. 2012, 139, 501–514. [Google Scholar] [CrossRef]
- Chybicki, A.; Łubniewski, Z.; Kamiński, L.; Bruniecki, K.; Markiewicz, L. Numerical weather prediction-data fusion to GIS systems and potential applications. In The Future with GIS. Katedra Systemow Geoinformatycznych; Krvatski Informsticki Zbor—GIS Forum: Zagreb, Croatia, 2011; pp. 56–61. [Google Scholar]
- Barbetta, S.; Coccia, G.; Moramarco, T.; Todini, E. Case Study: A Real-Time Flood Forecasting System with Predictive Uncertainty Estimation for the Godavari River, India. Water 2016, 8, 463. [Google Scholar] [CrossRef]
- Barge, J.; Sharif, H. An Ensemble Empirical Mode Decomposition, Self-Organizing Map, and Linear Genetic Programming Approach for Forecasting River Streamflow. Water 2016, 8, 247. [Google Scholar] [CrossRef]
- Peng, T.; Zhou, J.; Zhang, C.; Fu, W. Streamflow Forecasting Using Empirical Wavelet Transform and Artificial Neural Networks. Water 2017, 9, 406. [Google Scholar] [CrossRef]
- Sung, J.; Lee, J.; Chung, I.M.; Heo, J.H. Hourly Water Level Forecasting at Tributary Affected by Main River Condition. Water 2017, 9, 644. [Google Scholar] [CrossRef]
- Wang, J.; Shi, P.; Jiang, P.; Hu, J.; Qu, S.; Chen, X.; Chen, Y.; Dai, Y.; Xiao, Z. Application of BP Neural Network Algorithm in Traditional Hydrological Model for Flood Forecasting. Water 2017, 9, 48. [Google Scholar] [CrossRef]
- Li, B.; Yang, G.; Wan, R.; Dai, X.; Zhang, Y. Comparison of random forests and other statistical methods for the prediction of lake water level: A case study of the Poyang Lake in China. Hydrol. Res. 2016, 47, 69–83. [Google Scholar] [CrossRef]
- Albers, S.J.; Déry, S.J.; Petticrew, E.L. Flooding in the Nechako River Basin of Canada: A random forest modeling approach to flood analysis in a regulated reservoir system. Can. Water Resour. J. Rev. Can. Ressour. Hydr. 2015, 41, 250–260. [Google Scholar] [CrossRef]
- Francke, T.; López-Tarazón, J.; Schröder, B. Estimation of suspended sediment concentration and yield using linear models, random forests and quantile regression forests. Hydrol. Process. 2008, 22, 4892–4904. [Google Scholar] [CrossRef]
- Buttle, J. Soil moisture and groundwater responses to snowmelt on a drumlin sideslope. J. Hydrol. 1989, 105, 335–355. [Google Scholar] [CrossRef]
- Bengtsson, L.; Westerström, G. Urban snowmelt and runoff in northern Sweden. Hydrol. Sci. J. 1992, 37, 263–275. [Google Scholar] [CrossRef]
- Tyszewski, S.; Kardel, I. Studium Hydrograficzne Doliny Rzeki Białej z Wytycznymi Do Zagospodarowania Rekreacyjnowypoczynkowego I Elementami Małej Retencji Oraz Prace Hydrologiczne Niezbdne Do Sporzdzenia Dokumentacji Hydrologicznej; Pro Woda: Warsaw, Poland, 2009. (In Polish) [Google Scholar]
- Givati, A.; Lynn, B.; Liu, Y.; Rimmer, A. Using the WRF Model in an Operational Streamflow Forecast System for the Jordan River. J. Appl. Meteorol. Climatol. 2012, 51, 285–299. [Google Scholar] [CrossRef]
- Harr, R. Some characteristics and consequences of snowmelt during rainfall in western Oregon. J. Hydrol. 1981, 53, 277–304. [Google Scholar] [CrossRef]
- Chu, H.; Wei, J.; Li, J.; Qiao, Z.; Cao, J. Improved Medium- and Long-Term Runoff Forecasting Using a Multimodel Approach in the Yellow River Headwaters Region Based on Large-Scale and Local-Scale Climate Information. Water 2017, 9, 608. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Records, R.M. Large snowmelt versus rainfall events in the mountains. J. Geophys. Res. Atmos. 2015, 120, 2375–2381. [Google Scholar] [CrossRef]
- Berezowski, T.; Chormański, J.; Batelaan, O. Skill of remote sensing snow products for distributed runoff prediction. J. Hydrol. 2015, 524, 718–732. [Google Scholar] [CrossRef]
- Berezowski, T.; Nossent, J.; Chormanski, J.; Batelaan, O. Spatial sensitivity analysis of snow cover data in a distributed rainfall-runoff model. Hydrol. Earth Syst. Sci. 2015, 19, 1887–1904. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berezowski, T.; Chybicki, A. High-Resolution Discharge Forecasting for Snowmelt and Rainfall Mixed Events. Water 2018, 10, 56. https://doi.org/10.3390/w10010056
Berezowski T, Chybicki A. High-Resolution Discharge Forecasting for Snowmelt and Rainfall Mixed Events. Water. 2018; 10(1):56. https://doi.org/10.3390/w10010056
Chicago/Turabian StyleBerezowski, Tomasz, and Andrzej Chybicki. 2018. "High-Resolution Discharge Forecasting for Snowmelt and Rainfall Mixed Events" Water 10, no. 1: 56. https://doi.org/10.3390/w10010056
APA StyleBerezowski, T., & Chybicki, A. (2018). High-Resolution Discharge Forecasting for Snowmelt and Rainfall Mixed Events. Water, 10(1), 56. https://doi.org/10.3390/w10010056




