Abstract
We report flow tube measurements of the effective sulfuric acid diffusion coefficient at ranges of different relative humidities (from ∼4 to 70%), temperatures (278, 288 and 298 K) and initial H2SO4 concentrations (from 1 × 106 to 1 × 108 molecules·cm−3). The measurements were carried out under laminar flow of humidified air containing trace amounts of impurities such as amines (few ppt), thus representing typical conditions met in Earth’s continental boundary layer. The diffusion coefficients were calculated from the sulfuric acid wall loss rate coefficients that were obtained by measuring H2SO4 concentration continuously at seven different positions along the flow tube with a chemical ionization mass spectrometer (CIMS). The wall loss rate coefficients and laminar flow conditions were verified with additional computational fluid dynamics (CFD) model FLUENT simulations. The determined effective sulfuric acid diffusion coefficients decreased with increasing relative humidity, as also seen in previous experiments, and had a rather strong power dependence with respect to temperature, around ∝ T5.6, which is in disagreement with the expected temperature dependence of ∼T1.75 for pure vapours. Further clustering kinetics simulations using quantum chemical data showed that the effective diffusion coefficient is lowered by the increased diffusion volume of H2SO4 molecules via a temperature-dependent attachment of base impurities like amines. Thus, the measurements and simulations suggest that in the atmosphere the attachment of sulfuric acid molecules with base molecules can lead to a lower than expected effective sulfuric acid diffusion coefficient with a higher than expected temperature dependence.
1. Introduction
Sulfate aerosols play a major role in atmospheric chemistry and significantly influence humans’ health and Earth’s climate. Particulate matter contributes to air pollution and acts as seeds for cloud droplets, thus affecting cloud properties and radiation budget.Gaseous sulfuric acid H2SO4, formed via oxidation of SO2 by OH radicals, is the most important driver of new particle formation in the present-day atmosphere, and the concentration of H2SO4 vapour has a significant impact on atmospheric particle number [1]. While gas-phase H2SO4 is reduced by molecular cluster formation and nucleation, its main sink is condensation on newly formed and pre-existing aerosol particles. The condensation process affects both the growth dynamics of atmospheric particle populations, and the amount of H2SO4 available for new particle formation. A key parameter in atmospheric mass transport calculations is the gas-phase diffusion coefficient (D), to which the condensation rate of vapour onto particle surface is proportional and dependent on the particle size [2]. Assessments of vapour concentrations [3] and modelling of particle growth and composition [4] are thus dependent on the values used for the binary diffusion coefficients. Under certain circumstances, the gas phase diffusion can even limit the overall rates of condensation and reactions of trace gases with aerosol particles via influencing the uptake of gas molecules onto the surface. The extensive and detailed discussion on gas phase diffusion limitations is given in Introduction section of Tang et al. (2014) [5]. Hanson and Eisele (2000) [6] showed that hydration of sulfuric acid molecules in the atmosphere can significantly lower the sulfuric acid diffusion coefficient. However, gaseous sulfuric acid vapour can also undergo strong clustering in the presence of base impurities, as noted in several previous experiments (e.g., [7,8,9,10]). Ammonia is the most abundant atmospheric base, but it does not cluster very strongly with sulfuric acid, in contrast to amines [8]. Amines are strong organic bases, and the most common and abundant amines in the atmosphere being the low-molecular weight aliphatic amines with carbon numbers of 1–6. In this study we focus only on mono-methyl-amine (MMA), dimethyl-amine (DMA) , and tri-methyl-amine (TMA). The sources of amines can be various, both anthropogenic (e.g., animal husbandry, fish processing, food industry, sewage) and natural (e.g., biodegradation of organic matter, ocean, vegetation) [11]. As the oxidative lifetime of gas-phase amines is relatively short, amines are likely to be important mainly around their sources, including densely populated regions and ocean areas with high biological activity. While the measurements of atmospheric amine concentration are sparse, it appears that amine mixing ratios in Earth’s continental boundary layer vary between less than 1 to few tens of ppt and often exhibit a day-time peak [11,12]. At few ppt amine concentrations the total atmospheric sulfuric acid likely exists as a mixture of partly hydrated pure sulfuric acid monomers and partly hydrated sulfuric acid monomers bound to amines, with some further contributions from clusters containing several sulfuric acid molecules [13]. Clustering kinetics simulations have suggested that at such few ppt amine concentrations, the effective diffusion coefficient of sulfuric acid is lowered due to amine binding [14], which on the other hand may be sensitive to temperature.
The Chapman-Enskog theory on gas kinetics predicts the binary diffusion coefficient to depend on the temperature as D ∝T1.5 when approximating the gas molecules as hard spheres. Fuller et al. (1966) [15] used a semi-empirical method based on the best nonlinear least square fit for a compilation of 340 experimental diffusion coefficients, and obtained a temperature dependence of T1.75. According to a compilation work of Marrero and Mason (1972) [16], the temperature dependence of diffusion coefficients in binary gas mixtures in most cases varies between T1.5 and T2. The Fuller et al. method is known to yield the smallest average error, hence it is still recommended for use [17].
In this paper we report the first laboratory measurements, to our knowledge, of the temperature dependence of the diffusion coefficient of sulfuric acid. The diffusion coefficient of H2SO4 was estimated from the first order rate coefficients of the wall losses of H2SO4 in a flow tube. All previous measurements of the sulfuric acid diffusion coefficient have been carried out also in a flow tube, but at fixed temperatures varying between 295 and 303 K depending on the measurement, and by using nitrogen as the carrier gas [6,18,19,20]. Here, we use air at atmospheric pressure as a carrier gas, and vary the relative humidities (from 4 to 70%), temperatures (278, 288 and 298 K) and initial H2SO4 concentrations (from 1 × 106 to 1 × 108 molecules· cm−3). Base impurities such as di-methyl-amine (DMA) and tri-methyl-amine (TMA) were unavoidably present in our experiment in concentrations of few ppt (as shown in Supplementary Materials, Table ST1), and most probably they originated from the carrier gas and its humidification (e.g., [9,21,22]). Thus, our measurements represent a range of typical conditions met in many locations of the lower troposphere.
We use several approaches to verify the experimental method, and examine our results against the predictions of the semi-empirical Fuller formula as well as data from the previous experiments. In addition, we assess the effect of molecular cluster formation by cluster kinetics simulations with quantum chemical input data.
2. Methods
The experimental setup used in this study was described in detail in our previous work [23,24] and therefore only a brief description is given here. All experiments were conducted at Finnish Meteorological Institute in Helsinki, and thus all above mentioned major sources of atmospheric amines are in the vicinity of the laboratory. The whole experimental apparatus consists of four main parts: a saturator, a mixing unit, a flow tube and the sulfuric acid detection system—Chemical Ionization Mass Spectrometer (CIMS) [25], presented in Figure 1. The H2SO4 wall loss measurements were carried out in a laminar flow tube at three temperatures of 278.20 (±0.2), 288.79 (±0.2), and 298.2 (±0.2) K using purified, particle free and dry air as a carrier gas. The flow tube is a vertically mounted cylindrical tube made of stainless steel with an inner diameter (I.D.) of 6 cm and a total length of 200 cm. The whole flow tube was insulated and kept at a constant temperature with two liquid circulating baths (Lauda RK-20). The flow tube consists of two 1 meter long parts; one of them is equipped with 4 holes in the distance of 20 cm from each other, see Figure 1. Sulfuric acid vapour was produced by passing a stream of carrier gas through a saturator filled with 95–97% wt sulfuric acid (J.T. Baker analysed). As a saturator we used a horizontal iron cylinder with Teflon insert (I.D. 5 cm) and it was thermally controlled using a liquid circulating bath (LAUDA RC-6). The temperature inside the saturator was measured with a PT100 themperature sensor (±0.05 K). The carrier gas saturated with H2SO4 was then introduced with a flow rate from 0.1 to 1 L·min−1 into the mixing unit made of Teflon and turbulently mixed with a stream of humidified particle free air. The saturator temperature and the flow tube temperature were kept the same (isothermal conditions, see Figure 1), and the amount of sulfuric acid in the system was then governed by the amount of flow through the saturator and the subsequent mixing flow. The only part that was not temperature-controlled was the mixing unit. The mixing unit, which was −18 cm from the beginning of the flow tube (see Figure 1), was kept slightly warmer to avoid any condensation and particle formation in it. However, with the experiments taking relatively long (hours, one profile) the mixing unit cooled down a bit (at 278 and 288 K), and thus the temperature gradient was not prominent. The mixing unit had following dimensions: O.D. = 10 cm, I.D. = 7 cm and height = 6 cm. The flow rate of the mixing air varied in most of the experiments from about 7 to 10 L·min−1. The mixing air was humidified with one pair of Nafion humidifiers (Perma Pure MH-110-12) connected in parallel, where the flow of the mixing air was split into half for longer residence time and better humidification in both humidifiers. Ultrapure water (Millipore, TOC less than 10 ppb, resistivity 18.2 MΩ·cm @25 °C) circulating in both humidifiers was temperature controlled with liquid circulating bath (Lauda RC-6 CS). Both lines of the carrier gas (saturator and mixing air) were controlled by a mass flow controller to within ±3% (MKS type 250). The relative humidity was measured at the centre and far end of the flow tube with two humidity and temperature probes (Vaisala HMP37E and humidity data processor Vaisala HMI38) within accuracy of ±3%. The sulfuric acid diffusion coefficients were estimated as a function of relative humidity from the H2SO4 loss measured by CIMS along the flow tube. The detailed information regarding the operational principles and calibration of CIMS is given in [25,26,27] and therefore will not be given here again. The charging and detection efficiency of CIMS in the presence of trace concentrations of base impurities is discussed thoroughly theoretically (e.g., [13,28]) and also in recent experimental reports (e.g., [9,10]). Possible attachment of base and/or water molecules to single H2SO4 molecules (at levels of impurities of this work) is not expected to have a notable effect on their detection efficiency. However, both free H2SO4 molecules and those bound to base and/or water molecules are detected as single H2SO4 molecules by CIMS, since the ligands are quickly lost upon the chemical ionization (e.g., [28]). In this study the actual H2SO4 concentrations are not of particular interest, we focus here only on relative loss of H2SO4 along the flow tube. The concentration of sulfuric acid in gas phase was measured as 97 m/z Da using CIMS along the flow tube (see Figure 1) at the beginning (0 cm), in the middle (100 cm) and at the lower part in distances of 120, 140, 160, and 180 cm from the beginning and at the outlet (200 cm) of the flow tube in a wide range of relative humidities from 4 to 70%. The concentrations of H2SO4 are reported here as measured values. The CIMS sampling flow rate was set to 7 L·min−1. In order to measure the H2SO4 concentration along the whole flow tube, an additional CIMS inlet sampling tube was used—a stainless steel tube with I.D. 10 mm and whole length of 122 cm (100 cm straight + 22 cm elbow-pipe). Considering the H2SO4 losses, the sampling tube behaves in the same way as the flow tube, that is, for constant steady conditions the relative losses are constant (independent of H2SO4 concentration). The detailed separate experiments on H2SO4 losses within the sampling tube are discussed in detail by Brus et al. (2011) [29]. The inlet of the CIMS was about the mid-height of the flow tube (110 cm from ground), the sampling tube thus covered whole necessary length for sampling from top to bottom of the flow tube. The CIMS’ rack was equipped with wheels allowing movement, and the CIMS was moved in horizontal direction of maximum distance of about 1 m from the flow tube when the sampling tube was connected to mid-height port of the flow tube. The experimental measurement proceeded in the following way: First, all the experimental conditions (temperature of saturator and flow tube, flow rates, relative humidity) were adjusted. Then, when the steady state was reached, the CIMS’ inlet was connected to the lowest hole at 200 cm and concentration of sulfuric acid was recorded for at least 20 min. Afterwards the CIMS’ inlet was moved up to the hole at 180 cm, and the same procedure was repeated until the last hole at the top of the tube was reached. To confirm the reproducibility of the experimental data the H2SO4 concentration at any arbitrary distance along the flow tube was measured again. Moreover, the reproducibility was checked by exchanging the flow tube parts, so that the part with 4 holes was moved up, and H2SO4 losses were measured in the distances 0, 20, 40, 60, 80, 100 and 200 cm, respectively. The flow tube parts were exchanged only for experiments conducted at 298 K. At lower temperatures (288 and 278 K), we only used a setup where the flow tube part with sampling ports was at the lower position (100–200 cm). Further details on the flow tube operation tests are provided in the Supplementary Materials.
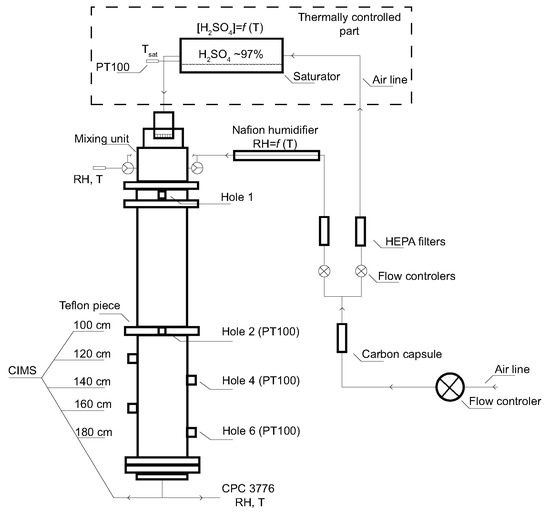
Figure 1.
The schematic figure of the FMI flow tube.
2.1. The CFD Simulations
To verify the assumption of laminar flow inside the tube, we applied the computational fluid dynamics (CFD) model FLUENT (Fluent version 16.2, ANSYS Inc., Canonsburg, PA, USA) which simulates flow based on the equations for mass and momentum conservation. These equations and the general operating principles of FLUENT are described in detail in [30,31,32,33]. It has to be noted that unlike the earlier studies, this work did not include the Fine Particle Model (FPM). Particle formation within the tube was thus not taken into account, and only sulfuric acid and water vapours are considered in the CFD FLUENT simulations. The simulations only considered the flow tube part of the experimental setup described in Section 2. Methods; the flow tube can be set up as an axisymmetric 2D problem. For the calculations presented here, we chose a resolution of 50 × 1000 cells. The same geometry has been used previously [32]. Boundary conditions (volumetric flow, wall temperatures, relative humidity, and initial sulfuric acid concentration) were set to match the experimental conditions , please see Supplementary Materials for details on boundary conditions and example profiles of H2SO4 concentration and velocity inside the flow tube. Generally, the wall was assumed to be an infinite sink for sulfuric acid, which means that the H2SO4 concentration at the walls was set to 0 in the simulations. However, we also carried out simulations where the wall was considered as a source of sulfuric acid; please see the discussion in the next section. The assigned properties for the sulfuric acid vapour were identical to the ones described in our earlier work [32]. Differing from Herrmann et al. (2010) [32], the setup was considered isothermal, i.e., there was no temperature gradient or buoyancy phenomena disturbing parabolic radial flow profile. An initial parabolic flow profile was used as the default flow profile for the all nominal simulations. To verify the proper operation of the experimental setup we applied the diffusion coefficient derived experimentally in this work in FLUENT simulations. The simulations yielded a profile of sulfuric acid concentration inside the flow tube which we compared back to the experimental results. This comparison was done to verify that the same assumptions used in the simulations and experiments (laminar flow and wall acting as an infinite sink) produced the same loss profiles.
2.2. Experimental Determination of the Diffusion Coefficient
We assume that the loss of H2SO4 to the walls of the flow tube is a diffusion controlled first-order rate process, which can be described by a simple equation:
where [H2SO4]0 is the initial concentration of H2SO4, [H2SO4]t is the concentration after time t and k (s−1) is the rate constant, which is given by the equation:
where r is the radius of the flow tube and D is the diffusion coefficient of H2SO4. Equation (2) is valid for diffusion in a cylindrical tube under laminar flow conditions and when the axial diffusion of the species investigated is negligible [34]. The slopes obtained from linear fits to the experimental data of ln([H2SO4]) as a function of the distance in the flow tube stand for the loss rate coefficient, kobs (cm−1), assuming that the first order loss to the flow tube wall is the only sink for the gas phase H2SO4. Multiplying the loss rate coefficient kobs with mean flow velocity in the flow tube (cm·s−1) yields the experimental first-order wall loss rate coefficient kw (s−1), from which the diffusion coefficients of H2SO4 were determined using Equation (2). The averaged values of mean flow velocities were 5.35 (±0.3), 5.27 (±0.2) and 4.5 (±1.1) for experiments at temperatures 278, 288 and 298 K, respectively. Most of the initial tests were carried out at 298 K, at which the spread of the mean flow velocities is wider. Hanson and Eisele (2000) [6] reported that the wall of the flow tube can act as a source of H2SO4 vapour after exposure in long lasting experiments and under very low relative humidity (RH ≤∼0.5%). The accuracy of our RH measurements is ±3% RH, so to avoid any influence of H2SO4 evaporation from the flow tube wall we only used data measured at RH ≥ 4% in the final analysis. Furthermore, we performed CFD FLUENT simulations at RH = 5% and T = 298 K, where we do not assume an infinite sink of H2SO4 on the wall, but instead apply several boundary conditions for the CFD model with increased H2SO4 concentrations on the flow tube wall (0–100% of [H2SO4]0), as shown in Figure 2. The comparison suggests that in our measurements the concentration on the flow tube wall is below 6% of the [H2SO4]0 under all conditions. When the H2SO4 concentration on the wall is ≤6% of [H2SO4]0, the resulting difference in the obtained diffusion coefficient is within 10% when compared to diffusion coefficient obtained with infinite sink boundary condition on the wall, as indicated by the shaded box in bottom left corner in Figure 2b. In other words, when the flow tube wall is emitting up to 6% of [H2SO4]0, we are not able to recognize it in our experiment, since the change in the obtained diffusion coefficient is smaller than our 10% experimental uncertainty. Any higher H2SO4 concentration at the wall than 6% of [H2SO4]0 would lead to a larger than 10% decrease in the obtained diffusion coefficient. Another experimental method to examine the assumption that the wall of the flow tube acts as an infinite sink is to measure the diffusion coefficient as a function of pressure (e.g., [35,36]). Since in systems including easily nucleating substances like H2SO4 a small change in the pressure can initiate strong new particle formation, i.e., secondary losses in the system, this method was not suitable for our study.
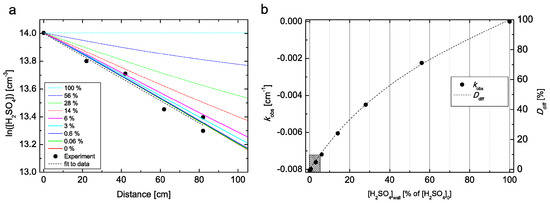
Figure 2.
Results from computational fluid dynamics (CFD) FLUENT simulations on the influence of increased H2SO4 concentration on the flow tube wall. (a) ln[H2SO4] as function of distance in the flow tube. (b) kobs and diffusion coefficient difference from the infinite sink boundary condition (Ddiff) as a function of the H2SO4 concentration on the wall expressed as % of the initial H2SO4 concentration, [H2SO4]0. The simulations conditions were RH = 5%, T = 298 K and Qtot = 7.6 L·min−1. When the H2SO4 concentration on the wall is ≤ 6% of [H2SO4]0, the resulting difference in the obtained diffusion coefficient is within 10% when compared to diffusion coefficient obtained with infinite sink boundary condition on the wall, as indicated by the shaded box in bottom left corner in Figure 2b. The H2SO4 concentrations are low, ranging from 6.5 × 105 to 1.2 × 106 molecules· cm−3, and the points at each distance are averaged over 20-min with a standard deviation of less than 10% of the average value.
2.3. Quantum Chemical Data and Cluster Kinetics Modelling
To assess the effects of base impurities on the measurement results, we performed clustering kinetics simulations using quantum chemical input data for the stabilities of H2SO4—base clusters as described by Olenius et al. (2014) [14]. Since recent theoretical studies (e.g., [13,37,38]) suggest and experiments (e.g., [8,10,23,39,40]) confirm that amines are more effective in stabilizing sulfuric acid clusters than ammonia, even taking into account the much higher abundance of ammonia, we focus only on the clustering of sulfuric acid with dimethylamine (DMA) and trimethylamine (TMA) and their hydrates (see also Section 3.2 Effect of Base Contaminants in Olenius et al. 2014) [14]. The cluster kinetics approach does not consider the 2D flow profile, but only the central stream line of the flow, from which clusters and molecules are lost by diffusion. This is considered a reasonable assumption for a laminar flow, as also indicated by the CFD FLUENT modelling results (see the Section 3). Detailed information on the simulations, as well as extensive discussion on the effects of clustering on the apparent diffusion coefficient can be found in the study by Olenius et al. (2014) [14], and the details of the present simulations are in the Supplementary Materials. The effective diffusion coefficient corresponding to the experimental approach was determined by simulating the time evolution of the molecular cluster concentrations using cluster evaporation rates based on quantum chemical calculations at the B3LYP/CBSB7//RICC2/aug-cc-pV(T+d)Z level of theory. The initial base concentration was considered to be a) constant during the experiment, or b) RH dependent, i.e., base molecules enter the system with the water vapour; such a scenario seems to be reasonable since it was observed in several experimental set-ups (e.g., [21,22,29] and also confirmed in our experiments, see Supplementary Materials. In the second case we set the initial base concentration [base]init to be linearly proportional to RH as
where the linear relationship was based on a fit to DMA concentrations measured at various RH, in a separate experiment, where only ultrapure water was used and no sulfuric acid involved. The DMA slope was chosen, since it was found steeper than TMA slope, thus providing higher estimate, see Supplementary Materials for a measurement method description. The measured dry values [base]dry were based on another separate experiment where only sulfuric acid at dry conditions was used, values at all three temperatures are tabulated in Supplementary Materials (Table ST1). The [base]dry values were found higher in experiment with sulfuric acid than ultrapure water, again higher estimates are used in Equation (3). The resulting initial base concentrations [base]init for DMA and TMA were 4 and 2 ppt, respectively, at dry conditions (RH = 0%), and 10 and 8 ppt at RH = 60%. However, we have to point out, that this RH dependence of amines is specific for the present set-up [41,42].
3. Results and Discussion
Figure 3 shows the diffusion coefficients of H2SO4, determined from the loss rate coefficients kw (s−1) using Equation (2) as a function of RH at the three temperatures of 278, 288 and 298 K. The measured points are accompanied with the fit and H2SO4–N2 data at 298 K reported by Hanson and Eisele (2000) [6], and Hanson (2005) [20] at 295 K. Initially, the increase in RH decreased the obtained diffusion coefficient, and the dependence of diffusion coefficient on RH flattens in the range of RH between 20 and 70%. These results indicate slower diffusion to the wall due to strong hydration of H2SO4 molecules [43] and possibly H2SO4 clustering with base impurities. There are four previously reported experimental values of the H2SO4 diffusion coefficient in nitrogen. Pöschl et al. (1998) [19] reported a value of 0.088 cm2·s−1 at T = 303 K and RH ≤ 3%, Lovejoy and Hanson (1996) [18] reported a value of 0.11 cm2·s−1 at T = 295 K and RH ≤ 1%, the study of Hanson and Eisele (2000) [6] yielded a value of 0.094 cm2·s−1 at T = 298 K, and Hanson (2005) [20] reported value of 0.088 cm2·s−1 at T = 295 K, both for RH ≤ 1%. The value of the diffusion coefficient of H2SO4 in air at T = 298 K and RH = 4% determined in this study is 0.08 cm2·s−1, which is in reasonable agreement with previously reported values, although the comparison is complicated because of slightly different experimental conditions and different carrier gases. The relatively larger scatter in our dataset compared to Hanson and Eisele (2000) [6] and Hanson (2005) [20] is because our experiments are carried out at close to atmospheric concentration of H2SO4 i.e., about two orders lower concentrations. In Figure 4 the H2SO4 losses simulated with the CFD FLUENT model described in Section 2.1 are compared with experimental values, which were measured in a separate set of experiments conducted at T = 278, 288 and 298 K. The linear fit to the experimental data represents the loss rate coefficients (kobs, cm−1).
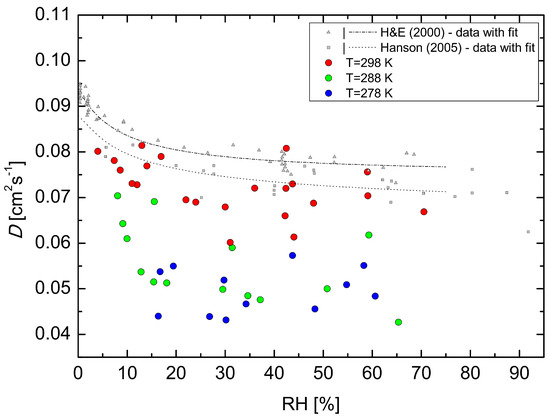
Figure 3.
Experimental diffusion coefficient of H2SO4 in air as a function of relative humidity at different temperatures compared with the data of Hanson and Eisele (2000) [6] at 298 K and Hanson (2005) [20] at 295 K of H2SO4 diffusion in N2.
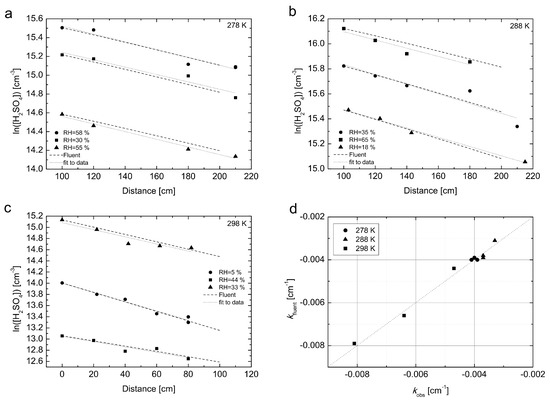
Figure 4.
The sulfuric acid losses simulated with CFD FLUENT model when the experimentally obtained diffusion coefficients are used as an input at (a) T = 278 K; (b) T = 288 K and (c) T = 298 K. (d) simulated losses rate coefficients compared with experimental values of kobs (cm−1) at T = 278, 288 and 298 K. The instances of each symbol in panel (d) represent loss rate coefficient at different relative humidities, the lowest relative humidity having the steepest slope (the highest absolute value of loss rate coefficient).
As can be seen from Figure 4, the model describes the behaviour of H2SO4 in the flow tube very well and confirms the validity of laminar flow approximation for all three temperatures. The maximum difference between the experimental and simulated values of the loss rate coefficient (kobs) was found 7%, see Figure 4d for details. Additionally, we made the following set of CFD simulations for all three temperatures and a constant mid-range RH ≈ 30%: (a) we used the diffusion coefficient obtained from the experiment, but with a constant (flat-plug type) flow profile as initial condition; (b) we used diffusion coefficients obtained from Equation (3) in Hanson and Eisele (2000) [6] with the temperature dependence of ∼T1.75 obtained from literature, and an initial parabolic flow profile. The simulations are summarized in Figure S4 in Supplementary Materials. Clearly, the two alternative approaches were not able to reproduce the measured loss profile. The losses are underestimated for case (a) and overestimated for case (b) compared to our above mentioned approach, where we use the experimentally obtained diffusion coefficient and initial parabolic flow profile.
Semi-empirical predictions for binary diffusion coefficients can be calculated from the Fuller et al. equation which is based on fits to experimental data of various gases as described by Fuller et al. (1966) [15] and Reid et al. (1987) [17]:
where DAB is the binary diffusion coefficient of species A and B (cm2·s−1), T is the temperature (K), P is the pressure (bar), MAB is 2((1/MA) + (1/MB))−1 (g·mol−1), where MA and MB are the molecular weights of species A and B (g·mol−1), and ∑v is calculated for each component by summing its atomic diffusion volumes [17]. The functional form of Equation (4) is based on the kinetic gas theory (the Chapman-Enskog theory), and the temperature dependence is obtained from a fit to a large set of experimental diffusion coefficients. A purely theoretical approach based on the kinetic gas theory with the hard-spheres approximation would yield a dependence of T1.5. The calculated values of the diffusion coefficients of H2SO4, dimethylamine- and trimethylamine-sulfate in dry air at 298 K using the Fuller method are 0.11, 0.08 and 0.074 cm2·s−1, respectively, which is in a reasonable agreement with our experimental data—the measured diffusion coefficient of H2SO4 at T = 298 K under close to dry conditions (RH 4%) is 0.08 (cm2·s−1). However, when calculating the diffusion coefficients of H2SO4 in dry air at lower temperatures (278 and 288 K) with the Fuller method, the agreement of the experimental values with the predictions deteriorates. The formula predicts significantly higher diffusion coefficients than those observed in the experiments. The calculated values of DAB for H2SO4 are 0.104 cm2·s−1 at T = 288 K and 0.098 cm2·s−1 at T = 278 K, and the measured values are 0.07 cm2·s−1 at (T = 288 K and RH = 8%) and 0.054 cm2·s−1 at (T = 278 K and RH = 16%), respectively. The temperature dependence of the experimental diffusion coefficients was found to be a power of 5.6 for the whole dataset and temperature range, when averaged over the RH between 15–70%. Since the data show a clear stepwise temperature dependence we provide also two separate fits to data from 278 to 288 K and from 288 to 298 K, with power dependencies of 1.9 and 9.4, respectively. These numbers are striking when compared to the empirical method of Fuller et al. (1966) [15], who obtained the best fit to 340 experimental diffusion coefficients with the power dependence of T1.75. In Figure 5 we show the temperature dependence of the experimental data obtained from literature [6,18,19], predictions of the Fuller method [15] for the diffusion coefficients of sulfuric acid, dimethylamine- and trimethylamine-sulfates in dry air, results of the clustering kinetics simulations using quantum chemical data for several simulated systems (discussed below), and the experimental data of this work. The data collected from literature, all obtained using laminar flow technique and N2 as the carrier gas, show a temperature dependence opposite to the one expected from theory. However, the range of temperatures at which the measurements were carried out is quite narrow (only 8 K) and different experimental set-ups could explain such behaviour.
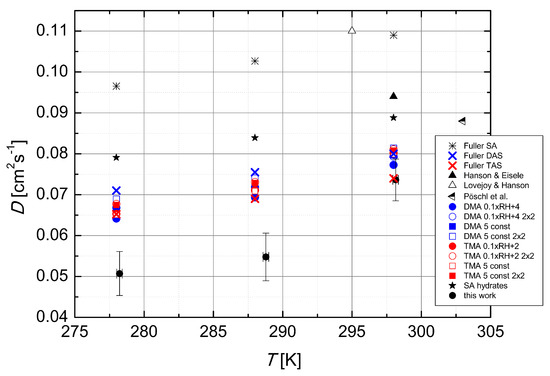
Figure 5.
The temperature dependence of the effective H2SO4 diffusion coefficient, calculated using the Fuller method for dry H2SO4 (SA), dimethylamine-(DAS) and trimethylamine-sulfate (TAS), both in dry air, data from literature, several assemblies of cluster population simulations (see text for details) and data measured experimentally in this work. The temperature dependence of the experimental diffusion coefficients was found to be a power of 5.6.
In order to explain the experimental observation of the temperature dependence of the diffusion coefficient, the dimer to monomer ratio at different temperatures was investigated. The CIMS was used to measure the concentrations of H2SO4 gas phase monomers and dimers during the experiments; larger clusters were outside the mass range of the CIMS used. The H2SO4 dimer formation is a result of H2SO4 monomer collisions, and thus the observed H2SO4 dimer CIMS signal depends on the H2SO4 monomer concentration and also on the residence time, which determinates the time available for the clustering to take place [7]. No significant temperature dependence of the dimer to monomer concentration ratio was observed in our experiments, which is in agreement with Eisele and Hanson (2000) [6], who reported a relatively constant H2SO4 dimer to monomer concentration ratio with lowering temperature (the temperature range investigated in their study was 235–250 K). On the other hand, they reported a substantial increase in the larger clusters’ (trimer and tetramer) concentration with decreasing temperature while the monomer concentration was almost constant. There are only a very few previously reported values of the sulfuric acid dimer to monomer ratio from laboratory experiments. Petäjä et al. (2011) [7] studied the close to collision-limited sulfuric acid dimer formation under experimental conditions similar to our study (T = 293 K, RH = 22%, initial H2SO4 concentrations from 106 to 108 molecule cm−3 with saturator containing liquid H2SO4 and in-situ H2SO4 using O3-photolysis as methods for producing gas phase H2SO4). They reported H2SO4 dimer to monomer concentration ratios ranging from 0.05 to 0.1 at RH = 22% and a residence time of 32 s. Petäjä et al. (2011) [7] speculate about the presence of a third stabilizing compound, and their experimental dimer formation rates correspond well to modelled rates at a DMA concentration of about 5 ppt. Almeida et al. (2013) [8] reported the dimer to monomer concentration ratios from 0.01 to 0.06 for the experiments in CLOUD chamber with addition of DMA (3–140 ppt, with the effect saturated for addition >5 ppt) and the dimer to monomer concentration ratios from 1 × 10−4 to 0.003 for pure binary H2SO4-water system, both at RH = 38% and T = 278 K. In our measurements the H2SO4 dimer to monomer concentration ratio under conditions T = 298 K, RH = 24% and a residence time of ∼37 s, spans the range from 0.03 to 0.11, which is in reasonable agreement with reported values [7,8], when trace impurity levels of DMA are present in the system.
The formation of particles inside the flow tube during the experiments was measured regularly using Ultrafine Condensation Particle Counter (UCPC model 3776, TSI Inc., Shoreview, MN, USA) with the lower detection limit of 3 nm. The highest determined concentration of particles was approximately 2 × 104 yielding the maximum nucleation rate J of ∼500 particles cm3·s−1 at T = 278 K and RH = 60%. Since the nucleation rate was increasing with decreasing temperature and elevated RH in the flow tube, the loss of gas phase sulfuric acid to the particles was more pronounced at temperatures of 288 and 278 K. The losses of H2SO4 to particles were minimal—units of percent [9,29] and cannot explain our experimental observation of increased H2SO4 diffusion coefficient temperature dependence. The additional losses of H2SO4 would lead to increased values of observed loss rate coefficient (kobs) and subsequently to higher diffusion coefficient. The origin of the discrepancy in the temperature dependence of the diffusion coefficient in our experiment remains unclear; however, a plausible explanation is the increased clustering of H2SO4 at lower temperatures (see explanation below) with base molecules such as amines. The cluster population simulations using quantum chemical data (see Figure 5 and Figure 6, Table 1) show that the presence of base impurities can decrease the effective H2SO4 diffusion coefficient via the attachment of base molecules to the acid molecule. Simulations considering only hydrated H2SO4 molecules and no bases give higher values for the diffusion coefficient, and also a notably less steep temperature dependence (Table 1). Also, the stepwise behaviour of temperature dependence can be found in cluster population simulations when fits are performed separately for temperatures 278–288 K and 288–298 K, see Table 1.
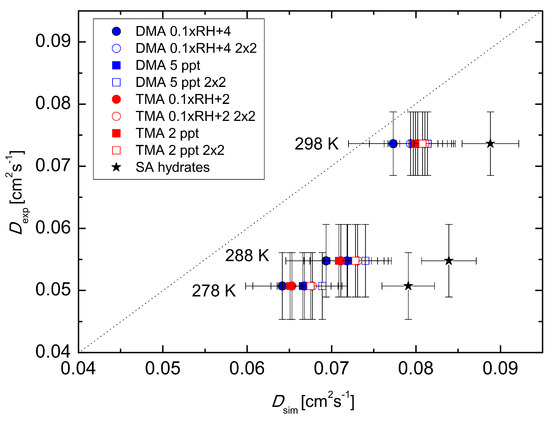
Figure 6.
Comparison of the experiment and the cluster population simulations at different temperatures, considered are also different levels and sources of impurities in the system. The formation of clusters containing up to two H2SO4 and two base molecules is denoted as “2 × 2” in the legend.

Table 1.
Summary of simulated and experimental averages (unweighted over the range of RH that is covered at all three temperatures (15–70%)) of the effective H2SO4 diffusion coefficients D (cm2·s−1) with standard deviations in parenthesis for three temperatures 278, 288 and 298 K. The initial base concentration [base]init is set to be either RH-dependent according to Equation (3) or RH-independent, and the simulations consider clusters containing up to one acid and one base molecule (1 × 1) or two acid and two base molecules (2 × 2) as well as hydrates of the clusters. Power dependencies with respect to the temperature, obtained as linear fits to the data, are also listed.
This stepwise behaviour corresponds to that obtained in the experiments. Overall, cluster population simulations demonstrate that temperature-dependent clustering can change the magnitude and temperature behaviour of the effective diffusion coefficient. Results obtained by simulating clusters containing H2SO4 and DMA are closer to the experimental diffusion coefficient values than those obtained using H2SO4 and TMA. On the other hand, the power dependence shows a better agreement for the H2SO4–TMA system (see Table 1). The best agreement between the simulations and the experiment was found for the temperature 298 K. Also, changing the base concentration according to Equation (3) shows a better performance than keeping the base concentration constant. Allowing the formation of clusters containing up to two H2SO4 and two base molecules has no significant effect. In principle, the larger clusters bind H2SO4 molecules and may thus increase the apparent diffusion coefficient, but here their effect is minor due to the relatively low initial H2SO4 concentration of 5 × 106 cm−3 used in the simulations. More analysis on the effects of the amines can be found in the work by Olenius et al. (2014) [14].
4. Conclusions
We have presented measurements of sulfuric acid diffusion coefficient in air derived from the first-order rate coefficients of wall loss of H2SO4. The experiments were performed in a laminar flow tube at temperatures of 278, 288 and 298 K, relative humidities from 4 to 70%, under atmospheric pressure and at initial H2SO4 concentrations from 106 to 108 molecules · cm−3. The carrier gas also contained trace amounts of impurities such as amines (few ppt). The chemical ionization mass spectrometer (CIMS) was used to measure H2SO4 gas phase concentration at seven different positions along the flow tube. The wall losses were determined from the linear fits to experimental ln[H2SO4] as a function of axial distance in the flow tube. The losses of H2SO4 inside the flow tube were also simulated using a computational fluid dynamics model (CFD FLUENT), in which the wall is assumed to be an infinite sink for H2SO4. The experimentally determined H2SO4 losses along the flow tube were in a very good agreement with profiles calculated using the FLUENT model, where experimentally obtained diffusion coefficients were used as an input. A maximum difference of 7% for experiments conducted at T = 278, 288 and 298 K and in the whole RH range was found when compared to model. The results of the fluid dynamics model (CFD FLUENT) also satisfactory confirm the assumption of fully developed laminar profile inside the flow tube and infinite sink boundary conditions on the wall for H2SO4 loss.
To explain an unexpectedly high power dependence of the H2SO4 diffusion coefficient on temperature observed in our system we accounted in our calculations for involvement of base impurities: dimethyl- (DMA) and trimethyl-amine (TMA). The semi-empirical Fuller formula [15] was used to calculate the diffusion coefficients at dry conditions for solely H2SO4, and H2SO4 neutralized with amine bases, namely dimethyamine- and trimethylamine-sulfate. Further, a molecular cluster kinetics model [14] with quantum chemical input data was used to simulate acid-base cluster formation that may lead to the observed behaviour. With the simulations we obtained an effective diffusion coefficient determined in the same way as in the experiments.
The experimental H2SO4 diffusion coefficients were found to be independent of different initial [H2SO4] and a wide range of total flow rates. The values of the diffusion coefficient were found to decrease with increasing relative humidity owing to stronger hydration of H2SO4 molecules. The observed power dependence of the experimental diffusion coefficients as a function of temperature was found to be of the order of 5.6 when the range of RH that is covered at all three temperatures (15–70%) is accounted for which is in a clear disagreement with predictions from the Fuller method [15] having a power dependence of 1.75. Since the experimental diffusion coefficients deviate more from the theory towards the lower temperatures of 278 and 288 K, we suggest that a plausible explanation for this discrepancy is involvement of impurities such as amines, capable of binding to acid molecules with the binding strength increasing with decreasing temperature. This hypothesis is qualitatively supported by clustering kinetics simulations performed using quantum chemical input data for H2SO4–dimethylamine and H2SO4–trimethylamine clusters. Our results indicate that the effective diffusion coefficient of H2SO4 in air exhibits a stronger temperature dependence than predicted from a theory that does not consider cluster formation. Neglecting this dependence might result in incorrect determination of residual H2SO4 concentration in laboratory experiments and lead to biases in atmospheric aerosol models in the presence of amines due to effects on the effective diffusion coefficient and thus on the condensation rate. However, more measurements are needed to gain a better understanding on the role of clustering and the magnitude of the temperature dependence of the H2SO4 diffusion coefficient.
Supplementary Materials
Tests of flow tube proper operation, impurity measurements and additional CFD simulations are available online at www.mdpi.com/2073-4433/8/7/132/s1.
Acknowledgments
Authors would like to acknowledge KONE foundation, project CSF No. P209/11/1342, ERC project 257360-MOCAPAF, the Academy of Finland Centre of Excellence (project number: 272041), Formas project 2015-749 and Academy of Finland (project number: 288440) for their financial support.
Author Contributions
D.B. and L.S. designed and performed the experiments; E.H. and T.T. run the CDF-FLUENT simulations, analyzed and interpreted the simulation data; T.O. performed the clustering kinetics simulations using quantum chemical data; U.M. performed the MS-MARGA chemical composition analysis, all authors contributed to synthesis of data and the article writting.
Conflicts of Interest
The authors declare no conflict of interest.The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CIMS | Chemical Ionization Mass Spectrometer |
| CFD | Computational Fluid Dynamics |
| FPM | Fine Particle Model |
| TOC | Total Organic Carbon |
| UCPC | Ultrafine Condensation Particle Counter |
| SA | Sulfuric Acid |
| MMA | Monomethylamine |
| DMA | Dimethylamine |
| TMA | Trimethylamine |
| DAS | Dimethylamine-sulfate |
| TAS | Trimethylamine-sulfate |
References
- Dunne, E.M.; Gordon, H.; Kürten, A.; Almeida, J.; Duplissy, J.; Williamson, C.; Ortega, I.K.; Pringle, K.J.; Adamov, A.; Baltensperger, U.; et al. Global atmospheric particle formation from CERN CLOUD measurements. Science 2016, 354, 1119–1124. [Google Scholar] [CrossRef] [PubMed]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change; John Wiley: New York, NY, USA, 1998. [Google Scholar]
- Pierce, J.R.; Adams, P.J. A Computationally Efficient Aerosol Nucleation/Condensation Method: Pseudo-Steady-State Sulfuric Acid. Aerosol Sci. Tech. 2009, 43, 216–226. [Google Scholar] [CrossRef]
- Hodshire, A.L.; Lawler, M.J.; Zhao, J.; Ortega, J.; Jen, C.; Yli-Juuti, T.; Brewer, J.F.; Kodros, J.K.; Barsanti, K.C.; Hanson, D.R.; et al. Multiple new-particle growth pathways observed at the US DOE Southern Great Plains field site. Atmos. Chem. Phys. 2016, 16, 9321–9348. [Google Scholar] [CrossRef]
- Tang, M.J.; Cox, R.A.; Kalberer, M. Compilation and evaluation of gas phase diffusion coefficients of reactive trace gases in the atmosphere: Volume 1. Inorganic compounds. Atmos. Chem. Phys. 2014, 14, 9233–9247. [Google Scholar] [CrossRef]
- Hanson, D.R.; Eisele, F.L. Diffusion of H2SO4 in humidified nitrogen: Hydrated H2SO4. J. Phys. Chem. A 2000, 104, 1715–1719. [Google Scholar] [CrossRef]
- Petäjä, T.; Sipilä, M.; Paasonen, P.; Nieminen, T.; Kurtén, T.; Ortega, I.K.; Stratmann, F.; Hanna Vehkamäki, H.; Berndt, T.; Kulmala, M. Experimental Observation of Strongly Bound Dimers of Sulphuric Acid: Application to Nucleation in the Atmosphere. Phys. Rev. Lett. 2011, 106, 228302. [Google Scholar] [CrossRef] [PubMed]
- Almeida, J.; Schobesberger, S.; Kürten, A.; Ortega, I.K.; Kupiainen-Määttä, O.; Praplan, A.P.; Adamov, A.; Amorim, A.; Bianchi, F.; Breitenlechner, M.; et al. Molecular understanding of sulphuric acid-amine particle nucleation in the atmosphere. Nature 2013, 502, 359–363. [Google Scholar] [CrossRef] [PubMed]
- Neitola, K.; Brus, D.; Makkonen, U.; Sipilä, M.; Mauldin III, R.L.; Sarnela, N.; Jokinen, T.; Lihavainen, H.; Kulmala, M. Total sulfate vs. sulfuric acid monomer concenterations in nucleation studies. Atmos. Chem. Phys. 2015, 15, 3429–3443. [Google Scholar] [CrossRef][Green Version]
- Rondo, L.; Ehrhart, S.; Kürten, A.; Adamov, A.; Bianchi, F.; Breitenlechner, M.; Duplissy, J.; Franchin, A.; Dommen, J.; Donahue, N.M.; et al. Effect of dimethylamine on the gas phase sulfuric acid concentration measured by Chemical Ionization Mass Spectrometry (CIMS). J. Geophys. Res. Atmos. 2016, 120, 3036–3049. [Google Scholar] [CrossRef] [PubMed]
- Ge, X.; Wexler, A.S.; Clegg, S.L. Atmospheric amines—Part I. A review. Atmos. Environ. 2011, 45, 524–546. [Google Scholar] [CrossRef]
- Hanson, D.R.; McMurry, P.H.; Jiang, J.; Tanner, D.; Huey, L.G. Ambient pressure proton transfer mass spectrometry: Detection of amines and ammonia. Environ. Sci. Technol. 2011, 45, 8881–8888. [Google Scholar] [CrossRef] [PubMed]
- Kupiainen-Määttä, O.; Olenius, T.; Kurtén, T.; Vehkamäki, H. CIMS Sulfuric Acid Detection Efficiency Enhanced by Amines Due to Higher Dipole Moments: A Computational Study. J. Phys. Chem. A 2013, 117, 14109–14119. [Google Scholar] [CrossRef] [PubMed]
- Olenius, T.; Kurtén, T.; Kupiainen-Määttä, O.; Henschel, H.; Ortega, I.K.; Vehkamäki, H. Effect of Hydration and Base Contaminants on Sulfuric Acid Diffusion Measurement: A Computational Study. Aerosol Sci. Technol. 2014, 48, 593–603. [Google Scholar] [CrossRef]
- Fuller, E.N.; Schettler, P.D.; Giddings, J.C. New method for prediction of binary gas-phase diffusion coefficients. Ind. Eng. Chem. 1966, 58, 18–27. [Google Scholar] [CrossRef]
- Marrero, T.R.; Mason, E.A. Gaseous Diffusion Coefficients. J. Phys. Chem. Ref. Data 1972, 1, 3–118. [Google Scholar] [CrossRef]
- Reid, R.C.; Prausnitz, J.M.; Polling, B.E. The Properties of Gases and Liquids, 4th ed.; Mc Graw-Hill Inc.: New York, NY, USA, 1987. [Google Scholar]
- Lovejoy, E.R.; Hanson, D.R. Kinetics and products of the reaction SO3 + NH3 + N2. J. Phys. Chem. 1996, 100, 4459–4465. [Google Scholar] [CrossRef]
- Pöschl, U.; Canagaratna, M.; Jayne, J.T.; Molina, L.T.; Worsnop, D.R.; Kolb, C.E.; Molina, M.J. Mass accommodation coefficient of H2SO4 vapor on aqueous sulphuric acid surfaces and gaseous diffusion coefficient of H2SO4 in N2H2O. J. Phys. Chem. A 1998, 102, 10082–10089. [Google Scholar] [CrossRef]
- Hanson, D.R. Mass accommodation of H2SO4 and CH3SO3H on water-sulfuric acid solutions from 6% to 97% RH. J. Phys. Chem. A 2005, 109, 6919–6927. [Google Scholar] [CrossRef] [PubMed]
- Benson, D.R.; Yu, J.H.; Markovich, A.; Lee, S.-H. Ternary homogeneous nucleation of H2SO4, NH3, and H2O under conditions relevant to the lower troposphere. Atmos. Chem. Phys. 2011, 11, 4755–4766. [Google Scholar] [CrossRef]
- Kirkby, J.; Curtius, J.; Almeida, J.; Dunne, E.; Duplissy, J.; Ehrhart, S.; Franchin, A.; Gagné, S.; Ickes, L.; Kürten, A.; et al. Role of sulphuric acid, ammonia and galactic cosmic rays in atmospheric aerosol nucleation. Nature 2011, 476, 429–433. [Google Scholar] [CrossRef] [PubMed]
- Neitola, K.; Brus, D.; Makkonen, U.; Sipilä, M.; Lihavainen, H.; Kulmala, M. Effect of addition of four base compounds on sulphuric-acid–water new-particle formation: A laboratory study. Boreal Env. Res. 2014, 19 (Suppl. B), 257–274. [Google Scholar]
- Skrabalova, L.; Brus, D.; Antilla, T.; Zdimal, V.; Lihavainen, H. Growth of sulphuric acid nanoparticles under wet and dry conditions. Atmos. Chem. Phys. 2014, 14, 1–15. [Google Scholar] [CrossRef][Green Version]
- Eisele, F.L.; Tanner, D. Measurement of the gas phase concentration of H2SO4 and methane sulphonic acid and estimates of H2SO4 production and loss in the atmosphere. J. Geophys. Res. 1993, 98, 9001–9010. [Google Scholar] [CrossRef]
- Mauldin, R.L., III; Frost, G.; Chen, G.; Tanner, D.; Prevot, A.; Davis, D.; Eisele, F. OH measurements during the First Aerosol Characterization Experiment (ACE 1): Observations and model comparisons. J. Geophys. Res. 1998, 103, 16713–16729. [Google Scholar] [CrossRef]
- Petäjä, T.; Mauldin, R.L., III; Kosciuch, E.; McGrath, J.; Nieminen, T.; Paasonen, P.; Boy, M.; Adamov, A.; Kotiaho, T.; Kulmala, M. Sulphuric acid and OH concentrations in a boreal forest site. Atmos. Chem. Phys. 2009, 9, 7435–7448. [Google Scholar] [CrossRef]
- Ortega, I.; Olenius, T.; Kupiainen-Määttä, O.; Loukonen, V.; Kurtén, T.; Vehkamäki, H. Electrical charging changes the composition of sulfuric acid–ammonia/dimethylamine clusters. Atmos. Chem. Phys. 2014, 14, 7995–8007. [Google Scholar] [CrossRef]
- Brus, D.; Neitola, K.; Hyvärinen, A.-P.; Petäjä, T.; Vanhanen, J.; Sipilä, M.; Paasonen, P.; Kulmala, M.; Lihavainen, H. Homogenous nucleation of sulfuric acid and water at close to atmospherically relevant conditions. Atmos. Chem. Phys. 2011, 11, 5277–5287. [Google Scholar] [CrossRef]
- Herrmann, E.; Lihavainen, H.; Hyvärinen, A.P.; Riipinen, I.; Wilck, M.; Stratmann, F.; Kulmala, M. Nucleation simulations using the fluid dynamics software FLUENT with the fine particle model FPM. J. Phys. Chem. A 2006, 110, 12448–12455. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, E.; Hyvärinen, A.P.; Brus, D.; Lihavainen, H.; Kulmala, M. Re-evaluation of the pressure effect for nucleation in laminar flow diffusion chamber experiments with fluent and the fine particle model. J. Phys. Chem. A. 2009, 113, 1434–1439. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, E.; Brus, D.; Hyvärinen, A.-P.; Stratmann, F.; Wilck, M.; Lihavainen, H.; Kulmala, M. A computational fluid dynamics approach to nucleation in the water-sulphuric acid system. J. Phys. Chem. A 2010, 114, 8033–8042. [Google Scholar] [CrossRef] [PubMed]
- Travnickova, T.; Havlica, J.; Zdimal, V. Description of fluid dynamics and coupled transports in models of a laminar flow diffusion chamber. J. Chem. Phys. 2013, 139, 14. [Google Scholar] [CrossRef] [PubMed]
- Brown, R.L. Tubular flow reactor with first-order kinetics. J. Res. Natl. Bur. Stand. 1978, 83, 1–6. [Google Scholar] [CrossRef]
- Fickert, S.; Adams, J.W.; Crowley, J.N. Activation of Br2 and BrCl via uptake of HOBr onto aqueous salt solutions. J. Geophys. Res. Atmos. 1999, 104, 23719–23727. [Google Scholar] [CrossRef]
- Liu, Y.; Ivanov, A.V.; Molina, M.J. Temperature dependence of OH diffusion in air and He. Geophys. Res. Lett. 2009, 36, L03816. [Google Scholar] [CrossRef]
- Ortega, I.K.; Kupiainen, O.; Kurtén, T.; Olenius, T.; Wilkman, O.; McGrath, M.J.; Loukonen, V.; Vehkamäki, H. From quantum chemical formation free energies to evaporation rates. Atmos. Chem. Phys. 2012, 12, 225–235. [Google Scholar] [CrossRef]
- Loukonen, V.; Kuo, I.-F.W.; McGrath, M.J.; Vehkamäki, H. On the stability and dynamics of (sulfuric acid) (ammonia) and (sulfuric acid) (dimethylamine) clusters: A first-principles molecular dynamics investigation. Chem. Phys. 2014, 428, 164–174. [Google Scholar] [CrossRef]
- Zollner, J.H.; Glasoe, W.A.; Panta, B.; Carlson, K.K.; McMurry, P.H.; Hanson, D.R. Sulfuric acid nucleation: Power dependencies, variation with relative humidity, and effect of bases. Atmos. Chem. Phys. 2012, 12, 4399–4411. [Google Scholar] [CrossRef]
- Kürten, A.; Jokinen, T.; Simon, M.; Sipilä, M.; Sarnela, N.; Junninen, H.; Adamov, A.; Almeida, J.; Amorim, A.; Bianchi, F.; et al. Neutral molecular cluster formation of sulfuric acid-dimethylamine observed in real-time under atmospheric conditions. Proc. Natl. Acad. Sci. USA 2014, 111, 15019–15024. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; McGraw, R.; Lee, S.H. Effects of amines on formation of sub-3 nm particles and their subsequent growth. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Erupe, M.E.; Viggiano, A.A.; Lee, S.H. The effect of trimethylamine on atmospheric nucleation involving H2SO4. Atmos. Chem. Phys. 2011, 11, 4767–4775. [Google Scholar] [CrossRef]
- Jaecker-Voirol, A.; Mirabel, P. Nucleation rate in binary mixture of sulphuric acid-water vapour: A re-examination. J. Phys. Chem. 1988, 92, 3518–3521. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).