Abstract
This paper presents a detailed analysis of the energy dynamics of the Mediterranean tropical-like cyclone, Medicane Ianos, by using a moist static energy (MSE) budget framework. Medicanes are hybrid cyclonic systems that share characteristics of both extratropical and tropical cyclones, making their classification and prediction challenging. Using high-resolution ERA5 reanalysis data, we analyzed the life cycle of Ianos, which is one of the strongest recorded medicanes, employing the vertically integrated MSE spatial variance budget to quantify the contributions of different energy sources to the cyclone’s development. The chosen study area was approximately 25002 km2, covering the entire track of the cyclone. The budget was calculated after tracking Ianos and applying Hart phase space analysis to assess the cyclone phases. The results show that the MSE budget can reveal that the cyclone development was driven by a delicate balance between convection and dynamical factors. The interplay between vertical and horizontal advection, in particular the upward transport of moist air and the lateral inflow of warm, moist air and cold, dry air, was a key mechanism driving the evolution of Ianos, followed by surface fluxes and radiative feedback. By analyzing what process contributes most to the increase in MSE variance, we concluded that Ianos can be assimilated in the tropical framework within a radius of 600 km around the cyclone center, but only during its intense phase. In this way, the budget can contribute as a diagnostic tool to the ongoing debate regarding medicanes classification.
1. Introduction
In the literature, Mediterranean hurricanes, mesoscale cyclones exhibiting tropical characteristics for at least a short portion of their lifespan, are often labeled as “medicanes” []. These mesoscale cyclonic systems exhibit many characteristics of tropical cyclones, including a warm core, spiral cloud bands, and occasionally an eye-like structure [,,]. Through the Hart cyclone phase space wind speed and geopotential criteria [] application to cyclone tracks from model simulations and reanalysis, it was found that these types of cyclone exhibit tropical features only in their mature phase and for a short period, from 6 to 12 h [,,,]. The low rate of occurrence of such events, as also confirmed by [,], implies that the mechanisms contributing to the formation and development of medicanes have been investigated in a relatively restricted set of case studies. The initiation phases of medicane life cycles exhibit similarities with all systems displaying growth through the interaction of an upper-tropospheric potential vorticity (PV) streamer and a low-level baroclinic region, as commonly observed in extratropical cyclones [,,]. However, air–sea interactions and convection during the mature stages may significantly influence cyclone development []. Deep convection and wind-induced surface heat exchanges have been found to sustain cyclonic circulation in several medicane cases [,,]. Indeed, moisture contributes to the intensification of vortices through condensation processes. When humidity is high, condensation generates latent heat, which increases cyclonic vorticity and can lead to stronger vortices, as demonstrated by a moist-convective rotating shallow-water model (mcRSW) []. However, medicanes are often accompanied by an upper tropospheric PV streamer or a cut-off also impacting their intense phase []. This might indicate that baroclinic forcing plays a significant role in their development and not only in the initial phase. Indeed, convection in a rotating environment enhances vertical vorticity through vortex-tube stretching, significantly influencing the cyclone’s structure and evolution. As suggested in [], the aggregation of convective vorticity anomalies plays a crucial role in vortex intensification. In particular, the interplay between convection and the boundary layer can lead to the formation of localized vorticity maxima, which may later merge into a dominant cyclonic circulation, contributing to the self-sustaining nature of the system. Such processes might be relevant in the classification of medicanes, especially for cases where diabatic heating and barotropic processes act synergistically.
In [], an attempt at a general classification was summarized, based on a limited number of cases and some previous work carried out by [], dividing medicanes into three groups. In the first group, baroclinic instability plays a significant role throughout the cyclones’ lifetime [], and warm seclusion is sufficient to explain the presence of the warm core []. In the second group, baroclinicity is relevant only in the initial stage, and, akin to tropical cyclones, the theory of wind-induced surface heat exchange (WISHE) [,] can explain their intensification [,]. Emanuel et al. (1986) [] emphasized the crucial role of heat flux from the ocean surface for tropical cyclones, arguing that the cyclone self-sustains through continuous oceanic heat transfer, allowing intensification. In [], they expanded this theory to show how even neutral or slightly unstable atmospheric conditions can lead to significant cyclogenesis under favorable air–sea interactions. The mature stage of a tropical cyclone is seen as a Carnot cycle, where the storm acts like a heat engine, where energy is derived from the difference in temperature between the warm ocean surface and the colder upper atmosphere. In this framework, the cyclone absorbs heat at the ocean’s surface (akin to the isothermal expansion of a Carnot cycle), works by generating wind, and releases energy through condensation in the upper troposphere []. Similarly to tropical cyclones, the medicanes of this group might operate like a heat engine, where surface heat fluxes from the relatively warm Mediterranean waters fuel cyclone intensification [,]. Then, the third group encompasses cyclones developing through a synergy between baroclinic and diabatic processes []. Given the lack of a precise physical definition, these classifications have relied on subjective criteria such as satellite imagery []. While previous studies have examined tropical-like characteristics in specific cases [,,], a systematic analysis quantifying baroclinic and barotropic contributions is still missing. Flaounas et al. (2021) [] proposed a PV-based approach focusing on the mature phase, yet a more comprehensive lifecycle analysis is needed.
To build on the previous literature, the objective of this study is to follow the whole development of the cyclone and carry out a quantitative analysis of the relative contribution of different baroclinic and barotropic processes. To do so, we focus on a thermodynamic variable that is used in modeling and meteorological diagnostics because it is approximately conserved in moist adiabatic processes, the moist static energy (MSE). MSE is defined as , where s is the dry static energy and the latent heat []. Given that MSE is indicative of the total energy acquired from a water basin as it comprises internal energy, latent heat energy, and potential energy, it can indeed be used to assess the variations of tropical cyclone intensity and structure, since they are closely related to the former energetic characteristic []. Warm ocean water provides the energy source for a TC, and through upward fluxes of sensible heat and latent heat, the TC increases in internal energy and latent energy. By converting the energy supplied by the ocean into kinetic energy via moist convection, the wind strengthens and, consequently, the TC intensifies []. Emanuel et al. (2004). [] identified that the concept of MSE is functional in deducing the theory of maximum potential intensity [,]. From the energy perspective, a TC cannot develop without eyewall updrafts transporting MSE upward from the boundary layer, as also found by []. Thus, a good candidate for the diagnostic study of cyclones from cyclogenesis to dissipation is the budget of vertically integrated MSE [,] and the spatial variance of vertically integrated MSE, which has been thoroughly applied to tropical cyclones [,]. This specific analysis framework was initially exploited by [] to understand the physical mechanisms of self-aggregation of convection in idealized simulations and then used by many others (e.g., [,,,,]).
Convective self-aggregation is the spontaneous organization of initially scattered convection into isolated convective clusters, where the feedback contributing to convective self-aggregation serves to transport moist static energy from dry to moist regions [,,]. In the presence of rotation, this can lead to spontaneous tropical cyclogenesis in radiative convective equilibrium (RCE) simulations in the tropics [,,,,,].
Within the budget, the vertically integrated moist static energy horizontal variance increase is connected to radiative, convective, moisture, and advection feedback [] since its mass-weighted vertical integral can only be changed by radiation, surface fluxes, and advection. This makes it possible to understand the relevant processes from cyclogenesis to cyclone development by studying which feedback increases the variance and correlates with moist static energy anomalies []. In particular, it can help to understand the nature of the mature phase of a medicane, focusing on whether or not moisture feedback associated with the crucial role of heat flux from the ocean surface (the above-mentioned wind-induced surface heat exchange: WISHE) mechanism plays a crucial role in the intensification of the cyclone [,], making the cyclone self-sustaining through continuous oceanic heat transfer, resembling its tropical counterpart. The moist static energy budget approach used in this paper provides insights into these types of processes happening during the life cycle of a cyclone by breaking down the key energy sources that drive cyclone growth. Furthermore, previous numerical studies [] have found that an increase in the variance of vertically integrated moist static energy is primarily driven by latent heat variance, reinforcing the idea that moisture feedback is a dominant energetic component. By incorporating these perspectives, we aim to assess whether or not medicanes can be interpreted within the tropical cyclone framework based on their energetic and convective characteristics.
The budget, previously employed in studies of convective organization [,,], has been successfully applied to tropical cyclones with both cloud-resolving model (CRM) idealized simulations of tropical cyclones [,] and general circulation model (GCM) realistic simulations of tropical cyclones [,]. In the context of idealized simulation with CRMs, Wing et al. (2016) [] found that the development of a tropical cyclone from an initially homogeneous environment is promoted by feedback involving radiation and cloud interaction and surface fluxes. The interaction between clouds and radiation can modify the MSE by trapping heat within the system, contributing to the energy build-up that aids cyclone formation and intensification. This was also found in [], who also highlighted that, after formation, the most important feedback for cyclone intensification is from surface fluxes, specifically, the latent heat flux. Indeed, they amplify the moist static energy within the storm’s core by enhancing the energy exchange between the ocean and atmosphere, fueling the cyclone’s growth, much like the WISHE. Similar results have been underlined in many studies using CRMs regarding tropical cyclone development [,]. However, Muller et al. (2018) [] urged the need to take into account large-scale environmental conditions and look into realistic boundary condition simulations. Studies like the one from [,,] followed this lead by directly analyzing GCM realistic simulations. Beucler (2014) [] found that latent heat fluxes were increasingly important in the mature stages of a tropical cyclone, with a second contribution from longwave cooling, while [] found that surface fluxes and cloud radiative feedback contributed to tropical cyclone development, with radiative feedback stronger in more intense tropical cyclones. Wing et al. (2019) [] also gave some insight into the role of MSE advection in bulk (horizontal and vertical together), which indicates large-scale features. They found that MSE advection exerted negative feedback on cyclone development, seen as a downgradient energy redistribution from the cyclone core to its outskirts. Lastly, Zhang et al. (2023) [] was able to detect the vertically varied contribution of both the horizontal and vertical advection term in the development of tropical cyclones, underlying how the role of different advective processes can impact the cyclone life-cycle, both positively (convergence and upward motion) and negatively (divergence and downward motion). Consequently, Zhang et al. (2023) [] underlined that the MSE variance budget can provide process-oriented information on physical processes associated with tropical cyclones under realistic boundary conditions.
That is exactly what we set out to do in this paper. Specifically, as a first step, we focus our attention on a single case study of a Mediterranean tropical-like cyclone, Ianos, both because it has been widely studied in the literature [,,,,] and because it is the medicane that reached one of the highest intensities [], equivalent to a category two hurricane on the Saffir–Simpson scale [,], making it the perfect candidate to validate its similarities with the tropical theory. To carry out Ianos tracking and analysis and to compute its budget, the high-resolution (0.25°) ERA5 reanalysis data [] released by the European Centre for Medium-Range Weather Forecasts (ECMWF) were used. ERA5 offers a highly accurate and consistent global climate dataset, making it useful for studying historical weather events and long-term climate changes [,]. Indeed, ERA5 offers the possibility to extend the same analysis performed here to other known medicanes.
The first objective of this study is to analyze the energy budget to investigate the feedback mechanisms that govern the lifecycle of medicanes. In particular, we aim to reconcile these mechanisms with both the large-scale features typically associated with Mediterranean cyclogenesis—such as the presence of an upper-level PV streamer, an upper-tropospheric cold trough, dry intrusions linked to strong gusts, low-level wind convergence, and the warm conveyor belt (WCB) with its slantwise ascent leading to precipitation [,,,,]—and the small-scale convective processes observed in the medicane core [,], similarly to the results found by employing different techniques, like the PV inversion one employed by []. The second goal of this work is to establish an objective method to determine whether and when medicanes can be assimilated into the tropical cyclone framework. To achieve this, we analyze the energy budget by examining the variance increase of each moist static energy term, providing a quantitative criterion for their classification.
Thus, we aim to answer the following questions:
- Can we quantitatively define which process is most important during the various stages of a medicane’s life through the MSE budget?
- Is it possible to objectively define when a medicane can be assimilated into the framework of tropical cyclones by analyzing the increase in variance of the moist static energy terms in the energy balance?
The paper is organized as follows: Section 2 describes the ERA5 reanalysis dataset and variables used for the budget computation, as well as Ianos’ characteristics and tracking. Section 3 presents the moist static energy budget framework and the Hart cyclone phase space used to analyze Ianos. In Section 4, the detailed analysis of the MSE variance terms and the MSE budget terms for Ianos is presented, and the area sensitivity analysis is outlined. In Section 5, the implications of the findings are discussed, and in Section 6 conclusions regarding the tropical-like characteristics of Ianos are drawn.
2. Data
2.1. ERA5 Reanalysis
The vertically integrated moist static energy (MSE) budget analysis during the evolution of Mediterranean cyclones was carried out using ECMWF reanalyses, ERA5 []. ERA5 provides hourly frequency data at a resolution of about 30 km. The temperature, specific humidity, geopotential, horizontal component of the wind, and vertical velocity fields are used to evaluate the moist static energy, h, the dry static energy, s, and the advective term of the budget. Then, the 1-h accumulated fluxes of net shortwave and net longwave radiation at the top of the atmosphere and the surface are used to evaluate the total column atmospheric radiative cooling, and the 1-h accumulated latent and sensible fluxes are used to close the budget.
2.2. Medicane Ianos
The Ianos cyclone, which occurred in September 2020 and lasted for several days (Table 1), was one of the most intense Mediterranean tropical-like cyclones that ever occurred []. It originated from a surface low-pressure system, intensified through convection over warm waters, and was supported by interactions with upper-level atmospheric disturbances []. As Ianos developed, it showed characteristics similar to tropical cyclones, such as a warm core, an eye-like structure, and strong rotational winds. The importance of convection and air–sea interactions in its development has been underlined in the literature [,].

Table 1.
Overview of cyclone Ianos and its characteristics: Year, Period, Duration, Region, and Central Pressure (CP).
By September 17, it had reached its peak, with wind gusts up to 54.1 m/s and a central pressure of 984 hPa [], making landfall in Greece and causing severe flooding, storm surges, and widespread damage []. It was a significant event, both scientifically and socially, offering valuable insights into the behavior of Mediterranean cyclones and the importance of accurate prediction models [].
2.3. Cyclone Tracking
The tracking method is based on [,]. The algorithm first aims to find the local minima of the sea level pressure field at each time step. Then, for each minimum, the sea level pressure gradient is computed along eight main directions (E, NE, N, NW, W, SW, S, SE) within a circle of radius 200 km. The computed gradient is then chosen to be lower than 5 hPa/200 km in at least six directions. After the minimum detection and filtering via selection through sea level pressure gradient, a proximity condition is applied to construct the complete trajectory. Starting from the first time step, each minimum is connected to the following one, at the following time step, which satisfies the condition of being closer than , with V = 50 km/h and = 3 h. If this condition is met, the two consecutive minima are considered to belong to the same trajectory. This condition was considered appropriate and was chosen according to the results of [].
3. Methods
3.1. The MSE Budget Framework
Moist static energy (MSE, h in the following equations) is conserved under moist adiabatic processes and the hydrostatic balance; thus, it is a useful quantity to understand moist convection. Under the standard approximation, its specific value (value per total air mass) is defined by [] as:
where is the geopotential, is the dry static energy (J/kg), q is the specific humidity (kg/kg), is the heat capacity of the dry air at constant pressure (1004 J kg−1 K−1), T is the temperature (K), L is the latent heat of vaporization of liquid water (2.5 · 106 J/kg), g is the acceleration of gravity, and z is the altitude. To derive a budget for h, we start from the equations for momentum, mass continuity, heat, and moisture budget, as written in pressure coordinates [,] for a moist atmosphere under hydrostatic balance. The derivation of the MSE budget and the assumptions made are reported in the Appendix (Appendix A), following the methodology by []. After having verified such assumptions, the budget for the mass-weighted vertical integral of the MSE is defined as:
where we define the integral operator as
where is the pressure at the model top and hPa. This operator represents a mass-weighted vertical integral through the entire atmospheric column. We can horizontally average the vertical integral of MSE over the domain to obtain the domain-averaged vertical integral budget of MSE and subtract the result from the total equation, and write an evolution equation for its anomaly. By defining the horizontal average operator as and the anomaly as , we find:
We recall that, in an atmosphere in radiative convective equilibrium, the following large-scale balance between surface fluxes and radiative cooling is satisfied: . Equation (5) can also be analyzed in terms of the different contributions of dry static energy and moist static energy as follows:
Finally, to track aggregation phenomena, such as the formation of Mediterranean cyclones, we multiply again Equation (5) by to obtain an equation for the variance of the vertically integrated MSE:
To understand which component of the MSE variance is more relevant, we will also analyze the MSE variance in terms of its components:
3.2. Hart Parameters
The thermal structure and thermal asymmetry of Ianos have been checked via the parameters of the three-dimensional cyclone phase space diagnostic []. These are the upper-level thermal wind, , a relevant parameter in distinguishing tropical-like cyclones from fully baroclinic cyclones [], and secondly, the thermal asymmetry, B. The thermal asymmetry is defined as the storm-motion-relative 900–600 hPa thickness asymmetry across the cyclone within its radius:
where z is the geopotential height, R is the right of the current storm motion, L is the left of the storm motion, and the overbar is the areal mean over a semicircle around the cyclone center. The threshold value of the thermal asymmetry for hurricanes has been set to m []. The is defined as:
where is computed between 700 hPa and 400 hPa as in equation Equation (9). The two pressure levels have been changed from 600 hPa to 700 hPa and from 300 hPa to 400 hPa due to the lower height of the tropopause in the midlatitudes []. The cyclone attains a deep upper-level warm core when becomes highly positive. These values are computed within a 200 km radius around the detected cyclone center, following the track of the cyclone, by using the geopotential height field. Thus, the deep warm core phase is represented by the asymmetry B being lower than 10 and closer to 0 and a highly positive value of .
4. Results
The results are presented as follows. First, we present the synoptic analysis for the Ianos cyclone, its evolution through the study of the Hart parameters, and the core central pressure (CP), with a small discussion on the chosen domain area for the MSE variance and budget computation. Then, this synoptic analysis is reconciled by first decomposing the vertically integrated moist static energy variance into the vertically integrated dry static energy and latent heat energy and their covariance, and second by analyzing each moist static energy budget term contribution.
4.1. General Characteristics and Warm Core Analysis
The combined analysis of the horizontal variance of the vertically integrated moist static energy , the Hart parameters, and the core central pressure (CP) is reported in Figure 1. The values of are computed in the squared area of 25002 km2 shown in Figure 1c. The choice of a fixed squared area was made to adhere to studies done using the MSE budget in both realistic and idealized simulations with CRMs and GCMs for tropical cyclones [,,,]. Additionally, selecting a fixed domain ensures that the analysis captures the initial phases of the cyclone’s life before a well-defined surface pressure minimum can be tracked, allowing for a more comprehensive assessment of its formation and evolution.
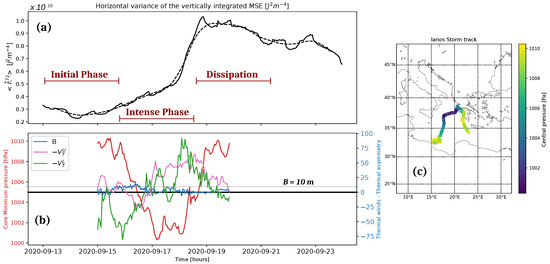
Figure 1.
Hart parameters and MSLP in (b), increase in the horizontal variance of moist static energy, , together with the different phases of Ianos life-cycle in (a), and storm track over the chosen area to compute in time in (c).
To validate this approach, we performed the same analysis using a moving domain centered on the cyclone at each timestep, with a radius of 1250 km (equivalent to half the fixed side of the 25002 km2 domain). The results (Supplementary Figure S1) indicate that both methods yield comparable MSE variance trends and budget terms, reinforcing the robustness of the fixed-domain approach. Furthermore, we explored sensitivity to spatial domain selection by computing the MSE variance terms and budget over different areas with a radius of 125 km, 300 km, 600 km, and 800 km (Supplementary Figures S2 and S3). The results are discussed thoroughly in Section 4.4; however, they confirm that increasing the domain size leads to a smoother representation of the MSE budget. The selected domain size of 25002 km2 is typically on the order of the Rossby deformation radius and about 10 times the climatological medicane radius (160–200 km []), ensuring that both the core structure of Ianos and its interaction with the surrounding environment are adequately captured.
From the Hart parameters combined with the CP (Figure 1b), one can define the different phases of Ianos’ life cycle, as highlighted in Figure 1a, aligning with an increase in . Indeed, the increase in has been observed in idealized CRMs simulations in the tropics associated with convective self-aggregation [,,]. The more convection is aggregated, the more the variance increases. Thus, low values of can be found when convection is sparse in a domain and when a cyclone is forming, and an increase would underline the progressive concentration of humidity and cloud in a single region, as happens in the mature stage of a cyclone.
The increase in variance combined with the development of a cyclone has been observed for tropical cyclones, both in idealized simulation [] and in climate models [], specifically during the cyclone’s intensification []. The same happens for Ianos in the intense phase (Figure 1a), between the 16th and the 19th of September, when the thermal symmetry is between 10 m and 0 m and the upper-level thermal wind becomes positive and reaches high values (Figure 1b). Here we report a brief analysis of Ianos’ life cycle by looking at Figure 1 and the synoptic analysis shown by looking at Figure 2 and Figure 3. During cyclogenesis, before the 16th of September, the variance is low, and after the cyclone dissipates, after the 19th of September, the convection at the cyclone core is consumed, and the variance starts slowly decreasing. More specifically, from the 13th of September 2020 there is a convective cluster due to a weak cut-off low, east and south of Sicily, and a weak surface low is present over Libya (Figure 2a). On the 14th of September, the convective cluster to the south of Sicily and the surface low approach each other (black and white lines in Figure 2b). There is a small increase in variance around the surface low center and over sea near northern Africa in Figure 2b. This might be related to cold air, relative to the sea surface, that starts moving over very warm sea (1.5 °C warmer than average []). On the 15th of September, the two structures merge off the Libyan coast (Figure 3c). This is marked by the increase of (Figure 2c) near the cyclone core. On the 16th of September, the cyclone moves northward and deepens quickly, while the convection redevelops, enhancing the variance in the region once more (Figure 2d). On the 17th of September, the cyclone attains its mature phase (the central eye is starting to show in Figure 3e), as also indicated by the Hart parameters in Figure 1b, when a Potential Vorticity streamer is wrapped around the surface cyclone (red lines in Figure 2e), as also underlined in the literature []. It exhibits a tropical appearance and turns eastward. It is in this phase that the values reported in Figure 1b for the thermal asymmetry and the thermal wind make Ianos a tropical cyclone []. It has been thoughtfully underlined in the literature that, in this phase, the cyclone was maintained by a diabatic process, resulting from the release of latent heat in the condensation process inside clouds and by the wind-induced surface heat exchange feedback [].
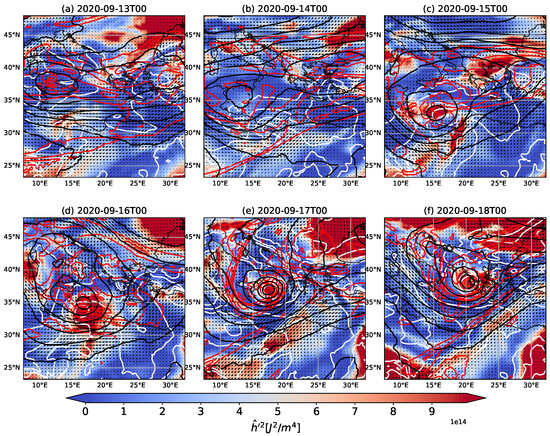
Figure 2.
Synoptic analysis of the Ianos cyclone in the same domain area of Figure 1, the chosen area of interest. The vertically integrated , in shading over different days during Ianos’ life cycle. Black lines represent 500 hPa geopotential height (from 5000 to 6000 m), red lines represent potential vorticity at 300 hPa (from 0 to 8 PVU), white lines represent MSLP (from 990 to 1010 hPa), and vectors represent 300 hPa wind in m/s.
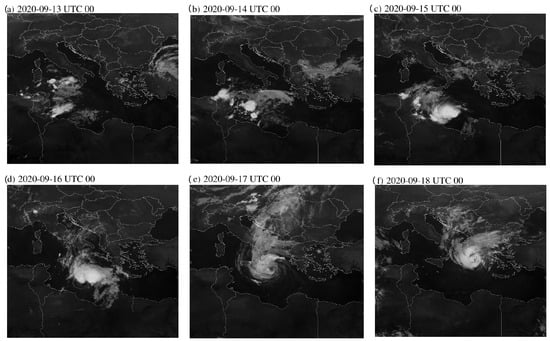
Figure 3.
Synoptic analysis of the Ianos cyclone. Eumetview satellite images (High Rate SEVIRI IR10.8 m Image—Meteosat Second Generation, MSG) for different days during Ianos’ life cycle.
In the following section, these latter processes will be discussed as responsible for the increased in the cyclone. On the 18th of September, the cyclone makes landfall over Greece. It is still associated with deep convection (Figure 2f, high values of in the cyclone, and the eye is still present). After the 19th of September, the cyclone turns southward and starts weakening. The high values of in Figure 1a after the cyclone dissipation are due to the presence of cold and moist air approaching the Mediterranean region after the 19th of September, increasing the variance given the contrast with the warm and dry air over northern Africa and the cyclone dissipation ( approaching zero inside the cyclone).
4.2. The Vertically Integrated MSE Variance Analysis
The increase in the vertically integrated MSE variance, hereafter referred to as , is examined in terms of its decomposition into the following terms, as outlined in Equation (8):
- Vertically integrated latent heat energy variance, : represents variations in the latent heat component of MSE, primarily due to moisture fluctuations and condensation processes;
- Vertically integrated dry static energy variance, : accounts for variations in the dry static energy term, related to temperature and geopotential height changes, indicating baroclinic contributions.
- Their covariance : describes interactions between thermal and moisture anomalies, which can either enhance or suppress convective processes. It can indicate the effect of large-scale features, like a cut-off low and the passing of a jet in the region, as will be discussed below.
By examining these components separately, we aim to clarify their role during different phases of the cyclone. As illustrated in Figure 4, where the data for Ianos reveals the observed increase of and its decomposition, it becomes evident that the growth in variance cannot be explained by the increase in alone. The latter happens, as mentioned, in the case of tropical cyclones [,], given the condition of weak temperature gradient in the tropics, and thus in the absence of thermal energy variance. In the case of midlatitude cyclones, both dry static energy and latent heat energy, as well as their covariance, are necessary to explain the increase in . More specifically, by comparing the areal average shown in Figure 4 with the vertically integrated MSE variance terms over the chosen area (Figure 5, Figure 6, Figure 7 and Figure 8), one can gain insight into the physical processes happening in the cyclone’s evolution.
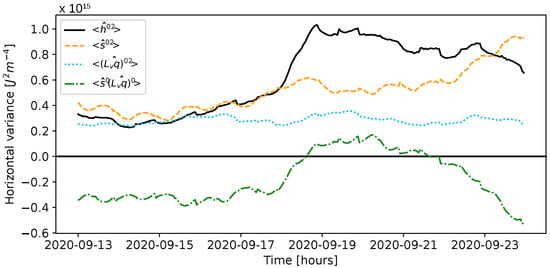
Figure 4.
Horizontal variance of the vertically integrated MSE terms as in Equation (8), over time, around the chosen area.
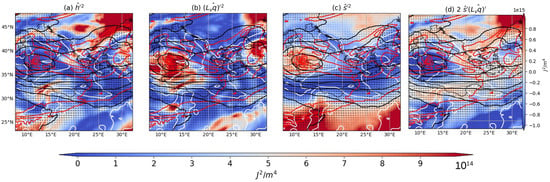
Figure 5.
Vertically integrated MSE terms over the chosen area for the 13 September 2020 at 00 UTC. In shading, (a) , (b) , (c) , and (d) . Black lines represent 500 hPa geopotential height (from 5000 to 6000 m), red lines represent potential vorticity at 300 hPa (from 0 to 8 PVU), white lines represent MSLP (from 990 to 1010 hPa), and vectors represent 300 hPa wind in m/s.
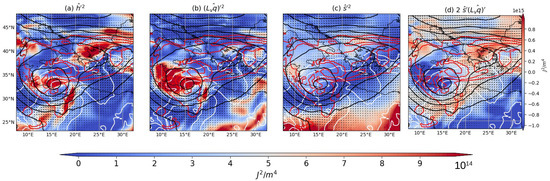
Figure 6.
Vertically integrated MSE terms over the chosen area for the 15 September 2020 at 00 UTC. In shading, (a) , (b) , (c) , and (d) . Black lines represent 500 hPa geopotential height (from 5000 to 6000 m), red lines represent potential vorticity at 300 hPa (from 0 to 8 PVU), white lines represent MSLP (from 990 to 1010 hPa), and vectors represent 300 hPa wind in m/s.
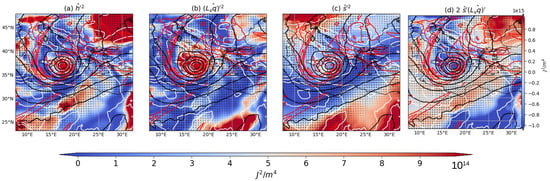
Figure 7.
Vertically integrated MSE terms over the chosen area for the 17 September 2020 at 00 UTC. In shading, (a) , (b) , (c) , and (d) . Black lines represent 500 hPa geopotential height (from 5000 to 6000 m), red lines represent potential vorticity at 300 hPa (from 0 to 8 PVU), white lines represent MSLP (from 990 to 1010 hPa), and vectors represent 300 hPa wind in m/s.
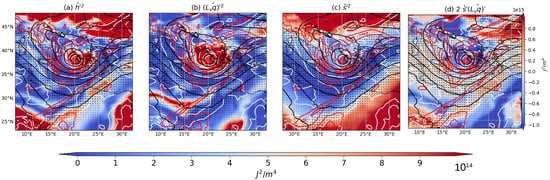
Figure 8.
Vertically integrated MSE terms over the chosen area for the 18 September 2020 at 00 UTC. In shading, (a) , (b) , (c) , and (d) . Black lines represent 500 hPa geopotential height (from 5000 to 6000 m), red lines represent potential vorticity at 300 hPa (from 0 to 8 PVU), white lines represent MSLP (from 990 to 1010 hPa), and vectors represent 300 hPa wind in m/s.
4.2.1. Initial Phase (13–15 September 2020)
As mentioned, the cyclogenesis of Ianos was due to the merging of a convective cluster due to a weak cut-off low south-east of Sicily and a weak surface low over Libya, which happened between the 13 September 2020 and the early morning of the 15th of September. Both and are positive, and their covariance term is negative (Figure 4). Figure 5, with positive values of and , and negative indicates the presence of strong convection surrounded by areas free of convection, as also seen in the satellite image in Figure 3a,b. The high value of (see Figure 5b) is due to the increase in humidity (convective cluster) and the high value of (Figure 5c), together with the negative (Figure 5d), indicate the presence of a cut-off low (black contours of geopotential height), which decreases temperature by bringing the cold air, and ignites convection. It is the increased humidity and decreased temperature in the cut-off region that generates a negative . This covariance term suggests upper-level cold air intrusion interacting with low-level moisture, promoting instability and enhancing convection. The presence of a cut-off low enhances dry static energy variance, supporting baroclinic forcing as a key contributor to early cyclogenesis. Cut-offs are common precursors for the development of medicanes []. They are cold-cored depressions that are produced by a westerly trough [,]. These systems are found in the upper troposphere (e.g., 500 hPa level) and are associated with cold air aloft. As the low approaches the Mediterranean environment with small baroclinicity (no surface low is present yet in Figure 5; see white lines), the temperature above decreases, increasing convective instability and lifting air masses []. Surface depressions may develop below these systems whilst cold air aloft promotes deep convection and cloud development, resulting in persistent heavy rainfall [].
Furthermore, until the 15th of September, there was increased horizontal advection of MSE, with strong moisture transport from north Africa supplying the system with warm, moist air. This is underlined in Figure 6, where the convective cluster and the surface low have approached one another, accompanied by an increase in in the cyclone region, mostly due to convection (Figure 6a,b). There, the presence of high MSE (warm and humid air) moving from northern Africa to the Mediterranean Sea and then being advected into the cyclone core (high positive values of and corresponding ) is apparent. The advection of high MSE air is happening both at the surface (between 850 and 900 hPa, as shown in Supplementary Figures S6 and S7) and at 600 hPa (Supplementary Figure S6). The advection of high MSE air is similar to what has been observed by [], where moist air was incorporated into cyclonic circulation, becoming a subsequent source for convection in medicanes and has been directly observed for other medicanes []. Specifically, moist air advection at the surface from north Africa has been found as an initial feature in other medicane cases []. As underlined in [], the greatest part of this moist air might be due to a cyclonic circulation from northern Africa towards the central Mediterranean Sea, given the preconditioning of moist air coming from the Atlantic. The high MSE transport of air at 600 hPa, instead, could be associated with the presence of the subtropical jet []. This advection of MSE air is underlined by the advective terms of the vertically integrated MSE variance budget, as will be shown in Section 4.3.
4.2.2. Intense Phase (16–18 September 2020)
As Ianos intensifies, the role of latent heat energy variance becomes more dominant in the core. Indeed, in the cyclone core, there is an increase of , corresponding to an increase of (Figure 7b), signaling increased convection. Then, the covariance term, , becomes positive at the time of Ianos’ transition to a tropical-like structure, where mid-upper level cold anomalies align with low-level moisture anomalies, allowing for enhanced convection. This intensification phase occurs during the arrival of a PV streamer from the west over the Ionian Sea [], in correspondence with positive values of , and specifically over Sardinia (Figure 7a,c,d). The PV streamer wraps around the surface cyclone and induces baroclinic interaction []. In Figure 7d, and are mostly increasing due to the presence of the PV. The covariance, , also underlines the presence of a frontal structure (black lines of the geopotential height) and the presence of an area of dry and cold air in the Black Sea. More specifically, during the intensification phase, the dryer columns () correspond to the coldest () since we see a positive signal from around the area of deep convection. This is related to drying linked to the dry intrusion from the stratosphere (PV streamer) passing through Sardinia and north Africa (and the subtropical jet coming from the south-west in Figure 7d), as also found in the literature [,]. A PV streamer can further trigger the convective instability of a Mediterranean tropical-like cyclone by alimenting the cyclone core with cold and dry air, increasing available potential energy []. The peak intensity during the 18th of September (Figure 8) is reached after the term has become positive, then it makes landfall in Greece. The increase in in the cyclone is now completely due to increase (Figure 8b) and over the whole area is mostly due to the temperature gradient between northern Africa and central Europe (Figure 8c). The former aspect is very relevant because it might underline the tropical-like nature of Ianos. Indeed, as mentioned for its tropical counterparts, the increase in moist static energy variance in the cyclone core is due to an increase in latent heat energy variance [,].
To dig deeper into the understanding of these similarities, we checked the behavior of one of the parameters of the tropical cyclone theory of [], the potential intensity (PI) in comparison with the increase of the (Supplementary Figure S4). Indeed, the PI is a direct consequence of assuming that a tropical cyclone acts as a Carnot engine [], where their steady-state maintenance can be idealized as a natural heat engine or Carnot cycle, with the heat input being largely in the form of the latent heat of vaporization acquired from the sea surface by the inwards airflow. PI comes directly from formulating and equating the mechanical energy available from this thermodynamic cycle and the turbulent dissipation in the storm’s atmospheric boundary layer (more information about its formulation and calculation can be found in []). In Supplementary Figure S4, it can be seen that, after cyclogenesis, PI increases as the MSE variance increases, making the use of the moist static energy variance increase suitable to investigate tropical cyclone intensification mechanisms.
The strongest increases in MSE variance occur near the cyclone core, corresponding to convective self-aggregation, which sustains the system’s warm-core structure. As will be explored in the next section, the increased importance of in the cyclone area is due to the release of latent heat inside clouds and by low-level diabatic processes (surface fluxes and convective motion) becoming important. Strong vertical motions during deep convection events close to the medicane’s center contribute to the intensification of the low-pressure system through latent heat release in moist ascent, thus warming the core of the medicane to a great vertical extent [].
4.2.3. Dissipation (19–21 September 2020)
During the dissipation phase, starts to decrease, both because of the decrease of due to the extinction of convection and because of the covariance term becoming negative again. However, it remains high, mainly because increases. This is due primarily to the strong temperature gradient in the chosen area that is no longer dampened by the presence of the heating produced by the cyclone with its warm core. But most importantly, by the arrival of a new large-scale disturbance, a new cut-off low over the Balkans, between Greece and the Black Sea (Supplementary Figure S5).
4.3. The Vertically Integrated MSE Variance Budget
The primary terms involved in the budget analysis, described in Equation (7), are outlined in Table 2 and used in this section according to their definition. These are averaged over the chosen area in Figure 1c, the same area as for Equation (8), and shown in time in Figure 9.

Table 2.
Vertically integrated moist static energy variance budget terms.
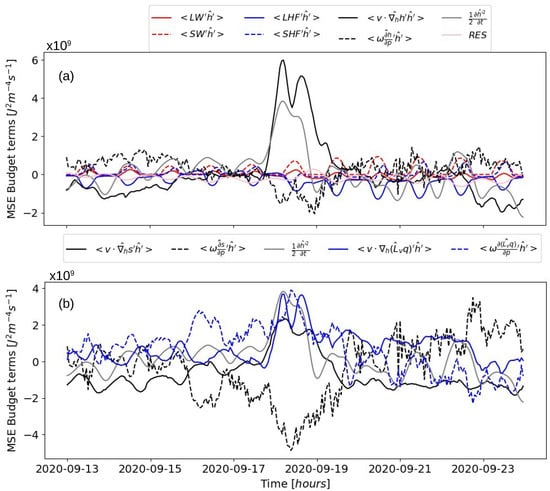
Figure 9.
Budget terms as in Equation (7). In (a), the moist static energy terms, and in (b), the dry static energy and the humidity advection in the vertical and the horizontal. In Pink is the residual term of the budget.
Firstly, the diurnal cycle is visible by looking at both the radiative and the surface fluxes. Secondly, from Figure 9a,b, it can be stated that, by separately computing both the vertical and horizontal advection of MSE, we can detect the dynamic processes involved in the cyclone life, cyclone genesis, and development. In Figure 10a–c, the relative contribution of each process is shown for each phase. The budget can indeed tell us the precise contribution of each term to the change in time of the MSE variance and can help us understand what is happening in every phase of Ianos’ life cycle. In the following, we detail each process for each phase.
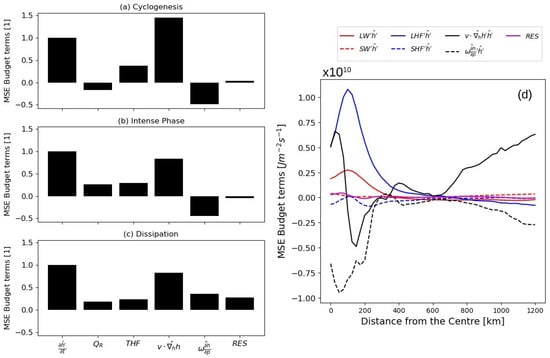
Figure 10.
The relative contribution of the normalized terms of the moist static energy variance budget. In (a), the terms for the initial phase are averaged over the chosen area, from the 15th of September at 00 UTC to the 16th of September at 23 UTC. In (b), the terms for the intense phase from the 17th of September at 00 UTC to the 19th of September at 00 UTC, and in (c), the terms for the dissipation, after the 19th of September. In (d), a special focus on the intense phase where the radial mean of each term, from the cyclone center to 1200 km, is reported.
4.3.1. Initial Phase
During the initial phase, the development of the cyclone is influenced mostly by surface flux feedback and advective processes (Figure 9a and Figure 10a). Regarding the surface fluxes anomalies, in general, the sensible heat flux anomaly (SHF’) is mostly positively correlated to over the whole region during the day (average value in Figure 9a) and the latent heat flux anomaly (LHF’) is mostly negatively correlated, especially over the terrain during the day (average value in Figure 9a), due to reduced moisture seeding to the atmosphere, especially in the northern Africa region, thus influencing the average value of the feedback (Figure 9a). However, both anomalies are positive around the core of the cyclones (Figure 11h,i). Specifically, the LHF is contributing to the increase of specifically in the cyclone core region, indicating that an increase in latent heat fluxes is helping the increase in inside the cyclone. In this phase, the surface fluxes’ anomalies in intensity are also mostly influenced by the humidity and temperature at the surface. At sea, the SST was anomalously high compared to the climatological SST of September (obtained by using the ERA5 reanalysis SSTs over the Mediterranean Basin from 1991 to 2020 in []), on average, 2 °C. The higher surface temperatures facilitate the transfer of moisture to the medicane via surface fluxes [], allowing the convection to develop more effectively [,], eventually making the two flux anomalies positively correlated with the increase in . On the other hand, the negative correlation between the surface flux anomalies and the MSE one can be owed to the air–sea enthalpy disequilibrium, as can be seen in Figure 11h,i. The boundary layer water vapor mixing ratio is larger in the moist regions, where it is positive, than in the dry regions. The air–sea disequilibrium is anomalously positive in the dry regions, enhancing surface fluxes there, and thereby reducing the .
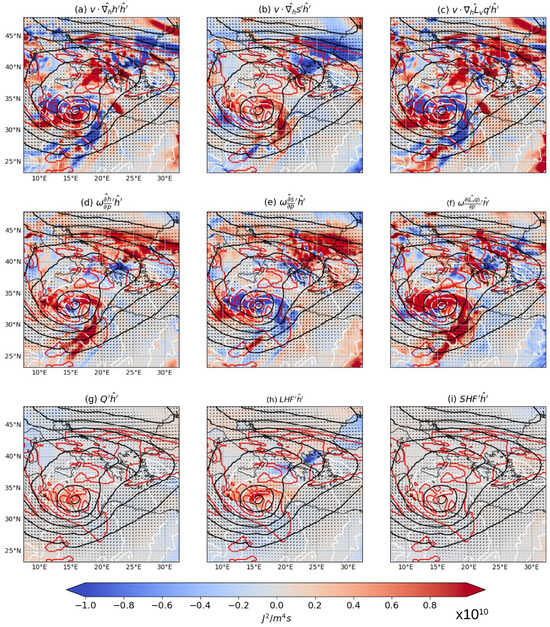
Figure 11.
Budget terms as in Equation (7) for the 15 September 2020 at 00 UTC. In shading, (a–c) show the horizontal advection term of moist static energy, dry static energy, and latent heat energy, respectively; (d–f) show the vertical advection term of moist static energy, dry static energy, and latent heat energy, respectively; (g) shows the radiative cooling term; (h) is the latent heat flux term; and (i) is the sensible heat flux term. Black lines represent 500 hPa geopotential height (from 5000 to 6000 m), red lines represent potential vorticity at 300 hPa (from 0 to 8 PVU), white lines represent MSLP (from 990 to 1010 hPa), and vectors represent 300 hPa wind in m/s.
The vertical and horizontal advection of moist static energy feedback on MSE anomaly, when divided into dry static energy and latent heat energy, as shown from Figure 9, Figure 10, Figure 11 and Figure 12, are linked to the mentioned large-scale features that affect cyclogenesis and cyclone development at midlatitudes (cutoff low and PV streamer interacting with the convection at the surface and in the mid-troposphere []). During cyclogenesis, the term is positive and is mostly due to (Figure 9a,b). If one looks at the values over the whole area, in Figure 11, is high in the cyclone core and at the eastern side of it, where is helping the increase of (Figure 11f). Keeping in mind that the advective anomalies shown in Figure 11 and Figure 12 are reported as in the Equation (with a minus), the positive values of the vertical advection of MSE anomalies mean a positive transport of MSE out of the boundary layer upward; instead, when it is negative, it can indicate subsidence. Thus, the increase in moist static energy in the vertical means that there is a vertical transport that advects high values of MSE to the mid and upper troposphere (the same happens for the latent heat energy), while it is the opposite for dry static energy (Figure 11e,f). This is because the values for dry static energy increase while going upward in the atmosphere. The increase the in the cyclone region (Figure 6). In the horizontal, a positive indicates a transport of warm air advection to a region of cold air or a cold air advection in a region of warm air (Figure 11b), and the same goes for . Indeed, the negative means that moist air is advected from northern Africa to the already moist Mediterranean (see Supplementary Figures S6 and S7 for humidity and cross-section, and Figure 11c). The opposite happens for the , where warm air is advected towards colder regions (Supplementary Figure S6 for temperature). The is negative on the eastern side of the cyclone and dominates the moist static energy advection anomaly correlation. Furthermore, on the 15th of September, the slight negative value at the center of the cyclone (Figure 11d) means subsidence (Supplementary Figure S7), as also suggested by the negative in Figure 11e. To sum up, during the initial phase of Ianos’ life cycle, both vertical anomalies align with the presence of the cut-off low. This situation is interpreted as the subsidence of dry air inside the cyclone’s eye, while outside the eye (at the eyewall), moistens the air and increases . Indeed, the local maximum of the field (Figure 2) corresponds to the latent heat flux peak (Figure 11).
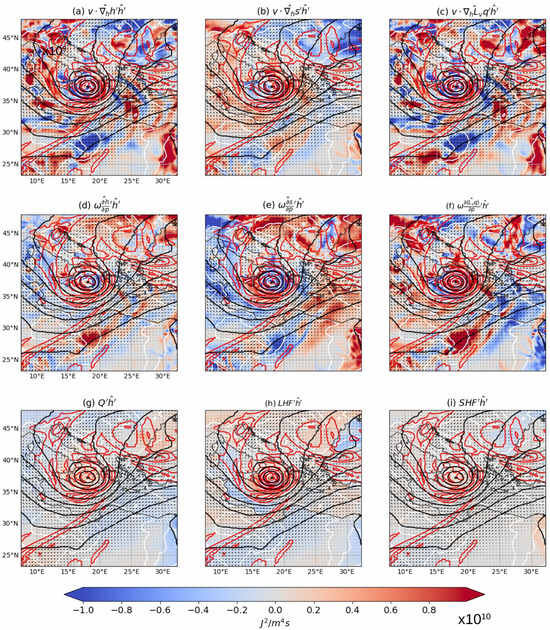
Figure 12.
Budget terms as in Equation (7) for the 17 September 2020 at 00 UTC. In shading, (a–c) show the horizontal advection term of moist static energy, dry static energy, and latent heat energy, respectively; (d–f) show the vertical advection term of moist static energy, dry static energy, and latent heat energy, respectively; (g) shows the radiative cooling term, (h) the latent heat flux term, and (i) the sensible heat flux term. Black lines represent 500 hPa geopotential height (from 5000 to 6000 m), red lines represent potential vorticity at 300 hPa (from 0 to 8 PVU), white lines represent MSLP (from 990 to 1010 hPa), and vectors represent 300 hPa wind in m/s.
Lastly, the contribution from the radiative fluxes is of secondary importance. The net-longwave (LW) and net-shortwave (SW) flux anomaly correlation with the MSE anomaly shown in Figure 9 are condensed into one term, the radiative cooling term, , as reported in Table 2 and Figure 10, Figure 11 and Figure 12. The term , indeed, has been computed as the difference between the net-longwave and the net-shortwave fluxes and represents their combined effect. The positive correlation between the positive cooling anomaly in cloudy regions and the positive anomaly of MSE, , makes positive in the cyclone core; thus, radiative cooling reinforces MSE anomalies in that area (Figure 11g). Figure 9a shows that, while the shortwave feedback on average remains mostly positive during all Ianos’ life cycle, thus also in the initial phase, the longwave feedback is positive during this phase and the intense phase only. The radiative feedback can be explained as follows. There is enhanced longwave cooling of the driest columns and decreased longwave cooling of the moistest columns, where all the deep clouds are, because the column longwave cooling is reduced by the longwave opacity and low temperature of high clouds [,] (Supplementary Figure S7). The shortwave feedback is mostly positive and results in a clear sky effect, where the driest regions absorb less shortwave than the cloudy ones, helping in maintaining the dry regions, keeping them drier and cooler ( < 0) [] (Supplementary Figure S7).
4.3.2. Intense Phase
Figure 10b shows that, in the intense phase, the dominant process is the horizontal advection of MSE with a secondary contribution of the surface fluxes and radiation in the whole area. In the case of radiative feedback, they are similar to what was previously described. is positively correlated with in the cyclone core area, as is visible on the 17th of September (Figure 12g and Supplementary Figure S9). The latent heat flux anomaly (LHF’) and sensible heat flux anomaly (SHF’) increase around the cyclone core, and by September 17th their impact becomes more pronounced (Figure 12h,i). While SHF’ remains mostly positive over the region during the day (Figure 9a), LHF’ is negatively correlated, except over the cyclone core, where increased latent heat fluxes contribute to intensification. Indeed, in this phase, the positive latent heat surface flux feedback can be interpreted firstly by the wind-induced surface heat exchange feedback (WISHE feedback []), whereby the pressure minimum intensifies the surface convergence, which enhances evaporation from the sea surface, upward movements, and, therefore, the release of latent heat, which, in turn, by warming the core of the system, intensifies the aforementioned upward movements and, therefore, the convergence in the lower layers, as was also found happening during Ianos development by []. Indeed, they found that the WISHE effect played a role in both the development and the intense phase, where the mass convergence associated with the convective cluster leads to an increase of the surface winds, and then of surface fluxes in surrounding areas, similarly to what happens in tropical cyclones [,]. This might explain the increase in the LHF and SHF anomalies, at least in the intense phase of the cyclone (Figure 12). Similarly to what happens in idealized simulations of tropical convection [,] and GCM simulations of cyclones [], while the surface flux-wind feedback is positive, it can be counteracted by a negative surface flux feedback due to variations in the air–sea enthalpy disequilibrium, as already explained. This can also be seen in Figure 12h,i, especially in the Mediterranean Sea. Nevertheless, the feedback between surface fluxes and wind, in the flow converging into the cyclone, is of great significance for the intense phase of the cyclone. This is analogous to what was found by [], with the majority of the feedback being positive within the cyclone area. This can be correlated to the vertical advection and horizontal advection anomalies of latent heat energy, shown in Figure 12c,f. The relative contribution of the surface fluxes for the cyclone only (in a 400 km area around the cyclone center) can be seen in Figure 10d, where the radial mean of each budget term is reported for the intense phase.
During the intense phase, the most important feature captured by the budget is the PV streamer. Generally, it is accompanied by a dry air intrusion from the stratosphere []. The presence of PV streamers has been documented in several studies on medicanes [,,,], indicating that such upper atmospheric structures may play a significant role in the intensification of these Mediterranean cyclones. Miglietta et al. (2017) [] analysed five medicanes and found the presence of an upper-level PV streamer in the early stages of each cyclone, located at the left exit of the jet stream. However, the evolution of the upper-level PV anomaly during the mature phase varied between cases, and only in the most intense cases did it help the intensification of the system.
In the budget, it is captured by the positive . This is clearly shown in Figure 9a,b, where the horizontal advection of MSE feedback is becoming the dominant term and is also in correspondence with the sudden increase in variance, as shown in Figure 4. The aligns directly with the PV streamer (Figure 12b), indicating that the advection of cool and dry air is increasing convective instability. The advective term also underlines the cyclonic circulation around the cyclone center (Figure 12a,c) in the intense phase (Supplementary Figure S8). In general, the horizontal advection of moist air is negatively correlated with the anomaly of moist static energy because it is underlying a decrease of MSE in the region downgradient of the direction of the advection and an increase in MSE upgradient (Figure 11c and Figure 12c). The same is true for the advection of dry air inside the cyclone, which instead is positively correlated with downgradient. In the case of dry static energy horizontal transport, when cold air is transported inside the cyclone from the north-west, the anomalies are positively correlated with the decrease of , as in the case of warm air coming from the south-east with the increase of , as shown in the initial phase (Figure 11b). Regarding vertical advective anomalies, a similar consideration for the initial phase holds. Furthermore, as mentioned in the previous section, the positive underlines the presence of strong vertical motions with latent heat release in moist ascent (as confirmed in the cross-section of Supplementary Figures S7 and S9). This warms the core of the medicane and is usually in correspondence with the surface flux feedback at the surface (Figure 12f,h).
4.3.3. Dissipation
After the intense phase is over, the LHF feedback decreases its importance due to the dissipation of the cyclone, while the SHF feedback turns negative on the 18th of September, when the cyclone made landfall. In Figure 9, it is made clear that, while the shortwave feedback remains mostly positive, the longwave one becomes negative in the dissipation phase of the cyclone, where clouds start disappearing over the core, thus increasing the longwave cooling over the entire area (). The advection terms also shift in importance. The vertical advection of latent heat energy, prominent in the intense phase, diminishes (Figure 12f). This decline in vertical and horizontal heat transport marks the cyclone’s dissipation (Figure 10c). Indeed, in the dissipation phase, the sign change in the vertical advection of MSE indicates the dissipation of convection, where a negative contribution from the vertical advection reflected a balance between a highly positive latent heat vertical advection and a strongly negative dry static energy vertical advection, signifying the conversion of moisture into heat, a process that halts after the intense phase.
4.4. Sensitivity to Area
Given the assumptions made in this paper regarding the choice of area, it was decided to check the sensitivity to this aspect. This is particularly important for considering the similarity between this type of Mediterranean cyclone, like Ianos, and its tropical counterparts. For tropical cyclones, it has been observed that an increase in the variance of vertically integrated MSE variance corresponds in magnitude to an increase in the variance of vertically integrated latent heat energy variance, [,], by considering smaller areal dimension to the one chosen ( in []). As seen in Figure 4, for an area of about 25002 km2, which corresponds to a radius of around 1250 km around the center of the cyclone, this is not confirmed, as the variance increases primarily due to the correlation term, . Additionally, the variance of dry static energy, , and latent heat energy, , are both relevant.
Figure 13 represents the sensitivity to the choice of area relative to the center for the different phases. The terms shown in Figure 13b are averaged over areas with different radii from the tracked center of Ianos on the day between September 17th and September 19th, the intense phase. What emerges is that moisture plays a significant role up to an area of about 600 km, approximately four times the radius of the cyclone’s core, with the integrated dry static energy variance term and the correlation counteracting each other. In the intense phase, the correlation term, , while always small, only cancels out within 200 km, in the cyclone’s core. A similar consideration can be made for the dissipation phase, Figure 13c, while in the initial phase the correlation term is significantly negative for all radii. Given this graph and the considerations already made in the previous sections, we can conclude that up to about 600 km, or within three times the radius of the core, Ianos behaves similarly to its tropical counterparts. However, in line with Figure 10, over larger areas, large-scale processes associated with dry static energy variations are as significant as moist processes, especially as horizontal advection of moist static energy becomes more relevant than surface fluxes. Nevertheless, by considering a larger area, we can account for all the processes and the relative importance of dynamics and thermodynamics in the development of the cyclone.
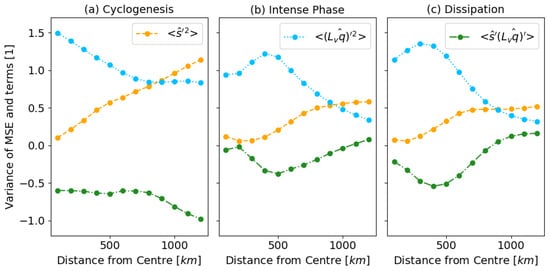
Figure 13.
Normalized terms of the moist static energy variance decomposition change with area. (a) The terms for the initial phase, from the 15th of September at 00 UTC to the 16th of September at 23 UTC. (b) The terms for the intense phase from the 17th of September at 00 UTC to 19 th of September at 00 UTC. (c), The terms for the dissipation, after the 19th of September.
As mentioned in Section 4.1, we also explored the sensitivity to spatial domain selection by computing the MSE variance terms and budget over different circular regions with a radius of 125 km, 300 km, 600 km, and 800 km (Supplementary Figures S2 and S3). As the domain size increases, the variability in MSE budget terms becomes smoother, and the residual term decreases. Similarly, the horizontal variance of MSE components follows this trend, with increasing spatial averaging reducing sharp variations, leading to a more gradual evolution over time. At smaller radii (e.g., 125 km), exhibits stronger oscillations and peaks, indicating rapid changes due to localized convection. At larger radii (e.g., from 800 km above), the variance smooths out, since the computed statistics are less influenced by localized fluctuations.
5. Discussion
In this study, the use of the budget of vertically integrated moist static energy was promoted as a diagnostic tool to primarily investigate processes that may be relevant to Mediterranean cyclones [,] and to assess their similarity to their tropical counterparts. Ianos was chosen because it represented the perfect candidate to examine the suggested tropicalization of Mediterranean cyclones [,,].
By looking at the decomposition, we found that was especially important during the intense phase of Ianos. This term reflects the role of moisture in the cyclone’s core, where the release of latent heat through condensation powered the storm’s intensification. This term also correctly indicates the presence of the initial convective activity that served as the initial condition for the development of the Ianos cyclone, as also mentioned in []. Our results also underlined that, unlike tropical cyclones, which primarily rely on latent heat energy variance due to the weak temperature gradients [], the in Ianos was significant from the early stages of cyclogenesis. This term captured the influence of midlatitude dynamics, such as the interaction with the potential vorticity (PV) streamer and cut-off low, as documented in the literature []. During cyclogenesis, the dry static energy variance increased as cold air from the upper atmosphere interacted with the warm sea surface [], creating a significant temperature contrast and then increasing . The term became particularly relevant during the later stages of Ianos’ development, during the interaction with the PV streamer, where it highlighted the role of cold, dry air being advected to the cyclone, as confirmed by the budget terms (specifically by the vertical advection of latent heat energy and horizontal advection of dry static energy (Figure 9b)). The positive values of this covariance during intensification indicated that the cyclone was benefiting from the combined effect of warming at the core (due to dry static energy) and moisture influx (due to latent heat energy), further fueling its intensification.
The budget terms properly captured the physical process behind Ianos’ life cycle. The Section 4.3 analysis revealed that the horizontal and vertical advection of MSE played the most important role in both the cyclogenesis and intense phases of Ianos (Figure 9a,b). However, the development of the warm core and the increase in vertically integrated MSE variance were also driven by diabatic processes, surface fluxes, and radiative flux feedback. The horizontal advection feedback captures the large-scale features. The positive horizontal advection of dry static energy (linked to temperature) indicates the transport of cold, dry air into the cyclone’s vicinity. This cold air increases convective instability by creating stronger temperature contrasts, which fuels further convective activity. In the intense phase, it marks the occurrence of a PV streamer and the associated dry air intrusion from the stratosphere. Meanwhile, in the initial phase, horizontal advection of moist air, especially from warm regions like northern Africa, contributes additional moisture to the cyclone core. Vertical advection of warm and moist air from the sea surface to the high troposphere fuels the convection needed for the storm’s growth. The interaction between these advection processes creates a delicate balance, where moist air fuels convection while cold, dry air from larger-scale systems enhances instability, both of which promote the cyclone’s intensification. The interplay between vertical and horizontal advection, particularly the upward transport of moist air and the lateral inflow of warm, moist air and cold, dry air, was a key mechanism driving the evolution of Ianos.
In [], the advective terms in the budget, calculated as a residual, exerted a negative feedback on the increase in variance, indicating that horizontal advection damps anomalies of moist static energy. This was further confirmed in [] by computing the advection term in a set of idealized simulations. Here, we found different results: horizontal advection of MSE is fundamental for the cyclone to reach its mature stage. Yu et al. (2019) [] found similar results regarding the positive feedback of vertical and horizontal advection of MSE in tropical cyclone cores using a high-resolution model like WRF. Moreover, in [], it was found that the order of magnitude of MSE convergence was much larger than that of radiation. Similarly to what was found in Ianos, the vertical component of MSE advection reflects the upward transport of MSE by convection in tropical cyclones. Positive vertical advection anomalies indicate that moist air is being lifted from the lower atmosphere, where it undergoes condensation and releases latent heat, thereby warming the cyclone’s core and intensifying it. This feedback is particularly important in the core of the cyclone, where strong upward motions are concentrated, and is closely tied to latent heat release during condensation, which warms the cyclone’s core and accelerates its intensification. This has also been found for other medicanes [] and makes Ianos truly resemble a tropical cyclone. However, the results found here underline the importance of the synergy between latent heat release and external factors (warm air lateral advection, PV streamer) in the intensification of the cyclone towards reaching the pure diabatic phase, as is commonly found in most medicanes [,,,].
Regarding the diabatic process role on cyclone intensification, we found that the wind-induced surface heat exchange mechanism was particularly relevant, similar to what was found in [], whereby the pressure drop and convergence at the cyclone’s core enhanced surface fluxes, which in turn drove convection and led to further intensification of the cyclone. This is indicated by the budget in Figure 9a, when looking at the surface fluxes feedback. The importance of surface flux feedback being positive for cyclone development was also noted in [] for GCMs, where it was found that more intense tropical cyclones exhibit greater positive surface flux feedback [,]. The positive surface flux feedback is also consistent with the results found in CRMs [,], reflecting robust wind-induced surface heat exchange feedback associated with tropical cyclones.
We found that the longwave cooling and shortwave heating effects primarily dominate the radiative feedback. In the cyclone’s core, the longwave cooling is reduced due to the presence of deep clouds, which trap infrared radiation, leading to a warming effect [,]. In contrast, the driest regions experience enhanced longwave cooling. This feedback is positive for cyclone intensification, as the reduced longwave cooling in the moist core increases the moist static energy (MSE), while the clear-sky regions allow for efficient cooling. The shortwave feedback, associated with solar radiation, is generally weaker but becomes important in keeping the dry regions dry and cooler, contributing to further destabilization of the environment around the cyclone core.
It should be emphasized here that the results found in this study regarding the roles of various feedback mechanisms in cyclogenesis and the maintenance of convection within the cyclone have been confirmed by multiple studies employing higher resolutions than the ERA5 reanalysis, making the conclusions of this work significant. Studies such as those by [,,], which used non-hydrostatic models like RAMS, SAM, and WRF while computing the same budget, have found similar radiative feedbacks during convective aggregation, cyclogenesis, and its maintenance. Similar findings were obtained using WRF by []. In their study, by implementing the moist static energy (MSE) budget on tropical cyclones, they observed similar behaviors regarding longwave feedback as well as the contributions of vertical and horizontal MSE transport feedbacks. Additionally, the WRF model has been used to simulate the evolution of moist static energy and secondary circulation during the rapid intensification of cyclones, such as Typhoon Yutu []. The study found a significant correlation between column-integrated MSE and changes in typhoon intensity, with rapid increases in MSE attributed to enhanced subsidence and convective heating, as observed in this study.
Regarding studies on medicane Ianos conducted with high-resolution models, we found that ref. [], using WRF at 3 km resolution, obtained similar results concerning the tropical transition of Ianos, including timing and Hart parameters. More recently, Sanchez et al. (2024) [], using the Met Office Unified Model (MetUM) at 2.2 km grid spacing, identified three key elements crucial to Ianos’ development: A low-valued potential vorticity (PV) area formed within a trough above the location where Ianos developed, as found here (Figure 4). Vorticity advection (corresponding to the PV streamer found in this study), is enhanced by the growth and advection of the low-PV region. Diabatic heating was dominated by deep convection, forming a vertical PV tower during Ianos’ intensification and continuing to produce diabatically induced divergent outflow aloft, which is recognized here as positive vertical MSE advection, thus sustaining Ianos’s development. Similar results regarding Ianos’s evolution were also found using a robust suite of high-resolution mesoscale models (WRF, BOLAM, MESONH, MOLOCH) run at 10 km and 2 km resolution by []. However, they pointed out the importance of resolving small-scale convective processes; reducing horizontal grid spacing from 10 km with parameterised convection to convection-permitting 2 km further improves the cyclone track and intensity. Indeed, Ianos’ intensity, regarding CP in this study, is underestimated. Higher resolution enhances convective activity, which improves the phasing of the cyclone with an upper-level jet and its subsequent intensification and evolution.
Lastly, the computation of the explicit budget also leaves a small residual, which is negligible for most of Ianos’ life-cycle (pink line in Figure 9a), suggesting that most of the key processes driving the cyclone’s evolution have been well captured through the analyzed terms. However, the residual may represent the influence of additional processes that were not considered but slightly contribute to the overall variance. Among these overlooked processes, temporal variations in kinetic energy and geopotential might play a role, though they are negligible (as discussion in Appendix A, Figure A1) compared to the moist static energy variation. Secondly, another possible source of the residual could stem from the neglect of surface momentum fluxes and differences in the calculation of horizontal derivatives. ERA5 uses its method to calculate horizontal gradients (more information on this can be found in both [] and in the IFS documentation []), which may introduce differences compared to our approach.
Given the results of the vertically integrated moist static energy and its terms, one can try to answer the validity of the tropical-like nature claim of Ianos and the cyclone similar to it. We performed a small sensitivity test on the area around the cyclone center, where the main outcome is that only for smaller areas (within three times the core radius), the cyclone displays characteristics similar to tropical cyclones, with latent heat energy variance dominating and surface fluxes playing a critical role in fueling convection and intensification (Figure 13). Once the area is increased, the influence of mid-latitude dynamics becomes more prominent, with dry static energy variance and the covariance term gaining importance. These terms highlight the impact of temperature gradients and large-scale atmospheric interactions, which are less relevant to tropical cyclones but crucial for extratropical cyclones like Ianos. However, only by taking into account large areas can one achieve a clearer insight into what is contributing to cyclone development in general, as also pointed out with the sensitivity of the budget to the changing area. This paper confirms that, while medicanes share many similarities with tropical cyclones, their development is also shaped by unique interactions with the mid-latitude process [].
Our classification results align with those found using other frameworks (e.g., the potential vorticity budget). Indeed, Flaounas et al. (2021) [] applied potential vorticity budget diagnostics and piecewise PV inversion to WRF model simulations of the mature stage of 100 intense Mediterranean cyclones, of which 10 were medicanes, giving a new definition of medicanes as systems that are sustained, or strongly driven, by diabatic processes. It has to be noted that their PV tendencies have been averaged within a radius of 100 km around cyclone centers; thus, their results are in line with what is shown in Figure 13. Miglietta et al. (2019) [], based on two different cases, divided medicanes into categories: those dominated in their mature stage by the WISHE mechanism and those where both mechanisms appear important even at later stages. They, however, found that, in both cases, the maximum intensity is reached at the time when the upper-level PV streamer completely wraps around the cyclone. They used both the equivalent potential temperature anomalies and potential vorticity isosurfaces for the medicane analysis. The analysis carried out here put Ianos in the first category, but can also detect the presence of the vorticity streamer with the dse advection term (Figure 9 and Figure 12) in the intense cyclone phase. Similar results were found by other case study analysis using potential vorticity as diagnostics [,,], including medicane Ianos []. For instance, Miglietta et al. (2017) [] qualitatively analyzed PV anomalies arising from the intrusion of dry stratospheric air and diabatic latent heating, highlighting their role in medicane formation and intensification, as is the case for what has been found by employing the MSE budget. Lastly, Givon et al. (2024) [] applied a PV budget clustering analysis for Mediterranean cyclones, including 12 medicanes, finding similar results to the [] classification. More importantly, they found that Ianos belonged to their category 6, which encompasses a PV cutoff structure, by analyzing the large-scale environment over a similar domain area as the one used in this study, confirming once again what we found in Figure 12. We leave as future study the possibility of being able to combine the two diagnostics, the MSE budget and the PV budget, to obtain more structured results.
The choice of area in MSE variance budget computations is therefore crucial for accurately capturing the balance between tropical-like and baroclinic influences on these cyclones. Thus, we suggest considering areas of around 1000 km2 of radius around the cyclone center. Despite providing a detailed analysis of the evolution of the Ianos cyclone and quantifying the processes’ contribution, this study focuses on a single case study, an exceptional and well-documented event through the moist static energy budget. Thus, future research will be extended to additional medicanes, allowing for a more robust verification of the identified dynamics. Lastly, our approach relies entirely on ERA5 reanalysis data, which, despite having been found valuable in predicting the structure of tropical cyclones in their intense phase [] and for mid-latitude cyclone tracking, convection and precipitation analysis [,] may introduce uncertainties in radiative and surface fluxes [,,] and has some biases in wind speed [] and humidity []. The surface flux biases may be due to the combined biases that ERA5 reanalysis presents in SST, near-surface wind speed, and humidity, which can affect flux estimations []. Additionally, ERA5 employs bulk flux parameterization [], which may not fully capture high-wind regimes, potentially leading to latent heat flux underestimation during medicane peak intensity []. Another important factor is the sea spray effect, which enhances latent heat fluxes but is not explicitly represented in ERA5, possibly leading to an underestimation of heat exchange in Ianos’ core []. Since direct observations of surface fluxes during medicanes are scarce, comparisons with satellite-derived data or observational networks [] and alternative reanalyses could help quantify uncertainties in future studies.
Nonetheless, this paper can still be used to distinguish the tropical-like phase of a cyclone, when the is correspondent to within the core of the cyclone (or up to three times the core radius), at least in the intense phase. Indeed, in both Figure 7 and Figure 12, the largest percentage of is explained by the moisture increase in the cyclone core region. The dominance of latent heat energy variance in this zone suggests that the cyclone’s energy sources are primarily linked to moisture-driven processes, such as condensation and convective motion, closely resembling tropical storm dynamics.
6. Conclusions
The increase in the vertically integrated variance was linked to the convective organization and intensification of the cyclone, confirming that medicanes like Ianos share similarities with tropical cyclones in terms of their internal energy processes [,]. Indeed, the overall increase in throughout the life-cycle of Ianos was a key indicator of its intensification [], where, similar to tropical cyclones, increased convection leads to the progressive concentration of humidity and cloud cover in a specific region []. During cyclogenesis, the MSE variance was initially low, but as the convective cluster and surface low merged, the variance began to rise, driven by the increase in latent heat energy and dry static energy variance. As the cyclone moved into its mature phase, the sharp increase in variance was associated with enhanced convection, moisture inflow, and the interaction with large-scale synoptic features like the PV streamer. The MSE variance growth, particularly during the intense phase, demonstrated the cyclone’s transition into a powerful system, with the latent heat and dry static energy components reinforcing each other through the covariance term.
The findings suggest that mid-latitude cyclones, particularly tropical-like cyclones such as Ianos, can be effectively analyzed within this framework traditionally applied to tropical cyclones []. The budget analysis revealed that, during cyclogenesis, the horizontal advection of moist static energy and surface fluxes are the most critical processes driving cyclone development. During the intense phase, the presence of a potential vorticity (PV) streamer—and consequently horizontal advection—remains significant, while surface fluxes and radiation contributions are of secondary importance (Figure 10).
The analysis carried out in this specific context enabled us to find a framework of process identification that can also be used for the classification of Mediterranean tropical-like cyclones in general. This makes it possible to understand whether or not these cyclones in bulk are similar to their tropical counterparts. By analyzing what process is mostly contributing to the cyclone reaching a deep warm core, an increase in or , we concluded that, if we consider the increase in MSE variance over large scales comparable to those typically used for tropical cyclones, Ianos cannot be directly associated with tropical cyclone theory. However, when analyzing smaller scales (under 600 km), Ianos can be assimilated within this framework, though only during its intense phase. By using the presented budget, we can extend our analysis to known cases of Mediterranean cyclones in the literature, by using reanalysis or via numerical simulation.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos16050562/s1, Section S1 provides figures for a deeper analysis of budget terms from Section 4, including MSE variance around the cyclone center and domain area sensitivity tests (Figures S1–S4). Section S1.2 enriches the analysis of Section 4.2 and Section 4.3 with variance terms during dissipation and atmospheric profiles on 15 and 17 September 2020 (Figures S5–S9).
Author Contributions
Conceptualization, M.S., L.S. and P.B.C.; Methodology, M.S., L.S. and P.B.C.; Formal analysis, M.S.; Investigation, M.S. and L.S.; Data curation, M.S. and L.S.; Writing—original draft, M.S. and L.S.; Writing—review & editing, M.S., L.S. and P.B.C.; Funding acquisition, P.B.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by the University of Perugia Fondi di ricerca di Ateneo—Edizioni 2021 e 2022. M.S. was funded by SSTAM/CIRIAF in co-operation with the Italian Ministryof Environment and Energy Security. P.B.C was funded by the European Union NextGenerationEUunder the Italian Ministry of University and Research (MUR) National Innovation Ecosystem grant ECS00000041—VITALITY—CUP J97G22000170005. Moreover, the Authors would like to thank the European Commission, MUR (Italy), Fapesc (Brazil), and FCT (Portugal) for funding in the frame of the collaborative international consortium MORE4WATER financed under the 2022 Joint callof the European Partnership 101060874—Water4all. L.S. was financed by the Italian Ministry of University and Research (MUR), through the PRIN 2022 PNRR Project P20229KW2R—SEAPLANE—“Simulation and modeling of interface fluxes in wind-wave flows for an improved climate science”, CUP E53D23017010001, funded by the National Recovery and Resilience Plan (PNRR), Italy, Mission04 Component 2 Investment 1.1—NextGenerationEU.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The ERA5 global reanalysis data can be freely downloaded from the online archive system at https://cds.climate.copernicus.eu/datasets/reanalysis-era5-complete?tab=overview (accessed on 19 February 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Derivation of the MSE Budget from Primitive Equations
To derive a budget for h, we start from the equations for momentum, mass continuity, heat, and moisture budget, as written in pressure coordinates [,] for a moist atmosphere under hydrostatic balance. We follow the exact formulation of the MSE budget by [], defining the material derivative as:
where is the pressure-coordinate vertical velocity (). In order to write the equation in a more compact form, we define the horizontal divergence operator as and the horizontal velocity vector as . We can write our system of equations as:
where, by using the hydrostatic condition Equation (A4), we can also write the thermodynamic energy equation by using the definition of dry static energy as follow:
and we also write the kinetic energy equation that is obtained by scalarly multiplying to the momentum equation:
where is the kinetic energy per unit mass. The source terms in the moisture and heat budget are the radiative heating rate , the condensation rate C of water vapour, the evaporation rate E of liquid water, and the dissipative heating D. The first assumption we made in deriving the system of Equations (A2)–(A8) is hydrostatic balance, which is valid as long as we consider large-scale motions. The second assumption is that we do not consider molecular diffusive processes. The third assumption is that phase changes of ice are neglected. The last assumption is to consider the gas constant independent on water vapor content. See [] for the accuracy of such approximations.
When solving this system of equations within a certain horizontal resolution, we need to include the effect of subgrid scales to obtain an appropriate energy budget. Therefore, we perform a running horizontal average on each variable to separate large, resolvable, and grid-scale quantities (in ERA5 we assume them to be of the order of the grid resolution, which is ≈31 km) from the sub-grid scale quantities:
where the running average follows the properties of the Reynolds average ( and ). Then, by decomposing the term in the main equations, with the aid of continuity and applying the average operator, we obtain:
We further simplify our system of equations by considering the lateral transport of heat and moisture by sub-grid scale eddies (associated with cumulus convection) negligible with respect to the horizontal transport by large-scale motions (see Equations (26)–(28) from []):
and the same assumptions are applied to the other variables, such as the lateral transport of kinetic energy and temperature. We note that this is a reasonable assumption for convection embedded in large-scale weather systems, as in the medicane Ianos studied in this paper. In our case, this assumption is equivalent to assuming that the effect of the lateral transport of heat and moisture by mesoscale eddies smaller than 31 km is negligible. However, subgrid-scale horizontal transport by the turbulence scheme is important for creating large-scale humidity perturbation and initiating deep convective aggregation in idealized simulations of radiative-convective equilibrium, where large-scale horizontal transport is absent and horizontal resolution is of the order of 1 km [].
On the other hand, we cannot ignore the vertical transport of moisture and heat by subgrid-scale eddies and convection (e.g., ). Taking into account such assumptions and with the aid of the continuity Equation (A10), we can rewrite our averaged equation in terms of the total derivative as:
where and are the apparent heat source and latent energy sink, as defined in [] (see their Equations (8) and (9)), with only the addition of dissipative heating in the definition of .
By considering the material derivative of the averaged geopotential:
we can add Equations (A17)–(A19), premultiplied by the factor L, to obtain the final expression for the averaged moist static energy () budget:
where for the sake of simplicity, from this point on, we refer to each variable as a large-scale variable without including the operator. Rearranging Equation (A20):
From this final equation, we see that both the geopotential time derivative and the lateral advection are present in the total MSE budget. To simplify such terms, we need to use the kinetic budget Equation (A16). Before adding the kinetic energy budget, we assume that the vertical subgrid scale flux of horizontal momentum is mainly downgradient, which is , where is a subgrid-scale eddy viscosity coefficient. With this assumption, we can express the subgrid vertical fluxes of horizontal kinetic energy as:
where we notice that the last term on the RHS is always negative and represents a dissipation of kinetic energy, which is the term D, which is compared to dissipative heating in Equation (A21). Then, we can rewrite the kinetic energy budget as:
Summing up the equation for the moist static energy, Equation (A21), with the kinetic energy, Equation (A23), we obtain an equation for the total energy of the system, E, the sum of kinetic energy and thermodynamic energy:
To simplify the treatment of subgrid turbulent fluxes, we integrate Equation (A24) over the column by defining the following integral operator:
where is the pressure at the model top and hPa. This operator represents a mass-weighted vertical integral through the entire atmospheric column. By assuming that there are no eddy fluxes at the model top, we can write the vertical integral of moist static energy fluxes as:
where and are the surface sensible and latent heat fluxes, respectively. Then, by integrating the kinetic energy eddy fluxes and representing them through a bulk aerodynamic formula:
where the vector is the horizontal surface velocity vector, is the momentum drag coefficient as modeled in ERA5 reanalysis, and is the surface air density.
The final vertical integral budget of the total energy can be written as:
However, the most common form used for the MSE budget in the tropics or self-aggregation of deep convection is:
which is derived by assuming that . To recover such a simpler formulation, we need to verify the following hypothesis:
- The vertically integrated tendency of geopotential must be much smaller in amplitude than the MSE tendency:
- Temporal and spatial fluctuations in K must be much smaller than those in MSE in order to have:
- Surface fluxes of kinetic energy are negatively small or can be neglected when compared to the sensible and latent heat surface fluxes:
These hypotheses were tested, as shown in Figure A1. Indeed, we computed the tendency of vertically integrated kinetic energy, , and the tendency of the vertically integrated geopotential, , and compared it to the tendency of vertically integrated MSE, , in ERA5. We found that the kinetic energy tendency is two orders of magnitude smaller than the MSE tendency during all of the Ianos life-cycle. Furthermore, we found that the geopotential tendency is at least one order of magnitude smaller than the MSE tendency for the whole period.
The small magnitude of the kinetic tendency relative to the MSE tendency gives us confidence that hypotheses 2 and 3 are fulfilled, and neglecting the tendencies does not seriously impact our results. Instead, the geopotential tendency being only one order of magnitude smaller than the MSE one suggests that this can be the main contribution to the residual we see in Figure 9a.
Figure A1.
The tendency of vertically integrated MSE, the tendency of vertically integrated kinetic energy, and the tendency of vertically integrated geopotential tendency.
References
- Emanuel, K. Genesis and maintenance of “Mediterranean hurricanes”. Adv. Geosci. 2005, 2, 217–220. [Google Scholar] [CrossRef]
- Cavicchia, L.; von Storch, H.; Gualdi, S. Mediterranean tropical-like cyclones in present and future climate. J. Clim. 2014, 27, 7493–7501. [Google Scholar] [CrossRef]
- Tous, M.; Romero, R. Meteorological environments associated with medicane development. Int. J. Climatol. 2013, 33, 1–14. [Google Scholar] [CrossRef]
- Fita, L.; Romero, R.; Luque, A.; Emanuel, K.; Ramis, C. Analysis of the environments of seven Mediterranean tropical-like storms using an axisymmetric, nonhydrostatic, cloud resolving model. Nat. Hazards Earth Syst. Sci. 2007, 7, 41–56. [Google Scholar] [CrossRef]
- Hart, R.E. A cyclone phase space derived from thermal wind and thermal asymmetry. Mon. Weather Rev. 2003, 131, 585–616. [Google Scholar] [CrossRef]
- Portmann, R.; González-Alemán, J.J.; Sprenger, M.; Wernli, H. How an uncertain short-wave perturbation on the North Atlantic wave guide affects the forecast of an intense Mediterranean cyclone (Medicane Zorbas). Weather Clim. Dyn. 2020, 1, 597–615. [Google Scholar] [CrossRef]
- Comellas Prat, A.; Federico, S.; Torcasio, R.C.; D’Adderio, L.P.; Dietrich, S.; Panegrossi, G. Evaluation of the Sensitivity of Medicane Ianos to Model Microphysics and Initial Conditions Using Satellite Measurements. Remote Sens. 2021, 13, 4984. [Google Scholar] [CrossRef]
- Saraceni, M.; Silvestri, L.; Bechtold, P.; Bongioannini Cerlini, P. Mediterranean tropical-like cyclone forecasts and analysis using the ECMWF ensemble forecasting system with physical parameterization perturbations. Atmos. Chem. Phys. 2023, 23, 13883–13909. [Google Scholar] [CrossRef]
- Cioni, G.; Cerrai, D.; Klocke, D. Investigating the predictability of a Mediterranean tropical-like cyclone using a storm-resolving model. Q. J. R. Meteorol. Soc. 2018, 144, 1598–1610. [Google Scholar] [CrossRef]
- Picornell, M.; Campins, J.; Jansà, A. Detection and thermal description of medicanes from numerical simulation. Nat. Hazards Earth Syst. Sci. 2014, 14, 1059–1070. [Google Scholar] [CrossRef]
- Gaertner, M.Á.; González-Alemán, J.J.; Romera, R.; Domínguez, M.; Gil, V.; Sánchez, E.; Gallardo, C.; Miglietta, M.M.; Walsh, K.J.; Sein, D.V.; et al. Simulation of medicanes over the Mediterranean Sea in a regional climate model ensemble: Impact of ocean–atmosphere coupling and increased resolution. Clim. Dyn. 2018, 51, 1041–1057. [Google Scholar] [CrossRef]
- Flaounas, E.; Davolio, S.; Raveh-Rubin, S.; Pantillon, F.; Miglietta, M.M.; Gaertner, M.A.; Hatzaki, M.; Homar, V.; Khodayar, S.; Korres, G.; et al. Mediterranean cyclones: Current knowledge and open questions on dynamics, prediction, climatology and impacts. Weather Clim. Dyn. 2022, 3, 173–208. [Google Scholar] [CrossRef]
- Nastos, P.; Papadimou, K.K.; Matsangouras, I. Mediterranean tropical-like cyclones: Impacts and composite daily means and anomalies of synoptic patterns. Atmos. Res. 2018, 208, 156–166. [Google Scholar] [CrossRef]
- Flaounas, E.; Gray, S.L.; Teubler, F. A process-based anatomy of Mediterranean cyclones: From baroclinic lows to tropical-like systems. Weather Clim. Dyn. 2021, 2, 255–279. [Google Scholar] [CrossRef]
- Dafis, S.; Rysman, J.F.; Claud, C.; Flaounas, E. Remote sensing of deep convection within a tropical-like cyclone over the Mediterranean Sea. Atmos. Sci. Lett. 2018, 19, e823. [Google Scholar] [CrossRef]
- Carrió, D.; Homar, V.; Jansa, A.; Romero, R.; Picornell, M. Tropicalization process of the 7 November 2014 Mediterranean cyclone: Numerical sensitivity study. Atmos. Res. 2017, 197, 300–312. [Google Scholar] [CrossRef]
- Chaboureau, J.P.; Pantillon, F.; Lambert, D.; Richard, E.; Claud, C. Tropical transition of a Mediterranean storm by jet crossing. Q. J. R. Meteorol. Soc. 2012, 138, 596–611. [Google Scholar] [CrossRef]
- Rostami, M.; Zeitlin, V. Evolution, propagation and interactions with topography of hurricane-like vortices in a moist-convective rotating shallow-water model. J. Fluid Mech. 2020, 902, A24. [Google Scholar] [CrossRef]
- Montgomery, M.T.; Smith, R.K. Recent developments in the fluid dynamics of tropical cyclones. Annu. Rev. Fluid Mech. 2017, 49, 541–574. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Rotunno, R. Development mechanisms for Mediterranean tropical-like cyclones (medicanes). Q. J. R. Meteorol. Soc. 2019, 145, 1444–1460. [Google Scholar] [CrossRef]
- Fita, L.; Flaounas, E. Medicanes as subtropical cyclones: The December 2005 case from the perspective of surface pressure tendency diagnostics and atmospheric water budget. Q. J. R. Meteorol. Soc. 2018, 144, 1028–1044. [Google Scholar] [CrossRef]
- d’Adderio, L.P.; Panegrossi, G.; Dafis, S.; Rysman, J.F.; Casella, D.; Sanò, P.; Fuccello, A.; Miglietta, M.M. Helios and Juliette: Two falsely acclaimed medicanes? Atmos. Res. 2024, 299, 107179. [Google Scholar] [CrossRef]
- Emanuel, K.A. An air-sea interaction theory for tropical cyclones. Part I: Steady-state maintenance. J. Atmos. Sci. 1986, 43, 585–605. [Google Scholar] [CrossRef]
- Rotunno, R.; Emanuel, K.A. An air–sea interaction theory for tropical cyclones. Part II: Evolutionary study using a nonhydrostatic axisymmetric numerical model. J. Atmos. Sci. 1987, 44, 542–561. [Google Scholar] [CrossRef]
- Mazza, E.; Ulbrich, U.; Klein, R. The tropical transition of the October 1996 medicane in the western Mediterranean Sea: A warm seclusion event. Mon. Weather Rev. 2017, 145, 2575–2595. [Google Scholar] [CrossRef]
- Bister, M.; Emanuel, K.A. Dissipative heating and hurricane intensity. Meteorol. Atmos. Phys. 1998, 65, 233–240. [Google Scholar] [CrossRef]
- Pytharoulis, I. Analysis of a Mediterranean tropical-like cyclone and its sensitivity to the sea surface temperatures. Atmos. Res. 2018, 208, 167–179. [Google Scholar] [CrossRef]
- Yano, J.I.; Ambaum, M.H. Moist static energy: Definition, reference constants, a conservation law and effects on buoyancy. Q. J. R. Meteorol. Soc. 2017, 143, 2727–2734. [Google Scholar] [CrossRef]
- Yu, L.; Wu, S.; Ma, Z. Evaluation of moist static energy in a simulated tropical cyclone. Atmosphere 2019, 10, 319. [Google Scholar] [CrossRef]
- Emanuel, K. Tropical cyclone energetics and structure. Atmos. Turbul. Mesoscale Meteorol. 2004, 8, 165–191. [Google Scholar]
- Rousseau-Rizzi, R.; Emanuel, K. An evaluation of hurricane superintensity in axisymmetric numerical models. J. Atmos. Sci. 2019, 76, 1697–1708. [Google Scholar] [CrossRef]
- Zhu, H.; Smith, R.K. The importance of three physical processes in a minimal three-dimensional tropical cyclone model. J. Atmos. Sci. 2002, 59, 1825–1840. [Google Scholar] [CrossRef]
- Yanai, M.; Esbensen, S.; Chu, J.H. Determination of bulk properties of tropical cloud clusters from large-scale heat and moisture budgets. J. Atmos. Sci. 1973, 30, 611–627. [Google Scholar] [CrossRef]
- Yanai, M.; Johnson, R.H. Impacts of cumulus convection on thermodynamic fields. In The Representation of Cumulus Convection in Numerical Models; Springer: Berlin/Heidelberg, Germany, 1993; pp. 39–62. [Google Scholar]
- Wing, A.A.; Camargo, S.J.; Sobel, A.H.; Kim, D.; Moon, Y.; Murakami, H.; Reed, K.A.; Vecchi, G.A.; Wehner, M.F.; Zarzycki, C.; et al. Moist static energy budget analysis of tropical cyclone intensification in high-resolution climate models. J. Clim. 2019, 32, 6071–6095. [Google Scholar] [CrossRef]
- Wing, A.A. Acceleration of tropical cyclone development by cloud-radiative feedbacks. J. Atmos. Sci. 2022, 79, 2285–2305. [Google Scholar] [CrossRef]
- Wing, A.A.; Emanuel, K.A. Physical mechanisms controlling self-aggregation of convection in idealized numerical modeling simulations. J. Adv. Model. Earth Syst. 2014, 6, 59–74. [Google Scholar] [CrossRef]
- Coppin, D.; Bony, S. Physical mechanisms controlling the initiation of convective self-aggregation in a general circulation model. J. Adv. Model. Earth Syst. 2015, 7, 2060–2078. [Google Scholar] [CrossRef]
- Holloway, C.E.; Woolnough, S.J. The sensitivity of convective aggregation to diabatic processes in idealized radiative-convective equilibrium simulations. J. Adv. Model. Earth Syst. 2016, 8, 166–195. [Google Scholar] [CrossRef]
- Shi, X.; Fan, Y. Modulation of the bifurcation in radiative-convective equilibrium by gray-zone cloud and turbulence parameterizations. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002632. [Google Scholar] [CrossRef]
- Cerlini, P.B.; Saraceni, M.; Silvestri, L. Competing effect of radiative and moisture feedback in convective aggregation states in two CRMS. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003323. [Google Scholar] [CrossRef]
- Silvestri, L.; Saraceni, M.; Bongioannini Cerlini, P. Numerical diffusion and turbulent mixing in convective self-aggregation. J. Adv. Model. Earth Syst. 2024, 16, e2023MS004151. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Blossey, P.N.; Khairoutdinov, M. An energy-balance analysis of deep convective self-aggregation above uniform SST. J. Atmos. Sci. 2005, 62, 4273–4292. [Google Scholar] [CrossRef]
- Holloway, C.E.; Wing, A.A.; Bony, S.; Muller, C.; Masunaga, H.; L’Ecuyer, T.S.; Turner, D.D.; Zuidema, P. Observing convective aggregation. Surv. Geophys. 2017, 38, 1199–1236. [Google Scholar] [CrossRef] [PubMed]
- Haerter, J.O.; Meyer, B.; Nissen, S.B. Diurnal self-aggregation. NPJ Clim. Atmos. Sci. 2020, 3, 30. [Google Scholar] [CrossRef]
- Khairoutdinov, M.; Emanuel, K. Rotating radiative-convective equilibrium simulated by a cloud-resolving model. J. Adv. Model. Earth Syst. 2013, 5, 816–825. [Google Scholar] [CrossRef]
- Muller, C.J.; Romps, D.M. Acceleration of tropical cyclogenesis by self-aggregation feedbacks. Proc. Natl. Acad. Sci. USA 2018, 115, 2930–2935. [Google Scholar] [CrossRef]
- Muller, C.; Bony, S. What favors convective aggregation and why? Geophys. Res. Lett. 2015, 42, 5626–5634. [Google Scholar] [CrossRef]
- Nolan, D.S.; Rappin, E.D.; Emanuel, K.A. Tropical cyclogenesis sensitivity to environmental parameters in radiative–convective equilibrium. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2007, 133, 2085–2107. [Google Scholar] [CrossRef]
- Reed, K.A.; Chavas, D.R. Uniformly rotating global radiative-convective equilibrium in the Community Atmosphere Model, version 5. J. Adv. Model. Earth Syst. 2015, 7, 1938–1955. [Google Scholar] [CrossRef]
- Wang, Q.; Kieu, C.; Vu, T.A. Large-scale dynamics of tropical cyclone formation associated with ITCZ breakdown. Atmos. Chem. Phys. 2019, 19, 8383–8397. [Google Scholar] [CrossRef]
- Khairoutdinov, M.F.; Emanuel, K. Intraseasonal variability in a cloud-permitting near-global equatorial aquaplanet model. J. Atmos. Sci. 2018, 75, 4337–4355. [Google Scholar] [CrossRef]
- Beucler, T. Self-Aggregation Phenomenon in Cyclogenesis; Technical Report; Massachusetts Institute of Technology: Cambridge, MA, USA, 2014. [Google Scholar]
- Wing, A.A.; Cronin, T.W. Self-aggregation of convection in long channel geometry. Q. J. R. Meteorol. Soc. 2016, 142, 1–15. [Google Scholar] [CrossRef]
- Wing, A.A.; Camargo, S.J.; Sobel, A.H. Role of radiative–convective feedbacks in spontaneous tropical cyclogenesis in idealized numerical simulations. J. Atmos. Sci. 2016, 73, 2633–2642. [Google Scholar] [CrossRef]
- Yao, L.; Yang, D.; Tan, Z.M. A vertically resolved MSE framework highlights the role of the boundary layer in convective self-aggregation. J. Atmos. Sci. 2022, 79, 1615–1631. [Google Scholar] [CrossRef]
- Smith, W.P.; Nicholls, M.E.; Pielke Sr, R.A. The role of radiation in accelerating tropical cyclogenesis in idealized simulations. J. Atmos. Sci. 2020, 77, 1261–1277. [Google Scholar] [CrossRef]
- Melhauser, C.; Zhang, F. Diurnal radiation cycle impact on the pregenesis environment of Hurricane Karl (2010). J. Atmos. Sci. 2014, 71, 1241–1259. [Google Scholar] [CrossRef]
- Zhang, B.; Soden, B.J.; Vecchi, G.A. A vertically resolved analysis of radiative feedbacks on moist static energy variance in tropical cyclones. J. Clim. 2023, 36, 1125–1141. [Google Scholar] [CrossRef]
- Lagouvardos, K.; Karagiannidis, A.; Dafis, S.; Kalimeris, A.; Kotroni, V. Ianos—A hurricane in the Mediterranean. Bull. Am. Meteorol. Soc. 2022, 103, E1621–E1636. [Google Scholar] [CrossRef]
- Zimbo, F.; Ingemi, D.; Guidi, G. The tropical-like cyclone “ianos” in September 2020. Meteorology 2022, 1, 29–44. [Google Scholar] [CrossRef]
- Panegrossi, G.; D’Adderio, L.P.; Dafis, S.; Rysman, J.F.; Casella, D.; Dietrich, S.; Sanò, P. Warm Core and Deep Convection in Medicanes: A Passive Microwave-Based Investigation. Remote Sens. 2023, 15, 2838. [Google Scholar] [CrossRef]
- Saffir, H.S. Hurricane wind and storm surge. Mil. Eng. 1973, 65, 4–5. [Google Scholar]
- Simpson, R.H. The hurricane disaster—Potential scale. Weatherwise 1974, 27, 169–186. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Silvestri, L.; Saraceni, M.; Brunone, B.; Meniconi, S.; Passadore, G.; Bongioannini Cerlini, P. Assessment of seasonal soil moisture forecasts over the Central Mediterranean. Hydrol. Earth Syst. Sci. 2025, 29, 925–946. [Google Scholar] [CrossRef]
- Silvestri, L.; Saraceni, M.; Bongioannini Cerlini, P. Links between precipitation, circulation weather types and orography in central Italy. Int. J. Clim. 2022, 42, 5807–5825. [Google Scholar] [CrossRef]
- Raveh-Rubin, S.; Wernli, H. Large-scale wind and precipitation extremes in the Mediterranean: Dynamical aspects of five selected cyclone events. Q. J. R. Meteorol. Soc. 2016, 142, 3097–3114. [Google Scholar] [CrossRef]
- Raveh-Rubin, S.; Flaounas, E. A dynamical link between deep Atlantic extratropical cyclones and intense Mediterranean cyclones. Atmos. Sci. Lett. 2017, 18, 215–221. [Google Scholar] [CrossRef]
- Claud, C.; Alhammoud, B.; Funatsu, B.M.; Chaboureau, J.P. Mediterranean hurricanes: Large-scale environment and convective and precipitating areas from satellite microwave observations. Nat. Hazards Earth Syst. Sci. 2010, 10, 2199–2213. [Google Scholar] [CrossRef]
- Miglietta, M.; Cerrai, D.; Laviola, S.; Cattani, E.; Levizzani, V. Potential vorticity patterns in Mediterranean “hurricanes”. Geophys. Res. Lett. 2017, 44, 2537–2545. [Google Scholar] [CrossRef]
- Dafis, S.; Claud, C.; Kotroni, V.; Lagouvardos, K.; Rysman, J.F. Insights into the convective evolution of Mediterranean tropical-like cyclones. Q. J. R. Meteorol. Soc. 2020, 146, 4147–4169. [Google Scholar] [CrossRef]
- Pantillon, F.; Davolio, S.; Avolio, E.; Calvo-Sancho, C.; Carrió, D.S.; Dafis, S.; Flaounas, E.; Gentile, E.S.; Gonzalez-Aleman, J.J.; Gray, S.; et al. The crucial representation of deep convection for the cyclogenesis of medicane Ianos. EGUsphere 2024, 2024, 1–29. [Google Scholar] [CrossRef]
- Ragone, F.; Mariotti, M.; Parodi, A.; Von Hardenberg, J.; Pasquero, C. A climatological study of western mediterranean medicanes in numerical simulations with explicit and parameterized convection. Atmosphere 2018, 9, 397. [Google Scholar] [CrossRef]
- Adames Corraliza, Á.F.; Mayta, V.C. On the accuracy of the moist static energy budget when applied to large-scale tropical motions. J. Atmos. Sci. 2023, 80, 2365–2376. [Google Scholar] [CrossRef]
- Hart, R.E.; Evans, J.L. A climatology of the extratropical transition of Atlantic tropical cyclones. J. Clim. 2001, 14, 546–564. [Google Scholar] [CrossRef]
- Miglietta, M.; Laviola, S.; Malvaldi, A.; Conte, D.; Levizzani, V.; Price, C. Analysis of tropical-like cyclones over the Mediterranean Sea through a combined modeling and satellite approach. Geophys. Res. Lett. 2013, 40, 2400–2405. [Google Scholar] [CrossRef]
- Muller, C.J.; Held, I.M. Detailed investigation of the self-aggregation of convection in cloud-resolving simulations. J. Atmos. Sci. 2012, 69, 2551–2565. [Google Scholar] [CrossRef]
- Porcù, F.; Carrassi, A.; Medaglia, C.M.; Prodi, F.; Mugnai, A. A study on cut-off low vertical structure and precipitation in the Mediterranean region. Meteorol. Atmos. Phys. 2007, 96, 121–140. [Google Scholar] [CrossRef]
- Miglietta, M.; Carnevale, D.; Levizzani, V.; Rotunno, R. Role of moist and dry air advection in the development of Mediterranean Tropical-Like Cyclones (Medicanes). Q. J. R. Meteor. Soc. 2021, 147, 876–899. [Google Scholar] [CrossRef]
- Bouin, M.N.; Lebeaupin Brossier, C. Surface processes in the 7 November 2014 medicane from air–sea coupled high-resolution numerical modelling. Atmos. Chem. Phys. 2020, 20, 6861–6881. [Google Scholar] [CrossRef]
- Coll-Hidalgo, P.; Pérez-Alarcón, A.; Nieto, R. Moisture sources for the precipitation of tropical-like cyclones in the Mediterranean Sea: A case of study. Atmosphere 2022, 13, 1327. [Google Scholar] [CrossRef]
- Koseki, S.; Mooney, P.A.; Cabos, W.; Gaertner, M.Á.; de la Vara, A.; Gonzáles Alemán, J.J. Modelling a tropical-like cyclone in the Mediterranean Sea under present and warmer climate. Nat. Hazards Earth Syst. Sci. Discuss. 2020, 21, 53–71. [Google Scholar] [CrossRef]
- Ernst, J.; Matson, M. A Mediterranean tropical storm? Weather 1983, 38, 332–337. [Google Scholar] [CrossRef]
- Rasmussen, E.; Zick, C. A subsynoptic vortex over the Mediterranean with some resemblance to polar lows. Tellus A 1987, 39, 408–425. [Google Scholar] [CrossRef]
- Palmen, E. On the formation and structure of tropical hurricanes. Geophysica 1948, 3, 26–38. [Google Scholar]
- Cioni, G.; Malguzzi, P.; Buzzi, A. Thermal structure and dynamical precursor of a Mediterranean tropical-like cyclone. Q. J. R. Meteorol. Soc. 2016, 142, 1757–1766. [Google Scholar] [CrossRef]
- Zhang, B.; Soden, B.J.; Vecchi, G.A.; Yang, W. The role of radiative interactions in tropical cyclone development under realistic boundary conditions. J. Clim. 2021, 34, 2079–2091. [Google Scholar] [CrossRef]
- Li, X.; Yang, J.; Han, G.; Ren, L.; Zheng, G.; Chen, P.; Zhang, H. Tropical Cyclone Wind Field Reconstruction and Validation Using Measurements from SFMR and SMAP Radiometer. Remote Sens. 2022, 14, 3929. [Google Scholar] [CrossRef]
- Sánchez, C.; Gray, S.; Volonté, A.; Pantillon, F.; Berthou, S.; Davolio, S. The impact of preceding convection on the development of Medicane Ianos and the sensitivity to sea surface temperature. Weather Clim. Dyn. 2024, 5, 1429–1455. [Google Scholar] [CrossRef]
- ECMWF. IFS Documentation CY41R2 - Part III: Dynamics and Numerical Procedures. In IFS Documentation CY41R2; ECMWF: Reading, UK, 2016. [Google Scholar]
- Givon, Y.; Hess, O.; Flaounas, E.; Catto, J.L.; Sprenger, M.; Raveh-Rubin, S. Process-based classification of Mediterranean cyclones using potential vorticity. Weather Clim. Dyn. 2024, 5, 133–162. [Google Scholar] [CrossRef]
- Malakar, P.; Kesarkar, A.; Bhate, J.; Singh, V.; Deshamukhya, A. Comparison of Reanalysis Data Sets to Comprehend the Evolution of Tropical Cyclones Over North Indian Ocean. Earth Space Sci. 2020, 7, e2019EA000978. [Google Scholar] [CrossRef]
- McErlich, C.; McDonald, A.; Renwick, J.; Schuddeboom, A. An Assessment of Southern Hemisphere Extratropical Cyclones in ERA5 Using WindSat. J. Geophys. Res. Atmos. 2023, 128, e2023JD038554. [Google Scholar] [CrossRef]
- Zhang, W.; Villarini, G.; Scoccimarro, E.; Napolitano, F. Examining the precipitation associated with medicanes in the high-resolution ERA-5 reanalysis data. Int. J. Climatol. 2021, 41, E126–E132. [Google Scholar] [CrossRef]
- Huang, H.; Huang, Y. Radiative sensitivity quantified by a new set of radiation flux kernels based on the ECMWF Reanalysis v5 (ERA5). Earth Syst. Sci. Data 2023, 15, 3001–3021. [Google Scholar] [CrossRef]
- Xin, Y.; Liu, J.; Liu, X.; Liu, G.; Cheng, X.; Chen, Y. Reduction of uncertainties in surface heat flux over the Tibetan Plateau from ERA-Interim to ERA5. Int. J. Climatol. 2022, 42, 6277–6292. [Google Scholar] [CrossRef]
- Urraca, R.; Huld, T.; Gracia-Amillo, A.; de Pison, F.J.M.; Kaspar, F.; Sanz-García, A. Evaluation of global horizontal irradiance estimates from ERA5 and COSMO-REA6 reanalyses using ground and satellite-based data. Sol. Energy 2018, 164, 339–354. [Google Scholar] [CrossRef]
- Slocum, C.; Razin, M.; Knaff, J.; Stow, J.P. Does ERA5 mark a new era for resolving the tropical cyclone environment? J. Clim. 2022, 35, 7147–7164. [Google Scholar] [CrossRef]
- Martens, B.; Schumacher, D.L.; Wouters, H.; Muñoz-Sabater, J.; Verhoest, N.E.; Miralles, D.G. Evaluating the land-surface energy partitioning in ERA5. Geosci. Model Dev. 2020, 13, 4159–4181. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Hui, F.M.; Vihma, T.; Granskog, M.A.; Cheng, B.; Chen, Z.Q.; Cheng, X. On the turbulent heat fluxes: A comparison among satellite-based estimates, atmospheric reanalyses, and in-situ observations during the winter climate over Arctic sea ice. Adv. Clim. Chang. Res. 2023, 14, 347–362. [Google Scholar] [CrossRef]
- Rizza, U.; Canepa, E.; Miglietta, M.M.; Passerini, G.; Morichetti, M.; Mancinelli, E.; Virgili, S.; Besio, G.; De Leo, F.; Mazzino, A. Evaluation of drag coefficients under medicane conditions: Coupling waves, sea spray and surface friction. Atmos. Res. 2021, 247, 105207. [Google Scholar] [CrossRef]
- Silvestri, L.; Saraceni, M.; Bongioannini Cerlini, P. Quality management system and design of an integrated mesoscale meteorological network in Central Italy. Meteorol. Appl. 2022, 29, e2060. [Google Scholar] [CrossRef]
- Arakawa, A.; Schubert, W.H. Interaction of a cumulus cloud ensemble with the large-scale environment, Part I. J. Atmos. Sci. 1974, 31, 674–701. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).