Abstract
This work analyzes the evolution of an urban thermal environment using measurements, in the form of time series, of atmospheric pollutants (PM10, PM2.5, CO) and meteorological variables (temperature (T), relative humidity (RH) and magnitude of wind speed (WS)) of three periods, each of 3.25 years: 2010–2013, 2017–2020 and 2019–2022. The study region is the capital of Chile, Santiago de Chile, located in a rugged basin geography. Of the total communes that make up the capital, six communes that are at different heights from sea level were selected for this study, providing 3,074,004 data records. These communes have been subject to an intensive urban densification process. The time series are analyzed through the chaos theory, demonstrating that they are chaotic through the calculation of the parameters: Lyapunov exponent (λ > 0), correlation dimension (DC < 5), Kolmogorov entropy (SK > 0), Hurst exponent (0.5 < H < 1), Lempel–Ziv complexity (LZ > 0). Based on these parameters, the following is constructed for each commune: the CK ratio, which results from the ratio between the entropies of the meteorological variables and the entropies of the pollutants; the loss of information (<ΔI> < 0) using the Lyapunov exponent; the fractal dimension (D) using the Hurst exponent. It is verified, when comparing the three periods for the six communes, that: CK evolves declining with height, with a greater influence of pollutants; the loss of information is faster in urban meteorology; an increase in fractality. The estimation of the entropic flows, based on the Clausius equation, confirm the trend. The descriptive framework shows the weakness of the mitigation measures.
Keywords:
air pollutants; urban meteorology; densification; entropy; loss of information; mitigation 1. Introduction
Santiago de Chile contains a little more than 40% of the total population of the country and has been the object, in recent years, of a very intense process of urban densification. The location of the city in a geographical basin of variable roughness, which produces a semi-enclosed condition, makes it relevant to measure urban meteorology and air pollution close to the ground in different periods for comparative studies. This makes it possible to analyze the evolution over time of urban thermal conditions at the level of the ordinary citizen.
This research uses the CK parameter (sum of the entropies of the time series of the urban meteorology variables/sum of the entropies of the time series of the pollutant concentration variables), whose behavior has been explored by the authors in two periods (2010–2013 and 2017–2020) of 3.25 years each [1,2,3,4,5]. The presence of confinement due to the SARS-CoV-2 pandemic (2020 until the beginning of 2022), with the reduction of human activities to a minimum (total confinement) in Santiago de Chile, represented a great opportunity to study the behavior of CK in a new period 2019–2022 given the significance that urban meteorology and air pollution have in its calculation. The CK parameter is based on extensive periods of measurements of variables of the urban meteorology system (characterized by temperature, relative humidity and magnitude of the wind speed) and of the atmospheric pollutants system (PM10, PM2.5, CO), which the authors have used to determine the effect of the polluting system on the urban meteorology system from the perspective of damping the entropy of the urban meteorology [1,2]. CK is of a localized nature and represents years of measurements, considering that any year has different seasons (autumn, winter, spring and summer) and may be affected by drought, heat waves, geography, human activity, etc. The procedure uses the measurements of six locations in the geographical basin of Santiago de Chile, according to three different periods: 2010–2013, 2017–2020, 2019–2022, with two periods sufficiently separated (2010–2013 and 2017–2020) and with two very close periods with partially overlapping data (2017–2020 and 2019–2022, last measurement). CK was also examined, calculating its values with data from two other countries (Mexico, Ecuador), in order to investigate its behavior in other geographic morphologies and contexts of human activity, such as mountains and coasts [3]. What is notable is that a similar behavior of CK was found in the geographic basin of Mexico City, but CK changes, as in Chile, on the coast and in the mountains (Ecuador, comparison country) [3]. The interest of this research is focused on Santiago de Chile, because it contains 40% of the country’s population, as pointed out. In Chile, CK declines from 2010 to the present, which informs us about the magnitude of the interactive process between the meteorological–pollutant systems, with dominance of the pollutants, also showing strong variation in the proximity to the ground. The characteristics that CK exhibits are compatible with behavior of the Kolmogorov cascade type: high turbulence in the proximity to the ground which attenuates with height [4,5]. Using the very rough basin geography, of variable surface height, of Santiago de Chile allows for locations of instruments for measuring urban meteorology and pollutants at different levels, proving that the interaction, summarized in the CK parameter, evolves over time with dependence of the height [4], of the entropy of the contaminants and of the entropy of the meteorological variables. A contrast study using the heat conduction equation and the Clausius equation for entropic flows [5] confirmed CK’s diagnosis of the interactive process. Forming a sufficiently fine grid of measurement locations, it is possible to build the CK layer that allows for visualization of the geometry, variable in time, of its configuration (in ). The layer in the vicinity of the earth’s surface, is highly dynamic or turbulent [5]. CK goes beyond the traditional daily air quality index since the proposed parameter indicates the magnitude of the disturbance, the effect on urban meteorology and the nature of the process (irreversible). The elaboration of CK, from very extended periods of time of measurements, shows in a more precise way the tendency of the interaction between the entropy of the pollutants and the entropy of urban meteorology, whose significant variables (temperature, magnitude of the velocity of the wind and relative humidity) are used to characterize properties of the atmosphere. If the third measurement period (2019–2022) confirms the trend described by CK in the two previous periods, CK attributes would allow for more informed and complex decisions to be made (regarding: changes in ground roughness due to tall buildings, effects of the mitigation measures in force, recovery of tributaries, modification of the energy matrix, etc.)
1.1. Urban Densification
The use of public data [6,7] allows for the study of the urban density that has a high incidence in the change in the roughness of the soils. From the official information [6,7], it is possible to estimate that the number of residential properties (N°) between the years (t) 2009–2020 grew exponentially: , .
By 2015, many of the buildings were 15 floors and in 2020 the majority were 30 floors. The supply of apartments (2020) increased by 77.3%. In the Metropolitan Region, there were 50 homes/hectare in 1990; in 2020 there were around 5000 homes/hectare [6,7]. According to census data from 1970, the proportion of apartments in Chile was only 7% (116,748). Since then, that alternative has been widely more accepted by Chileans, so that in 2002 that percentage reached 12.6% (474,199, according to the 2002 census). In 2018, they represented 17.5% of a total of 1,138,062 homes (552,678 more than in 2002) [5,6,8,9].
1.2. Mitigation Measures
Mitigation [10,11], in the sense that this research addresses it, corresponds to the set of measures that can be applied to counteract or minimize the negative environmental impacts that can be generated by anthropic interventions. These measures must be contained in a mitigation plan, which must be part of an environmental impact study [10,11]. A consequence of anthropogenic interventions, in a given geographical area, are the urban heat islands (UHI) generated by cities.
Urban heat islands are a phenomenon that occurs in those urban areas that experience higher temperatures than the surrounding areas due to human activity. The main reason is due to the partitioning of the energy flux of the earth’s surface according to Q* + QF = QH + QE + ΔQS + ΔQA, where Q* is the net radiation, QH and QE are the fluxes of the sensible and latent heat, respectively, QF represents the anthropogenic energy release within the control volume, ΔQA is the net advection through the lateral sides of the control volume, and ΔQS is the storage heat flux and represents all energy storage mechanisms within elements of the control volume, including air, trees, building fabrics, and soil [12,13,14]. Impervious surfaces can rarely experience cooling effects induced by latent heat, but much sensible heat induces temperature rise. Added to this, heat and pollution are generated by traffic and industry. All this aggravates the consequences of climate change in cities and decreases the quality of life of its inhabitants [15,16,17,18,19]. In the last 20 years, associated with climate change in Chile, there have been heat waves, which have intensified and increased in duration. Heat waves are becoming more frequent, especially in the central zone of the country, which is where the capital of Chile, Santiago de Chile, is located in a basin geography. According to the Report on the Evolution of the Climate in Chile 2021, carried out by the Chilean Meteorological Directorate, the last 11 years have been the warmest on record.
Chile has developed a strategy for the future (2050) and that is summarized in the Nationally Determined Contributions (NDC) [20] where the economic variable has an influential role. The NDC provides a framework of laws and actions for mitigation, covering areas such as inventories of climate pollutants, adaptation to climate change with capacity development, and international negotiation and financing. The problem, and this is what this research demonstrates through the measured data, is that human activity changes the initial conditions in the environment and in the geography (no matter how small the disturbance), causing great effects on the environment and on the health of the population in very short times [21].
This shows the relevance of having relatively simple techniques that allow for understanding the initial thermal condition of various communes before the arrival of heat waves, for example. This condition is built by urban micrometeorology, pollutants and a geographical environment subjected to intensive urban densification.
The study of dynamic systems according to chaos theory implies the evaluation of a series of parameters. Among them, due to the precision of its quantitative results and the relative ease of execution, the Kolmogorov entropy, which measures the loss of information throughout the evolution of the system, is of essential importance, especially in its application to systems of which there are only time series of values of some variable that is considered specific. This is applied to the study of polluting systems + urban meteorology, systems whose high dynamic complexity suggests the possibility that they are chaotic systems [22]. Kolmogorov entropy is a parameter that allows for determining the information content and gain in a given system. It is based on Shannon’s information theory [23] in which the concepts of storage capacity and information gain are defined and analyzed. The Kolmogorov entropy corresponds to an entropic flow, that is, it has a unit of time in the denominator.
Considering that the behavior of CK and the losses of information show the action of pollutants on urban meteorology and the effect of thermal conditions that affect urban life in the geographical basin studied in the periods 2010–2013 and 2017–2020, is it possible to extend its application to the new measurement period 2019–2022 considering that this period includes the forced confinement of the population due to SARS-CoV-2 and the reduction of activities to a minimum? This would allow us to examine CK and its reliability in conditions very different from the previous ones.
2. Materials and Methods
2.1. Measurement Recording Area
The capital city of Chile, Santiago de Chile, is located at 33.5° S and 70.8° W. It contains a population of 7,508,334 inhabitants, which represents 40% of the total population of the country, on a surface of approximately 641 km2. It is located in the middle of the country, at a height of about 520 m.a.s.l. The altitude above sea level increases from west to east. It is surrounded by two mountain chains: The Andes and the Chilean Coastal Range. Its climate is Mediterranean (Figure 1). The driest and warmest months are from December to February, reaching maximum temperatures of about 35 °C in the shade (air temperature in the sun). Figure 1 presents the measurement locations. Given its topography and the dominant meteorological conditions, there is, in general, a strong horizontal and vertical dispersion of pollutants generated by an important number of sources in the city (heating, vehicles, industries, etc.), especially during fall (20 March–21 June) and winter (21 June–23 September) [24]. The emissions have a tendency to increase given the also increasing population density, which implies an increase in fixed and mobile sources. In addition, the number of vehicles has increased rapidly in recent years. The automotive fleet in Santiago de Chile has added about 750,000 vehicles since 2010, totaling today about 2.15 million cars, according to the latest data available, for 2018, from the National Institute of Statistics of Chile (INE, in Spanish). Growth will continue, and by 2025, another 546,000 units would be added, which implies a 25% increase in that period.
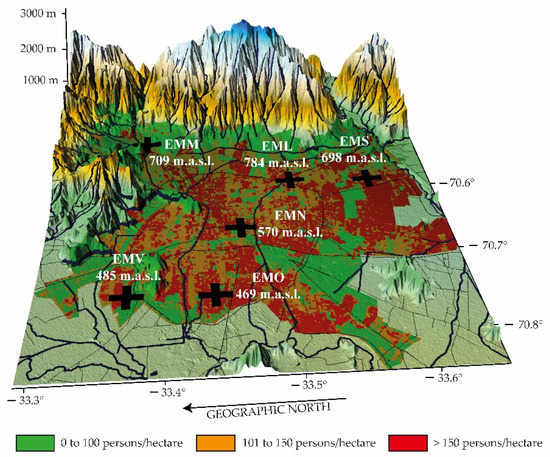
Figure 1.
Geographical distribution of the monitoring stations for this study (network of black crosses) and high urban densification [21] (in color for the areas with the persons/hectare; EML = La Florida, EMM = Las Condes, EMV = Quilicura, EMN = Santiago, EMS = Puente Alto, EMO = Pudahuel).
2.2. The Data
The measurements for the 2019–2022 period have the same amount as those for the 2010–2013 and 2017–2020 periods and were collected from the MACAM III Network of the National Air Quality Information System, under the Ministry of the Environment of Chile [25]. The data correspond to 3.25 years or 39 months of measurements of PM10, PM2.5, CO, temperature (T), relative humidity (HR) and wind speed magnitude (WV), totaling 28,463 data points for each variable, giving a total of 1,024,668 measurements for all communes in the 2019–2022 period (Table 1). The temporal resolution of the time series is one hour. If the other two periods used in this research are considered, 2010–2013 and 2017–2020, there are a total of 3,074,004 processed data points.

Table 1.
The continuous recording of the variables in this study is carried out at 2 m above the ground in all sensors, with the exception of the one measuring the magnitude of wind speed, which is at 10 m [5].
The measuring instruments used are calibrated and certified according to the EPA (USA) standard. The reason for this extreme care in its measurements is that in Chile, based on the measured data, an air quality index is built that determines restrictions on transportation, the use of fireplaces, student attendance at classes, etc. in the city. This is essentially important for the winter period. The city of Santiago de Chile, because it is in a geographical basin, has poor ventilation and in winter the thermal inversion layer occurs, which causes serious events in the respiratory tract, especially in children and the elderly population.
2.3. Kolmogorov Entropy and Loss Information
According to Farmer, one of the essential differences between chaotic and predictable behavior is that chaotic trajectories continuously generate new information while predictable trajectories do not [26,27]. The metric, or Kolmogorov–Sinai entropy, provides an upper bound on the information acquisition rate. Although in a context unrelated to dynamical systems, the metric entropy was originally defined by Shannon [28]. This quantity was later applied to dynamical systems, and shown to be a topological invariant by Kolmogorov [29] and Sinai [30].
According to Pesin’s identity [31], the sum of the positive Lyapunov exponents is the Kolmogorov–Sinai entropy (or invariant) or K-S entropy (or invariant) or metric entropy (or invariant). Kolmogorov [32] proposed to apply the concept of entropy to dynamical systems, and Sinai [30] gave a proof. More precisely, according to Ruelle’s inequality [33], the entropy of K-S is a lower bound on the sum of the Lyapunov exponents; however, they are equal when the natural measurement is continuous along the directions unstable, as is the usual case of chaotic flows.
This is related to the usual entropy of thermodynamics, which is a measure of the disorder of a system, since it measures the expansion of nearby trajectories into new regions of the space state. Unlike thermodynamic entropy, however, K-S entropy has inverse units of time (or inverse iterations for mappings) and is a measure of the average rate at which predictability is lost. Its inverse is a rough estimate of the expected time for a reasonable prediction. A purely random system has infinite entropy, and a periodic system has zero entropy.
Entropy can also be considered as the information creation rate when a chaotic system evolves, called Shannon entropy. The sensitive dependence of the initial conditions means that two points indistinguishably close in a spatial state move apart in time. As time progresses, we learn more and more about the initial condition as initially insignificant digits in its specification make themselves felt. A chaotic system is an endless source of new information [34]. Information is said to be a measure of the surprise of an occurrence or the distinguishability of a configuration, and entropy is the information that is not yet available. Entropy is always positive and can be large for a chaotic system. Sometimes this process is visualized as a loss of information, since the predictions from an initial state become less accurate as time progresses.
We consider a Markov process as a process that can be thought of as a source of information, so that it randomly generates one of n symbols at discrete timesteps [28,35]. The text from this response, for example, can be considered to constitute a Markov process. These symbols can be thought of as the outcome of sequential measurements. For convenience, assume that the n possible symbols are the integers from 0 to n − 1. If the occurrence of a given symbol s depends on m − 1 preceding symbols, then the Markov process is of mth order. Assume throughout that the Markov process is ergodic, so that time averages are independent of starting time, and are equal to ensemble averages. For an mth order process whose current symbol is sm, the sequence including the previous m-1 symbols, (s1 s2 … sm), can be represented as the m digit base n fraction s1 s2 … sm, abbreviated Sm. This number defines the state of the source. (This should not be confused with the state of a dynamical system) [28].
A sequence of numbers obtained by making a series of measurements may be thought of as the symbols emitted by a Markov source. A distinct symbol is assigned to each of the n elements of the partition induced by the measuring instrument. A measurement at time t = 0 determines that the state of the dynamical system is located somewhere inside a given element of the partition. A finite time Δt later, another measurement may give a different outcome, indicating that the state is in a different partition element. Thus, a series of measurements generates a sequence of symbols. The information rate per unit time for this symbol sequence may be calculated by taking the limit as of ΔIm/lΔt = Δl/Δt. Following Sinai [30], the metric entropy can be defined as the maximum information rate when the partition and sampling rate are varied:
To an observer with optimal measuring instruments taking samples at the optimal rate, the metric entropy is the average amount of new information gained per sample.
Considering a trajectory x(t) = [x1(t), x2(t) … xd(t)], according to Figure 2, in the phase space of dimension d of a dynamical system. This space is assumed to be divided into boxes of size ld with d the dimension of the space, the state of the system being measured at uniformly spaced time intervals τ. Let Pi be the joint probability that at time t = 0 the system is in box i0, at t = τ at i1… and at nτ at in. Using Shannon’s theory, the magnitude Kn is defined:
and is proportional to the information required to locate the system on a special trajectory that goes through the boxes i0 … in with a certain precision. The choice of coefficient k is a matter of convenience and amounts to the choice of a unit of measure.
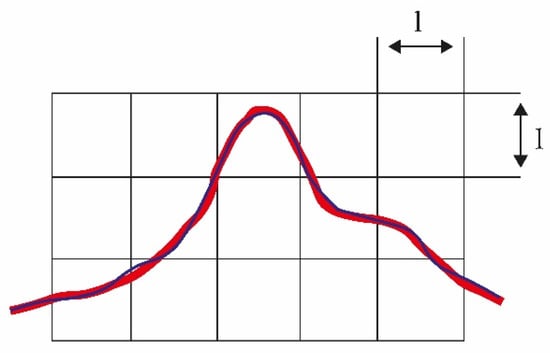
Figure 2.
The red–blue line represents a trajectory in phase space where there are n boxes with sides l.
Kn+1 − Kn represents the additional information required to know in which cell in+1 the system that was previously found in i0 … in will be found. From this it results that Kn+1 − Kn measures the loss of information about the system when passing from time nτ to (n + 1)τ. The Kolmogorov entropy is the average loss of information when l and τ are made as small as desired, that is, they tend to zero:
SK has units of information bits per second and bits per iteration in the case of a discrete system [36,37]. The limit process of Equation (1) develops according to the order: (i) n → ∞, (ii) l → 0, canceling the dependency of the selected partition (n is the number of cells or partitions) and (iii) τ →0, for continuous systems.
In summary, for the calculation of the Kolmogorov entropy, it is first verified that the entropy is between zero and infinity (0 < SK < ∞), which allows for verifying the presence of chaotic behavior. If the Kolmogorov entropy is equal to 0, no information is lost, and the system is regular and predictable. If SK ∞, the system is completely random, and it is impossible to make any predictions. Secondly, the amount of information required to predict the future behavior of two interacting systems is determined, in this case, by the atmosphere (represented by meteorological variables) and the hourly concentration of pollutants. In this way, the rate at which the system loses (or outdates) information over time can be estimated. Finally, the horizon of maximum predictability of the system can be established. This horizon is a limit frontier from which it is not possible to make predictions or formulate new scenarios [28].
The loss of information can be determined according to the equation:
is the average loss of information (I) in [bits/h]. NEW is the new data created and OLD is the old data, λ is the Lyapunov exponent. The Lyapunov exponent, λ(x0) represents the exponential separation between two trajectories, initially close, after N steps or iterations and which contains a quantity of information, I, referred to that separation I(x0). Due to notation considerations, λ0(t) remains.
The objective indicators of chaos are various and can be classified in a general way into two large groups: those that measure in some way how information is lost throughout evolution, such as the Lyapunov exponent, the Kolmogorov entropy, and even the transform Fourier, or those that refer to the fractal character of either the signal itself or its attractor in phase space. In this work we will deal with the first type of indicators and especially with the Kolmogorov entropy, due on the one hand to the ease of processing its calculation and on the other to the amount of information it provides.
Two types of <ΔI> must be calculated for each commune:
- (1).
- For each of the time series of the pollutants (P): PM10, PM2.5 and CO;
- (2).
- In the same way as in (1) for each meteorological variable (MV): temperature (T), magnitude of wind speed (WS) and relative humidity (RH) [3].
Flowchart
The applied technique requires two well-defined stages:
1. Time series with no missing data ideally each containing over 5000 data points (for stability reasons in the calculation [38]).
2. Prove that all series are chaotic.
For the second point to be fulfilled, it must necessarily happen that five parameters calculated, through chaos theory, to the time series are in the appropriate ranges:
Lyapunov exponent: λ > 0, correlation dimension: DC < 5, Kolmogorov entropy: SK > 0, Hurst exponent: 0.5 < H < 1 and Lempel–Ziv complexity: LZ > 0.
Figure 3 represents the process that allows for verifying the chaoticity of each time series (the total is 36 for the study period, 2019–2022) [5].
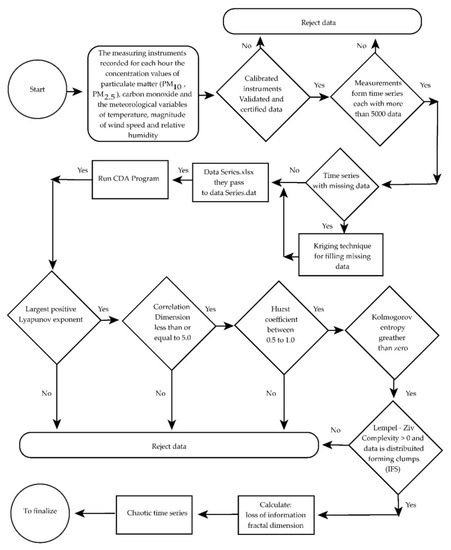
Figure 3.
Flowchart that allows for verification if each time series is chaotic and calculates the chaotic parameters of interest (Lyapunov exponent, correlation dimension, entropy, Hurst exponent, Lempel–Ziv complexity, fractal dimension and loss of information).
Some limitations of the method:
With respect to stages 1 and 2 indicated
- The time series of meteorological variables and concentration of pollutants with many data [38] were measured hourly and simultaneously in all locations (6) used in the study.
- There can be no missing data in the time series. There are filling methods such as Kriging [39].
- As it is a procedure based on measurements, the quality of the measurement instruments is fundamental (certification and calibration, Environmental Protection Agency (EPA) [25]).
- Using the software requires setting of parameters (for example, the embedding dimension) [40,41].
Constructing the equation:
the sum according to i indicates that the entropies of each meteorological variable are added in the numerator (temperature time series, relative humidity time series, wind speed magnitude time series) and the entropies are added in the denominator of each pollutant considered in the study (PM10 time series, PM2.5 time series, CO time series) of each commune (there are 6) where the monitoring station was located. Since it is a quotient between entropies (urban meteorology system/pollutant system) referring to similar properties, CK is a dimensioned quantity that compares the entropies of the two systems that interact during a period of 3.25 years, according to the height of each commune studied. In general, the ratio shows that for the three periods analyzed (2010–2013, 2017–2020, 2019–2022), the entropy of pollutants is dominant, in such a way that the polluting system shows a greater capacity to expand and connect with the environment.
3. Results
Table 2 presents the results of the calculation of the fundamental parameters: Lyapunov exponent (λ), correlation dimension (DC), Hurst exponent (H), Kolmogorov entropy (SK) and Lempel–Ziv complexity [40,41].

Table 2.
Parameters for chaos study of three pollution variables and three meteorological ones, in six monitoring stations (Santiago, Chile, 2019–2022 period).
Using Equation (6), a relationship is established between CK and the height of the different monitoring stations of meteorological and pollutant variables and, in addition, of the measurement periods (2010–2013 [1,2,4], 2017–2020 [1,2,4], 2019–2022), which appears in Table 3; the summary (Table 4) is plotted (columns 1, 2, 3 and 4) in Figure 4. Table 3 also shows a downward trend in the percentage of variation when comparing it between the periods 2017–2020 and 2019–2022, which indicates the effect of the 2019–2022 confinement on CK in proximity to the ground.

Table 3.
Percentage variations of the CK.

Table 4.
The CK results appear according to commune, height and period.
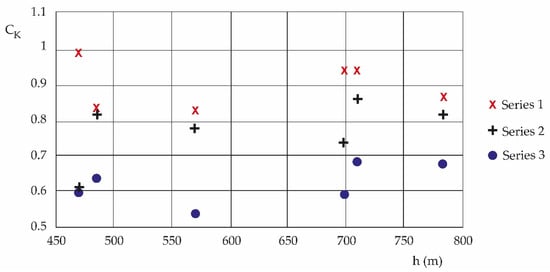
Figure 4.
Shows the CK curves which decrease as time evolves towards the most current period (2019–2022). Series 1: 2010–2013, Series 2: 2017–2020, Series 3: 2019–2022. On the other hand, the gaps between curves, according to periods, increase.
Figure 4 presents the distribution of CK by commune, height and according to the three study periods 2010–2013 [1,2,4], 2017–2020 [1,2,4] and 2019–2022. Figure 4 shows that the CK variable, a quotient between the entropies of the meteorological variables and the entropies of the pollutants, has evolved towards the present, maintaining and increasing the trend of deterioration of urban meteorology due to pollutants.
An important calculation is provided by the loss of information (<ΔI>) of pollutants and meteorological variables (Table 5) since it shows which system loses information faster and is becoming more chaotic. It also points out the persistence of contamination, since by incorporating the measurements of the confinement of the population (SARS-CoV-2 pandemic) and which are part of the 2019–2022 period, the loss of information from both systems (contaminant and meteorological variables) tends to a lower range of values (in absolute value) compared to the periods 2010–2013 and 2017–2020. What is new about the analysis of the recorded data is that in the 2019–2022 period, the loss of information on pollutants slows down and is comparable (at least in 4 out of 5 communes) with the 2017–2020 period, and is a manifestation of forced mitigation by confinement. Now, the urban meteorology, aggravated by a 30-year drought, would have a delay in recovering compared to previous measurement periods.

Table 5.
<ΔI> (bits/h) = loss information as the sum of the contribution of each P (pollutants: PM10, PM2.5, CO) and sum of contribution of each MV (meteorological variables: T, WV, RH).
Table 6 presents the temperature and relative humidity averages according to the different heights of each commune for the three periods of this study. Table 6 highlights the effect of the confinement of the population due to the SARS-CoV-2 pandemic (2020 until the beginning of 2022), since it led to the slight average drop in temperature and an improvement (rise) in relative humidity.

Table 6.
Average total temperature and relative humidity by commune and periods.
Table 7 makes it possible to compare, between measurement periods, the persistence (H = Hurst exponent) of the time series of both the polluting system and the urban meteorological system. H is the ability to influence the future, which declines in the period 2019–2022, which coincides with the confinement of the population due to the effect of the SARS-CoV-2 pandemic. However, there is an increase, in various communes, of chaoticity as shown by the fractal dimension (D).

Table 7.
Presents all the values of the Hurst exponent (H) and the fractal dimension (D), for all the variables of interest, the study communes and the three periods (2010–2013, 2017–2020 and 2019–2022).
From the perspective of localized measurements carried out in a geographical basin and applying the Clausius equation [42] δS = δQ/T, to estimate the entropic fluxes between meteorological and polluting variables, the following is obtained:
and the results are presented in Table 8 using the calculated values of the sum of entropies of the pollutants, the sum of the entropies of the meteorological variables and the average temperature of the period 2019–2022 of each commune from Table 2 and Table 6, respectively.

Table 8.
The product between the average temperature of each commune for the measurement period 2019–2022 and the difference in entropic flow of pollutants and urban meteorology, for which Equation (7) was applied. The last row are average values.
Table 9 allows for comparing Δ for the three periods, showing that the trend of higher flows at low altitudes is maintained (periods 2017–2020 and 2019–2022 compared to 2010–2013). Table 9 also shows that the greatest entropic flux comes from pollutants. As noted earlier, this is related to the usual thermodynamic entropy, which is a measure of the disorder of a system, since it measures the expansion of nearby trajectories into new regions of state space. However, unlike thermodynamic entropy, K-S entropy has inverse unit time and is a measure of the average rate at which predictability is lost.

Table 9.
Height according to measurement locations, periods and difference in entropic fluxes between pollutants and urban meteorology.
Figure 5 allows us to observe the behavior of the entropic flow curves according to the three measurement periods, locations and heights. However, it also shows, in some communes at lower altitudes, the effect of the decline in human activity and pollution (2019 beginning of 2022, Series 3 (between 450–500 m above sea level)) due to the SARS-CoV-2 pandemic.
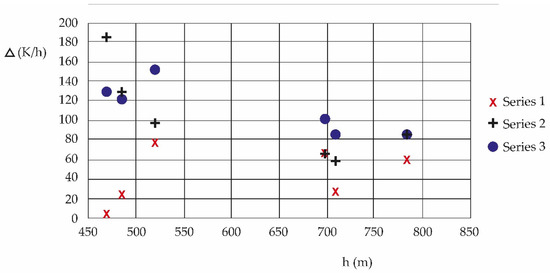
Figure 5.
Shows that Series 3 of the period 2019–2022 maintains the trend of greater entropic flux compared to the periods 2010–2013 (Series 1) and 2017–2020 (Series 2). It should be considered that in the 2019–2021 period, activity was reduced to a minimum due to the effect of SARS-CoV-2, recovering in 2022.
An approximate modeling, which depends essentially on the height, for Series 1 [4], Series 2 [4] of the CK quotient, is shown in Equations (8)–(10):
2017–2020 (Series 2, Table 4), produces Figure 6:
and 2019–2022 (Series 3, Table 4), produces Figure 7:
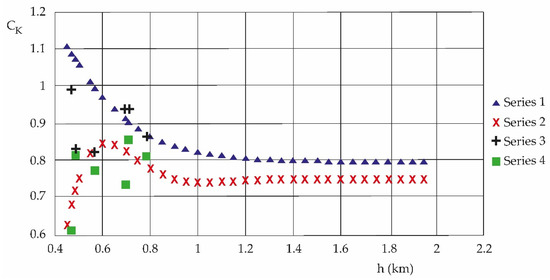
Figure 6.
Approximate modeling of the CK entropy ratio according to the study periods. Comparatively with the period 2010–2013 (Series 1), the period 2017–2020 (Series 2) had a strong increase in densification and high-rise construction. Series 3 and 4 are the experimental data from the periods 2010–2013 and 2017–2020, respectively [4].
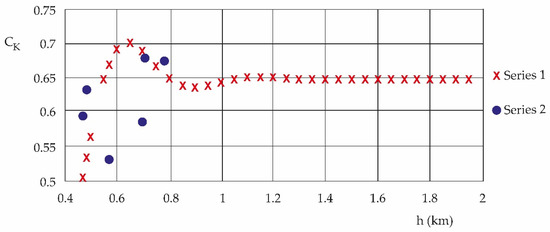
Figure 7.
Approximate modeling of the CK entropy ratio according to the study periods, Series 1. Series 2 are the experimental data from the periods 2019–2022.
4. Discussion
There are various records of the effect of other pollutants, aerosols and greenhouse gas emissions, which affect urban thermal dynamics.
Following [43], the urban heat island intensity (UHII) is the temperature difference between urban areas and their rural surroundings. It is usually attributed to changes in the underlying surface structure caused by urbanization. Air pollution caused by aerosol particles can affect the UHII by changing (i) the energy balance of the surface by the radiative effect of the aerosol (ARE) and (ii) the stability of the planetary boundary layer (PBL) and the intensity of the airflow by modifying the thermodynamic structure, which is called the aerosol dynamic effect (ADE). By examining satellite data and ground observations compiled between 2001 and 2010 in 35 cities in China and using the WRF-Chem model, [43] found that the impact of aerosols on UHII differs widely: it reduces UHII in summer, but increases the UHII in winter. These discoveries present new insights into the impact of the interaction between urbanization-induced surface changes and air pollution on urban climate.
In [44], they used a remote sensing thermal imagery time series and in situ measurements (stationary and mobile) combined with select geospatial predictor variables to model this atmospheric phenomenon in its most intensive season (summer). The data analysis indicated that climate change preventive actions in urban systems are urgently needed to mitigate high levels of heat stress and ensure a quality living environment for all social groups of citizens. The predictions, from locations that have several urban green areas and a large body of water, are not optimistic. Climate change and the UHI (urban thermal island) phenomenon are linked through a two-way interaction. First, global warming will increase UHI intensity in urban systems. Second, cooling strategies to reduce UHI intensity can help communities adapt to the impact of climate change, while also lowering the greenhouse gas emissions that cause climate change [45]
In the study [46], the results showed that the accumulated patients (2020–2022) regarding the SARS-CoV-2 pandemic, of the order of 400,000, belonged to the five communes (with a built area of approximately 300,000 m2 in recent years) that had the highest urban densification, which affected urban meteorology, favored the concentration of pollutants and made the SARS-CoV-2 pandemic more persistent. The “ideal” density of built housing should balance a pandemic and nullify its expansion.
Considering the results of the 2019–2022 measurements, the quotient between the entropies of urban meteorology and the entropies of pollutants, CK, is very sensitive to the effect of pollution on meteorology. As shown in Figure 4, the influence of pollutants on urban meteorology causes a significant evolutionary decay of CK for all communes (6) at the different heights studied (Table 4). The gap between curves maintains its tendency to separate.
Table 5 shows that the variable meteorological system in the 2010–2013 period loses less information, making it more predictable with respect to the polluting system. It should be considered that this period is at the beginning of the process of urban densification. Once this trend is consolidated, the period 2017–2020 shows an increase in the speed of the loss of information from urban meteorology regarding pollutants, that is, it is becoming more chaotic. Finally, the period 2019–2020 shows a hegemony of the polluting system over the urban meteorological system. The polluting system has become slower in the loss of information, increasing its predictability. That is, the polluting system is more homogeneous and hegemonic with respect to urban meteorology, a condition that is related to the growing urban densification with high-rise buildings and changes in soil roughness [47,48,49,50,51,52]. In the geographical basin studied, a large part of the natural tributaries, which facilitated the creation of thermal gradients and wind flows at the micrometeorological level, were channeled by means of concrete slabs and concrete tubes [53].
The period 2019–2022 corresponds to a strong contraction of human activity in Santiago de Chile due to the global pandemic of SARS-CoV-2 (confinement of people, reduction of vehicular traffic, people worked through the internet (on everything in education), etc.), which could be interpreted as a form of involuntary mitigation with, even, a certain irruption of wildlife in deserted cities [54,55]. This phenomenon is reflected in the total average values of temperature and relative humidity that trended downward (Table 6). However, despite the reduction of the polluting disturbance on the atmosphere during a period of almost two years (2020–2021), the atmospheric layer adjacent to the soil did not manifest resilience and returned to the initial condition, in the short term; Table 9 and Figure 5 show the entropic flows.
The damage to the atmosphere is very severe and the asymptotic decay of CK due to the influence of pollutants in the period 2019–2022, Figure 4 and Figure 5, shows an increase in the gap of the curve of that period with respect to the curves of the periods 2010–2013 and 2017–2020. This also indicates that in Chile mitigation actions are still very incipient and the pandemic was a way of putting them to the test. Table A1 presents a summary of mitigation measures applied in Chile. Table 7 shows that the persistence (H) [40,41], the ability to influence the future, of urban meteorology for the period 2019–2022 decreased when compared to the period 2010–2013 and its fractality [40,41] increased. A similar process was experienced by pollutants due to the decrease in human activities caused by the pandemic. Both systems, pollutant and urban meteorology, increased their fractal dimension and their chaoticity (2019–2022).
Various studies have been carried out using time series measurements of urban meteorology and pollution. From a historical perspective, [56] uses chaos theory to show the strong incidence of initial conditions in the prediction of the evolution of contamination events. In the most current article [57], an APS (air pollution scatterer) is defined as a city with a high indirect impact (CHSI) of air pollution and an entropy transfer network is proposed to investigate the APS from a perspective analysis of multiple time scales. However, the procedure of linking the entropies of the time series of pollutants with the entropies of the time series of urban meteorology to describe the dominance of one over the other, with the respective decay curves, according to measurement periods and heights, and with turbulence close to the ground, is not very common, which makes comparisons difficult. There are other techniques, such as the thermal conduction equation (temperature variation in time) and the Clausius equation (entropic flows) that lead to similar results and can be used as a check, as already pointed out in [5].
As pointed out before, the calculation of the CK parameter uses localized geophysical data (given that they correspond to a climatic and geographical environment, but also pollutants, vegetation, human activity, urban densification, etc.). This parameter shows, according to the mathematical technique used in the calculation of two of the variables that constitute it (SK,MV, SK,P), the generation of an interactive zone between pollutants and urban meteorology that, in a Cartesian spatial representation, acquires the shape of a layer that is distributed according to variable heights, evolving differently in each of the three measurement periods carried out in the study (Figure 8). In addition, in the three periods, the parameter shows great variability at very low altitudes. The strength of the applied procedure lies in the amount of data used (robustness), which gives a greater margin of confidence to the trend presented by CK.
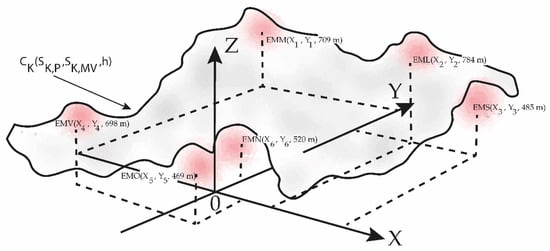
Figure 8.
The figure is a three-dimensional graphic representation of CK, general and approximate, according to the variation with the height of the interactive zone between pollutants and urban meteorology, which evolves differently according to the measurements of each of the three periods of 3.25 years (2010–2013, 2017–2020 and 2019–2022).
5. Conclusions
This research is carried out in a geographical basin and uses measurements from three different periods (2010–2013, 2017–2020, 2019–2022) in the form of time series that contain pollutant concentration data (PM10, PM2.5, CO) and urban meteorology (temperature, relative humidity and magnitude of wind speed). From the time series, it is shown that air pollution, in areas with high urban densification, is characterized by: persistence over time, irreversible process characteristics, low predictability, rapid loss of information (chaoticity) and entropic flows growing, which negatively influences urban meteorology, especially at low altitudes. By using the period of measurements from 2019 to the beginning of 2022, a period of confinement of the population and maximum reduction of industrial activity (SARS-CoV-2 pandemic), it is verified that the time of presence of the mitigation actions that may reduce the effects of pollution on the atmosphere (drop in temperature and increase in relative humidity) must be extremely long. On the other hand, urban densification, very active in the study periods 2010–2013 to 2017–2020, effectively increases the temperature, lowers the relative humidity and intensifies atmospheric deterioration due to pollution. The speed of loss of information from urban meteorology 2019–2022 is greater, in all communes, compared to the previous periods 2010–2013 and 2017–2020, that is, it is more chaotic despite the population confinement due to pandemic. This reveals that urban weather requires a long time (on a human scale) to return to its initial condition, which is also not ideal. As the loss of information from pollutants is slower, they become more homogeneous, more predictable and denser, which can favor more extreme climatic responses. From the perspective of a very approximate modeling, the parameter CK (SK,P, SK.MV, h) reveals the extreme variability, at heights very close to the ground and according to different measurement periods, of the urban thermal conditions (UTC). According to CK, the UTCs are revealed as very sensitive to initial conditions (chaotic systems) and with a Kolmogorov cascade behavior: a lot of turbulence close to the ground, which decays with height.
Author Contributions
Conceptualization, P.P.; methodology, P.P. and E.M.; software, P.P.; validation, P.P. and E.M.; formal analysis, P.P.; investigation, P.P.; resources, E.M.; data curation, E.M.; writing—original draft preparation, P.P.; writing—review and editing, P.P. and E.M.; visualization, E.M.; supervision, P.P.; project administration, P.P.; funding acquisition, P.P. All authors have read and agreed to the published version of the manuscript.
Funding
Project supported by the Competition for Research Regular Projects, year 2020, code LPR20-02, Universidad Tecnológica Metropolitana. This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data were obtained from the public network for online monitoring of air pollutant concentration and meteorological variables. In Chile: The network is distributed throughout all of Chile, without access restrictions. It is the responsibility of SINCA, the National Air Quality Information System, dependent on the Environment Ministry of Chile [25]. The data for the two study periods will be available for free use on the WEB page: URL: https://sinca.mma.gob.cl (accessed on 10 January 2023).
Acknowledgments
To the Research Directorate of the Universidad Tecnológica Metropolitana that made possible the progress of this study.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Instructions with mitigation procedures and application areas. ADP = Atmospheric Decontamination Plans; SPMSR = Sedimentary Particulate Material Sector Regulations; AEIL19300 = Atmospheric emission inventories within the framework of Law 19300; SSRGP = Specific Sectoral Regulations for gases and particles; APL = Clean Production Agreements; VR = Vehicular restriction; COC = Cessation of Operation of Companies; MMA = Ministry of Environment; MGAP = Ministry of Livestock, Agriculture and Fisheries; MINSAL = Ministry of Health; MINECON = Ministry of Economy, Development and Tourism.
Table A1.
Instructions with mitigation procedures and application areas. ADP = Atmospheric Decontamination Plans; SPMSR = Sedimentary Particulate Material Sector Regulations; AEIL19300 = Atmospheric emission inventories within the framework of Law 19300; SSRGP = Specific Sectoral Regulations for gases and particles; APL = Clean Production Agreements; VR = Vehicular restriction; COC = Cessation of Operation of Companies; MMA = Ministry of Environment; MGAP = Ministry of Livestock, Agriculture and Fisheries; MINSAL = Ministry of Health; MINECON = Ministry of Economy, Development and Tourism.
| Instrument | Pollutant | Responsible | Implementation |
|---|---|---|---|
| ADP | PM10, PM2.5, gases like SOx | MMA | In all Chile |
| SPMSR | PM30 | MGAP | Vallenar Province |
| AEIL19300 | PM10, PM2.5, gases like SOx, NOx, CHO | MMA, MINSAL, MGAP | In all Chile |
| SSRGP | PM10, PM2.5, gases like SOx, NOx, CHO | MINSAL | As primary regulation throughout Chile |
| CPA | Reducir GEI (Greenhouse effect gases) | MINECON, MMA, MINSAL | In all Chile |
| VR | PM10, PM2.5, gases like SOx, NOx, CHO | MINSAL | In localities of Chile with PDA |
| CFE | PM2.5, gases like SOx, NOx, CHO | MINSAL | In localities of Chile with PDA |
References
- Pacheco, P.R.; Salini, G.A.; Mera, E.M. Entropía y neguentropía: Una aproximación al proceso de difusión de contaminantes y su sostenibilidad. Rev. Int. Contam. Ambient. 2021, 37, 167–185. [Google Scholar] [CrossRef]
- Pacheco, P.; Mera, E.; Salini, G. Urban Densification Effect on Micrometeorology in Santiago, Chile: A Comparative Study Based on Chaos Theory. Sustainability 2022, 14, 2845. [Google Scholar] [CrossRef]
- Pacheco, P.; Mera, E. Relations between Urban Entropies, Geographical Configurations, Habitability and Sustainability. Atmosphere 2022, 13, 1639. [Google Scholar] [CrossRef]
- Pacheco, P.; Mera, E.; Fuentes, V.; Parodi, C. Initial Conditions and Resilience in the Atmospheric Boundary Layer of an Urban Basin. Atmosphere 2023, 14, 357. [Google Scholar] [CrossRef]
- Pacheco, P.; Mera, E.; Fuentes, V. Intensive Urbanization, Urban Meteorology and Air Pollutants: Effects on the Temperature of a City in a Basin Geography. Int. J. Environ. Res. Public Health 2023, 20, 3941. [Google Scholar] [CrossRef]
- INE-Plataforma de datos Estadísticos. 2020. Available online: https://www.ine.cl/docs/default-source/encuesta-suplementaria-deingresos/publicaciones-y-anuarios/sntesis-de-resultados/2019/sintesis-nacional-esi-2019.pdf (accessed on 1 December 2022).
- MVU—Ministerio de Vivienda y Urbanismo; y el Centro de Estudios de Ciudad y Territorio, (Housing and Urbanism Ministry and the Center for City and Territory Studies). 2020. Available online: https://observatoriourbano.minvu.gob.cl/estudios/ (accessed on 20 December 2022).
- Vergara, J.E. Verticalización. La edificación en altura en la región metropolitana de Santiago (1990–2014). Rev. INVI 2017, 32, 9–49. [Google Scholar] [CrossRef]
- PUBLICA. 2019. Available online: https://www.minvu.cl/wp-content/uploads/2019/06/CUENTA-PUBLICA-resumenejecutivo-2019-2.pdf (accessed on 8 January 2023).
- Stehr, N.; Von Storch, H. Introduction to papers on mitigation and adaptation strategies for climate change: Protecting nature from society or protecting society from nature? Environ. Sci. Policy 2005, 8, 537–540. [Google Scholar] [CrossRef]
- Stehr, N.; Von Storch, H. Adaptation and Mitigation and the Illusion of the Difference. GAIA—Ecol. Perspect. Sci. Soc. 2008, 17, 270–273. Available online: https://www.researchgate.net/publication/290922427 (accessed on 17 January 2023).
- Mirzaei, P.A.; Haghighat, F. Approaches to study urban heat island–abilities and limitations. Build. Environ. 2010, 45, 2192–2201. [Google Scholar] [CrossRef]
- Yuan, K.; Zhu, Q.; Riley, W.J.; Li, F.; Wu, H. Understanding and reducing the uncertainties of land surface energy flux partitioning within CMIP6 land models. Agric. For. Meteorol. 2022, 319, 108920. [Google Scholar] [CrossRef]
- Yuan, K.; Zhu, Q.; Zheng, S.; Zhao, L.; Chen, M.; Riley, W.J.; Cai, X.; Ma, H.; Li, M.; Wu, H. Deforestation reshapes land-surface energy-flux partitioning. Environ. Res. Lett. 2021, 16, 024014. [Google Scholar] [CrossRef]
- Balany, F.; Ng, A.W.; Muttil, N.; Muthukumaran, S.; Wong, M.S. Green Infrastructure as an Urban Heat Island Mitigation Strategy—A Review. Water 2020, 12, 3577. [Google Scholar] [CrossRef]
- Black, S.; Minnett, D.; Parry, I.; Roaf, J.; Zhunussova, K. A Framework for Comparing Climate Mitigation Effort across Countries; Working Paper 2022/254; International Monetary Fund: Washington, DC, USA, 2022. [Google Scholar]
- Fu, J.; Dupre, K.; Tavares, S.; King, D.; Banhalmi-Zakar, Z. Optimized greenery configuration to mitigate urban heat: A decade systematic review. Front. Archit. Res. 2022, 11, 466–491. [Google Scholar] [CrossRef]
- Yang, L.; Qian, F.; Song, D.-X.; Zheng, K.-J. Research on Urban Heat-island Effect. Procedia Eng. 2016, 169, 11–18. [Google Scholar] [CrossRef]
- Sun, Z.; Li, Z.; Zhong, J. Analysis of the Impact of Landscape Patterns on Urban Heat Islands: A Case Study of Chengdu, China. Int. J. Environ. Res. Public Health 2022, 19, 13297. [Google Scholar] [CrossRef]
- Palma Behnke, R.; Barría, C.; Basoa, K.; Benavente, D.; Benavides, C.; Campos, B.; de la Maza, N.; Farías, L.; Gallardo, L.; García, M.J.; et al. Chilean NDC Mitigation Proposal: Methodological Approach and Supporting Ambition; Mitigation and Energy Working Group Report; COP25 Scientific Committee; Ministry of Science, Technology, Knowledge and Innovation: Santiago, Chile, 2019. Available online: https://mma.gob.cl/wp-content/uploads/2020/03/Mitigation_NDC_White_Paper.pdf (accessed on 15 January 2023).
- Zhu, L.; Ge, X.; Chen, Y.; Zeng, X.; Pan, W.; Zhang, X.; Ben, S.; Yuan, Q.; Xin, J.; Shao, W.; et al. Short-term effects of ambient air pollution and childhood lower respiratory diseases. Sci. Rep. 2017, 7, 4414. [Google Scholar] [CrossRef]
- Martínez, J.A.; Vinagre, F.A. La Entropía de Kolmogorov; su Sentido Físico y su Aplicación al Estudio de Lechos Fluidizados 2D; Departamento de Química Analítica e Ingeniería Química, Universidad de Alcalá, Alcalá de Henares: Madrid, Spain, 2019; Available online: https://www.academia.edu/2479372/19/07/2019 (accessed on 23 September 2022).
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Rutland, J.; Garreaud, R. Meteorological air pollution for Santiago, Chile: Towards an objective episode forecasting. Environ. Monit. Assess. 1995, 34, 223–244. [Google Scholar] [CrossRef]
- MMA. Sistema de Información Nacional de Calidad del Aire. Ministerio del Medioambiente de Chile. 2020. Available online: https://sinca.mma.gob.cl/index.php (accessed on 9 January 2023).
- Farmer, J.D. Chaotic attractors of an infinite dimensional dynamical system. Phys. D 1982, 4, 366–393. [Google Scholar] [CrossRef]
- Farmer, J.D.; Otto, E.; Yorke, J.A. The dimension of chaotic attractors. Phys. D 1983, 7, 153–180. [Google Scholar] [CrossRef]
- Farmer, J.D. Information Dimension and the Probabilistic Structure of Chaos. Z. Nat. A 1982, 37, 1304–1326. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On Entropy per unit Time as a Metric Invariant of Automorphisms. Dokl. Akad. Nauk. SSSR 1959, 124, 754–755. [Google Scholar]
- Sinai, Y.G. On the concept of entropy of a dynamical system. Dolk. Akad. Nauk. SSSR 1959, 124, 768. [Google Scholar]
- Pesin, Y. Characteristic Lyapunov exponents and smooth ergodic theory. Russ. Math. Surv. 1977, 32, 55–114. [Google Scholar]
- Kolmogorov, A.N. A new invariant for transitive dynamical systems. Dokl. Akad. Nauk. Souiza Sovestkikh Sotsialisticheskikh Respuplik 1958, 119, 861–864. [Google Scholar]
- Ruelle, D. Thermodynamic Formalism; Addison-Wesley-Longman: Reading, MA, USA, 1978. [Google Scholar]
- Shaw, R. Strange aattractor, chaotic behavior, and information flow. Z. Nat. A 1981, 36, 80–112. [Google Scholar] [CrossRef]
- Abramson, N. Information Theory and Coding; McGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- Deco, G.; Schurmann, B. Information flow and chaotic dynamics. In Proceedings of the International Workshop on Neural Networks for Identification, Control, Robotics and Signal/Image Processing, Venice, Italy, 21–23 August 1996; IEEE: Venice, Italy, 1996; pp. 321–329. [Google Scholar] [CrossRef]
- Cohen, A.; Procaccia, I. Computing the Kolmogorov entropy from time signals of dissipative and conservative dynamical systems. Phys. Rev. A Gen. Phys. 1985, 31, 1872–1882. [Google Scholar] [CrossRef] [PubMed]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Emery, X. Simple and ordinary multigaussian Kriging for estimating recoverable reserves. Math. Geol. 2005, 37, 295–319. [Google Scholar] [CrossRef]
- Sprott, J.C. Chaos and Time-Series Analysis, 1st ed.; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Sprott, J.C. Chaos Data Analyzer Software, Version 2.1; EEUU: Madison, WI, USA, 1995. Available online: https://sprott.physics.wisc.edu./cda.htm (accessed on 7 January 2023).
- Clausius, R. Über die bewegende Kraft der Wärme. Ann. Der Phys. 1850, 79, 368–397, 500–524. [Google Scholar] [CrossRef]
- Han, W.; Li, Z.; Wu, F.; Zhang, Y.; Guo, J.; Su, T.; Cribb, M.; Fan, J.; Chen, T.; Wei, J.; et al. The mechanisms and seasonal differences of the impact of aerosols on daytime surface urban heat island effect. Atmos. Chem. Phys. 2020, 20, 6479–6493. [Google Scholar] [CrossRef]
- Žiberna, I.; Pipenbaher, N.; Donša, D.; Škornik, S.; Kaligarič, M.; Bogataj, L.K.; Črepinšek, Z.; Grujić, V.J.; Ivajnšič, D. The Impact of Climate Change on Urban Thermal Environment Dynamics. Atmosphere 2021, 12, 1159. [Google Scholar] [CrossRef]
- United States Government. Available online: https://www.epa.gov/heatislands/climate-change-and-heat-islands (accessed on 10 January 2023).
- Pacheco, P.; Mera, E. Study of the Effect of Urban Densification and Micrometeorology on the Sustainability of a Coronavirus-Type Pandemic. Atmosphere 2022, 13, 1073. [Google Scholar] [CrossRef]
- Fahed, J.; Kinab, E.; Ginestet, S.; Adolphe, L. Impact of urban heat island mitigation measures on microclimate and pedestrian comfort in a dense urban district of Lebanon. Sustain. Cities Soc. 2020, 61, 102375. [Google Scholar] [CrossRef]
- Battista, G.; de Lieto Vollaro, E.; Ocłoń, P.; de Lieto Vollaro, R. Effects of urban heat island mitigation strategies in an urban square: A numerical modelling and experimental investigation. Energy Build. 2023, 282, 112809. [Google Scholar] [CrossRef]
- Songok, J.; Mäkiranta, A.; Rapantova, N.; Pospisil, P.; Martinkauppi, B. Numerical simulation of heat recovery from asphalt pavement in Finnish climate conditions. Int. J. Therm. Sci. 2023, 187, 108181. [Google Scholar] [CrossRef]
- Wen, J.; Ignatius, M.; Xinzhu Chen, E.; Hien Wong, N. Impacts of a highly reflective stainless-steel façade on a surrounding building: A case study in Singapore. Sustain. Cities Soc. 2023, 90, 104377. [Google Scholar] [CrossRef]
- Gourfi, A.; Taïbi, A.N.; Salhi, S.; Hannani, M.E.; Boujrouf, S. The Surface Urban Heat Island and Key Mitigation Factors in Arid Climate Cities, Case of Marrakesh, Morocco. Remote Sens. 2022, 14, 3935. [Google Scholar] [CrossRef]
- Park, C.; Ha, J.; Lee, S. Association between Three-Dimensional Built Environment and Urban Air Temperature: Seasonal and Temporal Differences. Sustainability 2017, 9, 1338. [Google Scholar] [CrossRef]
- Marsh, T.; Harvey, C.L. The Thames flood series: A lack of trend in flood magnitude and a decline in maximum levels. Hydrol. Res. 2012, 43, 203–214. [Google Scholar] [CrossRef]
- Coman, I.A.; Cooper-Norris, C.E.; Longing, S.; Perry, G. It Is a Wild World in the City: Urban Wildlife Conservation and Communication in the Age of COVID-19. Diversity 2022, 14, 539. [Google Scholar] [CrossRef]
- Murray, M.H.; Byers, K.A.; Buckley, J.; Lehrer, E.W.; Kay, C.; Fidino, M.; Magle, S.B.; German, D. Public perception of urban wildlife during a COVID-19 stay-at-home quarantine order in Chicago. Urban Ecosyst. 2023, 26, 127–140. [Google Scholar] [CrossRef] [PubMed]
- Perez, P.; Salini, G. A Study of the Dynamic Behaviour of Fine Particulate Matter in Santiago, Chile. Aerosol Air Qual. Res. 2015, 15, 154–165. [Google Scholar] [CrossRef]
- Hu, H.; Tan, Z.; Liu, C.; Wang, Z.; Cai, X.; Wang, X.; Ye, Z.; Zheng, S. Multi-timescale analysis of air pollution spreaders in Chinese cities based on a transfer entropy network. Front. Environ. Sci. 2022, 10, 970267. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).