Abstract
The WRF-Solar Ensemble Prediction System (WRF-Solar EPS) and a calibration method, the analog ensemble (AnEn), are used to generate calibrated gridded ensemble forecasts of solar irradiance over the contiguous United States (CONUS). Global horizontal irradiance (GHI) and direct normal irradiance (DNI) retrievals, based on geostationary satellites from the National Solar Radiation Database (NSRDB) are used for both calibrating and verifying the day-ahead GHI and DNI predictions (GDIP). A 10-member ensemble of WRF-Solar EPS is run in a re-forecast mode to generate day-ahead GDIP for three years. The AnEn is used to calibrate GDIP at each grid point independently using the NSRDB as the “ground truth”. Performance evaluations of deterministic and probabilistic attributes are carried out over the whole CONUS. The results demonstrate that using the AnEn calibrated ensemble forecast from WRF-Solar EPS contributes to improving the overall quality of the GHI predictions with respect to an AnEn calibrated system based only on the deterministic run of WRF-Solar. In fact, the calibrated WRF-Solar EPS’s mean exhibits a lower bias and RMSE than the calibrated deterministic WRF-Solar. Moreover, using the ensemble mean and spread as predictors for the AnEn allows a more effective calibration than using variables only from the deterministic runs. Finally, it has been shown that the recently introduced algorithm of correction for rare events is of paramount importance to obtain the lowest values of GHI from the calibrated ensemble (WRF-Solar EPS AnEn), qualitatively consistent with those observed from the NSRDB.
1. Introduction
The value of numerical weather predictions (NWP) is nowadays well recognized by the renewable energy community [1,2,3]. NWPs represent a component of most solar and wind power prediction systems, providing reliable wind speed and solar irradiance forecasts up to three days ahead in broad geographic regions [4,5,6]. Predictions of intermittent natural resources such as wind and solar power facilitate their increasing penetration into the wider pool of energy generation technologies [7,8]. In fact, in countries with a high solar/wind production capacity, the electric transmission grid’s supply/demand can be kept in balance and disruptions of the energy distribution can be prevented if accurate planning of backup traditional dispatchable sources (coal, gas, hydro, etc.) is carried out. Another application of NWP is related to trading wind/solar energy in the day-ahead market. In many countries, producers have to sell their energy the day before, and they are subject to penalties if they do not deliver the production amounts previously committed [9,10,11].
An important feature enhancing NWP’s value for these applications is to provide uncertainty quantification, i.e., probabilistic information associated with the deterministic single-valued forecast [12,13]. Probabilistic forecasts of weather variables important for renewable energies have been traditionally generated using an ensemble of model runs with the members being different models (i.e., multi-model ensemble) [14,15], having different initial conditions [16,17], physics configurations (i.e., multi-physics) [18], and stochastic perturbations of the tendencies of physics parameterizations [19]. In these cases, the uncertainty of predicting a meteorological variable is represented by the ensemble spread, defined as the standard deviation of the members about the ensemble mean. Probabilities of exceeding a given value of any meteorological variable can be derived by the fraction of members larger than the value itself.
An alternative approach developed more recently in the last 15 years is to generate the ensemble members with statistical post-processing techniques such as the analog ensemble (AnEn) [20,21,22] or quantile regression [23]. In these cases, a historical dataset of observations of the variable to be predicted is needed at a specific location. It should be noted that the AnEn, as well as other post-processing techniques, have also been applied to reduce systematic errors (bias correct) and calibrate the existing ensemble [24,25,26,27]. Also, it is worth mentioning the work [2,28,29] where the AnEn is coupled with other machine learning (ML) techniques, [13,30,31,32,33] where the AnEn is used to predict regional solar power generation, and [34,35] where the AnEn’s computational efficiency has been optimized.
In this work, we will focus on developing and testing global horizontal irradiance (GHI) and direct normal irradiance (DNI) probabilistic prediction based on the version of the Weather Research and Forecasting (WRF) [36,37] model specialized for solar applications (WRF-Solar) [38,39]. Being a deterministic model, WRF-Solar does not inform about uncertainties associated with the irradiance predictions or probabilities of exceeding a given irradiance level. To avoid this limitation, WRF-Solar has been enhanced with a probabilistic component called the WRF-Solar Ensemble Prediction System (WRF-Solar EPS) [40,41,42,43]. WRF-Solar EPS generates the probabilistic forecasts introducing stochastic perturbations to state variables to account for uncertainties in the cloud, aerosol, and radiation processes. The variables were selected by developing tangent linear models of six WRF-Solar modules to identify the variables responsible for the most significant uncertainties in predicting surface solar irradiance and clouds [43]. Previous work has shown the necessity of calibration for WRF-Solar EPS predictions over the contiguous United States (CONUS). In fact, we have found that WRF-Solar EPS, like most of the NWP dynamical ensemble systems, is overconfident in the day-ahead predictions [40,42]. The calibration of the ensemble herein presented makes use of the AnEn post-processing system already applied in [21] to generate GHI and solar power probabilistic forecasts starting from a deterministic NWP. Herein we focus on applying the AnEn to a WRF-Solar EPS ensemble. A preliminary assessment of the use of AnEn coupled with WRF-Solar and WRF-Solar EPS has been briefly presented [42], and this work explores this approach in more detail, using a more extended dataset (three years), and includes an evaluation of the performances predicting DNI as well as GHI. More specifically, the AnEn will be applied to generate an ensemble forecast from the deterministic NWP output of WRF-Solar (WRF-Solar AnEn) and to calibrate WRF-Solar EPS (WRF-Solar EPS AnEn), improving its spread/skill consistency. It is necessary because the uncalibrated WRF-Solar EPS spread underestimates the error (root mean squared error) of the ensemble mean with respect to GHI observations [40]. As already mentioned, the AnEn needs an archive of past forecasts from an NWP model and past observations of the meteorological variables of interest, GHI or DNI, in this work. Past forecasts (analog forecasts) similar to the current one are selected based on some relevant meteorological variables (predictors). For each analog forecast, the verifying observations of the variable to be predicted (GHI or DNI) are used to build the ensemble prediction. The assumption is that these past observations can inform about future outcomes since they had occurred in similar meteorological conditions in the past. When calibrating the WRF-Solar EPS, the AnEn can also use, as predictors, variables derived from the ensemble members, such as the mean and the spread. Since the AnEn is based on just a single deterministic forecast in the WRF-Solar AnEn, it has the advantage of building an ensemble with fewer computational resources than the WRF-Solar EPS or WRF-Solar EPS AnEn.
The novel aspect of this work is that both the WRF-Solar AnEn and WRF-Solar EPS AnEn GHI and DNI forecasts are built using the National Solar Radiation Database (NSRDB) [44], a satellite-based solar irradiance observation dataset, which is based on the Geostationary Operational Environmental Satellite (GOES) observations and covers the CONUS region. Our previous work has quantified its adequacy in evaluating WRF-Solar predictions [45]. Therefore, using NSRDB gridded GHI and DNI data allows the AnEn to by applied at every grid point within the CONUS domain, resulting in calibrated systems over the entire model grid. A similar application of the AnEn for gridded 10 m wind speed forecasts was explored by [46], in which the wind speed gridded observations were derived from the European Center for Medium-Range Weather Forecasts (ECMWF) model analysis product. It should be noted that in past applications of the AnEn to GHI [21], the AnEn was applied only at specific locations corresponding to ground observation sites with radiometers, meaning that calibrated ensemble values of GHI or DNI were not available as gridded products covering large geographic areas. The use of NSRDB gridded data over CONUS allows setting up experiments to answer the following scientific questions: (1) Assessing and comparing WRF-Solar and WRF-Solar EPS performances in different climatic regions of the US in terms of deterministic GHI and DNI predictions. (2) Comparing the performance of the computationally cheaper ensemble, the WRF-Solar AnEn, against the more expensive WRF-Solar EPS. (3) Quantifying the improvements obtained by the AnEn calibration of the WRF-Solar EPS.
The paper is organized as follows: Section 2 describes the NSRDB observational dataset, WRF-Solar and WRF-Solar EPS, the AnEn, and the methodology used to calibrate the ensembles and to assess the performance of the GHI and DNI predictions. The results, including verification of the models’ performances and some case studies, are illustrated in Section 3, with the conclusions in Section 4.
2. Models and Dataset
2.1. The WRF-Solar Model
The WRF-Solar model was created to enhance the value of the WRF NWP model for solar energy applications [38]. The original emphasis was placed on improving the aerosol–cloud–radiation interactions with other physical additions to increase the value of solar applications [38,39]. The WRF-Solar community model was fully integrated into WRF in version 4.2. Recently, we have added a solar diagnostic package to provide 2-dimensional variables characterizing the cloud field and radiation. A more recent development is the addition of the multi-sensor advection diffusion (MAD)-WRF component [47] to improve short-range irradiance predictions. MAD-WRF improves the cloud initialization using a cloud parameterization based on the relative humidity in combination with observations of the cloud mask and the cloud top/base height if available. MAD-WRF has been shown to improve the short-term irradiance predictions over CONUS by 18% [47].
2.2. WRF-Solar Ensemble Prediction System
To extend the WRF-Solar capabilities [38,39,48] beyond deterministic forecasts, we have developed WRF-Solar EPS [40,41,42] First, we selected six parameterizations affecting solar irradiance and cloud processes: (1) Thompson microphysics [47], (2) Mellor–Yamada–Nakanishi–Niino planetary boundary layer parameterization [49], (3) the Noah land surface model [50], (4) Deng’s shallow cumulus parameterization [51], (5) the Fast-All-sky Radiation Model for Solar applications [52], and (6) a parameterization of the effects of unresolved clouds based on relative humidity. Then, we developed tangent linear models of these parameterizations to quantify sensitivities of the input variables to the parameterizations and select the ones introducing the most significant uncertainties in the output variables [43]. As a result of this analysis, we selected 14 state variables. In the final step, we introduced stochastic perturbations to these variables during the model integration in order to create the WRF-Solar EPS component. The characteristics of the perturbations and the variables/parameterizations to perturb are determined in configuration files, providing flexibility in generating the WRF-Solar EPS ensemble. The interested reader is referred to [40,41,42] for further details about the WRF-Solar EPS model.
2.3. National Solar Radiation Database
The National Solar Radiation Database (NSRDB) [44] is a satellite-based solar irradiance observation dataset, which has a 4 km horizontal resolution for each 30 min interval from 1998 to 2017 (https://nsrdb.nrel.gov accessed on 12 August 2022). From 2018 onwards, the NSRDB contains improved spatiotemporal resolution data (2 km of spatial resolution with up to 5 min of temporal resolution) which are in addition to the 4 km, 30 min NSRDB products. For this improved dataset, the NSRDB makes use of data from the new generation of GOES satellites [53,54,55] and covers the CONUS region (Figure 1). It has been shown to provide state-of-the-science retrievals of GHI (DNI). In [45], NSRDB and ground observations were compared to WRF-Solar predictions to confirm the adequacy of the NSRDB to assess the performances of WRF-Solar over CONUS. The NSRDB data are also used as an observation component of the AnEn calibration in this work. To efficiently implement the AnEn calibration, the NSRDB datasets covering 2016–2018 are aggregated to the 9 km WRF-Solar grid for each 30 min interval. For 2016 and 2017 datasets, the 9 km GHI (DNI) is obtained from spatially averaged 4 km NSRDB pixels, which are derived from 30 min, 4 km GOES-13 (East) and GOES-15 (West) data. For the 2018 dataset, additional procedures (e.g., spatiotemporal averaging; see details summarized in [41]) are applied to produce the 9 km GHI (DNI). Because the NSRDB is derived from the 30 min, 4 km GOES-15 and new GOES-East satellite data (i.e., GOES 16), which includes cloud properties retrieved from 15 min, 2 km satellite data. Comprehensive details for building up the 9 km GHI (DNI) are summarized in [41,45]. In Figure 1 a map of the 9 km GHI observations from the NSRDB on 1530 UTC 16 April 2018 within the WRF-Solar computational domain, is presented.
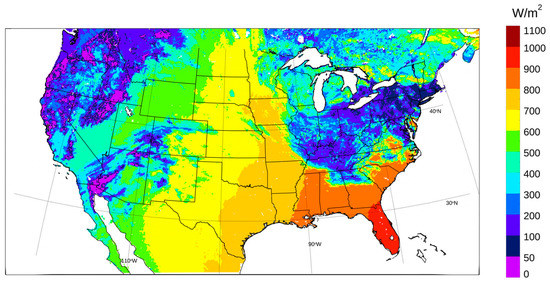
Figure 1.
GHI observations from NSRDB on 1530 UTC 16 April 2018 for WRF-Solar computational domain.
2.4. Forecast Dataset
WRF-Solar was configured to cover CONUS with 9 km grid spacing (Figure 1). The physics configuration follows those in the WRF-Solar [38], and one difference is the activation of the Fast-All-sky Radiation Model for Solar applications (FARMS) radiation scheme [52]. The National Centers for Environmental Prediction (NCEP) Global Forecast System (0.25° × 0.25°; 3-hourly intervals) forecast was used as the initial and boundary conditions, and 48 h forecasts were conducted and initialized every 06 UTC. This configuration is optimized for day-ahead forecasting. WRF-Solar EPS runs a stochastically generated ensemble with 10 members based on WRF-Solar.
The AnEn post-processing (hereafter described) focused on the GHI and DNI predictions over the 24–48 h lead time interval. Due to limitation in the storage and computational resources, the AnEn ran over a subsample of WRF-Solar grid points. Specifically, one of every fifth grid point has been considered for AnEn post-processing. Also, the AnEn was run every day of the verification period from 1 January to 29 December 2018 using the period from 1 January 2016 to 31 December 2017 as training; thus, in the verification period, there are 363 WRF-Solar and WRF-Solar EPS runs, and the corresponding post-processed WRF-Solar AnEn and WRF-Solar EPS AnEn runs.
2.5. The Analog Ensemble (AnEn)
A very brief description of the AnEn algorithm and its bias correction for rare events algorithms are presented here. We direct the reader to [21,56] for more details.
As previously explained, with the AnEn, the ensemble is built by searching for similar (analogs) forecasts to a current (target) forecast in an archive of historical deterministic predictions. The observed GHI (DNI) values verifying each selected forecast are used to generate the ensemble of GHI (DNI) predictions. The similarity is determined by a Euclidean distance that, in this application, is based on a few predictors. Following [21], after a few tests (not shown) carried out over the training period, no other predictors than GHI and DNI were found to add some skills. Therefore, only GHI and DNI were used for the AnEn post-processing of the WRF-Solar deterministic output of both GHI and DNI. In the case of WRF-Solar EPS post-processing, the GHI and DNI ensemble mean and ensemble standard deviation (spread) have been used as predictors. The Euclidean distance adopted to determine the similarity of the past forecasts with respect to the target one is computed over 3 h trends centered around the lead time of the target forecast. For instance, when predicting the GHI at 12 UTC (lead time 12 h) on 1 January 2018, GHI and DNI forecasts at 11 UTC, 12 UTC, and 13 UTC are used to compute the distances with all the past forecasts in the training dataset, from 1 January 2016 to 31 December 2017. The result is an array of 730 values (the number of days from 1 January 2016 to 31 December 2017), each representing the distance between the target forecast and each day’s forecast in the training dataset. After sorting these values in increasing order, the first n (number of ensemble members) dates are usually selected. The GHI (DNI) observed verifying values on these n dates are used to build the GHI (DNI) forecast’s ensemble values for 1 January 2018 12 UTC.
The ensemble members’ mean or median is commonly used to obtain a single-valued deterministic forecast. It is generally recommended to use the mean or the median of the ensemble distribution if the goal is to minimize the root mean squared error or the mean absolute error respectively [57]. Since the WRF-Solar EPS was run with 10 members due to computational capacity limits, the number of AnEn ensemble members was set to 10 to allow a fair comparison. After a few tests aimed at optimizing the performance at each grid point through brute force [21] by assigning different weights to the predictors, we decided to keep the same and equal weights. In fact, overfitting occurred at many grid points when trying to assign different weights, meaning that the AnEn performance improvement over the training dataset did not reflect over the verification dataset.
As already pointed out in [56,58], the AnEn introduces a negative/positive bias when predicting the right/left tails of the forecast distribution. Here, the bias correction techniques suggested by [58] have been adopted to mitigate these biases. They include extending the training dataset to lead times adjacent to that of the target forecast. For example, when predicting 12 h ahead, analogs are also searched at 11 h and 13 h (one-hour window). With this approach, the forecast sample from which analogs can be selected is increased by a factor of three. The other method is an adaptation to solar irradiance of what was proposed by [56] for wind speed. The forecasts in the distribution tails are adjusted by adding or subtracting a coefficient proportional to the difference between the target forecast and the mean of the analog forecasts. Hereafter in Section 3.3, it is shown that including this bias correction technique allowed us to have a more realistic prediction over an area affected by low irradiance, as observed by the NSRDB.
3. Results
3.1. Deterministic Verification
A first comparison between the models is presented here in terms of standard metrics such as bias, the root mean squared error (RMSE), and Pearson correlation [3]. For additional details about these standard metrics, the reader is referred to [3,59].
WRF-Solar, WRF-Solar EPS, WRF-Solar AnEn, and WRF-Solar EPS AnEn are evaluated in Figure 2, Figure 3 and Figure 4. The goal is to verify potential improvements achieved by using an ensemble with respect to a deterministic model (WRF-Solar EPS vs. WRF-Solar) both with and without the AnEn calibration. Also, the benefit of using an ensemble calibration process such as AnEn is assessed. In terms of bias (Figure 2) both WRF-Solar and WRF-Solar EPS have the tendency to overestimate GHI, which indicates that cloudiness is underestimated in general (see also [3]). Positive bias values are more significant in the Midwest and in subtropical areas facing the Gulf of Mexico than over the West coast. WRF-Solar and the WRF-Solar EPS performances are similar, with slightly higher peaks of bias from the latter of about 60 W/m2, and the overall total bias value obtained by pooling all the grid points and lead time together (Figure 2a,b) was larger in the WRF-Solar EPS (31.7 W/m2) than in WRF-Solar (22.8 W/m2). The benefit of the AnEn calibration is evident for both models, with a significant absolute bias reduction everywhere, and broad areas in the West with values virtually equal to zero in both the WRF-Solar AnEn and WRF-Solar EPS AnEn (Figure 2c,d).
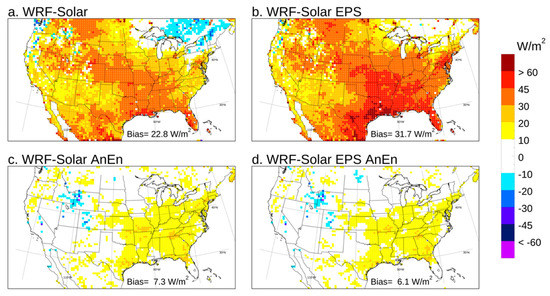
Figure 2.
Bias computed for GHI over 2018 for the forecast lead times from +24 to +48 h. The value in the legend at the bottom of each panel indicates the bias computed by pooling all the grid points and lead times together.
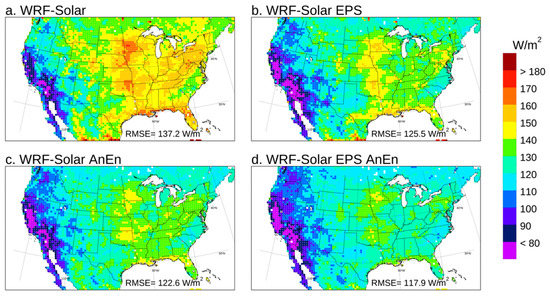
Figure 3.
Root mean squared error (RMSE) computed for GHI over the year 2018 for the forecast lead times from +24 to +48 h. The value in the legend at the bottom of each panel indicates the RMSE computed by pooling all the grid points and lead times together.
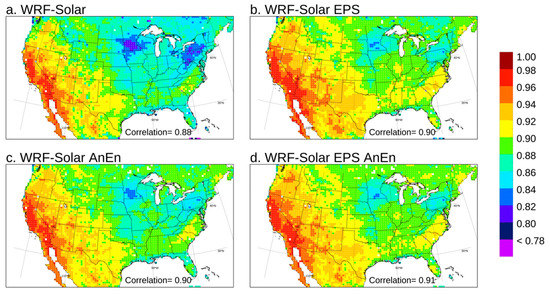
Figure 4.
Pearson correlation computed for GHI over the year 2018 for the forecast lead times from +24 to +48 h. The value in the legend at the bottom of each panel indicates the correlation computed by pooling all the grid points and lead times together.
Looking at the RMSE (Figure 3a,b), the WRF-Solar EPS improves upon WRF-Solar with a reduction of RMSE in many areas. Since the systematic component of RMSE (bias) is very similar in both models, or even higher in the WRF-Solar EPS than WRF-Solar, RMSE improvements can be attributed to a significant reduction of the random component of the RMSE in the WRF-Solar EPS. The AnEn calibration improves the RMSE in the Midwest regions for both models (Figure 3c,d), with more significant improvements over the West coast for WFR-Solar AnEn rather than for WRF-Solar EPS AnEn. The calibrated WRF-Solar AnEn (Figure 3c) is slightly better than the WRF-Solar EPS for RMSE (Figure 3b), with an overall RMSE value of 122.6 W/m2 against 125.5 W/m2. The WRF-Solar AnEn (Figure 3c) is slightly worse than the calibrated version the WRF-Solar EPS AnEn (Figure 3d), with an overall RMSE value of 122.6 W/m2 against 117.9 W/m2. The relative performances of the four different models for the correlation index (Figure 4) are very similar to those drawn for the RMSE. In conclusion, it is worth noting that the full potential of the WRF-Solar EPS is reached only after the AnEn calibration process that allows reaching the best performances in all three metrics (bias, RMSE, and correlation) among the four models examined. In fact, before the AnEn calibration, the WRF-Solar EPS is worse than the ensemble WRF-Solar AnEn in terms of RMSE and bias in particular. These results highlight the well-known importance of post-processing any NWP-based forecasts. Another conclusion is that the calibration process over the deterministic run (WRF-Solar) allows very competitive performances compared to its EPS versions without the need to run multiple numerical simulations.
The same plots regarding bias, RMSE, and correlation are presented in Appendix A for DNI. The conclusions drawn for DNI are almost identical to those already presented for GHI.
For a more detailed analysis, in Figure 5, RMSE, bias, and correlation are presented for the four models as time series of average daily values for 2018. In terms of bias, the benefit of calibration is clear most of the time. Especially in summer and winter, there is a clear benefit to having the AnEn coupled to WRF-Solar or the WRF-Solar EPS, which otherwise are affected by a more significant bias than in other seasons. In some cases, during spring and fall, there is a slight tendency of the AnEn to over-correct the positive bias resulting in negative values. In general, WRF-Solar exhibits a lower bias than the WRF-Solar EPS (Figure 5a), with the AnEn post-processing effectively reducing the systematic error, especially in summer, which is consistent with what is already seen in Figure 2. In terms of RMSE and correlation, the WRF-Solar EPS AnEn is the best model most days, confirming that the post-processing reduces the random component of the error more than in the calibrated WRF-Solar AnEn.
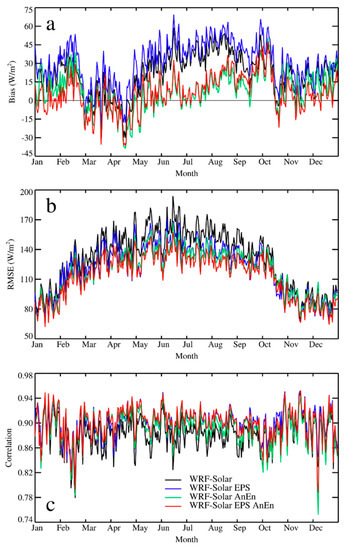
Figure 5.
Bias, RMSE, and correlations were computed for GHI for each day of the year 2018 for the forecast lead times from +24 to +48 h by pooling all the grid points together.
3.2. Probabilistic Verification
One of the main reasons for using ensemble prediction systems is to assess information dynamically regarding the accuracy of any forecast. A common practice to evaluate how effectively an EPS can provide accurate information about its own uncertainty is to compare the RMSE of the ensemble mean with the ensemble spread [60]. Historically, NWP-based EPSs have shown to be under-dispersive, at least up to 7 days ahead, meaning that the spread is lower than the RMSE [61]. EPS calibration procedures are aimed at not only reducing the bias but also at improving the RMSE/spread consistency.
In Figure 6, the ratio between the RMSE and spread is plotted for all the grid points by pooling all the forecast lead times from +24 h to +48 h and runs together. The ratio has been computed following [60]:
where is the ensemble mean at any of the N forecast events, is the observation, and is variance about the ensemble mean of the n ensemble members. The numerator of Equation (1) is the RMSE adjusted by a factor . This factor has been included to account for the limited number of members to properly compare the RMSE and the spread at the denominator of Equation (1), as demonstrated by [60]. The WRF-Solar EPS is under-dispersive, with values of the ratio larger than 2 everywhere, reaching peaks of 4 in the western US. Both the calibrated versions, WRF-Solar EPS AnEn and WFR-Solar AnEn, largely improve the RMSE/spread matching everywhere, with much lower values of the ratio between 1 and 1.4. These results indicate that the WRF-Solar EPS does not generate enough cloudiness variability across the members in the western US and East of the Rocky Mountains, in Wyoming and Colorado in particular.
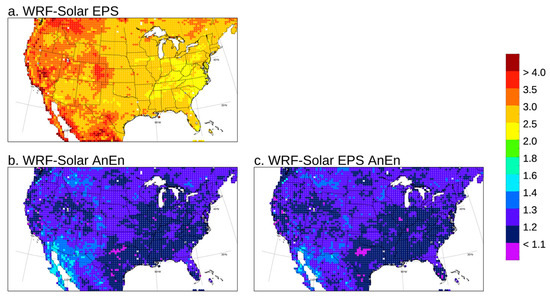
Figure 6.
RMSE/spread ratio computed for all the grid points pooling the forecast lead times from +24 to +48 h and forecast runs for 2018 together.
Another way to assess whether the probabilistic prediction system can quantify its own uncertainty is to compile a binned spread-skill diagram (Figure 7). In spread-skill diagrams, the ensemble spread is compared with the RMSE of the ensemble mean over small class intervals (i.e., bins) of spread [61]. A good correlation in the spread-skill diagram indicates that an ensemble system can predict its uncertainty. A perfect RMSE/spread matching is achieved at all bins for values resulting in a trend lying on the plot’s 1:1 diagonal. In Figure 7, a better spread skill consistency is clearly shown by the WRF-Solar AnEn and WRF-Solar EPS AnEn, with values closer to the 1:1 diagonal than for the WRF-Solar EPS. It is worth noticing that errors (RMSE) between 25 and 125 W/m2 for the WRF-Solar EPS correspond to an almost constant value of spread of about 10 W/m2. It means that a small value of spread around 10 W/m2 from the raw WRF-Solar EPS does not necessarily result in an accurate forecast, since the RMSE can likely take values up to 125 W/m2.
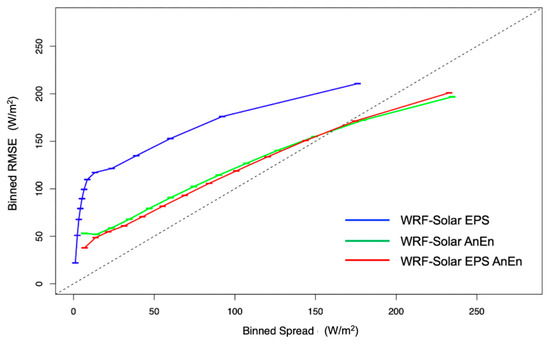
Figure 7.
Binned RMSE/spread diagrams computed pooling all the grid points for GHI forecasts, runs, and the forecast lead times from +24 to +48 h for 2018. The horizontal bars represent the 5–95% bootstrap confidence intervals of the spread for each considered bin.
So far, the metrics presented in this section were aimed at assessing only one attribute, i.e., the statistical consistency of the ensemble systems. The continuous ranked probability score (CRPS) [62,63] can be used to assess the overall quality of the probabilistic predictions. Details about the formulation of the CRPS and its components, reliability (REL), and potential CRPS (CRPSPOT) are presented in Appendix B. In Figure 8, Figure 9 and Figure 10, maps obtained from computing the CRPS, CRPSPOT and REL over all the grid points for the year 2018 and the +24 h, +48 h lead time interval are presented. The overall evaluation of the CRPS indicates the WRF-Solar EPS AnEn is the best model (lowest CRPS). The WRF-Solar EPS delivers the worst performance, and the WRF-Solar AnEn is slightly worse than the calibrated version the WRF-Solar EPS AnEn. When comparing the WRF-Solar EPS and its calibrated version (WRF-Solar EPS AnEn), it is possible to quantify the overall improvement achieved through the AnEn calibration, which is about 20%. The lack of reliability consistent with the under-dispersive characteristic already pointed out (Figure 6 and Figure 7) for the WRF-Solar EPS is evident looking at the reliability map. In fact, REL values are the highest (worst) for the WRF-Solar EPS, especially in the Midwest and Mexico. The WRF-Solar AnEn is very similar to the WRF-Solar EPS AnEn in terms of reliability, with values below 4 W/m2 everywhere. The WRF-Solar EPS exhibits the best (lowest) CRPSPOT values and, since CSPSPOT = UNC-RES holds, also the best (highest) resolution. It is worth recalling that the model resolution is the ability of the system to perform better than a climatological forecast, which can also be seen as the degree to which the forecasts separate the observed events in groups that are different from each other. Since WRF-Solar EPS forecasts are sharper (have a lower spread) than their calibrated version (WRF-Solar EPS AnEn), this is somehow reflected in a better resolution of the former. On the other hand, the improvement achieved by the calibration in terms of reliability abundantly compensates for the loss in resolution, leading to an overall (lower CRPS) improved probabilistic model. Given that the WRF-Solar AnEn and the WRF-Solar EPS AnEn show very similar reliability maps, the slightly overall worse CRPS in the former can be attributed to its lower resolution, highlighted by a higher CRPSPOT.
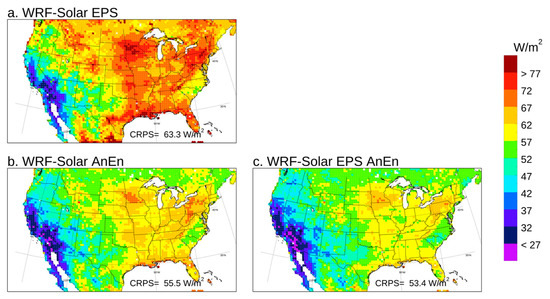
Figure 8.
Continuous ranked probability score (CRPS) map computed for GHI pooling runs and the forecast lead times from +24 to +48 h for 2018 together.
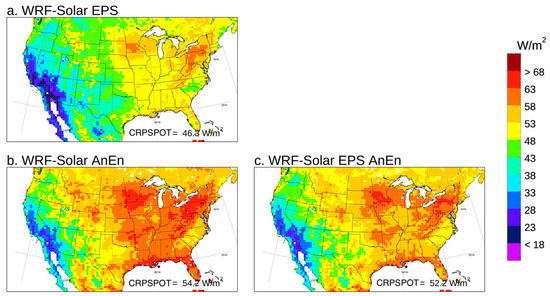
Figure 9.
Potential continuous ranked probability score (CRPSPOT) map computed for GHI pooling runs and the forecast lead times from +24 to +48 h for 2018 together.
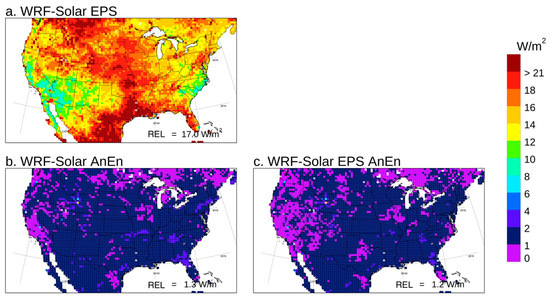
Figure 10.
Reliability (REL) map computed for GHI pooling runs and the forecast lead times from +24 to +48 h for 2018 together.
3.3. Case Study
In this section, an episode (1530 UTC July 29, 2018) in which NSRDB observations indicate a wide area affected by a very low GHI is investigated. In Figure 11, NSRDB estimates show a wide area across Arkansas, Missouri, and Illinois, with a GHI of less than 100 W/m2 and even under 50 W/m2 in a smaller region. Over the same area, the WRF-Solar EPS exhibits peaks of low GHI in the same range, even if the spatial pattern does not match exactly that of the NSRDB. After the calibration with the AnEn (Figure 11c), the overall bias is improved, and the average overestimation from WRF-Solar EPS of 41.2 W/m2 is reduced to −0.2 W/m2. Despite these general improvements when comparing with the NSRDB map (Figure 11a), a positive bias is introduced by the AnEn calibration (Figure 11c) over the area with a GHI lower than 100 W/m2 and, in particular, GHI values under 50 W/m2 are no longer generated. By using the bias correction for rare events (Figure 11d) described in Section 2.5 values under 50 W/m2 are introduced back in the forecast, consistently with the NSRDB and WRF-Solar EPS, while still keeping the overall improvement in terms of bias reduction (−0.8 W/m2) very similar to that of the AnEn without the correction for rare events (Figure 11c). It is worth recalling that the AnEn correction for rare events is applied only if the target forecast from the NWP model (WRF-Solar EPS ensemble mean in this case) is under a threshold value that, in this application, is set as the 10th quantile of the forecast distribution computed independently at each lead time and grid point. Hence, comparing the plots in Figure 11b–d, one can notice that GHI values under about 200 W/m2 in Figure 11b are modified with lower values in Figure 11d than in Figure 11c. The bias correction for rare events has been always included in the AnEn algorithm in all the applications previously presented in this work.
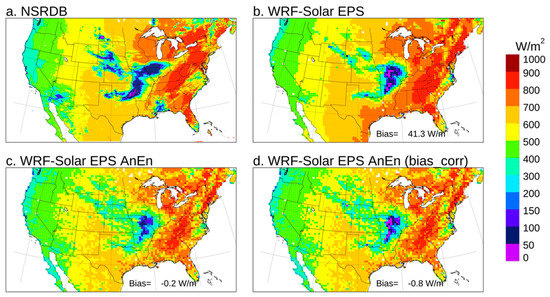
Figure 11.
NSRDB GHI map (a) at 1530 UTC on July 29, 2018. Model predictions from the ensemble mean of WRF-Solar EPS (b), WRF-Solar EPS AnEn (c), and WRF-Solar EPS AnEn with bias correction (d) are also reported for the same date.
4. Conclusions
In this work, the WRF version enhanced for solar energy applications, WRF-Solar, and its ensemble version, the WRF-Solar EPS, are evaluated using the National Solar Radiation Database (NSRDB), a satellite-based solar irradiance observation dataset. To handle the big datasets efficiently for evaluation of WRF-Solar and WRF-Solar EPS forecasts, the NSRDB observations covering 2016–2018 are aggregated from the native NSRDB grid (2 km or 4 km) to the WRF-Solar grid (9 km). Also, analog ensemble (AnEn) post-processing has been used to calibrate both models. In the case of the deterministic WRF-Solar model, the AnEn, besides removing the bias, also adds the capability of generating probabilistic predictions, since an ensemble is developed after the post-processing. For the WRF-Solar EPS, the AnEn ensemble members replace the original members that are output from the model, offering a calibrated version with a reduced bias and a better spread/skill consistency.
The first goal was to assess and compare WRF-Solar and WRF-Solar EPS performances in different climatic regions of the US in terms of deterministic GHI and DNI predictions. Both WRF-Solar and the WRF-Solar EPS overestimate GHI and DNI, which indicates that cloudiness is generally underestimated. Positive bias values are larger in the Midwest and in subtropical areas facing the Gulf of Mexico than over the West coast. For RMSE, the WRF-Solar EPS improves upon WRF-Solar both for DNI and GHI with a reduction in RMSE in many areas. Given the similar bias (a systematic component of the error) of the two models, the improvement in RMSE from the WRF-Solar EPS can be attributed to a reduction in the random component of the error.
The second goal was to compare the performance of the computationally cheaper ensemble, the WRF-Solar AnEn, against the more expensive WRF-Solar EPS. The WRF-Solar AnEn outperforms the WRF-Solar EPS both in terms of deterministic scores (lower bias and better RMSE) and probabilistic scores with improved statistical consistency and overall lover CRPS. These conclusions hold true for both GHI and DNI.
The third goal was to quantify the improvements obtained by the AnEn with respect to the raw models to which it is applied (WRF-Solar and WRF-Solar EPS). For deterministic verification, the benefit of the AnEn calibration is evident for both models, with a significant absolute bias reduction everywhere, and in broad areas in the West with bias values virtually equal to zero. The AnEn calibration improves the RMSE in the mid-West regions for both models, with more significant benefits over the West coast for WFR-Solar rather than the WRF-Solar EPS. The calibrated WRF-Solar AnEn is slightly better than the WRF-Solar EPS for RMSE and, generally, somewhat worse than the calibrated version of the WRF-Solar EPS (WRF-Solar EPS AnEn). For these reasons, the full benefit of using the WRF-Solar EPS is evident only after the AnEn calibration process, allowing better performances than the WRF-Solar AnEn in all three metrics (bias, RMSE, and correlation) for both GHI and DNI. For probabilistic verification, the WRF-Solar EPS is clearly under-dispersive, with values of the RMSE/spread ratio larger than 2 everywhere, reaching peaks of 4 in the western US. The calibrated version of the WRF-Solar EPS AnEn improves the RMSE/spread ratio everywhere. These results indicate that the WRF-Solar EPS does not generate enough cloudiness variability across the members in the western US and east of the Rocky Mountains in Wyoming and Colorado. The AnEn calibration process, despite slightly deteriorating the resolution of the WRF-Solar EPS due to the loss of sharpness, significantly increases its reliability, resulting in an overall improved ensemble system.
Finally, a test case involving an episode with a wide area of high cloudiness and very low GHI was examined. It has been shown that the recently introduced algorithm of correction for rare events is of paramount importance to obtain the lowest values of GHI from the WRF-Solar EPS AnEn, qualitatively consistent with those observed from the NSRDB.
Author Contributions
Conceptualization, S.A., P.A.J., J.-H.K. and J.D.; methodology, S.A., P.A.J., J.-H.K. and J.D.; software, S.A., P.A.J., J.-H.K. and J.D.; validation, S.A., P.A.J., J.-H.K. and J.D.; formal analysis, S.A. and J.-H.K.; investigation, S.A., P.A.J., J.-H.K. and J.D.; resources, S.A. and P.A.J.; data curation, J.-H.K. and J.Y.; writing—original draft preparation, S.A.; writing—review and editing, S.A., P.A.J., J.-H.K. and J.Y.; visualization, S.A. and J.-H.K.; supervision, S.A. and P.A.J.; project administration, P.A.J.; funding acquisition, P.A.J. and M.S.; All authors have read and agreed to the published version of the manuscript.
Funding
This work was authored in part by the National Renewable Energy Laboratory, operated by Alliance for Sustainable Energy, LLC, for the U.S. Department of Energy (DOE) under Contract No. DE-AC36-08GO28308. Funding provided by the U.S. Department of Energy Office of Energy Efficiency and Renewable Energy Solar Energy Technologies Office. The views expressed in the article do not necessarily represent the views of the DOE or the U.S. Government. The U.S. Government and the publisher, by accepting the article for publication, acknowledges that the U.S. Government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this work, or allow others to do so, for U.S. Government purposes. We would also like to acknowledge high-performance computing support from Cheyenne (https://doi.org/10.5065/D6RX99HX accessed on 2 February 2023) provided by NCAR’s Computational and Information Systems Laboratory, sponsored by the National Science Foundation. This material is based upon work supported by the National Center for Atmospheric Research, which is a major facility sponsored by the National Science Foundation under Cooperative Agreement No. 1852977.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In this section, the same metrics (bias, correlation, RMSE, spread/skill diagram, CRPS, reliability, CRPSPOT) presented for GHI are shown for DNI. As mentioned in the conclusion section, the same considerations drawn for GHI also hold for DNI.
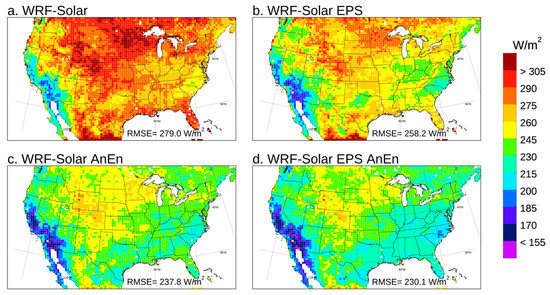
Figure A1.
Root mean squared error (RMSE) computed for DNI over the year 2018 for the forecast lead times from +24 to +48 h. The value in the legend at the bottom of each panel indicates the RMSE computed by pooling all the grid points and lead times together.
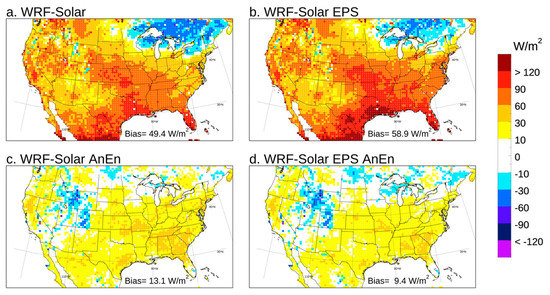
Figure A2.
Bias computed for DNI over the year 2018 for the forecast lead times from +24 to +48 h. The value in the legend at the bottom of each panel indicates the bias computed by pooling all the grid points and lead times together.
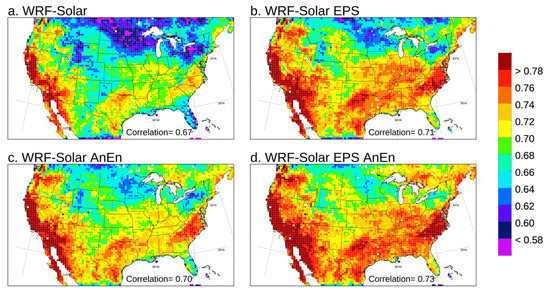
Figure A3.
Pearson correlation computed for DNI over the year 2018 for the forecast lead times from +24 to +48 h. The value in the legend at the bottom of each panel indicates the correlation computed by pooling all the grid points and lead times together.
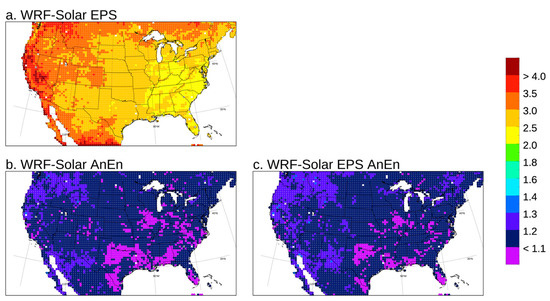
Figure A4.
RMSE/spread ratio computed for all the grid points for DNI by pooling the forecast lead times from +24 to +48 h and forecast runs for 2018 together.
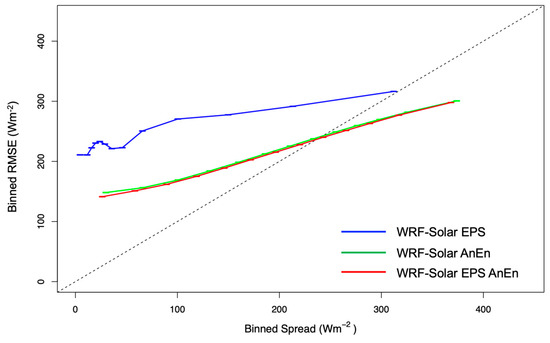
Figure A5.
Binned RMSE/spread diagrams are computed by pooling all the grid points for DNI forecasts, runs, and the forecast lead times from +24 to +48 h for 2018. The horizontal bars represent the 5–95% bootstrap confidence intervals of the spread for each considered bin.
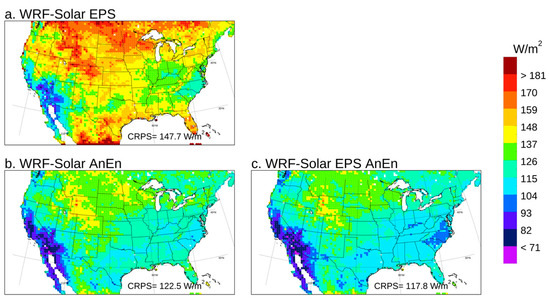
Figure A6.
Continuous ranked probability score (CRPS) map computed for DNI by pooling runs and the forecast lead times from +24 to +48 h for 2018 together.
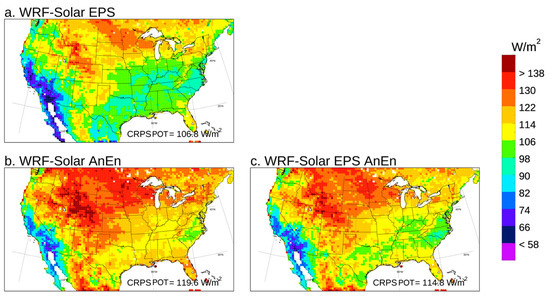
Figure A7.
Potential continuous ranked probability score (CRPSPOT) map computed for DNI pooling runs and the forecast lead times from +24 to +48 h for 2018 together.
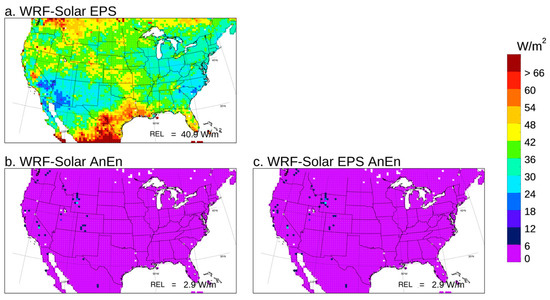
Figure A8.
Reliability (REL) map computed for DNI pooling runs and the forecast lead times from +24 to +48 h for 2018 together.
Appendix B
The continuous ranked probability score (CRPS) can be expressed as:
where is the cumulative distribution function (CDF) of the probabilistic forecast and is the CDF of the observation for the ith ensemble prediction/observation pair, and N is the number of available pairs. The CRPS reduces to the mean absolute error (MAE) if a deterministic (single-member) forecast is considered [64]. Like the MAE, a lower value of CRPS indicates better skill, with 0 as a perfect score. The CRPS has the same unit of measurement as the forecasted variable. Also, the CRPS can be obtained by integrating the Brier score [65] over all the possible threshold values [64] and it can be decomposed into three components: reliability (REL), resolution (RES), and uncertainty (UNC). The REL component measures the statistical consistency of the ensemble system (the lower, the better), that is, how well the forecasted probabilities match the observed frequencies. REL is closely connected to the rank histograms, which measure whether the frequency of the observations found in each ensemble bin is equal for all the bins [66]. The RES component measures how much better a system performs compared to a climatological forecast, where the climatological forecast is merely the single probability of an event as observed in the historical dataset. In general, the resolution attribute of a system reflects how well the different forecast frequency classes can separate the different observed frequencies from the climatological mean. The UNC component, which depends only on the observations, measures the variability of the observations reflecting the predictability associated with the available data set. More specifically, the CRPS can be expressed as CRPS = REL + CRPSPOT where CRPSPOT is the potential CRPS and can be defined as CRPSPOT = UNC − RES. The potential CRPS is the CRPS that could be obtained if a forecasting system becomes perfectly reliable (REL = 0). For the details about mathematical formulations of the three components, we direct the reader to [64].
References
- Mahoney, W.P.; Parks, K.; Wiener, G.; Liu, Y.; Myers, W.L.; Sun, J.; Delle Monache, L.; Hopson, T.; Johnson, D.; Haupt, S.E. A Wind Power Forecasting System to Optimize Grid Integration. IEEE Trans. Sustain. Energy 2012, 3, 670–682. [Google Scholar] [CrossRef]
- Haupt, S.E.; Kosović, B.; Jensen, T.; Lazo, J.K.; Lee, J.A.; Jiménez, P.A.; Cowie, J.; Wiener, G.; McCandless, T.C.; Rogers, M.; et al. Building the Sun4Cast System: Improvements in Solar Power Forecasting. Bull. Am. Meteorol. Soc. 2018, 99, 121–136. [Google Scholar] [CrossRef]
- Yang, D.; Alessandrini, S.; Antonanzas, J.; Antonanzas-Torres, F.; Badescu, V.; Beyer, H.G.; Blaga, R.; Boland, J.; Bright, J.M.; Coimbra, C.F.M.; et al. Verification of Deterministic Solar Forecasts. Sol. Energy 2020, 210, 20–37. [Google Scholar] [CrossRef]
- Sperati, S.; Alessandrini, S.; Pinson, P.; Kariniotakis, G. The “Weather Intelligence for Renewable Energies” Benchmarking Exercise on Short-Term Forecasting of Wind and Solar Power Generation. Energies 2015, 8, 9594–9619. [Google Scholar] [CrossRef]
- Giebel, G. The State-of-the-Art in Short-Term Prediction of Wind Power a Literature Overview, 2nd ed.; DOCUMENT TYPE Deliverable. 2019. Available online: https://www.osti.gov/etdeweb/servlets/purl/20675341 (accessed on 2 February 2023).
- Hong, T.A.O.; Member, S.; Fellow, P.P.; Zareipour, H.; Member, S. Energy Forecasting: A Review and Outlook. IEEE Open Access J. Power Energy 2020, 7, 376–388. [Google Scholar] [CrossRef]
- Marquis, M.; Wilczak, J.; Ahlstrom, M.; Sharp, J.; Stern, R.; Charles Smith, J.; Calvert, S. Forecasting the Wind to Reach Significant Penetration Levels of Wind Energy. Bull. Am. Meteorol. Soc. 2011, 92, 1159–1171. [Google Scholar] [CrossRef]
- Inman, R.H.; Pedro, H.T.C.; Coimbra, C.F.M. Solar Forecasting Methods for Renewable Energy Integration. Prog. Energy Combust. Sci. 2013, 39, 535–576. [Google Scholar] [CrossRef]
- Alessandrini, S.; Davò, F.; Sperati, S.; Benini, M.; Delle Monache, L. Comparison of the Economic Impact of Different Wind Power Forecast Systems for Producers. Adv. Sci. Res. 2014, 11, 49–53. [Google Scholar] [CrossRef]
- Zugno, M.; Pinson, P.; Onsson, T.J. Trading Wind Energy Based on Probabilistic Forecasts of Wind Generation and Market Quantities. Wind Energy 2012. [Google Scholar] [CrossRef]
- Roulston, M.S.; Kaplan, D.T.; Hardenberg, J.; Smith, L.A. Using Medium-Range Weather Forcasts to Improve the Value of Wind Energy Production. Renew Energy 2003, 28, 585–602. [Google Scholar] [CrossRef]
- Zugno, M.; Conejo, A.J. A Robust Optimization Approach to Energy and Reserve Dispatch in Electricity Markets. Eur. J. Oper. Res. 2015, 247, 659–671. [Google Scholar] [CrossRef]
- Carriere, T.; Kariniotakis, G. An Integrated Approach for Value-Oriented Energy Forecasting and Data-Driven Decision-Making Application to Renewable Energy Trading. IEEE Trans. Smart Grid 2019, 10, 6933–6944. [Google Scholar] [CrossRef]
- Ziehmann, C. Comparison of a Single-Model EPS with a Multi-Model Ensemble Consisting of a Few Operational Models Comparison of a Single-Model EPS with a Multi-Model Ensemble Consisting of a Few Operational Models, Tellus A: Dynamic Meteorology and Oceanography Comparison of a Single-Model EPS with a Multi-Model Ensemble Consisting of a Few Operational Models. T Ellus 2000, 52, 280–299. [Google Scholar] [CrossRef]
- Zemouri, N.; Bouzgou, H.; Gueymard, C.A. Multimodel Ensemble Approach for Hourly Global Solar Irradiation Forecasting. Eur. Phys. J. Plus 2019, 134, 594. [Google Scholar] [CrossRef]
- Toth, Z.; Kalnay, E. Ensemble Forecasting at NMC: The Generation of Perturbations. Bull. Am. Meteorol. Soc. 1993, 74, 2317–2330. [Google Scholar] [CrossRef]
- Molteni, F.; Buizza, R.; Palmer, T.N.; Petroliagis, T. The ECMWF Ensemble Prediction System: Methodology and Validation. Q. J. R. Meteorol. Soc. 1996, 122, 73–119. [Google Scholar] [CrossRef]
- Stensrud, D.J.; Bao, J.W.; Warner, T.T. Using Initial Condition and Model Physics Perturbations in Short-Range Ensemble Simulations of Mesoscale Convective Systems. Mon. Weather Rev. 2000, 128, 2077–2107. [Google Scholar] [CrossRef]
- Buizza, R.; Milleer, M.; Palmer, T.N. Stochastic Representation of Model Uncertainties in the ECMWF Ensemble Prediction System. Q. J. R. Meteorol. Soc. 1999, 125, 2887–2908. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S. Probabilistic Quantitative Precipitation Forecasts Based on Reforecast Analogs: Theory and Application. Mon. Weather Rev. 2006, 134, 3209–3229. [Google Scholar] [CrossRef]
- Alessandrini, S.; Delle Monache, L.; Sperati, S.; Cervone, G. An Analog Ensemble for Short-Term Probabilistic Solar Power Forecast. Appl. Energy 2015, 157, 95–110. [Google Scholar] [CrossRef]
- Delle Monache, L.; Eckel, F.A.; Rife, D.L.; Nagarajan, B.; Searight, K. Probabilistic Weather Prediction with an Analog Ensemble. Mon. Weather Rev. 2013, 141, 3498–3516. [Google Scholar] [CrossRef]
- Bremnes, J.B. Probabilistic Wind Power Forecasts Using Local Quantile Regression. Wind Energy 2004, 7, 47–54. [Google Scholar] [CrossRef]
- Junk, C.; Monache, L.D.; Alessandrini, S. Analog-Based Ensemble Model Output Statistics. Mon. Weather Rev. 2015, 143, 2909–2917. [Google Scholar] [CrossRef]
- Hamill, T.M.; Scheuerer, M.; Bates, G.T. Analog Probabilistic Precipitation Forecasts Using GEFS Reforecasts and Climatology-Calibrated Precipitation Analyses. Mon. Weather Rev. 2015, 143, 3300–3309. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S. Ensemble Calibration of 500-HPa Geopotential Height and 850-HPa and 2-m Temperatures Using Reforecasts. Mon. Weather Rev. 2007, 135, 3273–3280. [Google Scholar] [CrossRef]
- Odak Plenković, I.; Schicker, I.; Dabernig, M.; Horvath, K.; Keresturi, E. Analog-Based Post-Processing of the ALADIN-LAEF Ensemble Predictions in Complex Terrain. Q. J. R. Meteorol. Soc. 2020, 146, 1842–1860. [Google Scholar] [CrossRef]
- Abuella, M.; Chowdhury, B. Hourly Probabilistic Forecasting of Solar Power. In Proceedings of the 2017 North American Power Symposium, NAPS, Morgantown, WV, USA, 17–19 September 2017. [Google Scholar]
- Cervone, G.; Clemente-Harding, L.; Alessandrini, S.; Delle Monache, L. Short-Term Photovoltaic Power Forecasting Using Artificial Neural Networks and an Analog Ensemble. Renew Energy 2017, 108, 274–286. [Google Scholar] [CrossRef]
- Aryaputera, A.W.; Verbois, H.; Walsh, W.M. Probabilistic Accumulated Irradiance Forecast for Singapore Using Ensemble Techniques. In Proceedings of the Conference Record of the IEEE Photovoltaic Specialists Conference, Portland, OR, USA, 5–10 June 2016. [Google Scholar]
- Davò, F.; Alessandrini, S.; Sperati, S.; Delle Monache, L.; Airoldi, D.; Vespucci, M.T. Post-Processing Techniques and Principal Component Analysis for Regional Wind Power and Solar Irradiance Forecasting. Sol. Energy 2016, 134, 327–338. [Google Scholar] [CrossRef]
- Verbois, H.; Rusydi, A.; Thiery, A. Probabilistic Forecasting of Day-Ahead Solar Irradiance Using Quantile Gradient Boosting. Sol. Energy 2018, 173, 313–327. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Lu, S.; Hamann, H.F.; Hodge, B.M.; Lehman, B. A Solar Time Based Analog Ensemble Method for Regional Solar Power Forecasting. IEEE Trans. Sustain. Energy 2019, 10, 268–279. [Google Scholar] [CrossRef]
- Yang, D.; Alessandrini, S. An Ultra-Fast Way of Searching Weather Analogs for Renewable Energy Forecasting. Sol. Energy 2019, 185, 255–261. [Google Scholar] [CrossRef]
- Yang, D. Ultra-Fast Analog Ensemble Using Kd-Tree. J. Renew. Sustain. Energy 2019, 11, 053703. [Google Scholar] [CrossRef]
- Powers, J.G.; Klemp, J.B.; Skamarock, W.C.; Davis, C.A.; Dudhia, J.; Gill, D.O.; Coen, J.L.; Gochis, D.J.; Ahmadov, R.; Peckham, S.E.; et al. The Weather Research and Forecasting Model: Overview, System Efforts, and Future Directions. Bull. Am. Meteorol. Soc. 2017, 98, 1717–1737. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4; NCAR Technical Notes; NCAR: Boulder, CO, USA, 2019; Volume 145, p. 550. [Google Scholar]
- Jimenez, P.A.; Hacker, J.P.; Dudhia, J.; Haupt, S.E.; Ruiz-Arias, J.A.; Gueymard, C.A.; Thompson, G.; Eidhammer, T.; Deng, A. WRF-Solar: Description and Clear-Sky Assessment of an Augmented NWP Model for Solar Power Prediction. Bull. Am. Meteorol. Soc. 2016, 97, 1249–1264. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Alessandrini, S.; Haupt, S.E.; Deng, A.; Kosovic, B.; Lee, J.A.; Monache, L.D. The Role of Unresolved Clouds on Short-Range Global Horizontal Irradiance Predictability. Mon. Weather Rev. 2016, 144, 3099–3107. [Google Scholar] [CrossRef]
- Kim, J.H.; Jimenez Munoz, P.; Sengupta, M.; Yang, J.; Dudhia, J.; Alessandrini, S.; Xie, Y. The WRF-Solar Ensemble Prediction System to Provide Solar Irradiance Probabilistic Forecasts. IEEE J. Photovolt. 2022, 12, 141–144. [Google Scholar] [CrossRef]
- Yang, J.; Sengupta, M.; Jiménez, P.A.; Kim, J.H.; Xie, Y. Evaluating WRF-Solar EPS Cloud Mask Forecast Using the NSRDB. Sol. Energy 2022, 243, 348–360. [Google Scholar] [CrossRef]
- Kim, J.-H.; Jimenez, P.A.; Sengupta, M.; Yang, J.; Dudhia, J.; Alessandrini, S.; Xie, Y. The WRF-Solar Ensemble Prediction System To Provide Solar Irradiance Probabilistic Forecasts. In Proceedings of the 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), Fort Lauderdale, FL, USA, 20–25 June 2021; pp. 1233–1235. [Google Scholar] [CrossRef]
- Yang, J.; Kim, J.H.; Jiménez, P.A.; Sengupta, M.; Dudhia, J.; Xie, Y.; Golnas, A.; Giering, R. An Efficient Method to Identify Uncertainties of WRF-Solar Variables in Forecasting Solar Irradiance Using a Tangent Linear Sensitivity Analysis. Sol. Energy 2021, 220, 509–522. [Google Scholar] [CrossRef]
- Sengupta, M.; Xie, Y.; Lopez, A.; Habte, A.; Maclaurin, G.; Shelby, J. The National Solar Radiation Data Base (NSRDB). Renew. Sustain. Energy Rev. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Yang, J.; Kim, J.H.; Sengupta, M.; Dudhia, J. Assessing the WRF-Solar Model Performance Using Satellite-Derived Irradiance from the National Solar Radiation Database. J. Appl. Meteorol. Clim. 2022, 61, 129–142. [Google Scholar] [CrossRef]
- Sperati, S.; Alessandrini, S.; Delle Monache, L. Gridded Probabilistic Weather Forecasts with an Analog Ensemble. Q. J. R. Meteorol. Soc. 2017, 143, 2874–2885. [Google Scholar] [CrossRef]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; Thompson, G.; Lee, J.A.; Brummet, T. Improving the Cloud Initialization in WRF-Solar with Enhanced Short-Range Forecasting Functionality: The MAD-WRF Model. Sol. Energy 2022, 239, 221–233. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. Development of an Improved Turbulence Closure Model for the Atmospheric Boundary Layer. J. Meteorol. Soc. Jpn. Ser. II 2009, 87, 895–912. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an Advanced Land Surface-Hydrology Model with the Penn State-NCAR MM5 Modeling System. Part II: Preliminary Model Validation. Mon. Weather. Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Deng, A.; Seaman, N.L.; Kain, J.S. A Shallow-Convection Parameterization for Mesoscale Models. Part I: Submodel Description and Preliminary Applications. J. Atmos. Sci. 2003, 60, 34–56. [Google Scholar] [CrossRef]
- Xie, Y.; Sengupta, M.; Dudhia, J. A Fast All-Sky Radiation Model for Solar Applications (FARMS): Algorithm and Performance Evaluation. Sol. Energy 2016, 135, 435–445. [Google Scholar] [CrossRef]
- Buster, G.; Bannister, M.; Habte, A.; Hettinger, D.; Maclaurin, G.; Rossol, M.; Sengupta, M.; Xie, Y. Physics-Guided Machine Learning for Improved Accuracy of the National Solar Radiation Database. Sol. Energy 2022, 232, 483–492. [Google Scholar] [CrossRef]
- Buster, G.; Rossol, M.; Maclaurin, G.; Xie, Y.; Sengupta, M. A Physical Downscaling Algorithm for the Generation of High-Resolution Spatiotemporal Solar Irradiance Data. Sol. Energy 2021, 216, 508–517. [Google Scholar] [CrossRef]
- Habte, A.; Sengupta, M.; Gueymard, C.; Golnas, A.; Xie, Y. Long-Term Spatial and Temporal Solar Resource Variability over America Using the NSRDB Version 3 (1998–2017). Renew. Sustain. Energy Rev. 2020, 134, 110285. [Google Scholar] [CrossRef]
- Alessandrini, S.; Sperati, S.; Delle Monache, L. Improving the Analog Ensemble Wind Speed Forecasts for Rare Events. Mon. Weather Rev. 2019, 147, 2677–2692. [Google Scholar] [CrossRef]
- Gneiting, T. Making and Evaluating Point Forecasts. J. Am. Stat. Assoc. 2012, 106, 746–762. [Google Scholar] [CrossRef]
- Alessandrini, S. Predicting Rare Events of Solar Power Production with the Analog Ensemble. Sol. Energy 2022, 231, 72–77. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Fortin, V.; Abaza, M.; Anctil, F.; Turcotte, R. Corrigendum to Why Should Ensemble Spread Match the RMSE of the Ensemble Mean? J. Hydrometeor. 2014, 15, 1708–1713. [Google Scholar] [CrossRef]
- Hopson, T.M. Assessing the Ensemble Spread-Error Relationship. Mon. Weather Rev. 2014, 142, 1125–1142. [Google Scholar] [CrossRef]
- Brown, T.A. Admissible Scoring Systems for Continuous Distributions; The Rand Corporation: Santa Monica, CA, USA, 1974. [Google Scholar]
- Carney, M.; Cunningham, P. Evaluating Density Forecasting Models. 2006, pp. 1–12. Available online: https://www.scss.tcd.ie/publications/tech-reports/reports.06/TCD-CS-2006-21.pdf (accessed on 2 February 2023).
- Hersbach, H. Decomposition of the Continuous Ranked Probability Score for Ensemble Prediction Systems. Weather Forecast. 2000. [Google Scholar] [CrossRef]
- Brier, G.W. Verification of forecasts expressed in terms of probability. Mon. Weather Rev. 1950, 78. [Google Scholar] [CrossRef]
- Talagrand, O.; Vautard, R.; Strauss, B. Evaluation of Probabilistic Prediction Systems. Proc. ECMWF Workshop Predict. 1997, 1, 25. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).