Emissions and CO₂ Concentration—An Evidence Based Approach

Abstract

The relation between CO₂ emissions and atmospheric CO₂ concentration has traditionally been treated with more or less complex models with several boxes. Our approach is motivated by the question of how much CO₂ must necessarily be absorbed by sinks. This is determined by accepted measurements and the global carbon budget. Observations lead to the model assumption that carbon sinks, similar to oceans or the biosphere, are linearly dependent on CO₂ concentration on a decadal scale. In particular, this implies the falsifiable hypothesis that oceanic and biological CO₂ buffers have not significantly changed in the past 70 years and are not saturated in the foreseeable future. A statistical model with two parameters is built from the global carbon budget and two testable assumptions. This model explains the relation between CO₂ emission and historical CO₂ concentration data very well. The model gives estimates of the natural emissions, the pre-industrial CO₂ equilibrium concentration levels, the half-life time of an emission pulse, and the future CO₂ concentration level from a given emission scenario. It is validated by an ex-post forecast of the last 20 years. The important result is that, with the stated polices emission scenario of the International Energy Agency (IEA), the future CO₂ concentrations will not rise above 475 ppm. The model is compared with the carbon module of the Bern model, mapping their complex impulse response functions (IRFs) to a single time variant absorption parameter.

1. Introduction—A New Way of Looking at the Problem

Climate science is usually concerned about the question “How much CO${}_2$ remains in the atmosphere?”, given the anthropogenic emissions and the limited capability of oceans and biosphere to absorb the surplus CO${}_2$ concentration [1,2,3,4] This has led to conclusions of the kind that a certain increasing part of anthropogenic emissions will remain in the atmosphere forever. The frequently used notion of “airborne fraction” [5,6], which is the part of anthropogenic emissions remaining in the atmosphere, seems to suggest this. The Bern model explicitly includes a term that represents the fraction of the emissions remaining in the atmosphere forever [4].

We change the focus of attention by posing the logically equivalent question “How much CO${}_2$ does not remain in the atmosphere?”. Why is this so different? The amount of CO₂ that does not remain in the atmosphere can be calculated from direct measurements. We do not have to discuss each absorption mechanism from the atmosphere into oceans or plants. From the known global concentration changes and the known global emissions, we have a good estimate of the sum of actual yearly absorptions. These are related to the CO₂ concentration, motivating the guiding hypothesis for a linear model of absorption. It turns out that we do not need to know the actual coefficients of the individual absorption mechanisms—it is sufficient to assume their linear dependence on the current CO${}_2$ concentration.

Additionally, by changing the focus of attention from “how much remains in the atmosphere” to “how much is absorbed annually”, the formally equivalent estimation equations become much better conditioned. Both the known previous investigations based on a linear absorption model [7,8] had computational stability problems, which were noticeable in the large error bars of the resulting equilibrium concentration. Although the publications omit the computation of error bars, they can be reproduced from their data and equations. A third paper with a linear absorption model [9] uses apparently similar equations, but separates the estimation of the oceanic and biosphere absorption constants from the contribution of the anthropogenic emissions, which leads to the strange phenomenon that their main equation has no remaining free parameters to account for emission changes explicitly. We will discuss their approach in the appendix (Appendix B).

Overview of Methods

As a first step, we will derive the effective absorption from CO${}_2$ concentration growth and emissions based on the global carbon budget (Section 2.1). The plausibility and testability of the two model hypotheses are discussed (Section 2.3 and Section 2.4). Relating effective absorption to CO${}_2$ concentration by means of these hypotheses leads us to a statistical absorption model that can be estimated by ordinary least squares, providing robust parameter and error estimates (Section 2.5). Furthermore, model variations with temperature dependency or indirect temperature dependency via CO${}_2$ proxy are explored (Section 2.5.1). The model, which includes CO${}_2$ concentration at two different times, is applied to recursively predict future CO${}_2$ concentrations from current concentration and future emissions. Predicting the concentration of the last 20 years from prior data validates the model and shows its predictive quality (Section 2.5.4). This recursion is also applied to calculate the carbon pulse response and the CO${}_2$ adjustment time (Section 2.5.3 and Appendix A.1.1). A time-dependent generalization of the model is shown to be equivalent to the Bern model. This is proven in the appendix (Appendix A). While temperature prediction is not the main focus of the paper, a measurement based CO${}_2$ concentration proxy is estimated from the temperature and CO${}_2$ concentration data of the last 170 years as an upper bound temperature dependence on CO${}_2$ (Section 2.3.2). This allows for a maximum temperature estimate of future CO${}_2$ concentrations (Section 3.1).

2. The Absorption Model

2.1. Mass Conservation

From the Global Carbon Project [10], we obtain the emission and concentration data. A global mass balance representation of the yearly atmospheric CO${}_2$ flow is created, as it has been performed in [11], where they prove that the CO${}_2$ adjustment time is much larger than the CO${}_2$ residence time. The analysis of the airborne fraction and sink rate of anthropogenic emissions by [6] is also based on this global carbon budget (their Equation (1)).

For our purposes the components of the global carbon budget equation are

• C${}_i$ the CO${}_2$ concentration of the atmosphere at the end of year i,
• $E_i$ the global emissions of human origin during year i,
• $L_i$ the global land use net emissions during year i,
• $N_i$ the global natural net emissions during year i,
• $S_i$ other special causes of emissions, such as El Nino, volcanos, etc.,
• $A_i$ the global net absorption of CO${}_2$ during year i into the oceans and biosphere ($0<=i<n$):

$$\begin{array}{ccc}\hfill C_i& =& C_{i-1}+E{}_i+L_i+S_i+N_i-A{}_i\hfill \end{array}$$

(1)

Without explicit external information, $S_i$ cannot be discriminated from $L_i$ or $N_i$. Therefore, we set $S_i$ to 0 and include all inferred special causes in the unknown N${}_i$ in this investigation. With $S_i=0,$ the equation becomes

$$\begin{array}{ccc}\hfill E_i+L_i-(C_i-C_{i-1})& =& A_i-N_i\hfill \end{array}$$

(2)

This is not a model, but the formulation of the necessary mass conservation as seen from the atmosphere, similar to a bank account with cumulative yearly deposits and withdrawals, not directly dealing with the daily ups and downs or with the exact nature of the earning and spending processes. As a matter of fact, Equation (2) must be fulfilled at all time scales.

For consistency, all quantities have to be converted to the same unit (1 ppm = 2.124 GtC, 1 GtC = 3.664 Gt CO${}_2$ [10]). Here, all calculations are performed with the unit “ppm”. All CO${}_2$-related data, emissions, land use change, and CO${}_2$ concentration growth are from the Global Carbon Budget 2021, covering the years 1850–2020. Land use change data are subject to considerable uncertainty, with an error range of $\pm 0.4$ ppm.

We assume a value for land use change emission that is 0.2 ppm lower than the published mean value, as discussed further below. This is well within the error range and, therefore, justifiable.

Figure 1 shows that the total emissions ($E_i+L_i$, blue) come to exceed the yearly CO${}_2$ concentration growth ($C_i-C_{i-1}$, green), indicating that we have an increasingly effective absorption ($A_i-N_i$, red ) with growing CO${}_2$ concentration.

Another benefit of displaying these raw data is that, before 1900, the anthropogenic emissions were considerably smaller than other variations, such as land use change. In fact, there are roughly four historical phases:

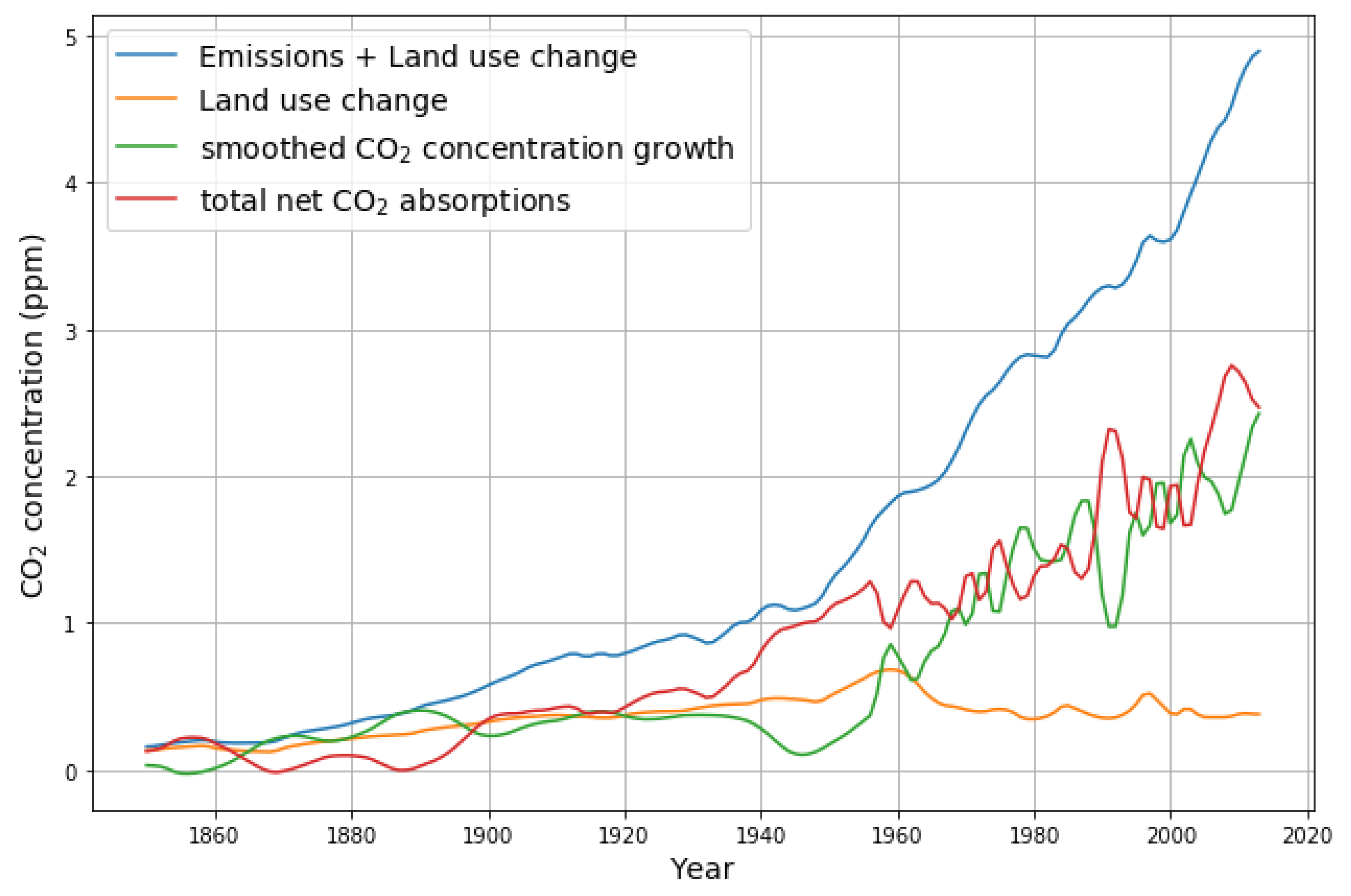
• The phase before 1900, where explicit emissions are smaller than implicit ones, due to land use change; however, there is a small, but increasing, CO${}_2$ concentration growth.
• The phase between 1900 and 1950 with growing emissions, but approximately constant CO${}_2$ concentration growth and slightly increasing land use change.
• The phase from 1950 to 2010 with growing emissions and growing concentration growth.
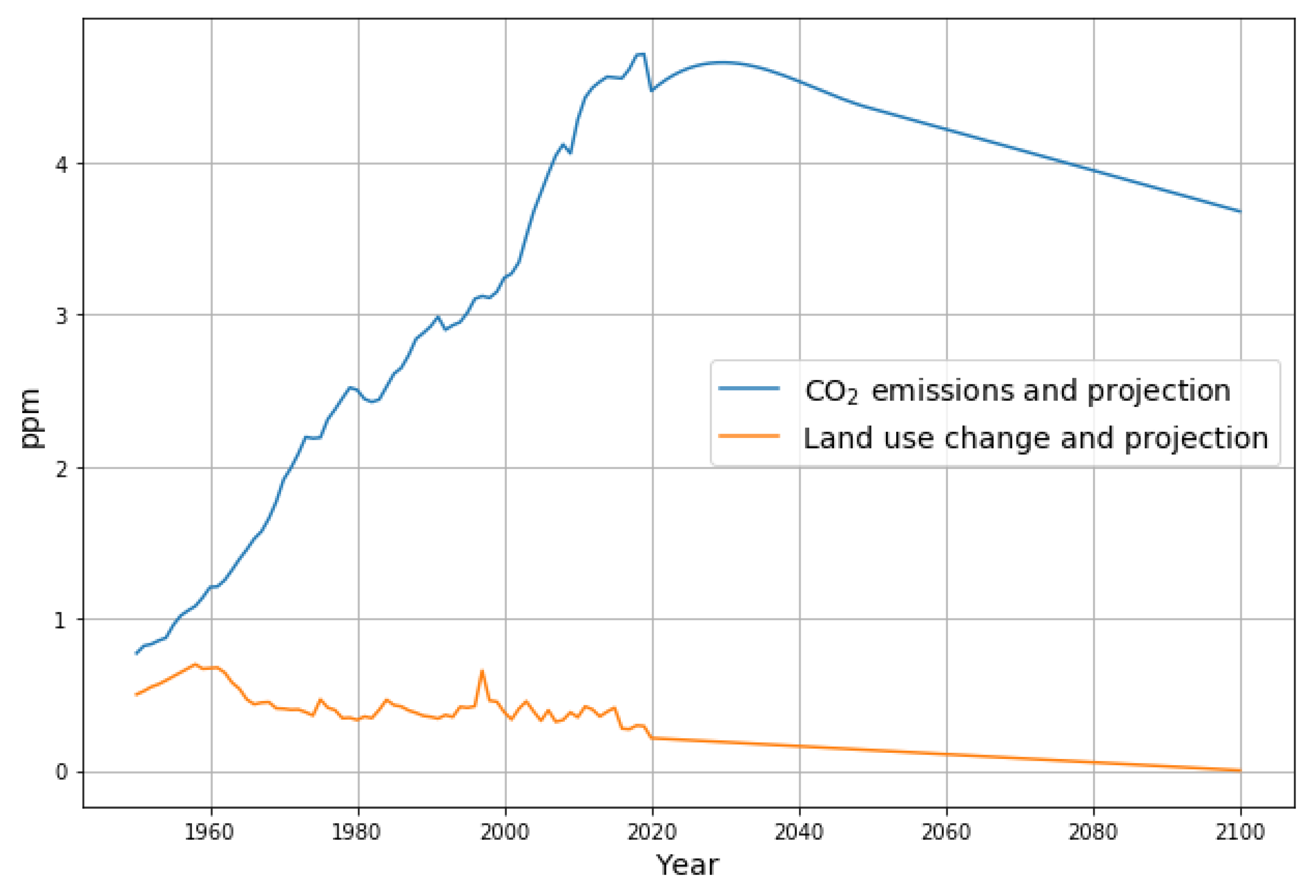
• Recent publications indicate that emissions have remained approximately constant since 2010 [12] and are expected to remain approximately constant for the forseeable future [13] (their Figure 2, stated policies scenario). The challenge is to estimate reasonable projections of CO${}_2$ concentration based on these emission assumptions.

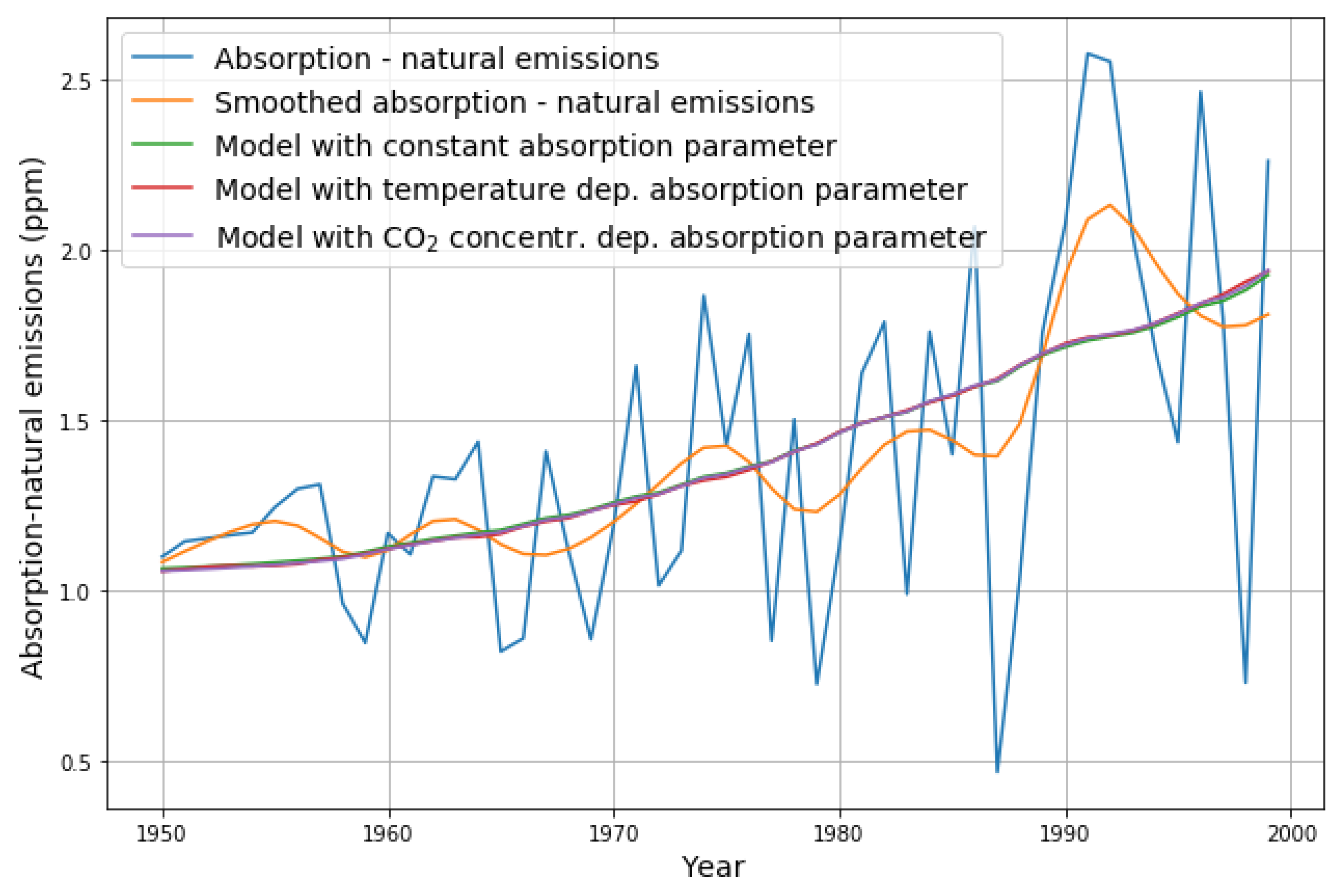
2.2. Exploratory Analysis

As a first exploratory analysis of these data, the scatter plot in Figure 2 relates the effective CO${}_2$ absorption to the CO${}_2$ concentration.

Qualitatively, we see a long-term linear dependence of the effective absorption on the atmospheric CO${}_2$ concentration with significant short-term deviations, where the effective zero-absorption line is crossed at approx. 280 ppm. This is considered to be the pre-industrial equilibrium CO${}_2$ concentration, where natural yearly emissions are balanced by the yearly absorptions. The average yearly absorption is approx. 2.5% of the CO${}_2$ concentration exceeding 280 ppm.

While the correlation coefficient of 0.97 is very high, there are clear non-random deviations from an ideal linear behaviour. With the large uncertainty of the land use change and contingent effects, such as volcano eruptions and influences such as ENSO (El Nino Southern Oscillation), it is not surprising that there are systematic deviations from a perfect line [8].

Regarding the predictions of future CO${}_2$ concentration, the key question is whether the deviations are averaging out or whether there is a systematic saturation trend that is limiting the absorption of CO${}_2$. Some climate researchers claim that the absorption will decline [14], but there are other papers providing evidence of increasing absorption [15].

We can see from these data that a reliable estimate of the historical equilibrium concentration requires the whole data range. An estimation based on all data above 310 ppm (year 1950) results in a smaller equilibrium value of 245 ppm.

Starting from the mass conservation Equation (2), above, on the basis of the preceding considerations, we state two hypotheses, from which the actual model is derived:

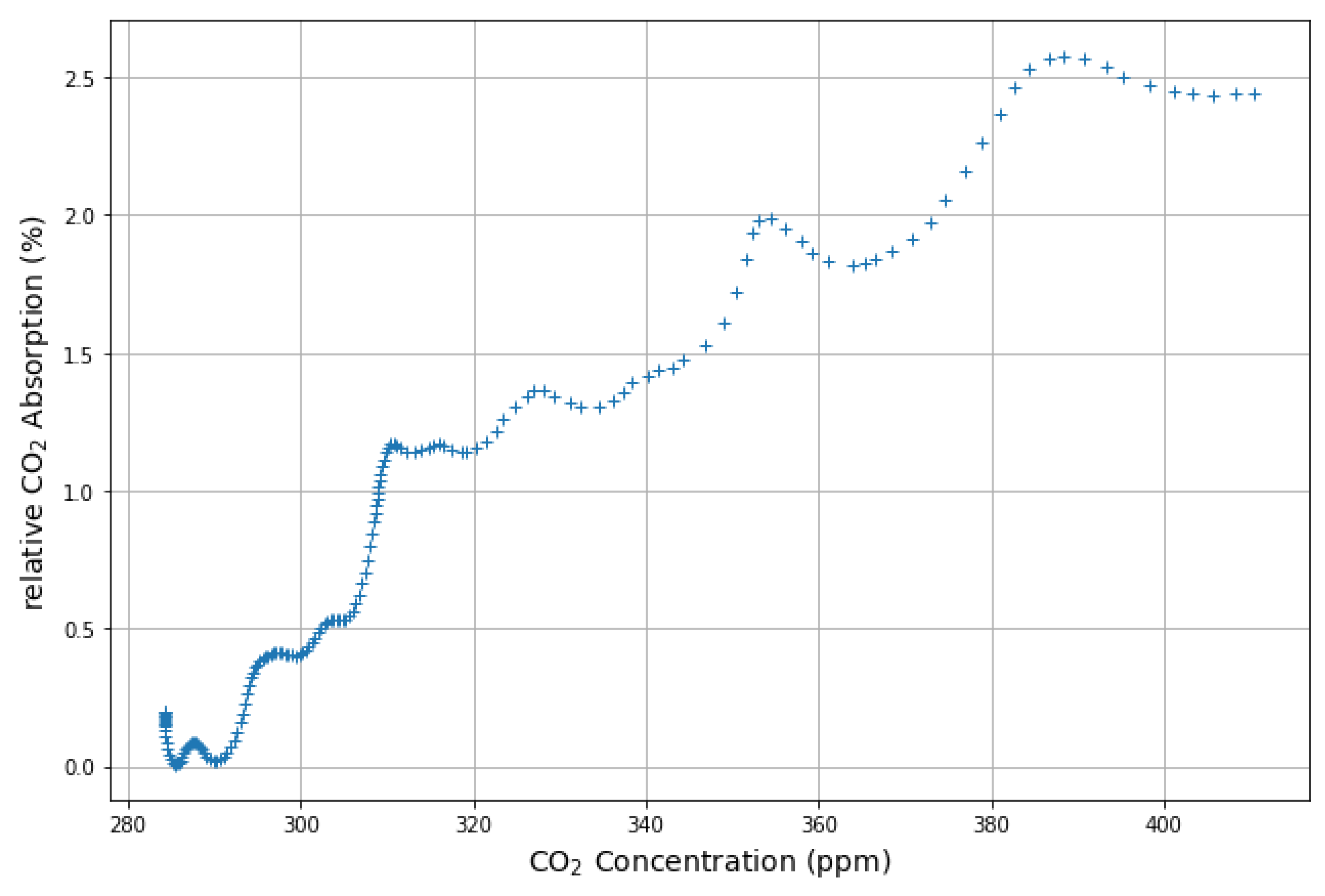
2.3. Hypothesis 1: The Absorption A${}_i$ Is Proportional to Previous CO${}_2$ Concentration

Formally this is

$$\begin{array}{ccc}\hfill A_i& =& a·C{}_{i-1}\hfill \end{array}$$

(3)

The physical justification for this assumption is the fact that the partial pressure of CO${}_2$, which is relevant for absorption processes, increases in proportion to concentration. It is also known that C${}_3$ plants, representing the majority of all plants, have a linear absorption property. The absorption property of C${}_4$ plants is nearly flat, but also linear in the range of 280–560 ppm, resulting in a linear behaviour when averaging over all plants. Halparin [7] analysed the different processes of gas transport into the ocean, with the conclusion that all relevant processes can be linearised (his Equation (14)):

• Net primary production of plants,
• Phytoplankton production, a smaller effect of dead biomass sinking to large depths of the ocean,
• Gas exchange with the deep ocean.

Assuming that there are different absorption constants for oceanic (a${}_{Ocean}$), phytoplankton (a${}_{Phytoplankton}$), and biospheric absorption (a${}_{Biosphere}$), under the linearity assumption, they can be added to a single constant a:

$$\begin{array}{ccc}\hfill a& =& a_{Ocean}+a_{Phytoplankton}+a_{Biosphere}\hfill \end{array}$$

(4)

Both the oceanic and biospheric processes may consist of multiple sub-processes, e.g., the photosynthesis of C${}_3$ plants has a much larger proportionality constant to that of C${}_4$ plants in the relevant CO${}_2$ concentration range of 280.. 560 ppm. As long as linearity holds, the net absorption constant is reflected by the sum of all elementary absorption constants.

This is a radical simplification of the box-diffusion model [16] referred to in [1]. Instead of assuming separate boxes for the mixed layer and for the biosphere, we assume a one-dimensional diffusion process between the atmosphere, ocean, and biosphere, with a single diffusion constant, making no explicit assumptions about the properties of the mixed layer nor the mechanism of the absorption in the biosphere. The advantage of this model is that we do not have to make any speculative assumptions about numerous possible model parameters, some of which are quite arbitrary (e.g., the thickness of the mixed layer), but instead, restrict the whole model to a single absorption parameter and an additive constant, both of which are estimated from measured data. While we do not know the contributing components, we can measure their total effect over time.

The authors of the Bern model claim that the “net primary production of the land biosphere and the surface ocean carbon uptake depend on atmospheric CO${}_2$ and surface temperature in a nonlinear way” [4] by assuming a superposition of four absorption processes. This statement contradicts our assumption of a single absorption process. We will show in the appendix that the impulse response functions of the Bern model ([4], their Equation (21)), can be mapped into the form of our model with a time varying absorption parameter, a (Appendix A). Statistical tests will decide if there is a need to actually introduce this time dependence or whether it is more appropriate to assume a constant absorption parameter, making relative absorption a linear function of CO${}_2$ concentration. Any deviations from the validity of a linear model will show up in the residual error. This gives our model a method of intrinsic validation, and the model can be extended when required.

2.3.1. Temperature Dependence of the Absorption Parameter

We have to consider the possibility that the absorption parameter, a, depends on temperature. Investigations of ice core data clearly indicate a temperature dependency of CO${}_2$ concentration [17]. The open question is whether there is a measurable dependency during the time scale and the temperature scale of our investigation. We will hypothetically test the temperature dependence of absorption parameter a with a linear dependency on sea surface temperature anomaly T with the HadSST2 temperature dataset T${}_i$ [18]. The linear dependence of the absorption parameter on the temperature anomaly is assumed, as in the Bern model [4]:

$$a_i=a_0+a_1·T_i$$

(5)

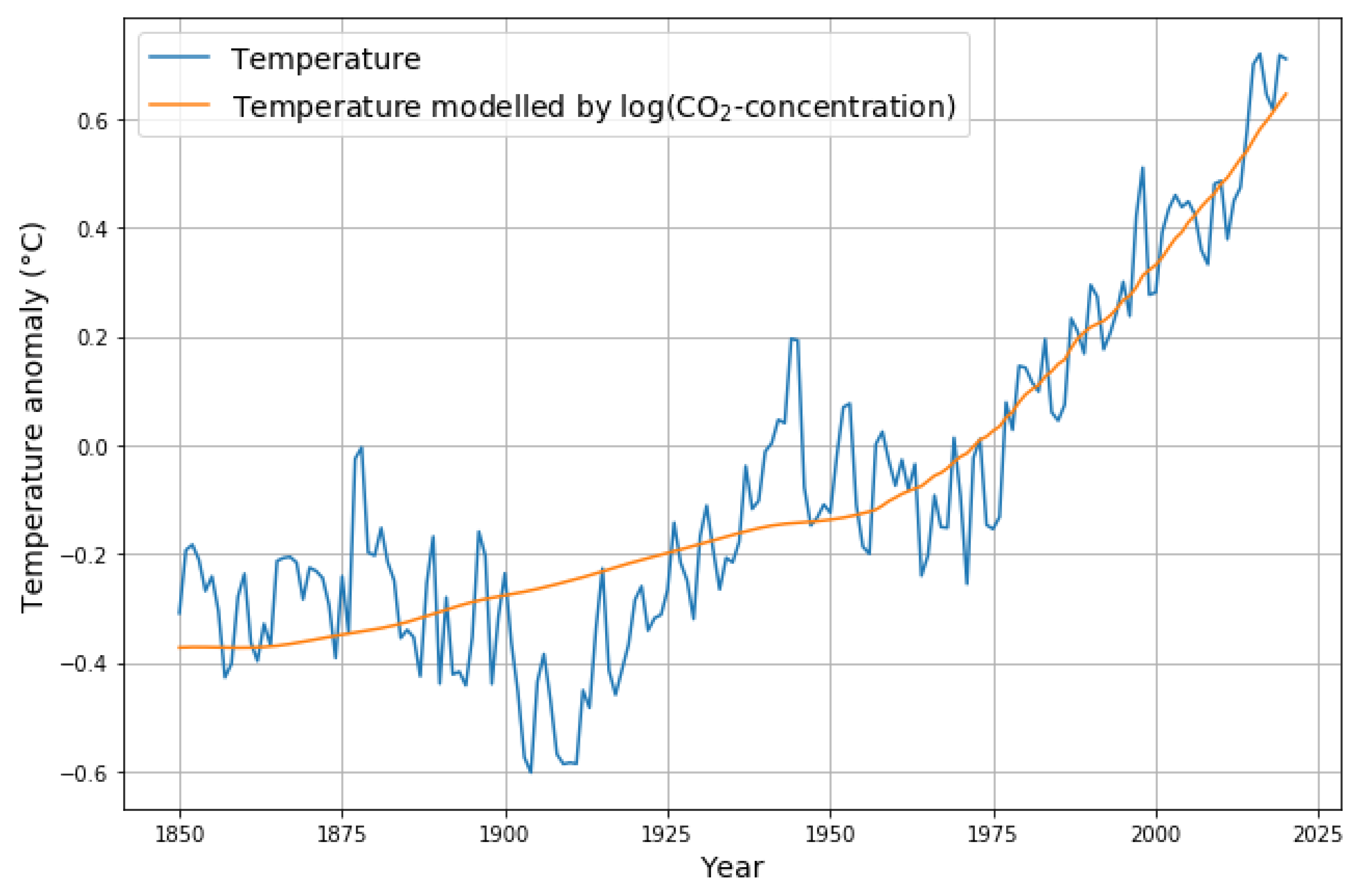
2.3.2. CO${}_2$ Concentration as a Hypothetical Proxy for Temperature

When we make predictions with hypothetical future CO${}_2$ emissions, we do not know the future temperatures. Without diving into the problematic discussion about the degree, how strong the influence of CO${}_2$ concentration is on temperature [19], we assume the “worst case” of full predictability of temperature effects by CO${}_2$ concentration (Figure 3).

Without making any assumptions about C${}_{i-1}\to$T${}_i$ causality, the estimated functional dependence of the temperature proxy from the regression on CO${}_2$ concentration was found to be

$$T_i^{proxy}=-16.0+2.77·ln\left(C_{i-1}\right)$$

(6)

We are aware that this is a very incomplete model. It ignores the obvious, significant, trend-reversing deviations between 1900 and 1975, and it also ignores the dominant contribution of cloud albedo reduction to global warming [20], whereby 80% of recent warming is caused by albedo reduction and only 20% by increase of CO${}_2$ concentration. Nevertheless, the proxy is still a suitable tool for estimating an upper bound of temperature dependence on CO${}_2$ concentration. Based on measured data, it avoids speculations and discussions about hypothetical feedback factors of CO${}_2$ sensitivity.

2.3.3. Corollary: Carbon Sinks Are Not Expected to Be Saturated in the Near Future

This is related to, and is a consequence of, the linearity assumption. Much of the debate about carbon sinks is concerned with numerous details about the possible saturation of various “boxes” in the models [21]. There are strong reasons to consider the atmosphere and the mixed layer, i.e., the top 75 m of the ocean as a single “box”, which exchanges gases with the deep ocean and the biosphere [7]. Due to the fact that the deep ocean contains more than 50 times the CO${}_2$ of the atmosphere, or 4000 times the yearly global emissions, this means that the whole atmospheric content is just about 2% of the ocean content. Therefore, we do not expect this huge “box” to be saturated any time soon.

There are four indications supporting the assumption that the up-taking reservoirs are not saturated:

(1)

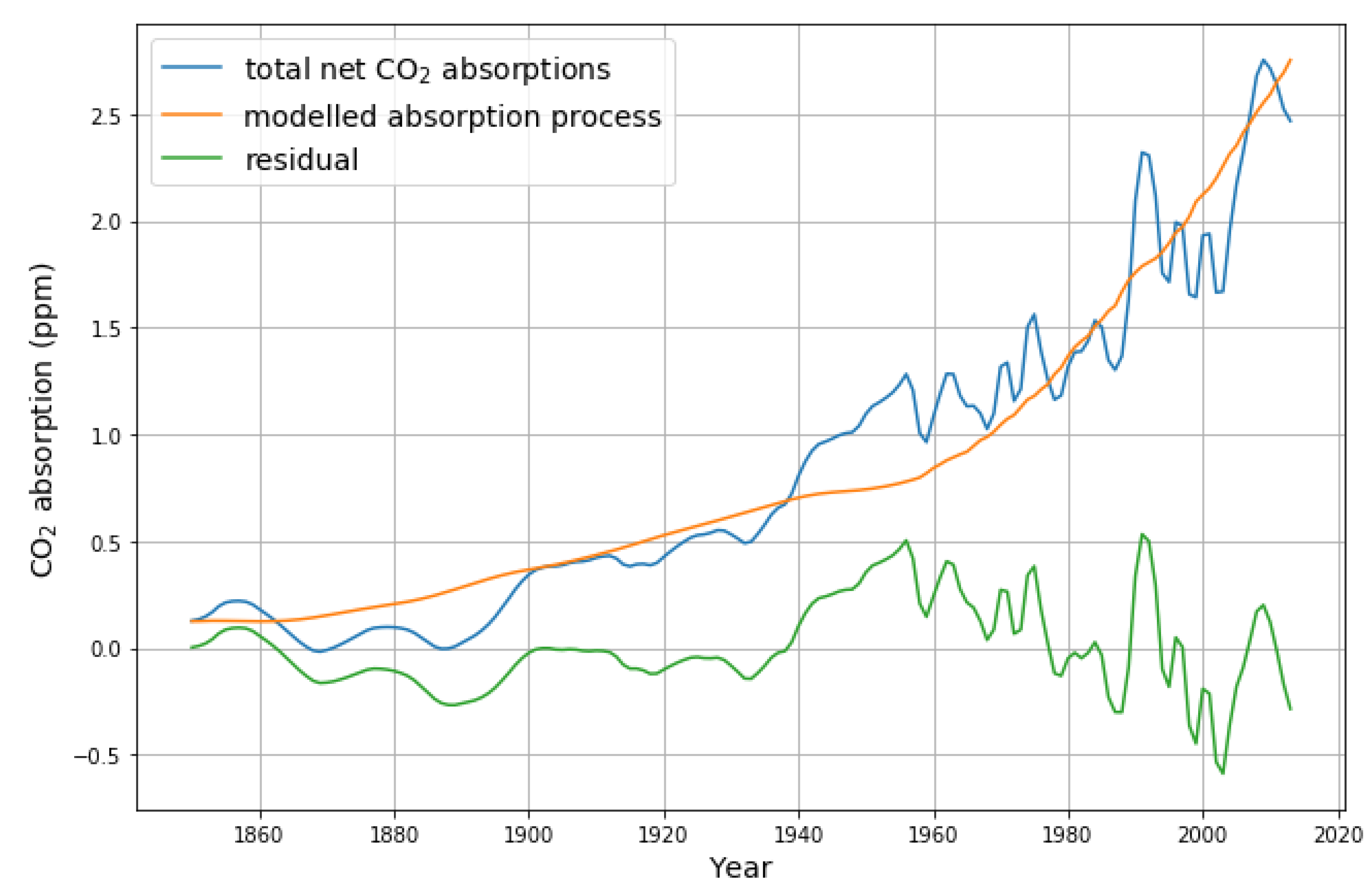
We can test the past 70 years for linearity. If there was any sign of saturation, this would have shown up as a deviation from the linearity assumption. We will see that, in the residual deviations from the model, if the actual absorption parameter decreased with time, the real CO${}_2$ concentration at the end would be larger than estimated by the model.

(2)

The global carbon budget [10] clearly shows an increasing trend in both the ocean sink, as well as the (biosphere) land sink.

(3)

A recent article revised the estimates of the ocean-atmosphere CO${}_2$ flux [15], making it consistent with the increasing ocean sink found in the global carbon budget.

(4)

We can make a rough estimation of the expected ocean uptake. The ocean has a total carbon inventory of 38,000 GtC ≈ 140,000 Gt CO${}_2$. If we assume the realistic scenario of constant future emissions at today’s level (37 Gt CO${}_2$ per year) and we assume that they are all absorbed by the ocean, by 2100 that would be approx. 3000 Gt CO${}_2$, just about 2% of the current ocean inventory.

Whatever our subjective opinion may be regarding future absorption, the measured data provide us with the current trend and its potential changes in the near future.

2.4. Hypothesis 2: Natural Emissions and Absorptions Are Balanced

This implies that, without anthropogenic emissions, C${}_i$ = C${}_{i-1}$ = C${}_0$, resulting in a constant equilibrium concentration C${}_0$. Equations (1)–(3) imply that global natural emissions are constant:

$$\begin{array}{ccc}\hfill N_i& =& a·C{}_0\hfill \end{array}$$

(7)

This relation makes a falsifiable statement about the magnitude of those natural emissions, which are not compensated by absorptions within the time unit of measurement, which is a year in this investigation. The statement of assumed constant equilibrium concentration requires further clarification. We know, e.g., from ice core investigations that historical CO${}_2$ concentration is not constant and most likely depends on temperature. A linear dependence on temperature can be mapped onto a linear dependence of the absorption parameter a on temperature, which is covered by Equation (5).

As we know, there are causes for systematic changes in the natural emissions, e.g., volcanic eruptions, ocean cycles, and changes of land use. We will see from the residual deviations of the measured data how significant these influences are and if the model needs to be adapted. For the time being, we initially assume no changes of natural emissions within the investigated time range 1850–2020. As with the previous assumption, the residual error of the model will lead to possible further fine-tuning of the model. Three possible deviations are possible:

• A systematic “trend” in the natural emissions. This would either increase or decrease the estimated absorption factor and the equilibrium concentration given a constant model of natural emissions,
• Short-term zero centered variations within a year. These variations do not show up in our model, due to the one year sampling interval,
• Long-term variations of more than a year are not averaged out. They are visible in the residual error of the predicted CO${}_2$ content.

2.5. The Modelling Equations

From Equations (2), (3), and (7), we obtain the final regression equation for an assumed constant absorption parameter, a:

$$E_i+L_i-(C_i-C_{i-1})=a·C_{i-1}-a·C_0+R_i$$

(8)

where the innovation or residual, $R_i$, is an unselfcorrelated random variable with zero mean. Equation (8) emphasises the fact that the effective absorption depends linearly on the difference between the actual and the equilibrium CO${}_2$ concentration C${}_0$. This implicitly includes the natural carbon cycle, described by the equilibrium concentration C${}_0$. Initially, we estimate $a·C_0$ as the constant natural emissions simultaneously with a in this regression equation, for estimating temperature-dependent models we assume a fixed known value for the equilibrium CO${}_2$ concentration $C_0$ and estimate the absorption function a.

Starting with the available data, from emissions $E_i$, land use change, $L_i$, CO${}_2$ growth, and the absorptions are modelled according to Equation (8) for the time interval 1850–2014,

For $L_i$, the emission change per year due to land use, the uncertainty is considerable [10]. Therefore, we have a certain amount of freedom to adapt its value, in order to satisfy other given constraints.

The absorption constant, a, and the natural equilibrium concentration $C_0$ in a given time interval are obtained through estimation with the least squares method, where the dependent variable is the left hand side of Equation (8), and the independent variable is $C_{i-1}$, by means of the Python module OLS (statsmodel-OLS-0.13.5). The results are shown in

Table 1. The result table of the Python linear regression model displays, for each regression variable, its estimated value (“Coef.”), its estimated standard error, the t-statistic for the variable being non-zero, and the error probability under the null hypothesis that the variable is non-zero. The last two columns show the error bounds, i.e., the 95% inter0val of the variable’s value.

	Coef.	Std.Err.	t	$\mathit{P}>\left|\mathit{t}\right|$	[0.025	0.975]
$-a·C_0$	−6.8952	0.2640	−26.1142	0.00	−7.4166	−6.3738
a	0.0247	0.0008	29.3485	0.00	0.0230	0.0264

.

This results in $C_0=279$ ppm, with error bounds [277, 282] ppm, and a half-life time of an emission pulse $t_{1/2}=\frac{ln\left(2\right)}{a}=28$ years, with error bounds [26, 30] years.

$C_0$ is very close, and its error bounds contain the widely accepted pre-industrial equilibrium CO${}_2$ concentration of 280 ppm. As can be seen from model Equation (8), we can substitute global variations of $L_i$ and $C_0:$

$$\Delta C_0=-\frac{1}{a}\Delta L$$

(9)

When using the center value of the land use change error band, i.e., on average 0.55 ppm, the calculated $C_0$ would have been $271\pm 2$ ppm, which we consider to be too small to be compatible with the accepted value of 280 ppm. Therefore, in the face of the large uncertainty of land use change estimates, we prefer to assume slightly lower average land use change-caused emissions (average 0.35 ppm) over an inconsistent equilibrium concentration. This substitution, however, only changes the equilibrium concentration.

Modelling the raw, noisy differential absorption data with this—simplest possible—model shows a fairly good approximation over the whole time span. The residual

$$R_i=E_i+L_i-(C_i-C_{i-1})-a·(C_{i-1}-C_0)$$

(10)

shows variations, but no systematic trend over the time span 1850–2014 (Figure 4).

The blue differential effective absorption data are approximated by the orange model curve, and the green curve shows the residual deviations. The standard deviation of the residuum is 0.2 ppm, the same order of magnitude as the uncertainty of emission and concentration measurements, in particular, $L_i$. We can, therefore, safely assume that the residual error reflects zero mean deviations of land use change or natural emissions, as discussed in [8].

We notice that, before 1900, the absorptions are smaller than this error, which means that analysing absorption values at times before 1900 is not meaningful. We also observe that, after 1950, when the quality of measurements dramatically increased, there is much more variability in the differential measurements of CO${}_2$ concentration. This justifies doubts about the data quality before 1950 and justifies a separate analysis of the much more reliable data after 1950.

Next, we investigate the possible dependence of the absorption parameter a on the sea surface temperature from the data set HadSST2 [18]. Using Equation (8) with temperature-dependent variable a from Equation (5) leads to a more complex three parameter estimation problem:

$$E_i+L_i-(C_i-C_{i-1})=(a_0+a_1·T_i)·(C_{i-1}-C_0)+R_i$$

(11)

This cannot be easily solved in closed form when $C_0$ is variable. After showing that the data are consistent with $C_{{}_0}=280$ ppm in the case for constant absorption a, we assume $C_0$ to be constant as an a priori condition and simplify the model equation by fixing $C_0$ to this value and only estimate the absorption parameters $a_0$ and $a_1$ from the data. Implicitly, this means that we make use of the assumption that the equilibrium concentration is constant. The results of the temperature-dependent, two-parameter absorption estimation problem are displayed in

Table 2. Estimation of temperature dependent absorption parameters with measured data from 1850 to 2014.

	Coef.	Std.Err.	t	$\mathit{P}>\left|\mathit{t}\right|$	[0.025	0.975]
a${}_0$	0.0263	0.0007	39.6674	0.00	0.0250	0.0276
a${}_1$	−0.0082	0.0025	−3.2074	0.00	−0.0132	−0.0031

.

The temperature-dependent parameter $a_1$ is statistically significant, and we obtain a slightly negative trend of the absorption parameter with increasing sea surface temperature since 1900.

The negative temperature dependence tells us that, before 1900, the absorption has no identifiable trend and that, between 1900 and 2000, the absorption appears to have decreased. The relative absorption in 1900 of 3% corresponds to the half-life time of 23 years for an emission pulse. However, in 2014, the relative absorption is still larger than 2.3% of the CO${}_2$ concentration, which corresponds to a half-life time of 30 years for an emission pulse. The fact that the absorption parameter changes with time in this model variant prohibits the use of a time-invariant convolution kernel for computing the CO${}_2$ concentration from emissions. Before we draw conclusions from this result, we need to validate the estimation.

2.5.1. Prediction and Model Validation

In order to validate the model, we are in the comfortable situation, in that there is a long time series, so we can perform an ex-post predictions by restricting the training data of the model to the year 2000 and make predictions of the CO${}_2$ concentration of the years 2001–2020, which are available for comparison.

In the validation process, we compare all 3 discussed model variants:

• Assumed constant absorption parameter;
• Assumed temperature-dependent absorption parameter;
• Assumed absorption parameter dependent on temperature modelled by CO${}_2$ concentration.

2.5.2. Estimation with Limited Data Range and Model Validation

The estimation results based on historical data may depend, to a certain extent, on the selected time interval, in particular, when we let the value of the equilibrium concentration of CO${}_2$ be determined from the data. This explains why previous authors arrive at such different results for the equilibrium concentration [7,8]. There are several reasons for constraining the data range:

• As stated above, there is no large variability of both CO${}_2$ emissions and CO${}_2$ concentration before the year 1900. Moreover, the measurements at that time were not really reliable. Therefore, the signal-to-noise ratio is so large that, for the determination of concentration changes as a function of CO${}_2$ emissions, it is better to dispense with these data.
• We want to evaluate the predictive quality of the data model. Therefore, we limit the training data to 1999 and compare the predicted CO${}_2$ concentration of the years 2000 to 2020 with the actual measurements.
• We further argue that the data of the first part of the 20th century are also not really reliable, indicated, e.g., by the nearly constant yearly change of CO${}_2$ concentration, despite growing emissions, as well as the extreme uncertainty of land use change data. We also know that CO${}_2$ concentration measurement methods have greatly improved in the 1950s [22]. We will, therefore, make an evaluation with training data from 1950 to 1999 and build the model based on these data.

We allow the investigated data interval to have its own equilibrium concentration, according to the available data. The equilibrium concentration is determined by the initial model with constant absorption parameter a.

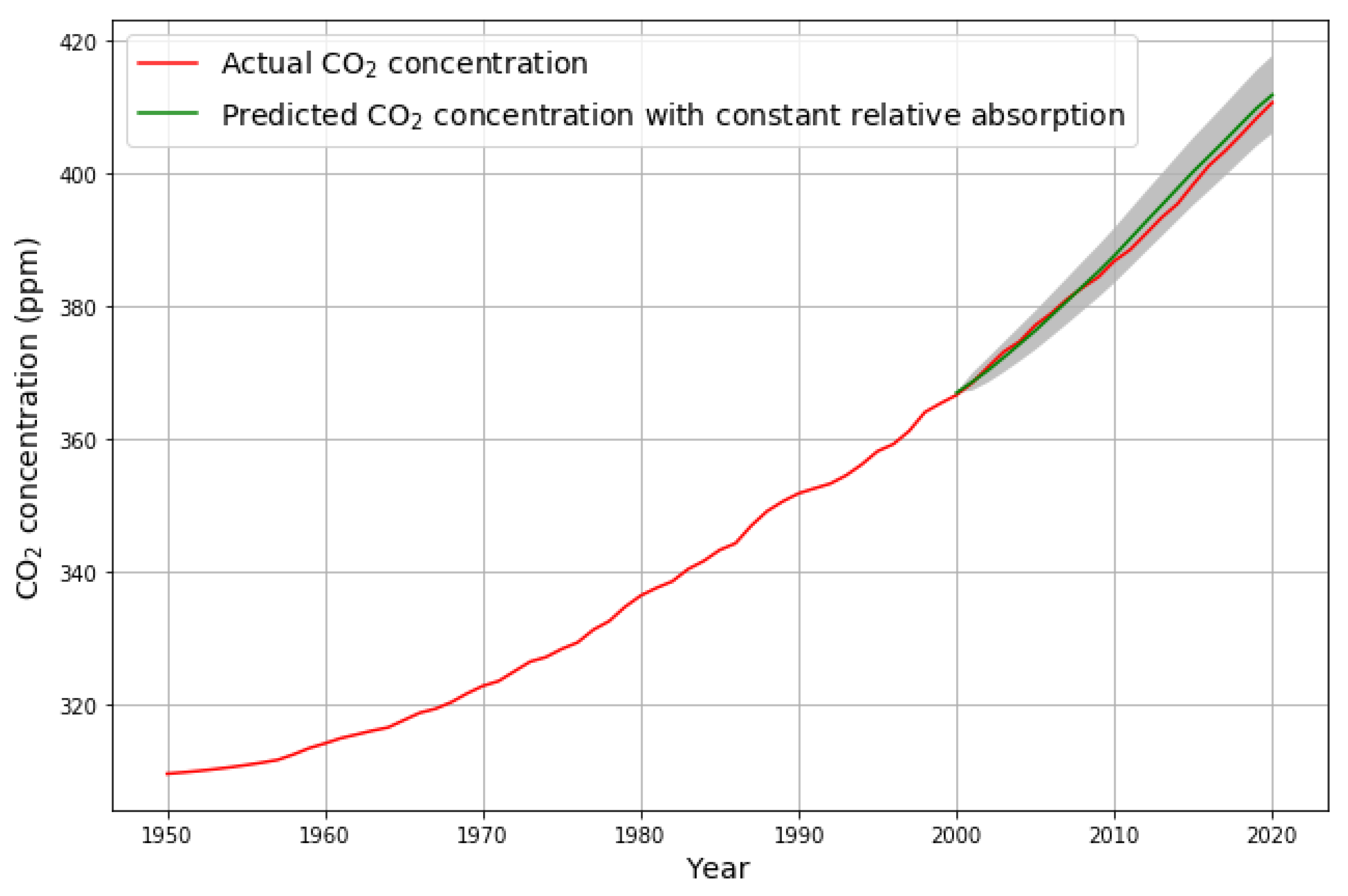
2.5.3. Estimation Based on Data from 1950 to 2000

The much better CO${}_2$ concentration measurements after 1950, in conjunction with the fact that the overwhelming bulk of anthropogenic emissions were released after 1950, justify investigating the second half of the 20th century separately. The result of the parameter estimation is displayed in

Table 3. Estimation of constant absorption parameters with measured data from 1950 to 2000.

	Coef.	Std.Err.	t	$\mathit{P}>\left|\mathit{t}\right|$	[0.025	0.975]
$-a·C_0$	−3.8188	0.2640	−14.4670	0.00	−4.3496	−3.2881
a	0.0158	0.0008	19.7789	0.00	0.0142	0.0174

.

This implies an equlibrilium CO${}_2$ concentration of C${}_0$ = 242 ppm with the error bounds [232, 251]. The half-life time of an emission pulse is 44 years with the 95% error bounds [39, 48].

The temperature-dependent estimation, according to Equation (11), with fixed C${}_0=242$ ppm, leads to the results of

Table 4. Estimation of temperature dependent absorption parameters with measured data from 1950 to 2000.

	Coef.	Std.Err.	t	$\mathit{P}>\left|\mathit{t}\right|$	[0.025	0.975]
a${}_0$	0.0157	0.0002	92.4536	0.00	0.0154	0.0161
a${}_T$	0.0005	0.0008	0.6142	0.54	−0.0011	0.0021

.

The temperature-dependent part of the absorption is clearly not significantly different from 0. When using the CO${}_2$ temperature proxy from Equation (6), we obtain the results in

Table 5. Estimation of absorption parameters depending on CO${}_2$ temperature proxy with measured data from 1950 to 2000.

	Coef.	Std.Err.	t	$\mathit{P}>\left|\mathit{t}\right|$	[0.025	0.975]
a${}_0$	0.0157	0.0002	90.0473	0.00	0.0154	0.0161
a${}_C$	0.0005	0.0010	0.4667	0.64	−0.0016	0.0025

.

Using the CO${}_2$ proxy for temperature, there is also no significant temperature dependence. Therefore, we are forced to take the model with constant absorption parameter as the best possible absorption model for the 50 years from 1950 to 2000 (Figure 5).

The diagram in Figure 5 confirms that there is no deviation from the constant absorption parameter curve when assuming a hypothetical temperature dependence.

2.5.4. Validation Based on Data from 1950 to 2000

Based on the model parameters from the 1950–2000 data, recursive evaluation of Equation (8) with future emission and land use data allows the prediction of future CO${}_2$ concentrations $C_i$ from $C_{i-1}$.

Figure 6 shows an excellent prediction in the center of the 95% gray error bar. There are small apparently periodical variations between the predictions and the actual data. Spencer [8] has explained these systematic deviations of up to 1 ppm with the Multivariate ENSO Index [23], further improving the already excellent fit. For projections of future emission scenarios, these small deviations, which are symmetric with respect to zero, do not play a significant role. Spencer also identifies volcanic activities, e.g., the Pinatubo eruption, but also these small deviations do not change the functional dependency between anthropogenic emissions and CO${}_2$ concentration in a significant way.

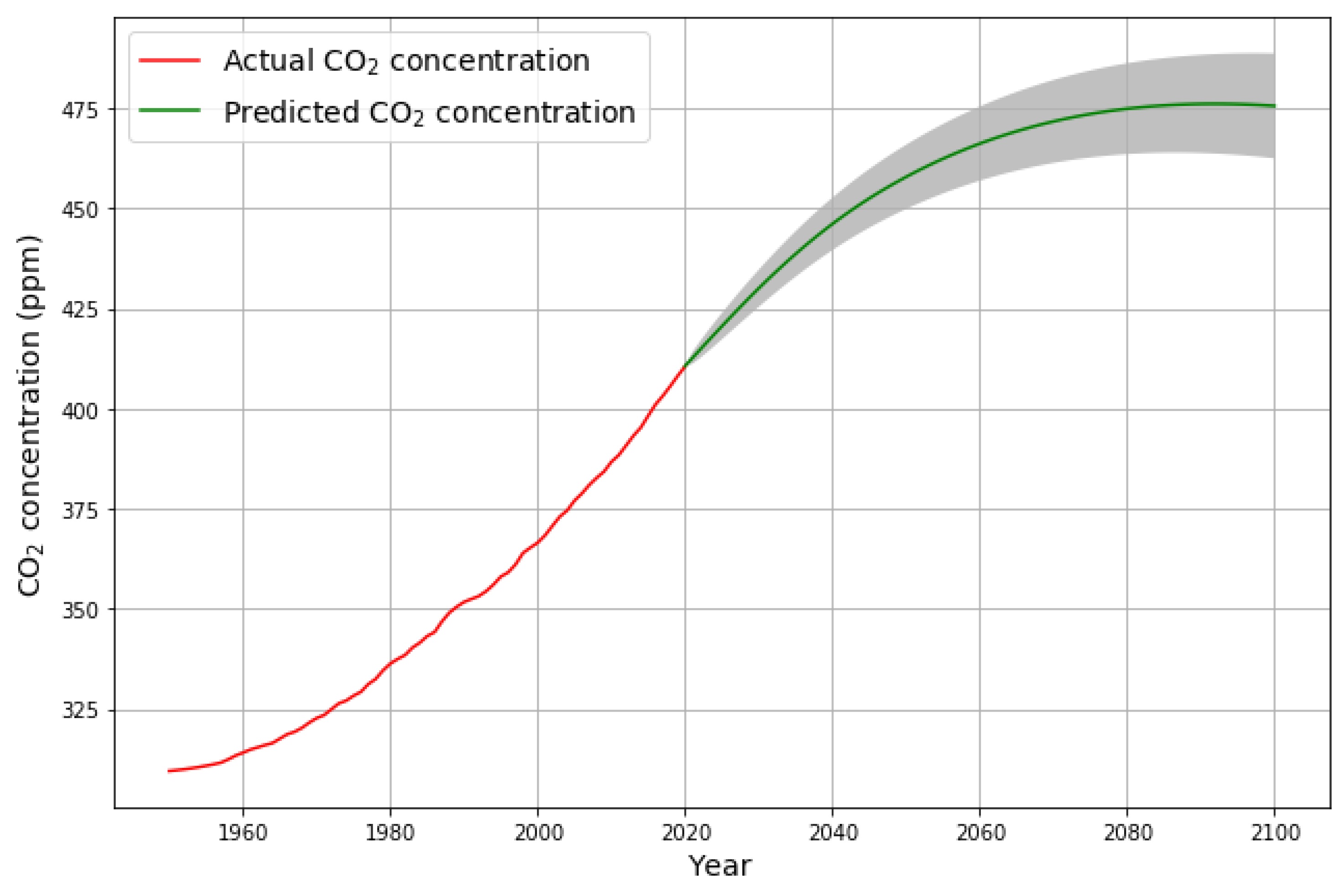
3. Prediction and Future Scenario

Due to the small error and excellent fit, the prediction of the future concentrations is based on model with constant absorption parameter, which is not temperature-dependent with data after 1950. The reproduction of the actual data is so good that we can trust this model not only within the 50 year time range of the measurements, but also due to the excellent ex post prediction of the concentrations of the last 20 years and the small residual error, we can confidently predict future concentrations.

For future predictions we expand the training data and use the full 70 years data range from 1950–2020 for the determination of the model parameters, as shown in

Table 6. Estimation of constant absorption parameters with measured data from 1950 to 2020.

	Coef.	Std.Err.	t	$\mathit{P}>\left|\mathit{t}\right|$	[0.025	0.975]
$-a·C_0$	−4.0355	0.1684	−23.9655	0.00	−4.3714	−3.6996
a	0.0165	0.0005	34.0113	0.00	0.0155	0.0174

.

This corresponds to an equilibrium concentration C${}_0$ = 245 ppm with 95% error bounds [239, 251], respectively, yearly net natural emissions of 4 ppm and a half-life time of 42 years for an emission pulse with the 95% error bounds [40, 45] years. This is consistent with the half-life time of 44 years from the 50 year time interval data.

3.1. Prediction of 2021–2100 CO₂ Concentration on the Basis of the 2021–2050 IEA Stated Policies Emission Scenario

To evaluate policy decisions, this model is applied to predict future CO${}_2$ levels based on the— most conservative and most likely—stated polices scenario of the International Energy Agency (IEA). This essentially means that the current energy consumption is continued, without significant further emission reductions beyond normal efficiency improvements. The stated policies scenarios can be regarded as the most realistic prediction, because it is based on policies that are actually in effect.

This scenario assumes global emissions remain approximately at the current maximum of 37 Gt/yr = 4.6 ppm, with a slight reduction of 3% per decade. Total budget to 2100:2640 Gt CO${}_2$, then 29 Gt/yr (excluding land use change). The actually used data set for a realistic future projection is created by trend extrapolating the stated policies beyond 2050 and assuming that the land use change data will follow the current trend and decrease to 0 by the year 2100 (Figure 7). Emissions will not be reduced to zero in the year 2100, but will remain close to the 2005 level.

The prediction for the CO${}_2$ concentration is based on the recursion of Equation (8) with the parameter a = 0.0165 and C${}_0$ = 245 ppm and R = 0, derived from the constant absorption parameter estimation with the 1950–2020 data and hypothetical emission data from the discussed extended IEA scenario.

Figure 8 shows that the IEA stated policies scenario, i.e., no special CO${}_2$ reduction policies, which implies that a CO${}_2$ concentration equilibrium of approx. 475 ppm will be reached during the second half of this century, with an 95% range of [463, 488] ppm. Based on the empirical CO${}_2$ temperature proxy Equation (6), this increase of the CO${}_2$ concentration from 410 ppm (in 2020) to 475 ppm corresponds to a temperature increase of 0.4 °C from 2020, or 1.4 °C from 1850.

4. Conclusions

The model and results derived in this paper are based on very general assumptions:

• The undeniable mass conservation of CO${}_2$,
• The assumption of approximate linearity of the relevant absorption processes w.r.t. CO${}_2$ concentration. This assumption has been relaxed to allow for temperature-dependent absorption,
• The assumption that CO${}_2$ concentration can be used as an upper limit proxy for temperature, i.e., a part of the temperature changes that can be explained by CO${}_2$ concentration,
• The assumption of constant natural emissions is within the time period of measurement. We observed, however, apparent changes of natural emissions in the first half of the 20th century, resulting in a large prediction uncertainty. Further investigations are required for a better understanding, because these changes cannot be distinguished from land use changes, which also have a large uncertainty.

Although the model allows for varying absorptions over time, the data of the last 70 years, which is the period of the bulk anthropogenic CO${}_2$ emissions, leads to the conclusion that relative CO${}_2$ absorption has no significant temperature or other time-dependent component, and a current CO${}_2$ emission pulse is absorbed with a 42 year half-life time.

The ex post validation of our model indicates that it predicts future CO${}_2$ concentration very well, on the basis of known emissions. In contrast, more than 40 years after their article was written, we see now that Oeschger’s complicated model, which explained the C${}_{14}$ content, including bomb test data, quite well, but failed badly for predicting future CO${}_2$ levels. Their predicted 2020 additional CO${}_2$ concentration beyond their assumed pre-industrial level of 295 ppm was more than 150% larger (590 ppm = 295 ppm + 295 ppm) than the actual additional concentration (410 ppm = 295 ppm + 115 ppm). It remains to be analyzed in detail whether the failure is due to overestimated emissions based on the unrealistic assumption of exponential emission growth or whether it is caused by the model itself.

The main conclusion of this evaluation is that, for the most likely IEA emission scenario of approximately constant, slightly decreasing global emissions, we can expect a maximum CO${}_2$ concentration level of approximately 475 ppm in the second half of this century. At this point, the emissions will be fully balanced by the absorptions, which is by definition the “net zero” situation.

Assuming the unlikely worst case that CO${}_2$ concentration is fully responsible for all global temperature changes, the maximum expected rise of global temperature caused by the expected CO${}_2$ concentration rise is 0.4 °C from now or 1.4 °C from the beginning of industrialisation.