Abstract
With the development of wireless communication technology, the electromagnetic interference (EMI) of artificial radio to weather radar increases significantly, which has a serious impact on the quality of radar data. Most of the research on detecting and suppressing electromagnetic interference was based on the primary product of the radar. This paper researches the effectiveness of deep convolutional neural networks (DCNN) to identify and suppress electromagnetic interference based on the I/Q data output from the front end of a radar receiver. Firstly, this paper selected UNet, ResNet with UNet structure, and DeepLab V3+ for the semantic segmentation of electromagnetic interference and other signals. After semantic segmentation, this paper used the linear interpolation method to suppress EMI. Finally, this paper selected the prediction precision of the model and compared the quality of primary products before and after EMI suppression to evaluate the effectiveness of DCNN. The results showed that all three models could effectively identify the electromagnetic interference and the quality of the data were improved after suppression. It suggests that the use of DCNN on the I/Q data output from the front end of a radar receiver can play a certain effect on the identification of electromagnetic interference.
1. Introduction
In recent years, with the development of wireless communication technology, the coverage of communication frequency bands has become wider, and the number of base stations and electronic devices used for wireless communication has increased, resulting in a significant increase in the electromagnetic interference of artificial radios on weather radars. Vaccarono et al. proposed that the quality of radar data is seriously affected because some frequency bands of telecommunication systems coincide with the operating frequency bands of C-band (4–8 GHz) weather radars [1]. In addition, the wireless communication industry also uses part of the S-band (2–4 GHz); therefore, it is unavoidable that electromagnetic interference affects the radar [2].
The influence of electromagnetic interference on the data quality of weather radar is becoming more and more serious. It affects the product generation and the identification of weather systems. Therefore, the identification and elimination of electromagnetic interference have become an important task of weather radar quality control. Cho proposed to suppress the interference by detecting abnormal increments in the spectrum [3]. Jiapeng Yin proposed a mobile dual-spectral linear depolarization ratio (MDsLDR) filter for mitigating narrowband disturbances in weather radar, which also included electromagnetic interference [4]. Additionally, V Lakshmanan obtained the features of non-weather echoes by processing data such as reflectivity, velocity, and velocity spectrum width by the neural network, then identified and processed them [5]. These methods have made obvious effectiveness in the suppression of electromagnetic interference. However, they are completed based on the primary product of the radar without processing of the I/Q data output from the front end of a radar receiver.
In a radar receiver, the quadrature phase detector is able to detect both amplitude and phase information of the signal. It decomposes the radar echo signal into the orthogonal components of I, Q. Therefore, the I/Q data also include the static and motion information of the scattered particles. Therefore, the processing of I/Q data also can affect the quality of the echo data. However, the present identification and suppression methods for electromagnetic interference on I/Q data are relatively simple. For the processing of I/Q data, the single-pulse anomaly detection filter is usually used to detect electromagnetic interference, and then the marked pulses are replaced by interpolation of adjacent pulses [6]. In I/Q data, electromagnetic interference may exist on only one pulse, but it may also keep repeating on several consecutive pulses with similar features. It shows that some of electromagnetic interference has spatial features. The original methods are identifying on individual pulses, and there is no advantage for the identification of electromagnetic interference with two-dimensional features. Thus, it is more effective to identify electromagnetic interference that can capture spatial information rather than an algorithm that identifies only from individual pulses.
It has been proved that the end-to-end DCNN has achieved great results for object detection and image classification. Classic deep convolutional neural networks such as VGG [7], AlexNet [8] are able to perform tasks such as image classification or target recognition well. Because they generally use a convolution-pooling structure in the first few layers of the network and the convolution-pooling structure can effectively capture the spatial information and depth information of the image by training. However, the final output classifier of these networks’ structure are one-dimensional vectors; therefore, the features obtained after convolution-pooling have to be further converted into a one-dimensional fully connected layer for classification. This type of network structure is not conducive to identifying and judging specific electromagnetic interference on a certain range gate based on I/Q data. Because the spatial information is lost after the process of converting the two-dimensional feature map obtained from convolution pooling to the fully connected layer. It is meaningless for the identification of electromagnetic interference which needs to obtain spatial information.
Jonathan Long proposed a fully convolutional network (FCN), which converts the original fully connected layers in the convolutional network into convolutional layers [9]. Compared with the classic convolutional neural network, The DCNN with fully connected layers avoid the loss of two-dimensional information of feature maps during the conversion from convolutional layers to fully connected layers. The emergence of fully convolutional networks opens up new directions for semantic segmentation. Chen suggested that convolutional neural networks need to continuously increase the receptive field through the convolution-pooling process, which is repeated in the process of capturing features. The signal would be continuously downsampled and information would be unavoidably lost. Downsampling does not affect the classification task, but limits the accuracy of localization for semantic segmentation tasks [10]. This disadvantage is showed by the difficulty of capturing fine features in the model. He proposed to improve the convolution by using atrous convolution instead of convolution-pooling [11]. Because the atrous convolution skips the pooling process. It can yield a larger receptive field, which results in more dense data. Larger receptive field can improve the effectiveness of small object identification in target detection and semantic segmentation tasks. Together, these studies provide important insights into semantic segmentation methods for two-dimensional signals.
Compared with the algorithm that can only identify the electromagnetic interference from a single pulse, The DCNN using the fully connected layer can more effectively identify and locate the electromagnetic interference with two-dimensional features.
In recent years, there are also cases of applying convolutional neural networks to non-computer vision fields [12,13]. Inspired by the application of deep convolutional neural networks (DCNNs) in computer vision work, this paper studies the effectiveness of using DCNNs for semantic segmentation of electromagnetic interference and other signals from I/Q data. Additionally, after the identification, this paper also suppresses the electromagnetic interference to achieve the purpose of quality control.
2. Materials and Methods
2.1. Experiment Procedure
The general experimental workflow in this paper is shown in Figure 1. The experimental procedure is composed of 5 parts, which are data pre-processing and dataset creation, design and creation of DCNN, model training, prediction and suppression of EMI, and evaluation.
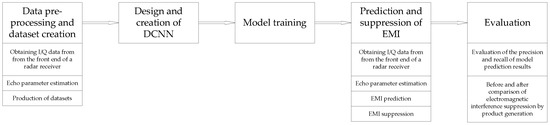
Figure 1.
Experimental procedure.
Data pre-processing and dataset creation is the step before the beginning of the experiment. It includes the obtaining of data and the production of datasets. The following steps are design and creation of DCNN and model training. After the model training is prediction and suppression of EMI. In this step, data are also obtained firstly, and the data are input to the model for EMI prediction. Then, the prediction results are used for EMI suppression. In the evaluation step, not only the prediction results of the model are evaluated, but also the results of the generated products after suppressing electromagnetic interference are compared. The effectiveness of the DCNN for the electromagnetic interference identification based on I/Q data is judged by the combined results of these two evaluations.
2.2. Echo Parameter Estimation
The static and motion information of the scattered particles is included in the I/Q data. Therefore, the I/Q data were used to estimate the echo parameters. This step could extract power spectrum, average Doppler velocity, and velocity spectral width from the I/Q data. The method used in this paper was the pulse pair processing algorithm (PPP) [14]. Compared with the FFT algorithm, the PPP algorithm is faster and requires less computer hardware. In addition, the input for DCNN training were the power spectrum data.
Let the number of sampling points on a pulse be , and the th range gate is represented as . The zero-delay autocorrelation function is as shown in Equations (1) [15,16].
The power spectrum of the signal can be obtained by the zero-delay autocorrelation function.
2.3. Semantic Segmentation Work in I/Q Data
The establishment of the electromagnetic interference identification model was similar to a fully convolutional. An encoder needed to be designed to perform multiple convolution and pooling operations on the data obtained by echo parameter estimation of the I/Q data. This process extracted the features of electromagnetic interference and other signals. Then, a decoder was designed to perform upsampling (deconvolution or interpolation). Expanded feature maps were obtained by the encoder in a certain way, so that the output size of the decoder was the same as the input. Finally, the predicted result was output through the softmax layer.
In this paper, UNet, ResNet with UNet structure and DeepLab V3+ were selected for semantic segmentation of electromagnetic interference in I/Q data. Additionally, the results were compared to research the effectiveness of DCNN in identifying electromagnetic interference on I/Q data.
Due to the great success of ResNet [17] in computer vision work. This paper learned from the residual structure and applied it to a fully convolutional network as an encoder. Such a structure could effectively deepen the network depth for downsampling work. In the decoder, upsampling was performed by directly scaling the rows and the columns of the feature map and filling the values of the adjacent range gates. This paper also combined the structure of UNet’s direct delivering feature map for semantic segmentation of electromagnetic interference [18].
Deeplab V3+ also has an encoder-decoder structure [19], but it is different from UNet [18] and ResNet with the UNet structure used in this paper. First of all, the backbone used by Deeplab V3+ is Xception [20]. The backbone compared with ResNet and UNet, it maintains fewer parameters. This model has a deeper network depth while being lighter. In the encoder, the atrous spatial pyramid pooling (ASPP) module [21,22] is used to extract features. It performs atrous convolution with different dilation rate for the same feature map separately to achieve the purpose of fusing multi-scale information. This convolution method can effectively increase the receptive field while reducing the loss of spatial information. The further fusion of low-level features and high-level features also improves the accuracy of segmentation edges. In the decoder, Deeplab V3+ directly outputs the feature map through the softmax layer and performs bilinear interpolation to obtain the result.
2.4. Production of Datasets
The I/Q data used in this paper were from the CMA Key Laboratory of Atmospheric Sounding, Chengdu, Sichuan, China. All the data containing electromagnetic interference were manually selected. As shown in Figure 2, the production process of the dataset was divided into two parts: automatic processing and manual identification. Automated processing included echo parameter estimation, unit conversion, normalization, edge enhancement, binarization. Additionally, the work after the automatic processing was manual identification.

Figure 2.
The procedure of producing dataset.
The first step was to estimate the echo parameters to obtain the raw power spectrum data . In this paper, the values in the raw power spectrum data span a large range; therefore, the units were converted to decibels in Equation (2). The converted data were used as the input of the network and assisted them in the visualization of the power spectrum when making labels.
Then, the power spectrum data were normalized to be between 0 and 255 to produce the normalized data , as shown in Equation (3).
where was the maximum value in the power spectrum data and was the minimum value in . From this step, the power spectrum data were converted into a grayscale image, which was only used for data visualization. The visualized data facilitated the labeling of training data and manual identification.
Edge enhancement was required to make the range gates with electromagnetic interference sharper. The and were the echo and background horizontal and vertical edge data, respectively. They were obtained by convolving the normalized power spectrum data with the Sobel kernel which detects the horizontal and vertical edges. The calculation process was shown in Equations (4) and (5) [23,24]. The obtained horizontal and vertical edges were combined to in Equation (6). After edge enhancement, data were obtained by combining data with the normalized power spectrum data , as shown in Equation (7).
The next step was the binarization. The threshold value used for binarization was obtained by manually observing the binarized visualization data. The threshold was judged by retaining the characteristics of electromagnetic interference and removing most of the noise. Through binarization, the electromagnetic interference and other weather echoes were separated from the background.
The final process was the manual identification of electromagnetic interference and weather echoes. Changing the gray value of the visualized power data to the training labels with the help of the binarization results. Set the gray value of the location of the ranging gate with electromagnetic interference to 1, representing a label with “electromagnetic interference”. Additionally, the gray value of the location of the ranging gate was set with weather echoes and the background to 0, representing a label with “other signals”. The division ratio of the training set to the test set was 8:2.
2.5. Data Cutting
In this paper, it was necessary to cut power spectrum data and labels due to the limitation of video memory. The cutting method would be described in detail below.
The power spectrum had range gates in one pulse, and there were pulses in a group of power spectrum data, then the input data size of the model was . Additionally, marked the size of the data obtained by cutting be . The output size of the model also corresponded to . Taking pulses and cutting them according to the length of range gates. After cutting, sliding down pulses to repeat the cutting process and recording the cutting sequence during each process. In addition, there might be cases where or were not an integer multiple of or during cutting. In this case, the size of the data obtained by cutting did not match the size used for model training or prediction. Therefore, when the data size did not match during model training, the power spectrum data and labels would be interpolated, and the size would be expanded to the size of before training. In the prediction work of the model, when the input size did not match , the input data were still expanded in size according to the previous steps, but the prediction result of the model needed to be compressed to the size of original input data size. After stitching the predictions of the model in the order of the records, the final prediction was obtained with the same size as the original power spectrum data.
In addition, different cut sizes can also influence the identification accuracy of the model. Although the size of the electromagnetic interference existing on each pulse is not large, the size of the weather echoes on the pulse is larger. The range gates of weather echoes present on each pulse are continuous and the number is large. When the size of the data that are obtained from the cut is smaller than the size of the weather echoes, the DCNN model is unable to learn the true weather echo features thus affecting the accuracy. Therefore, the size of the width in the cut data must be much larger than the number of range gates with weather echoes in each individual pulses. In this paper, due to video memory limitations, both and were set to 512.
2.6. Model Structure
Instead of dwelling on the structure of UNet and Deeplab V3+, this paper would describe the work of transforming ResNet50 into a fully convolutional network for semantic segmentation of electromagnetic interference and other signals.
The main characteristic of ResNet50 is that it can directly jump connect the network surface feature data to the deep layer, which can effectively solve the problem of gradient disappearance caused by too deep DCNN and improve the accuracy rate. ResNet50 is mainly divided into 5 stages; each stage can be regarded as the composition of two modules, the two modules are the Conv Block an Identity Block. The structure of the Conv Block and Identity Block are shown in Figure 3. Conv Block can change the dimension of the input. The module’s input channels are firstly compressed by the 1 × 1 convolution kernels. Additionally, the module’s input dimension is changed by 3 × 3 convolution kernels. Then, the module’s output number of channels is changed by 1 × 1 convolution kernels. In addition, the input has to be stacked with the output by acheiving the residual edge through the 3 × 3 convolution kernel. Additionally, Identity Block is used to deepen the network. The module’s input channels are compressed by the 1 × 1 convolution kernel. Then, they are convolved with 3 × 3 convolution kernel, but the padding method is set to “same” to keep the size of the convolved feature map constant. Finally, the 1 × 1 convolution kernels change the number of channels for output. In addition, the input has to be stacked with the output directly.
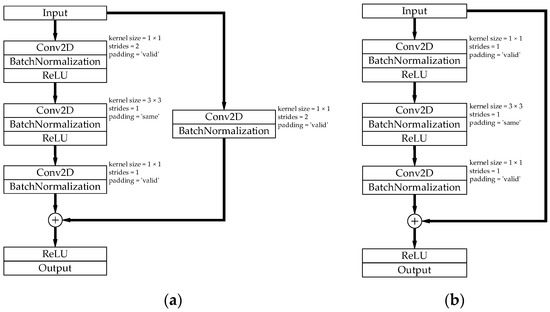
Figure 3.
(a) Conv Block; (b) Identity Block.
The structure of the semantic segmentation network improved by ResNet50 in this paper is shown in Figure 4. In the upsampling process, the idea of the UNet structure was borrowed: the feature maps obtained from each downsampling are directly delivered to the process of each upsampling. In the encoder, the network input was first convolved with the 7 × 7 convolution kernel to change the input scale and retain the feature map Feat1. Each stage in ResNet50 used the Conv Block and Identity Block modules mentioned above to change the input dimension and deepen the network. At the end of each stage, downsampling was completed, and each downsampling resulted in a feature map that needed to be preserved. Therefore, a total of 5 feature maps would be obtained after the encoder process: Feat1, Feat2, Feat3, Feat4, and Feat5. In the decoder, Feat5 would first be upsampled twice in width and length, and then stacked with Feat4. The number of channels was changed by convolution two times, and the result was upsampled twice as length and width. The results were stacked and upsampled with Feat3, Feat2, and Feat1, respectively, in the same steps. After downsampling and upsampling the residual module 5 times, the prediction result of the model was obtained through the softmax layer.
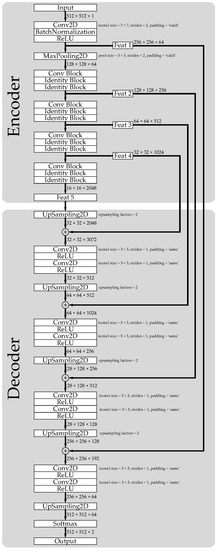
Figure 4.
ResNet semantic segmentation network with UNet structure.
2.7. Model Training
2.7.1. Loss Function
In this paper, all three networks were selected to solve the binary classification problem, i.e., semantic segmentation of the range gates where electromagnetic interference was existed and the range gates where electromagnetic interference was not existed. The number of range gates with electromagnetic interference was smaller than that of range gates without electromagnetic interference. Therefore, there was the problem of positive and negative sample imbalance. To deal with this problem, this paper adopted Combo Loss [25], which was a combination of dice loss [26] and cross-entropy loss, as the loss function of the neural network.
On the one hand, dice loss preferred to extract the foreground region, which was beneficial to solve the problem of positive and negative sample imbalance. However, dice loss would produce serious shocks when the positive sample was a small target. On the other hand, cross-entropy loss was the overall average, which would be more dependent on the negative sample location. Therefore, the combination of the two would be more conducive to the identification of electromagnetic interference.
2.7.2. Adjustment of Learning Rate
In this paper, the method of dynamically adjusting the learning rate was adopted in the three models. This method could dynamically adjust the learning rate according to the training steps to help the model speed up the convergence of the model and also jump out of the local optimal solution. The method used to dynamically adjust the learning rate was Cosine Annealing Warm Restarts [27]. The method was divided into two stages: warming up and cosine annealing. Added one step for each epoch completion and the learning rate needed to be adjusted. The current step count was marked as , and the total step counts of the model training process was marked as .
The warming up stage was a linear growth process in which the learning rate grew with a certain linear relationship during a fixed step count . At the end of the warming up stage and the beginning of the cosine annealing stage. The learning rate was marked as . Then, the learning rate adjustment formula for the warming up stage as shown in Equation (8).
When , the warm upstage was completed and the cosine annealing stage was entered. The simplified cosine annealing stage is shown in Equation (9). The minimum learning rate would be marked as and the maximum learning rate would be marked as in this paper, and them would be kept constant during the training process.
In this paper, the parameters of the dynamic learning rate were kept consistent among the three models taking , .
2.8. Suppression of Electromagnetic Interference
The work that follows the prediction of electromagnetic interference is the suppression of electromagnetic interference. The results obtained according to the model prediction was named which could be regarded as the specific location distribution of weather echoes and electromagnetic interference. Iterating between pulses at the same distance. When a label with the predicted result of electromagnetic interference was read, it was marked as at that position. Additionally, continue iterating down, when a label with weather echo was read, it was marked as at that position. Then, the range gates between contained electromagnetic interference, which needed to be interpolated and replaced. The value of the range gate at the same position of was read as and the value of the range gate at the same position of was read as in the I/Q data. Finally, the positions of all range gates between would be linearly interpolated. This work completed the suppression of electromagnetic interference between pulses at the same distance. Repeating this work at each distance completed the suppression of electromagnetic interference in a set of I/Q data.
2.9. Evaluation of Model
For the work studied in this paper, the main comparison evaluation indicators were precision and recall. Their formulas are as shown in Equations (10) and (11).
If the label of the range gates were “EMI” and the predicted result of the range gates were also “EMI”, then the range gates were marked as . If the label of the range gates were “EMI”, but the predicted result of the range gates were “other labels”, then the range gates were marked as . Similarly, if the range gates were labeled “other label”, but the predicted result of the range gates were “EMI”, then the range gates were marked as . If the label of the range gates were “other label” and the predicted result of the range gates were “other label”, then the range gates were marked as .
Among them, precision was more important than recall. Because the range gate without electromagnetic interference was identified as the range gate with electromagnetic interference, which had a great influence on the suppression work. If the range gate with weather echo was identified to be the range gate with electromagnetic interference, then the weather echo would be suppressed in the suppression work. Therefore, the impact of this situation on product generation was more serious than unidentified electromagnetic interference.
3. Results
3.1. Results of Model Evaluation
Table 1 shows the evaluation results of UNet, ResNet with UNet structure, and DeepLab V3+ for electromagnetic interference identification. It can be seen that the precisions of UNet and ResNet with UNet structured are higher than DeepLab V3+. Additionally, the previous two can locate the range gate with electromagnetic interference more accurately. However, DeepLab V3+ has the highest recall, which suggests that DeepLab V3+ could predict more range gates with electromagnetic interference among these three models. For the work of identifying electromagnetic interference, precision is more important. Thus, UNet and ResNet with the UNet structure were more effective.

Table 1.
Results of model evaluation of EMI label predictions.
3.2. Comparison of I/Q Data after the Suppression of Electromagnetic Interference
Figure 3 shows the identification and suppression effect of pulses with serious electromagnetic interference from I/Q data. As can be seen from the figure: After semantic segmentation of UNet, the edges are sharper and more accurate. Additionally, the edges after Deeplab V3+ semantic segmentation are more blurred and there are a lot of range gates that are mistaken identification. However, Deeplab V3+ is able to identify more range gates with ambiguous electromagnetic interference features compared to UNet. The edge accuracy of semantic segmentation of ResNet with UNet structure is a little inferior to UNet; but much better than Deeplab V3+. At the same time, it is also able to identify more range gates with ambiguous electromagnetic interference features compared to UNet. In Figure 5, DeepLab v3+ has the best suppression of electromagnetic interference after semantic segmentation, whereas the other two models have the second-best suppression.
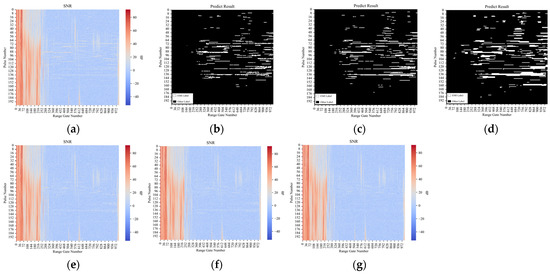
Figure 5.
Identification and suppression results of three models for electromagnetic interference. (a) Raw data; (b) semantic segmentation results of UNet; (c) semantic segmentation results of ResNet with UNet structure; (d) semantic segmentation results of DeepLab V3+; (e) EMI suppression results after UNet semantic segmentation; (f) EMI suppression results after ResNet semantic segmentation; (g) EMI suppression results after DeepLab V3+semantic segmentation.
For the suppression results, Deeplab V3+ with more blurred edges were better after suppression compared to the previous one which can predict more accurate edges, although there were a large number of mistaken identifications. Because blurred edges brought a larger interpolation range and a better suppression of electromagnetic interference with a wider range and higher intensity. However, inaccurate prediction of edges might cause potential problems for suppression. Figure 6 shows another set of identification and suppression results of electromagnetic interference. The black box shown in (g) of Figure 6 shows the problems that occurred after DeepLab V3+ identified the electromagnetic interference. The value of the range gate with electromagnetic interference might be used as the parameter needed for interpolation in the calculation, resulting in expansion of the effects of electromagnetic interference after interpolation.
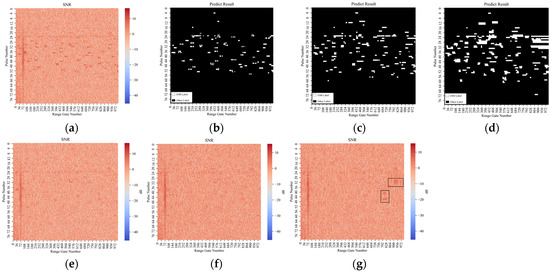
Figure 6.
Identification and suppression results of the problems among the three models. (a) Raw data; (b) semantic segmentation results of UNet; (c) semantic segmentation results of ResNet with UNet structure; (d) semantic segmentation results of DeepLab V3+; (e) EMI suppression results after UNet semantic segmentation; (f) EMI suppression results after ResNet semantic segmentation; (g) EMI suppression results after DeepLab V3+semantic segmentation.
3.3. Comparison of Products after the Suppression of Electromagnetic Interference
In the reflectivity, velocity spectrum width and Doppler velocity products, electromagnetic interference existed at the same location of the range gates. Therefore, in this paper, reflectivity products were used for the comparison of suppression effects. Figure 7 shows the comparison of the generated reflectivity products after the suppression of the three model identifications.
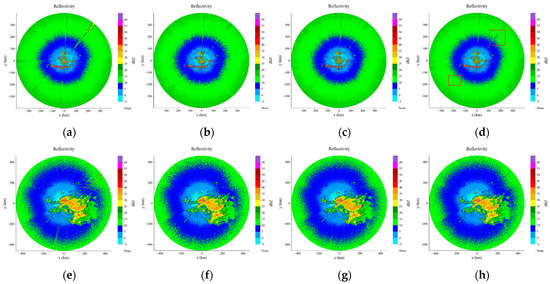
Figure 7.
Suppression results of three models for electromagnetic interference. (a) Raw data; (b) products generated by suppression of electromagnetic interference in (a) after UNet identification; (c) products generated by suppression of electromagnetic interference in (a) after ResNet identification; (d) products generated by suppression of electromagnetic interference in (a) after DeepLab V3+ identification; (e) original image; (f) products generated by suppression of electromagnetic interference in (e) after UNet identification; (g) products generated by suppression of electromagnetic interference in (e) after ResNet identification; (h) products generated by suppression of electromagnetic interference in (e) after DeepLab V3+ identification.
The PPI images of reflectance show that the products generated by suppressing electromagnetic interference through the prediction results of different models can significantly reduce the impact caused by electromagnetic interference. Additionally, the differences among the three are not very significant. It is worth noting that the red box in Figure 7d. It shows the expansion of electromagnetic interference after suppressing in the product.
In addition, the electromagnetic interference between 80 degrees and 90 degrees in Figure 7a and between 270 degrees and 280 degrees in Figure 7e is not suppressed by the identification of the three models. By viewing the identification effect of the location pulses corresponding to the I/Q data. Only DeepLab V3+ made few identifications, whereas the other two models hardly made any identifications. The reason is that the pulses in this region only have changes in pulse intensity at low frequencies compared to other region, and there are no other significant features. Therefore, the three models used in this paper are more difficult to identify this type of electromagnetic interference.
4. Discussion
According to the comparison of the identification results of pulses, it can be inferred that the deeper the depth of the network, the easier it can be to identify the electromagnetic interference features with obscure features. However, the accuracy of the semantic segmentation edge would be decreased. This paper infers that most of the electromagnetic interference features are relatively simple and have been captured in the superficial layers of the neural network. However, as the depth of the network grows, some information about the features of electromagnetic interference captured at the superficial layers is lost in the process of delivering the feature maps in the network. UNet structures preserve all the feature maps of each downsampling stage to deliver to the decoder directly. However, DeepLab V3+ delivers feature maps to the decoder after completing all atrous convolution. Therefore, the prediction results of UNet and ResNet with UNet structure can obtain higher precision in the evaluation compared to DeepLab V3+. For the task of electromagnetic interference identification based on I/Q data, most of the features that are captured by the model are simple features, which can be captured by the superficial layers of the neural network. Directly delivering the superficial features to the decoder for upsampling preserves more spatial information than delivering the features to the decoder after tedious downsampling; therefore, the edges of semantic segmentation are more accurate.
From the suppression results of I/Q data and products, the suppression for electromagnetic interference does not require high accuracy for semantic segmentation edges. Blurred edges achieve better results in most situations because the interpolation has a larger range. However, the inaccuracy of the predicted edges can lead to carrying the value of the range gate where electromagnetic interference exists into the calculation during interpolation. Additionally, the result obtained by interpolation will deteriorate the data quality. Therefore, the precision of the model prediction is still important, and to some extent, it can avoid data degradation caused by inaccurate localization in the interpolation process.
DCNN is effective in identifying and suppressing electromagnetic interference in most situations, and can improve data quality. When designing the DCNN application for identifying electromagnetic interference, the superficial feature map is preserved as much as possible for the recovery process in upsampling, which is beneficial to improving precision of localization. Additionally, the network does not benefit too deep to avoid as much as possible the loss of spatial information in the delivery of the network. However, the problem cannot be ignored is the large calculation amount, which has high requirements for hardware.
5. Conclusions
In this paper, deep convolutional neural networks were used to I/Q data from the front end of a radar receiver to explore the availability of DCNN for electromagnetic interference identification. The semantic segmentation of EMI on I/Q data was accomplished by selecting three DCNNs with different structures and suppressing electromagnetic interference after identification. The semantic segmentation networks were UNet, DeepLab V3+ and ResNet with UNet structure.
The research steps begin with the power spectrum data which was obtained by estimating the echo parameters from the I/Q data, and then the main work was made on the power spectrum data. The next step in the process was the preparation of the dataset used to train the model. The power spectrum data were normalized and then visualized to facilitate manual identification utilizing edge enhancement and binarization. After cutting the data and labels, the three semantic segmentation networks were trained individually. The three models were finally built by adjusting the parameters during the training. When the model had finished predicting, the electromagnetic interference was suppressed by linear interpolation. Finally, the evaluation of the effectiveness of a deep convolutional neural network for semantic segmentation of electromagnetic interference on I/Q data was completed by the calculation of precision and recall and the comparison of the suppression effect of the three models.
According to the evaluation results, the precision of UNet for EMI identification is 89.00%, the precision of ResNet using UNet is 87.54%, and the precision of DeepLab V3+ is 65.31%. Although DeepLab V3+ has the lowest precision of identification of electromagnetic interference among the three, it is more effective in capturing more ambiguous electromagnetic interference than the previous two. The other two DCNN semantic segmentations with UNet structure have sharper result edges and therefore are evaluated to obtain higher precision. It has been experimentally proven that networks with structures that can directly deliver superficial features to upsampling are more effective for the identification task of electromagnetic interference. After semantic segmentation, the suppression of electromagnetic interference is achieved by linear interpolation. Whether comparing the electromagnetic interference suppression effect of pulses from I/Q data or the effectiveness of primary products, all three can make a significant effect on electromagnetic interference suppression. Therefore, it is effective to use deep convolutional neural networks on I/Q data for semantic segmentation. Additionally, there is a significant improvement in data quality after the suppression of electromagnetic interference.
Author Contributions
Conceptualization, J.W.; methodology, J.W.; software, J.W.; validation, J.W.; formal analysis, J.W.; investigation, J.W., H.W. and Z.S.; resources, Z.S. and H.W.; data curation, Z.S. and H.W.; writing—original draft preparation, J.W.; writing—review and editing, H.W. and Z.S.; visualization, J.W.; supervision, H.W.; project administration, H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (award number U1733103).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets supporting the conclusions of this article are private, and it came from the CMA Key Laboratory of Atmospheric Sounding, Chengdu, Sichuan, China.
Acknowledgments
I would first like to thank my supervisor, Haijiang Wang, whose expertise was invaluable in formulating the research questions and methodology. Additionally, we would also like to acknowledge Zhaoping Sun for the provision of data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vaccarono, M.; Chandrasekar, C.V.; Bechini, R.; Cremonini, R. Survey on Electromagnetic Interference in Weather Radars in Northwestern Italy. Environments 2019, 6, 126. [Google Scholar] [CrossRef]
- Saltikoff, E.; Cho, J.Y.N.; Tristant, P.; Huuskonen, A.; Allmon, L.; Cook, R.; Becker, E.; Joe, P. The Threat to Weather Radars by Wireless Technology. Bull. Am. Meteorol. Soc. 2016, 97, 1159–1167. [Google Scholar] [CrossRef]
- Cho, J.Y.N. Signal Processing Algorithms for the Terminal Doppler Weather Radar: Build 2. 89. Available online: https://www.semanticscholar.org/paper/Signal-Processing-Algorithms-for-the-Terminal-Build-Cho/91c97e93e38798e4e0fd0c411f6c7626f0a5674b (accessed on 22 June 2022).
- Yin, J.; Unal, C.M.H.; Russchenberg, H.W.J. Narrow-Band Clutter Mitigation in Spectral Polarimetric Weather Radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4655–4667. [Google Scholar] [CrossRef]
- Lakshmanan, V.; Hondl, K.; Stumpf, G.; Smith, T. Quality Control of Weather Radar Data Using Texture Features and a Neural Network. 6. Available online: https://ieeexplore.ieee.org/document/7934116 (accessed on 20 June 2022).
- Cho, J.Y.N. A New Radio Frequency Interference Filter for Weather Radars. J. Atmos. Ocean. Technol. 2017, 34, 1393–1406. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556v6. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Shelhamer, E.; Long, J.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 640–651. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Semantic Image Segmentation with Deep Convolutional Nets and Fully Connected CRFs. arXiv 2016, arXiv:1412.7062. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Zhao, H.; Ma, X.; Tu, Y.; Wang, M. Adversarial Attacks in Modulation Recognition with Convolutional Neural Networks. IEEE Trans. Reliab. 2021, 70, 389–401. [Google Scholar] [CrossRef]
- Lin, Y.; Zhu, X.; Zheng, Z.; Dou, Z.; Zhou, R. The Individual Identification Method of Wireless Device Based on Dimensionality Reduction and Machine Learning. J. Supercomput. 2019, 75, 3010–3027. [Google Scholar] [CrossRef]
- Abeysekera, S.S. Efficient Frequency Estimation Using the Pulse-Pair Method at Different Lags. In Proceedings of the 2003 International Symposium on Circuits and Systems (ISCAS), Bangkok, Thailand, 25–28 May 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 4, pp. IV-109–IV-112. [Google Scholar]
- Mahapatra, P.R.; ZrniC, D.S. Practical Algorithms for Mean Velocity Estimation in Pulse Doppler Weather Radars Using a Small Number of Samples. IEEE Trans. Geosci. Remote Sens. 1983, GE-21, 491–501. [Google Scholar] [CrossRef]
- Nishiguchi, K.; Kobayashi, M. Improved Algorithm for Estimating Pulse Repetition Intervals. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 407–421. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. ISBN 978-3-319-24573-7. [Google Scholar]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Computer Vision–ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2018; Volume 11211, pp. 833–851. ISBN 978-3-030-01233-5. [Google Scholar]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. arXiv 2017, arXiv:1610.02357. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 6230–6239. [Google Scholar]
- Kanopoulos, N.; Vasanthavada, N.; Baker, R.L. Design of an Image Edge Detection Filter Using the Sobel Operator. IEEE J. Solid-State Circuits 1988, 23, 358–367. [Google Scholar] [CrossRef]
- Amer, G.M.H.; Abushaala, A.M. Edge Detection Methods. In Proceedings of the 2015 2nd World Symposium on Web Applications and Networking (WSWAN), Sousse, Tunisia, 21–23 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–7. [Google Scholar]
- Taghanaki, S.A.; Zheng, Y.; Kevin Zhou, S.; Georgescu, B.; Sharma, P.; Xu, D.; Comaniciu, D.; Hamarneh, G. Combo Loss: Handling Input and Output Imbalance in Multi-Organ Segmentation. Comput. Med. Imaging Graph. 2019, 75, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Rezatofighi, H.; Tsoi, N.; Gwak, J.; Sadeghian, A.; Reid, I.; Savarese, S. Generalized Intersection Over Union: A Metric and a Loss for Bounding Box Regression. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 658–666. [Google Scholar]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. arXiv 2017, arXiv:1608.03983. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).