Abstract
Corner modifications can reduce wind loads acting on supertall buildings and modify the corresponding flow structures. The present study investigated the aerodynamic shape optimization of the corner recession square cylinders with multiple geometric parameters in a large design space via the GA-GRNN surrogate model updating-based multi-objective optimization framework. Six typical optimal aerodynamic shape sections M1~M6 were selected from the Pareto optimal front, and the effects of multiple geometric parameters of these sections on the aerodynamic performance and flow field were analyzed. The results showed that the present multi-objective optimization framework can significantly reduce the computational load and time cost, and significantly improve the optimization efficiency in solving complex engineering problems. The optimal corner recession sections can obviously reduce the mean drag coefficient CD and root mean square lift coefficient CσL while significantly increasing the Strouhal number St of the square cylinder, and it is concluded that the aerodynamic shape optimization can significantly improve the aerodynamic performance of square-sectional supertall buildings. When compared with the benchmark section, the CD and CσL of the optimal section M1 can be reduced up to 45.7% and 84.5%, respectively. Based on the analysis of the flow structures around the optimal sections, the flow mechanism can be attributed to the fact that the corner recession modifications postpone the flow separation, and deflect the separated shear layer towards the side surfaces and suppress the development of vortex shedding in the wake, which leads to significant elongation of the wake length and reduction of the width of the recirculation region. The proposed multi-objective optimization framework in this study can provide an important reference for the aerodynamic shape optimization of building structures and relevant studies.
1. Introduction
Square cylinder is a typical shape widely adopted in supertall buildings and high-rise structures, which generally feature significant flexibility and low damping ratios. Such characteristics make the structures very susceptible to the action of wind, which leads to failure of the structural safety or discomfort of the occupants. Consequently, it is of great importance and necessity to explore aerodynamic control measures to mitigate the wind loads and wind-induced responses of these structures [1,2,3,4].
Aerodynamic control can be further divided into passive aerodynamic control and active aerodynamic control. The former is regarded as the most economical and efficient way to improve the wind resistance performance of supertall buildings. Passive aerodynamic control mainly mitigates the wind loads by changing the building’s exterior shapes. The passive aerodynamic control measures are mainly classified as minor modifications such as corner recession, corner chamfering, and corner rounding [5,6,7,8,9,10,11,12], and major modifications such as setbacks, tapering, twisting, openings, and global cross-section modification [13,14,15,16,17,18,19,20]. Corner modification is one of the most widely accepted aerodynamic control measures, as it only introduces slight changes to the overall building shape and is convenient for construction. In 1971, Davenport [21] took the lead in conducting experimental research on aerodynamic shape optimization of high-rise buildings such as square prisms, chamfered square prisms, and rectangular prisms, and a large number of subsequent related studies were carried out. Through wind tunnel tests of square and rectangular prisms, Kawai [6] studied the effects of corner chamfering, corner recession, and roundness of corners modifications on aeroelastic instability such as vortex-induced resonance and galloping vibration. Tamura and Miyagi [7] studied the aerodynamic characteristics of the basic square cylinder and square cylinders with chamfered and rounded corners under different types of incoming flows. The results showed that when compared with other shapes, it was apparent that the separated flow around the rounded corner square cylinder tended to reattach earlier to the side surface, which significantly reduces the fluctuating wind load of the structure in the across-wind direction. Tse et al. [8] studied the influence of aerodynamic modification on the economy of high-rise buildings, and it was concluded that although aerodynamic treatments would reduce the usable area of high-rise buildings, both corner-chamfered and corner recession modifications could effectively reduce the wind-induced response and eventually reduce the construction cost. Tanaka et al. [9] found that the corner chamfer, corner recession, and helical and cross opening models show superior aerodynamic behaviors in both safety and habitability design compared with the square model. Zhang et al. [10,11] studied the influence of recessed corner recession, chamfered corner, and rounded corner on the aerodynamic force coefficient of a high-rise building with a square section through the force-balance test and fitted the base-bending moment and torque correction coefficient of the model with a different corner recession ratio, corner-chamfered ratio, and rounded corner ratio. Cao et al. [22] studied the influence of corner chamfering, corner recession, and tapering on the along-wind aerodynamic damping ratio of square-sectional supertall buildings using the aeroelastic model test.
It is imperative to note that the previous aerodynamic shape modifications of super-tall buildings mainly rely on the trial-and-error method based on wind tunnel test or CFD numerical simulation. The optimal aerodynamic shape with the least wind loads and the wind-induced responses is determined through limited shape configurations, and the global optimal aerodynamic shape in the design space could not be obtained. With the continuous study on artificial intelligence technology in civil engineering, aerodynamic shape optimization of super-tall buildings through surrogate model is increasingly attractive. Bernardini et al. [17] established a multi-objective aerodynamic shape-optimization method for civil engineering structures by combining an evolutionary algorithm and the Kriging model based on CFD numerical simulation. Elshaer et al. [18] carried out aerodynamic optimization of the building corner by a coupling of optimization algorithm, large eddy simulation, and surrogate model based on the artificial neural network. The study showed that reductions in the order of more than 30% both in along-wind and across-wind responses were obtained through a two-surface chamfering that was constrained to 20% of the building width. Based on the assembled mathematical strategy of experimental design, Kriging surrogate model, ant colony, and genetic algorithm, Sun et al. [23] studied the optimal parameter scheme for the flutter performance of the streamlined box girder section of the Sutong Yangtze River Bridge. The results showed that the critical wind speed of the flutter for the optimal section was increased by 8%, and the inclination angle of the lower web had a more significant impact on flutter performance than the beam height. Wang et al. [24] studied the aerodynamic shape optimization of a square-sectional supertall building with corner recession by using the surrogate model-based multi-objective optimization framework.
In conclusion, studies on the optimization method based on the artificial neural network (ANN) surrogated model have been rarely conducted, and most studies improved the performance of multi-objective optimization by improving the surrogate model accuracy and adopting various sophisticated optimization algorithms. Therefore, this study aimed to propose an efficient multi-objective optimization framework based on the GA-GRNN surrogate model, updating and analyzing the effects of the corner recession modifications on the aerodynamic performance and flow structures. The outline of the present paper is organized as follows: Section 2 introduces the mathematical model and the related geometrical parameters to describe the aerodynamic shape optimization problem; Section 3 shows the solution strategy to the multi-objective aerodynamic shape optimization; Section 4 comprehensively analyzes the aerodynamic performance of and flow structures around the optimal corner recession square sections, and the improvement mechanism of the corner recession modifications on the aerodynamic performance is explored; the main conclusions are drawn in Section 5.
2. Description of the Aerodynamic Shape Optimization Problem
2.1. Mathematical Model of the Aerodynamic Shape Optimization
Aerodynamic shape optimization of the corner recession square cylinder is a multi-objective optimization problem, which can be described by the following mathematical model:
where f (X) is the objective function; g (X) and h (X) are the inequality functions and equality constraint functions respectively; m, p and q are the numbers of objective and constraint functions respectively; X is the design variable, and X1 and Xk are the lower and upper limits of the design variable interval.
The basic principles to determine the objective functions for the aerodynamic shape optimization are as follows:
- (1)
- The objective functions should quantitatively represent the aerodynamic performance of the cylinder, and change of the design variables should significantly impact the objective functions’ values.
- (2)
- To ensure the surrogate model’s optimization accuracy, the problem needs to be simplified by using a limited number of objective functions.
Based on the abovementioned considerations, the mean drag coefficient CD and the root mean square lift coefficient CσL of the corner recession square cylinder were selected as the objective functions. Therefore, f (X) can be defined as:
2.2. Geometric Parameters and Design Space
Corner recession modification is one of the most effective aerodynamic optimization measures at the cross-sectional level, which can effectively reduce the wind loads and wind-induced responses of square cylinders [3,4,7]. In order to further study the influence of corner recession modification on the aerodynamic force and flow field structure of the corner recession square cylinders, three geometric parameters, including the corner recession ratio, number of corner recessions n, and corner recession angle α, are defined to describe the shape of a 2D square cylinder with different corner recessions. The ratio ranges from 1% to 20% with an interval of 1%. The number of corner recession n ranges from 1 to 5 with the gradient of 1. The corner recession angle α ranges from 60° to 120°, and the gradient is 5°. Figure 1 depicts the geometric parameters of the 2D corner recession square cylinder, where the incoming wind direction angle is 0°.
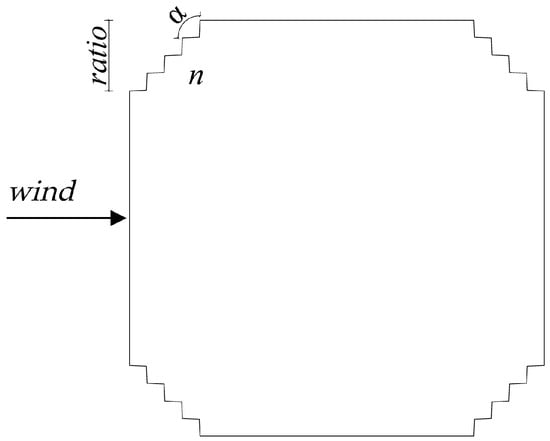
Figure 1.
Schematic diagram of the geometric parameters of the 2D square cylinder with corner recession.
According to the three parameters to describe the corner recession square cylinder, the total samples in the whole design space can be determined as high as 20 × 5 × 13 = 1300. If all the corner recession square cylinders are investigated, it will cost a lot of computation resources and time. Therefore, it is necessary to choose a reasonable solution strategy.
3. Solution Strategy
3.1. Proposal of the Surrogate Model Updating-Based Aerodynamic Shape Optimization Framework
In order to significantly reduce the time cost of aerodynamic shape optimization, a novel aerodynamic shape optimization framework based on the surrogate model updating was introduced. Instead of conducting the complete CFD numerical simulations for all the samples in the whole design space, aerodynamic force coefficients of a very small part of samples of the corner recession square cylinder, which is determined by the experiment design method, were computed by the CFD numerical simulations, and then a surrogate model for predicting the aerodynamic force coefficients was established; the aerodynamic shape optimization was carried out by minimizing the aerodynamic force coefficients of the corner recession square cylinders as the optimization objective, and the typical solutions were selected from the obtained Pareto optimal front as the potential optimization solutions.
The overall optimization process of the aerodynamic shape optimization framework is illustrated in Figure 2, which is summarized as follows.
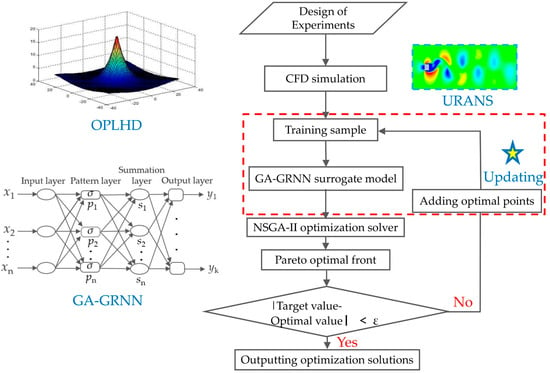
Figure 2.
Optimization process of aerodynamic shape for the square section with corner recession.
- (1)
- The optimal Latin hypercube design (OPLHD) [24,25,26] was adopted to sample the design space and generate the initial samples, and the aerodynamic force coefficients (including CD and CσL) of each initial sample were computed by CFD numerical simulation.
- (2)
- Based on the relation between input variables (geometric parameters) and output variables (aerodynamic force coefficients) of the initial sample points, the training set, validation set, and test set were allocated according to a certain proportion, and the GA-GRNN surrogate model was trained continuously until the test set verified that its prediction accuracy met the requirements.
- (3)
- To search for the objective functions (minimum CD and CσL) in the whole design space, based on the GA-GRNN surrogate model, the multi-objective non-dominated sorting genetic algorithm (NSGA-II) was adopted for the optimization, and the Pareto optimal front solutions were obtained, in which some of the solutions were selected for CFD verification.
- (4)
- If the prediction accuracy of the selected Pareto optimal front solutions satisfied the convergence criteria, the Pareto optimal front samples were added to the training samples, and a new round of training and optimization was carried out for the GA-GRNN surrogate model. The optimization accuracy was continuously improved through iterative updating until the convergence criteria were met, and finally the optimization solutions were acquired.
For more detailed information of the surrogate model-updating-based aerodynamic shape optimization framework, please refer to the literature [24].
3.2. CFD Simulation
Constructing a high-precision surrogate model is the key to realizing the aerodynamic shape optimization of the corner recession square cylinder. The CFD numerical simulation results directly affect the prediction accuracy of the surrogate model, which is the basis of the entire aerodynamic shape optimization process. Therefore, the appropriate setting of the computational domain and boundary conditions, high-quality mesh, and choice of turbulence model and solution method are crucial.
It should be noted that all CFD calculations in the entire aerodynamic shape optimization process were simulated by 2D numerical simulation, and the reasons are as follows:
- (1)
- The paper aimed to search for the cross-sectional configuration with the most favorable aerodynamics, and the specific numerical value of the section aerodynamic coefficient is not strictly required. Previous 2D and 3D numerical simulation studies show that the influence law of section shape change on the aerodynamic performance of the structure obtained by the two methods is consistent, but there are only numerical differences [3,4,24].
- (2)
- A large amount of CFD calculation is required in the optimization process, and the 3D numerical simulation is time-consuming, so it is very difficult to realize in the existing conditions. In addition, the method of simplifying the 3D model to the 2D model for aerodynamic shape optimization has been extended to the field of civil engineering [17].
The ICEM software was adopted to establish the two-dimensional computational model of the square cylinder. The side length D of the computational model was set as 0.1 m. In order to ensure the full development of the flow field around the square cylinder, the size of the computational domain (length × width) was set as 7 m × 4 m, in which the upstream length is 2 m and the downstream length is 5 m, as shown in Figure 3. The left inlet condition and the right outlet boundary condition of the computational domain were set as velocity-inlet and outflow respectively, and symmetry was used on the other walls, and wall was used on all the surfaces of the computational model.
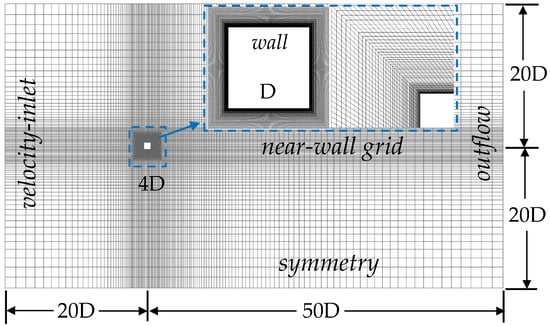
Figure 3.
Dimensions and mesh partition of the computational domain.
CFD numerical simulations were conducted by using the FLUENT 18.0 software platform, and the unsteady URANS method based on the SST k-ω turbulence model was adopted. The second-order upwind scheme was employed to discretize the turbulent kinetic energy and dissipation rate, the QUICK scheme was adopted to discretize the momentum term, and Standard was adopted for the pressure term. The SIMPLEC algorithm was employed to solve the coupled equation of pressure and velocity, and the skewness correction coefficient was set as 1.0. The convergence criteria for the iterative residuals of all parameters were set as less than 1 × 10−5, and the velocity and pressure of all monitoring points do not change. In order to ensure the accuracy and stability of CFD results, structured grids were adopted, and the zone near the square cylinder was refined (see Figure 3). It should be noted that, in order to capture the flow characteristics near the corner recession, the grid at the corner recession is locally refined. The total number of grids for different cases is between 100,000 and 350,000. The grid independence verification of the square cylinder without corner recession and its comparison with the existed experimental data and numerical simulation results were conducted, and due to the space limitations, more detailed information can be found in reference [24]. For the aerodynamic shape optimization in this paper, each time step of CFD simulation was set as 0.0005 s, and the total time steps was 5000.
The incoming wind speed V of the computational domain was set as 10 m/s and the turbulence intensity Iu was set as 10%, and the corresponding Reynolds number Re was 69,000. The turbulent kinetic energy k and specific dissipation rate ω were calculated by Equations (3) and (4).
The mean and fluctuating wind pressure coefficients and aerodynamic force coefficients of the corner recession square cylinders are defined by Equations (5)–(13).
where Cp(t), CD(t), and CL(t) are the time histories of wind pressure coefficient, drag coefficient, and lift coefficient, respectively; p(t), FD(t) and FL(t) are the time histories of wind pressure, drag force and lift force respectively; ρ is the air density; , , and are the mean wind pressure coefficient, mean drag coefficient, and mean lift coefficient, respectively, which are abbreviated as Cp, CD, and CL for convenience; Cσp, CσD, and CσL are the fluctuating wind pressure coefficient, root mean square drag coefficient, and root mean square lift coefficient, respectively.
The Strouhal number St is defined as:
where, f is the vortex shedding frequency (Hz).
3.3. GA-GRNN Surrogate Model
Given the highly nonlinear characteristics of aerodynamic shape optimization of the corner recession cross-section, the classical Generalized Regression Neural Network (GRNN) was selected to construct the surrogate model. GRNN has a strong nonlinear mapping ability and a high degree of fault tolerance and robustness. Even if the number of samples is small, the network output can converge to the optimal regression surface. Meanwhile, the smoothing factor σ of GRNN mainly relies on subjective experience and is manually set to a fixed value, so the generalization ability is poor [27]. In order to improve the generalization ability of GRNN and minimize the influence of human factors, the global random search feature of the genetic algorithm (GA) was used to search for the optimal σ, and the specific steps are shown in Figure 4 Compared with GRNN, the prediction accuracy and generalization ability of the GA-GRNN surrogate model are significantly improved [24]. The GA-GRNN surrogate model’s structure is divided into four layers: the input layer, the pattern layer, the sum layer, and the output layer, as shown in Figure 5.
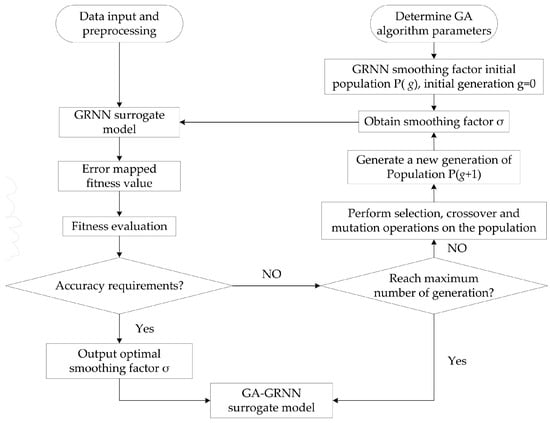
Figure 4.
Optimization process of the smoothing factor of the GA-GRNN surrogate model.
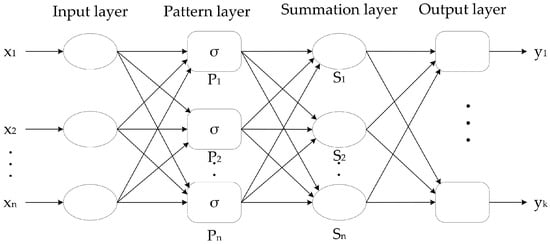
Figure 5.
Schematic diagram of the structure of the GA-GRNN surrogate model.
A well-established GA-GRNN surrogate model is the basic premise for obtaining reliable aerodynamic shape optimization results. Based on the existing wind tunnel test data of a supertall building model, the reasonable number of initial sample points and proportion division of sample data sets required by the GA-GRNN surrogate model is discussed, and more detailed information will be discussed in another paper. In this study, the number of the initial sample points was set as 40, and the sample data ratio of training set: validation set: test set was 7:2:1, which accounts for 28 training sample points, 8 validation sample points, and 4 test sample points, as shown in Table 1.

Table 1.
Initial sample points of the corner recession square cylinders and the corresponding aerodynamic coefficients.
Before optimization of the surrogate model, the test set was used to verify the performance of the constructed GA-GRNN surrogate model. The maximum absolute error (MAE), root mean square error (RMSE), and coefficient of determination R2 were selected as the indicators to evaluate the performance [28,29]. MAE evaluates the local prediction accuracy of the GA-GRNN model, RMSE evaluates the global prediction accuracy of the GA-GRNN surrogate model, and R2 evaluates the fit of the GA-GRNN surrogate model. The less the MAE or RMSE value is, the higher the GA-GRNN surrogate model’s prediction accuracy will be. The R2 value lies in the interval (0, 1). The closer the R2 value comes to 1, the better the fitting degree and the stronger the generalization ability of the GA-GRNN surrogate model will be. The three performance indicators can be expressed as follows.
where, N represents the number of sample points in the test set; yi and represent the CFD simulation result and the predicted value of the GA-GRNN surrogate model of the i-th test sample point, respectively; is the mean value of the CFD simulation result of the N test set sample points.
Figure 6 shows the comparisons of the predicted aerodynamic force coefficients of the test sample points and the corresponding CFD simulation results, where CD,CFD and CσL,CFD are the aerodynamic force coefficients obtained by the CFD simulation, and CD,GA-GRNN and CσL,GA-GRNN are the aerodynamic force coefficients predicted by the GA-GRNN surrogate model. It can be seen in the figure that the predicted values of CD and CσL are consistent with the CFD simulation results.
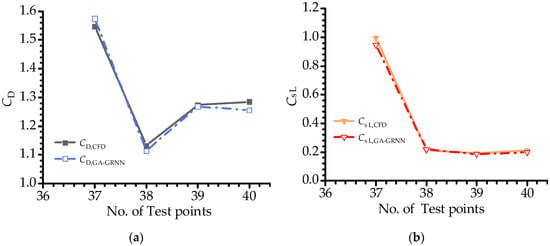
Figure 6.
The aerodynamic force coefficients of the test sample points in terms of (a) The mean drag coefficient CD and (b) The root mean square lift coefficient CσL.
Table 2 shows the performance indicators of the GA-GRNN surrogate model. It can be seen that MAE and RMSE for CD were only 0.032 and 0.023, and MAE and RMSE for CσL were also very small, with the values of 0.061 and 0.044, respectively. Therefore, it can be concluded that, in terms of either global accuracy or local accuracy, the GA-GRNN surrogate model has high prediction accuracy. Besides, the R2 values for CD and CσL were as high as 0.975 and 0.984, indicating that the GA-GRNN surrogate model has an excellent fitting effect and strong generalization ability.

Table 2.
Calculated values of performance indicators of the GA-GRNN surrogate model.
3.4. Convergence Criteria for the Aerodynamic Shape Optimization
To evaluate the aerodynamic shape optimization accuracy of the corner recession square cylinder, the relative error Er1~Er2 and the convergence criteria (see Equations (18) and (19)) were defined as the evaluation indexes of the optimization accuracy of aerodynamic force coefficients CD and CσL. It should be noted that the CD and CσL of the square cylinder are significantly reduced by the corner recession modification, and the CσL value is much smaller than the CD. Even though the absolute errors between the optimal minimum CσL predicted by the aerodynamic shape optimization and the CFD numerical simulation are small, the relative error is significant. Therefore, the prediction accuracy of the minimum CD is higher than that of minimum CσL. Thus, the convergence tolerance of Er1 and Er2 was set to ±2% and ±5%, respectively (see Figure 7). In order to ensure the accuracy and stability of the optimization results, when the aerodynamic coefficient optimization value of the surrogate model was updated two consecutive times and satisfies Equations (18) and (19), the optimization process ended.
where CDmin,GA-GRNN and CσLmin,GA-GRNN are the mean drag coefficient and root mean square lift coefficient respectively of the selected Pareto optimal front solution based on optimization of the GA-GRNN surrogate model; CDmin,CFD and CσLmin,CFD are the mean drag coefficient and root mean square lift coefficient respectively of the above optimal point obtained by CFD simulation, namely, the exact values.
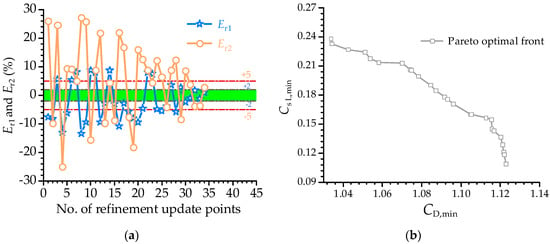
Figure 7.
(a) Updating process of the relative errors of the aerodynamic force coefficients and (b) Pareto-optimal set of the aerodynamic force coefficients.
In the process of aerodynamic shape optimization, when the surrogate model is updated, two optimal points are selected from the Pareto front solutions for CFD verification according to the objective functions of minimum CD and CσL respectively. If the prediction accuracy does not meet the convergence criteria, the two optimal points are added to the training sample set to reconstruct the GA-GRNN surrogate model. The iterative updating process will be continued until the convergence criteria are satisfied.
4. Results and Analysis
4.1. Aerodynamic Shape Optimization Results
Figure 7a shows the evolution of the relative errors Er1 and Er2 during the iterative updating process of the aerodynamic shape optimization. It can be seen in the figure that the relative errors are less than the corresponding convergence criteria after 17 iterations of updating, i.e., 34 refinement update points. Figure 7b shows the Pareto optimal front solutions of the two optimization objectives (minimum CD and CσL). As shown in the figure, the two optimization objectives were equally restricted, and the sample points on the Pareto optimal front can be regarded as the optimal solutions.
In the whole process of aerodynamic shape optimization, a total of 74 sample points were computed by the CFD simulation, accounting for 5.69% of the total number of samples (1300) in the whole design space. Therefore, the computational load and time cost were significantly reduced, and thus the computational efficiency was remarkably improved.
Based on the Pareto optimal front obtained by optimization of the GA-GRNN surrogate model, six optimal aerodynamic shape sections were selected and abbreviated as M1~M6, respectively. The geometric parameters of such sections are shown in Figure 8. It can be seen that the number of corner recessions for M1 and M2 were both 1, while the number of corner recessions for M3~M6 were 2, 3, 4, and 5 respectively.
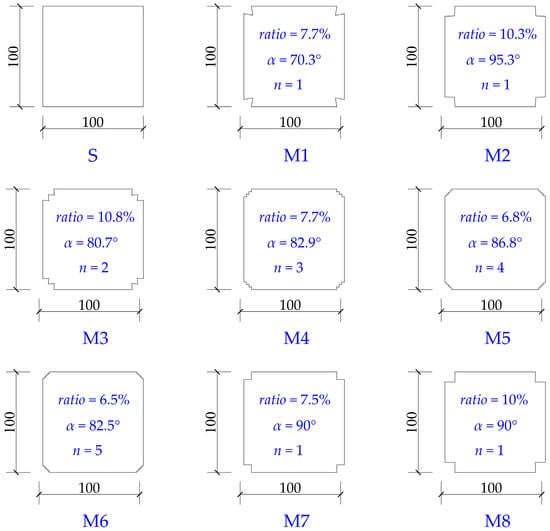
Figure 8.
Schematic diagram of the geometric parameters of the benchmark section and the sections M1~M8 (Unit: mm).
4.2. Aerodynamic Force Coefficients and Strouhal Number St
Existing studies have declared that the aerodynamic performance of the corner recession square cylinder, whose corner recession ratio is 7.5% [10] or 10% [12,30], and whose number of corner recession is 1 and corner recession angle is 90°, has an overwhelming advantage when compared with other limited corner recession square cylinders. For comparative analysis, the geometric parameters of the abovementioned two sections, which are abbreviated as M7~M8, are also shown in Figure 8.
To quantitatively evaluate the aerodynamic shape optimization effect of the sections M1~M8, the square section without corner recession was taken as the benchmark section, abbreviated as S (see Figure 8). The mean drag reduction coefficient CDR and the root mean square lift reduction coefficient CσLR respectively, which were calculated by Equations (20) and (21), were used to evaluate the aerodynamic performance.
where CDB and CσLB are the mean drag coefficient and the root mean square lift coefficient of the benchmark section S respectively; CDC and CσLC are the mean drag coefficient and the root mean square lift coefficient of the sections M1~M8 respectively.
Figure 9 shows the comparisons of the mean drag coefficient CD, the root mean square lift coefficient CσL, and Strouhal number St for the benchmark section S, and optimal sections M1~M8 at the wind direction angle of 0°. It can be illustrated in the figure that, when compared with the benchmark section S, the aerodynamic coefficients of optimal sections M1~M8 were significantly decreased, while the Strouhal number St was significantly increased.
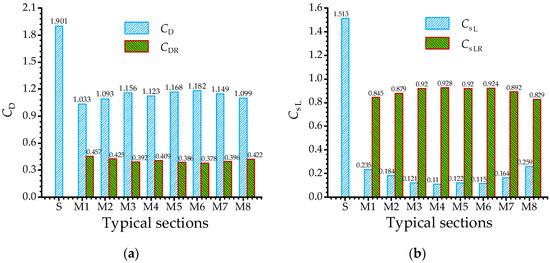
Figure 9.
Aerodynamic force coefficients and Strouhal number of the benchmark section and the sections M1~M8: (a) CD and CDR, (b) CsL and CsLR, and (c) St.
As is shown in Figure 9a, among the optimal sections M1~M8, the section with the minimum CD was M1, whose mean drag reduction coefficient CDR was 0.457; while the section with the maximum CD was M6, and its CDR reached 0.378. Compared with multi-corner recession square sections, the mean drag coefficient CD of the single-corner recession sections (M1, M2, M7, and M8) decreased significantly. By comparing the sections M1 and M7, as well as the sections M2 and M8, it was found that the corner recession angle α had an important influence on the CD of the sections. The CD value of M1 was significantly smaller than that of M7, while the CD value of M2 was quite close to that of M8, indicating that the decrease of α is more beneficial to reduce the CD when α is less than 90°, while the influence of corner recession angle α was not obvious when α was larger than 90°. As can be seen in Figure 9b, when compared with the benchmark section S, the reduction effect of the root mean square lift coefficient CσL of the sections M1~M8 was very significant, and the maximum root mean square lift reduction coefficient CσLR was as high as 0.928, which is observed at the section M4. By comparison of the aerodynamic performances of the sections M1~M8, it was found that the CσL of the multi-corner recession sections (M3~M6) were smaller than those of the single-corner recession sections (M1, M2, M7, and M8). By comparing the sections M1 and M7, as well as the sections M2 and M8, the CσL value of M1 was significantly larger than M7, while M2 was significantly smaller than M8. The results indicated that the increase of α is more beneficial to reduce the CσL when α is larger than 90°. According to the above analysis, it can be concluded that the corner recession modification can significantly reduce the CD and CσL, in which the single-corner recession (n = 1) and acute angle α (α < 90°) are beneficial to reduce CD. In contrast, the multi-corner recession (n = 2~5) and obtuse angle α (α > 90°) are more effective in reducing CσL.
As can be seen from Figure 9c, the effect of corner recession modification on the Strouhal number St is contrary to the variation trend of the aerodynamic force coefficients. Compared with the benchmark section S, the St of the optimal sections M1~M8 were significantly increased, and the maximum St was 0.216 for the section M1, which indicates that the vortex shedding frequency of the section M1 is the largest among all the sections. The increase of St will lead to larger critical wind speed so as to postpone the vortex shedding resonance of flexible supertall buildings. By comparison and analysis of Figure 9a–c, it can be seen that the CD decreased with the increase of the Strouhal number St, while the CσL first decreased sharply and then tended to be flat with the increase of the Strouhal number St.
According to the above analysis, the optimal corner recession sections obtained by the aerodynamic shape optimization can significantly improve the aerodynamic performance of the square cylinder. Additionally, it is also evident that the GA-GRNN surrogate model updating-based multi-objective optimization framework has wide perspective applications due to its advantage of significantly improving the optimization efficiency in solving complex engineering problems. In reference [24], the authors conducted a comprehensive study on aerodynamic shape optimization of a corner recession square cylinder with four design parameters, such as corner recession ratio, number of corner recession n, corner recession angle α, and wind direction angle θ. The total number of samples in the whole design space is 5200, which is much larger than the 1300 samples with three design parameters in this paper. Therefore, it is necessary to compare the aerodynamic performance of these two aerodynamic shape optimization results so as to validate the optimization accuracy.
The accuracy of the optimization results of the GA-GRNN surrogate model is the fundamental premise for improving the optimization efficiency. Therefore, the section M1 in this study was selected as the aerodynamic shape optimization result of the corner recession square cylinders with three design parameters, and the Section 1 in the reference [24], abbreviated as the section M9 in this paper, was selected as the aerodynamic shape optimization result of the corner recession square cylinders with four design parameters. The design parameters of the section M9 were set as follows: the corner recession ratio is 7.9%, the number of corner recessions n is 1, and the corner recession angle α is 67.2°.
Table 3 shows the aerodynamic coefficients and the Strouhal number of the sections M1 and M9. It can be seen that the aerodynamic coefficients and Strouhal number St of the section M1 were very close to those of the section M9, with the maximum error less than 3%. Therefore, it is concluded that the aerodynamic shape optimization results of the corner recession square cylinder based on the GA-GRNN surrogate model with three or four design parameters are highly consistent.

Table 3.
Aerodynamic force coefficients and Strouhal number of the sections M1 and M9.
4.3. Wind Pressure Coefficients Distributions
Figure 10 shows the distributions of the mean wind pressure coefficient Cp and fluctuating wind pressure coefficient Cσp for the benchmark section S and optimal sections M1~M8, respectively. The wind direction angle was 0°. Generally, each section’s wind pressure coefficient distribution curve had a similar overall trend, but the numerical differences were significant, especially for the fluctuating wind pressure coefficient.
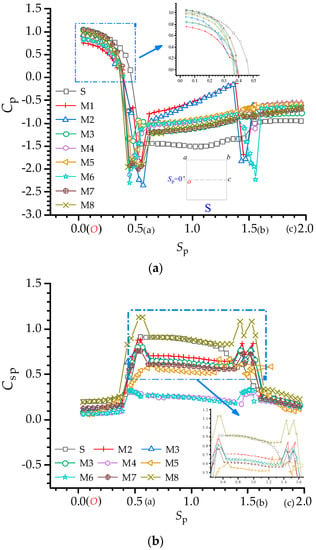
Figure 10.
Wind pressure coefficients distributions of the benchmark section S and optimal sections M1~M8: (a) Cp and (b) Cσp.
As can be seen from Figure 10a, on the windward surface (Oa), the mean wind pressure coefficient Cp of all the sections except for the corner modification regions were mainly positive and their variation trends were similar. Compared with the benchmark section S, the Cp of the sections M1~M8 decreased, in which the Cp of section M1 decreased the most. All the sections were subjected to negative pressures on the side (ab) and leeward (bc) surfaces. When compared with the benchmark section S, the absolute values of the Cp of the sections M1~M8, except for the corner modification regions, showed an obvious decrease. On the side surface (ab), the absolute values of the Cp of the sections M1~M2 decreased the most; while on the leeward surface (bc), the absolute values of the Cp of the sections M4~M6 decreased the most. The absolute values of the Cp of the sections M1~M8 showed a sudden increase in the corner recession modification region, and special attention should be paid to the corner modification region in the wind resistance design. Based on the analysis of Figure 10b, the influence of corner recession modification on the fluctuating wind pressure coefficient Cσp of the sections is basically consistent with the variation trend of the mean wind pressure coefficient, and the sections M4 and M6 were the most effective in reducing the Cσp. However, it should be noted that, compared with the benchmark section S, the Cσp of the section M8 showed an increasing trend, especially for the corner modification region.
4.4. Time-Averaged Flow Field
In this section, the flow-field visualization based on the CFD numerical simulation is used to analyze the time-averaged flow field around each section and explore the influence mechanism of corner recession modification on the aerodynamic performance of the square cylinder. Due to the space limitations, Figure 11 shows the time-averaged streamlines around the benchmark section S and optimal sections M1~M8. Meanwhile, for the convenience of analysis, Figure 11 also shows the wake length (L) and wake width (W) of each section and their reduction coefficients LR and WR. As shown in the figure S in Figure 11. The wake length L was defined as the horizontal distance from the section center to the free saddle point of the time-averaged streamlines; the wake width W was defined as the maximum width when the average wake velocity returns to half of the maximum velocity at the profile of x/D = 1, where x is the streamwise coordinate, and D is the side length of the reference square section [31].

Figure 11.
Time-averaged streamlines around different the benchmark section S and the optimal sections M1~M8.
According to Figure 11, the flow is separated at the corner recession on the windward surface of each section. The recirculation areas formed near the section’s upper and lower sides and the wake behind the section. By observing Figure 11, it can be seen that:
- (1)
- When compared with the benchmark section S, the wake lengths L of the sections M1~M8 were significantly increased, and the maximum L was 2.41D for the section M6. Increase of the wake length can be attributed to the backward shift of the separation point caused by the corner recession modification, and the vortices in the wake region were far away from the leeward surface, which led to a small absolute value of the mean wind pressure coefficient Cp on the leeward surface. Such a decrease of wind pressure resulted in reduction of the pressure drag of the corner recession sections, and thus the mean drag coefficient CD.
- (2)
- When compared with the benchmark section S, the corner recession correction made the separation point of the optimal sections M1~M8 move backwards, restraining the development of vortex shedding in the wake and deflecting the separated shear layer towards the side surfaces [4,7,32], and thus the width of the recirculation region of the sections M1~M8 was significantly reduced. The minimum wake width W was 1.09D for the section M1. As a result, the vortex shedding intensity was restrained, and the root mean square lift coefficient CσL was significantly reduced.
4.5. Instantaneous Flow Field
In order to further analyze the mechanism of aerodynamic performance improvement of the optimal sections M1~M8, Figure 12 shows the instantaneous vorticity contours around the benchmark section S and sections M1~M8. It can be seen from the figure that:
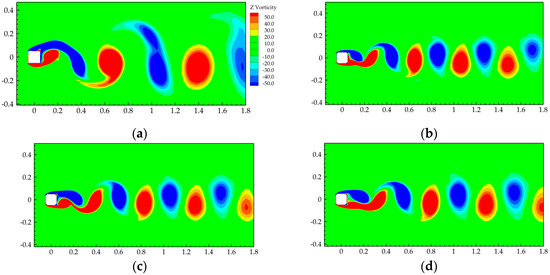
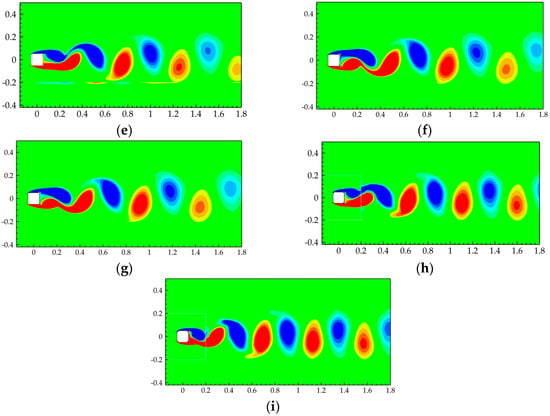
Figure 12.
Instantaneous vorticity contours around different sections: (a) S and (b–i) M1~M8.
- (1)
- There were plenty of vortex structures around the sections. The lower side was dominated by positive vortices, while negative vortices dominated the upper side. With vortices’ formation and development in the downstream, alternating vortex shedding occurred in the wake region, and the corner recession modification did not change the vortex development trend.
- (2)
- When compared with the benchmark section S, the width of vortex street in the wake region of the sections M1~M8 was significantly reduced, and the reason can be attributed to the corner recession modification promoting the reattachment of the separated shear layer, and the separated flows being brought closer to the side surface due to the entrainment of small vortices, accompanied by constraint of the separation angles, thus significantly reducing the mean drag coefficient CD. It can be concluded that the narrow vortex street width in the wake area is the main reason for the decrease in CD surfaces [7].
- (3)
- The length scales of vortex shedding for the sections M1~M8 were reduced when compared with the benchmark section S, and the number of vortex sheds increased. It can be concluded that the corner recession modification can suppress the vortex shedding to a certain extent, reduce the intensity of vortex shedding, and accelerate the vortex shedding with a larger Strouhal number St (vortex shedding frequency). Therefore, the CσL of the sections M1~M8 were significantly reduced.
5. Conclusions
Based on the GA-GRNN surrogate model updating and NSGA-II algorithm, the aerodynamic shape optimization of a square cylinder with corner recession modification was studied. Six optimal aerodynamic shape sections M1~M6 with different corner recession numbers were selected from the Pareto optimal front, and the aerodynamic performance and surrounding flow structures of these optimal sections were analyzed, and the improvement mechanism of corner recession modifications on the aerodynamic performance of square cylinder was analyzed. The main conclusions are summarized as follows.
- (1)
- In the whole process of aerodynamic shape optimization, a total of 74 sample points were computed by the CFD simulation, accounting for 5.69% of the total number of samples (1300) in the whole design space. Additionally, the aerodynamic shape optimization results based on the GA-GRNN surrogate model with three or four design parameters were highly consistent. It is concluded that the present GA-GRNN surrogate model updating-based multi-objective optimization framework can significantly improve the optimization efficiency in solving complex engineering problems, while still ensuring the prediction accuracy. The proposed multi-objective optimization framework in this study can provide an important reference for the aerodynamic shape optimization of building structures and relevant studies.
- (2)
- Compared with the benchmark section S, the mean drag coefficient CD and root mean square lift coefficient CσL of the sections M1~M6 were significantly reduced, and the maximum values of the reduction coefficients CDR and CσLR could reach 0.457 and 0.928, which appeared in the sections M1 and M4, respectively. The corner recession modifications significantly increased the Strouhal number St of the square cylinder, and the maximum St was 0.214 for the section M1. The increase of St will lead to larger critical wind speed so as to postpone the vortex shedding resonance of flexible supertall buildings.
- (3)
- Based on the analysis of the flow structures around the optimal sections M1~M8, it is concluded that the corner recession modifications can postpone the flow separation and deflects the separated shear layer towards the side surfaces, which leads to significant elongation of the wake length and reduction of the width of the recirculation region, and thus the CD is reduced. Besides, the corner recession modifications can suppress the intensity of vortex shedding and increase the number of shedding vortices, and accelerate the vortex shedding with a larger Strouhal number St (vortex shedding frequency), and thus the CσL of the sections M1~M8 are significantly reduced.
Author Contributions
Conceptualization, C.Z. and Y.W.; methodology, C.Z., Z.W. and Y.W.; software, Z.W. and J.A.M.; validation, Z.W. and J.A.M.; formal analysis, Z.W.; investigation, Z.W.; resources, C.Z.; data curation, Z.W. and J.A.M.; writing—original draft preparation, Z.W. and J.A.M.; writing—review and editing, C.Z. and Z.W.; visualization, Z.W.; supervision, C.Z.; project administration, C.Z.; funding acquisition, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by China State Construction Engineering Corporation (No. CSCEC-2020-Z-58-2); Heilongjiang Province Natural Science Foundation of China (No. LH2019E050).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data supporting this study’s findings are available from the corresponding author, [Zheng, C.R.], upon reasonable request.
Acknowledgments
The authors want to express their appreciation for the financial support provided by the China State Construction Engineering Corporation (No. CSCEC-2020-Z-58-2) and the Heilongjiang Province Natural Science Foundation of China (No. LH2019E050).
Conflicts of Interest
The authors declare no conflict of interest. There are no financial and personal relationships with other people or organizations that can inappropriately influence the work. There is no professional or other personal interest which could be construed as influencing the position presented in or the review of the manuscript.
References
- Kareem, A.; Kijewski, T.; Tamura, Y. Mitigation of motions of tall buildings with specific examples of recent applications. Wind Struct. 1999, 2, 201–251. [Google Scholar] [CrossRef]
- Irwin, P.A. Bluff body aerodynamics in wind engineering. J. Wind Eng. Ind. Aerodyn. 2008, 96, 701–712. [Google Scholar] [CrossRef]
- Zheng, C.R.; Xie, Y.; Khan, M.; Wu, Y.; Liu, J. Wind-induced responses of tall buildings under combined aerodynamic control. Eng. Struct. 2018, 175, 86–100. [Google Scholar] [CrossRef]
- Zheng, C.R.; Wang, Z.Y.; Zhang, J.; Wu, Y.; Jin, Z.; Chen, Y. Effect of the combined aerodynamic control on the amplitude characteristics of wind loads on a tall building. Eng. Struct. 2021, 245, 112967. [Google Scholar] [CrossRef]
- Kwok, K.C.S.; Wilhelm, P.A.; Wilkie, B.G. Effect of edge configuration on wind-induced response of tall buildings. Eng. Struct. 1988, 10, 135–140. [Google Scholar] [CrossRef]
- Kawai, H. Effect of corner modifications on aeroelastic instabilities of tall buildings. J. Wind Eng. Ind. Aerodyn. 1998, 74, 719–729. [Google Scholar] [CrossRef]
- Tamura, T.; Miyagi, T. The effect of turbulence on aerodynamic forces on a square cylinder with various corner shapes. J. Wind Eng. Ind. Aerodyn. 1999, 83, 135–145. [Google Scholar] [CrossRef]
- Tse, K.T.; Hitchcock, P.A.; Kwok, K.C.; Thepmongkorn, S.; Chan, C.M. Economic perspectives of aerodynamic treatments of square tall buildings. J. Wind Eng. Ind. Aerodyn. 2009, 97, 455–467. [Google Scholar] [CrossRef]
- Tanaka, H.; Tamura, Y.; Ohtake, K.; Nakai, M.; Kim, Y.C. Experimental investigation of aerodynamic forces and wind pressures acting on tall buildings with various unconventional configurations. J. Wind Eng. Ind. Aerodyn. 2012, 107, 179–191. [Google Scholar] [CrossRef]
- Zhang, Z.; Quan, Y.; Gu, M.; Xiong, Y. Effects of corner recession modification on aerodynamic coefficients of square high-rise buildings. China Civ. Eng. J. 2013, 46, 58–65. [Google Scholar]
- Zhang, Z.W.; Quan, Y.; Gu, M.; Xiong, Y. Effects of corner chamfering and rounding modification on aerodynamic coefficients of square tall buildings. China Civ. Eng. J. 2013, 46, 12–20. [Google Scholar]
- Zheng, C.R.; Zhang, J.T.; Zhang, Z.D. Experimental investigation on characteristics of mean wind loads of high-rise buildings controlled by corner recession and air-suction. J. Build. Struct. 2016, 37, 125–131. [Google Scholar]
- Kim, Y.; Kanda, J. Effects of taper and set-back on wind force and wind-induced response of tall buildings. Wind Struct. 2010, 13, 499–517. [Google Scholar] [CrossRef]
- Kim, Y.C.; Kanda, J. Wind pressures on tapered and set-back tall buildings. J. Fluids Struct. 2013, 39, 306–321. [Google Scholar] [CrossRef]
- Kim, Y.C.; Tamura, Y.; Tanaka, H.; Ohtake, K.; Bandi, E.K.; Yoshida, A. Wind-induced responses of super-tall buildings with various atypical building shapes. J. Wind Eng. Ind. Aerodyn. 2014, 133, 191–199. [Google Scholar] [CrossRef]
- Deng, T.; Yu, X.; Xie, Z. Aerodynamic measurements of across-wind loads and responses of tapered super high-rise buildings. Wind Struct. 2015, 21, 331–352. [Google Scholar] [CrossRef]
- Bernardini, E.; Spence, S.M.J.; Wei, D.; Kareem, A. Aerodynamic shape optimization of civil structures: A CFD-enabled Kriging-based approach. J. Wind Eng. Ind. Aerodyn. 2015, 144, 154–164. [Google Scholar] [CrossRef]
- Elshaer, A.; Bitsuamlak, G.; Damatty, A.E. Enhancing wind performance of tall buildings using corner aerodynamic optimization. Eng. Struct. 2017, 136, 133–148. [Google Scholar] [CrossRef]
- Elshaer, A.; Bitsuamlak, G. Multiobjective aerodynamic optimization of tall building openings for wind-induced load reduction. J. Struct. Eng. 2018, 144, 04018198. [Google Scholar] [CrossRef]
- Li, Y.G.; Zhang, M.Y.; Li, Y.; Li, Q.S.; Liu, S.J. Experimental study on wind load characteristics of high-rise buildings with opening. Struct. Des. Tall Spec. 2020, 29, e1734. [Google Scholar]
- Davenport, A.G. The response of six building shapes to turbulent wind. Philos. Trans. R. Soc. Lond. 1971, 269, 385–394. [Google Scholar]
- Cao, H.L.; Quan, Y.; Gu, M. Along-wind aerodynamic damping of high-rise buildings with aerodynamically modified square cross-sections. J. Vib. Shock 2012, 31, 84–89. [Google Scholar]
- Sun, Q.; Zhou, Z.Y.; Hu, C.X.; Qing, P.; Huang, D.M. Numerical aerodynamic shape optimization of streamlined box. J. Harbin Inst. Technol. 2021, 53, 93–100. [Google Scholar]
- Wang, Z.Y.; Zheng, C.R.; Joshua, A.M.; Wu, Y. Aerodynamic shape optimization of a square supertall building with corner recession based on Surrogate model. China Civ. Eng. J. 2022, 1–12. [Google Scholar] [CrossRef]
- Jin, R.C.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Inference 2005, 134, 268–287. [Google Scholar] [CrossRef]
- Jourdan, A.; Franco, J. Optimal Latin hypercube designs for the Kullback-Leibler criterion. Asta-Adv. Stat. Anal. 2010, 94, 341–351. [Google Scholar] [CrossRef]
- Vidya, S.; Janani, E.S.V. Tabu search algorithm based general regression neural network for long term wind speed predictions. Automatika 2020, 61, 657–669. [Google Scholar] [CrossRef]
- Cheng, M.; Jiang, P.; Hu, J.X.; Shu, L.; Zhou, Q. A multi-fidelity surrogate modeling method based on variance-weighted sum for the fusion of multiple non-hierarchical low-fidelity data. Struct. Multidiscip. Optim. 2021, 64, 3797–3818. [Google Scholar] [CrossRef]
- Ulaganathan, S.; Couckuyt, I.; Ferranti, F.; Laermans, E.; Dhaene, T. Performance study of multi-fidelity gradient enhanced. Struct. Multidiscip. Optim. 2015, 51, 1017–1033. [Google Scholar] [CrossRef]
- Miyashita, K.; Katagiri, J.; Nakamura, O.; Ohkuma, T.; Tamura, Y.; Itoh, M.; Mimachi, T. Wind-induced response of high-rise buildings: Effects of corner cuts or openings in square buildings. J. Wind Eng. Ind. Aerodyn. 1993, 50, 319–328. [Google Scholar] [CrossRef]
- Du, X.Q.; Tian, X.X.; Ma, W.Y.; Li, E.D. Effects of rounded corner on aerodynamics of square cylinders and its flow mechanisms. Chin. J. Appl. Mech. 2018, 50, 1013–1023. [Google Scholar]
- Sharma, A.; Mittal, H.; Gairola, A. Mitigation of wind load on tall buildings through aerodynamic modifications: Review. J. Build. Eng. 2018, 18, 180–194. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).