The Characteristics of Nonlinear Trends and the Complexity of Hydroclimatic Change in China from 1951 to 2014

Abstract

Hydroclimatic change across China has received considerable attention due to its vital significance for regional ecosystem stability and economic development, yet the spatiotemporal dynamics of its nonlinear trends and complexity have not been fully understood. Herein, the spatiotemporal evolution of Dai’s self-calibrating Palmer drought severity index (scPDSI) trends in China during the period from 1951 to 2014 is diagnosed using the ensemble empirical mode decomposition (EEMD) method. A persistent and noticeable drying has been identified in North and Northeastern China (NNEC) since the 1950s. Significant wetting in the north of the Tibetan Plateau (TP) and the south of the western parts of Northwestern China (WNWC) started sporadically at first and accelerated until around 1980. A slight wetting trend was found in Southwest China (SC) before 1990, followed by the occurrence of a dramatic drying trend over the following decades. In addition, we have found that the scPDSI variations in WNWC and the TP are more complex than those in NNEC and SC based on our application of Higuchi’s fractal dimension (HFD) analysis, which may be related to complex circulation patterns and diverse geomorphic features.

1. Introduction

Due to the diverse effects of complex topography and multiple climate forcings [1], hydroclimatic variability in China can vary dramatically across time and space. Despite this, one common feature is that extreme drought can hit any region across China, where dramatic and persistent moisture fluctuations are often accompanied by catastrophic societal and economic consequences for millions of people [2,3,4]. For instance, the 1630s–1640s drought was widespread over North China, contributing to the demise of the Chinese Ming dynasty [5,6,7]. A widely documented drought occurred in the late 1920s over Northwest China, resulting in the death of at least 4 million people [8,9]. In addition, as was clearly shown by the occurrence of severe drought events in the autumn of 2009 over southwest China and in the autumn of 2009 over South China [10,11], humid, subtropical China is not immune to water shortages either. Therefore, investigations concerning the spatial and temporal patterns of hydroclimatic variability across China are highly necessary to a better understanding of the underlying climate forcings.

A large body of research has examined hydroclimatic variation trends in specific regions of China [12,13,14,15] or the entirety China [16,17,18,19]. However, the shape of the trend found by many of these studies was basically determined a priori (e.g., by straight-line fitting), which can only extract a constant rate of variability over a timespan. In fact, time-unvarying changes cannot effectively exhibit the hidden, nonstationary nature of a time series since climatic changes are often uniform on different spatial and temporal scales. To address this problem, recent works have started to reflect the nonlinear trends of climatic change by using the ensemble empirical mode decomposition (EEMD) method [20,21,22]. The definition of a trend in a time series in EEMD requires the removal of any identifiable oscillatory components and the retention of one extremum, at most, within a given data-span [23]. To date, no studies have provided a reasonable diagnosis of the evolution of hydroclimatic variability on the different spatiotemporal scales across the entirety of China based on EEMD.

Climate can be identified as a set of atmospheric states of a dynamic chaotic system with deterministic nonlinear variability [24]. Although they have become increasingly more complex and capable of providing fairly reliable predictions of future climatic developments, climate models still cannot cover all potential mechanisms, and the outputs always include considerable uncertainties, especially for large-scale simulations [25]. Therefore, the interpretation of climate as a complex intervariable organization is a key option for better understanding the spatiotemporal evolution of dynamic systems [26,27]. To date, many concepts (e.g., entropy, fractals, chaos) have been introduced to explain the complexity of climatic change processes [28,29,30], yet the extension of these studies is still limited. Plus, considering hydroclimatic change as attenuated by more frequent extremes under global warming, the way in which to understand the spatiotemporal complexity of the hydroclimatic system in China tends to be a key issue that needs to be investigated.

In this context, the objective of the present study is to explore the spatial and temporal evolution of the nonlinear tendency and the complexity of hydroclimatic change across China. Section 2 presents the data and the methods employed in this study. In Section 3, Section 4, and Section 5, we investigate the spatial distribution of the EEMD time-varying trends and the fractal dimension from multiple timescales of the scPDSI series in China, and we discuss the potential driving mechanisms for these variations. The major findings are given in Section 6.

2. Dataset and Methods

2.1. Dataset Description

The hydroclimatic index used herein is Dai’s self-calibrating Palmer drought severity index (scPDSI), with potential evapotranspiration estimated by using the more sophisticated Penman–Monteith equation based on historical data [31]. The scPDSI is calculated from a water-balance model forced by observed monthly precipitation and temperature, and it is calibrated by local climatic conditions instead of the fixed coefficients used by Palmer [32]. Thus, the scPDSI is more spatially comparable than is the original PDSI developed by [33]. We use an updated version of the scPDSI, with global coverage based on a 2.5° × 2.5° gridding system, spanning the years from 1850 to 2014 (http://www.cgd.ucar.edu/cas/catalog/climind/pdsi.html, accessed on 13 March 2016). Since most of the meteorological stations in China were not established until the 1950s, we only use the scPDSI for the period from 1951 to 2014 (a total of 768 months). A total of 193 scPDSI grid points across China are used in this study (Figure 1).

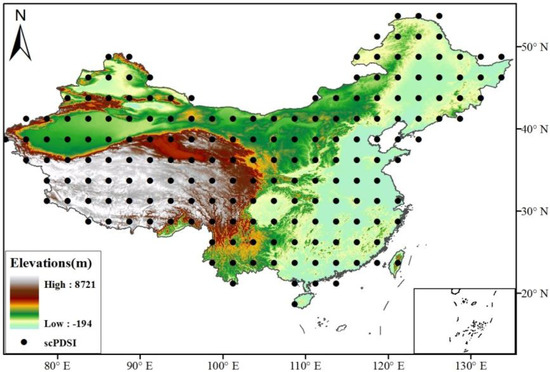
Figure 1. Map showing the locations of the gridded scPDSI across China. The scPDSI grid points were developed by Dai et al. (2011) for global coverage based on a 2.5° × 2.5° gridding system.

2.2. Ensemble Empirical Mode Decomposition

The original empirical mode decomposition method uses extrema information to separate the oscillations on different scales and the nonlinear trend from a time series [34], yet changes in extrema locations and values can easily result in different decompositions, leading totally different physical interpretations. The EEMD, a noise-assisted data-analysis method, is developed to improve the “mode mixing” problem [23]. In EEMD, a time series x(t) at a grid point is decomposed in terms of adaptively obtained, amplitude–frequency modulated oscillatory components Cj and a residual Rn, a curve either monotonic or containing only one extremum from which no additional oscillatory components can be extracted:

$$x\left(t\right)={\displaystyle \sum }_{j=1}^n{C}_j\left(t\right)+R_n\left(t\right)$$

(1)

The trend follows no a priori shape and changes over time after the intrinsic variability of various timescales is removed. It is also more sensitive to the extension of new data. The physical interpretation within specified time intervals does not vary with the addition of data, and the subsequent evolution of a physical system cannot also alter the reality of that which has already happened [23]. Based on the time-varying nature of the EEMD trend, we diagnose the variation at a given time (t) from a reference time of 1951:

$$Trend\left(t\right)=R_n\left(t\right)-R_n\left(1\right)$$

(2)

In addition, we also test the statistical significance of an EEMD trend at a given temporospatial location based on the Monte Carlo method introduced by Ji et al. [21].

2.3. Higuchi’s Fractal Dimension

An efficient algorithm for measuring the fractal dimension of a discrete signal directly in the time domain was proposed by [35]. This algorithm is simpler and faster than many other classical measures derived from chaos theory (e.g., correlation dimension) because the reconstruction of the attractor phase space is not essential [36]. Higuchi’s fractal dimension (HFD) has been widely employed to quantify the complexity and the self-similarity from a signal [37,38,39]. Its principle for computing the fractal dimension can be described in the following manner:

Given a one-dimensional time series X = {x(1), x(2), …, x(N)}, where N denotes the total number of samples, the algorithm that constructs k new time series $x_m^k$ is defined by:

$$x_m^k=\left\{x\left(m\right),x\left(m+k\right),\cdots ,x\left(m+\left[\frac{N-m}{k}\right]k\right)\right\}$$

(3)

where k and m are integers, [•] is the integer part of •, k indicates the discrete time interval between points, and $m=1, 2,\dots , k$ represents the initial time value. The length of each new time series can be calculated as:

$$L\left(m,k\right)=\frac{\left\{\left({{\displaystyle \sum }}_{i=1}^{\left[\left(N-m\right)/k\right]}\left|x\left(m+ik\right)-x\left(m+\left(i-1\right)k\right)\right|\right)\frac{N-1}{\left[\left(N-m\right)/k\right]k}\right\}}{k}$$

(4)

where N is the length of the original time series, and $\frac{N-1}{\left[\left(N-m\right)/k\right]k}$ is the normalization factor. The length of the series L(k) is obtained by averaging all of the subseries lengths L(m, k) that have been obtained for a given k value:

$$L\left(k\right)=\frac{1}{k}{\displaystyle \sum }_{m=1}^{k}L\left(m,k\right)$$

(5)

If $L\left(k\right)\propto k^{-D}$, that is, if it behaves as a power law, we regard the exponent D as the FD of the original series.

3. General Aspects of the scPDSI

The scPDSI values across China show a normal-like distribution (skewness = 0.028) with most values (79.3%) occurring at the near-normal conditions (−3 < scPDSI < 3), and the frequencies of the extreme dry (<−4) and wet (>4) regimes are 4.1% and 5.6%. The mean and median scPDSI values are −0.2 and −0.3, respectively, which are within the range of a “normal” moisture status (PDSI = 0.0 ± 0.5), as defined by Palmer [32]. The Jarque–Bera result for the scPDSI values is shown in Figure 2a, where the histogram of the scPDSI change is fitted by a Gaussian distribution, yet p < 0.05 reveals that the data are not normally distributed. This may be related to the high frequency of scPDSI in extremely, severely dry or wet regimes across China according to quantile–quantile plotting (Figure 2b).

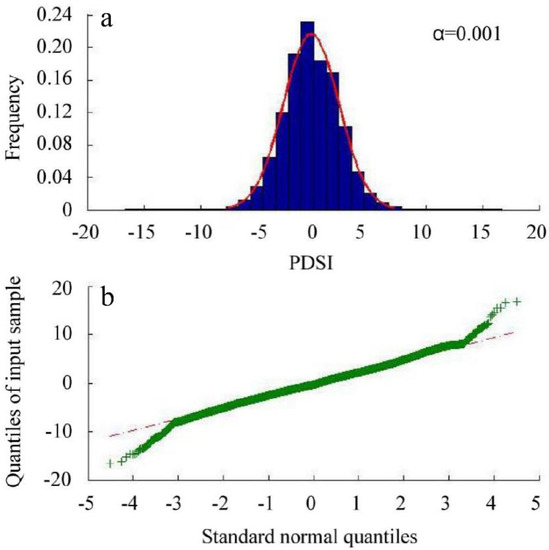
Figure 2. Normality tests for scPDSI variability across China from 1951 to 2014. The Jarque–Bera test results and the quantile–quantile plot are shown in (a,b), respectively.

In addition, special attention has been paid to extreme hydroclimatic change (|scPDSI| > 0.4) via an examination of their spatial distributions (Figure 3). As shown, the problem of the over-reporting of the extreme dry or wet conditions, which has been reported for the original PDSI dataset [2], still exists in the self-calibrated data. The over-reported extreme wet spells are not found in traditionally humid regions (e.g., South China), and instead are mainly found on the North Tibetan Plateau and in South Xinjiang (Figure 3a). Similarly, the extreme dry regimes are mainly represented in North and Southwest China instead of in traditionally semiarid and arid regions (e.g., Northwest China) (Figure 3b). In fact, the scPDSI was developed to describe the cumulative departure from the mean values in moisture supply and demand at the local surface level [31,33]. Therefore, persistent increases or decreases in moisture can give rise to the occurrence of clusters of extreme scPDSI values. This is in good agreement with many previous studies that have revealed that a persistent drying trend has been in place since the 1950s in North and Southwest China [19,40,41,42,43], while a remarkable wetting trend has been found in arid Central Asia [44].

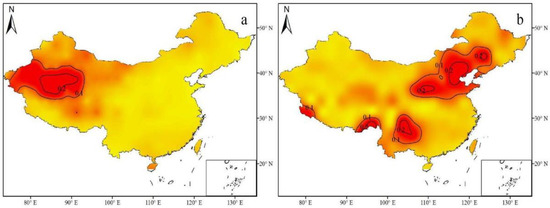
Figure 3. The frequency at which the scPDSI reported (a) an extreme wet spell (percentage of months with scPDSI < −4.0) and (b) an extreme dry spell (percentage of months with scPDSI > 4.0).

4. Spatiotemporal Evolution of Hydroclimatic Change Trends across China

The spatial evolution of the wetting or drying trends across China at a given time is presented in Figure 4. As shown, the hydroclimatic pattern in China can be termed as “eastern drying and western wetting” during the period from 1951 to 2014. The boundary of the drying land in Northern and Northeastern China (NNEC) has extended eastward, and Southwest China (SC) has also shown a drying trend in recent years. However, the Tibetan Plateau (TP) and Northwestern China (WNWC) have shown a wetting trend. In this study, only those regions with significant hydroclimatic variations are further discussed.

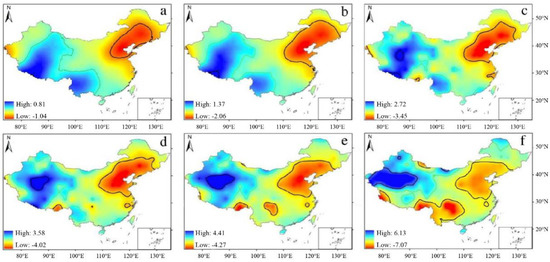
Figure 4. Spatial evolution of the EEMD-based trends of scPDSI across China ending in (a) 1960, (b) 1970, (c) 1980, (d) 1990, (e) 2000, and (f) 2014, respectively. Variations significant at the 0.05 level are highlighted by black lines. The green line symbolizes the change value of zero.

NNEC has been facing a significant and persistent downward trend in moisture availability over the past 60 years, which has caused enormous economic losses each year [45]. To alleviate the regional water-shortage problem, the South-to-North Water Diversion Project has been implemented by the central government. Previous studies have revealed that the recent decades correspond well to periods of East-Asian summer-monsoon failure which lead to deficient precipitation in NNEC [46,47]. The rapid warming in the Central and Eastern Pacific Ocean, as the primary cause for the decay of monsoon intensity, can suppress convective activity over the Philippine Sea via the descending limb of the Walker circulation [48]. The relatively cold Western Pacific Ocean and the subsidence over it weakens the Hadley circulation and thus reduces the western Pacific high, causing the failure of the summer monsoon and creating dry conditions in NNEC [22]. The recent cooling trend of the upper tropospheric temperature over East Asia was found to cause a weakening of the northward progression of regional summer-monsoon winds [49]. In addition, the radiative effects of significant increases in aerosols (e.g., black carbon) from urbanization and industrialization may stabilize the atmospheric convection, hence reducing regional monsoonal precipitation [50]. The boundary of the significantly drying land in NNEC has extended eastward to the eastern Loess Plateau and southward, close to the middle and lower reaches of the Yangtze River since 1990. This finding may be consistent with the dryland expansion experienced in northern China during the recent warming trend, as suggested by previous studies [51].

Recent decades have witnessed the most conspicuous increases in precipitation experienced on the TP over the course of the past millennium according to observations from regional tree-ring-based precipitation reconstructions [52]. However, the wetting tendency in most parts of the TP tends to be relatively moderate, except for in the northern part, which has experienced a significantly accelerated pace of wetting since 1980. One of the potential factors accounting for the wetting trends in the TP is related to large-scale oceanic and atmospheric patterns on interdecadal timescales, e.g., anomalies in the sea surface temperature (SST) of the North Indian Ocean. In recent years, the warming of the sea surface temperature in the North Indian Ocean has caused upward convection, which brings water vapor into the TP through the Walker circulation [53]. In addition, great moisture supply on the TP may be related to large-scale warming from a long-term perspective, as indicated by a significantly statistical association between moisture-sensitive tree-ring chronologies and the reconstructed Northern Hemisphere temperature [54,55,56].This warming may enhance the emissions of the biogenic volatile organic compounds from terrestrial vegetation that can increase the amount of secondary organic aerosols due to limited anthropogenic influence in the TP, contributing to the concentration of cloud condensation nuclei and leading to a regional precipitation increase [57]. It has been found that, in the past decade, the wetting regions have shrunk in the southern TP. This is mainly due to the anticyclonic trend that has appeared over the northeastern TP [58].

There were both moderate drying and weak wetting regions in the western parts of WNWC prior to 1980. Yet the drying regions shrank dramatically, and most of them turned into wetting regions over the next 3 decades. The strongest wetting rates occurred in the southern part of WNWC, especially the Tarim Basin. The moisture increase in this area was also evidenced by the observed precipitation records and other hydroclimatic data [59]. Closely associated with the regional moisture increase are two anomalous atmospheric teleconnection patterns that connect in WNWC. The zonal wave train along the middle latitudes resembles the “Silk Road Pattern”, and it induces an increase in the strength of the westerly winds, transporting moist air from the Atlantic Ocean and the Mediterranean Sea into this region [31]. The meridional pattern demonstrates a negative height anomaly in Central Asia, and positive height anomalies in tropical and subarctic areas. This wave train leads to anomalous southerly winds that bring abundant water vapor from the Arabian Sea into this area via the western boundary of the TP, and then they bend north and fuel regional precipitation development [60].

As for SC, regional moisture basically remained in a slight upward trend before 1990, and an abrupt trend reversal took place over the next 2 decades. The recent drying conditions in SC are considered to be the most dramatic over the past century [61]. The potential driving mechanisms for this dry spell seem to be quite complicated according to a large number of previous studies. The severe droughts over SC are closely linked with an anomalously strong western Pacific subtropical high (WPSH), which shifted to the north and west of its normal position. Subsidence prevailed in SC under the control of the WPSH and suppressed water-vapor transport towards this region [2]. Meanwhile, the South Asian high is stronger and lies to the east of its normal position, causing the failure of the summer southwest monsoon season [62]. The occurrence of the severe drought in SC is also related to anomalies in the westerlies’ circulation system, with anomalously high pressure over Lake Baikal and anomalously low pressure over East Asia, which can weaken the strength of southward cold air into SC and prevent the convergence of warm–moist air and cold–dry air over SC [63]. Plus, an anomalously high pressure ridge develops over the TP in very dry years, leading to the decline of the southwest monsoon and the prevalence of the dry northwesterly wind over SC [10]. In addition, the recent drying conditions in SC may be associated with the warming of the tropical oceans [64] and the Indian Ocean dipole [65].

5. Complexity of Hydroclimatic Variability in China

The spatial pattern of the HFD exponents for the scPDSI dataset over the entire domain is presented in Figure 5, which illustrates that the HFD values on a monthly scale range between 1.37 and 1.54 (Figure 5a), and the ones on an annual scale vary between 1.58 and 2.01 (Figure 5b). We found that none of HFD values is an integer, indicating that the hydroclimatic variations across the region are chaotic dynamic systems with fractal characteristics, and they are sensitive to the initial conditions [28,29,30]. A comparison of the HFD values reveals that the complexity of the hydroclimatic dynamics in China decreases along with an increase in the temporal scale. This result accords with many previous studies that demonstrated that the climate data with higher resolution often contain more details and thus are more complex [30].

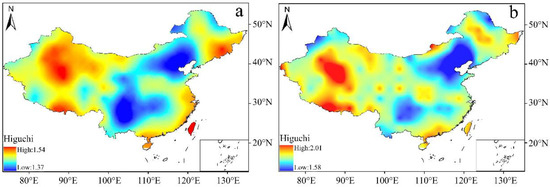
Figure 5. Spatial pattern of the HFD exponents for the scPDSI series on monthly (a) and annual (b) scales across China.

The higher HFD values are mainly distributed in WNWC and the TP, and the lower values mainly concentrate in NNEC and SC. This finding demonstrates that the hydroclimatic dynamics in WNWC and the TP are more complicated than those in NNEC and SC. This phenomenon is probably associated with the presence of atmospheric processes and landforms in different parts of the study region. Dong et al. revealed that the spatial distributions of higher fractal dimension values for temperature dynamics in the Tarim Basin were found in areas with complex landforms [66] Donner found that the spatial patterns of the HFD values for precipitation variability across the entirety of Germany were totally the opposite on the short (1–7 days) and long (10–100 days) timescales [67]. Xu et al. discovered that the complexity of temperature and precipitation dynamics in Xinjiang was positively related to elevations [28,29,30]. Previous evaluations of the circulation features of WNWC and the TP indicated that the regional moisture conditions are transported from the Indian Ocean, the Atlantic Ocean, giant lakes in Central Asia (e.g., the Caspian Sea and the Aral Sea), and the Arctic [22,29,51]. In addition, the two subareas have a unique geological feature, with an average elevation ranging from −155 m to 8848 m ASL, strongly influencing the monsoon and westerlies dynamics [68]. Therefore, the coupling of large-scale circulation and diverse geographic conditions possibly results in the poor stability and high complexity of the hydroclimatic change in WNWC and the TP.

6. Conclusions

From our study of the nonlinear characteristics of the hydroclimatic variability across China using the EEMD and the HFD method, several conclusions can be drawn, as follow:

(1) The hydroclimatic change is spatially and temporally non-uniform over the entire domain. NNEC has been facing a persistent and noticeable drying trend since the 1950s. The significant wetting conditions in the TP and WNWC started sporadically at first and strongly accelerated until around the 1980s. A slight wetting trend was found in SC before 1990, followed by the occurrence of a dramatic drying trend over the next 2 decades.

(2) None of the HFD values is an integer, which indicates that all of the hydroclimatic dynamics on the monthly and annual scales are chaotic dynamic systems with fractal characteristics, and they are sensitive to the initial conditions. The variations on a smaller temporal scale (e.g., a monthly scale) tend to be more complex than those on a larger temporal scale (e.g., an annual scale). Additionally, the hydroclimatic changes in WNWC and the TP are more complicated than those in NNEC and SC, which may be related to the complex circulation patterns and diverse geomorphic features that dominate them.