Abstract
Transportation sources are a major contributor to air pollution in urban areas, and the role of air quality modeling is vital in the formulation of air pollution control and management strategies. Many models have appeared in the literature to estimate near-field ground level concentrations from mobile sources moving on a highway. However, current models do not account explicitly for the effect of wind shear (magnitude) near the ground while computing the ground level concentrations near highways from mobile sources. This study presents an analytical model (SLINE 1.0) based on the solution of the convective–diffusion equation by incorporating the wind shear near the ground for gaseous pollutants. The dispersion coefficients for stable and unstable atmospheric conditions are based on the near-field parameterization. Initial vertical dispersion coefficient due to the wake effect of mobile sources is incorporated based on a literature review. The model inputs include emission factor, wind speed, wind direction, turbulence parameters, and terrain features. The model is evaluated based on the Idaho Falls field study (2008). The performance of the model is evaluated using several statistical parameters. Results indicate that the model performs well against this dataset in predicting concentrations under both the stable and unstable atmospheric conditions. The sensitivity of the model to compute ground-level concentrations for different inputs is presented for three different downwind distances. In general, the model shows Type III sensitivity (i.e., the errors in the input will show a corresponding change in the computed ground level concentrations) for most of the input variables using the ASTM (American Society for Testing and Materials) method. However, some recalibration of the model constants is needed using several field datasets to make sure that the model is acceptable for computing ground-level concentrations in engineering applications.
1. Introduction
Air pollution dispersion modeling is based on the physics and chemistry involved in the process of advection/dispersion of contaminants and could predict and estimate the concentrations of contaminants by considering source origin, composition, and emissions. Mathematical/numerical techniques are used to simulate ground-level concentrations in air quality models. Inputs of air quality modeling include source information, meteorological data, and the surrounding terrain [1,2]. An important meteorological parameter is atmospheric stability. The tendency to enhance and resist atmospheric motions is called atmospheric stability. Over the last 50 years, several methods have been proposed to classify atmospheric stability. Some of these methods are based on the variation in temperature with height, wind speed, insolation (day-time), and cloud cover (night-time). The concentration of pollutants is affected by the convective and mechanical turbulence. For unstable atmospheric conditions, more dilution is expected due to convective activities when compared with stable atmospheric conditions [3,4].
Air pollution dispersion modeling is typically an inexpensive approach when compared to field studies. Most dispersion models use computer programs to simulate the movement of air pollutants in the atmosphere and to estimate the pollutant concentrations in a geographic location. There are different types of models based on the nature of sources (such as point, line, area, and volume sources) [5]. “Line source models” are used to calculate and predict the concentration of pollutants that are continuously emitted from automobiles/trucks on highways. The effect of pollution from line sources is high in an urban environment due to their major contribution to local air quality. Vehicular density, vehicle speed, and emission rate are the major variables to be considered for the prediction analysis of air quality involving mobile sources [6,7,8].
The purpose of this paper is to develop and evaluate a line source model, SLINE 1.0, for gaseous pollutants by incorporating wind shear near the ground under stable and unstable atmospheric conditions. The change in wind velocity with height near the ground is defined as wind shear for the purpose of this development. The sensitivity of the model in predicting ground-level concentrations to input variables/parameters is also presented to identify how sensitive the model is towards the independent input variables/parameters.
2. Literature Review
The literature review indicated that many line source air quality models have been developed over the last 50 years. The mathematical formulation of these models can be analytical, statistical, or numerical. The solution of the convective–diffusion equation for a line source was available in the 1950s [8]. During the 1960s and 1970s, many Gaussian-based dispersion models were introduced. These formulations were a function of meteorology, receptor locations, and highway geometry. The differences in formulations were due to the assumptions made during the solution of the convective–diffusion equation or the specification of plume spread rates. However, these models did not perform very well when the predicted results were compared with the observed values. The primary reason was a difficulty in accounting for atmospheric dispersion and turbulence [9]. Subsequently, many experimental field studies have been conducted to improve the models.
HIWAY1 was developed in the early 1970s to predict mobile source emissions near roadways [10]. In 1978, Chock formulated General Motors’ (GM) line source model by incorporating wind speed correction and modified values for vertical dispersion coefficients to address wake turbulence from the vehicles [11]. In 1980, Rao and Keenan evaluated the existing models and suggested new dispersion curves for pollution dispersion near highways [12,13]. Model development continued from the 1980s onwards to address vehicle-induced turbulence, surface roughness, averaging time, new provisions for plume spread, and other turbulence mixing parameters [14].
The USEPA (United States Environmental Protection Agency) Office of Research and Development introduced a CALINE (California Line Source) dispersion model in 1972 based on the Gaussian plume model using Pasquill–Gifford (P–G) atmospheric stability classes. CALINE was developed by focusing on the prediction of CO concentration near roadways [15]. In 1975, formulations for depressed roadways were added to develop CALINE2 [16]. In 1979, the vertical and horizontal dispersion curves were revised along with updating vehicle-induced turbulence, averaging time, and introducing a finite line source to develop CALINE3 to reduce over-predictions. In 1984, CALINE4 was introduced with the addition of chemical reactions for NO2 and PM, intersections, and updating lateral plume spread and vehicle-induced turbulence. CALINE, CALINE2, and CALINE3 are open source models and are available freely to the public, unlike CALINE4 [17]. In 1989, Luhar and Patil developed a General Finite Line Source Model (GFLSM) based on the Gaussian diffusion equation and evaluated it based on data collected at intersections in Mumbai and New York [18]. Around the early 1990s, the CAL3QHC screening model was developed to auto-estimate the queue lengths of vehicles at the intersections. The enhanced version of CAL3QHC is CAL3QHR, a more flexible model than CAL3QHC with a two-tiered approach [19]. In the same decade, the ISCST2 (Industrial Source Complex Short Term 2) model was introduced by incorporating mixing height algorithms. It could estimate the concentration of pollutants with varying emission rates from point sources. According to Eerens, the CAR model was developed in 1993 and evaluated with the data collected in urban areas of the Netherlands [20]. ISCST3 was developed in 1995 by incorporating the new area source option and algorithms of dry deposition [21]. Later, the GFLSM was improved by Sharma based on experiments conducted at intersections in Delhi, India [22]. A road network dispersion model named CAR-FMI was developed similarly to a CAR model to predict concentrations of pollutants from automobiles near industrial areas [23]. The ROADWAY model was developed while studying vehicle wakes and the dispersion phenomena in pollutants from the vehicles [24]. COPERT and CEM are also major models used to calculate the concentration of pollutants from vehicular emissions [25]. During this period, the ADMS model was developed by CERC, UK [21]. The progress of these model developments has helped regulatory agencies to estimate the impacts of emissions.
A commonly used line source model, CALINE4, uses a range of traffic and fleet characteristics and a diffusion equation to assess the impacts of a road at a small scale. It is specifically designed for assessing air quality impacts at roadways or intersections and used to predict impacts of changing traffic volumes, signal phasing, or adding additional lanes to a roadway [26]. In New Zealand, a similar model named VEPM was developed, which uses real and lab-based emissions data to predict emissions up to the year 2040 from a roadway [27].
The research has continued to develop, assess, and evaluate the pre-existing models and to increase the scope of accuracy for future models. In 2005, the USEPA replaced the ISC model with AERMOD which contains an updated atmospheric stability scheme and the ability to characterize the planetary boundary layer through both surface and mixed layers [28]. In 2007, Gokhale developed a simple semi-empirical box model based on the traffic flow rate at the busiest traffic road intersections in Delhi. He estimated hourly average carbon monoxide (CO) concentrations and optimized specific vehicle emission rates based on vehicle category. Through this study, he was able to show that the nature of vehicle flows influence the rate and nature of the dispersion of pollutants which affect pollutant concentrations in the road vicinity [29]. In 2011, Xie conducted a study on both the daily and hourly concentration levels of CO, PM10, NO2, and O3 during the Beijing Olympic Games, conforming to the Grade II China National Ambient Air Quality Standards. A notable reduction in concentration levels was observed in different regions of Beijing, with the traffic-related air pollution in the downwind northern and western areas. According to Xie, the “Traffic Restriction Scheme (TRS) policy was effective in alleviating traffic-related air pollution and improving short-term air quality during the Beijing Olympic Games” [30]. In 2018, Milando conducted a study near high-traffic roads in Detroit. He evaluated the RLINE/AERMOD by comparing predicted concentrations of NOx, CO, and PM2.5. The model performance for CO and NOx was found to be best at sites close to major roads, during downwind conditions, during weekdays, and in certain seasons [31]. In 2018, Bowatte investigated longer-term effects of traffic-related air pollution exposure for individuals with or without existing asthma, and with or without lower lung function. Population groups who fall under middle age category and live less than 200 m from a major road, could be susceptible to both the development and persistence of asthma. These findings have public health implications for asthma prevention strategies in primary and secondary settings [32]. In 2018, Liang conducted a dorm room inhalation study due to vehicle emissions using a near-road monitor as a surrogate for true exposure and observed acute health effects. This study was conducted near a road, measuring several single traffic indicators at six indoor and outdoor sites [33]. In 2020, Amoatey conducted a comparative study between COPERT and CMEM models. The correlation coefficient for these two models was found to be statistically significant from 0 in the case of combined model comparison across all the traffic locations for both CO and NOx. He concluded that due to the terrain features of certain roads, weak performance was observed, and the influence of terrain needs to be considered in future studies [34].
Some of the popular air quality models related to transportation sources and their key features are mentioned in Table 1.

Table 1.
Various popular air quality models and some of their key features.
The literature review indicates that available line source dispersion models do not explicitly account for wind shear near the ground under different atmospheric conditions. Therefore, this study focused on developing a line source dispersion model considering wind shear near the ground under stable and unstable conditions. The model was applied to gaseous pollutants released from mobile sources on a highway. This paper presents a line source model (SLINE 1.0) by incorporating wind shear near the ground surface to predict the impact of mobile sources moving on a highway in nearby areas during stable and unstable atmospheric conditions. The sensitivity analysis was performed by considering the selected variables in the model which have an impact on the computed concentrations.
3. SLINE 1.0 Model Development
The basic approach to develop the SLINE 1.0 model was the incorporation of wind shear during the dispersion from a line source using the convective–diffusion equation. It is important to consider the variation of the wind velocity magnitude near the ground for the dispersion of pollutants released from the tailpipe of mobile sources. This physical phenomenon was incorporated in the derivation of the dispersion and transport equation for the SLINE 1.0 model. The model was based on the analytical solution of the convective-diffusion equation of a line source given in the book by Sutton, O.G. [8]. The assumptions used in deriving the equation were: (i) the wind direction is always perpendicular to the highway; (ii) the dispersion is of a non-fumigation type; (iii) the velocity profile with height above ground level is assumed to be the same for all downwind distances; (iv) a power-law profile is assumed for the velocity, i.e., the magnitude of the wind velocity near the ground level changes rapidly and follows a power law; (v) the eddy diffusivity profile is a conjugate of velocity profile as given in Equation (3) below; and (vi) the emission rate is constant.
3.1. Dispersion Model
The convective–diffusion equation representing the dispersion from mobile sources [8] is given as:
where C is the concentration of pollutants at a point (x,z), x is the downwind distance, z is the vertical height of the receptor above the ground, and and are the wind velocity and eddy diffusivity at the vertical height , respectively. The profiles of wind velocity and eddy diffusivity are given by Equations (2) and (3):
where and are the wind velocity and eddy diffusivity at a reference height , respectively. m is the exponent of the power-law velocity profile, and n is the exponent for the eddy diffusivity profile. Note that n = 1 − m to satisfy assumption (v) given above, and the value of m lies between 0 and 1.
The stability parameter (s) is calculated based on m and n using Equation (4):
The analytical solution of Equation (1) to calculate the concentration of pollutants at any downwind distance when the wind and eddy diffusivity profiles are given by Equations (2) and (3) [8] is given by Equation (5):
where q is the emission rate of the mobile source per unit length, and is the gamma function of s.
The value of is based on the field measurement, and is computed using Equation (6) used by Rao et al. [35] and Nimmatoori and Kumar [36]:
where is the standard deviation of concentration in the z-direction. Equations (5) and (6) are as follows if the wind is not perpendicular to the highway:
where θ is the angle between the wind direction and the line source.
Equations (3) and (8) indicate that K as well as are a function of downwind distance x. However, the derivation of Equation (1) assumes that the K profile is constant as the plume moves downwind. It is assumed during the application of Equation (7) that the concentration is predicted in the SLINE 1.0 model at a downwind distance by updating the value of in the model for that downwind distance. It is expected that this approach will improve the model performance.
The solution of Equation (1) for a constant wind velocity and eddy diffusivity at any point is given in the book by Wark et al. [1]:
Values of for Equation (9) are based on Pasquill–Gifford curves. Equation (9) is hereafter referred to as the SLSM (simple line source model) in the rest of the paper.
3.2. Turbulence Parametrization
is one of the critical components that affects estimations of the concentration of pollutants from the vehicular exhaust. It is important to incorporate the turbulence parameters related to the wake area created by mobile sources as well as the near-field while developing a line source dispersion model near the roadway. Figure 1 shows the conceptual turbulence model proposed in this paper as the plume moves downwind. The proposal is based on the findings in different studies on mobile sources. The turbulence model includes three flow regimes:
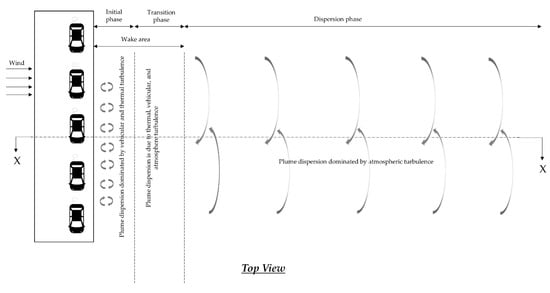
Figure 1.
Flow regimes of a line source plume.
- The first flow regime (Initial Phase) is near the mobile sources and the highway. The plume dispersion is dominated by vehicular and thermal turbulence in this phase. The downwind distance used is 6.5 m, as discussed in the following section;
- The second flow regime (Transition Phase) is in the wake area created by wind flow. The Transition Phase includes the effect of thermal turbulence, vehicular turbulence, and atmospheric turbulence. This phase is assumed from the downwind distances of 6.5 m to 50 m. The value of 50 m will depend on the type of vehicles on the highway and could be as high as 150 m for large trucks, as pointed by Yu et al. [37];
- The third flow regime (Dispersion Phase) is away from the vehicular wake area, and the plume dispersion is dominated by atmospheric turbulence.
Various studies indicate that the initial vertical plume spread, , depends on the vehicular turbulence, wind velocity, width of the road, residence time, the height and width of the mobile sources within the turbulent mixing zone, and other factors [1,38,39]. The width of the mixing zone (i.e., the Initial Phase) in the downwind direction was estimated by Benson as the width of the roadway and an additional 3 m [40]. It is assumed that is constant up to 6.5 m, which is based on the summation of the width of the road 3.5 m and 3 m from the edge of the road. The spread due to the wake turbulence is considered in the calculation of the vertical dispersion coefficient () in the SLINE 1.0 model by introducing the term to the equation.
The procedure for calculating from four different sources is given by Equations (10)–(13). Equation (10) was given by Chock et al. to calculate the vertical dispersion coefficient using the residence time (2.75 s) [41], Equation (11) is given in the paper by Benson by fitting the equation to the experimental data, Equation (12) is used in the AERMOD model by USEPA [42], and Equation (13) is given by Yu et al. [43].
where W is the width of the road (m), is the mean wind speed (m/s), ϕ is the wind angle concerning the road (), and is the abscissa of the fitted curve: to the field data.
where H is the height of the car.
The effective wake area is taken as the average vehicle height multiplied by the effective wake length.
The values of obtained from the above four procedures for a test case are shown in Table 2 using the width of the road as 3.5 m. The wind velocity considered was 1.4 m/s, the wind angle concerning the road was taken as 90°, and the average height of the vehicle was H = 1.65 m. The effective wake length was considered as 9.3 m, and the vehicle density on the roadway was 0.125 vehicles/m.

Table 2.
Comparison of from different studies [37,40,41,42].
Atmospheric stability influences the value of P–G stability was the most common method used to categorize atmospheric turbulence in the earlier literature. It is based on wind speed, incoming solar radiation (day-time), and cloud cover (night-time). Other methods have been used to define stability class, including Monin–Obukhov length, Richardson number, Bulk Richardson number, fluctuations in wind direction, and temperature gradient. Benson [40] and the Wake area model by Yu et al. [37] use P–G stability classes, AERMOD [41] uses the surface roughness length and the Monin–Obukhov length, and Chock [42] uses the Richardson Number to define stability class. Therefore, care should be taken in comparing the methods given in Table 2.
Table 2 shows that each of the methods gives different values of for different atmospheric conditions. The SLINE 1.0 model adopted the formulation for given in AERMOD [43], i.e., Equation (12).
The vertical dispersion coefficient for the Initial Phase is given by:
The vertical spread of the plume for stable and unstable conditions beyond 50 m downwind distance (Dispersion Phase) for low-level sources is based on theoretical considerations and experimental data and is given by Snyder et al. [43] as Equations (15) and (16).
where is the effective wind velocity, and is the surface friction velocity. The formulation for and are provided in Equations (2), (17), and (19), respectively. Equations (17)–(19) are considered from Snyder et al. [43]. The standard deviation of lateral wind component () is calculated using Equation (18). The best fit values for the empirical constants suggested by Snyder et al. for a, , and are considered in SLINE 1.0 [43].
where is the wind velocity at the reference height , is the height from the ground surface to the tailpipe (emission source) of the mobile source, and is the convective velocity scale.
For the current model for stable atmospheric conditions, because the value for stable conditions is approximately 0 (note that the heat flux is either very small or zero). For convective conditions, the value of is given by Equation (20) by Snyder et al. [44]:
The vertical spread of the plume in the Transition Phase should include the effect of thermal turbulence, vehicular turbulence, and atmospheric turbulence. The vehicles in motion on highways create turbulence which can increase the mixing of air pollutants and ambient air in the wake area behind the vehicles. There is a necessity to consider the additional spread due to the vehicles () on highways to maintain the accuracy of the model-predicted emissions. Therefore, the vertical spread in the SLINE 1.0 incorporates the additional spread due to the turbulence created by moving vehicles into Equations (15) and (16). The modified equation used to calculate is given in Equations (21) and (22) for stable and unstable atmospheric conditions, respectively.
Tentatively, the value () for mobile sources on the highway is calculated using Equation (12).
Note that the in the Transition Phase will have values varying with the downwind distance.
An expression of can be obtained as follows by substituting Equation (15) for the stable condition and Equation (16) for the unstable condition in Equation (8) with the help of Equation (3):
The expression for concentration for stable conditions will become:
The expression for unstable conditions will be:
Equations (25) and (26) represent the final developed concentration equations for the SLINE 1.0 line source dispersion model for the calculation of downwind concentrations under stable and unstable atmospheric conditions, respectively. The evaluation of SLINE 1.0 using statistical parameters is discussed in the following section.
4. Model Evaluation
SLINE 1.0 model’s ability to estimate air pollutant concentrations under changing conditions can only be evaluated after field measurements are taken under similarly changing conditions. In this study, the performance of the SLINE 1.0 model was determined by comparing the predicted values using the model and observed values from the Idaho Falls field study conducted in 2008 [45]. A total of 187 complete data points were available for unstable and stable atmospheric conditions. The remaining 25 data points in the field study did not have all the model inputs required for SLINE 1.0.
The usual way to evaluate predictions from a model is to draw a scatter diagram using predicted values (Cp) and observed values (Co). The correlation scatter plots between predicted concentration using SLINE 1.0 and observed concentrations at Idaho Falls data 2008 at stable and unstable conditions are plotted in Figure 2a,b, respectively. From the plots, it can be observed that the predicted concentrations of SLINE 1.0 are close to the observed concentrations at most of the data points. The graphical analysis gives a qualitative measure of the model performance.
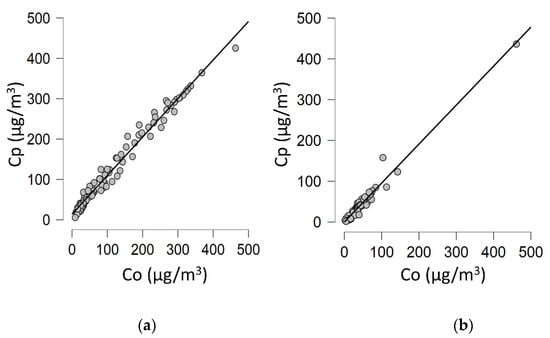
Figure 2.
Qualitative measures of the predicted and observed concentrations of SF6 from Idaho Falls data, 2008. (a) Scatter plot for predicted concentrations (SLINE 1.0) vs observed concentrations for stable atmospheric conditions. (b) Scatter plot for predicted concentrations (SLINE 1.0) vs observed concentrations for unstable atmospheric conditions.
Generally, the ratio (Cp/Co) of a good model should not exhibit large deviations from the unity, which implies a perfect match between the model predictions and observed values [46]. The plots in Figure 3a,b are for the Cp/Co ratio at different downwind distances. It can be observed from the plots that most of the ratios are close to unity. However, some points are showing over- and under-predictions by the model. This could be due to the model assumptions and experimental limitations. The ratios after 100 m indicate a need to review the constants used in equations.
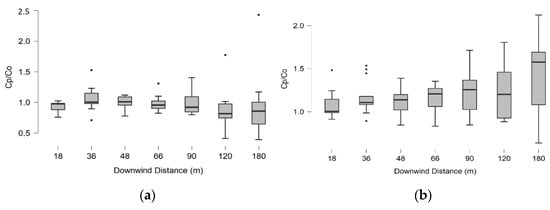
Figure 3.
The box plots of Cp/Co values with varying downwind distances. (a) The box plot between the ratio of predicted concentrations (SLINE 1.0) and observed concentrations for stable atmospheric conditions at varying downwind distances. (b) The box plot between the ratio of predicted concentrations (SLINE 1.0) and observed concentrations for unstable atmospheric conditions at varying downwind distances.
The quantitative performance of the model could be studied by computing the statistical indicators suggested in the literature over the last five decades. The performance measures of the SLINE 1.0 model used include model bias (MB), fractional bias (FB), normalized root mean square error (NMSE), correlation coefficient (r), geometric mean bias (MG), geometric variance (VG), and the factor of two (Fa2). These statistical performance measures are based on the suggestions given in the literature [47,48,49,50,51,52]. The formulation of the statistical indicators is as follows:
Fa2 = Fraction of data within a factor of 2.
The evaluation results for SLINE 1.0 using the 2008 Idaho Falls data as model inputs for the statistical indicators mentioned earlier are given in Table 3. This table also gives the ideal values of each indicator for a perfect model and evaluation results for the SLSM (simple line source model). The numerical result gives a quantitative relationship between observed and predicted values. The values with ‘✓’ denote the interpretation of statistical criteria which were satisfied by the suggested range from the literature for a better performing model.

Table 3.
Model evaluation results for the SLINE 1.0 model using Idaho Falls data, 2008.
MB is the mean error, which is defined as the observed value of concentration less than the predicted value. The computed MB values show that the mean error is 1.83 µg/m3 for unstable and −8.99 µg/m3 for stable atmospheric conditions, using the formulation given in Equations (25) and (26). The ideal case will have a 0.0 µg/m3 error and will be difficult to achieve in real life. The evaluation showed the FB values as 0.04 for unstable and −0.07 for stable atmospheric conditions. Computed FB is based on a linear scale and the systematic bias refers to the arithmetic difference between Cp and Co. For an acceptable model, FB should lie between −0.5 and +0.5.
NMSE emphasizes the scatter in the complete dataset. The normalization by the product of observed and predicted values ensures that the NMSE will not be biased towards a model that over-predicts or under-predicts the concentrations. NMSE reflects both systematic and unsystematic (random) errors in the concentrations. The NMSE values are 0.05 and 0.02 and are close to the ideal value.
The correlation coefficient, r, gives an indication of the linear relationship between the predicted and observed values. r is insensitive to either an additive or a multiplicative factor. A perfect r = 1 is necessary, but not a sufficient condition for a perfect model. Table 3 shows r values of 0.97 and 0.98.
MG is another measure of mean bias and indicates only systematic errors, while VG is another measure of scatter and reflects both systematic and random errors. For an acceptable model, the values of both MG and VG should lie between 0.75 and 1.25. The ideal value of MG and VG is 1.00. The results of the current model evaluation were 1.08 and 0.85 for MG, and 1.01 and 1.03 for VG.
The factor of two (Fa2) is defined as the percentage of predictions within a factor of two of the observed values. The ideal value for the factor of two is 1 (100%). Fa2 is the most robust statistical indicator. The value of Fa2 should be greater than 0.8 for an acceptable air quality model. The values of Fa2 for the current model were 0.94 and 0.99.
5. Analysis of Incorporating Wind Shear in SLINE 1.0
SLINE 1.0 incorporates the variation of wind velocity with height. The dispersion equations (Equations (25) and (26)) account for wind shear near the ground while computing concentrations from the mobile sources. The question arises: is there an improvement in model performance as compared to models that use uniform wind velocity? It is difficult to answer this question in absolute terms because SLINE 1.0 uses different dispersion coefficients, as discussed in Section 3.2. Therefore, an attempt has been made to compare the SLINE 1.0 results with a simple line source model (SLSM) that is available in a textbook. The SLSM uses Equation (9) from Wark et al. [1].
The evaluation results for SLSM are given in Table 3, and the heatmaps for observed and predicted concentrations at stable and unstable atmospheric conditions are given in Figure 4a,b. Additionally, complete descriptive statistics of the observed data versus the SLINE 1.0 and SLSM predictions are given in Table 4. From the observation of tabulated statistical indicators and heatmaps, it could be observed that the performance of SLINE 1.0 is better than SLSM. This is indirect evidence that the inclusion of wind shear along with an expanded turbulence model to specify sigma z are responsible for the improved performance of SLINE 1.0.
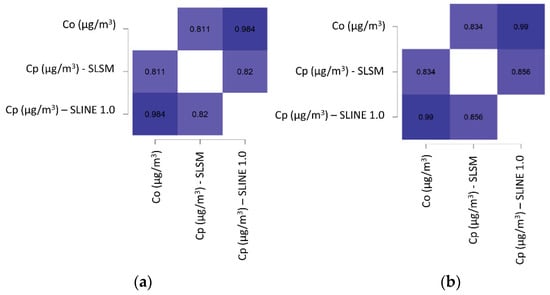
Figure 4.
Correlation heatmaps for the predicted and observed concentrations for SLINE 1.0 and SLSM. (a) Heatmap for observed and predicted concentrations for stable atmospheric conditions. (b) Heatmap for observed and predicted concentrations for unstable atmospheric conditions.

Table 4.
Descriptive statistics of model prediction comparison using JASP [53].
6. Sensitivity Analysis
The sensitivity analysis is the quantification of uncertainty in the model results (concentration in this study), based on its inputs and associated parameters. There are many techniques to perform sensitivity analysis. In this study, the sensitivity analysis was performed on SLINE 1.0 using the technique given in the ASTM Guide [54].
Two case studies were considered in this paper for the calculation of air pollutant concentrations downwind of the source, using SLINE 1.0 under stable and unstable atmosphere. The model inputs for the test case for each stability are provided in Table 5 and were used as a base case to conduct the sensitivity analysis.

Table 5.
Input data and associated parameters for the test case of the SLINE 1.0 model.
6.1. ASTM Guide (1994) Technique
The sensitivity of a model to a variable is classified into four categories, namely Type I, Type II, Type III, and Type IV (see Figure 5 and Table 6).
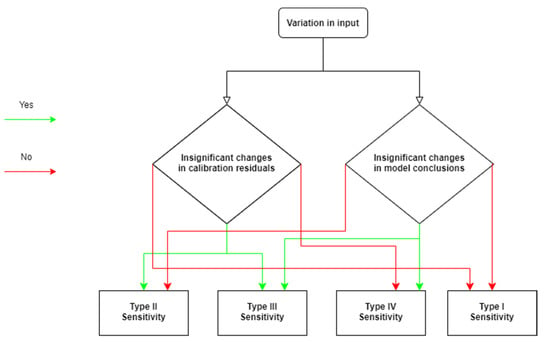
Figure 5.
Flowchart representing the four types of sensitivity analyses.

Table 6.
Standard input values considered for the sensitivity analysis.
The following steps were followed to complete the sensitivity analysis (Table 7). The important input variables/parameters required for running SLINE 1.0 include emission factor of the pollutant (EF), wind velocity at reference height (, the coefficient a, coefficient (only for stable conditions), coefficient (only for unstable conditions), surface friction velocity , and . These variables represent the emission rate, meteorology, and turbulence used in SLINE 1.0. The values in the considered range chosen for each variable/parameter were based on a trial-and-error process, which varied up to ±25%. One could choose another set of ranges. In general, the values were selected based on the possible errors in the specification of each variable. Sensitivity runs were performed on these variables/parameters for two different atmospheric stability conditions (stable and unstable) at near-field downwind distances of 10 m, 50 m and 250 m (Table 8). These three downwind distances were specifically chosen in the sensitivity analysis because, at 10 m, it represents the concentration near the Initial Phase (mixing zone near the source); at 50 m, it represents the concentration at the boundary of the Transition Phase (after which additional vertical spread due to the turbulence created by the vehicles is neglected); and at 250 m, it represents the concentration during the Dispersion Phase (where plume dispersion is dominated by atmospheric turbulence) (see Figure 1).

Table 7.
The categories’ sensitivity analysis and output changes.

Table 8.
Comparison of sensitivity analysis results for stable and unstable conditions.
The simulations were executed for each input to calculate predicted concentrations and calibration residuals by adjusting the variables in the considered range. The differences between the predicted concentrations and the base case concentrations are the calibration residuals. Figure 6 represents the changes in predicted concentration (also called model results) and calibration residuals for all the input variables/parameters. Note that the type of sensitivity (Type I, Type II, Type III, and Type IV) was determined for each variable/parameter depending on changes to the calibration residual values and predicted concentration values by studying the model runs [55,56]. The model runs for SLINE 1.0, varying the input variables/parameters, are plotted in Figure 6.
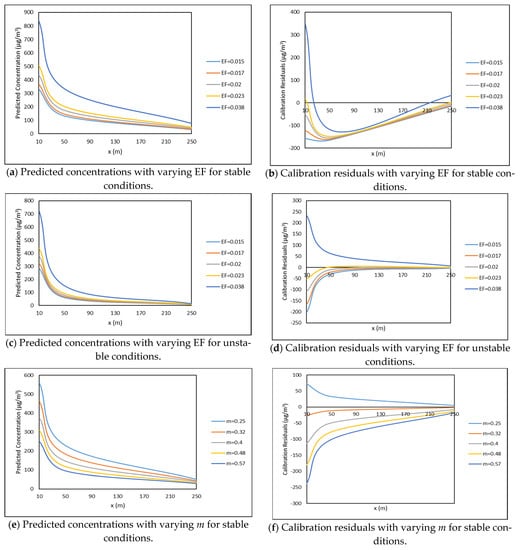
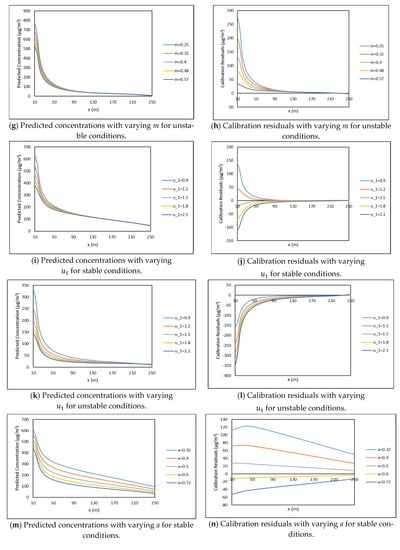
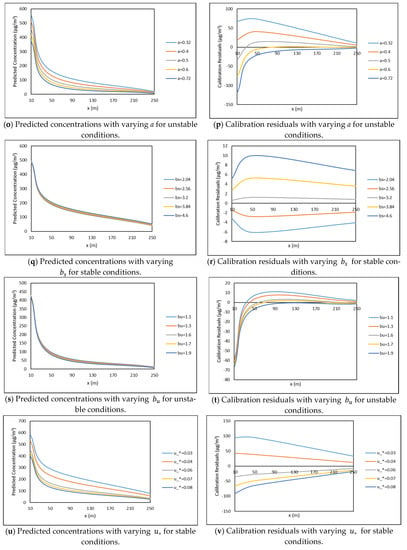
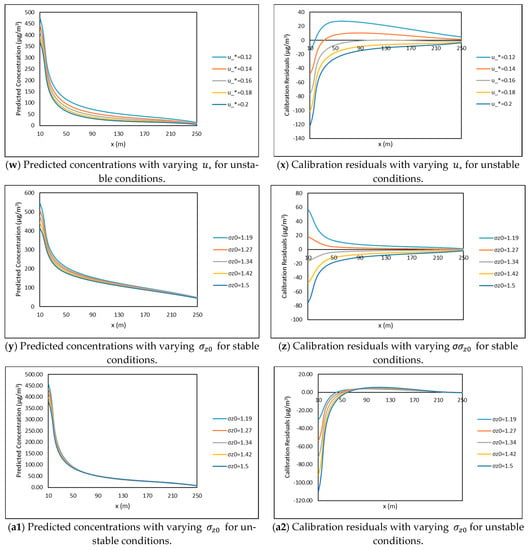
Figure 6.
Sensitivity plots of the SLINE 1.0 predicted concentrations and calibration residuals based on variations in input variables at incremental downwind distances. Note: The predicted concentrations in Figure 6 represent the model results of SLINE 1.0.
6.2. Discussion
The sensitivity plots of the SLINE 1.0 predicted concentrations and calibration residuals based on variation in input variables at incremental downwind distances are represented in Figure 6. The significant changes in predicted concentrations and calibration results are discussed at the following distances to identify the type of sensitivity:
- 10 m downwind distance, which is near the wake area and in the Initial Phase;
- 50 m downwind distance, which is near the Transition Phase;
- 250 m downwind distance, which is far away from the wake area and in the Dispersion phase.
If either the predicted concentrations (model results) or calibration residuals curves in the plots presented in Figure 6 show a considerable difference (does not overlap) when the input parameters/variables are varied in the considered range, then a significant change exists. If the curves are very close to each other and no considerable change in concentration (model results) or calibration residuals values, then there is not much significant change in model results with the variation of input variables/parameters in the considered range. The values in the considered range chosen for each variable/parameter were based on a trial-and-error process which varied up to ±25%.
6.2.1. The Sensitivity of Model Results to the Emission Factor of Pollutants (EF)
The base case value for the emission factor of an air pollutant is 0.0226 g/vehicle for both stable and unstable conditions. In the case of the emission factor of gaseous air pollutants, the model results for each downwind distance showed an increase with an increase in emission factor, as expected (see Figure 6a,c). The calculated model results and calibration residuals varied with the changes in the input. From Figure 6a–d, it can be observed that there are significant changes in predicted concentrations and calibration residuals at 10 m, 50 m, and 250 m for both the stable and unstable conditions. This indicates that the model shows Type III sensitivity at 10 m, 50 m, and 250 m. Concentration is linearly related to emission factor. Note that Type III is more pronounced at 10 m (near the wake area) and 250 m (far away from the wake area).
6.2.2. The Sensitivity of Model Results to the Exponent of Power-Law Velocity Profile (m)
The base case value for the exponent of the power-law velocity profile (m) considered was 0.3 for stable conditions and 0.85 for unstable conditions. For stable conditions, when the model results for different distances for varying exponent of the power-law velocity profile are compared, it was observed that the model results and residuals varied significantly at 10 m, 50 m, and 250 m (see Figure 6e,f). Overall, it was found that there are significant changes in the model results and calibration residuals at 10 m, 50 m, and 250 m. The model exhibited Type III sensitivity characteristics to the exponent of the power-law velocity profile in the Initial, Transition, and Dispersion Phases for a stable atmosphere.
For unstable conditions, it can be observed from Figure 6g,h that the model results and calibration residuals varied significantly at 10 m. Furthermore, there are significant changes observed in calibration residuals at 50 m downwind distances, but no significant changes observed in model results. However, there are no significant changes observed in either model results or calibration residuals at 250 m. Figure 6g,h indicate that the model showed Type III at 10 m, Type II at 50 m, and Type I sensitivity at 250 m for an unstable atmosphere. The results indicate that the model is not very sensitive to the exponent of the power-law velocity profile in the Dispersion Phase at large downwind distances for unstable atmosphere.
6.2.3. The Sensitivity of Model Results to Wind Velocity at a Reference Height ()
The base case value for wind velocity considered was 1.4 m/s for stable conditions and 0.7 m/s for unstable conditions. For stable conditions (see Figure 6i,j), significant changes were observed in model results and calibration residuals at 10 m and 50 m. However, at 250 m, no significant changes were observed in model results and calibration residuals. The curves in Figure 6i,j are very close to each other at 250 m. These characteristics show that the model exhibited Type III sensitivity at 10 m and 50 m, and Type I sensitivity at 250 m. This indicates that the model was least sensitive to wind velocity at the reference height at a downwind distance far away from the wake area for stable atmospheric conditions.
For unstable conditions (see Figure 6k,l), at 10 m and 50 m downwind distances there were significant changes observed in both model results and calibration residuals. However, at 250 m, no significant changes were observed in either model results or calibration residuals. This indicates that the model showed Type III sensitivity at 10 m and 50 m, but Type I sensitivity at 250 m. The results indicate that the model is more sensitive to the reference wind velocity in the Initial and Transition Phase than in the Dispersion Phase.
6.2.4. The Sensitivity of Model Results to Coefficient a
A base case value of 0.57 for the coefficient was considered for stable and unstable conditions. For stable conditions, the model results and calibration residuals varied significantly for 10 m, 50 m, and 250 m (see Figure 6m,n). However, due to the existence of considerable change in all the phases, the model showed Type III sensitivity to the coefficient at 10 m, 50 m, and 250 m.
For unstable conditions (see Figure 6o,p), there were significant changes observed in both model results and calibration residuals at all the considered downwind distances with the variation of coefficient a. This indicates that the model showed Type III sensitivity at 10 m, 50 m, and 250 m, i.e., the model is sensitive to coefficient a at all the downwind distances for unstable atmospheric conditions.
6.2.5. The Sensitivity of Model Results to Coefficient and
The current model used coefficient in stable conditions and coefficient in unstable conditions to predict the concentrations. The base case value considered for coefficient was 3 and for coefficient it was 1.5. For stable conditions (see Figure 6q,r), it can be observed that there was considerable significant change in the calibration residuals but not in model results at 10 m, 50 m, and 250 m. These characteristics indicate that model showed Type II sensitivity at all the Dispersion Phases to coefficient For unstable conditions (see Figure 6s,t), there were no significant changes in model results or calibration residuals at 10 m with varying coefficient . At 50 m and 250 m, there were considerable changes observed in calibration residuals but not in model results. This indicates that the model showed Type I sensitivity at 10 m, but Type II at 50 m and 250 m. The model showed limited sensitivity to coefficients and .
6.2.6. The Sensitivity of Model Results to Surface Friction Velocity ()
The base case value for surface friction velocity ( considered was 0.05 m/s for stable conditions and 0.15 m/s at unstable conditions. For stable conditions (see Figure 6u,v), the model results and calibration residuals varied significantly for all three downwind distances. Thus, the model showed Type III sensitivity to the surface friction velocity (). For unstable conditions (see Figure 6w,x), there were significant changes observed in both model results and calibration residuals at 10 m, 50 m, and 250 m downwind distances with the variation of surface friction velocity. At 10 m, there were significant changes observed in calibration residuals but not in the model results. This indicates that the model showed Type III sensitivity at 10 m, 50 m, and 250 m for unstable atmosphere.
6.2.7. The Sensitivity of Model Results to Initial Vertical Dispersion ()
The base case value considered for initial vertical dispersion () was 1.32 m for stable and unstable atmosphere conditions. For stable conditions (see Figure 6y,z), the plots indicate that there were noticeable changes in model results and calibration residuals at 10 m and 50 m. However, at 250 m, noticeable changes were observed in calibration residuals but not in model results. These results indicate that the model showed Type III sensitivity at 10 m and 50 m, but Type II at 250 m. This indicates that the initial vertical dispersion has considerably less of an impact on concentrations at larger downwind distances far away from the wake area. This is realistic because atmospheric turbulence is the dominant dispersion mechanism at large distances.
For unstable conditions (see Figure 6a1,a2), at 10 m there were significant changes observed in model results and calibration residuals. However, at 50 m, there were significant changes observed in calibration residuals but not in model results. However, at 250 m, there were no significant changes observed in either model results or calibration residuals. This indicates that the model showed Type III sensitivity at 10 m, Type II sensitivity at 50 m, and Type I sensitivity at 250 m downwind distances.
6.2.8. Summary
The above discussion shows that the computed concentrations and residuals changed significantly with the change in the value of the input in most cases. However, the sensitivity of the model was a function of the downwind distance for the reference velocity, bu, bs, and . The input variables showed Type III, Type I, and Type II sensitivity for the cases considered.
7. Conclusions
A new model, SLINE 1.0, has been presented to compute downwind concentrations from line sources on a highway. The model was evaluated with 2008 Idaho Falls data. The results indicate that SLINE 1.0 is an acceptable model based on qualitative analysis and quantitative analysis of model performance. Qualitative analysis showed that there was a strong correlation between the observed and predicted values. The statistical indicators representing the model performance of SLINE 1.0 were within the acceptable range of a better-performing model.
The most sensitive input variables were identified for SLINE 1.0. For stable atmospheric conditions, the model was sensitive to EF, m, , a, and near the Initial Phase; EF, m, , a, and right after the Transition Phase; and EF, m, a and in the Dispersion Phase. For unstable atmospheric conditions, the model was sensitive to EF, m, , a, and near the Initial Phase; EF, a and right after the Transition Phase; and EF, a and in the Dispersion Phase. Thus, the sensitivity analysis demonstrated that SLINE 1.0 shows Type III sensitivity for the majority of the input variables for both atmospheric conditions.
Recalibration of the model for the model constants used in Equations (14), (21), and (22) is needed so that the model shows Type III sensitivity for most of the variables and at all downwind distances. Recalibration will be performed based on available curves based on field studies reported over the last 50 years. It is further suggested that the model should be evaluated with multiple datasets to adjust model constants so that SLINE 1.0 could be used for a variety of engineering applications. Another potential area of research is to incorporate chemistry into the model in the future.
Author Contributions
Conceptualization, A.K., S.V.H.M.; Investigation, A.K., S.V.H.M.; Methodology, A.K., S.V.H.M.; Project administration, A.K.; Supervision, A.K.; Validation, A.K.; Writing—Original draft, S.V.H.M.; Writing—Review & editing, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data (Idaho Falls, 2008), used in the study were taken from the CMAS (Community Modeling and Analysis System). Link: https://www.cmascenter.org/r-line/ (accessed on 10 May 2021). Any other data are available from the authors.
Acknowledgments
The authors would like to thank The University of Toledo for providing the facilities to support this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wark, K.; Warner, C.F.; Wayne, T.D. Air Pollution: Its Origin and Control; Addison-Wesley: Boston, MA, USA, 1998. [Google Scholar]
- United Nation (DESA) Homepages. 68% Of the World Population Projected to Live in Urban Areas by 2050, Says UN. Available online: https://www.un.org/development/desa/en/news/population/2018-revision-of-world-urbanization-prospects.html (accessed on 27 August 2020).
- US EPA. Smog, Soot, and Other Air Pollution from Transportation, US EPA. 10 September 2015. Available online: https://www.epa.gov/transportation-air-pollution-and-climate-change/smog-soot-and-local-air-pollution (accessed on 7 November 2020).
- Timothy, S. Guidelines for Developing an Air Quality (Ozone and PM2.5) Forecasting Program; EPA-456/R-03-002; BiblioGov: Washington, DC, USA, June 2003. [Google Scholar]
- Karroum, K.; Lin, Y.; Chiang, Y.-Y.; Ben Maissa, Y.; El Haziti, M.; Sokolov, A.; Delbarre, H. A Review of Air Quality Modeling. MAPAN 2020, 35, 287–300. [Google Scholar] [CrossRef]
- Sharma, N.; Chaudhry, K.K.; Rao, C.V.C. Vehicular pollution prediction modelling: A Review of Highway Dispersion Models. Transp. Rev. 2004, 24, 409–435. [Google Scholar] [CrossRef]
- Cook, R.; Isakov, V.; Touma, J.S.; Benjey, W.; Thurman, J.; Kinnee, E.; Ensley, D. Resolving local-scale emissions for modeling air quality near roadways. J. Air Waste Manag. Assoc. 2008, 58, 451–461. [Google Scholar] [CrossRef]
- Sutton, O.G. Micrometeorology: A Study of Physical Processes in the Lowest Layers of the Earth’s Atmosphere; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Stockie, J.M. The Mathematics of Atmospheric Dispersion Modeling. SIAM Rev. 2011, 53, 349–372. [Google Scholar] [CrossRef]
- Zimmerman, J.R.; Thompson, R.S. User’s Guide for HIWAY: A Highway Air Pollution Model; US Environmental Protection Agency, Office of Research and Development: Research Triangle Park, NC, USA, 1975.
- Chock, D.P. A simple line-source model for dispersion near roadways. Atmos. Environ. 1978, 12, 823–829. [Google Scholar] [CrossRef]
- Rao, S.T.; Keenan, M.T. Suggestions for Improvement of the EPA-HIWAY Model. J. Air Pollut. Control. Assoc. 1980, 30, 247–256. [Google Scholar] [CrossRef]
- Rao, S.T.; Sistla, G.; Keenan, M.T.; Wilson, J.S. An Evaluation of Some Commonly Used Highway Dispersion Models. J. Air Pollut. Control. Assoc. 1980, 30, 239–246. [Google Scholar] [CrossRef]
- Watson, A.Y.; Bates, R.R.; Kennedy, D. Atmospheric transport and dispersion of air pollutants associated with vehicular emissions. In Air Pollution, the Automobile, and Public Health; National Academies Press: Washington, DC, USA, 1988. [Google Scholar]
- Heist, D.; Isakov, V.; Perry, S.; Snyder, M.; Venkatram, A.; Hood, C.; Stocker, J.; Carruthers, D.; Arunachalam, S.; Owen, R.C. Estimating near-road pollutant dispersion: A model inter-comparison. Transp. Res. Part D Transp. Environ. 2013, 25, 93–105. [Google Scholar] [CrossRef]
- Jones, K.; Wilbur, A. A User’s Manual for the CALINE-2 Computer Program; SE: Washington, DC, USA, 1976; Available online: https://trid.trb.org/view/56208 (accessed on 10 May 2021).
- Benson, P.E. Caline 4-A Dispersion Model for Predicting Air Pollutant Concentrations Near Roadways. 1984. Available online: https://trid.trb.org/view/215944 (accessed on 10 May 2021).
- Luhar, A.K.; Patil, R. A General Finite Line Source Model for vehicular pollution prediction. Atmos. Environ. 1989, 23, 555–562. [Google Scholar] [CrossRef]
- Eckhoff, P.A.; Braverman, T.N. Addendum to the User’s Guide to CAL3QHC Version 2.0 (CAL3QHCR User’s Guide). 1995. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.360.5544 (accessed on 10 May 2021).
- Boeft, J.D.; Eerens, H.; Tonkelaar, W.D.; Zandveld, P. CAR International: A simple model to determine city street air quality. Sci. Total Environ. 1996, 189-190, 321–326. [Google Scholar] [CrossRef]
- Hall, D.; Spanton, A.; Dunkerley, F.; Bennett, M.; Griffiths, R. A Review of Dispersion Model Inter-Comparison Studies Using ISC, R91, AERMOD and ADMS; Environment Agency: Durham, NC, USA, 2000. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.500.993&rep=rep1&type=pdf (accessed on 10 May 2021).
- Khare, M.; Sharma, P. Performance evaluation of general finite line source model for Delhi traffic conditions. Transp. Res. Part D Transp. Environ. 1999, 4, 65–70. [Google Scholar] [CrossRef]
- Kukkonen, J.; Harkonen, J.; Walden, J.; Karppinen, A.; Lusa, K. Validation of the dispersion model CAR-FMI against measurements near a major road. Int. J. Environ. Pollut. 2001, 16, 137. [Google Scholar] [CrossRef]
- Rao, S.; Sistla, G.; Eskridge, R.; Petersen, W. Turbulent diffusion behind vehicles: Evaluation of ROADWAY models. Atmos. Environ. 1986, 20, 1095–1103. [Google Scholar] [CrossRef]
- Bang, H.Q.; Khue, V.H.N.; Tam, N.T.; Lasko, K. Air pollution emission inventory and air quality modeling for Can Tho City, Mekong Delta, Vietnam. Air Qual. Atmos. Health 2018, 11, 35–47. [Google Scholar] [CrossRef]
- Kenty, K.L.; Poor, N.D.; Kronmiller, K.G.; McClenny, W.; King, C.; Atkeson, T.; Campbell, S.W. Application of CALINE4 to roadside NO/NO2 transformations. Atmos. Environ. 2007, 41, 4270–4280. [Google Scholar] [CrossRef]
- Bluett, J.; Kuschel, G.; Xie, S.; Unwin, M.; Metcalfe, J. The development, use and value of a long-term on-road vehicle emission database in New Zealand. Air Qual. Clim. Change 2013, 47, 17. [Google Scholar]
- US EPA. Air Quality Dispersion Modeling—Preferred and Recommended Models, US EPA. 2 November 2016. Available online: https://www.epa.gov/scram/air-quality-dispersion-modeling-preferred-and-recommended-models (accessed on 7 November 2020).
- Gokhale, S.; Pandian, S. A semi-empirical box modeling approach for predicting the carbon monoxide concentrations at an urban traffic intersection. Atmos. Environ. 2007, 41, 7940–7950. [Google Scholar] [CrossRef]
- Cai, H.; Xie, S. Traffic-related air pollution modeling during the 2008 Beijing Olympic Games: The effects of an odd-even day traffic restriction scheme. Sci. Total. Environ. 2011, 409, 1935–1948. [Google Scholar] [CrossRef]
- Milando, C.W.; Batterman, S.A. Operational evaluation of the RLINE dispersion model for studies of traffic-related air pollutants. Atmos. Environ. 2018, 182, 213–224. [Google Scholar] [CrossRef]
- Bowatte, G.; Lodge, C.J.; Knibbs, L.D.; Erbas, B.; Perret, J.L.; Jalaludin, B.; Morgan, G.G.; Bui, D.S.; Giles, G.G.; Hamilton, G.S.; et al. Traffic related air pollution and development and persistence of asthma and low lung function. Environ. Int. 2018, 113, 170–176. [Google Scholar] [CrossRef]
- Liang, D.; Golan, R.; Moutinho, J.L.; Chang, H.H.; Greenwald, R.; Sarnat, S.E.; Russell, A.G.; Sarnat, J.A. Errors associated with the use of roadside monitoring in the estimation of acute traffic pollutant-related health effects. Environ. Res. 2018, 165, 210–219. [Google Scholar] [CrossRef] [PubMed]
- Amoatey, P.; Omidvarborna, H.; Baawain, M.S.; Al-Mamun, A. Evaluation of vehicular pollution levels using line source model for hot spots in Muscat, Oman. Environ. Sci. Pollut. Res. 2020, 27, 31184–31201. [Google Scholar] [CrossRef] [PubMed]
- Rao, K.S. Analytical Solutions of a Gradient-Transfer Model for Plume Deposition and Sedimentation; Air Resources Lab.: Silver Spring, MD, USA, 1981.
- Nimmatoori, P.; Kumar, A. Development and evaluation of a ground-level area source analytical dispersion model to predict particulate matter concentration for different particle sizes. J. Aerosol Sci. 2013, 66, 139–149. [Google Scholar] [CrossRef]
- Yu, Y.T.; Xiang, S.; Noll, K.E. Evaluation of the Relationship between Momentum Wakes behind Moving Vehicles and Dispersion of Vehicle Emissions Using Near-Roadway Measurements. Environ. Sci. Technol. 2020, 54, 10483–10492. [Google Scholar] [CrossRef] [PubMed]
- Paine, R.; Lee, R.; Brode, R.W.; Wilson, R.; Cimorelli, A. AERMOD: Model Formulation and Evaluation Results; National Exposure Research Laboratory, Office of Research and Development: Research Triangle Park, NC, USA, 1999. Available online: https://cfpub.epa.gov/si/si_public_record_report.cfm?dirEntryId=63755&Lab=NERL (accessed on 10 May 2021).
- Zhang, K.; Batterman, S. Near-Road Air Pollutant Concentrations of CO and PM2.5: A comparison of MOBILE6.2/CALINE4 and generalized additive models. Atmos. Environ. 2010, 44, 1740–1748. [Google Scholar] [CrossRef]
- Benson, P.E. Modifications to the Gaussian Vertical Dispersion Parameter, σz, Near Roadways. Atmos. Environ. 1982, 16, 1399–1405. [Google Scholar] [CrossRef]
- Michelle, G.S.; David, K.H. User’s Guide for R-LINE Model Version 1.2 A Research LINE source model for near-surface releases. In Atmospheric Exposure Research Branch Atmospheric Modeling and Analysis Division; Research Triangle Park, NC, USA, 15 November 2013; Available online: https://www.cmascenter.org/r-line/documentation/1.2/RLINE_UserGuide_11-13-2013.pdf (accessed on 10 May 2021).
- Chock, D.P. General motors sulfate dispersion experiment. Bound. Layer Meteorol. 1980, 18, 431–451. [Google Scholar] [CrossRef]
- Snyder, M.G.; Venkatram, A.; Heist, D.K.; Perry, S.G.; Petersen, W.B.; Isakov, V. RLINE: A line source dispersion model for near-surface releases. Atmos. Environ. 2013, 77, 748–756. [Google Scholar] [CrossRef]
- Venkatram, A. Estimating the convective velocity scale for diffusion applications. Bound. Layer Meteorol. 1978, 15, 447–452. [Google Scholar] [CrossRef]
- CMAS: Community Modeling and Analysis System. Available online: https://www.cmascenter.org/help/documentation.cfm?.model=r-line&version=1.2 (accessed on 10 April 2021).
- Model Evaluation. Available online: http://www.eng.utoledo.edu/aprg/courses/dm/hmodel.html (accessed on 10 April 2021).
- Gudivaka, V.; Kumar, A. An evaluation of four box models for instantaneous dense-gas releases. J. Hazard. Mater. 1990, 25, 237–255. [Google Scholar] [CrossRef]
- Riswadkar, R.M.; Kumar, A. Evaluation of the Industrial Source Complex short-term model in a large-scale multiple source region for different stability classes. Environ. Monit. Assess. 1994, 33, 19–32. [Google Scholar] [CrossRef] [PubMed]
- Patel, V.C.; Kumar, A. Evaluation of Three Air Dispersion Models: ISCST2, ISCLT2, and Screen2 for Mercury Emissions in an Urban Area. Environ. Monit. Assess. 1998, 53, 259–277. [Google Scholar] [CrossRef]
- Kumar, A.; Bellam, N.K.; Sud, A. Performance of an industrial source complex model: Predicting long-term concentrations in an urban area. Environ. Prog. 1999, 18, 93–100. [Google Scholar] [CrossRef]
- Kumar, A.; Luo, J.; Bennett, G.F. Statistical evaluation of Lower Flammability Distance(LFD) using four hazardous release models. Process. Saf. Prog. 1993, 12, 1–11. [Google Scholar] [CrossRef]
- Ahuja, S. Evaluation of Mesopuff-II-SOx Transport and Deposition in the Great Lakes Region; University of Toledo: Toledo, OH, USA, 1996. [Google Scholar]
- JASP. Version 0.14.1.0; University of Amsterdam: Amsterdam, The Netherlands, 2020; Available online: https://jasp-stats.org/ (accessed on 8 April 2021).
- ASTM. Standard Guide for Conducting a Sensitivity Analysis for a Ground-Water Flow Model Application; ASTM: West Conshohocken, PA, USA, 1994; pp. 5611–5694. [Google Scholar]
- Madiraju, S.V.H.; Kumar, A. Development of a Line Source Dispersion Model for Gaseous Pollutants by Incorporating Wind Shear near the Ground under Stable Atmospheric Conditions. Environ. Sci. Proc. 2020, 4, 17. [Google Scholar] [CrossRef]
- Nimmatoori, P.; Kumar, A. Application and sensitivity analysis of two screening dispersion models (SCREEN3 and AERSCREEN) for a ground-level area source. Int. J. Environ. Sci. Eng. Res. 2013, 4, 12. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).