The Role of Physical Parameterizations on the Numerical Weather Prediction: Impact of Different Cumulus Schemes on Weather Forecasting on Complex Orographic Areas
Abstract
1. Introduction
2. Description of the Case Study
2.1. Synoptic Analysis
2.2. WRF Model
3. Results and Discussion
4. Performance Testing of WRF Model Simulations
- Accuracy (Hit rate): defined as the ratio between the number of cases in which the event was correctly predicted and the total number of cases considered (n). The value 0 indicates a bad forecast, the value 1 indicates a perfect forecast.
- Threat score (TS): an alternative to the hit rate, useful when the event considered has a substantially lower occurrence frequency than non-occurrence. If the threat score assumes the value 0, the forecast will be bad; otherwise, if it assumes the value 1, the forecast will be perfect.
- Bias: represents the ratio between the predicted and observed data average.
- False alarms ratio (FAR): illustrates that the model has made a forecast of rainfall for the valid period but it did not occur during the valid period. It is especially useful to verify the prediction ability of extreme events. If it assumes the value 0, the forecast will be perfect; if it assumes value 1, there will be the prediction of events that will not happen.
- Equitable threat score (ETS): based on TS; by definition ranging from −1/3 to 1 (perfect prediction).
- Hanssen–Kuipers discriminant: given by the ratio between the events correctly predicted and those actually occurred less the probability of having a false alarm. By definition ranging from −1 to 1 (perfect prediction).
- Probability of detection (POD): sensitive to hits, but ignores false alarms. Very sensitive to the climatological frequency of the event. Good for rare events. Should be used in conjunction with the FAR. Its range is between 0 and 1; if it assumes the value 1, the forecast will be perfect.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cassola, F.; Ferrari, F.; Mazzino, A. Numerical simulations of Mediterranean heavy precipitation events with the WRF model: A verification exercise using different approaches. Atmos. Res. 2015, 164–165, 210–225. [Google Scholar] [CrossRef]
- Caccamo, M.T.; Castorina, G.; Catalano, F.; Magazù, S. Ruchardt’s experiment treated by Fourier Transform. Eur. J. Phys. 2019, 40, 025703. [Google Scholar] [CrossRef]
- Castorina, G.; Caccamo, M.T.; Magazù, S. A new approach to the adiabatic piston problem through the arduino board and innovative frequency analysis procedures. In New Trends in Physics Education Research; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2018; pp. 133–156. [Google Scholar]
- Anthes, R.A. Regional Models of the atmosphere in the middle latitudes. Mon. Weather Rev. 1983, 111, 1306–1335. [Google Scholar] [CrossRef]
- Lackman, G. Mid-Latitude Synoptic Meteorology; American Meteorological Society: Boston, MA, USA, 2011. [Google Scholar]
- Markowski, P.; Richardson, Y. Mesoscale Meteorology in Mid-latitudes; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Altinbilek, D.; Barret, E.C.; Oweis, T.; Salameh, E.; Siccardi, F. Rainfall Climatology on the Mediterranean in EU-AVI 080 Project across—Analyzed Climatology Rainfall Obtained from Satellite and Surface Data in the Mediterranean Basin. 1997. Available online: http://www.diam.unige.it/idromet/avi080/altinb.html (accessed on 15 February 2021).
- Martin, J.E. Mid-Latitude Atmospheric Dynamics. A First Course; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Miglietta, M.M.; Buzzi, A. A numerical study of moist stratified flows over isolated topography. Tellus A 2001, 53, 481–499. [Google Scholar] [CrossRef]
- Davolio, S.; Buzzi, A.; Malguzzi, P. Orographic influence on deep convection: Case study and sensitivity experiments. Meteorol. Z. 2006, 15, 215–223. [Google Scholar] [CrossRef]
- Chu, C.; Lin, Y. Effects of orography on the generation and propagation of mesoscale convective systems in a two-dimensional unstable flow. J. Atmos. Sci. 2000, 57, 3817–3837. [Google Scholar] [CrossRef]
- Anthes, R.A.; Kuo, Y.-H.; Hisie, E.-Y.; Low-Nam, S.; Bettge, T.W. Estimation of skill and uncertainty in regional numerical models. Q. J. R. Meteorol. Soc. 1989, 115, 763–806. [Google Scholar] [CrossRef]
- Castorina, G.; Caccamo, M.T.; Magazù, S. Study of convective motions and analysis of the impact of physical parametrization on the wrf-arw forecast model. Atti Accad. Peloritana Pericolanti Cl. Sci. Fis. Mat. Nat. 2019, 97, A19. [Google Scholar] [CrossRef]
- Randall, D. An Introduction to Atmospheric Modelling; Department of Atmospheric Science, Colorado State University: Boulder, CO, USA, 2001. [Google Scholar]
- Kalnay, L. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Rizza, U.; Miglietta, M.M.; Mangia, C.; Ielpo, P.; Morichetti, M.; Iachini, C.; Virgili, S.; Passerini, G. Sensitivity of WRF-Chem model to land surface schemes: Assessment in a severe dust outbreak episode in the Central Mediterranean (Apulia Region). Atmos. Res. 2018, 201, 168–180. [Google Scholar] [CrossRef]
- Rizza, U.; Brega, E.; Caccamo, M.T.; Castorina, G.; Morichetti, M.; Munaò, G.; Passerini, G.; Magazù, S. Analysis of the ETNA 2015 Eruption Using WRF–Chem Model and Satellite Observations. Atmosphere 2020, 11, 1168. [Google Scholar] [CrossRef]
- Castorina, G.; Caccamo, M.T.; Magazù, S.; Restuccia, L. Multiscale mathematical and physical model for the study of nucleation processes in meteorology. Atti Accad. Peloritana Pericolanti Cl. Sci. Fis. Mat. Nat. 2018, 96. [Google Scholar] [CrossRef]
- Skamarock, W.C. A Description of the Advanced Research WRF Version 3 NCAR; Technical Note; University Corporation for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Caccamo, M.T.; Castorina, G.; Colombo, F.; Insinga, V.; Maiorana, E.; Magazù, S. Weather forecast performances for complex orographic areas: Impact of different grid resolutions and of geographic data on heavy rainfall event simulations in Sicily. Atmos. Res. 2017, 198, 22–33. [Google Scholar] [CrossRef]
- Castorina, G.; Colombo, F.; Caccamo, M.T.; Cannuli, A.; Insinga, V.; Maiorana, E.; Magazù, S. Cultural Heritage and Natural Hazard: How WRF Model Can Help to Protect and Safe Archaeological Sites. Int. J. Res. Environ. Sci. 2017, 3, 37–42. [Google Scholar] [CrossRef]
- Colombo, F.; Castorina, G.; Caccamo, M.T.; Insinga, V.; Maiorana, E.; Magazù, S. IT Technologies for Science Application: Using meteorological Local Area Model to Contrast the Hydrogeological Risks. Hydrol. Curr. 2017, 8, 1000284. [Google Scholar]
- Smith, R. The influence of mountains on the atmosphere. Adv. Geophys. 1979, 21, 87–230. [Google Scholar]
- Wallace, J.M.; Hobbs, P.V. Atmospheric Science: An Introductory Survey; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Kuo, H.L. Further studies of the parameterization of the effect of cumulus convection on large scale flow. J. Atmos. Sci. 1974, 31, 1232–1240. [Google Scholar] [CrossRef]
- Emanuel, K.A.; Raymond, D.J. The Representation of Cumulus Convection in Numerical Models; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Haltiner, G.; Williams, H. Numerical Prediction and Dynamic Meteorology; Wiley Sons Ltd.: Hoboken, NJ, USA, 1983. [Google Scholar]
- Stensrud, D.J. Parametrization Scheme; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Reeves, H.D.; Rotunno, R. Orographic flow response to variations in upstream humidity. J. Atmos. Sci. 2008, 66, 3557–3570. [Google Scholar] [CrossRef]
- Salby, M.L. Fundamentals of Atmospheric Physics; Academic Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Pielke, R.A.; Pearce, R.P. Mesoscale Modeling of the Atmosphere; American Meteorological Society: Boston, MA, USA, 1994. [Google Scholar]
- Ray, P. Mesoscale Meteorology and Forecasting; American Meteorological Society: Boston, MA, USA, 1986. [Google Scholar]
- Anthes, R.A. A cumulus parameterization scheme utilizing a one dimensional cloud model. Mon. Weater. Rev. 1977, 105, 270–286. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. The role of trigger function in numerical forecasts of mesoscale convective system. Meteorol. Atmos. Phys. 1992, 49, 93–106. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Betts, A.K. A new convective adjustment scheme. Part I. Observational and theoretical basis. Q. J. R. Meteorol. Soc. 1986, 112, 677–691. [Google Scholar]
- Betts, A.K.; Miller, M.J. A new convective adjustment scheme. Part II. Single column tests using GATE wave, BOMEX, ATEX and artic air-mass data sets. Q. J. R. Meteorol. Soc. 1986, 112, 693–709. [Google Scholar]
- Fritsch, J.M.; Chappel, C.F. Numerical prediction of convectively driven mesoscale pressure system. Part I: Convective parameterization. J. Atmos. Sci. 1890, 37, 1722–1733. [Google Scholar] [CrossRef]
- Arakawa, A.; Schubert, W.H. Interaction of a cumulus cloud ensamble with the large scale environment. Part I J. Atmos. Sci. 1974, 31, 674–701. [Google Scholar] [CrossRef]

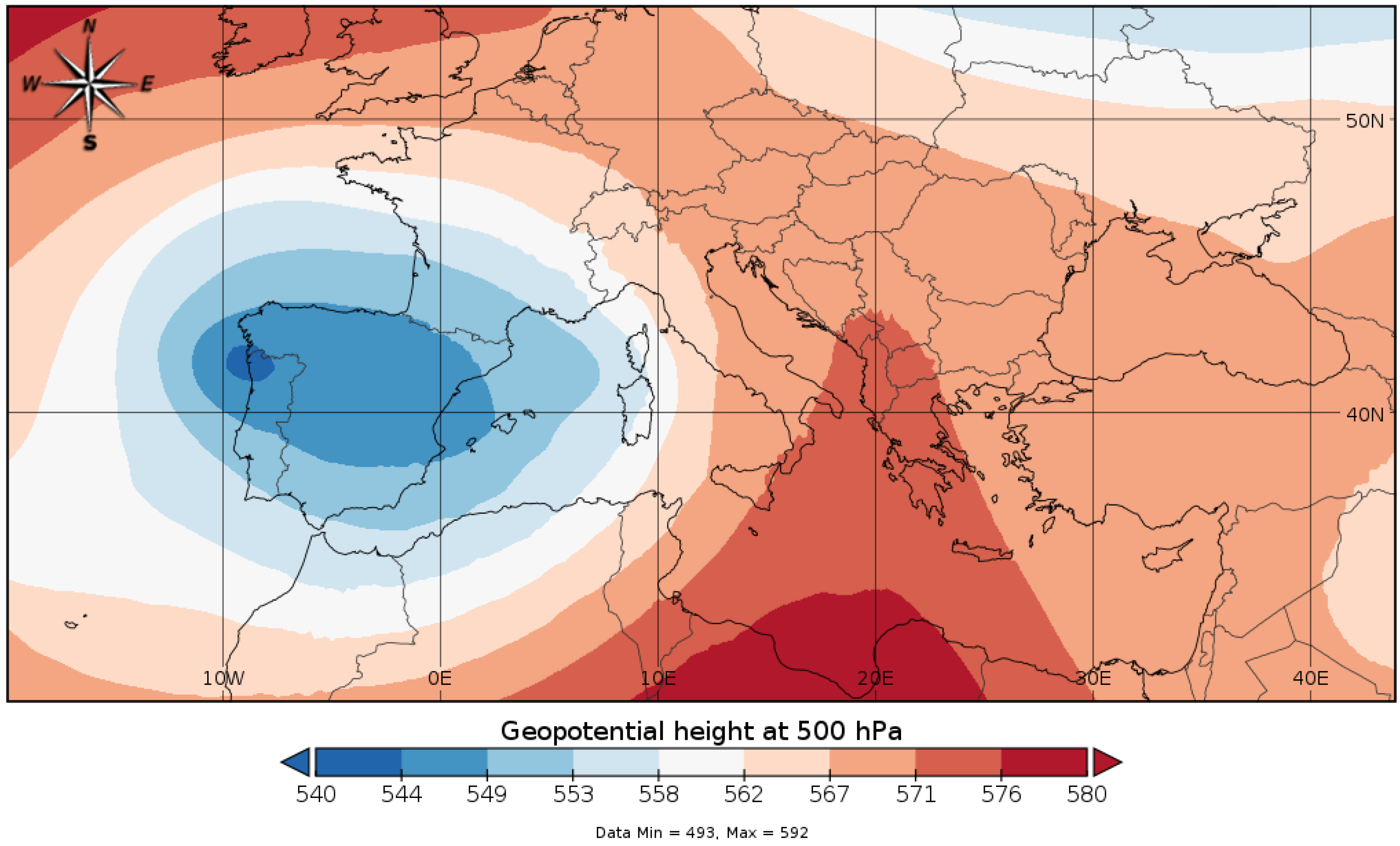



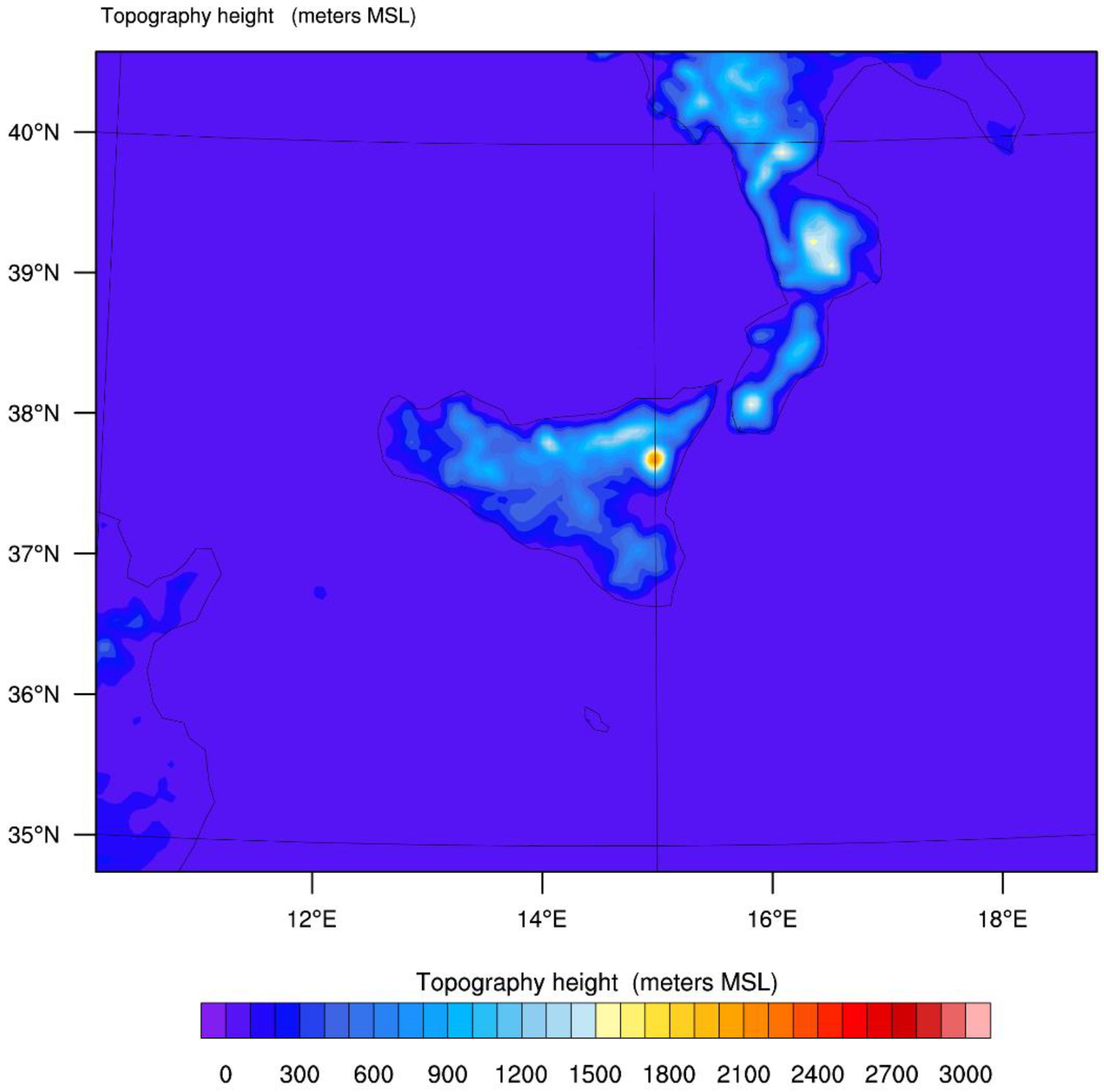

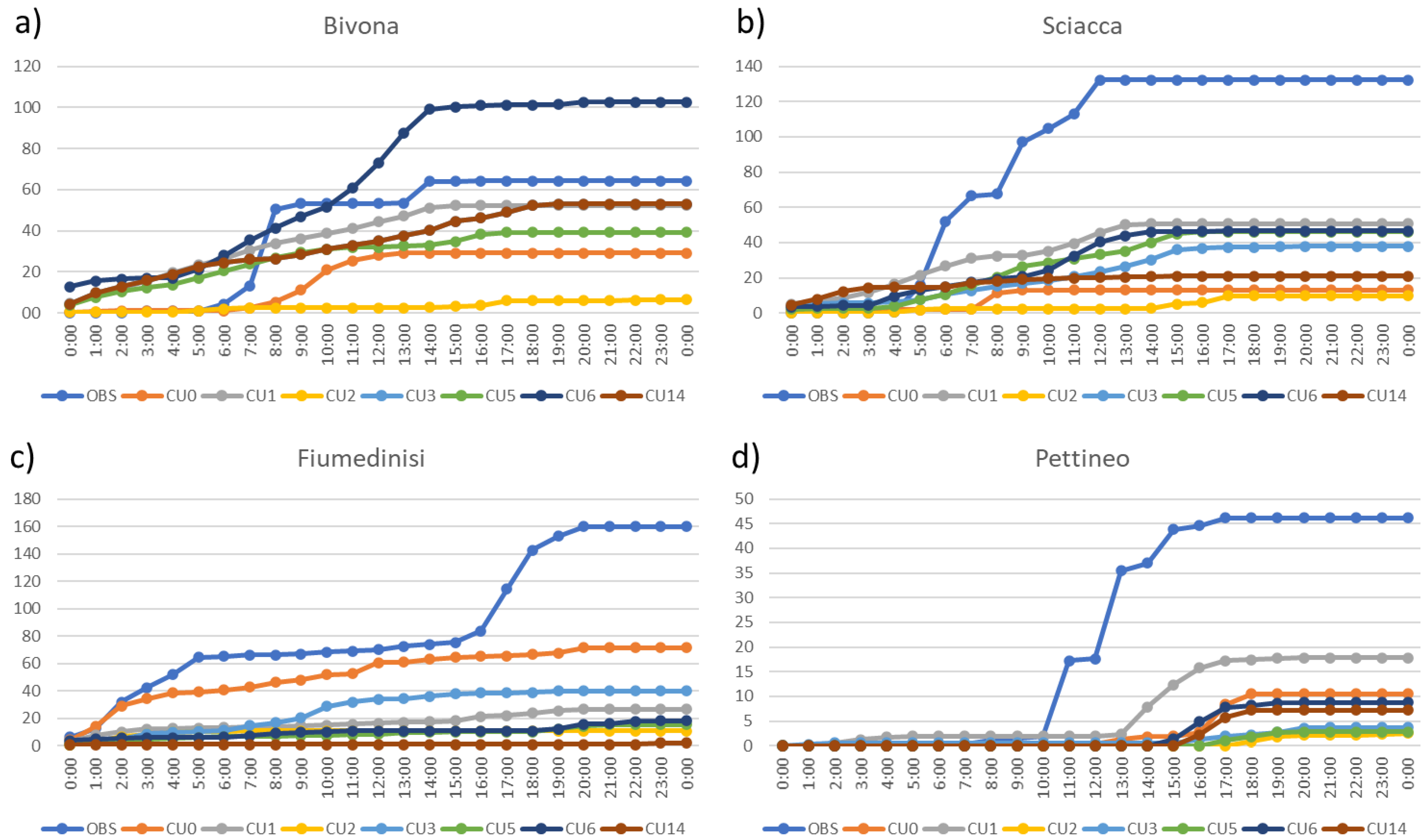


| Stations in the North of Sicily | 24 H Rain mm | 24 H Rain mm CU0 | 24 H Rain mm CU1 | 24 H Rain mm CU2 | 24 H Rain mm CU3 | 24 H Rain mm CU5 | 24 H Rain mm CU6 | 24 H Rain mm CU14 |
|---|---|---|---|---|---|---|---|---|
| Castelbuono | 74.1 | 2.3 | 12.2 | 3 | 1.7 | 8.5 | 18.5 | 7.6 |
| Lascari | 53.6 | 15.7 | 14.5 | 3.6 | 11.1 | 12.6 | 7.5 | 5.3 |
| Pettineo | 46.2 | 10.5 | 17.9 | 2.5 | 3.7 | 2.8 | 8.8 | 7.2 |
| Polizzi | 89.4 | 8.2 | 7.5 | 1.1 | 7.1 | 7.3 | 8.2 | 0.8 |
| Cefalù | 34.1 | 8.1 | 19.1 | 3 | 23.6 | 25.7 | 16.3 | 6.2 |
| Stations in the Northeast of Sicily | 24 H Rain mm | 24 H Rain mm CU0 | 24 H Rain mm CU1 | 24 H Rain mm CU2 | 24 H Rain mm CU3 | 24 H Rain mm CU5 | 24 H Rain mm CU6 | 24 H Rain mm CU14 |
|---|---|---|---|---|---|---|---|---|
| Antillo | 159.5 | 40.1 | 10.8 | 5.2 | 22.1 | 19.8 | 9.6 | 1.5 |
| Fiumedinisi | 153.8 | 71.3 | 26.5 | 10.8 | 40 | 15.3 | 18.1 | 2.1 |
| Linguaglossa | 92.1 | 50.1 | 1.4 | 0 | 2.1 | 0.5 | 0.4 | 1.2 |
| San Pier Niceto | 98.6 | 22 | 18.6 | 2.9 | 9.4 | 10.6 | 4.5 | 6.6 |
| Stations in the Soutwest of Sicily | 24 H Rain mm | 24 H Rain mm CU0 | 24 H Rain mm CU1 | 24 H Rain mm CU2 | 24 H Rain mm CU3 | 24 H Rain mm CU5 | 24 H Rain mm CU6 | 24 H Rain mm CU14 |
|---|---|---|---|---|---|---|---|---|
| Bivona | 64.3 | 29.1 | 52.5 | 6.6 | 53 | 39.3 | 102.6 | 53 |
| Giuliana | 163.2 | 33.3 | 39.0 | 9.8 | 41.3 | 29.3 | 53.6 | 53.6 |
| Ribera | 198.4 | 7.5 | 52.4 | 5 | 28.5 | 29.2 | 74.5 | 12.9 |
| Sciacca | 132.3 | 13.2 | 50.8 | 9.9 | 37.8 | 46.2 | 46.6 | 21 |
| CU0 | CU1 | CU2 | CU3 | CU5 | CU6 | CU14 | |
|---|---|---|---|---|---|---|---|
| Accuracy | 0.68 | 0.53 | 0.45 | 0.54 | 0.53 | 0.51 | 0.52 |
| TS | 0.49 | 0.43 | 0.12 | 0.38 | 0.35 | 0.30 | 0.26 |
| Bias | 0.95 | 1.47 | 0.49 | 1.13 | 1.07 | 0.91 | 0.73 |
| ETS | 0.22 | 0.04 | -0.06 | 0.05 | 0.03 | 0.01 | 0.01 |
| POD | 0.64 | 0.74 | 0.16 | 0.58 | 0.54 | 0.44 | 0.36 |
| FAR | 0.33 | 0.50 | 0.67 | 0.48 | 0.50 | 0.51 | 0.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castorina, G.; Caccamo, M.T.; Colombo, F.; Magazù, S. The Role of Physical Parameterizations on the Numerical Weather Prediction: Impact of Different Cumulus Schemes on Weather Forecasting on Complex Orographic Areas. Atmosphere 2021, 12, 616. https://doi.org/10.3390/atmos12050616
Castorina G, Caccamo MT, Colombo F, Magazù S. The Role of Physical Parameterizations on the Numerical Weather Prediction: Impact of Different Cumulus Schemes on Weather Forecasting on Complex Orographic Areas. Atmosphere. 2021; 12(5):616. https://doi.org/10.3390/atmos12050616
Chicago/Turabian StyleCastorina, Giuseppe, Maria Teresa Caccamo, Franco Colombo, and Salvatore Magazù. 2021. "The Role of Physical Parameterizations on the Numerical Weather Prediction: Impact of Different Cumulus Schemes on Weather Forecasting on Complex Orographic Areas" Atmosphere 12, no. 5: 616. https://doi.org/10.3390/atmos12050616
APA StyleCastorina, G., Caccamo, M. T., Colombo, F., & Magazù, S. (2021). The Role of Physical Parameterizations on the Numerical Weather Prediction: Impact of Different Cumulus Schemes on Weather Forecasting on Complex Orographic Areas. Atmosphere, 12(5), 616. https://doi.org/10.3390/atmos12050616








