Abstract
The COupled Snowpack and Ice surface energy and mass balance model in PYthon (COSIPY) was employed to investigate the relationship between the variability and sensitivity of the mass balance record of the Halji glacier, in the Himalayas, north-western Nepal, over a 40 year period since October 1981 to atmospheric drivers. COSIPY was forced with the atmospheric reanalysis dataset ERA5-Land that has been statistically downscaled to the location of an automatic weather station at the Halji glacier. Glacier mass balance simulations with air temperature and precipitation perturbations were executed and teleconnections investigated. For the mass-balance years 1982 to 2019, a mean annual glacier-wide climatic mass balance of −0.48 meters water equivalent per year (m w.e. a−1) with large interannual variability (standard deviation 0.71 m w.e. a−1) was simulated. This variability is dominated by temperature and precipitation patterns. The Halji glacier is mostly sensitive to summer temperature and monsoon-related precipitation perturbations, which is reflected in a strong correlation with albedo. According to the simulations, the climate sensitivity with respect to either positive or negative air temperature and precipitation changes is nonlinear: A mean temperature increase (decrease) of 1 K would result in a change of the glacier-wide climatic mass balance of −1.43 m w.e. a−1 (0.99 m w.e. a−1) while a precipitation increase (decrease) of 10% would cause a change of 0.45 m w.e. a−1 (−0.59 m w.e. a−1). Out of 22 circulation and monsoon indexes, only the Webster and Yang Monsoon index and Polar/Eurasia index provide significant correlations with the glacier-wide climatic mass balance. Based on the strong dependency of the climatic mass balance from summer season conditions, we conclude that the snow–albedo feedback in summer is crucial for the Halji glacier. This finding is also reflected in the correlation of albedo with the Webster and Yang Monsoon index.
1. Introduction
Since the 1850s, an overall glacier mass loss in High Mountain Asia (HMA), which accelerated in recent decades, has been observed (e.g., [1,2,3,4,5,6]). Shean et al. [7] estimate a total annual mass balance (MB) of a−1 or −0.19 ± 0.03 meters water equivalent per year (m w.e. a−1) and a contribution to sea-level rise of from 2000 to 2018. Glacier retreat is assumed to continue in the next decades. Rounce [8] projects a HMA glacier mass shrinkage between % (Representative Concentration Pathway 2.6) and % (Representative Concentration Pathway 8.5) for the period 2015 to 2100. The changes are caused by increased temperatures, changing precipitation amounts and changes in the ratio between liquid and solid precipitation (e.g., [9]). Wei and Fang [10] report a decadal warming rate of for the period 1961 to 2010. Nevertheless, due to heterogeneous topography, influence of large-scale circulation systems (e.g., [11,12,13,14,15,16,17,18]) and their interactions with local atmospheric circulation systems responses of glaciers largely vary in space (e.g., [19,20,21,22]). Winter-, spring- and summer-accumulation and mixed type glaciers can be found in HMA [23,24]. Summer-accumulation type glaciers are especially sensitive to changes in summer temperatures [25], e.g., due to snow–albedo feedback [26,27,28].
Changes in glacial lake patterns are a consequence of glacier change. These changes include the number of lakes, the lake area, the volume of glacier lakes and the spatial distribution of lakes. Wang et al. [29] have shown the correlation of decreasing glacier area and increasing number of lakes, with a peak in the elevations between 5500 and 6000 masl (see Figure 16, [29]) since the 1970s. With the increasing number of unstable glacier lakes and increasing water volume of existing lakes [30], the potential threat trough glacial lake outburst floods (GLOFs) (e.g., [31,32,33]) is increasing in the Hindu Kush Himalayas region and in particular in the Himalayas [34] and Nepal [35].
Due to the remoteness and harsh climate conditions in HMA, good documentation and in-situ analyses of glof are scarce. Halji village in northwestern Nepal [36] was affected by six GLOFs between 2004 and 2011 [37]. The village is located in Limi valley in the district Humla. Several buildings of the ∼400 inhabitants of the village were damaged [36,38], and as a result in 2010, a gabion wall was constructed to protect the village [38]. The wall was repaired after GLOF damage in 2011 and further extended in 2014 [38]. The source of the GLOFs is an ice-dammed basin located at the tongue of the Halji glacier (30.26° N, 81.47° E, see Figure 1), forming a potential glacier lake. The lake is drained by the Halji Khola (river) which flows through Halji Village. The linear distance between village (∼ 3800 ) and glacier (mean elevation 5500 ) is ∼6 .
The region is located north of the Himalayan main ridge. It is influenced by the westerlies [11] and south Asian monsoon systems [39,40], particularly the Indian Summer Monsoon [19]. Westerlies dominate in winter [11]. With the northward shift of the westerlies during summer, the area is mainly influenced by the monsoon [11,19]. According to the glacier accumulation regime classification of (see Figure 14 in [24]), the region lies within the transition zone from mostly winter-accumulation type glaciers further to the west, to glaciers with summer-accumulation and mixed accumulation regimes in Nepalese regions to the east.
In this study, we statistically downscale the European Centre for Medium-Range Weather Forecasts (ECMWF) reanalysis ECMWF Reanalysis fifth generation-Land (ERA5-L) [41] to the location of an automatic weather station (AWS) installed in the immediate vicinity of the glacier. This 40 year dataset was used to create distributed climate data input fields to force the COupled Snowpack and Ice surface energy and mass balance model in PYthon (COSIPY) [42] to the Halji glacier. COSIPY model development and testing details are provided by Sauter et al. [42]. It is the main tool of this study. With the resulting glacier mass balance fields, we analyzed the dominating atmospheric drivers and their influence on the interannual variability of the glacier’s mass budget. Moreover, simulations with temperature and precipitation perturbations were executed, and seasonal sensitivity characteristic after Oerlemans and Reichert [43] were calculated. The first method focuses on the impact of an overall change on the annual mass balance, while the latter refers to the impact on the annual mass balance from changes in individual months. Finally, to identify possible teleconnections, we investigated the monthly, seasonal and annual variability of the MB by correlating it with 22 different circulation and monsoon indices. The present study focuses on the atmospheric sensitivity of the Halji glacier in the transition zone between mainly monsoon influenced glaciers to the east and more westerly influenced glaciers to the west.
2. Halji Glacier
The Halji glacier extends between 5251 and 5658 (mean: 5430 ) [44] with an area of 2.3 km2 [45] in 2001. The glacier has an estimated maximum thickness of 83 ([22], dataset: [46]) and an estimated mean flow velocity of 2.3 m a−1 ([47], dataset: [48]) (see Appendix A Figure A1).
Kropáček et al. [38] determined an annual geodetic MB of a−1 between 2000 and 2013. Shean et al. ([7], dataset: [49]) calculated an annual geodetic MB of a−1 between 2000 and 2018. Both studies use digital elevation model (DEM) differencing but for different periods. As reported by Ye et al. [50], the glaciers in the Naimona’nyi region (∼25 km northwest of Halji glacier) have retreated at least since 1976. The only information about the Halji glacier development pre-millennial are glacier outlines derived from satellite data and the resulting glacier areas as displayed in Figure 1. The glacier area decreased from 3.1 km2 in 1974 [51] to 2.3 km2 in 2001 [45]. Between 2001 and 2010, the area was relatively stable with still 2.2 km2 in 2010 [52], but decreased to 1.9 km2 by 2018. The 2018 outline was derived from a Sentinel 2 [53] scene found with the Google Earth Engine Digitisation Tool developed by Lea [54]. According to the outline of the Randolph Glacier Inventory 6.0 (RGI6) [45], the glacier has two ice divides (see green lines Figure 1). All other outlines have been adjusted to these divides.

Figure 1.
The Halji glacier with multi-temporal glacier outlines and satellite image map in the background [55] (a) and photo of the automatic weather station (AWS) of the Chair of Climatology (Technische Universität Berlin) installed in 2018 with a part of the glacier in the background (b, photo by Benjamin Schröter). Colors within the inset map represent elevation [56].
3. Data and Methods
In the following section, the applied physically-based surface energy and mass balance model COSIPY is described. Afterwards, the AWS and the meteorological forcing of COSIPY with the applied downscaling approaches are presented in Section 3.2. The setup for the simulations in this study is summarized in Section 3.3. The applied statistics, the seasonal sensitivity characteristic (SSC) and circulating and monsoon indexes are presented in Section 3.4. An overview of all introduced symbols and constants with their units can be found in Appendix A.
3.1. COSIPY
COSIPY is of medium complexity within the range of available surface energy balance (SEB) and mb models [42]. It is physically based and combines SEB processes with an adaptive (non-equidistant) subsurface scheme. The possibility of the identification of important atmospheric MB drivers, the easy implementation on High-Performance Computing Clusters (HPCCs) and the modular structure (maximum traceability) are some of the key points focused on during the development of the model. The open-source model is written in Python 3. The source code is freely available on a git repository (https://github.com/cryotools/cosipy, accessed on 13 March 2021). We use version COSIPY v1.3 (https://doi.org/10.5281/zenodo.3902191, accessed on 13 March 2021) in the distributed setup. The temporal and spatial resolution of the simulations is scalable, depending on the temporal resolution of forcing variables and the spatial resolution of the applied DEM. The SEB is defined as the sum of all energy fluxes at the surface:
where QM is available melt energy, QSWin is incoming shortwave radiation, α is snow/ice albedo, is incoming longwave radiation, ) is outgoing longwave radiation, is sensible heat flux, is latent heat flux, is glacier heat flux and sensible heat flux of rain. and are input parameters of COSIPY whereby can be parametrized (see Equations (14) and (15), [42]). Cloud cover fraction is needed as input in the latter case. The decay of is calculated after Oerlemans and Knap [57] with the parameters presented and studied by Mölg et al. [58] in HMA. All other terms on the right-hand side of Equation (1) depend on the surface temperature . The resulting nonlinear equation is solved iteratively with an optimization algorithm. Due to physical constraints, ≤ melting point temperature must be fulfilled and therefore energy surplus results in when equals . If < , there is no available energy at the surface, i.e., . All energy fluxes are of positive (negative) algebraic sign towards (directed away from) the surface and presented in m−2.
The SEB is linked through as an upper Neumann boundary condition [59] to the heat equation of the subsurface module. Furthermore, surface melt and rain percolates through the snowpack and can result in refreezing within the snow layers. A small part of net shortwave radiation , penetrates the uppermost layers [60], warms these layers and result in subsurface melt, if the additional energy would otherwise result in inconsistent layer temperature > . Moreover, parametrizations for the densification of the snow [61,62] and the development of the snow/ice surface roughness [58] were implemented.
COSIPY is a one-dimensional point model that calculates in its distributed setup the mb at each point on the glacier and neglects exchange of lateral mass and energy transport. Processes at the base of the glacier are also neglected, which is why in the following, the simulated mb is referred to as the climatic mass balance in accordance with Cogley et al. [63]. It is the sum of mass changes through accumulation and ablation and therefore links climate variability to glacier-mass gain or loss [64]. It is calculated as follows [63]:
where surface accumulation is , surface ablation is , internal accumulation is , internal ablation is , surface mass balance is and internal mass balance is . Accumulated snowfall and deposition (resublimation) of water vapor result in . COSIPY does not consider direct sublimation during snowfall and processes associated with snowdrift. Therefore, frozen precipitation equals within COSIPY. surface ablation consists of sublimation and surface melt resulting from Equation (1). internal accumulation equals refreezing within the snowpack and equals subsurface melt through penetrating radiation. Mass balance components are positive (negative) if they are a mass gain (loss) in In accordance with Cogley et al. [63], a capital B denotes the glacier-wide MB (sum of all point balances) with the same suffixes than b. The annual climatic mass balance is . The cumulative climatic mass balance is . When we refer to the massbalance year (MB-year) of and other variables, we speak of the hydrological year, starting after the approximated end of the preceding ablation season on 1 October and ending on 30 September of the following year, whereby the year of the included January is used as name of the MB-year in accordance with Cogley et al. [63]. For further information on applied parametrizations, physical principles and technical infrastructure of COSIPY, please read Sauter et al. [42].
3.2. Climate Forcing Model Input
3.2.1. Automatic Weather Station Measurements
An AWS [65] was installed in December 2013 by the Chair of Climatology (Technische Universität Berlin) and was replaced by a new AWS in 2018 (see Figure 1). The AWS is located adjacent to the Halji glacier at an elevation of 5359 The data are continuously transmitted via Iridium satellite telemetry to a server of the Chair of Climatology at Technische Universität Berlin, Germany. Observations from 20 April 2018 until 2 November 2019 are used to statistically downscale atmospheric reanalysis data. Due to technical problems with total precipitation measurements, the available period starts in that case on 2 August 2018. The measured variables, measuring instruments and nominal accuracies are summarized in Table 1.

Table 1.
Variables, instruments, measuring range and nominal accuracies of the automatic weather station located at 5359 in the direct vicinity of Halji glacier. The full name of the instruments are Lufft WS501-UMB SmartWeather Sensor and Lufft WS100 Radar Precipitation Sensor.
Data of the first installed AWS from 1 December 2013 until 17 April 2018 were additionally used to evaluate downscaled surface pressure , air temperature at 2 and relative humidity at 2 RH2.
3.2.2. Downscaling ERA5-L
Required COSIPY forcing variables are derived from the atmospheric reanalyses ERA5-L produced by ECMWF within the Copernicus Climate Change Service. ERA5-L—a subversion of ERA5—provides ERA5 surface variables on a km grid, instead of the original km ERA5 grid. After producing ERA5, the Hydrology revised Tiled ECMWF Scheme for Surface Exchanges over Land (H-TESSEL) of the ERA5 integrated forecast system (IFS CY41R2) was re-executed with spatially interpolated (to a 9km grid) ERA5 variables to produce ERA5-L [66]. Air temperature at 2 and dewpoint temperature at 2 are the only COSIPY forcing variables that contain new information in comparison to ERA5. All other variables are also H-TESSEL forcing variables and therefore contain no new information [41,66,67]. We used hourly data from January 1981 until April 2020 from the grid cell, which represents the area between 30.25° N, 81.45° E and 30.35° N, 81.55° E. Halji glacier lies completely within this grid cell. ERA5-L data can be downloaded free of charge from the climate data store (https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-land?tab=form, accessed on 12 December 2020).
The preprocessing steps to start COSIPY simulations can be divided into two steps. An overview of the applied approaches is provided in Table 2. First, we downscale the ERA5-L data to the location of the installed AWS at the glacier. Second, the downscaled forcing variables at the location of the AWS are interpolated with a dem to the applied distributed fields on the glacier. The used ERA5-L grid cell has a model elevation of 5154 , which lies 205 below the elevation of the aws.

Table 2.
COupled Snowpack and Ice surface energy and mass balance model in PYthon (COSIPY) forcing variables with required units, applied downscaling approaches to ERA5-L data and approaches to create the distributed fields (interpolation) on the glacier. The second column denotes if the variable is also measured by the automatic weather station (AWS). A dash stands for no downscaling.
For surface pressure , we apply the barometric formula for both the downscaling to the elevation of the AWS and the interpolation to the distributed fields [69]:
where is atmospheric pressure at reference height, a thermal gradient, air temperature at reference height, h height difference, M average molar mass of air g gravitational acceleration and R gas constant (see Appendix List of constants).
We observed that the seasonal amplitude of ERA5-L’s is greater than the measured , resulting in a warm bias of temperature in summer and a cold bias in winter temperature. Therefore, we applied a quantile-mapping approach [70] to downscale the data to the AWS. For generation of the distributed fields, we use a lapse rate of (100 m). The lapse rate is calculated from the long-term mean (1981 to 2019) of of 121 ERA5-L grid cells around Halji glacier (see Appendix A Figure A2).
Derived ERA5-L relative humidity at 2 is calculated from saturation water vapor of and (see [71,72]). We use a constant value for all glacier grid points (GGPs) for the distributed fields on the glacier. For the two radiation components and we do not use downscaling from raw ERA5-L to the location of the aws. However, a radiation model after Wohlfahrt et al. [68] is used to calculate the distributed input fields of on the glacier. The model takes slope, aspect, timestamp, latitude, longitude of the GGPs and of ERA5-L as input and calculates for each GGPs. is taken constant in space for all GGPs without interpolation. To derive wind speed at 2 , first wind speed at 10 has to be calculated from u and v component of 10 wind, which is described on the ERA5 website (https://confluence.ecmwf.int/pages/viewpage.action?pageId=133262398, accessed on 12 December 2020). Afterwards, we use the logarithmic wind profile to calculate [73]:
where is surface roughness. We use a value of mm for , which is the mean between the upper and lower boundary condition (firn: 4 mm [74] and fresh snow: mm [75]) in the surface roughness parametrizations of COSIPY. We use a constant value for all GGPs for distributed fields on the glacier.
3.2.3. Comparison of Downscaled ERA5-L to Automatic Weather Station Measurements
Figure 2 presents the comparison between measured and ERA5-L downscaled variables , and specific humidity at 2 . For comparison, we use instead of , the forcing variable required by COSIPY, to exclude differences that are solely based on differences in and . The course of the year of all three measured variables can be reproduced by ERA5-L, which is displayed in the left panels. This is supported by the scatterplots in the middle panels and the statistics of the applied linear least-square regression with all coefficients of determination ≥0.9 (: 0.99, : 0.90, : 0.93), small root mean square errors (RMSE, : , : , : −1), small mean bias errors (MBE, : , : < , : −1) and regression line slopes close to 1 (: 1.1, : 0.94, : 1.18). All results are statistically significant with p-value < 0.01. The cumulative distribution functions in the right panels reveal that the downscaling approach in case of and result in a substantially improved agreement with AWS measurements. A decrease in MBE from to (RMSE: from to ) in case of and from to (RMSE: from to ) in case of could be achieved. In case of , almost no improvement (MBE: to −1) can be observed. The reason might be that mean of the measured values and the corresponding raw ERA5-L values differ only by % (Measured: 77.1%, ERA5-L: 76.8%).
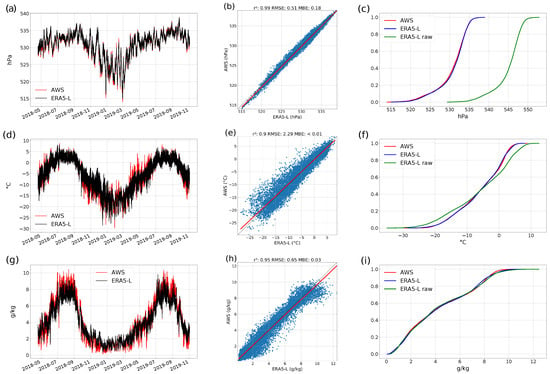
Figure 2.
Comparison between measurements of the automatic weather station (May 2018–October 2019) and the downscaled European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis fifth generation-Land (ERA5-L) variables air pressure (a–c), air temperature at 2 (d–f) and specific humidity (g–i) at the location of the automatic weather station. The time series are presented in the left panels (a,d,g), the scatterplots in the middle panels (b,e,h) and the cumulative distribution functions in the right panels (c,f,i). A linear least-square regression model is used for the scatterplots, where the red line shows the regression line. ERA5-L-raw denotes the unscaled ERA5-L variables. In all plots, hourly values are displayed.
As mentioned in Section 2, we additionally compared , and with measurements of the earlier installed AWS between 1 December 2013 and 17 April 2018. Due to measurement gaps, 65% of and 26% of and values could be used. The calculated of the linear least-square regression are again all > 0.9 (: 0.98, : 0.92, : 0.92), the RMSEs are within a tolerable range (: , : , : −1) and regression line slopes are acceptable (: 1.05, : 0.94, : 0.76).
We observed a distinct difference when comparing ERA5-L and measured . The hourly mean of measured is 5 times the ERA5 . Hourly values of are compared in Figure 3. Figure 3a shows the difference when comparing the data. It was not possible to apply a complex wind modeling approach within the scope of this study, also because of the lack of a highly resolved dem. Therefore, we applied a scale factor of 5 to ERA5-L , which is presented in Figure 3b. The cumulative distribution function in Figure 3c reveals the improvement in the distribution of scaled ERA5-L data in comparison with measured data. This is supported by the decrease of the MBE from to < −1.

Figure 3.
Measured (AWS) and ERA5-L wind speed at 2 . Time series without wind scaling (a, ERA5-L-raw), with wind scaling (b, ERA5-L), and the cumulative distribution functions (c) with unscaled and scaled ERA5-L wind speed at 2 . In all plots hourly values are displayed.
In the period from August 2018 to November 2019, measured total precipitation was twice the amount of ERA5-L . We used this as a scale factor (Figure 4). The scaling results in a decrease of MBE from mm to mm −1.
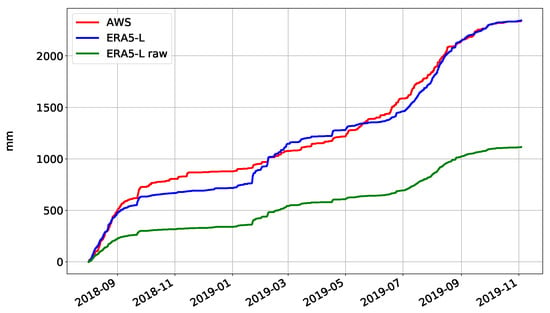
Figure 4.
Cumulative measured (AWS), unscaled (ERA5-L-raw) and scaled (ERA5-L) hourly total precipitation from 2 August 2018 to 2 November 2019.
3.3. COSIPY Simulations
As static data, a glacier outline and dem are required to start COSIPY simulations in the distributed setup. We used a time-invariant reference outline from RGI6 [45] (see Figure 1) for the simulation period October 1981–September 2019. Further, we used the 1 arcsecond global product [44] of the Shuttle Radar Topography Mission (SRTM) as dem. With the elevation information of all GGPs, we used the Geospatial Data Abstraction Library (GDAL) [76] to calculate all slopes and aspects of the GGPs needed as input for the radiation module of Wohlfahrt et al. [68]. Furthermore, we aggregated the dem with GDAL to spatial resolutions between and . The applied spatial resolutions in arcseconds and ∼ and the number of resulting GGP is summarized in Table 3.

Table 3.
Applied spatial resolutions and resulting glacier grid points (GGPs) for the Halji glacier. Not all applied resolutions are shown.
We created the distributed COSIPY input fields and started simulations for the whole available ERA5-L period from January 1981 to April 2020 at an hourly resolution for all spatial resolutions. We then calculated annual deviations of () to the 30 resolution simulation in order to identify the best trade-off between computational power and reasonable results. The deviations are presented in Figure 5.
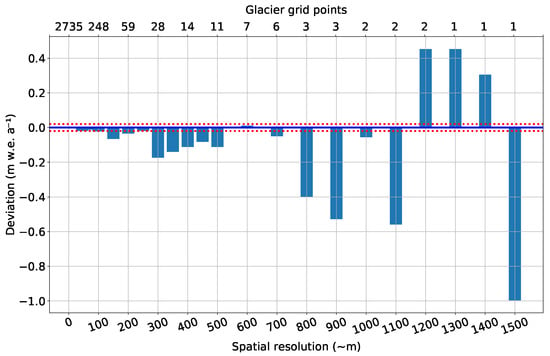
Figure 5.
Deviations of the mean annual glacier-wide climatic mass balance of the Halji glacier to the reference 30 simulation for the mass-balance years (MB-years) 1982 to 2019 for different spatial resolutions ranging from 60 to 1500 . Corresponding glacier grid points are on the second x-axis. The red dotted lines showing the selected threshold for deviations in a tolerable range ( −1).
All deviations until the resolution of m are within a tolerable range ( −1). Therefore, for all further simulations in this study, we used a spatial resolution of with the resulting 248 GGPs representing the entire Halji glacier. For all distributed simulations, we used the hpcc of the Climate Geography lab of Humboldt-Universität zu Berlin, Germany. A simulation with resolution and 248 GGPs has a runtime of less than two hours for the whole ERA5-L period from January 1981 to April 2020.
3.4. Sensitivity Studies and Large Scale Teleconnections
Statistics: To investigate the influence of the forcing variables on the interannual variability of , we calculate non-parametric Spearman’s rank correlation coefficients [77] between and the different forcing variables and the intermediate variables , and net longwave radiation . We define two significance levels with a 95% and 99% confidence interval and access the significance with the two-sided p-value of the Spearman’s rank correlation [77]. Furthermore, we start simulations with ±0.5, ±1.0, and ±5, ±10, % perturbations and analyzed the resulting annual deviations of to the original run.
Seasonal Sensitivity Characteristic (SSC): Oerlemans and Reichert [43] proposed calculating SSC to describe the dependency of of a glacier to the local seasonal climate in a uniform and structured manner. The SSC of a glacier is a 2 × 12 matrix quantifying the sensitivity to temperature and precipitation perturbations each in the 12 months of the year. For their calculation in the first step, the reference COSIPY simulation was adjusted so that the mean is zero. Therefore, the mean forcing temperature is adjusted in the range of . For the Halji glacier, we applied a offset of (see Appendix A Figure A3) to arrive at a zero for the period October 1981–September 2019. In the second step, 24 COSIPY simulations were forced with monthly perturbations of and 24 COSIPY simulations were forced with monthly perturbations of %. The resulting differences of between the positive and negative perturbation for each month are the 12 temperature values and the 12 precipitation values of the SSC. These 24 values are displayed as a bar plot. For further information, including the equations of the concept, please see Section 2, especially Equations (3) and (4) in Oerlemans and Reichert [43] and Section 3b in Reichert et al. [78].
Indexes: Finally, we calculate between and 22 common teleconnection indexes. The temporal resolution and coverage, short and long name, reference and download location of the indexes are summarized in Table A1 in the Appendix A. In doing so, we test the relationship between COSIPY-simulated Halji glacier and atmospheric drivers.
4. Results
The for MB-years 1982 to 2019 of Halji glacier and the corresponding (1 October 1981 to 30 September 2019) are displayed in Figure 6. The mean is −1 and is The most negative annual balance is −1 in 1990. The most positive is −1 in 2013. The overall standard deviation of −1 reflects the quantitative interannual varability in the mass balance time series. Between 1995 and 2007 all Halji glacier annual mass balances are negative (mean −1). In contrast, between 2008 and 2015, the glacier balance was in equilibrium (only two negative MB-years 2012 and 2014) with a mean of −1 over this period (see Figure 6b).
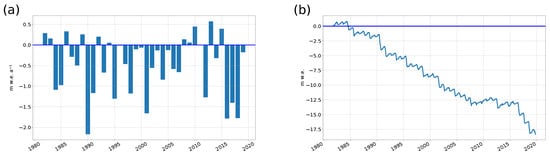
Figure 6.
Simulated annual glacier-wide climatic mass balance (a) and cumulative (b) glacier-wide climatic mass balance of the Halji glacier from 1982 to 2019.
4.1. Sensitivity to Climate Forcing Input Variables
Table 4 displays the non-parametric Spearman’s rank correlation coefficient rs between and the forcing variables as well as four intermediate (, , and ) variables.

Table 4.
Spearman’s rank correlation coefficients between monthly forcing (f) and intermediate (i) variables and annual glacier-wide climatic mass balance. Grey coefficients are not significant, normal font denotes significance level 0.05 and bold and italic fonts significance level 0.01. The aggregation metrics to calculate annual and monthly values are displayed in the second row.
On annual basis the forcing variables , and have the highest correlation with all > 0.4. Whereby, and by themselves are highly significantly correlated with an annual of 0.69 (not displayed in Table 4, p-value < 0.01). No significant annual correlation could be found between and , and and .
On a monthly basis, the October temperature at the beginning of the MB-year and the February, June and July temperature mainly determine the interannual variability. Interestingly, the monthly sum of in September before the MB-year starts explains the interannual variability with = 0.43 (p-value < 0.01). The high statistical significance between in June and results to some degree from the correlation ( = −0.37, p-value < 0.05, not displayed in Table 4) between and . A statistically significant correlation of and the forcing variables and could be found neither on annual nor monthly time scales. However, a significant correlation (p-value < 0.05) with the monthly mean of in February, May and June is present. Whereby, and are by themselves highly significant correlated in February ( = 0.47, p-value < 0.01), May ( = 0.74, p-value < 0.01) and June ( = 0.82, p-value < 0.01). The intermediate variables , and are superior in explaining interannual mb variability. The annual is mainly a result of the and variability. The interannual variance of is the dominating driver ( = 0.8, p-value < 0.01) of the long-term variability. The correlation of is in the same range because and are the strongest coupled variables with an annual of 0.98 (not displayed in Table 4, p-value < 0.01).
The monthly deviations in percent (absolute values in Appendix A Figure A5) of , , , , and to their long-term monthly mean from 1982 to 2019 are shown in Figure 7. Deviations that are positive for are blue, deviations with negative influence are red. deviations are most pronounced in summer from May/June until September/October. In the case of , it is roughly the opposite: the biggest deviations occur from October until May or June. Especially in July, August and September, there is a clear similarity in the patterns of the monthly and variability. The variability of is spread over the whole year, with two phases with low deviations in November and December and April and May. Monthly deviations from October to April/May are mostly negative from 1982 until 2003/2004 while being mostly positive compared to their long-term monthly mean. From June to September, and all monthly deviations do not show any clear pattern.
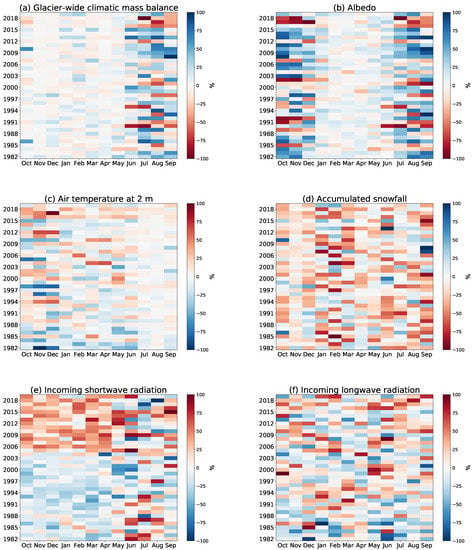
Figure 7.
Monthly mean deviations 1982 to 2019 from long-term monthly mean values in percent (% is maximum and minimum deviation) of glacier-wide climatic mass balance (a), albedo (b), air temperature at 2 (c), accumulated snowfall (d), incoming shortwave radiation (e) and incoming longwave radiation (f). The color bar is arranged so that deviations that act positively (negatively) on glacier-wide climatic mass balance are shown in blue (red).
4.2. Temperature and Total Precipitation Perturbations and Seasonal Sensitivity Characteristic
Figure 8 shows the resulting deviations of simulations with overall and perturbations. The results clearly show the nonlinear responses to positive and negative perturbations. A perturbation of results in a response roughly in the same range ( and −1). In contrast, a perturbation of results in a disproportionate mass response ( and −1). The same holds true in case of perturbations. A yearly positive response of −1 and a negative of −1 with a % change and a response of and −1 with % perturbation are found.
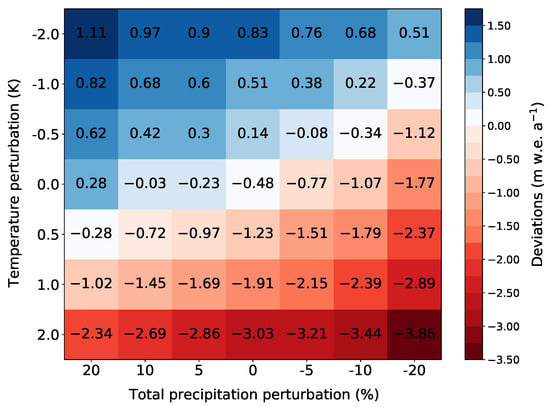
Figure 8.
Mean (1982–2019) annual glacier-wide climatic mass balance (−1) deviations from reference run ( = −1) for different overall temperature and total precipitation perturbations. The values within each pixel displays the actual mean of the corresponding perturbation simulation. Please note that the color bar of the deviations is not centered around zero, reflecting the nonlinear response to same positive and negative perturbations.
Figure 9 displays the SSC after Oerlemans and Reichert [43]. The sensitivity to is dominated by the months June to August and partly September. The peak in summer is also visible in sensitivity to monthly perturbations while it is not that pronounced as the sensitivity. The sensitivity to November perturbations is the lowest. is for both and most sensitive to July perturbations. The sum of the response to July and August is significantly greater than the response to all other months combined. In the case of , it is the sum of the response to July, August and September, which is greater than the sum of the response to all other months combined.
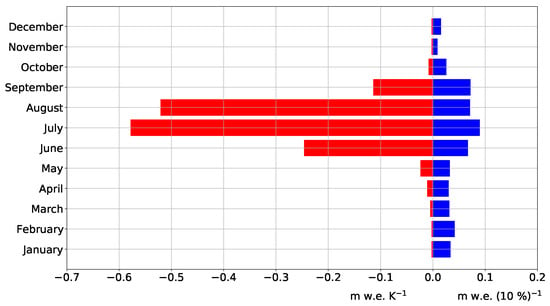
Figure 9.
Seasonal sensitivity characteristic (SSC) after Oerlemans and Reichert [43]. Red bars are the dependence of annual glacier-wide climatic mass balance on monthly temperature perturbations of 1 and blue the dependence of on monthly total precipitation perturbation of 10%.
4.3. Index Correlations
As presented in Section 3.4, we analyzed the response of to 22 circulation and monsoon indices. Analogous to the forcing variables, we calculated the non-parametric between and the indices. With exception of the Webster and Yang Monsoon index (WYM) and the Polar/Eurasia index (POL), no significant correlations could be found with any of the indexes. Figure 10 displays and the two indexes (annual values) that show significant correlations (p-value < 0.05) with . The WYM is calculated from the zonal wind shear between 850 and 200 [79] between 0° and 20° N and 40° and 110° E. It is a broad-scale monsoon index differentiating between strong and weak monsoon seasons [79].
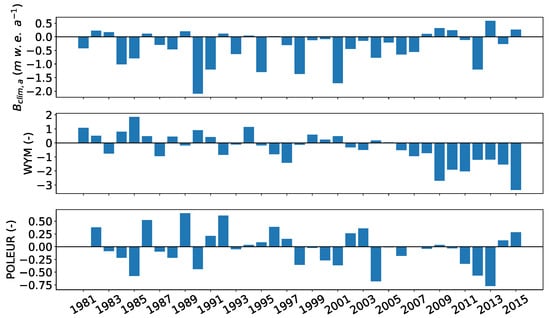
Figure 10.
Annual glacier-wide climatic mass balance (1982–2015) of the Halji glacier (upper panel), Webster and Yang Monsoon index (WYM, middle panel) and Polar/Eurasia index (POL, lower panel).
The POL links the Arctic polar vortex activity and mid-latitude circulation over the Asian continent [80,81] and is one of three modes describing anomalies that are derived from orthogonally rotated component analysis of the geopotential height at 700 north of 15° N in the northern hemisphere [82,83]. The annual (see Table 5) is 0.48 (p-value < 0.01) with POL and −0.42 (p-value < 0.05) with WYM. On a monthly bases, the highest values could be found between June values of POL and with = 0.56 (p-value < 0.01) and February with = 0.41 (p-value < 0.05). The highest correlation of the seasonal index WYM and is the combined June, July and August value with a of −0.44 (p-value < 0.01).

Table 5.
Spearman’s rank correlation coefficient between the annual glacier-wide climatic mass balance and the Polar/Eurasia index (POL) and the Webster and Yang Monsoon index (WYM). Empty cells mark months or seasons when the index does not exist. Grey coefficients are not significant, normal font denotes significance level 0.05 and bold and italic fonts significance level 0.01.
5. Discussion
5.1. Uncertainties
Model uncertainties can be separated in uncertainties stemming from forcing variables and uncertainties from the model itself.
5.1.1. Forcing Data Uncertainties
The statistical downscaling of the variables , and to the elevation of the AWS could be realised to a high degree of precision. The AWS is not located on the glacier and can therefore not account for possible dampening through melting glacier surface (e.g., [84]). With the current setup, we cannot assess this effect. At an elevation of 5350 the area around the AWS is temporally snow-covered even in summer and therefore can be damped as well. The lower summer AWS values compared to ERA5-L might be related to this effect. In the case of , the comparison between the ERA5-L and AWS values revealed a large difference. We scaled ERA5 to the location of the aws. When it comes to local wind patterns, the location of the AWS is not representative for the whole glacier and affected by small scale features. Without a highly resolved dem, we cannot achieve a better representation of . We have planned to implement a snowdrift scheme (e.g., [85]) to account for effects of drifting and blowing snow in future studies. The effects are redistribution of snow, changed albedo patterns, direct sublimation of drifting and blowing snow and modified vertical temperature and moisture profiles [85,86]. This will require highly resolved wind fields that can be used to improve the representation. With the current setup, it is not possible to access the uncertainties of . We used the radiation model after Wohlfahrt et al. [68] for the generation of the distributed fields, which corrects the input fields, mainly dependent on slope and aspect of the GGPs. Olson and Rupper [87] and Olson et al. [88] have shown that radiation modeling is most important for valley glaciers with steep surrounding terrain, for steep glaciers with high elevation differences and glaciers at high latitudes. The Halji glacier located at low latitude contradicts all these conditions as a relatively flat glacier with uninterrupted skyline. Therefore, the influence of the radiation modeling is assumed to be of minor importance.
As described in Section 3.2.2 from ERA5-L does not contain any new information in comparison with from ERA5. Taking from an atmospheric dataset with spatial resolution results in the largest uncertainty when it comes to the forcing variables especially in alpine regions with complex terrain and at high evaluations above 5000 (e.g., [89,90,91,92]). Immerzeel et al. [91] used an inverse approach to find the amount of precipitation, which is needed to sustain the measured glacier MBs. Precipitation in extreme cases in the upper Indus basin is assumed to be up to ten times higher than previously assumed according to their results. We scaled ERA5-L to the cumulative sum of measured by the AWS. We applied a constant scale factor of two to the ERA5-L data. After applying the scale factor, the timing of ERA5-L follows measured with some differences (see Figure 4). In follow-up studies, spatially higher-resolved atmospheric datasets (e.g., the High Asia Refined analysis version 2-2 m [92,93]) should be used to reduce uncertainties stemming from .
The applied dem and its resolution have an influence on the model results as well. The first reason is the influence on the radiation module [87,94]. Furthermore, the coarser the resolution, the less the resulting GGPs are representative for the different elevation ranges of the glacier. This is the reason for large and unsystematic deviations of resolutions with less than 30 GGPs ( ) for Halji glacier compared to the resolution of 30 m (see Figure 5). With the presented setup, the deviations of to the simulation are up to m resolution in a tolerable range (see Section 3.3).
5.1.2. COSIPY Simulation Uncertainties
COSIPY is a point model with no lateral exchange of energy and mass. In its distributed setup, at each GGP all processes are calculated without any exchange with neighboring grid cells. Furthermore, over a period of 40 years, ice-dynamics play an important role. Nevertheless, due to its very low flow velocities (see Appendix A Figure A1), mass balance response of the Halji glacier can be analyzed concerning meteorological forcing only. An approximated mean flow velocity of −1 ([47], dataset: [48]) would result in 90 ice movement over the whole period of 40 years. However, for further long-term integration of glacier change ice-dynamics will have to be integrated into the modeling framework. Snowdrift and direct sublimation of falling snow are further processes that are not resolved by the model. The model has been among others applied to the Zhadang glacier (see Section 5.1 in Sauter et al. [42]) and the Urumqi Glacier No. 1 (see Thiel et al. [95]), both located in HMA. The simulations in both cases revealed reasonable results. To assess the uncertainties stemming from all parameters and constants a full Monte Carlo simulation would have to be executed for the Halji glacier, which is not feasible in this study due to the enormous computational demand. A statistical error would affect single years, but not a long term cumulative value because the error would decrease according to the central limit theorem [96]. A systematic error would indeed affect the cumulative value of . Due to the significant correlation between and and experiences from Mölg et al. [58], Sauter et al. [42] and Thiel et al. [95], the Oerlemans and Knap [57] parametrization is crucial for model output. We used the parameters of Mölg et al. [58]. For a sensitivity test, we varied the values for fresh snow, firn and ice within the uncertainties of their study. The fresh snow variance results in ±0.5 −1 feedback, the firn variance in a ±0.43 −1 feedback and the ice variance in a ±0.17 −1 feedback. The test shows the high sensitivity to the albedo parametrization. Therefore, COSIPY simulated always has to be evaluated against remote-sensing based geodetic mass balance or mass balance derived from the glaciological method through direct observations on the ground. If lies within a reasonable range compared to the independent evaluation data, we understand the main purpose of applying COSIPY in identifying drivers of seasonal and interannual mass balance variability and in advancing process understanding of interactions between atmospheric drivers and . These analyses are feasible and justified when overall calculated falls within a reasonable range. This has also been demonstrated in other studies using medium complexity energy and mass balance models similar to COSIPY (e.g., [97,98,99,100,101,102,102]).
5.2. Glacier-Wide Climatic Mass Balance
Mean simulated of the MB-years 1982 to 2019 is −1. Model simulations can be compared to ice volume changes derived by remote sensing studies of Kropáček et al. [38] and Shean et al. [7] on the mass budget of the Halji glacier. Those values are summarized in Table 6. Corresponding simulated falls within the range of uncertainty in the case of the study by Kropáček et al. [38]. In the case of Shean et al. [7], the COSIPY simulated result is less negative than their estimate. Overall, the simulated negative falls within a reasonable range and is in line with observed reduction in area, presented by the various outlines in Figure 1, the general glacier retreat in HMA (e.g., [3,4,5,6]) and in particular in western Nepal (e.g., [19,103,104]). A possible explanation for the more negative result of the Shean et al. [7] study are the simulated extreme negative MB-years 2016, 2017 and 2018. which are included in their study period, while they are not included in the Kropáček et al. [38] study.

Table 6.
Comparison of simulated annual glacier-wide climatic mass balance (−1) with other studies using digital elevation model differences at the Halji glacier.
COSIPY simulations show a high interannual variability of with a standard deviation of −1. The simulated mass budget between 2001 and 2010 is clearly negative. Nevertheless, this finding is not that obvious in the changes of glacier outlines between 2001 and 2010. Possibly, in this period, the negative mass balance was mainly a result of glacier thinning as opposed to area reduction. With the currently available dataset, we cannot evaluate this possibility in more detail.
Concerning the COSIPY forcing variables, the variability of is mostly determined by and . The high correlation of with and can be explained with their co-correlations with . The clear shift in the pattern of monthly means of between October and April for the two periods before and after 2005/2006 seems to have no distinct influence on monthly deviations of . Especially, because the shift from 2005 on would be negative for the glacier budget whereas is most positive between 2008 and 2015. The intermediate variable is a result of the available amount of and . The latter separates in liquid and solid precipitation and determines together with the density of fresh snow within COSIPY. A high correlation (, p-value < 0.01) is found between the annual variability of and . The combination of and surface melt patterns determines the variability of , which has the highest correlation with with (p-value < 0.01) on annual bases. August is the second last month in the MB-year but still is extremely sensitive to variability in August with (p-value < 0.01). Monthly deviations to their long-term mean of in June, July and August reveal their strong coupling to monthly variability in the same months. July, August and September are the months with the highest monthly variability of in comparison with their long-term mean. Although monthly variability in the same months is smallest compared to the rest of the year this variability is nonetheless of major importance. These results are backed by the SSC, which reveal that peak in and sensitivity occurs during summer. In comparison with the SSC of the six glaciers from different mountain ranges in the world and including only Abramov glacier from HMA presented in Oerlemans and Reichert [43], Halji glacier is the only one with this behavior. Moreover, the difference between the sensitivity to December and November compared to September, August, and July is greater than for any glacier studied by Oerlemans and Reichert [43]. However, the applied mass balance model is not the same and differences resulting solely from the sensitivities of the applied models cannot be evaluated.
When looking at monthly mean deviations to their long-term mean in Figure 7, a possible explanation of the equilibrium state between 2008 and 2015 might be an increased amount, and therefore increased between June and September, resulting in a positive albedo feedback (see [28]). This feedback can partly be linked to the high correlation of the WYM and . The annual value of the WYM is ten years in a row negative between 2005 and 2015. In contrast, there are only three consecutive negative years of the WYM from 1984 to 2004. The WYM is a measure for the large-scale monsoon circulation intensity [79,105]. Besides the high correlations between WYM and , a high correlation with (p-value < 0.01) between June values of WYM and highlights again the importance of .
The correlations between and WYM and and the forcing variables emphasize the importance of timing and strength of the monsoon for the Halji glacier. The correlations among the forcing variables , , and in June are further indications of the importance of the monsoon. A strong monsoon with an unstable atmosphere is accompanied by higher , higher , higher and decreased . Remarkably, other than the WYM, none of the other monsoon (e.g., Indian Summer Monsoon index, Australian Monsoon Index) or monsoon related (e.g., Indian Ocean Dipol index, Southern Oscillation Index) indices revealed a significant correlation within this study. The analysis of possible reasons is beyond the scope of this study and would be speculative at this point.
A couple of studies have shown the connection between POL and precipitation patterns (e.g., [82,106,107]), whereby they focus on the central and whole Tibetan Plateau, North China or winter precipitation patterns in the Karakoram or western Himalaya. In contrast, in case of Halji glacier, the high correlation of POL in June and might rather be related to than to with (p-value < 0.01) between June values of and POL.
All results of this study reveal that a high amount of Halji glaciers interannual variability can be accounted to the variability of and in summer, which can be at least partly be due to monsoon patterns. This finding is in accordance with the literature (e.g., [19,108]). As a result, Halji glacier is extremely sensitive to temperatures changes. An increase in of results in a of −1 ( −1 difference compared to reference simulation), which mainly affects during summer. An increase in summer temperature has three main negative effects on the glacier mass budget for that kind of glacier [25]: (1) Enhanced melt, (2) lowered ratio between solid and liquid precipitation, which results in less surface accumulation, and (3) lower values of as a result of a decrease in , which enlarges and results in further enhancement of melt. The latter two effects are denoted as the snow-albedo feedback [26,27,28].
6. Conclusions
We simulated a of −1 between October 1981 and September 2019 for the Halji glacier in northwestern Nepal. Given the lack of direct mass balance observations, simulations were compared to geodetic mass balances derived from two remote sensing studies [7,38]. The simulation results are in a reasonable range compared to both of these remote sensing studies. The simulation also reveals high interannual variability of . All results revealed the importance of the monsoon and and in summer for the variability of . Only the combination of effects and resulting variability of can explain the pronounced variability in this season. The peak in summer of the calculated seasonal sensitivity characteristic back these findings. The variability of forcing variables in winter has a minor influence on .
Comparison of ERA5-L derived COSIPY forcing variables with AWS measured variables revealed that most input data related uncertainties arise from the amount of and that downscaling and scaling procedures are necessary in order to obtain reliable model forcing data. A decrease of 20% in results in an annual glacier-wide climatic mass balance of −1. Therefore, there is an urgent need in spatially higher resolved atmospheric datasets, to serve as forcing for long-term runs of mass balance models.
Presented approaches and statistics revealed that downscaling of , and is straight-forward given that some observations in the field are available. Furthermore, we recommend to investigate the influence of the applied spatial resolution on for each study site individually in order to identify the best trade-off between computational power and reasonable results.
COSIPY proves to be a powerful tool to identify climatic drivers of seasonal and interannual mass balance variability and to improve the process understanding of glacier responses to atmospheric forcing.
Author Contributions
Conceptualization, A.A. and C.S.; methodology, A.A. and C.S.; software, A.A.; validation, A.A., D.S. and C.S.; formal analysis, A.A.; investigation, A.A.; resources, D.S.; data curation, A.A. and D.S.; writing—original draft preparation, A.A.; writing—review and editing, C.S. and D.S.; visualization, A.A.; supervision, C.S.; project administration, A.A., D.S. and C.S.; funding acquisition, C.S. and D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Research Foundation’s (DFG) research grants ‘Precipitation patterns, snow and glacier response in High Asia and their variability on sub-decadal time scales, sub-project: snow cover and glacier energy and mass balance variability’ (prime-SG, SCHN 680/13-1), ‘Dynamic Response of Glaciers in the Qilian Shan to Climate Change’ (Dyn-Q, SCHN 680/17-1), and ’Glacial lake outburst floods in the Halji region, Nepal’ (Halji, SCHN 680/19-1 and SCHE 750/17-1).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We are grateful to Benjamin Schröter for organizing and supporting the field trips to Halji glacier. Further, we thank Tom Grassmann, Manfred Buchroithner, Nico Rohrbach and the community of Halji for their support of and contribution to field work. We would also like to thank the two anonymous reviewers and the editors, who substantially helped to improve the study. We acknowledge support by the German Research Foundation (DFG) and the Open Access Publication Fund of Humboldt-Universität zu Berlin.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following acronyms are used in this manuscript:
| AMI | Australian Monsoon Index |
| AMO | Atlantic Multi-decadal Oscillation |
| AO | Arctic Oscillation index |
| AWS | automatic weather station |
| COSIPY | COupled Snowpack and Ice surface energy and mass balance model in PYthon |
| DEM | digital elevation model |
| EA | East Atlantic index |
| EATL/WRUS | East Atlantic/West Russia index |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ERA5 | ECMWF Reanalysis fifth generation |
| ERA5-L | ECMWF Reanalysis fifth generation-Land |
| GDAL | Geospatial Data Abstraction Library |
| GGP | glacier grid point |
| GLOF | glacial lake outburst flood |
| H-TESSEL | Hydrology revised Tiled ECMWF Scheme for Surface Exchanges over Land |
| HMA | High Mountain Asia |
| HPCC | High-Performance Computing Cluster |
| IOD | Indian Ocean Dipol index |
| ISM | Indian Summer Monsoon index |
| MB | mass balance |
| MB-year | mass-balance year |
| MBE | mean bias error |
| MEI | Multivariate ENSO Index |
| NAO | North Atlantic Oscillation |
| Nino1+2 | Nino 1+2 index |
| Nino34 | Nino 3.4 index |
| Nino4 | Nino 4 index |
| ONI | Oceanic Nino Index |
| PDO | Pacific Decadal Oscillation |
| PNA | Pacific/North American index |
| POL | Polar/Eurasia index |
| RGI6 | Randolph Glacier Inventory 6.0 |
| RMSE | root mean square error |
| SCAND | Scandinavia index |
| SEB | surface energy balance |
| SOI | Southern Oscillation Index |
| SRTM | Shuttle Radar Topography Mission |
| SSC | seasonal sensitivity characteristic |
| TNI | Trans-Niño Index |
| WNPM | Western North Pacific Monsoon index |
| WP | West Pacific index |
| WYM | Webster and Yang Monsoon index |
The following constants are used in this manuscript:
| Symbol | Description | Unit | Default Value |
| M | average molar mass of air | mol−1 | 0.02897 |
| R | gas constant | kg m (s mol K) | 8.314462 |
| melting point temperature | 273.16 | ||
| g | gravitational acceleration | −2 | 9.80665 |
The following symbols are used in this manuscript:
| Symbol | Description | Unit |
| annual glacier-wide climatic mass balance | ||
| glacier-wide cumulative climatic mass balance | ||
| glacier-wide climatic mass balance | ||
| latent heat flux | W m−2 | |
| glacier heat flux | W m−2 | |
| sensible heat flux | W m−2 | |
| available melt energy | W m−2 | |
| sensible heat flux of rain | W m−2 | |
| incoming longwave radiation | W m−2 | |
| net longwave radiation | W m−2 | |
| outgoing longwave radiation | W m−2 | |
| incoming shortwave radiation | W m−2 | |
| net shortwave radiation | W m−2 | |
| relative humidity at 2 | % | |
| accumulated snowfall | ||
| specific humidity at 2 | −1 | |
| total precipitation | ||
| air temperature at reference height | ||
| layer temperature | ||
| surface temperature | ||
| air temperature at 2 | ||
| dewpoint temperature at 2 | ||
| wind speed at 2 | −1 | |
| wind speed at 10 | −1 | |
| snow/ice albedo | - | |
| internal ablation | ||
| surface ablation | ||
| a | thermal gradient | −1 |
| annual climatic mass balance | ||
| cumulative climatic mass balance | ||
| climatic mass balance | ||
| internal mass balance | ||
| surface mass balance | ||
| internal accumulation | ||
| surface accumulation | ||
| h | height difference | |
| atmospheric pressure at reference height | ||
| surface pressure | ||
| p-value | p-value | - |
| coefficient of determination | - | |
| Spearman’s rank correlation coefficient | - | |
| surface roughness |
Appendix A
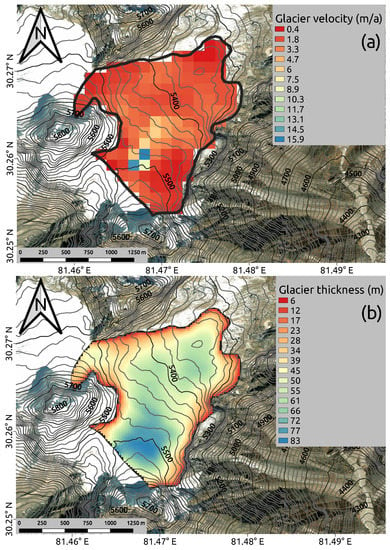
Figure A1.
Glacier velocity (a) according to Dehecq et al. ([47], dataset: [48]) and Glacier thickness (b) according to Farinotti et al. ([22], dataset: [46]) of Halji glacier with a satellite image map in the background [55]. For the location of Halji glacier please refer to Figure 1.
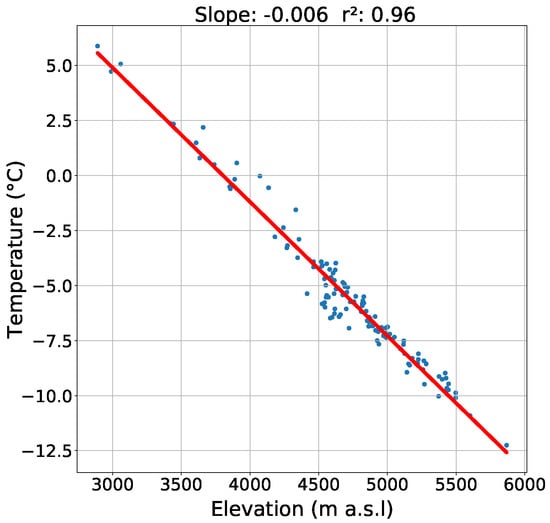
Figure A2.
Scatterplot of ERA5-L air temperature at 2 and model elevations of the 121 ERA5-L grid cells around the location of Halji glacier. The temperatures are the long-term means of each grid cell from 1981 to 2019.
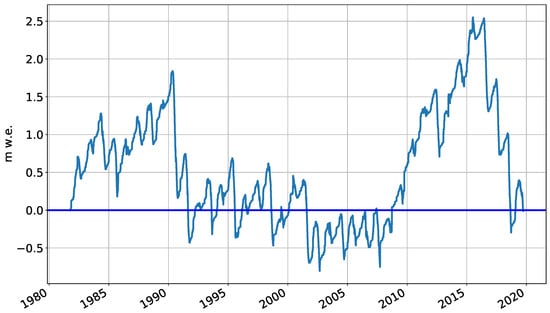
Figure A3.
Cumulative climatic mass balance of temperature adjusted simulation of Halji glacier from 1981 to 2020. We apply a temperature offset of to reach the long-term zero cumulative climatic mass balance which is needed for the computation of the seasonal sensitivity characteristic according to Oerlemans and Reichert [43].
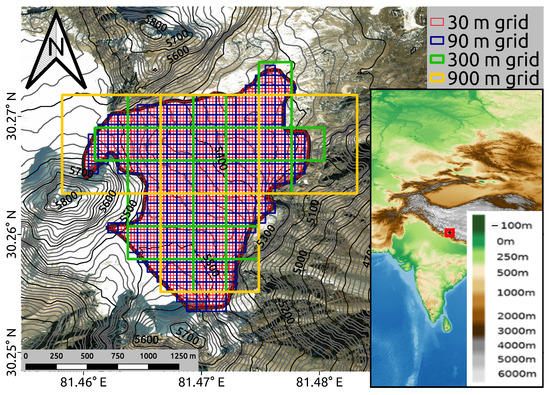
Figure A4.
Differently resolved spatial grids over Halji glacier based on the glacier outline from Randolph Glacier Inventory 6.0 [45] and with a satellite image map as background from [55]. Colors within the inset map represent elevation [56].

Table A1.
Investigated circulation, oscillation and monsoon indexes; The temporal resolution and coverage (status 1 August 2020) are displayed in the third column.
Table A1.
Investigated circulation, oscillation and monsoon indexes; The temporal resolution and coverage (status 1 August 2020) are displayed in the third column.
| Index | Description | Temporal Resolution and Coverage |
|---|---|---|
| AMI [109] | Australian Monsoon Index | Seasonal (DJF), 1948–2014 |
| http://apdrc.soest.hawaii.edu/projects/monsoon/seasonal-monidx.html, accessed on 22 March 2021 | ||
| AMO [110] | Atlantic Multi-decadal Oscillation | Annual, 1870–2010 |
| https://climatedataguide.ucar.edu/climate-data/atlantic-multi-decadal-oscillation-amo, accessed on 22 March 2021 | ||
| AO [111] | Arctic Oscillation index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/products/precip/CWlink/daily_ao_index/ao.shtml, accessed on 22 March 2021 | ||
| EA [80] | East Atlantic index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/ea.shtml, accessed on 22 March 2021 | ||
| EATL/WRUS [80] | East Atlantic/West Russia index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/eawruss.shtml, accessed on 22 March 2021 | ||
| IOD [112] | Indian Ocean Dipol index | Monthly, January 1870–December 2018 |
| http://www.bom.gov.au/climate/enso/indices/about.shtml, accessed on 22 March 2021 | ||
| ISM [113,114] | Indian Summer Monsoon index | Seasonal (JJAS), 1948–2015 |
| http://apdrc.soest.hawaii.edu/projects/monsoon/seasonal-monidx.html, accessed on 22 March 2021 | ||
| MEI [115] | Multivariate ENSO Index | Monthly, January 1979–December 2019 |
| https://psl.noaa.gov/enso/mei/, accessed on 22 March 2021 | ||
| NAO [116] | North Atlantic Oscillation | Monthly, January 1899–February 2020 |
| https://climatedataguide.ucar.edu/climate-data/hurrell-north-atlantic-oscillation-nao-index-pc-based, accessed on 22 March 2021 | ||
| Nino1+2 [117] | Nino 1+2 index | Monthly, January 1950–June 2020 |
| https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni, accessed on 22 March 2021 | ||
| Nino34 [117] | Nino 3.4 index | Monthly, January 1950–June 2020 |
| https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni, accessed on 22 March 2021 | ||
| Nino4 [117] | Nino 4 index | Monthly, January 1950–June 2020 |
| https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni, accessed on 22 March 2021 | ||
| ONI [117] | Oceanic Nino Index | Monthly, January 1950–May 2020 |
| https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni, accessed on 22 March 2021 | ||
| PDO [118] | Pacific Decadal Oscillation | Monthly, January 1854–February 2020 |
| https://www.ncdc.noaa.gov/teleconnections/pdo/, accessed on 22 March 2021 | ||
| PNA [119] | Pacific/North American index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/pna.shtml, accessed on 22 March 2021 | ||
| POL [80] | Polar/Eurasia index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/poleur.shtml, accessed on 22 March 2021 | ||
| SCAND [80] | Scandinavia index | Monthly, January 1950–June 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/scand.shtml, accessed on 22 March 2021 | ||
| SOI [120] | Southern Oscillation Index | Monthly, January 1951–December 2019 |
| https://www.ncdc.noaa.gov/teleconnections/enso/indicators/soi/, accessed on 22 March 2021 | ||
| TNI [117] | Trans-Niño Index | Monthly, January 1948–April 2020 |
| https://climatedataguide.ucar.edu/climate-data/nino-sst-indices-nino-12-3-34-4-oni-and-tni, accessed on 22 March 2021 | ||
| WNPM [113,114] | Western North Pacific Monsoon index | Seasonal (JJAS), 1948–2015 |
| http://apdrc.soest.hawaii.edu/projects/monsoon/seasonal-monidx.html, accessed on 22 March 2021 | ||
| WP [80,119] | West Pacific index | Monthly, January 1950–April 2020 |
| https://www.cpc.ncep.noaa.gov/data/teledoc/wp.shtml, accessed on 22 March 2021 | ||
| WYM [40] | Webster and Yang Monsoon index | Seasonal (JJAS), 1948–2015 |
| http://apdrc.soest.hawaii.edu/projects/monsoon/seasonal-monidx.html, accessed on 22 March 2021 | ||
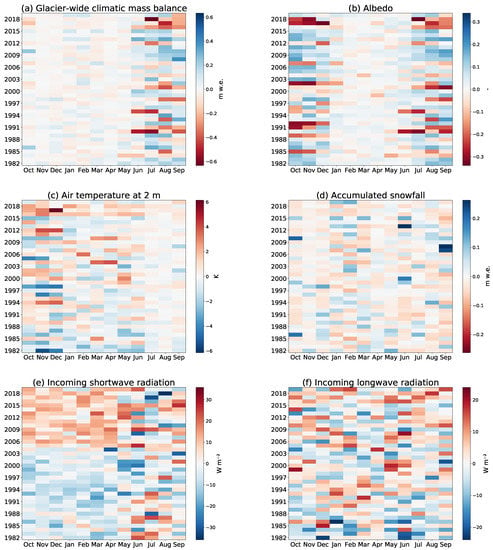
Figure A5.
Monthly mean deviations 1982 to 2019 from long-term monthly mean values of glacier-wide climatic mass balance (a), albedo (b), air temperature at 2 (c), accumulated snowfall (d), incoming shortwave radiation (e) and incoming longwave radiation (f). The color bar is arranged so that deviations that act positively (negatively) on glacier-wide climatic mass balance are shown in blue (red).
References
- Bolch, T.; Pieczonka, T.; Benn, D.I. Multi-decadal mass loss of glaciers in the Everest area (Nepal Himalaya) derived from stereo imagery. Cryosphere 2011, 5, 349–358. [Google Scholar] [CrossRef]
- Lei, Y.; Yao, T.; Yi, C.; Wang, W.; Sheng, Y.; Li, J.; Joswiak, D. Glacier mass loss induced the rapid growth of Linggo Co on the central Tibetan Plateau. J. Glaciol. 2012, 58, 177–184. [Google Scholar] [CrossRef]
- Neckel, N.; Kropáček, J.; Bolch, T.; Hochschild, V. Glacier mass changes on the Tibetan Plateau 2003–2009 derived from ICESat laser altimetry measurements. Environ. Res. Lett. 2014, 9, 014009. [Google Scholar] [CrossRef]
- Kang, S.; Wang, F.; Morgenstern, U.; Zhang, Y.; Grigholm, B.; Kaspari, S.; Schwikowski, M.; Ren, J.; Yao, T.; Qin, D.; et al. Dramatic loss of glacier accumulation area on the Tibetan Plateau revealed by ice core tritium and mercury records. Cryosphere 2015, 9, 1213–1222. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, L.; Jiang, H.; Wang, H.; Ma, N.; Xu, H. Accelerated glacier mass loss (2011–2016) over the Puruogangri ice field in the inner Tibetan Plateau revealed by bistatic InSAR measurements. Remote Sens. Environ. 2019, 231, 111241. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, L.; Zhang, Z.; Wang, H.; Ding, X. Recent Accelerating Glacier Mass Loss of the Geladandong Mountain, Inner Tibetan Plateau, Estimated from ZiYuan-3 and TanDEM-X Measurements. Remote Sens. 2020, 12, 472. [Google Scholar] [CrossRef]
- Shean, D.E.; Bhushan, S.; Montesano, P.; Rounce, D.R.; Arendt, A.; Osmanoglu, B. A Systematic, Regional Assessment of High Mountain Asia Glacier Mass Balance. Front. Earth Sci. 2020, 7, 363. [Google Scholar] [CrossRef]
- Rounce, D.R. Glacier Mass Change in High Mountain Asia Through 2100 Using the Open-Source Python Glacier Evolution Model (PyGEM). Front. Earth Sci. 2020, 7, 20. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Wang, B.; Sun, M.; Li, X. Recent changes in daily extremes of temperature and precipitation over the western Tibetan Plateau, 1973–2011. Quat. Int. 2013, 313–314, 110–117. [Google Scholar] [CrossRef]
- Wei, Y.; Fang, Y. Spatio-Temporal Characteristics of GlobalWarming in the Tibetan Plateau during the Last 50 Years Based on a Generalised Temperature Zone—Elevation Model. PLoS ONE 2013, 8, e60044. [Google Scholar] [CrossRef] [PubMed]
- Schiemann, R.; Lüthi, D.; Schär, C. Seasonality and interannual variability of the westerly jet in the Tibetan Plateau region. J. Clim. 2009, 22, 2940–2957. [Google Scholar] [CrossRef]
- Mölg, T.; Maussion, F.; Scherer, D. Mid-latitude westerlies as a driver of glacier variability in monsoonal High Asia. Nat. Clim. Chang. 2013, 4, 68–73. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, T.; Lu, C.; Guo, Y.; Chen, B.; Liu, R.; Li, Y.; Shi, X. An important mechanism sustaining the atmospheric “water tower” over the Tibetan Plateau. Atmos. Chem. Phys. 2014, 14, 11287–11295. [Google Scholar] [CrossRef]
- Curio, J.; Maussion, F.; Scherer, D. A 12-year high-resolution climatology of atmospheric water transport over the Tibetan Plateau. Earth Syst. Dyn. 2015, 6, 109–124. [Google Scholar] [CrossRef]
- Curio, J.; Scherer, D. Seasonality and spatial variability of dynamic precipitation controls on the Tibetan Plateau. Earth Syst. Dyn. 2016, 7, 767–782. [Google Scholar] [CrossRef]
- Ma, Y.; Lu, M.; Chen, H.; Pan, M.; Hong, Y. Atmospheric moisture transport versus precipitation across the Tibetan Plateau: A mini-review and current challenges. Atmos. Res. 2018, 209, 50–58. [Google Scholar] [CrossRef]
- Li, S.; Yao, T.; Yang, W.; Yu, W.; Zhu, M. Glacier Energy and Mass Balance in the Inland Tibetan Plateau: Seasonal and Interannual Variability in Relation to Atmospheric Changes. J. Geophys. Res. Atmos. 2018, 123, 6390–6409. [Google Scholar] [CrossRef]
- Wang, X.; Pang, G.; Yang, M. Precipitation over the Tibetan Plateau during recent decades: A review based on observations and simulations: PRECIPITATION ON THE TIBETAN PLATEAU. Int. J. Climatol. 2018, 38, 1116–1131. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.; Yang, W.; Yu, W.; Gao, Y.; Guo, X.; Yang, X.; Duan, K.; Zhao, H.; Xu, B.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Gardelle, J.; Berthier, E.; Arnaud, Y.; Kääb, A. Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999–2011. Cryosphere 2013, 7, 1263–1286. [Google Scholar] [CrossRef]
- Bonekamp, P.N.J.; de Kok, R.J.; Collier, E.; Immerzeel, W.W. Contrasting Meteorological Drivers of the Glacier Mass Balance Between the Karakoram and Central Himalaya. Front. Earth Sci. 2019, 7, 107. [Google Scholar] [CrossRef]
- Farinotti, D.; Huss, M.; Fürst, J.J.; Landmann, J.; Machguth, H.; Maussion, F.; Pandit, A. A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 2019, 12, 168–173. [Google Scholar] [CrossRef]
- Ageta, Y.; Higuchi, K. Estimation of Mass Balance Components of a Summer-Accumulation Type Glacier in the Nepal Himalaya. Geogr. Annaler. Ser. A Phys. Geogr. 1984, 66, 249. [Google Scholar] [CrossRef]
- Maussion, F.; Scherer, D.; Mölg, T.; Collier, E.; Curio, J.; Finkelnburg, R. Precipitation Seasonality and Variability over the Tibetan Plateau as Resolved by the High Asia Reanalysis*. J. Clim. 2014, 27, 1910–1927. [Google Scholar] [CrossRef]
- Naito, N. Summer Accumulation Type Glaciers. In Encyclopedia of Snow, Ice and Glaciers; Singh, V.P., Singh, P., Haritashya, U.K., Eds.; Encyclopedia of Earth Sciences Series; Springer: Dordrecht, The Netherlands, 2011; pp. 1107–1108. [Google Scholar] [CrossRef]
- Qu, X.; Hall, A. What Controls the Strength of Snow-Albedo Feedback? J. Clim. 2007, 20, 3971–3981. [Google Scholar] [CrossRef]
- Qu, X.; Hall, A. On the persistent spread in snow-albedo feedback. Clim. Dyn. 2014, 42, 69–81. [Google Scholar] [CrossRef]
- Ghatak, D.; Sinsky, E.; Miller, J. Role of snow-albedo feedback in higher elevation warming over the Himalayas, Tibetan Plateau and Central Asia. Environ. Res. Lett. 2014, 9, 114008. [Google Scholar] [CrossRef]
- Wang, X.; Siegert, F.; Zhou, A.G.; Franke, J. Glacier and glacial lake changes and their relationship in the context of climate change, Central Tibetan Plateau 1972–2010. Glob. Planet. Chang. 2013, 111, 246–257. [Google Scholar] [CrossRef]
- Treichler, D.; Kääb, A.; Salzmann, N.; Xu, C.Y. Recent glacier and lake changes in High Mountain Asia and their relation to precipitation changes. Cryosphere 2019, 13, 2977–3005. [Google Scholar] [CrossRef]
- Haeberli, W. Frequency and Characteristics of Glacier Floods in the Swiss Alps. Ann. Glaciol. 1983, 4, 85–90. [Google Scholar] [CrossRef]
- Björnsson, H. Jökulhlaups in Iceland: Prediction, characteristics and simulation. Ann. Glaciol. 1992, 16, 95–106. [Google Scholar] [CrossRef]
- Huggel, C.; Kääb, A.; Haeberli, W.; Teysseire, P.; Paul, F. Remote sensing based assessment of hazards from glacier lake outbursts: A case study in the Swiss Alps. Can. Geotech. J. 2002, 39, 316–330. [Google Scholar] [CrossRef]
- Veh, G.; Korup, O.; von Specht, S.; Roessner, S.; Walz, A. Unchanged frequency of moraine-dammed glacial lake outburst floods in the Himalaya. Nat. Clim. Chang. 2019, 9, 379–383. [Google Scholar] [CrossRef]
- Wester, P.; Mishra, A.; Mukherji, A.; Shrestha, A.B. (Eds.) The Hindu Kush Himalaya Assessment: Mountains, Climate Change, Sustainability and People; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Hovden, A. Who were the sponsors? Reflections on recruitment and ritual economy in three Himalayan village monasteries. In Tibetans Who Escaped the Historians Net: Studies in the Social History of Tibetan Societies; Ram ble, C., Schwieger, P., Travers, A., Eds.; Vajra Publications: Kathmandu, Nepal, 2013; pp. 209–230. [Google Scholar]
- Diemberger, H.; Hovden, A.; Yeh, E.T. The honour of the snow-mountains is the snow: Tibetan livelihoods in a changing climate. In The High-Mountain Cryosphere: Environmelt Changes and Human Risks; Huggel, C., Carey, M., Clague, J.J., Kaab, A., Eds.; Cambridge University Press: Cambridge, UK, 2015; pp. 249–271. [Google Scholar] [CrossRef]
- Kropáček, J.; Neckel, N.; Tyrna, B.; Holzer, N.; Hovden, A.; Gourmelen, N.; Schneider, C.; Buchroithner, M.; Hochschild, V. Repeated glacial lake outburst flood threatening the oldest Buddhist monastery in north-western Nepal. Nat. Hazards Earth Syst. Sci. 2015, 15, 2425–2437. [Google Scholar] [CrossRef]
- Benn, D.I.; Owen, L.A. The role of the Indian summer monsoon and the mid-latitude westerlies in Himalayan glaciation: Review and speculative discussion. J. Geol. Soc. 1998, 155, 353–363. [Google Scholar] [CrossRef]
- Webster, P.J.; Magaña, V.O.; Palmer, T.N.; Shukla, J.; Tomas, R.A.; Yanai, M.; Yasunari, T. Monsoons: Processes, predictability, and the prospects for prediction. J. Geophys. Res. Ocean. 1998, 103, 14451–14510. [Google Scholar] [CrossRef]
- Copernicus. Climate Data Store ERA5-Land Reanalysis. 2019. Available online: https://cds.climate.copernicus.eu/cdsapp#!/home (accessed on 11 January 2021).
- Sauter, T.; Arndt, A.; Schneider, C. COSIPY v1.3—An open-source coupled snowpack and ice surface energy and mass balance model. Geosci. Model Dev. 2020, 13, 5645–5662. [Google Scholar] [CrossRef]
- Oerlemans, J.; Reichert, B. Relating glacier mass balance to meteorological data by using a seasonal sensitivity characteristic. J. Glaciol. 2000, 46, 1–6. [Google Scholar] [CrossRef]
- Earth Resources Observation And Science (EROS) Center. Shuttle Radar Topography Mission (SRTM) 1 Arc-Second Global; U.S. Geological Survey: Reston, VA, USA, 2017. [CrossRef]
- Consortium, R.G.I. Randolph Glacier Inventory 6.0; NSIDC: Boulder, CO, USA, 2017. [Google Scholar] [CrossRef]
- Farinotti, D. A consensus estimate for the ice thickness distribution of all glaciers on Earth—Dataset. In Medium: Txt/Plain, Application/Zip, Image/Tiff, 12.48 GB; ETH: Zurich, Switzerland, 2019. [Google Scholar] [CrossRef]
- Dehecq, A.; Gourmelen, N.; Trouve, E. Deriving large-scale glacier velocities from a complete satellite archive: Application to the Pamir–Karakoram–Himalaya. Remote Sens. Environ. 2015, 162, 55–66. [Google Scholar] [CrossRef]
- Dehecq, A.; Gourmelen, N.; Trouvé, E. High Mountain Asia Glacier Velocities 2013–2015 (Landsat 8); Zenodo: Geneva, Switzerland, 2019. [Google Scholar] [CrossRef]
- Shean, D.; Bhushan, S. Zenodo, Geneva, Switzerland. Type: Dataset; 2020; Available online: https://zenodo.org/record/3600624#.YF1M_twRXIU (accessed on 22 March 2021). [CrossRef]
- Ye, Q.; Yao, T.; Kang, S.; Chen, F.; Wang, J. Glacier variations in the Naimona’nyi region, western Himalaya, in the last three decades. Ann. Glaciol. 2006, 43, 385–389. [Google Scholar] [CrossRef]
- Racoviteanu, A.S.; Bajracharya, S.A. GLIMS Glacier Database; NSIDC: Boulder, CO, USA, 2008. [Google Scholar] [CrossRef]
- Sakai, A.S.; Sakai, A.A. GLIMS Glacier Database; NSIDC: Boulder, CO, USA, 2018. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Lea, J.M. The Google Earth Engine Digitisation Tool (GEEDiT) and the Margin change Quantification Tool (MaQiT) – simple tools for the rapid mapping and quantification of changing Earth surface margins. Earth Surf. Dyn. 2018, 6, 551–561. [Google Scholar] [CrossRef]
- Microsoft. Bing Maps; Microsoft: Redmond, WA, USA, 2020. [Google Scholar]
- Terrestris GmbH & Co. KG. TOPOGRAPHIC WMS. 2021. Available online: https://www.terrestris.de/de/topographic-wms/ (accessed on 11 January 2021).
- Oerlemans, J.; Knap, W.H. A 1 year record of global radiation and albedo in the ablation zone of Morteratschgletscher, Switzerland. J. Glaciol. 1998, 44, 231–238. [Google Scholar] [CrossRef]
- Mölg, T.; Maussion, F.; Yang, W.; Scherer, D. The footprint of Asian monsoon dynamics in the mass and energy balance of a Tibetan glacier. Cryosphere 2012, 6, 1445–1461. [Google Scholar] [CrossRef]
- Mazumder, S. Numerical Methods for Partial Differential Equations: Finite Difference and Finite Volume Methods; OCLC: ocn913556966; Academic Press: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Bintanja, R.; Van Den Broeke, M.R. The Surface Energy Balance of Antarctic Snow and Blue Ice. J. Appl. Meteorol. 1995, 34, 902–926. [Google Scholar] [CrossRef]
- Anderson, E.A. A Point Energy and Mass Balance Model of a Snow Cover; Technical Report; National Weather Service (NWS): Silver Spring, MD, USA, 1976.
- Boone, A. Description du Schema de Neige ISBA-ES (Explicit Snow); Technical Report; Updated in November, 2009; Centre National de Recherches Météorologiques, Météo-France: Toulouse, France, 2004. [Google Scholar]
- Cogley, J.G.; Hock, R.; A Rasmussen, L.; Arendt, A.; Bauder, A.; J Braithwaite, R.; Jansson, P.; Kaser, G.; Möller, M.; Nicholson, L.; et al. Glossary of glacier mass balance and related terms. Int. Assoc. Cryospheric Sci. 2011. [Google Scholar] [CrossRef]
- Kaser, G.; Fountain, A.; Jansson, P. A Manual for Monitoring the Mass Balance of Mountain Glaciers; IHP-VI, Technical Documents in Hydrology No. 59; UNESCO: Paris, France, 2003. [Google Scholar]
- Neckel, N.; Kropáček, J.; Schröter, B.; Scherer, D. Effects of Cyclone Hudhud captured by a high altitude Automatic Weather Station in northwestern Nepal. Weather 2015, 70, 208–210. [Google Scholar] [CrossRef]
- ECMWF. ERA5-Land: Data Documentation; ECMWF: Reading, UK, 2020. [Google Scholar]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020. [Google Scholar] [CrossRef]
- Wohlfahrt, G.; Hammerle, A.; Niedrist, G.; Scholz, K.; Tomelleri, E.; Zhao, P. On the energy balance closure and net radiation in complex terrain. Agric. For. Meteorol. 2016, 226–227, 37–49. [Google Scholar] [CrossRef]
- Lente, G.; Ősz, K. Barometric formulas: Various derivations and comparisons to environmentally relevant observations. ChemTexts 2020, 6, 13. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- ECMWF. IFS Documentation CY41R2—Part IV: Physical Processes. 2016. Available online: https://www.ecmwf.int/node/16648 (accessed on 9 December 2020).
- ECMWF. ERA5-Land: Data Documentation; ECMWF: Reading, UK, 2021. [Google Scholar]
- Stull, R.B. (Ed.) An Introduction to Boundary Layer Meteorology; Springer: Dordrecht, The Netherlands, 1988. [Google Scholar] [CrossRef]
- Brock, B.W.; Willis, I.C.; Sharp, M.J. Measurement and parameterization of aerodynamic roughness length variations at Haut Glacier d’Arolla, Switzerland. J. Glaciol. 2006, 52, 281–297. [Google Scholar] [CrossRef]
- Gromke, C.; Manes, C.; Walter, B.; Lehning, M.; Guala, M. Aerodynamic Roughness Length of Fresh Snow. Bound. Layer Meteorol. 2011, 141, 21–34. [Google Scholar] [CrossRef]
- GDAL/OGR Contributors. GDAL/OGR Geospatial Data Abstraction Software Library; Open Source Geospatial Foundation: DE, USA, 2020. [Google Scholar]
- Zwillinger, D.; Kokoska, S. CRC Standard Probability and Statistics Tables and Formulae; Chapman & Hall/CRC: Boca Raton, FL, USA, 2000. [Google Scholar]
- Reichert, B.K.; Bengtsson, L.; Oerlemans, J. Midlatitude Forcing Mechanisms for Glacier Mass Balance Investigated Using General Circulation Models. J. Clim. 2001, 14, 18. [Google Scholar] [CrossRef]
- Webster, P.J.; Yang, S. Monsoon and Enso: Selectively Interactive Systems. Q. J. R. Meteorol. Soc. 1992, 118, 877–926. [Google Scholar] [CrossRef]
- Barnston, A.G.; Livezey, R.E. Classification, Seasonality and Persistence of Low-Frequency Atmospheric Circulation Patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Gao, N.; Bueh, C.; Xie, Z.; Gong, Y. A Novel Identification of the Polar/Eurasia Pattern and Its Weather Impact in May. J. Meteorol. Res. 2019, 33, 810–825. [Google Scholar] [CrossRef]
- Lin, Z. Intercomparison of the impacts of four summer teleconnections over Eurasia on East Asian rainfall. Adv. Atmos. Sci. 2014, 31, 1366–1376. [Google Scholar] [CrossRef]
- Gao, T.; Yu, J.y.; Paek, H. Impacts of four northern-hemisphere teleconnection patterns on atmospheric circulations over Eurasia and the Pacific. Theor. Appl. Climatol. 2017, 129, 815–831. [Google Scholar] [CrossRef]
- Carturan, L.; Cazorzi, F.; De Blasi, F.; Dalla Fontana, G. Air temperature variability over three glaciers in the Ortles—Cevedale (Italian Alps): Effects of glacier fragmentation, comparison of calculation methods, and impacts on mass balance modeling. Cryosphere 2015, 9, 1129–1146. [Google Scholar] [CrossRef]
- Sauter, T.; Möller, M.; Finkelnburg, R.; Grabiec, M.; Scherer, D.; Schneider, C. Snowdrift modelling for the Vestfonna ice cap, north-eastern Svalbard. Cryosphere 2013, 7, 1287–1301. [Google Scholar] [CrossRef]
- Groot Zwaaftink, C.D.; Cagnati, A.; Crepaz, A.; Fierz, C.; Macelloni, G.; Valt, M.; Lehning, M. Event-driven deposition of snow on the Antarctic Plateau: Analyzing field measurements with SNOWPACK. Cryosphere 2013, 7, 333–347. [Google Scholar] [CrossRef]
- Olson, M.; Rupper, S. Impacts of topographic shading on direct solar radiation for valley glaciers in complex topography. Cryosphere 2019, 13, 29–40. [Google Scholar] [CrossRef]
- Olson, M.; Rupper, S.; Shean, D.E. Terrain Induced Biases in Clear-Sky Shortwave Radiation Due to Digital Elevation Model Resolution for Glaciers in Complex Terrain. Front. Earth Sci. 2019, 7, 216. [Google Scholar] [CrossRef]
- Beck, H.E.; Vergopolan, N.; Pan, M.; Levizzani, V.; van Dijk, A.I.J.M.; Weedon, G.P.; Brocca, L.; Pappenberger, F.; Huffman, G.J.; Wood, E.F. Global-scale evaluation of 22 precipitation datasets using gauge observations and hydrological modeling. Hydrol. Earth Syst. Sci. 2017, 21, 6201–6217. [Google Scholar] [CrossRef]
- Kim, K.Y.; Kim, J.; Boo, K.O.; Shim, S.; Kim, Y. Intercomparison of precipitation datasets for summer precipitation characteristics over East Asia. Clim. Dyn. 2019, 52, 3005–3022. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Wanders, N.; Lutz, A.F.; Shea, J.M.; Bierkens, M.F.P. Reconciling high altitude precipitation in the upper Indus Basin with glacier mass balances and runoff. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 4755–4784. [Google Scholar] [CrossRef]
- Hamm, A.; Arndt, A.; Kolbe, C.; Wang, X.; Thies, B.; Boyko, O.; Reggiani, P.; Scherer, D.; Bendix, J.; Schneider, C. Intercomparison of Gridded Precipitation Datasets over a Sub-Region of the Central Himalaya and the Southwestern Tibetan Plateau. Water 2020, 12, 3271. [Google Scholar] [CrossRef]
- Wang, X.; Tolksdorf, V.; Otto, M.; Scherer, D. WRF-based dynamical downscaling of ERA5 reanalysis data for High Mountain Asia: Towards a new version of the High Asia Refined analysis. Int. J. Climatol. 2020. [Google Scholar] [CrossRef]
- Hopkinson, C.; Chasmer, L.; Munro, S.; Demuth, M.N. The influence of DEM resolution on simulated solar radiation-induced glacier melt. Hydrol. Process. 2010, 24, 775–788. [Google Scholar] [CrossRef]
- Thiel, K.; Arndt, A.; Wang, P.; Li, H.; Li, Z.; Schneider, C. Modeling of Mass Balance Variability and Its Impact on Water Discharge from the Urumqi Glacier No. 1 Catchment, Tian Shan, China. Water 2020, 12, 3297. [Google Scholar] [CrossRef]
- Gut, A. Probability: A Graduate Course; OCLC: 56096548; Springer: New York, NY, USA, 2005. [Google Scholar]
- Klok, E.; Oerlemans, J. Model study of the spatial distribution of the energy and mass balance of Morteratschgletscher, Switzerland. J. Glaciol. 2002, 48, 505–518. [Google Scholar] [CrossRef]
- Hock, R.; Holmgren, B. A distributed surface energy-balance model for complex topography and its application to Storglaciären, Sweden. J. Glaciol. 2005, 51, 25–36. [Google Scholar] [CrossRef]
- Machguth, H.; Paul, F.; Hoelzle, M.; Haeberli, W. Distributed glacier mass-balance modelling as an important component of modern multi-level glacier monitoring. Ann. Glaciol. 2006, 43, 335–343. [Google Scholar] [CrossRef]
- Reijmer, C.H.; Hock, R. Internal accumulation on Storglaciären, Sweden, in a multi-layer snow model coupled to a distributed energy-and mass-balance model. J. Glaciol. 2008, 54, 61–72. [Google Scholar] [CrossRef]
- Sicart, J.E.; Hock, R.; Ribstein, P.; Litt, M.; Ramirez, E. Analysis of seasonal variations in mass balance and meltwater discharge of the tropical Zongo Glacier by application of a distributed energy balance model. J. Geophys. Res. 2011, 116, D13105. [Google Scholar] [CrossRef]
- Van Pelt, W.J.J.; Oerlemans, J.; Reijmer, C.H.; Pohjola, V.A.; Pettersson, R.; van Angelen, J.H. Simulating melt, runoff and refreezing on Nordenskiöldbreen, Svalbard, using a coupled snow and energy balance model. Cryosphere 2012, 6, 641–659. [Google Scholar] [CrossRef]
- Yao, T.D.; Pu, J.C.; Tian, L.D.; Yang, W.; Duan, K.Q.; Ye, Q.H.; Thompson, L.G. Recent Rapid Retreat of the Naimona’nyi Glacier in Southwestern Tibetan Plateau. J. Glaciol. Geocryol. 2007, 29, 503–508. [Google Scholar]
- Zhu, D.; Tian, L.; Wang, J.; Wang, Y.; Cui, J. Rapid glacier retreat in the Naimona’Nyi region, western Himalayas, between 2003 and 2013. J. Appl. Remote Sens. 2014, 8, 083508. [Google Scholar] [CrossRef]
- Priya, P.; Krishnan, R.; Mujumdar, M.; Houze, R.A. Changing monsoon and midlatitude circulation interactions over the Western Himalayas and possible links to occurrences of extreme precipitation. Clim. Dyn. 2017, 49, 2351–2364. [Google Scholar] [CrossRef]
- Bothe, O.; Fraedrich, K.; Zhu, X. Tibetan Plateau summer precipitation: Covariability with circulation indices. Theor. Appl. Climatol. 2012, 108, 293–300. [Google Scholar] [CrossRef]
- Liu, W.; Wang, L.; Chen, D.; Tu, K.; Ruan, C.; Hu, Z. Large-scale circulation classification and its links to observed precipitation in the eastern and central Tibetan Plateau. Clim. Dyn. 2016, 46, 3481–3497. [Google Scholar] [CrossRef]
- Palazzi, E.; von Hardenberg, J.; Provenzale, A. Precipitation in the Hindu-Kush Karakoram Himalaya: Observations and future scenarios: PRECIPITATION IN HINDU-KUSH KARAKORAM HIMALAYA. J. Geophys. Res. Atmos. 2013, 118, 85–100. [Google Scholar] [CrossRef]
- Kajikawa, Y.; Wang, B.; Yang, J. A multi-time scale Australian monsoon index: A MULTI-TIME SCALE AUSTRALIAN MONSOON INDEX. Int. J. Climatol. 2010, 30, 1114–1120. [Google Scholar] [CrossRef]
- Enfield, D.B.; Mestas-Nuñez, A.M.; Trimble, P.J. The Atlantic Multidecadal Oscillation and its relation to rainfall and river flows in the continental U.S. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef]
- Thompson, D.W.J.; Wallace, J.M. The Arctic oscillation signature in the wintertime geopotential height and temperature fields. Geophys. Res. Lett. 1998, 25, 1297–1300. [Google Scholar] [CrossRef]
- Bureau of Meteorology, Commonwealth of Australia. About ENSO and IOD Indices; Online Resources (2021): Bureau of Meteorology, Commonwealth of Australia. Available online: http://www.bom.gov.au/climate/enso/indices/about.shtml (accessed on 22 March 2021).
- Wang, B.; Fan, Z. Choice of South Asian Summer Monsoon Indices*. Bull. Am. Meteorol. Soc. 1999, 80, 629–638. [Google Scholar] [CrossRef]
- Wang, B.; Wu, R.; Lau, K.M. Interannual Variability of the Asian Summer Monsoon: Contrasts between the Indian and the Western North Pacific–East Asian Monsoons*. J. Clim. 2001, 14, 4073–4090. [Google Scholar] [CrossRef]
- Zhang, T.; Hoell, A.; Perlwitz, J.; Eischeid, J.; Murray, D.; Hoerling, M.; Hamill, T.M. Towards Probabilistic Multivariate ENSO Monitoring. Geophys. Res. Lett. 2019, 46, 10532–10540. [Google Scholar] [CrossRef]
- Hurrell, J.W. Decadal Trends in the North Atlantic Oscillation: Regional Temperatures and Precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Stepaniak, D.P. Indices of El Niño Evolution. J. Clim. 2001, 14, 1697–1701. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R. The Pacific Decadal Oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the Geopotential Height Field during the Northern Hemisphere Winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. Southern Oscillation Index (SOI); Online Resources (2021): National Oceanic and Atmospheric Administration. Available online: https://www.ncdc.noaa.gov/teleconnections/enso/indicators/soi/ (accessed on 22 March 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).