Abstract
We report estimations of the Mexicali Valley (Mexico) mixing height for three seasons. Surface and upper air meteorological measurements were carried out nearby Cerro Prieto geothermal power plant during July 2010 (summer), January 2012 (winter), and October 2016 (autumn). Four different methods were applied to estimate the convective boundary layer (CBL) height from radiosonde (RS) profiles: the parcel method, the gradients method, the least-squares variational approach based on the slab model of the CBL structure, and a covariance method. For nocturnal conditions, we used diagnostic models based on friction velocity and Monin–Obukhov length. Under unstable conditions, we obtained (on average) mixing heights of 497 m at 06:00 LST, 1242 m at 12:00 LST, 1404 m at 15:00 LST, and 482 at 18:00 LST during summer; 754 m at 12:00 LST during winter; and 1195 m at 12:00 LST and 13:00 m between the 14:00 and 15:00 LST during the autumn. The results allowed adjusting a semiempirical model to evaluate mixing height from turbulent sensible heat flux and friction velocity data. Our results provide practical tools that could facilitate the application of regulatory dispersion models to assess air quality in the region.
1. Introduction
Pollution in the Mexicali Valley (Mexico) is not a simple phenomenon. It involves factors that play essential roles in the region, both in the economic development and the environment, such as landfills, cement and smelting industries, agricultural burning, and power plants nearby [1,2,3,4]. The Cerro Prieto geothermal power plant, which is the primary source of energy in the state of Baja California (BC, Mexico), is frequently considered as the principal source of pollution in the region. However, the environmental impact of the geothermal plant is controversial, with divergent opinions from the Comisión Federal de Electricidad (CFE), scholars, and social sectors [5,6,7,8].
Air quality impact assessment is an essential activity for determining the relative contribution to ground-level pollutant concentrations of specific current or future source emissions at receptor sites. Its main tools are air quality monitoring and modeling techniques. Air pollution models also play a pertinent role in risk analysis, emergency planning, and source apportionment studies. Air pollution modeling is the technique widely used to estimate the mixing and dilution of pollution in the atmosphere. It concerns itself mainly with dispersion in the atmospheric boundary layer, which is that portion of the atmosphere where the direct effect of the surface is felt because of the turbulent transfer. In practice, it is a computer simulation approach used to investigate and assess the dynamics and relationships between the physical properties of the pollutant sources, emission rates, meteorology, terrain features, air quality, and health problems.
Monitoring air pollutants furnishes important, quantitative, and reliable information about the air quality, but it only concerns a few specific locations and times, with no clear identification of the origin of the problem. Air pollution modeling, alternatively, provides a more complete and deterministic description of the prevailing air quality conditions, including an analysis of the main factors and causes, and gives guidance for implementing mitigation strategies and measures. The choice of techniques, which apply to a particular situation, is intimately related to the problem to be assessed. A review of relevant modeling techniques has been presented in [9], with emphasis placed on Gaussian plume models because of their ease of use and broad applicability, but also with suggestions of alternative modeling techniques when departures from the Gaussian plume occurs or when more detailed information on atmospheric chemistry, deposition, or long-range transport is required.
An air quality standard is an upper limit on the average concentration of a given pollutant in the air over a given time (1 h, 24 h, or some other). Therefore, because of this statistical view of the air quality standards application, in general, we need a long-time meteorological series representative of the specific site of interest to carry out air quality assessment. Very often, however, this data is unavailable, and we are obligated to carry out short-term meteorological campaigns at the selected site. These campaigns include surface and upper-air meteorological measurements to obtain the turbulence parameters and the vertical profiles of pressure, temperature, and relative humidity to estimate the hourly input data required by the regulatory air pollution models.
The mixing height is a fundamental parameter to characterize the structure of the lower troposphere, and therefore, it is one of the essential variables for air pollution modeling. It is the height of the layer adjacent to the ground over which pollutants or any constituents emitted within this layer or entrained into it become vertically dispersed by convection or mechanical turbulence within the time scale of about an hour [10].
The mixing height is not a directly measurable variable, and the development and improvement of mixing height estimation models and methods are part of active research areas in meteorology. Nowadays, remote sensing systems, such as wind profilers, and SODAR, RASS, and LIDAR systems, are successfully used for that purpose; however, in many developing countries, such expensive equipment is not widely available for estimating mixing height, particularly for short-term and site-specific air quality studies. Consequently, the radiosonde ascents still provide the most common source of data for operational determination of the mixing height [10].
The main objective of this paper is to provide data and practical tools that can facilitate the application of regulatory dispersion models to assess the Mexicali Valley air quality. We reported the estimates of mixing height we made from the surface and upper-air meteorological measurements carried out for July 2010, January 2012, and October 2016. We applied complementary reckoning approaches for both convective and stable conditions. The results allowed adjusting a semiempirical diagnostic method to evaluate the mixing height and its evolution from surface measurements of sensible heat flux, friction velocity, and Monin–Obukhov length.
2. Study Area
The Mexicali Valley is located in a Colorado River delta plain, between 114°45’ to 115°40’ west longitude and 31°40’ to 32°40’ north latitude, with an altitude between 5 and 28 meters above sea level (masl). It is in the northeast corner of BC, 50 km to the south of Calexico, California, with a total surface of 207,000 ha [11]. Sierra Cucapah, a range 90 km long with 800 m height above ground, is located to the west. The valley relief is slightly flat and large cultivated surface. Figure 1 gives a general view of the Mexicali Valley.
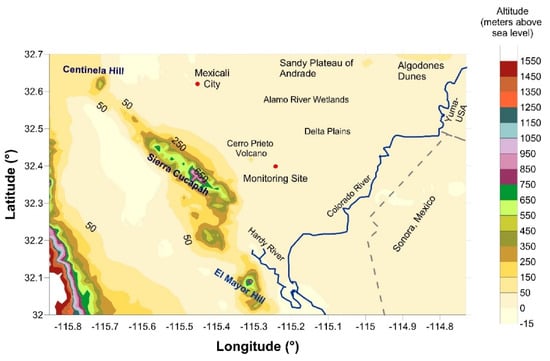
Figure 1.
The Mexicali Valley. Monitoring site and its surroundings. Altitude scale in meters.
Following the climatology [12,13], the mean seasonal temperatures in the region are 13 °C in winter, 19 °C in spring, 28 °C in summer, and 19 °C in autumn. The windier part of the year extends from March to June, with average wind speeds of more than 3.3 m/s, and the calmer period lasts from July to February, with average wind speeds around 2.8 m/s. The cloudy period in Mexicali extends from November to March. The day length varies significantly over the year. On average, the sunrise occurred at 06:30 LST (sunset: 17:15 LST) in winter, at 05:00 LST (sunset: 18:25 LST) in spring, at 05:00 LST (sunset: 18:30 LST) in summer, and at 06:00 LST (sunset: 17:00 LST) in autumn. The average daily incident shortwave solar energy experiences extreme seasonal variation over the year. The brighter period of the year extends from middle April to the end of July, and the darker period runs from beginning November to beginning February. The Mexicali local standard time (LST) is UTC-8 (Coordinated Universal Time 8).
3. Materials and Methods
We performed this study with the support of surface and upper-air meteorological data obtained from short-term experimental campaigns carried out nearby of Cerro Prieto power plant in summer, autumn, and winter. In the first part of this section, we described the experimental campaigns and data obtained, whereas in the second part, we presented the methods we used to estimate the boundary layer heights.
3.1. Meteorological Campaigns
We carried out three short-term experimental campaigns in an open rural site located at 32°24.0015’ N and 115°14.0065’ W, with an altitude of 10 meters (above sea level), within the facilities of the Cerro Prieto geothermal power plant, 700 m to the west of the geometrical center of the emission sources distribution, approximately. We made surface meteorological measurements throughout July 2010 (summer), January 2012 (winter), and October 2016 (autumn), and we launched atmospheric radiosondes during the periods of 17–28 July 2010, 25–29 January 2012, and 11–15 October 2016.
3.1.1. Surface Meteorological Measurements
We used a 3D ultrasonic anemometer (USA-1, METEK GmbH, Elmshorn) to measure the wind velocity components and temperature at z = 12 m above ground with a sampling rate of 10 Hz. No significant obstacles were around the monitoring site. From this high-frequency data, following the methods described in [14], we calculated 1-h averages of the turbulent parameters, such as friction velocity (), sensible heat flux (H0), Monin–Obukhov length (L), and turbulent kinetic energy (ε), among others. Using 1-min sets of data, we carried out two rotations on the ordinary velocity components (vx, vy, vz) to obtain the mean streamwise velocity and the turbulent fluctuations and of the velocity components and (sonic) temperature (T). Then, we used the following equations to estimate the turbulent parameters from the covariance between the turbulent fluctuations [14]:
Here, ρ and cp are the density and specific heat of the air, k is the von Karman constant, and g is the gravity acceleration.
We calculated the wind speed (WSP) and wind direction (WDR) from the wind velocity components. Using conventional instruments, we also measured atmospheric pressure (p), temperature (T), and relative humidity (RH) with a 1 Hz sampling rate. We calculated the 1-h averages of all variables.
3.1.2. Atmospheric Soundings
From the atmospheric soundings, we obtained the vertical profiles of pressure, temperature, relative humidity, and dew point temperature. From the radiosonde (RS) data profiles, we calculated the virtual potential temperature (VPT) and specific humidity (SH) profiles. We used the Vaisala’s MW21 DigiCORA III upper air sounding system with radiosondes RS92-SGP [15], for the sounding campaigns of July 2010 and January 2012 and a GRAW ground station GS-B sounding system with radiosondes DFM09 [16], for the October 2016 campaign. The numbers of launched radiosondes were 25 in the period of 17–28 July 2010; 13, during 25–29 January 2012; and 14 during 11–15 October 2016. These launchings were performed mainly at the sunrise, noon, afternoon, sunset, and midnight.
In Table 1, we summarized the number of atmospheric soundings we carried out during the upper-air measurement campaigns. The color of the cells indicates the sunlight conditions during the radiosoundings (RS).

Table 1.
Number and launching time of the soundings carried out during the campaigns. The color of the cells indicates the sunlight conditions during the radiosoundings (RS): yellow cells indicate diurnal RS, whereas blue cells indicate nocturnal RS.
3.2. Estimation Methods
We provided in this section a brief description of the methods we used to estimate the atmospheric boundary layer (ABL) depth for both the diurnal (convective) and nocturnal (stable) conditions from the RS profiles and the surface meteorological measurements.
We used the surface measurements of Monin–Obukhov length and friction velocity to estimate the stability parameters and , where z is the height where L is measured and f the Coriolis parameter. We also estimated the near-surface temperature lapse rate of the RS temperature profiles. With these three parameters, we organized the RS according to the atmospheric stability. Near the transition hours (sunrise and sunset), we used only the near-surface temperature lapse rates of the T-profiles for reckoning the stability conditions of the soundings. Qualitatively, the near-surface atmospheric conditions were labeled as unstable, neutral, and stable conditions when , , and , respectively. In terms of the other stability parameter, following the proposal of Arya [17], we labeled the atmospheric conditions according to Table 2.

Table 2.
Stability classes, as suggested by Arya [17]. Sonic at z = 12 m.
To avoid mistaking free tropospheric features for the top of the ABL, we restricted the RS profiles to the lowest 4000 meters above ground level (magl). We smoothed all the RS profiles to reduce the effect of extreme values (outliers). Specifically, if is the set of data points for the temperature profile obtained by RS, the smoothed value at a given zk was the sum of the values of temperature at zk-1 multiplied by 0.25, at the zk of interest multiplied by 0.5, and at zk+1 multiplied by 0.25:
3.2.1. Convective Boundary Layer
We applied four different methods to estimate the convective boundary layer (CBL) height from the radiosonde data. Two of them were traditional approaches often encountered in the ABL literature: the parcel method (PM) [10,18,19], which requires only the temperature profiles, and the gradient method (GM), which is applied to the VPT [20,21,22] and SH [23] vertical profiles. The other two methods were the least-squares variational approach (LSVA) [24] that carries out the best fitting of slab model profiles to the VPT and SH vertical profiles and a covariance method (CM) that identifies the mixing height with the level of the minimum covariance between the VPT and SH profiles.
The Parcel Method
The PM is a procedure widely used to estimate the mixing height from RS data, with no need for wind profile. The original method (Holzworth) determines the maximum daily value of mixing height from the intersection between the dry adiabatic profile, which starts at the maximum surface temperature, and the RS temperature profile observed at sunrise (generally, from 05:00 through 07:00 LST, approximately) [10,18,19]. It is ordinary an interpretation of the estimated height as the equilibrium level of a hypothetical rising parcel of air representing a thermal. This method strongly depends on the surface temperature, and high uncertainty in the estimated height may result in situations without a pronounced inversion at the top of the CBL. A fixed meteorological station measures the surface temperature.
In this work, we did not attempt estimating the maximum daily value of mixing height [18], which sometimes finds application in air quality modeling, or the minimum daily value [19], which provides a worst-case scenario for estimating surface concentrations of air pollutant emissions. Instead, we used the parcel method as described by Seidel et al. [25], and we evaluated the mixing height at the time of the atmospheric sounding. No intersection between the dry adiabatic profile and the RS temperature profile will exist if the lower part of the T-profile exhibits a subadiabatic lapse rate; therefore, no direct estimation of mixing height can be provided by the PM in this case.
Gradient Methods
Several methods are available to determine the convective mixing height from the gradient profiles of the RS data. In this work, for estimating the mixing height under unstable conditions, we applied gradient methods to the vertical profiles of virtual potential temperature and specific humidity. The identification procedures are as follows:
(a) Virtual potential temperature: The CBL height is estimated to be the level of the maximum vertical gradient of virtual potential temperature, which is characteristic of a transition from a convectively less stable region below to a more stable region above. [20,23,26].
(b) Specific humidity: The CBL height is estimated to be the height where the minimum of the vertical gradient of the specific humidity profile occurs [23].
The gradient approaches are most effective when the CBL is capped with a well-defined inversion layer with the VPT increasing and the SH decreasing sharply above the top. However, the local gradient approach could lead to an ambiguous height determination for scenarios where a sharp inversion layer is absent, or where a cloud layer tops the ABL, or where there are multiple layers in the troposphere with strong gradients.
Slab Model of CBL and the Least-Squares Fitting Approach to the Mixing Height
The basic structure of the CBL comprises a few stacked atmospheric layers: the surface layer, where the vertical profiles of the principal meteorological quantities follow the similarity laws; the mixing layer, which is in the middle, characterized by intense turbulence of thermal origin (convection); and the entrainment layer, marked by a temperature inversion that suppresses the turbulence and buffers the free atmosphere above [20,21,22]. This layered structure of CBL is frequently evident in the vertical profiles of VPT and SH. This feature especially holds for VPT, but with minor restrictions also for SH [27].
The slab model assumes that, under convective conditions (z/L < 0), the entrainment layer has an infinitesimal thickness, and that the vertical profiles of VPT and SH display simple shape profiles (Figure 2), which we can use to estimate the convective mixing height [20].
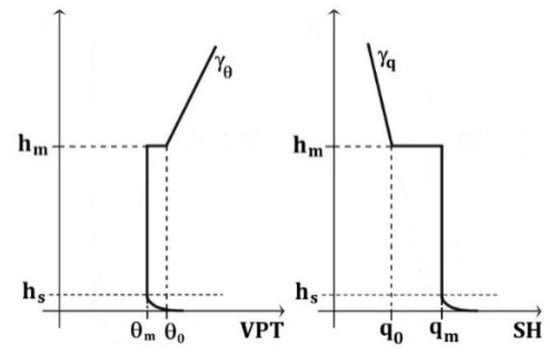
Figure 2.
Idealized profiles of virtual potential temperature (VPT) and specific humidity (SH) from the standpoint of the slab model of the convective boundary layer (CBL).
We applied the least-squares variational approach (LSVA) proposed in [24] to estimate the mixing height from the VPT profile under convective conditions. We also used an extension of this method with the SH profile. The basis of LSVA is on the slab model of the CBL structure [20], but with the additional assumption that the thickness hs of the surface layer is infinitesimal (negligible).
Radiosonde ascents provide the atmospheric vertical profiles of temperature (T), pressure (p), and dew point temperature (Tdew), and these basic profiles allow us to calculate the specific humidity q and the virtual potential temperature using standard relations [20,22].
Let the set of data points obtained by RS for the VPT profile Then, according to LSVA, if no residual layer is present, the profile exhibits only three sections [20,24]. The mixing layer, where the VPT is assumed to be constant and equal to from (earth surface) to (mixing height); the entrainment zone, whose thickness is assumed infinitesimal, located at where the VPT has a discontinuity, jumping from to ; and the free atmosphere, for , where VPT increases linearly with a slope γ.
The following equation describes the model profile (solid line in Figure 3):
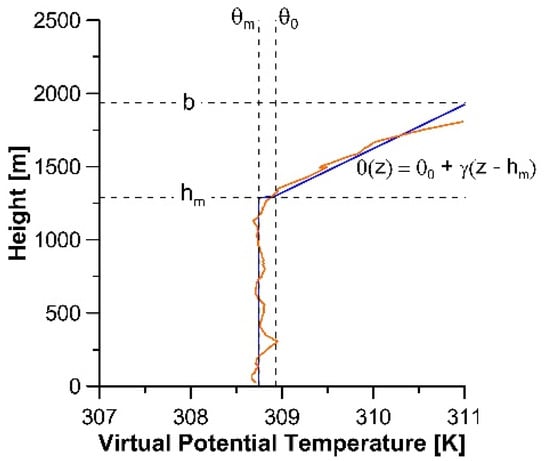
Figure 3.
Slab model for the vertical profile of VTP under convective conditions. The thickness of both the entrainment zone and the surface layer is assumed infinitesimal (negligible). The straight dark lines represent the model VPT profile. We used a similar model for the SH profile.
Here, H(x) is the Heaviside function, which is 0 for negative argument values and one otherwise.
From the standpoint of the LSVA, the estimating procedure of mixing height consists of finding the values of the parameters , which define the best fitting of the model profile to the set P of the data points obtained from RS for the VPT profile . It is a parametric estimation problem that the LSVA solves through nonlinear least-squares [24].
The values of that minimize the functional
under the next five restrictions,
define the best choice of the VPT model profile. The limit b of the integral in Equation (7) is a cutting height subjectively imposed on the balloon ascent. It is an adjusting parameter worked (by a skilled user) to select the portion of the virtual potential temperature profile free of residual layers.
In principle, the following set of nonlinear equations provide the solution of the problem [24]:
However, due to the experimental nature of the VTP profile , we used a numerical procedure to obtain the minimizing set . With the Equations (9)–(12), we reduced the functional (7) to another one that depends only on the parameters and b. Given b, we varied over the interval until obtaining the minimum of F. The minimizing set defines the best fitting of the model VTP profile to the experimental data. For a given b, the minimizing represents the best choice for the mixing height.
This approach takes into account all the VTP profile up to the cutting height b. Then, if the VPT profile shows the existence of multiple layers in the troposphere with strong gradients, different values of b can result in different estimations of mixing height. In this work, we also used a direct extension of the LSVA to estimate the mixing height from the SH profile.
Covariance Method
One of the main characteristics of the mixing layer is that an intense vertical mixing tends to leave the conserved properties such as virtual potential temperature and specific humidity nearly constant with height [27]. Otherwise, in the entrainment layer (the transition zone between the mixing layer and the stably stratified, quasi-nonturbulent free atmosphere above), the typical features are a significant positive temperature lapse rate, a sharp decrease of specific humidity, and sometimes considerable vertical wind shear [27]. The sharp gradients of VPT and SH (positive, the first and negative, the second) in the entrainment layer compel to a joint covariance of VPT and SH with an ample negative value in the capping inversion of the CBL. The level it occurs identifies the mixing height. We refer to this approach as the covariance method (CM).
3.2.2. Stable Boundary Layer
In contrast to the daytime convective boundary layer, under stable nocturnal conditions, the situation is more complicated and less straightforward to determine the height of the stable boundary layer (SBL). Turbulence is gradually suppressed during stable conditions and may show an intermittent behavior [28]. Some other processes, such as longwave radiation flux divergence [29], gravity waves, wave breaking [30], baroclinicity [31], and low-level jet [32], may affect the structure of the nocturnal boundary layer (NBL). Therefore, no straightforward interpretation exists of temperature and wind speed profiles, and both the measurement and prediction of the nighttime mixing height have proven to be far more complicated and less reliable. When direct measurements (using instruments like SODAR, RASS, and LIDAR) of mixing height are not available, as it is the case for most routine meteorological observations, one estimates the height of the SBL through parametrical relations that express it as a function of some boundary layer parameters [33,34].
Parametrizations of the Turbulent SBL
Many parameterizations for the height of the turbulent SBL have been suggested in the literature. Both diagnostic and prognostic relationships have been proposed, but no agreement exists on which type is the most suitable [10,27]. Several diagnostic models for estimating the height of the turbulent SBL from turbulence parameters such as friction velocity and Monin–Obukhov length have been proposed [17,35,36,37,38,39,40,41,42]. The main models to estimate the SBL height were discussed and summarized by Seibert et al. [27], and Lena and Desiato [43] performed an intercomparison of several indirect appraisal methods to estimate of the stable mixing height for urban air pollution modeling. They also compared the results of the models against mixing heights derived from wind (SODAR) and temperature (RASS) profiles measured in the Milan urban area during spring and summer 1996.
In Table 3, we presented three of the most popular diagnostic equations (based on scaling arguments) [10]. These equations correspond to the classical parametrization models of Zilitinkevich [35], Nieuwstadt [38], and Arya [17]. Most of the verification studies done in the past do not seem to favor the application of more elaborated parameterizations [10].

Table 3.
Stable mixing height diagnostic algorithms. The equations give stable mixing height () as a function of friction velocity () Monin–Obukhov length (L), and the Coriolis parameter (f).
The Nieuwstadt parametrization, N1981, was derived for the height of the stationary boundary layer during stable lapse rate conditions. It satisfies the conventional limits for neutral conditions and large values of stability [38]. The parametrization Z1972 was first suggested by Zilitinkevich in 1972 [35] as a model of the nocturnal atmospheric boundary layer, and several authors confirmed it from 1974 to 1978 [44,45,46,47]. The parametrization A1981 was suggested by Benkley and Schulman [36] as a simple relation for routine operational use. Both simple relations were studied by Arya [17], who found functional correlations of with and . Arya concluded that Z1972 is adequate for moderately stable conditions, whereas A1981, is satisfactory for all but extremely stable () nighttime conditions. Both diagnostic models, Z1972 and A1981, can be obtained from the N1981 as asymptotic limits of (very stable conditions) and (neutral conditions), respectively [27]. A1981 provides the simplest parametrization for the nocturnal mixing height, and it is suggested frequently for practical applications, but with the prescription of a convenient lower threshold value [43].
Venkatram [37] and Nieuwstadt [41] proposed other simpler diagnostic algorithms where the SBL height is proportional to the 3/2-power of friction velocity and the 10 m-wind-speed. The US-EPA processors AERMET [48] and CALMET [49] use these relations; however, they show underestimation or overestimation in low and high wind conditions, respectively [43].
Other diagnostic models have been proposed using the time scale 1/NBV, defined by the Brunt-Vaisala frequency, instead of 1/f or where the diagnostic formulae considering the bulk structure of the SBL are based on the assumption that turbulence production must vanish at the SBL top and the Richardson number must, therefore, exceed its critical value [10]. However, these and other available methods (see [10] for a review) involve information not available from radiosondes, such as cloud base height, micrometeorological covariance statistics, or turbulence flux profiles.
In this work, we used Equations (N1981, Z1972, A1981) to estimate the nocturnal mixing height from surface measurements of friction velocity and Monin–Obukhov length. In practice, we considered Z1972 and A1981 with the proportionality constants equal to the average of the respective constants recommended by the different authors. In the case of the monitoring site in the Mexicali Valley (with latitude around 32°24’ N), the Coriolis parameter is f = 7.79 × 10−5 s−1. Then, Z1972 became to
and Equation A1981 became to
These equations, which will be referred to as Z1972S and A1981S, give hm in meters if is in m/s, and L is in meters. Friction velocity in A1981S is limited to m/s [50].
Surface-Based Inversions
Longwave radiation flux divergence may affect the structure of the NBL [29]. At nighttime, under clear skies, the net radiative-flux divergence is a potentially crucial cooling phenomenon that affects the boundary layer structure. When the sun goes down, the ground loses heat very quickly, and this cools the air above the ground. This cooling of the ground continues over more extended periods during the wintertime nights, which are much longer than the summertime nights. Weak winds prevent air mixing near the surface, and clear skies increase the rate of cooling at the Earth’s surface. Stable conditions inhibit vertical and horizontal mixing near the ground and, consequently, favor the development of a strong surface-based temperature inversion, where the near-surface temperature lapse rate is positive. A surface-based T inversion is a clear indicator of a stable boundary layer, whose top can define an ABL height. If a surface-based inversion (SBI) is found in a sounding, the previous methods are not evaluated, as they assume a different NBL structure [25]. The top of the SBI can be defined by the height above which temperature first decreased with elevation [25,51].
3.2.3. Estimation of Mixing Height from the Sensible Heat Flux
A straightforward semiempirical model was proposed in 2001 by Yi, Davis, Berger, and Bakwin (YDBB) [52] to estimate the convective mixing height as a linear function of the square root of the energy accumulation due to the turbulent sensible heat flux :
Here, a and b are constants to be empirically determined by fitting to measurements. The YDBB model can be used to predict mean mixing height during that period of the day when the mixing layer grows due to surface heating.
The lower limit t0 in the integral of Equation (15) denotes the instance when H0 changes sign from negative to positive (at the sunrise). When t = t0, we have . Then, the constant a represents the value of mixing height at the sunrise. The upper limit t is the time of interest, for which, we want to evaluate the mixing height, t0 < t ≤ tm + 2 h. tm is the time when the sensible heat flux reaches its maximum value [52]. From the standpoint of YDBB, the mixing height gets the most significant value when t ≈ tm + 2 h, approximately. However, in [52], the authors underlined that it might occur (in northern Wisconsin) that the weather is generally transparent or partly cloudy on days when maximum mixing height is reached 4 h after the maximum . Moreover, with clear skies in the summertime, the mixing layer can continue to grow for 5 or 6 h after the maximum .
3.2.4. The Time Evolution of the Mixing Height
The time behavior of mixing height follows a diurnal cycle. It also depends on the meteorology parameters, the turbulent surface fluxes, and the physiographic characteristics of the site. The diurnal cycle of heating of the earth’s surface by the direct influence of the insolation creates thermal turbulence and causes the recurrent mixing layer growth with a period of 24 h. However, the underlying diurnal behavior of mixing height is known not to be purely harmonic (i.e., it does not occur in a simple sinusoidal way) [20]. For convective conditions, the YDBB model can be used to obtain an estimation of the temporal evolution of the mixing height during its growing phase from the surface values of turbulent sensible heat flux. For nighttime conditions, on the other hand, estimations of mixing height can be obtained from the surface values of friction velocity and Monin–Obukhov length using one of the models presented in Table 3.
Then, we can use the YDBB and the stable parametrizations, complementarily, to establish a procedure that allows the hourly estimations of the diurnal mixing heights from the surface values of sensible heat flux, and nocturnal mixing heights from friction velocity and Monin–Obukhov length:
Here, π(t) is the rectangle function, which is equal to 1 if t0 < t ≤ tm + 2 h and 0 otherwise. The function hs is one convenient parametrization (N1972, Z1981, A1981, or any other) that allows estimating the nocturnal value of hm.
4. Results and Discussion
4.1. Surface Meteorological Data
Figure 4 and Figure 5 show the hourly trends of the minimal, mean, and maximal values of temperature, relative humidity, wind speed, sensible heat flux, friction velocity, and the stability parameters ( and ). For each sounding campaign (17–28 July 2010, 25–29 January 2012, and 11–15 October 2016), we determined hour by hour the minimum, mean, and maximum values of the surface meteorological variables measured during its period. Figure 5 also shows the hourly trends of sensible heat flux and friction velocity for the corresponding month.
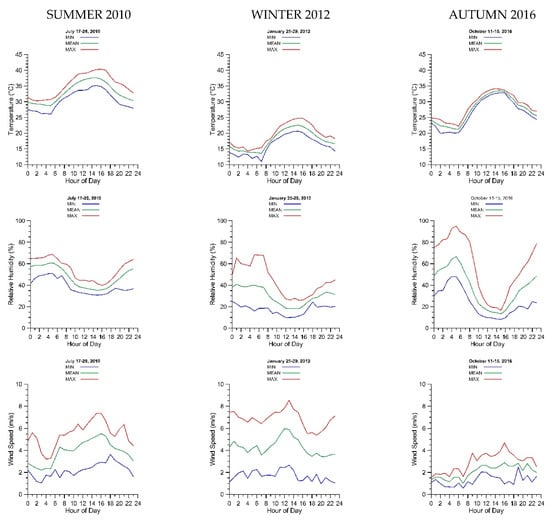
Figure 4.
Hourly behaviors of the minimum, mean, and maximum values of temperature, relative humidity, and wind speed during the Cerro Prieto (Mexicali) summer, winter, and autumn campaigns.
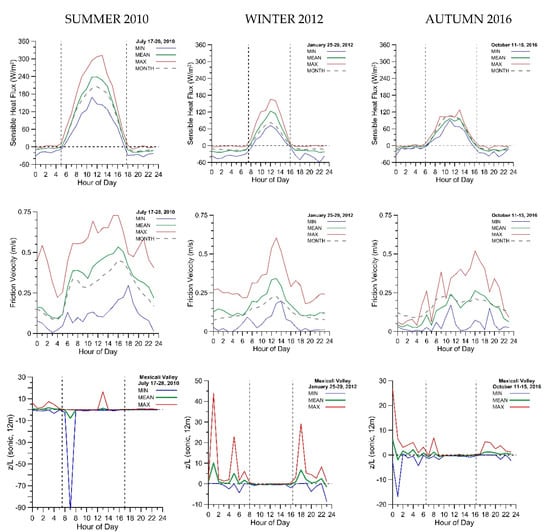

Figure 5.
Hourly behaviors of the minimum, mean, and maximum values of sensible heat flux, friction velocity, and the stability parameters during the Cerro Prieto (Mexicali) summer, winter, and autumn campaigns.
In Figure 4, we observed that the larger values of temperature and relative humidity prevailed in summer, while in winter, the smaller ones. On average, the minimum, mean and maximum temperatures were 30, 33, and 35 °C in summer, 16, 18, and 19 °C in winter, and 26, 27, and 29 °C in autumn. For relative humidity, the values were 39%, 48%, and 55% in summer, 17%, 30%, and 44% in winter, and 24%, 38%, and 58% in autumn. These results are consistent with the Mexicali Valley climatology [13]. For wind speed, the averages of the minimum, mean, and maximum values were 2.2, 3.9, and 5.5 m/s for summer, 1.7, 4.3, and 6.8 m/s for winter, and 1.3, 2.1, and 2.9 m/s for autumn, with the larger values in winter and the smaller ones in autumn. Regarding the Mexicali climatology [13], the mean wind speeds obtained for the summer and autumn campaigns fell within the 25th to 75th percentile band, but for the winter campaign fell in the 10th to 90th percentile band.
In Figure 5, the plots in rows 3 and 4 show that, with very few exceptions, the stability parameters (at z = 12 m) and were negative from 05:30 to 17:00 LST in summer, from 08:00 to 16:15 LST in winter, and from 06:30 to 16:15 LST in autumn. Therefore, during these periods, unstable atmospheric conditions prevailed in the surface with possible near-neutral conditions at the ends [53]. Moreover, the plots of the first row of Figure 5 show that the sensible heat flux was positive on average during the periods 05:00–17:45 LST in summer, 07:30–16:00 LST in winter, and 06:00–16:30 LST in autumn. During these periods, the surface heating produced thermal turbulence (convection). These results with H0 > 0 are consistent with the observations of ζ < 0 and μ < 0, corroborating the unstable atmospheric conditions. On average, H0 reached its maximum at noon, independently of the seasonal period, with values of 239, 123, and 96 W/m2 in the summer, winter, and autumn RS-campaigns, respectively. At midday, the surface upward turbulent transport of thermal energy was more abundant in summer than in winter and autumn campaigns.
It is striking that the maximum value of H0 at noon was higher in winter than in autumn, but this is reflecting only that on the day January 28, the average value of H0 registered from 10:00 LST to 13:00 LST was 142 W/m2 against the average of 88 W/m2 registered during the rest of the campaign. Moreover, we can observe that the hourly trends of H0 averaged over the month revealed maximums of 205 W/m2 in summer, 82 W/m2 in winter, and 106 W/m2 in autumn at noon, which are consistent with the expected seasonal differences. Accordingly, we expect that the convective mixing heights reveal the seasonal differences correctly.
The mean values of friction velocity also were more significant in summer than winter and autumn. On average, the values were 0.32, 0.17, and 0.13 m/s in the summer, winter, and autumn measurement periods, respectively. Then, the downward turbulent transport of momentum was more significant in the summer than in the winter and autumn RS-campaigns. We observed the smaller values of friction velocity in the nighttime, especially during the dawn hours. On the monthly average, the temporal evolutions of the mean friction velocity exhibit trends with peaks of 0.4514, 0.2255, and 0.2326 m/s around the 16:00 LST, 13:00 LST, and 11:00 LST during the summer, winter, and autumn, respectively.
4.2. Vertical Profiles of Temperature
We carried out 52 RS under different stability conditions during the three campaigns (25 in summer 2010, 13 in winter 2012, and 14 in autumn 2016). In Table 1, we highlighted the sunlight conditions. In Figure 6, we presented the average temperature profiles obtained from the RS carried out under sunlight conditions. The only case we carried out diurnal RS for all seasons (summer, autumn, and winter) was that of the 12:00 LST soundings (Figure 6b,e,f). Because of the variability of the sunrise moment at the Mexicali latitudes, we obtained diurnal RS early in the morning (06:00 LST) only in the summer 2010 campaign.
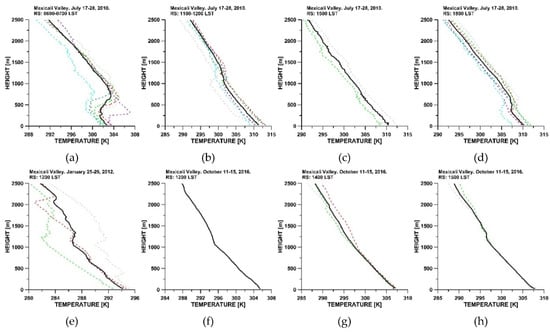
Figure 6.
Temperature profiles obtained from the RS during daylight conditions. (a) 06:00 LST, (b) 12:00 LST, (c) 15:00 LST, and (d) 18:00 LST from the summer RS campaign; (e) 12:00 LST from the winter campaign; and (f) 12:00 LST, (g) 14:00 LST, and (h) 15:00 LST from the autumn campaign. The solid line represents the average profile. We carried out only one RS at 12:00 LST during the autumn campaign.
For each RS, from the surface measurement campaigns, we determined the mean values of Monin–Obukhov length, friction velocity, sensible heat flux, and the stability parameters ( and ) over the sounding duration. We also estimated the near-surface temperature lapse rates (Γ) of the T-profiles. In Table 4, Table 5 and Table 6, we presented the values of the main parameters for all the RS that we considered during unstable conditions. The RS revealed quasi-adiabatic and superadiabatic lapse rates,. Otherwise, in Table 7, Table 8 and Table 9, we gave the values of the same parameters for the RS that we considered under stable conditions. These RS revealed subadiabatic lapse rates,.

Table 4.
Estimation of the Mexicali Valley convective mixing height from atmospheric soundings.

Table 5.
Estimation of the Mexicali Valley convective mixing height from atmospheric soundings.

Table 6.
Estimation of the Mexicali Valley convective mixing height from atmospheric soundings.

Table 7.
The summer stable mixing height of the Mexicali Valley estimated with the surface mean values of friction velocity and Monin–Obukhov length according to the N1981, Z1972S, and A1981S. Here, we also included the mean surface values of the stability parameters and sensible heat flux, and the near-surface temperature lapse rate of the radiosonde (RS).

Table 8.
The nocturnal stability conditions of the Mexicali Valley during the winter 2012 campaign. The height of the stable boundary layer (SBL) estimated from surface-based inversion.

Table 9.
The nocturnal stability conditions of the Mexicali Valley during the autumn 2016 campaign. The height of the SBL estimated from surface-based inversion.
4.3. Estimation of the Convective Mixing Height with the LSVA, GM, CM, and PM
In Table 4, Table 5 and Table 6, we present the evaluations of the Mexicali Valley mixing height under unstable conditions for summer 2010, winter 2012, and autumn 2016 sounding campaigns. The estimates were done from the VPT and SH profiles, which we calculated from the temperature (T), pressure (p), and dew point temperature (Tdew) vertical profiles from the RS. In Table 4, Table 5 and Table 6, we labeled the application of the LSVA and GM as LSVA/VPT, GM/VPT, LSVA/SH, and GM/SH. The CM requires both profiles, VPT and SH. The PM was applied directly to the RS and dry adiabatic temperature profiles. We measured the surface temperature in situ with an RTD thermometer (RM Young, model 43347) at 12 m above ground, with 1 Hz sampling rate and 1-h averaging times.
Table 4, Table 5 and Table 6 include the date and time of the RS, the average values of the stability parameters, the sensible heat flux measured in the surface during the RS, the near-surface lapse rate of the RS temperature profile, and the estimations of the convective mixing height from the VPT, SH, and T vertical profiles. The last column gives the mean mixing height over all the methods.
On average, the sunrise and sunset in the Mexicali Valley occurred at 05:49 LST and 19:45 LST during the summer 2010 campaign, at 06:40 LST and 17:10 LST during the winter 2012 campaign, and at 06:44 LST and 18:10 LST, during the autumn 2016 campaign, respectively.
The RS presented in Table 4, Table 5 and Table 6 were carried out during sunlight hours. All of them, excepting the soundings carried out at 18:00 LST during the summer 2010 campaign, were done under atmospheric surface conditions with ζ < 0, μ < 0, and H0 > 0, which indicate unstable atmospheric conditions near the ground. The soundings of the 18:00 LST were performed under surface conditions with ζ > 0, μ > 0, and H0 < 0, which indicate stable conditions. However, as we can observe, the near-surface temperature lapse rates of these RS were superadiabatic, indicating that they found unstable conditions in the first 100–200 m above ground. The radiosoundings of the 18:00 LST were carried out during the transition period of the sunset, which explains the small positive values of the stability parameters and the small negative values of H0.
The atmospheric conditions for the 06:00 LST soundings carried out during the summer 2010 campaign were unstable according to the stability criteria (ζ < 0, μ < 0), but the near-surface lapse rates of these temperature profiles were quasi-adiabatic or subadiabatic, indicating that they found stable conditions in the first 100–200 m above ground. In this case, however, the diagnostic parametrizations based on the friction velocity and Monin–Obukhov length cannot be applied since the formulae assume L > 0. Therefore, we used the LSVA, GM, CM, and PM to obtain the mixing height from the RS profiles. In order to apply the PM, however, we built the dry adiabatic profile with the surface temperature increased (subjectively) in 3 K (otherwise, no intersection would be found between the temperature profiles of the RS and dry adiabatic).
The graphs in Figure 7, Figure 8 and Figure 9 illustrate the application of the LSVA, GM, CM, and PM to the VPT, SH, and T profiles obtained from the RS carried out at 12:00 LST during the sounding campaigns. In these Figures, the red lines indicate the VTP and SH profiles, the green lines represent their gradient profiles, and the blue lines represent the VPT and SH slab model profiles given by the LSVA. The graphs in the third column show the covariance (magenta lines) between the VPT and SH profiles. The last column illustrates the application of the PM for the 12:00 LST temperature profiles (solid lines). The dotted line denotes the dry adiabatic profiles.
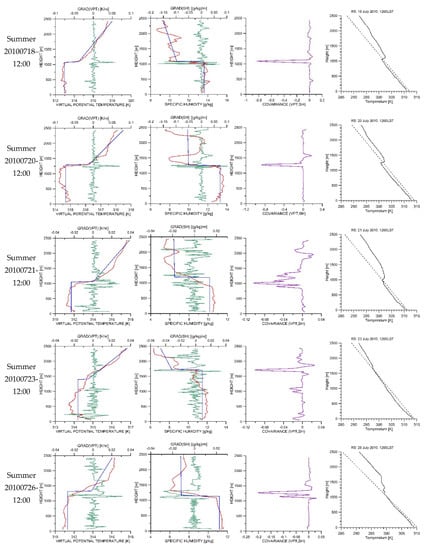
Figure 7.
Application of the estimation methods to the VPT, SH, and T profiles of the 12:00 LST of the days 18, 20, 21, 23, and 26 of July 2010. First column: LSVA/VPT and GM/VPT. Second column: LSVA/SH and GM/SH. Third column: CM. Fourth column: PM.
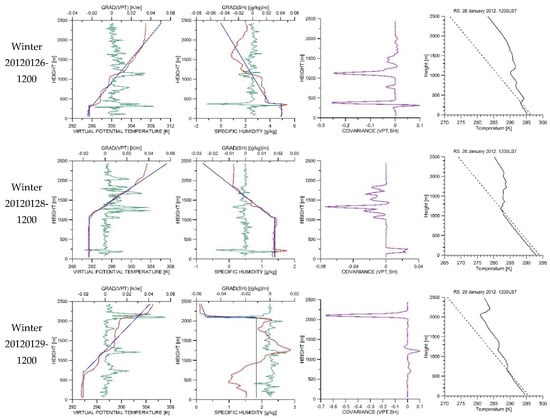
Figure 8.
Application of the LSVA, GM, CM, and PM to the VPT, SH, and T profiles of the 12:00 LST of the days 26, 28, and 29 of January 2012. First column: LSVA/VPT and GM/VPT. Second column: LSVA/SH and GM/SH. Third column: CM. Fourth column: PM.
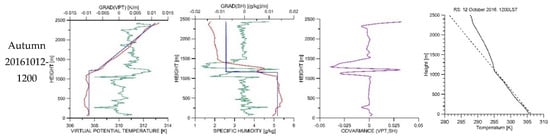
Figure 9.
Application of the LSVA, GM, CM, and PM to the VPT, SH, and T profiles of the 12:00 LST of October 12, 2016. First column: LSVA/VPT and GM/VPT. Second column: LSVA/SH and GM/SH. Third column: CM. Fourth column: PM.
Comparing the plots of the VPT and SH profiles in Figure 7, Figure 8 and Figure 9, we observed that the SH profiles were less regular than the VPT profiles. Then, the idealized slab model (Figure 2) provided a better representation of the actual VPT profiles than the actual SH profiles. Nevertheless, the application of the LSVA to the SH profiles gave reasonable mixing height values, similar to those of the other methods, excepting the 12:00 LST case of 29 January 2012.
In Figure 8, the VPT profile of the RS identified as 20120129-1200 reveals the presence of three inversions aloft at 730, 1210, and 2110 m, with VPT gradients of 0.022, 0.032, and 0.055 K/m, respectively. Probably, the third one is an inversion by subsidence, which are common in the Imperial County and the Mexicali Valley between November and June and relatively absent between July and October [54,55]. The presence of the semipermanent cyclonic cell of the Pacific Ocean can cause the fall of air masses. When these air masses descend, they undergo heating by compression, reaching temperatures that are higher than those of the layers that are closer to the ground surface. The intensity of these highly stable atmospheric conditions makes them difficult to disrupt and can persist for one or more days. These inversions may occur at heights between 2000 and 6000 m. The second inversion resembles a reminiscence of the day before. Therefore, we accepted the mean value of 706 m from the LSVA/VPT, GM/VPT, and PM as the valid one for 12:00 LST of 29 January 2012 (Table 4).
Table 4, Table 5 and Table 6, and the plots in Figure 10, reveal similar results among the convective mixing height estimations obtained with the LSVA/VPT, GM/VPT, LSVA/SH, GM/SH, CM, and PM, for the same atmospheric sounding.
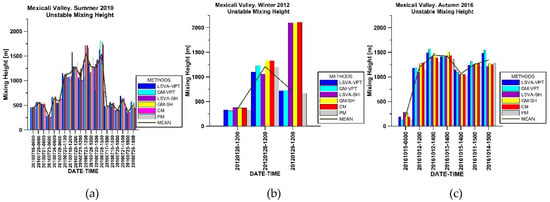
Figure 10.
Estimations of the convective mixing height with the LSVA/VPT, GM/VPT, LSVA/SH, GM/SH, CM, and PM. (a) Summer 2010, (b) winter 2012, and (c) autumn 2016. The graphs also show the mean value (solid line) over all the methods. The estimations obtained with the SH profile of the 12:00 LST sounding of 29 January 2012, reflected an atypical behavior of the specific humidity profile, and we discarded them when calculating the mixing height mean value.
All the methods we used to estimate the convective mixing height gave similar results when the CBL was capped with a well-defined inversion layer with the VPT increasing and the SH decreasing sharply above the top, indicating a marked transition from a convectively less stable region below to a more stable region above. The local gradient approach and the LSVA lead to ambiguous estimations with scenarios where a sharp inversion layer is absent or where multiple layers in the troposphere with strong gradients were present. In general, the VPT profile under unstable conditions fits better the slab model profile than the SH profile, then the LSVA/VPT provided more reliable results than LSVA/SH. The reliability of the CM depends on the regularity of both profiles, VPT and SH.
From Table 4, Table 5 and Table 6, we observed that, on average, the convective mixing height in the Mexicali Valley ranged from 400 to 1400 m. These results are in agreement with the mixing height values (ranging from 300 to 1500 m) that Bei et al. [56] determined in 2010 at the Parque Morelos (PQM, Tijuana Municipal System Theme Park in the center of Tijuana).
Summarizing, the average values of mixing height that we obtained under unstable conditions were: 497 m at the 06:00 LST (1 RS), 1242 m at the 12:00 LST (6 RS), 1407 m at the 15:00 LST (2 RS), and 482 m at the 18:00 LST (6 RS) during the summer 2010 campaign; 754 m at the 12:00 LST (3 RS) during the winter 2012 campaign; and 198 m at 08:00 LST (1 RS), 1195 m at the 12:00 LST (1 RS), 1311 m at the 14:00 LST (3 RS), and 1300 m at the 15:00 LST (2 RS) during the autumn 2016 campaign.
4.4. Estimation of the Stable Boundary Layer Height
4.4.1. Summer 2010 Campaign
During the summer 2010 campaign, we carried out nocturnal atmospheric soundings at 00:00 LST. Therefore, the atmospheric conditions for these RS were expected to be stable. On average, during this set of RS, the observed values of the sensible heat flux and the stability parameters were H0 = −9 W/m2, ζ = 0.525, and μ = 59 (Table 7). These observations indicate that the 00:00 LST soundings were done under very stable atmospheric conditions. The near-surface lapse rates of the temperature profiles were subadiabatic (Γ = −0.0027 K/m, on average). We used N1981, Z1972S, and A1981S to estimate the Mexicali Valley midnight stable mixing height from the friction velocity and the Monin–Obukhov length. Table 7 and Figure 11 summarize the results.
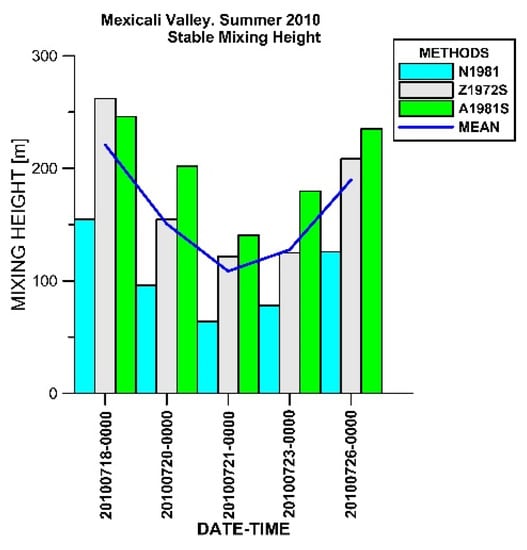
Figure 11.
Estimations of the Mexicali Valley mixing height under the 00:00 LST stable atmospheric conditions during the summer 2010 campaign. We observe that the A1981S parametrization, Equation (14), overestimated the mixing height in comparison with the other two models during very stable conditions (μ > 50).
In Table 7 and Figure 11, we noticed that N1981, Z1972S, and A1981S provided similar estimations for the 00:00 LST stable mixing height. The smaller estimations were obtained with N1981, which was derived for stable lapse rate conditions with a wide range of stabilities, from near neutral to very stable [38]. However, as A1981S was derived in the limit of neutral or near-neutral conditions, it overestimated the mixing height in comparison with the other two models for the cases with very stable conditions (50 < μ < 100), but revealed a small difference for Z1972S in the case (20100718-00:00) with a moderately stable condition (10 < μ < 50). On average, the nocturnal (00:00 LST) mixing height value was 160 m.
4.4.2. Winter 2012 and Autumn 2016 Campaigns
For the winter 2012 and autumn 2016 campaigns, all the nocturnal RS were done under stable conditions. It is evidenced by the average surface values of the stability parameters and the near-surface temperature lapse rates of the RS profiles. Table 8 and Table 9 summarize the results.
During the winter 2012 sounding campaign, we carried out nocturnal soundings at 00:00 LST, 06:00 LST, 18:00 LST, and 21:00 LST. For this part, during the autumn 2016 campaign, we carried out soundings at 06:00 LST and 18:00 LST, again under nocturnal conditions. In Table 8 and Table 9, we summarized the nocturnal stability conditions in the Mexicali Valley during the periods of these experimental campaigns. For all the RS, we observed that the surface values of the stability parameters were positive and large, indicating that the atmospheric conditions on the surface were from very stable to extremely stable. We also observed that the near-surface temperature lapse rates of the RS profiles were all positive, revealing the presence of surface-based inversions (SBI).
An SBI is a clear indicator of a stable boundary layer, whose top can define an ABL height [25]. If an SBI is found in a sounding, none of the previous diagnostic parametrizations can be applied because they assume a different ABL structure [25]. Turbulence is suppressed, and no mixing height exists.
We evaluated the SBI as the height where the temperature changes from increasing to decreasing with the elevation. Ideally, at this height, the vertical gradient of the temperature profile becomes zero: (
Table 8 and Table 9 and Figure 12 and Figure 13 show our estimations of the SBI. On average, the SBI values were from 53 m at 18:00 LST to 183 m at 06:00 LST during the winter 2012 campaign, whereas in the autumn 2016 campaign, the values were from 132 m at 18:00 LST to 370 m at 06:00 LST. As we can observe in Figure 14 and the first row of Table 6, these inversions seem to break-off 1 h after sunrise (~ 08:00 LST).
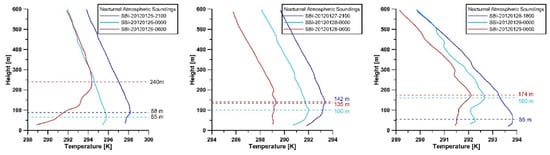
Figure 12.
Estimation of the height of the stable boundary layer (SBL) of the Mexicali Valley from the surface-based inversions during the winter 2012 campaign. The graphs show the evolution of the surface-based inversion (SBI) from the first hours after sunset to 1 h before sunrise of the next day.
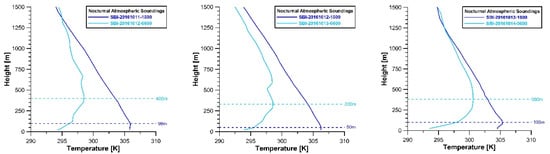
Figure 13.
Estimation of the height of the SBL of the Mexicali Valley from the surface-based inversions during the autumn 2016 campaign. The graphs illustrate the change of the SBI from the sunset to 1 h before sunrise of the next day.
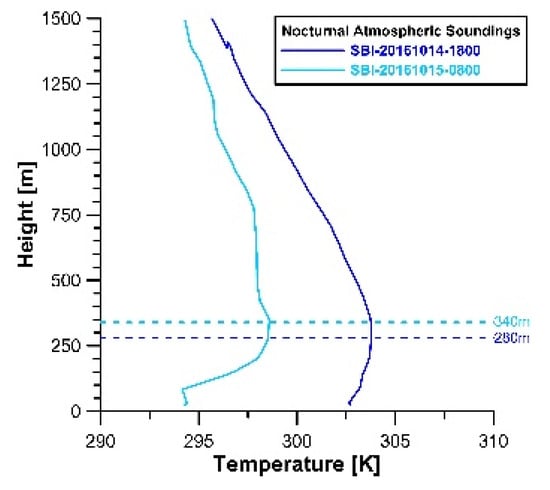
Figure 14.
Breaking-off of the surface-based inversion developed from the sunset of 14 October to the early morning of 15 October, during the summer 2010 campaign in the Mexicali Valley. As we observed in Table 6, the radiosonde (RS) profile 20161015-08:00 revealed a subadiabatic near-surface temperature lapse rate of Γ = −0.0046 K/m.
4.5. Estimation of the Mixing Layer Growth with the YDBB Model
The YDBB model [52] allows calculating the mixing height during its growing phase in terms of the time series of sensible heat flux H0(t). We determined the sensible heat flux as the covariance between the turbulent fluctuations of temperature and the vertical wind component measured with a 3D ultrasonic anemometer at z = 12 m, using Equation (2).
With the H0 data collected during the surface meteorological campaigns and the estimations of the convective and stable mixing heights, the parameters a and b of the YDBB model were determined. In the case of the summer 2010 campaign (the longer one), the results for the convective conditions included 14 estimations of the mixing height for the 06:00 LST (6 RS), 12:00 LST (6 RS), and 15:00 LST (2 RS). For the winter 2012 campaign, we obtained only three estimations of the convective mixing height for the 12:00 LST. For the autumn 2016 campaign, we had estimations of convective mixing height for the 08:00 LST (1 RS), 12:00 LST (1 RS), 14:00 LST (3 RS), and 15:00 LST (2 RS). No RS soundings were available for sunrise during the winter and autumn campaigns. Therefore, we used the friction velocity surface measurements to estimate the mixing height at 07:00 LST (each day of these campaigns) with the diagnostic parametrization A1981S. In Table 10, we presented the results obtained for the YDBB model parameters, including the determination coefficient R2. In Figure 15, we showed the results of the application of the YDBB model (Equation (16)) to calculate the mixing height for all hours during the sounding campaigns.

Table 10.
Parameters of the Yi, Davis, Berger, and Bakwin (YDBB) model obtained from measurements of H0 and estimations of mixing height from convective atmospheric soundings and surface measurements of friction velocity.
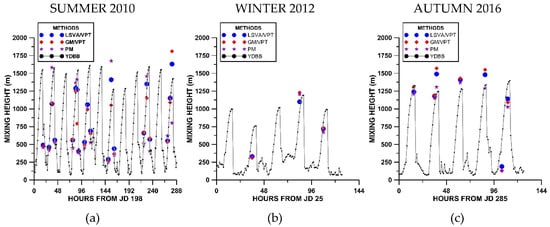
Figure 15.
Application of the Yi, Davis, Berger, and Bakwin (YDBB) model described by Equation (16) to estimate the hourly growth of the mixing height throughout the periods of (a)17–28 July 2010, (b) 25–29 January 2012, and (c) 11–15 October 2016. We also presented the mixing height estimations with the LSVA/VPT, GM/VPT, and PM methods. The abscissae represent the number of hours past from the start (expressed by the Julian day) of the RS campaign.
For comparison purposes, the graphs included the estimations of the convective mixing height with the LSVA/VPT, GM/VPT, and PM approaches. With a few exceptions, the YDBB model gave results in agreement with the estimations of these appraisal methods. On average, the diurnal mixing heights estimated with this model were 1095 m in summer 2010, 779 m in winter 2012, and 936 m in autumn 2016.
5. Conclusions
The main goal of this work was to show that simple and straightforward methods can be applied to obtain reasonable estimations of the hourly mixing height that regulatory dispersion models require to carry out air pollution modeling studies. The use of sophisticated equipment (SODAR, RASS, and LIDAR) is more and more frequent in experimental research campaigns to study the structure of the atmospheric boundary layer; however, for air quality assessment based on short-term pollutants dispersion modeling, usually one estimates the mixing height from a more conventional approach, such as atmospheric sounding. Unfortunately, radiosondes involve some interference with aircraft flight plans, and long campaigns are not always allowed, nor with the necessary characteristics. Therefore, it often occurs that one has to carry out the air pollution modeling with a limited set of mixing height observations, which are mainly representative of daylight conditions.
In this paper, we reported the estimation of mixing height in the Mexicali Valley from RS temperature profiles and surface data of sensible heat flux, friction velocity, and Monin–Obukhov length, which we measured during the periods of 17–28 July 2010, 25–29 January 2012, and 11–15 October 2016. For unstable atmospheric conditions, we used four different approaches: the parcel and gradient methods [27], a least-squares variational approach [24], and a covariance method. For the turbulent SBL height, we used the parametrizations of Nieuwstadt [38], Zilitinkevich [35], and Arya [17], which allow estimations of mixing height from friction velocity and Monin–Obukhov length.
These complementary methods provided a set of mixing height values, which we used to implement a semiempirical model (YDBB) for the diagnostic of the mixing height growing as a function of sensible heat flux [52]. These models allowed estimating the hourly time evolution of mixing height during the periods of interest. A comparison of the YDBB estimations against the results of the PM, GM, and LSVA approaches showed reasonable agreements. In practice, the regulatory models (such as AERMOD and US-EPA) require hour by hour, the value of mixing height as input to perform the estimation of the hourly surface concentrations of the pollutants. However, an atmospheric sounding campaign will provide only a small number of RS a day during the campaign. In general, it would be too expensive and technically prohibitive to carry out one RS each hour of the day, even only during the sunlight hours. Then, the YDBB model may be considered as a practical tool to build up the hourly series of mixing height from the available RS. We also found good agreement with the mixing height values (ranging from 300 to 1500 m) that Bei et al. [56] determined in 2010 at the Parque Morelos (PQM, Tijuana Municipal System Theme Park in the center of Tijuana).
On the other hand, the nocturnal RS we carried out during the winter and autumn campaigns revealed the development of surface-based temperature inversions from sunset to 1 h before sunrise of the next day, with their breaking-off 1 h after sunrise, approximately.
Author Contributions
Conceptualization, A.S.; formal analysis, A.S., T.C., O.P, and R.-S.S.-G.; Investigation, A.-T.C.-M., N.H.-F., G.-A.T.-F., and M.-A.M.-F.; methodology, A.S,; project administration, A.-T.C.-M. and S.C.-S.; software, S.C.-S.; supervision, A.S., A.-T.C.-M., T.C., and O.P.; validation, A.-T.C.-M.; visualization, S.C.-S.; writing—original draft, A.S. and S.C.-S; writing—review and editing, A.-T.C.-M., T.C., O.P., and R.-S.S.-G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors thank the Comisión Federal de Electricidad for the facilities granted to carry out field measurements.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Reyna Carranza, M.A.; Quintero Núñez, M.; Collins, K. Correlation Study of the Association of PM10 with the Main Respiratory Diseases in the Populations of Mexicali, Baja California and Imperial County, California. Rev. Mex. Ing. Bioméd. 2005, XXVI, 22–36. [Google Scholar]
- Reyna, M. Air Quality in Mexicali, Baja California. Epidemiology 2008, 16, S17. [Google Scholar]
- Sánchez-Duque, A.; Bautista, F.; Goguitchaichvili, A.; Cejudo-Ruiz, R.; Reyes-López, J.A.; Amílcar Solís-Domínguez, F.; Morales-Contreras, J.J. Evaluación de la contaminación ambiental a partir del aumento magnético en polvos urbanos. Caso de estudio en la ciudad de Mexicali, México. Rev. Mex. Cienc. Geológicas 2015, 32, 501–513. [Google Scholar]
- Quintero, M.; Meza, L.; Canales, M.; Ahumada, S. The Program to Improve the Air Quality of Mexicali, Baja California, Mexico 2010-2015. Procedia Environ. Sci. 2010, 2, 800–813. [Google Scholar] [CrossRef]
- Comisión Federal de Electricidad, G. Inicia Nueva Etapa de Diálogo Entre la CFE, las Comunidades Aledañas a la Planta Geotérmica de Cerro Prieto, y Actores Políticos del Estado de Baja California 2016; CFE-BP-27/16vf; CFE Gerencia de Comunicación Social: Mexico City, Mexico, 2016. [Google Scholar]
- Moncada-Aguilar, A.M.; Ramírez-Hernández, J.; Quintero-Núñez, M.; Avendaño-Reyes, L. Origin of Salinity in Groundwater of Neighboring Villages of the Cerro Prieto Geothermal Field. Water Air Soil Pollut. 2010, 213, 389–400. [Google Scholar] [CrossRef]
- Peralta, O.; Castro, T.; Durón, M.; Salcido, A.; Celada-Murillo, A.-T.; Navarro-González, R.; Márquez, C.; García, J.; de la Rosa, J.; Torres, R.; et al. H2S emissions from Cerro Prieto geothermal power plant, Mexico, and air pollutants measurements in the area. Geothermics 2013, 46, 55–65. [Google Scholar] [CrossRef]
- Asamblea Nacional de Afectados Ambientales Valle de Mexicali: A 4 años de la Catástrofe. Available online: http://www.afectadosambientales.org/valle-de-mexicali-a-4-anos-de-la-catastrofe/ (accessed on 2 November 2019).
- Clark, A.I.; McIntyre, A.E.; Lester, J.N.; Perry, R. Air quality impact assessment. Environ. Monit. Assess. 1984, 4, 205–232. [Google Scholar] [CrossRef]
- Seibert, P.; Beyrich, F.; Gryning, S.-E.; Joffre, S.; Rasmussen, A.; Tercier, P. Review and intercomparison of operational methods for the determination of the mixing height. Atmos. Environ. 2000, 34, 1001–1027. [Google Scholar] [CrossRef]
- Rojas-Caldelas, R.I.; Pena-Salmon, C.A.; Ley-Garcia, J. Cultural landscape planning: The Mexicali Valley, Mexico. WIT Trans. Ecol. Environ. 2012, 155, 457–468. [Google Scholar] [CrossRef]
- Ruíz Corral, J.A.; Díaz Padilla, G.; Guzmán Ruíz, S.D.; Medina García, G.; Silva Serna, M.M. Estadísticas climatológicas básicas del Estado de Baja California (Periodo 1961–2003); Centro de Investigación Regional del Noroeste, INIFAP-CIRNO: Ciudad Obregón, Mexico, 2006. [Google Scholar]
- Weather Spark. Average Weather in Mexicali, Mexico (1980–2016). Available online: https://weatherspark.com/y/2211/Average-Weather-in-Mexicali-Mexico-Year-Round (accessed on 3 November 2019).
- Sozzi, R.; Favaron, M. Sonic anemometry and thermometry: Theoretical basis and data-processing software. Environ. Softw. 1996, 11, 259–270. [Google Scholar] [CrossRef]
- Luukkonen, K. DigiCORA III Sounding System with Radiotheodolite and GPS Windfinding. Vaisala News 2001, 155, 38–40. [Google Scholar]
- GRAW-Radiosondes Upper Air Sounding Systems. RADIOSONDE DFM-09. Available online: http://www.pecindia.com/upper-air-sounding-system.html (accessed on 3 November 2019).
- Arya, S.P.S. Parameterizing the Height of the Stable Atmospheric Boundary Layer. J. Appl. Meteorol. 1981, 20, 1192–1202. [Google Scholar] [CrossRef]
- Holzworth, G.C. Estimates of mean maximum mixing depths in the contiguous United States. Mon. Weather Rev. 1964, 92, 235–242. [Google Scholar] [CrossRef]
- Holzworth, G.C. Mixing Heights, Wind Speeds, and Potential for Urban Air Pollution throughout the Contiguous United States; Research Triangle Park, North Carolina: Environmental Protection Agengy, Office of Air Programs: Washington, DC, USA, 1972. [Google Scholar]
- Stull, R.B. An Introduction to Boundary Layer Meteorology.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988; ISBN 9789027727695. [Google Scholar]
- Sorbjan, Z. Structure of the Atmospheric Boundary Layer; Prentice Hall: Upper Saddle River, NJ, USA, 1989; ISBN 9780138535575. [Google Scholar]
- Garrat, J.R. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1994; ISBN 0-521-38052-9. [Google Scholar]
- Ao, C.O.; Chan, T.K.; Iijima, B.A.; Li, J.L.; Mannucci, A.J.; Teixeira, J.; Tian, B.; Waliser, D.E. Planetary boundary layer information from GPS radio occultation measurements. In ECMWF GRAS SAG Workshop on Applications of GPSRO Measurements; ECMWF: Shinfield Park, Reading, 2008. [Google Scholar]
- Salcido, A.; Sozzi, R.; Castro, T. Least squares variational approach to the convective mixing height estimation problem. Environ. Model. Softw. 2003, 18, 951–957. [Google Scholar] [CrossRef]
- Seidel, D.J.; Ao, C.O.; Li, K. Estimating climatological planetary boundary layer heights from radiosonde observations: Comparison of methods and uncertainty analysis. J. Geophys. Res. 2010, 115, D16113. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Routledge, Ed.; Halsted Press: New York, NY, USA, 1988; ISBN 978-0415043199. [Google Scholar]
- Seibert, P.; Beyrich, F.; Gryning, S.E.; Joffre, S.; Rasmussen, A.; Tercier, P. Mixing layer depth determination for dispersion modelling. In COST Action 710-Final Report: Harmonisation of the Pre-Processing of Meteorological Data for Atmospheric Dispersion Models; Fisher, B.E.A., Erbrink, J.J., Finardi, S., Jeannet, P., Joffre, S., Morselli, M.G., Pechinger, U., Seibert, P., Thomson, D.J., Eds.; European Comission: Brussels, Belgium, 1998; ISBN 92- 828-3302-X. [Google Scholar]
- Holtslag, A.A.M.; Nieuwstadt, F.T.M. Scaling the atmospheric boundary layer. Boundary-Layer Meteorol. 1986, 36, 201–209. [Google Scholar] [CrossRef]
- Garratt, J.R.; Brost, R.A. Radiative Cooling Effects within and above the Nocturnal Boundary Layer. J. Atmos. Sci. 1981, 38, 2730–2746. [Google Scholar] [CrossRef]
- Newsom, R.K.; Banta, R.M. Shear-Flow Instability in the Stable Nocturnal Boundary Layer as Observed by Doppler Lidar during CASES-99. J. Atmos. Sci. 2003, 60, 16–33. [Google Scholar] [CrossRef]
- Zilitinkevich, S.S.; Esau, I.N. The effect of baroclinicity on the equilibrium depth of neutral and stable planetary boundary layers. Q. J. R. Meteorol. Soc. 2003, 129, 3339–3356. [Google Scholar] [CrossRef]
- Banta, R.M. Stable-boundary-layer regimes from the perspective of the low-level jet. Acta Geophys. 2008, 56, 58–87. [Google Scholar] [CrossRef]
- Vickers, D.; Mahrt, L. Evaluating Formulations of Stable Boundary Layer Height. J. Appl. Meteorol. 2004, 43, 1736–1749. [Google Scholar] [CrossRef]
- Beyrich, F. Sodar observations of the stable boundary layer height in relation to the nocturnal low-level jet. Meteorol. Z. 1994, 3, 29–34. [Google Scholar] [CrossRef]
- Zilitinkevich, S.S. On the determination of the height of the Ekman boundary layer. Boundary-Layer Meteorol. 1972, 3, 141–145. [Google Scholar] [CrossRef]
- Benkley, C.W.; Schulman, L.L. Estimating Hourly Mixing Depths from Historical Meteorological Data. J. Appl. Meteorol. 1979, 18, 772–780. [Google Scholar] [CrossRef]
- Venkatram, A. Estimating the Monin-Obukhov length in the stable boundary layer for dispersion calculations. Boundary-Layer Meteorol. 1980, 19, 481–485. [Google Scholar] [CrossRef]
- Nieuwstadt, F.T.M. The steady-state height and resistance laws of the nocturnal boundary layer: Theory compared with cabauw observations. Boundary-Layer Meteorol. 1981, 20, 3–17. [Google Scholar] [CrossRef]
- Mahrt, L.; Andre, J.C.; Heald, R.C. On the Depth of the Nocturnal Boundary Layer. J. Appl. Meteorol. 1982, 21, 90–92. [Google Scholar] [CrossRef]
- Nieuwstadt, F.T.M.; Tennekes, H. A Rate Equation for the Nocturnal Boundary-Layer Height. J. Atmos. Sci. 1981, 38, 1418–1428. [Google Scholar] [CrossRef]
- Nieuwstadt, F.T.M. Some aspects of the turbulent stable boundary layer. Boundary-Layer Meteorol. 1984, 30, 31–55. [Google Scholar] [CrossRef]
- Derbyshire, S.H. Nieuwstadt’s stable boundary layer revisited. Q. J. R. Meteorol. Soc. 1990, 116, 127–158. [Google Scholar] [CrossRef]
- Lena, F.; Desiato, F. Intercomparison of nocturnal mixing height estimate methods for urban air pollution modelling. Atmos. Environ. 1999, 33, 2385–2393. [Google Scholar] [CrossRef]
- Businger, J.A.; Arya, S.P.S. Height of the Mixed Layer in the Stably Stratified Planetary Boundary Layer. Adv. Geophys. 1975, 18, 73–92. [Google Scholar]
- Wyngaard, J.C. Progress in research on boundary layers and atmospheric turbulences. Rev. Geophys. 1975, 13, 716–720. [Google Scholar] [CrossRef]
- Brost, R.A.; Wyngaard, J.C. A Model Study of the Stably Stratified Planetary Boundary Layer. J. Atmos. Sci. 1978, 35, 1427–1440. [Google Scholar] [CrossRef]
- Rao, K.S.; Snodgrass, H.F. Some parameterizations of the nocturnal boundary layer. Boundary-Layer Meteorol. 1979, 17, 15–28. [Google Scholar] [CrossRef]
- US Environmental Protection Agency. User’s Guide for the AERMOD Meteorological Preprocessor (AERMET): EPA-454/B-19-028; United States Environmental Protection Agency, Air Quality Assessment Division: Research Triangle Park, NC, USA, 2019. [Google Scholar]
- US Environmental Protection Agency. A user’s guide for the CALMET meteorological model; EPA-454/B-95-002; United States Environmental Protection Agency, Office oa Air Quality Planning and Standards: Research Tringle Park, North Carolina, USA, 1995.
- Sozzi, R. (Agenzia Regionale Protezione Ambiente Lazio, Lazio, Italy). Personal communication, 2000.
- Bradley, R.S.; Keimig, F.T.; Diaz, H.F. Recent changes in the North American Arctic boundary layer in winter. J. Geophys. Res. Atmos. 1993, 98, 8851–8858. [Google Scholar] [CrossRef]
- Yi, C.; Davis, K.J.; Berger, B.W.; Bakwin, P.S. Long-Term Observations of the Dynamics of the Continental Planetary Boundary Layer. J. Atmos. Sci. 2001, 58, 1288–1299. [Google Scholar] [CrossRef]
- Sathe, A.; Gryning, S.-E.; Peña, A. Comparison of the atmospheric stability and wind profiles at two wind farm sites over a long marine fetch in the North Sea. Wind Energy 2011, 14, 767–780. [Google Scholar] [CrossRef]
- Fields, G.P.; Houdashelt, C.L.; Carlson, P. State Implementation Plan for PM-10 in the Imperial Valley. Pechan Report No. 93.04.006/449; Pechan and Associates, Inc.: Rancho Cordoba, CA, USA, 1993. [Google Scholar]
- INE-SEMARNAT. Programa para Mejorar la Calidad del Aire en Mexicali 2000–2005; INE-SEMARNAT: Mexicali, Baja California, Mexico, 1999. [Google Scholar]
- Bei, N.; Li, G.; Zavala, M.; Barrera, H.; Torres, R.; Grutter, M.; Gutiérrez, W.; García, M.; Ruiz-Suarez, L.G.; Ortinez, A.; et al. Meteorological overview and plume transport patterns during Cal-Mex 2010. Atmos. Environ. 2013, 70, 477–489. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).