Abstract
Observations from radiosondes or from vertically pointing remote sensing profilers are often used to estimate the vertical flux of momentum due to gravity waves. For planar, monochromatic waves, these vertically integrated fluxes are equal to the phase averaged flux and equivalent to the horizontal averaging used to deduce momentum flux from aircraft data or in numerical models. Using a simple analytical solution for two-dimensional hydrostatic gravity waves over an isolated ridge, it is shown that this equivalence does not hold for mountain waves. For a vertical profile, the vertically integrated flux estimate is proportional to the horizontally integrated flux and decays with increasing distance of the profile location from the mountain. For tilted profiles, such as those obtained from radiosonde ascents, there is a further sampling error that increases as the trajectory extends beyond the localised wave field. The same sampling issues are seen when the effects of the Coriolis force on the gravity waves are taken into account. The conclusion of this work is that caution must be taken when using radiosondes or other vertical profiles to deduce mountain wave momentum fluxes.
1. Introduction
Atmospheric gravity waves play a key role in the atmosphere in transporting energy and momentum. The drag exerted by gravity waves acts as an important brake on atmospheric circulations, and failure to account for this drag properly in global weather and climate models can lead to significant biases. Often however, these waves are not explicitly resolved, either due to model resolution or because the model numerical scheme acts to damp the wave motion (e.g., [1]). As a result, gravity wave drag has to be parametrised in weather and climate models. Parametrisations for orographically generated gravity wave (mountain wave) drag have been widely used since the 1980s [2,3,4], and many models also include parametrisations for non-orographic gravity wave drag [5,6]. As model resolutions increase, there is also a need for “scale aware” schemes that can smoothly deal with wave fields where the large scale waves are resolved, but shorter wavelength waves are not [7]. The need to understand and quantify gravity wave drag better has led to a number of international field campaigns in recent years including Concordiasi [8], DEEPWAVE [9], GW-LCYCLE [10] and SGWEX [11], as well as new developments in satellite and remote sensing retrievals of gravity wave characteristics (e.g., [12]).
Validation and tuning of gravity wave drag parametrisation schemes ideally need observations of gravity wave momentum fluxes, although often, the parametrisations are tuned to climatology [13]. The work in [13] gave a review of the different methods and platforms used to measure the momentum flux. Analytically, the two components of the vertical flux of horizontal momentum are defined as:
where is the density of air and are the three components of the wave induced velocity perturbations. Some methods use velocity directly, while others instead use the gravity wave polarization relationship and temperature fluctuations, , to derive and sometimes also [14]. Radiosondes can measure both velocity and temperature perturbations directly; however, other remote sensing techniques often just measure temperature perturbations. The work in [15] showed that the different ways of calculating the momentum flux are sensitive to different frequencies of gravity waves. One feature of the method of [14] is that it uses the rotation of wind vectors with height due to the Coriolis force to estimate the wave frequency, and so, it only works for inertia gravity waves, i.e., for long enough horizontal wavelength (or sufficiently low frequency) waves that the Coriolis force becomes important. A similar method was used for retrieving gravity wave momentum fluxes from satellite observations of temperature [16].
For quasi-2D wave fields (e.g., generated by flow over a mountain ridge), Equation (1) can be approximated to a reasonable degree by one or several horizontal profiles measured from an aircraft [17] or quasi-Lagrangian balloon [18]. In 3D wave fields, there will be a sampling error due to the spatial variability (see, e.g., [17,19]). Due to the requirement for expensive aerial platforms, such observations are rare, typically only taken during field campaigns. As a result, use is often made of ground based (quasi-)vertical profiles from radiosondes [15,20,21,22] or remote sensing techniques such as radio occultation [23] to determine wave characteristics. The work in [24] compared observations of gravity wave momentum flux from a variety of methods, including radiosondes, with wave flux in several climate models. Like many other studies, they discussed a number of limitations of the observations, including the different wavelengths/frequencies observed by different techniques, but not the impact of sampling errors. The work in [25] discussed some of the challenges in interpreting LiDAR observations of gravity wave wave packets due to their localisation in space and time, but did not explicitly consider the retrieval of momentum fluxes.
This paper aims to assess the potential impact of the sampling error from using radiosondes or other vertical profiles to determine momentum flux. For simplicity, profiles are taken from analytical gravity wave solutions where the true momentum flux is known. Section 2 briefly presents the results for a simple two-dimensional planar monochromatic wave field. In Section 3, the case of an isolated source of mountain waves is examined using the solution of [26] for two-dimensional hydrostatic flow over a Witch of Agnesi mountain. This is extended to include the impact of the Coriolis force in Section 4. Section 5 discusses the results and the impact this may have on the observational measurement of gravity wave momentum flux in the real atmosphere. Although the focus of this paper is on direct calculation of momentum fluxes from the perturbations in the velocity field, the same sampling errors occur for retrievals that use the polarization equations where the velocity perturbations are assumed proportional to the temperature fluctuations, .
2. Sampling a Planar Monochromatic Wave Field
For a two-dimensional stationary planar monochromatic wave field:
where k and m are the horizontal and vertical wavenumbers, respectively [27]. In general,
where U is the horizontal wind, N is the Brunt–Väisälä frequency, and f is the Coriolis parameter. In the large Rossby number limit () where Coriolis effects are negligible, this reduces to . The wave momentum flux estimated by sampling along a profile at position x between heights and is:
where is the depth averaged flux. We now substitute in and and consider the case where the profile is obtained with a radiosonde with constant ascent rate, W, which drifts with the background wind, so that . Integrating then gives:
where is the correct vertical momentum flux obtained by averaging over a whole number of wavelengths in the horizontal and . For a truly vertical profile, . The second term in the bracketed expression in (6) is the relative error due to sampling the flux over a non-integer number of wavelengths. This term is oscillatory, but the amplitude decreases as the number of wavelengths sampled over increases, i.e., increases; so, the error is largest for sampling depths of less than around one third of a wavelength along the path. Note that for a monochromatic planar wave, this result is true whether or not the effects of the Coriolis force are included, although the value of m will be different in the two cases.
3. Isolated Mountain Waves without Coriolis Force
Here, we examine how the momentum flux obtained by sampling in the vertical, or along a slanted trajectory such as that of a radiosonde, relates to a flux sampled in the horizontal, for example along an aircraft leg or in a numerical model simulation. For simplicity, we considered the Queney solution [26] for an idealised two-dimensional hydrostatic mountain wave without the inclusion of the Coriolis force. Further, the effects of changing density with height were ignored, and both background wind speed and Brunt–Väisälä frequency were assumed constant. Strictly speaking, the radiosonde retrieval techniques assumed inertia gravity waves in order to retrieve vertical velocity fluctuations from temperature fluctuations. The solutions including the Coriolis force were more complicated, however, and did not admit a simple analytical solution, so we will first illustrate the importance of sampling in the non-rotating case, before considering the impact of the Coriolis force in the following section.
The Queney solution [26] for hydrostatic flow over a Witch of Agnesi mountain is:
where and are the horizontal and vertical velocity perturbations, non-dimensionalized on the background wind speed U, and are non-dimensionalized by the horizontal length scale of the hill, a, is the terrain height, H is the maximum mountain height (both non-dimensionalized by a), and is the inverse Froude number based on mountain width with background stability N. Both U and N were assumed independent of height. Note the non-dimensional vertical wavelength of all waves was , irrespective of horizontal wavenumber, since the hydrostatic assumption () was made.
An isolated mountain wave field such as that given by (7)–(9) consists of multiple horizontal wavelengths, and there is no single wavelength over which to measure a (reference) horizontally averaged flux. The relevant length scale is instead the mountain length scale, a. We first considered how the measured total flux on a horizontal leg converged as a function of the integral length. The total flux is defined as:
where is the non-dimensional integral length and is relative to the position of the mountain summit. Substituting for and and evaluating the integral give:
where is the total non-dimensional flux, integrating to infinity. The first term in brackets tends to one for large , and the second term tends to zero; so, for large , the total flux is recovered as expected. Taking gave a maximum error of less than 2.5% in the total flux across a range of cross-section heights, as shown in Figure 1. Aircraft horizontal flight legs should therefore ideally sample from at least upstream of the summit to downstream in order to sample the momentum flux accurately from an isolated mountain wave field.
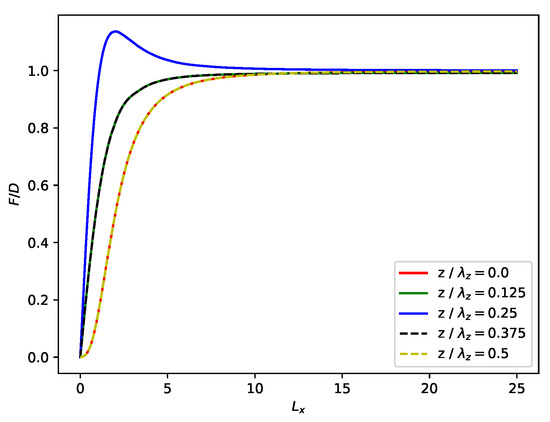
Figure 1.
Relative total momentum flux as a function of integral length at different heights. Note: periodicity means the and lines correspond exactly to the and lines, respectively.
To compare with the vertically integrated mean flux, we need to average the total flux D over some horizontal length scale. The obvious length scale is the mountain half width, which is unity in non-dimensional form, and so, we define the horizontally integrated mean flux .
Virtual profiles are sampled from the analytic wave solution for different values of (0.1, 0.2, 0.5, ∞). Note that (i.e., an infinitely fast ascent rate) equates to a vertical profile. Figure 2 shows the trajectories superimposed on a contour plot of vertical velocity perturbations for the and cases. For the hydrostatic wave solution of [26], the waves are stacked vertically above the mountain, and so, a vertical profile will continually sample the wavefield, while a sounding with a finite ascent rate will drift out of the wavefield. This problem is worse for smaller values of A as the radiosonde drifts out of the main wave field sooner.
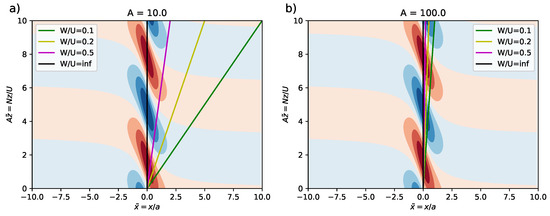
Figure 2.
Vertical velocity from the Queney mountain wave solution for (a) and (b) . Plotted on top are the virtual radiosonde trajectories for non-dimensional ascent rates, , and ∞ (a vertical profile).
For each profile, the integrated mean flux in this case is:
where s is the distance along the trajectory. For a vertical profile, this integral can be evaluated analytically and divided by the total horizontally averaged flux, D, to give:
assuming goes from zero to . The second and third terms in the bracket decay for large , i.e., sampling over several vertical wavelengths, in which case, asymptotically, the non-dimensional vertically integrated mean momentum flux is related to the non-dimensional horizontally averaged mean flux by:
For tilted profiles, the vertically integrated mean momentum flux cannot be evaluated analytically, and so, numerical solutions (calculated using the fft routines in the Python Numpy library) were used.
Figure 3 shows the flux, normalised by the horizontal mean flux , as a function of the height to which the integral was calculated, for three different launch locations (), for different ascent rates (), and for different non-dimensional mountain widths (). The differences between different ascent rates were (as might be expected) more pronounced for smaller values of A. As in the planar wave case, the fluxes for a vertical profile appeared to converge towards a constant mean value, with some sinusoidal error due to sampling an incomplete number of wavelengths. Unlike the planar wave case, this value depended on the sample location and was not equal to the horizontal mean flux . For tilted profiles (like a radiosonde trajectory), the mean flux did not converge, but decayed with increased trajectory length as the trajectory moved out of the peak localised wave field. Note that in all but the wide () mountain case where the radiosonde was launched from the summit, the flux estimates obtained from vertical profiles significantly underestimated the true horizontally averaged value. These flux profiles were also not independent of height, and this could be incorrectly interpreted as implying wave dissipation and transfer of momentum to the mean flow.
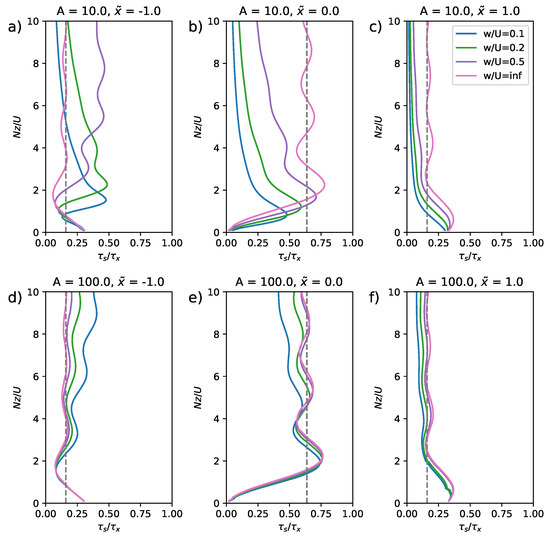
Figure 3.
The along-trajectory integrated mean momentum flux, , normalized by the horizontal total flux, , as a function of the normalised height, , for the Queney mountain wave solution. Subplots are for launch locations (a,d) (b,e), (c,f), and for (a–c) and (d–f). In each subplot, results are shown for a range of non-dimensional ascent rates, W/U, of 0.1, 0.2, 0.5, and ∞ (a vertical profile). The dotted vertical line shows the asymptotic correction factor for a vertical profile in each case.
4. Isolated Mountain Waves with Coriolis Force
In many applications, the Rossby number is sufficiently small that the Coriolis force cannot be neglected completely. The wave equation for an isolated Witch of Agnesi hill, including the effects of the Coriolis force, does not permit such simple analytical solutions as the case with presented in Section 3, but the solutions can be evaluated numerically using a fast Fourier transform to calculate the contribution of different wavenumbers in the topography to the wave spectrum. Figure 4 is the equivalent of Figure 2 including the effects of the Coriolis force. For the smaller () width hill with , the solutions with and without the Coriolis force were very similar (Figure 4a). With , the effect of the Coriolis force was to tilt the longer wavelength components of the wave downstream. In this case, the tilt was such that the different radiosonde trajectories all sampled the wave better, rather than passing out of the wavefield as in the case without Coriolis force. As a result the along-trajectory integrated fluxes in Figure 5 showed much less dependence on the balloon ascent rate than for the case without Coriolis force, and also less dependence on whether a whole number of vertical wavelengths was sampled. On the other hand, as the wave field was tilted, the vertically integrated fluxes did not converge to a constant value, even for a truly vertical profile. Any estimate of the flux would therefore always be sensitive to the height over which the integral was calculated. Again, the estimated fluxes were always much smaller than the horizontally integrated flux. Unlike the limiting case without Coriolis force (the dashed line), the downwind shift in the wave field meant that the vertically integrated fluxes (along vertical profiles) were not symmetrical about the summit of the mountain. Upwind and near the summit, they were reduced compared to the limiting case, while downwind, they may be larger.
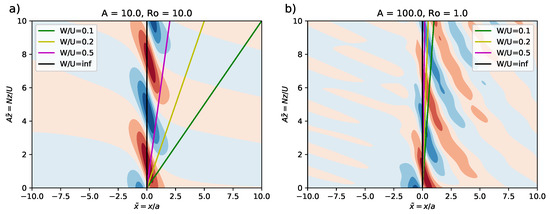
Figure 4.
Vertical velocity for the mountain wave solution for the (a) , and (b) , cases. Plotted on top are the virtual radiosonde trajectories for non-dimensional ascent rates, and ∞ (a vertical profile).
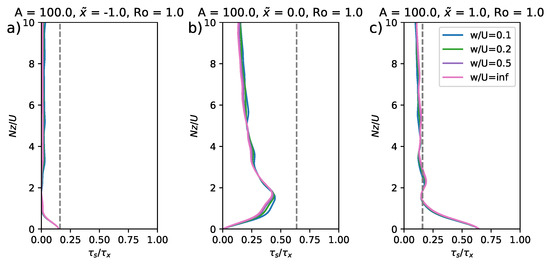
Figure 5.
As in Figure 3, but for the case with , . Results are plotted at (a) , (b) , and (c) . The dotted vertical line shows the asymptotic correction factor for a vertical profile in the case without Coriolis force.
5. Discussion and Conclusions
These simple calculations highlighted the impact of sampling on estimated mountain wave momentum fluxes from radiosondes or other systems for vertical profiling. For monochromatic, planar waves, the horizontally and vertically integrated momentum fluxes were equivalent, even for tilted profiles (such as a radiosonde trajectory), simply because these sampled the full phase of the waves. Errors were solely due to sampling a non-integer number of wavelengths, and this decreased with an increase in the path length.
In contrast, for isolated mountain waves in which rotation was unimportant, there were a number of complicating factors that made it difficult to obtain accurate estimates of the momentum flux from profile sampling:
- For the Queney solution, the vertically integrated mean flux (for ) at the summit of the orography was not equal to the horizontally integrated mean momentum flux, but was related by a factor of .
- Vertically averaged fluxes, (for ), were strongly dependent on the horizontal location of the profile relative to the summit of the orography, decaying like in dimensional form.
- Integrating along a tilted path (e.g., a radiosonde trajectory) led to an additional sampling error as the trajectory would move out of the localised wave field. This effect was worse for smaller values of A, i.e., shorter horizontal wavelengths/narrower topography and higher wind speeds.
These issues may seem obvious, yet they are frequently overlooked when interpreting momentum fluxes inferred from measurements. Using a simple analytical solution, we were able to quantify the impacts. For truly vertically profiles from, e.g., remote sensing instruments, then the instrument should be located as close to the summit of the topography as possible. Assuming the relationship for the Queney solution, the measured vertically integrated momentum flux could then, in theory, be corrected to give the total horizontal momentum flux assuming the width of topography, a, is known. For instruments not sited at the summit, an additional correction factor would be required to account for the decay of the wave field with distance from the summit.
For tilted profiles such as radiosonde trajectories, even this did not work, and so, it was hard to relate the measured along-path integral momentum flux to the horizontal momentum flux. For large values of A (wide topography, long horizontal wavelengths) and for faster ascent rates, the impact was less, and so, the profile may be assumed quasi-vertical, as was the case for shown above. For smaller values of A, this was not a good assumption.
The effect of the Coriolis force mitigated some of these issues. In particular, it led to less sensitivity of the along-trajectory integrated flux to the balloon ascent speed, although the fluxes no longer converged. The values were however still strongly dependent on the balloon launch location relative to the hill and were less than the horizontally averaged momentum flux.
These issues all acted to reduce the measured vertically integrated momentum flux compared to the horizontally averaged flux, and so, there was a likelihood that gravity wave momentum fluxes would be underestimated by radiosonde measurements as a result of sampling errors. There was some evidence of this in the literature. The work in [21] showed that radiosonde derived momentum fluxes were a factor of 5–6 smaller than previous satellite derived momentum fluxes over the island of South Georgia. The radiosonde launch site on South Georgia’s east coast was located approximately from the summit, suggesting that estimates of momentum flux obtained from radiosonde measurements of mountain waves could actually be a factor 40 times smaller than those that would have been obtained from horizontal sampling (neglecting Coriolis effects). One would expect the satellite retrieved fluxes to be smaller than the true flux due to their relative coarse resolution (see, e.g., [11]), and so, the factor of 5–6 noted by [21] was likely an underestimate of the true error in the radiosonde derived fluxes.
The assumptions of constant wind speed and Brunt–Väisälä frequency in this study were of course somewhat limiting, as was the use of very simple idealised 2D mountain profiles. Changes in the wind speed and Brunt–Väisälä frequency would lead to the wave ray path bending with height. This could further exacerbate the sampling issues discussed here. Further, we did not consider the impact of transient wave packets in time, which as pointed out by [25], may also be important when interpreting observations of gravity waves. Nonetheless, we would expect that the gravity wave fields generated by real isolated mountains would share at least qualitatively the features of the idealised wave fields considered here, and so, these same sampling issues would be relevant to more complex real-world situations.
Most satellite retrievals of gravity wave momentum flux (e.g., [12,16]) use horizontal fluctuations in temperature at a particular height level and so do not suffer from the sampling issues discussed here. They do however have their own limitations, for example not being able to resolve the shorter wavelength parts of the wave spectrum, which carry much of the momentum, as demonstrated by [11].
Even if relating the vertically integrated gravity wave momentum fluxes from radiosondes to a horizontally averaged flux from an aircraft or model is difficult, these data sources are still immensely useful. They provide the only routine in situ measurements of gravity wave activity globally in the troposphere and so are key for identifying spatial and temporal variations in wave activity. They are also essential for validating high resolution models. Such models give access to the whole 3D wave field and its temporal evolution in a way that is not possible with any observational techniques, and so, they are increasingly being used to develop, tune, and test gravity wave parametrisation schemes (e.g., [28]).
Author Contributions
The authors both contributed equally to all aspects of the research and the writing of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the U.K. Natural Environment Research Council Grant Number NE/K012584/1.
Acknowledgments
The authors would like to thank Corwin Wright for useful discussion and suggestions.
Conflicts of Interest
The authors declare no conflict of interests.
References
- Shutts, G.J.; Vosper, S.B. Stratospheric gravity waves revealed in NWP model forecasts. Quart. J. R. Meteorol. Soc. 2011, 137, 303–317. [Google Scholar] [CrossRef]
- Lott, F.; Miller, M.J. A new subgrid-scale orographic drag parametrization: Its formulation amd testing. Quart. J. R. Meteorol. Soc. 1997, 123, 101–127. [Google Scholar] [CrossRef]
- Scinocca, J.F.; McFarlane, N.A. The parametrization of drag induced by stratified flow over anisotropic orography. Quart. J. R. Meteorol. Soc. 2000, 126, 2353–2393. [Google Scholar] [CrossRef]
- Webster, S.; Brown, A.R.; Cameron, D.R.; Jones, C.P. Improvements to the representation of orography in the Met Office Unified Model. Quart. J. R. Meteorol. Soc. 2003, 129, 1989–2010. [Google Scholar] [CrossRef]
- Lott, F.; Guez, L.; Maury, P. A stochastic parametrization of non-orographic gravity waves: Formalism and impact on the equatorial stratosphere. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Eckermann, S.D. Explicitly stochastic parameterization of nonorographic gravity wave drag. J. Atmos. Sci. 2011, 123, 1749–1765. [Google Scholar] [CrossRef]
- Vosper, S.B. Mountain wave and wakes generated by South Georgia: Implications for drag parametrization. Quart. J. R. Meteorol. Soc. 2015, 141, 2813–2827. [Google Scholar] [CrossRef]
- Walterscheld, R.L.; Gelinas, L.J.; Mechoso, C.R.; Schubert, G. Spectral distribution of gravity wave momentum fluxes over the Antarctic Peninsula from Concordiasi superpressure balloon data. J. Geophys. Res. Atmos. 2016, 121, 7509–7527. [Google Scholar] [CrossRef]
- Fritts, D.C.; Smith, R.B.; Taylor, M.J.; Doyle, J.D.; Eckermann, S.D.; Dörnbrack, A.; Rapp, M.; Williams, B.P.; Pautet, P.D.; Bossert, K.; et al. The deep propagating gravity wave experiment (DEEPWAVE): An airborne and ground based exploration of gravity wave propagation and effects from their sources through the lower and middle atmosphere. Bull. Am. Met. Soc. 2016, 97, 425–453. [Google Scholar] [CrossRef]
- Wagner, J.; Dörnbrack, A.; Rapp, M.; Gisinger, S.; Ehard, B.; Bramberger, M.; Witschas, B.; Chouza, F.; Rahm, S.; Mallaum, C.; et al. Observed versus simulated mountain waves over Scandinavia—Improvement of vertical winds, energy and momentum fluxes by enhanced model resolution? Atmos. Chem. Phys. 2017, 17, 4031–4052. [Google Scholar] [CrossRef]
- Jackson, D.R.; Gadian, A.; Hindley, N.P.; Hoffmann, L.; Hughes, J.; King, J.; Moffat-Griffin, T.; Moss, A.C.; Ross, A.N.; Vosper, S.B.; et al. The South Georgia wave experiment SG-WEX—A means for improving analysis of gravity waves and low-level wind impacts generated from mountainous islands. Bull. Am. Met. Soc. 2018, 99, 1027–1040. [Google Scholar] [CrossRef]
- Wright, C.; Hindley, N.P.; Hoffmann, L.; Alexander, M.J.; Mitchell, N.J. Exploring gravity wave characteristics in 3-D using a novel S-transform technique: AIRS/Aqua measurements over the Southern Andes and Drake Passage. Atmos. Chem. Phys. 2017, 17, 8553–8575. [Google Scholar] [CrossRef]
- Alexander, M.J.; Geller, M.; McLandress, C.; Polavarapu, S.; Preusse, P.; Sassi, F.; Sato, K.; Eckermann, S.; Ern, M.; Hertzog, A.; et al. Recent developments in gravity wave effects in climate models and the global contribution of gravity wave momentum flux from observations and models. Quart. J. R. Meteorol. Soc. 2010, 136, 1103–1124. [Google Scholar] [CrossRef]
- Vincent, R.A.; Allen, S.J.; Eckermann, S.D. Gravity Wave Parameters in the Lower Atmosphere. In Gravity Wave Processes: Their Parameteriztion in Global Climate Models; Hamilton, K., Ed.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 7–25. [Google Scholar] [CrossRef]
- Geller, M.A.; Gong, J. Gravity wave kinetic, potential, and vertical fluctuation energies as indicators of different frequency gravity waves. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Ern, M.; Preusse, P.; Alexander, M.J.; Warner, C.D. Absolute values of gravity wave momentum flux derived from satellite data. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Smith, R.B.; Nugent, A.D.; Kruse, C.G.; Fritts, D.C.; Doyle, J.D.; Eckermann, S.D.; Taylor, M.J.; Dörnbrack, A.; Uddstrom, M.; Cooper, W.; et al. Stratospheric gravity wave fluxes and scales during DEEPWAVE. J. Atmos. Sci. 2016, 73, 2851–2869. [Google Scholar] [CrossRef]
- Hertzog, A.; Boccara, G.; Vincent, R.A.; Vial, F.; Cocquerez, P. Estimation of gravity wave momentum flux and phase speeds from quasi-lagrangian stratospheric balloon flights. Part II: Results from the Vorcore campaign in Antarctica. J. Atmos. Sci. 2008, 65, 3056–3070. [Google Scholar] [CrossRef]
- Vosper, S.B.; Mobbs, S.D. Momentum fluxes due to three-dimensional gravity waves: Implications for measurements and numerical modelling. Quart. J. R. Meteorol. Soc. 1998, 124, 2755–2769. [Google Scholar] [CrossRef]
- Wang, L.; Geller, M.A.; Alexander, M.J. Spatial and temporal variations of gravity wave parameters. Part I: Intrinsic frequency, wavelength, and vertical propagation direction. J. Atmos. Sci. 2005, 62, 125–142. [Google Scholar] [CrossRef]
- Moffat Griffin, T.; Wright, C.J.; Moss, A.C.; King, J.C.; Colwell, S.R.; Hughes, J.K.; Mitchell, N.J. The South Georgia wave experiment (SG-WEX): Radiosonde observations of gravity waves in the lower stratosphere. Part I: Energy density, momentum flux and wave propagation direction. Quart. J. R. Meteorol. Soc. 2017, 143, 3279–3290. [Google Scholar] [CrossRef]
- Yoo, J.H.; Choi, T.; Chun, H.Y.; Kim, Y.H.; Song, I.S.; Song, B.G. Inertia-gravity waves revealed in radiosonde data at Jang Bogo station, Antarctica (74∘26′ S, 164∘13′ E). Part I: Characteristics, energy, and momentum flux. J. Geophys. Res. Atmos. 2018, 123, 13305–13331. [Google Scholar] [CrossRef]
- Gubenko, V.N.; Pavelyev, A.G.; Salimzyanov, R.R.; Pavelyev, A.A. Reconstruction of internal gravity wave parameters from radio occultation retrievals of vertical temperature profiles in the Earth’s atmosphere. Atmos. Meas. Tech. 2011, 4, 2153–2162. [Google Scholar] [CrossRef]
- Geller, M.A.; Alexander, M.J.; Love, P.T.; Bacmeister, J.; Ern, M.; Hertzog, A.; Manzini, E.; Preusse, P.; Sato, K.; Scaife, A.A.; et al. A comparison between gravity wave momentum fluxes in observations and climate models. J. Clim. 2013, 26, 6383–6405. [Google Scholar] [CrossRef]
- Dörnbrack, A.; Gisinger, S.; Kaifler, B. On the interpretation of gravity wave measurements by ground-based LiDAR. Atmosphere 2017, 8, 49. [Google Scholar] [CrossRef]
- Queney, P. The problem of airflow over mountains: A summary of theoretical studies. Bull. Am. Met. Soc. 1948, 29, 16–26. [Google Scholar] [CrossRef]
- Nappo, C.J. An Introduction to Atmospheric Gravity Waves, 2nd ed.; Elsevier: Oxford, UK, 2013; p. 359. [Google Scholar]
- Vosper, S.B.; van Niekerk, A.; Elvidge, A.; Sandu, I.; Beljaars, A. What can we learn about orographic drag parameterization from high-resolution models? A case study over the Rocky mountains. Quart. J. R. Meteorol. Soc. 2019. accepted. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).