A Fuzzy Credibility-Constrained Fuzzy Multi-Objective Programming Model for Optimizing Irrigation Strategies to Balance Citrus Yield and Quality Under Uncertainty
Abstract
1. Introduction
2. Methodology
- (1)
- Water volume significantly impacts not only crop yield but also quality, which necessitates the integration of water–yield and water–quality response relationships into the optimization of limited irrigation resources.
- (2)
- Farmers’ income is jointly influenced by yield and market prices determined by fruit quality and the supply–demand of markets. However, the intricate influence of yield and various quality metrics on income is ambiguous. The interrelationship of water, yield, and quality metrics makes it even more complicated. The allocation of irrigation water resources in districts should simultaneously account for the yield and the diverse quality indicators.
- (3)
- Irrigation water resource optimization is a complex system. The stochastic characteristics of rainfall and runoff, decision-makers’ forecasting tendencies towards available water (optimistic, moderate, pessimistic), and decision-making preferences (yield priority, quality priority) all influence decision-making schemes. Incorporating these factors into the allocation schemes of water resources in irrigation districts merits further research.
2.1. Rao Model for Simulating Water–Yield and Water–Quality Relationships
2.2. Interval-Valued Intuitionistic Fuzzy TOPSIS (IVIF-TOPSIS)
- (1)
- Create a decision-maker group which consists of M decision-makers (DMs);
- (2)
- Collect the importance judgment of each decision-maker towards different criteria (C), which are formulated by their knowledge and expertise;
- (3)
- Formulate the judgment matrix according to the correspondence of linguistic variables and interval-valued intuitionistic fuzzy numbers (Table 1). The judgment matrix can be expressed as follows:
| Linguistic Variables | Interval-Valued Intuitionistic Fuzzy Numbers |
|---|---|
| Very important (VI) | ([0.80, 0.90], [0.05, 0.10]) |
| Important (I) | ([0.65, 0.75], [0.10, 0.20]) |
| Medium (M) | ([0.45, 0.55], [0.35, 0.45]) |
| Unimportant (U) | ([0.25, 0.35], [0.55, 0.65]) |
| Very unimportant (VU) | ([0.00, 0.10], [0.80, 0.90]) |
- (4)
- Calculate average interval fuzzy number () of Mth decision-makers through the following equation [21]:
- (5)
- Calculate interval-valued intuitionistic fuzzy positive ( ) and negative ( ) ideal rating.
- (6)
- Calculate the distance between the aggregated fuzzy weight of each criterion and the best () or worst () values using Euclidean distance as follows [26]:
- (7)
- Generate the closeness coefficient (CC) of each criterion as follows:
- (8)
- Obtain the weight (wn) of each criterion as follows:
2.3. Fuzzy Credibility-Constrained Fuzzy Multi-Objective Programming Model
- (1)
- Formulate the FCC-FMOP model.
- (2)
- Transform the fuzzy credibility constraints as general linear constraints [29]. When the fuzzy numbers are triangular fuzzy numbers such as , , and , the fuzzy credibility constraints and can be converted as and , respectively. After determining the value of β, the FCC-FMOP model can be transformed into a typical FMOP model.
- (3)
- Collect the judgment about the importance of different objectives, and calculate the importance weight wn of each objective through IVIF-TOPSIS.
- (4)
- Establish the membership function of objectives as follows [30]:
- (5)
- Transform the FMOP model as the following single-objective model with the goal of maximizing satisfaction λn based on wn and the membership function of objectives [31]:
- (6)
- Code the above optimization model in software (such as MATLAB, GAMS, and LINGO) to generate the optimization results.
- (7)
- Change the credibility level β and solve the model under each credibility level.
- (8)
- Obtain the solution set of the FCC-FMOP model under different decision-making preferences of decision-makers.
2.4. Model Performance Evaluation Method
3. Case Study
3.1. Study Area
3.2. Model Formulation
3.2.1. Objectives
3.2.2. Constraints
3.3. Data Collection
4. Results Analysis and Discussion
4.1. The Importance Weights of Yield and Quality Indicators
4.2. Optimal Irrigation Strategies Balancing Yield and Quality
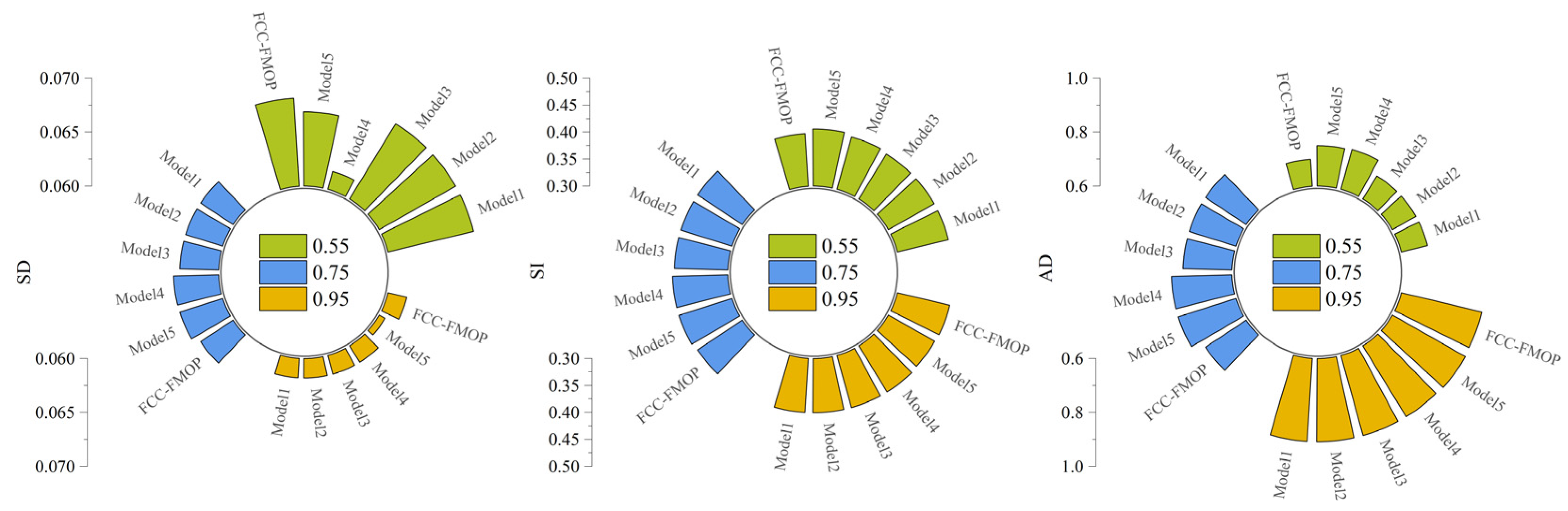
4.3. Performance Evaluation of the FCC-FMOP Model
4.4. Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ramírez-Pérez, L.J.; Morales-Díaz, A.B.; Benavides-Mendoza, A.; De-Alba-Romenus, K.; González-Morales, S.; Juárez-Maldonado, A. Dynamic modeling of cucumber crop growth and uptake of N, P and K under greenhouse conditions. Sci. Hortic. 2018, 234, 250–260. [Google Scholar] [CrossRef]
- Zhou, B.; Xu, Y.; Wu, J.; Dong, S.; Shi, Y. Changes in temperature and precipitation extreme indices over China: Analysis of a high-resolution grid dataset. Int. J. Climatol. 2016, 36, 1051–1066. [Google Scholar] [CrossRef]
- Velez, J.E.; Intrigliolo, D.S.; Castel, J.R. Scheduling deficit irrigation of citrus trees with maximum daily trunk shrinkage. Agric. Water Manag. 2007, 90, 197–204. [Google Scholar] [CrossRef]
- Chen, F.; Cui, N.; Jiang, S.; Wang, Z.; Li, H.; Lv, M.; Wang, Y.; Gong, D.; Zhao, L. Multi-objective deficit drip irrigation optimization of citrus yield, fruit quality and water use efficiency using NSGA-II in seasonal arid area of Southwest China. Agric. Water Manag. 2023, 287, 108440. [Google Scholar] [CrossRef]
- Shirgure, P. Research review on Irrigation scheduling and water requirement in citrus. Sci. J. Rev. 2013, 2, 113–121. [Google Scholar]
- Abbas, F.; Fares, A. Best Management Practices in Citrus Production. Tree For. Sci. Biotechnol. 2009, 3, 1–11. [Google Scholar]
- Liu, X.; Zhu, X.; Pan, Y.; Bai, J.; Li, S. Performance of different drought indices for agriculture drought in the North China Plain. J. Arid. Land. 2018, 10, 507–516. [Google Scholar] [CrossRef]
- Khedkar, D.D. Minimal volume irrigation scheduling for citrus cultivation in warud tehsil, maharashtra, india. Agric. Agric. Sci. Procedia 2015, 4, 365–371. [Google Scholar] [CrossRef]
- Zhong, Y.; Fei, L.; Li, Y.; Zeng, J.; Dai, Z. Response of fruit yield, fruit quality, and water use efficiency to water deficits for apple trees under surge-root irrigation in the Loess Plateau of China. Agric. Water Manag. 2019, 222, 221–230. [Google Scholar] [CrossRef]
- Silveira, L.K.; Pavão, G.C.; Dos Santos Dias, C.T.; Quaggio, J.A.; Pires, R.C.D.M. Deficit irrigation effect on fruit yield, quality and water use efficiency: A long-term study on Pêra-IAC sweet orange. Agric. Water Manag. 2020, 231, 106019. [Google Scholar] [CrossRef]
- Panigrahi, P.; Srivastava, A.K. Effective management of irrigation water in citrus orchards under a water scarce hot sub-humid region. Sci. Hortic. 2016, 210, 6–13. [Google Scholar] [CrossRef]
- Kuscu, H.; Turhan, A.; Demir, A.O. The response of processing tomato to deficit irrigation at various phenological stages in a sub-humid environment. Agric. Water Manag. 2014, 133, 92–103. [Google Scholar] [CrossRef]
- Obenland, D.; Campisi-Pinto, S.; Arpaia, M.L. Determinants of sensory acceptability in grapefruit. Sci. Hortic. 2018, 231, 151–157. [Google Scholar] [CrossRef]
- Pérez-Pastor, A.; Ruiz-Sánchez, M.C.; Domingo, R. Effects of timing and intensity of deficit irrigation on vegetative and fruit growth of apricot trees. Agric. Water Manag. 2014, 134, 110–118. [Google Scholar] [CrossRef]
- Romero, C.C.; Dukes, M.D.; Baigorria, G.A.; Cohen, R. Comparing theoretical irrigation requirement and actual irrigation for citrus in Florida. Agric. Water Manag. 2009, 96, 473–483. [Google Scholar] [CrossRef]
- Levy, Y. Citrus Irrigation; Institute Agronomique & Veterinaire Hasssan II: Rabat, Morocco, 1998. [Google Scholar]
- Zhang, F.; Guo, S.; Liu, X.; Wang, Y.; Engel, B.A.; Guo, P. Towards sustainable water management in an arid agricultural region: A multi-level multi-objective stochastic approach. Agric. Syst. 2020, 182, 102848. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, F.; Engel, B.A.; Wang, Y.; Guo, P.; Li, Y. A distributed robust optimization model based on water-food-energy nexus for irrigated agricultural sustainable development. J. Hydrol. 2022, 606, 127394. [Google Scholar] [CrossRef]
- Zhang, F.; Cui, N.; Guo, S.; Yue, Q.; Jiang, S.; Zhu, B.; Yu, X. Irrigation strategy optimization in irrigation districts with seasonal agricultural drought in southwest China: A copula-based stochastic multiobjective approach. Agric. Water Manag. 2023, 282, 108293. [Google Scholar] [CrossRef]
- Herman, J.D.; Quinn, J.D.; Steinschneider, S.; Giuliani, M.; Fletcher, S. Climate Adaptation as a Control Problem: Review and Perspectives on Dynamic Water Resources Planning Under Uncertainty. Water Resour. Res. 2020, 56, e24389. [Google Scholar] [CrossRef]
- Clark, M.P.; Vogel, R.M.; Lamontagne, J.R.; Mizukami, N.; Knoben, W.J.M.; Tang, G.; Gharari, S.; Freer, J.E.; Whitfield, P.H.; Shook, K.R.; et al. The Abuse of Popular Performance Metrics in Hydrologic Modeling. Water Resour. Res. 2021, 57, e2020WR029001. [Google Scholar] [CrossRef]
- Shi, R.; Wang, J.; Tong, L.; Du, T.; Shukla, M.K.; Jiang, X.; Li, D.; Qin, Y.; He, L.; Bai, X.; et al. Optimizing planting density and irrigation depth of hybrid maize seed production under limited water availability. Agric. Water Manag. 2022, 271, 107759. [Google Scholar] [CrossRef]
- Rao, N.H.; Sarma, P.B.S.; Chander, S. A simple dated water-production function for use in irrigated agriculture. Agric. Water Manag. 1988, 13, 25–32. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Set. Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Izadikhah, M. Group Decision Making Process for Supplier Selection with TOPSIS Method under Interval-Valued Intuitionistic Fuzzy Numbers. Adv. Fuzzy Syst. 2012, 2012, 407942. [Google Scholar] [CrossRef]
- Xiao, Z.; Wei, G. in Application interval-valued intuitionistic fuzzy set to select supplier. In Proceedings of the 2008 Fifth International Conference on Fuzzy Systems and Knowledge Discovery, Jinan, China, 18–20 October 2008; pp. 351–355. [Google Scholar]
- Zhang, X.; Guo, P.; Zhang, F.; Liu, X.; Yue, Q.; Wang, Y. Optimal irrigation water allocation in Hetao Irrigation District considering decision makers’ preference under uncertainties. Agric. Water Manag. 2021, 246, 106670. [Google Scholar] [CrossRef]
- Amid, A.; Ghodsypour, S.H.; O’Brien, C. A weighted max–min model for fuzzy multi-objective supplier selection in a supply chain. Int. J. Prod. Econ. 2011, 131, 139–145. [Google Scholar] [CrossRef]
- Zhang, F.; Cai, Y.; Tan, Q.; Wang, X. Spatial water footprint optimization of crop planting: A fuzzy multiobjective optimal approach based on MOD16 evapotranspiration products. Agric. Water Manag. 2021, 256, 107096. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–55. [Google Scholar] [CrossRef]
- Afzali, A.; Rafsanjani, M.K.; Saeid, A.B. A Fuzzy Multi-objective Linear Programming Model Based on Interval-valued Intuitionistic Fuzzy Sets for Supplier Selection. Int. J. Fuzzy Syst. 2016, 18, 864–874. [Google Scholar] [CrossRef]
- Chen, F.; Cui, N.; Jiang, S.; Li, H.; Wang, Y.; Gong, D.; Hu, X.; Zhao, L.; Liu, C.; Qiu, R. Effects of water deficit at different growth stages under drip irrigation on fruit quality of citrus in the humid areas of South China. Agric. Water Manag. 2022, 262, 107407. [Google Scholar] [CrossRef]







| Indices | Definition |
|---|---|
| i | Index of growth stage (i = 1, 2, 3, 4) |
| t | Index of irrigation period (t = 1, 2, …, 36) |
| max | Abbreviation for maximum |
| min | Abbreviation for minimum |
| Decision variables | |
| IWt | Water consumption of fruit trees during period t |
| IRRt | Irrigation water amount during period t |
| Parameters | |
| Empirical coefficient of single fruit weight, hue angle, fruit water content, and soluble sugar, respectively | |
| Available water for irrigation citrus (mm) | |
| Surplus available water (mm) | |
| Relative water deficit value of single fruit weight, hue angle, fruit water content, and soluble sugar during growth stage i, respectively | |
| Rao’s water deficit sensitivity index of single fruit weight, hue angle, fruit water content, and soluble sugar during growth stage i, respectively | |
| Maximum irrigation quota under deficit irrigation, which is a fuzzy number (mm) | |
| EPi and EPt | Effective precipitation during growth stage i and irrigation period t (mm) |
| ETcki | Evapotranspiration of control treatment during growth stage i (mm) |
| F1, …, F5 | Objective function of yield (kg), single fruit weight (g), hue angle, fruit water content (%), and soluble sugar (mg/mL), respectively |
| Minimum water demand during irrigation period t (mm) | |
| Yck, SFWck, HAck, FWCck, and SSck | Yield (kg), single fruit weight (g), hue angle, fruit water content (%), and soluble sugar (mg/mL) under control treatment, respectively. |
| β | Credibility level of fuzzy event |
| γi | Rao’s water deficit sensitivity index |
| η | Irrigation water use efficiency |
| Items | Parameters | Growth Stage of Citrus | Empirical Coefficient A0 | |||
|---|---|---|---|---|---|---|
| Stage I | Stage II | Stage III | Stage IV | |||
| Single fruit weight | Ci | −0.461 | 0.603 | 0.683 | 0.395 | 1.019 |
| Bi | 0.000 | 0.038 | 0.000 | 0.072 | ||
| Hue angle | Ci | 0.218 | 0.439 | 0.352 | 0.335 | 0.985 |
| Bi | 0.173 | 0.000 | 0.066 | 0.158 | ||
| Fruit water content | Ci | 0.012 | 0.238 | 0.186 | 0.018 | 1.005 |
| Bi | 0.000 | 0.154 | 0.003 | 0.000 | ||
| Soluble sugar | Ci | −0.227 | 0.643 | 0.508 | 1.651 | 1.099 |
| Bi | 0.263 | 0.124 | 0.000 | 0.233 | ||
| Yield | γi | 0.101 | 0.157 | 0.376 | 0.115 | - |
| Items | Fuzzy Numbers |
|---|---|
| I (mm) | (142.5, 172.5, 202.5) |
| Yield (kg) | (33,500, 34,000, 34,500) |
| Single fruit weight (g) | (170, 180, 190) |
| Hue angle | (64, 64.5, 65) |
| Fruit water content (%) | (74.5, 75, 75.5) |
| Soluble sugar (mg/mL) | (110, 120, 130) |
| Criteria | DM1 | DM2 | DM3 | DM4 | Aggregated Fuzzy Weight | d+ | d− | CCj | Wj | Rank |
|---|---|---|---|---|---|---|---|---|---|---|
| Yield | VI | VI | VI | VI | ([0.80, 0.90], [0.05, 0.10]) | 0.02 | 0.66 | 0.98 | 0.215 | 1 |
| Single fruit weight | I | VI | I | VI | ([0.74, 0.84], [0.08, 0.15]) | 0.03 | 0.61 | 0.95 | 0.209 | 2 |
| Hue angle | M | I | M | I | ([0.66, 0.77], [0.16, 0.25]) | 0.12 | 0.48 | 0.80 | 0.177 | 5 |
| Fruit water content | VI | I | M | VI | ([0.70, 0.82], [0.15, 0.23]) | 0.05 | 0.57 | 0.92 | 0.203 | 3 |
| Soluble sugar | VI | I | I | M | ([0.77, 0.87], [0.06, 0.13]) | 0.06 | 0.55 | 0.89 | 0.197 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Zhang, X.; Wu, Z.; Guo, S.; Wang, S. A Fuzzy Credibility-Constrained Fuzzy Multi-Objective Programming Model for Optimizing Irrigation Strategies to Balance Citrus Yield and Quality Under Uncertainty. Agronomy 2025, 15, 2739. https://doi.org/10.3390/agronomy15122739
Zhang F, Zhang X, Wu Z, Guo S, Wang S. A Fuzzy Credibility-Constrained Fuzzy Multi-Objective Programming Model for Optimizing Irrigation Strategies to Balance Citrus Yield and Quality Under Uncertainty. Agronomy. 2025; 15(12):2739. https://doi.org/10.3390/agronomy15122739
Chicago/Turabian StyleZhang, Fan, Xinyu Zhang, Zihan Wu, Shanshan Guo, and Sufen Wang. 2025. "A Fuzzy Credibility-Constrained Fuzzy Multi-Objective Programming Model for Optimizing Irrigation Strategies to Balance Citrus Yield and Quality Under Uncertainty" Agronomy 15, no. 12: 2739. https://doi.org/10.3390/agronomy15122739
APA StyleZhang, F., Zhang, X., Wu, Z., Guo, S., & Wang, S. (2025). A Fuzzy Credibility-Constrained Fuzzy Multi-Objective Programming Model for Optimizing Irrigation Strategies to Balance Citrus Yield and Quality Under Uncertainty. Agronomy, 15(12), 2739. https://doi.org/10.3390/agronomy15122739







