Diffusion Probabilistic Models for NIR Spectral Data Augmentation in Precision Agriculture

Abstract

Near-infrared (NIR) spectroscopy is a rapid, non-destructive tool widely used in agriculture, but limited labeled spectra often constrain model robustness. To address this, we propose using denoising diffusion probabilistic models (DDPMs) for NIR data augmentation. Leveraging the SpectraFood leek dataset, a conditional MLP-DDPM was trained to generate realistic synthetic spectra guided by dry matter content. Incorporating 1000 generated spectra into the training set improved the predictive performance of PLSR, RF, and XGBoost models, demonstrating enhanced generalization and robustness. Compared with WGAN, DDPM offered higher stability and fidelity, effectively expanding the calibration space without introducing unrealistic patterns. Future work will explore conditional and hybrid diffusion frameworks, integrating environmental and physiological covariates, and cross-domain spectral transfer, extending the applicability of DDPMs for diverse crops and precision agriculture scenarios.

1. Introduction

Near-infrared (NIR) spectroscopy has become a widely adopted analytical tool in agriculture for its advantages of being rapid, non-destructive, and cost-efficient once established [1]. Applications span from monitoring crop quality and predicting chemical compositions such as moisture, protein, or sugar content, to supporting precision agriculture and postharvest management [1,2]. With the increasing demand for sustainable and data-driven solutions in agriculture, NIR spectroscopy is playing a critical role in bridging the gap between field-level observations and laboratory-based chemical analyses.

However, despite its promise, the effective utilization of NIR spectroscopy faces a fundamental challenge: the scarcity and cost of acquiring high-quality spectral datasets. Unlike conventional imaging, NIR measurements often require specialized instruments, controlled sampling protocols, and time-intensive calibration procedures [3]. Moreover, the diversity of agricultural products and environmental conditions further increases the need for large and representative datasets [4]. In practice, the limited availability of labeled NIR spectra often constrains the robustness of machine learning models, leading to overfitting and reduced generalization ability in real-world scenarios [5].

To address data scarcity, various strategies have been explored. Traditional data augmentation techniques—such as spectral shifting, scaling, or noise injection—introduce limited variability and may not accurately reflect realistic spectral patterns [6]. More advanced generative models, such as Variational Autoencoders (VAEs) and Generative Adversarial Networks (GANs), have shown potential in synthesizing realistic data. For example, researchers have demonstrated that training GANs on limited Vis–NIR datasets allows the synthesis of additional spectra that effectively improve nutrient prediction models for soils under challenging field conditions [7]. Similarly, in viticulture studies, synthetic NIR hyperspectral data generated by GANs has been shown to capture maturity-related spectral variations, thereby enhancing the robustness of grape quality assessment [8]. In addition, researchers developed a conditional VAE (CVAE) framework to guide spectral data augmentation for calibration modeling in in situ measurements. In this approach, the CVAE is trained to generate virtual spectra that expand the training dataset, while a semi-supervised ladder network (S2-LN) regression model leverages both generated and real spectra. These studies highlight the capacity of GANs and VAE to expand dataset diversity while preserving meaningful chemical and structural information embedded in NIR and hyperspectral signals. However, both GAN and VAE suffer from drawbacks such as mode collapse, training instability, and difficulties in capturing fine-grained spectral structures. As a result, there is a growing demand for more powerful generative frameworks capable of producing high-fidelity synthetic spectra that can augment limited datasets [9,10].

Denoising Diffusion Probabilistic Models (DDPMs) have recently emerged as a new class of generative models that demonstrate state-of-the-art performance in image and audio [11]. For example, researchers used a stable diffusion model as an image augmentation method to synthesize multi-class weed images to improve the weed detection performance [9]. Unlike GANs, diffusion models are based on a gradual denoising process that transforms Gaussian noise into realistic data samples, ensuring both stability and diversity in generation [12]. Their probabilistic framework allows for better coverage of the underlying data distribution, making them particularly attractive for scientific domains where data realism and variability are critical. Beyond image augmentation, diffusion-based frameworks have also been explored for tabular data generation, demonstrating their ability to model heterogeneous features and complex data distributions in industrial and biomedical datasets [13].

However, near-infrared (NIR) spectroscopy data pose unique challenges compared to conventional tabular datasets. NIR spectra are high-dimensional, highly correlated, and physically constrained by molecular absorption mechanisms. Unlike typical tabular data, where features are independent or weakly correlated, NIR signals exhibit smooth and structured variations across wavelengths, and small distortions may significantly affect their interpretability. Consequently, directly applying diffusion models designed for unstructured tabular data may not fully capture the intrinsic spectral continuity and domain-specific characteristics of NIR measurements. This motivates our investigation into adapting DDPMs for agricultural NIR data augmentation, aiming to exploit their generative power while preserving the underlying physical and chemical information inherent in spectral data.

The main contributions of this study are twofold: (1) we propose, for the first time, a diffusion-based framework for augmenting agricultural NIR spectroscopy data, and (2) we conduct a systematic evaluation of generated spectra in terms of both statistical similarity and downstream predictive performance.

2. Materials and Methods

2.1. NIR Dataset

In this study, NIR spectral data were obtained from the publicly available SpectroFood dataset, which contains hyperspectral measurements and corresponding dry matter measurements for leek. The leek samples were captured using a dual-camera setup consisting of the Specim FX10 (398–931 nm) and Specim FX17 (936–1717 nm) (Specim, Oulu, Finland), providing a combined spectral range from 398 to 1717 nm with a total of 421 spectral bands. The full width at half maximum (FWHM) ranged from 2.62 to 3.58 nm, and the sample–camera distance was maintained at 60 cm to minimize illumination variability. A total of 288 leek samples were included in this subset, each associated with a measured dry matter content (DMC).

All hyperspectral data in the SpectroFood dataset were preprocessed by the data providers to correct for radiometric and reflectance distortions using the standard white–dark reference calibration:

$$R_c= {\displaystyle \frac{R_o-D}{W-D}} \times 100$$

(1)

where $R_o$ is the raw hyperspectral measurement, $W$ is the white reference image, $D$ is the dark reference, and $R_c$ is the calibrated reflectance value.

After calibration, dead pixels and spikes were removed using fixed thresholding, and non-sample background regions were excluded using manual segmentation [14]. The resulting dataset thus consists of 288 samples × 421 wavelengths, each paired with its corresponding dry matter measurement, forming the basis for subsequent diffusion-based data augmentation and predictive modeling.

2.2. Diffusion Model

To address the limited availability of near-infrared (NIR) spectral data in agricultural research, we employed a denoising diffusion probabilistic model (DDPM) implemented with a lightweight multilayer perceptron (MLP) architecture. Unlike image-based diffusion models, which rely on convolutional networks, our approach adopts a fully connected network tailored for one-dimensional spectral vectors, enabling efficient generation of realistic NIR spectra conditioned on dry matter content.

2.2.1. Model Architecture

The diffusion framework follows the standard forward–reverse denoising process (Figure 1), where Gaussian noise is progressively added to the clean spectral data $x_0$ over a predefined number of timesteps $T$. The corrupted spectrum at step $t$ is defined as follows:

$$x_t= \sqrt{{\overline{a}}_t}{x}_0+ \sqrt{1- {\overline{a}}_t}ϵ, ϵ ~ \mathcal{N} (0, I)$$

(2)

where ${\overline{a}}_t= {\prod }_{i=1}^t(1-{\beta }_i)$, and ${\beta }_i$ are linearly spaced noise variance parameters.

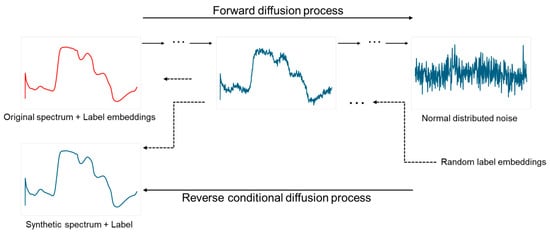
Figure 1. Label conditional DDPM process.

The goal of the denoising model is to learn the reverse mapping ${\rho }_{\theta }\left(x_{t-1}\right|x_t,y)$, conditioned on the target variable $y$. The denoising network is an MLP, denoted as $f_{\theta }$, which predicts the clean spectral signal ${\widehat{x}}_0$ given the noisy input and timestep embedding. The input to the model is the concatenation of $y$ and noisy spectrum $x_t$. The network consists of several fully connected layers with dropout regularization, implemented as follows:

$$Input:\left[y, x_t\right]\in {\mathbb{R}}^{d+1} \to f_{\theta }\left(\left[y, x_t\right], t\right)\to {\widehat{x}}_0$$

(3)

2.2.2. Training Objective

The denoising network was trained to minimize the mean squared error (MSE) between the predicted clean spectrum and the original uncorrupted input:

$$\mathcal{L}={\mathbb{E}}_{x_0, t,ϵ}[\parallel f_{\theta }\left(y, x_t, t\right)- x_0{\parallel }_2^2]$$

(4)

2.2.3. Conditional Sampling

During inference, the trained MLP-Diffusion model generates synthetic spectra via a deterministic DDIM sampling process. Given a desired target variable $y_{cond}$, random noise is gradually denoised through $T_{DDIM}$ reverse steps to yield the generated spectrum $x_0^{’}$:

$$x_{t-1}= \sqrt{{\overline{a}}_{t-1}}{f}_{\theta }\left(y_{cond}, x_t, t\right)+\sqrt{1-{\overline{a}}_{t-1}}{ϵ}_t$$

(5)

where ${ϵ}_t~\mathcal{N}$ (0, I). This conditional generation mechanism allows the creation of synthetic NIR spectra corresponding to specific chemical or physical properties, effectively augmenting the training dataset for downstream regression tasks.

Synthetic spectra were generated by sampling across the full range of observed DMC values, ensuring that the augmented dataset adequately covers the calibration space of interest. The number of synthetic samples per DMC value was chosen to provide sufficient variability while remaining computationally feasible. This conditioning mechanism enables the DDPM to produce spectra that are not only realistic in shape but also consistent with the associated chemical property.

2.2.4. Model Training

The NIR dataset of leek samples was first randomly divided into training and testing subsets with an 8:2 ratio. This splitting procedure was repeated three times using different random seeds to better assess the robustness of the results. The testing subset was reserved exclusively for downstream regression tasks to evaluate the predictive performance of generated spectra with real samples. Within the 80% training portion, the data were further split into training and validation sets (7:3) for optimizing the diffusion model and preventing overfitting. The MLP-based denoising diffusion model (DDPM) was implemented using PyTorch 2.8 and trained on an NVIDIA RTX 4060 GPU. Model optimization was performed using the Adam optimizer with a cosine annealing learning rate schedule. The main hyperparameters, including network depth, hidden dimensions, number of diffusion steps, dropout rate, and learning rate, are summarized in Table 1. The best-performing DDPM used the following settings: learning rate = 0.001, batch size = 512, diffusion timesteps = 500, training iterations = 2000, number of MLP layers = 4, and MLP nodes per layer = 256.

Table 1. The list of main hyperparameters for MLP-DDPM.

Hyperparameters	Search Space
Learning rate	0.0001–0.003
Batch size	256, 512, 1024
Diffusion timesteps	200, 500, 1000
Training iterations	2000, 5000, 10,000
Number of MLP layers	2, 4, 6
MLP nodes	125, 256, 512, 1024

During training, the model progressively learned to reconstruct clean spectral features from noisy inputs, minimizing the mean squared error (MSE) between the reconstructed and original spectra. The best-performing checkpoint, based on validation loss, was saved for subsequent conditional sampling and data augmentation experiments.

2.3. Conditional Wasserstein Generative Adversarial Network

To provide a comparative baseline for evaluating the performance of the diffusion-based approach, a Conditional Wasserstein Generative Adversarial Network (WGAN) was implemented for NIR data generation. The WGAN consists of a generator, a discriminator, and an auxiliary classifier that are jointly trained in an adversarial and conditional learning setup. The generator is designed to synthesize realistic NIR spectra conditioned on specific dry matter content (DMC) values, thereby capturing the underlying relationship between spectral variation and physicochemical properties. The discriminator learns to differentiate between real and synthetic spectra, encouraging the generator to produce more physically plausible outputs. Meanwhile, the classifier enforces the conditional constraint by ensuring that the generated spectra are not only visually and statistically realistic but also consistent with their target DMC values.

The generator, discriminator and classifier were implemented as fully connected multilayer perceptrons (MLPs) with leaky rectified linear unit (ReLU) activation functions and layer normalization to enhance stability. The WGAN model was trained using the same 80% training subset of the leek dataset employed for DDPM training, with a batch size of 64, learning rate of 1 × 10⁻⁴.

The WGAN-generated spectra were later compared with DDPM-generated data in terms of visual spectral consistency, distributional similarity, and downstream regression performance. This comparison provides a clear evaluation of the relative merits of diffusion-based versus adversarial-based generative frameworks for NIR data augmentation.

2.4. Evaluation of DDPM and WGAN

To comprehensively assess the quality and realism of the synthetic NIR spectra generated by the DDPM and WGAN models, multiple quantitative and visual evaluation metrics were employed. The Spectral Angle Mapper (SAM) score was used to measure the angular difference between synthetic and real spectra, providing an index of spectral similarity that is invariant to illumination intensity. Cosine similarity was additionally computed to quantify the alignment of spectral vectors, serving as a complementary measure to SAM. The Root Mean Square Error (RMSE) between synthetic and reference spectra was calculated to evaluate absolute spectral reconstruction accuracy. Furthermore, the Maximum Mean Discrepancy (MMD) with a radial basis function (RBF) kernel was applied to assess the overall distributional similarity between real and generated data in a high-dimensional feature space. To facilitate visual comparison of spectral distributions, Principal Component Analysis (PCA) was performed on the combined real and synthetic datasets, enabling inspection of how closely the generated samples aligned with the real data manifold in the reduced feature space. Together, these metrics provide a robust multi-perspective evaluation of spectral fidelity, structural consistency, and diversity of the synthetic datasets produced by both generative models.

2.5. Machine Learning Model Evaluation

To evaluate the quality of the synthetic NIR spectra generated by the DDPM and WGAN, this study adopted a downstream regression task using DMC as the target variable. The underlying assumption is that models trained on high-quality synthetic and real data should be competitive with models only trained on real data. Therefore, two experiments were conducted: (1) using only the original training dataset, and (2) using the original training dataset plus DDPM or WGAN synthetic dataset. Three regression algorithms with complementary learning mechanisms were adopted: Partial Least Squares Regression (PLSR), Random Forest (RF), and XGBoost. PLSR was selected for its strong interpretability and suitability for high-dimensional, collinear spectral data [15]; RF served as a non-linear ensemble baseline with robustness to noise and overfitting [14]; and XGBoost, a gradient boosting algorithm, provided an advanced non-linear modeling framework capable of capturing complex spectral–chemical relationships [16].

Model performance was evaluated on the 20% hold-out test set, which was never used during diffusion model training or augmentation, ensuring an unbiased evaluation. The predictive accuracy was quantified using the coefficient of determination (R²) and root mean square error (RMSE):

$$R^2=1- {\displaystyle \frac{{\sum }_{i=1}^n{(y_i- {\widehat{y}}_i)}^2}{{\sum }_{i=1}^n{(y_i- \overline{y})}^2}}$$

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

where $n$ is the number of samples used to fit the model, $y_i$ is the ground truth value of the $i$th sample, ${\widehat{y}}_i$ is the model estimated value of the $i$th sample, and $\overline{y}$ is the mean response value.

3. Results

3.1. Evaluation of DDPM and WGAN

This study was conducted using the SpectraFood dataset, which provides visible and NIR spectra collected from leek. The spectra cover the wavelength range of 398 to 1717 nm (Figure 2). To train the diffusion model, 80% of the leek samples (230 samples) were randomly selected for DDPM training and evaluation, while the remaining 20% were reserved for evaluating the synthetic spectra in downstream regression tasks. Figure 3 shows the distribution of DMC in the training dataset. The DMC values range from 0.08 to 0.19, indicating a moderate variation across the leek samples, which provides sufficient diversity for training the diffusion model.

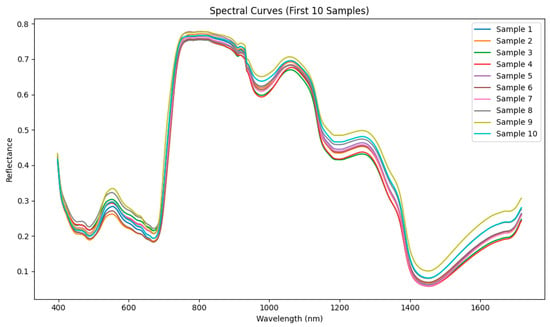
Figure 2. Representative NIR spectra of leek samples (first ten samples) from the SpectraFood dataset.

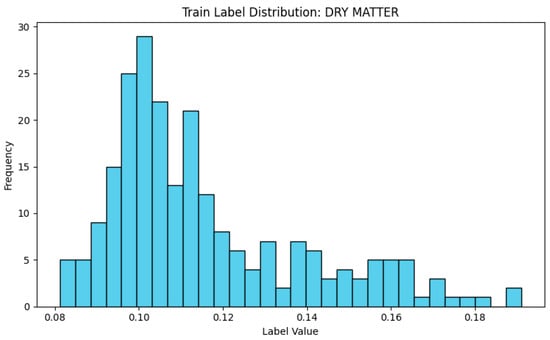
Figure 3. The distribution of dry matter content in the training dataset.

Within the training portion (230 samples) of the dataset, a further 8:2 split was applied to create the training and validation subsets for the diffusion model. The model was trained on the training subset while its performance was monitored on the validation subset to ensure stable learning. The diffusion process was run for 2000 epochs, during which the MSE loss progressively decreased and eventually reached a plateau, indicating that the model had effectively converged and captured the underlying NIR spectral distribution (Figure 4).

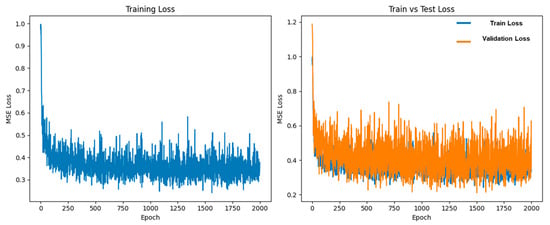
Figure 4. MSE loss curve over 2000 epochs during DDPM training.

Once the diffusion model was trained, it was employed to generate new NIR spectra by performing the reverse diffusion process guided by the target dry matter (DMC) values. The generation started from random Gaussian noise and progressively denoised it through a series of learned reverse steps. At each step, the model estimated and removed the noise component, gradually recovering realistic spectral patterns conditioned on the given DMC level (Figure 5). In this study, the best number of reverse diffusion steps was set to 200, which provided a good balance between computational cost and the quality of the generated spectra. After training convergence, the well-trained DDPM was used to generate 1000 synthetic NIR samples, conditioned on DMC values ranging from 0.08 to 0.18, which aligns with the observed range in the original dataset. These synthetic spectra were then combined with the 230 real training samples to form an augmented dataset (Figure 6). This expanded dataset was subsequently used for downstream regression experiments to evaluate whether the diffusion-generated samples could enhance model performance and improve prediction robustness.

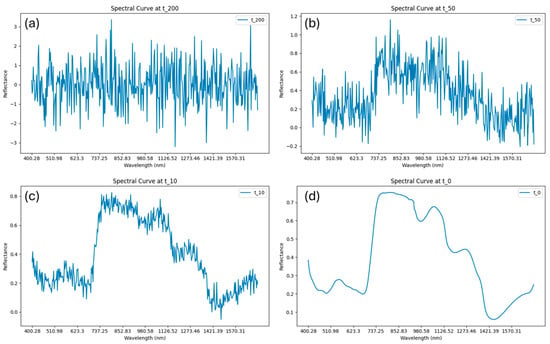
Figure 5. Example illustration of the spectral denoising process in time step 200 (a), 50 (b), 10 (c), 0 (d).

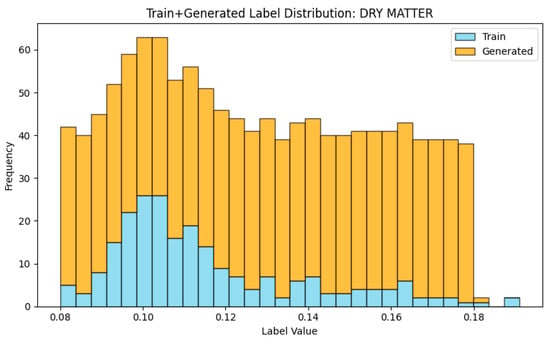
Figure 6. The distribution of dry matter content in the training plus DDPM synthetic dataset.

To benchmark the performance of the diffusion-based method, WGAN was implemented for comparison. WGAN was trained using the same training subset as the DDPM for fair comparison. The generator, discriminator, and classifier were jointly optimized in an adversarial framework for 10,000 epochs. The generated spectra captured the general shape and absorption features of the real NIR signals but exhibited slightly higher local noise and weaker smoothness when compared with DDPM (Figure 7). In addition, Figure 7 shows that the spectra generated by DDPM closely match the real samples, particularly in the 700–950 nm range, where they almost overlap. This range is sensitive to the dry matter content (DMC) of leek, indicating that DDPM effectively captures water-related spectral features.

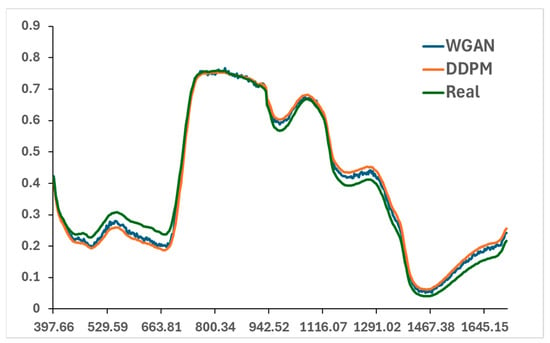
Figure 7. Comparison of real and synthetic NIR spectra generated by WGAN and DDPM at a DMC value of 0.0811.

To comprehensively assess the generative quality of WGAN and DDPM, several quantitative and qualitative metrics were employed, including Spectral Angle Mapper (SAM), Cosine Similarity, Root Mean Square Error (RMSE) between real and generated spectra, and Maximum Mean Discrepancy (MMD) with a Radial Basis Function (RBF) kernel (Table 2). In addition, PCA visualization was used to examine the distributional overlap between synthetic and real spectra (Figure 8). Compared with WGAN, the DDPM-generated spectra demonstrated higher similarity to the real data, with lower SAM and RMSE values and a larger cosine similarity, suggesting a better match in both spectral shapes for individual samples. However, DDPM exhibits a larger MMD than WGAN, suggesting that although individual samples are realistic, the overall distribution may deviate from the real data in some respects. In contrast, WGAN spectra are noisier at the sample level, but the overall distribution is closer to that of the real data. PCA projection further confirmed that the DDPM-synthesized spectra were more closely aligned with the real spectra cluster, whereas WGAN samples showed slightly larger dispersion and boundary deviations (Figure 8). These results indicate that diffusion-based generation can produce smoother and more physically consistent NIR spectra compared with adversarial-based approaches.

Table 2. Evaluation of DDPM and WGAN.

	SAM	Cosine Similarity	RMSE	MMD
DDPM	0.364	0.934	0.198	0.166
WGAN	0.614	0.817	0.473	0.075

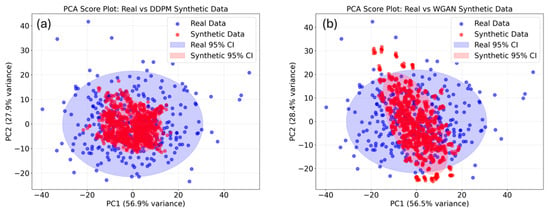
Figure 8. PCA score plot of DDPM (a) and WGAN (b) synthetic spectra data.

3.2. Evaluation on Downstream Regression Tasks

After training DDPM and WGAN, the best checkpoints of each model were used to generate synthetic NIR spectra. For each model, three different random seeds were employed, producing three sets of synthetic data, each containing 1000 samples. To evaluate the performance of the synthetic NIR dataset generated by DDPM and WGAN, this study incorporated the 1000 generated spectra into the original training set, forming an augmented dataset referred to as the synthetic-augmented training set. Three regression models, PLSR, RF, and XGBoost, were then trained separately using both the original training set and the synthetic-augmented training set. The predictive performance of each model was evaluated on the same hold-out test set. The comparison between these two training strategies allows for assessing the effectiveness of DDPM-based and WGAN-based data augmentation in improving model generalization and prediction accuracy. Table 3 shows the regression performance of three ML models trained on the synthetic-augmented training set and the original training set. Compared with RF and XGBoost, PLSR shows the best regression performance with an R² of 0.809 and RMSE of 0.011 based on the original training set. After adding DDPM-generated synthetic NIR dataset, PLSR, RF and XGBoost resulted in higher regression performance compared to training on the original training set, with average R² of 0.833, 0.695 and 0.494, respectively. After adding WGAN-generated synthetic NIR dataset, PLSR, RF and XGBoost resulted in higher regression performance compared to training on the original training set, with average R² of 0.81, 0.655 and 0.45, respectively. Overall, both DDPM- and WGAN-based data augmentation improved the regression performance across all three models compared with training on the original dataset. However, the improvements achieved by DDPM were generally more pronounced than those from WGAN, particularly for PLSR and RF. Despite these trends, statistical analysis using paired t-tests indicated that the performance gains from DDPM were not statistically significant (p = 0.17 for R² and p = 0.19 for RMSE), suggesting that while DDPM-generated spectra enhanced model performance, the improvement was not substantial enough to reach statistical significance. The detailed regression results of the best-performing model, PLSR, are illustrated in Figure 9, showing the relationship between the predicted and measured DMC values using both the original and synthetic-augmented datasets.

Table 3. Evaluation of DDPM and WGAN on downstream regression tasks.

	Model	R2	RMSE
Original	PLSR	0.809	0.011
	XGBoost	0.402	0.02
	RF	0.602	0.016
DDPM	PLSR	0.834 ± 0.02	0.01 ± 0.001
	XGBoost	0.494 ± 0.01	0.018 ± 0.001
	RF	0.695 ± 0.01	0.014 ± 0.001
WGAN	PLSR	0.81 ± 0.01	0.011 ± 0.001
	XGBoost	0.45 ± 0.02	0.019 ± 0.001
	RF	0.655 ± 0.01	0.015 ± 0.001

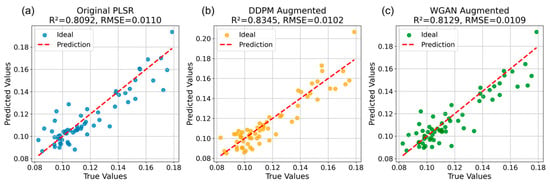
Figure 9. Regression results of the best-performing model (PLSR) using the original (a) and synthetic-augmented NIR datasets generated by DDPM (b) and WGAN (c).

4. Discussion

The results demonstrate that the proposed DDPM-based framework can effectively generate realistic NIR spectra and improve regression performance in downstream prediction tasks. Compared with traditional generative methods such as generative adversarial networks (GANs) and variational autoencoders (VAEs), diffusion probabilistic models exhibit superior stability and fidelity in reproducing the intrinsic variability of NIR spectra. Previous studies have reported that GAN-based spectral data augmentation could enhance soil nutrient estimation and fruit quality prediction, yet these methods often suffer from mode collapse and limited diversity in generated samples, particularly when the available training data are scarce [7,17,18,19]. Similarly, VAE-based approaches, while capable of learning latent spectral distributions, tend to produce overly smoothed spectra that lack fine-grained reflectance variations critical for accurate regression modeling [20,21].

In this study, we quantitatively compared DDPM with WGAN in generating synthetic NIR spectra. During training, WGAN proved more difficult to fit and required careful tuning to avoid instability. While WGAN-generated spectra generally preserved the overall spectral shape and trends, they exhibited higher noise levels compared with DDPM-generated spectra (Figure 7). The diffusion model adopted in this study provides a more stable generative process by explicitly modeling noise addition and denoising steps (Table 2, Figure 8). The iterative denoising mechanism allows the model to reconstruct spectral signatures that preserve both local smoothness and global spectral shape, yielding synthetic spectra that closely follow the real data distribution. As shown in Table 3, all three regression models—PLSR, RF, and XGBoost—achieved improved predictive performance when trained on the DDPM-augmented dataset compared with the original training set and the WGAN-augmented dataset. This suggests that the synthetic samples contribute meaningful spectral variability, helping to regularize the model and prevent overfitting, especially under data-scarce conditions typical in agricultural datasets [22].

The improvement observed in PLSR performance is particularly noteworthy, since linear models are more sensitive to spectral variability and noise. The enhanced accuracy after augmentation indicates that the diffusion-generated spectra effectively enriched the calibration space while maintaining realistic correlations between spectral patterns and dry matter content. This aligns with recent findings in other fields where DDPM-based augmentation was shown to outperform GANs in terms of data fidelity and downstream prediction accuracy [13]. Regarding DDPM architecture, a simple MLP was employed due to its computational efficiency. Despite its simplicity, the MLP-DDPM effectively captured spectral continuity and fine-grained absorption features, as evidenced by the close alignment with real spectra and downstream regression performance. However, statistical analysis using paired t-tests showed that the gains achieved by the MLP-based DDPM were not statistically significant (p = 0.17 for R² and p = 0.19 for RMSE), indicating that although DDPM-generated spectra contributed meaningful variability and tended to enhance model performance, the improvement was not sufficient to reach statistical significance in this study. Future studies need to explore using more complex architectures, such as 1-D convolutional networks or transformers, to enhance the capacity to model local and long-range spectral dependencies, which could be explored in future work.

Overall, the results confirm the potential of diffusion probabilistic models as a robust approach for spectral data augmentation. By learning the underlying data manifold through gradual denoising, DDPMs can generate realistic and diverse synthetic samples without requiring adversarial optimization or complex latent regularization. To further strengthen this work, future studies could perform ablation analyses, such as varying the number of generated samples, diffusion steps, or conditioning variables, to systematically assess the robustness of results, identify optimal hyperparameters, and extend comparisons with VAEs and other GAN variants. While smaller or larger numbers of synthetic samples were not exhaustively tested in this study, this represents a potential avenue for future work, where systematic exploration of the optimal number of generated spectra could help maximize downstream regression performance and further improve calibration-space coverage.

5. Conclusions

This study presents a novel application of denoising diffusion probabilistic models (DDPMs) for NIR spectral data augmentation in agricultural analysis. Using the SpectraFood leek dataset as a case study, the DDPM successfully learned the underlying spectral distribution and generated realistic synthetic spectra conditioned on dry matter content. The inclusion of these synthetic samples in the training dataset improved the predictive performance of three regression models—PLSR, RF, and XGBoost—highlighting the potential of diffusion-based generative modeling to mitigate data scarcity in spectroscopy-driven agricultural research.

Compared with conventional generative frameworks such as WGAN, the diffusion-based approach demonstrated higher stability and data fidelity, effectively expanding the calibration space without introducing unrealistic noise. This makes DDPM particularly suitable for small-sample or domain-limited agricultural spectroscopy tasks, where obtaining large numbers of labeled samples is costly and time-consuming.

Future work will focus on extending the proposed framework to conditional and hybrid diffusion architectures, integrating environmental and physiological covariates to guide spectral generation more precisely. Additionally, exploring cross-domain generalization—for instance, transferring learned spectral priors from one crop type to another—may further enhance the practicality of DDPMs for broader agricultural sensing applications. The combination of diffusion-based generative modeling and precision agriculture analytics thus holds promise for improving model robustness, interpretability, and scalability in data-limited real-world scenarios.