Abstract
Recent progress in computational materials science in the area of semiconductor epitaxial growth is reviewed. Reliable prediction can now be made for a wide range of problems, such as surface reconstructions, adsorption-desorption behavior, and growth processes at realistic growth conditions, using our ab initio-based chemical potential approach incorporating temperature and beam equivalent pressure. Applications are examined by investigating the novel behavior during the hetero-epitaxial growth of InAs on GaAs including strain relaxation and resultant growth mode depending growth orientations such as (111)A and (001). Moreover, nanowire formation is also exemplified for adsorption-desorption behaviors of InP nanowire facets during selective-area growth. An overview of these issues is provided and the latest achievement are presented to illustrate the capability of the theoretical-computational approach by comparing experimental results. These successful applications lead to future prospects for the computational materials design in the fabrication of epitaxially grown semiconductor materials.
1. Introduction
Computational materials science is now popular among researchers including experimentalists to predict the physical properties of materials. This reflects recent developments in the computer software using electronic theory to explain many experimental results and to predict the physical properties of materials without actually synthesizing them. During the last several decades, semiconductor technology has made it possible to create artificial materials whose physical properties are on the atomic scale such as quantum dots and nanowires fabricated by various epitaxial growth techniques. In particular, crystal growth processes during molecular beam epitaxy (MBE) and metal-organic vapor phase epitaxy (MOVPE) have been paid much attention from a number of theorists to work in the field of semiconductor epitaxial growth, since these epitaxial growth techniques realize highly non-equilibrium conditions where the growth is governed by the diffusive kinetics of the source atoms within the crystalline surfaces in contrast with bulk-growth processes which proceed near thermodynamic equilibrium conditions. Thus, a fundamental understanding of the growth processes in these techniques not only leads to better growth techniques but also gives guiding-principles for the fabrication of the novel materials that are not found in nature.
As a physical process, the growth of thin films is controlled by various growth processes that involve adsorption of atoms or molecules onto a surface, their subsequent diffusion across the surface, dissociation of molecules, and desorption, etc. at the gas-solid interface in the growth front. It is well known that reconstructed structures appear on the growth front (surfaces) of semiconductor materials [1]. Therefore, we have to understand the atomic structures on the surfaces to control the interface mass transfer. To this end, so far a lot of theoretical works have been carried out to investigate the surface structures of semiconductors using ab initio calculation that is a promising tool for clarifying the complicated growth processes because of its ability to calculate electronic structures and total energy [2,3,4]. Kaxiras et al. [2] studied the lowest-energy geometry for GaAs(111) with different stoichiometries. Qian et al. [3] discussed relationship between the stoichiometry and the surface reconstruction on GaAs(001) by means of chemical potentials. Northrup [4] classified the stable structures on Si(001)H using H chemical potential. However, all these approaches discussed about the static structural stability on the surfaces at 0 K.
Generally, vapor phase epitaxy such as MBE and MOVPE is performed under finite temperatures and gas-pressures. This implies that it is indispensable to consider the ambient conditions to predict the reconstructed structures on the growth surfaces. We [5,6] proposed ab initio-based chemical potential approach that incorporates the free energy of gas phase. Therefore, the theoretical analysis is useful to analyze the influence of temperatures and gas-pressure on the stability of reconstructed surfaces. By the application of this method, epitaxial growth processes can be investigated for various semiconductors including GaAs and GaN [7,8,9]. Controlling the growth processes, recent developments in semiconductor technology made it possible to create artificial nanostructures such as nanodots, nanowire, and nanosheet fabricated by various thin film growth techniques including MBE and MOVPE. In this article, we focus on the nanostructures to exemplify the feasibility of the chemical potential approach to their actual growth systems such as MBE growth for lattice mismatched InAs and selective-area growth of InP nanowires (NWs). Surface phase diagram calculations as functions of temperature and gas-pressure are performed for InAs(001), InAs(111)A, InP(111)A, and facets of InP NWs with wurtzite (WZ) structure. Furthermore, the growth modes of heteroepitaxial InAs/GaAs system are also investigated using macroscopic free energy theory incorporating surface energy and misfit dislocation formation energy obtained by the ab initio and the empirical interatomic potential calculations. The adsorption-desorption behavior during growth of InP NWs, which are crucial in determining their crystal structure, are also investigated using Monte Carlo (MC) simulations combined with surface phase diagrams calculations. Comparative studies between calculated and experimental results are shown to check the versatility of the chemical potential approach to predictions of phase diagram and novel adatom behavior on various semiconductor surfaces.
2. Computational Methods
We proposed an ab initio-based approach that incorporates the free energy of ideal gas per one particle (chemical potential) μgas [5,6]. The adsorption-desorption behavior of In atom and As molecule on these surfaces can be determined by comparing μgas with the adsorption energy Ead. An impinging atom (molecule) can adsorb on the surface if the free energy of the atom (molecule) in the gas phase is larger than its adsorption energy. In contrast, an impinging atom (molecule) desorbs if its gas-phase free energy is smaller than the adsorption energy. The μgas can be computed using quantum statistical mechanics as functions of temperature and pressure. The adsorption energy can be obtained using ab initio calculations. Exemplifying In atom and As4 molecule, the chemical potential μgas of ideal gas is given by the following Equations:
μIn = −kBT(kBT/pIn × g × ζtrans),
μAs4 = −kBT(kBT/pAs4 × g × ζtrans × ζrot × ζvib).
Here, kB is the Boltzmann’s constant, T the gas temperature, g the degree of degeneracy of electron energy level, p the beam equivalent pressure (BEP) of In atom or As molecule (As4), and ζtrans, ζrot, and ζvib are the partition functions for translational, rotational, and vibrational motions, respectively. In general, both μIn and μAs4 decrease with temperature and increases with BEP. The adsorption energy Ead is obtained by
where Etotal is the total energy of the surface with adatoms, Esubstrate the total energy of the surface without adatoms, and Eatom is the total energy of isolated atoms. We note that the Gibbs free energy of formation vibrational contribution is very small compared with the energy difference between a given structure and the ideal surface. The gas-phase entropy difference is also considerably larger than the surface entropy change, when the temperature or pressure is varied. Therefore, only the entropic effects of the gas phase are considered throughout our theoretical approach. Using the chemical potential and the adsorption energy, the adsorption and desorption behaviors on the surfaces under growth conditions are obtained as functions of T and p, i.e., the structure corresponding to adsorbed surface is favorable when Ead is less than μgas, whereas desorbed surface is stabilized when μgas is less than Ead. Based on these results, we obtain adsorption-desorption boundaries for In and As and surface phase diagrams of the InAs WL.
Ead = Etotal − Esubstrate − Eatom,
Indeed, this method has been successfully applied to determine the reconstructions on GaAs(001) surfaces [5]. It has been found that the μgas of Ga atom using Equation (1) decreases with temperature and increases with BEP. By comparing the adsorption energy of Ga atom (−3.3 eV) using Equation (3), the μgas of Ga atom becomes lower than the adsorption energy when temperatures is higher than 1000 K for Ga-BEP at 1.0 × 10−5 Torr. This suggests that the critical temperature for Ga adsorption is ~1000 K for Ga-BEP at 1.0 × 10−5 Torr. The surface phase diagram for Ga adsorption obtained by the comparison of μgas with Ead thus suggest that the Ga-droplet appear under low temperature and high Ga-BEP conditions, while GaAs-(4 × 2)β2 surface is stabilized under high temperature and low Ga-BEP conditions. The calculated results are consistent with the observation of Ga-droplet under ~900 K during the MBE growth of GaAs under Ga-rich conditions and Ga desorption above ~970 K after turning off the Ga flux, suggesting that ab initio-based approach that incorporates the free energy of the gas phase is feasible for investigating surface structures, while previous calculations [2,3,4] are unable to incorporate temperature and pressure.
In this study, the total-energy calculations are performed within the generalized gradient approximation (GGA) [10] within the density functional theory. Norm-conserving pseudopotentials with partial core corrections are used to describe electron-ion interaction [11]. The conjugate-gradient minimization technique is used for both the electronic-structure calculation and the geometry optimization [12]. The geometry is optimized until the remaining forces acting on the atoms are less than 5.0 × 10−3 Ry/Å. The valence wave functions are expanded by the plane-wave basis set with a cutoff energy of 16 Ry. We take the model with slab geometries of six atomic layers for the InAs(111)A and InP(111)A and eight atomic layers for the InAs(001), WZ-InP() and WZ-InP() with artificial H atoms [13] and a vacuum region equivalent to nine atomic layer thickness. The k-point sampling corresponding to 36 points in the irreducible part of the 1 × 1 surface Brillouin zone, which provides sufficient accuracy in the total energies, is employed. The computations are carried out using Tokyo Ab initio Program Package [12].
According to our macroscopic theory for growth mode [14], the free energies F for various growth modes such as two-dimensional coherent growth (2D-coherent), 2D growth with misfit dislocation (2D-MD) and (b) 2D growth with stacking-fault tetrahedron (2D-SFT), and Stranski-Krastanov growth (SK-coh) are given by
where γ is the surface energy, M the effective elastic constant, ε0 the intrinsic strain (=0.072) [14], h the layer thickness, Ed the dislocation formation energy, l0 the average dislocation spacing (=58.76 (Å) [14]), ESFT the SFT formation energy, Aunit the area of 14 × 14 planar unit cell used in the system energy calculations for the 2D-MD with l0 and the 2D-SFT, and β and −α are the effective energy increase in surface energy of the epitaxial layer and the effective decrease in strain energy due to SK-island formation.
F2D-coherent(h) = γ + Mε02h/2,
F2D-MD(h) = γ + Ed/l0 − Ed2/2(Mε02l02h),
F2D-SFT(h) = γ + Mε02h/2 + ESFT/Aunit,
FSK-coh(h) = γ(1 + β) + M(1 − α)ε02h/2,
In order to obtain the parameter values of M, Ed, and ESFT, we employ a simple formula for estimating system energy E for computational models such as the 2D-coherent, the 2D-MD, and the 2D-SFT as follows.
where E0 is the cohesive energy estimated by Kohr–Das Sarma-type empirical interatomic potential Vij within the second-neighbor interactions [15]. The potential parameters A, β, Ri, γ, θ, B0, λ, η, and α are determined by reproducing equilibrium interatomic bond lengths, elastic stiffness for zinc blende structure, and relative stability among zinc blende, rocksalt, and CsCl structures [16]. Stacking-fault energy ∆ESF is described as the summation of electrostatic energies consisting of repulsive interaction between covalent bond charges Zb (=−2) and attractive interaction between ionic charges Zi (=±3 for III–V compound semiconductors) depending on ionicity fi (=0.298 for InAs) [17]. The value of coefficient K is determined to be 8.7 (meV·Å) by reproducing energy difference 25.3 (meV/atom) between diamond and hexagonal structures for C with fi = 0 obtained by ab initio calculations. In the system energy calculations, the lattice parameter a of InAs is fixed to be that of GaAs(111) for the 2D-coherent and the 2D-SFT or relaxed value of a for the 2D-MD, and the lattice parameter c and the atomic positions are varied to minimize the system energy in a 14 × 14 planar unit cell with increase of layer thickness h.
E = E0 + ∆ESF,
E0 = 1/2 × ∑i,jVij,
Vij = Aexp[−β(rij − Ri)γ][exp(−θrij) − B0exp(−λrij)G(η)/Ziα],
∆ESF = K [3/2 × (1 − fi) × Zb2/rbb − fi × Zi2/rii].
Furthermore, we employ stochastic MC simulations [18] in order clarify the growth mechanism of nanowires. The MC simulations take temperature and pressure into account. In the MC procedure, the probability of adsorption, migration, and desorption (, , and , respectively) at adsorption site are estimated by
where Δμ(x) is the energy difference between adsorption energy Ead (x) and μgas at adsorption site x, R is diffusion prefactor taken to be kBT/πћ [19], ΔE(x→x’) is the local migration barrier involving the adatom hopping from site x to x’ and Ede(x) is desorption energy at site x. The probability for surmounting the activation energy is reduced (or enhanced) by a weighting function of exp{Δμ(x)/kBT}, which corresponds to the local-thermal equilibrium desorption probability. In the simulation procedure, we adopt extensive surfaces as growth substrates which are 30,000 × 30,000 times as large as the surface unit cells. The atoms and molecules with pressure p are supplied from gas phase to these surfaces at an interval of Δtgas per surface area that is derived from Maxwell’s law of velocity distribution given by
where is the mass of the adsorbate. The evaluation of adsorption using Equation (15) are repeated during the simulation. Events for adatoms on the surface are determined by
where Kdiff(x→xi) is the relative diffusion probability from site x to another site xi and Kde(x) is the relative desorption probability at site x. The sum is carried out all over the neighboring site xj. Events for adatoms are taken place with a time increment Δt expressed in Equation (18).
Pad(x) = exp{−Δμ(x)/kBT}/[1 + exp{−Δμ(x)/kBT}],
Pdiff(x→x’) = Rexp{ΔE(x→x’)/kBT},
Pde(x) = Rexp[−{Ede(x) − Δμ(x)}/kBT],
Δtgas = (2mkBT/p)1/2
Kdiff(x→xi) = Pdiff(x→xi)/{Σj Pdiff(x→xj) + Pde(x)},
Kde(x→xi) = Pde(x→xi)/{Σj Pdiff(x→xj) + Pde(x)},
Δt = 1/{Σj Pdiff(x→xj) + Pde(x)},
3. Hetero-Epitaxial Growth of InAs on GaAs
Semiconductor hetero-epitaxial systems grown by molecular beam epitaxy (MBE) are crucial for fabricating low-dimensional semiconductor nanostructures such as three-dimensional (3D) island shaped quantum dots (QDs) in InAs grown on GaAs(001). Despite a constant lattice mismatch, InAs thin films fabricated on the GaAs(111)A exhibit two-dimensional (2D) growth. Many studies have been done to investigate the InAs/GaAs growth using reflection high-energy electron-diffraction (RHEED) and scanning tunneling microscopy (STM). Joyce et al. [20] found that an intermediate wetting layer (WL) is formed on the (001)-oriented substrates prior to the formation of QDs while strain relaxation involving misfit dislocation formation causes a continuous 2D growth mode on the (111)A. For the InAs/GaAs(111), Yamaguchi et al. [21] reported experimental measurements using STM on the mechanisms of strain relaxation in InAs/GaAs(111)A hetero-epitaxy to propose a possible model for the resulting semicoherent interface structure. Ohtake et al. [22] studied strain-relaxation processes in the InAs/GaAs(111)A using rocking-curve analysis of reflection high-energy electron diffraction. Zepeda-Ruiz et al. [23] theoretically analyzed the strain relaxation at the semicoherent interface structure consisting of a network of interacting misfit dislocations. We have also investigated the stacking-fault tetrahedron (SFT) formation in the InAs/GaAs(111)A using empirical interatomic potentials to clarify the contribution of strain relaxation stabilizing it [24]. These previous studies have mainly focused on the strain relaxation at the InAs/GaAs(111)A interface without incorporating surface related phenomena. Taguchi and Kanisawa have studied the surface structures and adsorption-desorption behavior on the InAs(111)A surface using ab initio calculations [25]. Moreover, it should be noted that the stability of surface structures and adsorption behavior have never been clarified on the InAs/GaAs(111)A.
The formation of the WL on the (001) as a function of substrate temperature, reconstruction, and the amount of InAs deposition has been investigated in detail by Belk et al. [26]. Their RHEED results indicate that the surface in InAs/GaAs changes its structure from substrate GaAs(001)-c(4 × 4) to InAs(001)-(2 × 4) via (1 × 3)/(2 × 3) WL with increase of InAs coverage over the temperature range of 350–500 °C. Grabowski et al. [27] observed a complete transition into (2 × 3) at InAs coverage of 0.76 ± 0.07 monolayer (ML) with many missing dimers at 450 °C in STM. Eisele et al. [28] found that the (4 × 3) surface unit cells are arranged either in-line or brick-lined at about 2/3 ML of InAs deposited on the GaAs(001)-c(4 × 4) surface. Moreover, Konishi and Tsukamoto [29] found that the domains of (1 × 3)/(2 × 3) and (2 × 4) are distributed in an ordered pattern closely related to the density of QD precursors just after nucleation on the basis of in-situ STM observations. Although many studies have been also done for surface structures on the InAs/GaAs(001) from theoretical viewpoints, there have been only a few theoretical studies for the (2 × 3) surfaces. Kratzer et al. [30] showed that the (2 × 3) reconstruction can be regarded as the main building unit of the InAs WL. In contrast with InAs/GaAs(111), there have been very few studies for the strain relaxation on the InAs WL. We have successfully investigated various semiconductor surface structures and the elemental growth processes on them using ab initio-based approach incorporating MBE growth conditions such as temperature T and beam equivalent pressure p [8,9,31,32,33,34]. In this chapter, we systematically discuss the novel behavior in hetero-epitaxial growth of InAs on GaAs(111)A and GaAs(001) surfaces including adsorption/desorption behavior and strain relaxation during MBE growth.
3.1. Surface Reconstructions on InAs(111)A WL
Figure 1 shows top view of InAs (111)A-(2 × 2) with In vacancy (VIn), As-adatom, and As-trimer (TAs) WL surface structures considered in this study. Figure 2 shows the calculated surface phase diagrams for (a) InAs(111)A WL surface (InAs(111)-WL) and (b) fully relaxed (FR) surface without interface structure of InAs/GaAs (InAs(111)-FR) as functions of temperature T and BEP of As4 molecules pAs4. Here, we assume that the BEP of In atom pIn in gas phase is pIn~10−7 Torr. The (2 × 2) with TAs is stabilized only at low temperatures, while the (2 × 2) with VIn appears at high temperatures. The stable temperature ranges for the (2 × 2) with VIn (beyond 550–600 K) on the InAs(111)-WL are consistent with MBE growth temperature range of 723–773 K (black area) at which the (2 × 2) with VIn is observed experimentally [20,35,36]. It should be noted that the InAs(111)-WL with As-adatom surface newly appears between stable regions of the (2 × 2) with VIn and the (2 × 2) with TAs, where the As adatom stably resides in the interstitial site bonding with three substrate In atoms. The large decrease in the charge density is found at surface As atoms on the In-vacancy surface [31]. This is because the electronegativity of In on the surface is smaller than that of Ga at the interface [37]. This results in breaking the electron counting model (ECM) [38,39] to destabilize the In-vacancy surface. The As-adatom surface makes up this deficiency in charge density, where the charge density around the As adatom is transferred to the substrate In atom to strengthen the interatomic bond between the In and As atoms. Therefore, the As-adatom surface appears as a stable phase between VIn and TAs on the InAs(111)-WL, while the InAs(111)-FR without interface Ga does not favor the As-adatom surface.
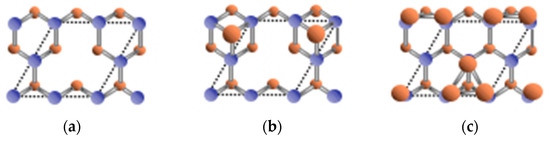
Figure 1.
Schematics of top view of InAs(111)A-(2 × 2) with (a) In-vacancy; (b) As-adatom; and (c) As-trimer surfaces considered in this study. Blue and orange atoms denote In and As, respectively.
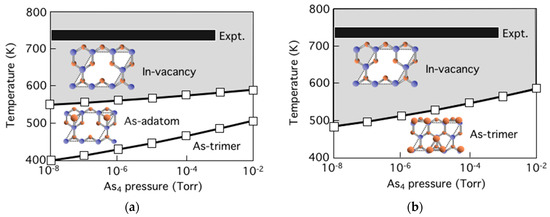
Figure 2.
Calculated surface phase diagrams for (a) InAs(111)A WL surface and (b) fully relaxed surface without interface structure of InAs/GaAs as functions of temperature and BEP of As4. Black area denotes the temperature range of the conventional MBE growth.
3.2. Growth Process on InAs(111)A WL
Figure 3 shows the calculated adsorption-desorption boundaries for In atom without (dotted line) and with simultaneous As adsorption (solid line) on the (2 × 2) with VIn of (a) the InAs(111)-WL and (b) the InAs(111)-FR as functions of T and pIn. These figures reveal that In adsorption on the In-vacancy surface does not occur without simultaneous As adsorption under conventional growth temperatures in the range of 723–773 K (black area). This is because In adsorption energies on the In vacancy surface dramatically decrease after As adsorption such as −1.76 eV without As to −4.17 eV with As on the InAs(111)-FR and −1.46 eV to −3.27 eV for the InAs(111)-WL. These findings thus imply that In adsorption is promoted only when As atoms are adsorbed on the InAs(111)A-(2 × 2) surface and the InAs growth proceeds with the adsorption of As atoms. This reveals that the self-surfactant effect is crucial for the growth processes similarly to the GaAs growth [40,41]. Moreover, it is found that relative stability among the surface lattice sites and adsorption energies for In adatom do not strongly depend on the layer thickness [31]. Therefore, it is expected that the strain in the WL does not significantly affect the adsorption-desorption transition curve and the kinetic behavior of In adatom. Considering the fact that the misfit dislocation is formed at 4–7 ML of InAs [23,24], these results suggest that strain accumulated in the WL is not significant for the hetero-epitaxial growth on the InAs(111)A to keep 2D growth at the initial growth stage.
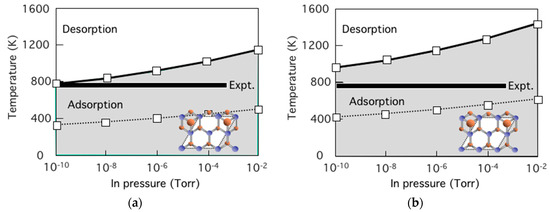
Figure 3.
Calculated adsorption-desorption boundaries for In atom without (dotted line) and with simultaneous As adsorption (solid line) on the (2 × 2) with In-vacancy of (a) the InAs(111)-WL and (b) the InAs(111)-FR as functions of temperature and BEP of In. Black area denotes the temperature range of the conventional MBE growth.
3.3. Strain Relaxation on InAs(111)A WL
In order to clarify the strain relaxation in the InAs/GaAs(111)A system, we employ the computational models including 2D growth with MD (2D-MD), 2D growth with SFT (2D-SFT), and the 2D coherent growth (2D-coherent). Figure 4 shows the calculated energy difference ∆EMD between the 2D-coherent and the 2D-MD as a function of layer thickness h [42]. Here, the MD core with five- and seven-member rings (5/7 core) are inserted at the interface between InAs and GaAs(111), as shown in Figure 4a. The 5/7 core is often found in transmission electron microscopy (TEM) observations [43], and is recognized to be the stable core structure in the MD formation energy calculations for compound semiconductors [44,45,46]. This reveals that the ∆EMD changes its sign from positive to negative at 7 ≤ h ≤ 8 ML, where the strain in InAs thin layers is relaxed to stabilize the 2D-MD. The critical layer thickness 7 ≤ h ≤ 8 ML for the MD generation agrees well with its value of h about 7 ML estimated from People-Bean’s formula to minimize energy in the entire crystal at thermodynamic equilibrium [47]. Using the calculated results shown in Figure 4a, the parameter values used in Equations (4) and (5) are determined to be M = 2.63 × 1010 (N/m2) and Ed = 0.675 (eV/Å).
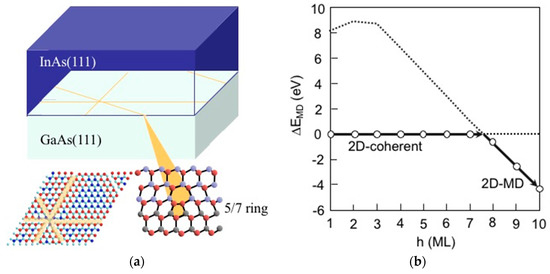
Figure 4.
(a) Schematic of the 2D growth with dislocation (5/7-ring core structure) network formation at the interface; (b) Calculated energy difference between the 2D coherent growth (2D-coherent) and the growth with MD (2D-MD) as a function of layer thickness h.
The calculated energy difference ∆ESFT between the 2D-coherent and the 2D-SFT as a function of layer thickness is shown in Figure 5 [42] along with the schematic of the SFT consisting of the face with stacking-fault and the ridge corresponding to stair-rod dislocation along the (110) direction, similarly to the SFT in Si [48]. The ∆ESFT with negative at h ≥ 4 ML suggests that the SFT formation acts as a strain relaxation mechanism near the surface as well as the MD formation at the interface in InAs/GaAs(111)A system. The ∆ESFT results from the competition between energy profit in the face region and energy deficits in the face and the ridge regions. The face region dramatically decreases the system energy due to strain relaxation, inducing upward displacements of atoms in the SFT that overwhelm the energy deficit due to the stacking-fault formation. In the ridge region, however, the stair-rod dislocation increases system energy due to its energetically unfavorable dimers along the ridge line, shown in Figure 5b. The calculated results shown in Figure 5b approximately determine the parameter value of ESFT = 0.014h − 0.0011h2 (eV) as a function of layer thickness h.
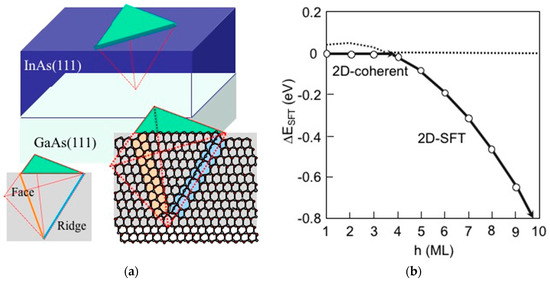
Figure 5.
(a) Schematic of the 2D growth with formation of stacking-fault tetrahedron (SFT) consisting of ridge and face; (b) Calculated energy difference between the 2D coherent growth (2D-coherent) and the growth with SFT (2D-SFT) as a function of layer thickness h.
3.4. Hetero-Epitaxial Growth of InAs on GaAs(111)A
Figure 6 depicts the calculated free energy differences ∆F between the 2D-coherent and various growth modes such as the 2D-MD and the 2D-SFT as a function of layer thickness h. It should be noted that the ∆F for the 2D-MD becomes negative at h about 6 ML different from 7 ≤ h ≤ 8 ML shown in Figure 4b. This means that the first isolated dislocation formation occurs at h ~ 6 ML, and the dislocation spacing l gradually decreases according to l = l0/(1 − hcMD/h) approaching the average dislocation spacing l0 (=58.76 Å) with increase of h, where hcMD is estimated by Ed/(Mε02l0) [21]. Figure 6 implies that the InAs growth on the GaAs(111)A proceeds along the lower energy path from the 2D-coherent (h ≤ 4 ML) to the 2D-MD (h ≥ 7ML) via the 2D-SFT (4 ML ≤ h ≤ 7 ML). This is consistent with STM observations, where faulted triangle domains containing stacking-faults appear with the MD network at 5 ML on the InAs/GaAs(111) [21]. Furthermore, a similar process was found in molecular dynamics simulations for (111)-oriented heteroepitaxial Al films forming a local disorder zone like the SFT near surface layers followed by the MD nucleation [49]. Experimental results, however, indicate that strain is gradually relieved beyond 1–2 ML, contradicting our calculated results with 4 ML [21,22]. This discrepancy can be interpreted by considering the fact that our computational model is not optimized for 2D-SFT. The 14 × 14 unit cell used in this study is not set for the SFT, but for the MD with geometrically optimized dislocation spacing. If the SFT spacing is optimized, the ∆ESFT becomes lower to give smaller layer thickness for the SFT formation. Moreover, employing the MD consisting of faulted and unfaulted domains observed by STM [21], further strain relaxation may occur at smaller layer thickness [23]. Consequently, our calculated results suggest that the first strain relaxation occurs near the surface due to the SFT formation before the MD formation at the interface. Assuming γ = 42 (meV/Å2) for the InAs(111)A, β = 0.084, and α = 0.748 extracted from the previously reported results for the InAs/GaAs(001) [50], the calculated free energy difference ∆F between the 2D-coherent and the SK-coherent is also shown in Figure 6. Although the ∆F for the SK-coherent becomes negative at 5 ML ≤ h ≤ 6 ML that is energetically competitive with the 2D-MD, the SK-coherent does not appear due to the 2D-SFT preceding the SK-coherent.
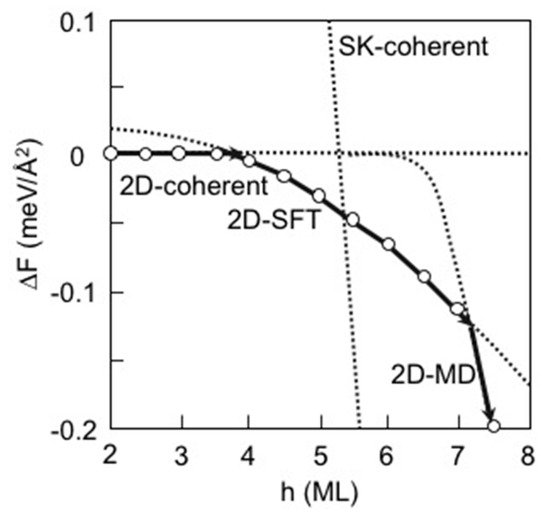
Figure 6.
Calculated free energy differences ∆F for various growth modes for the InAs/GaAs(111)A as a function of layer thickness h.
3.5. Surface Reconstructions on InAs(001) WL
The RHEED and the STM observations for InAs on GaAs(001) have clarified that the surface changes its structure from initial GaAs(001)-c(4 × 4)α surface to final InAs(001)-(2 × 4)α2 via InAs(001)-(1 × 3)/(2 × 3) with increase of InAs coverage [26]. On the basis of these results, the surface structural change is schematically shown in Figure 7 obtained by counting the number of In and As atoms deposited on the initial GaAs(001)-c(4 × 4)α with Ga-As surface dimers. The intermediate InAs(001)-(2 × 3) surface with In0.375Ga0.625As interface reasonably appears after 0.625 ML InAs deposited on the GaAs(001)-c(4 × 4)α. This is consistent with experimental findings where 2/3 ML InAs deposition creates the (2 × 3) surface with In1/3Ga2/3As [26,51,52,53]. Further deposition with 0.708 ML InAs realizes the (2 × 4) surface that is also consistent with the RHEED observations where the (2 × 4) appears supplying ~1.3–1.4 ML InAs on the GaAs(001)-c(4 × 4)α [26]. Here it should be noted that the desorption of 0.375 ML As is indispensable to realize the (2 × 4) surface during the structural change from the (2 × 3) to the (2 × 4). Figure 8a shows the calculated surface phase diagram for the InAs(001)-(2 × 3) and (n × 3) WL surfaces (n = 4, 6, and 8) as functions of T and pAs4. Here the (2 × 3) surface is fully covered by As-dimers on the surface while one As-dimer is missing every n As-dimers on the (n × 3) surfaces to approach satisfying the ECM at n = 8. This implies that the (2 × 3) surface is unstable at growth conditions, since desorption energy of As-dimer on the (2 × 3) surface is very small such as 1.12 eV to easily desorb from the WL surface to change its structure from the (2 × 3) to the (8 × 3) even at low temperatures. Figure 8b shows the calculated surface phase diagram for the InAs(001)-(2 × 4) WL surfaces as functions of T and pAs4. The phase boundary between the (001)-(2 × 4)α2 and the (001)-(2 × 4)β2 is ranging from 470 to 600 K. The stable temperature range of these structures is consistent with experimental conditions during MBE growth [52,54]. This reveals that (2 × 4)α2 is stable at the conventional growth conditions such as T~700–750 K and pAs4~10−7–10−6 Torr.
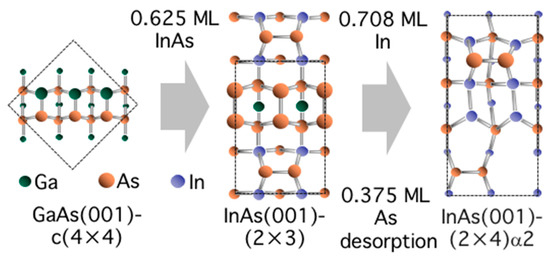
Figure 7.
Schematic of structural change during MBE growth from initial GaAs(001)-c(4 × 4) to InAs(001)-(2 × 4)α2 via InAs(001)-(2 × 3). Green, blue, and orange atoms denote Ga, In, and As, respectively.
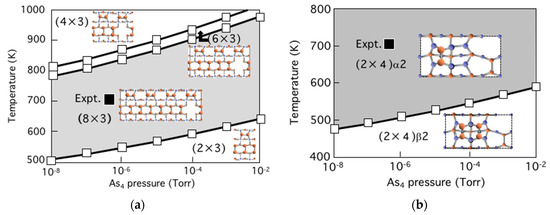
Figure 8.
Calculated surface phase diagrams for InAs(001) WL surfaces such as (a) (2 × 3) and (b) (2 × 4) as functions of temperature and BEP of As4. Black square denotes the t conventional MBE growth conditions.
3.6. Growth Process on InAs(001) WL
Calculated adsorption-desorption boundaries of In on the InAs(001)-(n × 3) WL surfaces is shown in Figure 9a as functions of T and pIn. This indicates that In adsorption does not occur on the (2 × 3) but is allowed on the (4 × 3), the (6 × 3), and the (8 × 3) at growth conditions. This is because the adsorption energy for In atom is very large such as −1.68 eV on the (2 × 3) in contrast with −3.87 eV on the (4 × 3), −3.66 eV on the (6 × 3), and −3.33 eV on the (8 × 3). This is because the stable adsorption site of In on the (2 × 3) is around the center position between upper As-dimer and lower As-dimer quite different from the missing As-dimer site on the (n × 3) as shown in Figure 9a. Figure 9b shows the calculated adsorption-desorption boundaries for As dimer on the stable In-adsorbed InAs(001)-(n × 3) WL surfaces as functions of T and pAs4. This implies that In adsorption does not induce As desorption, indispensable for InAs growth to change the surface structure from the (2 × 3) to the (2 × 4)α2, on the (4 × 3) and (6 × 3). Although As dimer desorption can be found on the (8 × 3) shown in Figure 9b schematically, it should be noted that newly appeared missing dimer is quickly occupied by In adatom to form the surface structure equivalent to the In-adsorbed (4 × 3) also schematically shown in Figure 9b. Moreover, it is found that further In adsorption also no longer occurs to prevent InAs growth on these (n × 3) WL surfaces.
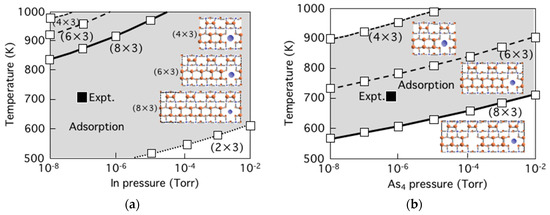
Figure 9.
Calculated adsorption-desorption boundaries for (a) In atom and (b) As-dimer on the InAs(001)-(n × 3) WL surfaces as functions of temperature and BEP of In and As4, respectively.
According to the results shown in Figure 9, another growth processes should be considered to allow In adsorption with simultaneous As desorption. On the (4 × 3), for example, it is found that In-As dimers stably reside on the (4 × 3) instead of As dimers at the conventional growth conditions [34]. Desorption of As dimer after forming In-As dimer in the missing dimer region is due to the fact that desorption energy of As dimer (1.44 eV) dramatically decreases from 2.84 eV on the initial (4 × 3) and 2.38 eV on the In-adsorbed (4 × 3). This is because adsorption of In-As dimer with bond length ~1.5 Å larger than As dimer largely deforms As dimer to destabilize it on the (4 × 3). Furthermore, In-As dimer adsorption replacing As dimer increases the number of In-As interatomic bond energetically more favorable than As-As interatomic bond to stabilize the (4 × 3). Figure 10 summarizes the sequence between for As dimer desorption and In-As dimer formation reflecting the change in the number of electrons in the surface dangling bonds (EC) on the (n × 3). It should be noted that In adsorption on the (8 × 3) induces As-dimer desorption to enhance further In adsorption to form In adsorbed (4 × 3) with subsequent As adsorption to form In-As dimer on the (4 × 3). Therefore, considering this In-As dimer formation process, the (8 × 3) is equivalent to the (4 × 3). Finally, the (4 × 3) consisting of three In-As dimers and one missing dimer, and the (6 × 3) with three In-As and two As dimers and one missing dimer appear on the InAs(001) WL surface. If we assume the existence ratio of the (4 × 3) and the (6 × 3) units satisfying 0.375 ML desorption of As to realize the (2 × 4)α2 as shown in Figure 7, the calculated f(4×3) = 0.70 and f(6×3) = 0.30 can be favorably compared with f(4×3) = 0.83 and f(6×3) = 0.17 estimated by directly counting the number of the units from Figure 2 in Ref. 27. Therefore, the (4 × 3) with three In-As dimers is most likely to appear among the (n × 3) WL surfaces during MBE growth. In order to realize the (2 × 4) α2 on the (4 × 3), further 0.5 ML In adsorption is necessary. It should be noted, however, In atoms are no longer incorporated on the (4 × 3) unless the strain is relaxed similar to the (2 × 4) α2 [33]. These results suggest that strain relaxation might occur at InAs coverage less than about 0.9 ML, contradicting well-known SK growth mode, to continue InAs growth.
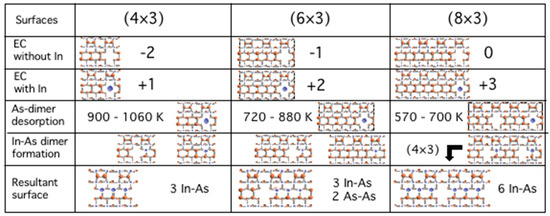
Figure 10.
Summary of the growth processes on the (n × 3) surfaces obtained in this study.
3.7. Strain Relaxation on InAs(001) WL
Figure 11 shows the calculated energy E for the 2D-coherent, the 2D-MD with 5/7-ring core, and 2D-MD with 8-ring core as a function of layer thickness h along with computational model used in this study. Here, the MD cores are inserted at the interface between InAs and GaAs(001) similarly to the InAs/GaAs(111)A. This reveals that the energy difference ∆EMD between the energies for the 2D-coherent and the 2D-MD with 5/7-core changes its sign from positive to negative at h~1.3 ML, where the strain in InAs thin layers is relaxed to stabilize the 2D-MD with 5/7-core [55]. Using the calculated results shown in Figure 11b, the parameter values used in the free energy formula are determined to be M = 5.72 × 1011 (N/m2) and Ed = 1.51 (eV/Å). These values easily lead the layer thickness for the first MD generation hc2D−MD using the relationship of hc2D−MD = Ed/(Mε02l0) [14]. The calculated results suggest that the first MD formation occurs at 0.5 ML and the MD spacing l2D−MD gradually decreases with increase of the layer thickness according to l2D−MD = l0/(1 − hc2D−MD/h) to effectively relax the strain accumulated in the InAs layers. Therefore, the MD formation is one of possible mechanisms of eliminating lattice strain to proceed the growth on the InAs(001)-(n × 3) WL surfaces.
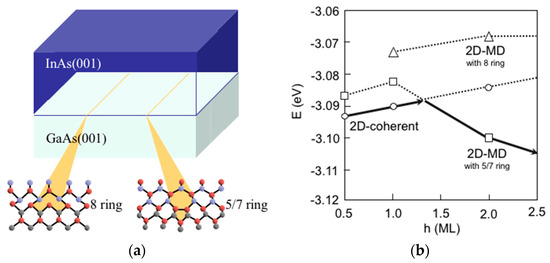
Figure 11.
(a) Schematic of the 2D growth with dislocation (8-ring core and 5/7-ring core) formation at the interface; (b) Calculated energy for the 2D coherent growth (2D-coherent) and the 2D growth with MD (2D-MD with 8-ring and 2D-MD with 5/7-ring) as a function of layer thickness h.
3.8. Hetero-Epitaxial Growth of InAs on GaAs(001)
On the basis of physical quantities γ = 51 (meV/Å2) for the InAs(001), β = 0.076, and α = 0.188 extracted from the previously reported results for the InAs/GaAs(001) [50], Figure 12 shows the calculated free energy differences ∆F between the 2D-coherent and various growth modes such as the 2D-MD and the SK-coherent as a function of layer thickness h. It is found that the ∆F for the 2D-MD becomes negative at 0.46 ML, while negative ∆F appears at 0.75 ML for the SK-coherent. This suggests that the initial 2D coherent growth mode changes into the 2D growth mode with MD formation. Therefore, strain relaxation occurs at early growth stage before the SK island formation. This is not consistent with well-known QD formation mechanism due to the SK island formation but is consistent with the fact that strain accumulated in InAs(001)-(n × 3) WL should be relaxed at InAs coverage less than about 0.9 ML to continue InAs growth as pointed out in Section 3.6. Although further careful investigations incorporating surface reconstructions as a submonolayer phenomenon are necessary for confirming the strain relaxation for the InAs/GaAs(001), the calculated results for the InAs/GaAs systems suggest that the strain relaxation due to the MD formation to produce the 2D growth is competitive with the SK-island formation inducing the 3D growth during MBE growth.
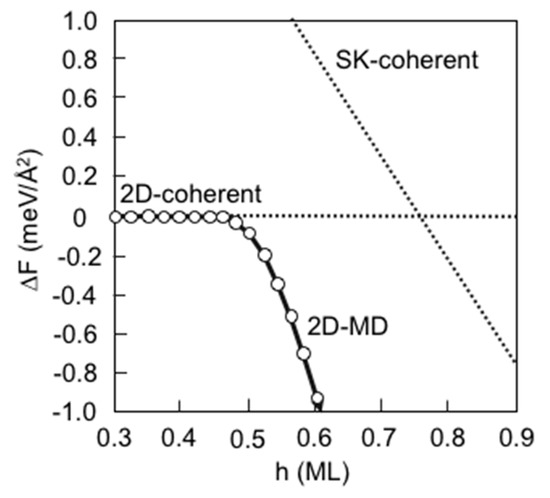
Figure 12.
Calculated free energy differences ∆F for various growth modes for the InAs/GaAs(001) as a function of layer thickness h.
3.9. Quantum Dot Formation of InAs
Using Equations (5) and (7), the boundary between the 2D-MD and the SK-coherent is simply described as β/α = 1/(2γ)(Ed/l0). Using the MD formation energy Ed = 0.675 (eV/Å) for InAs/GaAs(111)A and 1.51 (eV/Å) for InAs/GaAs(001) obtained by our empirical potential calculations, Figure 13 shows the growth mode boundaries for the InAs/GaAs system depending growth orientations as functions of β/α and surface energy γ. This reveals that the stable region of the 2D-MD in the InAs/GaAs(111)A is larger than that in the InAs/GaAs(001) because of its smaller MD formation energy. Furthermore, the larger the β/α and γ, the more favourable the 2D-MD. This is because the energy increase in surface energy γβ tends to overwhelm the decrease in strain energy −Mαε02h/2 due to SK-island formation. According to these facts, the surface energy γ in addition to Ed is a crucial factor for determining the growth mode, since the change in γ is related not only to γ itself but also to β/α through γβ. Figure 13 also includes the boundary denoted by dotted line for the InAs/GaAs(110) with Ed = 0.96 (eV/Å) obtained by ab initio calculations [14]. The InAs/GaAs(110) system has been extensively examined using RHEED, TEM, and STM for a wide range of film thickness where the growth follows a layer-by-layer mode irrespective of thickness and strain relaxation occurs solely by the formation of MD [20,56]. However, self-assembled InAs QD has been realized on GaAs(110) using MBE with buffer layer insertion [57] and MOVPE with optimizing growth temperature [58], where the strain reduction is considered to be a crucial origin of the QD formation. This novel QD formation can be interpreted by considering the change in γ. It is known that the strain reduction lowers the surface energy by 10–20 (meV/Å2) [50]. Assuming β/α = 0.2 and γ = 50 (meV/Å2) (denoted by closed diamond in Figure 13), the 2D-MD is favourable without strain relaxation while decrease in γ due to strain relaxation with the buffer-layer insertion easily changes favourable growth mode from the 2D-MD to the SK-coherent found in the (110). Although the dependence of β/α and γ on strain relaxation should be rigorously investigated using ab initio calculations, Figure 13 gives an insight on the growth modes among different oriented InAs/GaAs systems such that (001), (110), and (111)A favours the 3D growth, the 2D and the 3D growths depending on the strain relaxation, and the 2D growth, respectively. Consequently, the QD formation on the InAs/GaAs can be qualitatively interpreted by considering γ and Ed.
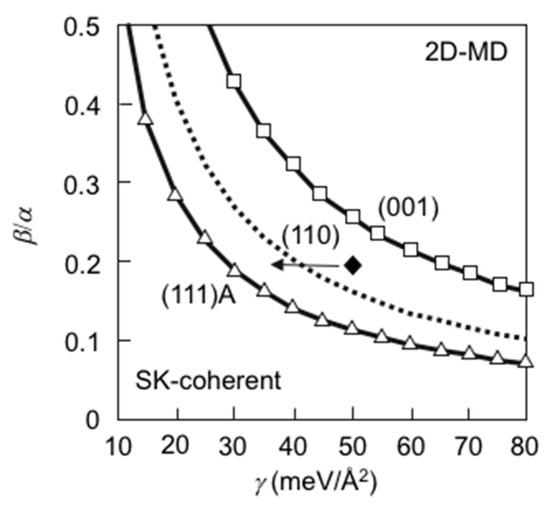
Figure 13.
Calculated growth mode boundaries as functions of β/α and γ for the InAs/GaAs systems with different orientations. Open square and open triangle denote the results for the (001)- and the (111)A-oriented InAs/GaAs, respectively. The growth mode boundary (dotted line) and the data (closed diamond) for the InAs/GaAs(110) are also shown in this figure.
4. Growth Processes of InP NWs
Semiconductor NWs have great potential to understand the fundamental roles of reduced dimensionality and size in optical, electrical, and mechanical properties and their wide range of potential applications in nanoscale devices. So far, semiconductor NWs have been fabricated by various growth methods such as MOVPE [59,60], MBE [61,62,63], and laser assisted catalytic growth [64,65,66]. In particular, InP NWs are intriguing targets in fiber optic communications, high-speed electronic applications, and photovoltaic devices, such as p–n junction light-emitting diodes [67], field effect transistors [67], one-dimensional polarization-sensitive photodetectors [65], solar cells [68], and so on. It has been reported that semiconductor NWs grown in the [111] direction have some structural characteristics different from those of bulk crystals: semiconductor NWs often incorporate the WZ segments as stacking faults in the zinc blende (ZB) structure [69,70,71,72,73,74,75,76,77,78,79,80,81,82,83], which is called a rotational twin structure, as shown in Figure 14. It has also been suggested that rotational twins significantly affect the electronic properties of the NWs: discontinuity of the electron wave function occurs at the stacking fault, leading to a reduced mobility of carriers [84]. Therefore, the structural stability of InP NWs has been intensively discussed because of the small energy difference between the ZB and WZ structures in bulk form [85].
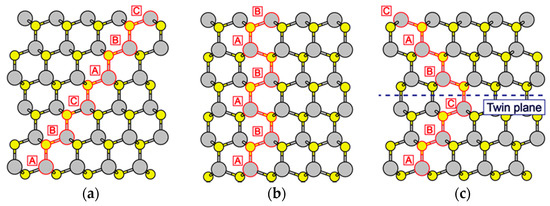
Figure 14.
Schematics of crystal structures of III-V compound semiconductors. Large and small circles represent cations and anions, respectively. Stacking sequences of (a) zinc blende (ZB) and (b) wurtzite (WZ) structures are and , respectively, while (c) rotational twins are formed in semiconductor nanowires (NWs). Dashed line denote a twin plane.
Despite these experimental findings, twinning formation processes in InP NWs have not been clarified from theoretical viewpoint. The relative stability between the ZB and WZ structures in InP NWs have been clarified using empirical interatomic potential calculations: the WZ structure can be stabilized when the contribution of NW side facets to the cohesive energy is prominent, and the WZ structure is more stable than the ZB structure for NWs with small diameters [86,87]. Glas et al. have theoretically suggested that the growth processes affect the formation of the WZ structure in NWs [88,89]. However, elementary processes such as adsorption and desorption behaviors of In and P atoms at the growth forefront have never been studied at present. In particular, it is still unclear how the atoms are adsorbed at the lattice sites of the WZ structure at the top layer of NWs under growth conditions. Another important characteristics of InP NWs is that the plane direction of substrates depends on experimental methods. InP NWs fabricated by selective-area MOVPE (SA-MOVPE) are grown on the InP(111)A substrates [90,91]. On the other hand, InP(111)B substrates are used for InP NWs synthesized by vapor–liquid–solid (VLS) growth [70,85,92]. Mohan et al. have reported that InP NWs with the pure WZ structure are synthesized by the SA-MOVPE [90]. Kitauchi et al. have revealed that the crystal structure of InP NWs grown by the SA-MOVPE depends on growth conditions such as temperature and partial pressure of the supplied gas [91]. InP NWs grown for high temperature and low P pressure take the pure WZ structure, whereas those with rotational twins are fabricated for low temperature and high P pressure. Furthermore, these results suggest the formation of the WZ crystal phase even in (111)A planar layers. These experimental results imply that the growth process of InP layers on InP(111)A surface in itself affects the crystal structure of InP NWs. In spite of these experimental findings, temperature and pressure dependence of structural stability of InP layers on InP(111)A surface still remains unclear. In the SA-MOVPE, it can be considered that not only side facets but also the growth mechanism of InP layers on the surface is quite important for determining their crystal structure. However, little is known about the elemental growth processes of InP layers on InP(111) surface. The knowledge for adsorption and desorption behavior of In and P atoms on InP(111) surfaces is lacking.
Furthermore, Kitauchi et al. have also revealed that InP NWs are composed of side facets (see Figure 15a) for high temperature (660 °C) and low V/III ratio, where the lateral growth does not occur. On the other hand, the growth in the lateral direction takes place for low temperatures (600 °C) and high V/III ratio, and InP NWs with lateral growth consist of side facets (see Figure 15b). It has also been reported that InP NWs consisting of side facets without lateral growth are fabricated for intermediate temperature (625 °C) and V/III ratio. A similar structural characteristic has been found in InP NWs grown by both the SA-MOVPE and the VLS growth. InP NWs grown by VLS growth consist of ( in cubic crystal) or {111} side facets without the lateral growth [76,79,84]. In addition, it has been reported that GaAs NWs fabricated by VLS growth are composed of ( in cubic crystal) side facets with the lateral growth [78]. However, temperature and pressure dependence of the shapes in semiconductor NWs still remains unclear.
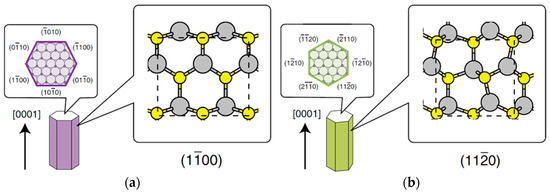
Figure 15.
Schematics of InP NWs consisting of (a) and (b) side facets. Cross-sectional views and side views of NW facets are also shown. Dashed red lines in the top views represent unit cells. Large gray and small yellow circles represent In and P atoms, respectively.
In this chapter, focusing on the top layer of growing NWs, we discuss the adsorption and desorption behaviors of In and P atoms during SA-MOVPE, taking account of the effects of NW side facets. By using our ab initio based approach incorporating growth conditions such as temperature T and pressure p, [8,9] we determine whether the adatoms are adsorbed at the lattice site of the ZB or the WZ structure on the top layer. We also discuss the growth processes of InP epitaxial layers on InP(111)A P-stabilized surface. In particular, adsorption–desorption behavior on InP(111)A surface is calculated by our ab initio-based approach. We demonstrate temperature and pressure dependence of structural stability of InP layers, leading to the formation of rotational twins at low temperature and high V/III ratio conditions. Furthermore, focusing on the side facets of InP NWs grown by the SA-MOVPE, we investigate the initial growth processes on both and side facets surfaces. Assuming the WZ structure is assumed because the WZ structure is feasible compared with the ZB structure in InP NWs. In particular, adsorption–desorption behavior on these facets is calculated by our first-principles-based approach which incorporates the growth conditions such as temperature and pressure. We compare the growth rates of and surfaces using Monte Carlo (MC) simulations and clarify temperature and pressure dependence of the shapes in InP NWs.
4.1. Nanowire Growth on the Basis of Classical Nucleaton Theory
In this section, we briefly explain the conventional nanowire growth model using classical nucleation theory, which have been successfully applied for NWs synthesis with WZ structure by the VLS growth [79,88,89,93]. During the VLS growth, we assume a two-dimensional nucleus with semicircles shape at the interface between top layer of NW and liquid catalysis, and NWs are formed according to the formation of two dimensional nuclei. The Gibbs free energy of a nucleus with ZB structure ΔG(r) is given by
where r is radius of nucleus with semicircle shape, Δμliquid-solid is chemical potential difference (per unit area) between liquid and solid phases, σint is the interface energy per area between nucleus and nanowire top layer, and Γstep is the contribution of the step energy caused by a two-dimensional nucleus. According to Equation (19), the critical radius for nucleation r* satisfy the condition, ∂G(r)/∂r = 0. Therefore, r* and activation energy for nucleation ΔG* are written as
ΔG(r) = −πr2Δμliquid-solid/2 + πr2σint/2 + rΓstep,
r* = Γstep/π(Δμliquid-solid − σint),
ΔG* = Γstep2/(2πΔμliquid-solid).
On the other hand, the activation enegy for nulceation with WZ structure, ΔG*WZ, is also written as
where ΓWZstep is the contribution of the step energy caused by two dimensional growth with WZ structure, and σWZint is the interface energy for WZ structure. The WZ structure is formed satisfying ΔG* < ΔG*WZ, and the boundary between ZB and WZ structure in NWs are obtained using the step energy difference ΔΓstep = Γstep − ΓWZstep, as
ΔG*WZ = ΓWZstep2/{2πΔμliquid-solid − σWZint}},
(1 − ΔΓstep/Γstep)−2 = (1 − σWZint/Δμliquid-solid)−1
Using this relationship, we find that NWs with WZ structure is stabilized when ΔΓstep and/or Δμliquid-solid is large. Figure 16 shows the estimated phase diagram for crystal structure of InP NWs as functions of Δμliquid-solid and ΔΓstep/Γstep using the energy difference between ZB and WZ structures in bulk InP (6.8 meV/atom) [86] for σWZint. Actually, this figure manifests that the WZ structure is stabilized if Δμliquid−solid is large and ΔΓstep/Γstep takes positive value. Similar results have been obtained if we take more sophisticated nucleation model into account to evaluate the free energies [88,89,91]. These results suggest that the stability of the step and driving force for nucleation during the VLS growth are crucial for the formation of NWs with WZ structure.
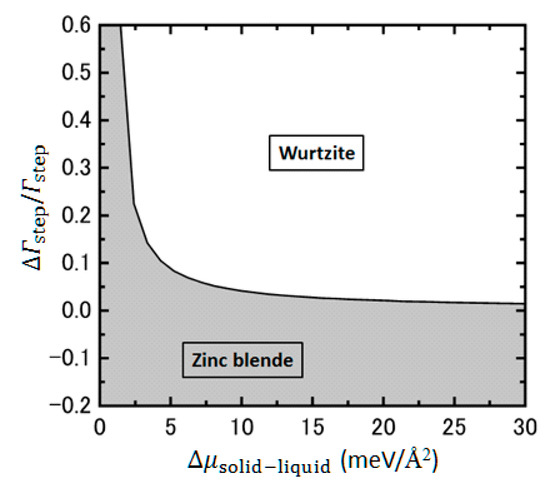
Figure 16.
Phase diagram for crystal structure of InP NWs as functions of chemical potential difference between liquid and solid phases Δμliquid-solid and normalized step energy difference between ZB and WZ structures ΔΓstep/Γstep, using the energy difference between ZB and WZ structures in bulk InP (6.8 meV/atom) [87] for interface energy per area between nucleus and nanowire top layer for WZ structure σWZint. White and grey areas denote the stable regions for WZ and ZB structures, respectively.
4.2. Effect of Side Facets on Adsorption–Desorption Behaviors at Top Layers in InP NWs
In order to clarify the effects of NW side facets during the SA-MOVPE, we have to consider adsorption-desorption behavior on two kinds of growth regions. One is a central area on the top layer of InP NWs, where we adopt the (2 × 2) surface with P trimer as a calculation model. It is expected that the the (2 × 2) surface with P trimer appears because it satisfies the ECM [38,39], and previous theoretical calculations also support the stabilization of the P trimer on the InP(111)A surface under P-rich conditions [94]. Since the InP NWs are grown under high P pressures [91], this surface could be a possible surface reconstruction during the growth of NWs. In addition, investigating adsorption–desorption behavior on the (2 × 2) is quite important since the adsorption site of In atoms determines the crystal structure. Another growth area we have to consider is a side area, where the calculation model of the side area consists of both (111)A and surfaces. Here, we assume the (2 × 2) surface with P trimer on the top surface of the side area. For the central area of NWs, the calculated adsorption energy of P atom is a positive value (2.26 eV). This indicates that the adsorption of a single P atom does not occur even at 0 K. Thus, it is reasonable to consider the adsorption of a P atom on an In-preadsorbed surface, which corresponds to the self-surfactant effect [40,41]. We also find that the adsorption of a P atom with one and two In atoms is also inhibited under the typical growth conditions. The adsorption occurs only below 200 °C Figure 17 shows the calculated adsorption of a P atom with three In atoms (3 In-P), which has the highest adsorption probability [90].
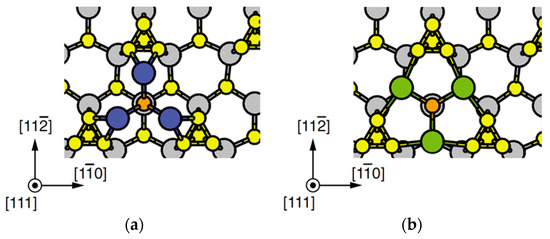
Figure 17.
Top views of (a) 3In-P occupying the ZB lattice sites (3In-ZB-P) and (b) 3In-P occupying the WZ lattice sites (3In-WZ-P) on the InP(111)A surface. Large and small circles represent In and P atoms, respectively. Blue and green circles denote the In adatoms that occupy the lattice sites of the ZB and WZ structures, respectively. Orange circles represent the P adatoms. Reprinted with permission from [95]. Copyright (2011) by the Japan Society of Applied Physics.
This kind of adsorption process is similar to those on the GaAs(111)A surface, in which the surface with three Ga and one As atom appears in the growth process on the GaAs(111)A-(2 × 2) surface [96]. The calculated adsorption energy difference between the three In atoms occupying the ZB lattice sites (3In-ZB-P shown in Figure 17a) and those occupying the WZ lattice sites (3In-WZ-P shown in Figure 17b) is very small (0.07 eV). Figure 18 displays the calculated phase diagrams of the 3In-ZB-P and 3In-WZ-P adsorbed surfaces, respectively, as functions of temperature and P2 pressure. The pressure of In is taken to be Torr, which corresponds to a typical growth condition [90,91]. These surface phase diagrams for the adsorption P atoms exhibits little difference in the adsorption probability between 3In-ZB-P and 3In-WZ-P. The small energy difference is due to similar bonding configurations, where both 3In-ZB-P and 3In-WZ-P form nine In-P bonds regardless of the adsorption site. These results imply that the WZ structure as well as the ZB structure can be formed when nucleation occurs away from the NW side facets.
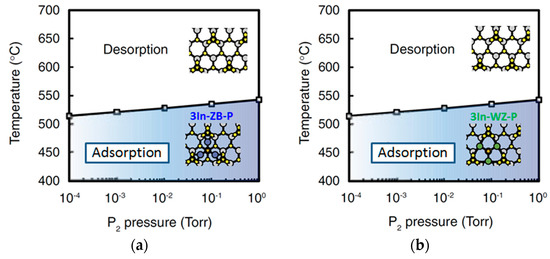
Figure 18.
Calculated phase diagrams of (a) 3In-ZB-P and (b) 3In-WZ-P adsorbed surfaces as functions of temperature and P2 pressure. In pressure is taken to be Torr. Colored regions correspond to the atom-adsorbed regions. Reprinted with permission from [95]. Copyright (2011) by the Japan Society of Applied Physics.
The calculations for the adsorption–desorption behavior in the side area demonstrate that the calculated adsorption energy is positive though the adsorption of a P atom at its lattice site is necessary. Therefore, we can expect the self-surfactant effect [40,41] in the same way as in the central area. The calculations for the adsorption of a P atom with In atoms demonstrate that the adsorption probability of two P atoms with four In adatoms has the highest value. Figure 19 shows the geometries of two P adatoms with four In adatoms occupying the ZB (4In-ZB-2P) and WZ (4In-WZ-2P) lattice sites near the side facet, respectively. The adsorption energy of 4In-ZB-2P is found to be higher than that of 4In-WZ-2P by 0.46 eV. There is a two-coordinated In adatom in 4In-ZB-2P, shown in Figure 20a, whereas all the In adatoms in 4In-WZ-2P are three-coordinated. The three-coordinated In adatom at the side facet in 4In-WZ-2P originates from the formation of an In-P bond with the P atom in the second layer, as shown in Figure 20b. Therefore, the formation of the three-coordinated In adatom results in the stabilization of the surface with 4In-WZ-2P. Figure 21 shows the calculated phase diagrams for the adsorption of the surface with 4In-ZB-2P and 4In- WZ-2P, respectively. These surface phase diagrams suggest that the stable temperature range of the surface with 4In-WZ-2P is higher than that with 4In-ZB-2P by 25 K. It is thus expected that the WZ structure is preferentially formed when the nucleation occurs near the NW side facets.
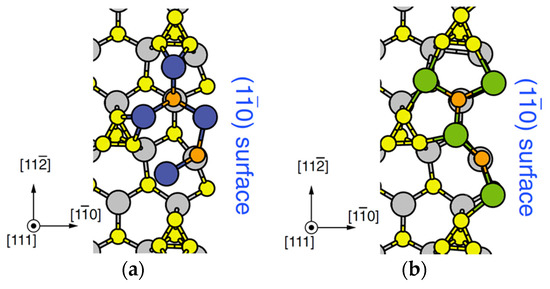
Figure 19.
Top views of (a) 4In-2P occupying the ZB lattice sites (4In-ZB-2P) and (b) 4In-2P occupying the WZ lattice sites (4In-WZ-2P) near the side facet. There is a two-coordinated In adatom indicated by the red circle in 4In-ZB-2P, whereas all the In adatoms in 4In-WZ-2P are three-coordinated. The three-coordinated In adatom at the side facet in 4In-WZ-2P is due to the formation of In-P bonds with the P atom in the second layer. Reprinted with permission from [95]. Copyright (2011) by the Japan Society of Applied Physics.
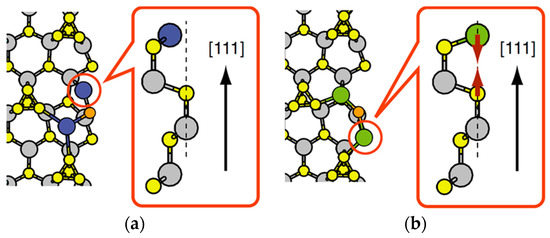
Figure 20.
Top views of (a) 4In-ZB-2P and (b) 4In-WZ-2P adsorbed surfaces in the side area. There is a two-coordinated In adatom indicated by the red circle in 4In-ZB-2P, whereas all the In adatoms in 4In-WZ-2P are three-coordinated. The three-coordinated In adatom at the side facet in 4In-WZ-2P is due to the formation of In-P bonds with the P atom in the second layer. Reprinted with permission from [96]. Copyright (2011) by the Japan Society of Applied Physics.
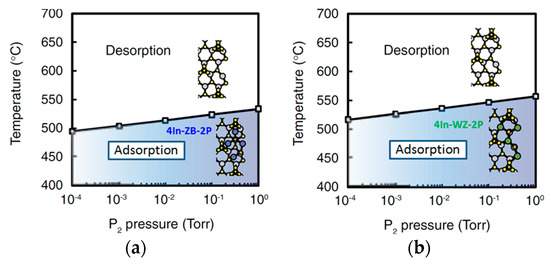
Figure 21.
Calculated phase diagrams of (a) 4In-ZB-2P and (b) 4In-WZ-2P adsorbed surfaces as functions of temperature and P2 pressure. In pressure is taken to be Torr. Colored regions correspond to the atom-adsorbed regions. Reprinted with permission from [95]. Copyright (2011) by the Japan Society of Applied Physics.
To determine the predominant area for the nucleation, we estimate the difference in adsorption probability between the central and side areas. By comparing the phase diagram shown in Figure 18 with that in Figure 21b, it is concluded that the difference in the adsorption probability between the central and side areas to be negligible, so that adsorption occurs in both the central and side areas. Since the ratio of the central area is large for NWs with large diameters, the crystal structure in NWs with large diameters is mainly dominated by the nucleation at the central area. The small energy difference between the ZB and WZ structures at the central area could results in the formation of rotational twins for NWs with large diameters. In contrast, most of the top layer consists of side facets for NWs with small diameters. The crystal structure in NWs with small diameters is thus dominated by the nucleation on the side facets, resulting in the preference of NWs with WZ structure under the growth conditions. The preference of the WZ structure over the ZB structure in InP NWs with small diameters is qualitatively consistent with the experimental results [90,91].
4.3. Nanowire Growth Processes under Epitaxial Growth Condirions
Figure 22 shows the lattice sites of In atoms for the WZ and ZB structures on the surface with P trimer [91]. Focusing on these adsorption sites, we discuss adsorption–desorption behavior of In and P atoms under growth conditions. On the basis of experimental results, we here consider two types of growth conditions: high temperature and low V/III ratio (660 °C and V/III ratio is 18, condition (A) hereafter) and low temperature and high V/III ratio (600 °C and V/III ratio is 55, condition (B) hereafter) [91]. Figure 23 shows contour plots of adsorption energies for In and P atoms, respectively [97]. The values of contour plots are measured from the values of chemical potentials μgas in Equations (1) and (2) under the growth condition (B) which are −2.5 and −1.2 eV for In and P, respectively. There are four adsorption sites for an In atom labeled 1, 2, 3, and 4 in Figure 23a. Three of them (sites 1, 2, and 3) are symmetrically equivalent and correspond to the adsorption sites for the ZB structure, and the other (site 4) corresponds to the adsorption site for the WZ structure. The adsorption energy difference among the adsorption sites for the WZ and ZB structure is negligible (0.06 eV). The positive values of adsorption energy (0.60 and 0.66 eV) indicate that the adsorption hardly occurs under typical growth conditions [90,91]. The calculated adsorption probability estimated using Equation (12) of an In atom under the growth condition (B) is found to be less than 0.03%. However, even if the adsorption probability is 0.03%, the adsorption occurs. This is because of the stabilization of the P trimer. The P trimer on (2 × 2) surface hardly desorbs under typical growth conditions. Indeed, the MC simulations for adsorption, migration and desorption of an In atom on the P trimer surface demonstrate that the adsorption of an In atom occurs even under the growth conditions (A) and (B), and surface lifetime and diffusion length of an In adatom are relatively large. The relatively large values in lifetime and diffusion length is due to low migration barriers on the (2 × 2) surface with P trimer less than 0.13 eV.
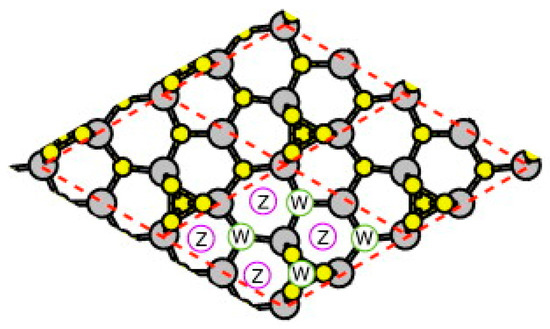
Figure 22.
Top view of the surface with P trimer surface. Red dashed lines correspond to the (2 × 2) unit cells. Large and small circles represent In and P atoms, respectively. Symbols of W and Z stand for In lattice sites in the WZ and ZB structures, respectively. Reprinted with permission from [97]. Copyright (2013) by Elsevier.
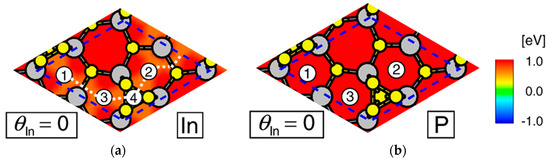
Figure 23.
Contour plots of adsorption energies for (a) In and (b) P atoms on the P trimer surface. These contour plots are indicated by colors with respect to μgas under the growth condition (B) which is displayed in green region. Atoms tend to adsorb (desorb) in blue (red) colored regions under the growth condition (B). Encircled numbers represent adsorption sites. The coverage of In (θIn) and a kind of atom for contour plots are denoted at the lower left and right, respectively. Dotted white lines in (a) denotes a possible migration path of In adatom. Reprinted with permission from [98]. Copyright (2013) by Elsevier.
The migration path of In adatom corresponds to the orange-colored region in Figure 23a. Moreover, this also supports that the number of atoms consisting of the critical nuclei on InP(111)A surface is estimated to be small (10 at most) [98]. The small number of atoms implies that nucleation on the surface can be formed under typical growth conditions. Figure 23b shows that there are three symmetrically equivalent adsorption sites (labeled by encircled numbers such as 1, 2, and 3) for a P atom. The calculated adsorption energies at these sites in Figure 23b are 0.91 eV. The adsorption probability of a P atom under growth condition (B) (5 × 10−4%) is much lower than that of an In atom. From these results, the adsorption of an In atom is obviously feasible compared with that of a P atom on the (2 × 2) surface with P trimer. It is thus concluded that the crystal growth on the (2 × 2) surface starts with the adsorption of an In atom. Further investigations for the adsorption of In and P atoms on the In-adsorbed surfaces clarify that there are two types of plausible growth processes depending on the growth conditions.
Figure 24 shows the growth process which is feasible under the growth conditions (A) and (B), leading to the formation of an InP monolayer belonging to the WZ structure. First, the adsorption of an In atom occurs at the site 4 on the surface with In coverage of zero (θIn = 0). There are three symmetrically equivalent and stable adsorption sites for an In atom on the surface with θIn = 1/4, which correspond to the WZ structure. The calculated adsorption energy is −0.54 eV. The surface with θIn = 2/4 represents the surface after adsorption of an In atom at the site 1 on the surface with θIn = 1/4. After the formation of the surface with θIn = 2/4, the adsorption of an In atom with calculated adsorption energy of −0.06 eV subsequently occurs at one of the two symmetrically equivalent. The surface after the adsorption of a P atom is the surface with In vacancy surface which is well known as a stable surface satisfying the ECM [38,39]. It should be noted that this In vacancy surface has an InP monolayer belonging to the WZ structure. In order to verify whether this process is likely under the growth conditions, we have calculated phase diagrams as functions of temperature and pressures. Figure 25a illustrates the adsorption–desorption behavior of an In atom on the surface with θIn = 1/4 shown in Figure 24. This calculated phase diagram manifests that the adsorption of an In atom easily occurs and stabilizes the surface under both the growth conditions (A) and (B). The adsorption of an In atom at θIn = 1/4 originates from the fact that the In-adsorbed surface corresponding to θIn = 2/4 satisfies the ECM [38,39]. As shown in Figure 25b, the adsorption of an In atom occurs on the surface with θIn = 2/4 under the growth condition (B) (red triangle), while the growth condition (A) is located near the boundary between adsorption and desorption (red circle). However, the adsorption possibility of an In atom under the growth condition (A) is relatively high (15%). The adsorption of an In atom certainly occurs even under the growth condition (A). In addition, once the adsorption of an In atom occurs, a P atom adsorbs easily and stabilizes the surface as shown in Figure 25c. The growth process shown in Figure 24 indeed occurs under both the growth conditions (A) and (B), suggesting that an InP monolayer belonging to the WZ structure is formed.
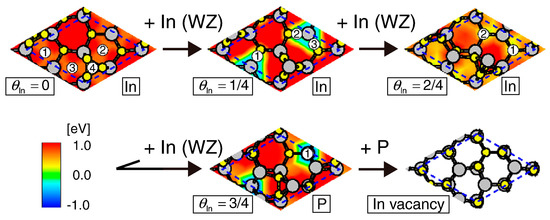
Figure 24.
Growth process which is plausible under the growth conditions (A) and (B). The adsorption of a P atom occurs on the surface with θIn = 3/4. This growth process results in formation of an InP monolayer belonging to the WZ structure. Reprinted with permission from [97]. Copyright (2013) by Elsevier.
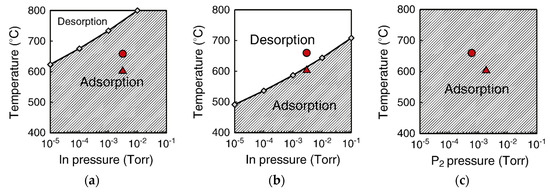
Figure 25.
Calculated phase diagrams as functions of temperature and pressure in the growth process shown in Figure 21. Panels (a) and (b) show adsorption–desorption behavior of an In atom on the surface with θIn = 1/4 and 2/4, respectively. Panel (c) illustrates adsorption–desorption behavior of a P atom on the surface with θIn = 3/4. Regions with hatched lines correspond to atom-adsorbed regions. Red circles and triangles represent the growth conditions (A) and (B), respectively. Reprinted with permission from [97]. Copyright (2013) by Elsevier.
Figure 26 shows the growth process which is feasible only under the growth condition (B), leading to the formation of an InP monolayer belonging to either the WZ or ZB structure. The adsorption of an In atom occurs at the adsorption site for the ZB structure (the site 3 in Figure 26) on the P trimer surface (θIn = 0). There are two symmetrically equivalent adsorption sites for a P atom on the surface with θIn = 1/4, which are located at near P lattice sites, whose adsorption energy is −0.02 eV. The P-adsorbed surface with = 1/4 represents the surface after adsorption of a P atom at the site 2. The adsorption of an In atom subsequently occurs after the formation of the P-adsorbed surface. Although there are three adsorption sites for an In atom on the P-adsorbed surface, these three sites are no longer equivalent, so that calculated adsorption energies at the sites 1, 2, and 3 are different with each other (−0.07, −0.05, and 0.37 eV, respectively). The positive value at the site 3 indicates that the adsorption of an In atom hardly occurs. Consequently, this growth process splits into two sub-processes with almost the same probabilities after the adsorption of a P atom. One of the two sub-processes starts with the adsorption of an In atom at the site 1 which corresponds to the adsorption site for the WZ structure. The adsorption of an In atom (the calculated adsorption energy is −2.00 eV) at site 1 easily occurs on the surface with θIn = 2/4 in this sub-process, leading to the formation of the In vacancy surface which has an InP monolayer belonging to the WZ structure. The other sub-process begins with the adsorption of an In atom at the site 2, which corresponds to the adsorption site for the ZB structure, on the P-adsorbed surface with θIn = 1/4. The calculated adsorption energy of an In atom at site 1 on the surface with θIn = 2/4 is −1.95 eV, resulting in the formation of the In vacancy surface which has an InP monolayer belonging to the ZB structure.
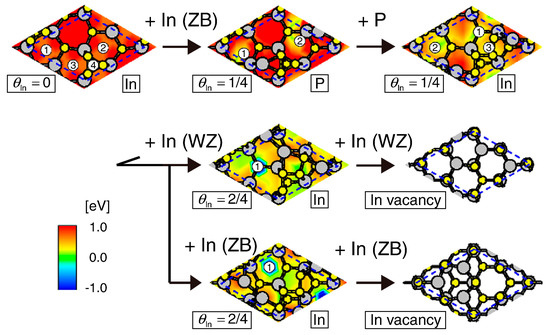
Figure 26.
Growth process which is feasible only under the growth condition (B). The adsorption of a P atom occurs on the surface with θIn = 1/4. This growth process splits into two sub-processes after the adsorption of a P atom, and results in the formation of an InP monolayer belonging to the WZ or ZB structure. Reprinted with permission from [97]. Copyright (2013) by Elsevier.
Figure 27 shows calculated phase diagram for the adsorption of a P atom on the surface with θIn = 1/4 in the growth process shown in Figure 26. The phase diagram indicates that a P atom can adsorb on the surface with = 1/4 only under the growth condition (B). Therefore, this growth process can occur only under the growth condition (B). The adsorption of a P atom on the surface with θIn = 1/4 under the growth condition (B) is predominant for the growth process shown in Figure 26, which is quite different from that in the growth process shown in Figure 24. This is because the P-adsorbed surface satisfies the ECM [38,39], and is stabilized only for low temperatures and high P pressures. Although the adsorption probability of a P atom under the growth condition (A) might not be zero, the growth process shown in Figure 24 must be dominant under the growth condition (A) as shown in Figure 25a). The growth process shown in Figure 26 occurs only under the growth condition (B), leading to the formation of InP layers with both WZ and ZB structures. Both WZ and ZB structures can be grown with the same probability under growth condition (B).
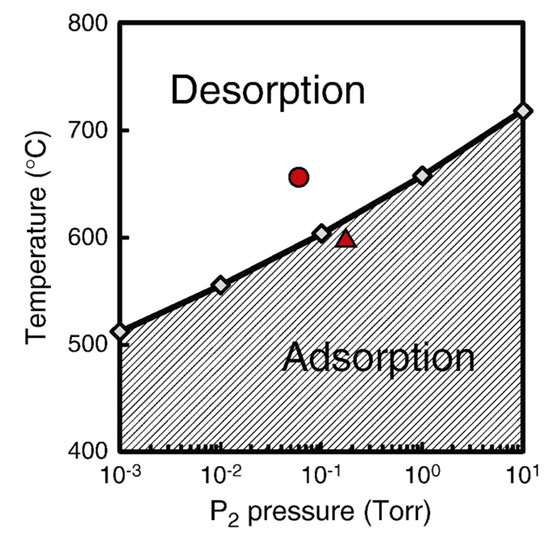
Figure 27.
Calculated phase diagrams functions of temperature and pressure for adsorption–desorption behavior of a P atom in the growth process shown in Figure 26. Red circle and triangle represent the growth conditions (A) and (B), respectively. Reprinted with permission from [98]. Copyright (2013) by Elsevier.
Figure 28 shows the relative adsorption probabilities of a P atom, Pre(P), on the surface with θIn = 1/4 as functions of temperature and pressure estimated by the MC simulations. Here, we note that Pre(P) + Pre(In) = 100%, where Pre(In) is relative adsorption probabilities of an In atom. Because of high V/III ratio, the adsorption of a P atom on the surface at θIn = 1/4 is dominant under the growth condition (B) compared with that of an In atom, leading to the growth process shown in Figure 26. From these results, it can be concluded that the growth process shown in Figure 24 is dominant for high temperatures and low P pressures, while the growth process shown in Figure 26 is dominant for low temperatures and high P pressures. Hence, it can also be concluded that InP layers grown for high temperatures and low P pressures (low V/III ratio) take the WZ structure, while those grown for low temperatures and high P pressures (high V/III ratio) include both the WZ and ZB layers with rotational twins. These results are consistent with the experimental result [91]. It is thus concluded that adsorption of P atoms depending on temperature and pressure is an important factor determining crystal structures of InP layers on InP(111)A surface. If the nucleation occurs on the InP(111)A top layer of InP NWs far from side facets, the growth processes depending on the growth conditions could strongly affect the structural stability of InP NWs. We believe that this scenario is applicable to clarify the crystal structure of InP NWs on InP(111)A substrates depending on growth conditions [91].
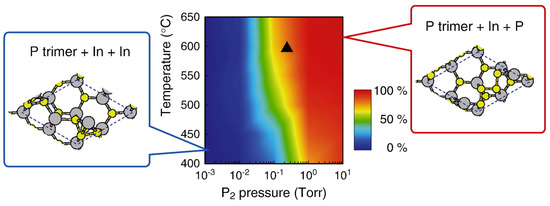
Figure 28.
Relative adsorption probabilities of a P atom, , on the surface with θIn = 1/4 as functions of temperature and pressure. It should be noted that Pre(P) + Pre(In) = 100%. In pressure is fixed at 3.3 × 10−3 Torr which corresponds to both the growth conditions (A) and (B). Triangle represents the growth condition (B). Reprinted with permission from [97]. Copyright (2013) by Elsevier.
4.4. Effects of Growth Condition on InP NW Shape
Figure 29 shows the calculated adsorption sites and migration barriers for an In atom on and ( surfaces for clarifying the effects of growth condition on the shape of InP NWs. There are two symmetrically equivalent adsorption sites on both and surfaces. The calculated adsorption energy difference between and surfaces is almost zero and the value of the adsorption energy is taken to be −1.90 eV. The adsorption probability calculated by Equation (12) for the low temperature and high V/III ratio is found to be less than 0.03%. This low probability indicates that it is difficult for an In atom to adsorb on the surface. However, the MC simulations support that the adsorption of an In atom occurs even under those growth conditions.
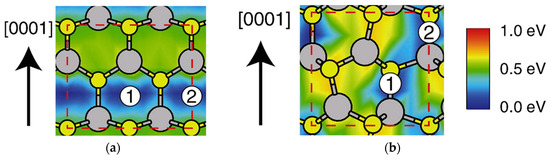
Figure 29.
Adsorption sites and migration barriers for an In atom on (a) and (b) surfaces. Encircled numbers and contour plots represent adsorption sites and migration barriers, respectively. Large gray and small yellow circles represent In and P atoms, respectively. Reprinted with permission from [99]. Copyright (2013) by Elsevier.
Figure 30 shows temperature dependence of surface lifetime τ and diffusion length Ldiff, respectively, for an In adatom on and surfaces obtained by the MC simulations. Here, surface lifetime is defined by the time during the migration, and diffusion length Ldiff is the distance between the adsorption site and the desorption site. Furthermore, In pressure is fixed at 3.3 × 10−3 Torr, which corresponds to the experimental growth conditions [90,91]. It is found that once the adsorption of an In atom occurs, the In adatom can migrate a certain distance (101–103 nm) with certain life time of 10−8–10−6 s under the experimental growth conditions. The values of τ and Ldiff are long enough to grow at relatively low temperatures. Furthermore, both τ and Ldiff on surface are larger than those on surface, although there is little orientation dependence in the adsorption energy. This is because the migration barriers on surface (0.27 eV) is smaller than that on surface (0.32 eV) as shown in Figure 29. For a P atom, the calculated adsorption sites are the same as those for an In atom, and calculated adsorption energies on ) and surfaces are 0.36 and 0.43 eV, respectively. These positive values indicate that the adsorption of a P atom does not occur even at 0 K. This is because the P-adsorbed surfaces have more excess electrons, which does not satisfy the ECM [38,39], compared to the In-adsorbed surfaces. Hence, the growth on both and surfaces starts from the adsorption of an In atom. In order to proceed the lateral growth on the surfaces, either In adatoms on the surface encountering each other caused by migration or additional adsorption on the In-adsorbed surfaces is necessary before vaporization of adsorbed In adatoms.
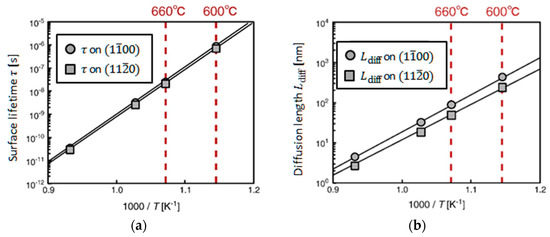
Figure 30.
Temperature dependence of (a) surface lifetime and (b) diffusion length for an In adatom on and surfaces. In pressure is fixed at Torr, which corresponds to the experimental growth conditions [90,91]. Reprinted with permission from [99]. Copyright (2013) by Elsevier.
Figure 31 shows the calculated adsorption sites and migration barriers for In and P atoms on the In-adsorbed surface. There are two symmetrically equivalent adsorption sites for In and P atoms on the In-adsorbed surface. The calculated adsorption energies at these sites for In and P atoms are −2.75 and −1.30 eV, respectively. Using these adsorption energies, the phase diagrams for adsorption–desorption behavior of In and P atoms on the In-adsorbed surface are obtained as shown in Figure 32. The surface phase diagram shown in Figure 32a demonstrates that an In atom can adsorb on the surface under the experimental growth conditions which are symbolized by red circles, squares, and triangles in Figure 32. In contrast, a P atom can adsorb only at the low temperature and high V/III ratio denoted by the red triangle in Figure 32b.
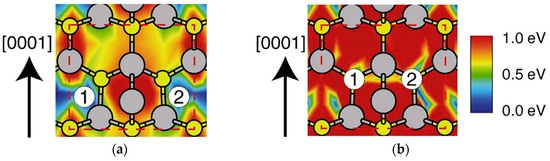
Figure 31.
Calculated adsorption sites and migration barriers on the In-adsorbed surface for (a) In and (b) P atoms. Encircled numbers and contour plots represent adsorption sites and migration barriers, respectively. Large gray and small yellow circles represent In and P atoms, respectively. Reprinted with permission from [99]. Copyright (2013) by Elsevier.
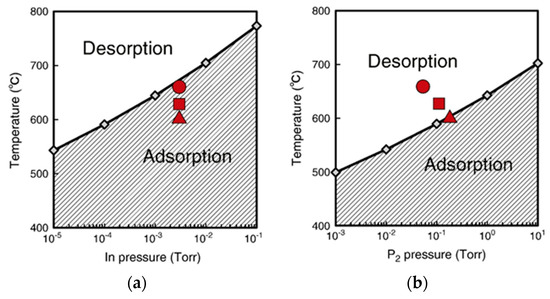
Figure 32.
Calculated phase diagrams as functions of temperature and pressure on the In-adsorbed surface for adsorption of (a) In and (b) P atoms. Regions with hatched lines correspond to atom-adsorbed regions. Red circles, squares, and triangles represent the growth conditions for the high temperature and low V/III ratio, the intermediate temperature and V/III ratio, and the low temperature and high V/III ratio, respectively. In pressure is fixed at 3.3 × 10−3 Torr which corresponds to the experimental growth conditions [90,91]. Reprinted with permission from [99]. Copyright (2013) by Elsevier.
Figure 33 shows the calculated adsorption sites and migration barriers for In and P atoms on the In-adsorbed surface. There is only one adsorption site for each atom on the In-adsorbed surface. The calculated adsorption energies for In and P atoms are −2.43 and −1.27 eV, respectively, which are slightly higher than those on the In-adsorbed surface. Figure 34 shows the calculated phase diagrams for adsorption–desorption behavior of In and P atoms on the In-adsorbed surface. The calculated phase diagrams indicate lower adsorption probabilities on the In-adsorbed surface compared with those on the In adsorbed surface. Under specific experimental condition (red circles in Figure 34) at 600 °C with V/III ratio of 55, however, the calculated adsorption probabilities for In and P atoms are 27% and 40%, respectively. These adsorption probabilities imply that this adsorption could occur at the low temperatures with high V/III ratio.
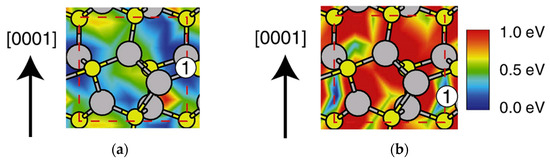
Figure 33.
Calculated adsorption sites and migration barriers on the In-adsorbed surface for (a) In and (b) P atoms. Encircled numbers and contour plots represent adsorption sites and migration barriers, respectively. Large gray and small yellow circles represent In and P atoms, respectively. Reprinted with permission from [100]. Copyright (2013) by Elsevier.
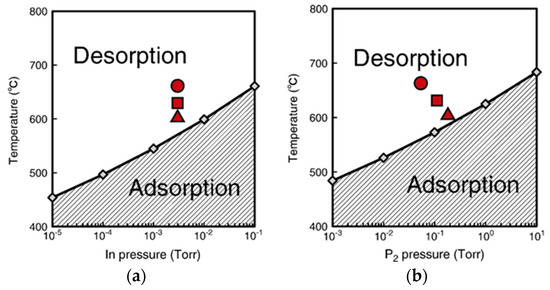
Figure 34.
Calculated phase diagrams as functions of temperature and pressure on the In-adsorbed surface for adsorption of (a) In and (b) P atoms. Regions with hatched lines correspond to atom-adsorbed regions. Red circles, squares, and triangles represent the growth conditions for the high temperature and low V/III ratio, the intermediate temperature and V/III ratio, and the low temperature and high V/III ratio, respectively. In pressure is fixed at 3.3 × 10−3 Torr which corresponds to the experimental growth conditions [90,91]. Reprinted with permission from [99]. Copyright (2013) by Elsevier.
Table 1 shows relative adsorption probabilities of a P atom on the In-adsorbed and surfaces, Pre(1–100)(P) and Pre(11–20)(P), respectively, which are percentages calculated by nP/(nIn + nP). Here, nIn and nP are the number of the formation of In and P adatoms using MC simulations, respectively, on the In-adsorbed surfaces during the MC sampling (nIn + nP = 1000). Both Pre(1–100) (P) and Pre(11–20)(P) increase with temperature up to 550 °C, because In adatoms hardly encounter each other as seen in the decrease in τ and Ldiff in Figure 30. On the In-adsorbed surface, Pre(1–100) (P) shifts to decrease around 550–600 °C. This is because a P atom hardly adsorbs beyond 600 °C. On the In-adsorbed surface, a P atom as well as an In atom hardly adsorbs beyond 600 °C. These results demonstrate that the probability of P/In atoms is higher, indicating that the adsorption of a P atom is dominant on the In-adsorbed surfaces. Although adsorption probability of an In atom on the In-adsorbed ) surface is higher than that of a P atom as shown in Figure 32, P atoms frequently attach on the surface owing to high V/III ratio, as seen in the estimated using Equation (15) shown in Table 2. It is found that in most cases, the adsorption of a P atom occurs on the In-adsorbed surfaces. From the calculated results by the MC simulations, we can deduce the initial growth process, such as a sequence of adsorption, migration, and desorption of In atoms, which iteratively occur on and surfaces, and the adsorption of P atom supplied from gas phase with In adatoms. Therefore, there are two reasons for the growth rate difference between and surfaces. One is the longer τ and Ldiff of In adatoms on surface as shown in Figure 30 because In adatoms are necessary for the adsorption of a P atom. The other is higher adsorption probability of a P atom on the In-adsorbed surface compared with that on surface, as shown in Figure 29b and Figure 31b. The latter is more important than the former, since adsorption behavior of P atoms is sensitive around the critical temperature and pressure. It is expected that at 600 °C P atoms tend to adsorb on the In-adsorbed surface whereas P atoms tend to desorb on the In-adsorbed surface. The difficulty in P adsorption on the In-adsorbed surface beyond 600 °C causes the growth rate difference. If we consider successful epitaxial growth of semiconductor NWs, the growth in the axial direction should be faster than that in the lateral directions. The difference in growth rate in InP.

Table 1.
Relative adsorption probabilities of a P atom on the In-adsorbed and surfaces, Pre(1–100)(P) and Pre(11–20)(P), respectively, obtained by MC simulations. It should be noted that Pre(1–100)(In) + Pre(1–100)(P) = Pre(11–20)(In) + Pre(11–20)(P) = 100%, where Pre(1–100) (In) and Pre(11–20)(In) are relative adsorption probabilities of an In atom on the In-adsorbed surfaces. Here, we assume that pressure is 0.1 Torr.

Table 2.
Values of Δtgas for In and P obtained by Equation (15). Here, we assume that In and P pressures are 3.3 × 10−3 and 0.1 Torr, respectively.
NWs can be clarified by comparing with the results on InP(111)A surface discussed in Section 4.3 [98]. Although the calculated adsorption energy difference of an In atom on bare (111)A, , and surfaces is insignificant, τ and Ldiff of an In adatom on the (111)A surface are longer than those on other surfaces. The remarkable values in τ and Ldiff on the (111)A surface originates from lower migration barriers on the (111)A, as shown in Table 3. Furthermore, the calculated adsorption energies of an In and a P atom on an In-adsorbed (111)A surface are lower than those on the In-adsorbed and surfaces.

Table 3.
Values of τ and Ldiff obtained by MC simulations, and migration barriers of In adatom on bare (111)A, , and surfaces using Figure 23 and Figure 29. Here, we assume that temperature and In pressure are 600 °C and 3.3 × 10−3 Torr, respectively. The lowest values for migration barriers are taken on each surface.
The adsorption energies of an In and a P atom on the In-adsorbed (111)A surface are −3.04 and −1.32 eV, respectively, while those of a single In (P) atom on the In-adsorbed and surfaces are −2.75 (−1.30) and −2.45 (−1.27) eV, respectively. Therefore, it is clear that the growth in the axial direction is faster than that in the lateral direction. The MC calculations indeed demonstrate that the difference in growth rate between and surfaces can be realized depending on the growth conditions. It is considered that facets with higher growth rate disappear and those with lower growth rate remain [100]. Thus, the lower growth rate of surface results in the formation of InP NWs consisting of no side facets for lower temperatures. Using surface phase diagrams shown in Figure 32b and Figure 34b and MC calculation results, we can deduce NW growth modes which are related to the shape of InP NWs.
Figure 35 shows the phase diagram for growth modes of InP NWs as functions of temperature and P pressure, derived from the comparisons of the calculated results among (111)A, , and surfaces. Region I in Figure 35 corresponds to the growth of InP NWs consisting of side facets without lateral growth. In this region, due to its growth conditions with high temperatures and low P pressures, P atoms hardly adsorb either on or surfaces, and the side facets emerge due to their low surface energy compared with surface [101,102]. Region II in Figure 32 corresponds to the growth of InP NWs consisting of side facets without lateral growth. In this region, P atoms adsorb on surface, resulting in annihilation of side facets and emergence of the side facets. It should be noted that the lateral growth of side facets does not occur since P atoms hardly adsorb on the surface in this region. Finally, in region III of Figure 32, P atoms tend to adsorb on both and surfaces due to low temperatures and high P pressures. This leads to the lateral growth and the formation of NWs with large diameters. In this region, InP NWs consisting of side faces are preferentially grown due to the low growth rate on surface compared with that on surface. The experimentally reported growth modes of InP NWs under the conditions at the red circle, square, and triangle in Figure 35. Trends of the calculated phase diagram qualitatively agrees with the experimental results [91], although the criteria for adsorption of a P atom (boundary lines in Figure 35) could be underestimated. We note that the possibility of In adsorption on the In-adsorbed surface, which facilitates the growth of surface for high temperatures cannot be ruled out (see Figure 32a). Even if it is true, the boundary between regions I and II in Figure 35 might shift toward higher temperatures, resulting in expansion of region II. However, our conclusions still agree with the experiments qualitatively. It is thus expected that the shape of InP NWs grown by the SA-MOVPE can be predicted on the basis of this phase diagram.
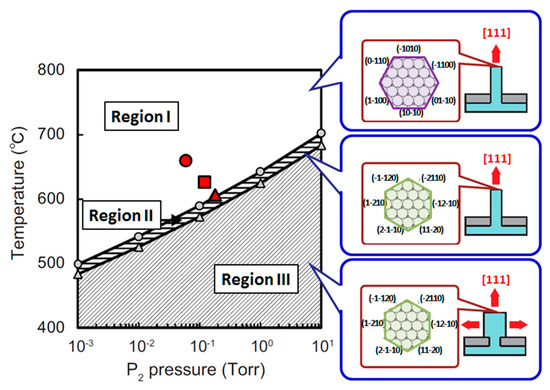
Figure 35.
Phase diagram for growth modes of InP NWs as functions of temperature and pressure. Red circle, square, and triangle represent the experimental growth conditions for the high temperature and low V/III ratio, the intermediate temperature and V/III ratio, and the low temperature and high V/III ratio, respectively [90,91].
5. Concluding Remarks
In this article, we have exemplified the applicability of the chemical potential approach with the aid of the macroscopic theory and MC simulations for fundamental understanding of the growth processes of nanostructures for InAs and InP. The power of this approach is not only on understanding the epitaxial growth processes but also on producing fundamental data such as surface phase diagrams as functions of growth conditions. Surface phase diagrams and elemental growth processes have been extensively investigated using similar approach for various semiconductors except InAs and InP such as GaAs [18,41,103,104,105,106,107,108] and III-Nirides [7,8,9,109,110,111,112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,128]. Figure 36 summarizes the calculated surface phase diagrams with different orientations for AlN and GaN under H-rich conditions during MOVPE growth. It is found that the phase diagrams change whole situation depending on materials and orientations. This suggests that MOVPE growth stably proceeds without depending on growth conditions on polar , nonpolar , and nonpolar for AlN, and polar , semipolar , and semipolar for GaN, since these phase diagrams are simple with small number of phases. On the other hand, AlN semipolar surfaces give complicated phase diagrams strongly depending on growth conditions in contrast with those of GaN. Therefore, careful control of growth conditions is necessary to keep stable AlN MOVPE growth on the semipolar surfaces. This is just an example for the availability of the chemical potential approach and surface phase diagrams as fundamental data for the epitaxial growth.
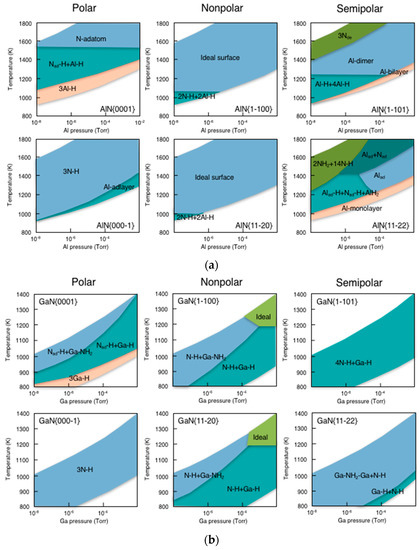
Figure 36.
Surface phase diagrams for H-adsorbed (a) AlN and (b) GaN with different orientations as functions of temperature and pressure.
The applicability of our approach has also been exemplified for various NWs including SiC, GaP, GaAs, InAs, ZnS, and ZnSe [98,101,102,129,130,131]. Furthermore, owing to ab initio calculations our studies are easily able to be extended to computational modeling and predictions of the electronic and optical properties of NWs. Such kinds of studies have been carried out for GaN and ZnO NWs, as seen in Figure 37 [131]. The calculated results demonstrate that the band gap energy of NWs becomes large compared with the calculated bulk energy gap due to quantum confinement effects. Moreover, the calculated imaginary part of their dielectric functions exhibit strong anisotropy and there are several side peaks near the absorption edge caused by valence electronic states around the highest-occupied band involved in the large dipole matrix elements. These calculated results provide a firm theoretical framework to predict microscopic properties of various semiconductor NWs. Consequently, the chemical potential approach enables us to interpret and predict epitaxial growth for semiconductors from a quantum mechanical viewpoint, such as hetero-epitaxial growth and nanowire growth in understanding their surface reconstructions through surface phase diagrams and growth processes including adsorption-desorption and migration behavior of atoms and molecules on the surfaces. Success will lead to more realistic simulations of epitaxial growth to give guiding principles for their fabrications as functions of growth conditions such as temperature and gas pressure. Recent progress in fabrication techniques will make it possible to create various new materials, including nanosheet in addition to nanodots and nanowires by controlling the atomic arrangements during epitaxial growth. Under these circumstances, the chemical potential approach will be an essential technique in the future of materials design to interpret and predict dynamic changes of the material properties because of its availability of predicting atomic arrangements during epitaxial growth.
Figure 37.
Calculated band structure and imaginary part of dielectric function of (a) GaN and (b) ZnO NWs with diameter of 1.3 nm. Energies are measured from the highest occupied state. Solid and dashed lines in dielectric function represent the imaginary part of dielectric function polarized along the nanowire axis and that in the orthogonal plane.
Acknowledgments
This work was supported in part by the JSPS KAKENHI Grant No. 21560032, No. 24560025, No. JP16K04962, No. JP16H06418, and CREST-JST (No. 16815710). One of the authors (Toru Akiyama) would like to thank the Toyota Physical and Chemical Research Institute for financial support. The computations were performed using Research Center for Computational Science (National Institutes of Natural Sciences) and Research Institute for Information Technology (Kyushu University).
Author Contributions
All the authors participated in conceiving and designing the review articles; Tomonori Ito and Toru Akiyama designed the calculations for the hetero-epitaxial growth and nanowire growth, respectively. Toru Akiyama conducted the calculations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Däweritz, L.; Hey, R. Reconstruction and defect structure of vicinal GaAs(001) and AlxGa1-xAs surfaces during MBE growth. Surf. Sci. 1990, 236, 15–22. [Google Scholar] [CrossRef]
- Kaxiras, E.; Bar-Yam, Y.; Joannopoulos, J.D.; Pandey, K.C. Ab initio theory of polar semiconductor surfaces. I. Methodology and the (2 × 2) reconstructions of GaAs(111). Phys. Rev. B 1987, 35, 9625–9635. [Google Scholar] [CrossRef]
- Qian, G.X.; Martin, R.M.; Chadi, D.J. Stoichiometry and surface reconstruction: An ab initio study of GaAs(001) surfaces. Phys. Rev. Lett. 1988, 60, 1962–1965. [Google Scholar] [CrossRef] [PubMed]
- Northrup, J.E. Structure of Si(100)H: Dependence on the H chemical potential. Phys. Rev. B 1991, 44, 1419–1422. [Google Scholar] [CrossRef]
- Kangawa, Y.; Ito, T.; Taguchi, A.; Shiraishi, K.; Ohachi, T. A new theoretical approach to adsorption-desorption behavior of Ga on GaAs surfaces. Surf. Sci. 2001, 493, 178–181. [Google Scholar] [CrossRef]
- Kangawa, Y.; Ito, T.; Hiraoka, Y.S.; Taguchi, A.; Shiraishi, K.; Ohachi, T. Theoretical approach to influence of As2 pressure on GaAs growth kinetics. Surf. Sci. 2002, 507, 285–289. [Google Scholar] [CrossRef]
- Ito, T.; Akiyama, T.; Nakamura, K. Ab initio-based approach to reconstruction, adsorption and incorporation on GaN surfaces. Semicond. Sci. Technol. 2012, 27, 024010. [Google Scholar] [CrossRef]
- Kangawa, Y.; Akiyama, T.; Ito, T.; Shiraishi, K.; Nakayama, T. Surface stability and growth kinetics of compound semiconductors: An ab initio-based approach. Materials 2013, 6, 3309–3360. [Google Scholar] [CrossRef]
- Ito, T.; Kangawa, Y. Ab Initio-Based Approach to Crystal Growth: Chemical Potential Analysis. In Handbook of Crystal Growth, 2nd ed.; Nishinaga, T., Rudolph, P., Kuech, T.F., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; Volume IA, pp. 477–520. [Google Scholar]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1997, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Louie, S.G.; Froyen, S.; Cohen, M.L. Nonlinear ionic pseudopotentials in spin-density-functional calculations. Phys. Rev. B 1982, 26, 1738–1742. [Google Scholar] [CrossRef]
- Yamauchi, J.; Tsukada, M.; Watanabe, S.; Sugino, O. First-principles study on energetics of c-BN(001) reconstructed surfaces. Phys. Rev. B 1996, 54, 5586–5603. [Google Scholar] [CrossRef]
- Shiraishi, K. A new slab model approach for electronic structure calculation of polar semiconductor surface. J. Phys. Soc. Jpn. 1990, 59, 3455–3458. [Google Scholar] [CrossRef]
- Shiraishi, K.; Oyama, N.; Okajima, K.; Miyagishima, N.; Takeda, K.; Yamaguchi, H.; Ito, T.; Ohno, T. First principles and macroscopic theories of semiconductor epitaxial growth. J. Cryst. Growth 2002, 237–239, 206–211. [Google Scholar] [CrossRef]
- Khor, K.E.; das Sarma, S. Proposed universal interatomic potential for elemental tetrahedrally bonded semiconductors. Phys. Rev. B 1988, 38, 3318–3822. [Google Scholar] [CrossRef]
- Ito, T.; Khor, K.E.; das Sarma, S. Systematic approach to developing empirical potentials for compound semiconductors. Phys. Rev. B 1990, 41, 3893–3896. [Google Scholar] [CrossRef]
- Ito, T. Simple criterion for wurtzite-zinc-blende polytypism in semiconductors. Jpn. J. Appl. Phys. 1998, 37, L1217–L1220. [Google Scholar] [CrossRef]
- Kangawa, Y.; Ito, T.; Taguchi, A.; Shiraishi, K.; Irisawa, T.; Ohachi, T. Monte Carlo simulation for temperature dependence of Ga diffusion length on GaAs(001). Appl. Surf. Sci. 2002, 190, 517–520. [Google Scholar] [CrossRef]
- Itoh, M.; Bell, G.R.; Avery, A.R.; Jones, T.S.; Joyce, B.A.; Vvedensky, D.D. Island nucleation and growth on reconstructed GaAs(001) surfaces. Phys. Rev. Lett. 1998, 81, 633–636. [Google Scholar] [CrossRef]
- Joyce, B.A.; Sudijono, J.L.; Belk, J.G.; Yamaguchi, H.; Zhang, X.M.; Dobbs, H.T.; Zangwill, A.; Vvedensky, D.D.; Jones, T.S. A scanning tunneling microscopy-reflection high energy electron diffraction-rate equation study of the molecular beam epitaxial growth of InAs on GaAs(001), (110) and (111)A-quantum dots and two-dimensional modes. Jpn. J. Appl. Phys. 1997, 36, 4111–4117. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Belk, J.G.; Zhang, X.M.; Sudijono, J.L.; Fay, M.R.; Jones, T.S.; Pashley, D.W.; Joyce, B.A. Atomic-scale imaging of strain relaxation via misfit dislocation in highly mismatched semiconductor heteroepitaxy: InAs/GaAs(111)A. Phys. Rev. B 1997, 55, 1337–1340. [Google Scholar] [CrossRef]
- Ohtake, A.; Ozeki, M. Strain relaxation in InAs/GaAs(111)A heteroepitaxy. Phys. Rev. Lett. 2000, 84, 4665–4668. [Google Scholar] [CrossRef] [PubMed]
- Zepeda-Ruiz, L.A.; Maroudas, D.; Weinberg, W.H. Semicoherent interface formation and structure in InAs/GaAs(111)A heteroepitaxy. Surf. Sci. 1998, 418, L68–L72. [Google Scholar] [CrossRef]
- Joe, H.; Akiyama, T.; Nakamura, K.; Kanisawa, K.; Ito, T. An empirical potential approach to the structural stability of InAs stacking-fault tetrahedron in InAs/GaAs(111). J. Cryst. Growth 2007, 301–302, 837–840. [Google Scholar] [CrossRef]
- Taguchi, A.; Kanisawa, K. Stable reconstruction and adsorbates of InAs(111)A surface. Appl. Surf. Sci. 2006, 252, 5263–5266. [Google Scholar] [CrossRef]
- Belk, J.G.; McConville, C.F.; Sudijono, J.L.; Jones, T.S.; Joyce, B.A. Surface alloying at InAs/GaAs interfaces grown on (001) surfaces by molecular beam epitaxy. Surf. Sci. 1997, 387, 213–226. [Google Scholar] [CrossRef]
- Grabowski, J.; Prohl, C.; Höpfner, B.; Dähne, M.; EIsele, H. Evolution of the InAs wetting layer on GaAs(001)-c(4 × 4) on the atomic scale. Appl. Phys. Lett. 2009, 95, 233118. [Google Scholar] [CrossRef]
- Eisele, H.; Höpfner, B.; Prohl, C.; Grabowski, J.; Dähne, M. Atomic structure of the (4 × 3) reconstructed InGaAs monolayer on GaAs(001). Surf. Sci. 2010, 604, 283–289. [Google Scholar] [CrossRef]
- Konishi, T.; Tsukamoto, S. Statistical analysis of surface reconstruction domains on InAs wetting layer preceding quantum dot formation. Nanoscale Res. Lett. 2010, 5, 1901–1904. [Google Scholar] [CrossRef] [PubMed]
- Kratzer, P.; Penev, E.; Scheffler, M. Understanding the growth mechanisms of GaAs and InGaAs thin films by employing first-principles calculations. Appl. Surf. Sci. 2003, 216, 436–446. [Google Scholar] [CrossRef]
- Ito, T.; Ishimure, N.; Akiyama, T.; Nakamura, K. Ab initio-based approach to adsorption-desorption behavior on the InAs(111)A heteroepitaxially grown on GaAs substrate. J. Cryst. Growth 2011, 318, 72–75. [Google Scholar] [CrossRef]
- Ito, T.; Ogasawara, K.; Sugitani, T.; Akiyama, T.; Nakamura, K. Ab initio-based approach to elemental growth process on the InAs wetting layer grown on GaAs substrate. J. Cryst. Growth 2013, 362, 2–5. [Google Scholar] [CrossRef]
- Ito, T.; Hirai, K.; Akiyama, T.; Nakamura, K. Ab initio-based approach to novel behavior of InAs wetting layer grown on GaAs(001). J. Cryst. Growth 2013, 378, 13–16. [Google Scholar] [CrossRef]
- Ito, T.; Akiyama, T.; Nakamura, K. Ab initio-based approach to structural change in InAs(001)-(2 × 3) wetting layer surfaces during MBE growth. e-J. Surf. Sci. Nanotechnol. 2015, 13, 190–194. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Homma, Y.; kanisawa, K.; Hirayama, H. Drastic improvement in surface flatness properties by using GaAs(111)A substrates in molecular beam epitaxy. Jpn. J. Appl. Phys. 1999, 38, 635–644. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Sudijiono, J.L.; Joyce, B.A.; Jones, T.S.; Gatzke, C.; Stradling, R.A. Thickness-dependent electron accumulation in InAs thin films on GaAs(111)A: A scanning tunneling-spectroscopy study. Phys. Rev. B 1998, 58, 4219–4222. [Google Scholar] [CrossRef]
- Phillips, J.C. Ionicity of the chemical bond in crystals. Rev. Mod. Phys. 1970, 42, 317–356. [Google Scholar] [CrossRef]
- Farrell, H.H.; Harbison, J.P.; Peterson, L.D. Molecular-beam epitaxy growth mechanisms on GaAs(100) surfaces. J. Vac. Sci. Technol. B 1987, 5, 1482–1489. [Google Scholar] [CrossRef]
- Pashley, M.D. Electron counting model and its application to island structures on molecular-beam epitaxy grown on GaAs(001) and ZnSe(001). Phys. Rev. B 1989, 40, 10481–10487. [Google Scholar] [CrossRef]
- Shiraishi, K.; Ito, T. Ga-adatom-induced As rearrangement during GaAs epitaxial growth: Self-surfactant effect. Phys. Rev. B 1998, 57, 6301–6304. [Google Scholar] [CrossRef]
- Tatematsu, H.; Sano, K.; Akiyama, T.; Nakamura, K.; Ito, T. Ab initio-based approach to initial growth processes on GaAs(111)B-(2 × 2) surfaces: Self-surfactant effect of Ga adatoms revisited. Phys. Rev. B 2008, 77, 233306-1-4. [Google Scholar] [CrossRef]
- Ito, T.; Akiyama, T.; Nakamura, K. Theoretical investigations for strain relaxation and growth mode of InAs thin layers on GaAs(111)A. Condens. Matter 2016, 1, 4. [Google Scholar] [CrossRef]
- Potin, V.; Ruterana, P.; Nouet, G.; Pond, R.C.; Morkoç, H. Mosaic growth of GaN on (0001) sapphire: A high-resolution electron microscopy and crystallographic study of threading dislocations from low-angle to high-angle grain boundaries. Phys. Rev. B 2000, 61, 5587–5589. [Google Scholar] [CrossRef]
- Ichimura, M. Stillinger-Weber potentials for III-V compound semiconductors and their application to the critical thickness calculation for InAs/GaAs. Phys. Status Solidi A 1996, 153, 431–437. [Google Scholar] [CrossRef]
- Béré, A.; Serra, A. Atomic structure of dislocation cores in GaN. Phys. Rev. B 2002, 65, 205323. [Google Scholar] [CrossRef]
- Kawamoto, K.; Suda, T.; Akiyama, T.; Nakamura, K.; Ito, T. An empirical potential approach to dislocation formation and structural stability in GaNxAs1-x. Appl. Surf. Sci. 2005, 244, 182–185. [Google Scholar] [CrossRef]
- People, B.; Bean, J.C. Calculation of critical layer thickness versus lattice mismatch for GexSi1-x/Si strained-layer heterostructures. Appl. Phys. Lett. 1985, 47, 322–324. [Google Scholar] [CrossRef]
- Kobayashi, R.; Nakayama, T. First-principles study on crystal and electronic structures of stacking-fault tetrahedron in epitaxial Si films. J. Cryst. Growth 2004, 278, 500–504. [Google Scholar] [CrossRef]
- Zhou, N.; Zhou, L. A fusion-crystalization mechanism for nucleation of misfit dislocations in FCC epitaxial films. J. Cryst. Growth 2006, 289, 681–685. [Google Scholar] [CrossRef]
- Wang, L.G.; Kratzer, P.; Moll, N.; Scheffler, M. Size, shape, and stability of InAs quantum dots on the GaAs(001) substrate. Phys. Rev. B 2000, 62, 1897–1904. [Google Scholar] [CrossRef]
- Kita, T.; Wada, O.; Nakayama, T.; Murayama, M. Optical reflectance study of the wetting layers in (In, Ga)As self-assembled quantum dot growth on GaAs(001). Phys. Rev. B 2002, 66, 195312. [Google Scholar] [CrossRef]
- Patella, F.; Nufris, S.; Arciprete, F.; Fanfoni, M.; Placidi, E.; Segarlata, A.; Balzarotti, A. Tracing the two- to three-dimensional transition in the InAs/GaAs(001) heteroepitaxial growth. Phys. Rev. B 2003, 67, 205308. [Google Scholar] [CrossRef]
- Xu, C.; Temko, Y.; Suzuki, T.; Jacobi, K. InAs wetting layer evolution on GaAs(001). Surf. Sci. 2005, 580, 30–38. [Google Scholar] [CrossRef]
- Yamaguchi, H.; Horikoshi, Y. Unified model for structure transition and electrical properties of InAs(001) surfaces studied by scanning tunneling microscopy. Jpn. J. Appl. Phys. 1994, 33, L1423–L1426. [Google Scholar] [CrossRef]
- Kaida, R.; Akiyama, T.; Nakamura, K.; Ito, T. Theoretical study for misfit dislocation formation at InAs/GaAs(001) interface. J. Cryst. Growth 2016. [Google Scholar] [CrossRef]
- Joyce, B.A.; Vvedensky, D.D. Self-organized growth on GaAs surfaces. Mater. Sci. Eng. R 2004, 46, 127–176. [Google Scholar] [CrossRef]
- Blumin, M.; Ruda, H.E.; Savelyev, I.G.; Shik, A.; Wang, H. Self-assembled InAs quantum dots and wires grown on a cleaved-edge GaAs(110) surface. J. Appl. Phys. 2006, 99, 093518. [Google Scholar] [CrossRef]
- Aierken, A.; Hakkarainen, T.; Sopanen, M.; Riikonen, J.; Sormunen, J.; Mattila, M.; Lipsanen, H. Self-assembled InAs island formation on GaAs(110) by metalorganic vapor phase epitaxy. Appl. Surf. Sci. 2008, 254, 2072–2076. [Google Scholar] [CrossRef]
- Yazawa, M.; Koguchi, M.; Muto, A.; Ozawa, M.; Hiruma, K. Effect of one monolayer of surface gold atoms on the epitaxial growth of InAs nanowhiskers. Appl. Phys. Lett. 1992, 61, 2051–2053. [Google Scholar] [CrossRef]
- Hiruma, K.; Yazawa, H.; Katuyama, T.; Ogawa, K.; Koguchi, M.; Kakibayashi, H. Growth and optical properties of nanometer-scale GaAs and InAs whiskers. J. Appl. Phys. 1995, 77, 447–462. [Google Scholar] [CrossRef]
- Li, H.; Wu, J.; Wang, Z. High-density InAs nanowires realized in situ on (100) InP. Appl. Phys. Lett. 1999, 75, 1173–1175. [Google Scholar] [CrossRef]
- Wu, Z.H.; Mei, X.Y.; Kim, D.; Blumin, M.; Ruda, H.E. Growth of Au-catalyzed ordered GaAs nanowire arrays by molecular-beam epitaxy. Appl. Phys. Lett. 2002, 81, 5177–5179. [Google Scholar] [CrossRef]
- Wu, Z.H.; Sun, M.; Mei, X.Y.; Ruda, H.E. Total reflection amorphous carbon mirrors for vacuum ultraviolet free electron lasers. Appl. Phys. Lett. 2004, 84, 657–659. [Google Scholar] [CrossRef]
- Morales, A.M.; Lieber, C.M. A Laser ablation method for the synthesis of crystalline semiconductor nanowires. Science 1998, 279, 208–211. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Gudiksen, M.S.; Duan, X.; Cui, Y.; Lieber, C.M. Highly polarized photoluminescence and photodetection from single indium phosphide nanowires. Science 2001, 293, 1455–1457. [Google Scholar] [CrossRef] [PubMed]
- Gudiksen, M.S.; Lauhon, L.J.; Wang, J.; Smith, D.C.; Lieber, C.M. Growth of nanowire superlattice structures for nanoscale photonics and electronics. Nature 2002, 415, 617–620. [Google Scholar] [CrossRef] [PubMed]
- Duan, X.; Huang, Y.; Cui, Y.; Wang, J.; Lieber, C.M. Indium phosphide nanowires as building blocks for nanoscale electronic and optoelectronic devices. Nature 2001, 409, 66–69. [Google Scholar] [CrossRef] [PubMed]
- Goto, H.; Nosaki, K.; Tomioka, K.; Hara, S.; Hiruma, K.; Motohisa, J.; Fukui, T. Growth of core–shell InP nanowires for photovoltaic a lication by selective-area metal organic vapor phase epitaxy. Appl. Phys. Express 2009, 2, 035004. [Google Scholar] [CrossRef]
- Ohlsson, B.J.; Björk, M.T.; Magnusson, M.H.; de ert, K.; Samuelson, L.; Wallenberg, L.R. Size-, shape-, and position-controlled GaAs nano-whiskers. Appl. Phys. Lett. 2001, 79, 3335–3337. [Google Scholar] [CrossRef]
- Bhunia, S.; Kawamura, T.; Watanabe, Y.; Fujikawa, S.; Tokushima, K. Metalorganic vapor-phase epitaxial growth and characterization of vertical InP nanowires. Appl. Phys. Lett. 2003, 83, 3371–3373. [Google Scholar] [CrossRef]
- Motohisa, J.; Noborisaka, J.; Takeda, J.; Inari, M.; Fukui, T. Catalyst-free selective-area MOVPE of semiconductor nanowires on (111)B oriented substrates. J. Cryst. Growth 2004, 272, 180–185. [Google Scholar] [CrossRef]
- Li, Q.; Gong, X.; Wang, C.; Wang, J.; Ip, K.; Hark, S. Size-dependent periodically twinned ZnSe nanowires. Adv. Mater. 2004, 16, 1436–1440. [Google Scholar] [CrossRef]
- Johansson, J.; Karlsson, L.S.; Svensson, C.P.T.; Martensson, T.; Wacaser, B.A.; Deppert, K.; Samuelson, L.; Seifert, W. Structural properties of <111>B-oriented III–V nanowires. Nat. Mater. 2006, 5, 574–580. [Google Scholar] [CrossRef]
- Tomioka, K.; Motohisa, J.; Hara, S.; Fukui, T. Crystallographic Structure of InAs nanowires studied by transmission electron microscopy. Jpn. J. Appl. Phys. 2007, 46, L1102–L1104. [Google Scholar] [CrossRef]
- Tomioka, K.; Mohan, P.; Noborisaka, J.; Hara, S.; Motohisa, J.; Fukui, T. Growth of highly uniform InAs nanowire arrays by selective-area MOVPE. J. Cryst. Growth 2007, 298, 644–647. [Google Scholar] [CrossRef]
- Cornet, D.M.; Mazzetti, V.G.M.; la Pierre, R.R. Onset of stacking faults in InP nanowires grown by gas source molecular beam epitaxy. Appl. Phys. Lett. 2007, 90, 013116. [Google Scholar] [CrossRef]
- Spirkoska, D.; Arbiol, J.; Gustafsson, A.; Conesa-Boj, S.; Glas, F.; Zardo, I.; Heigoldt, M.; Gass, M.H.; Bleloch, A.L.; Estrade, S. Ga-assisted catalyst-free growth mechanism of GaAs nanowires by molecular beam epitaxy. Phys. Rev. B 2008, 77, 155326. [Google Scholar]
- Plante, M.C.; la Pierre, R.R. Au-assisted growth of GaAs nanowires by gas source molecular beam epitaxy: Tapering, sidewall faceting and crystal structure. J. Cryst. Growth 2008, 310, 356–363. [Google Scholar] [CrossRef]
- Algra, R.E.; Verheijen, M.A.; Borgström, M.T.; Feiner, L.; Immink, G.; van Enckevort, W.J.P.; Vlieg, E.; Bakkers, E.P.A.M. Twinning superlattices in indium phosphide nanowires. Nature 2008, 456, 369–372. [Google Scholar] [CrossRef] [PubMed]
- Paiman, S.; Gao, Q.; Tan, H.H.; Jagadish, C.; Pemasiri, K.; Montazeri, M.; Jackson, H.E.; Smith, L.M.; Yarrison-Rice, J.M.; Zhang, X.; et al. The effect of V/III ratio and catalyst particle size on the crystal structure and optical properties of InP nanowires. Nanotechnology 2009, 20, 225606. [Google Scholar] [CrossRef] [PubMed]
- Caroff, P.; Dick, K.A.; Johansson, J.; Messing, M.E.; Deppert, K.; Samuelson, L. Controlled polytypic and twin-plane superlattices in III–V nanowires. Nat. Nanotechnol. 2009, 4, 50–55. [Google Scholar] [CrossRef] [PubMed]
- Cantoro, M.; Brammertz, G.; Richard, O.; Bender, H.; Clemente, F.; Leys, M.; Degroote, S.; Caymax, M.; Heyns, M.; de Gendt, S. Controlled III/V nanowire growth by selective-area vapor-phase epitaxy. J. Electrochem. Soc. 2009, 156, H860–H868. [Google Scholar] [CrossRef]
- Vogel, A.T.; de Boor, J.; Wittemann, J.V.; Mensah, S.L.; Werner, P.; Schmidt, V. Fabrication of high-quality InSb nanowire arrays by chemical beam epitaxy. Cryst. Growth Des. 2011, 11, 1896–1900. [Google Scholar] [CrossRef]
- Bao, J.; Bell, D.C.; Capasso, F.; Wagner, J.B.; Måttensson, T.; Trägårdh, J.; Samuelson, L. Optical properties of rotationally twinned InP nanowire heterostructures. Nano Lett. 2008, 8, 836–841. [Google Scholar] [CrossRef] [PubMed]
- Yeh, C.-Y.; Lu, Z.W.; Froyen, S.; Zunger, A. Predictions and systematizations of the zinc-blende-wurtzite structural energies in binary octet compounds. Phys. Rev. B 1992, 45, R12130–R12133. [Google Scholar] [CrossRef]
- Akiyama, T.; Sano, K.; Nakamura, K.; Ito, T. An empirical potential a roach to wurtzite-zinc-blende polytypism in group III–V semiconductor nanowires. Jpn. J. Appl. Phys. 2006, 45, L275–L278. [Google Scholar] [CrossRef]
- Akiyama, T.; Nakamura, K.; Ito, T. Structural stability and electronic structures of InP nanowires: Role of surface dangling bonds on nanowire facets. Phys. Rev. B 2006, 73, 235308. [Google Scholar] [CrossRef]
- Glas, F.; Harmand, J.-C.; Patriarche, G. Why does wurtzite Form in nanowires of III–V zinc blende Semiconductors? Phys. Rev. Lett. 2007, 99, 146101. [Google Scholar] [CrossRef] [PubMed]
- Glas, F. A simple calculation of energy changes upon stacking fault formation or local crystalline phase transition in semiconductors. J. Appl. Phys. 2008, 104, 093520. [Google Scholar] [CrossRef]
- Mohan, P.; Motohisa, J.; Fukui, T. Controlled growth of highly uniform, axial/radial direction-defined, individually addressable InP nanowire arrays. Nanotechnology 2005, 16, 2903–2907. [Google Scholar] [CrossRef]
- Kitauchi, Y.; Kobayashi, Y.; Tomioka, K.; Hara, S.; Hiruma, K.; Fukui, T.; Motohisa, J. Structural transition in indium phosphide nanowires. Nano Lett. 2010, 10, 1699–1703. [Google Scholar] [CrossRef] [PubMed]
- Wagner, R.S.; Elis, W.C. Vapor-liquid-solid mechanism of single crystal growth. Appl. Phys. Lett. 1964, 4, 89–90. [Google Scholar] [CrossRef]
- Johansson, J.; Karlsson, L.S.; Dick, K.A.; Bolinsson, J.; Wacaser, B.A.; Deppert, K.; Samuelson, L.; Seifert, W. Effects of supersaturation on the crystal structure of gold seeded III–V nanowires. Cryst. Growth Des. 2009, 9, 766–773. [Google Scholar] [CrossRef]
- Akiyama, T.; Kondo, T.; Tatematsu, H.; Nakamura, K.; Ito, T. Ab initio approach to reconstructions of the InP(111)A surface: Role of hydrogen atoms passivating surface dangling bonds. Phys. Rev. B 2008, 78, 205318. [Google Scholar] [CrossRef]
- Yamashita, T.; Akiyama, T.; Nakamura, K.; Ito, T. Theoretical investigation of effect of side facets on adsorption–desorption behaviors of In and P atoms at top layers in InP nanowires. Jpn. J. Appl. Phys. 2011, 50, 55001. [Google Scholar] [CrossRef]
- Taguchi, A.; Shiraishi, K.; Ito, T.; Kangawa, Y. Theoretical investigations of adatom adsorptions on the As-stabilized GaAs(111)A surface. Surf. Sci. 2001, 493, 173–177. [Google Scholar] [CrossRef]
- Yamashita, T.; Akiyama, T.; Nakamura, K.; Ito, T. Theoretical investigation on temperature and pressure dependence of structural stability of InP thin layers grown on InP(111)A surface. Surf. Sci. 2013, 610, 16–21. [Google Scholar] [CrossRef]
- Yamashita, T.; Sano, K.; Akiyama, T.; Nakamura, K.; Ito, T. Theoretical investigations on the formation of wurtzite segments in group III–V semiconductor nanowires. Appl. Surf. Sci. 2008, 254, 7668–7671. [Google Scholar] [CrossRef]
- Yamashita, T.; Akiyama, T.; Nakamura, K.; Ito, T. Growth of side facets in InP nanowires: First-principles-based approach. Surf. Sci. 2013, 609, 207–214. [Google Scholar] [CrossRef]
- Kangawa, Y.; Akiyama, T.; Ito, T.; Shiraishi, K.; Kakimoto, K. Theoretical approach to structural stability of c-GaN: How to grow cubic GaN. J. Cryst. Growth 2009, 311, 3106–3109. [Google Scholar] [CrossRef]
- Yamashita, T.; Akiyama, T.; Nakamura, K.; Ito, T. Effects of facet orientation on relative stability between zinc blende and wurtzite structures in group III–V nanowires. Jpn. J. Appl. Phys. 2010, 49, 55003. [Google Scholar] [CrossRef]
- Yamashita, T.; Akiyama, T.; Nakamura, K.; Ito, T. Theoretical investigation on the structural stability of GaAs nanowires with two different types of facets. Phys. E 2010, 42, 2727–2730. [Google Scholar] [CrossRef]
- Ito, T.; Ishizaki, H.; Akiyama, T.; Nakamura, K.; Shiraishi, K.; Taguchi, A. An ab initio-based approach to phase diagram calculations for GaAs(001) surfaces. e-J. Surf. Sci. Nanotechnol. 2005, 3, 488–491. [Google Scholar] [CrossRef]
- Ito, T.; Nakamura, T.; Akiyama, T.; Nakamura, K. An ab initio-based approach to phase diagram calculations for GaAs(001)-(2 × 4)γ surfaces. Appl. Surf. Sci. 2008, 254, 7663–7667. [Google Scholar] [CrossRef]
- Akiyama, T.; Tatematsu, H.; Nakamura, K.; Ito, T. A first-principles surface-phase diagram study for Si-adsorption processes on GaAs(111)A surface under low As-pressure condition. Surf. Sci. 2010, 604, 171–174. [Google Scholar] [CrossRef]
- Murase, I.; Akiyama, T.; Nakamura, K.; Ito, T. Ab initio-based approach to initial incorporation of Bi on GaAs(001)-c(4 × 4)α surfaces. J. Cryst. Growth 2013, 378, 21–24. [Google Scholar] [CrossRef]
- Sugitani, T.; Akiyama, T.; Nakamura, K.; Ito, T. Ab initio-based approach to incorporation of nitrogen on GaAs(001) surfaces. J. Cryst. Growth 2013, 378, 29–33. [Google Scholar] [CrossRef]
- Ito, T.; Sugitani, T.; Akiyama, T.; Nakamura, K. Ab initio-based approach to N-pair formation on GaAs(001)-(2 × 4) surface. e-J. Surf. Sci. Nanotechnol. 2014, 12, 6–10. [Google Scholar] [CrossRef]
- Ito, T.; Akiyama, T.; Nakamura, K. An ab initio-based approach to phase diagram calculations for GaN(0001) surfaces. Appl. Surf. Sci. 2008, 254, 7659–7662. [Google Scholar] [CrossRef]
- Ito, T.; Akiyama, T.; Nakamura, K. An ab initio-based approach to the stability of GaN(0001) under Ga-rich condition. J. Cryst. Growth 2009, 311, 3093–3096. [Google Scholar] [CrossRef]
- Akiyama, T.; Ammi, D.; Nakamura, K.; Ito, T. Surface reconstructions on GaN and InN semipolar (10-1-1) surfaces. Jpn. J. Appl. Phys. 2009, 48, 100201-1-3. [Google Scholar] [CrossRef]
- Akiyama, T.; Ammi, D.; Nakamura, K.; Ito, T. Stability of magnesium-incorporated semipolar GaN(10-1-1) surfaces. Jpn. J. Appl. Phys. 2009, 48, 110202-1-3. [Google Scholar] [CrossRef]
- Yamashita, T.; Akiyama, T.; Nakamura, K.; Ito, T. Surface reconstructions on GaN and InN semipolar (11-22) surfaces. Jpn. J. Appl. Phys. 2009, 48, 120201-1-3. [Google Scholar] [CrossRef]
- Akiyama, T.; Yamashita, T.; Nakamura, K.; Ito, T. Ab initio-based study for adatom kinetics on semipolar GaN(11-22) surfaces. Jpn. J. Appl. Phys. 2009, 48, 120218-1-3. [Google Scholar] [CrossRef]
- Yamashita, T.; Akiyama, T.; Nakamura, K.; Ito, T. Surface reconstructions on GaN and InN semipolar (20-21) surfaces. Jpn. J. Appl. Phys. 2010, 49, 0180014-1-2. [Google Scholar] [CrossRef]
- Ito, T.; Ito, T.; Akiyama, T.; Nakamura, K. Ab initio-based Monte Carlo simulation study for the structural stability of AlN grown on 4H-SiC(11–20). e-J. Surf. Sci. Nanotechnol. 2010, 8, 52–56. [Google Scholar] [CrossRef]
- Akiyama, T.; Yamashita, T.; Nakamura, K.; Ito, T. Stability and indium incorporation on In0.25Ga0.75 N surfaces under growth conditions: First-principles calculations. Jpn. J. Appl. Phys. 2010, 49, 030212-1-3. [Google Scholar] [CrossRef]
- Akiyama, T.; Ammi, D.; Nakamura, K.; Ito, T. Surface reconstruction and magnesium incorporation on semipolar GaN(1-101) surfaces. Phys. Rev. B 2010, 81, 245317-1-6. [Google Scholar] [CrossRef]
- Akiyama, T.; Nakamura, K.; Ito, T. Stability of hydrogen on nonpolar and semipolar nitride surfaces: Role of surface orientation. J. Cryst. Growth 2011, 318, 79–83. [Google Scholar] [CrossRef]
- Akiyama, T.; Nakamura, K.; Ito, T. Stability of carbon incorporated semipolar GaN(1-101). Jpn. J. Appl. Phys. 2011, 50, 080216-1-3. [Google Scholar]
- Akiyama, T.; Obara, D.; Nakamura, K.; Ito, T. Reconstructions on AlN polar surfaces under hydrogen rich conditions. Jpn. J. Appl. Phys. 2012, 51, 018001-1-2. [Google Scholar] [CrossRef]
- Akiyama, T.; Saito, Y.; Nakamura, K.; Ito, T. Stability of nitrogen incorporated Al2O3 surfaces: Formation of AlN layers by oxygen desorption. Surf. Sci. 2012, 606, 221–225. [Google Scholar] [CrossRef]
- Akiyama, T.; Obara, D.; Nakamura, K.; Ito, T. Reconstructions on AlN nonpolar surfaces in the presence of hydrogen. Jpn. J. Appl. Phys. 2012, 51, 048002-1-2. [Google Scholar] [CrossRef]
- Akiyama, T.; Nakamura, K.; Ito, T. Ab initio-based study for adatom kinetics on AlN 0001) surfaces during metal-organic vapor-phase epitaxy growth. Appl. Phys. Lett. 2012, 100, 251601-1-3. [Google Scholar] [CrossRef]
- Akiyama, T.; Saito, Y.; Nakamura, K.; Ito, T. Nitridation of Al2O3 surfaces: Chemical and structural change triggered by oxygen desorption. Phys. Rev. Lett. 2013, 110, 026101-1-5. [Google Scholar] [CrossRef] [PubMed]
- Takemoto, Y.; Akiyama, T.; Nakamura, K.; Ito, T. Systematic theoretical investigations on surface reconstructions and adatom kinetics on AlN semipolar surfaces. e-J. Surf. Sci. Nanotechnol. 2015, 13, 239–243. [Google Scholar] [CrossRef]
- Takemoto, Y.; Akiyama, T.; Nakamura, K.; Ito, T. Ab initio-based study for surface reconstructions and adsorption behavior on semipolar AlN(11-22) surfaces during metal-organic vapor-phase epitaxial growth. Jpn. J. Appl. Phys. 2015, 54, 085502-1-5. [Google Scholar] [CrossRef]
- Akiyama, T.; Takemoto, Y.; Nakamura, K.; Ito, T. Theoretical investigations for initial growth processes on semipolar AlN(11-22) surfaces under metal-organic vapor-phase epitaxiy growth conditions. Jpn. J. Appl. Phys. 2016, 55, 05FM06-1-4. [Google Scholar] [CrossRef]
- Ito, T.; Sano, K.; Akiyama, T.; Nakamura, K. A simple approach to polytypes of SiC and its application to nanowires. Thin Solid Films 2006, 508, 243–246. [Google Scholar] [CrossRef]
- Akiyama, T.; Sano, K.; Nakamura, K.; Ito, T. An Empirical Interatomic Potential Approach to Structural Stability of ZnS and ZnSe Nanowires. Jpn. J. Appl. Phys. 2007, 46, 1783–1787. [Google Scholar] [CrossRef]
- Akiyama, T.; Freeman, A.J.; Nakamura, K.; Ito, T. Electronic structures and optical properties of GaN and ZnO nanowires from first principles. J. Phys. Conf. Ser. 2008, 100, 052056. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).