Broadband Seismic Metamaterials Based on Gammadion-Shaped Chiral Structures

Abstract

Controlling seismic wave propagation to protect critical infrastructure through metamaterials has emerged as a frontier research topic. The narrow bandgap and heavy weight of a resonant seismic metamaterial (SM) limit its application for securing buildings. In this research, we first develop a two-dimensional (2D) seismic metamaterial with gammadion-shaped chiral inclusions, achieving a high relative bandgap width of 77.34%. Its effective mass density is investigated to clarify the generation mechanism of the bandgap due to negative mass density between 12.53 and 28.33 Hz. Then, the gammadion-shaped pillars are introduced on a half-space to design a three-dimensional (3D) chiral SM to attenuate Rayleigh waves within a wider low-frequency range. Further, time-frequency analyses for real seismic waves and scaled experimental tests confirm the practical feasibility of the 3D SM. Compared with common resonant SMs, our chiral configurations offer a wider attenuation zone and lighter weight.

1. Introduction

As a natural disaster, earthquakes represent significant threats to human infrastructure, and millions of earthquakes occur annually worldwide. Therefore, reinforcing the building through the implementation of a supplementary passive energy dissipation system holds significant importance. However, conventional damping methods often fail to meet the practical aseismic demands due to the inaccuracies of structural design and the complexity of its nonlinear cracking mechanism [1,2]. In addition, it is not applicable to existing buildings or ancient buildings. Thus, people prefer to seek a way to control the seismic waves before they reach the buildings.

Metamaterials [3,4,5], as artificially engineered composites with wave manipulation capabilities, have evolved from electromagnetic field over two decades ago [6] to elastic and acoustic fields rapidly [7,8,9]. The bandgap is one of their important properties, which means waves cannot propagate through the metamaterials in a specific frequency range [10]. Numerous attempts have been undertaken to create metamaterials aimed at obtaining targeted bandgap properties [11,12,13]. Younes et al. [14,15] conducted theoretical studies on acoustic wave transmission through a two-dimensional (2D) configuration of cylindrical pillars located on a half-space substrate surface, while experimentally validating two distinct bandgap categories: locally resonant and Bragg-type bandgaps. It is well known that the locally resonant metamaterial is more suitable for seismic waves as it can offer a low-frequency bandgap, which means it is able to manipulate longer wavelengths through compact structural configurations. Therefore, locally resonant metamaterials open a new way for earthquake prevention, which can attenuate seismic waves in the bandgap before they reach our target buildings. Metamaterials applied in seismic wave manipulation are described as seismic metamaterials (SMs).

In the last decade, SMs based on resonant structures have been designed and tested to produce low-frequency bandgaps. Palermo et al. [16] introduced the SM, developed through embedding sub-wavelength-scale resonant structures beneath the ground surface. Du et al. [17] proposed a 2D SM composed of periodically arranged steel pillars filled with concrete and embedded within a soil medium, achieving a protective barrier against guided Lamb waves and surface waves. Li et al. [18] and Zeng et al. [19] proposed a SM based on inertial amplification to generate low-frequency bandgaps. Zhao et al. [20] proposed a multi-point mass resonance metamaterial for low-frequency surface wave attenuation. However, these works mainly focus on realizing low-frequency bandgaps and have the problem of narrow bandwidth due to the inherent defect of resonant structures. To solve this problem, Zeng et al. [21] and Du et al. [22] continuously optimized the shapes of the resonant structures of SMs. More recently, Chen et al. [23] proposed a gradient-index SM achieving an omnidirectional, low-frequency, and ultra-broadband wave attenuation. Ahmed et al. [24] proposed a lightweight design using auxetic geometry, which further lowers the bandgap frequencies of SM and enhances its practical feasibility.

Chirality or handedness has played an important role in optics, biology, and medicine for decades. Recently, chirality has started to play a role in the field of mechanics. Kuang et al. [25] and Dong et al. [26] comprehensively discussed the progress and prospects of chiral materials. We noticed that chiral structures, which are characterized by unique mechanical properties including high shear rigidity and negative mass density, were regarded as a superior choice for engineering applications [27]. Chiral topology metamaterials were proposed for energy absorption [28]. Auxetic metamaterials based on chiral structures with high auxeticity and stiffness were usually used for the application of vibration isolation because of their special directional propagation mechanism [29,30].

Elastic chiral metamaterial has also been proven to have a significant effect on its dispersion curves, attaining a wide bandgap at low frequencies [31,32]. Zhu et al. [33] explored an elastic metamaterial beam incorporating a chiral lattice architecture, demonstrating the capability to enable broadband vibration suppression while maintaining its structural load-bearing performance. Tan et al. [34] developed an improved three-ligament chiral structure with flexure hinges for a better attenuation zone. Li et al. [35] presented a hybrid acoustic metamaterial consisting of chiral and anti-chiral ligaments, which was verified to have good vibration attenuation performance. Zhang et al. [36] investigated the wave behavior of the octa-chiral lattices with local resonators. Inspired by recent presentations of chiral metamaterials with broad bandgap property, we try to combine local resonance mechanisms with chiral SMs for seismic wave attenuation. The inherent rotation–translation coupling effect within chiral structures can activate additional torsional degrees of freedom, enabling the generation of ultra-wide bandgaps. We propose that this integration could achieve superior seismic wave attenuation while maintaining engineering feasibility.

In this paper, we design two types of chiral SMs, including an embedded SM and a pillar-type SM, for two-dimensional and three-dimensional situations, respectively. The wave attenuation performance is systematically analyzed through finite element simulations in harmonic regimes, complemented by time-frequency analysis of historical seismic records to establish real-world spectral characteristics. Band structure calculations and transmission coefficient analyses are conducted to, respectively, characterize bandgap properties and quantify attenuation magnitude. Compared to non-chiral structures, the relative bandgap width of chiral structures increased by 77.34%. Modal analysis clearly revealed the torsional effects induced by the chiral structure, thereby demonstrating the mechanism by which chirality broadens the bandgap. To validate practical applicability, scaled prototypes fabricated through 3D printing undergo experimental testing, creating a cross-verification framework between numerical simulations and experimental measurements.

2. Model and Method

The metamaterial is constructed by periodically embedding gammadion-shaped chiral structures into the substrate on a two-dimensional (2D) square lattice (lattice constant is a). Geophysical survey data show that the wavelengths of natural seismic waves are in the order of 100 m; thus, we consider the lattice constant a to be 5 m, which is about λ/20 of the seismic waves. Figure 1a shows the schematic diagram of the gammadion-shaped chiral structure unit, and its corresponding geometric parameters are labeled on it.

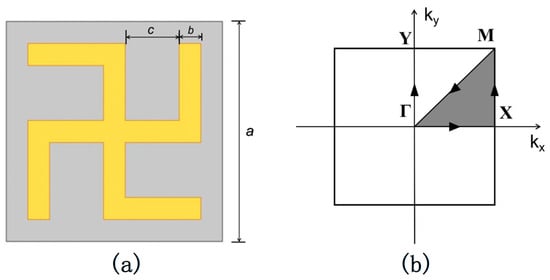
Figure 1. (a) The structure unit of 2D chiral SM, where the yellow part is steel and the gray part is the soil. Lattice constant is a, the structure’s arm width is b and c is the structural arm length. (b) The first irreducible Brillouin zone for the periodic composites with a square lattice: Γ = (0, 0), X = (π/a, 0), M = (π/a, π/a), Y = (0, π/a). The arrow indicates the path during scanning of the Brillouin zone.

Considering the feasibility of practical applications, soil is designated as the substrate medium, and conventional construction material, such as steel, is selected for the material of the structure. It is postulated that both materials are linear elastic, isotropic, and homogeneous. It is also worth mentioning that soil in a geophysical setting exhibits viscoelastic effects due to the existence of underground water, oil, and gas, while the viscoelasticity of the ground will not only improve the wave attenuation but also enhance the shielding bandwidth of the SM (see [37] for details). The parameters of the materials are given in Table 1, and the geometric parameters are listed in Table 2.

Table 1. Material parameters of the unit cell.

Material	Density (kg/m3)	Young’s Modulus (Pa)	Poisson’s Ratio
steel	7800	2.06 × 1011	0.3
soil	1800	2 × 107	0.3

Table 2. Geometric parameters of unit cell.

a (m)	b (m)	c (m)
5	0.5	1.25

The dispersion behavior of elastic waves in periodic lattices is characterized by the dispersion relation ω(k), linking angular frequency ω to wave vector k. This relation is obtained by solving the frequency-domain elastic wave equation under time-harmonic excitation [21].

Suppose that the seismic waves propagate along the x–y plane. In a time-harmonic field, displacement can be written as:

$$\mathit{u}(\mathit{r},t)=\mathit{u}\left(\mathit{r}\right)e^{-i\omega t}$$

(1)

where u denotes the displacement vector, r means the position vector, and ω signifies the angular frequency. The elastic wave propagation in inhomogeneous materials can be expressed by:

$$\mathsf{\nabla }·\left(\mathit{C}:\mathsf{\nabla }\mathit{u}\right)=-\rho \left(\mathit{r}\right){\omega }^2\mathit{u}$$

(2)

where C represents the fourth-order elasticity tensor, and ρ signifies the mass density of the material.

According to Bloch’s theorem and Floquet periodic boundary conditions, the displacement in the unit cell can be written as:

$$\mathit{u}\left(\mathit{r}+\mathit{R}\right)=\mathit{u}\left(\mathit{r}\right)e^{i\mathit{k}·\mathit{R}}$$

(3)

where R is the lattice translation vector, and k is the wave vector.

Substituting Equations (2) and (3) into (1) via the Galerkin method transforms the partial differential equations into a discrete generalized eigenvalue problem. The unit cell’s discretized equation of motion can be expressed in the following matrix form:

$$(\mathit{K}-{\omega }^2\mathit{M})\mathit{u}=0$$

(4)

where M and K are the global mass and stiffness matrices, respectively.

In order to obtain the band structures and the transmission coefficient of the proposed structures, the numerical analysis technique in this work is the finite element method. The representative computed unit cell can be meshed based on structure variations and partitioned into finite elements interconnected via nodes. Here, by using mesh, Equation (4) is discretized and subsequently solved to determine the unknowns ω and u with wave vector k sweeping the edges of the first irreducible Brillouin zone. The first irreducible Brillouin zone for the periodic composite with the square lattice is shown in Figure 1b.

3. Discussion

3.1. Band Structures of the 2D Chiral SM

For the embedded SM with a gammadion-shaped chiral steel inclusion, its band structures are calculated to predict its bandgap properties. We use COMSOL Multiphysics 5.1 to perform finite element simulation calculations. Select the solid module and apply periodic boundary conditions in the x-direction and y-direction of the structure. The characteristic frequency is chosen for study. Use a free triangular mesh for partitioning; the maximum element size must be less than one-tenth of the wavelength to ensure convergence of the study. For convenience, the mesh may be controlled either through the system’s predefined ultra-fine mesh or via the physical field. The structure is shown in Figure 1a, and the band structures are shown in Figure 2. It is easily found that one complete bandgap with a width of 15.80 Hz is obtained, which is produced between the third and fourth bands. To evaluate the property of the bandgap more accurately, we calculate the relative bandwidth of the bandgap (RBW): the ratio of the total width (Δω) to the center frequency of the bandgap (ω₀). To highlight the advantage of chiral inclusion, we also compute the band structures of the SM with an achiral inclusion at the same duty ratio. As we can see from Figure 2, the RBW of the chiral SM is up to 77.34% (Figure 2a), while the RBW of the achiral SM is only 26.96% (see Figure 2b). Both structures generate bandgaps via local resonance, and under the same duty ratio, bandgap differences are attributed to chirality. Clearly, gammadion-shaped chiral inclusions significantly widen the bandgap compared to achiral ones.

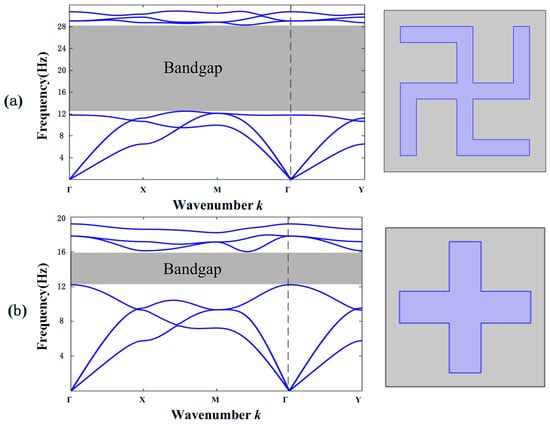
Figure 2. Band structures of SMs with different inclusions: (a) gammadion-shaped chiral inclusion, (b) cross-shaped inclusion.

3.2. Effective Mass Density of the Chiral SM

In this section, the dynamic effective mass density of our designed chiral seismic metamaterial is numerically determined. This analysis is based on the effective medium theory [17,21,38] under the low-frequency assumption, where the wavelength is much larger than the size of the resonant unit. Four boundaries of the unit cell (depicted in Figure 1a) are considered to experience an x-direction global displacement. Analyze using the frequency domain, where the average reaction force and displacement are software-provided functions, calculated numerically via integration functions along the boundaries. Thus, the effective mass of the unit cell can be numerically calculated through the averaged reaction force in the boundaries, which can be written as [39]:

$$m_{eff}(\omega )={\displaystyle \frac{\left|\mathit{F}\right|}{-{\omega }^2\left|\mathit{u}\right|}},$$

(5)

where the m_eff is the effective mass, and F is the average reaction force in the four boundaries. The u denotes the displacement vector, and ω signifies the angular frequency. The effective mass density is defined as the volume-averaged mass, formulated as:

$${\rho }_{eff}(\omega )={\displaystyle \frac{m_{eff}\left(\omega \right)}{v_{cell}}}\mathrm{with} v_{cell}=a^{2}h,$$

(6)

where ρ_eff is the effective mass density, v_cell is the volume of the unit cell, and h is the thickness of the structure.

As shown in Figure 3, when the frequency of the incidence wave gradually increases, the resonant response is excited by the chiral inclusion at 12.98 Hz. It can be easily found that the negative effective mass density is obtained in the range from 12.98 Hz to 28.33 Hz, which agrees with the bandgap in Figure 2a. From this point, it can be inferred that the generation mechanism of the bandgap is a negative effective mass density based on the dipole resonance of the chiral structure.

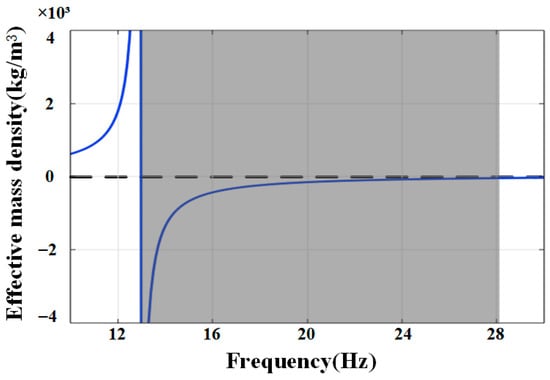
Figure 3. Effective mass density of the chiral SM, where the gray area represents the negative value part.

3.3. Effects of Geometric Parameters

Based on the preceding analysis, it is evident that the generation of a wide bandgap in the system originates from the local resonance of the chiral structure. Regarding the emergence of the bandgap, the chiral structure’s geometric parameters play a fundamental role. In the following section, we will analyze the effects of geometric parameters on the bandgap characteristics. When the value of the structure’s arm width b varies, while other parameters are maintained consistent with prior specifications, the effect on the bandgap width is depicted in Figure 4a. It is observed that both the lower and upper boundaries of the bandgap shift to higher frequencies as b increases. The upper boundary exhibits a more pronounced upward trend compared to the lower boundary, with the bandgap width coming to the largest when b is 0.6 m. In Figure 4b, we increase the structural arm length c while keeping other parameters constant. This causes both the upper and lower bandgap boundaries to shift upward progressively. Further increase reveals that the upward shift in the upper boundary tends to stabilize. The widest bandgap arises when c is 1.35 m. The progression pattern of these bandgaps indicates that the geometric parameters of the chiral structure exert a substantial influence on the location and width of bandgaps.

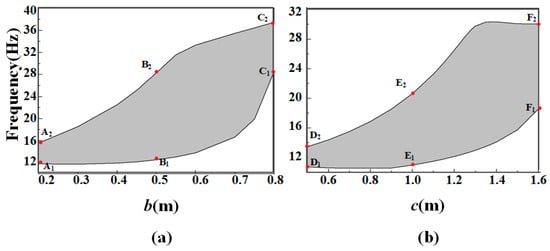
Figure 4. Effect of geometrical parameters on bandgap extension. The gray shades represent the bandgap. (a) Bandgap changes when parameter b is modified. (b) Bandgap changes when parameter c is modified.

In order to clarify the effect of parameter changes on the bandgap, we select several sets of parameters to observe the vibration modes of the corresponding structures, as shown in Figure 5. It can be seen that, at low frequencies, the structures can be regarded as periodic scatterers (steel) connected by narrow connectors (soil). At the lower boundary state of the bandgap (the modes of A₁–F₁ marked in Figure 4), the displacement is mainly concentrated in the scatterer, and the arrows on the surface clearly show the rotation of the scatterer. At this time, the bandgap opens mainly due to the rotation of the chiral scatterer. Since the scatterer has a relatively large mass, the local resonance bandgap is at a low frequency. At the upper boundary state (the modes of A₂–F₂ marked in Figure 4), the chiral structure guides and concentrates energy into the soil within its grooves. The color, which represents the displacement amplitude, illustrates the locality of the displacement, while the arrows on the surface indicate the direction of energy flow. Due to the relatively low soil mass, the localized resonance bandgap is at a higher frequency. When the scatterer’s arm length is thin (i.e., small b value, such as the A₂ mode) or short (i.e., small c value, such as the D₂ mode), the guiding effect of the scatterer on displacement is relatively weak, and energy may flow around the scatterer. When the scattering body’s arm length is thicker (i.e., larger b value, such as the C₂ mode) or longer (i.e., larger c value, such as the F₂ mode), the guiding effect on displacement is more pronounced, with displacement being largely confined within the groove formed by the scattering body’s chiral arms. These modes indicate that the bandgap is generated by local resonance, and the chirality plays a very important role in the formation of the bandgap.

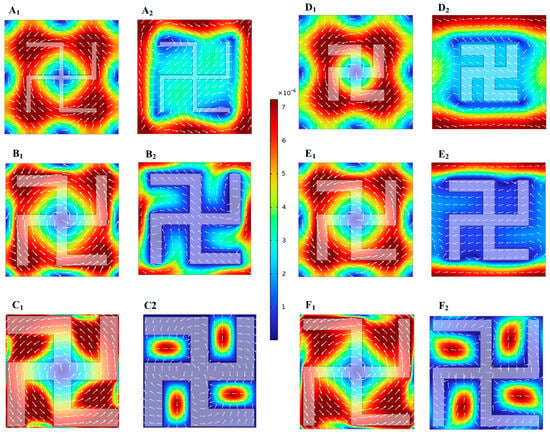
Figure 5. Vibration modes at the upper and lower boundaries of the bandgap when modifying parameters. The color represents the displacement amplitude, and the arrows on the surface indicate the direction of energy flow. The (A–C) group shows the cases where only parameter b is changed, and the (D–F) group shows the cases where only parameter c is changed. The mode with subscript 1 is at the lower boundary of the bandgap, and subscript 2 represents the mode at the upper boundary.

3.4. Frequency Domain Analysis

Next, we further verify the shielding results of the chiral SM by calculating the transmission coefficient of seismic wave propagation in a 2D finite system. Additionally, the incident and transmitted wave displacement field distributions are analyzed to demonstrate the shielding capability of the proposed SM. The model used in frequency domain calculations is a finite system composed of 50 unit cells sandwiched by two homogeneous parts of the soil, as shown in Figure 6a. The cells are arranged in a 2D array with 10 rows in the x-direction and five columns in the y-direction. The unit cell parameters are kept consistent with those mentioned above, as shown in Table 1 and Table 2. Perfectly matched layers (PMLs) are implemented at both ends along the x-direction to minimize reflections originating from the model domain boundaries. Periodic boundary conditions are imposed on the finite periodic composite in the y-direction. A specified displacement is applied as a line source on the left side of the model to excite incident waves, which is marked as a blue line in Figure 6a. The wave is captured at the red line after passing through the structures.

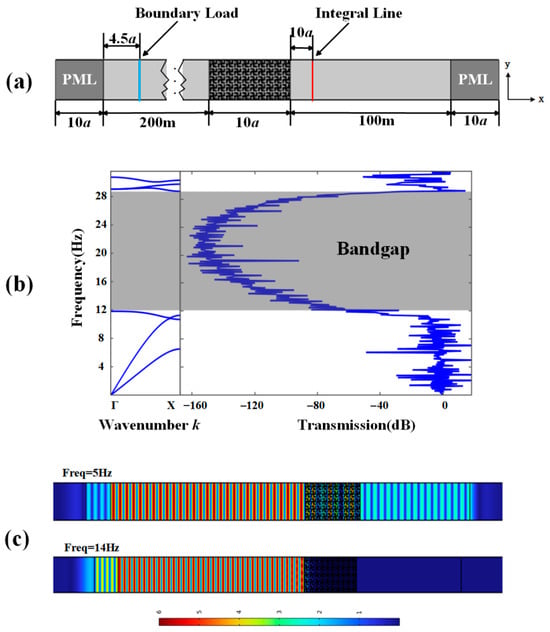
Figure 6. (a) Model used in frequency domain calculations. (b) The band structure of the chiral SM in the ΓX direction and the TS of the periodic array of the chiral SM, where the gray areas indicate the bandgap and attenuation zone. (c) The displacement field distributions at 5 Hz and 14 Hz, respectively.

For a more quantitative analysis, a frequency domain analysis spanning 0 Hz to 32 Hz is conducted, with the transmission coefficient versus frequency along the Γ–X direction being computed. The transmission spectrum (TS) is processed as:

$$TS=20\times log{\displaystyle \frac{u_1}{u_0}},$$

(7)

where u₁ is the displacement with structures and u₀ is the displacement without structures. The TS along the ΓX direction is calculated, and the result is shown in Figure 6b, in which the attenuation region agrees well with the bandgap in Figure 2a.

To demonstrate the shielding capability of the SM, the total displacement fields of incident waves both within and beyond the bandgap are extracted, respectively, as shown in Figure 6c. At 5 Hz beyond the bandgap, the incident wave is partially reflected and partially passes through the SM. In contrast, the incident wave can barely penetrate the SM when the frequency is 14 Hz within the bandgap. This result demonstrates that the vibration is attenuated efficiently for seismic waves within the bandgap.

3.5. Attenuation Characteristics for the 3D Chiral SM

Actually, seismic waves originate from the interplay between bulk and surface waves resulting from complex underground geological configurations, among which Rayleigh waves are the most dangerous surface waves for buildings. Thus, we also develop a three-dimensional (3D) chiral SM for Rayleigh waves. Here, we mainly focus on whether the attenuation effect still exists for surface waves in a half-space. In order to figure out the transmission coefficient, 10 unit cells are arranged on a substrate with a thickness of 20a. The geometry model is presented in Figure 7a, in which the gray and blue areas represent soil and steel, respectively. A periodic boundary condition is implied to achieve an infinite array of units in the y direction. Week reflective boundary conditions are applied on the boundaries of the substrate. A boundary load along the z-direction is applied on the line source to model an incident surface wave. Given that introducing Rayleigh damping would merely accentuate the attenuation effect without altering the bandgap behavior itself, we shall disregard the impact of damping for computational convenience [37]. After passing through the structures, the wave is captured at the integral area. The transmission coefficient is calculated in the same way as in the 2D SM. The attenuation regions are presented in Figure 7b. A low-frequency broadband attenuation zone from 2.3 to 18 Hz can be seen provided by the structure. Additionally, the total displacement fields for the incident waves within and beyond the bandgaps are also withdrawn, as shown in Figure 7c. From the displacement field, it can be seen that the incident wave is a Rayleigh wave, and the structure can indeed prevent the propagation of the wave. For instance, at 1.5 Hz beyond the bandgaps, the incident wave is partially localized on the structures and partially passes through the structures. However, at 5.5 Hz in the bandgap, the incident surface wave is significantly attenuated and almost unable to propagate through the 4th unit cell. Therefore, previously designed structures still have a very significant attenuation in a half-space for surface waves.

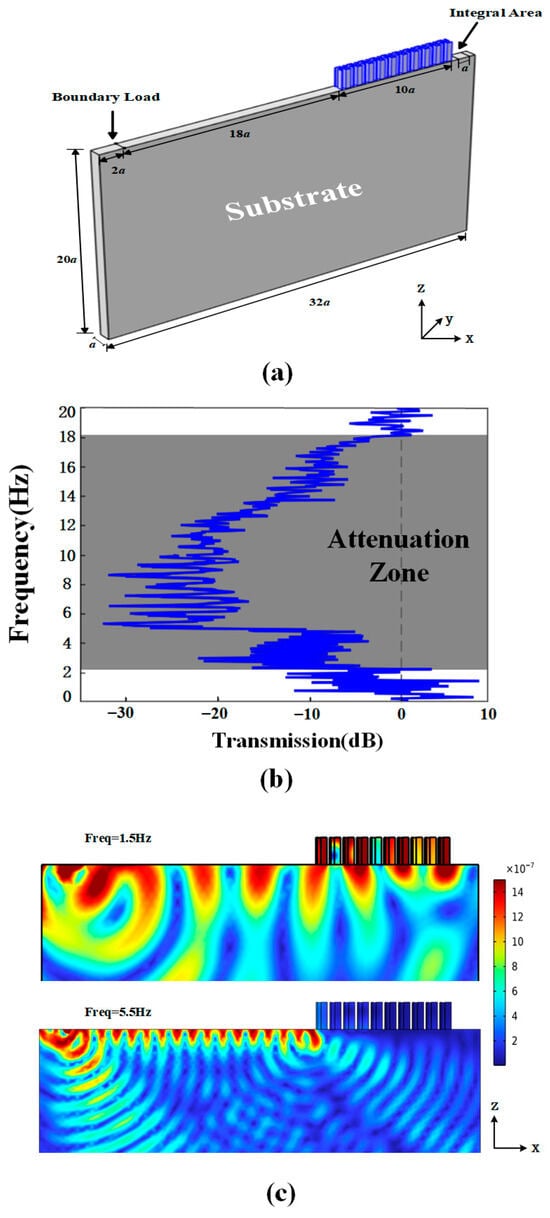
Figure 7. (a) Schematic picture of a finite system used for transmission calculations. (b) The transmission coefficient of the structure. The gray area is the attenuation zone. (c) The displacement field distributions at 1.5 Hz and 5.5 Hz, respectively.

3.6. Robustness Analysis

The influence of the insertion depth into the surface for gammadion-shaped pillars is not considered in the model mentioned above. However, in actual engineering, the insertion depth of the structure is a factor that cannot be ignored. In order to prove the applicability of the designed structure, we conduct research on its robustness.

As shown in Figure 8a, we modify the depth of the pillar insertion into the ground based on Figure 7a. To comprehensively simulate various scenarios, we test multiple cases with half-buried underground, fully buried, not buried, and buried at random depths. The transmission spectrum calculation results are shown in Figure 8b. In the cases of partial insertion with different depths, the insertion depth has a negligible impact on the transmission spectrum; only when fully buried will it have a slight effect on the result. Introducing randomness can even result in slightly better outcomes. However, overall, these slight differences do not affect the attenuation effect of the structure. The results demonstrate that the insertion depth only has a tiny impact on the effectiveness of the structures in attenuating waves, and the structures exhibit good robustness. For simplicity of calculation, the influence of insertion depth will no longer be considered in subsequent experiments.

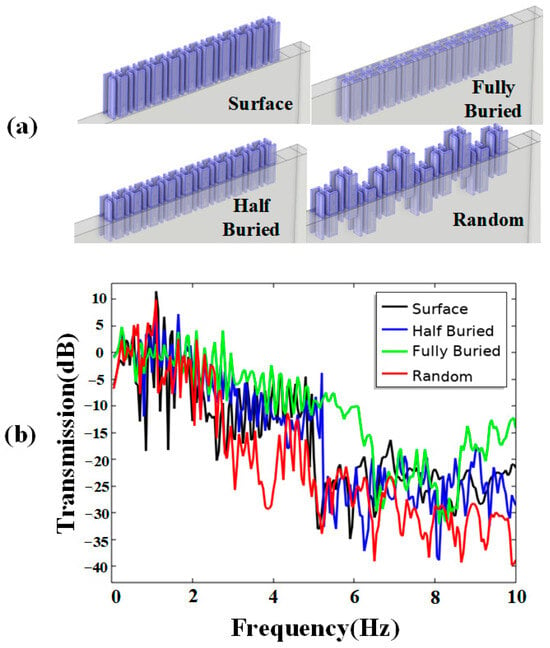
Figure 8. (a) Schematic diagram of finite element models with different insertion depths. (b) The corresponding transmission coefficients.

3.7. Time Domain Analysis

To further validate the shielding effect of our proposed 3D SM for Rayleigh waves, a time-transient harmonic analysis is conducted. The computed model is the same as that in Figure 7a, where an amplitude modulation (AM) wave source in the z-direction is applied as the boundary load, and the attenuated displacements are collected in the integral region behind the structures. The wave source emits a 5 Hz amplitude-modulated wave with 19-cycle Hanning-shaped modulation, active for 30 s. To highlight the attenuation effects, the displacements without and with the SM structures are overlaid on the same graph for comparison, in which the black line is the displacement without SM, and the red line is the displacement with SM, as shown in Figure 9. It can be seen that the SM has a very significant attenuation effect with a 76.45% attenuation at the peaks.

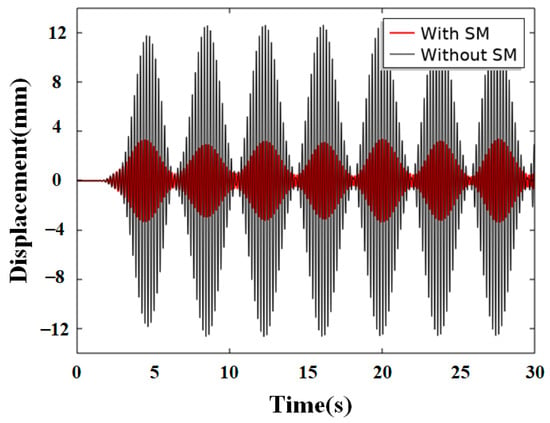
Figure 9. AM wave attenuation results, where the black line is the displacement without SM, and the red line is the displacement with SM attenuation. The model used is the same as Figure 7a.

Different from the AM wave source, the real seismic excitation is characterized by randomness and low-frequency dominance. In order to be more relevant to the real situation, we further choose a classical seismic wave signal (1952, Northern Calif-02) in our simulation experiments [40]. Figure 10a,b shows the time-domain profile of the seismic signal and its corresponding frequency content spectrum, in which the main excitation is predominantly concentrated within the frequency range of 0.1 Hz to 15 Hz and concentrates in the first 30 s. The seismic signal is applied on the boundary load along the z-direction, and the acceleration values for the cases with and without SM at the integral region in both time and frequency domains are calculated shown in Figure 11, in which the black curves represent cases without SM and the red ones depict those with SM. These results prove that the seismic waves are effectively suppressed after introducing the SM structures.

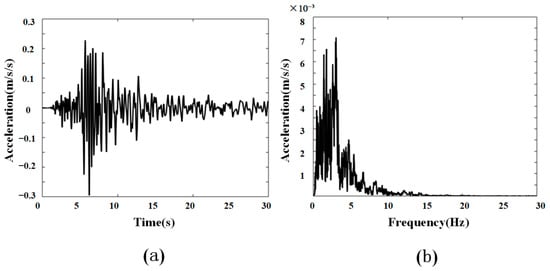
Figure 10. Seismic excitation signal: (a) temporal variation; (b) frequency domain composition.

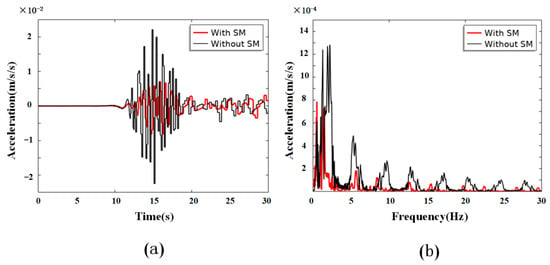
Figure 11. Dynamic response of the excitation signal: (a) temporal response of the seismic wave; (b) spectral response of the seismic wave. The black curves represent cases without SM, and the red ones depict results with SM attenuation.

4. Experimental Results

In the previous sections, the effectiveness of the proposed structure for seismic wave attenuation has been fully demonstrated theoretically and via simulation. In this part, the validity and feasibility of the proposed SM are verified by experiments. The sample of the unit cell is custom-made through 3D printing technology, as shown in Figure 12a. A 1:100 scaled experimental platform is built, and the epoxy is selected as the material of the SM instead of steel. The material parameters of epoxy are density of 1180 kg/m³, Young’s modulus of 4.35 × 10⁹ Pa, and Poisson’s ratio of 0.368 [41,42]. Theoretically, reducing the lattice constant by a factor of 100 should correspond to a 100-fold increase in the working frequency. However, since we replaced the steel with epoxy resin, both the density and Young’s modulus decrease significantly, resulting in a bandgap frequency amplification far smaller than the anticipated 100-fold increase. The bandgap width likewise narrowed slightly.

Figure 12. Experimental setups. (a) Dimensions of a 1:100 reduced epoxy sample. (b) Installation of experimental equipment. (c) Arrangement of the samples. (d) Model for finite element simulation.

The experimental substrate configuration is fabricated as a glass box (dimensions: 1.2 m × 0.5 m × 0.5 m), filled with sand to basically simulate the half-space environment. Due to the surface waves’ operating wavelength being substantially greater than the sand particle dimensions, the sand–SM interaction is deemed negligible. The glass box is high enough so that the body waves and the surface waves can be separated. Place pebbles along the surrounding boundaries of the box to minimize reflections from the walls. The entire experimental setups are shown in Figure 12b. However, due to the difficulty of eliminating the reflective influence of the walls, we changed the arrangement of the structural units. As shown in Figure 12c, the samples are periodically arranged in a 4 × 5 manner, with two samples in the middle removed and replaced with an accelerometer (X&K Tech., XK101S, Qinhuangdao, China), labeled as D in Figure 12b, to pick up the signals. Another accelerometer is placed in a symmetrical position as a comparison group without structural function, labeled as E. By altering the frequency in small increments, we achieve the effect of a frequency domain scan. As the transmission spectrum focuses on ratios, we employ acceleration in place of displacement for our calculations. The experimental setup is implemented as follows: A single-frequency sinusoidal excitation signal, generated by a signal generator (uT, uT8904FRS-DY, Wuhan, China) labeled as A, undergoes a frequency sweep from 30 Hz to 230 Hz and is subsequently amplified by a power amplifier (SP, Inc., YE5874A, Yangzhou, China) labeled as B. Through a vibration exciter (SP, Inc., JZK-50, Yangzhou, China) labeled as C positioned near the sand surface on one side of the glass box, wave excitation is introduced. Vertical surface acceleration peak components with and without SM configurations are captured at measurement points D and E as mentioned above, using two accelerometers which are connected to a signal acquisition unit (uT, uT8904FRS-DY). The acceleration data, denoted as A_d at point D and A_e at point E, are processed via analysis software (uT, uTekSs) labeled as F, enabling the calculation of the transmission spectrum (TS) defined by:

$$TS=20\times log{\displaystyle \frac{{\mathit{A}}_{\mathbf{d}}}{{\mathit{A}}_{\mathbf{e}}}}$$

(8)

Meanwhile, the corresponding numerical simulations are performed to match the experimental model, whose computed model is shown in Figure 12d, with the same dimensions as the experimental equipment. The transmission spectrum is shown in Figure 13, with numerical simulation results of this model also overlaid as a comparison. The first attenuation zone exists in the frequency range of 63–138 Hz, which shows a significant attenuation, even better than the simulation results. The second attenuation zone in the range of 175–210 Hz is in good agreement with the simulation results, and the attenuation effect is also obvious.

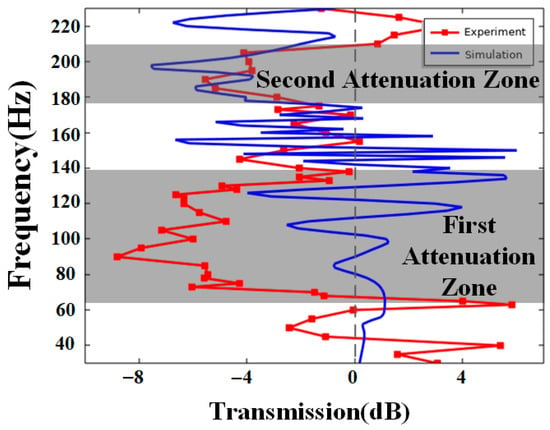
Figure 13. Experimental results. The blue curve is the finite element simulation results, and the red curve is the experimental results.

Although good agreement between numerical simulations and experimental measurements is achieved for the higher-frequency bandgap, a discrepancy exists in the lower-frequency region, where an attenuation band is observed experimentally but not predicted numerically. This discrepancy may stem from systematic errors, which are not fully accounted for in the idealized numerical model but are inherent to the practical experimental setup. Their effects are often amplified under low-frequency conditions.

The materials used in the simulation are assumed to be homogeneous, isotropic estimates based on the literature. In reality, spatial inhomogeneity in the substrate and moisture distribution can cause parameters to change. Such variations in material parameters can significantly affect the overall dynamic response of the system, particularly in the low-frequency range. Moreover, the sandy soil is adopted as the substrate in our experiment, and its inherent damping can lead to wave attenuation, contributing to discrepancies between the experimental and simulated results.

The simulation assumes perfectly bonded connections between pillar structures and the substrate. In practice, interfaces between samples and soil involve minute gaps or slippage, leading to more complex energy dissipation mechanisms than the theoretical model. This may enhance the attenuation of low-frequency vibrational energy.

5. Conclusions

In summary, we have proposed gammadion-shaped chiral metamaterials for full-mode seismic waves for protecting target buildings against earthquake damage. Chiral materials provide a bandgap of 12.53–28.33 Hz, within which the material exhibits negative effective mass density. It is found that our SM based on the gammadion-shaped chiral structures has a larger RBW (77.31%) than the SM with common non-chiral structures under the condition of the same duty ratio. Multiphysics simulations combining band structure analysis, transmission characterization, and negative mass density identification systematically verify both their shielding efficacy and wave attenuation mechanisms for the SM under the bulk wave incidence. In time-domain analysis, SM has a very significant attenuation effect with a 76.45% attenuation at the amplitude-modulated wave peaks. Importantly, a 3D SM for surface waves is exploited through a validation framework, incorporating real seismic signal reconstruction and 3D-printed scaled prototype testing, which confirms the SM system’s operational robustness across theoretical predictions and experimental measurements. This work demonstrates chiral SM’s promising potential applications in seismic shielding.