Photothermal Heat Transfer in Nano-Hydroxyapatite/Carbon Nanotubes Composites Modeled Through Cellular Automata

Abstract

Modeling elementary diffusion processes in nanostructured materials is essential for developing platforms capable of interacting with high-speed physical signals. In this work, the photothermal response of a nano-hydroxyapatite/carbon nanotube (nHAp/CNT) composite was experimentally characterized and modeled through a cellular automaton (CA) framework designed to capture the thermal propagation of the hybrid system. Synthesizing nHAp/CNT composites enables the combination of the biocompatible and piezoelectric nature of nHAp with the enhanced photothermal response introduced by CNTs. UV–Vis reflectance measurements confirmed that CNT incorporation increases the optical absorption of the ceramic matrix, resulting in more efficient photothermal conversion. The composite was irradiated with a nanosecond pulsed laser, and the resulting thermal transients were compared with CA simulations based on a D2Q9 lattice configuration. The model accurately reproduces experiments, achieving R² > 0.991 and NRMSE below 2.4% for all tested laser powers. This strong correspondence validates the CA approach for predicting spatiotemporal heat diffusion in heterogeneous nanostructured composites. Furthermore, the model revealed a sensitive thermal coupling when two heat sources were considered, indicating synergistic enhancement of local temperature fields. These findings demonstrate both the effective integration of CNTs within the nHAp matrix and the capability of CA-based modeling to describe their photothermal behavior. Overall, this study establishes a computational–experimental basis for designing controlled thermal-wave propagation and guiding future multi-frequency or multi-source photothermal mixing experiments.

1. Introduction

One of the current challenges in physics and engineering is the modeling and prediction of the behavior of systems composed of many interconnected elements, often involving two or more scales of analysis. Such systems may range from macroscopic structures, as those present in the cosmos, to microscopic processes involving the interaction of elementary particles in materials far from thermodynamic equilibrium. In particular, the microscopic behavior of particle dispersion in novel nanomaterials and the calculation of the propagation of physical perturbations are challenging. Two-wave mixing excitation from mixing physical mechanisms in nanostructures, such as optics, electronics, or phononics, can create nonlinear dispersions between elementary particles [1,2]. Accurately predicting these behaviors enables the development of systems with potential scientific and technological applications, including ultrafast logic gates, sensors, and solar cells [3,4,5].

The scattering of elementary particles within the crystalline lattice of a material under excitation behaves analogously to a colliding gas and can be described using a phenomenological approach known as the Lattice Boltzmann Method (LBM). This method evaluates the average response of microscopic perturbations and predicts the mesoscopic response through a global evolution scheme [6]. Depending on the nature of the perturbation, optical, electrical, thermal, or magnetic, the particle interactions follow specific physical laws that are usually expressed as nonlinear differential equations, making it difficult to represent and visualize their temporal evolution [7]. For this reason, the use of cellular automata (CA) models to predict time and space physical behavior has gained attention in science to solve a large number of particle interactions [8].

A CA is a discrete model in which each cell of a lattice evolves according to local rules that collectively define the global state of the system [9]. By updating cell states iteratively, CA can reproduce complex dynamics, including nonlinear and chaotic behavior, arising from simple local interactions. This computational framework has been successfully applied to a wide range of physical problems [5,10], offering an effective way to model systems whose behavior emerges from heterogeneous or multi-scale interactions. Such capabilities are particularly valuable when studying nanostructured materials whose thermal behavior depends strongly on local variations in composition and interfacial coupling.

A material of interest in biotechnology is nano-hydroxyapatite (nHAp), which exhibits bone-regeneration properties due to its piezoelectricity [11]. The cellular growth in nanocrystalline minerals was promoted for the reorientation of polar groups [12]. Despite its relevant biocompatibility properties, the manufacturing of new sensors and actuators using nHAp is limited due to its low strength and brittle nature. Therefore, novel materials such as carbon nanotubes (CNTs) have been incorporated into the ceramic matrix to enhance its mechanical, electrical, and thermal properties [13]. Moreover, nHAp is well known for its osteoconductive behavior, and recent studies indicate that controlled laser irradiation can activate biochemical pathways associated with bone repair [14]. Therefore, understanding how heat is deposited and diffuses through nHAp-based composites under laser excitation is a fundamental precursor for the development of optically activated regenerative devices. The addition of CNTs increases optical absorption, improving photothermal conversion efficiency, critical for these photonic processes. The present work serves as a preliminary step toward these applications by establishing the thermal behavior of the nHAp/CNT system under controlled laser perturbation.

In heterogeneous nanomaterials, heat transport is governed by local interactions that continuous models fail to capture. CA addresses this limitation by representing the material as discrete interacting units, where local energy-exchange rules naturally account for nanoscale interfaces and optical absorption contrasts. This makes CA particularly suitable for modeling photothermal diffusion in hybrid nHAp/CNT, since previous frameworks have been successfully applied to describe phonon-driven thermal transport in other nanostructured materials [15]. These precedents support the implementation of CA to analyze thermal propagation in complex composites, enabling controlled perturbations and numerical exploration of material behavior under different excitation conditions.

In this work, we propose a CA framework capable of reproducing the photothermal dynamics of an nHAp/CNT composite subjected to localized laser excitation. The composite surface is discretized into a lattice where each cell represents a region of the material and evolves according to rules that emulate energy exchange and thermal relaxation. By initializing the automaton with a pulsed heat source, we numerically evaluate the spatial and temporal diffusion of heat and compare it with experimental photothermal measurements. This strategy enables a physically grounded representation of thermal transport in a heterogeneous nanostructured bioceramic, overcoming the limitations of classical continuum models. Beyond providing understanding into the heat propagation mechanisms of the nHAp/CNT system, the developed CA model establishes a computational foundation for future investigations, which includes a two-wave mixing configuration to photothermally excite biocompatible materials with potential regenerative applications [16].

2. Materials and Methods

2.1. Nanocomposites Synthesis

To obtain the nHAp/CNT material, first, CNTs were synthesized via spray pyrolysis using ferrocene and toluene as precursors, which were injected as a mist using argon as the carrier gas into a horizontal tubular furnace. This reaction was carried out at 850 °C for 30 min. Afterward, the CNTs were collected and subjected to a purification process. They were mixed with a nitric/sulfuric acid mixture for 15 min under magnetic stirring to remove amorphous carbon and any remaining catalytic particles from the synthesis process. Finally, they were washed repeatedly with distilled water until a neutral pH was achieved. The resulting material was then placed in an oven at 90 °C for 2 h to remove excess water. Subsequently, nHAp was synthesized using co-precipitation method, where a phosphoric acid solution was added dropwise to a 1 wt% CNTs mixture of calcium hydroxide. The mixture was kept under mechanical stirring for 5 h, with the pH of the resulting solution being monitored. After stirring, the solution was vacuum filtered and dried in a furnace at 120 °C for 5 h. The resulting powder was further used to fabricate sintered wafers by using a 1.0 cm steel press die. The compaction was performed under a controlled pressure route using a hydraulic press, gradually increasing in steps of ~128.5 MPa every 5 min until reaching a final pressure of 900 MPa. The wafers were sintered in a tubular furnace at 500 °C in 500 sccm Ar flow for 5 h.

The incorporation of CNTs as a reinforcing material in nHAp ceramic matrix is particularly important because, although there are reports in the formation of these composite materials with CNTs loadings ranging from 0.5 to 5 wt% [17], a two-step experimental procedure is required: one step focused to obtaining the ceramic matrix and an additional step for incorporating of reinforcing material. This work reports the properties of an nHAp composite reinforced with 1 wt% CNTs obtained in a single-step process. This concentration (≤2 wt%) is considered adequate to improve the optical and structural response of HAp-based materials without altering the ceramic phase and without requiring additional incorporation steps. The experimental procedure applied to obtain the resulting material (nHAp/CNTs) allows a homogeneous dispersion of the reinforcing material (CNTs), so its mass fraction is 1 wt% in the ceramic matrix.

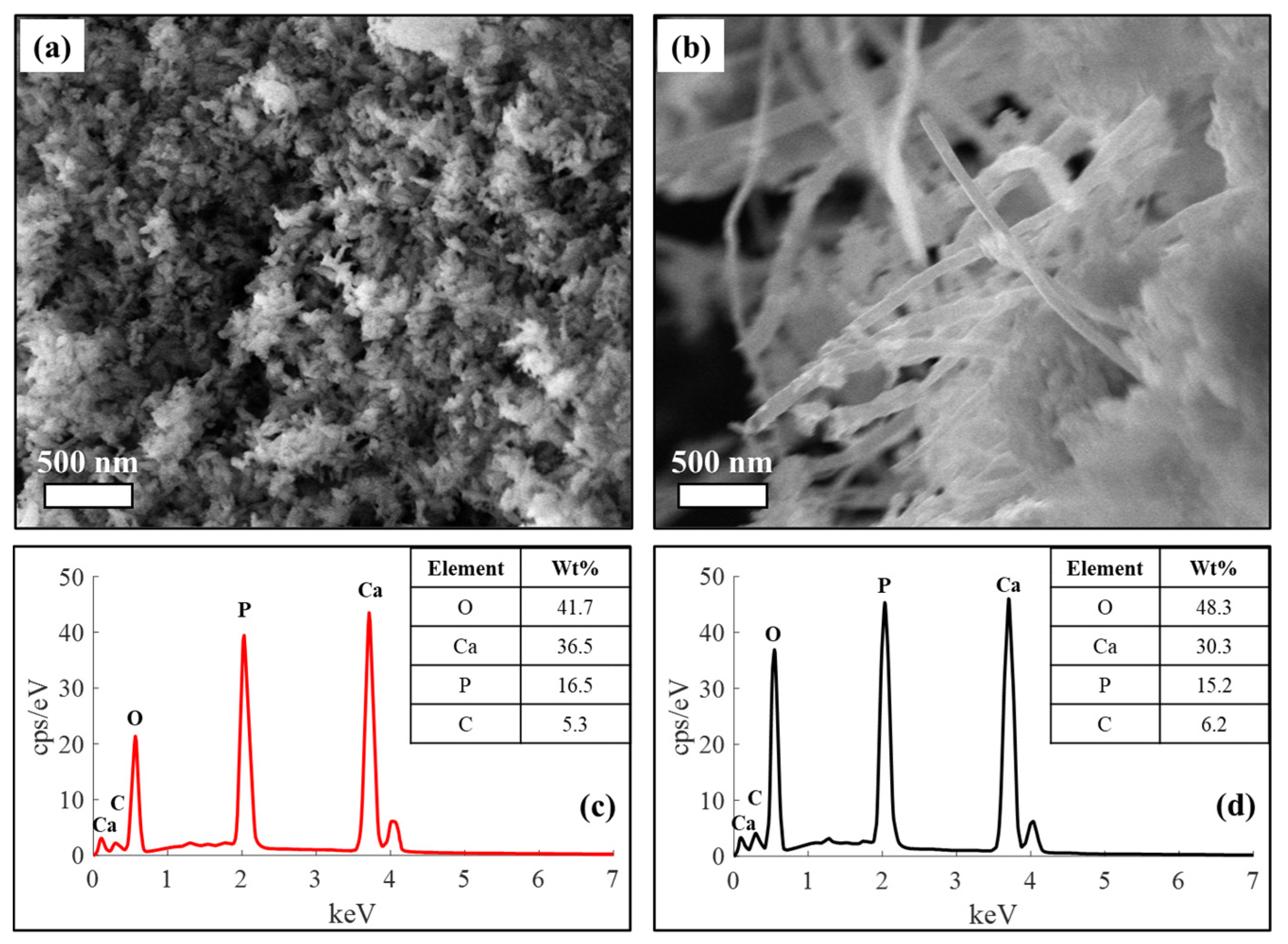
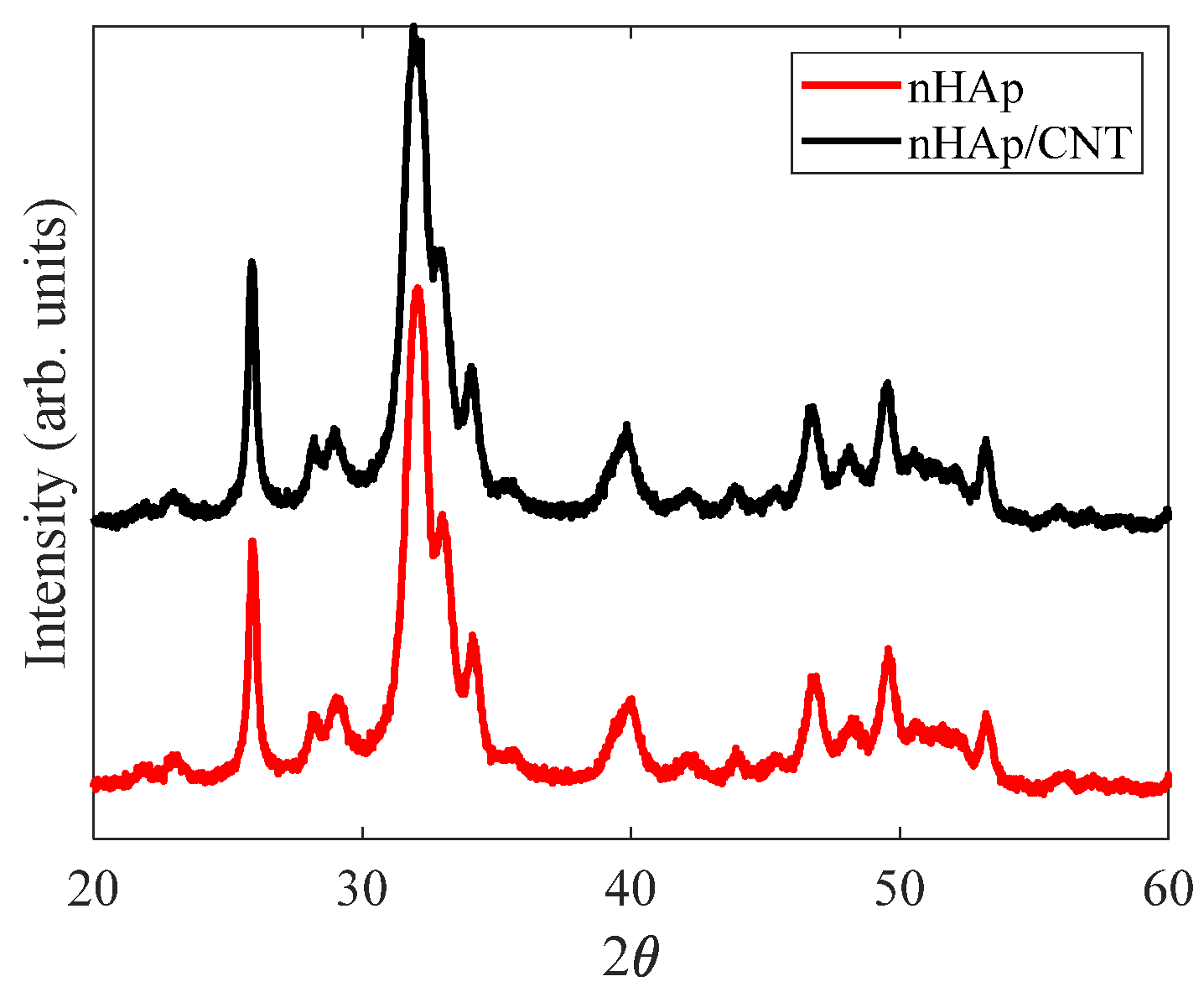
2.2. Characterizations

The morphology and composition of the nHAp materials were analyzed with field-emission scanning electron microscopy (FESEM) and energy dispersive X-ray spectroscopy (EDS), respectively. Those analyses were performed using a GeminiSEM 360 FESEM (ZEISS, Wetzlar, Germany). The crystalline phase was examined using X-ray diffraction (Bruker D8 FOCUS diffractometer, Billerica, MA, USA) with Cu-Ka radiation (l = 1.54056 Å). The optical properties were explored in a UV-Vis range total reflectance dispersion using a spectrophotometer (model HR-2XR200-25, Ocean Optics, Dunedin, FL, USA).

2.3. Photothermal Measurement Methodology

The photothermal response of the sample was evaluated by irradiating its central region using a near-infrared laser source with a wavelength of 1064 nm (Laserglow, Toronto, ON, Canada). The laser operated at variable optical powers ranging from 28 mW to 83 mW, with a beam diameter of approximately 1 mm. Each irradiation cycle lasted 60 s, during which the surface temperature evolution was monitored in real time. Temperature measurements were performed using an MLX90614 (Melexis, Ypres, Belgium) infrared sensor with a resolution of 0.2 °C, positioned at an angle of 45° relative to the sample surface and at a distance of 5 mm to minimize reflection and ensure accurate thermal detection. The data was acquired with an Arduino UNO board (Arduino, Monza, Italy), with a sampling rate of 0.1 s. The setup was mounted on an opto-mechanical platform to ensure stability and reproducibility during measurements, while ambient conditions were kept constant to reduce convective and radiative losses. A scheme of the setup is shown in Figure 1.

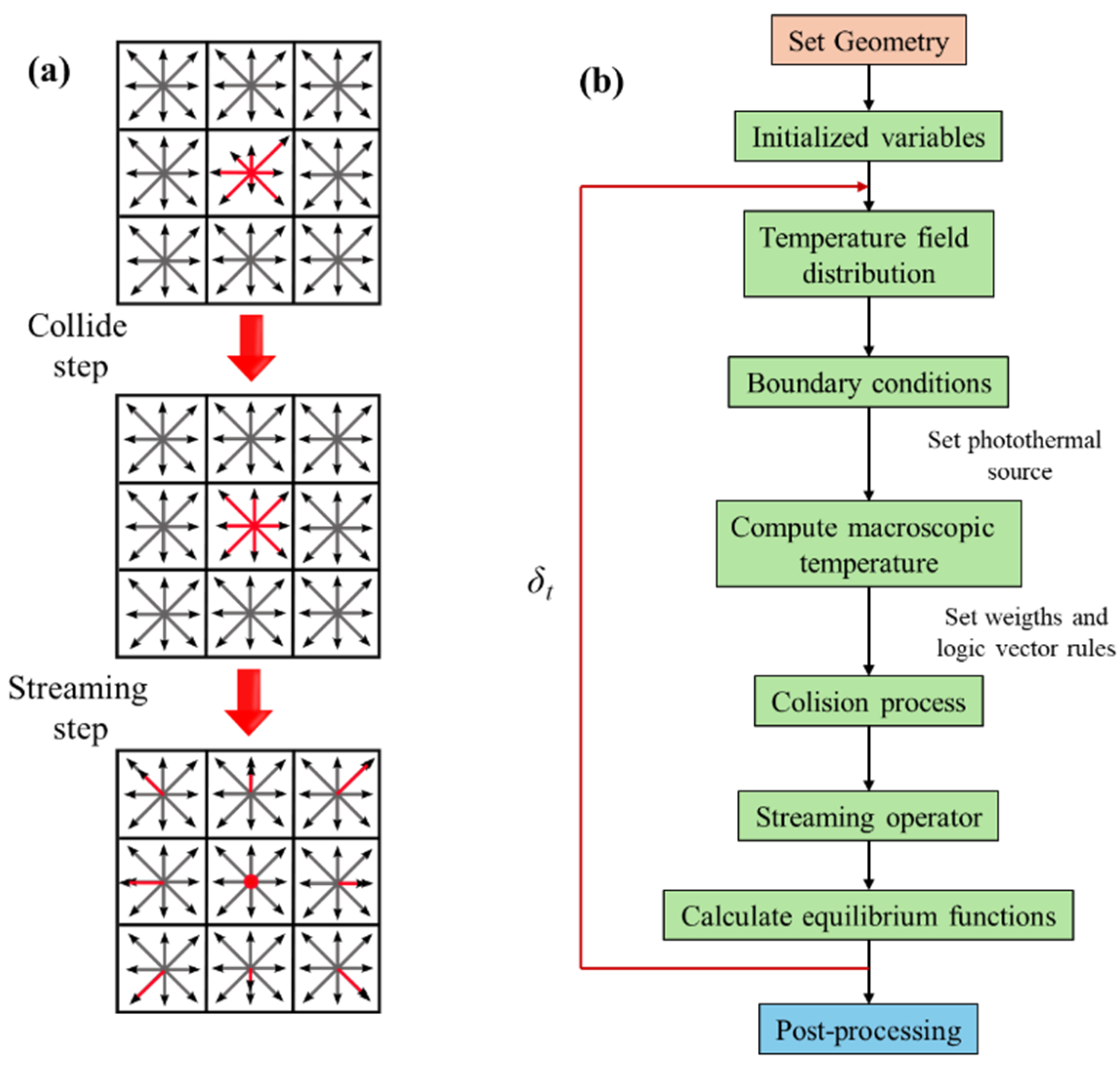
2.4. Cellular Automata Description

The extension of Boolean cellular dynamics into real numerical representations led to the LBM, which preserves the discrete lattice concept while incorporating continuous state variables. Based on this framework, a D2Q9 (2-dimensions, 9-directions) CA was developed to reproduce the experimentally observed photothermal diffusion. The description of particle populations in a quantized system is described according to the Boltzmann lattice equation. The physical system is established in both discretized space and time, and the entire computational domain is composed of a large number of identical cells. The Boltzmann equation describes the equilibrium condition of the distribution function. When an external force is considered, it can be expressed as [18]:

$${\displaystyle \frac{\partial f}{\partial t}}+F{\displaystyle \frac{\partial f}{\partial p}}+{\displaystyle \frac{p}{m}}\nabla f=\Omega$$

(1)

where f is the particle distribution function, F is the force field, p is the momentum vector, m is the particle mass, and Ω is the collision operator. Equation (1) represents the change in position and momentum of particles after collisions and depends on a relaxation time. Furthermore, to analyze phonon scattering and thermal transport properties, the equation is rescaled as [18]:

$${\displaystyle \frac{\partial f}{\partial t}}+v_g\nabla f=\Omega (f)$$

(2)

where f is now the phonon distribution function, v_g is the group velocity vector, and Ω(f) is the collision operator that describes changes in phonon position and momentum. The collision term is generally approximated through a relaxation-time model [18]:

$$\Omega \left(f\right)=-{\displaystyle \frac{f-f^{eq}}{{\tau }_R}}$$

(3)

where f^eq is calculated using the Planck equilibrium distribution, and ${\tau }_R$ is the relaxation time.

The relationship between the Boltzmann equation and a CA can be established by defining discrete transition rules that mimic particle collisions and propagation. For the implementation of LBM through CA dynamics, the Hardy–Pomeau–de Pazzis (HPP) rule can be used. In this model, point particles move through a discrete lattice according to a set of rules that imitate a discrete molecular dynamic. The CA rule governing the evolution of the system is defined through two sequential stages: collision and propagation. During the collision phase, particles within the same cell interact and redistribute their directions, while in the propagation phase, they move to adjacent cells according to their updated velocities. This two-step decomposition ensures locality of interactions and simplifies computational implementation. From this framework, the discrete Boltzmann equation can be written as [18]:

$$n_i\left(r+v_i{\delta }_t,t+{\delta }_t\right)=n_i\left(r,t\right)+\Omega \left(n\left(r,t\right)\right)$$

(4)

where $v_i$ is the velocity vector and δ_t is the discrete step. For the present study, a configuration of nine possible velocity directions allows for representing the phonon scattering and heat diffusion in the solid network [19], as shown in Figure 2a.

The computational procedure followed in the thermal LBM simulation is summarized in the flowchart shown in Figure 2. The algorithm begins with the definition of the lattice parameters, relaxation times, and D2Q9 velocity vectors. The temperature field is initialized uniformly at 300 K, and the distribution functions are set according to the equilibrium condition $f_i={\omega }_{i}T$. A circular photothermal inclusion is then introduced by assigning a different local relaxation time (${\tau }_{photon}$) within its region, while the surrounding matrix maintains a base value $\left({\tau }_{base}\right)$. A localized heat source is positioned at the center of the domain to generate a periodic thermal pulse. Each time step involves two main operations: (i) the collision process, in which the distributions relax toward their local equilibrium with spatially dependent relaxation rates, and (ii) the streaming process, where distributions propagate along the discrete lattice directions defined by the vectors $(c_x,c_y)$. Fixed-temperature boundary conditions (300 K) are imposed at the edges, while the central source alternates between 326 K and 452 K to simulate the pulsed heating obtained experimentally. The discrete velocity model implemented in this algorithm is D2Q9, and the boundary conditions consist of the bounce-back for solid-fluid interfaces and periodic boundary conditions for lateral sides [20].

3. Results

Figure 3 presents the morphology of the synthesized powders of nHAp and nHAp/CNT, obtained by FESEM. In Figure 3a, the nHAp powders exhibit a well-defined nanostructured morphology, characterized by agglomerated nanorods. The pure nHAp powders were synthesized using the same co-precipitation procedure described in Section 2.1, but without CNT addition. Figure 3b shows the nHAp/CNT composite, where the nanotubes are clearly visible and appear uniformly integrated within the HAp matrix, forming an interconnected hybrid network. The CNTs showed an outer diameter of 75 ± 12 nm, and their multi-walled nature is supported by previous reports of CNTs produced with comparable spray-pyrolysis parameters [21]. This microstructural complexity highlights the intrinsic heterogeneity of the composite, where the combination of organic (carbon-based) and inorganic (phosphate-based) phases generates a material with properties that are difficult to predict using conventional models. Such structural intricacy is particularly relevant for understanding and modeling its photothermal behavior, which depends strongly on the nanoscale arrangement and the interfacial coupling between CNTs and the biocrystalline matrix. Furthermore, Figure 3c,d display the EDS spectra of the nHAp and nHAp/CNT powders, respectively. The analysis confirmed the presence of oxygen, calcium, phosphorus, and carbon, with a Ca/P atomic ratio of approximately 2:1, consistent with the stoichiometry of HAp (Ca₁₀(PO₄)₆(OH)₂). The small carbon signal observed in the EDS spectrum of nHAp arises from the carbon tape used for sample mounting and from adventitious carbon adsorbed on the surface, a common feature in FESEM analyses. In the composite sample, the oxygen and carbon signals increased nearly in the same proportion due to the incorporation of CNT. The higher oxygen signal reflects both the oxygen in the HAp lattice, and the surface oxygenated functional groups present on CNTs [22]. Despite this increase, the overall Ca/P ratio remained unchanged, indicating that the addition of CNTs did not alter the intrinsic composition of the HAp phase. This chemical stability supports the effective integration of the nanostructures without compromising the structural integrity of the base material.

The crystalline structure of the powders was analyzed by XRD. The diffraction patterns of nHAp and nHAp/CNT are present in Figure 4. The well-defined peaks at 2θ = 26° (002), 32° (211), 33° (300), 34° (202), and 40° (310), corresponding to the characteristic reflections of the hexagonal HAp phase, are in good agreement with standard reference data [23]. These results confirm the successful formation of nanocrystalline HAp with no detectable secondary phases. The XRD pattern of the nHAp/CNT composite displayed the same characteristic peaks as pure nHAp, indicating that the incorporation of nanotubes did not alter the crystal structure of the biocrystal. However, no distinct peaks related to the CNTs were identified, likely due to their low content and the overlapping of their broad graphitic reflections with the background signal, which limits the detection of CNT crystallinity within the composite.

The characterization of the nHAp/CNT wafer samples is presented in Figure 5. Figure 5a shows a handheld photograph of the composite pellets. The samples were pressed with a load of 0.1 g in the die, resulting in an average thickness of 500 ± 5 µm and a density of 2.54 g/cm³. The black appearance of the nHAp/CNT sample arises from the incorporation of CNTs, which are well known for their strong absorption across the visible spectrum. Figure 5b compares the UV–Vis reflectance spectra of the pure nHAp and the nHAp/CNT pellets. As expected for a white ceramic, the nHAp sample exhibits a relatively high reflectance across the full spectral range, consistent with its strong scattering and low intrinsic optical absorption. In contrast, the nHAp/CNT composite shows a decrease in reflectance throughout the UV–Vis region, with values of ~65% in the UV region, decreasing to ~60% toward the NIR. Although the polished, compacted surface of the pellets increases specular reflectance, the CNTs reduce this effect by absorbing UV–Vis radiation, thereby enhancing the composite’s photothermal conversion efficiency.

Furthermore, SEM analysis was conducted on the sample surface to evaluate its homogeneity and nanostructural arrangement after the sintering process. Figure 5c presents a far view, where some pores are visible, but the overall surface exhibits low roughness. Moreover, Figure 5d shows a zoom image, revealing compacted nHAp crystals that exhibit slight fusion due to the 500 °C sintering temperature. This morphology suggests good intergranular contact, promoting efficient in-plane heat propagation and mechanical integrity. The resulting surface regularity facilitates accurate heat-wave propagation for correlation with the CA simulation. Meanwhile, the preserved nanostructured crystals form a complex conductive network with non-trivial thermal behavior [2], providing an ideal configuration for analyzing nonlinear dynamic propagation through the LBM-derived CA approach.

Additionally, the photothermal response of the nHAp/CNT sample was experimentally measured to derive the CA rules that best represent the physical mechanism of heat transport. Figure 6 shows the temporal evolution of the surface temperature of the composite under laser irradiation at different optical powers. In this experiment, the laser beam was irradiated at the center of the sample, and the temperature variation was recorded over time. A clear correlation between laser power and thermal response is observed: as irradiance increases, the maximum temperature rise becomes more pronounced and occurs in shorter times. This behavior reveals enhanced heat absorption and diffusion within the material. Overall, the temperature rise exhibits an approximately linear dependence on laser power, as expected for a photothermal response. However, slight deviations are observed between some curves. These differences can be attributed to physical factors that introduce nonlinearities during heat propagation, such as temperature-dependent properties. This variation can be changes in thermal conductivity, convective heat losses to the surrounding air, and/or surface emissivity. Although these effects are not explicitly included in the simplified CA model, their influence remains small, and the general trend clearly shows a monotonic increase in ΔT with increasing optical power. The progressive temperature increase with higher laser power confirms the strong coupling between optical excitation and thermal transport in the nHAp/CNT system. The structural complexity of the nanocomposite limits the applicability of classical heat-transfer models for determining its thermo-optical properties, since CNTs are heterogeneously distributed within the ceramic matrix. Therefore, the proposed CA approach was employed to establish a set of rules capable of describing the photothermal behavior of this complex material.

Figure 7 presents the series of seven photothermal responses obtained experimentally and their corresponding fits using the CA model. Figure 7a–g represents the temporal evolution of the temperature under a specific laser power: 28 mW, 38 mW, 53 mW, 63 mW, 70 mW, 74 mW, and 83 mW, respectively. The markers represent the experiment data, and the continuous lines the CA approximation. The fittings show excellent agreement between the measured data and the numerical simulation. The close correspondence between experimental and simulated profiles demonstrates that the proposed CA accurately reproduces the heat propagation dynamics in the nHAp/CNT composite. This validation confirms that the numerical model effectively captures both the transient and steady-state components of the thermal process. The resulting set of automaton rules therefore provides a reliable framework for describing photothermal transport in heterogeneous nanostructured systems and can serve as a basis for extending the model to more complex geometries or multi-physical interactions in future studies.

Table 1. Parameters obtained from experimental and numerical CA approach.

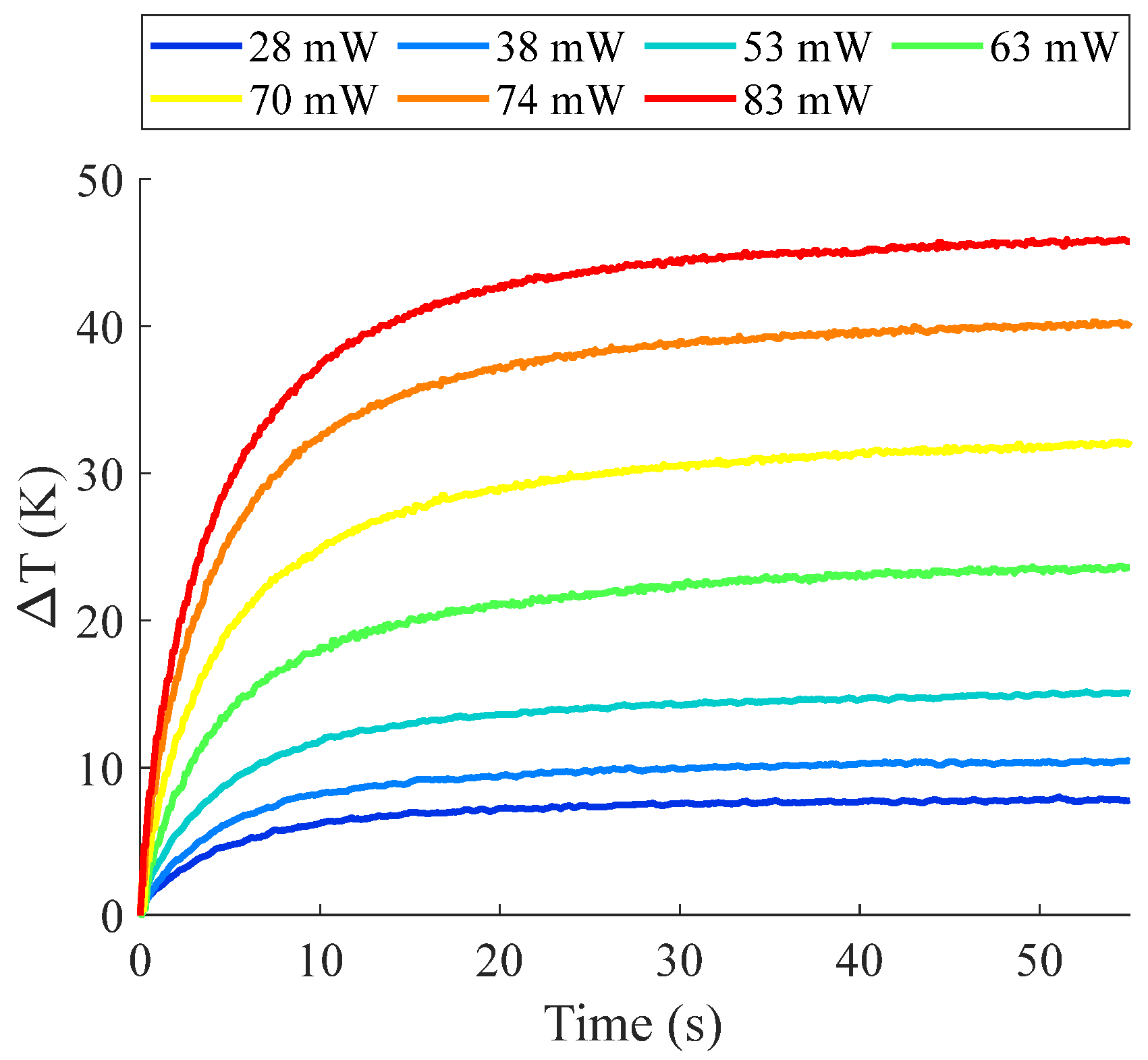
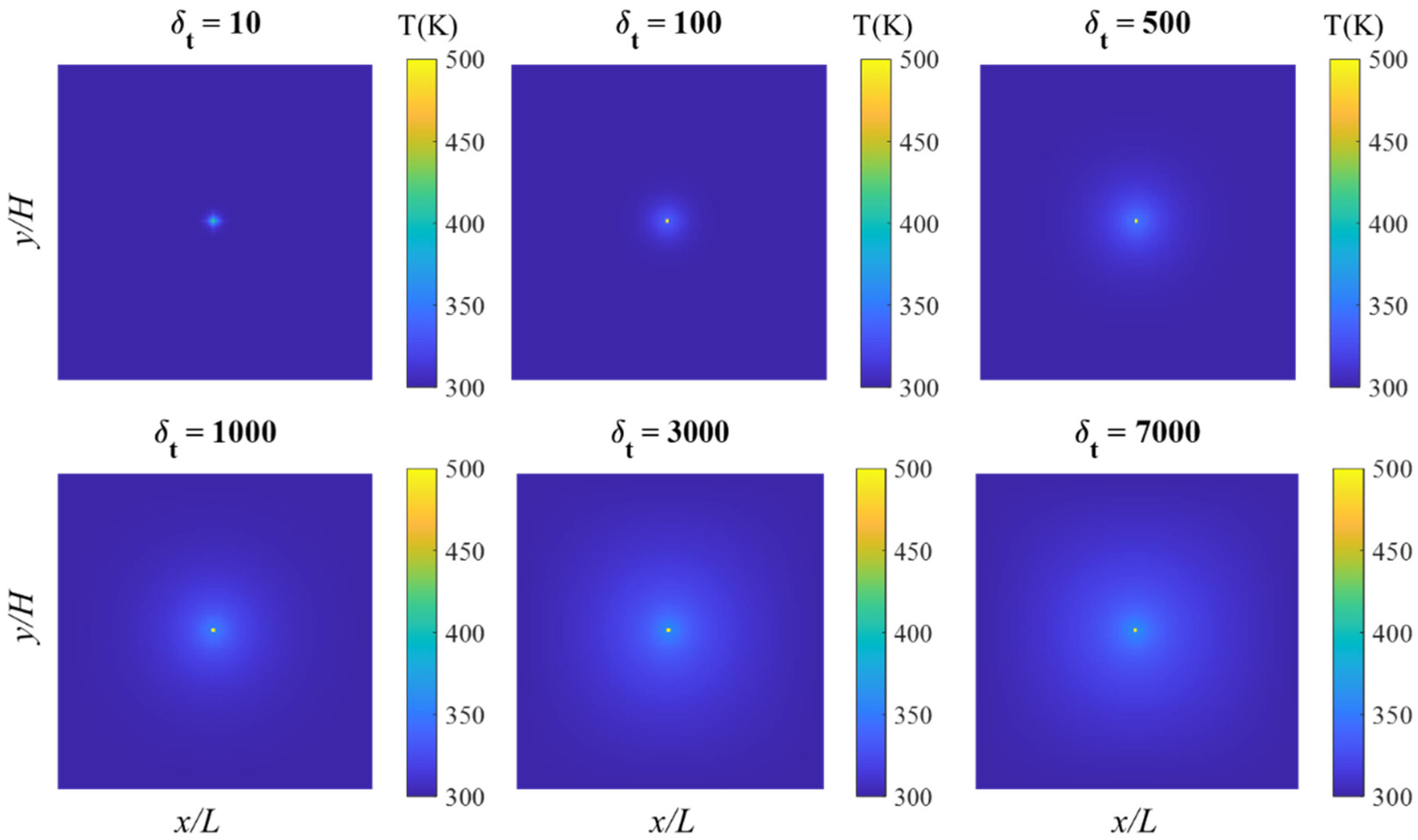
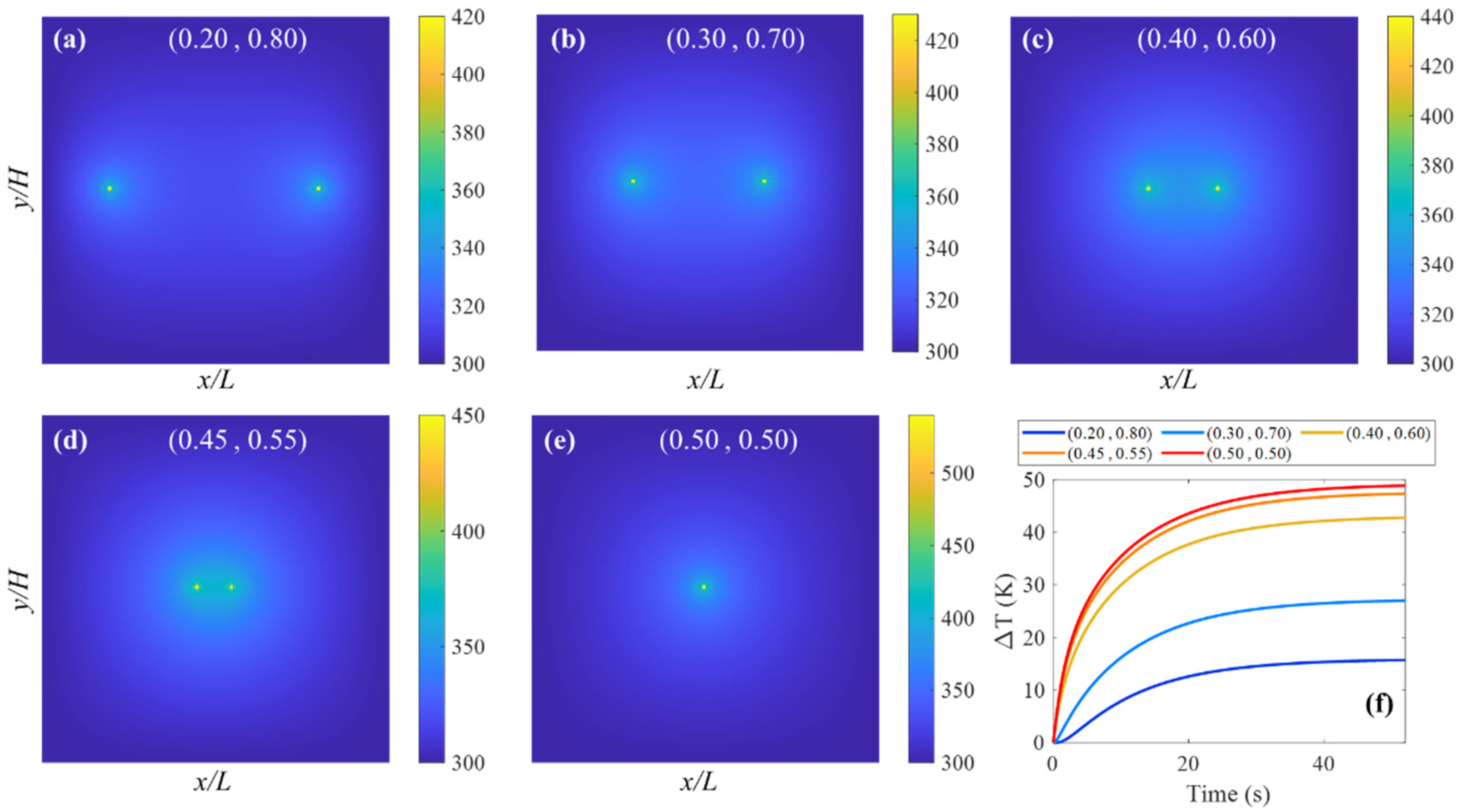
Laser Power (mW)	Experimental Tmax (K)	CA Tpulse (K)	NRMSE (%)	R2
28	302.05	347	1.93	0.991
38	305.17	362	1.64	0.992
53	309.65	390	1.40	0.994
63	317.95	440	1.28	0.996
70	326.49	492	1.22	0.996
74	334.67	543	1.91	0.992
83	340.47	576	2.25	0.992

summarizes the key parameters obtained from the experimental and numerical analysis of the photothermal response as a function of laser power. The maximum temperature (T_max) corresponds to the peak value measured in the heat transport experiment, as presented in Figure 6. The temperature used in the CA model to reproduce the experimental behavior is denoted as T_pulse, representing the expected temperature at the laser irradiation spot sample surface. Since the sensor aperture is larger than the laser spot, this consideration is physically consistent. The Normalized Root Mean Square Error (NRMSE) was employed to evaluate the agreement between experimental and simulated data, providing a dimensionless measure of relative deviation. The NRMSE slightly increased for laser powers of 74 mW and 83 mW, which may be attributed to temperature-dependent variations in the thermal diffusivity of the nanocomposite within the irradiated region. These effects are not accounted for in the CA model, where material properties remain fixed through the relaxation parameter (${\tau }_R$). Similarly, the coefficient of determination (R²) was used to assess the consistency between experimental and simulated results. The obtained R² values ranged from 0.991 to 0.996, confirming an overall strong correlation. The highest agreement was observed for most conditions, while slightly lower correlations at 74 mW and 83 mW suggest minor deviations likely related to local thermal variability or boundary effects.

Figure 8 illustrates the temporal evolution of the simulated temperature field obtained from the CA model. The nine sequential frames represent the spatial propagation of heat across the surface of the nHAp/CNT composite, starting from the initial irradiation point at the center of the domain. The coordinate axes represent a dimensionless unit according to the CA representation. At early stages, the temperature distribution is highly localized, corresponding to the laser spot region. As time progresses, the thermal field expands radially, revealing the characteristic diffusion pattern governed by the local interaction rules of the automaton. The progressive homogenization of the temperature map indicates the transition from transient heating to a steady-state regime. This simulation provides a clear visualization of how heat diffuses through the nanostructured composite, validating the capacity of the CA approach to reproduce the spatiotemporal dynamics of thermal transport observed experimentally. To relate the CA simulation to physical units (seconds, meters, and kelvins), a scaling procedure based on the real thermal diffusivity of the material was applied. The physical relation for heat conduction in the lattice framework is given by [24]:

$$\alpha ={c_s}^2\left(\tau -0.5\right){\displaystyle \frac{∆x^2}{∆t}}$$

(5)

where α represents the thermal diffusivity, ${c_s}^2=1/3$ is the squared lattice sound speed, τ is the relaxation time expressed in lattice units, $∆x$ is the lattice spacing, and $∆t$ is the discrete time step. This formulation allows transforms the numerical results of the CA into real physical scales, enabling the estimation of the effective thermal diffusivity of the nHAp/CNT composite. The relaxation parameter that fits the experimental data was found to be $\tau =2.8$. Additionally, $∆x$ and $∆t$ were chosen as $100\times {10}^{-6} \mathrm{m}$, and 0.0137 s, respectively, to fit the real dimensionality of the system. With these parameters, the thermal diffusivity was computed around $1\times {10}^{-6} {\mathrm{m}}^2/\mathrm{s}$, which is in concordance with HAp ceramics [25]. Therefore, the model provides a realistic approximation of the material’s heat transport properties, correlating the numerical and experimental domains.

To explore the implications of heat transfer generated by multiple excitation sources, a second laser beam with identical characteristics was introduced at different spatial positions on the surface of the nHAp/CNT composite. The separation between beams varied along the normalized x/L-axis to analyze the effect of spatial interference on the thermal field. The 2D temperature maps at the steady-state condition (δ_t = 7000) for different beam configurations are shown in Figure 9a–e, corresponding to symmetric separations at x/L = (0.2, 0.8), (0.3, 0.7), (0.4, 0.6), (0.45, 0.55), and (0.5, 0.5), respectively. Since the system exhibits a linear response with respect to laser power, the diffusivity in the 2D maps behaves as expected, forming circular thermal halos around each irradiation point. As the beams approach each other, the temperature fields progressively merge, leading to an overlapping thermal distribution in the central region. The superposition of the heat waves results in a local enhancement of the surrounding temperature, which in turn increases the temperature at the laser spot itself. When both sources coincide spatially (x/L = 0.5, 0.5), a strong photothermal interaction is observed, reaching a maximum surface temperature of approximately 550 K.

This behavior demonstrates that the photothermal coupling between adjacent heat sources can significantly modify the local thermal gradients and the overall energy distribution within the material. Such analysis is particularly relevant for studying nonlinear optical effects arising from long-range optical interactions, as these phenomena may influence both the photothermal conversion efficiency and the optical transmittance of the nanostructured system. To better visualize this effect, a central region of the sample was analyzed for all source configurations, and the transient temperature evolution is shown in Figure 9f. As observed, the temperature difference (ΔT) at the midpoint increases as the two beams move closer together. For the widest separation, the system exhibits a second-order thermal response with an amplitude of approximately 15 K, whereas when both beams coincide spatially, the response becomes first-order with an amplitude near 50 K. This transition reflects the progressive coupling between the photothermal fields generated by each laser, resulting in a synergistic enhancement of heat accumulation in the overlapping region. These findings suggest a promising route for precise thermal modulation at a given analysis point by adjusting either the power or spatial position of one beam relative to the other. In future implementations, one beam can act as the pump, providing the primary photothermal excitation, while the second serves as the probe, monitoring the induced thermal and optical variations. Although in the present simulation both sources share identical parameters, this configuration establishes the conceptual basis for a pump–probe photothermal model capable of analyzing localized nonlinear optical effects and their influence on energy transport and transmittance in complex nanostructured systems [26,27].

4. Discussion

The photothermal behavior demonstrated in the nHAp/CNT composite has important implications for future bioactivation strategies, particularly in applications of bone regeneration through controlled laser stimulation [28,29,30]. Since nHAp exhibits osteoconductive and osteoinductive responses when subjected to opto-mechanical activation, the ability to predict spatial and temporal heat distribution becomes essential for defining safe and effective irradiation parameters [16]. The enhanced optical absorption provided by CNTs enables more localized heating, suggesting that tailored composite formulations may be engineered to achieve targeted thermal stimuli without exceeding thresholds that could induce thermal damage or adverse biological responses. In this context, the CA framework developed here provides an initial predictive platform capable of estimating thermal gradients that may modulate biochemical interactions for tissue repair. However, the present model relies on fixed relaxation parameters and does not account for temperature-dependent properties such as thermal diffusivity, optical absorption, or coupling between mechanical, electrical, and thermal fields that may arise in real biological environments [31]. Moreover, the model does not incorporate convective heat losses, vascular heat dissipation, or the multiphasic architecture of living tissues, all of which will influence the thermal response during in vivo or clinically relevant laser exposure. Future work should therefore expand the CA approach by integrating multi-physics modules, such as thermal Lattice Boltzmann flux solvers [32], optical absorption maps derived from real microstructures [33], and bio-heat transfer models [34], to more accurately reproduce the conditions of phototherapies. Such developments will allow the framework established here to evolve into a more comprehensive predictive tool for designing and optimizing laser-based activation protocols in bioceramic and hybrid biomaterials.

In summary, the present findings highlight the ability of the CA framework to reproduce key features of the photothermal response in heterogeneous nHAp/CNT composites. An important aspect of this behavior is that the incorporation of CNTs enhances the optical absorption and photothermal output of the ceramic matrix without altering its crystalline structure, allowing the composite to exhibit more distinct and measurable temperature transients. These enhanced signals were essential for establishing a robust correlation between the experimental response and the CA predictions. Beyond this, the distinctive contribution of the present work lies in extending a D2Q9-based cellular automaton, typically applied to fluid dynamics or phonon transport [35,36], to the case of laser-induced heat diffusion in a bioceramic matrix reinforced with CNTs. To our knowledge, this is the first implementation of a CA model that captures both the transient experimental behavior and the thermal coupling between multiple excitation sources in such a hybrid system. This establishes a computational approach that can be further expanded toward optical activation mechanisms and multi-wave mixing studies in functional bioceramics.

5. Conclusions

This work demonstrated that the photothermal behavior of the nHAp/CNT composite can be accurately described through a CA framework specifically adapted to capture heterogeneous thermal diffusion. The carbon nanostructures were successfully incorporated into the nHAp matrix through the in situ chemical precipitation method, enhancing the optical absorption of the base ceramic and enabling localized, efficient heating. The experimental measurements under 1064 nm laser excitation exhibited a strong correlation with the numerical predictions, with R² values above 0.99 and NRMSE below 2.4%. For laser powers above 74 mW, slight deviations from linearity were observed, likely associated with temperature-dependent variations in the thermal properties of the composite. Additionally, the dual-source analysis revealed sensitive thermal coupling effects that could be exploited in nonlinear optical circuits or two-wave mixing calibration setups. These results establish a reliable computational–experimental basis for future studies involving controlled heat-wave propagation and provide a conceptual foundation for designing photothermal experiments in nanostructured bioceramics.