Abstract
The ferroaxial moment, a time-reversal-even axial dipole degree of freedom, plays a key role not only in conventional quantum states of matter but also in anomalous off-diagonal cross-correlated responses. Here, we theoretically demonstrate that a skyrmion crystal with a swirling non-coplanar spin texture can exhibit ferroaxiality. In particular, we show that a hybrid skyrmion crystal, formed by the superposition of Néel- and Bloch-type vortices, hosts a finite ferroaxial moment. The degree of ferroaxiality is quantified by calculating the expectation value of the electric toroidal dipole within a multi-orbital tight-binding model based on multipole representation theory. We further reveal characteristic off-diagonal responses associated with magnetic and magnetic toroidal multipoles under external magnetic fields. These results establish the hybrid skyrmion crystal as a promising platform for exploring the fundamental nature of ferroaxial moments.
1. Introduction
Multipole degrees of freedom provide a unifying framework for classifying complex electronic orders and cross-correlation responses in solids [1,2,3,4,5,6,7,8]. Beyond conventional electric and magnetic multipoles, electric toroidal and magnetic toroidal multipoles have emerged as key factors of anisotropic spin and orbital degrees of freedom in an atomic scale, together with their unconventional couplings to external fields [8]. Among them, the magnetic toroidal dipole, which is characterized as a time-reversal-odd polar vector, has been extensively studied from both atomic and thermodynamic perspectives [9,10,11], since it often gives rise to unconventional cross-correlation phenomena [12,13], including the linear magnetoelectric effect [14,15,16,17,18,19,20], asymmetric magnon excitations [21,22,23], and the nonlinear spin Hall effect [24,25].
In contrast, the ferroaxial moment represents a distinct axial degree of freedom, characterized as a time-reversal-even axial dipole [26,27]. Unlike magnetic toroidal dipoles, which embody parity-breaking magnetic responses, the ferroaxial moment encodes the sense of static rotation or twisting of a system and thus serves as an axial-order parameter associated with structural asymmetries [28,29,30]. From a symmetry standpoint, ferroaxiality can be regarded as the ferroic alignment of electric toroidal dipoles. It has been classified as one of the fundamental ferroic orders, on equal footing with ferroelectricity, ferromagnetism, and ferrotoroidicity, and it is allowed in crystallographic point groups lacking mirror symmetry. This degree of freedom couples to anomalous off-diagonal cross-correlation responses [31], such as the antisymmetric thermopolarization [32], intrinsic longitudinal spin current generation [31,33], and transverse nonlinear magnetic responses [34]. Recent experimental efforts have identified ferroaxial moments in a wide range of materials, which includes Co3Nb2O8 [35], CaMn7O12 [36], RbFe(MoO4)2 [28,37], NiTiO3 [37,38,39,40], Ca5Ir3O12 [41,42,43,44], BaCoSiO4 [45], K2Zr(PO4)2 [40,46], Na2Hf(BO3)2 [47], Na-superionic conductors [48], Na2BaM(PO4)2 ( Mg, Mn, Co, and Ni) [49], MnTiO3 [50], NiCo2TeO6 [51], and rare-earth tritellurides [52].
In the present study, we investigate an alternative route to induce the ferroaxial moment by focusing on magnetic phase transitions [53]. We demonstrate that a hybrid skyrmion crystal, which is defined as a spin texture formed by the superposition of Néel- and Bloch-type skyrmions, can host a finite ferroaxial moment even in the absence of structural rotational distortions. By analyzing a multi-orbital tight-binding model on a two-dimensional square lattice, we evaluate the expectation value of the electric toroidal dipole as a quantitative measure of ferroaxility and reveal that spin–orbit coupling plays a crucial role in inducing the atomic-scale ferroaxial moment. Furthermore, the hybrid skyrmion crystal exhibits magnetic field-induced cross-correlation responses characteristic of ferroaxiality and relevant odd-parity multipoles, such as transverse magnetization and magnetic toroidal dipoles. These findings establish the hybrid skyrmion crystal as a fertile platform for exploring ferroaxial physics in magnetism, thereby extending the scope of ferroaxiality beyond crystallographic distortions.
The remainder of this paper is organized as follows: in Section 2, we introduce the multi-orbital tight-binding model consisting of s and p orbitals on a two-dimensional square lattice, together with the spin texture of the hybrid skyrmion crystal, and discuss the associated symmetry reduction under magnetic ordering. In Section 3, we present our results on the emergence of ferroaxiality in the hybrid skyrmion crystal and clarify the role of relativistic spin–orbit coupling. Then, in Section 4, we discuss magnetic field-induced off-diagonal responses, including transverse magnetization and magnetic toroidal dipoles. Finally, Section 5 provides a conclusion of the present paper.
2. Model
We consider a multi-orbital tight-binding model on a two-dimensional square lattice. To explicitly incorporate the ferroaxial moment in the low-energy Hilbert space, we study an s-p hybridized system, in which the electric toroidal dipole degree of freedom, corresponding to the atomic-scale ferroaxial moment, is naturally included as described below. The tight-binding Hamiltonian is given by
We define the fermionic operators and as creating and annihilating an electron with spin on orbital (, , , or , , ) at square lattice site i, respectively; throughout this paper, the lattice constant is set to unity.
The kinetic energy part of the Hamiltonian function, given in the first term, includes several nearest-neighbor hopping processes, including between s orbitals, between and orbitals, between orbitals, and between the s and orbitals. These transfer integrals are chosen to ensure that the Hamiltonian function respects the tetragonal symmetry of the square lattice. To reduce complexity, orbital-dependent onsite potentials are omitted. The second part of the Hamiltonian function accounts for the atomic spin–orbit coupling within the p-orbital manifold, represented by the matrix . The specific expression of is given by
with basis . () denotes the Pauli matrices acting in the spin space. Unless otherwise noted, the following parameter values are employed: , , , , and . The adopted parameter set is designed to represent a generic situation where orbital hybridization and spin–orbit coupling occur at comparable energy scales. The hopping amplitudes correspond to typical energy scales of –1 eV in transition metal systems, while the strength of the spin–orbit coupling corresponds to tens to hundreds of meV depending on the d-orbital character. We note that the qualitative conclusions of this study are not sensitive to the fine details of these parameters: the ferroaxial moment robustly appears in the hybrid skyrmion crystal whenever the spin–orbit coupling is finite, whereas it vanishes in the pure Néel- and Bloch-type cases. Changing the relative magnitudes of the hopping integrals modifies quantitative values but does not alter these essential symmetry-based results. The overall energy scale of the model is measured in units of . The third part of the Hamiltonian function describes the coupling to magnetic mean fields originating from skyrmion spin textures, with the coupling constant fixed at . Here, the coupling constant J represents the effective interaction between the itinerant electron spins and the localized moments forming the skyrmion crystal texture, as described below. Physically, J corresponds to a local exchange field that enforces the alignment of the conduction electron spin with the background magnetic texture, analogous to Hund’s coupling or Kondo coupling in itinerant electron models [54,55,56]. In typical transition metal compounds, J is of the order of 0.01–1 eV depending on the localization of the magnetic moments.
We model the effective site-dependent field of the skyrmion crystal, which corresponds to the fixed localized spins , as follows:
where the double-Q structure is defined by the two modulation wave vectors and ; we schematically illustrate the momentum space positions of and in the square lattice Brillouin zone in Figure 1d, where these two vectors are related by the rotational symmetry of the lattice and their superposition gives rise to the double-Q structure that corresponds to the hybrid skyrmion crystal. In this representation, is the position vector of site i, serves as a variational parameter associated with a uniform magnetization, and enforces the normalization condition . The parameter controls the helicity of the skyrmion spin texture; the state with denotes the Néel-type skyrmion crystal, that with denotes the Bloch-type skyrmion crystal, and that with denotes the hybrid skyrmion crystal. The resulting spin configurations for , and are illustrated in Figure 1a, Figure 1b, and Figure 1c, respectively.
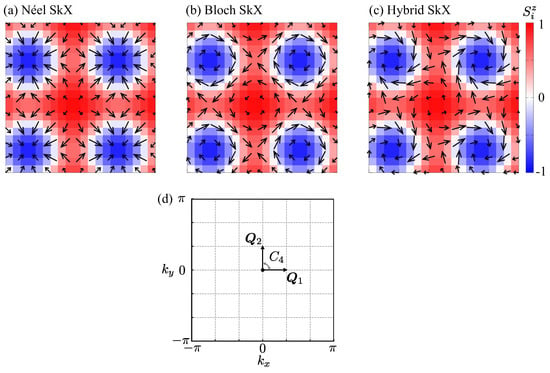
Figure 1.
Real-space spin configurations of (a) the Néel-type skyrmion crystal, (b) the Bloch-type skyrmion crystal, and (c) the hybrid skyrmion crystal. The arrows indicate the directions of magnetic moments at each lattice site, while the color scale represents the z component of the spin. The spin textures correspond to (a) , (b) , and (c) in Equation (3). SkX denotes the skyrmion crystal. (d) Momentum space sketch of the two modulation vectors and in the square lattice Brillouin zone. The symmetry relating and is shown.
The skyrmion spin texture described above has been observed in various materials since its discovery in chiral and polar magnets [57,58,59,60,61,62,63,64]; Néel-type skyrmion crystals are typically realized in polar magnets [65,66,67,68], whereas Bloch-type skyrmion crystals are stabilized in chiral magnets [57,58,59,60,62], consistent with the Lifshitz invariants in free energy [69,70,71,72]. In particular, square lattice skyrmion crystals have been reported in noncentrosymmetric compounds such as [73,74,75,76,77] and Cu2OSeO3 [78,79], as well as in centrosymmetric compounds such as GdRu2Si2 [80,81,82,83,84] and GdRu2Ge2 [85]. Several stabilization mechanisms for square skyrmion crystals have been proposed theoretically [86]. In noncentrosymmetric cases, the Dzyaloshinskii–Moriya interaction [87,88] plays a central role in inducing the skyrmion crystal [89,90,91,92], whereas in centrosymmetric cases, frustrated exchange interactions combined with bond-dependent anisotropic interactions and/or dipolar interactions are essential [93,94,95]. Although most skyrmion crystals are classified as either Néel- or Bloch-type, recent theoretical studies have suggested the possibility of hybrid skyrmion crystals arising from competing interactions in the momentum space [96] and crystalline-dependent magnetic anisotropy [97]. Experimentally, hybrid skyrmion crystals have been identified in synthetic multilayers [98,99,100] and in bulk magnets such as EuNiGe3 [101,102], which can exhibit peculiar helicity-dependent dynamics [103,104].
The resulting magnetic point group symmetry depends on the helicity of the skyrmion. For the Néel-type skyrmion crystal in Figure 1a, the magnetic point group symmetry is reduced from to . Since the presence of symmetry forbids a ferroaxial moment parallel to the mirror plane, the Néel-type skyrmion crystal does not host a ferroaxial moment. Similarly, in the Bloch-type skyrmion crystal in Figure 1b, the ferroaxial moment is prohibited due to the combined symmetry of the twofold rotational operation about the x and y axes with the time-reversal operation. Indeed, the time-reversal-even axial vector oriented along the z axis does not transform as the identity irreducible representation of the magnetic point group in the Bloch-type skyrmion crystal. In contrast, the hybrid skyrmion crystal belongs to the magnetic point group 4, which breaks both and symmetries. Consequently, the z component of the ferroaxial moment is symmetry-allowed in the hybrid skyrmion crystal. We summarize the relation between the magnetic point groups of the three skyrmion textures and the symmetry-allowed multipoles relevant to the present study in Table 1. This overview highlights that the ferroaxial moment is uniquely allowed in the hybrid skyrmion crystal, while the Néel-type and Bloch-type skyrmion crystals only support the magnetic monopole and magnetic toroidal dipole, respectively.

Table 1.
Magnetic point groups (MPGs) of Néel-, Bloch-, and hybrid-type skyrmion crystals (SkX) and the corresponding allowed and forbidden multipoles. denotes the ferroaxial moment (electric toroidal dipole), the magnetic monopole, and the magnetic toroidal dipole. The irreducible representation (Irrep.) under is also shown in the rightmost column.
3. Ferroaxiality Under Skyrmion Spin Textures
We begin by examining the ferroaxiality under skyrmion spin textures. Figure 2a shows the dependence of the expectation value with respect to the z component of the electric toroidal dipole at the chemical potential . The operator expression of the z-directional electric toroidal dipole is given by [105]
where and represent the orbital components of the magnetic dipole, whose matrix forms for the basis are represented by
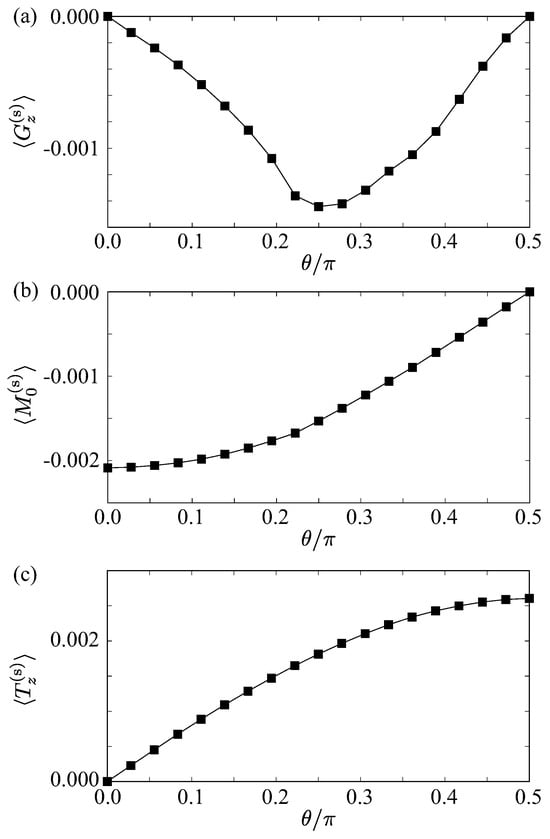
Figure 2.
dependence of the expectation values of (a) the electric toroidal dipole , (b) the magnetic monopole , and (c) the magnetic toroidal dipole .
Equation (4) corresponds to the definition of the electric toroidal dipole introduced in Ref. [105], where the operator is defined at the single-ion level. In the present study, multipole operators are defined on each lattice site in terms of the spin and orbital degrees of freedom, following the conventional single-atom definitions. The system-averaged multipoles shown here are obtained by taking the expectation value of these operators in the mean-field electronic state and summing them over all lattice sites, normalized by the total number of sites, where we take sites. Equivalently, this corresponds to evaluating the component of the corresponding multipole operator in reciprocal space.
The atomic-scale electric toroidal dipole moment is defined as the vector product of spin and orbital angular momenta. As shown in Figure 2a, becomes nonzero except for and ; the corresponding real-space configurations of are shown in Figure 3d–f, where density waves in terms of can be found in all cases. In other words, the ferroaxial moment with the same symmetry as the electric toroidal dipole is induced in the hybrid skyrmion crystal but not in the Néel- and Bloch-type skyrmion crystals, which is in agreement with the symmetry analysis in Table 1. These results demonstrate that the ferroaxial moment can be activated by a magnetic phase transition through symmetry lowering, even in the absence of rotational distortions of ligand ions [106]. The expectation value reaches its maximum around , highlighting the importance of the coupling between the Néel- and Bloch-type helicities. With respect to the model parameters, remains nonzero when , but it vanishes for . This behavior highlights the crucial role of spin–orbit coupling in the present model. Although a non-coplanar spin texture can induce orbital hybridization, the emergence of a ferroaxial moment requires an additional microscopic channel that couples spin and orbital sectors. The spin–orbit interaction provides this channel by mixing orbitals of different symmetries, thereby converting the non-coplanar spin texture into an electric toroidal dipole moment. In the absence of SOC (), this spin–orbital entanglement is lost, and the ferroaxial moment consequently vanishes.
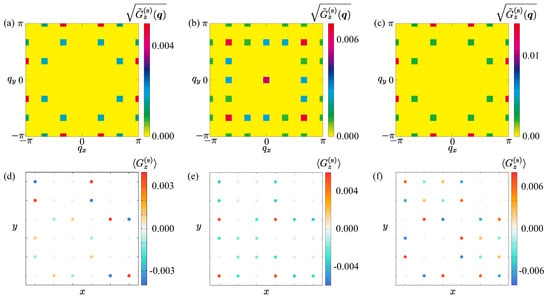
Figure 3.
The structure factor in terms of the electric toroidal dipole at (a) , (b) , and (c) . The presence of intensity at indicates a ferroic alignment of electric toroidal dipoles. Panels (d–f) show the real-space distributions of the local ferroaxial moment at each lattice site i, evaluated from Equation (6). The color scale encodes positive and negative values, and the horizontal/vertical axes indicate the lattice coordinates , allowing the skyrmion positions [Figure 1a–c] to be identified from the ferroaxial density modulations.
To highlight the distinct behavior of for different values, we evaluate its structure factor defined as
where is the wave vector and means the expectation value at site i. Physically, the structure factor in Equation (6) quantifies the spatial correlations of the electric toroidal dipole moments across the lattice, analogous to how the spin structure factor measures correlations of spins. A peak at corresponds to a ferroaxial alignment, i.e., a uniform ordering of electric toroidal dipoles, whereas peaks at finite vectors indicate modulated or antiferroaxial arrangements. This quantity allows us to identify whether the skyrmion textures host uniform or spatially modulated ferroaxial moments.
Figure 3a–c represents the structure factors of at , , and , respectively. The data for the hybrid skyrmion crystal in Figure 3b exhibits the intensity at , while those for the Néel-type skyrmion crystal in Figure 3a and the Bloch-type skyrmion crystal in Figure 3c do not. In all cases, however, finite- components such as remain visible. These results indicate that the Néel- and Bloch-type skyrmion crystals accompany the antiferroic alignment of the axial moment without a net uniform component. The corresponding real-space configurations of , i.e., the spatial distribution of the ferroaxial moment, are shown in Figure 3d–f. These maps visualize how the ferroaxial moment forms density wave-like patterns depending on the helicity, thereby providing a complementary picture to the spin textures in Figure 1 and facilitating a comparison with experimental imaging techniques such as second-harmonic generation microscopy.
In addition to the electric toroidal dipole, the skyrmion spin texture also induces other odd-parity multipoles. As examples, we present the dependence of the expectation value of the magnetic monopole in Figure 2b and that of the z component of the magnetic toroidal dipole in Figure 2c. Their operator expressions are given by
where represents the atomic-scale electric dipole operators, defined as
Equations (7) and (8) represent the magnetic monopole operator and magnetic toroidal dipole operator, respectively, in the convention of Ref. [105].
The data show that the magnetic monopole is activated in the Néel-type skyrmion crystal, while the magnetic toroidal dipole is activated in the Bloch-type skyrmion crystal. This trend is consistent with the real-space spin textures shown in Figure 1a,b: in the case of the Néel-type skyrmion crystal, the in-plane spins are arranged radially around the core, reflecting the symmetry of a magnetic monopole. In contrast, for the Bloch-type skyrmion crystal, the in-plane spins form a vortex-like configuration around the core, which corresponds to the symmetry of a magnetic toroidal dipole. The appearance of the magnetic monopole (magnetic toroidal dipole) implies the longitudinal (transverse) magnetoelectric effect [97,107]. Since the hybrid skyrmion crystal hosts both odd-parity multipoles, multiple components of the magnetoelectric tensor become finite.
4. Transverse Responses Under an External Magnetic Field
Next, we examine the cross-correlation responses associated with the ferroaxial moment under an external magnetic field. To this end, we add a Zeeman term to the Hamiltonian function in Equation (1):
where represents the in-plane external magnetic field. We consider the hybrid skyrmion spin texture with .
Figure 4a presents the x component of the spin magnetization under a magnetic field applied along the x direction, i.e., and . Here, the component of the spin magnetization is defined as
where
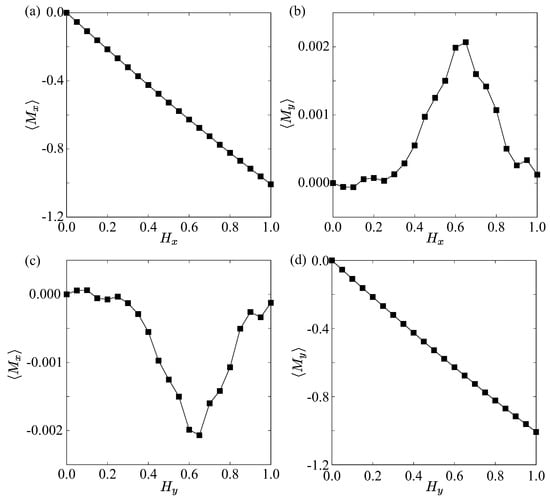
Figure 4.
The magnetic field dependence of the in-plane spin magnetization at . The x-directional magnetic field is applied in (a,b), and the y-directional magnetic field is applied in (c,d). The induced spin magnetization is shown for the x component in (a,c), while that for the y component is shown in (b,d).
The expectation value of the magnetization increases linearly with , consistent with the standard response of a physical quantity to its conjugate external field. A similar response is obtained when the magnetic field is applied along the y direction ( and ), where exhibits a linear dependence on , as shown in Figure 4d. The equivalence between the x and y directional responses reflects the fourfold rotational symmetry of the hybrid skyrmion crystal.
Meanwhile, the presence of the ferroaxial moment leads to additional off-diagonal transverse responses. In this case, the y component of the spin magnetization is induced by the x-directional magnetic field, as shown in Figure 4b, and the x component is induced by the y-directional magnetic field, as shown in Figure 4c [34]. It is noted that the sign of the induced spin magnetization is opposite for different magnetic field directions. Such a transverse response vanishes for the Néel- and Bloch-type skyrmion crystals, since the ferroaxial moment is not present. In other words, such a transverse response is a hallmark of the hybrid skyrmion crystal.
Moreover, additional cross-correlation responses arise from other active odd-parity multipole moments in the skrmion spin texture [108]. As an illustrative example, we focus on the magnetic field-induced toroidal dipole in the hybrid skyrmion spin texture. Figure 5a–d displays the magnetic field dependence of the induced magnetic toroidal dipole moment under the hybrid skyrmion spin texture. Here, the magnetic toroidal dipoles and are defined as
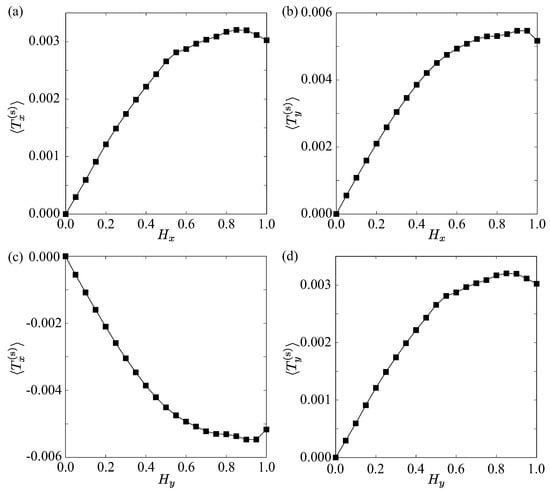
Figure 5.
The magnetic field dependence of the in-plane magnetic toroidal dipole at . The x-directional magnetic field is applied in (a,b), and the y-directional magnetic field is applied in (c,d). The induced magnetic toroidal dipole is shown for the x component in (a,c), while that for the y component is shown in (b,d).
The behavior of the induced magnetic toroidal dipole follows that of the induced magnetization shown in Figure 4. In the longitudinal channel, where , the induced magnetic toroidal dipole has the same sign and magnitude, as shown in Figure 5a,d, while in the transverse channel, where , the induced magnetic toroidal dipole has the same magnitude but opposite sign, as shown in Figure 5b,c. Since the magnetic toroidal dipole becomes the microscopic origin of the nonlinear nonreciprocal transport [109,110,111,112,113], one may anticipate the nonreciprocal conductivity along both x and y directions in the hybrid skyrmion spin texture under the external in-plane magnetic field.
The emergence of the longitudinal magnetic toroidal dipole parallel to the applied magnetic field can be ascribed to the activation of the electric toroidal monopole, which mediates an inner-product coupling between polar and axial vector quantities as . In contrast, the emergence of the transeverse magnetic toroidal dipole perpendicular to the magnetic field originates from the activation of the electric dipole, giving rise to an outer-product coupling between the polar and axial vector quantities as . Since the electric toroidal monopole and electric dipole are activated in the Bloch-type and Néel-type skyrmion crystals, respectively, the hybrid skyrmion crystal exhibits both contributions. Thus, the hybrid skyrmion crystal serves as a unique platform in which longitudinal and transverse magnetic toroidal dipole responses coexist.
From an experimental perspective, promising candidate systems for realizing such hybrid skyrmion crystals include synthetic multilayers [98,99,100] and bulk polar magnets such as EuNiGe3 [101,102], where hybrid helicities have already been reported. In these materials, the coexistence of hybrid skyrmions and ferroaxial moments is anticipated. Detecting ferroaxial responses may be possible via nonlinear optical techniques, such as second-harmonic generation microscopy that can directly image ferroaxial domains [50]. This probe offers complementary approaches to test the theoretical predictions presented in this study.
It is worth noting that the activation of the ferroaxial moment through the electric toroidal dipole is not limited to skyrmion textures [53]. In principle, other non-coplanar multiple-Q spin states that break the same set of mirror and twofold symmetries [114] can also induce ferroaxiality, even if they do not carry a quantized skyrmion number. The hybrid skyrmion crystal serves as a representative case in which these symmetry conditions are naturally realized.
5. Conclusions
We have theoretically demonstrated that the ferroaxial moment, a time-reversal-even axial dipole, can be induced in a hybrid skyrmion crystal without relying on structural rotational distortions. By employing a multi-orbital tight-binding model with s and p orbitals on a square lattice, we quantified ferroaxiality through the expectation value of the electric toroidal dipole. Our analysis revealed that the hybrid skyrmion texture, formed by the superposition of Néel- and Bloch-type vortices, breaks the relevant symmetries and gives rise to a finite ferroaxial moment, in contrast to the pure Néel- or Bloch-type cases. We further clarified that relativistic spin–orbit coupling is essential for inducing this ferroaxiality at the atomic scale.
In addition to establishing the ferroaxial moment, we identified characteristic magnetic field-induced cross-correlation responses in the hybrid skyrmion crystal. These include a transverse spin magnetization originating from the electric toroidal dipole, as well as longitudinal and transverse magnetic toroidal dipoles induced by electric toroidal monopoles and electric dipoles, respectively. Such responses arise from the dual Néel- and Bloch-type characteristics inherent in the hybrid spin texture. Taken together, our results establish the hybrid skyrmion crystal as a promising platform for exploring magnetic-order-driven ferroaxial physics, opening avenues for future applications in spintronics and multiferroics.
Funding
This research was supported by JSPS KAKENHI grant numbers JP21H01037, JP22H00101, JP22H01183, JP23H04869, JP23K03288, and JP23K20827 and by JST CREST (JPMJCR23O4) and JST FOREST (JPMJFR2366).
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Dubovik, V.; Cheshkov, A. Multipole expansion in classical and quantum field theory and radiation. Sov. J. Part. Nucl. 1975, 5, 318–337. [Google Scholar]
- Dubovik, V.; Tugushev, V. Toroid moments in electrodynamics and solid-state physics. Phys. Rep. 1990, 187, 145–202. [Google Scholar] [CrossRef]
- Gorbatsevich, A.; Kopaev, Y.V. Toroidal order in crystals. Ferroelectrics 1994, 161, 321–334. [Google Scholar] [CrossRef]
- Kuramoto, Y.; Kusunose, H.; Kiss, A. Multipole orders and fluctuations in strongly correlated electron systems. J. Phys. Soc. Jpn. 2009, 78, 072001. [Google Scholar] [CrossRef]
- Santini, P.; Carretta, S.; Amoretti, G.; Caciuffo, R.; Magnani, N.; Lander, G.H. Multipolar interactions in f-electron systems: The paradigm of actinide dioxides. Rev. Mod. Phys. 2009, 81, 807–863. [Google Scholar] [CrossRef]
- Suzuki, M.T.; Ikeda, H.; Oppeneer, P.M. First-principles theory of magnetic multipoles in condensed matter systems. J. Phys. Soc. Jpn. 2018, 87, 041008. [Google Scholar] [CrossRef]
- Kusunose, H.; Hayami, S. Generalization of microscopic multipoles and cross-correlated phenomena by their orderings. J. Phys. Condens. Matter 2022, 34, 464002. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H. Unified description of electronic orderings and cross correlations by complete multipole representation. J. Phys. Soc. Jpn. 2024, 93, 072001. [Google Scholar] [CrossRef]
- Gao, Y.; Vanderbilt, D.; Xiao, D. Microscopic theory of spin toroidization in periodic crystals. Phys. Rev. B 2018, 97, 134423. [Google Scholar] [CrossRef]
- Shitade, A.; Watanabe, H.; Yanase, Y. Theory of orbital magnetic quadrupole moment and magnetoelectric susceptibility. Phys. Rev. B 2018, 98, 020407(R). [Google Scholar] [CrossRef]
- Gao, Y.; Xiao, D. Orbital magnetic quadrupole moment and nonlinear anomalous thermoelectric transport. Phys. Rev. B 2018, 98, 060402(R). [Google Scholar] [CrossRef]
- Kopaev, Y.V. Toroidal ordering in crystals. Physics-Uspekhi 2009, 52, 1111–1125. [Google Scholar] [CrossRef]
- Spaldin, N.A.; Fiebig, M.; Mostovoy, M. The toroidal moment in condensed-matter physics and its relation to the magnetoelectric effect. J. Phys. Condens. Matter 2008, 20, 434203. [Google Scholar] [CrossRef]
- Popov, Y.F.; Kadomtseva, A.; Belov, D.; Vorob’ev, G.; Zvezdin, A. Magnetic-field-induced toroidal moment in the magnetoelectric Cr2O3. J. Exp. Theor. Phys. Lett. 1999, 69, 330–335. [Google Scholar] [CrossRef]
- Schmid, H. On ferrotoroidics and electrotoroidic, magnetotoroidic and piezotoroidic effects. Ferroelectrics 2001, 252, 41–50. [Google Scholar] [CrossRef]
- Ederer, C.; Spaldin, N.A. Towards a microscopic theory of toroidal moments in bulk periodic crystals. Phys. Rev. B 2007, 76, 214404. [Google Scholar] [CrossRef]
- Yanase, Y. Magneto-Electric Effect in Three-Dimensional Coupled Zigzag Chains. J. Phys. Soc. Jpn. 2014, 83, 014703. [Google Scholar] [CrossRef]
- Thöle, F.; Spaldin, N.A. Magnetoelectric multipoles in metals. Philos. Trans. R. Soc. A 2018, 376, 20170450. [Google Scholar] [CrossRef]
- Saito, H.; Uenishi, K.; Miura, N.; Tabata, C.; Hidaka, H.; Yanagisawa, T.; Amitsuka, H. Evidence of a New Current-Induced Magnetoelectric Effect in a Toroidal Magnetic Ordered State of UNi4B. J. Phys. Soc. Jpn. 2018, 87, 033702. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Emergent odd-parity multipoles and magnetoelectric effects on a diamond structure: Implication for the 5d transition metal oxides AOsO4 (A = K, Rb, and Cs). Phys. Rev. B 2018, 97, 024414. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Nonreciprocal Directional Dichroism and Toroidalmagnons in Helical Magnets. J. Phys. Soc. Jpn. 2012, 81, 023712. [Google Scholar] [CrossRef]
- Miyahara, S.; Furukawa, N. Theory of magneto-optical effects in helical multiferroic materials via toroidal magnon excitation. Phys. Rev. B 2014, 89, 195145. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Asymmetric Magnon Excitation by Spontaneous Toroidal Ordering. J. Phys. Soc. Jpn. 2016, 85, 053705. [Google Scholar] [CrossRef]
- Kondo, H.; Akagi, Y. Nonlinear magnon spin Nernst effect in antiferromagnets and strain-tunable pure spin current. Phys. Rev. Res. 2022, 4, 013186. [Google Scholar] [CrossRef]
- Hayami, S.; Yatsushiro, M.; Kusunose, H. Nonlinear spin Hall effect in PT-symmetric collinear magnets. Phys. Rev. B 2022, 106, 024405. [Google Scholar] [CrossRef]
- Hlinka, J. Eight Types of Symmetrically Distinct Vectorlike Physical Quantities. Phys. Rev. Lett. 2014, 113, 165502. [Google Scholar] [CrossRef] [PubMed]
- Hlinka, J.; Privratska, J.; Ondrejkovic, P.; Janovec, V. Symmetry Guide to Ferroaxial Transitions. Phys. Rev. Lett. 2016, 116, 177602. [Google Scholar] [CrossRef]
- Jin, W.; Drueke, E.; Li, S.; Admasu, A.; Owen, R.; Day, M.; Sun, K.; Cheong, S.W.; Zhao, L. Observation of a ferro-rotational order coupled with second-order nonlinear optical fields. Nat. Phys. 2020, 16, 42–46. [Google Scholar] [CrossRef]
- Cheong, S.W.; Lim, S.; Du, K.; Huang, F.T. Permutable SOS (symmetry operational similarity). npj Quantum Mater. 2021, 6, 58. [Google Scholar] [CrossRef]
- Cheong, S.W.; Huang, F.T.; Kim, M. Linking emergent phenomena and broken symmetries through one-dimensional objects and their dot/cross products. Rep. Prog. Phys. 2022, 85, 124501. [Google Scholar] [CrossRef]
- Hayami, S.; Oiwa, R.; Kusunose, H. Electric Ferro-Axial Moment as Nanometric Rotator and Source of Longitudinal Spin Current. J. Phys. Soc. Jpn. 2022, 91, 113702. [Google Scholar] [CrossRef]
- Nasu, J.; Hayami, S. Antisymmetric thermopolarization by electric toroidicity. Phys. Rev. B 2022, 105, 245125. [Google Scholar] [CrossRef]
- Roy, A.; Guimarães, M.H.D.; Sławińska, J. Unconventional spin Hall effects in nonmagnetic solids. Phys. Rev. Mater. 2022, 6, 045004. [Google Scholar] [CrossRef]
- Inda, A.; Hayami, S. Nonlinear Transverse Magnetic Susceptibility under Electric Toroidal Dipole Ordering. J. Phys. Soc. Jpn. 2023, 92, 043701. [Google Scholar] [CrossRef]
- Johnson, R.D.; Nair, S.; Chapon, L.C.; Bombardi, A.; Vecchini, C.; Prabhakaran, D.; Boothroyd, A.T.; Radaelli, P.G. Cu3Nb2O8: A Multiferroic with Chiral Coupling to the Crystal Structure. Phys. Rev. Lett. 2011, 107, 137205. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.D.; Chapon, L.C.; Khalyavin, D.D.; Manuel, P.; Radaelli, P.G.; Martin, C. Giant Improper Ferroelectricity in the Ferroaxial Magnet CaMn7O12. Phys. Rev. Lett. 2012, 108, 067201. [Google Scholar] [CrossRef]
- Hayashida, T.; Uemura, Y.; Kimura, K.; Matsuoka, S.; Hagihala, M.; Hirose, S.; Morioka, H.; Hasegawa, T.; Kimura, T. Phase transition and domain formation in ferroaxial crystals. Phys. Rev. Mater. 2021, 5, 124409. [Google Scholar] [CrossRef]
- Hayashida, T.; Uemura, Y.; Kimura, K.; Matsuoka, S.; Morikawa, D.; Hirose, S.; Tsuda, K.; Hasegawa, T.; Kimura, T. Visualization of ferroaxial domains in an order-disorder type ferroaxial crystal. Nat. Commun. 2020, 11, 4582. [Google Scholar] [CrossRef] [PubMed]
- Yokota, H.; Hayashida, T.; Kitahara, D.; Kimura, T. Three-dimensional imaging of ferroaxial domains using circularly polarized second harmonic generation microscopy. npj Quantum Mater. 2022, 7, 106. [Google Scholar] [CrossRef]
- Bhowal, S.; Spaldin, N.A. Electric toroidal dipole order and hidden spin polarization in ferroaxial materials. Phys. Rev. Res. 2024, 6, 043141. [Google Scholar] [CrossRef]
- Hasegawa, T.; Yoshida, W.; Nakamura, K.; Ogita, N.; Matsuhira, K. Raman Scattering Investigation of Structural Transition in Ca5Ir3O12. J. Phys. Soc. Jpn. 2020, 89, 054602. [Google Scholar] [CrossRef]
- Hanate, H.; Hasegawa, T.; Hayami, S.; Tsutsui, S.; Kawano, S.; Matsuhira, K. First Observation of Superlattice Reflections in the Hidden Order at 105 K of Spin–Orbit Coupled Iridium Oxide Ca5Ir3O12. J. Phys. Soc. Jpn. 2021, 90, 063702. [Google Scholar] [CrossRef]
- Hayami, S.; Tsutsui, S.; Hanate, H.; Nagasawa, N.; Yoda, Y.; Matsuhira, K. Cluster Toroidal Multipoles Formed by Electric-Quadrupole and Magnetic-Octupole Trimers: A Possible Scenario for Hidden Orders in Ca5Ir3O12. J. Phys. Soc. Jpn. 2023, 92, 033702. [Google Scholar] [CrossRef]
- Hanate, H.; Tsutsui, S.; Yajima, T.; Nakao, H.; Sagayama, H.; Hasegawa, T.; Matsuhira, K. Space-Group Determination of Superlattice Structure Due to Electric Toroidal Ordering in Ca5Ir3O12. J. Phys. Soc. Jpn. 2023, 92, 063601. [Google Scholar] [CrossRef]
- Xu, X.; Huang, F.T.; Admasu, A.S.; Kratochvílová, M.; Chu, M.W.; Park, J.G.; Cheong, S.W. Multiple ferroic orders and toroidal magnetoelectricity in the chiral magnet BaCoSiO4. Phys. Rev. B 2022, 105, 184407. [Google Scholar] [CrossRef]
- Yamagishi, S.; Hayashida, T.; Misawa, R.; Kimura, K.; Hagihala, M.; Murata, T.; Hirose, S.; Kimura, T. Ferroaxial Transitions in Glaserite-type Compounds: Database Screening, Phonon Calculations, and Experimental Verification. Chem. Mater. 2023, 35, 747–754. [Google Scholar] [CrossRef]
- Nagai, T.; Kimura, T. Chemical Switching of Ferroaxial and Nonferroaxial Structures Based on Second-Order Jahn–Teller Activity in (Na,K)2Hf(BO3)2. Chem. Mater. 2023, 35, 4109–4115. [Google Scholar] [CrossRef]
- Nagai, T.; Mochizuki, Y.; Yoshida, S.; Kimura, T. Chemical Aspect of Displacive-Type Ferroaxial Phase Transition from Perspective of Second-Order Jahn–Teller Effect: NASICON Systems as an Example. J. Am. Chem. Soc. 2023, 145, 8090–8098. [Google Scholar] [CrossRef]
- Kajita, Y.; Nagai, T.; Yamagishi, S.; Kimura, K.; Hagihala, M.; Kimura, T. Ferroaxial transitions in glaserite-type Na2BaM(PO4)2 (M = Mg, Mn, Co, and Ni). Chem. Mater. 2024, 36, 7451–7458. [Google Scholar] [CrossRef]
- Sekine, D.; Sato, T.; Tokunaga, Y.; Arima, T.h.; Matsubara, M. Second harmonic imaging of antiferromagnetic domains and confirmation of absence of ferroaxial twins in MnTiO3. Phys. Rev. Mater. 2024, 8, 064406. [Google Scholar] [CrossRef]
- Martinez, V.A.; Gao, Y.; Yang, J.; Lyzwa, F.; Liu, Z.; Won, C.J.; Du, K.; Kiryukhin, V.; Cheong, S.W.; Sirenko, A.A. Ferroaxial phonons in chiral and polar NiCo2TeO6. Phys. Rev. B 2025, 112, 064411. [Google Scholar] [CrossRef]
- Alekseev, S.; Ghorashi, S.A.A.; Fernandes, R.M.; Cano, J. Charge density waves with nontrivial orbital textures in rare earth tritellurides. Phys. Rev. B 2024, 110, 205103. [Google Scholar] [CrossRef]
- Hayami, S. Ferroaxial moment induced by vortex spin texture. Phys. Rev. B 2022, 106, 144402. [Google Scholar] [CrossRef]
- Zener, C. Interaction between the d-Shells in the Transition Metals. II. Ferromagnetic Compounds of Manganese with Perovskite Structure. Phys. Rev. 1951, 82, 403–405. [Google Scholar] [CrossRef]
- Anderson, P.W.; Hasegawa, H. Considerations on double exchange. Phys. Rev. 1955, 100, 675. [Google Scholar] [CrossRef]
- Hewson, A.C. The Kondo Problem to Heavy Fermions; Cambridge Studies in Magnetism Series; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Mühlbauer, S.; Binz, B.; Jonietz, F.; Pfleiderer, C.; Rosch, A.; Neubauer, A.; Georgii, R.; Böni, P. Skyrmion lattice in a chiral magnet. Science 2009, 323, 915–919. [Google Scholar] [CrossRef]
- Yu, X.Z.; Onose, Y.; Kanazawa, N.; Park, J.H.; Han, J.H.; Matsui, Y.; Nagaosa, N.; Tokura, Y. Real-space observation of a two-dimensional skyrmion crystal. Nature 2010, 465, 901–904. [Google Scholar] [CrossRef] [PubMed]
- Yu, X.Z.; Kanazawa, N.; Onose, Y.; Kimoto, K.; Zhang, W.; Ishiwata, S.; Matsui, Y.; Tokura, Y. Near room-temperature formation of a skyrmion crystal in thin-films of the helimagnet FeGe. Nat. Mater. 2011, 10, 106–109. [Google Scholar] [CrossRef]
- Seki, S.; Yu, X.Z.; Ishiwata, S.; Tokura, Y. Observation of skyrmions in a multiferroic material. Science 2012, 336, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Heinze, S.; von Bergmann, K.; Menzel, M.; Brede, J.; Kubetzka, A.; Wiesendanger, R.; Bihlmayer, G.; Blügel, S. Spontaneous atomic-scale magnetic skyrmion lattice in two dimensions. Nat. Phys. 2011, 7, 713–718. [Google Scholar] [CrossRef]
- Adams, T.; Chacon, A.; Wagner, M.; Bauer, A.; Brandl, G.; Pedersen, B.; Berger, H.; Lemmens, P.; Pfleiderer, C. Long-Wavelength Helimagnetic Order and Skyrmion Lattice Phase in Cu2OSeO3. Phys. Rev. Lett. 2012, 108, 237204. [Google Scholar] [CrossRef]
- Nagaosa, N.; Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. [Google Scholar] [CrossRef]
- Tokura, Y.; Kanazawa, N. Magnetic Skyrmion Materials. Chem. Rev. 2021, 121, 2857. [Google Scholar] [CrossRef]
- Kézsmárki, I.; Bordács, S.; Milde, P.; Neuber, E.; Eng, L.M.; White, J.S.; Rønnow, H.M.; Dewhurst, C.D.; Mochizuki, M.; Yanai, K.; et al. Neel-type skyrmion lattice with confined orientation in the polar magnetic semiconductor GaV4S8. Nat. Mater. 2015, 14, 1116–1122. [Google Scholar] [CrossRef] [PubMed]
- Bordács, S.; Butykai, A.; Szigeti, B.G.; White, J.S.; Cubitt, R.; Leonov, A.O.; Widmann, S.; Ehlers, D.; von Nidda, H.A.K.; Tsurkan, V.; et al. Equilibrium skyrmion lattice ground state in a polar easy-plane magnet. Sci. Rep. 2017, 7, 7584. [Google Scholar] [CrossRef] [PubMed]
- Fujima, Y.; Abe, N.; Tokunaga, Y.; Arima, T. Thermodynamically stable skyrmion lattice at low temperatures in a bulk crystal of lacunar spinel GaV4Se8. Phys. Rev. B 2017, 95, 180410. [Google Scholar] [CrossRef]
- Kurumaji, T.; Nakajima, T.; Ukleev, V.; Feoktystov, A.; Arima, T.h.; Kakurai, K.; Tokura, Y. Néel-Type Skyrmion Lattice in the Tetragonal Polar Magnet VOSe2O5. Phys. Rev. Lett. 2017, 119, 237201. [Google Scholar] [CrossRef]
- Dzyaloshinskii, I. Theory of helicoidal structures in antiferromagnets. I. Nonmetals. Sov. Phys. JETP 1964, 19, 960–971. [Google Scholar]
- Kataoka, M.; Nakanishi, O. Helical spin density wave due to antisymmetric exchange interaction. J. Phys. Soc. Jpn. 1981, 50, 3888–3896. [Google Scholar] [CrossRef]
- Bogdanov, A.N.; Yablonskii, D.A. Thermodynamically stable “vortices” in magnetically ordered crystals: The mixed state of magnets. Sov. Phys. JETP 1989, 68, 101. [Google Scholar]
- Bogdanov, A.; Hubert, A. Thermodynamically stable magnetic vortex states in magnetic crystals. J. Magn. Magn. Mater. 1994, 138, 255–269. [Google Scholar] [CrossRef]
- Tokunaga, Y.; Yu, X.; White, J.; Rønnow, H.M.; Morikawa, D.; Taguchi, Y.; Tokura, Y. A new class of chiral materials hosting magnetic skyrmions beyond room temperature. Nat. Commun. 2015, 6, 7638. [Google Scholar] [CrossRef]
- Karube, K.; White, J.; Reynolds, N.; Gavilano, J.; Oike, H.; Kikkawa, A.; Kagawa, F.; Tokunaga, Y.; Rønnow, H.M.; Tokura, Y.; et al. Robust metastable skyrmions and their triangular–square lattice structural transition in a high-temperature chiral magnet. Nat. Mater. 2016, 15, 1237. [Google Scholar] [CrossRef]
- Karube, K.; White, J.S.; Morikawa, D.; Dewhurst, C.D.; Cubitt, R.; Kikkawa, A.; Yu, X.; Tokunaga, Y.; Arima, T.h.; Rønnow, H.M.; et al. Disordered skyrmion phase stabilized by magnetic frustration in a chiral magnet. Sci. Adv. 2018, 4, eaar7043. [Google Scholar] [CrossRef]
- Karube, K.; White, J.S.; Ukleev, V.; Dewhurst, C.D.; Cubitt, R.; Kikkawa, A.; Tokunaga, Y.; Rønnow, H.M.; Tokura, Y.; Taguchi, Y. Metastable skyrmion lattices governed by magnetic disorder and anisotropy in β-Mn-type chiral magnets. Phys. Rev. B 2020, 102, 064408. [Google Scholar] [CrossRef]
- Henderson, M.E.; Bleuel, M.; Beare, J.; Cory, D.G.; Heacock, B.; Huber, M.G.; Luke, G.M.; Pula, M.; Sarenac, D.; Sharma, S.; et al. Skyrmion alignment and pinning effects in the disordered multiphase skyrmion material Co8Zn8Mn4. Phys. Rev. B 2022, 106, 094435. [Google Scholar] [CrossRef]
- Chacon, A.; Heinen, L.; Halder, M.; Bauer, A.; Simeth, W.; Mühlbauer, S.; Berger, H.; Garst, M.; Rosch, A.; Pfleiderer, C. Observation of two independent skyrmion phases in a chiral magnetic material. Nat. Phys. 2018, 14, 936–941. [Google Scholar] [CrossRef]
- Takagi, R.; Yamasaki, Y.; Yokouchi, T.; Ukleev, V.; Yokoyama, Y.; Nakao, H.; Arima, T.; Tokura, Y.; Seki, S. Particle-size dependent structural transformation of skyrmion lattice. Nat. Commun. 2020, 11, 5685. [Google Scholar] [CrossRef] [PubMed]
- Khanh, N.D.; Nakajima, T.; Yu, X.; Gao, S.; Shibata, K.; Hirschberger, M.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Peng, L.; et al. Nanometric square skyrmion lattice in a centrosymmetric tetragonal magnet. Nat. Nanotechnol. 2020, 15, 444. [Google Scholar] [CrossRef]
- Khanh, N.D.; Nakajima, T.; Hayami, S.; Gao, S.; Yamasaki, Y.; Sagayama, H.; Nakao, H.; Takagi, R.; Motome, Y.; Tokura, Y.; et al. Zoology of Multiple-Q Spin Textures in a Centrosymmetric Tetragonal Magnet with Itinerant Electrons. Adv. Sci. 2022, 9, 2105452. [Google Scholar] [CrossRef]
- Matsuyama, N.; Nomura, T.; Imajo, S.; Nomoto, T.; Arita, R.; Sudo, K.; Kimata, M.; Khanh, N.D.; Takagi, R.; Tokura, Y.; et al. Quantum oscillations in the centrosymmetric skyrmion-hosting magnet GdRu2Si2. Phys. Rev. B 2023, 107, 104421. [Google Scholar] [CrossRef]
- Wood, G.D.A.; Khalyavin, D.D.; Mayoh, D.A.; Bouaziz, J.; Hall, A.E.; Holt, S.J.R.; Orlandi, F.; Manuel, P.; Blügel, S.; Staunton, J.B.; et al. Double-Q ground state with topological charge stripes in the centrosymmetric skyrmion candidate GdRu2Si2. Phys. Rev. B 2023, 107, L180402. [Google Scholar] [CrossRef]
- Eremeev, S.; Glazkova, D.; Poelchen, G.; Kraiker, A.; Ali, K.; Tarasov, A.V.; Schulz, S.; Kliemt, K.; Chulkov, E.V.; Stolyarov, V.; et al. Insight into the electronic structure of the centrosymmetric skyrmion magnet GdRu2Si2. Nanoscale Adv. 2023, 5, 6678–6687. [Google Scholar] [CrossRef]
- Yoshimochi, H.; Takagi, R.; Ju, J.; Khanh, N.; Saito, H.; Sagayama, H.; Nakao, H.; Itoh, S.; Tokura, Y.; Arima, T.; et al. Multistep topological transitions among meron and skyrmion crystals in a centrosymmetric magnet. Nat. Phys. 2024, 20, 1001. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Stabilization mechanisms of magnetic skyrmion crystal and multiple-Q states based on momentum-resolved spin interactions. Mater. Today Quantum 2024, 3, 100010. [Google Scholar] [CrossRef]
- Dzyaloshinsky, I. A thermodynamic theory of “weak” ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. [Google Scholar] [CrossRef]
- Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960, 120, 91. [Google Scholar] [CrossRef]
- Rößler, U.K.; Bogdanov, A.N.; Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 2006, 442, 797–801. [Google Scholar] [CrossRef] [PubMed]
- Binz, B.; Vishwanath, A.; Aji, V. Theory of the Helical Spin Crystal: A Candidate for the Partially Ordered State of MnSi. Phys. Rev. Lett. 2006, 96, 207202. [Google Scholar] [CrossRef]
- Binz, B.; Vishwanath, A. Theory of helical spin crystals: Phases, textures, and properties. Phys. Rev. B 2006, 74, 214408. [Google Scholar] [CrossRef]
- Yi, S.D.; Onoda, S.; Nagaosa, N.; Han, J.H. Skyrmions and anomalous Hall effect in a Dzyaloshinskii-Moriya spiral magnet. Phys. Rev. B 2009, 80, 054416. [Google Scholar] [CrossRef]
- Utesov, O.I. Thermodynamically stable skyrmion lattice in a tetragonal frustrated antiferromagnet with dipolar interaction. Phys. Rev. B 2021, 103, 064414. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Lin, S.Z.; Batista, C.D. Meron, skyrmion, and vortex crystals in centrosymmetric tetragonal magnets. Phys. Rev. B 2021, 103, 104408. [Google Scholar] [CrossRef]
- Hayami, S. Multiple skyrmion crystal phases by itinerant frustration in centrosymmetric tetragonal magnets. J. Phys. Soc. Jpn. 2022, 91, 023705. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Degeneracy Lifting of Néel, Bloch, and Anti-Skyrmion Crystals in Centrosymmetric Tetragonal Systems. J. Phys. Soc. Jpn. 2020, 89, 103702. [Google Scholar] [CrossRef]
- Hayami, S.; Yambe, R. Helicity locking of a square skyrmion crystal in a centrosymmetric lattice system without vertical mirror symmetry. Phys. Rev. B 2022, 105, 104428. [Google Scholar] [CrossRef]
- Legrand, W.; Chauleau, J.Y.; Maccariello, D.; Reyren, N.; Collin, S.; Bouzehouane, K.; Jaouen, N.; Cros, V.; Fert, A. Hybrid chiral domain walls and skyrmions in magnetic multilayers. Sci. Adv. 2018, 4, eaat0415. [Google Scholar] [CrossRef]
- Li, W.; Bykova, I.; Zhang, S.; Yu, G.; Tomasello, R.; Carpentieri, M.; Liu, Y.; Guang, Y.; Gräfe, J.; Weigand, M.; et al. Anatomy of skyrmionic textures in magnetic multilayers. Adv. Mater. 2019, 31, 1807683. [Google Scholar] [CrossRef]
- Liyanage, W.L.N.C.; Tang, N.; Quigley, L.; Borchers, J.A.; Grutter, A.J.; Maranville, B.B.; Sinha, S.K.; Reyren, N.; Montoya, S.A.; Fullerton, E.E.; et al. Three-dimensional structure of hybrid magnetic skyrmions determined by neutron scattering. Phys. Rev. B 2023, 107, 184412. [Google Scholar] [CrossRef]
- Singh, D.; Fujishiro, Y.; Hayami, S.; Moody, S.H.; Nomoto, T.; Baral, P.R.; Ukleev, V.; Cubitt, R.; Steinke, N.J.; Gawryluk, D.J.; et al. Transition between distinct hybrid skyrmion textures through their hexagonal-to-square crystal transformation in a polar magnet. Nat. Commun. 2023, 14, 8050. [Google Scholar] [CrossRef]
- Matsumura, T.; Kurauchi, K.; Tsukagoshi, M.; Higa, N.; Nakao, H.; Kakihana, M.; Hedo, M.; Nakama, T.; Ōnuki, Y. Helicity Unification by Triangular Skyrmion Lattice Formation in the Noncentrosymmetric Tetragonal Magnet EuNiGe3. J. Phys. Soc. Jpn. 2024, 93, 074705. [Google Scholar] [CrossRef]
- Leonov, A.O.; Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 2015, 6, 8275. [Google Scholar] [CrossRef]
- Kim, K.W.; Moon, K.W.; Kerber, N.; Nothhelfer, J.; Everschor-Sitte, K. Asymmetric skyrmion Hall effect in systems with a hybrid Dzyaloshinskii-Moriya interaction. Phys. Rev. B 2018, 97, 224427. [Google Scholar] [CrossRef]
- Kusunose, H.; Oiwa, R.; Hayami, S. Complete Multipole Basis Set for Single-Centered Electron Systems. J. Phys. Soc. Jpn. 2020, 89, 104704. [Google Scholar] [CrossRef]
- Inda, A.; Hayami, S. Emergent cross-product-type spin-orbit coupling under ferroaxial ordering. Phys. Rev. B 2025, 111, L041104. [Google Scholar] [CrossRef]
- Bhowal, S.; Spaldin, N.A. Magnetoelectric Classification of Skyrmions. Phys. Rev. Lett. 2022, 128, 227204. [Google Scholar] [CrossRef]
- Hayami, S.; Kusunose, H.; Motome, Y. Spontaneous parity breaking in spin-orbital coupled systems. Phys. Rev. B 2014, 90, 081115. [Google Scholar] [CrossRef]
- Sawada, K.; Nagaosa, N. Optical Magnetoelectric Effect in Multiferroic Materials: Evidence for a Lorentz Force Acting on a Ray of Light. Phys. Rev. Lett. 2005, 95, 237402. [Google Scholar] [CrossRef] [PubMed]
- Kawaguchi, H.; Tatara, G. Effective Hamiltonian theory for nonreciprocal light propagation in magnetic Rashba conductor. Phys. Rev. B 2016, 94, 235148. [Google Scholar] [CrossRef]
- Watanabe, H.; Yanase, Y. Nonlinear electric transport in odd-parity magnetic multipole systems: Application to Mn-based compounds. Phys. Rev. Res. 2020, 2, 043081. [Google Scholar] [CrossRef]
- Suzuki, Y. Tunneling spin current in systems with spin degeneracy. Phys. Rev. B 2022, 105, 075201. [Google Scholar] [CrossRef]
- Yatsushiro, M.; Oiwa, R.; Kusunose, H.; Hayami, S. Analysis of model-parameter dependences on the second-order nonlinear conductivity in PT-symmetric collinear antiferromagnetic metals with magnetic toroidal moment on zigzag chains. Phys. Rev. B 2022, 105, 155157. [Google Scholar] [CrossRef]
- Ullah, A.; Li, X.; Jin, Y.; Pahari, R.; Yue, L.; Xu, X.; Balasubramanian, B.; Sellmyer, D.J.; Skomski, R. Topological phase transitions and Berry-phase hysteresis in exchange-coupled nanomagnets. Phys. Rev. B 2022, 106, 134430. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).