Abstract
Pyrazinamide may exist in at least four known polymorphic forms, which were obtained experimentally. One of these polymorphs, (α), shows outstanding mechanical properties, demonstrating a significant anisotropic plasticity in a three-point bending test, while the δ form was brittle. Despite a δ → α transition as well as β and γ behavior being experimentally studied, the relative stability of pyrazinamide polymorphs remains unclear and even controversial. In this work we provide a pure computational study of the thermodynamic relationships between all four polymorphs as a function of temperature using periodic DFT calculations. It was shown that the β but not the δ form is the most stable at low temperatures. Moreover, the relative stability of the δ form in comparison to α is questioned, showing that the “brittle to bending” δ → α transition was kinetically hindered in the experiments. We show that α and γ polymorphs were stabilized at higher temperatures due to an entropy term. Finally, the calculated stability of the bending α form of pyrazinamide at room temperature was in perfect agreement with previous experiments, which showed a transformation of all other forms to α during six month storage or grinding.
1. Introduction
Polymorphism is a widespread phenomenon for organic molecular crystals [1,2]. Different crystal structures determine the distinction in physicochemical properties, such as the shelf-life stability [3,4], solubility [5,6,7,8], bioavailability [9,10], tableting [11,12,13,14], etc. These properties are crucial for pharmaceutics, where polymorph screening is an almost mandatory procedure during drug discovery and development [15,16]. Polymorphism control helps to produce and preserve a desired form with known properties during the shelf-life and medication use [17,18,19].
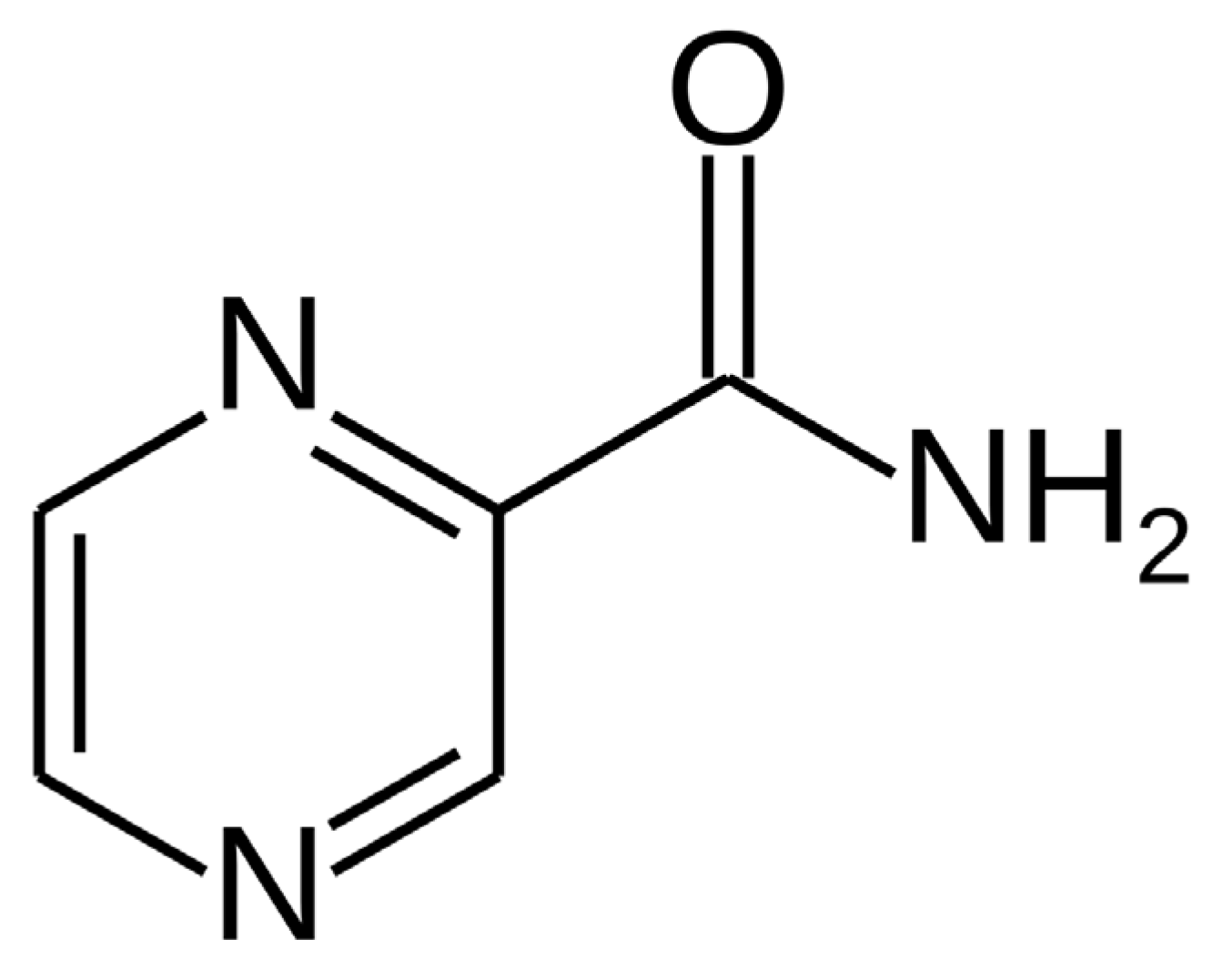
Pyrazinamide (pyrazine-2-carboxamide) is an antimicrobial agent that is commonly used for the treatment of active tuberculosis during the initial phase of therapy alone or in combination with other agents (Scheme 1) [20,21,22].
Scheme 1.
Molecular structure of pyrazinamide (pyrazine-2-carboxamide).
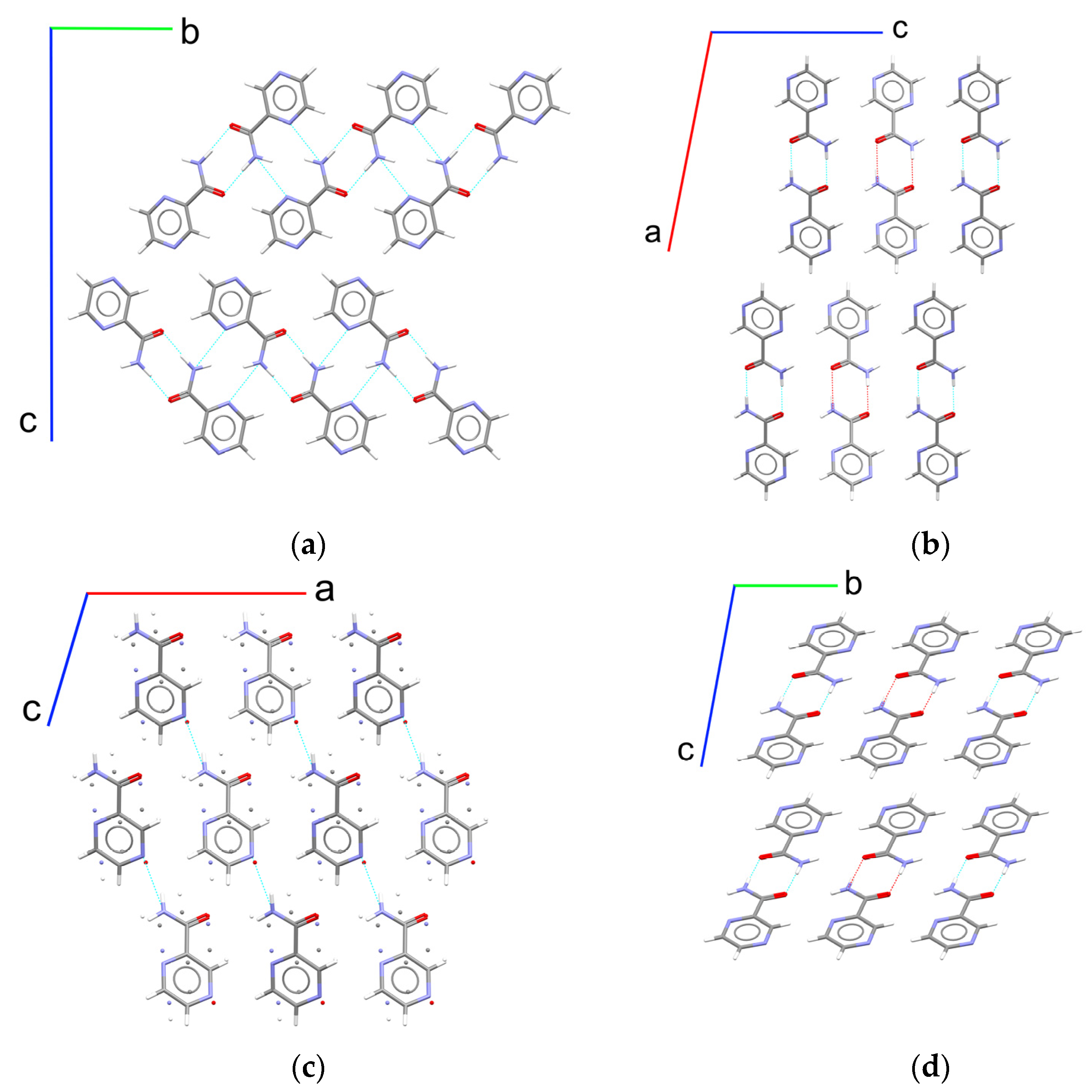
It may crystallize in four different polymorphs (α, β, γ, and δ), whereas only the α form is commercially available and used in therapy (Figure 1) [23,24,25,26]. It was shown that a transformation in the “real-world” conditions typical of pharmaceutical processing (e.g., milling and tableting) and storage (at a near ambient temperature and various humidity) leads to the formation of the α polymorph from the other three crystal structures [27]. It is valuable to note that the α form shows outstanding mechanical properties, being the only confirmed polymorph of pyrazinamide, which has a significant anisotropic plasticity (a “bending” crystal) [28,29]. Taking into account a highly nonequilibrium grinding process and a significant amount of supplied energy during tableting, mechanical responsiveness may play a key role in product formation. Thus, these experiments cannot be treated as a clear way of thermodynamic stability estimation and need additional confirmation.
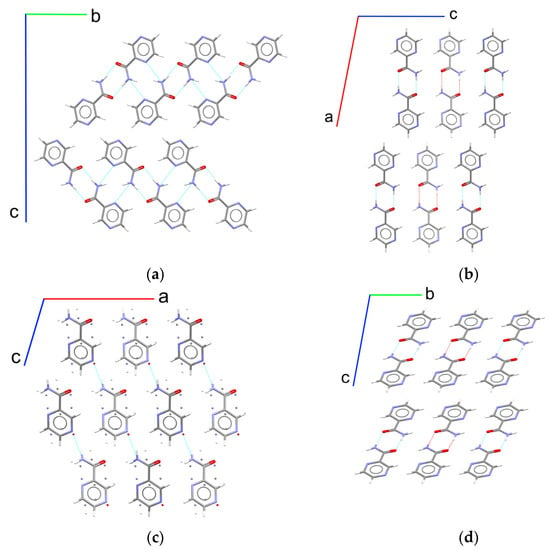
Figure 1.
Fragments of crystal structures of pyrazinamide polymorphs: (a) α form viewed along the a axis; (b) β form viewed along the b axis; (c) γ form viewed along the b axis, where disordered atom positions are marked as single atoms; and (d) δ form viewed along the a axis. The H-bonds are marked via dashed blue lines.
Multiple experimental methods can be used to address polymorphism, including single crystal and powder X-Ray diffraction, FT-IR and Raman spectroscopy, optical and electron microscopy, etc. Nevertheless, differential scanning calorimetry (DSC) helps to follow the phase transitions directly, which suggests a relative stability for the different polymorphs and provides enthalpies of the polymorphic transitions. Castro et.al shows direct phase transitions of β → γ at 368 K (95 °C), δ → α at 393 K (120 °C), δ → γ at 408 K (135 °C), and α → γ at 418 K (145 °C) [30]. Cherukuvada et al. reported β (+γ) → γ at 372 K (99 °C), δ → γ at 404 K (131 °C), and α → γ at 428 K (155 °C), as well as melting γ at 462 K (189 °C) [27]. These data are summarized in Table 1.

Table 1.
Experimental phase transition temperatures and enthalpies determined using DSC.
Later, Wahlberg et al. tried to estimate the relative stability order of all four polymorphs at 0 K using a dispersion-corrected periodic DFT with different approaches: providing full optimization, only ions (atom) positions relaxation with a unit cell fixed (adopted from an experimental 122 K measurement), and only H-atoms being optimized (where the unit cell and heavy atom positions are fixed as in the experimental structures at 122 K) [31]. All three options are summarized in Table 2 and show a different order of the polymorphs’ stability. No temperature dependence was studied in this work [31].

Table 2.
Relative electronic structure energies (kJ/mol) of pyrazinamide polymorphs obtained using different DFT optimization procedures. Results showed no consistency in relative stability using the different procedures.
Hoser et al. provided the structure information of all four polymorphs at 10 K temperatures, electronic energies and the Gibbs energy—temperature diagrams which take into account zero-point energies (ZPE) and thermal effects via phonon calculations [33]. Nevertheless, phonon calculations were provided at a 6–31 G (d, p) basis set and using the cell parameters from the 122 K XRD measurements with a further NoMoRe procedure [33]. These calculations led to different results of the polymorphs’ stability at 0–550 K depending on the DFT optimization procedure used, in accordance with Wahlberg et al.
Important to note is that other computational approaches, such as various force fields [34,35], the usage of bond critical point parameters obtained from the Bader analysis [36], and binding energies [37,38,39], may be used and adopted for a pyrazinamide system. Nevertheless, direct calculations of the total energies using a periodic DFT is still the most straightforward and well-proved method for a polymorphs comparison, including in extreme conditions [40]. Thus, this approach was used by Wahlberg et.al. and Hoser et al. to calculate the pyrazinamide polymorphs’ stability order.
Summing up, DSC provides valuable experimental data on pyrazinamide polymorphs, but does not take into account the kinetic hindering of solid–solid phase transitions and can hardly be used for systems where polymorphs have no direct transformations. Computational methods, therefore, should be used to supplement these data and clarify the relative stability of different forms. The theoretical investigations provided in the literature have controversial data and do not take into account the temperature factor to the full extent of the DFT power and they rely on multiple constraints. Thus, an additional “pure” computational study of pyrazinamide polymorphs’ stability is desired. Finally, special attention in this work is pointed to the stability of the brittle δ and bending α forms and their (brittle–bending) phase transition as an intriguing perspective of designing materials, and changing the mechanical properties by temperature tuning [41,42,43].
2. Computational Details
2.1. Crystallographic Structures
The crystal structures of the pyrazinamide polymorphs were chosen from the CCDC database with the lowest R-factors (<4%) solved and refined at a 100 K temperature: PYRZIN22 (α) [44], PYRZIN18 (β) [27], PYRZIN19 (γ) [27], and PYRZIN16 (δ). The disordered γ form was treated as two independent structures with “A” and “B” positions only and the energies were calculated by further summing the energies in the ratio of 0.866 and 0.134, respectively. These structures were used as the starting guesses for all further calculations. All the pyrazinamide structures were converted to a VASP format using the CIF2Cell code [45] for periodic DFT calculations.
2.2. Periodic DFT Calculations
All the periodic DFT calculations were performed using the Vienna ab initio simulation package (VASP 5.4.4) [46,47,48,49] using the Perdew, Burke and Ernzerhof (PBE) functional [50], a plane-wave basis set with a kinetic energy cutoff of 550 eV and projector augmented wave (PAW) atomic pseudopotentials [51,52]. Dense k-point Monkhorst–Pack meshes [53] of 5 × 2 × 1, 1 × 6 × 2, 3 × 7 × 2 and 4 × 4 × 2 were used for the α, β, γ (both “A” and “B”) and δ forms, respectively. A typical energy convergence criteria of 0.1 meV/atom and the additional criteria of 0.1 kJ/mol was used to achieve a tighter convergence. Gaussian smearing was chosen (ISMEAR = 0) with 0.1 eV width smearing (SIGMA = 0.1). Dispersion correction was used for the electronic structure calculations: Grimme D3 with a Becke–Johnson damping function (D3BJ) [54] for the PBE functional, alongside the nonlocal rev-vdW-DF2 functional of Hamada also known as vdW-DF2-B86R [55]. All the structures were fully optimized, with both the unit cell and ion positions (ISIF = 3). The difference between the experimental and optimized using PBE-D3BJ crystal structures may be found in Table S1, showing a good agreement.
The temperature dependence of the Gibbs free energy was treated by computing the second order derivatives of the total energy with respect to the position of the ions using a finite differences approach (IBRION = 6) for the PBE functional with a D3BJ dispersion correction. Symmetry was used to reduce the number of displacements. A supercell of 3 × 2 × 1 (α), 1 × 3 × 1 (β), 2 × 3 × 1 (γ), and 2 × 2 × 2 (δ) was constructed for the finite differences approach to increase the accuracy of the performed calculations. K-point meshes were chosen of 2 × 1 × 1, 1 × 2 × 2, 2 × 2 × 2 and 2 × 2 × 1 and were used for the α, β, γ and δ forms, respectively. The finite difference approach using the D3BJ dispersion correction scheme was performed to save the computational resources in comparison to the density-functional-perturbation theory (DFPT) using a rev-vdW-DF2 dispersion correction, while taking into account the good agreement of these methods for full electronic energy calculations (see Table 3).
The dynamical matrix that was constructed and diagonalized, and the phonon modes and frequencies of each system were reported in the OUTCAR file. Hessian elements from vasprun.xml were further extracted to proceed with the Phonopy 2.17.1 package [56,57] to calculate the zero-point energy correction term (ZPE), temperature dependent vibrational energy, entropy and free energy. Mesh samplings of the reciprocal space used for the calculations of the thermal properties in Phonopy were equal to the meshes used for the electronic calculations in VASP.
2.3. Molecular Mechanics Calculations
Additional calculations were provided using the robust CrystalExplorer 21 (CE) software [58], which uses crystal structures without any optimization except for hydrogen position normalization (as a default). The molecular cluster of 32 Å was used for all forms, providing a convergence tighter than 0.1 kJ/mol. The lattice energy calculations employed the CE-B3LYP/6–31 G (d, p) model intermolecular interaction energies incorporated in CrystalExplorer 21, using the Gaussian 09 program suite [59] as a backend.
3. Results and Discussion
3.1. Lattice and Total Electronic Energies
Calculations of the electronic structure energies at 0 K are frequently used as a first step in ranking polymorphs’ stability, especially at extreme conditions [40,60]. The lattice energies of these pyrazinamide polymorphs were calculated using various methods at 0 K, not taking into account any vibrational modes to rationalize the polymorphs’ stability. The results show a good agreement between the plain-wave periodic DFT calculations using different methods (shown in Table 3). These calculations were also supplemented with CE results. In this method, a cell is mandatorily constrained to the experimental (100 K), and only the intermolecular interactions are calculated to estimate the lattice energy; thus giving different results in comparison to DFT. Despite several works with a successful application of the CE algorithm for polymorphs’ stability ranking being presented in the literature [61,62], it is more reasonable to use the original energy framework concept only to visualize and rationalize the supramolecular architecture of molecular crystal structures, as it was performed in ref. [33].
All our DFT calculations showed that the β form was the most stable at 0 K according to full electronic energies. This coincides well with the previous results of Wahlberg et al. for a full optimization procedure, and Hoser et al., where the unit cell was constrained at 10 K experimental structures using the B3LYP-D3 and PBE0-D3 functionals with a TZVP basis set. The relative stability of δ (being more stable) and α (being less stable) forms based on full electronic energies were also confirmed in a recent study of Hoser et al. Nevertheless, ZPE is mandatory to include for estimating thermodynamic stability at any temperature.

Table 3.
Relative electronic structure energies (kJ/mol) of pyrazinamide polymorphs obtained using plane-wave periodic DFT with different methods and relative lattice energies via the CrystalExplorer 21 algorithm. The results show consistency in the relative stability using the DFT method, where a full (unit cell and ions positions) optimization procedure was provided.
Table 3.
Relative electronic structure energies (kJ/mol) of pyrazinamide polymorphs obtained using plane-wave periodic DFT with different methods and relative lattice energies via the CrystalExplorer 21 algorithm. The results show consistency in the relative stability using the DFT method, where a full (unit cell and ions positions) optimization procedure was provided.
| Calculation Method | α | β | γ (A) | γ (B) | γ | δ |
|---|---|---|---|---|---|---|
| DFT-PBE-D3BJ, kJ/mol | 2.1 (III) | 0.0 (I) | 2.0 | 7.0 | 2.6 (IV) | 1.1 (II) |
| DFT-rev-vdW-DF2, kJ/mol | 3.0 (III) | 0.0 (I) | 3.3 | 10.4 | 4.3 (IV) | 2.5 (II) |
| * CE-B3LYP/6–31 G (d, p), kJ/mol | 0.9 (III) | 0.0 (II) | 13.5 ** | 28.3 ** | 15.5 ** (IV) | −2.3 (I) |
* CrystalExplorer 21 should not be considered analogous to periodic DFT calculations since it has a very different approach and treats experimental structures. ** Lattice energies are very sensitive to crystallographic data and may give overestimated energies.
3.2. Gibbs Free Energies at Different Temperatures
Gibbs free energy is a useful thermodynamic potential for estimating the relative stability of polymorphs at finite temperatures. Adding the ZPE to the total electronic energies levels out the difference in the internal energy (U) between the α and δ forms (Table 4). The β form proves to be the most stable at 0 K.

Table 4.
Relative Gibbs free energies of pyrazinamide polymorphs at 0 K calculated as a sum of full electronic energies and ZPE vibrations using a finite difference approach (i.e., D3BJ dispersion correction).
These findings raise a question of the presence of any temperature interval of the thermodynamic stability of the δ form, which was suggested previously based on DSC data and the crystallization resulting from warming the amorphous state up to 260 K [63]. To answer this question, the temperature contributions were calculated directly from the second-order derivatives of the total energy with respect to the position of the ions using a finite differences approach. Thus, it was possible to obtain the Gibbs energies and their terms and to find the relative stabilities in the 0–470 K range.
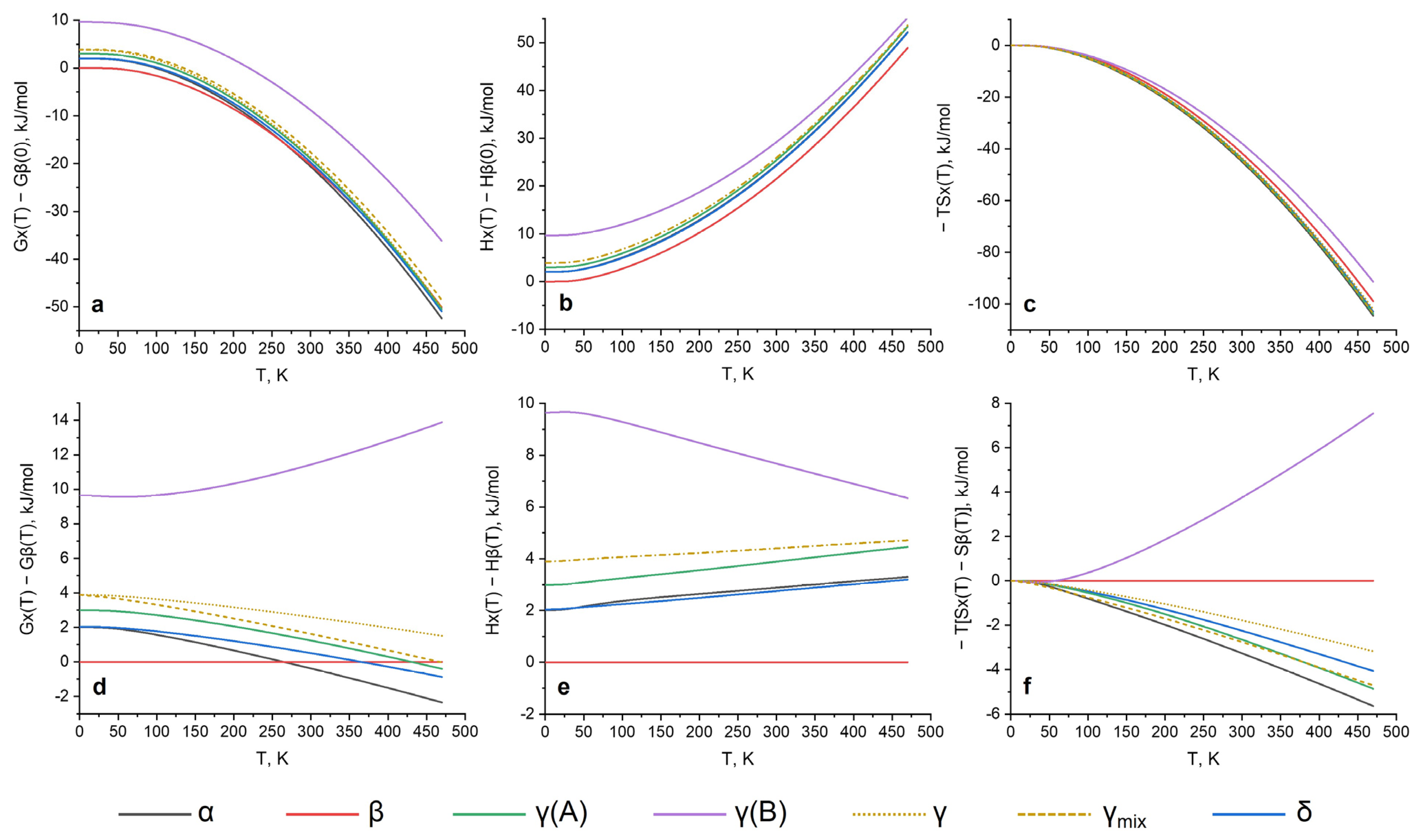
The Gibbs free energies showed that the β form was the most stable at 0–264 K followed by the highest stability of the α form of 264 K up to a melting temperature. A previously reported δ polymorph was suggested as being more stable than the α, β and γ forms, and was proved to be metastable in the whole temperature range. This coincides well with the results of the periodic DFT with a unit cell fixed, as reported in ref. [33] as the Model 1. It was also shown that the 0 K enthalpies of the α and δ forms were extremely close and there was no possibility to prove one’s stability unambiguously. To better understand the behavior of the system at higher temperatures and possible phase transitions, the enthalpy and entropy terms should be examined separately.
The enthalpy differences were almost constant, except for the γ (B) form. The entropy term (−T × S) was more demonstrative for temperature dependencies. Nevertheless, it is important to state several technical aspects of such calculations. Supercell usage is highly recommended for these purposes, and it significantly influences the results due to obtaining a converged dynamical matrix (as it was shown for the pyrazinamide system (Figure S1 see Supplementary Materials)); thus, a finite difference approach with supercells was used. Accurate calculations show stability decreases of the β and δ polymorphs, which was also proved in previous experiments (DSC) and DFT calculations. Temperature dependencies (G and −TS) show that the β form became less stable at a much higher rate in comparison to δ (which is contrary to previous DFT work) and fully coincides with experimental studies, showing a lower temperature of β → γ than a δ → γ phase transition. Our calculations were also in good agreement with an experimental transformation of γ → δ during storage for 6 months, due to an ~1–2 kJ/mol higher stability of the δ form at room temperature (depending on how the γ form energy is calculated as reported below). Direct calculations of the enthalpy differences between the forms at experimental phase transition temperatures were also performed, and showed a very good quantitative agreement of 0.1 kJ/mol (Table 5).

Table 5.
Experimental and calculated enthalpies for pyrazinamide polymorphs phase transitions at experimental temperatures.
Nevertheless, the simulation of the γ form, which became most stable at higher temperatures according to the DSC results, was not straightforward. No previous, nor has this study predicted a α → γ phase transition before or near the melting point according to Gibbs free energies. A single crystal diffraction showed a disorder in the crystal structure of the γ polymorph, which can be treated in multiple ways during DFT calculations [31]. The most straightforward option is to simulate disorder as two independent structures (denoted as γ (A) and γ (B) in Figure 2), and to sum the energies as a superposition of these models (denoted as γ). A disorder stabilization of the γ structure by increasing the entropy can be partly considered as the entropy of mixing, which was performed and plotted as the γmix analogous to ref. [33]. This quantitatively helps to increase the stability of the γ form at higher temperatures. Nevertheless, we would like to highlight that, according to the Gibbs free energy (as well as the −T × S term), the γ(A) structure is more preferable than the γmix in the whole temperature rate and increase, as it is relative to the γmix stability at higher temperatures after 390–400 K. Taking into account that the crystal structure of the γ form was obtained from saturated solutions, a disordered structure may be a consequence of highly nonequilibrium crystallization. Phase transitions from other polymorphs at different temperatures may process without the formation of a disordered structure. Based on our calculations, one can speculate γ(A) as being the only form at high temperatures after the occurred phase transitions. Finally, it is important to note that the real crystal morphology is not known and that the γ form may have domains of γ(A) and γ(B), or may have various superpositions at the supramolecular level; thus, it is not possible to provide the same level of calculations as for the other pyrazinamide structures. Nevertheless, an overall trend in an increasing stability via the entropy term was qualitatively proved and coincided well with previous studies.
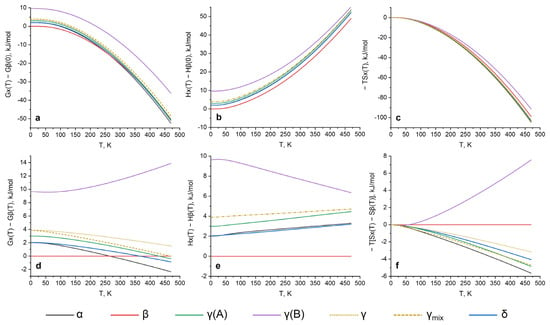
Figure 2.
Calculated relative thermodynamic parameters for pyrazinamide polymorphs as a function of temperature (where the lower it is the more stabilizing it is): (a,d) Gibbs free energy; (b,e) enthalpy of crystal structures; (c,f) entropy as −T × S term. β form energies at 0 K are taken as zero for the upper row. The lower part shows the differences in energies with respect to the β form, which becomes horizontal and equal to 0. The γ form is treated separately as γ (A), γ (B), γ and γ (mix) where: γ is calculated as a superposition of disordered structures proportional to their ration in the final structure γ = x1 × γ (A) + x2 × γ (B); γ (mix) is γ, corrected by T × Smix., where Smix is calculated as the standard entropy of mixing Smix = R × [x1 × ln(x1) + x2 × ln(x2)], where x1 = 0.866, and x2 = 0.134 for the A disorder and B disorder, correspondingly.
4. Overview
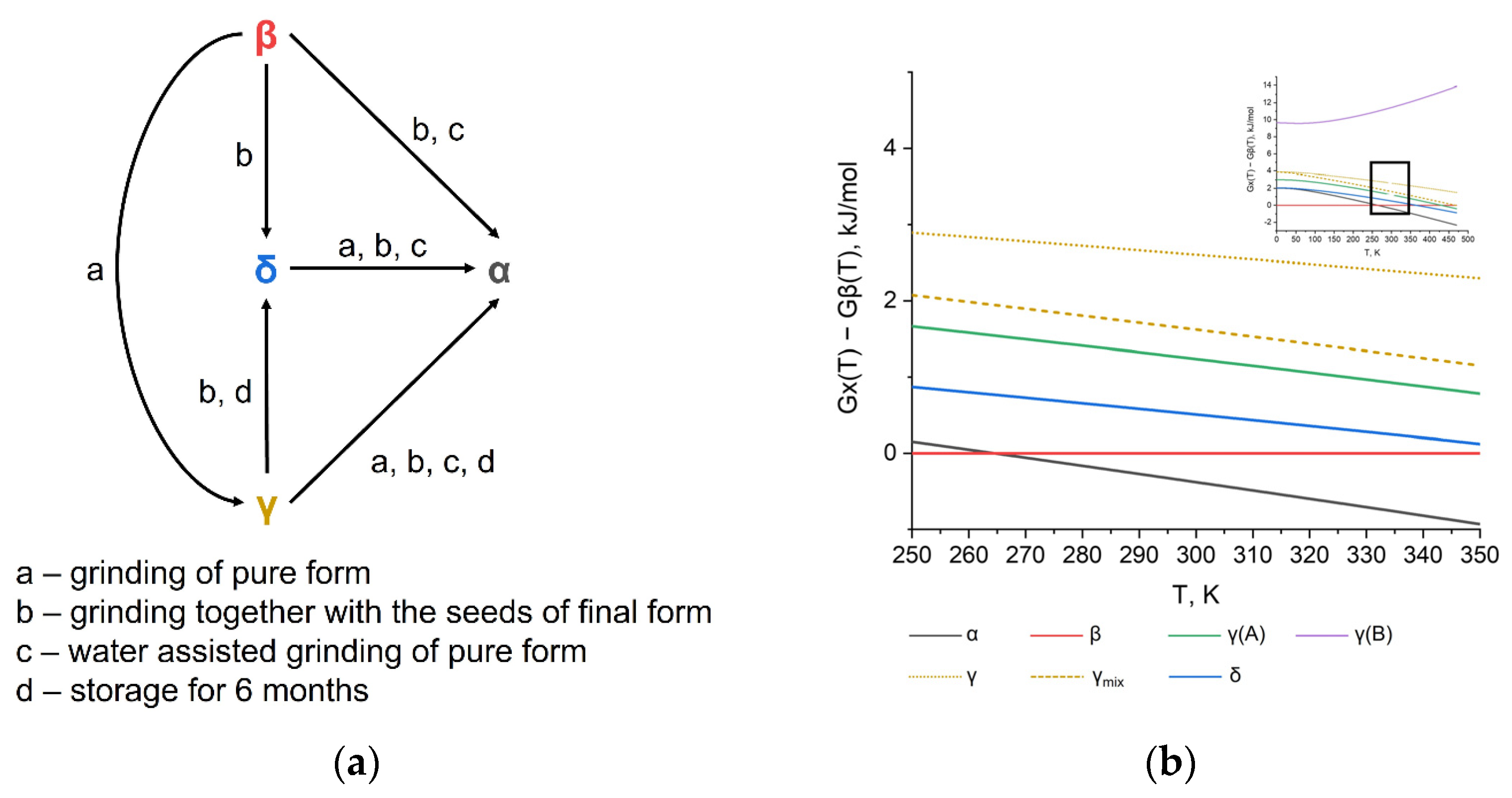
In this contribution, we provide a pure computational study of pyrazinamide polymorphs without any constrains to the crystal structures in contrast to previous works. The thermodynamic stability of four different forms was calculated and analyzed with special attention paid to the temperature dependence. Our calculations are in a very good agreement with experimental phase transitions data at room temperature, showing the α form as being the most stable (Figure 3). The transition of the γ → δ form is also consistent with the calculated energies, while β → γ and β →δ are predicted at higher temperatures according to the G(T) trends of these polymorphs (Figure 2d). This might be the result of a slight overestimation of the β form stability in ours and in previous calculations.
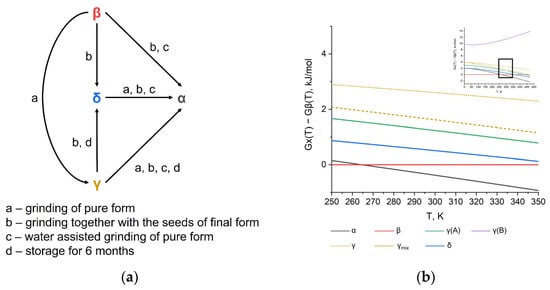
Figure 3.
(a) Experimental phase transition scheme at room temperature based on data from ref. [27]. (b) Calculated relative thermodynamic stability (Gibbs free energies) of four pyrazinamide polymorphs near room temperature as a function of temperature.
Another qualitative agreement is an increase of the α and γ stability at higher temperatures due to a higher entropy in respect to the β and δ polymorphs. A previously reported experimental low-temperature stability of the δ form seems to be metastability, because of a more advantageous internal energy of the β crystal structure. This conclusion coincides well with previous DFT studies of 10 K structures with constrained unit cell parameters and a full optimization in earlier work.
Finally, we have highlighted several valuable computational details in Gibbs energies calculations for polymorphs’ stability ranking, taking pyrazinamide as an example (i.e., ZPE and supercell usage). The ZPE contribution may significantly change the lattice energies, leveling out a difference in electronic energy, as it was shown for the α and δ forms, consequently becoming very close in terms of their stability. In our calculations, a bending α polymorph has a higher stability than a brittle δ in the whole temperature range, proving that the δ → α phase transition is hindered by kinetics in DSC experiments.
5. Conclusions
The relative stability of pyrazinamide polymorphs over a wide temperature range has been studied using computational methods. Electronic structure and phonon calculations were performed to obtain the temperature dependence of the thermodynamic properties of α, β, γ and δ pyrazinamide. It was confirmed that the α form was a stable polymorph at room temperature, whereas the β-form appeared to be a low-temperature form instead of the previously suggested δ-form, which appeared to be metastable in all temperature ranges. The relevance of our model was confirmed by the very good agreement between the calculated and experimental enthalpies of polymorphic transitions, as well as the relative agreement of the order of transition temperatures. The discrepancy between the experimental and calculated transition temperatures between the γ and the other forms is explained by the complexity of the accurate simulation of the disordered γ-form.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst13040617/s1, Figure S1: Calculated relative Gibbs free energies using full unit cell (no supercell) (a) finite difference approach using PBE-D3BJ functional, (b) DFPT approach using nonlocal rev-vdW-DF2 functional; Table S1: Comparison between initial parameters of experimental crystallographic data and optimized crystal structures for the of α(PYRZIN22), β(PYRZIN18), γ(PYRZIN19) and δ form (PYRZIN16) calculated using DFT-PBE-D3BJ level of theory. Difference in % is given in brackets.
Author Contributions
Conceptualization, D.A.R.; methodology, A.S.D. and D.A.R.; software, A.S.D. and D.A.R.; validation, A.S.D. and D.A.R.; formal analysis, A.S.D.; investigation, A.S.D. and D.A.R.; resources, D.A.R.; data curation, A.S.D.; writing—original draft preparation, A.S.D. and D.A.R.; writing—review and editing, D.A.R.; visualization, A.S.D.; supervision, D.A.R.; project administration, D.A.R.; funding acquisition, D.A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, grant number 21-73-00094, (https://rscf.ru/project/21-73-00094/, accessed on 7 March 2023).
Data Availability Statement
The data presented in this study are available in the Supplementary Information section and on request from the corresponding author.
Acknowledgments
The Siberian Branch of the Russian Academy of Sciences (SB RAS) Siberian Supercomputer Center (http://www.sscc.icmmg.nsc.ru/, accessed on 7 March 2023) is gratefully acknowledged for providing access to their supercomputer facilities. The authors also acknowledge the Supercomputing Center of the Novosibirsk State University (http://nusc.nsu.ru, accessed on 7 March 2023) for providing computational resources.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bernstein, J. Polymorphism—A Perspective. Cryst. Growth Des. 2011, 11, 632–650. [Google Scholar] [CrossRef]
- Cruz-Cabeza, A.J.; Reutzel-Edens, S.M.; Bernstein, J. Facts and fictions about polymorphism. Chem. Soc. Rev. 2015, 44, 8619–8635. [Google Scholar] [CrossRef]
- Dunitz, J.D.; Bernstein, J. Disappearing Polymorphs. Acc. Chem. Res. 1995, 28, 193–200. [Google Scholar] [CrossRef]
- Bučar, D.-K.; Lancaster, R.W.; Bernstein, J. Disappearing Polymorphs Revisited. Angew. Chem. Int. Ed. 2015, 54, 6972–6993. [Google Scholar] [CrossRef]
- Nicoud, L.; Licordari, F.; Myerson, A.S. Estimation of the Solubility of Metastable Polymorphs: A Critical Review. Cryst. Growth Des. 2018, 18, 7228–7237. [Google Scholar] [CrossRef]
- Park, K.; Evans, J.M.B.; Myerson, A.S. Determination of Solubility of Polymorphs Using Differential Scanning Calorimetry. Cryst. Growth Des. 2003, 3, 991–995. [Google Scholar] [CrossRef]
- Pudipeddi, M.; Serajuddin, A.T.M. Trends in solubility of polymorphs. J. Pharm. Sci. 2005, 94, 929–939. [Google Scholar] [CrossRef]
- Vázquez Marrero, V.R.; Piñero Berríos, C.; De Dios Rodríguez, L.; Stelzer, T.; López-Mejías, V. In the Context of Polymorphism: Accurate Measurement, and Validation of Solubility Data. Cryst. Growth Des. 2019, 19, 4101–4108. [Google Scholar] [CrossRef]
- Scarpignato, C.; Blandizzi, C.; Viscomi, G.C. Impact of crystal polymorphism on the systemic bioavailability of rifaximin, an antibiotic acting locally in the gastrointestinal tract, in healthy volunteers. Drug Des. Devel. Ther. 2014, 9, 1. [Google Scholar] [CrossRef]
- Censi, R.; Di Martino, P. Polymorph Impact on the Bioavailability and Stability of Poorly Soluble Drugs. Molecules 2015, 20, 18759–18776. [Google Scholar] [CrossRef]
- Singaraju, A.B.; Bahl, D.; Wang, C.; Swenson, D.C.; Sun, C.C.; Stevens, L.L. Molecular Interpretation of the Compaction Performance and Mechanical Properties of Caffeine Cocrystals: A Polymorphic Study. Mol. Pharm. 2020, 17, 21–31. [Google Scholar] [CrossRef]
- Yadav, J.P.; Yadav, R.N.; Sihota, P.; Chen, H.; Wang, C.; Sun, C.C.; Kumar, N.; Bansal, A.; Jain, S. Single-Crystal Plasticity Defies Bulk-Phase Mechanics in Isoniazid Cocrystals with Analogous Coformers. Cryst. Growth Des. 2019, 19, 4465–4475. [Google Scholar] [CrossRef]
- Bag, P.P.; Chen, M.; Sun, C.C.; Reddy, C.M. Direct correlation among crystal structure, mechanical behaviour and tabletability in a trimorphic molecular compound. CrystEngComm 2012, 14, 3865. [Google Scholar] [CrossRef]
- Wang, C.; Paul, S.; Wang, K.; Hu, S.; Sun, C.C. Relationships among Crystal Structures, Mechanical Properties, and Tableting Performance Probed Using Four Salts of Diphenhydramine. Cryst. Growth Des. 2017, 17, 6030–6040. [Google Scholar] [CrossRef]
- Lee, E.H. A practical guide to pharmaceutical polymorph screening & selection. Asian J. Pharm. Sci. 2014, 9, 163–175. [Google Scholar] [CrossRef]
- Hasa, D.; Jones, W. Screening for new pharmaceutical solid forms using mechanochemistry: A practical guide. Adv. Drug Deliv. Rev. 2017, 117, 147–161. [Google Scholar] [CrossRef]
- Bauer, J.; Spanton, S.; Henry, R.; Quick, J.; Dziki, W.; Porter, W.; Morris, J. Ritonavir: An extraordinary example of conformational polymorphism. Pharm. Res. 2001, 18, 859–866. [Google Scholar] [CrossRef]
- Morissette, S.L.; Soukasene, S.; Levinson, D.; Cima, M.J.; Almarsson, O. Elucidation of crystal form diversity of the HIV protease inhibitor ritonavir by high-throughput crystallization. Proc. Natl. Acad. Sci. USA 2003, 100, 2180–2184. [Google Scholar] [CrossRef]
- Wang, C.; Rosbottom, I.; Turner, T.D.; Laing, S.; Maloney, A.G.P.; Sheikh, A.Y.; Docherty, R.; Yin, Q.; Roberts, K.J. Molecular, Solid-State and Surface Structures of the Conformational Polymorphic Forms of Ritonavir in Relation to their Physicochemical Properties. Pharm. Res. 2021, 38, 971–990. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, W.; Zhang, W.; Mitchison, D. Mechanisms of Pyrazinamide Action and Resistance. Microbiol. Spectr. 2014, 2, 1–12. [Google Scholar] [CrossRef]
- Zhang, N.; Savic, R.M.; Boeree, M.J.; Peloquin, C.A.; Weiner, M.; Heinrich, N.; Bliven-Sizemore, E.; Phillips, P.P.J.; Hoelscher, M.; Whitworth, W.; et al. Optimising pyrazinamide for the treatment of tuberculosis. Eur. Respir. J. 2021, 58, 2002013. [Google Scholar] [CrossRef] [PubMed]
- Chang, K.C.; Yew, W.W.; Zhang, Y. Pyrazinamide Susceptibility Testing in Mycobacterium tuberculosis: A Systematic Review with Meta-Analyses. Antimicrob. Agents Chemother. 2011, 55, 4499–4505. [Google Scholar] [CrossRef] [PubMed]
- Takaki, Y.; Sasada, Y.; Watanabé, T. The crystal structure of α-pyrazinamide. Acta Crystallogr. 1960, 13, 693–702. [Google Scholar] [CrossRef]
- Rø, G.; Sørum, H. The crystal and molecular structure of β-pyrazinecarboxamide. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1972, 28, 991–998. [Google Scholar] [CrossRef]
- Tamura, C.; Kuwano, H. Crystallographic data of carboxylic acids and carboxyamides of picoline and pyrazine derivatives. Acta Crystallogr. 1961, 14, 693–694. [Google Scholar] [CrossRef]
- Rø, G.; Sørum, H. The crystal and molecular structure of δ-pyrazinecarboxamide. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1972, 28, 1677–1684. [Google Scholar] [CrossRef]
- Cherukuvada, S.; Thakuria, R.; Nangia, A. Pyrazinamide polymorphs: Relative stability and vibrational spectroscopy. Cryst. Growth Des. 2010, 10, 3931–3941. [Google Scholar] [CrossRef]
- Reddy, C.M.; Gundakaram, R.C.; Basavoju, S.; Kirchner, M.T.; Padmanabhan, K.A.; Desiraju, G.R. Structural basis for bending of organic crystals. Chem. Commun. 2005, 1, 3945. [Google Scholar] [CrossRef]
- Reddy, C.M.; Padmanabhan, K.A.; Desiraju, G.R. Structure−Property Correlations in Bending and Brittle Organic Crystals. Cryst. Growth Des. 2006, 6, 2720–2731. [Google Scholar] [CrossRef]
- Castro, R.A.E.; Maria, T.M.R.; Évora, A.O.L.; Feiteira, J.C.; Silva, M.R.; Beja, A.M.; Canotilho, J.; Eusébio, M.E.S. A New Insight into Pyrazinamide Polymorphic Forms and their Thermodynamic Relationships. Cryst. Growth Des. 2010, 10, 274–282. [Google Scholar] [CrossRef]
- Wahlberg, N.; Ciochoń, P.; Petriĉek, V.; Madsen, A.Ø. Polymorph Stability Prediction: On the Importance of Accurate Structures: A Case Study of Pyrazinamide. Cryst. Growth Des. 2014, 14, 381–388. [Google Scholar] [CrossRef]
- Bursch, M.; Mewes, J.; Hansen, A.; Grimme, S. Best-Practice DFT Protocols for Basic Molecular Computational Chemistry. Angew. Chem. 2022, 1, 202205735. [Google Scholar] [CrossRef]
- Hoser, A.A.; Rekis, T.; Madsen, A.Ø. Dynamics and disorder: On the stability of pyrazinamide polymorphs. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2022, 78, 416–424. [Google Scholar] [CrossRef]
- Marchese Robinson, R.L.; Geatches, D.; Morris, C.; Mackenzie, R.; Maloney, A.G.P.; Roberts, K.J.; Moldovan, A.; Chow, E.; Pencheva, K.; Vatvani, D.R.M. Evaluation of Force-Field Calculations of Lattice Energies on a Large Public Dataset, Assessment of Pharmaceutical Relevance, and Comparison to Density Functional Theory. J. Chem. Inf. Model. 2019, 59, 4778–4792. [Google Scholar] [CrossRef] [PubMed]
- Wen, S.; Beran, G.J.O. Accurate Molecular Crystal Lattice Energies from a Fragment QM/MM Approach with On-the-Fly Ab Initio Force Field Parametrization. J. Chem. Theory Comput. 2011, 7, 3733–3742. [Google Scholar] [CrossRef] [PubMed]
- Vener, M.V.; Levina, E.O.; Koloskov, O.A.; Rykounov, A.A.; Voronin, A.P.; Tsirelson, V.G. Evaluation of the Lattice Energy of the Two-Component Molecular Crystals Using Solid-State Density Functional Theory. Cryst. Growth Des. 2014, 14, 4997–5003. [Google Scholar] [CrossRef]
- Wang, S.; Ren, C.; Tian, H.; Yu, J.; Sun, M. MoS 2/ZnO van der Waals heterostructure as a high-efficiency water splitting photocatalyst: A first-principles study. Phys. Chem. Chem. Phys. 2018, 20, 13394–13399. [Google Scholar] [CrossRef]
- Wang, S.; Tian, H.; Ren, C.; Yu, J.; Sun, M. Electronic and optical properties of heterostructures based on transition metal dichalcogenides and graphene-like zinc oxide. Sci. Rep. 2018, 8, 12009. [Google Scholar] [CrossRef]
- Wang, S.; Chou, J.-P.; Ren, C.; Tian, H.; Yu, J.; Sun, C.; Xu, Y.; Sun, M. Tunable Schottky barrier in graphene/graphene-like germanium carbide van der Waals heterostructure. Sci. Rep. 2019, 9, 5208. [Google Scholar] [CrossRef]
- Rychkov, D.A. A Short Review of Current Computational Concepts for High-Pressure Phase Transition Studies in Molecular Crystals. Crystals 2020, 10, 81. [Google Scholar] [CrossRef]
- Skakunova, K.D.; Rychkov, D.A. Low Temperature and High-Pressure Study of Bending L-Leucinium Hydrogen Maleate Crystals. Crystals 2021, 11, 1575. [Google Scholar] [CrossRef]
- Arkhipov, S.G.; Losev, E.A.; Nguyen, T.T.; Rychkov, D.A.; Boldyreva, E.V. A large anisotropic plasticity of l-leucinium hydrogen maleate preserved at cryogenic temperatures. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2019, 75, 143–151. [Google Scholar] [CrossRef] [PubMed]
- Brock, A.J.; Whittaker, J.J.; Powell, J.A.; Pfrunder, M.C.; Grosjean, A.; Parsons, S.; McMurtrie, J.C.; Clegg, J.K. Elastically Flexible Crystals have Disparate Mechanisms of Molecular Movement Induced by Strain and Heat. Angew. Chem.-Int. Ed. 2018, 57, 11325–11328. [Google Scholar] [CrossRef] [PubMed]
- Rajalakshmi, G.; Hathwar, V.R.; Kumaradhas, P. Intermolecular interactions, charge-density distribution and the electrostatic properties of pyrazinamide anti-TB drug molecule: An experimental and theoretical charge-density study. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2014, 70, 568–579. [Google Scholar] [CrossRef]
- Björkman, T. CIF2Cell: Generating geometries for electronic structure programs. Comput. Phys. Commun. 2011, 182, 1183–1186. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Hamada, I. van der Waals density functional made accurate. Phys. Rev. B 2014, 89, 121103. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Togo, A. First-principles Phonon Calculations with Phonopy and Phono3py. J. Phys. Soc. Jpn. 2023, 92, 1. [Google Scholar] [CrossRef]
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Smirnova, V.Y.; Iurchenkova, A.A.; Rychkov, D.A. Computational Investigation of the Stability of Di-p-Tolyl Disulfide “Hidden” and “Conventional” Polymorphs at High Pressures. Crystals 2022, 12, 1157. [Google Scholar] [CrossRef]
- Thomas, S.P.; Spackman, M.A. The Polymorphs of ROY: A Computational Study of Lattice Energies and Conformational Energy Differences. Aust. J. Chem. 2018, 71, 279. [Google Scholar] [CrossRef]
- Thomas, S.P.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. Accurate Lattice Energies for Molecular Crystals from Experimental Crystal Structures. J. Chem. Theory Comput. 2018, 14, 1614–1623. [Google Scholar] [CrossRef] [PubMed]
- Borba, A.; Albrecht, M.; Gómez-Zavaglia, A.; Suhm, M.A.; Fausto, R. Low Temperature Infrared Spectroscopy Study of Pyrazinamide: From the Isolated Monomer to the Stable Low Temperature Crystalline Phase. J. Phys. Chem. A 2010, 114, 151–161. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).