Abstract
Using a hierarchy of three sigmoid growth models with increasing complexity, i.e., number of parameters, we reanalyzed kinetic data for heterogeneous nucleation—the number of nuclei N(t) vs. time t—from archetypical experiments on the electrodeposition of mercury on platinum by I. Markov and E. Stoycheva, to obtain two scales: Nmax and τ. The universal character of the studied phenomenon was revealed when replotting the original data as α ≡ N(t)/Nmax vs. t/τ. Yet the simplest model, the recently introduced α21 model which is aimed to describe diffusion-limited growth in 2D, α21 = tanh2(2t/τ21), fits all datasets with an R2 ≥ 0.989. This can be rationalized by attracting the non-classical notion of two-step nucleation—the nuclei form in a metastable phase which, in this case, grows on the electrode surface. Beyond the universality, we find the dependence of the two obtained scales on the overvoltage, which is increased systematically from 83 to 88 mV to generate the six N(t) datasets for each of the two electrode types—planar and hemispherical. Surprisingly, for one of them, the planar electrode, there is a discontinuity in the dependence—an almost horizontal jump from 85 to 86 mV, while for the hemispherical electrode, τ decreases smoothly.
1. Introduction
Here, we develop a detailed program that uses a hierarchy of three sigmoid growth models, shortly called the Hierarchy of Models which is thus abbreviated in what follows as HoM. The notion of hierarchy comes from the increasing complexity, i.e., from the increasing number of parameters—2, 3 and 4—suited here to reanalyze nucleation data published by Ivan V. Markov and Evgenia Stoycheva in [1] in terms of N(t)-curves. While finding the corresponding parameters from all three models with high numerical precision, our study remains neutral with respect to the current achievements in the field of electrochemical nucleation [2,3] and growth [4], and we do not engage with analyzing the classical theories in the field [5]. Rather, based on the rationalization of the numerical data, we conclude that it is the growth of a metastable phase preceding the nucleation itself that determines the particular outcome from our numerical analysis. Therefore, we use the models in a numerically straightforward manner, not trying to suit them to conform to classical notions of the nucleation theory, such as the induction time and the stationary nucleation rate, especially when not obtaining them as a numerical result. This approach has proven successful; yet, the simplest model from the hierarchy, the one with 2 parameters, the so called α21 model, which is a particular solution of the general model of crystal growth αDg in decaying supersaturation [6], shows a fit with high numerical precision of all 12 datasets from [1]. Further, we will show that the additional parameters from the more complex models do not show a clear dependence on the overpotential, the control parameter that is varied systematically in the experiment to produce the different datasets. Thus, more parameters do not bring more understanding of the phenomenon of heterogeneous nucleation in the electrodeposition of mercury on platinum and could even hide the true understanding of the phenomena whilst lacking a physical insight. Eventually, we conclude with the hypothesis that the numerically obtained behavior from the α21 model is a clear manifestation of the non-classical two-step nucleation process [7]—the nuclei form uniformly in the growing two-dimensional metastable phase and its growth is described by the α21 model.
The thorough and precise study of Markov and Stoycheva provides, in our view, a unique opportunity to analyze the nucleation kinetics in terms of the so-called “N(t)-curves” by counting the number of nuclei on the time-scale of milliseconds. In [8] and in the further papers by C. Nanev on the same subject, the logistic dependence was employed to study the kinetics of insulin nucleation. Our present study not only implements a well-thought hierarchy of models with an increasing number of parameters, i.e., complexity, it, in particular, uses a generalization of the logistic model or Verhulst model [9]—the so-called Richards model [10], in which an additional “tweaking” exponent is introduced. Another elaboration beyond [8] is that here, after finding the two scales towards transforming the data into universal forms, we continue by studying the dependencies of the scales used in this transformation on the parameter that makes the several data sets different: the driving force of the process, the overvoltage (in [8] it is the supersaturation). In this way, the program initiated in [8] unfolds to show its full strength.
In principle, the idea to fit sigmoid models to growth and nucleation data is not new [11,12,13,14]; however, having not found clear analogues between these studies and our hierarchy of models, we leave the task of a systematic review for further studies.
2. Hierarchy of Models (HoM)
For the reanalysis of the nucleation data by I. Markov and E. Stoycheva [1], we use a set of three models with a different number of fitting parameters. Two of them are always Nmax—the maximal number of the observed nuclei at the end of the process and the timescale of the phenomenon generally denoted by τ. The α21-model contains only these two parameters, which means that after using these two scales to re-scale the original data they should collapse onto a single or master curve defined by the mathematical expression of the model without any parameters in it. In the model of Johnson–Mehl–Avrami–Kolmogorov (JMAKn), an additional “tweaking” parameter is used—the so called Avrami exponent n to which the ratio of the time and the timescale is raised, denoted by τJ. The dimensionless equation of the Richards model contains two more parameters in addition to Nmax and τR (which itself is composed by the fit parameters)—the additional power q and the dimensionless constant K, a combination of three of the model parameters but Nmax—the power q and the two particular timescales, the time to the inflection point ti, and the inverse of the kinetic coefficient τk. Anticipating a main result from our study, it is not the number of parameters that improves the fit quality! In opposite, the use of the two more complex models, JMAKn and Richards, does not increase the numerical precision but results in values for the exponents n and q, respectively, that do not allow a consistent treatment. Thus, we can conclude that the two more complex models are “artificially good” [6] in describing the concrete experimental data and, even worse, the high numerical precision of their output can hide the physics behind the phenomenon observed.
2.1. The α21 Model [6]
The α21 model is a particular case of the αDg model, introduced recently in [6] to describe two-dimensional, D = 2, diffusion-limited, g = 1, crystal growth with exhaustion of the initial supersaturation. It is suited for the purposes of our present study as the following:
N(t) = Nmaxtanh2(2t/τ21)
The core of the integral version of the model, tanh2(2t/τ21), results from the integration of the following differential equation:
Further, it should be noted that α21 = (l/lmax)2 where l is the side length of the growing in 2D square(s) and lmax is the maximal size achievable with the initial supersaturation. Thus, in the right hand side of Equation (2) the positive feedback becomes 4l/lmax, which is the perimeter of the growing square(s).
The αDg model is a further development of the idea behind the model of crystallization in three dimensions, describing the evolution of the rescaled size of the growing cube(s) [15] to obtain a differential equation for the size or, as in [6], for the transformation ratio α. In the context of this study, α could be defined as α ≡ N/Nmax.
The model derivation starts [6,15] with a conservation law for the exhausted concentration in time t as spread among N equally sized crystals and continues with a kinetic law for the remaining part of the concentration, linking the normal growth velocity to the supersaturation raised to a power g, the so-called growth order. In the index of α and τ above, Equation (1), 2 stands for the spatial dimension, i.e., 2D, and 1 stands for g = 1. The time t is multiplied by the coefficient of 2 and this follows naturally from the model derivation. The crystal grows simultaneously in the two opposite directions with the same normal velocity, and the coefficient of 2 is not “hidden” in the timescale, thus keeping the inflection point, in the present context, (ti, Ni) closer to, but not on the line, N(t)/Nmax = t/τ21:
Ni/Nmax = 1/3
ti = 0.329τ21
The value of 0.329 can easily be mistaken for 1/3 (one third) [6], but it is numerically different from 1/3. Still, the inflection point (0.329, 1/3), formulated in terms of rescaled quantities, is far from the (1/2, 1/2), which is the inflection point of the logistic dependence used in [8], and this difference can help to distinguish between the models and to go even further from pure numerical considerations to identify the different physics behind the models.
The α21 model is the model with the lowest number of parameters from the HoM, only Nmax and τ21, and we will use these scales first to rescale the number of nuclei N and the time t, a program that is already constructed in [8] to study protein nucleation. The rescaling operation of the N-axis can also be considered as another formulation of the so-called transformation ratio, defined for the purpose of the present study as α ≡ N/Nmax. Ideally, all the rescaled data should collapse onto the same master curve and a failure to conform to this expectation for some of the datasets should be considered a failure of the model to adequately describe this particular dataset. An important aspect in favor of the α21 model is that it is lacking a “tuning exponent” as in the other two models from our hierarchy. Therefore, only the α21 model naturally provides a master curve N/Nmax = tanh2(2t/τ21), while for the other two more complex models, JMAKn and Richards, the “master curves” are as many as there are different values obtained for the “tuning exponents”—n and q, correspondingly. In such situations, one could force the collapse by fixing the excessive parameter(s) to certain presumed value(s), but this has consequences. Conceptually, this means judgement that is outside the numerical procedure. Numerically, this would eventually lead to a decrease in the numerical precision, and we will see an example below.
Another complementary part of the program is initiated in [8], and is yet to be developed in detail to study the dependence on the supersaturation of the scales τ and Nmax found along the two axes t and N, respectively. A similar strategy was adopted in [16] to study the cloud condensation nuclei (CCN) as counted in 20 boxes by size at 6 different supersaturations. Then, to map them onto universal distributions after rescaling each of the 20 counts by the total number of CCN, in order to study further the peculiarities of the scale, using one for each value of the supersaturation the “total number of CCN” (corrected to concentration in this particular case [16]) and how it correlates with the meteo-elements.
From the autonomous Equation (2), one can derive a more useful expression in practical context for the rate of transformation as time dependent:
where in the right-hand side of (1) α21 is substituted with tanh2(2t/τ21).
Building a model of dynamical system is not completed by introducing/deriving only the integral and differential forms of the mode, as there is also the so-called chaotic map, an iterative scheme based on the discretization of the corresponding differential equation. In the case of the present model, and in analogy with the archetypical logistic map, the chaotic map would be introduced as the following:
Only a further study devoted specifically to the αDg model(s) could reveal the links between the three different parts of the model(s) for different combinations of the concrete, presumably integer values of D and g. Here, we should point out only that the value of the fully developed chaos r = 2.6, see Figure 1, is less than the coefficient of 4 in (2). Thus, one could integrate (2) with a general coefficient of r instead of 4 to obtain a family of curves, one for each value of r, in order to follow how the generalization reflects on the integral behavior of the model.
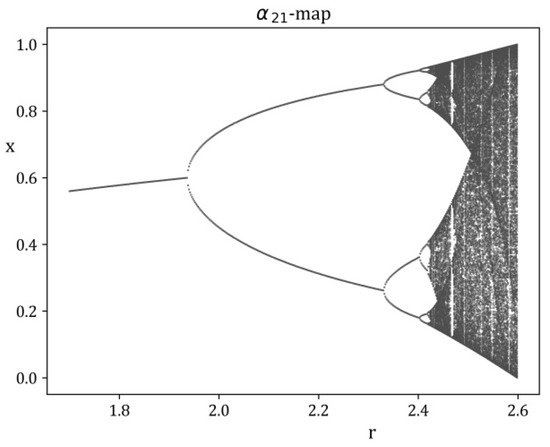
Figure 1.
The α21 chaotic map.
2.2. The Johnson–Mehl–Avrami–Kolmogorov Model (JMAKn)
This model is most used in theoretical studies in the field of crystallization, which was introduced in the 1930’s by Kolmogorov [17], Johnson and Mehl [18], and Avrami [19] and is adopted here as:
Note the use of a third parameter in the model, the power n. In [6] it is incorporated in the abbreviation of the model to eventually extend it to JMAKn. Originally, n is the spatial dimensionality D and n = D + k where k = 0, 1 to account for the (lack of) nucleation during the growth, respectively. With the years and with its extensive use in a broad range of mainly experimental contexts, see for example [20,21,22,23], n is at present considered more as an additional fitting parameter, and its non-integer values are considered as challenging further conceptual developments and discussions of why it is not integer as predicted and why it is varying from experiment to experiment, and even from one upper value of α to another to which values the concrete fitting is carried. See [6] for a detailed study of this last mentioned effect. The link between JMAKn and α21 is also studied in detail in [6] and, in particular, it is found that the conversion factor between the two timescales is as follows:
τJMAK1.725 ≈ 1.1τ21
As anticipated, there is no constant conversion factor between the two models introduced so far and the next one, the model of Richards.
The differential form of the JMAKn model is derived in [6]:
and, applying the same procedure that leads to (6), we can infer the chaotic map of the JMAKn model:
and in Figure 2 a particular case when d is set to 1.725 is shown:

Figure 2.
The JMAK1.725 chaotic map.
Note that the value of r where the map reaches the fully developed chaos, r ≈ 2.19, is less than the coefficient of 3.5 in (9) (when n = 1.725). This again points at a direction for further study, in which the dynamic behavior of the two models may be compared.
2.3. Richards Model
This is another general model that describes sigmoid growth [10] under the combined action of two feedback mechanisms: positive and negative ones (the differential forms of the two models above are discussed and studied in [6]):
and this could easily be seen in the differential version of the model:
Note that in (12) tk, the inverse the kinetic coefficient k, is used. Thus, the positive feedback in Equation (13), when q > 1, is represented by kN/(q − 1), while the negative one is −k/[(q − 1)]. When q < 1, the role of the two feedbacks is reverted. This is the value of q that fine-tunes the position of the inflection point of the model and, in [10], the exact dependence is found: . This points at the way of finding the model’s timescale τR when using the second timescale in (12) and the time to the inflection point ti, which comes into the model only after finding the integration constant from the integration of Equation (13):
to obtain the non-dimensional version of the model:
where K is defined as K = q1/(q−1)ti/tk and remains the only parameter in addition to q. This non-dimensionalization procedure brings the inflection point of the model to the line α ≡ N/Nmax = t/τR, independent of K. Note that the inflection point is the same for a fixed value of q for any value of K, and that this provides the basis of a further study by considering the subtle connection between the integral curve and the corresponding chaotic map. In the “map-language”, K is usually denoted by r as in the two chaotic maps shown above. It is also worth mentioning here that the inflection points of the two previous models from the HoM are only close to the line α ≡ N/Nmax=t/τR [6]. In addition, it is worth stressing that for the non-dimensionalization of the differential Equation (13), namely, the time-scale τR, Equation (14), is to be used.
The Richards model has two commonly used special cases on its own: the logistic model of Verhulst [9], with q = 2, used in the context of protein nucleation by Nanev et al. [8], and the Gomperz model [24], with q = 1. Note that the inflection point of the Gomperz model is (1/3, 1/3) which is close enough to (0.329, 1/3), which is the inflection point of the α21 model. Thus, one can re-visit concrete situations where the Gomperz model was used but the α21 model was possibly applicable as well, not only in the technical sense but also in terms of the physics behind [6].
The Richards model also generates chaotic maps for each value of q, and the most famous of them, the logistic map, is built when q = 2. For each value of q, there is a family of curves for different values of K that show the cusp catastrophe [25] type of behavior and the critical value of Kc = qq/(q−1), for which the model curve still crosses the line N/Nmax = t/τR once the value of K or r is the same as in the corresponding chaotic map showing the fully developed chaos. For K > Kc, the integral curve of the model with a fixed value of q crosses the line N/Nmax = t/τR three times already, with the midpoint of these three points being the inflection point.
With this, we conclude the ad hoc building of the HoM, although further tweaking is possible. For example, one could fit the Richards model with uniform datasets drawn by the αDg model with concrete values of D = 1, 2, 3 and g = 1, 2 in order to bracket the studies in which the Richards model was used. However, one could also try the αDg model to reanalyze the datasets used there. Anticipating such a study, when fitting α21 with the Richards model one obtains q = 0.823, far below the logistic model with q = 2, and K = 3.842, well beyond the value of Kc = 2.474, see Figure 3 (also for the slow decrease of R2 apart from q = 0.823).
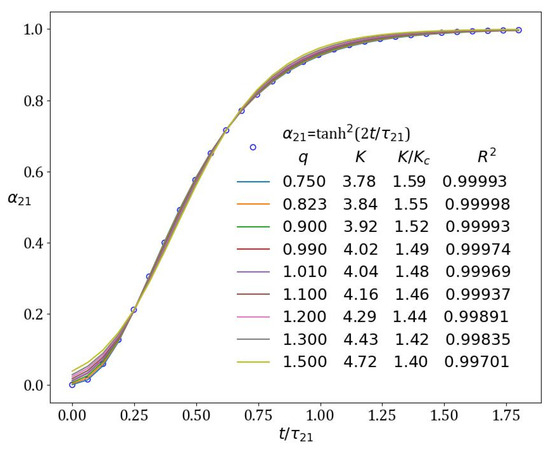
Figure 3.
Fitting a dataset of 30 points drawn from the α21-model with the Richards model. It is evident that R2 cannot distinguish between the values of q taken in a large interval.
3. Results
After introducing the hierarchy of models (HoM) to be used in analyzing the nucleation data, the first practical step of our reanalysis was to digitize the N(t) data for the “plane structureless platinum electrode” or, simply, planar electrode (Figure 5 in [1]) and “hemispherical single-crystal electrode”, or simply hemispherical electrode (Figure 6 in [1]) from the paper of I.V. Markov and E. Stoycheva published in 1976 [1]. There are numerous tools for digitization, ranging from standalone applications such as DataThief and Engauge Digitizer to special packages from the high-level programming languages as R.
Further, one can use the curve_fit function from SciPy in Python or nls() in R for fitting the data.
We provide, in full detail, the results from the α21 model, while the other two models serve more to verify the results from the simplest one in the HoM. For them we give only specific details of general interest in the Appendix A such as the rescaled data according to the scales found and the values of n and q, respectively.
3.1. Fitting with the α21 Model
We used a python code to both fit (with curve_fit) and plot (with Matplotlib) the results.
3.2. Summary of the Fitting Procedure
Here, we provide the results from the fitting procedure, as illustrated in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, in a data format that permits further comparisons. Thus, the values of the parameters as found from fitting the experimental data from Figure 5 in [1] are given in Table 1, while in Table 2 are listed these found when fitting data from Figure 6 in [1] from the same study. Note that the high values of R2 obtained do not allow for discrimination between the models in our hierarchy and, thus, physical considerations must come into the play.

Figure 4.
Fitting the experimental data for the planar electrode, digitized from Figure 5 from [1], with α21.
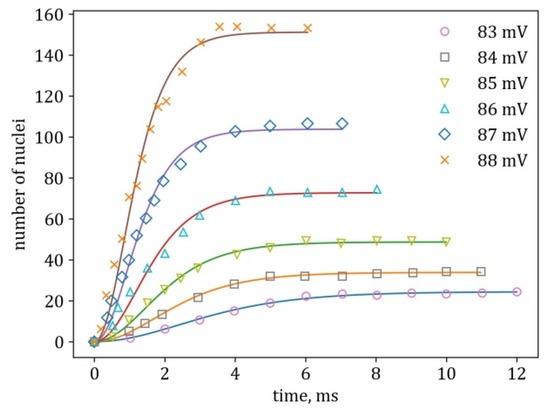
Figure 5.
Fitting the data for hemispherical electrode, digitized from Figure 6 from [1], with α21.

Figure 6.
Rescaling the data for the planar electrode in [1] with the fit parameters obtained from α21. The dotted line is N/Nmax = t/τ21 and the solid curve is the “master curve” N/Nmax = tanh2(2t/τ21).

Figure 7.
Rescaling the data for the hemispherical electrode in [1] with the fit parameters from α21. The dotted line is N/Nmax = t/τ21 and the solid curve is N/Nmax = tanh2(2t/τ21).

Figure 8.
Parameters from fitting the data for the planar electrode (from Figure 5 [1]) with α21. Circles are for Nmax and squares—for τ21. The slope of the solid line is ~−1, while the slope of the dotted line is ~−0.5.

Figure 9.
Parameters from fitting the data for hemispherical electrode (from Figure 6 in [1]) with α21. Circles are for Nmax and squares—for τ21.

Table 1.
Parameter values found from fitting Figure 5 from [1], that was obtained from the planar electrode, with the models from the HoM. Note that the timescale from the Richards model is not obtained directly from the fit, see Equation (14), and since no conclusions are drawn based on the values of ti, tk and K = q1/(q−1)ti/tk, they are not shown in the tables.

Table 2.
Parameter values found from fitting Figure 6 from [1] from the models of the hierarchy. Note that the timescale from the Richards model is not obtained directly from the fit, see Equation (14).
4. Discussion and Conclusions
Here, our study adds a solid argument to the discussion on the existence of an autocatalytic loop in the N(t) dependence next to the one in [8] by attracting the notion of the two-step nucleation [7]. It is modified in the experiments we reanalyze the data from here by the heterogenous substrates: the nuclei form within a growing along the electrode two-dimensional metastable phase. It is the growth of this phase that is described by the recently introduced α21 model of crystallization, which has an autocatalytic loop by definition.
Note that in the first from the set of two papers [26], I. Markov provides an expression for the saturation density but does not provide theoretical ground of how to treat the obtained timescales nor of how they are obtained explicitly.
Our study is intended to remain on a mainly methodological ground, providing correct numerical analysis. However, we also attribute the phenomenon of heterogeneous nucleation observed by Markov and Stoycheva in [1] to the non-classical two-step nucleation pathway. We used a hierarchy of models (HoM) to achieve numerically correct estimations of the two scales, describing the phenomenon of nucleation—the maximal number of nuclei Nmax and the time-scale τ—for a given (and fixed) driving force (overvoltage) of the phenomenon. Thus, it is tempting to study the obtained data in a quantitative manner. A major result of this study is the dependence of the obtained time-scales on the overvoltage, smoothly decreasing for one of the cathodes—the hemispherical one, and discontinuous for the planar electrode. The combination of the two behaviors resembles the so-called “cusp catastrophe” known to the general public from the isotherms drawn from the Van der Waals equation above and below Tc.
It is our expectation that the HoM and the template we built on it will become a part of the toolbox used to study experimental situations where sigmoid growth is observed and, in particular, those where non-classical nucleation is expected.
Author Contributions
Conceptualization, V.T. and J.E.P.; methodology, V.T., V.V.I., F.H. and V.K.; software, V.T. and V.V.I.; validation, V.T. and V.V.I.; formal analysis, V.T. and V.V.I.; investigation, all; writing—original draft preparation, V.T and J.E.P.; writing—review and editing, V.T., V.V.I. and J.E.P. All authors have read and agreed to the published version of the manuscript.
Funding
Mercator Fellowship (VT) from the German Research Foundation (DFG); Bulgarian NSF—grants KΠ-06-H54/2/15.11.2021 and KΠ-06-ДO02/1/18.05.2023; Spanish Grant PID2021-124585NB-C31 funded by MCIN/AEI/10.13039/501100011033; and by ERDF “A way of making Europe”.
Data Availability Statement
Acknowledgments
Peter Vekilov (UH) has made a last-moment suggestion for the title of our manuscript, thanks! It was taken into account only in part. Our precise numerical study was possible only due to the preceding precise experiments of the late Evgenia Stoycheva (Armyanova). This paper is dedicated to the memory of Ivan Vesselinov Markov (1941–2022), who made significant contributions to the general field of Crystallization including the books he published [27,28].
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The results from fitting the experimental datasets of Markov and Stoycheva [1] with the two more complex models—the JMAKn and Richards model—are separated in an appendix because they do not bring a deeper insight beyond the one obtained using the simplest of the three models from the Hierarchy of Models(HoM), the α21 model. Hence, they are eliminated by the action of a thinking experiment, the so called “Ockham’s razor”. The referenced sources and equations are presented in the main text.
Appendix A.1. Fitting with the JMAKn Model
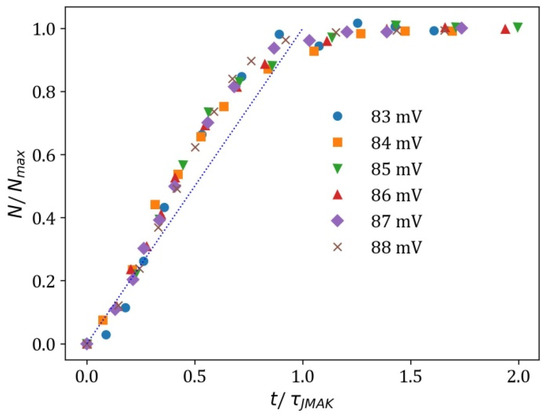
Figure A1.
Rescaling the data for the planar electrode (Figure 5 in [1]) with the fit parameters from JMAKn, see also Table 1, Equation (7), the dotted line is . There is no master curve since n is different for each value of the overpotential.
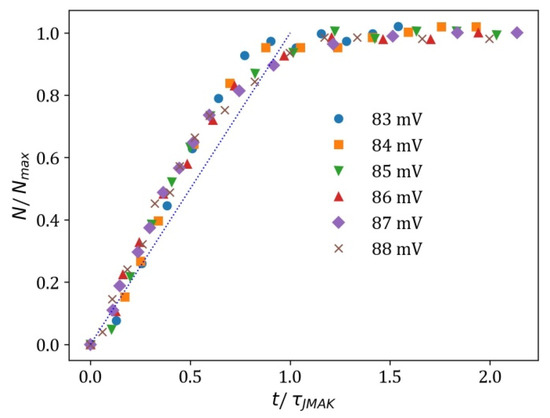
Figure A2.
Rescaling the data for the hemispherical electrode (Figure 6 in [1]) with the fit parameters from JMAKn, see Table 2, Equation (7), the dotted line is . As in the previous plot, no master curve could be drawn.
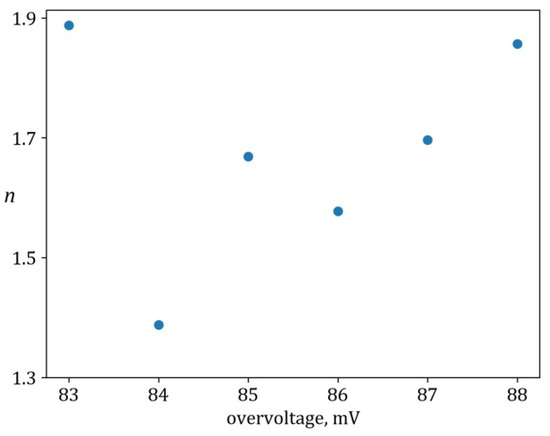
Figure A3.
Values of n from (7) used to fit data for the planar electrode (from Figure 5) in [1] with the JMAKn model.
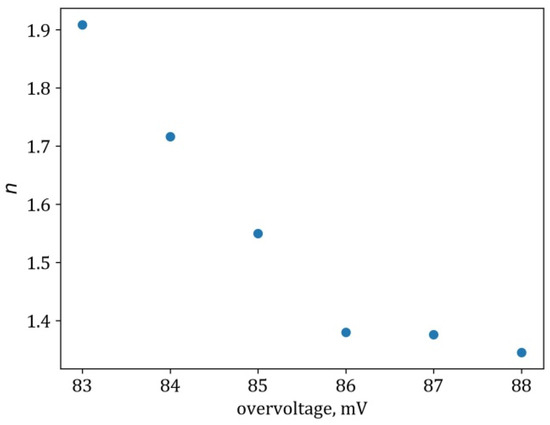
Figure A4.
Values of n from (7) used to fit data for the hemispherical (from Figure 6) [1] with the JMAKn model.
Appendix A.2. Fitting with the Richards Model
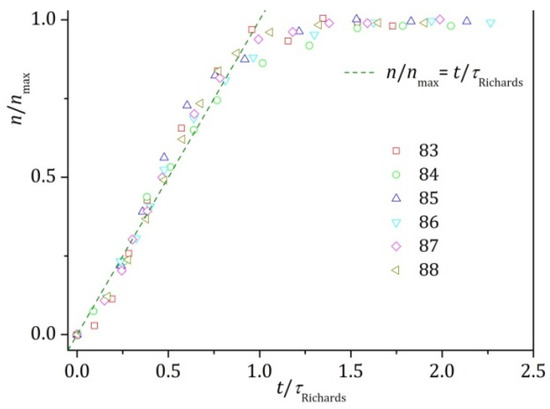
Figure A5.
Rescaling the data for the planar electrode (Figure 5 in [1]) with the fit parameters from the Richards model, Equation (12). Since there is not a fixed single value of q (see the figure below), there is no master curve in the usual sense.
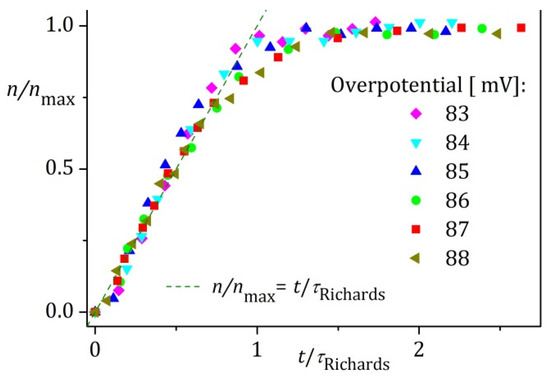
Figure A6.
Rescaling the data for the hemispherical electrode (Figure 6 in [1]) with the fit parameters from the Richards model, Equation (12). Here, the failure of the data collapse is clearly seen, especially when compared to the fits with the previous models from the HoM.
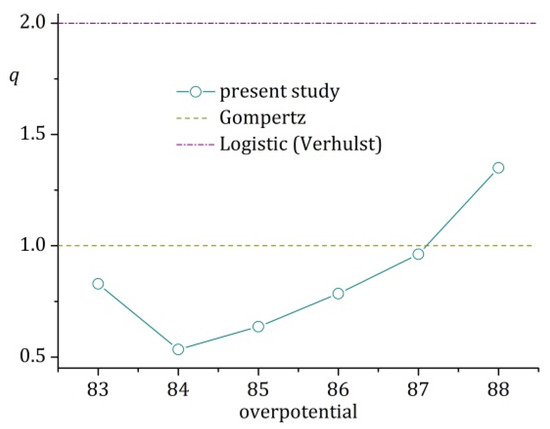
Figure A7.
Values of the “tuning” exponent q in the Richards model, Equation (12), as obtained from fitting Figure 5 in [1].
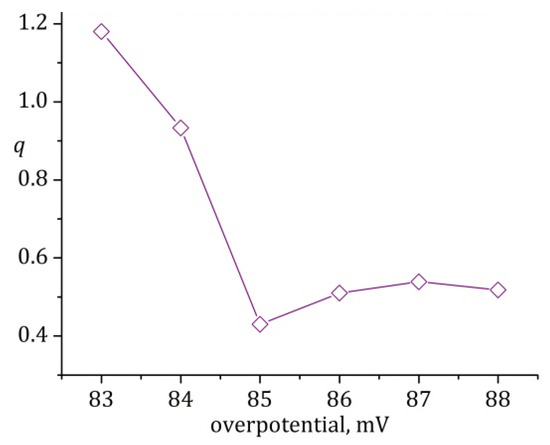
Figure A8.
Values of the “tuning” exponent q in the Richards model, Equation (12), as obtained from fitting Figure 6 in [1].
We do not provide a plot in Avrami coordinates here because, again, the only master curve would be the one from α21, while in order to plot curves from the Richards model, one should chose values not only for q but also for K!
References
- Markov, I.; Stoycheva, E. Saturation Nucleus Density in the Electrodeposition of Metals onto Inert Electrodes II. Experimental. Thin Solid Film. 1976, 21, 35. [Google Scholar] [CrossRef]
- Budevski, E.; Staikov, G.; Lorenz, W. Electrocrystallization: Nucleation and Growth Phenomena. Electrochim. Acta 2000, 2559, 45. [Google Scholar]
- Milchev, A. Nucleation Phenomena in Electrochemical Systems: Kinetic Models. ChemTexts 2016, 4, 2. [Google Scholar] [CrossRef]
- Popov, K.I.; Djokić, S.S.; Nikolić, N.D.; Jović, V.D. Morphology of Electrochemically and Chemically Deposited Metals; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Milchev, A. Thermodynamics of Electrochemical Nucleation; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Ivanov, V.V.; Tielemann, C.; Avramova, K.; Reinsch, S.; Tonchev, V. Modelling Crystallization: When the Normal Growth Velocity Depends on the Supersaturation. J. Phys. Chem. Solids 2023, 111542, 181. [Google Scholar] [CrossRef]
- Vekilov, P.G. The Two-Step Mechanism of Nucleation of Crystals in Solution. Nanoscale 2010, 2346, 2. [Google Scholar] [CrossRef] [PubMed]
- Nanev, C.N.; Tonchev, V.D. Sigmoid Kinetics of Protein Crystal Nucleation. J. Cryst. Growth 2015, 48, 427. [Google Scholar] [CrossRef]
- Verhulst, P.-F. Notice Sur La Loi Que La Population Suit Dans Son Accroissement. Corresp. Math. Phys. 1838, 113, 10. [Google Scholar]
- Tjørve, E.; Tjørve, K.M. A Unified Approach to the Richards-Model Family for Use in Growth Analyses: Why We Need Only Two Model Forms. J. Theor. Biol. 2010, 417, 267. [Google Scholar] [CrossRef]
- Watzky, M.A.; Finke, R.G. Transition Metal Nanocluster Formation Kinetic and Mechanistic Studies. A New Mechanism When Hydrogen Is the Reductant: Slow, Continuous Nucleation and Fast Autocatalytic Surface Growth. J. Am. Chem. Soc. 1997, 10382, 119. [Google Scholar] [CrossRef]
- Bentea, L.; Watzky, M.A.; Finke, R.G. Sigmoidal Nucleation and Growth Curves across Nature Fit by the Finke–Watzky Model of Slow Continuous Nucleation and Autocatalytic Growth: Explicit Formulas for the Lag and Growth Times plus Other Key Insights. J. Phys. Chem. C 2017, 5302, 121. [Google Scholar] [CrossRef]
- Barlow, D.A. The Kinetics of Multi-Step Protein Crystal Growth from Solution. Horiz. World Phys. 2021, 306, 151–186. [Google Scholar]
- Barlow, D.; Gregus, J. The Kinetics of Homogeneous and Two-Step Nucleation during Protein Crystal Growth from Solution. Int. J. Chem. Kinet. 2019, 840, 51. [Google Scholar] [CrossRef]
- Nanev, C.N.; Tonchev, V.D.; Hodzhaoglu, F.V. Protocol for Growing Insulin Crystals of Uniform Size. J. Cryst. Growth 2013, 10, 375. [Google Scholar] [CrossRef]
- Kleshtanova, V.; Tonchev, V.; Stoycheva, A.; Angelov, C. Cloud Condensation Nuclei and Backward Trajectories of Air Masses at Mt. Moussala in Two Months of 2016. J. Atmos. Sol.-Terr. Phys. 2023, 106004, 243. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On the Statistical Theory of the Crystallization of Metals. Bull. Acad. Sci. USSR Math. Ser. 1937, 355, 1. [Google Scholar]
- Johnson, W.; Mehl, R. Reaction kinetics in processes of nucleation and growth. Trans. Metall. Soc. AIME 1939, 135, 416–442. [Google Scholar]
- Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 1939, 1103, 7. [Google Scholar] [CrossRef]
- Málek, J. Kinetic Analysis of Crystallization Processes in Amorphous Materials. Thermochim. Acta 2000, 239, 355. [Google Scholar] [CrossRef]
- Avramov, I. Kinetics of Distribution of Infections in Networks. Phys. A Stat. Mech. Its Appl. 2007, 615, 379. [Google Scholar] [CrossRef]
- Dill, E.D.; Folmer, J.C.; Martin, J.D. Crystal Growth Simulations to Establish Physically Relevant Kinetic Parameters from the Empirical Kolmogorov–Johnson–Mehl–Avrami Model. Chem. Mater. 2013, 3941, 25. [Google Scholar] [CrossRef]
- Shirzad, K.; Viney, C. A Critical Review on Applications of the Avrami Equation beyond Materials Science. J. R. Soc. Interface 2023, 20, 20230242. [Google Scholar] [CrossRef] [PubMed]
- Gompertz, B. XXIV. On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies. In a Letter to Francis Baily, Esq. FRS &c; Philosophical Transactions of the Royal Society of London: London, UK, 1825; Volume 513. [Google Scholar]
- Zeeman, E.C. Catastrophe Theory, in Structural Stability in Physics: Proceedings of Two International Symposia on Applications of Catastrophe Theory and Topological Concepts in Physics Tübingen, Fed. Rep. of Germany, May 2–6 and December 11–14, 1978; Springer: Berlin/Heidelberg, Germany, 1979; pp. 12–22. [Google Scholar]
- Markov, I. Saturation Nucleus Density in the Electrodeposition of Metals onto Inert Electrodes I. Theory. Thin Solid Films 1976, 11, 35. [Google Scholar]
- Markov, I.V. Crystal Growth for Beginners: Fundamentals of Nucleation, Crystal Growth and Epitaxy; World Scientific: Singapore, 2016. [Google Scholar]
- Markov, I.V. Ivan Stranski—The Grandmaster of Crystal Growth; World Scientific: Singapore, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).