Abstract
Random quasi-phase matching (RQPM) in polycrystalline materials has been considered as an important technique for nonlinear optical frequency conversion, especially in wideband laser generation involving femtosecond lasers. In this paper, optical rectification (OR) based on RQPM in ZnSe ceramics was investigated for the first time, which could convert ultrashort optical pulses to broadband terahertz waves. A theoretical model of RQPM OR was built, with which the effects of material grain size, thickness, pump wavelength and pump pulse duration on terahertz generation, were simulated and discussed. It was found that RQPM OR in ZnSe is indeed effective in terahertz generation but insensitive to the material grain size and pump wavelength RQPM OR is even better than traditional single crystals such as ZnTe in bandwidth and robustness. The results can be a reference to optimize the RQPM OR nonlinear process, and hopefully, this work will promote the application of costless polycrystalline materials in the hot field of terahertz generation.
1. Introduction
Terahertz waves, defined as electromagnetic waves in the frequency range of 0.1–10 THz (30–3000 μm), have gained much attention, from basic research to industry uses in the past two decades, such as in communications, radar, spectroscopy, and nondestructive testing [1,2,3,4,5]. Among all kinds of terahertz sources, ultrashort terahertz pulses driven by femtosecond lasers enable the time-domain spectroscopy (TDS) system [6], which has the unique ability to characterize the complete electric field of a terahertz pulse with full phase and amplitude information, thus the complex dielectric properties of a sample can be acquired directly [7]. TDS is now among the most commercialized techniques in the terahertz field, enabling various applications with its powerful ability in spectroscopy and imaging [8,9].
There are mainly two methods to obtain ultrashort terahertz pulses for TDS, that is, through photoconductive switching or optical rectification (OR) [10]. Compared with the former one, OR is more promising in high-intensity and broadband terahertz generation, which are favorable in enhancing the signal-to-noise ratio and extending measurable sample species and spectroscopic details. OR originates from the second-order nonlinearity and can be regarded as difference-frequency mixing among the Fourier components within the spectral bandwidth of the ultrashort pump laser pulses [11]. It is well known that the effective generation of terahertz waves via OR requires both phase and group velocity matching between the pump and the terahertz waves. For this purpose, or phase matching (PM), identically, we can make use of the birefringence of nonlinear crystals or microstructures with periodically reversed nonlinearity, known as birefringence phase matching (BPM) and quasi-phase matching (QPM), respectively [10]. Sometimes the terahertz refractive index is significantly larger than the optical group index, represented by LiNbO3, and the tilted-pulse-front method has been proposed and proved to be effective in strong-field broadband terahertz generation [12], with the expense of much higher cost and complexity. If the crystal has cubic structure, e.g., ZnTe, the most famous material for OR pumped by the Ti:Sapphire laser [11], natural anomalous dispersion from optical to terahertz is necessary, otherwise phase matching can never be achieved. It is similar for GaP pumped by Yb-doped 1 μm lasers [13], and GaAs pumped by Er-doped 1.56 μm fiber lasers [14]. An inevitable problem is that it is almost impossible to change the pump wavelength which is strictly determined by the material dispersion of such crystals. An additional electric field induced Pockels effect would be helpful to modulate the refractive indices, but it is effective only in difference frequency mixing requiring two incident beams rather than OR, as demonstrated in our previous study [15].
Another feasible approach for efficient OR can resort to random quasi-phase matching (RQPM), which occurs in disordered polycrystalline materials such as ZnSe ceramics. RQPM was firstly proposed for difference frequency generation in 2004 [16]. Since then, RQPM has been extensively studied in both theory and experiment [17,18,19,20,21,22,23,24]. A qualitative explanation for RQPM is from the view of QPM that the grain size distribution in a wide range provides massive reciprocal lattice vectors to compensate for the phase mismatch [22]. The conversion efficiency of RQPM generally follows a linear relation to interaction length [17], thus it is much lower than that of BPM and QPM. However, if intense ultrashort lasers are involved, the significance of RQPM would be greatly enhanced. On one hand, the material length should be short enough to reduce dispersion, and the gap of net gain between RQPM and BPM/QPM becomes very limited; on the other hand, the damage threshold (in W/cm2) of ultrashort laser pulses in the femtosecond range is much higher than that of nanosecond laser pulses, so the nonlinear gain can be obviously increased by tight focusing. Meanwhile, the most remarkable advantage of RQPM in bandwidth can be fully exploited to support frequency conversion of ultrashort laser pulses. Effective wideband generation from visible to infrared based on RQPM three-wave interactions have been reported [18,19,20], but its application in terahertz sources via OR has not been touched yet.
In this paper, the theoretical model of terahertz generation by RQPM OR was built and quantitative simulations were performed. With the help of “Neper”, a professional software for polycrystal generation, the impacts of material (grain size and sample thickness) and pump laser (central wavelength and pulse duration) on terahertz generation were analyzed. We also studied the conversion efficiency of RQPM OR from the view of photon fluence. Combining with the material characterization on refractive index and absorption coefficients, the results in this paper would be helpful in designing a broadband terahertz source in the 0.1–5 THz range based on RQPM OR in costless polycrystalline ZnSe ceramics.
2. Modeling
2.1. Polycrystalline ZnSe Sample and Grain Morphology
Polycrystalline ZnSe is a preferred material for lenses, windows, and optical systems for its low absorption at the infrared range and its visible transmission. ZnSe is non-hygroscopic and chemically stable, unless treated with strong acids. After synthesis by chemical vapor deposition (CVD), crystalline grains in the size from ten- to hundred-level microns are inlaid together to form a transparent ceramic after sintering and pressing under high temperature. Polycrystalline ZnSe is highly industrialized with much lower cost than single crystals. A typical sample which was cut and polished from a core-drilled blank produced by II-VI Inc. (Saxonburg, PA, USA), is shown in Figure 1a. As an essential requisite for terahertz generation via OR, the refractive index and absorption coefficients in the terahertz range were characterized by a time-domain spectroscopy (TDS) system (TAS 7500 TS, Advantest Corp. (Tokyo, Japan), effective measurable range 0.1–4 THz), as shown in Figure 1b,c. The measured refractive index from 0.3 to 4 THz fitted well with that calculated from the Sellmeier equation [25]. The low absorption in this range also indicated that terahertz waves can be effectively coupled out once generated.
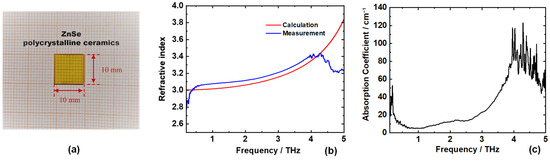
Figure 1.
Polycrystalline ZnSe and its optical property in the terahertz range: (a) photo of the sample; (b) refractive index; (c) absorption coefficient.
For a comprehensive simulation on a nonlinear process based on RQPM, a realistic model of polycrystalline ZnSe model is required, which can be generated by the software “Neper” using the grain growth module [26,27]. After model generation, it was meshed with the step of 10 μm, shown by Figure 2a,b. Microscopically, RQPM OR is affected by two random factors: one is the random distribution of the grain morphology and the other is the random orientation of the grains on the optical beam path. The former factor determines the interaction length and the latter corresponds to deff of every grain. The data of the grain morphology can be directly obtained from the software output. For example, Figure 2c,d gives the grain size distribution of two different samples, which generally followed lognormal functions.
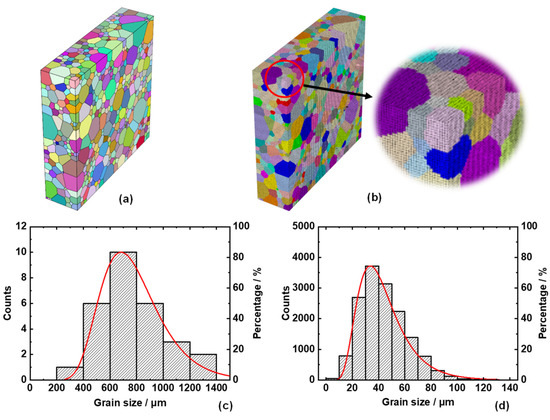
Figure 2.
Polycrystalline ZnSe, its meshed morphology and the grain size distribution: (a) original sample; (b) meshed sample; (c,d) histograms of grain size distributions of a 3 × 3 × 1 mm3 sample and a 1 × 1 × 1 mm3 sample with an average grain size of approximately 800 and 40 μm, respectively.
2.2. Theoretical Model of RQPM OR in Polycrystalline ZnSe
The wave equation of OR in nonlinear medium incident by a Gaussian laser beam under the condition of slowly varying envelope approximation and no absorption can be simplified as [28]
where E(Ω, z) is the Fourier component of the terahertz field at the angular frequency Ω, E0 is the time-domain electric field of the pump laser, z is the interaction length, χ(2) is the nonlinear susceptibility of the material, τ is the duration of the pump pulse, c is the light speed in vacuum, nΩ is the refractive index of the terahertz wave, and Δk is the wave vector mismatch. Δk can be expressed as Δk = kω + kΩ − kω+Ω from the view of three-wave mixing, where kω, kΩ and kω+Ω are the wave vectors of two optical frequencies ω, ω + Ω and a terahertz frequency Ω. Considering Ω << ω,
which leads to
where ng,ω is the group refractive index of the pump laser, expressed as
in which nω and λω are the phase refractive index and wavelength at the laser angular frequency ω. Consequently, the coherent length Lc of OR is given by
It should be noted that Δk and Lc is independent to crystalline orientation for cubic ZnSe material. Under undepleted pump approximation, the terahertz electric field is obtained by direct integration of Equation (1):
where deff is the effective nonlinear coefficient and it is assumed that χ(2) = 2deff. deff is dependent on z due to the variation of crystalline orientation in different grains of a polycrystalline material. If there are m grains along the beam path, the integration in Equation (6) is divided into m parts, written as
where deff,n is the effective nonlinear coefficient of each grain (n is an integer and 1 ≤ n ≤ m), and the integration range from zn−1 to zn is the interaction length in the nth grain. The major difference of a RQPM process compared with BPM and QPM is that deff is totally random in polycrystalline materials. The mathematical model, called spherical random pointing [29,30], can be used to describe the random nonlinearity. Once the distribution of deff is determined, the terahertz field can be calculated either from step-to-step integration with Equation (7) or based on the Fourier transform method [31].
The energy conversion efficiency of OR can be given by comparing the pump fluence Fpump and terahertz fluence FTHz, which are expressed as follows [28]:
Thus, the analytical expression for the OR conversion efficiency is
3. Results and Discussion
Here, we discuss the terahertz generation based on RQPM in polycrystalline ZnSe. The main factors that affect terahertz generation via OR can be classified into two categories, material related and pump related. The former includes the average grain size and sample thickness, while the latter contains the pump wavelength and pulse duration. The conversion efficiency of OR is also discussed by comparing the terahertz and pump photon fluence in this part. The ZnSe samples used for simulation were all generated by “Neper” with the meshing step of 10 μm, which is adequate to guarantee good space resolution. All the simulation data of the terahertz field were obtained using the step-to-step integration method and statistically averaged over all the beam paths of each meshing grid within the cross section. The power losses at both the pump and terahertz ranges were not considered to highlight the basic rules of the RQPM OR process.
3.1. Dependence of Terahertz Generation on Polycrystalline Parameters
3.1.1. Grain Size Distribution
Basically, there are two factors to characterize the polycrystalline grain, the grain size and sphericity. However, previous studies of RQPM processes have shown that the average grain size plays the key role and the effect of sphericity is negligible [23]. A complete description of the grain size distribution requires both the mean value (μ) and standard deviation (σ). The values of |E|2, which indicates the generated terahertz intensity in the frequency domain, is shown in Figure 3, including the simulation results of seven different polycrystalline ZnSe samples. The mean value of grain size ranged from tens to hundreds of microns while the standard deviation should allow the construction of a realistic polycrystalline model, both directly obtained from Neper output. The frequency dependence is also given in Figure 3 to depict the frequency-domain profile and the bandwidth. The central wavelength of the pump laser was λ0 = 1064 nm which can be realized by Yb3+-doped fiber lasers, with the time-domain pump intensity of I0 = 30 GW/cm2 and the pump pulse duration of τ = 100 fs. The samples had an identical thickness of 1 mm, which is a common size for various single crystals and is also acceptable in simulation time while ensuring sufficient grain number, but different cross sections to guarantee adequate grains for statistical analysis.
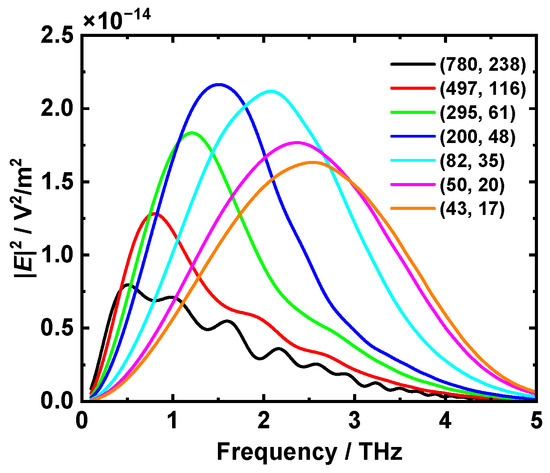
Figure 3.
Terahertz intensity generated by RQPM OR with different 1 mm-thick polycrystalline ZnSe samples. The grain size distribution is written as (μ, σ), where μ and σ are the mean value and standard deviation in micron, respectively. The cross section for the (780, 238) sample was 3 × 3 mm2, it was 2 × 2 mm2 for the (497, 116) and (295, 61) samples, and it was 1 × 1 mm2 for all the left samples.
It is apparent that broadband terahertz waves spanning from 0.1 to 5 THz can be generated in polycrystalline ZnSe materials based on RQPM. For each spectrum, the terahertz intensity rises first and then declines, which can be explained by Equation (7), that is, the generated terahertz field is contributed by both the wave vector mismatch ∆k and the terahertz frequency Ω for a given sample. The frequency-dependent ∆k is calculated and shown in Figure 4a. The lower terahertz frequency, the smaller ∆k, and the stronger terahertz field, but the part outside the summation notation of Equation (7) first rises and then declines due to the varied value of Ω. In addition, if the average grain size is reduced, the spectrum generally moves towards the high-frequency part. The reason is that the OR efficiency is related to the coherent length Lc, and it has been proved that the highest efficiency occurs when the average grain size is close to the coherent length. As shown in Figure 4b, the higher terahertz frequency, the smaller Lc. Therefore, smaller average grain size benefits high-frequency terahertz generation, and the location of the spectral peak moves towards higher frequency monotonically.
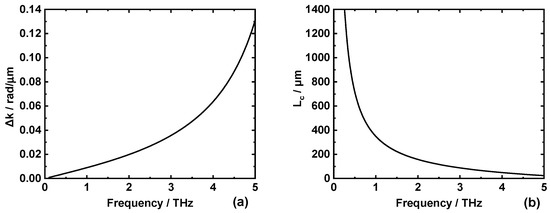
Figure 4.
Wave vector mismatch ∆k (a) and coherent length Lc (b) of OR in ZnSe pumped at 1064 nm.
It is noticeable that there are abnormal leaps on the curves correspond to the samples with large average grain sizes (e.g., 780 and 497 μm), due to the random nature of RQPM nonlinear interactions. Considering the computing power of a personal computer, only the samples with limited dimensions could be successfully generated by Neper. However, the grain quantity would be quite limited given the size of the polycrystalline ZnSe sample is small and the average grain size is large, resulting deviation from ideal statistical results. Nevertheless, the general tendency of these simulations can reflect the basic rule of RQPM OR in polycrystalline ZnSe.
3.1.2. Sample Thickness
The theory of RQPM nonlinear frequency conversions indicates that output signal grows linearly with the interaction length (sample thickness) under the condition of monochromatic interactions [17]. However, both the ultrashort pump laser and the terahertz waves are far beyond the monochromatic approximation during an OR process. Here, we discussed the wideband terahertz generation based on RQPM OR, taking ZnSe samples with the grain size distribution of μ = 82 μm and σ = 35 μm as examples with the same cross section of 1 × 1 mm2. Such samples would contain thousands of grains to guarantee the accuracy of statistical analysis. The simulation results are shown in Figure 5.
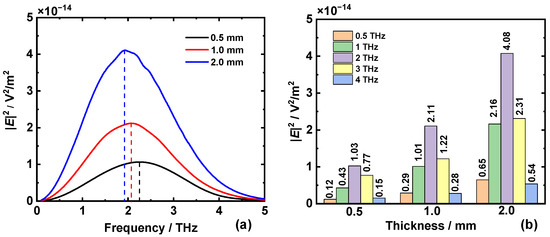
Figure 5.
Terahertz intensity generated by RQPM OR in polycrystalline ZnSe samples with different thickness: (a) terahertz spectrum; (b) nonlinear terahertz signal growth at certain frequencies. The grain size distribution (μ, σ) was (82, 35) in micron.
It is absolutely reasonable that the terahertz field grows with interaction length as shown in Figure 5a, but clearly, it is not a strict linear relation shown by Figure 5b. With the increase in terahertz frequency, the proportion of signal increase once the sample thickness is doubled (0.5/1.0/2.0 mm), demonstrates a declining trend. In other words, the curve profile in Figure 5a generally moves to the low-frequency part. The signal peak is at 2.26, 2.08, and 1.94 THz when the sample thickness is 0.5, 1.0, and 2.0 mm, respectively. This phenomenon is ascribable to ∆k or Lc: at low frequencies, ∆k is smaller; thus, the signal accumulation is faster with the increase in interaction length.
3.2. Dependence of Terahertz Generation on Pump Laser Parameters
3.2.1. Central Wavelength of the Pump Laser
Different from single crystals that strictly require specific pump wavelengths to satisfy the PM condition [11,12,13,14], the advantage of RQPM nonlinear interactions in polycrystals is that it is insensitive to pump wavelength as the grain size spreads over a wide range. Using an identical 1 × 1 × 1 mm3 ZnSe sample with the grain size distribution of μ = 82 μm and σ = 35 μm, the terahertz generation was investigated under pump wavelengths of 800, 1064, 1550, 1900 and 2350 nm, respectively, all of which had the same pulse duration of 100 fs and the pump intensity of 30 GW/cm2. All such lasers are readily available in commercial solid-state or fiber mode-locked laser products. The simulation results are shown in Figure 6.
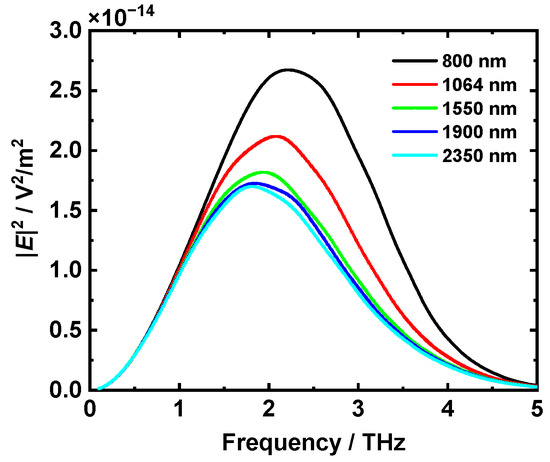
Figure 6.
Terahertz intensity generated by RQPM OR in a polycrystalline ZnSe sample pumped at different wavelengths. The grain size distribution (μ, σ) was (82, 35) in micron, the pump pulse duration was 100 fs and the pump intensity was 30 GW/cm2.
The insensitivity of RQPM OR can be reflected from Figure 6 because neither the terahertz spectrum profile nor the absolute intensity varied much pumped at different wavelengths. Compared with OR in ZnTe single crystals [32], the changes of peak intensity and bandwidth are lower than half while the pump wavelength is varied in a much larger scope from 800 to 2350 nm. However, we can see the total terahertz power become lower at longer pump wavelength, which is related to ∆k or Lc as well. Figure 7 gives the distribution of ∆k and Lc related to both the pump wavelength from 800 to 2400 nm and terahertz frequency from 0.1 to 5 THz. At the low-frequency region of the terahertz spectrum (e.g., 0.1–1 THz), the coherent length is much larger than the grain size whatever pump wavelength is used, so that the spectral intensity is almost independent to pump wavelength. At the terahertz frequency range of 2–4 THz, Lc is close to the average grain size. In this case, ∆k becomes larger and Lc gets smaller with the increase in pump wavelength, causing the decline of terahertz spectral intensity and the move of the spectral peak to the high-frequency part. All the results are consistent with that in Figure 6.
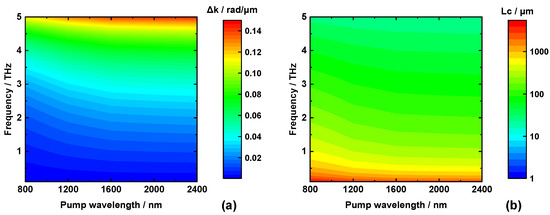
Figure 7.
Pump-wavelength-dependent wave vector mismatch ∆k (a) and coherent length Lc (b) of OR in ZnSe.
3.2.2. Pump Pulse Duration
The dependence of terahertz generation via RQPM OR on pump pulse duration mainly lies in the different spectral bandwidth and spectral intensity for a certain time-domain pump field. Supposing the time-domain pump intensity was 30 GW/cm2 at 1064 nm, its spectra with Lorentz type is shown by Figure 8a when the pump pulse duration is increased from 50 to 500 fs. Since the OR process can be regarded as intra-pulse difference frequency mixing, the shorter pump pulse, the more frequency components, so the lower peak spectral intensity and broader terahertz spectrum generation. The simulation results of RQPM OR using a 1 × 1 × 1 mm3 ZnSe sample with the grain size distribution of μ = 82 μm and σ = 35 μm is shown in Figure 8b. The spectrum peak moves from 2.5 THz towards the low-frequency part to 0.6 THz when the pump pulse duration is increased from 50 to 500 fs. At the same time, the high-frequency components of terahertz filed become weaker, resulting in degraded spectrum bandwidth and enhanced peak spectral intensity when the pump pulse duration is increased.
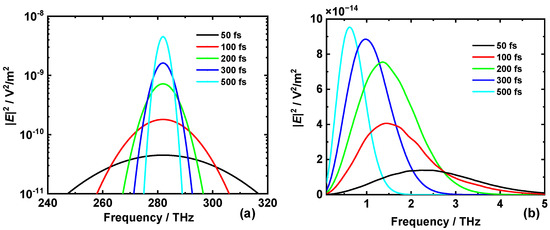
Figure 8.
The spectra of the pump pulse at different pulse durations (a) and the corresponding generated terahertz spectra (b). The pump intensity was 30 GW/cm2 at 1064 nm.
3.3. Conversion Efficiency of RQPM OR
The overall optical-to-optical power or energy conversion efficiency is an important indicator of nonlinear frequency conversion. Based on the above theoretical model of RQPM OR, the effects of pump laser and polycrystalline ZnSe sample on conversion efficiency were discussed in detail by comparing the photon fluence at terahertz and pump wavelengths. Figure 9 gives the conversion efficiency in 1 mm-thick ZnSe simples as a function of grain size at different central pump wavelengths of 800 nm, 1064 nm, 1550 nm, 1900 and 2350 nm, respectively. The pump pulse duration and pump intensity were identical at 100 fs and 30 GW/cm2, respectively. The conversion efficiency reaches 10−4, which is comparable to OR with single crystals [33].
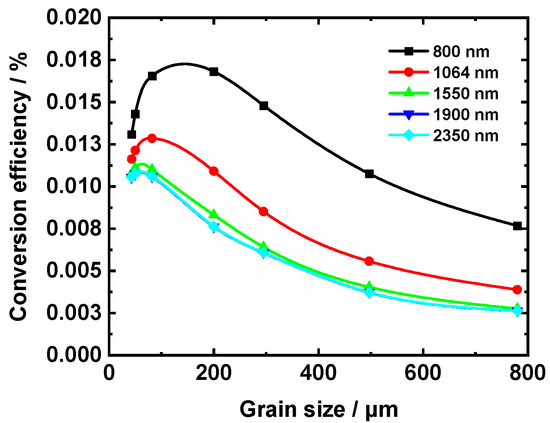
Figure 9.
The conversion efficiency of RQPM OR versus ZnSe grain size at different central pump wavelengths of 800, 1064, 1550, 1900 and 2350 nm. Note the curves of 1900 and 2350 nm are overlapped.
The grain size distributions of all the samples is consistent with that shown Figure 3. As discussed in Section 3.1.1, the generated terahertz field is contributed by both the wave vector mismatch ∆k and the terahertz frequency Ω for a given sample. Consequently, the OR conversion efficiency increases first and then decreases if the grain size gets larger. The maximum conversion efficiency appears at the average grain size of lower than 200 μm when the central pump wavelength is 800 nm, and the peak moves towards smaller grain size if the pump wavelength is longer. In addition, if we step back to Figure 7a, which shows that the shorter pump wavelength, the smaller ∆k, and the better phase matching, leading to monotonically declined conversion efficiency with the increase in pump wavelength. In this sense, we can maximize the generated terahertz field by choosing a shorter central pump wavelength of 800 nm and optimizing the grain size distribution. Since the value of ∆k has little difference when the central pump wavelength is changed from 1800 to 2400 nm, the efficiency curves pumped at 1900 and 2350 nm are almost identical. The RQPM OR efficiency, which declines by half or so when the grain size is changed by an order of magnitude, is also confirmed to be insensitive to the polycrystalline sample.
Figure 10a shows the conversion efficiency of RQPM OR versus grain size at different pump pulse durations with 1 mm-thick ZnSe samples, where the central pump wavelength was 1064 nm and the pump intensity was 30 GW/cm2. The pump fluence is given in Figure 10b, demonstrating an increasing trend as the pulse durations increases, so that the conversion efficiency can be reflected by comparing Figure 8b and Figure 10b. There is an optimized average grain size for different pulse durations, and the optimal size value is larger when the pump pulse duration gets longer. The OR efficiency varies a lot with pulse durations, where a shorter pulse duration benefits higher terahertz pulse energy. Generally, shorter pump wavelength and pulse duration is good for enhancing the conversion efficiency, but high-order nonlinear effects such as the two-photon absorption and cross-phase modulation would be major problems affecting the RQPM OR efficiency.
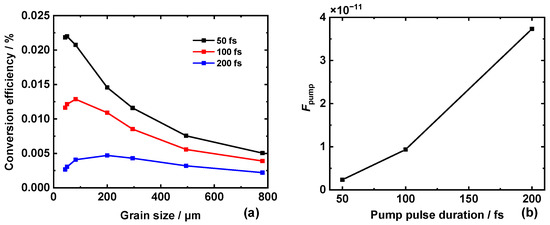
Figure 10.
The conversion efficiency of RQPM OR versus ZnSe grain size (a) pumped at different pulse durations, with the pump fluence at different pulse durations (b) given as a reference.
4. Conclusions
RQPM OR, which can be used to generate broadband terahertz waves in polycrystalline materials pumped by femtosecond lasers, is discussed for the first time. A theoretical model was built for RQPM OR and the impacts of material- and pump-related parameters on terahertz generation were studied in detail. It was indicated that the terahertz bandwidth is mainly determined by the average grain size and pump pulse duration. The smaller grain size and the shorter pump pulse duration, the broader terahertz bandwidth, and meanwhile, the terahertz spectral peak moves to higher frequency. The terahertz field intensity corresponds to material thickness, pump wavelengths, pulse duration, etc. The conversion efficiency of RQPM was proved to be comparable to that with single crystals but insensitive to the polycrystalline grain size, which should be a great advantage. Simulations showed that shorter pump wavelength and pulse duration are favorable to conversion efficiency; however, they would result in high-order nonlinear effects and require further study in both theory and experiment. It should also be noted that the terahertz absorption was not considered, but it plays a minor role because the sample was as thin as 1 mm. It is believed that the industrialized polycrystalline ZnSe can be a promising material in OR to achieve efficient terahertz sources spanning from 0.1 to 5 THz, even advantageous over single crystals in bandwidth, cost and robustness. Meanwhile, a large number of polycrystalline materials such as ZnS, ZnO, and GaN, which possess good physical, optical and nonlinear optical properties, can also be used in RQPM OR to generate terahertz waves with desired spectrum given suitable samples and pump lasers are available.
Author Contributions
S.W. and K.Z. presented the idea and performed the theoretical analysis. H.Q. and F.L. investigated the relevant literature and reports. D.X., J.L. and J.Y. were responsible for supervision. All authors contributed to the results, discussion, and manuscript writing. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grantnumber 62175184, and Key Laboratory of Micro Opto-electro Mechanical System Technology, Ministry of Education.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- O’Hara, J.F.; Ekin, S.; Choi, W.; Song, I. A perspective on terahertz next-generation wireless communications. Technologies 2019, 7, 43. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.Q.; Deng, B.; Qin, Y.L. Review of terahertz radar technology. J. Radars 2018, 7, 1–21. [Google Scholar]
- D’Arco, A.; Di Fabrizio, M.; Dolci, V.; Petrarca, M.; Lupi, S. THz pulsed imaging in biomedical applications. Condens. Matter 2020, 5, 25. [Google Scholar] [CrossRef] [Green Version]
- Vaks, V.L.; Anfertev, V.A.; Balakirev, V.Y.; Basov, S.A.; Domracheva, E.G.; Illyuk, A.V.; Kupriyanov, P.V.; Pripolzin, S.I.; Chernyaeva, M.B. High resolution terahertz spectroscopy for analytical applications. Physics-Uspekhi 2020, 63, 708–720. [Google Scholar] [CrossRef]
- Bogue, R. Sensing with terahertz radiation: A review of recent progress. Sens. Rev. 2018, 38, 216–222. [Google Scholar] [CrossRef]
- Neu, J.; Schmuttenmaer, C.A. Tutorial: An introduction to terahertz time domain spectroscopy (THz-TDS). J. Appl. Phys. 2018, 124, 231101. [Google Scholar] [CrossRef] [Green Version]
- Zhong, K.; Liu, C.; Wang, M.R.; Shi, J.; Kang, B.; Yuan, Z.R.; Li, J.N.; Xu, D.G.; Shi, W.; Yao, J.Q. Linear optical properties of ZnGeP2 in the terahertz range. Opt. Mater. Express 2017, 7, 3571–3579. [Google Scholar] [CrossRef]
- Fischer, B.; Hoffmann, M.; Helm, H.; Modjesch, G.; Uhd Jepsen, P. Chemical recognition in terahertz time-domain spectroscopy and imaging. Semicond. Sci. Technol. 2005, 20, S246–S253. [Google Scholar] [CrossRef] [Green Version]
- Naftaly, M.; Miles, R.E. Terahertz time-domain spectroscopy for material characterization. Proc. IEEE 2007, 95, 1658–1665. [Google Scholar] [CrossRef]
- Zhong, K.; Shi, W.; Xu, D.G.; Liu, P.X.; Wang, Y.Y.; Mei, J.L.; Yan, C.; Fu, S.J.; Yao, J.Q. Optically pumped terahertz sources. Sci. China Technol. Sci. 2017, 60, 1801–1818. [Google Scholar] [CrossRef]
- Vidal, S.; Degert, J.; Tondusson, M.; Freysz, E.; Oberlé, J. Optimized terahertz generation via optical rectification in ZnTe crystals. J. Opt. Soc. Am. B 2014, 31, 149–153. [Google Scholar] [CrossRef]
- Helling, J.; Stepanov, A.G.; Almási, G.; Bartal, B.; Kuhl, J. Tunable THz Pulse generation by optical rectification of ultrashort laser pulses with tilted pulse fronts. Appl. Phys. B 2004, 78, 593–599. [Google Scholar] [CrossRef]
- Aoki, K.; Savolainen, J.; Havenith, M. Broadband terahertz pulse generation by optical rectification in GaP crystals. Appl. Phys. Lett. 2017, 110, 201103. [Google Scholar] [CrossRef]
- Nagai, M.; Tanaka, K.; Ohtake, H.; Bessho, T.; Sugiura, T.; Hirosumi, T.; Yoshida, M. Generation and detection of terahertz radiation by electro-optical process in GaAs using 1.56 μm fiber laser pulses. Appl. Phys. Lett. 2004, 85, 3974–3976. [Google Scholar] [CrossRef]
- Zhong, K.; Li, F.J.; Qiao, H.Z.; Zhang, X.Z.; Xu, D.G.; Yao, J.Q. Wideband collinear phase matching in cubic semiconductors via the linear electro-optic effect: A theoretical study. Crystals 2022, 12, 764. [Google Scholar] [CrossRef]
- Baudrier-Raybaut, M.; Haïdar, R.; Kupecek, P.; Lemasson, P.; Rosencher, E. Random quasi-phase-matching in bulk polycrystalline isotropic nonlinear materials. Nature 2004, 432, 374–376. [Google Scholar] [CrossRef]
- Videl, X.; Martorell, J. Generation of light in media with a random distribution of nonlinear domains. Phys. Rev. Lett. 2006, 97, 013902. [Google Scholar] [CrossRef] [Green Version]
- Vasilyev, S.; Moskalev, I.; Mirov, M.; Smolski, V.; Mirov, S.; Gapontsev, V. Ultrafast middle-IR lasers and amplifiers based on polycrystalline Cr:ZnS and Cr:ZnSe. Opt. Mater. Express 2017, 7, 2636–2650. [Google Scholar] [CrossRef]
- Ru, Q.T.; Lee, N.; Chen, X.; Zhong, K.; Tsoy, G.; Mirov, M.; Vasilyev, S.; Mirov, S.B.; Vodopyanov, K.L. Optical parametric oscillation in a random polycrystalline medium. Optica 2017, 4, 617–618. [Google Scholar] [CrossRef]
- Zhang, J.W.; Fritsch, K.; Wang, Q.; Krausz, F.; Mak, K.F.; Pronin, O. Intra-pulse difference-frequency generation of mid-infrared (2.7–20μm) by random quasi-phase-matching. Opt. Lett. 2019, 44, 2986–2989. [Google Scholar] [CrossRef] [Green Version]
- Ru, Q.T.; Kawamori, T.; Lee, N.; Chen, X.; Zhong, K.; Mirov, M.; Vasilyev, S.; Mirov, S.B.; Vodopyanov, K.L. Optical paramet-ric oscillation in a random poly-crystalline medium: ZnSe ceramic. Proc. SPIE 2018, 10516, 166–174. [Google Scholar]
- Kawamori, T.; Ru, Q.T.; Vodopyanov, K.L. Comprehensive model for randomly phase-matched frequency conversion in zinc-blende polycrystals and experimental results for ZnSe. Phys. Rev. Appl. 2019, 11, 054015. [Google Scholar] [CrossRef]
- Liu, K.F.; Zhong, K.; Lu, Z.T.; Xu, D.G.; Yao, J.Q. Effects of grain morphology on nonlinear conversion efficiency of random quasi-phase matching in polycrystalline materials. IEEE Photonics J. 2020, 12, 2200910. [Google Scholar] [CrossRef]
- Müller, J.S.; Morandi, A.; Grange, R.; Savo, R. Modeling of random quasi-phase-matching in birefringent disordered media. Phys. Rev. Appl. 2021, 15, 064070. [Google Scholar] [CrossRef]
- Li, H.H. Refractive index of ZnS, ZnSe, and ZnTe and its wavelength and temperature derivatives. J. Phys. Chem. Ref. Data 1984, 13, 103–150. [Google Scholar] [CrossRef]
- Quey, R.; Renversade, L. Optimal polyhedral description of 3D polycrystals: Method and application to statistical and synchrotron X-ray diffraction data. Comput. Methods Appl. Mech. Eng. 2018, 330, 308–333. [Google Scholar] [CrossRef] [Green Version]
- Neper: Polycrystal Generation and Meshing. Available online: http://neper.info/ (accessed on 11 August 2022).
- Vodopyanov, K.L. Optical generation of narrow-band terahertz packets in periodically-inverted electro-optic crystals: Conversion efficiency and optimal laser pulse format. Opt. Express 2006, 14, 2263–2276. [Google Scholar] [CrossRef]
- Marsaglia, G. Choosing a point from the surface of a sphere. Ann. Math. Stat. 1972, 43, 645–646. [Google Scholar] [CrossRef]
- Muller, M.E. A note on a method for generating points uniformly on n-dimensional spheres. Commun. ACM 1959, 2, 19–20. [Google Scholar] [CrossRef]
- Zhong, K.; Wang, S.J.; Liu, K.F.; Xu, D.G.; Yao, J.Q. Fourier transform analysis on random quasi-phase-matched nonlinear optical interactions. IEEE Photonics J. 2022, 14, 3005505. [Google Scholar] [CrossRef]
- Li, D.; Ma, G. Pump-wavelength dependence of terahertz radiation via optical rectification in (110)-oriented ZnTe crystal. J. Appl. Phys. 2008, 103, 123101. [Google Scholar] [CrossRef]
- Meng, Q.L.; Ye, R.; Zhong, Z.Q.; Yu, J.L.; Zhang, B. Analysis on THz radiation generation efficiency in optical rectification by tilted-pulse-front pumping. J. Infrared Millim. Terahertz Waves 2015, 36, 866–875. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).