Ab Initio Study of Chiral Phonons in Ternary YAlSi Compound

Abstract

Ternary compound YAlSi crystallizes with orthorhombic Cmcm symmetry. This structure contains Y–Si pairs of atoms, creating honeycomb-like sublattices. In this paper, we investigate the dynamical properties of the system, focusing on the chiral modes. These modes are associated with the circular motion of the atoms. We show that the chiral modes can be realized in the YAlSi compound, and it makes this compound suitable for further experimental study of the chiral phonons.

1. Introduction

Systems with hexagonal three-fold rotational symmetry can host exotic types of chiral phonons [1], associated with circular motion of the atoms around the equilibrium position. In such cases, phonons have a finite pseudoangular momentum [2], which can interact with the external magnetic field to give rise to the phonon Hall effect [3]. Chiral phonons were studied in many two-dimensional (2D) lattices, like honeycomb lattice [4], kukelé lattice [5], and kagome lattice [6]. Recently, chiral phonons were also studied in three-dimensional (3D) systems, e.g., dichalcogenides [7], multiferroics [8,9], magnetic topological insulators [10], CoSn-like kagome metals [11], or binary compounds ABi ($A=$ K, Rb, Cs) [12], using the ab initio (DFT) technique. Due to a finite pseudoangular momentum and a definite handedness, chiral phonons interact selectively with other chiral objects like circularly polarized light. This fact is exploited in experimental studies of chiral phonons [13,14,15,16].

The initial studies of chiral phonons were restricted to lattices having hexagonal symmetry (i.e., threefold rotational symmetry). However, a recent study went beyond the hexagonal symmetry to predict the presence of chiral phonons in systems having, e.g., fourfold rotational symmetry [17]. Here, we show that a system with orthorhombic Cmcm symmetry (i.e., two-fold rotational symmetry) can also host the chiral phonons [11]. In this context, it is worth mentioning some systems containing chiral chains, like $\alpha$-SiO${}_2$ [18], $\alpha$-HgS [19], binary compounds ABi ($A=$ K, Rb, Cs) [12], or nonsymmorphic systems [20]. Chiral phonons can also be observed in a system under strain [21]. In this case, the uniaxial strain can lead to structural phase transition (e.g., from P6/mmm to Cmmm symmetry in the case of CoSn-like compounds [11]), without vanishing chiral phonons.

In this paper, we discuss the basic ternary YAlSi compound with orthorhombic Cmcm symmetry (Figure 1). Recently, many representatives of the ternary compounds containing Al and Si were studied, e.g., RAlSi or RAlGe, where R is a rare earth atom. In the case of RAlSi compounds, systems crystallize in two type of structures [22], with orthorhombic symmetry (DyAlGe [23], HoAlSi [24], HoAlGe [23], TmAlSi [25], LuAlSi [22,25,26]) or tertragonal symmetry (DyAlSi [27], PrAlGe [28], CeAlGe [28,29], CeAlSi [30], GdAlSi [26], GdAlGe [24,31]). Here, the orthorhombic phase is isostuctural to the YAlGe [32].

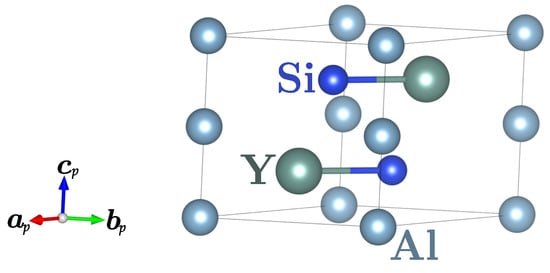
Figure 1. Primitive cells of YAlSi with orthorhombic Cmcm symmetry.

In the case of RAlSi, physical properties of the system are associated with the realization of topological band structure, which is also the reason behind the occurrence of massless Weyl fermions in these compounds (e.g., LaAlSi [33,34], LaAlGe [35], CeAlSi [36], CeAlGe [29,37], PrAlGe [38,39]). Contrary to this, in TAlSi (T is transition metal), the topological electronic properties were not reported. However, due to the realized space group (Cmcm), YAlSi can exhibit interesting dynamical properties. The dynamical properties of the ternary YAlSi compound have not yet been studied. In fact, there are two two-fold rotational symmetry axes (around y or z direction), that allow the realization of the chiral phonons.

The paper is organized as follows. At first, we shortly describe the used techniques (Section 2). Next, in Section 3, we present our results. In particular, we investigate the dynamical properties of the system (Section 3.1) and the chiral phonons (Section 3.2). We conclude our discussion in Section 4.

2. Methods

First-principles (DFT) calculations [40,41] were preformed using the projector augmented-wave (PAW) potentials [42] implemented in the Vienna Ab initio Simulation Package (vasp) code [43,44,45]. The calculations are made within the generalized gradient approximation (GGA) in the Perdew, Burke, and Ernzerhof (PBE) parametrization [46]. For the summation over the reciprocal space, $12\times 8\times 12$ k–grid in the Monkhorst–Pack scheme [47] was used. The energy cutoff for the plane-wave expansion was set to 400 eV. In calculations, the valence electron configurations: $5s^{2}4d^1$ (with additional semi-core $4s^{2}4p^6$ states treated as valence), $3s^{2}3p^1$, and $3s^{2}3p^2$, for Y, Al, and Si, respectively, were used. The crystal structure, as well as the atom positions, were optimized in the conventional unit cell containing two primitive unit cells. The condition for the break of the optimization loop was the energy difference of ${10}^{-6}$ eV and ${10}^{-8}$ eV for ionic and electronic degrees of freedom for subsequent steps, respectively. The crystal symmetry was analyzed using FindSym [48] and SpgLib [49], while the momentum space analysis was conducted using SeeK-path tools [50].

Dynamical properties were investigatied within the direct Parlinski-Li-Kawazoe method [51], implemented in phonopy [52], and evaluated by alamode software [53,54]. In this method, the Hellmann–Feynman forces calculated for displacement atoms, are used to find the interatomic force constants (IFC). Next, the IFCs are used to contruct the dynamical matrix, to study the dynamical properties of the system. In our calculations we used a supercell containing $2\times 2\times 1$ conventional cells (i.e., eight primitive cells).

3. Results

The described system crystallizes in the Cmcm YAlGe-type structure (space group No. 63) [32]. In the primitive unit cell (Figure 1), Al atoms create two layers of a triangular lattice (with angle between ${\mathit{a}}_p$ and ${\mathit{b}}_p$ equal to 42.5°, i.e., smaller than in ideal triangular lattice). Similarly, we can distinguish two pairs of Y–Si pairs, creating two dimensional honeycomb-like lattices (in the ${\mathit{a}}_p$–${\mathit{b}}_p$ plane). This honeycomb-like Y–Si lattices are positioned alternately along the ${\mathit{c}}_p$ direction. The conventional cell is described by the lattice vectors $\mathit{a}={\mathit{a}}_p-{\mathit{b}}_p$, $\mathit{b}={\mathit{a}}_p+{\mathit{b}}_p$, and $\mathit{c}={\mathit{c}}_p$.

The theoretically-obtained lattice parameters ($a=4.0053$ Å, $b=10.3064$ Å, and $c=5.7184$ Å) were in excellent agreement with the experimental ones, i.e., $a=3.9948$ Å, $b=10.2983$ Å, and $c=5.7085$ Å [22]. Positions of the atoms were found as $4c$ (0, 0.3049, 0.25) for Y, $4a$ (0, 0, 0) for Al, and $4c$ (0, 0.5989, 0.25) for Si, while the experimental values [22] were $4c$ (0, 0.3058, 0.25) for Y, $4a$ (0, 0, 0) for Al, and $4c$ (0, 0.5992, 0.25) for Si.

The electronic band structure and density of states (elDOS) of YAlSi is presented in Figure 2. Here, the high symmetry points in the scaled units have the coordinates: ${\mathrm{A}}_0=(0.28776,0.28776,1/2)$; ${\mathrm{C}}_0=(-0.28776,0.71224,0)$; ${\mathrm{E}}_0=(-0.28776,0.71224,1/2)$; $\mathsf{\Gamma }=(0,0,0)$; $\mathrm{R}=(0,1/2,1/2)$; $\mathrm{S}=(0,1/2,0)$; ${\mathsf{\Sigma }}_0=(0.28776,0.28776,0)$; $\mathrm{T}=(-1/2,1/2,1/2)$; $\mathrm{Y}=(-1/2,1/2,0)$; and $\mathrm{Z}=(0,0,1/2)$, while their positions with respect to the first Brillouin zone are presented in the inset of Figure 2. Additionally, the system did not exhibit any magnetic order, while the spin–orbit coupling effects were negligible (in practice, the band splitting induced by the spin–orbit coupling was not visible in the electronic band structure). The elDOS exhibited metallic properties (see right panel in Figure 2).

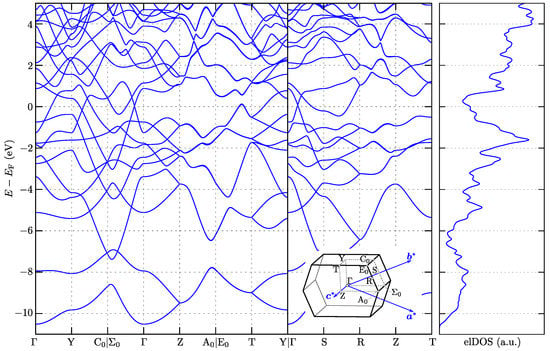
Figure 2. Electronic band structure and density of states (elDOS) of YAlSi with orthorhombic Cmcm symmetry. Inset presents Brillouin zone with high symmetry points for Cmcm symmetry.

3.1. Dynamical Properties

The lattice dynamics of the system were studied using the dynamical matrix:

$$\begin{array}{c}\hfill D_{\alpha \beta }^{j{j}^{\prime }}\left(\mathit{q}\right)=\frac{1}{\sqrt{m_j{m}_{j^{\prime }}}}\sum _n{\Phi }_{\alpha \beta }(j0,j^{\prime }n)exp\left(i\mathit{q}·{\mathit{R}}_{j^{\prime }n}\right),\end{array}$$

(1)

where $\mathit{q}$ is the phonon wave vector, while $m_j$ denotes the mass of the jth atom. IFC tensor between the jth atom in the initial cell “0” and the $j^{\prime }$ th atom in the nth cell is denoted by ${\Phi }_{\alpha \beta }(j0,j^{\prime }n)$, where $\alpha$ and $\beta$ describe directions (x, y, and z). The phonon spectrum can be found as an eigenvalue problem of the dynamical matrix:

$$\begin{array}{c}\hfill {\omega }_{ϵ\mathit{q}}^2{\mathrm{e}}_{ϵ\mathit{q}\alpha j}=\sum _{j^{\prime }\beta }{D}_{\alpha \beta }^{j{j}^{\prime }}\left(\mathit{q}\right){\mathrm{e}}_{ϵ\mathit{q}\beta j^{\prime }},\end{array}$$

(2)

where branch $ϵ$ for wave vector $\mathit{q}$ has polarization vector $\mathrm{e}\equiv {\mathrm{e}}_{ϵ\mathit{q}\alpha j}$. Moreover, each component of the polarization vector e contains information about the displacement of the jth atom in the $\alpha$ direction.

The phonon dispersion for YAlSi is presented in Figure 3. The system is stable in orthorhombic Cmcm symmetry (there are no imaginary soft modes). The phonon modes at the $\mathsf{\Gamma }$ point can be decomposed into the irreducible representations as follows:

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_{\mathrm{acoustic}}=& =& B_{1\mathrm{u}}+B_{2\mathrm{u}}+B_{3\mathrm{u}}\hfill \\ \hfill {\mathsf{\Gamma }}_{\mathrm{optic}}=& =& 2A_{\mathrm{g}}+A_{\mathrm{u}}+2B_{1\mathrm{g}}+3B_{1\mathrm{u}}+3B_{2\mathrm{u}}+2B_{3\mathrm{g}}+2B_{3\mathrm{u}}.\hfill \end{array}$$

(3)

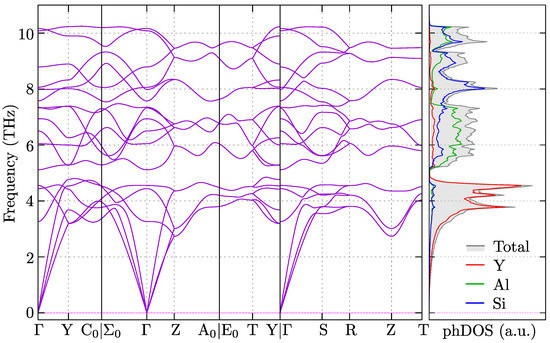
Figure 3. Phonon dispersion and the density of states for YAlSi with Cmcm symmetry.

Modes $3B_{1\mathrm{u}}+3B_{2\mathrm{u}}+2B_{3\mathrm{u}}$ are infrated active, while modes $2A_{\mathrm{g}}+2B_{1\mathrm{g}}+2B_{3\mathrm{g}}$ are Ramman active. As we can see, all optical modes are non-degenerate. The acoustic branches show linear dispersion around the $\mathsf{\Gamma }$ point.

Analysis of the phonon density of states (phDOS, right panel on Figure 3) uncovers the nature of the branches. First, the vibrations with low frequencies (below 5 THz) are realized mostly by the Y atoms. Next, the intermediate branches (from 5 THz to $7.5$ THz) are realized by Al atoms, while the Si atoms contribute to the higher frequency modes (from $7.5$ THz to 9 THz). Finally, modes above 9 THz are associated with vibrations shared between Al and Si atoms. Moreover, we can distinguish lower and upper bands separated by a gap located around 5 THz.

3.2. Chiral Phonons

The polarization vector e contains information about the vibrations of each $ϵ$ branch at the $\mathit{q}$ wave vector. Each e can be rewritten in terms of the circular polarization vectors. The ideal circular motion of an atom can be realized by two oscillators of equal magnitude, but oscillating with a phase difference of $\pm \pi /2$. In the case of a magnitude imbalance, elliptic motion was realized. Let us define the new basis: $|R_1⟩=\frac{1}{\sqrt{2}}\left(1i0\cdots \right)$; $|L_1⟩=\frac{1}{\sqrt{2}}\left(1-i0\cdots \right)$; $|Z_1⟩=\left(001\cdots \right)$; ⋯; $|R_j⟩=\frac{1}{\sqrt{2}}\left(\cdots 1i0\cdots \right)$; and $|L_j⟩=\frac{1}{\sqrt{2}}\left(\cdots 1-i0\cdots \right)$; $|Z_j⟩=\left(\cdots 001\cdots \right)$. In this case, we investigate the chiral modes realized in the $xy$ plane (perpendicular to $\mathit{c}$ direction). Our new basis denotes right-handed and left-handed circulation ($|R_j⟩$ and $|L_j⟩$, respectively) of the jth atom. Now, each each polarization vector e can be reexpressed in the form:

$$\begin{array}{c}\hfill \mathrm{e}=\sum _j\left({\alpha }_j^R|R_j⟩+{\alpha }_L^j|L_j⟩+{\alpha }_j^Z|Z_j⟩\right),\end{array}$$

(4)

where ${\alpha }_j^V=⟨V_j|\mathrm{e}⟩$, for $V\in \{R,L,Z\}$.

The operator for phonon circular polarization along the z-axis can be defined as:

$$\begin{array}{c}\hfill {\widehat{S}}^z\equiv \sum _{j=1}^N{s}_j^z=\sum _{j=1}^N\left(|R_j⟩⟨R_j|+|L_j⟩⟨L_j|\right),\end{array}$$

(5)

and the phonon circular polarization is equal to:

$$\begin{array}{c}\hfill s_{\mathrm{ph}}^z={\mathrm{e}}^{†}{\widehat{S}}^z\mathrm{e}=\sum _{j=1}^N{s}_j^z\hslash =\sum _{j=1}^N\left(|{\alpha }_j^R{|}^2-{\left|{\alpha }_j^L\right|}^2\right)\hslash ,\end{array}$$

(6)

with $|s_{\mathrm{ph}}^y|\le 1$, since ${\sum }_j\left(|{\alpha }_j^R{|}^2+{\left|{\alpha }_j^L\right|}^2\right)=1$. Here, we introduce $s_j^z$, which denotes the contribution of each atom to the phonon circular polarization. In the case of $|s_j^z|=1$, the jth atom realizes motion along an ideal circle around the equilibrium position; for $|s_j^z|=0$, ordinary vibrations are realized, and for $0<|s_j^z|<1$, elliptic orbits are realized.

In Figure 4, we present the results of our calculations. In particular, we show the phonon circular polarization from Y and Si atoms [Figure 4a,b, respectively], and the total phonon circular polarization of the system [Figure 4c]. As we can see, both atoms in the honeycomb-like sublattice realize the chiral phonon modes: Y atoms in the low frequency range [Figure 4a], and Si atoms in the high frequency range [Figure 4b]. Moreover, in both cases, the phonon circular polarization has a value smaller than the nominal one (i.e., $0<|s_i^z|<1$), which is related to the realization of vibrations along elliptic orbits. Additionally, for some path in the reciprocal space, the total phonon circular polarization was non-zero (e.g., along Z-A${}_0$|E${}_0$-T path). From this, YAlSi realizes the modes with non-zero total pseudo-angular momentum (PAM). This is possible due to the contribution of the triangular-like Al atom sublattice. For some wave vector $k$, atoms in the sublattice realize circular motions with the same polarization. This situation looks similar to the transition metal dichalcogenides, where circular motion of the chalcogenides with different phases but the same circular polarization allow realization of the chiral modes with non-zero PAM.

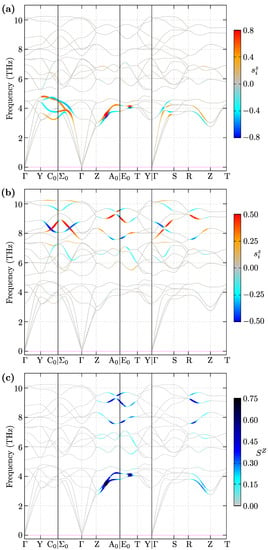
Figure 4. Phonon ciruclar polarization for (a) Y and (b) Si atoms. Panel (c) presents total phonon circular polarization of YAlSi with orthorhombic Cmcm symmetry.

4. Summary

In this paper, we investigate the ternary YAlSi compound, which crystallizes with orthorhombic Cmcm symmetry. In this structure, Y–Si pairs form honeycomb-like sublattice of the atoms with different masses. Our theoretical study based on the ab initio (DFT) study directly shows that the chiral phonons can be realized in YAlSi. Depending on the mode frequency, chiral modes were realized by either the Y or Si atom (in the range of low and high frequencies, respectively) in the vicinity of the $\mathsf{\Gamma }$ point. Realization of the chiral phonons in a system with orthorhombic symmetry and in absence of the three-fold rotational symmetry, opens up a new direction for experimental studies of these modes.