Ab Initio Study of Chiral Phonons in Ternary YAlSi Compound
Abstract
:1. Introduction
2. Methods
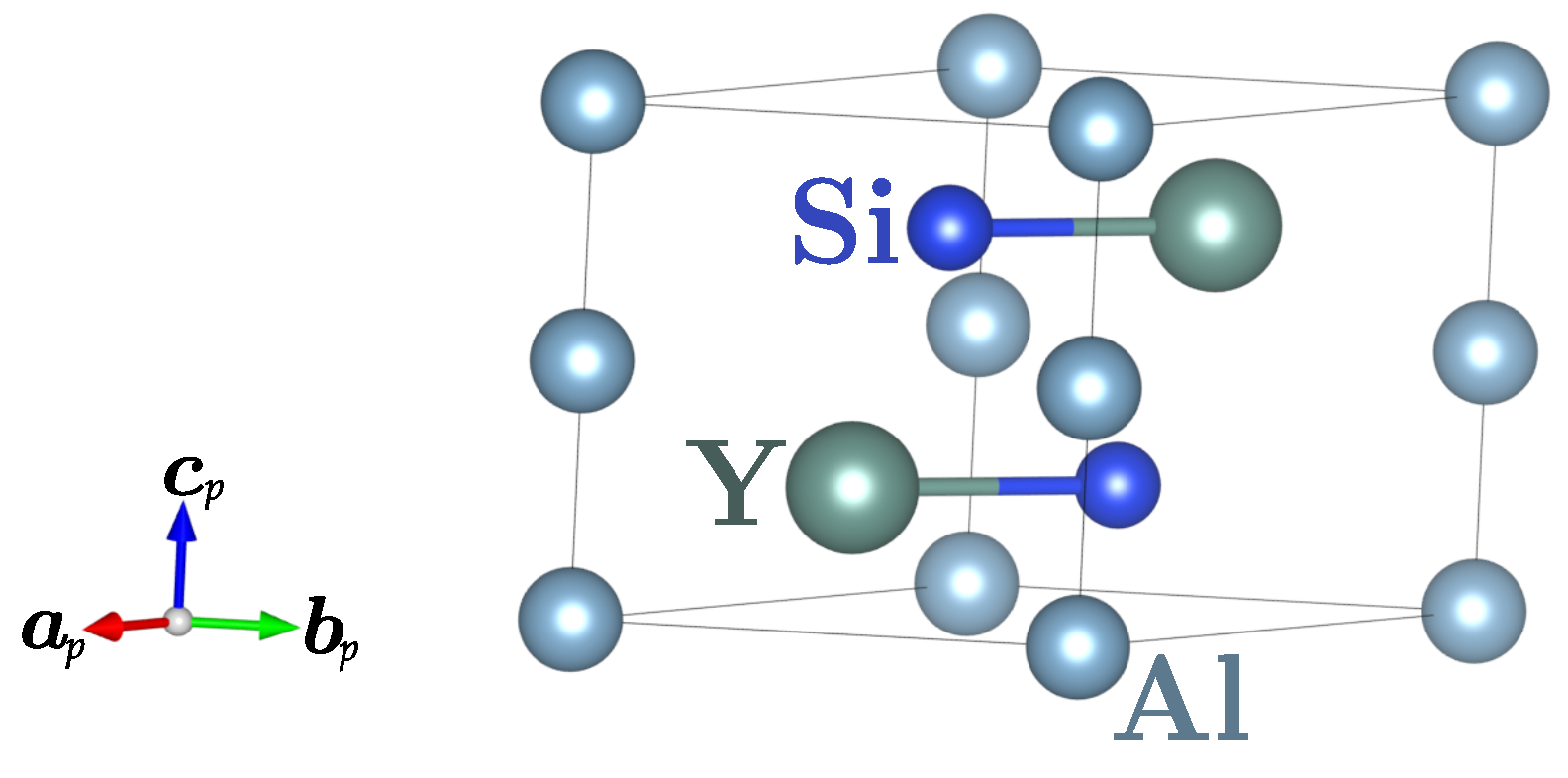
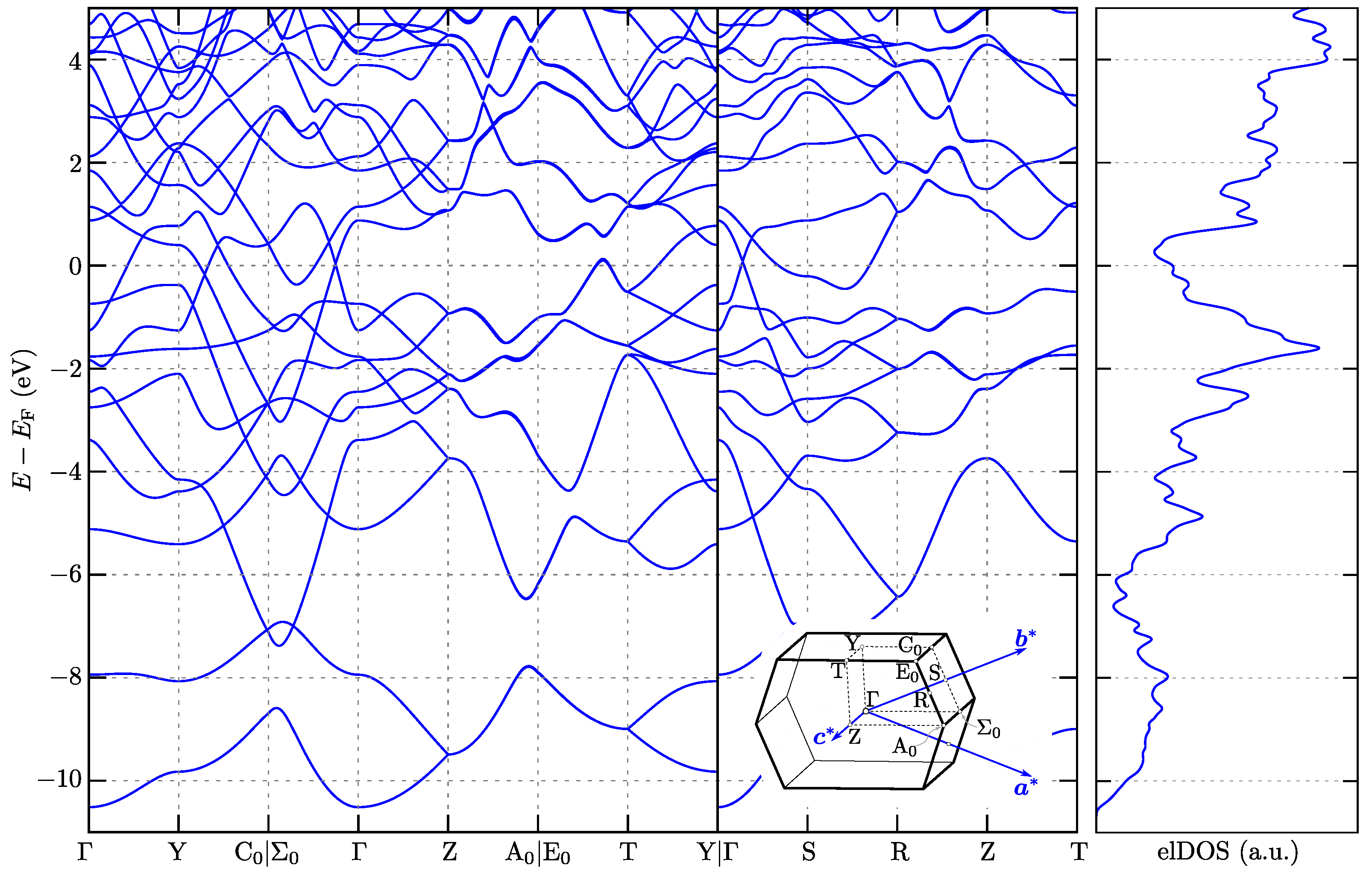
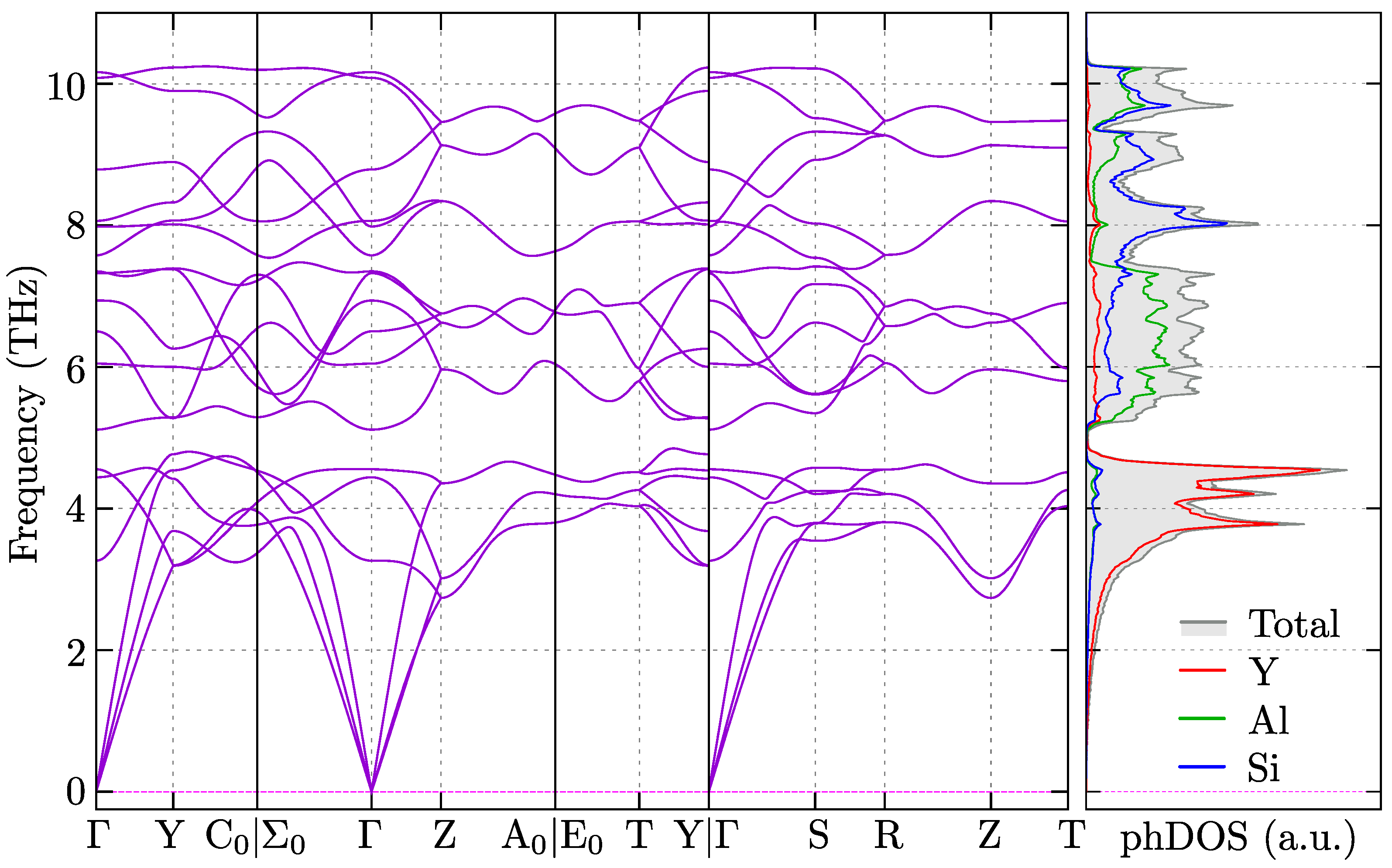
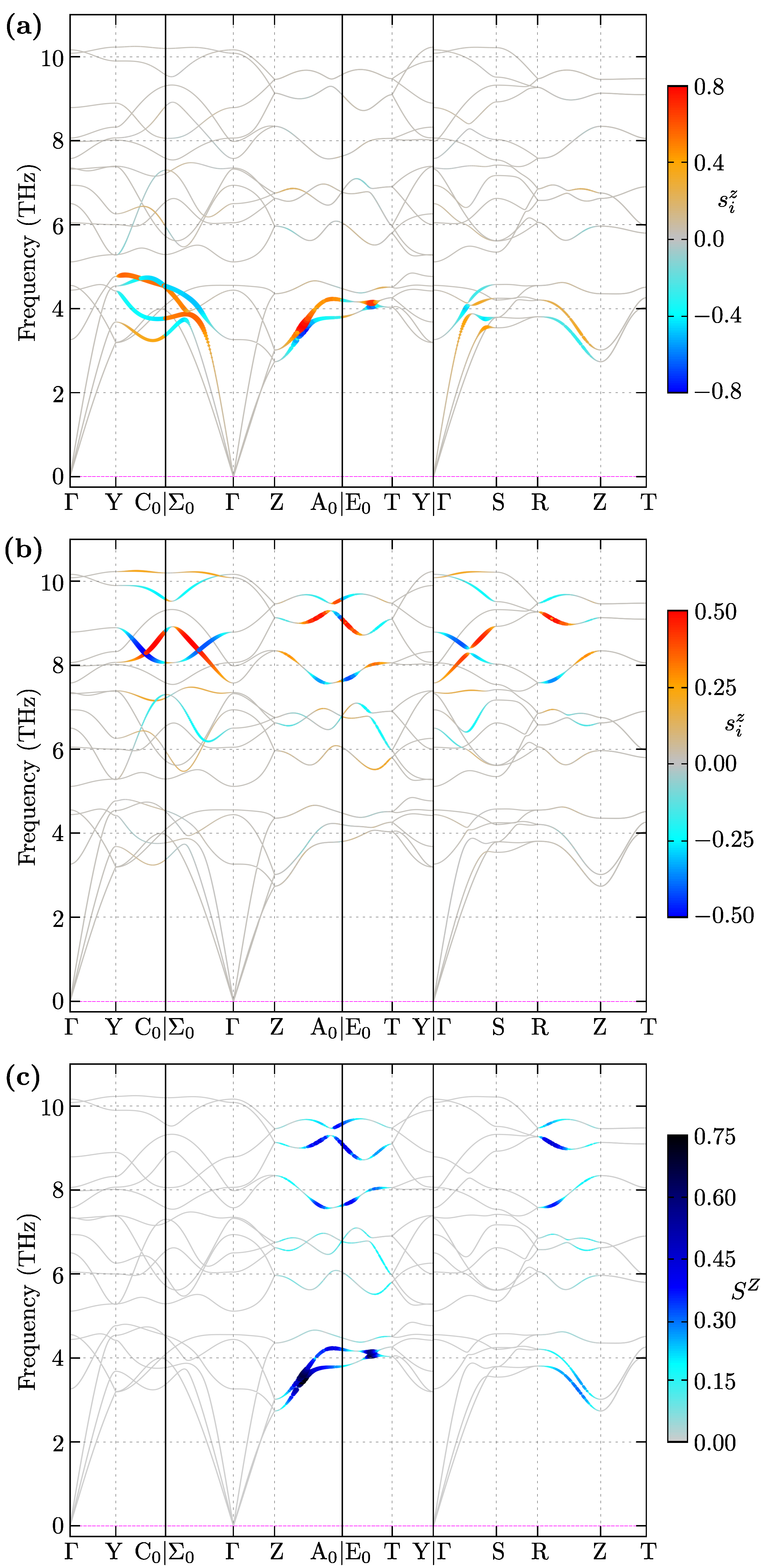
3. Results
3.1. Dynamical Properties
3.2. Chiral Phonons
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Coh, S. Classification of materials with phonon angular momentum and microscopic origin of angular momentum. arXiv 2019, arXiv:1911.05064. [Google Scholar]
- Zhang, L.; Niu, Q. Angular Momentum of Phonons and the Einstein–de Haas Effect. Phys. Rev. Lett. 2014, 112, 085503. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Ren, J.; Wang, J.S.; Li, B. Topological Nature of the Phonon Hall Effect. Phys. Rev. Lett. 2010, 105, 225901. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Niu, Q. Chiral Phonons at High-Symmetry Points in Monolayer Hexagonal Lattices. Phys. Rev. Lett. 2015, 115, 115502. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Lian, C.S.; Li, Y.; Xu, Y.; Duan, W. Pseudospins and Topological Effects of Phonons in a Kekulé Lattice. Phys. Rev. Lett. 2017, 119, 255901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, H.; Wu, W.; Yang, S.A.; Li, X.; Zhang, L. Chiral phonons in kagome lattices. Phys. Rev. B 2019, 100, 094303. [Google Scholar] [CrossRef]
- Zhang, W.; Srivastava, A.; Li, X.; Zhang, L. Chiral phonons in the indirect optical transition of a MoS2/WS2 heterostructure. Phys. Rev. B 2020, 102, 174301. [Google Scholar] [CrossRef]
- Juraschek, D.M.; Fechner, M.; Balatsky, A.V.; Spaldin, N.A. Dynamical multiferroicity. Phys. Rev. Mater. 2017, 1, 014401. [Google Scholar] [CrossRef]
- Juraschek, D.M.; Spaldin, N.A. Orbital magnetic moments of phonons. Phys. Rev. Mater. 2019, 3, 064405. [Google Scholar] [CrossRef] [Green Version]
- Kobiałka, A.; Sternik, M.; Ptok, A. Dynamical properties of magnetic topological insulator TBi2Te4 (T=Mn, Fe): Phonons dispersion, Raman active modes, and chiral phonons study. arXiv 2022, arXiv:2203.03337. [Google Scholar]
- Ptok, A.; Kobiałka, A.; Sternik, M.; Łażewski, J.; Jochym, P.T.; Oleś, A.M.; Stankov, S.; Piekarz, P. Chiral phonons in the honeycomb sublattice of layered CoSn-like compounds. Phys. Rev. B 2021, 104, 054305. [Google Scholar] [CrossRef]
- Skórka, J.; Kapcia, K.J.; Jochym, P.T.; Ptok, A. Chiral phonons in binary compounds ABi (A = K, Rb, Cs) with P21/c structure. arXiv 2022, arXiv:2203.05524. [Google Scholar]
- Chen, S.Y.; Zheng, C.; Fuhrer, M.S.; Yan, J. Helicity-Resolved Raman Scattering of MoS2, MoSe2, WS2, and WSe2 Atomic Layers. Nano Lett. 2015, 15, 2526–2532. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, H.; Yi, J.; Li, M.Y.; Xiao, J.; Zhang, L.; Yang, C.W.; Kaindl, R.A.; Li, L.J.; Wang, Y.; Zhang, X. Observation of chiral phonons. Science 2018, 359, 579. [Google Scholar] [CrossRef] [Green Version]
- Du, L.; Tang, J.; Zhao, Y.; Li, X.; Yang, R.; Hu, X.; Bai, X.; Wang, X.; Watanabe, K.; Taniguchi, T.; et al. Lattice Dynamics, Phonon Chirality, and Spin–Phonon Coupling in 2D Itinerant Ferromagnet Fe3GeTe2. Adv. Funct. Mater. 2019, 29, 1904734. [Google Scholar] [CrossRef] [Green Version]
- Cheng, B.; Schumann, T.; Wang, Y.; Zhang, X.; Barbalas, D.; Stemmer, S.; Armitage, N.P. A Large Effective Phonon Magnetic Moment in a Dirac Semimetal. Nano Lett. 2020, 20, 5991–5996. [Google Scholar] [CrossRef]
- Wang, Q.; Li, S.; Zhu, J.; Chen, H.; Wu, W.; Gao, W.; Zhang, L.; Yang, S.A. Chiral phonons in lattices with C4 symmetry. Phys. Rev. B 2022, 105, 104301. [Google Scholar] [CrossRef]
- Chen, H.; Wu, W.; Zhu, J.; Gong, W.; Gao, W.; Yang, S.A.; Zhang, L. Chiral Phonons in Chiral Materials. arXiv 2021, arXiv:2109.08872. [Google Scholar]
- Ishito, K.; Mao, H.; Kousaka, Y.; Togawa, Y.; Iwasaki, S.; Zhang, T.; Murakami, S.; Kishine, J.I.; Satoh, T. Truly chiral phonons in α-HgS observed by circularly polarised Raman spectroscopy. arXiv 2021, arXiv:2110.11604. [Google Scholar]
- Zhang, T.; Murakami, S. Chiral phonons and pseudoangular momentum in nonsymmorphic systems. Phys. Rev. Res. 2022, 4, L012024. [Google Scholar] [CrossRef]
- Rostami, H.; Guinea, F.; Cappelluti, E. Strain-driven chiral phonons in two-dimensional hexagonal materials. arXiv 2022, arXiv:2201.04909. [Google Scholar]
- Pukas, S.; Lutsyshyn, Y.; Manyako, M.; Gladyshevskii, E. Crystal structures of the RAlSi and RAlGe compounds. J. Alloy. Compd. 2004, 367, 162. [Google Scholar] [CrossRef]
- Wang, C.; Guo, Y.; Wang, T. Dynamic evolution from positive to negative magnetoresistance of RAlGe (R= Dy, Ho) with disordered orthorhombic structure. J. Alloy. Compd. 2022, 902, 163623. [Google Scholar] [CrossRef]
- Wang, C.; Guo, Y.Q.; Wang, T.; Yang, S.W. Crystal structure and electromagnetic responses of tetragonal GdAlGe. Chin. Phys. B 2020, 29, 127502. [Google Scholar] [CrossRef]
- Tobash, P.H.; Bobev, S. Synthesis, flux crystal growth, structure and properties of the new rare-earth compounds EuAl4-xSix (x∼1), TmAlSi and LuAlSi. J. Alloy. Compd. 2006, 418, 58. [Google Scholar] [CrossRef]
- Bobev, S.; Tobash, P.H.; Fritsch, V.; Thompson, J.D.; Hundley, M.F.; Sarrao, J.L.; Fisk, Z. Ternary rare-earth alumo-silicides—single-crystal growth from Al flux, structural and physical properties. J. Solid State Chem. 2005, 178, 2091. [Google Scholar] [CrossRef] [Green Version]
- He, W.; Zhang, J.; Zeng, L. New structure of the ternary compound DyAlSi. J. Alloy. Compd. 2006, 424, 105. [Google Scholar] [CrossRef]
- Puphal, P.; Mielke, C.; Kumar, N.; Soh, Y.; Shang, T.; Medarde, M.; White, J.S.; Pomjakushina, E. Bulk single-crystal growth of the theoretically predicted magnetic Weyl semimetals RAlGe (R = Pr, Ce). Phys. Rev. Mater. 2019, 3, 024204. [Google Scholar] [CrossRef] [Green Version]
- Hodovanets, H.; Eckberg, C.J.; Zavalij, P.Y.; Kim, H.; Lin, W.C.; Zic, M.; Campbell, D.J.; Higgins, J.S.; Paglione, J. Single-crystal investigation of the proposed type-II Weyl semimetal CeAlGe. Phys. Rev. B 2018, 98, 245132. [Google Scholar] [CrossRef] [Green Version]
- Dhar, S.; Pattalwar, S. Structural and magnetic properties of CeAlxSi2-x and CeAlxGe2-x alloys. J. Magn. Magn. Mater. 1996, 152, 22. [Google Scholar] [CrossRef]
- Wang, C.; Guo, Y.; Wang, T. Magnetic and transport properties of orthorhombic rare-earth aluminum germanide GdAlGe. J. Magn. Magn. Mater. 2021, 526, 167739. [Google Scholar] [CrossRef]
- Zhao, J.T.; Parthé, E. Structure of YAlGe and isotypic rare-earth–aluminium germanides. Acta Crystallogr. C 1990, 46, 2276. [Google Scholar] [CrossRef]
- Ng, T.; Luo, Y.; Yuan, J.; Wu, Y.; Yang, H.; Shen, L. Origin and enhancement of the spin Hall angle in the Weyl semimetals LaAlSi and LaAlGe. Phys. Rev. B 2021, 104, 014412. [Google Scholar] [CrossRef]
- Su, H.; Shi, X.; Yuan, J.; Wan, Y.; Cheng, E.; Xi, C.; Pi, L.; Wang, X.; Zou, Z.; Yu, N.; et al. Multiple Weyl fermions in the noncentrosymmetric semimetal LaAlSi. Phys. Rev. B 2021, 103, 165128. [Google Scholar] [CrossRef]
- Xu, S.Y.; Alidoust, N.; Chang, G.; Lu, H.; Singh, B.; Belopolski, I.; Sanchez, D.S.; Zhang, X.; Bian, G.; Zheng, H.; et al. Discovery of Lorentz-violating type II Weyl fermions in LaAlGe. Sci. Adv. 2017, 3, e1603266. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piva, M.M.; Souza, J.C.; Brousseau-Couture, V.; Pakuszewski, K.R.; John, J.K.; Adriano, C.; Côté, M.; Pagliuso, P.G.; Nicklas, M. Tuning the nontrivial topological properties of the Weyl semimetal CeAlSi. arXiv 2021, arXiv:2111.05742. [Google Scholar]
- Puphal, P.; Pomjakushin, V.; Kanazawa, N.; Ukleev, V.; Gawryluk, D.J.; Ma, J.; Naamneh, M.; Plumb, N.C.; Keller, L.; Cubitt, R.; et al. Topological Magnetic Phase in the Candidate Weyl Semimetal CeAlGe. Phys. Rev. Lett. 2020, 124, 017202. [Google Scholar] [CrossRef] [Green Version]
- Destraz, D.; Das, L.; Tsirkin, S.S.; Xu, Y.; Neupert, T.; Chang, J.; Schilling, A.; Grushin, A.G.; Kohlbrecher, J.; Keller, L.; et al. Magnetism and anomalous transport in the Weyl semimetal PrAlGe: Possible route to axial gauge fields. Npj Quantum Mater. 2020, 5, 5. [Google Scholar] [CrossRef]
- Liu, W.; Zhao, J.; Meng, F.; Rahman, A.; Qin, Y.; Fan, J.; Pi, L.; Tian, Z.; Du, H.; Zhang, L.; et al. Critical behavior of the magnetic Weyl semimetal PrAlGe. Phys. Rev. B 2021, 103, 214401. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef] [Green Version]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Stokes, H.T.; Hatch, D.M. FindSym: Program for identifying the space-group symmetry of a crystal. J. Appl. Cryst. 2005, 38, 237. [Google Scholar] [CrossRef] [Green Version]
- Togo, A.; Tanaka, I. SpgLib: A software library for crystal symmetry search. arXiv 2018, arXiv:1808.01590. [Google Scholar]
- Hinuma, Y.; Pizzi, G.; Kumagai, Y.; Oba, F.; Tanaka, I. Band structure diagram paths based on crystallography. Comput. Mater. Sci. 2017, 128, 140. [Google Scholar] [CrossRef] [Green Version]
- Parlinski, K.; Li, Z.Q.; Kawazoe, Y. First-Principles Determination of the Soft Mode in Cubic ZrO2. Phys. Rev. Lett. 1997, 78, 4063. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1. [Google Scholar] [CrossRef] [Green Version]
- Tadano, T.; Gohda, Y.; Tsuneyuki, S. Anharmonic force constants extracted from first-principles molecular dynamics: Applications to heat transfer simulations. J. Phys. Condens. Matter 2014, 26, 225402. [Google Scholar] [CrossRef] [PubMed]
- Tadano, T.; Tsuneyuki, S. First-Principles Lattice Dynamics Method for Strongly Anharmonic Crystals. J. Phys. Soc. Jpn. 2018, 87, 041015. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. vesta3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basak, S.; Ptok, A. Ab Initio Study of Chiral Phonons in Ternary YAlSi Compound. Crystals 2022, 12, 436. https://doi.org/10.3390/cryst12030436
Basak S, Ptok A. Ab Initio Study of Chiral Phonons in Ternary YAlSi Compound. Crystals. 2022; 12(3):436. https://doi.org/10.3390/cryst12030436
Chicago/Turabian StyleBasak, Surajit, and Andrzej Ptok. 2022. "Ab Initio Study of Chiral Phonons in Ternary YAlSi Compound" Crystals 12, no. 3: 436. https://doi.org/10.3390/cryst12030436
APA StyleBasak, S., & Ptok, A. (2022). Ab Initio Study of Chiral Phonons in Ternary YAlSi Compound. Crystals, 12(3), 436. https://doi.org/10.3390/cryst12030436





