Between Harmonic Crystal and Glass: Solids with Dimpled Potential-Energy Surfaces Having Multiple Local Energy Minima
Abstract
:1. Introduction
2. Models with Dimpled Potentials
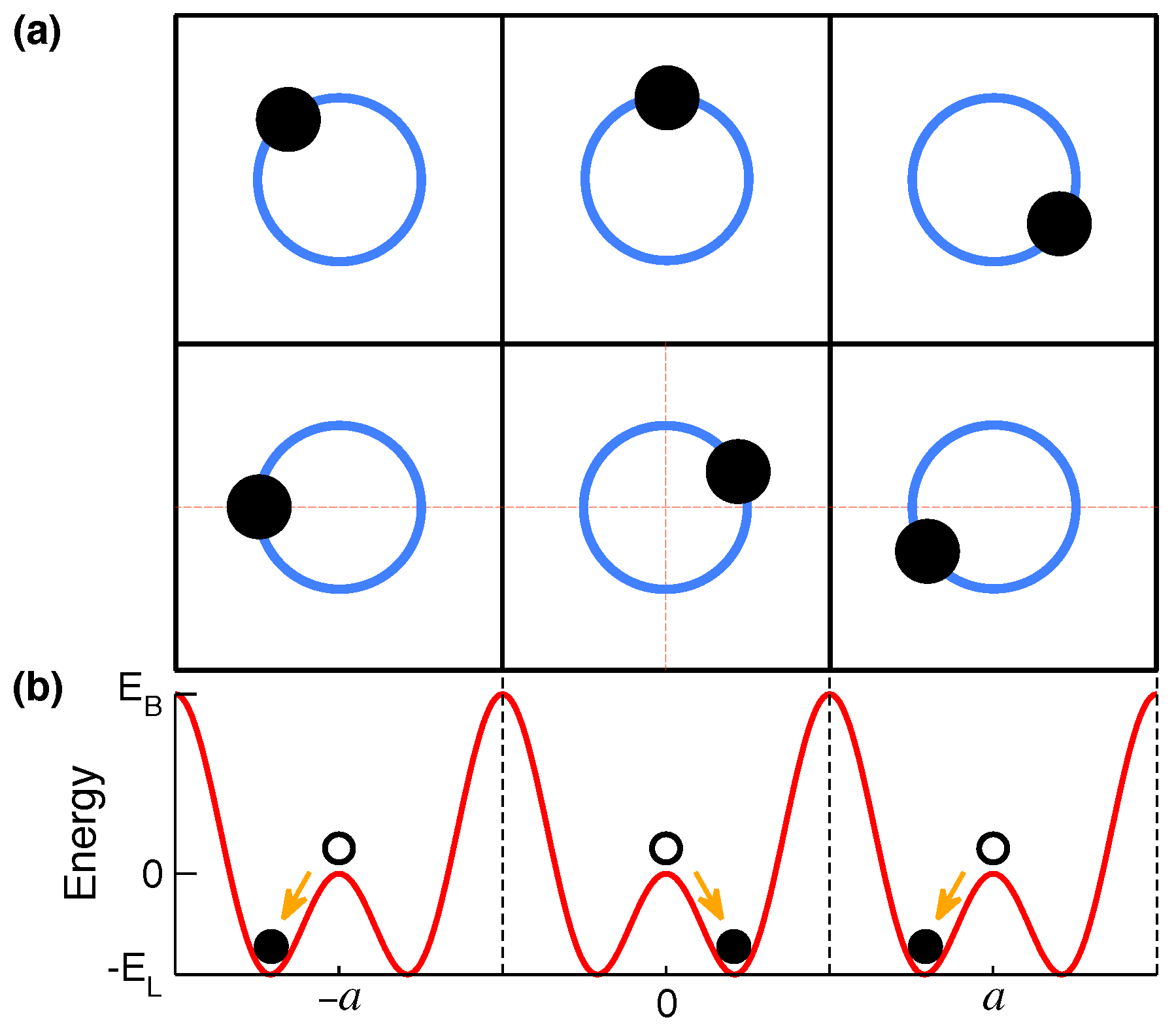
2.1. Networks of LPEM in MLM Solids
2.2. Symmetry-Breaking Phase Transition
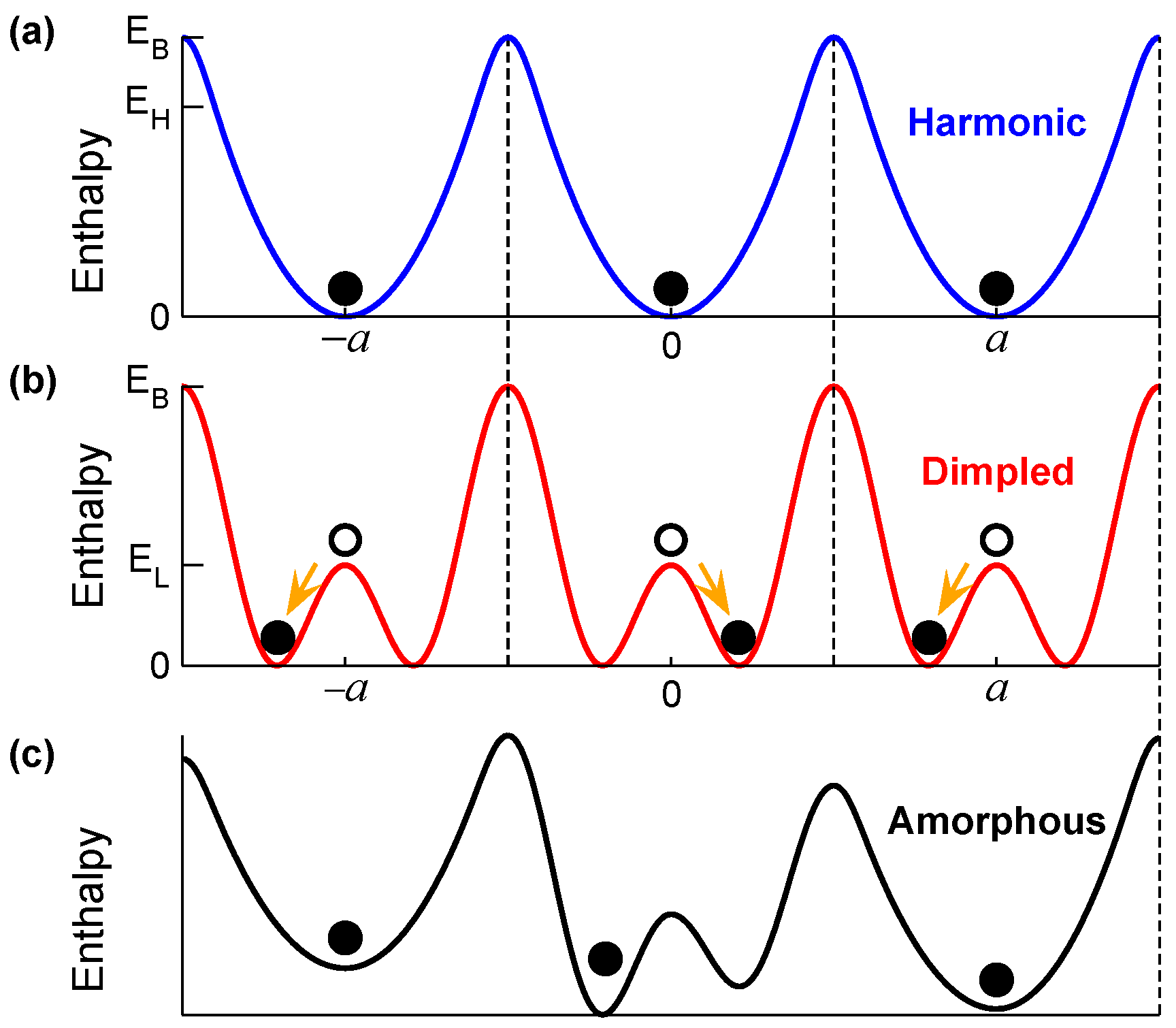
2.3. Expected Thermal Atomic Motion
- : harmonic vibration around a single LPEM. The small-displacement method can provide phonons at a LPEM (see Appendix B).
- : anharmonic vibration around a single LPEM.
- : motion covers several LPEMs in the same basin. If such LPEMs are distributed symmetrically around , then the time-averaged atomic position is .
- : motion covers a significant part of the PE basin, including neighborhoods of and multiple LPEMs. If the PE surface has a negligible roughness () at the bottom of a nearly harmonic potential, then a finite atomic displacement method can be used to calculate phonons around , see Appendix B.
- : atomic motion is no longer restricted by a PE basin; the solid has melted or sublimated.
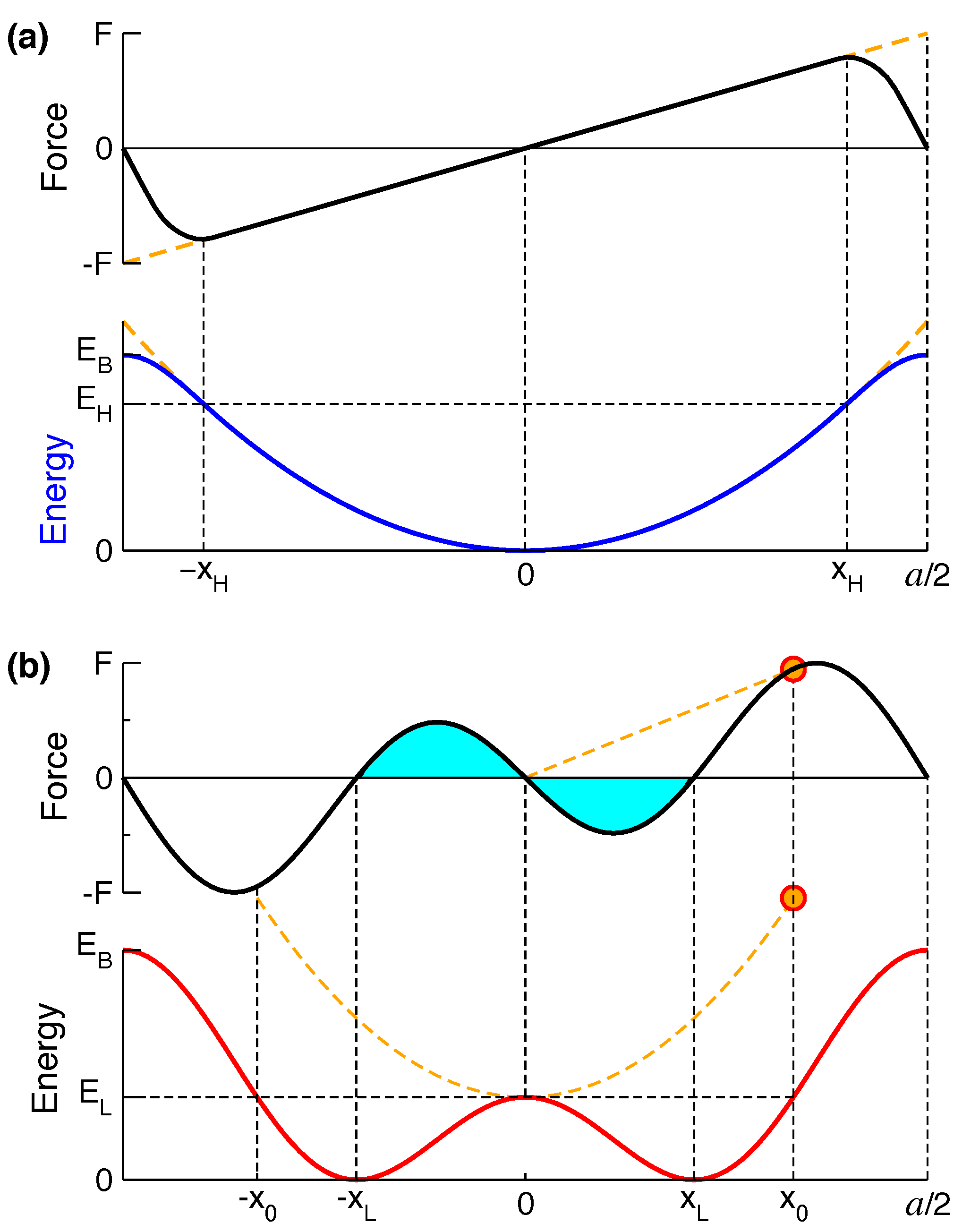
2.4. Atomic Forces in MLM Solids
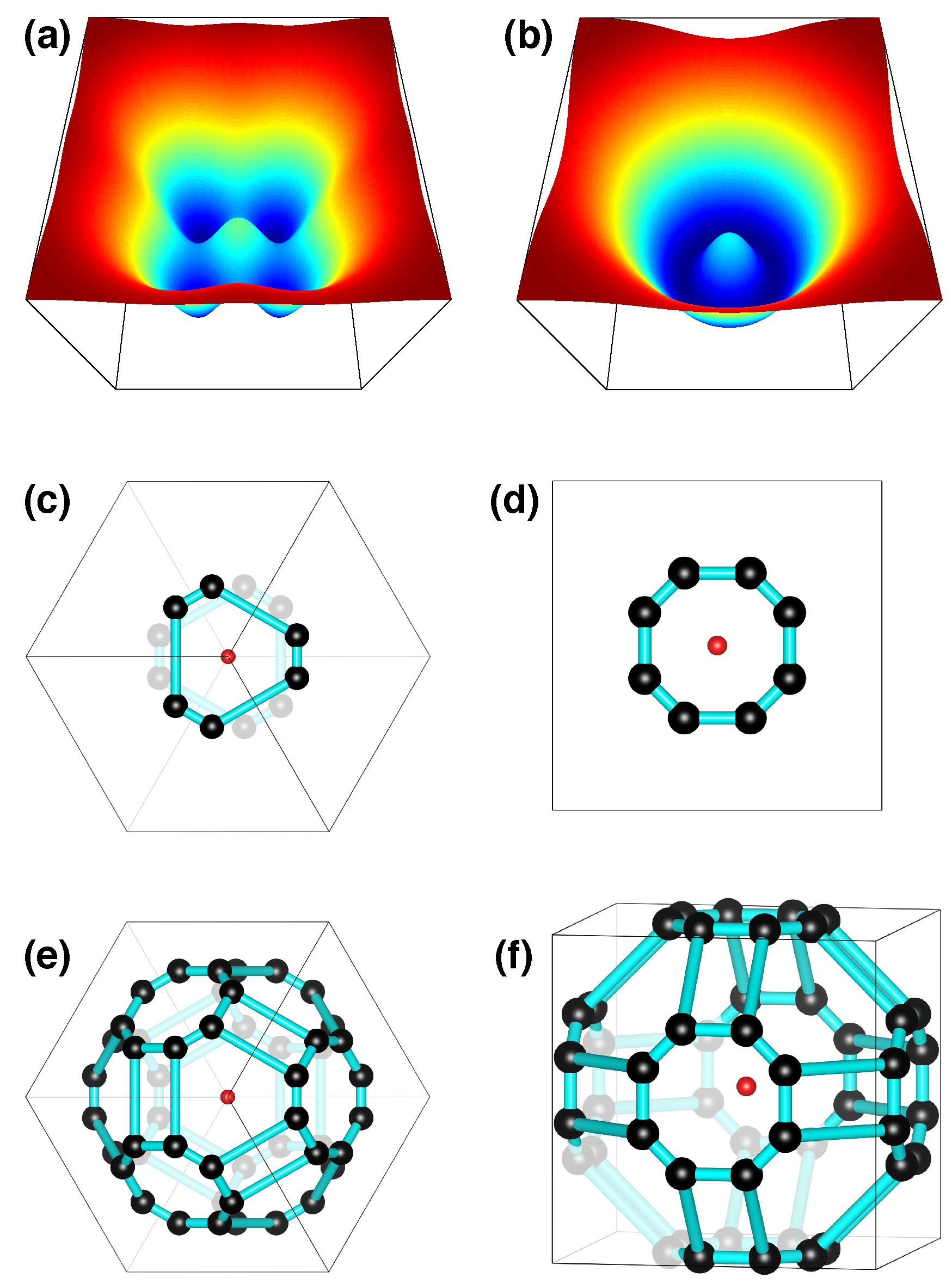
2.5. Examples for Corrugated-Sombrero Potentials
2.6. Diffraction from MLM Solids
3. Example Applications
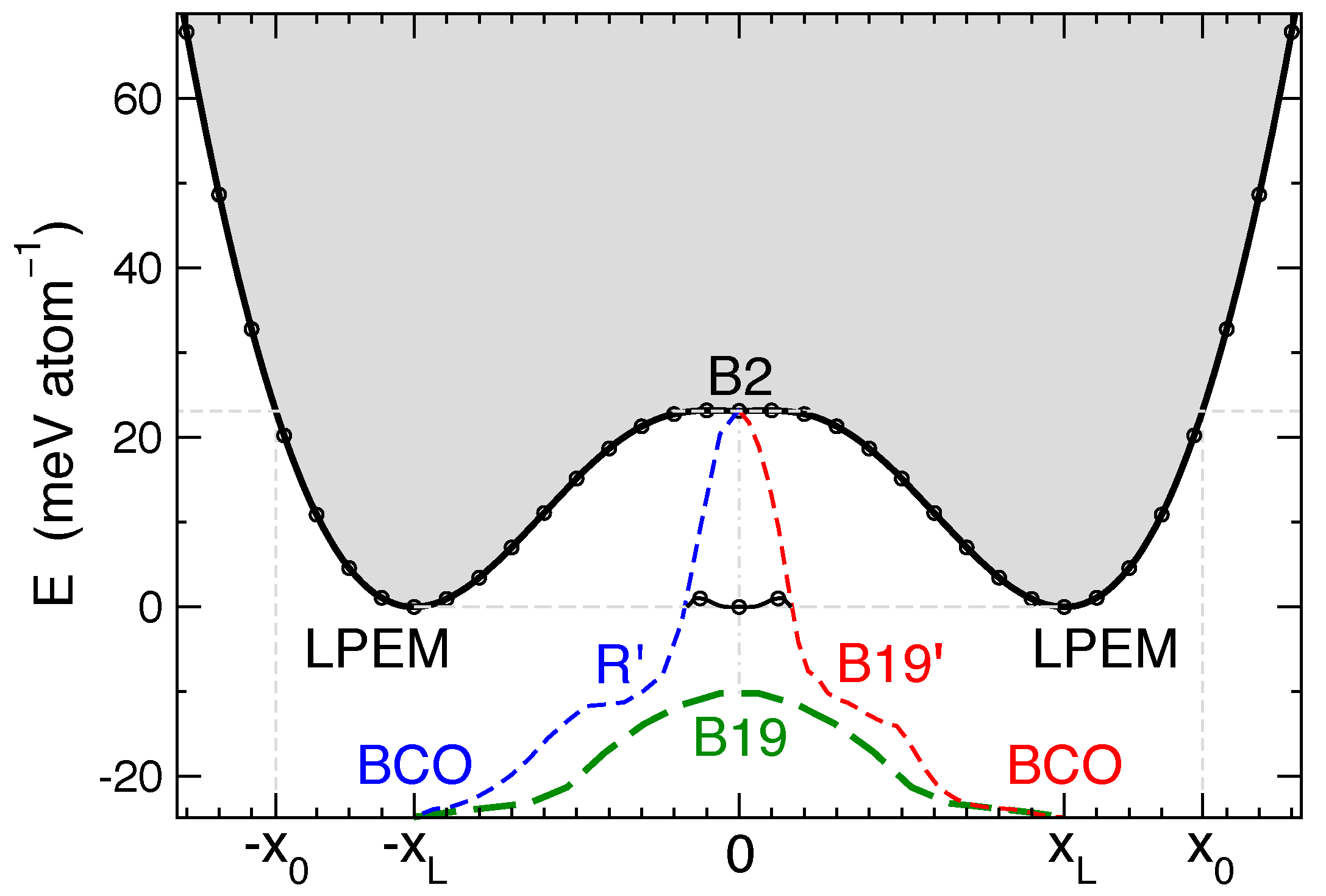
3.1. NiTi Austenite
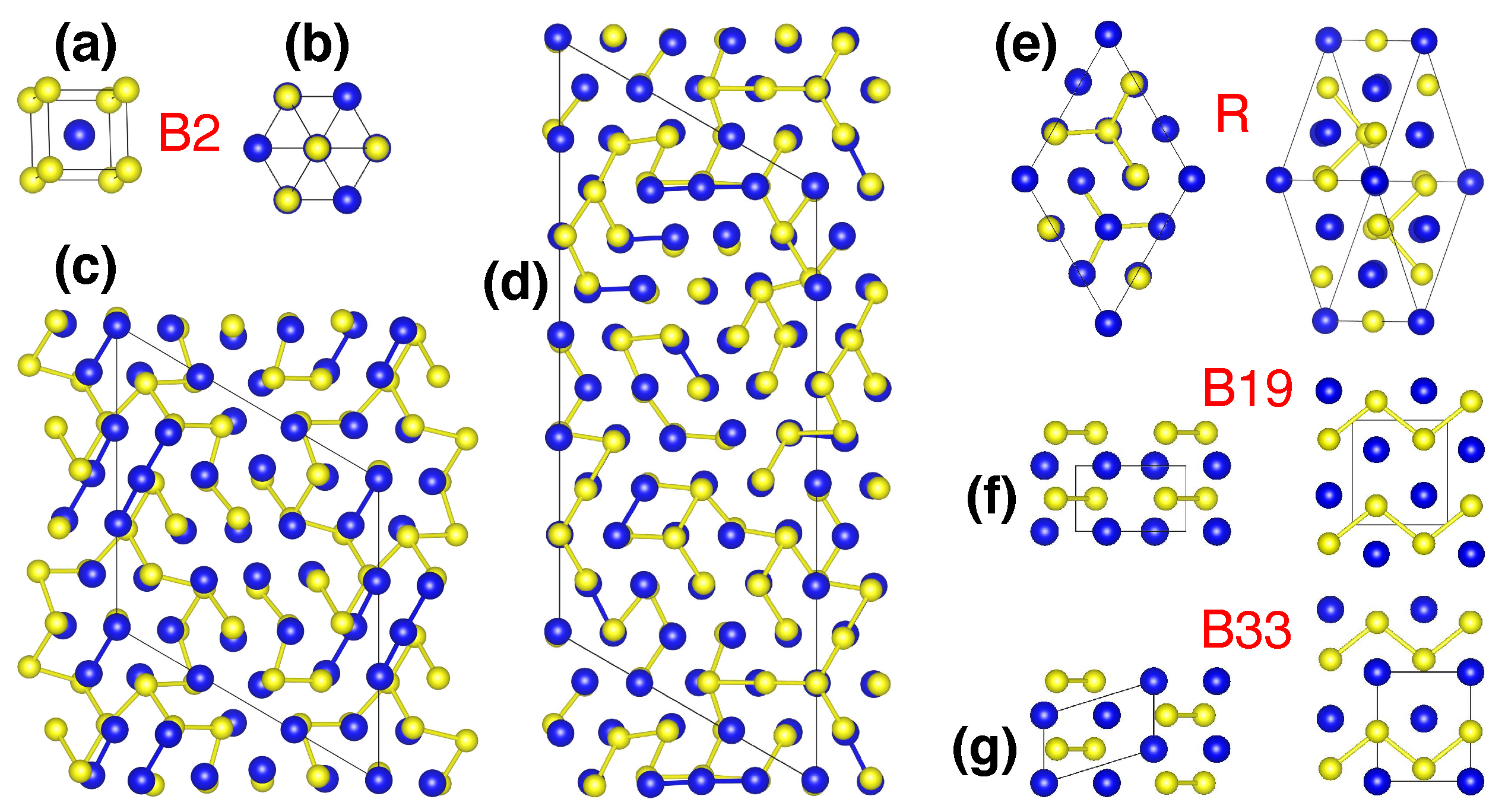

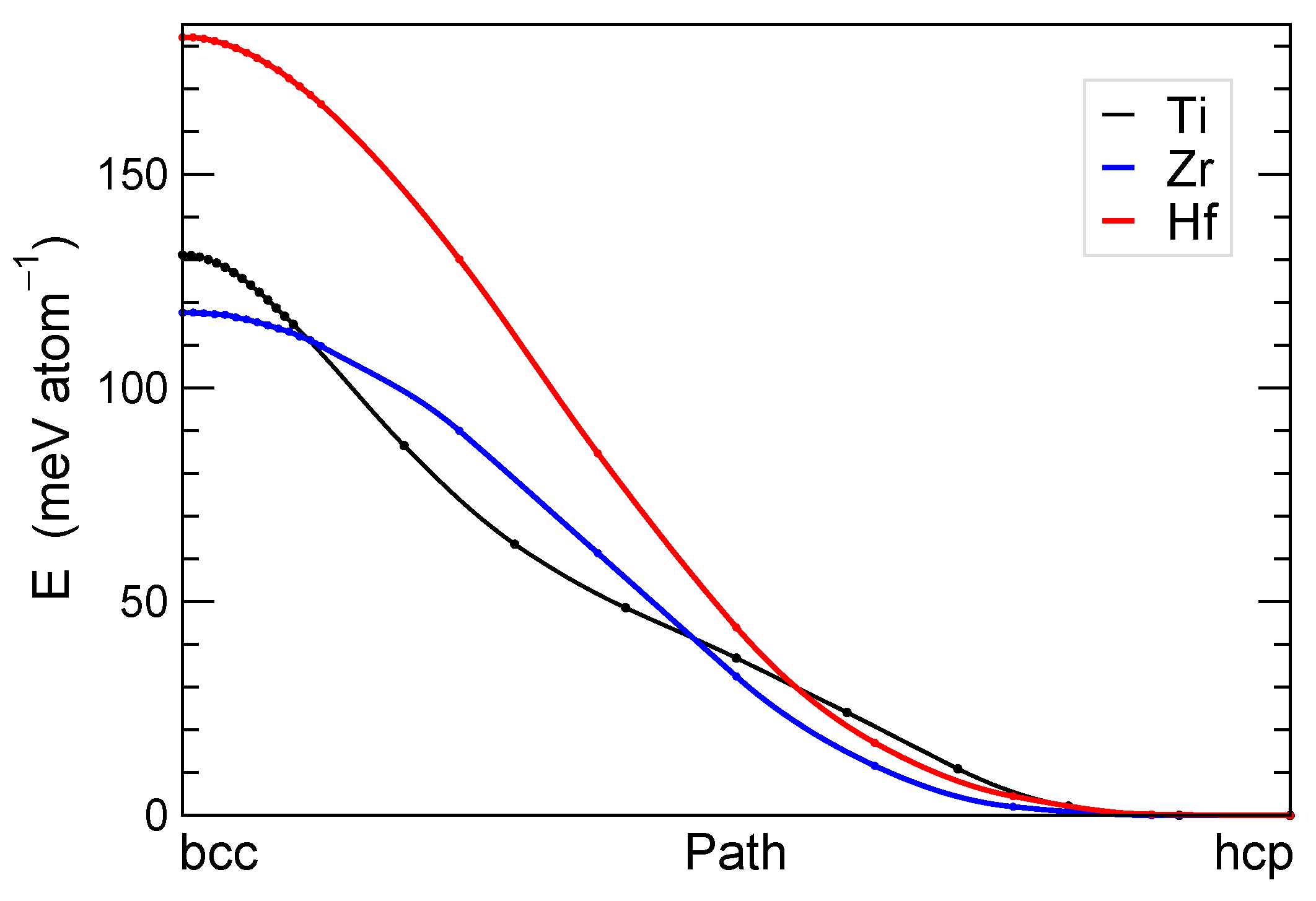
3.2. Group 4 Metals: Ti, Zr, and Hf
3.3. 1T-TaS2 Layered Crystal
3.4. Ubiquity
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NASA | National Aeronautics and Space Administration |
| DOE | U.S. Department of Energy |
| USA | United States of America |
| BCO | base-centered orthorhombic |
| bcc | body-centered cubic |
| hcp | hexagonal close-packed |
| CDW | charge-density wave |
| DOS | density of states |
| LPEM | local potential-energy minimum |
| MLM | multiple local minima |
| MD | molecular dynamics |
| MEP | minimal-enthalpy path |
| NEB | nudged elastic band |
| PE | potential energy |
| QHA | quasiharmonic approximation |
| T | temperature |
Appendix A. Computational Details
Appendix B. Phonon Calculations
Appendix B.1. Small-Displacement Method
Appendix B.2. Finite-Displacement Method
Appendix B.3. Phonons at Fixed Temperature
References
- Zarkevich, N.A. Theoretical and computational methods for accelerated materials discovery. Mod. Phys. Lett. B 2021, 35, 2130003. [Google Scholar] [CrossRef]
- Grimvall, G.; Magyari-Köpe, B.; Ozolins, V.; Persson, K. Lattice instabilities in metallic elements. Rev. Mod. Phys. 2012, 84, 945–986. [Google Scholar] [CrossRef] [Green Version]
- Jonsson, H.; Mills, G.; Jacobsen, K.W. Nudged Elastic Band Method for Finding Minimum Energy Paths of Transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne, B.J., Ciccotti, G., Coker, D.F., Eds.; World Scientific: Singapore, 1998. [Google Scholar]
- Sheppard, D.; Xiao, P.H.; Chemelewski, W.; Johnson, D.D.; Henkelman, G. A generalized solid-state nudged elastic band method. J. Chem. Phys. 2012, 136, 074103. [Google Scholar] [CrossRef] [PubMed]
- Zarkevich, N.A.; Johnson, D.D. Nudged-elastic band method with two climbing images: Finding transition states in complex energy landscapes. J. Chem. Phys. 2015, 142, 024106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Born, M. On the stability of crystal lattices. I. Math. Proc. Camb. Philos. Soc. 1940, 36, 160–172. [Google Scholar] [CrossRef]
- Karplus, M.; Kushick, J.N. Method for estimating the configurational entropy of macromolecules. Macromolecules 1981, 14, 325–332. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Johnson, D.D. Shape-Memory Transformations of NiTi: Minimum-Energy Pathways between Austenite, Martensites, and Kinetically Limited Intermediate States. Phys. Rev. Lett. 2014, 113, 265701. [Google Scholar] [CrossRef] [PubMed]
- Zarkevich, N.A.; Chen, H.; Levitas, V.I.; Johnson, D.D. Lattice Instability during Solid-Solid Structural Transformations under a General Applied Stress Tensor: Example of Si I→Si II with Metallization. Phys. Rev. Lett. 2018, 121, 165701. [Google Scholar] [CrossRef] [Green Version]
- Frenkel, A.; Stern, E.A.; Voronel, A.; Qian, M.; Newville, M. Buckled crystalline structure of mixed ionic salts. Phys. Rev. Lett. 1993, 71, 3485–3488. [Google Scholar] [CrossRef]
- Sluchanko, N.; Bogach, A.; Bolotina, N.; Glushkov, V.; Demishev, S.; Dudka, A.; Krasnorussky, V.; Khrykina, O.; Krasikov, K.; Mironov, V.; et al. Rattling mode and symmetry lowering resulting from the instability of the B12 molecule in LuB12. Phys. Rev. B 2018, 97, 035150. [Google Scholar] [CrossRef] [Green Version]
- Haskins, J.B.; Lawson, J.W. Finite temperature properties of NiTi from first principles simulations: Structure, mechanics, and thermodynamics. J. Appl. Phys. 2017, 121, 205103. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Johnson, D.D.; Pecharsky, V.K. High-throughput search for caloric materials: The CaloriCool approach. J. Phys. D Appl. Phys. 2018, 51, 024002. [Google Scholar] [CrossRef] [Green Version]
- Zarkevich, N.A.; Zverev, V.I. Viable Materials with a Giant Magnetocaloric Effect. Crystals 2020, 10, 815. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Johnson, D.D. FeRh ground state and martensitic transformation. Phys. Rev. B 2018, 97, 014202. [Google Scholar] [CrossRef] [Green Version]
- Zarkevich, N.A.; Johnson, D.D. Reliable thermodynamic estimators for screening caloric materials. J. Alloys Compd. 2019, 802, 712–722. [Google Scholar] [CrossRef] [Green Version]
- Fultz, B. Vibrational thermodynamics of materials. Prog. Mater. Sci. 2010, 55, 247–352. [Google Scholar] [CrossRef] [Green Version]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; Wiley: Hoboken, NJ, USA, 2004; ISBN 9780471415268. [Google Scholar]
- Souvatzis, P.; Eriksson, O.; Katsnelson, M.I.; Rudin, S.P. Entropy Driven Stabilization of Energetically Unstable Crystal Structures Explained from First Principles Theory. Phys. Rev. Lett. 2008, 100, 095901. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Johnson, D.D. Stable atomic structure of NiTi austenite. Phys. Rev. B 2014, 90, 060102. [Google Scholar] [CrossRef] [Green Version]
- Smith, T.M.; Zarkevich, N.A.; Egan, A.J.; Stuckner, J.; Gabb, T.P.; Lawson, J.W.; Mills, M.J. Utilizing local phase transformation strengthening for nickel-base superalloys. Commun. Mater. 2021, 2, 106. [Google Scholar] [CrossRef]
- Fisher, E.S.; Renken, C.J. Single-Crystal Elastic Moduli and the hcp-bcc Transformation in Ti, Zr, and Hf. Phys. Rev. 1964, 135, A482–A494. [Google Scholar] [CrossRef]
- Petry, W. Phonons at martensitic phase transitions of bcc-Ti, bcc-Zr and bcc-Hf. Phase Transit. 1991, 31, 119–136. [Google Scholar] [CrossRef]
- Gooding, R.J.; Krumhansl, J.A. Theory of the bcc-to-9R structural phase transformation of Li. Phys. Rev. B 1988, 38, 1695–1704. [Google Scholar] [CrossRef]
- Mahan, G.D. Crystal. In Encyclopedia Britannica; Encyclopædia Britannica: Chicago, IL, USA, 2021; (published online 26 July 1999; revised 5 March 2021); Available online: https://www.britannica.com/science/crystal (accessed on 9 December 2021).
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College: Philadelphia, PA, USA, 1976. [Google Scholar]
- Bragg, W.H.; Bragg, W.L. The Reflection of X-rays by Crystals. Proc. R. Soc. Lond. A 1913, 88, 428–438. [Google Scholar] [CrossRef]
- Overhauser, A.W. Crystal Structure of Lithium at 4.2 K. Phys. Rev. Lett. 1984, 53, 64–65. [Google Scholar] [CrossRef]
- Petry, W.; Heiming, A.; Trampenau, J.; Alba, M.; Herzig, C.; Schober, H.R.; Vogl, G. Phonon dispersion of the bcc phase of group-IV metals. I. bcc titanium. Phys. Rev. B 1991, 43, 10933–10947. [Google Scholar] [CrossRef]
- Prokoshkin, S.; Korotitskiy, A.; Brailovski, V.; Turenne, S.; Khmelevskaya, I.; Trubitsyna, I. On the lattice parameters of phases in binary Ti-Ni shape memory alloys. Acta Mater. 2004, 52, 4479–4492. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Besnard, C.; Kunčická, L.; Kocich, R.; Korsunsky, A.M. In situ neutron diffraction investigation of texture-dependent Shape Memory Effect in a near equiatomic NiTi alloy. Acta Mater. 2021, 202, 135–148. [Google Scholar] [CrossRef]
- Moine, P.; Allain, J.; Renker, B. Observation of a soft-phonon mode and a pre-martensitic phase in the intermetallic compound Ti50Ni47Fe3 studied by inelastic neutron scattering. J. Phys. F Met. Phys. 1984, 14, 2517–2523. [Google Scholar] [CrossRef]
- Mercier, O.; Melton, K.N.; Gremaud, G.; Hägi, J. Single-crystal elastic constants of the equiatomic NiTi alloy near the martensitic transformation. J. Appl. Phys. 1980, 51, 1833–1834. [Google Scholar] [CrossRef]
- Ren, X.; Miura, N.; Zhang, J.; Otsuka, K.; Tanaka, K.; Koiwa, M.; Suzuki, T.; Chumlyakov, Y.; Asai, M. A comparative study of elastic constants of Ti-Ni-based alloys prior to martensitic transformation. Mater. Sci. Eng. A 2001, 312, 196–206. [Google Scholar] [CrossRef]
- Sedlák, P.; Janovská, M.; Bodnárová, L.; Heczko, O.; Seiner, H. Softening of Shear Elastic Coefficients in Shape Memory Alloys Near the Martensitic Transition: A Study by Laser-Based Resonant Ultrasound Spectroscopy. Metals 2020, 10, 1383. [Google Scholar] [CrossRef]
- Bradley, D. Sound Propagation in Near-Stoichiometric Ti-Ni Alloys. J. Acoust. Soc. Am. 1965, 37, 700–702. [Google Scholar] [CrossRef]
- Hasiguti, R.R.; Iwasaki, K. Internal Friction and Related Properties of the TiNi Intermetallic Compound. J. Appl. Phys. 1968, 39, 2182–2186. [Google Scholar] [CrossRef]
- Sandrock, G.D. Premartensitic behavior of the electrical resistivity of NiTi. Metall. Mater. Trans. B 1974, 5, 299. [Google Scholar] [CrossRef]
- Araki, H.; Matake, N.; Chalermkarnnon, P.; Shirai, Y. Pre-Martensitic Phenomenon in NiTi Studied by Positron Lifetime Spectroscopy. Mater. Sci. Forum 2000, 327–328, 437–440. [Google Scholar] [CrossRef]
- Sandrock, G.D.; Perkins, A.J.; Hehemann, R.F. The premartensitic instability in near-equiatomic TiNi. Metall. Trans. 1971, 2, 2769–2781. [Google Scholar] [CrossRef]
- Moine, P.; Michal, G.; Sinclair, R. A morphological study of “Premartensitic” effects in TiNi. Acta Metall. 1982, 30, 109–123. [Google Scholar] [CrossRef]
- Michal, G.; Moine, P.; Sinclair, R. Characterization of the lattice displacement waves in premartensitic TiNi. Acta Metall. 1982, 30, 125–138. [Google Scholar] [CrossRef]
- Haskins, J.B.; Malmir, H.; Honrao, S.J.; Sandoval, L.A.; Lawson, J.W. Low-Temperature Mechanical Instabilities Govern High-Temperature Thermodynamics in the Austenite Phase of Shape Memory Alloy Constituents: Ab Initio Simulations of NiTi, NiZr, NiHf, PdTi, and PtTi. Acta Mater. 2021, 212, 116872. [Google Scholar] [CrossRef]
- Bogdanoff, P.D.; Fultz, B. The role of phonons in the thermodynamics of the martensitic transformation in NiTi. Philos. Mag. B 2001, 81, 299. [Google Scholar] [CrossRef]
- Ling, H.C.; Roy, K. Stress-Induced Shape Changes and Shape Memory in the R and Martensite Transformations in Equiatomic NiTi. Metall. Trans. A 1981, 12, 2101–2111. [Google Scholar] [CrossRef]
- Zarkevich, N.A. ThermoPhonon. 2014. Available online: http://lib.dr.iastate.edu/ameslab_software/2/ (accessed on 9 December 2021).
- Lindemann, F.A. Über die Berechnung molekularer Eigen-frequenzen. Phys. Z. 1910, 11, 609–612. [Google Scholar]
- Huang, X.Y.; Ackland, G.J.; Rabe, K.M. Crystal structures and shape-memory behaviour of NiTi. Nat. Mater. 2003, 2, 307. [Google Scholar] [CrossRef]
- Jardine, A.P.; Ashbee, K.H.G.; Bassett, M.J. Effects of cooling rate on the shape memory effect thermodynamics of NiTi. J. Mater. Sci. 1988, 23, 4273–4281. [Google Scholar] [CrossRef]
- Demidova, E.; Belyaev, S.; Resnina, N.; Shelyakov, A. Influence of the holding temperature on the kinetics of the isothermal B2–B19’ transformation in (TiNi)-based shape memory alloy. J. Therm. Anal. Calorim. 2020, 139, 2965–2970. [Google Scholar] [CrossRef]
- Persson, K.; Ekman, M.; Ozoliņš, V. Phonon instabilities in bcc Sc, Ti, La, and Hf. Phys. Rev. B 2000, 61, 11221–11224. [Google Scholar] [CrossRef] [Green Version]
- Trubitsin, V.Y. Effect of strongly anharmonic longitudinal and transverse vibrations with wave vector k = 2/3(111) on the structural stability of β-Zr under pressure. Phys. Rev. B 2006, 73, 214303. [Google Scholar] [CrossRef]
- Zhang, S.; Zhu, Y.; Zhang, X.; Zhang, S.; Qi, L.; Liu, R. First-principles study on the structural stabilities, electronic and elastic properties for zirconium under pressure. Comput. Mater. Sci. 2010, 50, 179–183. [Google Scholar] [CrossRef]
- Abriata, J.P.; Bolcich, J.C.; Peretti, H.A. The Hf-Zr (Hafnium-Zirconium) system. J. Phase Equilibria 1982, 3, 29–34. [Google Scholar] [CrossRef]
- Saxena, S.K.; Upadhyaya, S.C.; Upadhyaya, J.C.; Shyam, R.; Agrawal, R.M. Phonons in bcc Zr at various temperatures. Solid State Comm. 1996, 99, 519–523. [Google Scholar] [CrossRef]
- Antolin, N.; Restrepo, O.D.; Windl, W. Fast free-energy calculations for unstable high-temperature phases. Phys. Rev. B 2012, 86, 054119. [Google Scholar] [CrossRef] [Green Version]
- Souvatzis, P.; Eriksson, O.; Katsnelson, M.I.; Rudin, S.P. The self-consistent ab initio lattice dynamical method. Comput. Mater. Sci. 2009, 44, 888. [Google Scholar] [CrossRef]
- Hellman, O.; Abrikosov, I.A.; Simak, S.I. Lattice dynamics of anharmonic solids from first principles. Phys. Rev. B 2011, 84, 180301. [Google Scholar] [CrossRef] [Green Version]
- Scruby, C.B.; Williams, P.M.; Parry, G.S. The role of charge density waves in structural transformations of 1T TaS2. Philos. Mag. J. Theor. Exp. Appl. Phys. 1975, 31, 255–274. [Google Scholar] [CrossRef]
- Law, K.T.; Lee, P.A. 1T-TaS2 as a quantum spin liquid. Proc. Natl. Acad. Sci. USA 2017, 114, 6996–7000. [Google Scholar] [CrossRef] [Green Version]
- Zarkevich, N.A. Double Climbing Image Nudge Elastic Band Method, 1st ed.; 2014; Available online: http://lib.dr.iastate.edu/ameslab_software/1/ (accessed on 9 December 2021).
- Zarkevich, N.A.; Johnson, D.D. Predicting Enthalpies of Molecular Substances: Application to LiBH4. Phys. Rev. Lett. 2008, 100, 040602. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P. Generalized gradient approximation for the fermion kinetic energy as a functional of the density. Phys. Lett. A 1992, 165, 79. [Google Scholar] [CrossRef]
- Johnson, D.D. Modified Broyden’s method for accelerating convergence in self-consistent calculations. Phys. Rev. B 1988, 38, 12807–12813. [Google Scholar] [CrossRef]
- Zarkevich, N.A. Structural Database for Reducing Cost in Materials Design and Complexity of Multiscale Computations. Complexity 2006, 11, 36–42. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Zarkevich, N.A.; Johnson, D.D. Titanium α-ω phase transformation pathway and a predicted metastable structure. Phys. Rev. B 2016, 93, 020104(R). [Google Scholar] [CrossRef] [Green Version]
- Togo, A.; Oba, F.; Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 2008, 78, 134106. [Google Scholar] [CrossRef] [Green Version]
- Savrasov, S.Y. Linear-response theory and lattice dynamics: A muffin-tin-orbital approach. Phys. Rev. B 1996, 54, 16470–16486. [Google Scholar] [CrossRef] [Green Version]
- Zarkevich, N.A.; Majzoub, E.H.; Johnson, D.D. Anisotropic thermal expansion in molecular solids: Theory and experiment on LiBH4. Phys. Rev. B 2014, 89, 134308. [Google Scholar] [CrossRef] [Green Version]
- Haskins, J.B.; Thompson, A.E.; Lawson, J.W. Ab initio simulations of phase stability and martensitic transitions in NiTi. Phys. Rev. B 2016, 94, 214110. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zarkevich, N.A.; Johnson, D.D. Between Harmonic Crystal and Glass: Solids with Dimpled Potential-Energy Surfaces Having Multiple Local Energy Minima. Crystals 2022, 12, 84. https://doi.org/10.3390/cryst12010084
Zarkevich NA, Johnson DD. Between Harmonic Crystal and Glass: Solids with Dimpled Potential-Energy Surfaces Having Multiple Local Energy Minima. Crystals. 2022; 12(1):84. https://doi.org/10.3390/cryst12010084
Chicago/Turabian StyleZarkevich, Nikolai A., and Duane D. Johnson. 2022. "Between Harmonic Crystal and Glass: Solids with Dimpled Potential-Energy Surfaces Having Multiple Local Energy Minima" Crystals 12, no. 1: 84. https://doi.org/10.3390/cryst12010084
APA StyleZarkevich, N. A., & Johnson, D. D. (2022). Between Harmonic Crystal and Glass: Solids with Dimpled Potential-Energy Surfaces Having Multiple Local Energy Minima. Crystals, 12(1), 84. https://doi.org/10.3390/cryst12010084






