Abnormal Shear Performance of Microscale Ball Grid Array Structure Cu/Sn–3.0Ag–0.5Cu/Cu Solder Joints with Increasing Current Density

Abstract

The shear performance and fracture behavior of microscale ball grid array structure Cu/Sn–3.0Ag–0.5Cu/Cu solder joints with increasing electric current density (from 1.0 × 10³ to 6.0 × 10³ A/cm²) at various test temperatures (25 °C, 55 °C, 85 °C, 115 °C, 145 °C, and 175 °C) were investigated systematically. Shear strength increases initially, then decreases with increasing current density at a test temperature of no more than 85 °C; the enhancement effect of current stressing on shear strength decreases and finally diminishes with increasing test temperatures. These changes are mainly due to the counteraction of the athermal effect of current stressing and Joule heating. After decoupling and quantifying the contribution of the athermal effect to the shear strength of solder joints, the results show that the influence of the athermal effect presents a transition from an enhancement state to a deterioration state with increasing current density, and the critical current density for the transition decreases with increasing test temperatures. Joule heating is always in a deterioration state on the shear strength of solder joints, which gradually becomes the dominant factor with increasing test temperatures and current density. In addition, the fracture location changes from the solder matrix to the interface between the solder matrix and the intermetallic compound (IMC) layer (the solder/IMC layer interface) with increasing current density, showing a ductile-to-brittle transition. The interfacial fracture is triggered by current crowding at the groove of the IMC layer and driven by mismatch strain at the solder/IMC layer interface, and the critical current density for the occurrence of interfacial fracture decreases with increasing test temperatures.

1. Introduction

Solder joints provide electrical, thermal, and mechanical connections among different components and various circuits in electronic products and devices, which are considered the weakest link in electronics [1]. The failure of one solder joint usually results in malfunction or total breakdown of electronics. Therefore, the reliability of solder joints is essential for the optimum function of electronics.

After fabrication of electronics, the reliability of solder joints is mainly determined by the serving conditions. One of the main serving conditions is electric current stressing. Once current is applied to a solder joint, Joule heating alters the thermal condition; then, the shear stress generates at the interfaces owing to the coefficient of thermal expansion (CTE) mismatch between different materials in the solder joint [2]. Therefore, the shear property under current stressing is critical in evaluating the reliability of solder joints in service.

Electric current stressing brings not only a thermal effect due to Joule heating, but also athermal effects due to electron-lattice interaction (momentum transfer) in solder joints [3]. The influence of Joule heating on the shear performance of solder joints is usually determined by studying the effect of the Joule heating-induced temperature (T_Joule). Previous studies have shown that the shear property and fracture behavior of solder joints are affected significantly by temperature [4,5,6]. For example, as temperature and aging time increase, the shear strength of Cu/Sn–3.0Ag–0.5Cu/Cu (Cu/SAC305/Cu) solder joints declines monotonically, and the fracture location gradually changes from the solder matrix to an intermetallic compounds (IMC) layer, clearly showing a ductile-to-brittle transition [4]. In contrast, the most prominent phenomenon induced by the athermal effect of current stressing in solder joints is electromigration (EM), which is known as an enhanced directional metal atoms transport process [7].

Many studies have reported that EM can cause dramatic microstructure change, such as the polarity growth of IMC, phase segregation, grain rotation, hillocks, and formation of voids and cracks, which will accelerate solder joint failure [8,9,10]. After EM, the shear strength of the lap–type Cu/SAC387/Cu solder joints shows a sharp decrease with increasing current stressing time, and the maximum descent rate of shear strength reaches 58.5% after 3100 h [11]. Similar phenomena also occur in other solder joints [12,13,14,15,16]. Moreover, the fracture location changes from the solder matrix to the cathode interface with a ductile-to-brittle transition [11,12,13]. In brief, both Joule heating and the athermal effect of current stressing have a significant influence on the shear performance and fracture behavior of solder joints.

However, Joule heating and the athermal effect of current stressing are usually applied to in-service solder joints simultaneously. Thus, a mechanical test under current stressing should be more valuable for evaluating the reliability of solder joints in service. Therefore, numerous investigations have been conducted on the creep [17,18,19], thermal fatigue [20,21,22], and tensile [23,24,25] behaviors of solder joints under current stressing, while the shear behavior of solder joints under current stressing has received less attention. A recent study reported that the shear strength of dual-interface ball grid array (BGA) Cu/SAC305/Cu solder joints decreases as the current density increases from 6.0 × 10³ to 1.1 × 10⁴ A/cm², and the fracture location changes from the solder matrix to the interface between the solder matrix and IMC layer (the solder/IMC layer interface) [26]. Owing to the excessively high current density, severe Joule heat is generated in the solder joints, which causes the athermal effect of current stressing being easily concealed and ignored in the analysis. In fact, the current density following through solder joints in industry may be much lower [27], which can also influence the shear performance of solder joint. When a low current density of 7.0 × 10² A/cm² is applied to the single-interface SAC105/Cu solder joints, the shear strength of solder joint under current stressing is about 9.5% higher than that at a corresponding T_Joule [28]. This indicates that the athermal effect of current stressing may enhance shear performance. More current densities used in the related studies are shown in Table S1 in the Supplementary Materials. Nevertheless, the quantified contribution of Joule heating and athermal effect on the shear strength remains unclear, and the dual-interface solder joint is more common in practical applications than the single-interface solder joint, while it remains uncertain whether a similar shear strength increase will appear in the dual-interface solder joint.

In this study, the shear deformation and fracture behavior of the BGA structure Cu/SAC305/Cu solder joints with increasing current density from 1.0 × 10³ to 6.0 × 10³ A/cm² were investigated. The influences of Joule heating and the athermal effect on the shear strength of solder joints were decoupled and quantified for a thorough discussion.

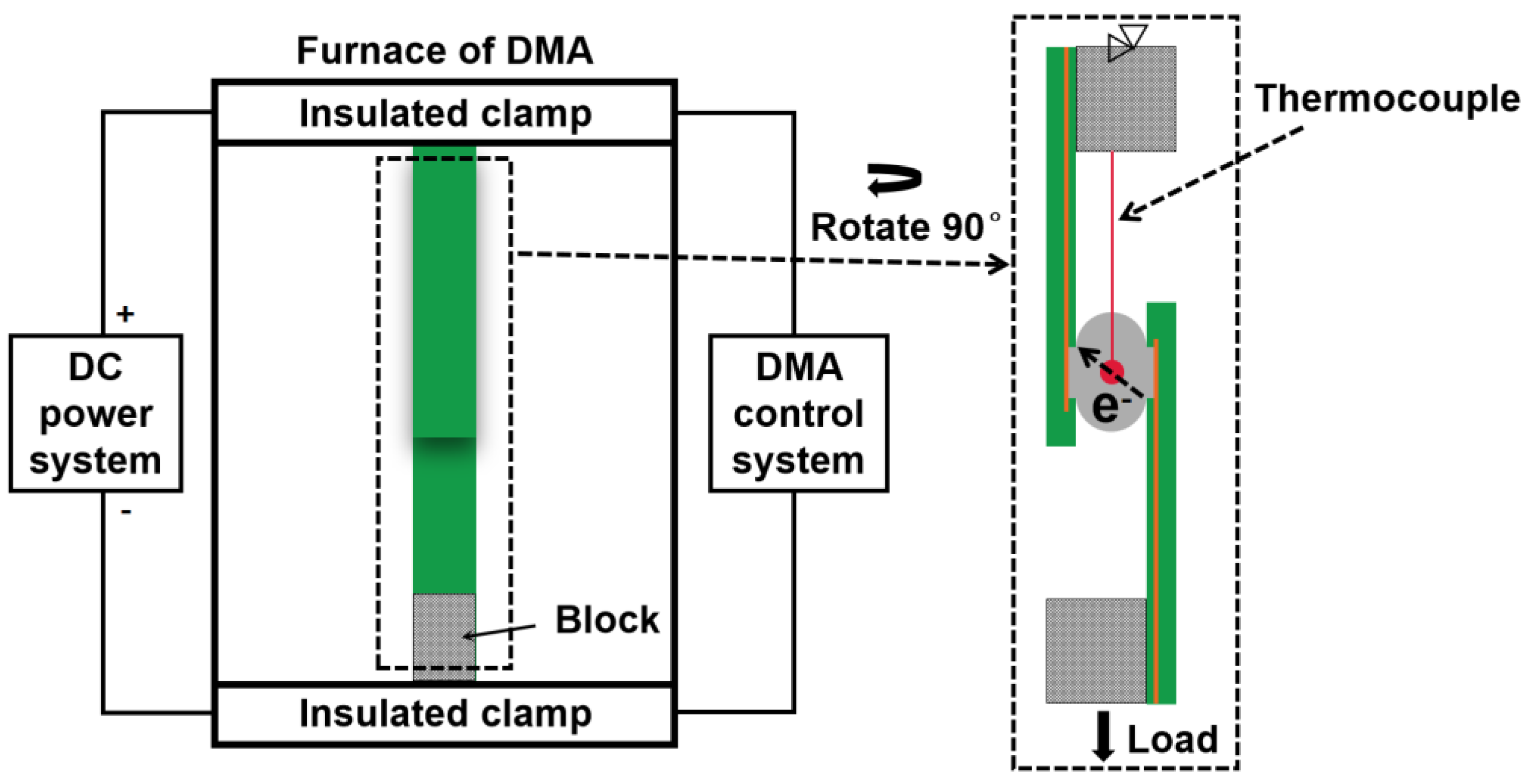
2. Experimental Procedure and Simulation Model

Dual-interface BGA structure solder joints were fabricated and used. The diameter of the SAC305 ball was 600 μm. Bismaleimide triazine (BT) epoxy-based substrate with a surface finish of copper-organic solderability preservatives (Cu-OSP) was chosen for the fabrication. The opening diameter of the pad was 480 μm. The fabrication procedure of the joint was the same as it was in our previous study [29].

The shear test of the solder joint under current stressing was performed on a dynamic mechanical analyzer (DMA Q800, TA, New Castle, DE, USA). During the shear test, the temperature of the DMA chamber was first heated to a test temperature (i.e., 25 °C, 55 °C, 85 °C, 115 °C, 145 °C, and 175 °C). Then, direct current with a density of 1.0 × 10³ A/cm², 2.0 × 10³ A/cm², 3.0 × 10³ A/cm², 4.0 × 10³ A/cm², 5.0 × 10³ A/cm², or 6.0 × 10³ A/cm² was applied to the solder joint by a constant current power supply (ANS1560D, China). After three minutes, shear force was applied to the solder joint with a constant rate of 1.0 N/min. During the procedure, the contacting parts of the circuit with the furnace and clamp were well-insulated. Moreover, a temperature measurement system consisting of a multi-channel capture card (KIC X5-9, China) and an Omega type K thermocouple (TT-K-40-SLE, 80 μm, China) was used to record the temperature of the solder joint, as illustrated in Figure 1. In addition, the shear strength of the joints at different test temperatures without electric current was tested, with the test temperatures corresponding to the T_Joule for the solder joints at different current densities. After testing, the failed joint was characterized using a scanning electron microscope (SEM, Quanta 450, FEI, USA) equipped with an energy-dispersive spectrometer (EDS).

Because of the small dimension of microscale solder joints, the local temperature and strain in a solder joint can be barely detected by experiments. Thus, a two-dimensional model of a single BGA joint was established, using COMSOL finite element (FE) analysis software. The model of the BGA joint is shown in Figure 2a, where L₀ = 500 µm, L₁ = 16 µm, L₂ = 480 µm, L₃ = 780 µm, L₄ = 300 µm, and L₅ = 37 µm. The thickness of the IMC layer was set at 5 µm. These values were consistent with those of the test sample (see Figure 2b). The length (L₆) of the model was set at 880 µm. All elements in the model were three-node free triangular elements, and the area near the IMC layer was refined, as shown in Figure 2c. The model contained 53,329 elements, where the minimum and maximum element sizes were 0.066 µm and 17.6 µm, respectively. The average element quality of the mesh was 0.8276. The mesh convergence analysis for different mesh types and sizes was carried out to prove the validity of the result. (More details can be found in the Supplementary Materials). The electric current inlet was set at the edge of the upper Cu layer (x = 1/2L₆, 2L₁ + L₄ < y < 2L₁ + L₄ + L₅), and the electric current outlet was set at the edge of the bottom Cu layer (x = −1/2L₆, −L₅ < y < 0). The electromagnetic heating and thermal expansion multi-physics coupling were used for FE calculations, involving the electric current, the heat transfer in solids, and the solid mechanics interfaces. All procedures were performed under steady-state conditions. According to the EDS results shown in Section 3.2, the interfacial IMC between Cu and SAC305 solder was Cu₆Sn₅. The material parameters used in the simulation are listed in

Table 1. Material parameters used in simulation.

Properties	SAC305	Cu	Cu6Sn5	FR4
Electrical conductivity (107 S/m)	0.87 [26]	6.00 [26]	0.57 [26]	4.00 × 10−10 [26]
Thermal conductivity (W/(m·K))	57.3 [26]	398.0 [30]	34.1 [26]	0.3 [26]
Density (g/cm3)	7.38 [31]	8.94 [31]	8.28 [30]	1.90 [26]
Young’s modulus (GPa)	45.6 [32]	117.0 [30]	85.6 [30]	22.0 [26]
Poisson’s ratio	0.36 [31]	0.35 [26]	0.31 [26]	0.15 [26]
CTE (10−6/k)	21.2 [30]	17.1 [30]	16.3 [30]	18.0 [26]
Specific heat capacity (J/(kg·K))	222.1 [30]	385.2 [30]	286.0 [30]	1369.0 [26]

.

3. Results

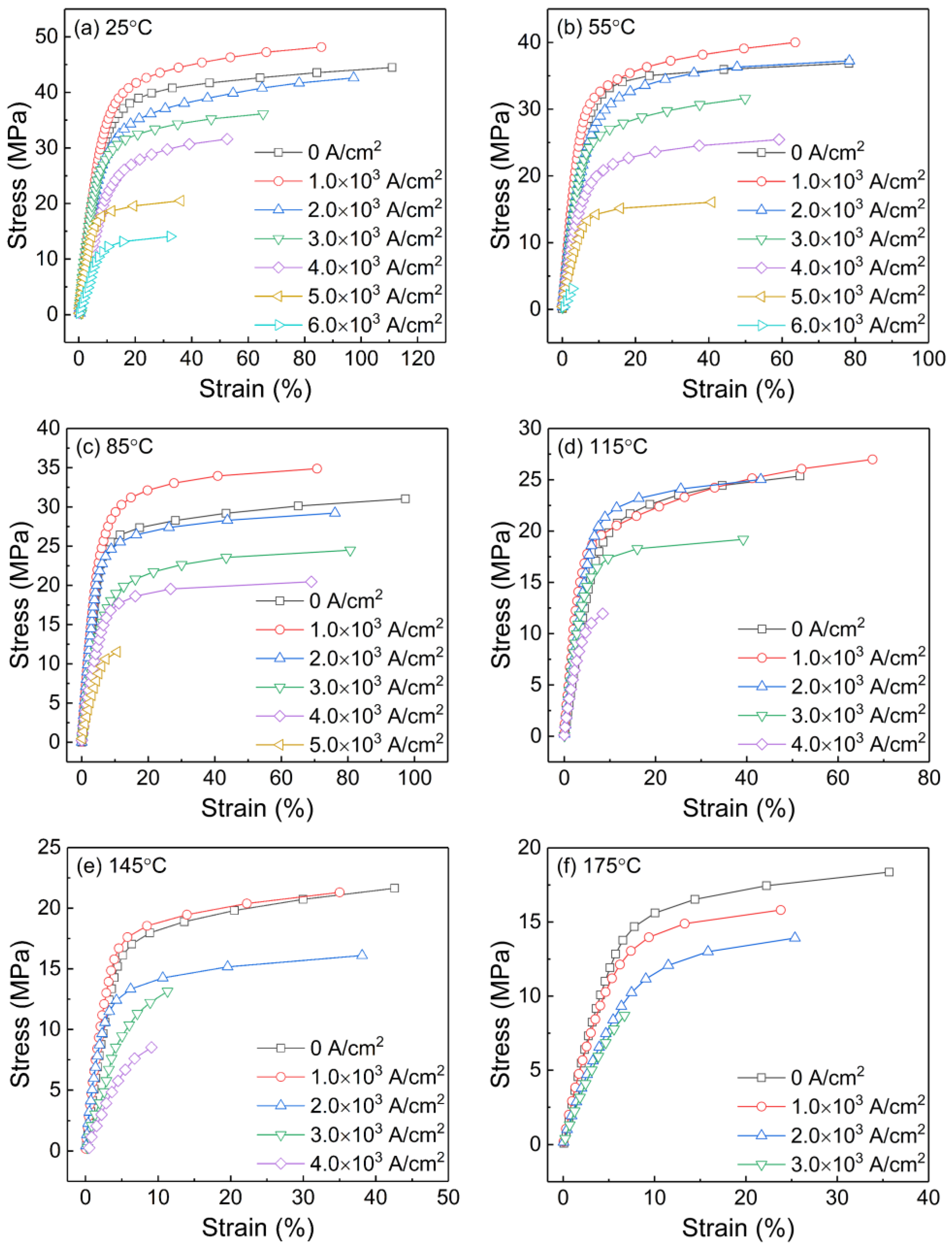
3.1. Deformation of Solder Joints under Current Stressing

The typical stress-strain curves of solder joints with different current densities are shown in Figure 3. At a test temperature of 25 °C, the deformation of solder joints appears in linear and non-linear stages at all current densities, as shown in Figure 3a. When the test temperature is 55 °C, the linear and non-linear deformation stages still exist at a current density of no more than 5.0 × 10³ A/cm². However, only the linear stage, with a small strain, appears in the deformation of the solder joint at a current density of 6.0 × 10³ A/cm², as shown in Figure 3b, indicating that a brittle fracture may have occurred in the solder joint. As the test temperatures increase, the critical current density for the disappearance of the non-linear deformation stage decreases to 5.0 × 10³ A/cm² at the test temperature of 85 °C; to 4.0 × 10³ A/cm² at test temperatures of 115 °C and 145 °C; and to 3.0 × 10³ A/cm² at the test temperature of 175 °C, as shown in Figure 3c–f, respectively.

Based on the stress-strain curves, the shear strength was obtained and shown in Figure 4. Clearly, the shear strength decreased monotonically with increasing test temperatures. Moreover, the shear strength first increased and then decreased with increasing current density at 25 °C, in which the peak value of shear strength appeared at 1.0 × 10³ A/cm². Similar phenomena were observed at test temperatures of 55 °C and 85 °C, while the enhancement effect on shear strength decreased gradually as the test temperature increased from 25 °C to 85 °C. As the test temperature increased to 115 °C, 145 °C, and 175 °C, the shear strength decreased monotonically with increasing current density; the increase in shear strength of solder joints at a current density of 1.0 × 10³ A/cm² diminished. In general, the shear strength of the solder joint was determined by test temperature and current density.

It is known that the T_Joule is usually higher than test temperatures. To clarify the influence of Joule heating on the shear strength of solder joints, the dynamic temperature of the solder joint with different current densities was captured at a test temperature of 25 °C, and the temperature distribution in the solder joint was obtained by FE simulation, as presented in Figure 5. The temperature difference in the solder joint was no more than 0.01 °C, i.e., the T_Joule in the solder joint was in a nearly homogeneous state. In addition, the measured temperature was quite close to that obtained in the FE simulation. Thus, the measured temperature could be used as the T_Joule of the solder joint. In addition, the measured temperature increased with increasing current density at all test temperatures, as shown in Figure 6.

Assuming that the shear strength of solder joints under current stressing is σ_j and that of solder joints at the T_Joule is σ_T, the strength-temperature curves can be obtained as shown in Figure 7. Obviously, even if the T_Joule in the solder joint is the same as that without current stressing, there is a difference in the shear strength. At test temperatures of 25 °C, 55 °C, 85 °C, and 115 °C, the difference between σ_j and σ_T changes from σ_j > σ_T (stage I) to σ_j < σ_T (stage II) with increasing temperatures. As the test temperature increases to 145 °C and 175 °C, σ_j is always less than σ_T. These changes indicate that shear strength is affected by the athermal effect of current stressing, and that this influence is non-monotonic.

Furthermore, the contribution of the athermal effect of current stressing (C_athermal) to the shear strength of solder joints can be defined as

$$C_{athermal}=\frac{{\sigma }_j-{\sigma }_T}{{\sigma }_j}\times 100\%$$

(1)

Specifically, when C_athermal > 0, the athermal effect elevates shear strength; when C_athermal = 0, the shear strength is not affected by the athermal effect and the corresponding current density is called the critical current density; when C_athermal < 0, the athermal effect lowers shear strength. It is worth noting that Equation (1) can only be applied to solder joints with fracture occurring in the solder matrix. As the fracture only occurred at the solder/IMC layer interface at 175 °C, as discussed in Section 3.2, Equation (1) does not apply to such solder joints.

Applying Equation (1), the C_athermal at various test temperatures with increasing current density can be calculated, as shown in Figure 8. Clearly, the maximum C_athermal is obtained at a test temperature of 25 °C near 1.0 × 10³ A/cm²; then, C_athermal decreases with increasing current density, and eventually becomes negative. In other words, the contribution of the athermal effect gradually changes from an enhancement state to a deterioration state with increasing current density. Moreover, the critical current density for this change decreases with increasing test temperatures. When the test temperature reaches 145 °C, C_athermal is nearly equal to 0, even if the current density does not exceed 1.0 × 10³ A/cm², indicating the disappearance of the enhancement state of the athermal effect on shear strength.

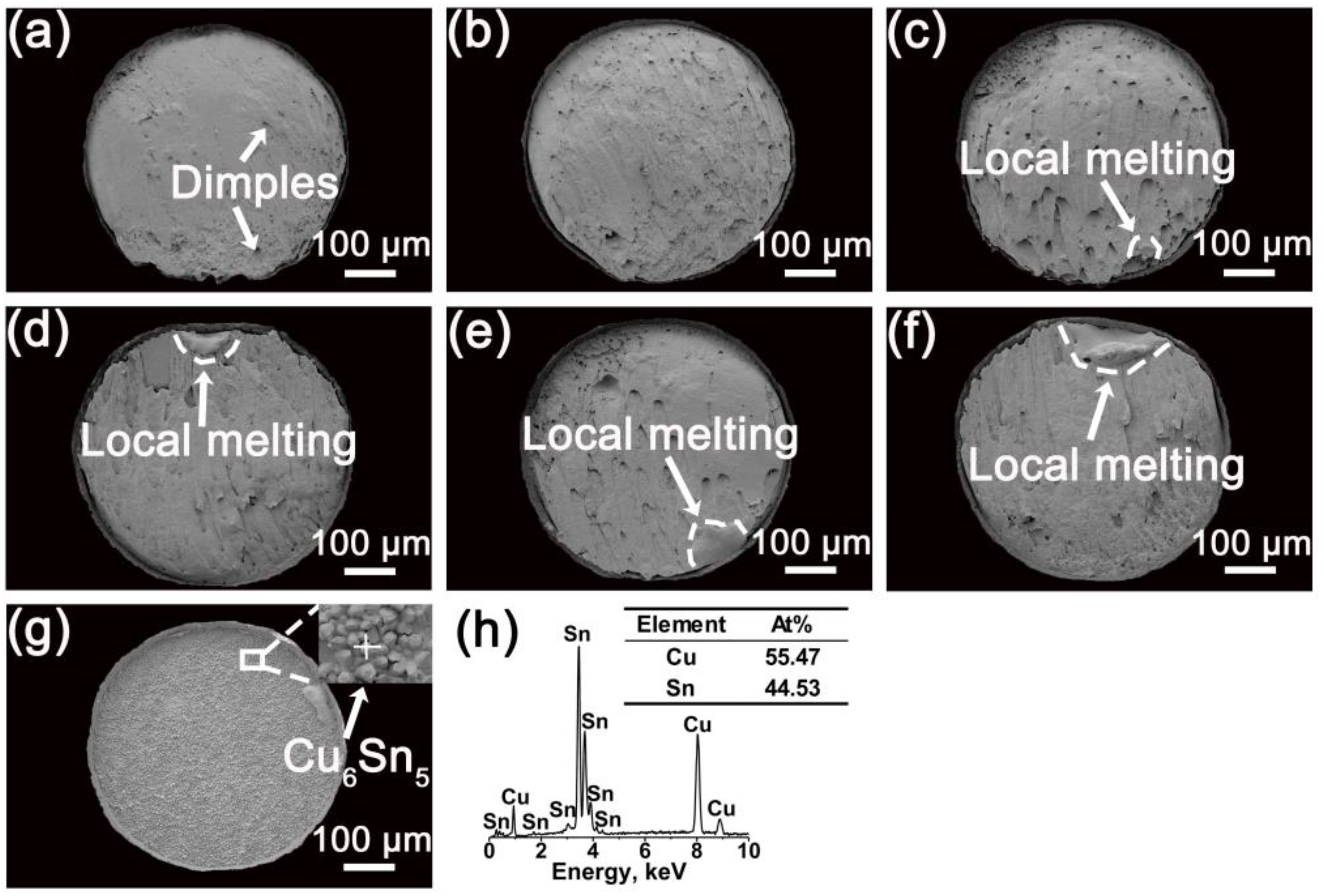
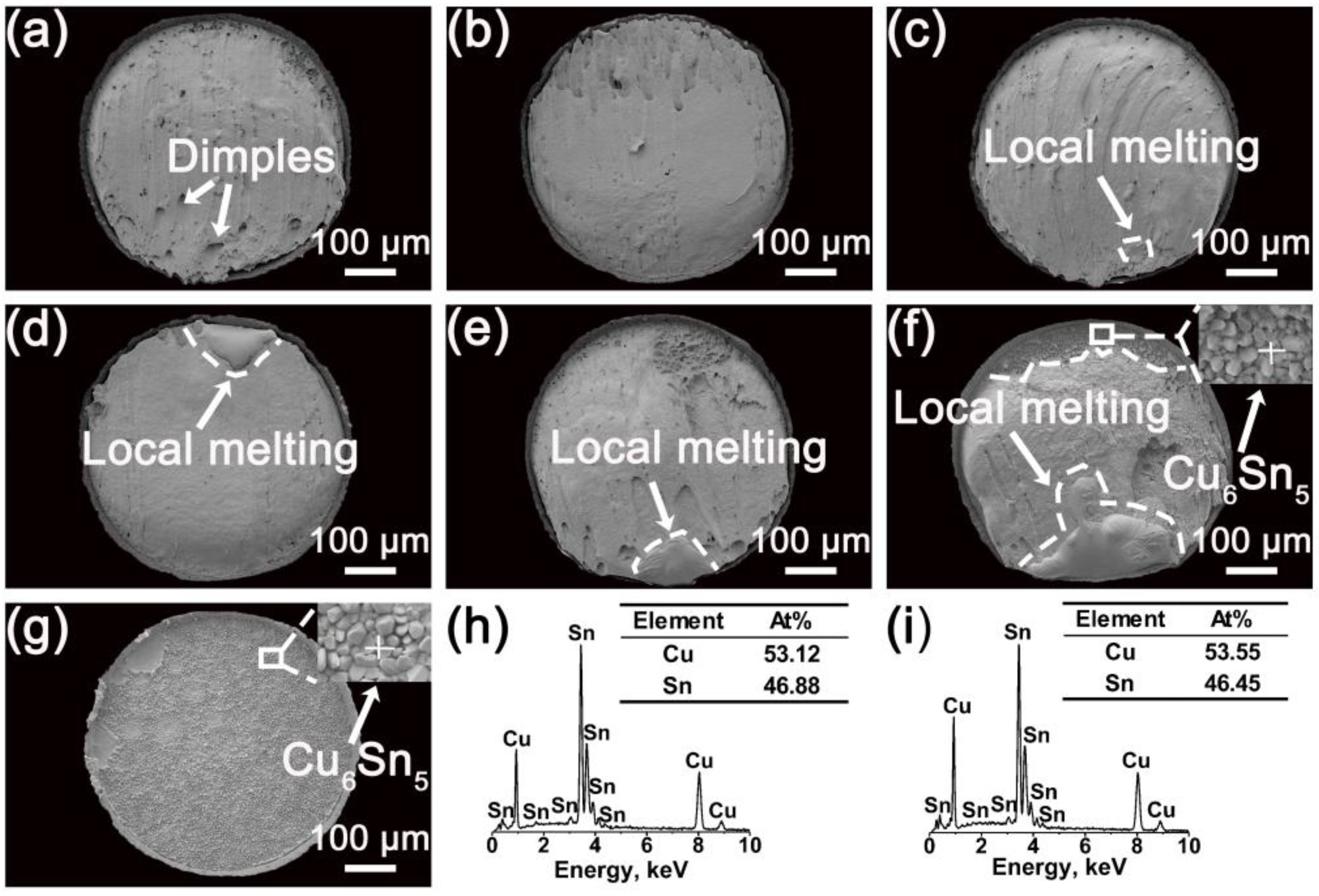
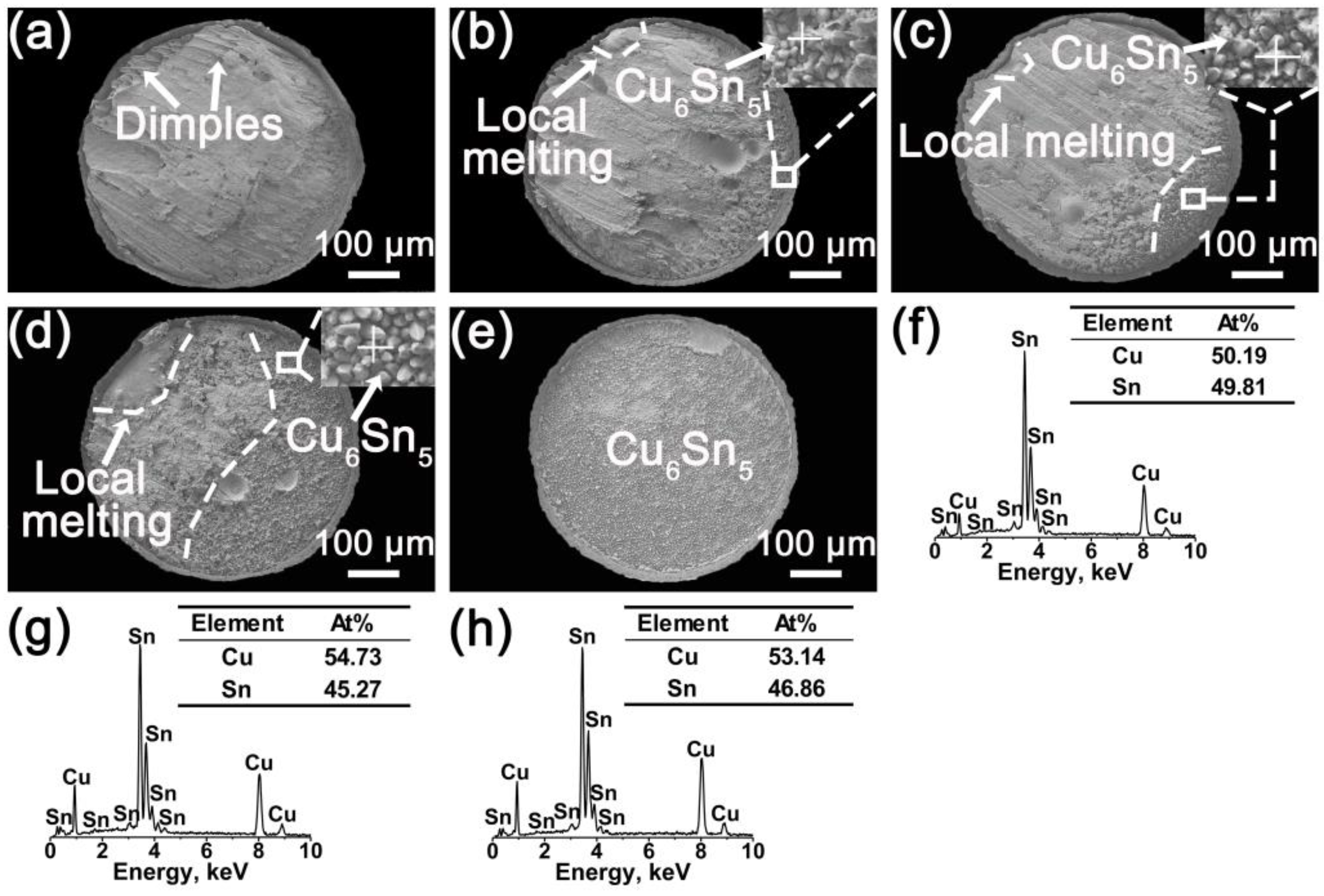
3.2. Fracture of Solder Joints under Current Stressing

The fracture morphology of solder joints with different current densities at a test temperature of 25 °C is shown in Figure 9. In general, the fracture location changed from the solder matrix to the solder/IMC layer interface, and the fracture mode of the solder joints underwent a ductile-to-brittle transition with increasing current density. Specifically, when the current density was no more than 5.0 × 10³ A/cm², the fracture occurred in the solder matrix with many dimples on the surface, which is a typical ductile fracture feature [33]. No local melting zone was observed at 1.0 × 10³ A/cm², while the local melting zone initiated and expanded with increasing current density from 2.0 × 10³ A/cm² to 5.0 × 10³ A/cm², as shown in Figure 9a–f. When the current density reached 6.0 × 10³ A/cm², the fracture occurred at the solder/IMC layer interface with numerous exposed particles, presenting a brittle fracture feature [34] as shown in Figure 9g. The EDS results of particles in Figure 9g show that the atomic ratio of Cu and Sn was nearly 6:5, indicating that the particles were Cu₆Sn₅, as shown in Figure 9h.

As the test temperature gradually increased to 55 °C, 85 °C, 115 °C, 145 °C, and 175 °C, the fracture remained in the solder matrix for joints without current stressing, and the variation on the fracture features of solder joints with different current densities was generally similar to those obtained at 25 °C, as shown in Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. Two points need to be noted: (1) the fracture location changed from the solder matrix to a site with a partial solder matrix and a partial solder/IMC layer interface, eventually changing to the solder/IMC layer interface; (2) the critical current density for the interfacial fracture decreased with increasing test temperatures. With respect to the first point, although the critical current density for the interfacial fracture decreased to 5.0 × 10³ A/cm² when the test temperature was 55 °C or 85 °C, as shown in Figure 10 and Figure 11, the area of the interfacial fracture part at the test temperature of 85 °C was larger than the area of the interfacial fracture part at the test temperature of 55 °C, as shown in Figure 10f and Figure 11f. In other words, the area of the interfacial fracture part in the mixed fractured solder joint at the same current density increased with increasing test temperatures. With respect to the second point, as the test temperatures increased, the critical current density for the interfacial fracture decreased, to 4.0 × 10³ A/cm² at the test temperature of 115 °C (see Figure 12); then to 3.0 × 10³ A/cm² at the test temperature of 145 °C (see Figure 13); and finally to 1.0 × 10³ A/cm² at the test temperature of 175 °C (see Figure 14). Apparently, the interfacial fracture is more likely to occur under the coupling effect of high test temperatures and current stressing with high current density, and the critical current density for the ductile-to-brittle transition of solder joints decreases with increasing temperatures.

4. Discussion

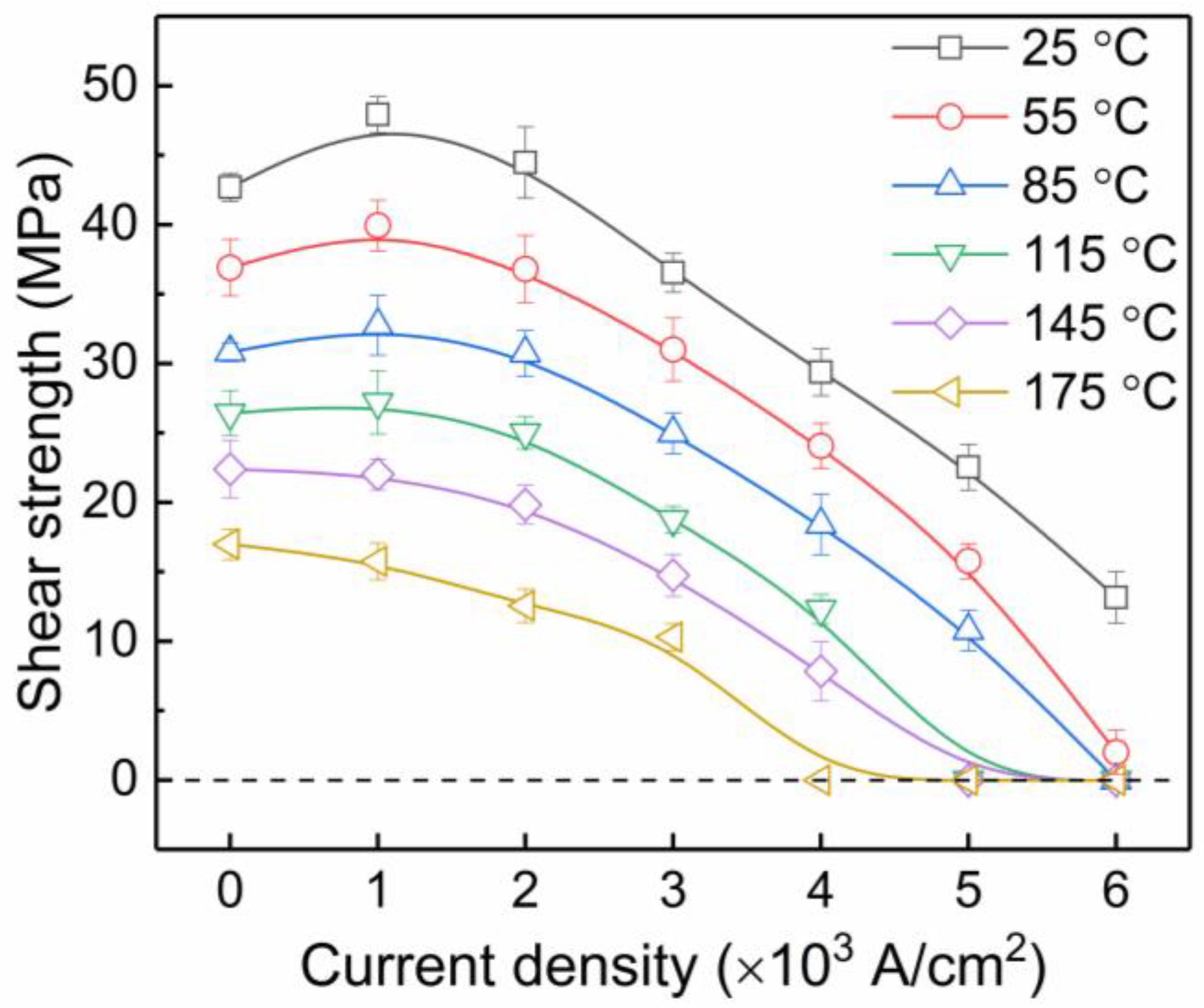
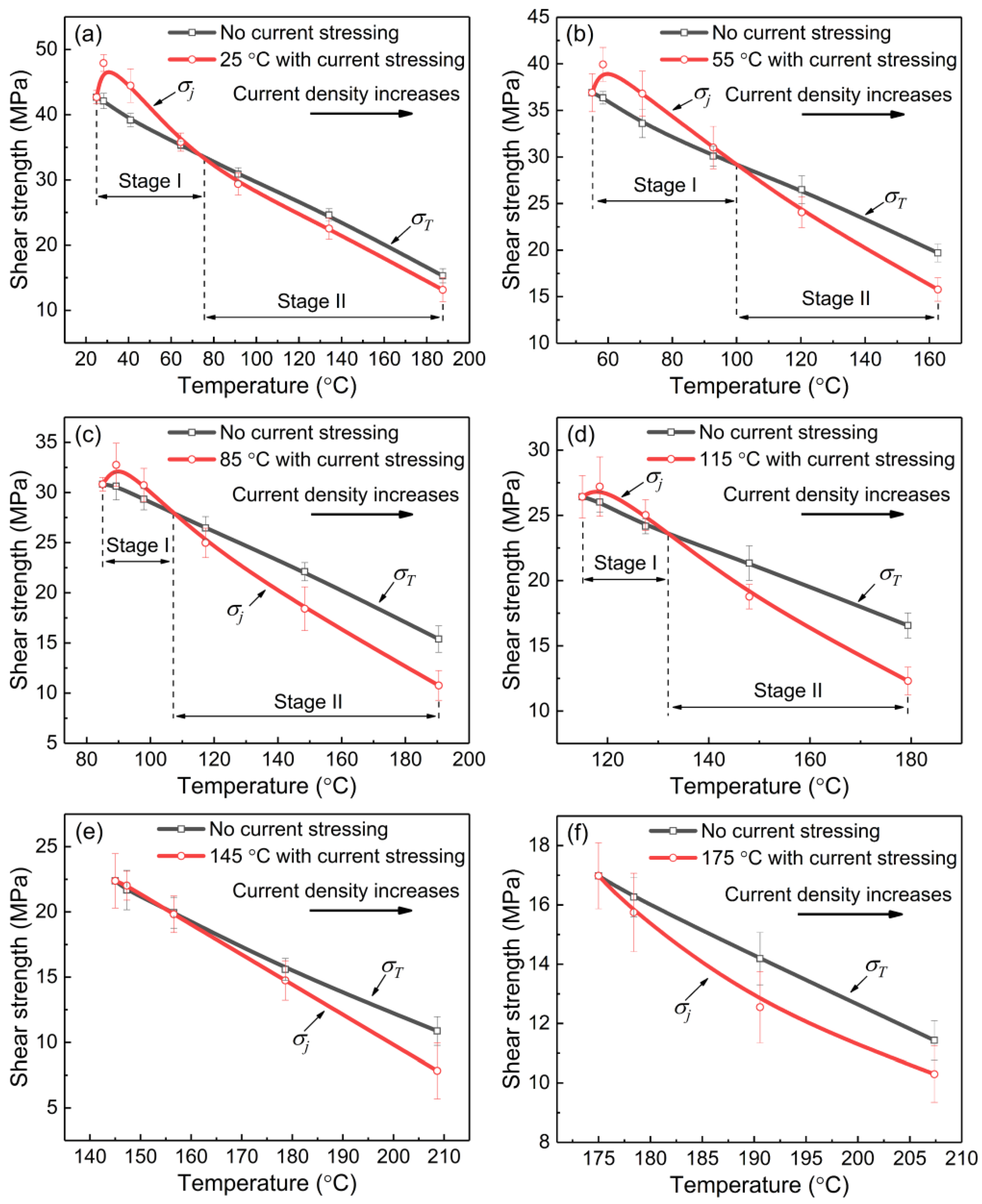
4.1. Shear Strength

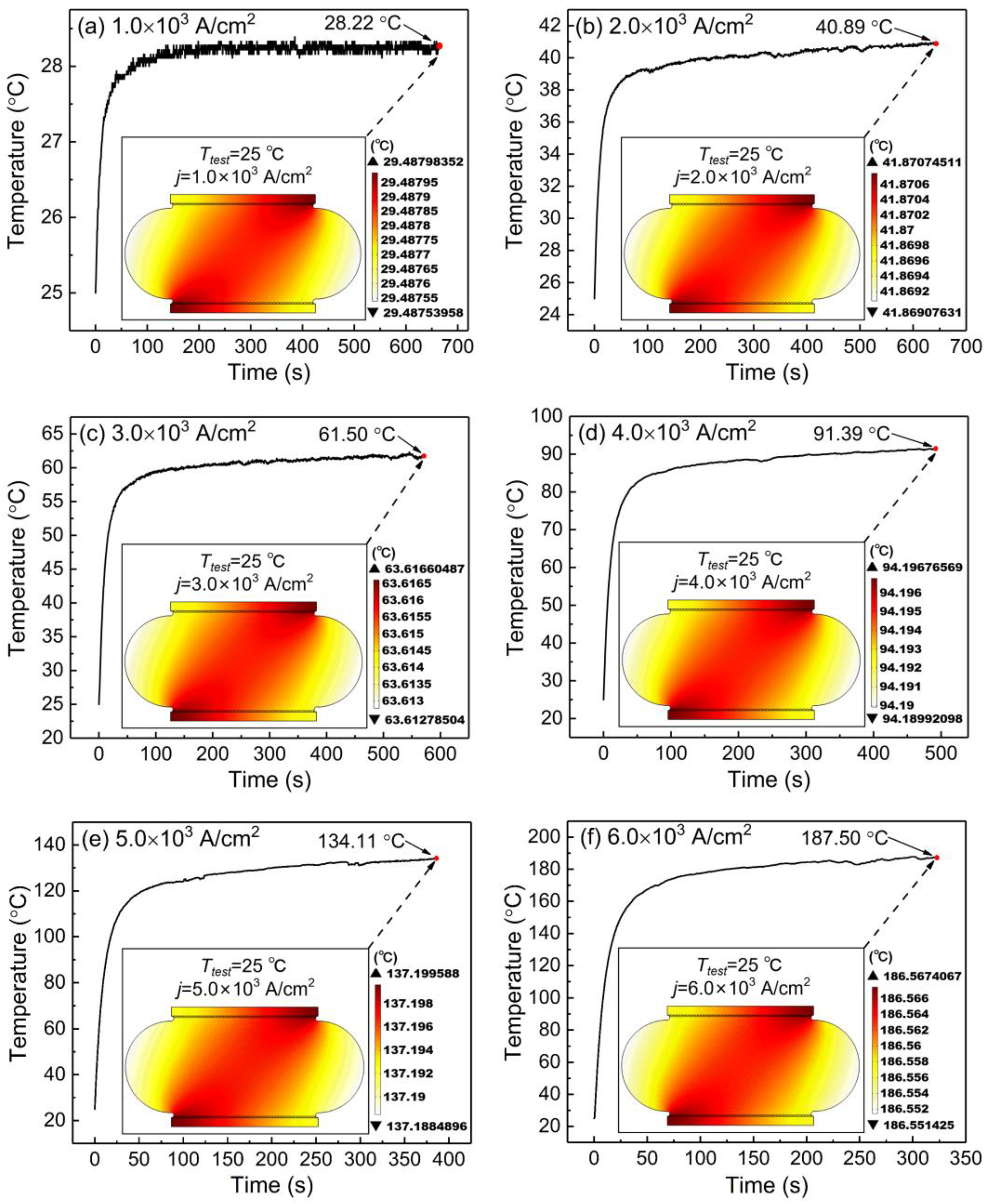
4.1.1. Influence of Joule Heating on the Shear Strength

As the simulation and measurement results of temperature in solder joints under current stressing are quite close (see Figure 5), the influence of Joule heating on the shear strength of solder joints can be estimated through the influence of the T_Joule on shear strength. The T_Joule in the BGA structure solder [26] joints can be expressed as:

$$T_{\mathrm{Joule}}=\frac{{\pi }^2{j}^2{D}^{4}Rt}{16\left(hSt+Cm\right)}$$

(2)

where j is the current density, D is the opening diameter of the pad, R is the electrical resistance, t is the electric current stressing time, h is the heat transfer coefficient, S is the surface area where heat transfer occurs, C is the specific heat of solder, and m is the mass of the solder. Clearly, the T_Joule increases with increasing current density and is proportional to the square of the current density, as verified by the measured data in Figure 6. According to the temperature-dependent yield strength theory, the stress required for dislocation movement, Peierls-Nabarro stress (τ_p), can be expressed as a function of temperature [35,36]:

$${\tau }_p(T)=\frac{2G}{1-\nu }{e}^{-\frac{2\pi a}{b\left(1-\nu \right)}}\{1-a{\left[\frac{T^2\left(1-\nu \right)}{2G^2}\right]}^{1/4}{e}^{\frac{\pi a}{2b(1-\nu )}}\}$$

(3)

where G is the shear modulus, ν is the Poisson ratio, a is the distance between adjacent atomic surfaces parallel to the slip surface, b is the Burgers vector, and T is the temperature. Applying Equation (3), the increase in temperature will result in a decrease in Peierls-Nabarro stress, thus facilitating the initiation of a dislocation slip. An easier slip of dislocations will render the solder joints more susceptible to deformation with a lower shear strength.

Furthermore, according to the force-heat energy density equivalence principle [37], the fracture strength of the solder joint can be expressed as a function of temperature:

$${\sigma }_{th}(T)={\left[\frac{E(T)}{E_0}\left[1-\frac{1}{{\displaystyle \int {}_0^{T_m}{C}_p(T)dT}}{\displaystyle \underset{0}{\overset{T}{\int }}{C}_p(T)dT}\right]\right]}^{1/2}{\sigma }_{th}^0$$

(4)

where σ_th(T), E(T), and C_p(T) are the fracture strength (MPa), Young’s modulus (GPa), and the specific heat capacity (J/(Kg × K)) at temperature T, respectively, T_m is the melting temperature, and ${\sigma }_{th}^0$ is the fracture strength at 0 °C. The various parameters used in Equation (4) are as follows: E₀ = 45.59 GPa [32], T_m = 217 °C [38], $E\left(T\right)=45.59-0.11T+8.37\times {10}^{-5}{T}^2$ (GPa) [32], and $C_p\left(T\right)=223.84+0.14T$ (J/(Kg × K)) (calculated by JMatPro). After substituting these parameters into Equation (4), Equation (4) can be written as:

$${\sigma }_{th}(T)={\sigma }_{th}^0(1-6.73\times {10}^{-3}T+1.09012\times {10}^{-5}{T}^2-4.6953\times {10}^{-9}{T}^3-2.484\times {10}^{-12}{T}^4{)}^{1/2}$$

(5)

Applying Equation (5), the shear strength of solder joints in the temperature range of 25 °C to 215.36 °C (the maximum T_Joule in present study) was calculated as shown in Figure 15. Clearly, the shear strength shows a nearly linear decrease with the temperature, which is also verified by the results in Figure 7. Therefore, it is certain that Joule heating only presents a deterioration state on shear strength.

4.1.2. Influence of Athermal Effect on Shear Strength

In addition to Joule heating, when solder joints are subjected to current stressing, the metal atoms in the solder matrix will be subjected to a force in the direction of the electron flow, i.e., the electron wind force. The electron wind force (F_ew) can be expressed as [39]:

$$F_{ew}=Z^{\ast }e\rho j$$

(6)

where Z* is the effective charge (−18 [40]), e is the electronic charge, and ρ is the resistivity (1.09 × 10⁻⁵ Ωcm [41]). Applying Equation (6), the electron wind force is elevated from 3.14 × 10⁻¹⁸ N to 1.89 × 10⁻¹⁷ N when the current density is increased from 1.0 × 10³ A/cm² to 6.0 × 10³ A/cm². For Sn metal, the activation energy of diffusion is 107.1 kJ/mol in the direction parallel to the c-axis, which is higher than that in the direction of the a/b-axis, 105 kJ/mol [42]. Thus, the activation energy of diffusion in the direction parallel to the c-axis can be used as the criterion for the diffusion of Sn atoms. Accordingly, the activation energy for the diffusion of per Sn atom is 1.78 × 10⁻¹⁹ N·m. This means that the electron wind force under a current density of 1.0 × 10³ A/cm² is sufficient to cause the diffusion of Sn atoms and thus the formation of dislocation [43]. The generation of dislocations will cause lattice stress in the solder matrix. The lattice stress (σ) can be described as a function of dislocation density (d) according to Taylor’s relation [44]:

$$\sigma =\alpha Gb{d}^{1/2}$$

(7)

where α is the dislocation interaction constant. Moreover, the relationship between lattice stress and microhardness (H_v) can be expressed as [45]:

$$H_v=3\sigma =3\alpha Gb{d}^{1/2}$$

(8)

Clearly, the increase in dislocation density is conducive to improving the microhardness of the solder matrix [3]. According to the general relationship between microhardness and strength, the strength of metal materials is positively correlated with hardness [46]. Thus, the shear strength of solder joints will increase with an increase in dislocation density.

Nevertheless, electron wind force also promotes the movement of dislocations [47]. The force exerted by electrons on the dislocation per unit length (F_ew/l₀) can be expressed as [48]:

$$\frac{F_{ew}}{l_0}=K_{ew}j={\tau }_{ew}b$$

(9)

where K_ew is the coefficient of electron wind force and τ_ew is the shear stress on dislocation. Applying Equation (9), static dislocation may be activated into dynamic dislocation with an increase in current density. Concurrently with the applied shear stress (τ), the climbing rate of dislocation (ν_c) is [49]:

$${\nu }_c=\frac{2\pi r{\nu }_a}{R_{d}b}\cdot \frac{D_s}{kT}\cdot \left(\tau +{\tau }_{ew}b\right)$$

(10)

where r is the dislocation line curvature radius, ν_a is the atomic volume, R_d is the distance from the source of the dislocation on the grain boundary to the place where the dislocation disappears, D_s is the atomic self-diffusion coefficient, and k is the Boltzmann constant. Applying Equations (6) and (10), the dislocations increase more readily at a high current density, resulting in a decrease in the shear strength of solder joints.

4.1.3. Influence of Current Stressing on Shear Strength

Based on the above analysis, Joule heating and athermal effect may be counteractive with respect to the variation of shear strength of solder joints. In addition, Joule heating favors eliminating dislocations induced by the athermal effect [50]; i.e., Joule heating can weaken the enhancement state of the athermal effect on shear strength. Specifically, the athermal effect of current stressing favors producing dislocations as a result of electron-lattice interaction, thus inducing lattice stress, but Joule heating favors relaxing the stress, resulting in a dynamic recovery of dislocations, which can be considered as a stress relaxation process controlled by the thermal-activated mechanism [51]. When Joule heating is generated, lattice stress in the solder matrix will be lowered; the correlation between lattice stress and temperature is as following [52]:

$$\sigma ={\sigma }_0-\frac{kT}{V_{\alpha }}\ln \left(1+\frac{t}{t_0}\right)$$

(11)

where σ₀ is the lattice stress at t = 0, V_α is the activation volume for recovery events, t is the current stressing time, and t₀ is a reference time [51]. Applying Equations (7) and (11), as the temperature of the solder matrix increases, the lattice stress will decrease, leading to a reduction of dislocation density. When the current density is 1.0 × 10³ A/cm², the T_Joule rise in solder joints does not exceed 4 °C; thus, Joule heating-induced shear strength decrease may be not obvious. In contrast, the athermal effect of current stressing can induce an increase in dislocation density at this current density, leading to a prominent increase in shear strength. Therefore, the shear strength shows a slight increase.

As the current density continues to increase, both Joule heating and the athermal effect have been enhanced. Applying Equations (2) and (6), the T_Joule is proportional to the square of current density, while the electric wind force is proportional to the first power of the current density. The influence of Joule heating on shear strength may gradually become more significant than that of the athermal effect, and eventually become the dominant factor. When the increment and recovery of the dislocation reach an equilibrium state, the influence of the athermal effect on shear strength will be offset by Joule heating, i.e., C_athermal = 0. Like the T_Joule, the test temperature contributes to lowering the dislocation density; therefore, the enhancement state in shear strength at 1.0 × 10³ A/cm² will be weakened and eventually disappear as the test temperatures increase. Consequently, the critical current density for reaching the equilibrium state decreases with increasing test temperatures, as shown in Figure 8.

As the current density further increases, Joule heating becomes dominant on the variation of shear strength. Moreover, the athermal effect may assist the slip of dislocations, and the deformation of solder joints is further promoted. Therefore, the athermal effect gradually changes from an enhancement state to a deterioration state with increasing current density, and the shear strength also exhibits a continuous decrease.

4.2. Fracture Behavior

The above results on fracture behaviors show that the fracture location changed gradually from the solder matrix to the solder/IMC layer interface, as shown in Figure 16 for all three fracture types. For fracture type I, the crack initiates and then propagates in the solder matrix, as shown in Figure 16a. For fracture type II, the crack initiates at the solder/IMC layer interface and then propagates first along the solder/IMC layer interface and then into the solder matrix, as shown in Figure 16b. For fracture type III, the crack initiates and propagates along the solder/IMC layer interface until complete fracture, as shown in Figure 16c.

When the solder joints are loaded without current stressing, the stress concentration occurs in the solder matrix at the corner of the joint, due to the constraints from the substrate and the solder mask, where the crack is initiated. Since the stress concentration remains in the solder matrix along the corners of the joint near the same substrate, the crack propagates there until complete fracture. Thus, a fracture surface remains, with its distance to the substrate close to the height of the solder mask.

As electric current is applied, current crowding occurs due to the inhomogeneous configuration and IMC layers of the BGA structure solder joint, and it becomes more pronounced with increasing current density [26]. To better understand the influence of electric current on fracture behavior, the current density distribution in the solder joint under an applied current density of 6.0 × 10³ A/cm² was obtained using FE simulation, as shown in Figure 17. Clearly, the most serious current crowding occurs at the groove of the Cu₆Sn₅ grains closest to the electron flow entrance or exit, and the current density at the groove of the IMC grains decreases gradually when far away from the electron flow entrance or exit, as shown in Figure 17a. Moreover, the maximum current density (1.12 × 10⁴ A/cm²) at the groove of the Cu₆Sn₅ grains is nearly twice the applied current density, as shown in Figure 17b, where a hot spot is likely to form due to the serious Joule heat [53]. When the temperature of the hot spot exceeds the melting point of the solder, a crack will be preferentially initiated at the melting site under shear stress.

In addition to the inhomogeneity in the current density distribution and the thermal state, due to the different CTE between the SAC305 solder and the Cu₆Sn₅ [30], a thermal strain mismatch occurs at the solder/IMC layer interface in the joint under current stressing, as shown in Figure 18, and the maximum mismatch strain is near the maximum current crowding site. In addition, the mismatch strain increases with increasing current density, as shown in Figure 19. Thus, when the strain mismatch is large enough, the crack propagates along the interface. Otherwise, the crack will propagate into the solder matrix once again. Therefore, a complete interfacial fracture is more likely to occur at high current densities. As the mismatch strain also increases with increasing test temperatures, see Figure 19, the current density needed for the interfacial fracture decreases at higher test temperatures. In general, the interfacial fracture is triggered by the current crowding induced hot spot at the groove of the IMC grains and driven by the mismatch strain at the solder/IMC layer interface, and the corresponding critical current density for the fracture position changing from the solder matrix to the solder/IMC layer interface decreases with increasing temperatures.

5. Conclusions

The shear performance of microscale BGA structure Cu/SAC305/Cu solder joints with increasing current density (from 1.0 × 10³ to 6.0 × 10³ A/cm²) at various test temperatures (25 °C, 55 °C, 85 °C, 115 °C, 145 °C, and 175 °C) were investigated. The conclusions can be summarized as follows:

(1)

The shear strength first increases then decreases with increasing current density at relatively low test temperatures (25–85 °C). The shear strength increase is weakened and gradually diminished as temperatures increase.

(2)

The abnormal variation of shear strength is induced by the counteraction of Joule heating and the athermal effect of current stressing. Joule heating dominates at the higher current densities and presents a deterioration state on the shear strength, while the contribution of the athermal effect of current stressing on shear strength changes from an enhancement state to a deterioration state with increasing current density, and the critical current density for this change decreases with increasing temperatures.

(3)

The fracture location of solder joints gradually shifts from the solder matrix to the solder/IMC layer interface, with increasing current density and showing an obvious ductile-to-brittle transition. The critical current density for this transition decreases with increasing temperatures.