Abstract
Numerical simulations are a valuable tool for the design and optimization of crystal growth processes because experimental investigations are expensive and access to internal parameters is limited. These technical limitations are particularly large for ammonothermal growth of bulk GaN, an important semiconductor material. This review presents an overview of the literature on simulations targeting ammonothermal growth of GaN. Approaches for validation are also reviewed, and an overview of available methods and data is given. Fluid flow is likely in the transitional range between laminar and turbulent; however, the time-averaged flow patterns likely tend to be stable. Thermal boundary conditions both in experimental and numerical research deserve more detailed evaluation, especially when designing numerical or physical models of the ammonothermal growth system. A key source of uncertainty for calculations is fluid properties under the specific conditions. This originates from their importance not only in numerical simulations but also in designing similar physical model systems and in guiding the selection of the flow model. Due to the various sources of uncertainty, a closer integration of numerical modeling, physical modeling, and the use of measurements under ammonothermal process conditions appear to be necessary for developing numerical models of defined accuracy.
1. Introduction
The ammonothermal method has initially been developed as a tool for the synthesis and recrystallization of metal amides and metal nitrides, taking advantage of enhanced solubilities of inorganic substances in supercritical ammonia containing mineralizers [1]. Starting from 1995 [2], the ammonothermal process has been increasingly researched as a method for the growth of GaN bulk crystals [3,4,5,6,7,8]. Depending on the choice of mineralizer, it is possible to obtain GaN in its cubic or wurtzite structure [9], although most research has focused on wurtzite GaN. The ammonothermal method is recognized as particularly promising for the growth of GaN with high structural quality by using near-equilibrium conditions [6,10]. On the contrary, impurity concentration and thus conductivity control are particularly challenging due to the closed growth system [11]. GaN has already found widespread commercial application in blue light-emitting diodes, though LEDs are usually grown on foreign substrates [12]. Development of growth technologies for bulk GaN is driven by those device applications for which high dislocation density in the heteroepitaxial nitride structures is a critical issue, such as laser diodes and power electronic devices (in particular, vertical high-power transistors and diodes) [13,14,15,16]. Like the very successful hydrothermal method for the growth of oxides such as quartz and ZnO [1,17], the ammonothermal method also has the potential to grow a large number of crystals simultaneously [17]. Due to its scalability, the ammonothermal method is still believed to have the potential to become a strong competitor for halide vapor phase epitaxy (HVPE), which is the most common method for bulk GaN growth at present [13]. Recent progress in ammonothermal GaN growth includes a demonstration of scalability to pilot production for simultaneous growth of likely about 100 boules in one reactor [6], a masking technique for circumventing issues related to growth on different facets [18], growth of nearly bow-free crystals (radius of curvature: 1460 m) at pressures as low as 100 to 120 MPa [19], and growth of nearly 4-inch size crystals while keeping off-angle distributions as small as ±0.006° along both a-axis and m-axis [20]. Besides its use for the growth of bulk GaN, the ammonothermal technique is increasingly being utilized for exploratory syntheses of various binary, ternary, and multinary nitride and oxynitride materials [21,22,23], including nitride semiconductors composed of earth-abundant elements [24].
A technical challenge for understanding and optimizing ammonothermal syntheses lies in the difficulty of experimental access to the interior of the autoclave during the process, which is due to the experimental parameters of about 600 °C and 100 to 400 MPa. Therefore, numerical modeling is an important tool for clarifying the actual experimental conditions such as temperature distribution and flow field inside the autoclave. A number of research groups have conducted numerical studies of temperature and flow field [25,26,27,28], partially including further aspects such as the concentration of metastable intermediates [29] and growth rates [29,30]. However, critical issues have not been studied thoroughly in the literature, and validation has been applied only to an extremely limited extent. Therefore, the accuracy of such numerical results remains unclear, preventing simulations from delivering their full potential impact on further development and use of the ammonothermal method for bulk crystal growth. Moreover, it should be noted that natural convection in cylindrical enclosures with laterally heated walls in general is not well studied to date [28,31].
The ammonothermal growth conditions and growth process represent a complex multiphysics problem. For a glossary of common terms and information on multiphysics simulations in general, the reader is referred to a respective review [32]. Moreover, a recent review on conjugate heat transfer simulations can be found in [33], and solvers for coupled porous media flow have recently been reviewed in [34].
Besides the difficult experimental access to internal conditions, the limited number of experiments also represents a bottleneck for scientific and technological progress. Costs for growth experiments are driven by investment costs for corrosion-resistant high-pressure equipment and costs for consumables including seeds and gaskets. A breakthrough in the trustworthiness of numerical simulations of growth conditions and ideally also the growth process itself could therefore tremendously speed up further development.
In the second section of this review, the general functionality of ammonothermal bulk growth of GaN will be described. The third section gives an overview and discussion of numerical studies of flow and temperature field in the literature. Simulations of the growth process or subprocesses thereof beyond the thermal and flow field are reviewed in Section 4. The fifths section covers approaches for validation of ammonothermal simulations. The sixth section shines some light on further, potentially relevant aspects that may affect the accuracy of current CFD (Computational Fluid Dynamics) simulations of ammonothermal growth systems. Finally, a brief conclusion and outlook is be given.
2. Functionality of the Ammonothermal GaN Growth Process
If employed for bulk crystal growth, the ammonothermal method is based on the use of buoyancy as the driving force for convective mass transport and a solubility difference as the driving force for recrystallization (i.e., dissolution of the nutrient and crystallization on the seed crystals). Figure 1 schematically illustrates the functionality of ammonothermal growth in the current common understanding, for growth in the temperature range of retrograde solubility. It should be noted that the transport of gallium requires the assistance of a mineralizer to promote its solubility, likely by the formation of complex ions [35,36,37,38], which appear to aggregate under ammonothermal process conditions [38,39]. The temperature dependence of solubility depends on the mineralizer and may comprise both a range of normal solubility at lower temperatures and retrograde solubility at higher temperatures. Such transitions from normal to retrograde solubility have been observed experimentally at least when using the ammonium halides NH4Cl [40] or NH4F [4]. Besides high-temperature versions of ammonoacidic growth, ammonobasic growth also operates in the retrograde solubility range [9], albeit at lower absolute temperatures and higher pressures than ammonoacidic growth.
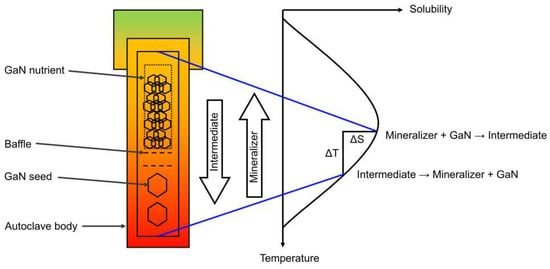
Figure 1.
Basic functionality of ammonothermal GaN bulk growth process. Recrystallization of GaN takes place in an autoclave using a temperature gradient to create a driving force for dissolution and crystallization in different zones of the autoclave. Mass transport of Ga is achieved by the formation of soluble intermediates and their transport by natural convection of the fluid.
Although numerical simulations have so far focused on the (quasi-)steady stage of the growth process, one should be aware that this is not the only relevant stage of an ammonothermal growth run. Experimental procedures suggest that etch-back of the seeds during early stages of the experiment is also important, given that experimenters deliberately use a back-etching step prior to allowing nucleation on the seeds [41]. Therefore, transient stages of the experiment such as ramp-up and sometimes a process step with inverted external temperature gradient appear to be critical steps of the process. A schematic representation of a temperature program suitable for growth in the retrograde solubility range is depicted in Figure 2, following the temperature program presented by Grabianska et al. for basic ammonothermal crystallization developed at Institute of High Pressure Physics Polish Academy of Sciences [41]. Besides giving an example of the externally applied temperature program, Figure 2 also illustrates the fact that internal temperatures differ from externally controlled temperatures. The schematically indicated mean internal temperatures are based on the assumption that convective heat transfer will reduce internal thermal gradients compared to the externally applied ones, which is in agreement with a numerical study by Chen et al. [42], among others. The inset in Figure 2 visualizes an effect that is not only likely relevant to the growth process itself but also of practical importance for numerical simulations. Several numerical studies suggest that the fluid flow can be highly oscillatory, at least in certain regions of the autoclave, such as in the vicinity of the baffle. This is in agreement with experimental observations, though the experimental results suggest that the temperature and flow fluctuations may not follow a regular, oscillatory pattern [43]. From a growth point of view, instabilities of fluid flow may have different effects depending on their location. Mirzaee et al. consider them to be potentially beneficial for mass transport across the baffle if occurring in that region but assume them to be detrimental if occurring in the vicinity of the seeds [29]. In the authors′ opinion, instability of fluid flow should not be required even in the baffle area if the areas with upward and downward flows are well-balanced and allow for sufficient mass flow; however, it does not seem fully clarified whether they are avoidable under all other constraints. From the viewpoint of numerical simulations, the fluid flow′s susceptibility to instability poses a challenge because it makes transient simulations prone to requiring rather small timesteps while instable flow occurs. The need for small timesteps, in turn, makes it difficult to keep computation times of transient process simulations in a reasonable order of magnitude.
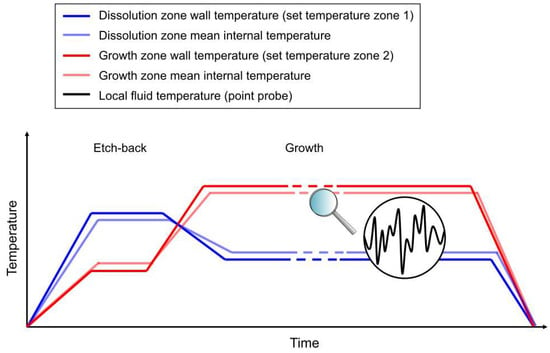
Figure 2.
Schematic representation of the temperature program used for ammonothermal growth of GaN in the retrograde solubility range. The externally controlled temperature program (set temperatures) is based on [41]. The mean internal temperatures are not known but intended to indicate that there is a difference between internal and external temperatures, with the internal gradient likely being smaller than the externally applied gradient due to convective heat exchange between the two zones. The round inset visualizes that local fluid temperatures are often unstable and may not even follow a strictly oscillatory pattern, on the basis of [43] and references therein.
3. Simulations of Fluid Flow and Temperature Field
In the following, literature on simulations of fluid flow and temperature field will be reviewed. A description of ammonothermal equipment will also be included at the beginning, in order to explain and discuss common simplifications in simulations.
3.1. Simulation Domain and Geometry
The experimental geometry of ammonothermal setups for bulk growth of GaN is generally some variation of the setup depicted in Figure 3a, which is based on several articles from the literature [4,20,44,45] and the experience of the authors. The internal configuration shown in the figure is valid for the case of retrograde solubility of GaN. Essential elements of an ammonothermal growth setup comprise the autoclave in the vertical orientation, a furnace that allows a temperature gradient to be established in the axial direction of the autoclave, and a head assembly with peripheral devices. The latter are needed for pressure monitoring and the removal and introduction of gaseous substances and are usually connected by stainless steel pipes.
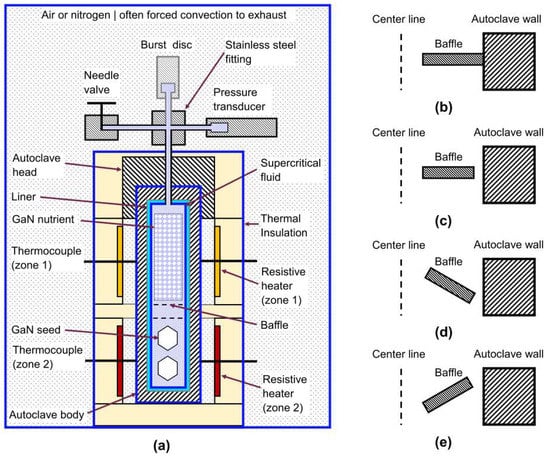
Figure 3.
Setup for bulk crystal growth of GaN using an ammonothermal method. (a) Complete setup consisting of autoclave with head assembly in a furnace, which are usually surrounded by some enclosure filled either with ambient air or nitrogen. The illustration assumes retrograde temperature dependence of solubility (in case of normal solubility, the locations of GaN seeds and nutrient would be inverted). Thick blue lines represent possible choices for the boundaries of the simulation domain. Parts drawn with gray line color (burst disc, insulation of autoclave head, liner) are optional and may not be used, depending on the mineralizer and safety concept. (b–e) Baffle geometries considered in simulation literature: (b) ring-shaped baffle directly attached to the autoclave wall, (c) ring-shaped baffle with a gap between baffle and autoclave wall, (d) funnel-shaped baffle with a gap between baffle and autoclave wall.
The entire setup is commonly run inside an enclosure (or adequate separate room free of personnel) in order to protect operators from shrapnel and toxic gases in case of mechanical failure of high-pressure parts. Such enclosures may be run as a fume-hood-like system with ambient air if permittable from a safety point of view. Since common safety concerns include prevention of formation of explosive gas mixtures in the proximity of possible sources for ignition and leakage of toxic gases outside the enclosure, high air turnovers are usually chosen if using air-filled enclosures [46]. Alternatively, enclosures can be designed to provide an oxygen-free (e.g., nitrogen) atmosphere, e.g., for autoclaves made of molybdenum alloys [47].
Besides the reaction medium, the interior of the autoclave contains GaN nutrient, GaN seeds, and (ideally inert) parts for flow control and for positioning GaN nutrient and seeds. Flow control is achieved using one (e.g., [48]) or more (e.g., [44,45]) baffles, which are often axially symmetric. However, examples of non-axially symmetric baffle assemblies are occasionally shown [45]. Numerical simulations have focused on axially symmetric baffles [25,26,27,29,30,42,49,50,51,52,53], in part likely for taking advantage of axial symmetry in 2D simulations. Different types of baffle configurations that have been applied in the simulation literature of ammonothermal GaN growth are depicted in Figure 3b–e. Specifically, experimental setups typically exhibit a thin gap in between the inner autoclave wall and the outer edge of the baffle (Figure 3c). Some numerical studies have neglected this gap (likely for simplifying the mesh and avoiding related issues). However, others have included it and found significant flow to occur through this gap [27,52,54], which is in accordace with an experimental observation by Masuda et al. that a small gap between baffle and autoclave wall is required for successful crystal growth experiments [53]. Moreover, funnel-shaped baffles (Figure 3d–e) have been studied numerically in 2D [51] and 3D [26] but there seem to be no experimental studies on inclined baffle geometries.
For numerical simulations, different sub-regions of the experimental setup can in principle be selected as the simulation domain, depending on the questions to be answered as well as on computational resources. Domain boundary choices found in the literature are the inner or outer autoclave wall, the wall of the furnace or a gas volume surrounding the furnace and head assembly. The implications of these choices as well as examples are discussed in Section 3.3, as the definition of domain boundary is closely linked to the definition of domain boundary conditions.
Components that have so far usually been neglected in simulation literature comprise the liner or corrosion-resistant capsule (if applicable), as well as the head assembly. However, Moldovan studied an ammonothermal setup with a silver liner [55]. Moreover, simplifications of geometry are applied, especially for obtaining axial symmetry. Typical examples are the head assembly and pipes, which are completely neglected in most models, as well as the seed crystals. The effects of the head assembly, and especially its horizontal parts with the biggest lack of axial symmetry, can be expected to have rather symmetric effects on the thermal field inside the autoclave. In the author′s opinion, the most relevant effect of the head assembly should be thermal losses, because the parts are not insulated and kept at temperatures from room temperature to about 150 °C due to the limited high-temperature strength of stainless steels. Changes in the magnitude of heat losses through the head assembly have been found to trigger changes in the crystallization of reaction products inside the nickel base alloy tube that connects the autoclave head and the central fitting of the head assembly [56]. The magnitude of such heat losses must be expected, depending on the temperature of the ambient in its surrounding, the gas turnover in the vicinity of the furnace, and on the presence of heat-conducting connections to cooler parts (such as for filling or for fixing the setup mechanically, depending on the specific facilities). Those heat losses are likely approximately axial symmetric. However, they are likely not negligible, and thus, sound estimates of their magnitude may be necessary for obtaining accurate results.
3.2. Axisymmetric 2D Calculations versus 3D Calculations
It should be noted that there is still an active discussion on the need for 3D calculations and the limitations of 2D calculations for simulations of thermal field and flow field in ammonothermal systems. Several groups have so far focused on 2D calculations [25,27,29,57], taking advantage of their much lower computational cost. In their 2008 review on modeling of crystal growth processes in general, Chen et al. suggest the coupling of a 2D axisymmetric global thermal field model with a 3D model for the fluid flow, among others, for ammonothermal growth modeling [58]. Experimentally validated simulations of an ambient pressure model of a hydrothermal crystal growth reactor reveal transient 3-dimensional fluid flow but also conclude that the time-averaged flow and temperature fields are axially symmetric, if only axially symmetric solids are considered [59]. However, it appears reasonable to expect a need for 3D calculations at least if effects of not axially symmetric parts are considered. This is the case for seeds, which are usually flat cuboids initially and tend to develop facets during the growth run [5]. Very recently, there have been reports on the use of round seeds and limiting the growth to one direction in order to eliminate the stress generated in crystals due to inhomogeneous incorporation of impurities [41]. In this case, however, it appears that the axis of the round seeds remains perpendicular to the axis of the autoclave and thus the symmetry axis of the simulation domain. Thus, the seeds remain a not axially symmetric element. One of the objects with the largest deviations from axial symmetry therefore also constitutes a primary region of interest to the crystal grower. A few groups have done 3D calculations and concluded that 3D calculations are necessary for obtaining accurate results on the heat and mass transport inside the autoclave [26,31]. It should be noted that these simulations did not even contain any not axially symmetric solids [26,31]. The study by Enayati et al. uses an experimental model with water as both the working fluid inside the enclosure and as a means of wall temperature control [31]. Using this experimental transparent setup, Enayati et al. present validation data obtained using tracer particles and a laser-based imaging system [31]. The validation data fit the experimental data rather well, supporting the numerical results as well as the chosen heater-long constant temperatures as a boundary condition. It should, however, be noted that the adiabatic walls at the bottom and especially at the top of the enclosure may represent a major deviation from actual ammonothermal growth setups. As recently reported by Schimmel et al. thermal losses through the autoclave head and head assembly appear to have a significant influence on the temperature distribution of the autoclave walls [57]. Therefore, both the experimental and the numerical model may not be an accurate representation of a typical solvothermal growth reactor. Despite the decent validation, it is therefore not clear to what extent the results can be applied to ammonothermal growth. The study by Erlekampf et al. provides validation data by several internal temperature measurements in an actual ammonothermal autoclave [26]; however, the temperature configuration used (inverted temperature gradient in relation to common practice in solvothermal bulk crystal growth) raises the question of whether the agreement between numerical and experimental data remains similar if a buoyancy-promoting orientation of the temperature gradient was used.
3.3. Boundary Conditions
Depending on the choice of simulation domain, boundary conditions can be fixed temperatures at the domain boundaries or other objects, heat sources of fixed or adjustible power density, and conditions pertaining to gas exchange and radiative heat losses across the domain boundaries. A schematic overview of types of boundary condition found in the literature is given in Figure 4.
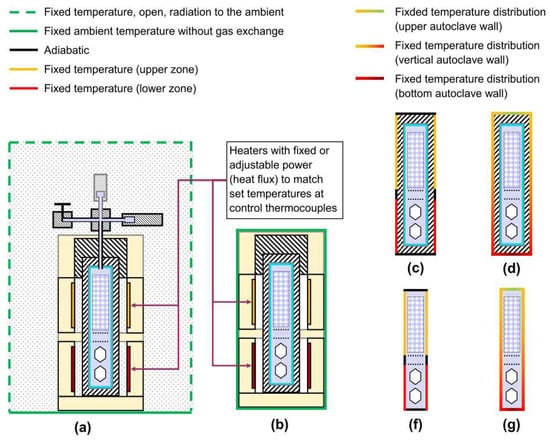
Figure 4.
Boundary conditions for different choices of the simulation domain. (a,b): fixed heater power densities; (a) allows for gas exchange via open boundaries as well as radiative losses to the ambient, whereas (b) uses a fixed temperature of the domain boundary, (c,f) heater-long constant fixed temperatures and adiabatic walls elsewhere, (d,g), fixed temperature distributions at all walls, and (c,d) show simulation domain including the autoclave wall, whereas (f,g) represent simulation domain excluding the autoclave walls.
Until recently, almost all simulation studies in the literature chose either the inner or the outer autoclave wall as the boundary of the simulation domain [25,27,29,60]. Most studies employ fixed temperatures for major sections of the outer autoclave walls [25,29,50], usually corresponding to the length of heaters. A study of hydrothermal fluid flow uses a step function to account for thermal gradients in autoclave walls but fixes temperature at the inner wall of the autoclave [61], therefore completely neglecting the influence of convective heat transfer on inner wall temperatures. A validated simulation of a hydrothermal model system has been reported by Ursu et al. and works with fixed temperatures for hot and cold zone [62]. However, the model setup used by Ursu et al. can be expected to create rather homogeneous wall temperatures because a recirculating water bath is used for heating. Thus, the model setup may be an accurate representation of the numerical model but not necessarily of the actual hydrothermal growth setup. Erlekampf et al. were the first to publish a numerical study of an ammonthermal reactor that includes the furnace in a 2D simulation of the global thermal field and uses heater power density as the heat source [26]. Moreover, they provided at least some validation using the actual ammonothermal setup [26]. However, convective heat transfer was apparently neglected in the 2D simulation. For their subsequent 3D simulation, Erlekampf et al. chose the inner autoclave wall as the domain boundary, using the temperature distribution from their 2D model as the boundary condition [26]. Most recently, Schimmel et al. reported a first 2D simulation that expands the domain boundary even further in order to investigate the temperature distribution in the autoclave walls [57].
In summary, the different groups made different choices about what to neglect in order to create a sufficiently simple model. However, there is no comprehensive information in the literature as to which choices are most reasonable and how they affect the results. Based on the recent publication by Schimmel et al. [57], it appears that outer wall temperatures can be an effective and reasonably efficient choice but require knowledge of the temperature distribution in the outer autoclave walls rather than just knowledge of the heater set temperatures.
3.4. Physics and Models Thereof
In principle, the physics involved that may influence the thermal field and flow fields include heat conduction in solids and fluids, natural convection, and potentially radiative heat transfer. The relative importance of those effects depends on the choice of simulation domain. Specifically, radiation is relevant if the furnace is included in the simulation and if the setup features air-filled gaps in between heat sources and autoclave walls as in [57]. In most published studies, however, the border of the simulation domain was placed at the outer or inner autoclave walls, and radiation was not deemed to be relevant.
Regarding natural convection inside the autoclave, appropriate models for the fluid flow must be chosen for the solid-free regions as well as for the porous medium constituted by the nutrient. In principle, the Navier-Stokes equations need to be solved. As recently discussed in further detail in [57], fluid flow under ammonothermal process conditions is likely in the transition range between laminar and turbulent flow, and turbulent flow is very likely to occur at least in some regions of the cavity or under some experimental conditions. In practice, with limited computational resources, it is important to apply suitable approximations rather than Direct Numerical Simulation (DNS), which simulates the whole range of the turbulent statistical fluctuations at all relevant physical scales [63]. Approximations for turbulent flow include Large Eddy Simulation (LES) and Reynolds Averaged Navier-Stokes (RANS) models ([63], p. 90). The former, LES, directly simulates turbulent fluctuations above a certain length scale and models those below this length scale ([63], p. 87). The modeling at the so-called subgrid scale employs semi-empirical laws ([63], p. 87). The latter, RANS, is restricted to the simulation of time-averaged turbulent flow ([63], p. 90). While being computationally most efficient, it should be noted that RANS simulations require empirical or at least semi-empirical information on the turbulence structure and its relation to the averaged flow ([63], p. 88f). A review of RANS models can be found in [64]. Regarding simulations of solvothermal flow fields, Enayati et al. used 3D LES, among others, for studying the effects of baffle on temperature distribution and flow field [31,49] as well as for studying the effects of a rack and seeds [65] and of reactor size [60]. For comparing the results of 2D and 3D calculations, Enayati et al. employed a RANS model [31]. Likewise, the majority of ammonothermal flow and temperature field calculations have utilized different RANS models. Pendurti et al. estimated the flow to be turbulent and applied a renormalized group k-ε model [30]. Masuda et al. use a modified production k-ε model to model turbulent flow in ammonothermal and hydrothermal growth, which compensates for the over estimation of the formation near the stagnation point that appears in the standard k-ε equations [51,66]. Enayati et al. apply k-ω shear stress transport (SST) turbulent model for studying the effects of position and permeability of a porous medium in a laterally heated reactor for crystal growth [67]. Recently, Schimmel et al. have applied the relatively simple, yet computationally efficient LVEL (Length-VELocity) turbulence model for studying global heat transfer in an ammonothermal growth setup including the furnace [57]. The LVEL model constitutes a zero-equation low Reynolds number turbulence model, which is valid over the laminar, transitional, and turbulent flow regimes and is particularly well-suited for fluid domains cluttered with solids [68], thus facilitating the study of the complete ammonothermal growth setup in a computationally affordable way. Viewing these studies, it is, however, important to keep in mind that there is a lack of knowledge on fluid properties under process conditions, which causes uncertainties in the dimensionless numbers characterizing the flow. Given the lack of experimentally validated flow simulations in conjunction with the uncertainties in fluid properties, it remains uncertain what flow models should be applied, and whether those remain the same for all experimental conditions. Quantification of uncertainties due to various modeling assumptions (including but not limited to turbulence models) is also lacking. For RANS models in general CFD applications, however, a review of the quantification of model uncertainty has recently been published by Xiao et al. [69].
Besides models for free laminar or turbulent flow, porous media flow occurs within the GaN nutrient and is coupled with the free flow through all other fluid-filled regions of the cavity. Grain sizes of nutrients in experimental research are rarely disclosed; however, Pimputkar et al. state 1.0 to 2.8 mm nutrient grain sizes for a 25 mm by 280 mm cavity, for ammonobasic growth using sodium as the mineralizer [70]. The scarcity of disclosure by experimenters suggests that nutrient grain size is a critical variable. This appears perfectly reasonable, knowing that the flow in the nutrient depends on the product of the Grashof and Darcy numbers, which is proportional to the square of the average diameter of particles [71]. The flow strength in the porous layer can be enhanced by increasing the size of the particles, or by putting particles in bundles as in the hydrothermal growth [71]. Indications of applying such a bundling approach appear occasionally in figures in publications on experimental results (e.g., Figure 5a in [41]), but no details or underlying considerations are commonly given. In numerical simulations, Masuda et al. considered a porous medium with a grain diameter of 5 mm and a (nondimensional) porosity of 0.7 [53]. In their model, the drag that is produced by the fluid passing through the porous medium is considered as pressure drop, which is determined by the equation of Ergun [53]. Darcy′s equation with Brinkman extension to account for viscous diffusion [72] (relevant in the vicinity of interfaces [73]) and Forchheimer extension for inertial effects at the microscale [73,74] was applied by Mirzaee et al. [29], Chen et al. [52] and Enayati et al. [67]. Erlekampf et al. used the Darcy model with only the Forchheimer extension [26]. Both Forchheimer and Ergun equations include both viscous and inertial effects that can describe porous media flow in low- to high-velocity regimes for laminar, transitional, and turbulent flow [75]. Deviations appear to occur if the flow has a pronounced contracting/expanding character, which is better captured by the Forchheimer equation [76]. A contracting/expanding character of the flow is promoted by high localization of the pressure drop in the gap between adjacent particles and thus is most pronounced at low porosities close to maximum packing [76]. Therefore, using Ergun or Darcy′s law with Forchheimer extension appears equally justified if the porosity of the nutrient is not exceptionally low. As for Brinkman′s extension, Auriault showed in a focused analysis that the domain of validity is limited to flows through swarms of fixed particles or fixed beds of fibers at very low concentration and under further specific conditions [77]. Similarly, Battiato et al. conclude that the validity domain of Brinkman′s equation corresponds to porous media with very large porosity and very small solid concentration [74]. Thus, there appears to be no benefit of using Brinkman extension unless the porous medium has or develops a large porosity (which may, however, occur at late stages of a growth run).
3.5. Discretization in Space and Time
Discretization in space is usually done by the finite volume method (FVM). This method discretizes the integral formulation of the conservation laws directly in physical space and uses cell-averaged values as its main numerical quantities ([63], p. 203), with the unknowns defined either at the cell centers or at the mesh nodes (termed cell-centered and vertex-centered, respectively) [78]. An alternative approach would be the use of the finite element method (FEM), which uses the local function values at mesh points as its main numerical quantities ([63], p. 203). The reasons for the popularity of the FVM in CFD are its generality, its conceptual simplicity, and its ease of implementation for arbitrary structured or unstructured grids ([63], p. 203). Regarding the computational costs, there are relatively few studies, with contradictory results. Gohil et al. who compared FVM and FEM calculations of a complex geometry using an unstructured mesh and considering both steady and oscillatory flows, state that their FEM calculation arrived at the pre-specified target accuracy much faster than its FVM counterpart [79]. Gohil et al. conclude that the faster convergence of FEM is likely in part due to the coupled treatment of the mass and momentum equations, which is a fundamental property of FEM [79]. Others have reported opposite observations [80,81]. However, the computation time to reach a specified accuracy is rarely reported, even though it appears to be the most reasonable metric for such a comparison.
While structured grids offer advantages in the efficient use of memory and potentially also time, structured grids have drawbacks when complex geometries are to be meshed [82]. In the case of the ammonothermal method, this becomes increasingly relevant as one attempts a more realistic implementation of internal solids (such as several seeds, seeds in 3D, baffles that are not necessarily always axially symmetric, etc.). Moreover, structured grids cannot grade cell size as rapidly as unstructured grids, causing an increased number of cells [82] if there are regions that require very different cell sizes. In the ammonothermal case, this can, for instance, be relevant to global heat transfer simulations because of the different length scales inside the autoclave, in the furnace and outside the furnace.
For the interior of the autoclave, some estimates of functional cell sizes can be extracted from the literature, though they can of course vary considerably depending on the model and question to be answered. Pendurti et al. state that a mesh size of 0.4 mm is sufficient to resolve the laminar sublayer within the turbulent boundary layer in the proximity of a seed crystal [30]. Mirzaee et al. who employed a quadrilateral mesh, chose a mesh size of 50 × 250 in radial and vertical directions on the basis of a mesh convergence study using GaN growth rate as the monitored quantity for determining mesh convergence [29,83]. This corresponds to average cell dimensions of 0.762 mm in the radial and 1.524 mm in vertical directions, respectively. Mesh concentration was applied near the inner autoclave walls to account for larger temperature and velocity gradients expected near solid walls, whereas a uniform mesh was used for the region surrounding the seeds [83]. Moreover, a fine grid was used in proximity of the baffle, where oscillatory flow was observed [83].
In their large eddy simulation of a laterally heated enclosure for crystal growth, Enayati et al. observe a closer agreement of an intermediately fine mesh with experimental results [31], which is unusual given that the accuracy of a numerical simulation generally improves for a finer mesh. They ascribe this effect to insufficient sampling resolution of the experimental data [31].
In the case of transient simulations, a discretization in time is also required. While the growth process itself is transient in nature (albeit slow), there is no evidence of whether fully stable temperature and flow fields develop under specific conditions. This is of practical interest for three reasons. Firstly, if a stable flow and temperature field exists during the main part of a growth run at constant set temperatures, numerical studies addressing temperature and flow field in this main part of the growth run can be investigated by steady computations. Secondly, the stability of the flow and temperature field is also expected to influence the growth process because it will affect the stability of mass transport and the driving force for crystallization. Thirdly, the ability to obtain a steady solution can have practical implications if certain software functionalities are available only for steady or only for transient studies in commercial CFD software. Several numerical studies have shown that the flow shows oscillatory features, at least under certain conditions [26,27,29,50]. More recently, an experimental study has provided experimental evidence that significant fluctuations of local fluid temperature can indeed occur, and the experimental data do not show a strictly oscillatory behavior of these temperature fluctuations [43]. However, these numerical and experimental occurrences of flow instability do not necessarily imply that stable conditions never exist. Masuda et al. have presented steady-state temperature and flow fields for an ammonothermal system with normal solubility [25]. Jiang et al. conducted transient calculations with a variety of open/space ratios of a ring baffle and found that there are oscillations in volume flux [27]. According to their results, the amplitude of oscillations varies with the open/space ratio, and thus this ratio can be used to establish comparatively stable flow conditions [27], though none of them appears to be fully stable. It should be noted that there are two qualitatively different ways in which the flow can be transient under quasi-steady conditions (we define quasi-steady conditions by stable wall temperatures at the control thermocouple locations over an extended period of time). The first possibility is that flow speed fluctuates but flow directions are stable. The second possibility is that flow speeds oscillate around zero, thus changing the direction of flow at a specific location over time. Such oscillations have been reported by Chen et al. [42]. From a general CFD viewpoint, C. Hirsch recommends the use of transient equations unless one can be assured that the flow will remain steady ([63], p. 142f), at least if there is no major advantage in using steady equations.
3.6. Results
In the following, selected results from the literature on flow and temperature field simulations of ammonothermal growth reactors are reviewed. Note that the intent is rather to draw the reader′s attention to likely relevant aspects than to provide a complete overview.
Chen et al. have shown that the position of the nutrient strongly affects the temperature field inside the autoclave and point out that the inversed positioning of dissolution and growth zones for normal and retrograde solubility causes distinctly different temperature fields [42] (not shown here). Moreover, Chen et al. investigated the fluid flow in the vicinity of the baffle for the normal solubility case for different inner diameters of the autoclave [52]. The setup considered by Chen et al. is depicted in Figure 5a. The temperature field is shown in Figure 5b. The average flow velocities in the center hole of the baffle and in the ring-shaped gap between the baffle and autoclave wall are shown in Figure 5c (presumably averaged over the respective cross-section areas). As it can be seen from c, average flow velocities are subject to major fluctuations over time, which vary with the inner diameter of the autoclave [52] and the open-to-space ratio [42]. In spite of the fluctuations in flow velocity, the flow largely remains upward in the center hole and downward in the ring gap [52]. However, Chen et al. also report a case in which the flow direction in the center hole alternates over time [42].
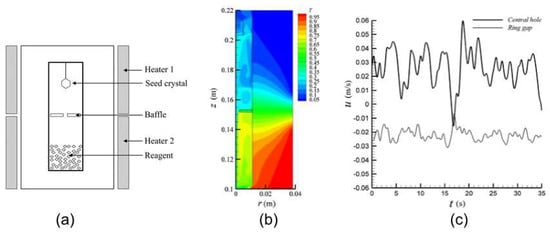
Figure 5.
Setup (a) and simulation results (b,c) by Chen et al. for a reactor with an inner diameter of 2.22 cm and baffle opening of 10%: dimensionless temperature field (b) and average velocity in the central hole and ring gap (c). Reprinted with permission from Springer Nature Customer Service Centre GmbH: Springer Nature Research on Chemical Intermediates [52], Copyright 2011.
Gaps between autoclave wall and baffle as well as between autoclave wall and nutrient have been neglected in some numerical studies; however, as pointed out by Mirzaee et al. the presence of such a gap is a fact of experimental research [29]. Moreover, Masuda et al. cite their empirical knowledge that a small gap is necessary between autoclave wall and baffle [25]. Mirzaee et al. investigated the influence of the gap between autoclave wall and nutrient and concluded that it induces a circulating flow through the nutrient, which lowers the temperature difference but greatly enhances the transport of Ga-containing solutes out of the porous medium [29]. Although the solubility data, flow model and boundary conditions used by Mirzaee may not yet be accurate, this conclusion appears highly plausible. The importance of the gap between autoclave wall and baffle has previously been pointed out by Pendurti et al. who investigated transport in ammonothermal growth [30]. It can be concluded that although thin gaps are undesirable from a meshing viewpoint, it is essential to include the gaps between the autoclave wall and baffle as well as between the autoclave wall and nutrient basket.
Masuda et al. have investigated how the flow field and temperature distribution in the growth zone change with increasing crystal size [25]. They find a transition from one flow pattern to another flow pattern at a specific crystal radius and observe that this change in flow pattern also leads to changes in the temperature distribution in and around the crystal (see Figure 6). Similarly, Mirzaee et al. have also reported significant effects of the geometrical changes of growing crystals on the flow field [29].
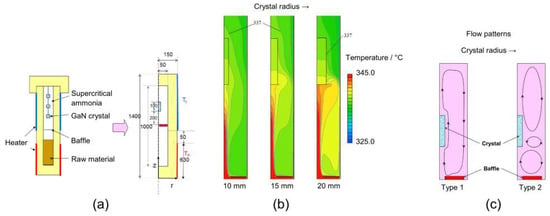
Figure 6.
Effects of crystal size increase in a 2D simulation by Masuda et al. (a) Considered experimental setup and chosen axisymmetric model thereof, (b) temperature distribution in the vicinity of the seed and above the baffle, (c) schematic of the two types of convection patterns that were found to develop for crystal radii below and above about 15 mm, respectively. Reprinted with permission from [25]. Copyright (2016) The Japan Society of Applied Physics.
Erlekampf et al. as well as Enayati et al. have concluded that the fluid flow is three-dimensional even for an axisymmetric simulation domain [26,31]. However, it remains unknown how much those fluctuations on a small timescale affect the results of a growth run. Either way, one can expect three-dimensional flow to have practically relevant effects in the vicinity of the not axisymmetric seeds, where effects of the 3D geometry of the seeds are likely to also affect the time-averaged flow and temperature fields.
In practice, another relevant lack of axial symmetry may arise from the imprecise alignment of the axis of the thermal field of the furnace and the axis of the autoclave. Such alignment issues have been studied for hydrothermal growth by Li et al. who studied an industrial-scale autoclave [84]. Based on measured temperature deviations of around 2 K, Li et al. estimated the heat flux on the outer autoclave wall to vary by as much as 10% [84]. Li et al. conclude that the circumferential temperature variations in an industrial hydrothermal growth reactor are sufficient to establish an asymmetric flow [84]; however, they do not report whether the flow in a 3D model with symmetric boundary conditions and axial symmetry is symmetric or not.
Recently, a study on the effects of thermal boundary conditions was conducted by Schimmel et al. [57]. Following the boundary condition approach illustrated in Figure 4a, a global simulation of the temperature and flow fields was used to determine a realistic temperature distribution at the outer autoclave wall [57]. This temperature distribution was then used as a thermal boundary condition for a less complex model using the approach visualized in Figure 4d. For comparison, the otherwise same model was also solved with heater-long fixed temperatures and otherwise adiabatic walls (corresponding to the approach shown in Figure 4c. The resulting temperature and flow fields are depicted in Figure 7. Two aspects are of general importance. Firstly, the outer wall temperature distributions shown Figure 7a,c are remarkably different from the temperature distribution shown in Figure 7b. This indicates that at least for the studied ammonothermal setup with two heating zones and an uninsulated autoclave head, the wall temperature distribution differs significantly from the idealization of heater-long fixed temperatures and otherwise adiabatic walls [57]. Secondly, it should be noted that the modified thermal boundary conditions do have a pronounced effect on the temperature distribution and fluid flow field in the autoclave cavity [57]. For achieving simulations with reasonable agreement with experimental results, it therefore appears crucial to use more realistic thermal boundary conditions than those that have most commonly been applied in the literature [57]. Figure 5d–f show the corresponding flow fields in the cavity.
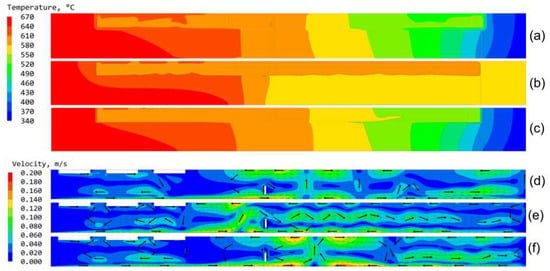
Figure 7.
Comparison of the effects of different thermal boundary conditions applied to the outer autoclave walls. (a,d) show temperature and flow fields of a global field simulation including the furnace and its surroundings, (b,e) temperature and flow fields with heater-long fixed wall temperatures and otherwise adiabatic walls. (c,f) have been obtained using wall temperature distributions extracted from a global field simulation including the furnace and its surroundings with a simulation domain limited to the autoclave. In all cases, three seed crystals and a ring-shaped baffle were considered in an axisymmetric 2D simulation. Major arrows are normalized and serve as a guide to the eye for better visibility. Reprinted from [57].
4. Simulations of the GaN Crystal Growth Process
Pendurti et al. have presented steady-state growth rates for the case of transport-limited growth, on the basis of early solubility data for ammonobasic growth [30]. They note that their predicted transport-limited growth rates are in the order of hundreds of microns per hour, whereas experimentally observed growth rates are in the order of hundreds of microns per day, and ascribe this deviation to neglecting dissolution and growth kinetics [30]. The fact that the grown crystals usually show formation of facets [20,85,86] and the observation that nutrient loss mass flux does not covary with seed mass flux [44] both imply that seeded GaN growth is likely surface-reaction-limited in state-of-the-art growth processes. It is interesting that this holds for both ammonobasic and ammonoacidic process variants, suggesting that there might be a common limiting factor for the growth kinetics. Griffiths et al. pointed out that (at least for ammonobasic growth with Na mineralizer) polar growth rates dominate at low growth zone fluid temperature, whereas nonpolar growth rates begin to approach polar growth rates as temperature increases [44]. However, transport limited growth appears to occur in industrial hydrothermal growth of quartz crystals [84]. Regardless of the limiting factor for growth rates, it should be noted that the simulation by Pendurti et al. is a transient simulation over many hours, as they simulated how etch-back transitions into growth and how stable growth rates are approached [30]; however, it does not constitute a complete simulation of the growth process (such as with a time-dependent temperature program at the autoclave walls). Rather, a transient simulation is used to study how a steady temperature, fluid flow, and concentration field develop, starting from initial conditions, and which steady-state transport-limited growth rate is established as a result.
Mirzaee et al. however, have presented an actual process simulation over a growth time of 100 h and including the advancement of the crystal-solution interface [29], which represents a significant advancement compared to earlier studies that had purely focused on the quasi-steady phase of a growth run without accounting for geometrical changes of internal solids. Specifically, fluid flow, heat transfer, GaN metastable phase transport, dissolution and crystallization rates, and crystal formation have been included in the model by Mirzaee et al. [29]. In agreement with the experience of the first author of the present paper, they state that the needed time step size and thus computation times depend critically on the stability of the fluid flow inside the autoclave [29]. Per 24 h of the growth process, Mirzaee et al. needed CPU times from 0.5 to 3 days, depending on the stability of fluid flow, in spite of using a 2D model (on an Intel (R) 3.52 GHz CPU Seven desktop) [29]. Thus, computation times for the 100 h long process that they considered must have varied from 2 to 12.5 days.
5. Approaches to Validation
At present, there is a lack of experimental validation of simulations that study the ammonothermal growth of GaN, and studies that include only temperature and flow fields are no exception. This issue originates from the difficulty of experimental access to the interior of the autoclave, which represents a critical issue because it affects numerical simulations not only through the lack of validation data but also through a lack of accurate knowledge on physical and chemical quantities of the system. Over the last decade, significant progress has been made in the area of in situ monitoring technology for ammonothermal autoclaves. Alt et al. not only demonstrated local internal temperature measurements using thermocouples but also developed an optical cell suitable for optical measurements such as video optical observations and spectroscopical measurements [87]. Optical cells were further developed by Steigerwald et al. and used for investigating the decomposition of ammonia and ammonobasic solutions under supercritical conditions via UV/vis and Raman Spectroscopy [88]. Besides the optical applications, optical cells have also enabled in situ X-ray imaging with moderate X-ray energies, which has been applied primarily for studying dissolution kinetics and solubility of GaN under a variety of experimental conditions [56,89]. Due to the good X-ray transparency of the applied window materials [90,91], the in situ X-ray imaging method developed by Schimmel et al. allows even for tracking local concentration changes of Ga-containing solutes [39]. More recently, Schimmel et al. have also demonstrated that internal temperature measurements contain additional information beyond fluid temperatures, namely information on the stability of fluid flow and on chemical reactions associated with enthalpy changes [43]. Despite those encouraging developments, a few difficulties for their use for validating numerical simulations remain. Firstly, it would be highly desirable to validate temperature and flow fields; however, both fields are notoriously difficult to obtain with a good special resolution, for the entire interior of an autoclave and without influencing the flow by the introduction of measurement devices such as thermocouples. The latter issue can in principle be addressed by introducing the thermocouples also in the numerical simulation; however, it can require significant adaptation of the mesh, and it becomes problematic for rotational symmetry if thermocouples are to be placed away from the centerline of the autoclave.
Enayati et al. [31] and Moldovan et al. [28] presented an interesting approach of validation via the design of a geometrically and dynamically similar experimental setup that allows for particle image velocimetry-based flow visualizations and thus yields actual flow fields. Moldovan et al. found the flow to be oscillatory in nature but with steady time-averaged patterns [28]. They used the standard deviation of fluid temperatures to assess the magnitude of fluctuations at different locations, and found the fluctuations to be most pronounced in the mixing region between the hot and cold sections [28]. However, it should be noted that two uncertainties remain in this case. Firstly, it is difficult to ensure similarity of ammonothermal growth setup and experimental model due to the limited knowledge of the physics of the ammonothermal system, in particular its fluid properties under process conditions. Secondly, while the model is designed to provide similar thermal boundary conditions as the numerical model, there appears to be a high probability that those boundary conditions may differ significantly from those of the actual ammonothermal growth experiment (see Section 3.6. and [57]). In the author′s opinion, the most important advantage of using a physical model reactor with particle image velocimetry is that it allows for visualizing large parts of the flow field. Although visual access could in principle be implemented for growth reactors, any method that relies on nonmetallic windows (see e.g., [87,88]) will remain restricted in the area of view for the typical pressure and temperature conditions of ammonothermal processes, which represents a severe limitation specifically for flow visualization. The confidence in the similarity of a physical model system would benefit from more detailed knowledge on the outer wall temperatures of the ammonothermal autoclave and on the fluid properties of the ammonothermal fluid mixture. The approach of using time-averaged patterns and local standard deviations of fluid temperatures should also be transferable to in situ validation experiments using internal thermocouples under actual process conditions, such as the one recently presented by Schimmel et al. [43].
Mirzaee et al. state that their code underwent validation by a variety of means as follows. Firstly, the code was tested on natural convection problems for which experimental validation data exist [29], albeit using fluids with better-known properties such as glycerin and water [92]. While being perfectly reasonable for validating most aspects of the natural convection problem, this approach does not represent a complete validation because the uncertainty about fluid properties of the solute-containing supercritical fluid mixture under ammonothermal process conditions is not eliminated. In addition, one also needs to keep in mind that the calculation of supersaturation is based on early experimental solubility data published by Wang et al. in 2006 [93] and that the solubility of GaN under various process conditions remains an active area of research and scientific discussion [56,94]. A second step of validation taken by Mirzaee et al. is using it on a flow pattern in a retrograde solubility ammonothermal crystal growth system that had been presented by Chen et al. [42]. The data published by Chen et al. [42], however, represent a numerical study of unknown accuracy in itself and therefore do not allow for a complete validation either. For validating the interface advancement, Mirzaee et al. utilize the experimentally validated problem of the deformation of the solid–fluid–gas interface in water upon the entry of a solid sphere into water [95]. While the authors of this review wish to encourage all reasonable validation approaches even if yielding only a partial validation, neither one of the validation approaches conducted by Mirzaee et al. can fully confirm the accuracy of their simulation, which is largely due to a lack of knowledge on fundamental aspects such as fluid properties and solubility.
To the knowledge of the authors, no simulation of the entire ammonothermal GaN growth process with comprehensive experimental validation exists to date. Such simulations appear to be limited to much more well-investigated crystal growth processes such as Czochralski growth of silicon, and even for this extremely well-established growth process, they are still an active area of research [96]. It is furthermore interesting to note that even for such well-established crystal growth processes, validation of simulations using physical models also remains an active area of research, as indicated by a recent review by Dadzis et al. [97]. This indicates that even with comparatively well-established material properties, it is not always clear which simplifying assumptions yield the right balance of computational speed and accuracy. The proper choice of assumptions, however, is crucial for developing a simulation that is of full practical use for engineering a crystal growth process.
6. Open Questions That May Affect the Accuracy of Simulation Results
In case of ammonothermal crystal growth and the conditions in respective high-pressure reactors, there are a variety of possible causes for significant deviations of simulation results from experimental observations. Some potentially major sources of uncertainty are discussed in this section. Unfortunately, validation by comparing simulation results to experimental data is feasible only to a limited extent because of the technical difficulty of measuring temperatures, flow velocities, and other simulated quantities during ammonothermal experiments. In addition, while hydrothermal crystal growth benefits from synergies with geological research, this is not the case for the ammonothermal growth of nitrides. Hence, the thermodynamics, kinetics, and fluid properties in ammonothermal systems are still underexplored. Thus, there is a particularly high risk of making inadequate assumptions without noticing it.
In the following, potentially critical issues will be discussed. Related experimental observations will also be mentioned where available.
6.1. Fluid Properties
Ammonothermal crystal growth utilizes supercritical ammonia as a solvent. Pure substance properties will be illuminated first, followed by a discussion of possible deviations due to the presence of decomposition products of ammonia and solutes. Thermophysical data for pure ammonia are available up to 426.9 °C in a database of the National Institute of Standards and Technology (NIST) [98]. To give an overview of how different fill levels alter the pure substance properties of ammonia, Figure 8 shows density, pressure, specific heat capacity, dynamic viscosity, and thermal conductivity at the upper end of the temperature range for which data are available in the database by NIST [98]. The fill level refers to the volume fraction of the reactor filled with liquid ammonia at the boiling point of ammonia (−33.36 °C). It should be noted that even for the temperature range available in the database by NIST, basic properties are still updated occasionally as more accurate data become available [99]. Specifically, the thermal conductivity has recently been found to be about 6% lower than the respective database values [99].
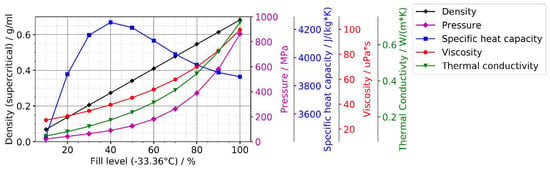
Figure 8.
Properties of supercritical ammonia at 426.08 °C as a function of fill level (data from National Institute of Standards and Technology (NIST) database [98]).
The fill level represents a common quantity used by experimenters for obtaining a specific density of supercritical ammonia or a specific pressure at a specified mean temperature. Figure 9 shows the system pressure resulting from different fill levels as a function of temperature. Fill levels for ammonothermal growth of GaN are typically in the range of 30 to 70%, with those for ammonoacidic growth being lower than those for ammonobasic growth.
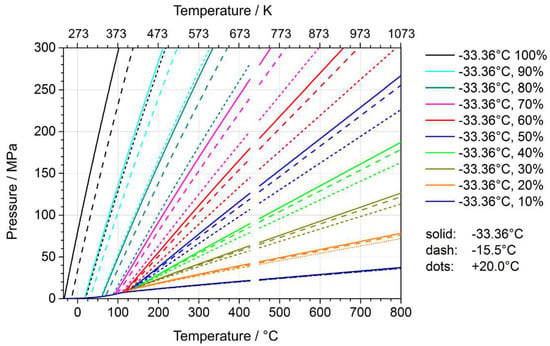
Figure 9.
System pressure for ammonia in a closed system as a function of temperature for fill levels from 10 to 100%, with fill levels referring to three different reference temperatures (reprinted from [46]). The reference temperatures correspond to the boiling point, a typical temperature for the introduction of liquified ammonia using a pressurized system, and room temperature, respectively [46].
Since ammonothermal experiments employ temperatures typically up to 600 °C and sometimes even higher temperatures, extrapolated data are typically used [26,51]. An alternative approach is to simulate the fluid properties themselves. For instance, Masuda et al. have calculated liquid thermal conductivity and liquid viscosity of supercritical ammonia using the chemical process simulator VMGSim produced by Virtual Materials Group [25].
It should be noted that ammonothermal crystallization of GaN is conducted at rather unusual process parameters. Most applications of supercritical fluids, in particular extraction processes, utilize a parameter range that is characterized by a high isothermal compressibility [100]. Specifically, temperatures are typically in the range of 1.01 Tc < T < 1.2 Tc, and pressures are usually in the range of 1.01 pc < p < 1.5 pc [100,101], with Tc and pc representing the critical temperature and critical pressure of the fluid, respectively. For ammonia, this range would be 133.7 °C to 158.9 °C and 11.4 MPa to 17.0 MPa, which is far from the parameter range of ammonothermal growth of GaN [46]. This is illustrated in Figure 10b, which shows the pressure as a function of specific volume for different temperatures.
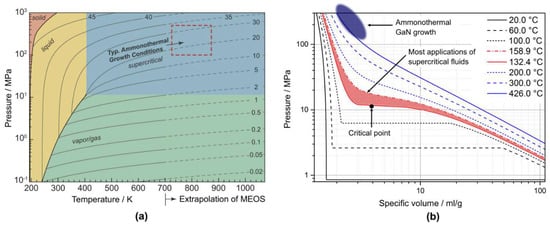
Figure 10.
(a) Phase diagram of pure ammonia with contour lines of density (mol/l) and superimposed phases present at equilibrium. Calculated and extrapolated beyond 700 K using the reference multiparameter equation of state (MEOS) as provided by the National Institute of Standards and Technology (NIST). Reprinted from [102], Copyright 2016, with permission from Elsevier. (b) Pressure as a function of specific volume of ammonia for selected temperatures (reprinted from [46], data from NIST database [98]). The hatched area in red marks the typical application range of supercritical fluids whereas the dark blue region approximately indicates the parameter range of ammonothermal GaN growth.
Given the existence of a much further developed but similar method, the hydrothermal growth of oxides, it appears reasonable to consider whether lacking data can be derived from the knowledge on that method. A comparison of exemplary process parameters for hydrothermal and ammonothermal crystal growth processes shows that the hydrothermal methods operate much closer to the critical temperature. However, both hydrothermal and ammonothermal crystal growth operate at pressures outside the typical application range for supercritical fluids, although this is more pronounced in the case of the ammonothermal method. The described comparison is substantiated by the data given in Table 1.

Table 1.
Process parameters of hydrothermal and ammonothermal growth. In the case of the ammonothermal method, the reports with the highest growth rates as of 2018 were chosen. The temperature dependency of solubility refers to the temperature range used in the growth process. TCZ refers to the crystallization zone temperature, ΔT to the temperature difference between growth and dissolution zones. Reprinted from [46].
In conclusion, it is not clear how accurate extrapolations and simulations of fluid data are, and thus, experimental data on fluid properties would significantly contribute to an increased confidence in the results of numerical simulations of ammonothermal reactors.
While extrapolation of the pure substance properties to higher temperatures may be reasonably accurate for pure ammonia, the question arises whether properties of pure ammonia are a reasonably accurate assumption. During ammonothermal growth, part of the ammonia decomposes, leading to a mixture of NH3, N2, and H2 [102]. Pimputkar et al. have studied this decomposition reaction in a combined numerical and experimental approach to determine an accurate description for the equilibrium constant for the ammonia decomposition reaction as a function of pressure and temperature and verified it against experimental data [102]. The determined equilibrium constant as a function of inverse temperature is shown in Figure 11a. For selected fill densities, the calculated mole fractions of ammonia in equilibrium as a function of temperature are depicted in Figure 11b alongside experimental data. Depending on the materials of the pressure-bearing materials, hydrogen may leave the otherwise closed system by diffusion [102]. When considering the composition of the ammonothermal reaction medium during actual GaN growth experiments, it is important to be aware that different ammonothermal growth environments may cause vastly different kinetics of ammonia decomposition. In other words, any ammonia mole fraction from 1.0 down to the equilibrium value may be present at some point in time during a growth experiment, and there is also a possibility that equilibrium is never reached. The kinetics of ammonia decomposition can be expected to depend heavily on the presence or absence of materials that can act as a catalyst for the decomposition reaction. Specifically, Ni is known to catalyze ammonia decomposition [107]. GaN growth is typically conducted in autoclaves made from nickel-base [9,20,44,48] and sometimes molybdenum-base alloys [47]; however, the autoclave wall is not necessarily in direct contact with ammonia. In order to prevent corrosion of the autoclave wall, as well as in order to minimize the introduction of transition metal impurities, hermetically sealed [108] or pressure-balanced [3,109] liners or capsules of different, more corrosion-resistant materials are often applied. Depending on the mineralizer, platinum [9,40,106], silver [19], or molybdenum [70] are used as liner materials for bulk GaN growth. Besides the catalytic properties of the inner wall, there is also a possibility that the mineralizer itself may affect ammonia decomposition [46]. Given that chlorine is known to poison catalysts of ammonia synthesis and decomposition [110,111,112], NH4Cl (and possibly further acidic mineralizers) might hinder ammonia decomposition [46]. In conclusion, it is not fully clarified how quickly ammonia decomposes under specific growth conditions of GaN. Consequently, it is not always clear which mole fractions of ammonia, nitrogen, and hydrogen should be assumed. To the author′s knowledge, there are also no numerical studies that account for the presence of nitrogen and hydrogen. Moreover, the sensitivity of simulation results to changes in ammonia, nitrogen, and hydrogen mole fractions has not been investigated yet.
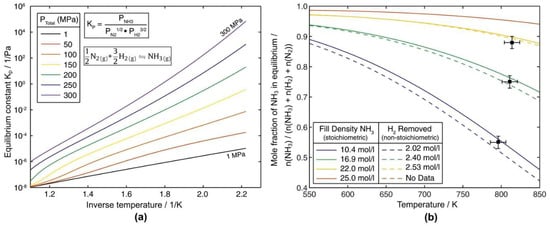
Figure 11.
Data on ammonia decomposition at conditions relevant to ammonothermal GaN growth calculated by Pimputkar et al.: (a) equilibrium constant Kp for the ammonia decomposition reaction as a function of inverse temperature calculated for various total system pressures ranging from 1 to 300 MPa., (b) calculated equilibrium mole fraction of ammonia as a function of temperature and initial fill density, overlaid with three experimentally determined data points. Both reprinted from [46], Copyright 2016, with permission from Elsevier.
Moreover, solutes such as mineralizers and intermediates are essential components of ammonothermal reaction media. In situ measurements of Ga-intermediate concentrations and diffusive transport velocity indicate that there may be a significant increase in fluid viscosity when mineralizer and Ga-containing intermediates are present in the solution [39]. In situ measurements using a rolling ball viscosimeter have been shown to be feasible [113], but no viscosity data for typical solutions are available in the literature yet.
Besides the unknown influence of solutes on fluid viscosity, there is also uncertainty about the optical properties of the solution and hence about the relevance of heat transfer to and through the fluid via radiation. In simulations, the fluid is commonly assumed to be clear [29] and radiation is usually neglected. However, at least with NH4Cl mineralizer, optical in situ measurements have shown that the optical transparency of the fluid decreases rapidly as temperature is increased, which is ascribed to increasing concentrations of solutes [87]. Though no measurements of transparency of infrared radiation have been reported, significant absorption of the fluid cannot be excluded and may be specific to the chemical species present.
An additional possibility is an altered heat capacity in the presence of solutes, as suspected by Alt et al. who performed temperature measurements with thermocouples directly in the fluid and compared experiments with and without NH4Cl mineralizer [87]. However, Alt et al. do not comment on the reproducibility of their experiments, and the temperature deviations cannot unambiguously be assigned to a possible change of heat capacity.
Last but not least, there is also a possibility that the ammonothermal reaction medium contains nanoparticles, as suspected in a study that combined experimental observations by in situ X-ray imaging with molecular dynamics simulations [39]. In recent years, nanofluids have been researched intensively as heat transfer liquids, as they often exhibit a strongly increased thermal conductivity with respect to the base fluid [114]. Moreover, thermophoresis plays a significant role in heat transfer and convection in nanofluids, as shown by J. Buongiorno [115] and studied further from a thermodynamics viewpoint by E. Bänsch [116]. Thermophoresis leads to a reduced concentration of particles in the proximity of hot walls, if they exhibit a significant thermal gradient to the fluid [115,116] (which can be expected in the case of autoclave walls, especially in the growth zone in ammonothermal growth). The locally reduced particle concentration in turn leads to a locally reduced viscosity; thus, thermophoresis enhances transport in the boundary layer [115,116]. Potential effects of nanoparticles in the solution have not been considered in any macroscale simulations so far.
6.2. Possible Relevance of Solutal Buoyancy
Since there are strongly deviating data on solubility of Ga (see Section 6.3, Solubility of the Metal), a possible contribution of solutal buoyancy can only be gauged with limited accuracy. Solutal buoyancy may have different effects for growth in the normal and retrograde solubility regimes, as the targeted transport direction of the metal is inversed with respect to gravity. A solutal contribution to convection should be more pronounced at low ammonia densities for a given Ga concentration; however, this may be compensated by the increase of solubility with increasing solvent density. For a rough estimate of whether solutal buoyancy can be expected to play a significant role, we attempt to quantify the range of local density differences under ammonothermal growth conditions of GaN based on thermal gradients and resulting differences in solute concentration. For local density differences of ammonia, we build on internal temperature measurements in an actual growth setup presented by Griffiths et al. [44]. According to this ammonobasic GaN growth study, growth becomes transport-limited at fluid density differences below 1.2 mol/L between dissolution and growth zone (based on extrapolation of NIST fluid density data of pure NH3). For lack of data on Ga concentration differences under actual growth conditions, we utilize data on the solubility limit of Ga, which were obtained under ammonoacidic conditions using NH4F mineralizer [39]. While the effect of solutal buoyancy may be smaller in reality (as there is likely no region in the autoclave with zero concentration of dissolved Ga), this consideration should be sufficient to elucidate whether solutal convection is likely to be of relevance. The results of this estimation are presented in Table 2. Accordingly, solutal buoyancy may very well have a significant impact, as the density increase due to Ga-containing solutes reaches the same order of magnitude as the density difference of pure ammonia that is induced by thermal gradients.

Table 2.
Estimate of temperature-induced density differences (labeled “supercritical NH3”) between growth and dissolution zone, and solute-induced density differences (labeled “dissolved Ga”).
6.3. Solubility of the Metal
For simulations that include mass transport of the metal (which has already been attempted [29]), an additional uncertainty arises from the limited and deviating data on the solubility of the metal. An overview of available data and investigated parameter ranges is given in Table 3. Although there are several reports on GaN solubility under ammonothermal conditions, the different reports cover widely scattered but not nearly comprehensive parameter ranges regarding important variables such as solvent density or pressure, mineralizer concentration, mineralizer substance, and temperature. Different methods have been applied, aiming at obtaining reliable quantitative solubility data; however, data do not appear to be in good agreement yet, and there is an ongoing discussion on causes of measurement errors [56,89,94,117]. There are two aspects that are especially important to numerical simulations of the growth process: the temperature dependency of solubility and its absolute magnitude. The existing solubility studies have mostly focused on limited parameter ranges to function as guidance for experimental research in individual laboratories, for which the semi-quantitative change of solubility with certain parameters such as temperature or mineralizer concentration is most important.

Table 3.
Overview of data range of GaN solubility under ammonothermal conditions (reprinted from [46] with added data from new publication [117]). Values marked with an asterisk have been converted to the respective unit. For normalization to volume, the volume of the reactor was used.
The temperature dependency of solubility governs the (super-)saturation field and is therefore critical for the driving forces for both dissolution and crystallization. If only a single solute species dominates solubility for a range of temperature, the heat of solution is directly related to the temperature dependency of solubility via van ′t Hoff equation, and for such cases, the heat of solution has been determined experimentally [9,117,118].
The absolute magnitude of solubility for a given set of parameters is also relevant because it governs the concentration field. The concentration field together with the flow field determines the mass transport by diffusion and convection. In addition, the absolute magnitude also affects the question of whether solutal buoyancy plays a relevant role or not.
It remains to be said that a comprehensive database of solubility would be valuable, especially for numerical studies of the growth process. In such a database, solubility should be available as a function of solvent density, mineralizer concentration (or possibly acidity or alkalinity of the solution), mineralizer substance, temperature, and possibly pressure. In hydrothermal systems (studied in geological contexts), the solubility of different minerals is known to depend either primarily on acidity/alkalinity or primarily on pressure and temperature, and solubilities have also been studied through numerical modeling [119]. A combination of further clarification of solution chemistry, numerical modeling, and experimental validation of selected conditions may eventually provide comprehensive data on ammonothermal solutions with sufficient accuracy for the use in growth process modeling. Both experimental and numerical investigations in the context of ammonothermal solution chemistry have recently been conducted [38,120,121] and represent important first steps in this direction.
6.4. Dissolution and Growth Kinetics
Regarding growth kinetics, Griffiths et al. have investigated growth kinetics in a kinetically limited ammonobasic regime and determined activation energies by Arrhenius analysis of the temperature dependency of seed mass flux [44]. Dissolution kinetics appear to be more difficult to analyze based on growth runs. Griffiths et al. mention the complication that source loss flux includes not only contributions to seeded growth but also contributions to parasitic deposition and Ga loss e.g., to autoclave walls [44]. In addition, in our view, it appears difficult to distinguish dissolution limited by surface kinetics from dissolution limited by transport in a growth experiment. In a methodically different approach in the context of solubility studies, dissolution kinetics of GaN under selected ammonothermal conditions have been investigated by in situ X-ray imaging [46,56,89]. While this yields direct, nearly real-time observation, the sluggish thermal response of the thermal mass of the autoclave and the difficulty of distinguishing kinetically and transport-limited regimes so far have prevented the extraction of kinetic parameters such as activation energies from in situ X-ray monitoring results. Altogether, data on dissolution and growth kinetics in ammonothermal GaN growth remain sketchy and do not yet provide a sufficient basis for growth process modeling for most experimental parameters.
7. Conclusions and Outlook
In conclusion, progress in the following three areas is required before a fully trustworthy numerical simulation with known accuracy and known limitations can be realized. Firstly, a variety of physical and chemical questions need to be addressed. Secondly, technical issues of numerical simulations need to be resolved. Thirdly, validation data need to be obtained via in situ measurement techniques and physical model systems. In particular, sound knowledge on fluid properties of the respective solute-containing mixtures under process conditions (or, alternatively, a proof of negligible deviation in properties from pure substance data in the available temperature range) would significantly increase the confidence in the results of both numerical simulations and physical models.
While establishing numerical simulations of known accuracy represents a great challenge, one should keep in mind that once those obstacles have been overcome, numerical simulations could become an incredibly useful tool for the further development of ammonothermal crystallization processes. Besides facilitating scale-up in the industrial use of the method, numerical simulations also hold the potential to achieve comparability of results from laboratories around the world through the sharing of internal experimental conditions. This could tremendously speed up development, especially in collaborative research. At least within collaborations, data exchange is often feasible, but there is often a lack of comparability or knowledge of the internal process conditions. Since experimental setups often cannot follow identical designs due to different requirements of each collaborative project or measurement technique, reliable numerical simulations would be extremely helpful for comparing or combining results from different experimental setups in a meaningful way.
Given the number of unknowns, validation of simulations is deemed to be essential for establishing reliable simulations of known accuracy. A feasible approach for obtaining rather comprehensive validation data for numerical simulations, including mass transfer of GaN is seen in the application of high-energy computed tomography [125] in conjunction with internal temperature measurements [43,44] while using outside wall temperature measurements for heater control. It is, however, important to note that a transient simulation, ideally even in 3D, would be necessary in order to take full advantage of such an approach for validation. The reason is that the information that becomes accessible by computed tomography for the entire autoclave volume is the distribution of solid GaN as a function of time. Therefore, the obtainable primary information is essentially validation data for a transient simulation of the entire growth process. Due to the number of unknowns as well as the need for balancing computational cost and accuracy, it is entirely possible that the agreement of simulation results and experimental validation data will initially be mediocre or possibly even poor. It would then be necessary to identify those unknowns that are likely to cause the observed deviations and to address the underlying issues (for instance by determining fluid properties). Hereby, the accuracy of simulations could incrementally be improved until a sufficient agreement of experimental validation data and numerical model is achieved.
While a physics-based simulation of the entire growth process will clearly be complex, different opportunities for speedup exist or are likely to become available in the foreseeable future. While computation times will likely remain an issue on workstation PCs, one should keep in mind that access to advanced computing resources such as supercomputers is still on the rise. In addition, recent progress in the area of artificial intelligence is increasingly being utilized for novel approaches in the field of computational fluid dynamics. This includes the use of deep convolutional neural networks for determining closure terms for spanwise-averaged Navier–Stokes equations, which allows us to account for 3D turbulence effects at a greatly reduced computational cost [126]. Specifically in the field of crystal growth, machine learning has already successfully been applied for speeding up numerical modeling of supersaturation and flow field in SiC solution growth using the results of physics-based simulations as training data for machine learning [127]. Integrated approaches utilizing a combination of machine learning and knowledge of physical laws (for example, physics-informed neural networks) are also increasingly researched for a variety of applications and can make machine learning more data-efficient [128]. In the long run, there is also a prospect of a disruptive expansion in available computing power through the advent of quantum computing, which may eventually provide tremendous speedup also for computational fluid dynamics and multiphysics simulations [129,130].
Once sound knowledge of the internal growth conditions has been obtained, it may also become feasible to utilize numerical simulations to improve the understanding of defect formation and impurity incorporation. For instance, the effects of inhomogeneous impurity incorporation, pressure and temperature changes, and other causes of stress may be worth investigating. Such studies have already yielded instructive insights for mitigating defect formation in more mature crystal growth techniques, such as Hydride Vapor Phase Epitaxy (HVPE) of GaN [131] and Physical Vapor Transport (PVT) growth of SiC [132].
Author Contributions
Conceptualization, S.S. and D.T.; methodology, S.S.; formal analysis, S.S.; investigation, S.S; resources, S.S., D.T., Y.H., and H.A.; data curation, S.S.; writing—original draft preparation, S.S.; writing—review and editing, S.S., D.T., T.I., Y.H., S.C., and H.A.; visualization, S.S.; supervision, D.T., Y.H., H.A., and S.C.; project administration, S.S., D.T., Y.H., and H.A.; funding acquisition, S.S., D.T., Y.H., and H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JAPAN SOCIETY FOR THE PROMOTION OF SCIENCE (JSPS), grant number P19752 (Postdoctoral Fellowships for Research in Japan (Standard)). This research is supported by the MEXT “Program for research and development of next-generation semiconductor to realize energy-saving society” Program Grant Number JPJ005357.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
The authors would like to thank Mitsubishi Chemical Corporation and The Japan Steel Works, Ltd. for their continuous support. The first author (S.S.) would also like to thank collaborators from previous ammonothermal projects, including, but not limited to, Peter Wellmann, Rainer Niewa, Wolfgang Schnick, Eberhard Schlücker, Elke Meissner, Thomas G. Steigerwald, Dietmar Jockel, and last but not least Siddha Pimputkar for fruitful discussions on various aspects of ammonothermal crystal growth. Such discussions have contributed to gaining a more comprehensive understanding of existing limitations of knowledge that may affect the accuracy of numerical simulations. In addition, the first author (S.S.) would like to thank the Alexander von Humboldt-Foundation for the nomination for the JSPS fellowship.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Juza, R.; Jacobs, H.; Gerke, H. Ammonothermalsynthese von Metallamiden und Metallnitriden. Berichte der Bunsengesellschaft für Phys. Chemie 1966, 70, 1103–1105. [Google Scholar] [CrossRef]
- Dwiliński, R.; Wysmołek, A.; Baranowski, J.; Kamińska, M.; Doradziński, R.; Garczyński, J.; Sierzputowski, L.; Jacobs, H. GaN Synthesis by Ammonothermal Method. Acta Phys. Pol. A 1995, 88, 833–836. [Google Scholar] [CrossRef]
- Pimputkar, S.; Kawabata, S.; Speck, J.S.S.; Nakamura, S. Improved Growth Rates and Purity of Basic Ammonothermal GaN. J. Cryst. Growth 2014, 403, 7–17. [Google Scholar] [CrossRef]
- Bao, Q.; Saito, M.; Hazu, K.; Furusawa, K.; Kagamitani, Y.; Kayano, R.; Tomida, D.; Qiao, K.; Ishiguro, T.; Yokoyama, C.; et al. Ammonothermal Crystal Growth of GaN Using an NH 4 F Mineralizer. Cryst. Growth Des. 2013, 13, 4158–4161. [Google Scholar] [CrossRef]
- Zajac, M.; Kucharski, R.; Grabianska, K.; Gwardys-bak, A.; Puchalski, A.; Wasik, D.; Litwin-Staszewska, E.; Piotrzkowski, R.; Z Domagala, J.; Bockowski, M. Basic Ammonothermal Growth of Gallium Nitride–State of the Art, Challenges, Perspectives. Prog. Cryst. Growth Charact. Mater. 2018, 64, 63–74. [Google Scholar] [CrossRef]
- Key, D.; Letts, E.; Tsou, C.-W.; Ji, M.-H.; Bakhtiary-Noodeh, M.; Detchprohm, T.; Shen, S.-C.; Dupuis, R.; Hashimoto, T. Structural and Electrical Characterization of 2” Ammonothermal Free-Standing GaN Wafers. Progress toward Pilot Production. Materials 2019, 12, 1925. [Google Scholar] [CrossRef]
- Li, T.; Ren, G.; Su, X.; Yao, J.; Yan, Z.; Gao, X.; Xu, K. Growth Behavior of Ammonothermal GaN Crystals Grown on Non-polar and Semi-polar HVPE GaN Seeds. CrystEngComm 2019, 21, 4874–4879. [Google Scholar] [CrossRef]
- Ehrentraut, D.; Pakalapati, R.T.; Kamber, D.S.; Jiang, W.; Pocius, D.W.; Downey, B.C.; McLaurin, M.; D’Evelyn, M.P. High Quality, Low Cost Ammonothermal Bulk GaN Substrates. Jpn. J. Appl. Phys. 2013, 52, 08JA01. [Google Scholar] [CrossRef]
- Wang, B.; Callahan, M.J. Ammonothermal Synthesis of III-nitride Crystals. Cryst. Growth Des. 2006, 6, 1227–1246. [Google Scholar] [CrossRef]
- Dwiliński, R.; Doradziński, R.; Garczyński, J.; Sierzputowski, L.P.; Puchalski, A.; Kanbara, Y.; Yagi, K.; Minakuchi, H.; Hayashi, H. Excellent Crystallinity of Truly Bulk Ammonothermal GaN. J. Cryst. Growth 2008, 310, 3911–3916. [Google Scholar] [CrossRef]
- Suihkonen, S.; Pimputkar, S.; Sintonen, S.; Tuomisto, F. Defects in Single Crystalline Ammonothermal Gallium Nitride. Adv. Electron. Mater. 2017, 3. [Google Scholar] [CrossRef]
- Amano, H. Growth of GaN Layers on Sapphire by Low-Temperature-Deposited Buffer Layers and Realization of p-type GaN by Magesium Doping and Electron Beam Irradiation ( Nobel Lecture ). Angew. Chemie Int. Ed. 2015, 54, 7764–7769. [Google Scholar] [CrossRef] [PubMed]
- Kucharski, R.; Sochacki, T.; Lucznik, B.; Bockowski, M. Growth of Bulk GaN Crystals. J. Appl. Phys. 2020, 128. [Google Scholar] [CrossRef]
- Paskova, T.; Evans, K.R. GaN Substrates-progress, Status, and Prospects. IEEE J. Sel. Top. Quantum Electron. 2009, 15, 1041–1052. [Google Scholar] [CrossRef]
- Amano, H. Progress and Prospect of the Growth of Wide-Band-Gap Group III Nitrides: Development of the Growth Method for Single-Crystal Bulk GaN. Jpn. J. Appl. Phys. 2013, 52, 050001. [Google Scholar] [CrossRef]
- Amano, H.; Baines, Y.; Beam, E.; Borga, M.; Bouchet, T.; Chalker, P.R.; Charles, M.; Chen, K.J.; Chowdhury, N.; Chu, R.; et al. The 2018 GaN Power Electronics Roadmap. J. Phys. D. Appl. Phys. 2018, 51, 163001. [Google Scholar] [CrossRef]
- Fukuda, T.; Ehrentraut, D. Prospects for the Ammonothermal Growth of Large GaN Crystal. J. Cryst. Growth 2007, 305, 304–310. [Google Scholar] [CrossRef]
- Grabianska, K.; Kucharski, R.; Puchalski, A.; Sochacki, T.; Bockowski, M. Recent Progress in Basic Ammonothermal GaN Crystal Growth. J. Cryst. Growth 2020, 547, 125804. [Google Scholar] [CrossRef]
- Tomida, D.; Bao, Q.; Saito, M.; Osanai, R.; Shima, K.; Kojima, K.; Ishiguro, T.; Chichibu, S.F. Ammonothermal Growth of 2 Inch Long GaN Single Crystals Using an Acidic NH4F Mineralizer in a Ag-lined Autoclave. Appl. Phys. Express 2020, 13, 055505. [Google Scholar] [CrossRef]
- Mikawa, Y.; Ishinabe, T.; Kagamitani, Y.; Mochizuki, T.; Ikeda, H.; Iso, K.; Takahashi, T.; Kubota, K.; Enatsu, Y.; Tsukada, Y.; et al. Recent Progress of Large Size and Low Dislocation Bulk GaN Growth. In Proceedings of SPIE, Proceedings of the Gallium Nitride Materials and Devices XV, San Francisco, CA, USA, 4–6 February 2020; Morkoç, H., Fujioka, H., Schwarz, U.T., Eds.; SPIE-International Society for Optics and Photonics: Bellingham, WA, USA; Volume 1128002, p. 1.
- Häusler, J.; Schnick, W. Ammonothermal Synthesis of Nitrides: Recent Developments and Future Perspectives. Chem. A Eur. J. 2018, 24, 11864–11879. [Google Scholar] [CrossRef]
- Richter, T.; Niewa, R. Chemistry of Ammonothermal Synthesis. Inorganics 2014, 2, 29–78. [Google Scholar] [CrossRef]
- Hertrampf, J.; Becker, P.; Widenmeyer, M.; Weidenkaff, A.; Schlücker, E.; Niewa, R. Ammonothermal Crystal Growth of Indium Nitride. Cryst. Growth Des. 2018, 18, 2365–2369. [Google Scholar] [CrossRef]
- Mallmann, M.; Niklaus, R.; Rackl, T.; Benz, M.; Chau, T.G.; Johrendt, D.; Minár, J.; Schnick, W. Solid Solutions of Grimm-Sommerfeld Analogous Nitride Semiconductors II-IV-N2 with II = Mg, Mn, Zn; IV = Si, Ge – Ammonothermal Synthesis and DFT Calculations. Chem. A Eur. J. 2019, 2, 15887–15895. [Google Scholar] [CrossRef] [PubMed]
- Masuda, Y.; Sato, O.; Tomida, D.; Yokoyama, C. Convection Patterns and Temperature Fields of Ammonothermal GaN Bulk Crystal Growth Process. Jpn. J. Appl. Phys. 2016, 55, 3–6. [Google Scholar] [CrossRef]
- Erlekampf, J.; Seebeck, J.; Savva, P.; Meissner, E.; Friedrich, J.; Alt, N.S.A.; Schlücker, E.; Frey, L. Numerical Time-dependent 3D Simulation of Flow Pattern and Heat Distribution in an Ammonothermal System with Various Baffle Shapes. J. Cryst. Growth 2014, 403, 96–104. [Google Scholar] [CrossRef]
- Jiang, Y.N.; Chen, Q.S.; Prasad, V. Numerical Simulation of Ammonothermal Growth processes of GaN Crystals. J. Cryst. Growth 2011, 318, 411–414. [Google Scholar] [CrossRef][Green Version]
- Moldovan, S.I.; Balasoiu, A.M.; Braun, M. Experimental Investigation of Natural Convection Flow in a Laterally Heated Vertical Cylindrical Enclosure. Int. J. Heat Mass Transf. 2019, 139, 205–212. [Google Scholar] [CrossRef]
- Mirzaee, I.; Charmchi, M.; Sun, H. Heat, Mass, and Crystal Growth of GaN in the Ammonothermal Process: A Numerical Study. Numer. Heat Transf. Part A Appl. 2016, 70, 460–491. [Google Scholar] [CrossRef]
- Pendurti, S.; Chen, Q.S.; Prasad, V. Modeling Ammonothermal Growth of GaN Single Crystals: The Role of Transport. J. Cryst. Growth 2006, 296, 150–158. [Google Scholar] [CrossRef][Green Version]
- Enayati, H.; Chandy, A.J.; Braun, M.J.; Horning, N. 3D Large Eddy Simulation (LES) Calculations and Experiments of Natural Convection in a Laterally-heated Cylindrical Enclosure for Crystal Growth. Int. J. Therm. Sci. 2017, 116, 1–21. [Google Scholar] [CrossRef]
- Keyes, D.E.; McInnes, L.C.; Woodward, C.; Gropp, W.; Myra, E.; Pernice, M.; Bell, J.; Brown, J.; Clo, A.; Connors, J.; et al. Multiphysics Simulations: Challenges and Opportunities. Int. J. High Perform. Comput. Appl. 2013, 27, 4–83. [Google Scholar] [CrossRef]
- John, B.; Senthilkumar, P.; Sadasivan, S. Applied and Theoretical Aspects of Conjugate Heat Transfer Analysis: A Review. Arch. Comput. Methods Eng. 2019, 26, 475–489. [Google Scholar] [CrossRef]
- Nägel, A.; Logashenko, D.; Schroder, J.B.; Yang, U.M. Aspects of Solvers for Large-Scale Coupled Problems in Porous Media. Transp. Porous Media 2019, 130, 363–390. [Google Scholar] [CrossRef]
- Zhang, S.; Alt, N.S.A.; Schlücker, E.; Niewa, R. Novel Alkali Metal Amidogallates as Intermediates in Ammonothermal GaN Crystal Growth. J. Cryst. Growth 2014, 403, 22–28. [Google Scholar] [CrossRef]
- Zhang, S.; Hintze, F.; Schnick, W.; Niewa, R. Intermediates in Ammonothermal GaN Crystal Growth under Ammonoacidic Conditions. Eur. J. Inorg. Chem. 2013, 5387–5399. [Google Scholar] [CrossRef]
- Hertrampf, J.; Schlücker, E.; Gudat, D.; Niewa, R. Dissolved Intermediates in Ammonothermal Crystal Growth: Stepwise Condensation of [Ga(NH 2) 4]−toward GaN. Cryst. Growth Des. 2017, 17, 4855–4863. [Google Scholar] [CrossRef]
- Becker, P.; Wonglakhon, T.; Zahn, D.; Gudat, D.; Niewa, R. Approaching Dissolved Species in Ammonoacidic GaN Crystal Growth: A Combined Solution NMR and Computational Study. Chem. A Eur. J. 2020, 26, 7008–7017. [Google Scholar] [CrossRef]
- Schimmel, S.; Duchstein, P.; Steigerwald, T.G.; Kimmel, A.-C.L.; Schlücker, E.; Zahn, D.; Niewa, R.; Wellmann, P. In situ X-ray Monitoring of Transport and Chemistry of Ga-containing Intermediates under Ammonothermal Growth Conditions of GaN. J. Cryst. Growth 2018, 498, 214–223. [Google Scholar] [CrossRef]
- Yoshida, K.; Aoki, K.; Fukuda, T. High-temperature Acidic Ammonothermal Method for GaN Crystal Growth. J. Cryst. Growth 2014, 393, 93–97. [Google Scholar] [CrossRef]
- Grabianska, K.; Jaroszynski, P.; Sidor, A.; Bockowski, M.; Iwinska, M. GaN Single Crystalline Substrates by Ammonothermal and HVPE Methods for Electronic Devices. Electronics 2020, 9, 1342. [Google Scholar] [CrossRef]
- Chen, Q.S.; Pendurti, S.; Prasad, V. Modeling of Ammonothermal Growth of Gallium Nitride Single Crystals. J. Mater. Sci. 2006, 41, 1409–1414. [Google Scholar] [CrossRef]
- Schimmel, S.; Kobelt, I.; Heinlein, L.; Kimmel, A.L.; Steigerwald, T.G.; Schlücker, E.; Wellmann, P. Flow Stability, Convective Heat Transfer and Chemical Reactions in Ammonothermal Autoclaves—Insights by In Situ Measurements of Fluid Temperatures. Crystals 2020, 10, 723. [Google Scholar] [CrossRef]
- Griffiths, S.; Pimputkar, S.; Kearns, J.; Malkowski, T.F.; Doherty, M.F.; Speck, J.S.; Nakamura, S. Growth Kinetics of Basic Ammonothermal Gallium Nitride Crystals. J. Cryst. Growth 2018, 501, 74–80. [Google Scholar] [CrossRef]
- Malkowski, T.F.; Pimputkar, S.; Speck, J.S.; DenBaars, S.P.; Nakamura, S. Acidic Ammonothermal Growth of Gallium Nitride in a Liner-free Molybdenum Alloy Autoclave. J. Cryst. Growth 2016, 456, 21–26. [Google Scholar] [CrossRef]
- Schimmel, S. In situ Visualisierung des Ammonothermalen Kristallisationsprozesses Mittels Röntgenmesstechnik. Ph.D. Thesis, Friedrich-Alexander-Universität (FAU), Erlangen-Nürnberg, Germany, 2018. Available online: urn:nbn:de:bvb:29-opus4-102649 (accessed on 29 March 2021).
- Tomida, D.; Kagamitani, Y.; Bao, Q.; Hazu, K.; Sawayama, H.; Chichibu, S.F.; Yokoyama, C.; Fukuda, T.; Ishiguro, T. Enhanced Growth Rate for Ammonothermal Gallium Nitride Crystal Growth Using Ammonium Iodide Mineralizer. J. Cryst. Growth 2012, 353, 59–62. [Google Scholar] [CrossRef]
- Letts, E.; Hashimoto, T.; Hoff, S.; Key, D.; Male, K.; Michaels, M. Development of GaN wafers via the Ammonothermal Method. J. Cryst. Growth 2014, 403, 3–6. [Google Scholar] [CrossRef]
- Enayati, H.; Chandy, A.J.; Braun, M.J. Numerical Simulations of Transitional and Turbulent Natural Convection in Laterally Heated Cylindrical Enclosures for Crystal Growth. Numer. Heat Transf. Part A Appl. 2016, 70, 1195–1212. [Google Scholar] [CrossRef]
- Chen, Q.S.; Pendurti, S.; Prasad, V. Effects of Baffle Design on Fluid Flow and Heat Transfer in Ammonothermal Growth of Nitrides. J. Cryst. Growth 2004, 266, 271–277. [Google Scholar] [CrossRef][Green Version]
- Masuda, Y.; Suzuki, A.; Mikawa, Y.; Kagamitani, Y.; Ishiguro, T.; Yokoyama, C.; Tsukada, T. Numerical Simulation of GaN Single-crystal Growth Process in Ammonothermal Autoclave—Effects of Baffle Shape. Int. J. Heat Mass Transf. 2010, 53, 940–943. [Google Scholar] [CrossRef]
- Chen, Q.-S.; Jiang, Y.-N.; Yan, J.-Y.; Li, W.; Prasad, V. Modeling of Ammonothermal Growth Processes of GaN Crystal in Large-size Pressure Systems. Res. Chem. Intermed. 2011, 37, 467–477. [Google Scholar] [CrossRef][Green Version]
- Masuda, Y.; Suzuki, A.; Ishiguro, T.; Yokoyama, C. Numerical Simulation of Heat and Fluid Flow in Ammonothermal GaN Bulk Crystal Growth Process. Jpn. J. Appl. Phys. 2013, 52, 08JA05. [Google Scholar] [CrossRef]
- Chen, Q.-S.; Prasad, V.; Hu, W.R. Modeling of Ammonothermal Growth of Nitrides. J. Cryst. Growth 2003, 258, 181–187. [Google Scholar] [CrossRef]
- Moldovan, S.I. Numerical Simulation and Experimental Validation of Fluid Flow and Mass Transfer in an Ammonothermal Crystal Growth Reactor. Ph.D. Thesis, University of Akron, Akron, OH, USA, May 2013. [Google Scholar]
- Schimmel, S.; Koch, M.; Macher, P.; Kimmel, A.C.L.; Steigerwald, T.G.; Alt, N.S.A.; Schlücker, E.; Wellmann, P. Solubility and Dissolution Kinetics of GaN in Supercritical Ammonia in Presence of Ammonoacidic and Ammonobasic Mineralizers. J. Cryst. Growth 2017, 479, 59–66. [Google Scholar] [CrossRef]
- Schimmel, S.; Tomida, D.; Saito, M.; Bao, Q.; Ishiguro, T.; Honda, Y.; Chichibu, S.; Amano, H. Boundary Conditions for Simulations of Fluid Flow and Temperature Field during Ammonothermal Crystal Growth—A Machine-Learning Assisted Study of Autoclave Wall Temperature Distribution. Crystals 2021, 11, 254. [Google Scholar] [CrossRef]
- Chen, Q.; Jiang, Y.; Yan, J.; Qin, M. Progress in modeling of Fluid Flows in Crystal Growth Processes. Prog. Nat. Sci. 2008, 18, 1465–1473. [Google Scholar] [CrossRef]
- Li, H.; Braun, M.J.; Xing, C. Fluid Flow and Heat Transfer in a Cylindrical Model Hydrothermal Reactor. J. Cryst. Growth 2006, 289, 207–216. [Google Scholar] [CrossRef]
- Enayati, H. Effect of Reactor Size in a Laterally-Heated Cylindrical Reactor. Int. J. Heat Technol. 2020, 38, 275–284. [Google Scholar] [CrossRef]
- Li, H.; Evans, E.A.; Wang, G.X. Flow of Solution in Hydrothermal Autoclaves with Various Aspect Ratios. J. Cryst. Growth 2003, 256, 146–155. [Google Scholar] [CrossRef]
- Ursu, D.; Negrila, R.; Popescu, A.; Grozescu, I.; Vizman, D. Numerical and Experimental Studies of Fluid Flow and Heat Transfer in a Model Experiment for Hydrothermal Growth. Solid State Phenom. 2016, 254, 237–242. [Google Scholar] [CrossRef]
- Hirsch, C. Numerical Computation of Internal and External Flows, 2nd ed.; Elsevier: Burlington, MA, USA, 2007; ISBN 9780750665940. [Google Scholar]
- Alfonsi, G. Reynolds-averaged Navier-Stokes Equations for Turbulence Modeling. Appl. Mech. Rev. 2009, 62, 1–20. [Google Scholar] [CrossRef]
- Enayati, H.; Chandy, A.; Braun, M.J. Three-dimensional Large Eddy Simulations of Natural Convection in Laterally Heated Cylindrical Enclosures with Racks and Seeds for Crystal Growth. In Proceedings of the Second Thermal and Fluids Engineering Conference, Las Vegas, NV, USA, 2–5 April 2017; pp. 719–732. [Google Scholar]
- Masuda, Y.; Suzuki, A.; Mikawa, Y.; Chani, V.; Yokoyama, C.; Tsukada, T. Numerical Simulation of Hydrothermal Autoclave for Single-Crystal Growth Process. J. Therm. Sci. Technol. 2008, 3, 540–551. [Google Scholar] [CrossRef]
- Enayati, H.; Braun, M.J.; Chandy, A.J. Numerical Simulations of Porous Medium with Different Permeabilities and Positions in a Laterally-heated Cylindrical Enclosure for Crystal Growth. J. Cryst. Growth 2018, 483, 65–80. [Google Scholar] [CrossRef]
- Malin, M.R. Brian Spalding: Some Contributions to Computational Fluid Dynamics During the Period 1993 to 2004. In 50 Years of CFD in Engineering Sciences; Springer: Singapore, 2020; pp. 3–39. [Google Scholar]
- Xiao, H.; Cinnella, P. Quantification of Model Uncertainty in RANS Simulations: A Review. Prog. Aerosp. Sci. 2019, 108, 1–31. [Google Scholar] [CrossRef]
- Pimputkar, S.; Speck, J.S.; Nakamura, S. Basic Ammonothermal GaN Growth in Molybdenum Capsules. J. Cryst. Growth 2016, 456, 15–20. [Google Scholar] [CrossRef]
- Springer Handbook of Crystal Growth; Dhanaraj, G., Byrappa, K., Prasad, V., Dudley, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-540-74182-4. [Google Scholar]
- Prasad, V.; Kulacki, F.A.; Keyhani, M. Natural Convection in Porous Media. J. Fluid Mech. 1985, 150, 89–119. [Google Scholar] [CrossRef]
- Alloui, Z.; Vasseur, P. Convection in Superposed Fluid and Porous Layers. Acta Mech. 2010, 214, 245–260. [Google Scholar] [CrossRef]
- Battiato, I.; Ferrero V, P.T.; O’ Malley, D.; Miller, C.T.; Takhar, P.S.; Valdés-Parada, F.J.; Wood, B.D. Theory and Applications of Macroscale Models in Porous Media. Transp. Porous Media 2019, 130, 5–76. [Google Scholar] [CrossRef]
- Mao, D.; Karanikas, J.M.; Fair, P.S.; Prodan, I.D.; Wong, G.K. A Different Perspective on the Forchheimer and Ergun Equations. SPE J. 2016, 21, 1501–1507. [Google Scholar] [CrossRef]
- Papathanasiou, T.D.; Markicevic, B.; Dendy, E.D. A Computational Evaluation of the Ergun and Forchheimer Equations for Fibrous Porous Media. Phys. Fluids 2001, 13, 2795–2804. [Google Scholar] [CrossRef]
- Auriault, J.-L. On the Domain of Validity of Brinkman’s Equation. Transp. Porous Media 2009, 79, 215–223. [Google Scholar] [CrossRef]
- McBride, D.; Croft, T.N.; Cross, M. A Coupled Finite Volume Method for the Computational Modelling of Mould Filling in Very Complex Geometries. Comput. Fluids 2008, 37, 170–180. [Google Scholar] [CrossRef]
- Gohil, T.; McGregor, R.H.P.; Szczerba, D.; Burckhardt, K.; Muralidhar, K.; Székely, G. Simulation of Oscillatory Flow in an Aortic Bifurcation Using FVM and FEM: A Comparative Study of Implementation Strategies. Int. J. Numer. Methods Fluids 2011, 66, 1037–1067. [Google Scholar] [CrossRef]
- Jeong, W.; Seong, J. Comparison of Effects on Technical Variances of Computational Fluid Dynamics (CFD) Software Based on Finite Element and Finite Volume Methods. Int. J. Mech. Sci. 2014, 78, 19–26. [Google Scholar] [CrossRef]
- Molina-Aiz, F.D.; Fatnassi, H.; Boulard, T.; Roy, J.C.; Valera, D.L. Comparison of Finite Element and Finite Volume Methods for Simulation of Natural Ventilation in Greenhouses. Comput. Electron. Agric. 2010, 72, 69–86. [Google Scholar] [CrossRef]
- Bern, M.; Plassmann, P. Mesh Generation. In Handbook of Computational Geometry; North Holland: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Mirzaee, I. Computational Investigation of Gallium Nitrite Ammonothermal Crystal Growth. Ph.D. Thesis, University of Massachusetts Lowell, Lowell, MA, USA, 2015. [Google Scholar]
- Li, H.; Evans, E.A.; Wang, G.X. A Three-dimensional Conjugate Model with Realistic Boundary Conditions for Flow and Heat Transfer in an Industry Scale Hydrothermal Autoclave. Int. J. Heat Mass Transf. 2005, 48, 5166–5178. [Google Scholar] [CrossRef]
- Zajac, M.; Kucharski, R.; Grabiańska, K.; Gwardys-Bąk, A.; Puchalski, A.; Boćkowski, M. Ammonothermal GaN Substrates for Microwave Electronics and Energoelectronics. In Proceedings of SPIE, Proceedings of the Radioelectronics Systems Conference, Jachranka, Poland, 14–16 November 2017; SPIE-International Society for Optics and Photonics: Bellingham, WA, USA. [CrossRef]
- Pimputkar, S.; Kawabata, S.; Speck, J.S.; Nakamura, S. Surface Morphology Study of Basic Ammonothermal GaN Grown on Non-polar GaN Seed Crystals of Varying Surface Orientations from m-plane to a-plane. J. Cryst. Growth 2013, 368, 67–71. [Google Scholar] [CrossRef]
- Alt, N.; Meissner, E.; Schlücker, E.; Frey, L. In situ Monitoring Technologies for Ammonthermal Reactors. Phys. Status Solidi Curr. Top. Solid State Phys. 2012, 9, 436–439. [Google Scholar] [CrossRef]
- Steigerwald, T.G.; Balouschek, J.; Hertweck, B.; Kimmel, A.-C.L.; Alt, N.S.A.; Schluecker, E. In situ Investigation of Decomposing Ammonia and Ammonobasic Solutions under Supercritical Conditions via UV/vis and Raman Spectroscopy. J. Supercrit. Fluids 2018, 134, 96–105. [Google Scholar] [CrossRef]
- Schimmel, S.; Lindner, M.; Steigerwald, T.G.; Hertweck, B.; Richter, T.M.M.; Künecke, U.; Alt, N.S.A.; Niewa, R.; Schlücker, E.; Wellmann, P.J. Determination of GaN Solubility in Supercritical Ammonia with NH4F and NH4Cl Mineralizer by in situ X-ray Imaging of Crystal Dissolution. J. Cryst. Growth 2015, 418, 64–69. [Google Scholar] [CrossRef]
- Schimmel, S.; Künecke, U.; Meisel, M.; Hertweck, B.; Steigerwald, T.G.; Nebel, C.; Alt, N.S.A.; Schlücker, E.; Wellmann, P. Chemical Stability of Carbon-based Inorganic Materials for in situ X-ray Investigations of Ammonothermal Crystal Growth of Nitrides. J. Cryst. Growth 2016, 456, 33–42. [Google Scholar] [CrossRef]
- Schimmel, S.; Wellmann, P. In situ Visualization of the Ammonothermal Crystallization Process by X-ray Technology. In Ammonothermal Synthesis and Crystal Growth of Nitrides–Chemistry and Technology; Niewa, R., Meissner, E., Eds.; Springer International Publishing: Berlin, Germany, 2021; Volume 304, ISBN 978-3-030-56305-9. [Google Scholar]
- Beckermann, C.; Viskanta, R.; Ramadhyani, S. Natural Convection in Vertical Enclosures Containing Simultaneously Fluid and Porous Layers. J. Fluid Mech. 1988, 186, 257–284. [Google Scholar] [CrossRef]
- Wang, B.; Callahan, M.J.; Rakes, K.D.; Bouthillette, L.O.; Wang, S.Q.; Bliss, D.F.; Kolis, J.W. Ammonothermal Growth of GaN Crystals in Alkaline Solutions. J. Cryst. Growth 2006, 287, 376–380. [Google Scholar] [CrossRef]
- Griffiths, S.; Pimputkar, S.; Speck, J.S.; Nakamura, S. On the Solubility of Gallium Nitride in Supercritical Ammonia–sodium Solutions. J. Cryst. Growth 2016, 456, 5–14. [Google Scholar] [CrossRef]
- Mirzaii, I.; Passandideh-Fard, M. Modeling Free Surface Flows in Presence of an Arbitrary Moving Object. Int. J. Multiph. Flow 2012, 39, 216–226. [Google Scholar] [CrossRef]
- Liu, X.; Harada, H.; Miyamura, Y.; Han, X.F.; Nakano, S.; Nishizawa, S.I.; Kakimoto, K. Transient Global Modeling for the Pulling Process of Czochralski Silicon Crystal Growth. I. Principles, Formulation, and Implementation of the Model. J. Cryst. Growth 2020, 532, 125405. [Google Scholar] [CrossRef]
- Dadzis, K.; Pätzold, O.; Gerbeth, G. Model Experiments for Flow Phenomena in Crystal Growth. Cryst. Res. Technol. 2020, 55, 1–7. [Google Scholar] [CrossRef]
- Lemmon, E.W.; McLinden, M.O.; Friend, D.G. Thermophysical Properties of Fluid Systems; Linstrom, P.J., Mallard, W.G., Eds.; Available online: http://http//webbook.nist.gov/chemistry (accessed on 5 June 2017).
- Tomida, D.; Yoshinaga, T. Thermal Conductivity Measurements of Liquid Ammonia by the Transient Short-Hot-Wire Method. Int. J. Thermophys. 2020, 41, 53. [Google Scholar] [CrossRef]
- Brennecke, J.F.; Eckert, C.A. Phase Equilibria for Supercritical Fluid Process Design. AIChE J. 1989, 35, 1409–1427. [Google Scholar] [CrossRef]
- Supercritical Fluids; Arai, Y., Sako, T., Takebayashi, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; ISBN 978-3-642-62515-2. [Google Scholar]
- Pimputkar, S.; Nakamura, S. Decomposition of Supercritical Ammonia and Modeling of Supercritical Ammonia-nitrogen-hydrogen Solutions with Applicability toward Ammonothermal Conditions. J. Supercrit. Fluids 2016, 107, 17–30. [Google Scholar] [CrossRef]
- Hosaka, M.; Taki, S. Hydrothermal Growth of Quartz Crystals in Pure Water. J. Cryst. Growth 1981, 51, 640–642. [Google Scholar] [CrossRef]
- Hervey, P.R.; Foise, J.W. Syntheic Quartz Crystal—A Review. Miner. Metall. Process. 2001, 18, 1–4. [Google Scholar]
- Ehrentraut, D.; Sato, H.; Kagamitani, Y.; Sato, H.; Yoshikawa, A.; Fukuda, T. Solvothermal Growth of ZnO. Prog. Cryst. Growth Charact. Mater. 2006, 52, 280–335. [Google Scholar] [CrossRef]
- Bao, Q.; Saito, M.; Hazu, K.; Kagamitani, Y.; Kurimoto, K.; Tomida, D.; Qiao, K.; Ishiguro, T.; Yokoyama, C.; Chichibu, S.F. Ammonothermal Growth of GaN on a Self-nucleated GaN Seed Crystal. J. Cryst. Growth 2014, 404, 168–171. [Google Scholar] [CrossRef]
- Duan, X.; Qian, G.; Fan, C.; Zhu, Y.; Zhou, X.; Chen, D.; Yuan, W. First-principles Calculations of Ammonia Decomposition on Ni(110) Surface. Surf. Sci. 2012, 606, 549–553. [Google Scholar] [CrossRef]
- D’Evelyn, M.P.; Ehrentraut, D.; Jiang, W.; Kamber, D.S.; Downey, B.C.; Pakalapati, R.T.; Yoo, H.D. Ammonothermal Bulk GaN Substrates for Power Electronics. ECS Trans. 2013, 58, 287–294. [Google Scholar] [CrossRef]
- Hertweck, B.; Schimmel, S.; Steigerwald, T.G.; Alt, N.S.A.; Wellmann, P.J.; Schluecker, E. Ceramic Liner Technology for Ammonoacidic Synthesis. J. Supercrit. Fluids 2015, 99, 76–87. [Google Scholar] [CrossRef]
- Bajus, S. Ammoniakzersetzung mit Salzmodifizierten Katalysatoren. Ph.D. Thesis, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen-Nürnberg, Germany, June 2014. [Google Scholar]
- Lu, K.; Tatarchuk, B.J. Activated Chemisorption of Hydrogen on Supported Ruthenium. II. Effects of Crystallite Size and Adsorbed Chlorine on Accurate Surface Area Measurements. J. Catal. 1987, 106, 176–187. [Google Scholar] [CrossRef]
- Shlflett, W.K.; Dumeslc, J.A. Ammonia Synthesis as a Catalytic Probe of Supported Ruthenium Catalysts: The Role of the Support and the Effect of Chlorine. Ind. Eng. Chem. Fundam. 1981, 20, 246–250. [Google Scholar] [CrossRef]
- Steigerwald, T.G.; Alt, N.S.A.; Hertweck, B.; Schluecker, E. Feasibility of Density and Viscosity Measurements under Ammonothermal Conditions. J. Cryst. Growth 2014, 403, 59–65. [Google Scholar] [CrossRef]
- Keblinski, P.; Eastman, J.A.; Cahill, D.G. Nanofluids for Thermal Transport. Mater. Today 2005, 8, 36–44. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective Transport in Nanofluids. J. Heat Transfer 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Bänsch, E. A Thermodynamically Consistent Model for Convective Transport in Nanofluids: Existence of Weak Solutions and Fem Computations. J. Math. Anal. Appl. 2019, 477, 41–59. [Google Scholar] [CrossRef]
- Tomida, D.; Kuroda, K.; Nakamura, K.; Qiao, K.; Yokoyama, C. Temperature Dependent Control of the Solubility of Gallium Nitride in Supercritical Ammonia Using Mixed Mineralizer. Chem. Cent. J. 2018, 12, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Tomida, D.; Kuroda, K.; Hoshino, N.; Suzuki, K.; Kagamitani, Y.; Ishiguro, T.; Fukuda, T.; Yokoyama, C. Solubility of GaN in Supercritical Ammonia with Ammonium Chloride as a Mineralizer. J. Cryst. Growth 2010, 312, 3161–3164. [Google Scholar] [CrossRef]
- Bushmin, S.A.; Azimov, P.; Lvov, S. Numerical Modelling of the Metamorphic Mineral Solubility in Hydrothermal Solutions at 400-800 C, 1-5 kbar and Various Fluid Acidity. Mineral. Collect. 2004, 54, 94–116. [Google Scholar]
- Zahn, D. On the Solvation of Metal Ions in Liquid Ammonia: A Molecular Simulation Study of M(NH2)x(NH3)y Complexes as a Function of pH. RSC Adv. 2017, 7, 54063–54067. [Google Scholar] [CrossRef]
- Zahn, D. A Molecular Simulation Study of the Auto-protolysis of Ammonia as a Function of Temperature. Chem. Phys. Lett. 2017, 682, 55–59. [Google Scholar] [CrossRef]
- Ehrentraut, D.; Kagamitani, Y.; Yokoyama, C.; Fukuda, T. Physico-chemical Features of the Acid Ammonothermal Growth of GaN. J. Cryst. Growth 2008, 310, 891–895. [Google Scholar] [CrossRef]
- Hashimoto, T.; Saito, M.; Fujito, K.; Wu, F.; Speck, J.S.; Nakamura, S. Seeded Growth of GaN by the Basic Ammonothermal Method. J. Cryst. Growth 2007, 305, 311–316. [Google Scholar] [CrossRef]
- Hashimoto, T.; Letts, E. Development of Cost-Effective Native Substrates for Gallium Nitride-Based Optoelectronic Devices via Ammonothermal Growth. Optoelectron. Devices Appl. 2012, 95–106. [Google Scholar] [CrossRef]
- Schimmel, S.; Künecke, U.; Baser, H.; Steigerwald, T.G.; Hertweck, B.; Alt, N.S.A.; Schlücker, E.; Schwieger, W.; Wellmann, P. Towards X-ray in-situ Visualization of Ammonothermal Crystal Growth of Nitrides. Phys. Status Solidi Curr. Top. Solid State Phys. 2014, 11, 1439–1442. [Google Scholar] [CrossRef]
- Font, B.; Weymouth, G.D.; Nguyen, V.-T.; Tutty, O.R. Deep Learning of the Spanwise-averaged Navier–Stokes Equations. J. Comput. Phys. 2021, 434, 110199. [Google Scholar] [CrossRef]
- Tsunooka, Y.; Kokubo, N.; Hatasa, G.; Harada, S.; Tagawa, M.; Ujihara, T. High-speed Prediction of Computational Fluid Dynamics Simulation in Crystal Growth. CrystEngComm 2018, 20, 6546–6550. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Givi, P.; Daley, A.J.; Mavriplis, D.; Malik, M. Quantum Speedup for Aeroscience and Engineering. AIAA J. 2020, 58, 3715–3727. [Google Scholar] [CrossRef]
- Bharadwaj, S.S.; Sreenivasan, K.R. Quantum Computation of Fluid Dynamics. 2020. Available online: https://arxiv.org/abs/2007.09147 (accessed on 29 March 2021).
- Bockowski, M.; Iwinska, M.; Amilusik, M.; Fijalkowski, M.; Lucznik, B.; Sochacki, T. Challenges and Future Perspectives in HVPE-GaN Growth on Ammonothermal GaN Seeds. Semicond. Sci. Technol. 2016, 31, 093002. [Google Scholar] [CrossRef]
- Gao, B.; Kakimoto, K. Three-dimensional Modeling of Basal Plane Dislocations in 4H-SiC Single Crystals Grown by the Physical Vapor Transport Method. Cryst. Growth Des. 2014, 14, 1272–1278. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).