Abstract
Individuals have a strong tendency to coordinate with all their neighbors on social and economics networks. Coordination is often influenced by intrinsic preferences among the available options, which drive people to associate with similar peers, i.e., homophily. Many studies reported that behind coordination game equilibria there is the individuals’ heterogeneity of preferences and that such heterogeneity is given a priori. We introduce a new mechanism which allows us to analyze the issue of heterogeneity from a cultural evolutionary point of view. Our framework considers agents interacting on a multiplex network who deal with coordination issues using social learning and payoff-driven dynamics. Agents form their heterogeneous preference through learning on one layer and they play a pure coordination game on the other layer. People learn from their peers that coordination is good and they also learn how to reach it either by conformism behavior or sorting strategy. We find that the presence of the social learning mechanism explains the rising and the endurance of a segregated society when members are diverse. Knowing how culture affects the ability to coordinate is useful for understanding how to reach social welfare in a diverse society.
JEL Classification:
C22; C73; D83; D85; Z13
1. Introduction
In a globalized and constantly changing world the evolution of coordination and social connections is a complex dynamic. Coordination is important for many social and economic decisions. For example, as the workforce becomes more diverse1, organizations wishing to obtain the benefits associated with diversity must also learn how to manage diversity in order to facilitate coordination. People from different backgrounds may use different heuristics when trying to coordinate with others. Knowing how culture affects the ability to coordinate will be useful for understanding how to reach social welfare in a diverse society. People from the same culture are likely to share similar norms and perhaps find it easier to predict the behavior of others, thus improving coordination. On the other hand, when interacting with someone from a different culture, individuals may be unfamiliar with each other’s norms and need to rely on cultural cues to try to predict the opponent’s behavior.
Empirical evidence shows that clusters of people looking the same, acting the same, behaving the same, pervade the whole society [7]. There are strong evolutionary and selective pressures that push humans toward coordinating their behaviors or identities. Social pressure and individual preferences for conformity or homophily, i.e., the tendency of individuals to associate and bond with similar others2, are few of the many motivating factors for coordination. There are two main strategies to implement the coordination that are sorting actions, i.e., people selecting and moving towards people like them, or adoption, i.e., people conforming to the most common action within their neighborhood. However, in many settings, individuals interact with new people over time and thus must draw on other cues to guide their behavior and resolve strategic uncertainty related to how the others will play. To this end, societies can appeal to cultural traits to guide their behaviors and help them coordinate in settings in which there are multiple possible stable outcomes. Such traits, like national culture, gender culture, corporate culture and religion influence how we conduct work and our behavior and style when we interact with others. Those traits, of course, are not given but they have history. They are, firstly, transmitted, then learned and finally endorsed by people. Hence, when individuals interact with new people for the first time, they are not acting randomly but, rather, they implement what they have learned in their social neighborhood. In other words, people are using the learned cultural trait, and the behaviors associated with it as a focal point affecting their interactions with strangers. Eventually, during the interactions with strangers their understanding of which behavior is the most acceptable will be enriched, although this does not occur always or easily. Indeed, what is focal for some individuals belonging to a specific culture might not be shared by some others associated with other culture, and their interactions could lead to costly coordination or cause segregation3. Moreover, culture will not only inform individuals about what is the socially accepted behavior to implement but also how to implement it for coordinating with their similar peers. Hence, individual preferences for conformity or homophily can be the expression of a learning process too. The question is how behavior is changed when we interact with a person we know very well compared to an acquaintance, or a person we are only minimally tied with (e.g., a perfect stranger).
Following the above observations, the purpose of this paper is to analyze how cultural transmission in large scale social structures can inform the level of coordination in it. To accomplish this task we merge two main approaches that economists and social scientists have developed to study the transmission and diffusion of cultural traits and the behavioral coordination in social networks. Namely, the two approaches involve the social learning and the game theory frameworks on multi-layered, or multiplex, networks. We investigate the influence of the network structure and social learning dynamics on the evolution of heterogeneous behavior agents in a coordination game played on multiplex networks.
We find that the multi-layered network structure and the presence of the social learning mechanism modulate the rising of segregated societies with members of different groups choosing diverse actions. We highlight that the presence of social learning and heterogeneity of cultural intolerance works in favor of states where there is segregation between actions. The social system converges to a multi-equilibria state in which the two different actions are segregated. Segregation state is the one with the higher social welfare where individuals are satisfied with the actions of their neighbors. We show that segregation is an evolutionary stable state for both actions and strategies. This happens for three reasons: the topology of both hidden and evident layers, the presence of intolerant individuals and the presence of the social learning mechanism. The result of multiple configurations crucially depend on the multi-layered structure of our system. Our results offer a novel mechanism that provides an evolutionary explanation for the phenomenon of segregation and stratification between cultural groups.
2. Literature Review
Coordination games are characterized by the presence of multiple equilibria that are often equivalent in terms of payoff. Predicting which of the many equilibria will be selected has been the object of many studies. The literature suggests two criteria for the prediction. The first is related to the structural properties of the game such as risk and payoff dominance [10], or path-dependence [11]. The second pertains to the theory of focal points [12] that states that in some games there are natural reasons (possibly outside the payoff structure of the game) that cause the players to focus on one of the Nash equilibria. Such reasons could be represented by culture. Although cultural differences in coordination games have not yet been studied extensively, some related literature has demonstrated the importance of social norms [13] and group identity [14,15,16,17,18] for coordination game outcomes. According to this literature, culture and social identity concur to be an explanation for the heterogeneous preferences that very often are the cause of multiple equilibria in coordination games. Coordination in these works entails integration of cultural traits and it can occur by imposing a common identity that motivates people towards a shared purpose. For instance, this happens in companies when the governance decides to impose the corporate culture to its employees (i.e., adoption mechanism) to coordinate their effort to the common goal of corporate productions [16]. Another way to drive people’s coordination is by allowing them to choose (i.e., sorting mechanism) with whom to interact in a more effective way [19] or to sort themselves into working groups with the same cultural treat [17]. In these works, both strategies, the adoption and the sorting, are fixed. We are interested in investigating further both mechanisms but in a scenario in which they are not imposed by a central authority, i.e., the corporate governance, but they are rather learned from an evolutionary learning process from peers. In a nutshell, in our model individuals learn from their peers which is the most successful strategy to coordinate with people that are different from them. Hence, the strategies are dynamic and not fixed. Furthermore, our work contributes to the literature of coordination on social networks, either static [20,21,22,23,24,25] and dynamic [26,27,28,29,30,31,32,33] structures4.
With respect to this literature we make three relevant contributions. The first contribution consists of assuming the heterogeneity of strategies rather than preferences and the strategies themselves are not given but they result from a social learning process. The second difference pertains the dynamics on the network and the study of the topology of the network structure. For realistic considerations, instead of studying in a separate way the static and the dynamic configuration of the network, our population can, in principle, use both a static (i.e., keeping the neighbors’ set) and a dynamic (i.e., changing the neighbors’ set one person at the time) strategy. Moreover, always for realistic reasons we study the model by changing the social learning topology from a lattice through a small-world and to a random graph. The third upgrade is related to the type of the network structure. Instead of specifying the entire social network of an individual with strong and weak ties to identify her closed friends from her acquaintances, we will create two different social structures to force the division of the two dynamics: on one level, the individual will learn from her neighborhood the strategy of how to deal with other people that differs from her, and on another level, she will coordinate with strangers by applying the learned strategy. The two-level social structure has a name, i.e., it is called multiplex network, and it is derived from communications theory which defines multiplexity as the combination of multiple signals or ties into one structure in such way that it is still possible to separate the individual signals if needed [7,34].
Recently, the area of multi-layered social networks has started attracting more and more attention in research conducted within different domains [34,35,36]. The meaning of multiplex networks has expanded in order to cover not only social relationships but any kind of connection, e.g., based on geography, occupation, kinship, hobbies [37]. The applications of multi-layered social networks to game theory models have increased with a large attention devoted to cooperative games to study the duration of cooperative behavior across different social connections [38,39,40]. Among the new strand of literature few studies have undergone the path of studying where both cooperative [41,42] and coordinating [43] behaviors come from by including different dynamics of social learning or social pressure. With respect to this literature, we study the evolution of coordination by allowing the individuals to choose between two strategies that lead to it: conforming to everyone else around them or selecting their neighbors. Both strategies will be the results of a social learning process. Hence, the main questions of the paper are: can the interplay between social learning and game theoretical decisions inform us about the level of coordination in the society? Does the network topology play any role? In order to answer to these questions, we present a multiplex model in which each layer contains the same set of nodes endowed with different links. The two layers are called hidden and evident and on top of them we model, respectively, the dynamics of social learning and the coordination game. Hence, the individual learns in the hidden layer how to coordinate with acquaintances in the evident one, where the payoff is calculated. The relationship between the two levels is identified in the link between learned strategies and payoff calculation.
3. Model
We consider multiplex networks of N nodes, hereinafter agents, having two layers that we call hidden and evident ones. Each agent i is characterized by a profile , where is agent’s action and is agent’s strategy. For the sake of simplicity, we consider only two possible actions, that is, , and two possible strategies that we call rewiring (R) and staying (S). All agents exist on both multiplex layers having the sets of neighbors , where () is the set of neighbors in the evident (hidden) layer. Note that the intersection can be empty. Agents play a pure coordination game on the evident layer where each link with a neighbor having the same action gives them a unitary payoff , while being linked to a neighbor with a different action does not produce any benefit to them. Thus, the payoff matrix of the pure coordination game played in the evident layer is given by:
| A | B | |
| A | (1,1) | (0,0) |
| B | (0,0) | (1,1) |
On the other hand, the behavior of the agents in the evident layer is influenced by the strategy that they learn in the hidden layer. On the hidden layer agents adopt the strategy of their most successful neighbor , that is, the one with the largest payoff collected in the evident layer. Thus, the actions have to be considered only in the evident layer for accumulating the game payoffs while the strategies are learned through payoff-driven imitation in the hidden layer and implemented in the evident one.
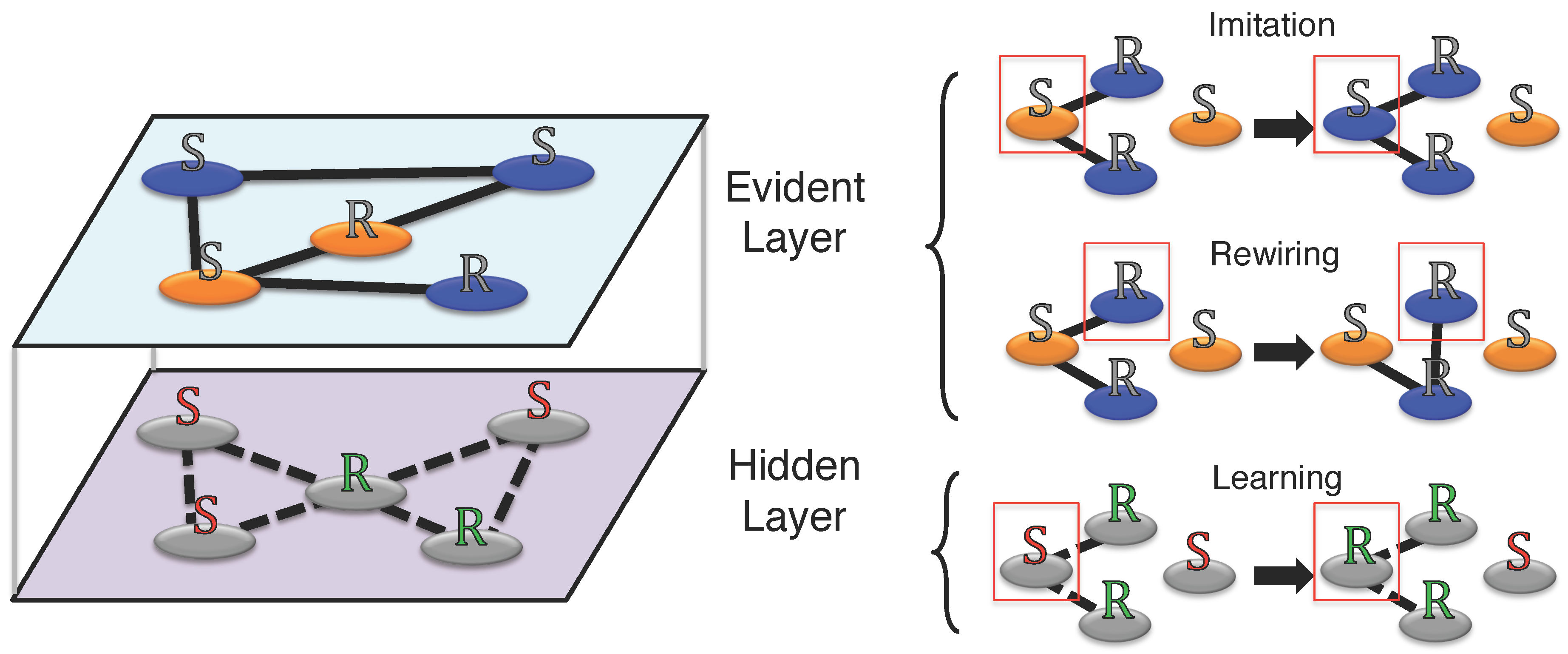
We report in Figure 1 the model dynamics. The R-agents have preferences for keeping their action and sorting themselves out into groups of agents using the same action. For an R-agent the match with another agent of different action represents a missing gain caused by the mis-coordination outcome. Hence, since cutting and creating links is costless for all agents in the system, R-agents prefer to modify their neighborhoods rather than remaining attached to the same neighbors waiting for coordination. More precisely, an R-agent cuts a link with a neighbor having a different action, if any, and creates a link with another randomly chosen one, assuming the risk of linking again to someone of a different action (i.e., risk of mismatching). In fact, the new agents’ action is revealed only after the connection (i.e., imperfect observability of the action). The rewiring strategy is constrained such that agents can only have a limited number of links to maintain a constant average degree of the network. Conversely, S-agents prefer adopting the most common action within their neighborhood without changing their links.
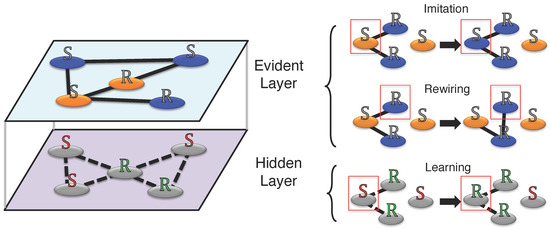
Figure 1.
Visualization of the adaptive multiplex network model. The coordination with neighbor actions dynamics happens in the evident layer through imitation (according to S-agents) and rewiring (for R-agents), while the learning dynamics occurs in the hidden layer through payoff-driven strategy imitation. Actions are represented as node colors (orange and blue) while strategies are represented as node labels (R for rewiring agents, S for staying ones). Imitation refers to the coordination game according to which agents update their actions on the evident layer. Rewiring indicates the possibility, on the evident layer, for an agent to cut a link with a neighbor of opposite action and then create a link with another randomly chosen agent. Learning denotes the propagation of strategies over the hidden layer.
The coevolutionary model dynamics consists of two stages repeated at a different rate. In the first stage, i.e., the learning dynamics, agents learn their strategy from the neighbors in the hidden layer. In the second stage, i.e., the game dynamics, they implement their strategy and they play the game accumulating the payoff with the neighbors in the evident layer. The learning dynamics are implemented with probability while the game dynamics with probability . We consider both stages as asynchronous dynamics, i.e., the update of strategies, neighborhoods and actions are done for one agent at a time. Each macro-step considers N micro-steps, i.e., the update of a randomly chosen agent.
We run computer simulations for multiplex networks of agents, where the starting evident layer is an Erdös–Rényi random network [44] of average degree and the hidden layer topology is generated using the Watts–Strogatz model [45] with parameter and average degree . Conventionally, we can consider the hidden layer as a regular lattice when , a random graph when , and a small-world network for intermediate values . We begin the simulation by distributing at random a fraction of R-agents in the multiplex network.
4. Results
We first present the global results quantifying the influence of the hidden layer, the learning dynamics and the initial fraction of rewiring strategies on the segregation level and the final fraction of R-agents and dominant action. In order to measure action segregation in the evident layer we computed the segregation matrix index (SMI) [46,47] across different instances of the model, for different topologies of the hidden layer (), different time-scales of learning dynamics () and different values of initial rewiring strategies (). The SMI serves as a measure of the cohesiveness of a group and it is defined as , where is the density of same-action links and is the density of opposite-action links [47]. Higher values of SMI mean that agents interact more frequently with other agents having the same action. Perfect segregation is reached when only agents having the same action are linked to each other and it corresponds to the value .
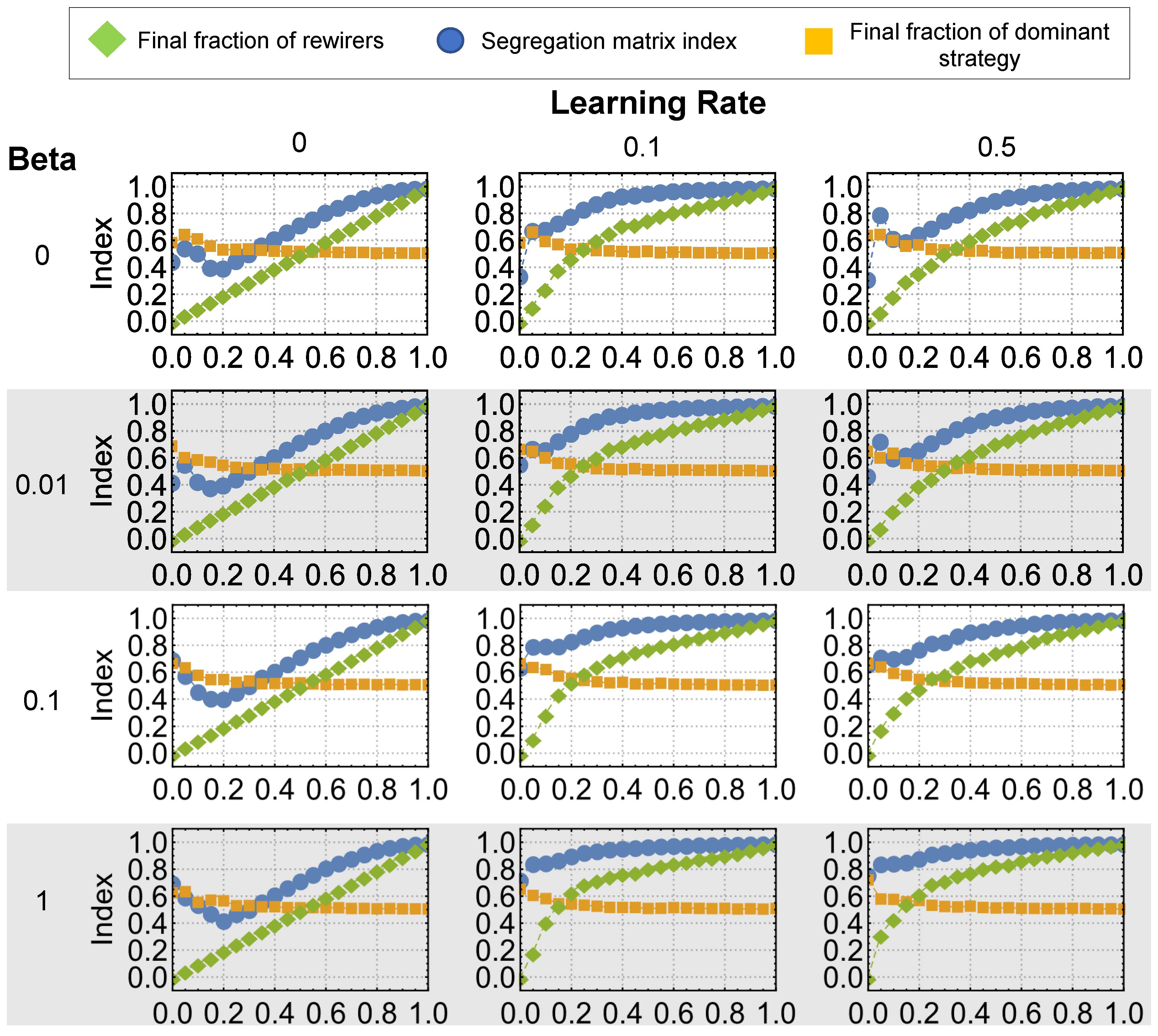
Figure 2 reports results for , and . We plot SMI between groups of actions in the evident layer (blue lines). Note that the SMI can also be interpreted as the cumulated payoffs of agents playing the pure coordination game in the evident layer, that is to say, high levels of segregation between actions imply high social welfare for the involved agents.
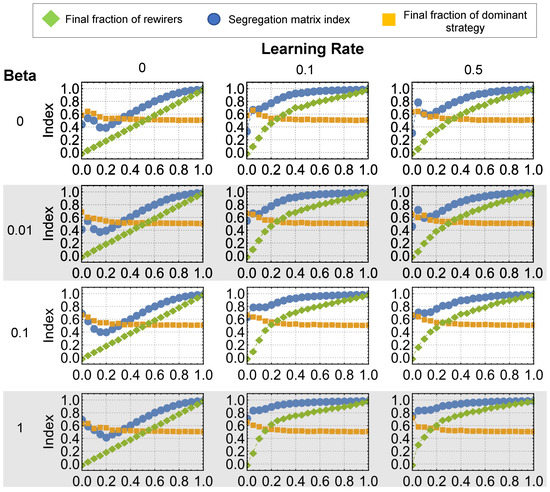
Figure 2.
Panel of segregation matrix indexes (SMI) over different values of initial densities of rewirers (R0) for different values of rewiring parameter and learning parameter . Every data point is averaged over 50 different replicates. Error bars were not reported since they are of the same size of dots.
When there was no learning in the system (, i.e., first column), there was no strategy imitation and the final fraction of R-agents (green lines) was maintained. The outcomes were qualitatively the same and they were independent on the topology of the hidden layer. Notice that all the SMI curves display a single minimum around . Furthermore, the final fraction of the dominant action (orange lines) was slightly higher when only S-agents are present. This is due to the fact that in some simulations the system converges to one single action reaching full consensus. When the learning dynamics were occurring (i.e., ), we obtained higher SMI values and final fractions of R-agents for all values of with respect to the case. In this case the rewiring strategy spread successfully in the hidden layer since R-agents connected more easily to same action’s agents accumulating higher payoffs than S-agents.
Finally, the hidden topology played an important role too. In fact, when (i.e., lattice), rewiring strategies did not diffuse enough given the spatiality of the hidden topology and the final fraction of R-agents did not reach the values of the case. When the hidden layer topology looks more like a random graph , the diffusion of rewiring strategies is enhanced reflecting to higher values of SMI and thus of social wealth. Simulations confirm this pattern: with the same model parameters, systems having a lattice hidden layer topology did not reach the same segregation levels of the others and they produced less of final fraction of R-agents than random graphs and small-world networks. The lower density of R-agents driven by the lattice topology translated into a less frequent rewiring, which in turn reduced segregation in the evident layer. Hence, the multiplex interplay in terms of learning between actions and strategies can lead to the topology of the hidden layer influencing and possibly reducing the action consensus observed in the evident layer.
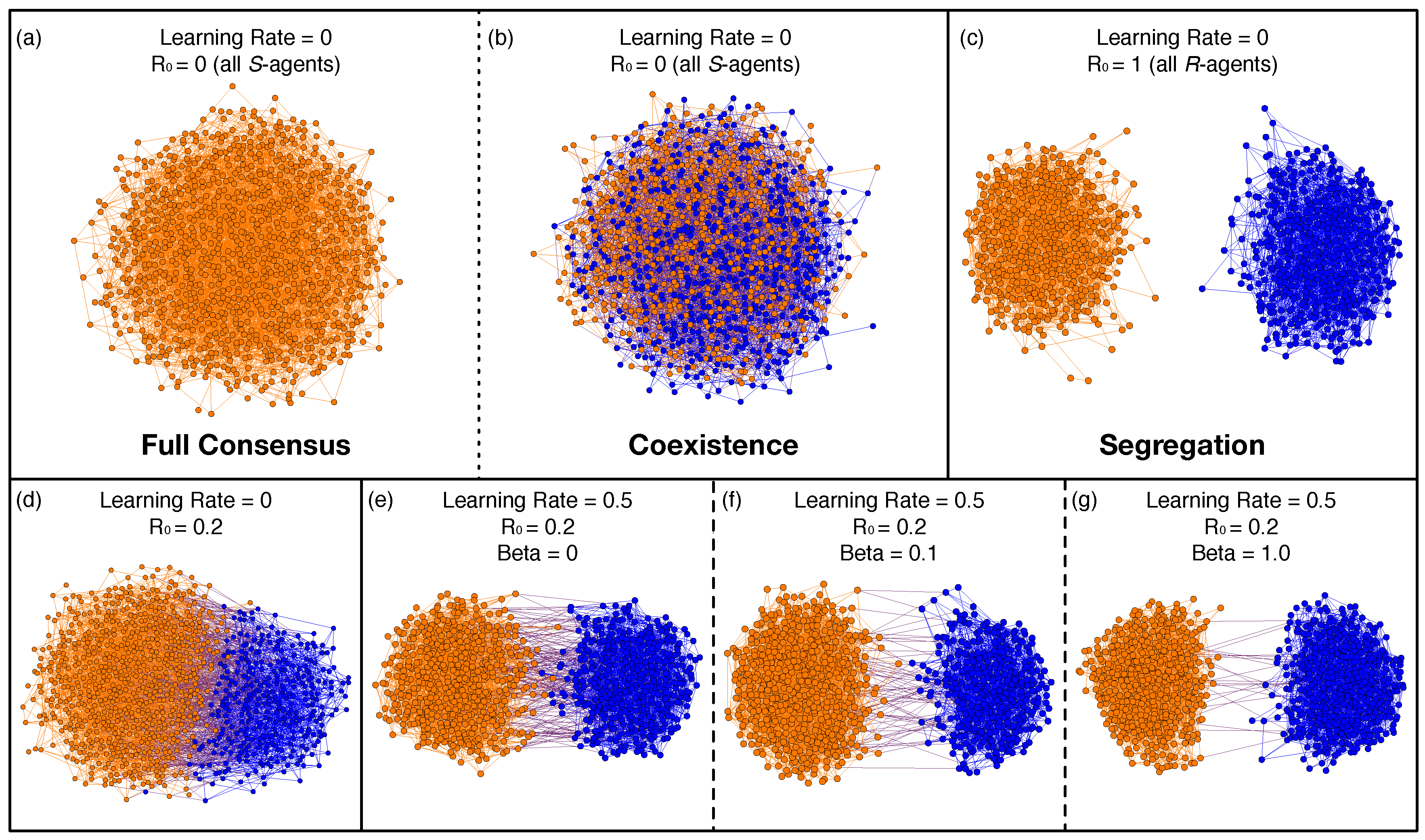
All the possible final outcomes of the evident layer are resumed in Figure 3 showing the typical action and links configurations for different parameters of the model. When learning and R-agents are not present, see panels (a,b), we obtained full consensus to one single action (a) or coexistence of both action types (b). This is due to the fact that S-agents can reach a stable equilibrium having both actions because they are more tolerant than R-agents in accepting neighbors of the opposite action. However, systems of S-agents can eventually converge to one single action if that equilibrium is not stable enough. On the other hand, when all agents have R-strategy and learning was not present, we always obtained segregation of the two actions and of the two network community, see panel (c). A mix of segregation and coexistence of the two actions can be found in all the other panels (d–g). In fact, links between two action communities are present at different frequencies according to the initial fraction of R-agents, see panel (d), and to the hidden layer topology, see panels (e–g).
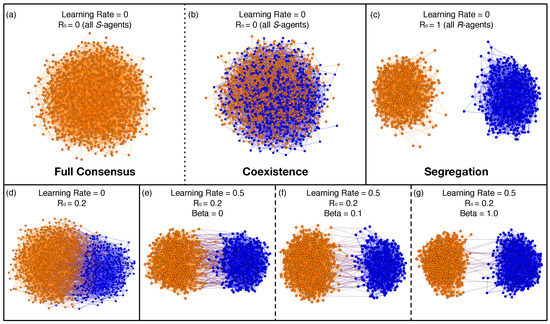
Figure 3.
Final configuration states of the multiplex evident layer. Visualization of the actions (color codes) and link disposition according to model parameters (learning dynamics rate), (hidden layer topology) and (initial fraction of R-agents). Full consensus (a) can only occur when only S-agents are present in the system, but not always; coexistence (b) is obtained otherwise, while segregation (c) and more profitable social outcomes in terms of game payoffs are reached when R-agents spread in the population. Other panels (d–g) show outcomes having an heterogeneous initial distribution.
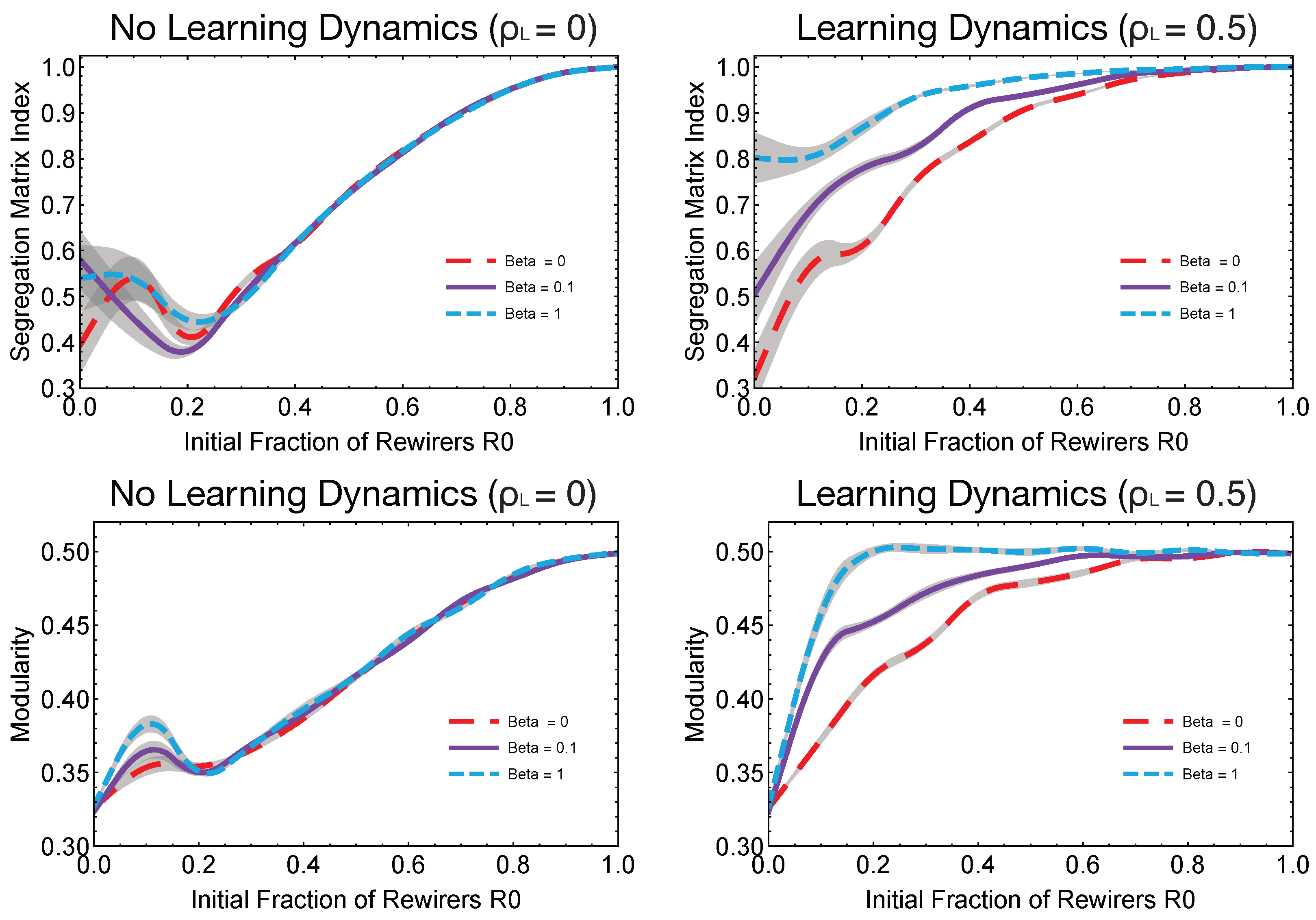
As we have seen above, the presence of learning alters dramatically the segregation dynamics. Figure 4 (top panels) highlight the SMI curves for three different topologies (lattices, , small-world networks, and random graphs, ) of the hidden layer. Different hidden topologies display different SMI curves and the minimum segregation is again observed around when no learning dynamics occurred. When learning is actively present in the system and strategies can evolve over time, then the multiplex interplay between actions and strategies increases the action segregation in the system. This phenomenon of increasing segregation is also present when the hidden layer topology is modified. In fact, lattices displayed a rather regular structure, had a larger mean network distance and a higher graph distance entropy compared to random graphs and small-worlds, making the propagation of rewiring strategies slower with respect to the other hidden topologies. The more frequent presence of R-agents also produced higher values of modularity, see Figure 4 (bottom panels), where one can observe that the final evident layer topologies were more clustered for increasing values of and .
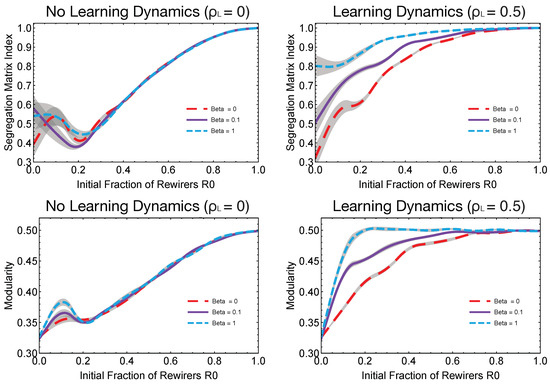
Figure 4.
Segregation results for different hidden layers and R-agents. Segregation matrix indexes (SMI) (top row) and modularity (bottom row) for different values of initial fractions of R-agents (), hidden layer topologies () and either for no learning in the system (left panels) or learning rate (right panels). Every data point is averaged over 50 different replicates. Error bars are represented as gray overlays. When no learning is present in the system, consensus is reduced across all topologies when an optimal number of R-agents is initially present in the system. Hence, there is an optimal number of for reducing segregation. Above that value, the more R-agents in the system the more segregation is present and all curves converge on the same trajectory. The presence of learning destroys this overall convergence so that different hidden topologies display different levels of segregation.
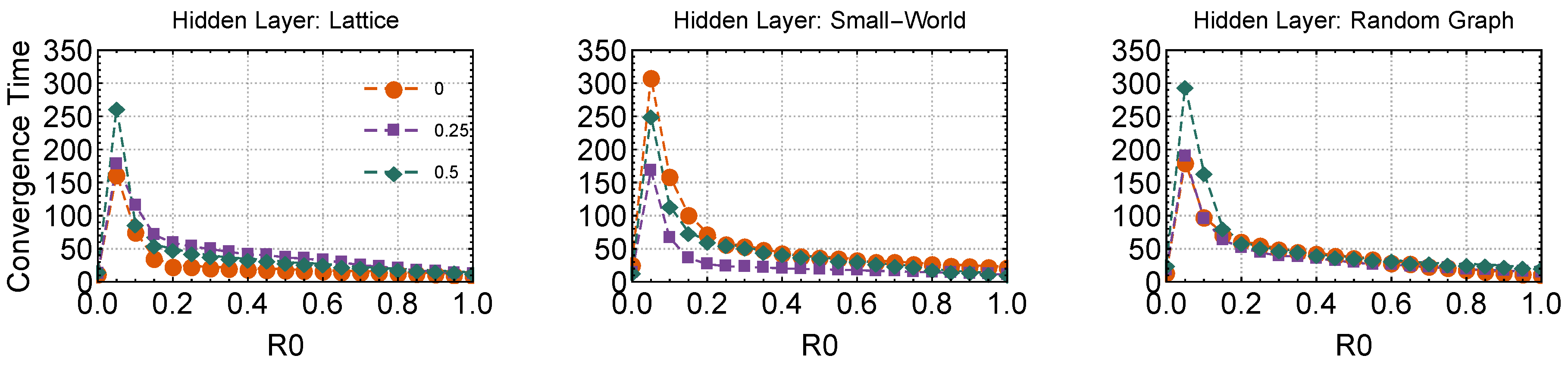
Figure 5 reports the number of simulation macro-steps necessary for the system to converge to the equilibrium configuration where every agent is satisfied. Independently of the topology of the hidden layer, the addition of initial R-agents from to dramatically increased the convergence time. However, when more R-agents were inserted in the system, the equilibrium configuration was reached in smaller times, with a monotonous decreasing trend. Figure 5 also indicates that the presence of learning increased the convergence time when the hidden layer was either a lattice or a random graph.
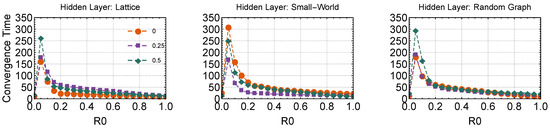
Figure 5.
Convergence simulation time. Results over the initial fraction of R-agents , for three different hidden layer topologies: (i) a lattice (, left), (ii) a Watts–Strogatz small-world () and (iii) a random graph (). Data points are relative to no social learning (orange circles), moderate social learning (purple squares) and high-rate social learning (green diamonds). Every data point is averaged over 50 different replicates. Error bars are of the same size of dots.
5. Discussion
In this study we have explored the case in which the preference for interacting with individuals having the same behavior (or action) stems from social learning mechanism informing individuals on how to respond to cultural intolerance. By cultural intolerance we mean the cost faced when individuals interact with others of different cultures [7]. We have found that the presence of social learning based on a payoff-driven update process and heterogeneity of cultural intolerance works in favor of states where there is segregation between actions. A segregation state is the one with the higher social welfare where both S-agents and R-agents are satisfied of the actions of their neighbors. We have found that the studied system converges to a multi-equilibria state in which the two different actions are segregated. This happens for three main reasons.
The first cause is the initial topology of the evident layer. Our baseline configuration, that has no learning and no R-agents, can be considered as the exogenous treatment in [33], but unlike the latter, the final configuration of the system does not always predict a conformism on the majority preferred action. In fact, the random graph topology that we have used does not always assure the convergence of the system towards one action because of the (less frequent) possibility of the formation of two connected clusters having different actions. As presented in Figure 3a,b, such topology produces two types of outcome configurations: on one hand, the system reaches full consensus on one action (either blue or orange), on the other hand, it converges to an equilibrium of coexistence of the two actions.
The second reason is the presence of R-agents, i.e., intolerant individuals. The higher their number the more likely a segregation occurs, as reported in Figure 2. In Figure 3c, even when there is no learning from the hidden layer and regardless the topology of the evident, the presence of R-agents determines the segregated characterization of the equilibrium. Figure 4 (lower panels) shows that the presence of R-agents alters also the modularity of the evident layer. If we compare such results with those graphically showed in Figure 3e–g, we can see that with the same values of and with the same learning rate, the two communities have less links between each other with the increasing of the modularity rate, causing a sharp segregation. The presence of R-agents alters the distribution of the links within each community. One result of [33] says that when costs of linking are low but positive, subjects choose a segregated network and diversity of actions. When the costs of linking are zero, subjects choose an almost fully integrated network, but persist with diverse action choices. In our paper the cost of rewiring is null as the one of meeting someone with a different action. However, since the number of links is limited we did not obtain fully integrated networks as in [33]. It will be of interest to study the system adding a cost to R-agents whenever they cut and/or create new links assuming the risk of not finding same action individuals.
The third reason for segregation is the presence of the social learning mechanism. It performs the function of reinforcing the best strategy for solving the cultural intolerance, thus accelerating the segregation as shown in Figure 3d–g, and in Figure 5. We have shown that in this framework the most successful strategy comes out to be the rewiring one, given the fact that both the cost of cutting and forming a link is zero, and given the fact that the payoff for interacting with an alike agent is zero. The social learning mechanism, in the hidden layer, promotes rewiring as the best strategy to gain higher payoffs in the evident layer. Such promotion happens at faster time scales, making the segregation more evident, when we pass from a lattice topology to a random graph and even if the number of R-agents is low as shown in Figure 2.
We believe that our results are also empirically relevant. Our findings can account for the coexistence of equilibria of multiple actions, as well as for the segregation in actions of the two cultural groups. Both these patterns are often observed in real-world systems. For example, it is well documented and analyzed the segregation phenomenon in the United States [48] that brought the rise and the persistence of “ghetto culture”, which, in turn, is associated with a poor work ethic [49]. Another identification of such phenomenon is based on the hypothesis of “acting white” by [50], who argue that some minorities are discouraged from achieving in school (coordinating with good-students) by the negative prejudices of ethnic peers. Our model provides an alternative explanation for the phenomenon as a consequence of both a learning mechanism and a strategic choice: because of strategy-assortativity, that is the outcome of the social learning, avoiding effort prevents a member of these cultural groups from being estranged from their own cultural group members. In this regard, we stress that our model can explain why, even in the presence of strong anti-discrimination intervention, we may observe segregation and stratification between cultural groups. Such a result is made salient by the presence of the multi-level structure that integrate the two dynamics of learning and strategic coordination.
Author Contributions
All authors conceived the study. F.L. and A.A. wrote the code to run computer simulations. All authors performed data analysis, discussed the results, drew conclusions and wrote the manuscript.
Funding
A.A. gratefully acknowledges the financial support of the Ministerio de Economía y Competitividad of Spain under grant no. FJCI-2016-28276.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsor had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
References
- Nemeth, C.J. Differential contributions of majority and minority influence. Psychol. Rev. 1986, 93, 23. [Google Scholar]
- Tushman, M.L. Special boundary roles in the innovation process. Adm. Sci. Q. 1977, 22, 587–605. [Google Scholar] [CrossRef]
- Van Der Zee, K.; Paulus, P. Social psychology and modern organizations: Balancing between innovativeness and comfort. In Applied Social Psychology: Understanding and Managing Social Problems; Cambridge University Press: Cambridge, UK, 2008; pp. 271–290. [Google Scholar]
- Hong, L.; Page, S.E. Problem solving by heterogeneous agents. J. Econ. Theory 2001, 97, 123–163. [Google Scholar] [CrossRef]
- Pelled, L.H.; Eisenhardt, K.M.; Xin, K.R. Exploring the black box: An analysis of work group diversity, conflict and performance. Adm. Sci. Q. 1999, 44, 1–28. [Google Scholar] [CrossRef]
- Zizzo, D.J. You are not in my boat: Common fate and discrimination against outgroup members. Int. Rev. Econ. 2011, 58, 91–103. [Google Scholar] [CrossRef]
- Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications; Cambridge University Press: Cambridge, UK, 1994; Volume 8. [Google Scholar]
- McPherson, M.; Smith-Lovin, L.; Cook, J.M. Birds of a feather: Homophily in social networks. Annu. Rev. Sociol. 2001, 27, 415–444. [Google Scholar] [CrossRef]
- Bruch, E.E.; Mare, R.D. Preferences and pathways to segregation: Reply to van de Rijt, Siegel, and Macy. Am. J. Sociol. 2009, 114, 1181–1198. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Selten, R. A General Theory of Equilibrium Selection in Games; MIT Press Books; The MIT Press: Cambridge, MA, USA, 1988; Volume 1. [Google Scholar]
- Van Huyck, J.B.; Cook, J.P.; Battalio, R.C. Adaptive behavior and coordination failure. J. Econ. Behav. Organ. 1997, 32, 483–503. [Google Scholar] [CrossRef]
- Schelling, T.C. The Strategy of Conflict; Harvard University Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Singh, T.B. Social Norms and Interpersonal Trust. SSRN Electron. J. 2009. [Google Scholar] [CrossRef]
- Jackson, M.O.; Xing, Y. Culture-dependent strategies in coordination games. Proc. Natl. Acad. Sci. USA 2014, 111, 10889–10896. [Google Scholar] [CrossRef]
- Benjamin, D.J.; Choi, J.J.; Strickland, A.J. Social identity and preferences. Am. Econ. Rev. 2010, 100, 1913–1928. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Chen, Y. The potential of social identity for equilibrium selection. Am. Econ. Rev. 2011, 101, 2562–2589. [Google Scholar] [CrossRef]
- Chen, Y.; Li, S.X.; Liu, T.X.; Shih, M. Which hat to wear? Impact of natural identities on coordination and cooperation. Games Econ. Behav. 2014, 84, 58–86. [Google Scholar] [CrossRef]
- Charness, G.; Rigotti, L.; Rustichini, A. Individual behavior and group membership. Am. Econ. Rev. 2007, 97, 1340–1352. [Google Scholar] [CrossRef]
- Brede, M.; Stella, M.; Kalloniatis, A.C. Competitive influence maximization and enhancement of synchronization in populations of non-identical Kuramoto oscillators. Sci. Rep. 2018, 8, 702. [Google Scholar] [CrossRef] [PubMed]
- Pestelacci, E.; Tomassini, M.; Antonioni, A. Coordination games on small-worlds: Artificial agents vs. experiments. In Proceedings of the ECAL 2011, Paris, France, 8–12 August 2011; pp. 654–661. [Google Scholar]
- Antonioni, A.; Cacault, M.P.; Lalive, R.; Tomassini, M. Coordination on networks: Does topology matter? PLoS ONE 2013, 8, e55033. [Google Scholar] [CrossRef]
- Hernandez, P.; Munoz-Herrera, M.; Sanchez, A. Heterogeneous network games: Conflicting preferences. Games Econ. Behav. 2013, 79, 56–66. [Google Scholar] [CrossRef]
- Attanasi, G.; Hopfensitz, A.; Lorini, E.; Moisan, F. Social connectedness improves co-ordination on individually costly, efficient outcomes. Eur. Econ. Rev. 2016, 90, 86–106. [Google Scholar] [CrossRef]
- Buskens, V.; Snijders, C. Effects of network characteristics on reaching the payoff-dominant equilibrium in coordination games: A simulation study. Dyn. Games Appl. 2016, 6, 477–494. [Google Scholar] [CrossRef]
- Mazzoli, M.; Sanchez, A. Equilibria, information and frustration in heterogeneous network games with conflicting preferences. J. Stat. Mech. Theory Exp. 2017, 2017, 113403. [Google Scholar] [CrossRef]
- Goyal, S.; Vega-Redondo, F. Network formation and social coordination. Games Econ. Behav. 2005, 50, 178–207. [Google Scholar] [CrossRef]
- Jackson, M.O.; Watts, A. On the formation of interaction networks in social coordination games. Games Econ. Behav. 2002, 41, 265–291. [Google Scholar] [CrossRef]
- Antonioni, A.; Sanchez, A.; Tomassini, M. Global information and mobility support coordination among humans. Sci. Rep. 2014, 4, 6458. [Google Scholar] [CrossRef]
- Advani, A.; Reich, B. Melting Pot or Salad Bowl: The Formation of Heterogeneous Communities; Technical report, IFS Working Papers; IFS: Peterborough, UK, 2015. [Google Scholar]
- Bojanowski, M.; Buskens, V. Coordination in dynamic social networks under heterogeneity. J. Math. Sociol. 2011, 35, 249–286. [Google Scholar] [CrossRef]
- Ellwardt, L.; Hernandez, P.; Martınez-Cánovas, G.; Munoz-Herrera, M. Conflict and segregation in networks: An experiment on the interplay between individual preferences and social influence. Dyn. Games 2016, 3, 191–216. [Google Scholar] [CrossRef]
- Riedl, A.; Rohde, I.M.; Strobel, M. Efficient coordination in weakest-link games. Rev. Econ. Stud. 2015, 83, 737–767. [Google Scholar] [CrossRef]
- Goyal, S.; Hernández, P.; Martínez-Cánovasz, G.; Moisan, F.; Muñoz-Herrera, M.; Sánchez, A. Integration and Segregation; Cambridge Working Papers in Economics; University of Cambridge: Cambridge, UK, 2017; Volume 1721. [Google Scholar]
- Kazienko, P.; Musial, K.; Kajdanowicz, T. Multidimensional social network in the social recommender system. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2011, 41, 746–759. [Google Scholar] [CrossRef]
- Szell, M.; Lambiotte, R.; Thurner, S. Multirelational organization of large-scale social networks in an online world. Proc. Natl. Acad. Sci. USA 2010, 107, 13636–13641. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, M.A.; Shinavier, J. Exposing multi-relational networks to single-relational network analysis algorithms. J. Informetr. 2010, 4, 29–41. [Google Scholar] [CrossRef]
- Battiston, F.; Nicosia, V.; Latora, V. The new challenges of multiplex networks: Measures and models. Eur. Phys. J. Spec. Top. 2017, 226, 401–416. [Google Scholar] [CrossRef]
- Wang, Z.; Szolnoki, A.; Perc, M. Evolution of public cooperation on interdependent networks: The impact of biased utility functions. EPL (Europhys. Lett.) 2012, 97, 48001. [Google Scholar] [CrossRef]
- Gómez-Gardenes, J.; Reinares, I.; Arenas, A.; Floría, L.M. Evolution of cooperation in multiplex networks. Sci. Rep. 2012, 2, 620. [Google Scholar] [CrossRef] [PubMed]
- Matamalas, J.T.; Poncela-Casasnovas, J.; Gómez, S.; Arenas, A. Strategical incoherence regulates cooperation in social dilemmas on multiplex networks. Sci. Rep. 2015, 5, 9519. [Google Scholar] [CrossRef] [PubMed]
- Pereda, M. Evolution of cooperation under social pressure in multiplex networks. Phys. Rev. E 2016, 94, 032314. [Google Scholar] [CrossRef] [PubMed]
- Amato, R.; Díaz-Guilera, A.; Kleineberg, K.K. Interplay between social influence and competitive strategical games in multiplex networks. Sci. Rep. 2017, 7, 7087. [Google Scholar] [CrossRef] [PubMed]
- Lugo, H.; San Miguel, M. Learning and coordinating in a multilayer network. Sci. Rep. 2015, 5, 7776. [Google Scholar] [CrossRef]
- Erdos, P.; Rényi, A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 1960, 5, 17–60. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of small-world networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef]
- Fershtman, M.; Chen, M. The segregation matrix: A new index for measuring sociometric segregation. Megamot 1993, 34, 563–581. [Google Scholar]
- Fershtman, M. Cohesive group detection in a social network by the segregation matrix index. Soc. Netw. 1997, 19, 193–207. [Google Scholar] [CrossRef]
- Massey, D.S.; Denton, N.A. American Apartheid: Segregation and the Making of The Underclass; Harvard University Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Sáez-Martı, M.; Zenou, Y. Cultural transmission and discrimination. J. Urban Econ. 2012, 72, 137–146. [Google Scholar] [CrossRef]
- Fordham, S.; Ogbu, J.U. Black students’ school success: Coping with the burden of acting white. Urban Rev. 1986, 18, 176–206. [Google Scholar] [CrossRef]
| 1 | The literature on the link between group diversity and group performance is vast and not univocal. While it is true that increasing diversity in groups elicits positive outcomes such as enhancing thoughtful decision processes [1], expanding access to social networks and resources [2], promoting innovation [3], and facilitating problem solving [4], it has been also proved that increasing diversity introduces group biases that may contribute to conflict among group members [5,6]. |
| 2 | In a social network environment homophily means that contact between similar people occurs at a higher rate than among dissimilar people [8]. In static terms homophily and segregation correspond to the same network phenomenon. |
| 3 | We refer to segregation as the non-random allocation of people who belong to different groups into social positions and the associated social and physical distances between groups [9]. |
| 4 | The cited works can be also classified by the type of coordination game implemented such as pure coordination, stag-hunt, anti-coordination and battle of the sexes. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).