Abstract
Contrary to what is represented in geospatial databases, places are dynamic and shaped by events. Point clustering analysis commonly assumes events occur in an empty space and therefore ignores geospatial features where events take place. This research introduces relational density, a novel concept redefining density as relative to the spatial structure of geospatial features rather than an absolute measure. Building on this, we developed Space-Time Plume, a new algorithm for detecting and tracking evolving event clusters as smoke plumes in space and time, representing dynamic places. Unlike conventional density-based methods, Space-Time Plume dynamically adapts spatial reachability based on the underlying spatial structure and other zone-based parameters across multiple temporal intervals to capture hierarchical plume dynamics. The algorithm tracks plume progression, identifies spatiotemporal relationships, and reveals the emergence, evolution, and disappearance of event-driven places. A case study of crime events in Dallas, Texas, USA, demonstrates the algorithm’s performance and its capacity to represent and compute criminogenic places. We further enhance metaball rendering with Perlin noise to visualize plume structures and their spatiotemporal evolution. A comparative analysis with ST-DBSCAN shows Space-Time Plume’s competitive computational efficiency and ability to represent dynamic places with richer geographic insights.
1. Introduction
While digital maps or geospatial databases represent places as static geometric objects (e.g., points or polygons), places are dynamic: they appear and disappear (e.g., periodic markets), expand, shift, or contract (e.g., urban sprawl, gentrification, or depopulation), and emerge or decease (e.g., new opportunities zones or ghost towns). The dynamics of a place reflect human experiences in response to geospatial events that can attract people (e.g., festivals), repel people (e.g., hazards), or drive spill-over or cascading effects on the same or different geospatial event types to the dynamic place. As such, events are placemaking signals and drivers. Many studies in geography, sociology, tourism, and related fields have shown how events shape people and loci, give rise to places, and evolve along the process [1,2,3,4]. While the literature offers fruitful discussions on the conceptual bases of the constructs and relationships, empirical studies have been limited to case-based investigations and lack advances in the representation and computation of dynamic places by capturing changes in the spatial distribution of events over time.
This research operationalizes dynamic places in geospatial databases by developing a space-time plume (ST-Plume) algorithm that detects and tracks spatial clustering of events over time. We posit that the extent and context of geospatial event clusters over time represent the geographic progression of a dynamic place. The conceptual construct of a plume captures the place’s varying properties, geometries, and locations over time. The algorithm consists of two primary stages: (1) detect spatial clusters to identify the footprints of a dynamic place over time, and (2) temporally relate the footprints over time to form a plume representation. Popular density-based spatial clustering algorithms consider point-to-point distances to determine whether two points belong to a cluster. Density-Based Spatial Clustering of Applications with Noise (DBSCAN) assumes that two points within the predetermined maximum distance, also known as the reachability distance, () belong to a spatial cluster if and only if the cluster has the predetermined minimum number of points (n) [5]. One major drawback of DBSCAN is its inability to detect clusters of varying densities. The Ordering Points to Identify the Cluster Structure (OPTICS) algorithm overcomes the issue by introducing an additional parameter, the core distance, to the core-point idea, and adjusting reachability according to iterative updates of nearest-neighbor distances [6]. By updating the reachability distance, OPTICS captures the varying density structure among points and allows the delineation of spatial clusters of varying densities.
Nevertheless, the varying densities in a spatial cluster may reflect higher-level structures among these points. Instead of an ordered list of points by their nearest-neighbor distances, Hierarchical DBSCAN (or HDBSCAN) computes mutually reachable distances for every pair of points to consider all possible values in determining clusters under a fixed minimum number of points and displays the results as a dendrogram [7,8]. Over the years, researchers have developed various density-based algorithms with computational capabilities and efficiency to detect complex clustering patterns from large-scale and streaming data [9,10]. Prominent algorithms include Shared Nearest Neighbors (SNNs) [11], ST-DBSCAN [12], Minimum Spanning Tree-based clustering (MST) [13], Clustering by Fast Search and Find of Density Peaks (CFSFDP) [14], Hierarchical Clustering Algorithm based on Density-Distance Cores [15], and many more. Common to all density-based algorithms is the unspoken assumption that points are distributed in an empty space. Therefore, points can occur in any infinitesimal location anywhere, and distance can be used as an absolute measure of density.
However, the real world is not an empty space and is populated with geographic features and heterogeneous landscapes. The conventional density-based algorithms will likely overlook clusters of mail thefts in areas of single-family homes in a city with apartment complexes, even if packages were stolen in every single-family home, for example. As such, we introduced a new premise to account for the influence of underlying geographic structures on identifying spatial clusters. We developed the ST-Plume algorithm and used crime events and criminogenic places for proof of concepts. Like most geospatial events, crime reports are geocoded to buildings with addresses. With the same number of reported crimes, areas of higher building density are associated with denser addresses and likely have denser reported crimes. The ST-Plume algorithm continuously adapts a threshold for spatial reachability (i.e., the spatial epsilon parameter used in DBSCAN) to account for the varying densities and sizes of building footprints as the algorithm moves across a study area and identifies spatial clusters of various densities, reflecting the spatial structure underlying places in the study area. The following sections present the proposed algorithm (Section 2), demonstrate the algorithm in a case study with real-world crime data (Section 3), discuss the algorithm performance (Section 4), conclude with the research contributions to the representation and computation of dynamic places broadly, and suggest future research directions (Section 5).
2. The Proposed Space-Time Plume Algorithm for Dynamic Places
Central to the proposed ST-Plume algorithm is the consideration of geographic space in which events take place. Features in a geographic space differ in size, geometry, and arrangement. Some events can only occur in certain feature types, such as soccer games on a soccer field. Some events frequently occur in the same venue (e.g., meetups in a cafe), but other events rarely repeat at the same location (e.g., burglary in a house). Consequently, the event density depends on the spatial distribution and temporal availability of the geographic features that can host, afford, or be susceptible to the events. Spatial heterogeneity, temporal variability, and multi-scalar manifestation are intrinsic to the ST-Plume algorithm and are implemented in three stages: (1) delineate zones of low heterogeneous geographic structures and determine spatial reachability based on the feature density in each zone; (2) determine temporal intervals based on event’s periodicity of interest (e.g., daily, weekly, monthly, seasonally, etc.) and apply both spatial reachability and temporal intervals to cluster events within each zone; (3) identify event clusters in neighboring zones and merge event clusters across neighboring zones if events are within temporal intervals and spatial reachability distances from either zone.
2.1. Geographic Heterogeneity and Lacunarity
Geographic objects are diverse in type, appearance, and separation. For example, there are many different types of buildings. A large building may be the size of multiple small buildings. Some buildings may be next door to each other, and others may be far away in isolation. Geographic worlds possess high variability and complexity, which makes an area of spatial homogeneity hypothetical only. A practical approach is to delineate zones of low spatial heterogeneity with proper cut-off values. Since Mandelbrot’s introduction in 1982 [16], the concept of lacunarity has evolved from a measure for fractals of the same dimension but with different textures to a scale-dependent measure of heterogeneity or texture of any object or phenomenon, regardless of fractals [17]. Lacunarity indices have been used to measure landscape textures [18], sea ice fractures [19], forest structures [20], building density [21], the spatial extent of geographic context for environmental exposure [22], and many more applications. Complementary to fractals for space-filling properties, lacunarity measures the “gappiness” of a spatial distribution and provides an estimation of the density and spacing of either binary or quantitative features [21,23].
The gliding-box algorithm [17] is a common way to calculate scale-dependent lacunarity as the measure represents the width of the probability distribution of mass (i.e., non-gap) over a predefined unit (i.e., the gliding box). A spatial pattern with holes of all sizes is expected to be very lacunar and will have a wide probability distribution of mass per unit. We adopted the gliding-box implementation for the spatial pattern analysis [23]. The length r of the gliding box should be much smaller than the spatial pattern by a scale factor. The box glides one unit step (i.e., a cell) at a time across the entire study area composed of occupied and void spaces. The mass s of an occupied space can be one () or some quantity, and there is no mass () in any void space. The gliding box moves across the spatial pattern and calculates the mass at each stop. After the gliding box has passed through the entire spatial pattern, a probability function of mass values () is built for the spatial pattern based on the frequency distribution of calculated mass values (s). The lacunarity measure () is defined by the first and second moments (Z(1) and Z(2)) of the mass probability function (). In the original study [17], Allain and Cloitre used a binary example (s = 0 or 1). Therefore, their differs slightly from the generic equation below.
Lacunarity for the entire spatial pattern characterizes its overall gappiness. Local lacunarity, in contrast, differentiates where high or low spatial heterogeneity is present in the spatial pattern. When there are zones of spatial homogeneity, areas around the zonal boundaries are characterized by varying hole sizes and are expected to be more lacunar. Local lacunarity detects the boundary area by subsetting an analysis window around each unit location (i.e., a cell) and applying the gliding-box algorithm to calculate the lacunarity within an analysis window for every location across a spatial pattern [24]. The procedures for generating a raster of local lacunarity values are described in Algorithm 1 with nested Algorithms 2 and 3.
| Algorithm 1: Generate a raster of local lacunarity for the entire study area. |
 |
A raster dataset is a 2D grid composed of equally sized square cells. The three algorithms calculate local lacunarity at every cell based on an analysis window centering on the cell (Algorithm 2 across the study area. Edge cells (or boundary cells) can only partially expand internally and result in a partial analysis window. Therefore, the spatial extent of the input raster dataset should be expanded to at least around the study area to avoid edge effects [25] that cause computation problems on boundary cells.
| Algorithm 2: Calculate local lacunarity in each analysis window. |
 |
Conceptually, the analysis window in Algorithm 2 can be any size larger than the gliding box and smaller than the spatial extent of the raster data representing the pattern. For ease of computation, common sizes for an analysis window are odd numbers of multiples of the raster’s cell size (e.g., or ). Eliciting high-lacunarity locations delineates the entire spatial pattern into similar gappy zones, whose average gap can be a reachability distance () for the respective zone in density-based clustering. Algorithm 2 extracts an analysis window for each and calls Algorithm 3 to develop a mass probability function, calculate the lacunarity value for each analysis window, and return the value to Algorithm 1 where the lacunarity value is assigned to individual cells on the output raster.
| Algorithm 3: Calculate the local lacunarity value in an analysis window. |
 |
The output raster of local lacunarity values exhibits the spatial distribution of heterogeneity: locations with higher lacunarity values are surrounded by higher degrees of heterogeneity. Geographically, these locations represent the boundaries between homogeneous zones. Zone delineation of similar gappiness can be determined heuristically by iteratively adjusting lacunarity thresholds for optimal boundaries. Similarly, lacunarity is scale-dependent and varies by the window size and box size in Algorithms 1–3. A case study in Section 4 demonstrates the heuristic processes.
2.2. Zone Delineation Based on Lacunarity
Lacunarity values increase towards zonal boundaries where the lacunarity value reaches a maximum, and then the values decrease when transitioning to another zone. Transitions from low to high values in the output raster of lacunarity are indicative of zones with low lacunarity values internally and high lacunarity values on boundaries. If an analysis window is homogeneous (all cell values are 0 or 1), the revised lacunarity value from Algorithms 1–3 at its center cell is 1 (the minimum lacunarity value). If every gliding box in an analysis window has different mass values, the lacunarity value at the center cell derived from the analysis window is maximal: , which is the number of all possible mass combinations for a raster . If the input is a squared (that is, ) binary raster of cell values, i.e., 1 or 0 (representing feature or gap, respectively), the maximal lacunarity value is in the output raster of local lacunarity. In the simplest case, the input squared raster has one boundary line of single-cell width in an analysis window, and the maximal lacunarity in the output raster is or . Therefore, cells with values between and are considered boundary cells. Cells with values less than reside within zones.
2.3. Space-Time Plumes (ST-Plumes) of Events to Elicit Dynamic Places
We developed the Space-Time Plume (ST-Plume) algorithm to identify dynamic places. Expanding upon Space-Time DBSCAN (ST-DBSCAN), the ST-Plume algorithm incorporates key thematic differences to determine the inclusion or exclusion of observations to a plume:
- -
- Adaptive spatial reachability distance () according to the underlying spatial structure of the zone where observations reside;
- -
- Zone-based iterations for local neighbor search;
- -
- Temporal interval selection and multiscale temporal clustering with across-scale linkages;
- -
- Optional parameters for adaptive minimum points based on the zone’s spatial structure to consider if an observation should be considered in a cluster.
2.3.1. Zone-Adaptive Spatial Reachability Distance
The spatial structure of feature density and gappiness in a zone constrains the minimal separation for events to occur across features within the zone, and the minimal separation limits the maximum possible event density if events can only take place at these features. Some events may occur in the same feature multiple times (e.g., parties in a house), but the event density remains influenced by the feature’s spatial structure and distribution. Consequently, a density-based clustering analysis of these events should adapt to the spatial density of relevant features embedded in each zone; that is the concept of relational density. We designed a zonal modifier () to implement the relational density by modifying a predefined base spatial reachability parameter in ST-DBSCAN to determine a zone-adjusted spatial reachability distance in a given zone i. We tailored the relationship between and to reflect the underlying spatial processes and constraints on event occurrences.
We implemented a transformation of to a multiplier to increase or decrease the reachability distance required to find a spatial neighbor (Equations (4)–(6)). Zones composed of sparse features (e.g, single-family homes) require a larger reachability measure to effectively identify potential neighbors, whereas zones of dense features (e.g., apartment complexes) need smaller reachability measures. utilizes the observed mean distance of all pairwise features within a zone instead of average nearest-neighbor distances commonly used in spatial clustering. Therefore, distinguished from spatial clusters of similar densities by the conventional density-based methods, the ST-Plume algorithm can detect plumes that capture transitions from relatively sparse to dense zones, as event densities inherited from these areas of sparse, transitional, and dense features may reveal unique spatial dynamics and intra-zone interactions.
where
- -
- : Sparse zone flag is 1 if the zone is classified as sparse and 0 otherwise, based on the defined lacunarity threshold.
- -
- is the sparse zone modifier, a predefined boost parameter to calibrate the contrast between sparse and dense zones. The dot product aims to indicate the relative importance of sparse vs. dense categories. The modifier increases the for regions with sparse features (i.e., ) and has no effect for regions with dense features (i.e., ). Hence, the modifier adds separation between the sparse and dense regions.
- -
- (default = 0.1) is an adjustable modifier for spatial density (clustering vs. dispersion).
- -
- (default = 0.5) is an adjustable modifier for observed mean distance between neighbors (see Section 3.3 for details on calibrating and parameters).
- -
- is the Inverse Density of the features that influence event distribution. In our case study, the features are buildings.Since we consider events that can only take place in the features of interest, zones without features, by definition, cannot be part of any ST-Plume. Therefore, the feature count (N) must be 1 or greater. captures the average area per feature, and the logarithmic transformation () transforms it to a dimensionless measure with values that approximate a normal distribution. The added 1 to the logarithmic transformation is to account for cases with approaching 0. The term is a measure internal to a given zone.
- -
- ObsMD is the observed mean distance of all pairwise building distances within the zone.
- -
- is the maximum observed mean distance across all zones, used to scale mean distances in individual zones.
- -
- is the weight for the observed mean distance (ObsMD) and can be adjusted.
The product of attends to the relativity of the zone’s mean feature distance to the maximum one in the study area. The term is a relative measure of the zone to other zones in the study area. The transformation of into a multiplier is achieved by scaling reachability values within the range :
The parameter (k) represents the maximum amplification factor for the spatial reachability distance (). Sparse regions should have a higher amplification, approaching (k), while the denser a region is, the closer the amplification is to 1. Finally, the zonal adjusted spatial reachability distance () for is:
Applying the popular “spatial join” operation, we can identify which zone contains an event and assign the identified zone ID to that event. When determining potential spatial neighbors, events use the zonal adjusted spatial reachability distance from their assigned zone.
2.3.2. Zone-Based Computation
ST-Plume leverages events’ zonal assignments for efficient algorithm iterations. Zonal assignments improve computational efficiency by searching neighboring events locally in the same zone or across the neighboring zones only without a global search of all other events and ensure that the clustering process considers the local spatial structures pertinent to each event. The algorithm loops through all zones and events within zones, iteratively creating plumes and searching for potential space-time neighboring events. Zone-based processing allows the algorithm to finish processing all events in one zone before moving on to another. Neighbor searches extend beyond an event’s zone, incorporating neighboring zones based on the zonal modifier () to the zone’s base reachability distance (). Since neighboring events may come from different zones with different reachability constraints, we compare bi-directional relationships. The spatial reachability between two events in two zones is evaluated from both perspectives. If reachability exists in either direction, the two events are considered spatial neighbors, and the algorithm continues to the temporal filter. For example, if Event A is in Zone 1, and Event B is in Zone 2, using the reachability modifier from Zone 1 for Event A, Event B is out of reach of Event A. However, Event A is within the reach of Event B using the reachability modifier from Zone 2. As such, Event A and Event B are spatially reachable.
2.3.3. Multiscale Temporal Clustering
Temporal reachability () can be defined using daily, weekly, monthly, seasonal, or custom intervals. The ST-Plume algorithm deems two events are in the same temporal cluster if the events are reachable within the considered temporal interval. A smaller temporal reachability interval () may cause a spatial cluster to break apart temporally for a time gap larger than the temporal interval under consideration. However, a larger temporal reachability interval allows for more events to be included in the same temporal cluster, which can help reduce the fragmentation of clusters but may lead to excessively large plumes, which diminishes the plumes’ analytical value. To address this, we developed a hierarchical system to link plumes based on progressively increasing temporal reachability intervals. The hierarchical system of plumes makes explicit the multi-scalar nature of ST-Plumes. For instance, a 28-day plume may emerge from the convergence of 14-day plumes when increasing the temporal reachability. The hierarchy system links the 28-day plume branching into the 14-day plumes in a parent–child relationship. The locations, shapes, sizes, and duration of these plumes may vary as one moves up or down in the temporal hierarchy of plumes. In essence, the plume hierarchy encodes a hierarchy of dynamic places characterized by the events of interest and changes in their locations and spatial footprints over time.
2.3.4. Dynamic Space-Time Reachability
The ST-Plume algorithm defines the dynamic space-time reachability by both zone-adaptive spatial reachability distance and the predetermined temporal reachability intervals. Two events are in the same plume if they are spatially and temporally reachable. Since the ST-Plume algorithm first identifies clusters of events reachable in space, the subsequent filter for temporal reachability operates within individual spatial clusters.
If a sole temporal interval is considered, ST-Plume operates similarly to the ST-DBSCAN algorithm. With multiple values (e.g., 7 days, 14 days, 21 days, etc.), the algorithm iterates each event to search for the event’s space-time neighboring events within each from the shortest to the longest temporal intervals to form plumes at these temporal intervals and builds a temporal hierarchy of these plumes. The ST-Plume algorithm keeps track of plume assignments and event object visitation (per temporal interval) through a dictionary property that is part of each Event object. The dictionary operates as a hash table with keys, , and values, the Plume object identifiers. Below is an example of :
2.3.5. Scaling and Filtering of Plumes via Adaptive MinPts and Event Count Thresholds
ST-Plume allows single events to serve as the base unit for plume formation because certain events, such as a homicide in a remote location, carry a distinct spatial and temporal meaning even in isolation. Unlike density-based algorithms (e.g., ST-DBSCAN) that label unclustered points as noise, ST-Plume assigns every event to a plume for each temporal epsilon, even if it is the only event in that plume. This behavior is analogous to k-means clustering, where every point belongs to a cluster regardless of its proximity to others.
This full assignment structure ensures that the ST-Plume algorithm can capture the full spectrum of spatiotemporal scales inherent in event data. Plumes naturally grow in extent as the algorithm progressively relaxes spatial and temporal reachability thresholds. With sufficiently large thresholds, a plume may expand across a large area or the entire study area, which becomes a runaway plume with overly expanded volumes that no longer reflect localized activity patterns. Because ST-Plume aims to detect “places” across varying resolutions, it is important to carefully determine spatial and temporal reachability thresholds that can capture the granularity and cohesion of those places. To constrain spatial–temporal expansion for analytically relevant clusters, the ST-Plume algorithm includes two complementary mechanisms: (1) the Adaptive MinPts parameter and (2) Plume Event Count Threshold (PECT).
The Adaptive MinPts mechanism mirrors DBSCAN’s idea that a minimum number of neighbors is required for a point to initiate or participate in a plume. However, this runs counter to ST-Plume’s core philosophy that even isolated events may represent meaningful places. For that reason, the Adaptive MinPts is an optional parameter that may be useful for cases where aggregation strength is a necessary condition for inclusion. When activated, the MinPts value is dynamically adjusted based on the normalized zonal modifier (), which captures the local spatial structure in a zone. The adjustment follows an inverse relationship: In dense urban areas (lower ), a higher MinPts value helps prevent over-expansion. In sparser areas (higher ), a lower MinPts supports the formation of place-like clusters even with limited nearby events.
where
- -
- is the normalized Zone Index for the current event;
- -
- and are the minimum and maximum expected Zone Index values;
- -
- is a user-defined upper limit (e.g., 5);
- -
- The base MinPts is fixed at 1.
The PECT is a post-processing filter applied after the completion of clustering procedures to retain those that meet a user-defined minimum event count threshold for downstream analysis. ST-Plume guarantees a plume assignment for every event. In sparse regions or when adaptive constraints are active, this can result in many singleton plumes (i.e., plumes containing only one event). The Plume Event Count Threshold filters out small or analytically insignificant plumes.
2.3.6. Putting It All Together: The ST-Plume Algorithm
In essence, the ST-Plume algorithm takes Event objects and Zone objects (Algorithm 4) to generate Plume objects (Algorithm 5) that capture the space-time dynamics of event-driven places. Each Zone object represents a spatial unit that contains Event objects and maintains structural relationships with neighboring zones. Each Event object denotes the time and location together, offering the affordance for an event to take place. Each Plume object represents a spatiotemporal cluster of events and is linked to other Plume objects in the hierarchy based on the given set of temporal intervals. Event objects, Zone objects, and Plume objects are defined as follows:
| [Event Object] | |
| : | Unique Event object identifier. |
| : | A dictionary with key–value mapping |
| each providing a temporal interval (key) | |
| to the assigned Plume object ID (value), ordered by temporal intervals. | |
| : | Timestamp of when the event occurred |
| stored in date/time format. | |
| X and Y: | Spatial coordinates of the event location. |
| Z: | Temporal coordinate, implemented as an integer |
| converted from the timestamp . | |
| : | Identifier for the Zone object in which the event resides. |
| [Zone Object] | |
| : | Unique Zone object identifier. |
| : | Normalized zone modifier to spatial reachability |
| : | List of event objects within this zone. |
| n: | Number of events in the list. |
| : | Spatial index (KDTree) built for events within this zone |
| only if n > 1; no otherwise. | |
| : | A dictionary with linked neighbor Zone objects (key) and distances |
| (value) between this Zone object and the linked neighborZone objects, | |
| ordered by distance. |
| [Plume Object] | |
| : | Unique Plume object identifier. |
| : | Temporal interval |
| : | List of references to event objects assigned to this Plume object. |
| n: | Number of events in list. |
| : | Set of Parent Plume object ID(s) from the next |
| larger temporal interval. | |
| : | Set of children Plume ID(s) from the immediate |
| smaller temporal interval. |
Algorithm 4 creates Event objects from input event data of interest (e.g., crime incidents or disease cases) and initiates Zone objects based on lacunarity (Algorithm 1) and zone delineation (Section 3.2). Before the algorithms, the event data and zone data are preprocessed using the geospatial function Spatial Join: (1) Spatial Join events to zones so that each event obtains a zone ID in which the event took place in the output Event–Zone table; and (2) Spatial Join zones to zones within a specific distance (boundary to boundary) so that each zone obtains neighboring zones within the distance in the output NeighborZones table. Both tables are used in Algorithm 4. The Event–Zone table provides Zone ID for corresponding Event and Zone objects. The NeighborZones table links each zone to its neighboring zones and distances, essential to creating a dictionary for each Zone object to facilitate event search across zones. The definition of neighboring zones is domain-dependent. Commonly used definitions include adjacency or within a specific distance. If the predetermined distance is set to zero, only immediately adjacent zones are neighbors.
| Algorithm 4: Preprocess event and zone datasets into objects |
 |
The Space-Time Plume algorithm is comprised of a main processing flow and several helper functions, as detailed in Algorithms 5–8. Algorithm 5 iterates through Zone objects and their respective Event objects calling subprocesses to initialize (Algorithm 6) and expand (Section 2.3.4) Plume objects by using a neighbor queue and Breadth-First Search (BFS) approach. After plume expansion for a particular event is exhausted, Algorithm 5 calls Algorithm 8 to capture the plume temporal hierarchy and continues to the next event. This logic flow is detailed in Figure 1.
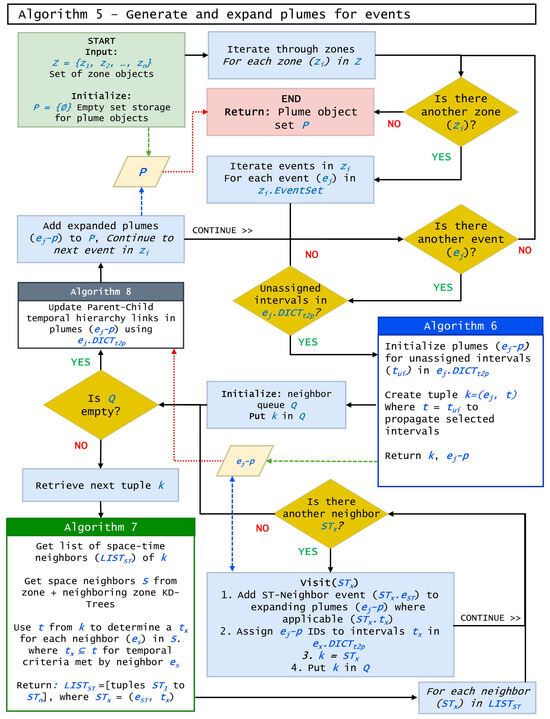
Figure 1.
Data and logic flow of Algorithm 5: generate space-time plumes for events.
During the Event object creation, its property, , is initialized as an empty hash table, whose values are populated through plume generation (Algorithms 5 and 6). This property provides three key functionalities for ST-Plume: (1) support for the plume expansion process across multiple temporal intervals simultaneously, (2) a mechanism to track event object visitation per temporal interval, and (3) a reference for plume linkage in the temporal hierarchy.
The plume expansion process is similar to ST-DBSCAN with a few modifications. The algorithm initializes a queue data structure, instead of a stack, to explore potential space-time neighbor Event objects. The queue structure was chosen due to its earlier propagation of nearer relationships, resembling the first law of geography that closer things are more related than those further away [26].
Event object’s and Zone object’s , , , and facilitate the search for and queuing of the next neighboring events within spatial and temporal reachability. If MinPts is specified, the algorithm calculates adaptive MinPts during neighbor consideration before determining plume assignment (Section 2.3.5).
| Algorithm 5: Generate space-time plumes of events |
 |
Algorithm 6 initializes plumes for active expansion from unassigned temporal intervals in an event . The process only creates plumes for temporal intervals that do not have an assignment; previously assigned temporal intervals are skipped. After plume initialization, the algorithm builds a tuple k composed of the event and the list of temporal intervals that were unassigned t. This data structure is integral to the multiscale temporal hierarchy procedures. As events pass through the algorithms, they carry a subset of temporal intervals that are applicable to their space-time neighbor searches (Algorithm 7) to ensure only relevant plumes are expanded and space-time neighbors are filtered appropriately. Figure 2 demonstrates this logic visually.
| Algorithm 6: Initialize plumes for an event |
 |
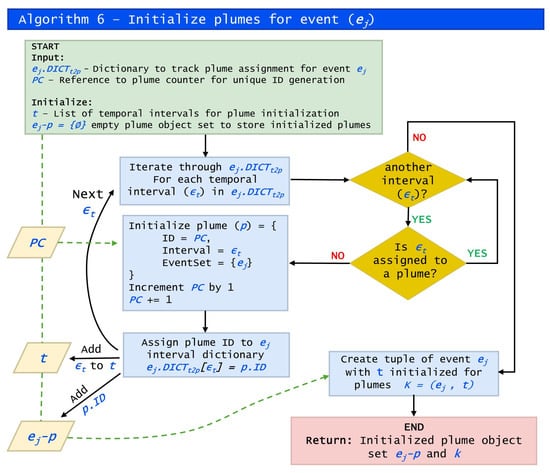
Figure 2.
Data and logic flow of Algorithm 6: initialize plumes for events.
ST-Plume utilizes a two-step approach to identify spatiotemporal neighbors of a given tuple k. First, spatial candidates (S) are retrieved from the input event’s zone as well as neighboring zones (up to ) via KD-tree queries. The algorithm considers bi-directional reachability to ensure all neighbors are found. A temporal filter is applied to each spatial candidate based on the list of temporal intervals t from tuple k. Unlike ST-DBSCAN, which uses the fixed intervals of 1 day and the same day the following year [12], ST-Plume calculates the absolute date difference, allowing users to define custom temporal thresholds.
| Algorithm 7: Obtain space-time neighbors of an event |
 |
For each spatial candidate event , the algorithm constructs a tuple (), where includes only the temporal intervals satisfied by . The subset allows the algorithm to propagate temporal intervals forward for further sub-consideration (i.e., searching for st-neighbors of ). These valid spatiotemporal neighbor tuples are aggregated into a list and returned. a flowchart highlighting this approach is provided in Figure 3.
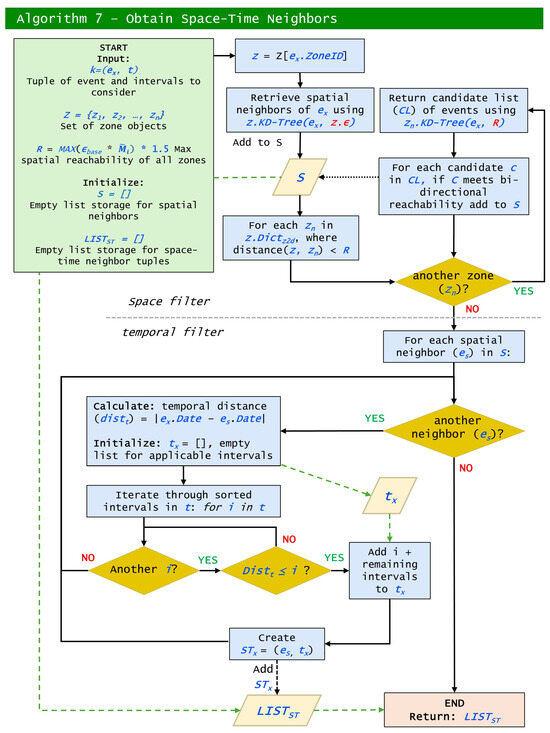
Figure 3.
Data and logic flow of Algorithm 7: obtain space-time neighbors.
Algorithm 8 establishes a temporal hierarchy for recently expanded plumes . Algorithm 5 has completed expanding these plumes that were initiated by event . Algorithm 8 iterates through assigning plume IDs to the children and parent properties of the plume objects. For a given interval in , the child plume (child) object is retrieved from P using ; . Likewise, the parent plume (parent) object is retrieved from P using ; .
Together these algorithms form the foundation to identify and expand plumes from a given set of events and zones. Other features and functions of the ST-Plume program, such as data loading and export, MinPts calculations, and minor tasks can be reviewed in the published codebase. See the data and availability statement.
| Algorithm 8: Set plume parent–child links for an event |
 |
3. ST-Plumes of Crime Events and Criminogenic Places
The lacunarity and ST-Plume algorithms were implemented with reported crime events in 2018–2022 from the Dallas Police Department. With lacunarity-guided clustering, ST-Plume adapted to neighborhoods of high and low spatial densities and manifested the presence, progression, and interactions of all identified space-time plumes of reported crime events. Each plume represented a swarm of crime events taking place over time; the event density internal to the swarm could vary, but collectively, the swarm progressed as a unity. The analysis of the plume’s changing geospatial characteristics and its interactions with other plumes elicited how criminogenic places evolved in the city of Dallas. These criminogenic places rendered geographic affordances and situations contributing to crime happenings or lack thereof. The evolution of criminogenic places gave empirical insights into Crime Displacement Theory (Reppetto 1976) and informed place-based policy for crime prevention. Generally speaking, the ST-Plume algorithm computes latent interplays between places and events: event-affording places and place-making events. The rest of this section details the computation procedures and result analysis of the case study.
3.1. Geospatial Data Processing and Parameters Determination
The data used in the case study included reported crime events and building footprints in Dallas, Texas, USA. The Dallas Police Department provided all reported events from 1 January 2018 to 31 December 2022 (5 years) and geocoded the events based on incident addresses. After removing non-criminal records and offenses with addresses corresponding to police stations, hospitals, or Lake Ray Hubbard and North Lake, the dataset contained 479,669 unique crime events. Since all these crime events were geocoded with addresses, varying building densities across the city were influential to spatial crime clusters. We applied Algorithms 1–3 to geospatial data of building footprints to delineate zones of similar building densities in Dallas. Specifically, the case study used Dallas building footprints from Open Street Map (OSM), which is in the process of incorporating Microsoft AI-derived building footprints from Maxar (formerly DigitalGlobe), Airbus, and IGN France imagery. Cross-referencing OSM building footprints with National Agriculture Imagery from the U.S. Department of Agriculture (accessed through Texas Geographic Information Office-TNRIS) indicated the current OSM Dallas building data were of higher detail in polygon shapes, positional accuracy, and completeness compared to the Microsoft AI-derived building footprints. The finding was consistent with a similar comparative study that assessed OSM building footprints in Lombardy, Italy and concluded the adequacy of OSM buildings for direct use, including urban analysis at an accuracy corresponding to 1:5000 maps [27]. Reviews of data quality suggested the high accuracy of OSM buildings in large urban areas [28]. Furthermore, the position accuracy of the OSM building footprints improved from an average error of 3.7 m in 2018 to 2.3 m in 2023 based on five cities in Québec, Canada [29].
The building footprints, represented as a polygon layer (vector) in NAD 1983 State Plane Texas N Central Coordinate system in U.S. feet, were converted to a binary raster of building locations or otherwise in a matrix. The conversion of polygon feature classes to raster datasets is a classical GIS topic [30,31,32]. Cell value assignment is influenced by the geometric relationship between the vector polygons and the origin, orientation, and spatial resolution of the raster structure as well as the chosen value assignment rule [33]. This study retained the orientation of the city of Dallas, extended the origin two miles (3220 m) northwest, and selected a cell size of 10 feet by 10 feet (3 m × 3 m) to balance the spatial accuracy of building footprints (an order of magnitude greater than 10 feet in dimensions) and processing efficiency. The large shift (two miles) in the origin, in comparison to the cell size (10 feet), ensured minimal, if any, bias on the cell value assignment. The selected cell size preserved most buildings’ polygon features in Dallas. Smaller cell sizes typically render fewer errors along feature boundaries but require greater computational resources. Following the Rule of Maximum Area, the study assigned a cell to a building polygon (value = 1) or a void space (value = 0) whichever occupied the largest portion of the cell’s area. All building footprints within Dallas and up to two miles outward were considered, in order to reduce potential edge effects [25], which have a significant impact on lacunarity calculations [34]. Algorithm 1 ingested the building raster to compute the output raster of local lacunarity with the following parameters: a cell size of , analysis window size of (or ), and gliding-box size of (or ).
3.2. Parameters Determination for Local Lacunarity Analysis
Parameters for the lacunarity analysis were heuristically determined based on the relationships between each parameter and the calculated local lacunarity measure in a test raster purposefully subsetted from the study area to include varied building sizes and gaps, the run times for the possible combinations of window sizes were 5, 7, 9, 11, 13, 15, 17, 19, 21, and 23, and the box sizes were 3, 5, 7, 9, 11, 13, 15, 17, 19, and 21, where the box size was strictly less than the window size, for example, a window size of with a box size of , a window size of with box sizes of and , etc. Note that Algorithm 3 augmented the output local lacunarity by one unit. Hence, the local lacunarity value for areas with homogeneous gaps would be equal to one, and greater than one otherwise. The test raster consisted of 3298 rows and 5860 columns of cells. For each combination of window size and box size, we computed statistical metrics of local lacunarity values and their correlations with window sizes and box sizes (Figure 4).
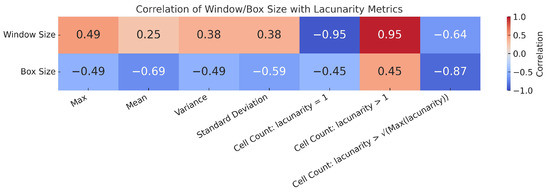
Figure 4.
Correlation of window and box sizes with local lacunarity statistics. A larger window size is highly correlated (0.95) with a higher number of boxes with local lacunarity > 1, while a smaller window size is highly correlated (−0.95) with a lower number of local lacunarity = 1. A larger box size is highly correlated (−0.87) with a lower number of local lacunarity > the squared root of the maximum lacunarity value.
The analysis informed the sensitivity of the analysis window size and gliding-box size in the local lacunarity distribution on the output raster. Increasing the window size would lead to a higher maximum, mean, and variance of the lacunarity, which could reflect larger buildings, varying building sizes and gaps, and likely bigger building clusters. However, there would also be fewer clusters of neighborhoods of similar building sizes and gaps (indicated by fewer cells with lacunarity = 1). In contrast, a smaller window size was shown to better capture more clusters of similar densities with lower lacunarity statistics and greater counts of lacunarity = 1. The box size exhibited a counter-effect to the window size. A larger box size resulted in smaller lacunarity statistics and more clusters of similar gaps. The correlation coefficients suggested a much stronger effect (0.95 and −0.95) of the window size than the effects of the box size on identifying clusters of similar building densities. With the same box size (), varying window sizes (5 × 5, 9 × 9, and 13 × 13) delineated zones of varying similar densities and extents, among which a window size of resulted in zones with the most uniform gaps (Figure 5).

Figure 5.
Effects of window sizes (5, 9, and 13) with the same box size (=3) on the lacunarity distribution. The background has lacunarity values of 0–1.
We ran the lacunarity algorithms (Algorithms 1–3) for all combinations with a box size smaller than the window size among window sizes (5, 7, 9, …, 23) and box sizes (3, 5, 7, …, 21) on the test raster (Figure 6). While run time demands were comparable among the smallest box sizes for each window size, the run time increased for increasing box sizes with each window size; the smaller the window size, the faster the increase. Combinations with a window size of and box size of were among the ones that incurred the lowest run time (200 s). The run time analysis (Figure 6), the correlation analysis (Figure 4), and the zoning results (Figure 5) heuristically led us to conclude that the smallest window size () with the smallest box size () was the most effective at capturing microtransitions in building density, ensuring that apartment buildings and single-family residential buildings did not mix within the same zone and having comparably faster processing time.
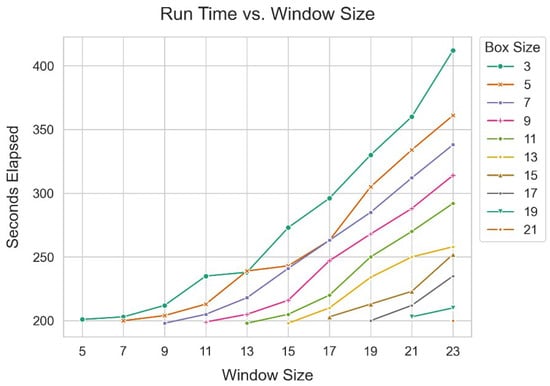
Figure 6.
Run time analysis of Algorithms 1–3 on the combinations of window sizes and box sizes in the experiment with 64 GB DDR4 RAM and a 12th Gen Intel i7-12700K, 3610 Mhz, 12-core processor with parallel processing on the test raster with 3298 rows and 5860 columns.
3.3. Zone Delineation, Zonal Reachability Modifier, and Neighboring Zones
We examined lacunarity behaviors in transitions between building clusters and in between open spaces to identify lacunarity thresholds for zone delineation. If an analysis window is homogeneous (all cell values are zero or one), the revised lacunarity value from Algorithms 1–3 is one (the minimum lacunarity value). Lacunarity values greater than one () suggest variation in building occurrences and open spaces. An examination of these lacunarity values uncovered unique properties within our input binary matrix. Considering the input building footprint data, the conversion to a binary matrix (zero, one) creates a unique schema for clustered patterns. Occurrences (ones) are tightly packed together, representing building footprints, with gaps (zeros) in between. The analysis window of the lacunarity algorithm interacts with these tightly packed “clusters” in several ways.
With the adjustment of adding one to the lacunarity value in Algorithm 3, the maximum lacunarity value of a given analysis window is a function of the window size w and the box size b: . When an entire edge row or column of the analysis window is composed of buildings (ones) and the other cells fall in gap spaces (zeros), the window’s lacunarity value w. In the empirical study, we opted for the second-smallest window–box combination (five, three), since the smallest combination (three, one) led to mostly spatially homogeneous windows and obscured zonal boundaries. We extracted cells between and from the calculated lacunarity grid as zonal boundaries and generated zones accordingly.
For each zone, we calculated with Equations (4), introduced in Section 2.3.1. This study focused on the calibrations of and to balance effects from density variations () and neighbor distances () on clustering. The goal was to ensure that the resulting values would reflect a meaningful clustering behavior across the zones, particularly in areas of high and low density. The calibration was based on the building footprints in Dallas, USA. A combination of high and low values resulted in an over-emphasized density and disadvantaged areas with sparse structures. Conversely, low and high values tended to under-emphasize the density and advantaged areas with sparse structures. Empirical tests suggested optimal ranges of values (0.5–1.5) for gradual and meaningful increases in for low-density areas and values (0.2–1.0) for the influences from neighbor distances without making distant points dominant. The combination of , , and resulted in a good balance between density variations, observed mean distances, and adjustments for areas of sparse buildings. Furthermore, was scaled to (Equation (6)) in the range of 1–3 as a multiplier to adjust spatial reachability distance in a zone. To facilitate plume formation across zones, we applied a popular spatial-join function to create a NeighborZones table with pairs of zone neighbors within 1500 feet of their shortest edge-to-edge distance. The table was used to populate for each Zone object.
3.4. Creating ST-Plumes of Crime Events in Dallas
First, we ran Algorithm 4 to create event objects and zone objects. Testing spatial reachability values between 150 and 328 feet suggested 200 feet resulted in a reasonable balance between capturing sparse areas while controlling excessive expansion in areas with dense buildings. was scaled to the range of 1–3 for all zones for three weights to differentiate the underlying spatial structures. We considered temporal intervals of 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, and 91 days and found that intervals within the range of 21–42 days offered a good balance, preventing excessive fragmentation while capturing plumes across different spatial densities. Hierarchical relationships between plumes are linked by temporal intervals in parents and children’s lists as discussed in Section 2.3.3.
Events assigned to separate plumes at a short temporal interval (e.g., 21 days) could expand into the same plume at a longer temporal epsilon (e.g., 42 days) as the ST-Plume algorithm processed multiple temporal epsilons simultaneously, dynamically linking plumes to create a plume hierarchy as discussed in Section 2.3.3. To focus on significant plumes, we applied an event count threshold of 30 to discard small plumes with less than 30 crime events. The applied base spatial reachability distance (200 feet) and temporal intervals of 14, 28, and 42 days resulted in no pronounced runaway plumes in the empirical study. Therefore, the optional MinPts parameter was dismissed. The numbers of plumes and their composing events varied with the temporal intervals (Table 1).

Table 1.
Summary of plumes by temporal intervals.
The run time for the selected parameter combination was 363.32 s or 6 min with 64 GB DDR4 RAM and a 12th Gen Intel Core i7-12700K, 3610 Mhz, 12-core processor. A full analysis of the run time with different parameter combinations is provided in Section 4.
3.5. Plumes Across and Within Regions of Varying Densities
With an adaptive spatial framework, the proposed ST_Plume Algorithm 5 identified criminogenic places in sparsely populated regions while maintaining contextual relevance. The selection of parameters, including the base spatial reachability distance , the zone-adaptive index , and the temporal intervals , influenced the ability to detect plumes within sparsely structured spatial areas. As and were relaxed, plumes became more prevalent in low-density regions, whereas more restrictive values limited their formation in high-density regions to account for heterogeneity in the underlying spatial structure.
Additionally, the algorithm allowed plumes to span across regions of varying densities, integrating both sparse and dense regions into a composite swarm. This relationship was particularly interesting, as plumes were not strictly confined to spatially structured regions but could form organically to capture placial relationships between dense urban areas and their surrounding sparse regions, potentially reflecting spillover effects or spheres of influence. The spatial projection of a 42-day plume (ID: 2365) bounded by the blue outline, for example, expanded space-time neighboring events among multiple 28-day plumes in various shades distributed across heterogeneous zones from 1 January 2018 to 31 December 2022 (Figure 7).
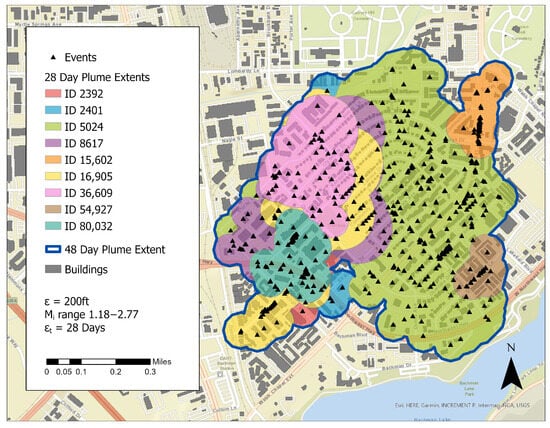
Figure 7.
A plume spanning zones of heterogeneous spatial structures with large and small buildings.
3.6. Visualizing ST-Plumes
ST-Plumes gradually transition through space and time. To better present this gradual transition between inclusion and exclusion of events, we combined three-dimensional spherical metaballs (hereafter, 3D metaballs) with Perlin noise perturbations. Metaballs (also known as blobby objects) are computer graphics shapes to render isosurfaces in volumetric data, and in particular, metaballs in proximity can merge into a single, continuous object with a blobby appearance [35]. Perlin noise attempts to create naturally appealing textures for visual effects in computer graphics [36] and is capable of capturing neutral landscapes [37]. Specifically, we applied a Gaussian Kernel function as in Kernel Density Estimation (KDE) with the spherical to capture the surface around each crime event in the event cloud. We adopted the idea that each event’s influence exponentially decayed over space in a level set framework for 3D surface editing [38]. However, we applied the exponential decay function for an event inside a metaball instead, to blur plume’s boundaries. The 3D metaballs captured the density and spatial–temporal structure of event distributions, whereas Perlin noise introduced naturalistic perturbations that reflected the uncertainty and irregularity in swarm boundaries. In combination, the 3D metaballs with Perlin noise exhibited a probabilistic and flowing visualization of dynamic event swarms, preserving both their structure and inherent uncertainty.
With metaballs and Perlin noise perturbations, Figure 8 provides three perspectives of a 3D visualization of wrapped fuzzy clouds around the events to mirror the way smoke plumes billow and disperse in response to environmental conditions. The crime events defined the cores of each plume while allowing for smooth transitions at the edges rather than abrupt cutoffs. By integrating spatial, temporal, and probabilistic influences, the 3D visualization captured the conceptual framework of placial dynamics, where place-based influence continuously shaped event clusters rather than defining them with rigid constraints.
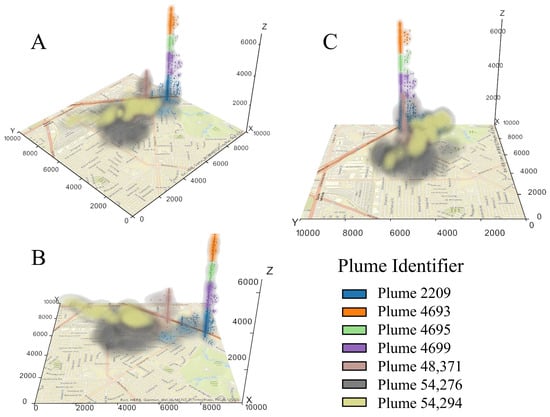
Figure 8.
Perspective views of plumes visualized with 3D metaballs and Perlin noise perturbations: (A–C) are different perspectives of the same collection of plumes. See text for details.
The three perspectives (A, B, and C) in Figure 8 illustrate the dynamic nature of the plumes and their interactions with the surrounding environment. Each plume is symbolized with a unique color. The apparent multi-colored stack is composed of four plumes in a time sequence, from the latest to the earliest plume IDs: 4693 (orange), 4695 (green), 4699 (purple), and 2209 (blue). The narrow stack captures the overall persistent, yet intermittent with breaks, nature of the localized criminogenic place over time. The plume (ID: 54276) in a grayish color covers an extensive place. After a break in time, another plume (ID: 54294) in a yellowish color emerges and progresses across a much narrower area over time. The progression captures the shift in the corresponding criminogenic place, and the space-time gradient as shown in Perspective C in Figure 8 suggests the plume’s speed of dispersion.
4. Algorithm Performance Based on the Case Study
Since ST_Plume builds upon ST_DBSCAN and by proxy DBSCAN, we compared their key differences in computational efficiency, particularly in spatial and temporal neighbor searches, expansion methods, and indexing structures.
ST_DBSCAN and DBSCAN have a run-time complexity of where n is equal to the number of data points [12]. This is due to the usage of , where the height of the tree is in the worst case. At most, each data point in n has a single region query, and the region query is expected to remain small in comparison to the database, hence .
To analyze the complexity of ST_Plume, we consider its core functional components built upon the ST_DBSCAN framework: (1) zone-based iteration, (2) plume initialization per event, (3) spatial and temporal neighbor queries, (4) plume expansion using breadth-first search, and (5) hierarchical linkage across temporal scales.
Zone-based iteration allows ST_Plume to spatially localize its computations by processing events spatially, one zone at a time. While the algorithm loops through each zone , each event is assigned to exactly one zone, ensuring that every event is processed once in the zone iteration. As a result, the overall iteration remains linear in the number of events, i.e., . This design choice reduces the randomness of event selection and ensures localized plume formation is completed before shifting to other areas. This improves spatial coherence, enhances memory efficiency (by keeping neighbor searches spatially constrained), and supports more predictable expansion behavior.
Plume initialization for an event involves iterating through its associated temporal interval dictionary , which contains at most temporal intervals. Since the number of temporal thresholds is typically small and constant, this step introduces only a minor overhead. As a result, its contribution to overall complexity remains within , which is asymptotically less than the current dominant spatial query term and therefore does not affect the leading-order complexity of the algorithm.
Spatial neighbor searches in ST_Plume consist of two components: (1) retrieving neighbors within the current zone using a KD-tree, based on the zone’s scaled distance threshold , and (2) retrieving neighbors from adjacent zones, each with its own KD-tree, using the maximum spatial reachability value R, while also checking bi-directional reachability constraints.
KD-trees are built once during the initial construction of zone objects (see Algorithm 4), which requires complexity on average per zone, where n is the number of events in that zone. Since the trees are static and not updated after construction, they incur no additional maintenance cost during the clustering process. Each spatial neighbor query then runs in , where k is the number of neighbors returned.
The number of adjacent zones queried per event is limited by the spatial reachability parameter R, which bounds the search radius. In practice, this means that global searches are avoided unless R exceeds the entire study area extent. Examining bi-directional spatial reachability requires comparisons after each neighbor zone KD-tree query, where k is the number of candidate neighbors returned. This step ensures that both the source and neighbor events fall within each other’s spatial thresholds, enforcing symmetry in plume formation. Since k is typically small due to localized spatial constraints, this check adds minimal overhead to the overall neighbor search process.
Compared to R-trees, which are better suited for dynamic datasets, KD-trees provide more efficient localized range queries. This makes them well suited for ST_Plume, where spatial searches are zone-specific and benefit from static, precomputed indexing. The result is a spatial neighbor search process that is both efficient and scalable within the algorithm’s localized spatial structure.
Plume expansion in ST_Plume is performed using a breadth-first search (BFS) strategy rather than depth-first search (DFS). This choice does not alter the algorithm’s complexity, as both BFS and DFS operate in , where v represents the number of events and e the number of spatial–temporal edges determined through KD-tree neighbor queries. While standard BFS visits each vertex only once, ST_Plume includes a mechanism to revisit an event in rare cases where an earlier temporal link is discovered. Such revisits are bounded by (), which is typically a small constant. Furthermore, only the newly found temporal link is processed, not the full interval set, reducing unnecessary processing. As a result, the plume expansion phase remains asymptotically less than . Thematically, BFS was selected because it better reflects geographic relationships, where nearby events are more likely to be linked, and it supports earlier propagation of temporally earlier connections, aligning with the real-world unfolding of spatial–temporal phenomena.
For the plume hierarchy linkage, the algorithm iterates through an event’s which has at most () entries. Since this operation is only performed for events that had at least one unprocessed temporal interval in Algorithm 5, the overall cost remains linear at . Given that () is typically small, this step does not introduce any additional complexity beyond the algorithm’s dominant terms.
In the worst case, ST_DBSCAN and ST_Plume approach complexity, though in practice, complexity remains . ST_Plume has a minor overhead due to its additional thematic functionality, including bi-directional spatial reachability, multiscale temporal clustering, and linkage, which scales by a small constant factor . In practice, since is typically small, the algorithm behaves as . However, as increases, the algorithm performs more plume initializations, temporal filter checks, and hierarchical linkages per event. To account for this scaling behavior, we express the complexity as , acknowledging the role of multiscale temporal processing in the algorithm’s run time.
Although ST_Plume incurs a slight additional computational overhead compared to ST_DBSCAN, its adaptive spatial scaling, temporal multi-resolution clustering, and hierarchical plume formation provide additional thematic functionality. Several described optimizations mitigate the increased complexity to ensure that ST_Plume remains scalable for large event datasets.
Runtime Performance and Sensitivity Analysis
We conducted two experiments to evaluate ST_Plume’s run-time performance and the impact on plume counts while varying the spatial reachability distances (), temporal intervals (), and MinPts parameter (Table 2 and Table 3). The experiments ran on a workstation running Windows 11 with 64 GB DDR4 RAM and a 12th Gen Intel Core i7-12700K, 3610 Mhz, 12-core processor.

Table 2.
Algorithm performance with a fixed temporal interval (28 days), a fixed spatial reachability distance (200 ft), and varying MinPts values.

Table 3.
Analysis of plume clustering with a fixed temporal interval (28 days), varying spatial reachability distances , and the maximal number of plumes = 479,669.
ST_Plume’s run-time performance was sensitive to the choice of the maximal MinPts values and spatial reachability distance () (Figure 9). The plume count increased linearly with the adaptive maximal MinPts values, and the run time increased linearly with the spatial reachability distance (). A reverse relationship was observed between the plume count and the spatial reachability distance (). The relationship between the run time and adaptive maximal MinPts values was more complex, starting with a nonlinear negative correlation and reflecting a slightly positive correlation at a larger maximal MinPts value.
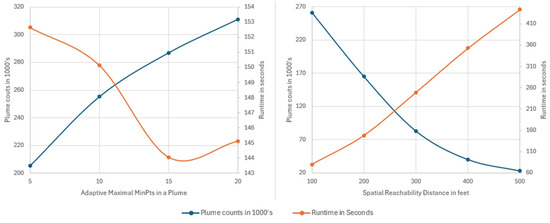
Figure 9.
Runtime performance of ST_Plume with varying maximal MinPts values and spatial reachability distances ().
ST_Plume run-time performance also depended on the cumulative temporal intervals () in consideration (Figure 10). Because ST_Plume aimed at a hierarchical structure of plumes, the cumulative run time was analyzed from shorter to longer temporal intervals. The cumulative run time exhibited a linear increase with the cumulative consecutive temporal intervals in the sequence of 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, and 91 days, in the combinations of 7, (7,14), (7,14,21), (7, 14, 21, 28), …(7, 1,4, 21, 28, …, 91). This behavior aligns closely with the theoretical complexity of our algorithm for approximately linear complexity relative to the number of temporal thresholds evaluated. Such linear scaling suggests that, although multiple temporal thresholds may enhance thematic depth and clustering effectiveness, each additional threshold incurs a measurable computational cost. Therefore, an optimal approach is to implement a select few temporal thresholds that balance thematic utility with computational efficiency to mitigate the risk of excessive run-time increases without sacrificing substantial analytical quality.
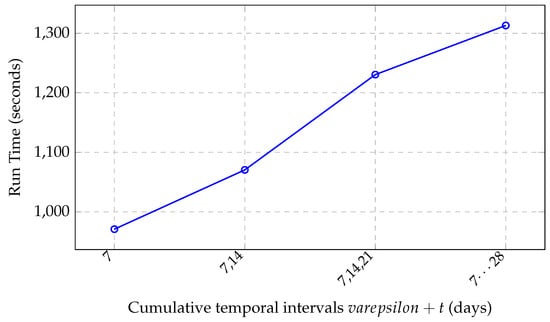
Figure 10.
Cumulative run time with cumulative temporal intervals with increments of 7 days. The spatial reachability distance is fixed at 200 ft).
5. Conclusions
The ST-Plume algorithm derives its name from the way smoke rises and dissipates in the atmosphere. Just as smoke is influenced by external forces—wind, pressure, and turbulence—spatiotemporal event swarms are shaped by dynamic influences that push, pull, or anchor them in place. Places in this conceptualization are not rigidly bounded; they exist within a continuum of influence, where fuzzy edges define the extent of a swarm rather than strict cutoffs. Traditional clustering methods often impose hard boundaries, but real-world event distributions are fluid and interact with each other and the environment across varying degrees of intensity.
This study proposed the Space-Time Plume (ST_Plume) algorithm to identify dynamic places emerging from event data, using a case study of crime events in Dallas, Texas. ST_Plume was developed on the premise that the underlying spatial structure of locations influenced both event occurrence and spacing, making spatial structure a crucial factor for detecting clusters of varying densities. Unlike traditional clustering methods, ST_Plume integrates zone-based spatial adaptation, allowing for more nuanced cluster formation across different urban environments. ST_Plume sets forth a new concept, “relational density”, where event density cannot be fully understood without considering the environmental context that affords events to take place. The idea of relational density was implemented by adaptive spatial reachability, multiscale temporal clustering, and hierarchical plume formation in the ST_Plume algorithm. While this added complexity slightly increased computational demands compared to ST-DBSCAN, we mitigated performance concerns through algorithmic optimizations. ST-Plume represents a novel step toward adaptive, structure-aware spatiotemporal clustering, offering new ways to analyze event-driven place formation. By incorporating spatial context, adaptive thresholds, and dynamic zone scaling, it provides a more flexible and interpretable approach to detecting transient yet meaningful places in event datasets.
With the case study of crime events in Dallas, Texas, USA, we demonstrated the algorithm’s capability to successfully capture plumes across diverse spatial structures, adapting to different density scenarios based on user-defined parameters. We used 3D metaballs and Perlin noise perturbations to visualize the plumes in space and time to draw insights into the dynamic nature of event-driven places. Going beyond the conventional event hotspot analysis, ST_Plume contributes to understanding how event-driven places evolve over space and time and provides a new framework for analyzing the spatiotemporal dynamics of events with an emphasis on event–environment interactions. Nevertheless, the ST_Plume algorithm is inherently domain-independent, making it applicable across a wide range of disciplines. While this study focused on crime events, the methodology can be adapted to analyze various types of spatiotemporal event data, such as infections and the study of places. The flexibility of the algorithm allows it to be tailored to different data types and clustering needs, making it a valuable tool for diverse research fields.
There are a few limitations to consider. ST_Plume is based on the assumption that events cannot occur without geospatial features, and therefore, the event distribution is constrained by the underlying spatial structure of these geospatial features. For crime events geocoded to building addresses, the distribution of buildings constrains the locations and densities of these crime events. As such, ST_Plume’s output depends on the quality of geocoded events and the geospatial data representing the geospatial features (e.g., building footprints from Open Street Map in the case study).
Several directions remain open for future development of ST-Plume. First, alternative zonal modifiers for spatial reachability may improve objectivity and refine spatial adaptation further. Second, an adaptive temporal density criterion could enhance plume formation by dynamically adjusting the temporal epsilon to account for variations in duration, such as increasing daylight time in summer or individuals with varying availability for activities to account for relational temporal intensity. The new ideas of relational spatial density and relational temporal intensity allow for space-time clustering adapting to the environmental and situational affordances to event occurrences and draw insights into the dynamics of event-driven places and place-making processes.
Author Contributions
Conceptualization, B.D. and M.Y.; methodology, B.D. and M.Y.; software, B.D.; validation, B.D.; formal analysis, B.D.; writing—original draft preparation, B.D.; writing—review and editing, M.Y.; visualization, B.D.; supervision, M.Y.; project administration, B.D.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This research, with permission, included the use of classified police incident data from Dallas Police Department. A public sample of this dataset is provided on the Dallas Open Data Portal https://www.dallasopendata.com/Public-Safety/Police-Incidents/qv6i-rri7/about_data (accessed on 17 March 2025). The ST-Plume algorithm python package is available at https://github.com/LucernaResearch/ST-PLUME (deposited on 27 June 2025) and includes a demonstration using the sample police incident data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jones, C. Major events, networks and regional development. Reg. Stud. 2005, 39, 185–195. [Google Scholar] [CrossRef]
- Misener, L.; Mason, D.S. Creating community networks: Can sporting events offer meaningful sources of social capital? Manag. Leis. 2006, 11, 39–56. [Google Scholar] [CrossRef]
- Richards, G. From place branding to placemaking: The role of events. Int. J. Event Festiv. Manag. 2017, 8, 8–23. [Google Scholar] [CrossRef]
- Harrison, S.; Tatar, D. Places: People, events, loci–the relation of semantic frames in the construction of place. Comput. Support. Coop. Work (CSCW) 2008, 17, 97–133. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the KDD 96: Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. ACM Sigmod Rec. 1999, 28, 49–60. [Google Scholar] [CrossRef]
- Campello, R.J.; Moulavi, D.; Sander, J. Density-based clustering based on hierarchical density estimates. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Gold Coast, QLD, Australia, 14–17 April 2013; pp. 160–172. [Google Scholar]
- Campello, R.J.; Moulavi, D.; Zimek, A.; Sander, J. Hierarchical density estimates for data clustering, visualization, and outlier detection. ACM Trans. Knowl. Discov. Data (TKDD) 2015, 10, 1–51. [Google Scholar] [CrossRef]
- Campello, R.J.; Kröger, P.; Sander, J.; Zimek, A. Density-based clustering. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2020, 10, e1343. [Google Scholar] [CrossRef]
- Bhattacharjee, P.; Mitra, P. A survey of density based clustering algorithms. Front. Comput. Sci. 2021, 15, 1–27. [Google Scholar] [CrossRef]
- Ertoz, L.; Steinbach, M.; Kumar, V. A new shared nearest neighbor clustering algorithm and its applications. In Proceedings of the Workshop on Clustering High Dimensional Data and Its Applications at 2nd SIAM International Conference on Data Mining, Arlington, VA, USA, 13 April 2002; Volume 8. [Google Scholar]
- Birant, D.; Kut, A. ST-DBSCAN: An algorithm for clustering spatial–temporal data. Data Knowl. Eng. 2007, 60, 208–221. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Wilkes, D.M. A divide-and-conquer approach for minimum spanning tree-based clustering. IEEE Trans. Knowl. Data Eng. 2009, 21, 945–958. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Yang, Q.F.; Gao, W.Y.; Han, G.; Li, Z.Y.; Tian, M.; Zhu, S.H.; Deng, Y.-h. HCDC: A novel hierarchical clustering algorithm based on density-distance cores for data sets with varying density. Inf. Syst. 2023, 114, 102159. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Allain, C.; Cloitre, M. Characterizing the lacunarity of random and deterministic fractal sets. Phys. Rev. A 1991, 44, 3552. [Google Scholar] [CrossRef] [PubMed]
- Plotnick, R.E.; Gardner, R.H.; O’Neill, R.V. Lacunarity indices as measures of landscape texture. Landsc. Ecol. 1993, 8, 201–211. [Google Scholar] [CrossRef]
- Scott, R.; Kadum, H.; Salmaso, G.; Calaf, M.; Cal, R.B. A lacunarity-based index for spatial heterogeneity. Earth Space Sci. 2022, 9, e2021EA002180. [Google Scholar] [CrossRef]
- Malhi, Y.; Román-Cuesta, R.M. Analysis of lacunarity and scales of spatial homogeneity in IKONOS images of Amazonian tropical forest canopies. Remote Sens. Environ. 2008, 112, 2074–2087. [Google Scholar] [CrossRef]
- Zhou, Y.; Lin, C.; Wang, S.; Liu, W.; Tian, Y. Estimation of building density with the integrated use of GF-1 PMS and Radarsat-2 data. Remote Sens. 2016, 8, 969. [Google Scholar] [CrossRef]
- Tian, T.; Kwan, M.P.; Vermeulen, R.; Helbich, M. Geographic uncertainties in external exposome studies: A multi-scale approach to reduce exposure misclassification. Sci. Total Environ. 2024, 906, 167637. [Google Scholar] [CrossRef] [PubMed]
- Plotnick, R.E.; Gardner, R.H.; Hargrove, W.W.; Prestegaard, K.; Perlmutter, M. Lacunarity analysis: A general technique for the analysis of spatial patterns. Phys. Rev. E 1996, 53, 5461. [Google Scholar] [CrossRef] [PubMed]
- Dong, P. Test of a new lacunarity estimation method for image texture analysis. Int. J. Remote Sens. 2000, 21, 3369–3373. [Google Scholar] [CrossRef]
- Ting, Z.; Shaolin, P. Spatial scale types and measurement of edge effects in ecology. Acta Ecol. Sin. 2008, 28, 3322–3333. [Google Scholar] [CrossRef]
- Tobler, W. A Computer Movie Siumulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Brovelli, M.A.; Zamboni, G. A new method for the assessment of spatial accuracy and completeness of OpenStreetMap building footprints. ISPRS Int. J. Geo-Inf. 2018, 7, 289. [Google Scholar] [CrossRef]
- Herfort, B.; Lautenbach, S.; Porto de Albuquerque, J.; Anderson, J.; Zipf, A. A spatio-temporal analysis investigating completeness and inequalities of global urban building data in OpenStreetMap. Nat. Commun. 2023, 14, 3985. [Google Scholar] [CrossRef] [PubMed]
- Moradi, M.; Roche, S.; Mostafavi, M.A. Evaluating OSM Building Footprint Data Quality in Québec Province, Canada from 2018 to 2023: A Comparative Study. Geomatics 2023, 3, 541–562. [Google Scholar] [CrossRef]
- Van Der Knaap, W.G. The vector to raster conversion:(mis) use in geographical information systems. Int. J. Geogr. Inf. Syst. 1992, 6, 159–170. [Google Scholar] [CrossRef]
- Carver, S.; Brunsdon, C. Vector to raster conversion error and feature complexity: An empirical study using simulated data. Int. J. Geogr. Inf. Syst. 1994, 8, 261–270. [Google Scholar] [CrossRef]
- Huo, X.; Zhou, C.; Xu, Y.; Li, M. A methodology for balancing the preservation of area, shape, and topological properties in polygon-to-raster conversion. Cartogr. Geogr. Inf. Sci. 2022, 49, 115–133. [Google Scholar] [CrossRef]
- Shortridge, A.M. Geometric variability of raster cell class assignment. Int. J. Geogr. Inf. Sci. 2004, 18, 539–558. [Google Scholar] [CrossRef]
- Feagin, R.; Wu, X.; Feagin, T. Edge effects in lacunarity analysis. Ecol. Model. 2007, 201, 262–268. [Google Scholar] [CrossRef]
- Blinn, J.F. A generalization of algebraic surface drawing. ACM Trans. Graph. (TOG) 1982, 1, 235–256. [Google Scholar] [CrossRef]
- Perlin, K. Improving noise. In Proceedings of the 29th Annual Conference on Computer Graphics and Interactive Techniques, San Antonio, TX, USA, 23–26 July 2002; pp. 681–682. [Google Scholar]
- Etherington, T.R. Perlin noise as a hierarchical neutral landscape model. Web Ecol. 2022, 22, 1–6. [Google Scholar] [CrossRef]
- Museth, K.; Breen, D.E.; Whitaker, R.T.; Barr, A.H. Level set surface editing operators. In Proceedings of the 29th Annual Conference on Computer Graphics and Interactive Techniques, San Antonio, TX, USA, 23–26 July 2002; pp. 330–338. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).