DEVS Closure Under Coupling, Universality, and Uniqueness: Enabling Simulation and Software Interoperability from a System-Theoretic Foundation
Abstract
1. Introduction
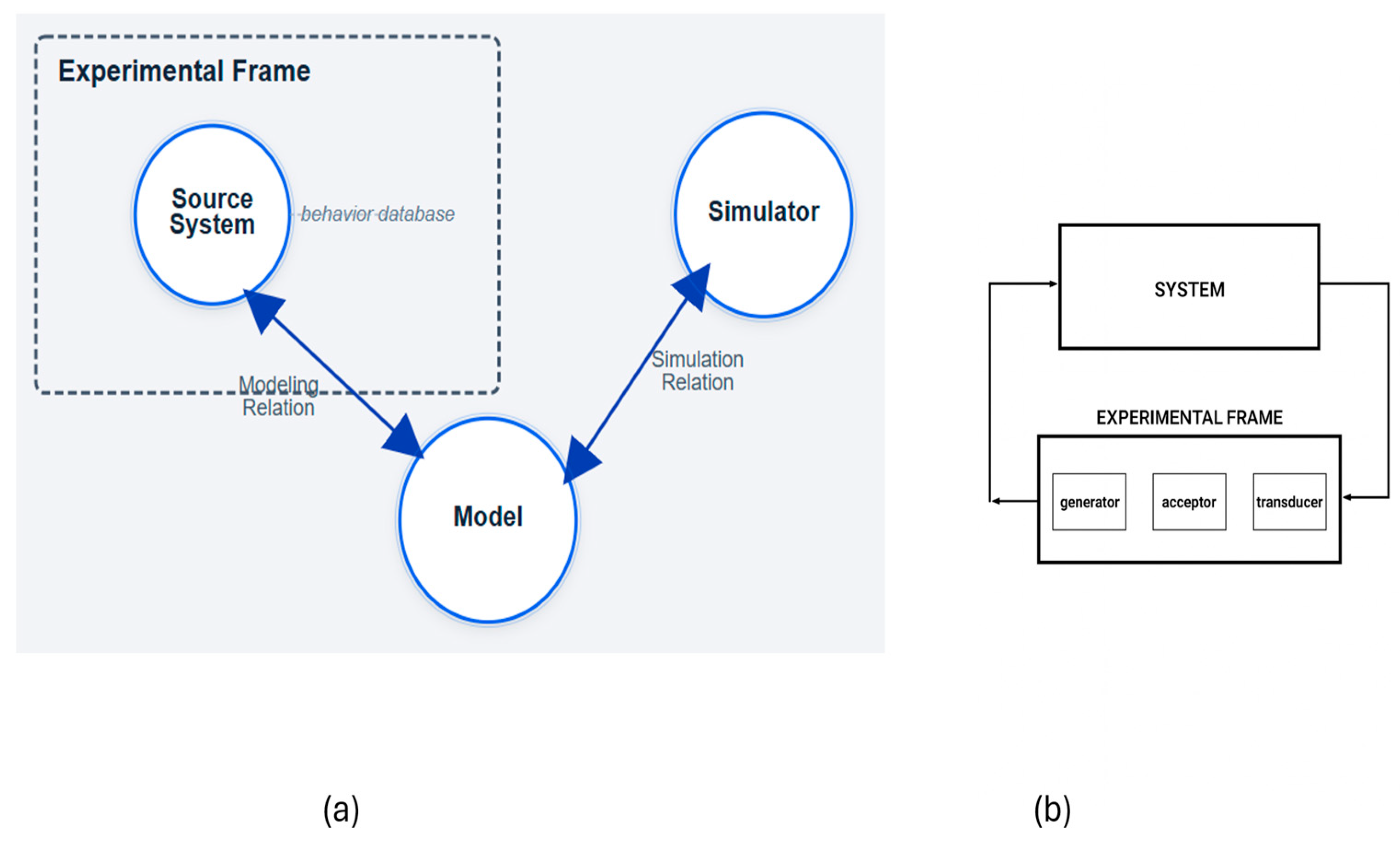
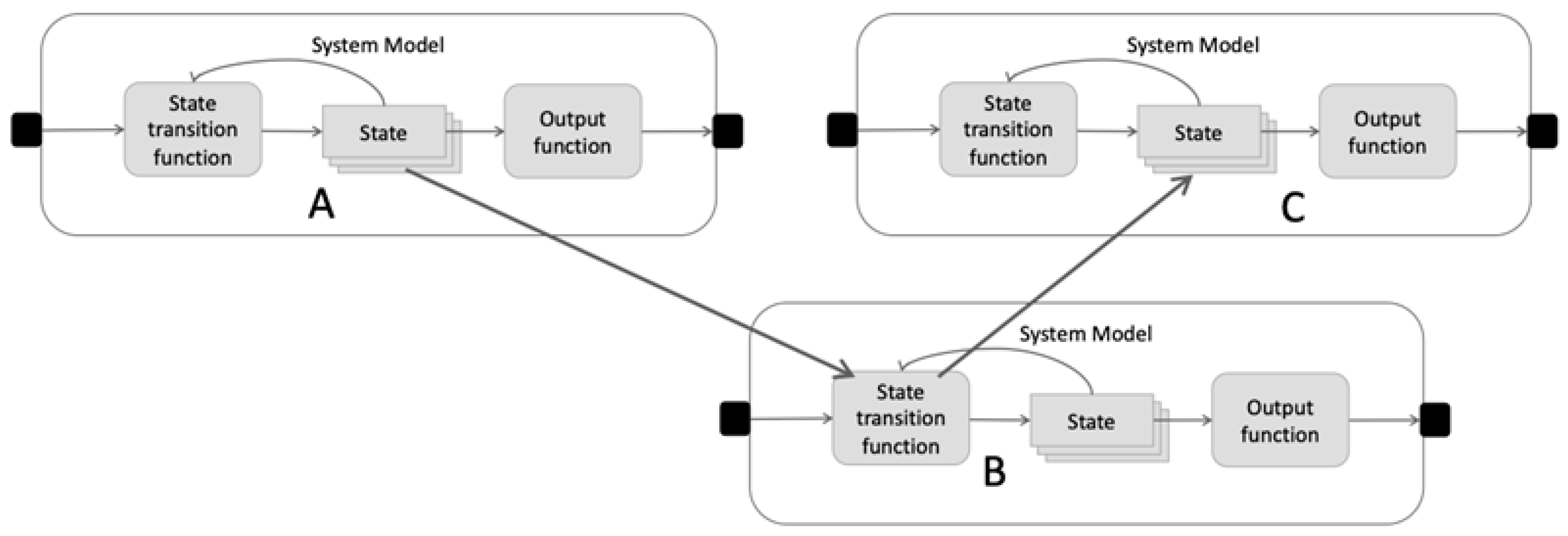
2. Background: Modeling and Simulation Framework and DEVS Theory
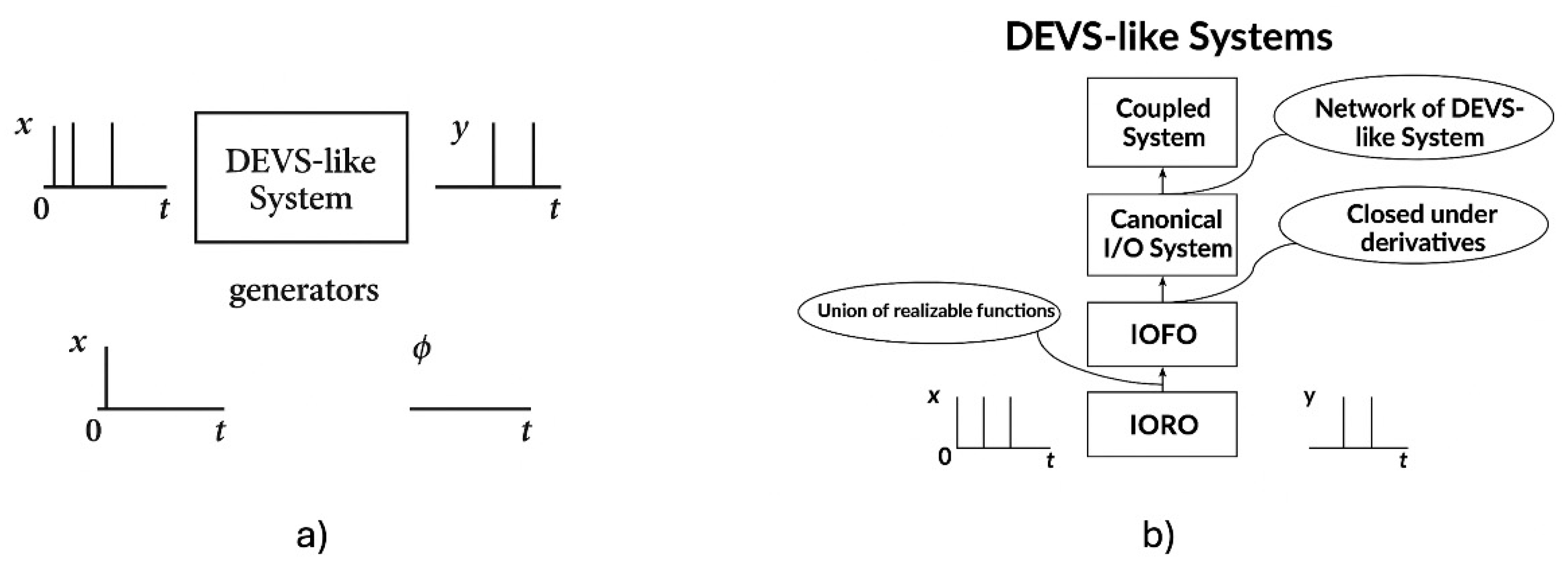
2.1. DEVS Universality and Uniqueness
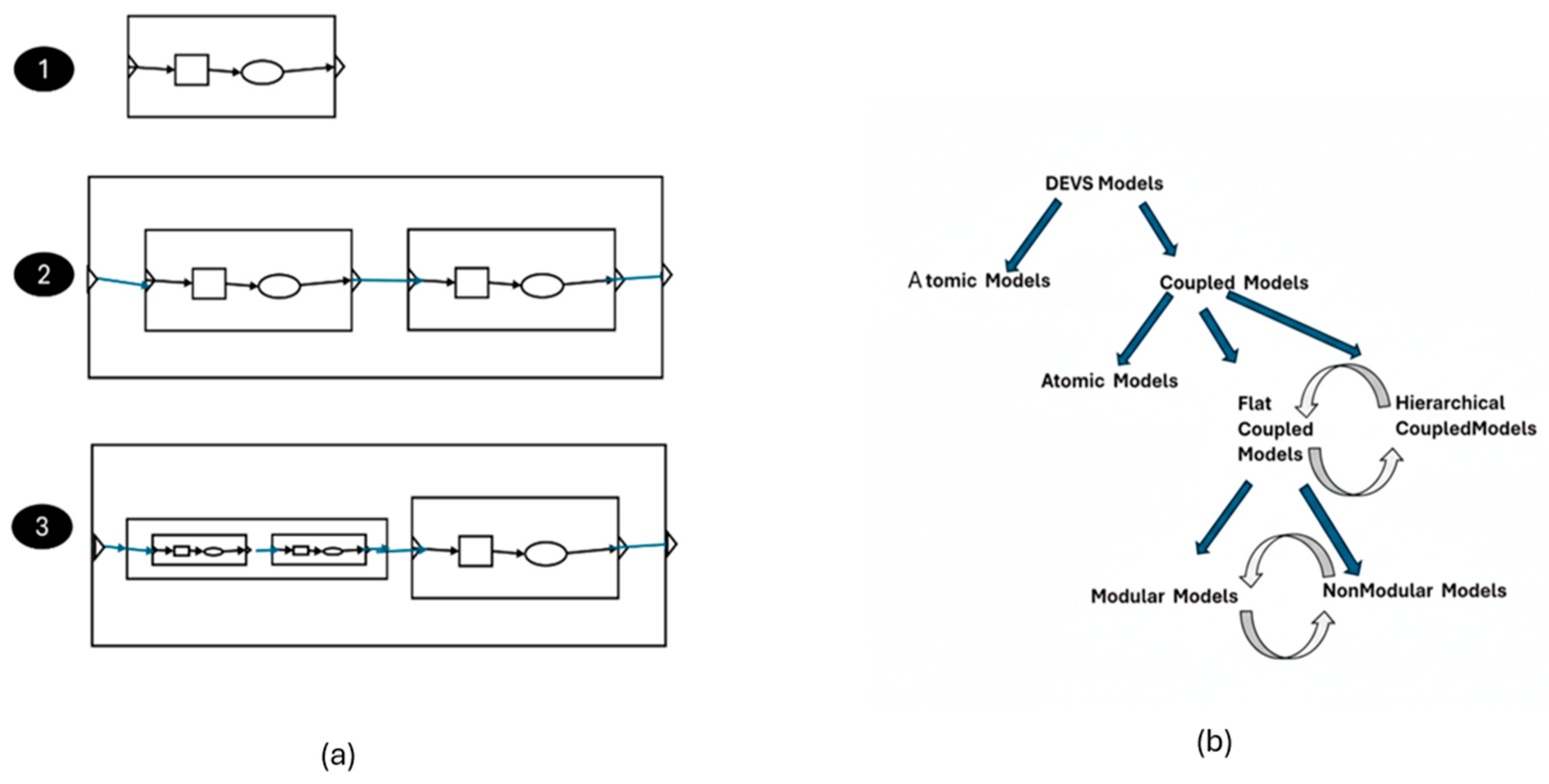
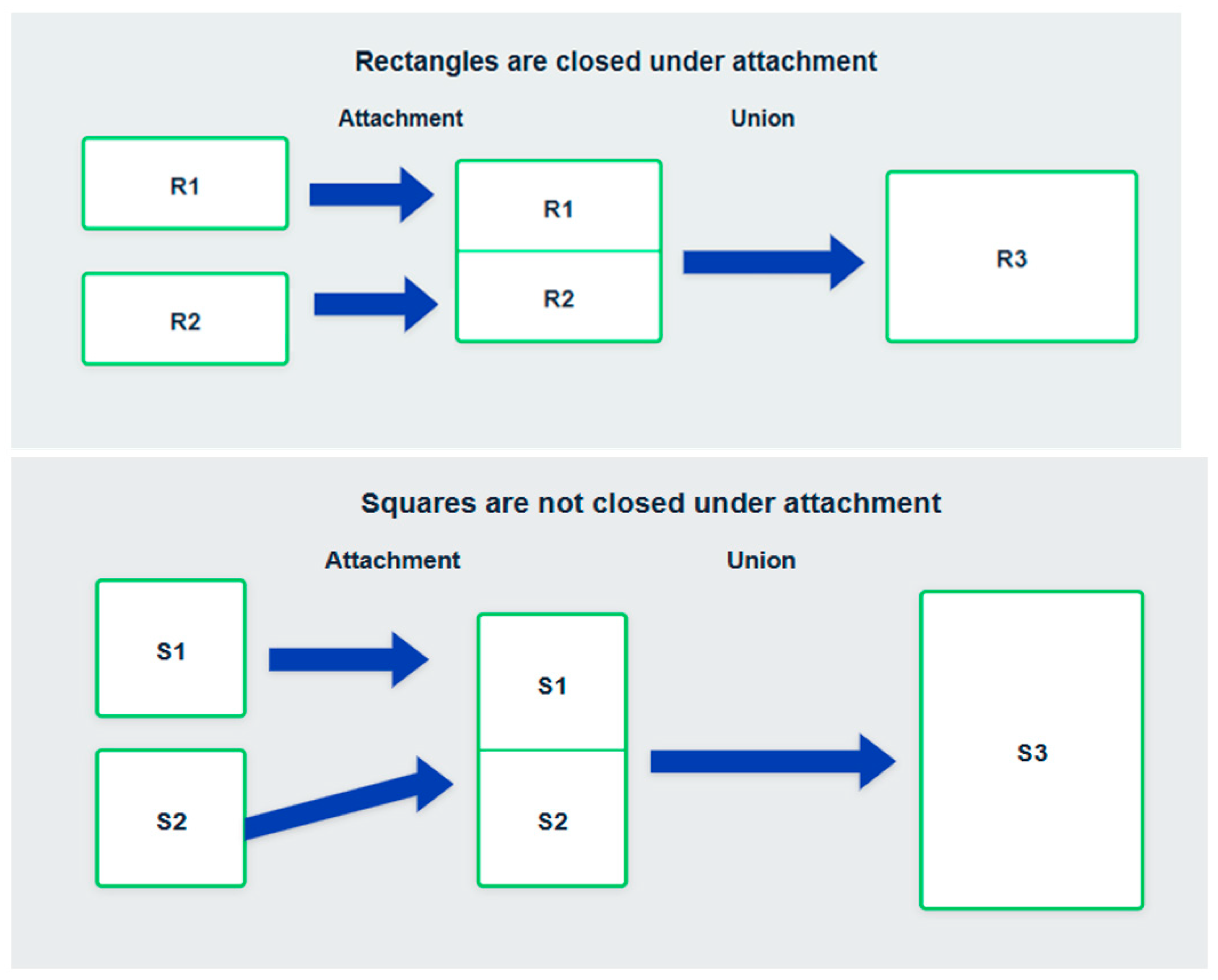
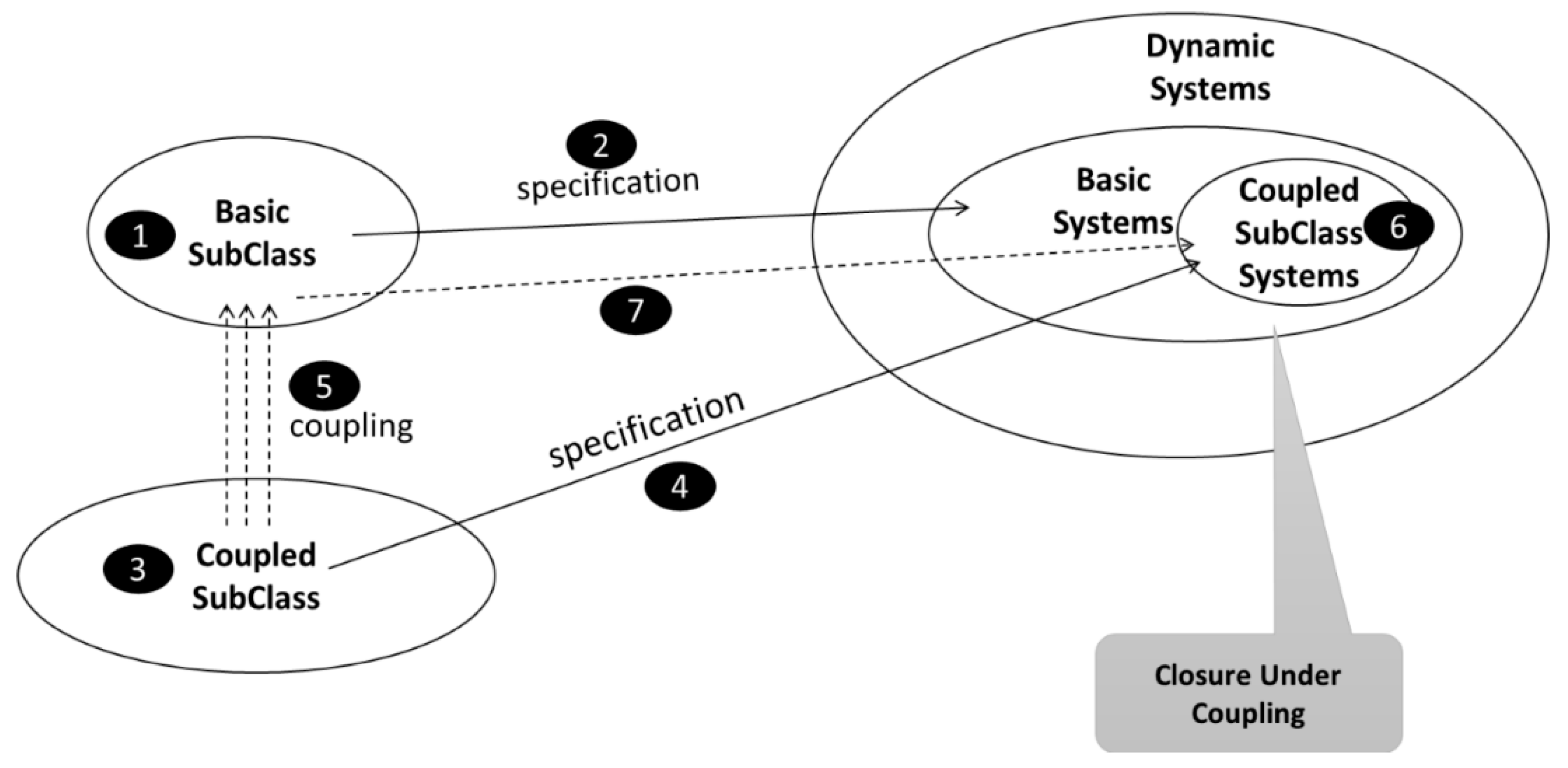
2.2. Background on Closure Under Coupling
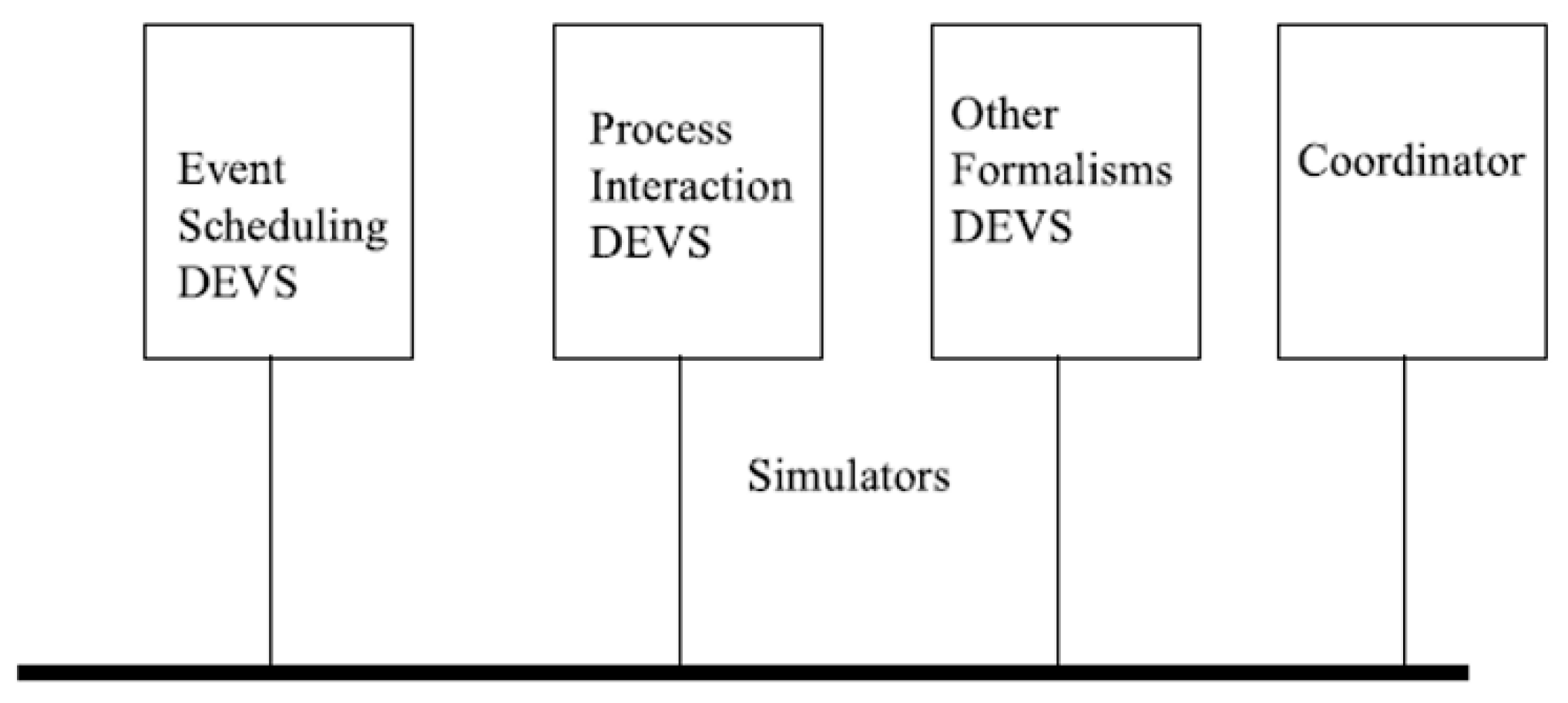
3. DEVS Simulation Protocol/Abstract Simulator
- i.
- Maintain time synchronization across components by keeping track of the elapsed time for each component.
- ii.
- Compute the minimum time advance to determine the next event, correctly route messages between components, and apply internal, external, or confluent transition functions correctly.
- (1)
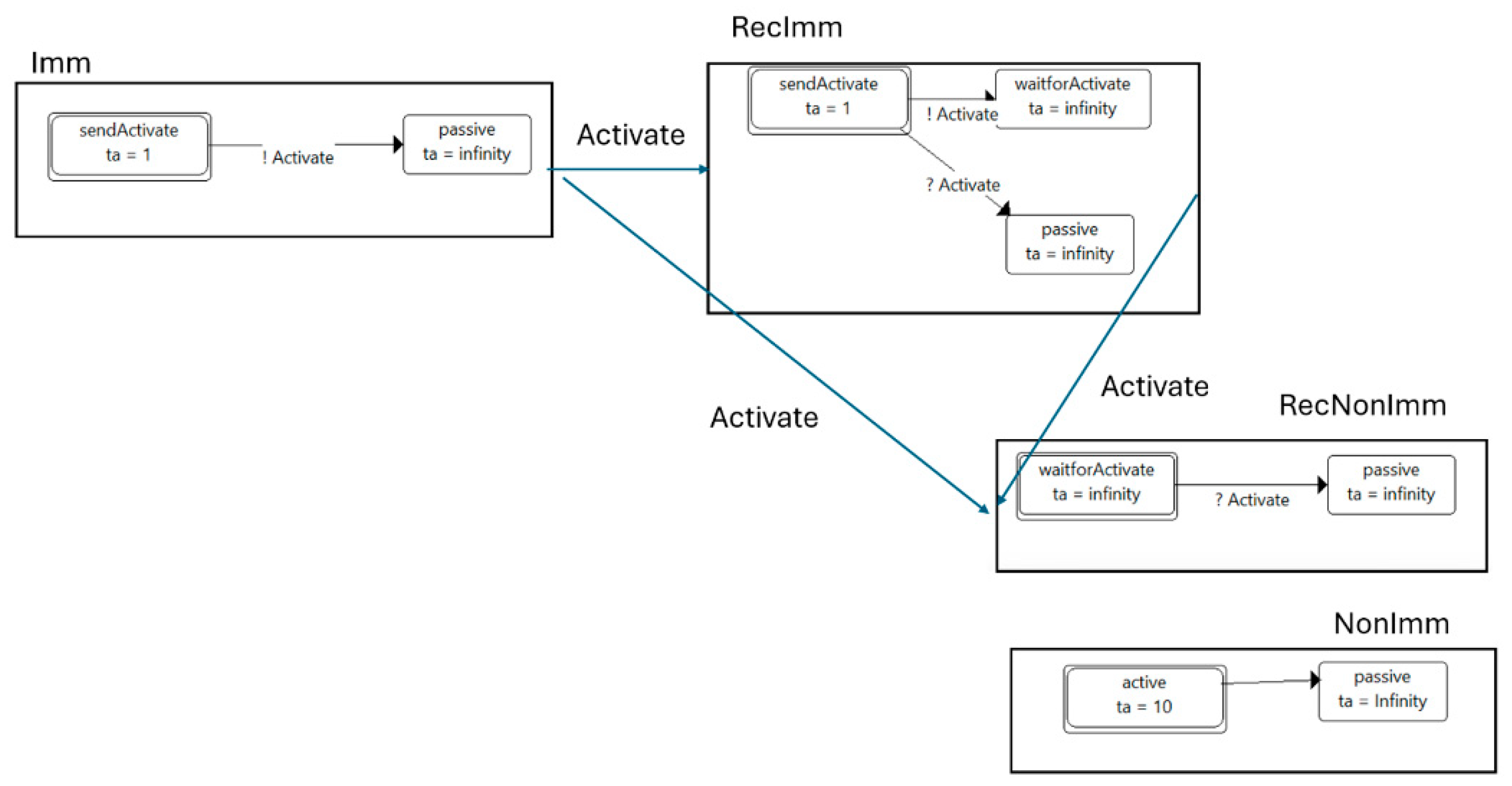
- The time advance of the next internal event is determined: The internal transition function defined by the proof of closure under Coupling computes the time advance to the next internal event and its effect on the state described in the table. The resultant time advance is the minimum of the time advances of the components, which is 1. The simulation clock, having originally been set to 0, 0 will now be advanced to 1. The imminent components (those having the minimum) are Imm and RecImm. To determine the next state after that time has advanced, the following steps take place:
- (2)
- The outputs of the imminent components are computed: Here these are both the Activate outputs from Imm and RecImm whose outputs are determined by their output functions applied to their current states.
- (3)
- Using the coupling table illustrated inTable 2, the outputs are routed to the recipients: Here the table depicts the three 4-tuples that are derived from the coupled model specification of Figure 6. Such tuples are of the form (source, outport, destination, inport) with the interpretation that an output message originating from the source component on its output port output should be routed instantaneously to appear on the input port inport of the destination. For example, the first row in the table dictates that an output message appearing on the activate outport of the source Imm will be placed on the input port Activate of the RecImm component. Likewise the second line differs only in the recipient and its input port from the first row. The last tuple states that an output produced by RecImm on its output port Activate must be placed on the input port Activate of the component NonImm.
- (4)
- The effects of transmitted outputs (now inputs) are computed:
- a.
- Since RecImm is imminent and receives an input, it uses its confluent function to compute its next state as waitForActivate (here the confluent function computes the external transition before the internal transition)
- b.
- Since RecNonImm is not imminent, it uses its external transition function to compute its next state as passive.
- (5)
- Imminent components that are not receivers apply their internal transition functions—here Imm transitions to passive.
- (6)
- Components that are neither imminent nor receive inputs update their time advances to reflect the passage of the elapsed time. Here NonImm updates its time advance to 9. (10 − 1).
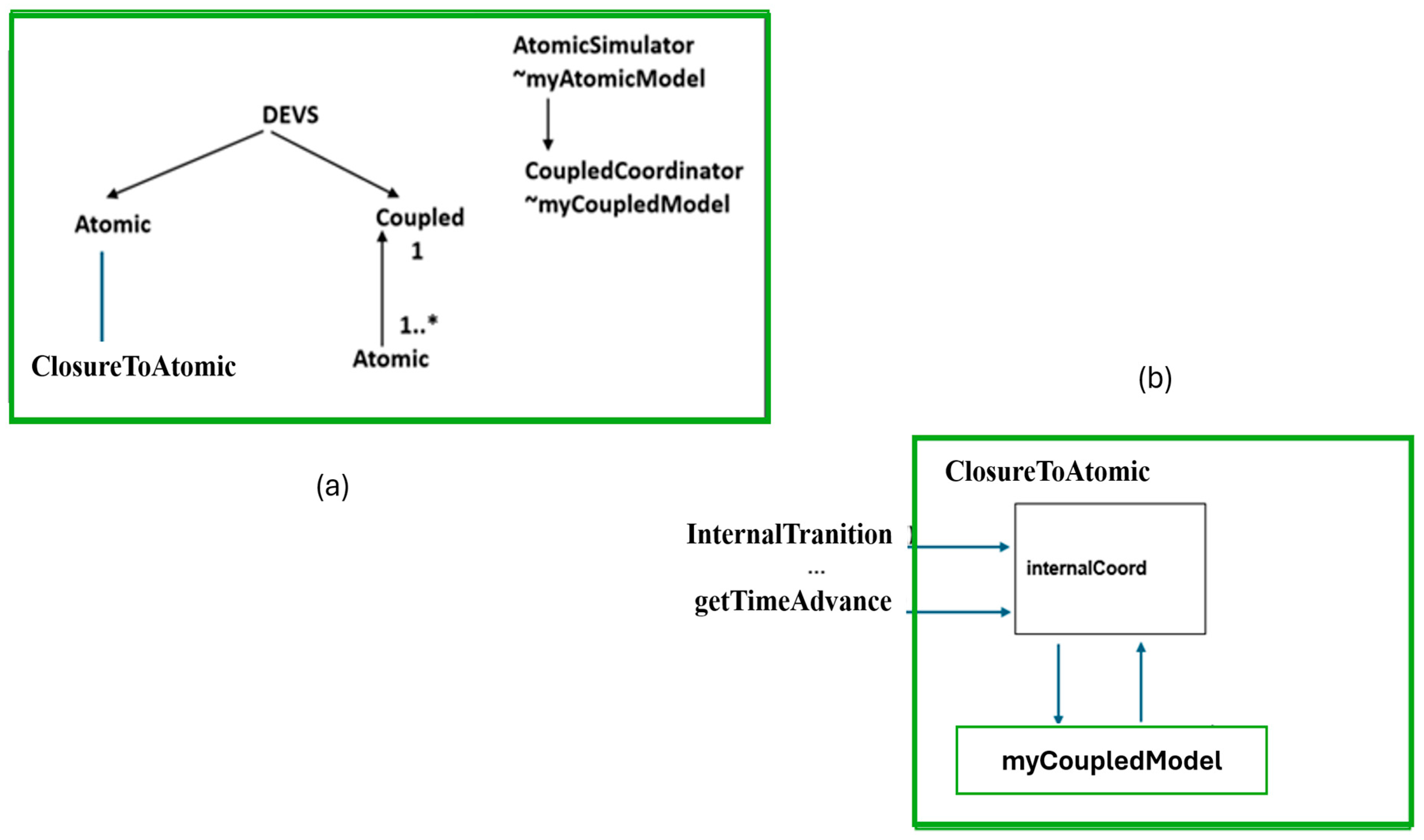
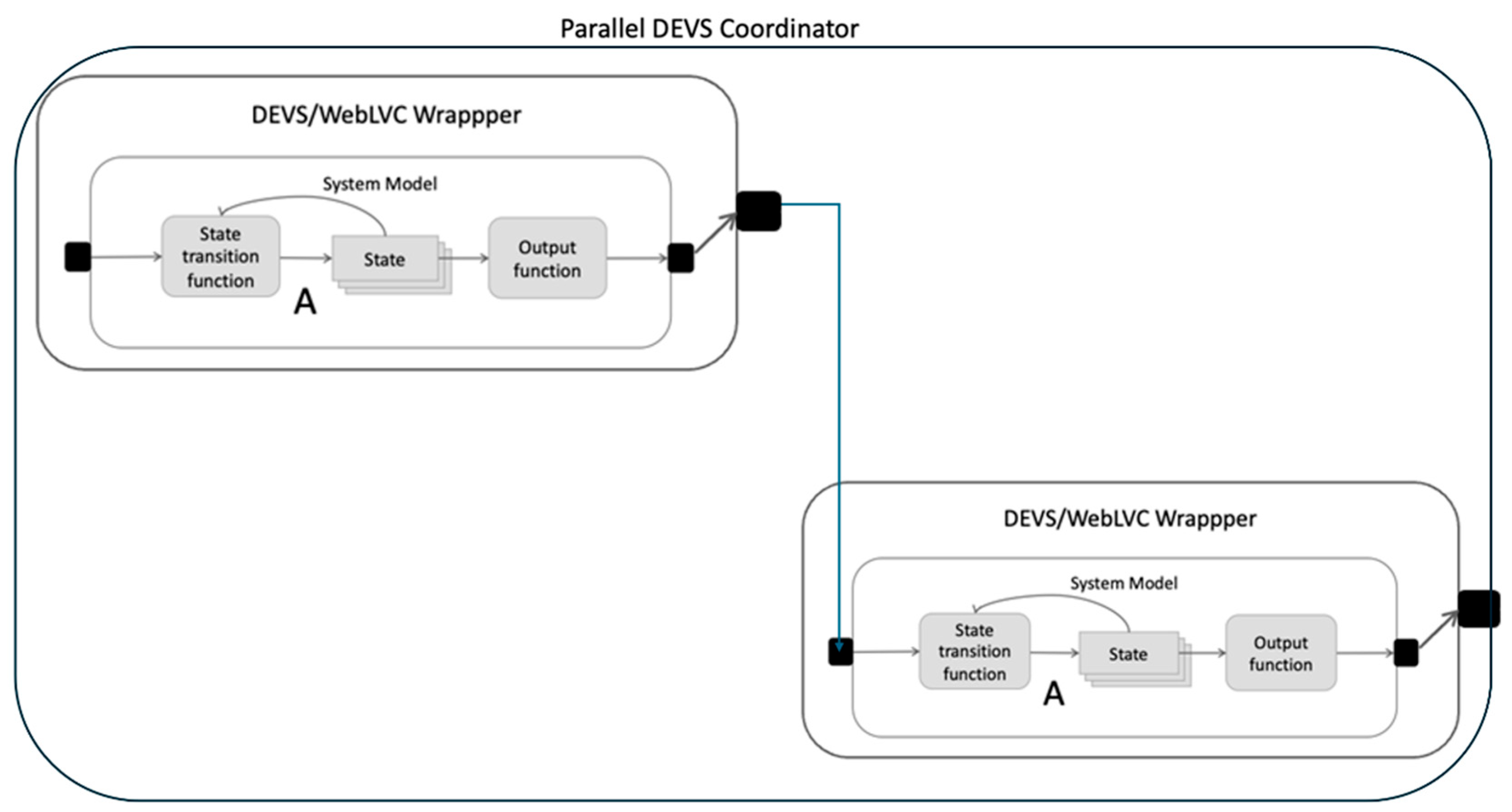
Object-Oriented Implementation of DEVS Abstract Simulator
4. DEVS BUS and Model Transformation
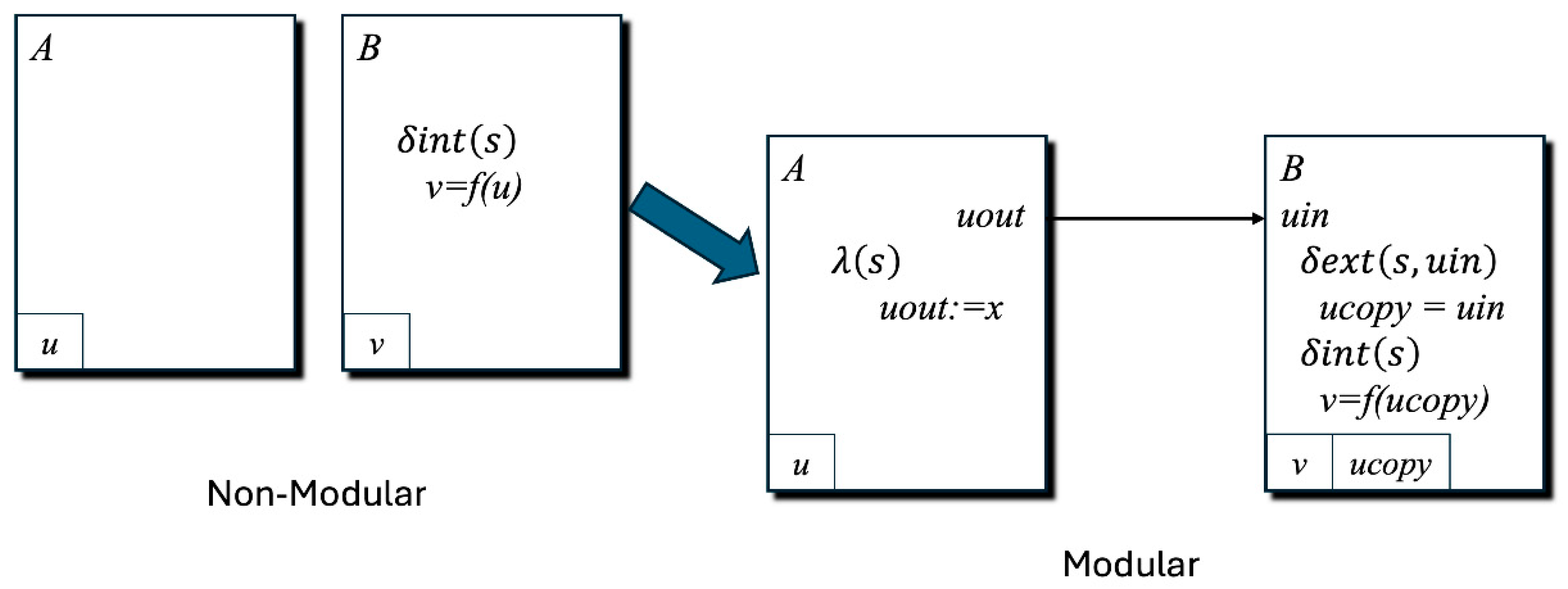
4.1. Transforming Non-Modular Multi-Component DEVS Models into Modular Form
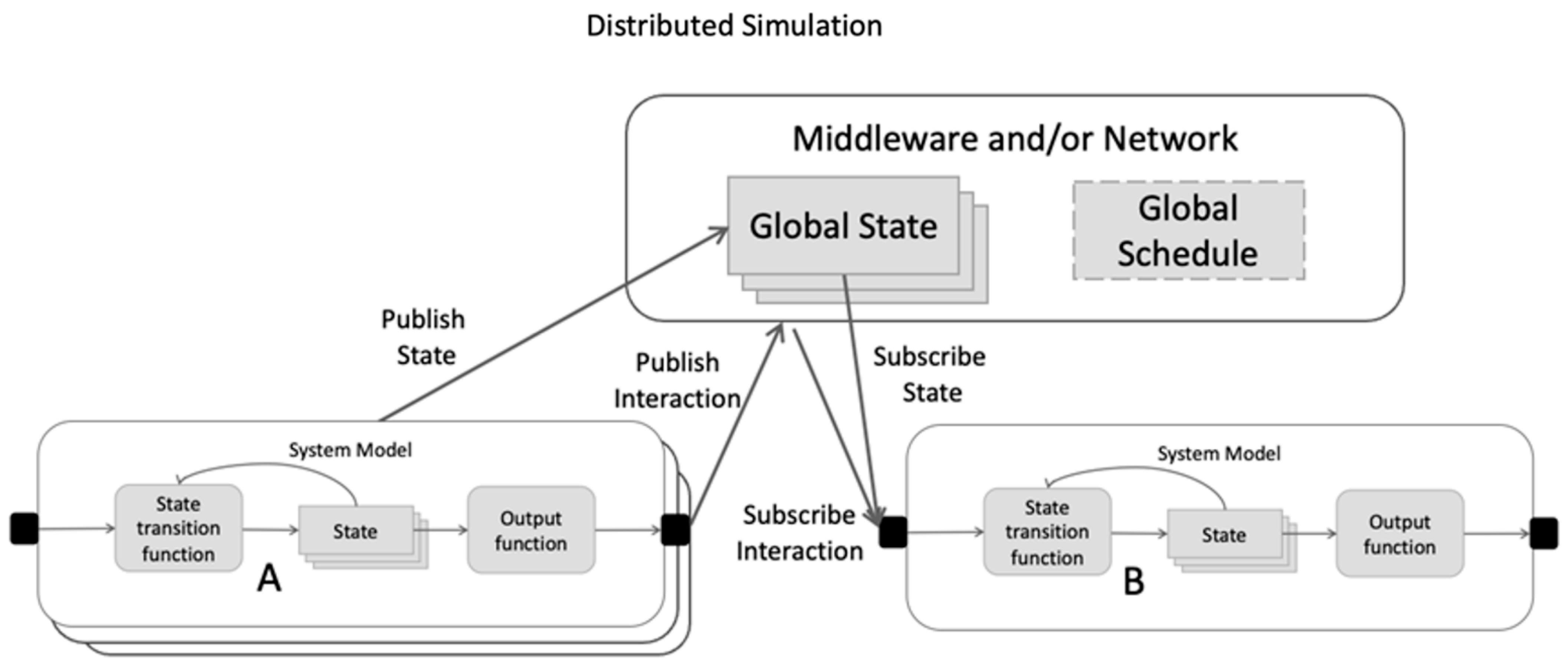
4.2. Non-Modular Non-DEVS Models in Distributed Simulation
- (1)
- Convert the atomic constituents of the coupled model to modular form so that they, as well as the coupled model, can be reused.
- (2)
- Treat the existing simulator as a DEVS-like system and wrap it so that it appears as an atomic model to the coordinator of the enclosing coupled model.
4.3. DEVS Co-Simulation
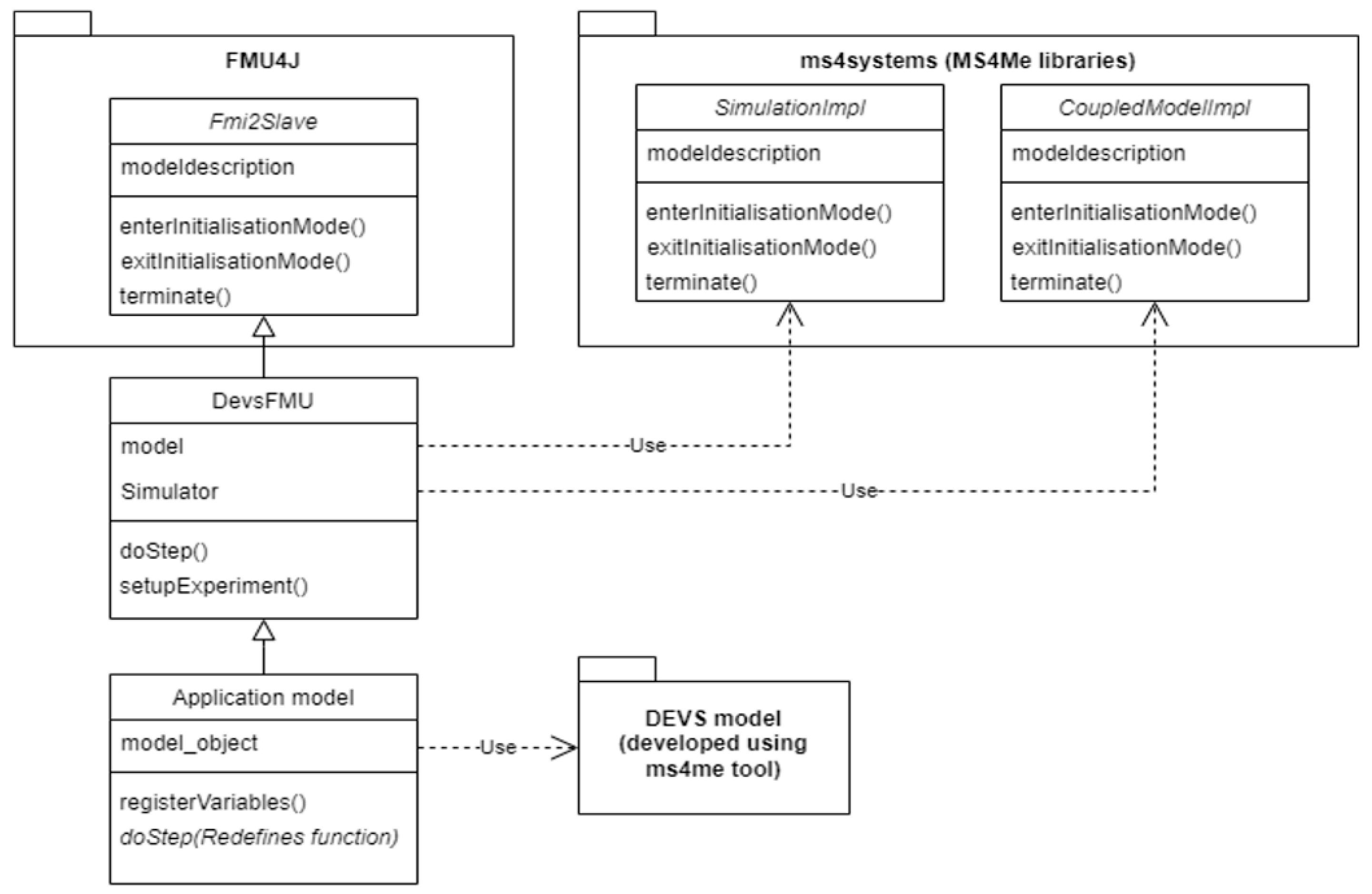
4.3.1. Functional Mockup Unit (FMU) and Interface (FMI)
4.3.2. Exporting DEVS Models as DEVS FMUs
5. Operations on DEVS Model Structure
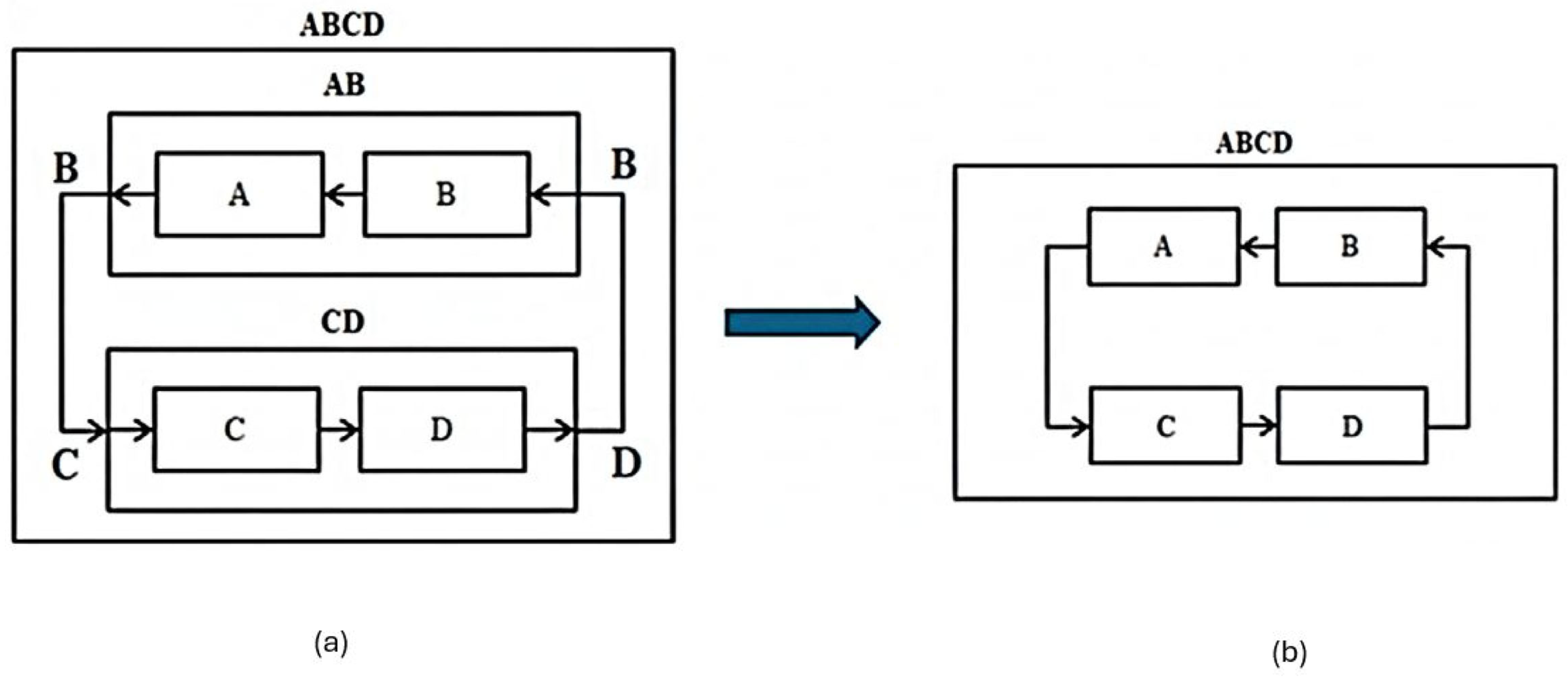
5.1. Flattening and Its Inverse, Deepening
5.2. Deepening
5.3. Implications of Flattening for Design of DEVS Models and Simulators
6. DEVS Closure Under Coupling in Relation to Other System Formalism/Frameworks
6.1. Wymore’s Mathematical Systems Theory
6.2. Automata Theory and Formal Languages
6.3. Process Algebras (e.g., CSP, CCS, π-Calculus [87,88])
7. Discussion and Directions for Research
7.1. Hierarchical Modular Construction and Multi-Resolution Modeling
- Simplified development and maintenance through smaller, manageable modules and clear focus on core functionality.
- Support for parallel development with controlled interactions among collaborators.
- Flexible hierarchical modeling allowing representation at different levels of detail.
- Improved software reuse, enabling standardized models and libraries for future applications.
7.2. Empirical Applications and Validation of DEVS Support for Interoperability
7.3. Formal Theory Extensions
7.3.1. Extending Closure Under Coupling Theory and Applying It to Important Classes of Models
7.3.2. Exploiting Uniqueness of DEVS Representation for Basic Building Blocks
7.4. Support for Model and Simulation-Based System Engineering
- Generalizing co-simulation frameworks to hybrid systems, reexamining the general concept without reference to FMIs. A DEVS simulator can execute in synchrony with an HLA federation where each can share global state variable data with the other. Problems not yet mentioned are the quantized state representation of continuous trajectories [134,135,136,137,138,139,140,141,142,143,144,145] and the location of state events [146] in coupling of hybrid component. Camus [59] presents a co-simulation framework employing the universality of DEV&DESS and its formally defined approach to locating state events in differential equation components attaining the capability to modify event-detection functions and to handle discrete internal transitions. The Heterogeneous Flow System Specification [26,147] provides a more general approach that is not fully integrated within DEVS, limiting its effectiveness. Research is needed to identify modes of global state sharing that are effective and efficient where non-modular models possibly expressed in different formalisms are involved as they are in hybrid systems.
- Implementing DEVS simulations using data distribution middleware, mapping message semantics to Quality of Service (QoS) profiles and event streaming systems such as Kafka, while ensuring causal delivery, latency guarantees, and backpressure handling.
7.5. Flattening and Deepening
7.6. DEVS Standard for Interoperable Simulation Modules
7.6.1. Continuing Research in Tool Development and Language Interoperability
7.6.2. Continuing Validation, Benchmarking, and Use Case Development
7.6.3. Continuing Integration of DEVS into M&S Community and Standards
7.7. Towards a Framework for Modeling and Simulation Complexity
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DESS | differential equation system specification |
| DEV | DESS, DEVS, and DESS |
| DEVS | discrete-event system specification |
| DTSS | discrete-time system specification |
| FMI | Functional Mock-up Interface |
| M&S | modeling and simulation |
| MOSA | modular open system approach |
| SES | system entity structure |
Appendix A
Closure of Rectangles Under Attachment
Appendix B
Sketch of Proof of Closure Under Coupling

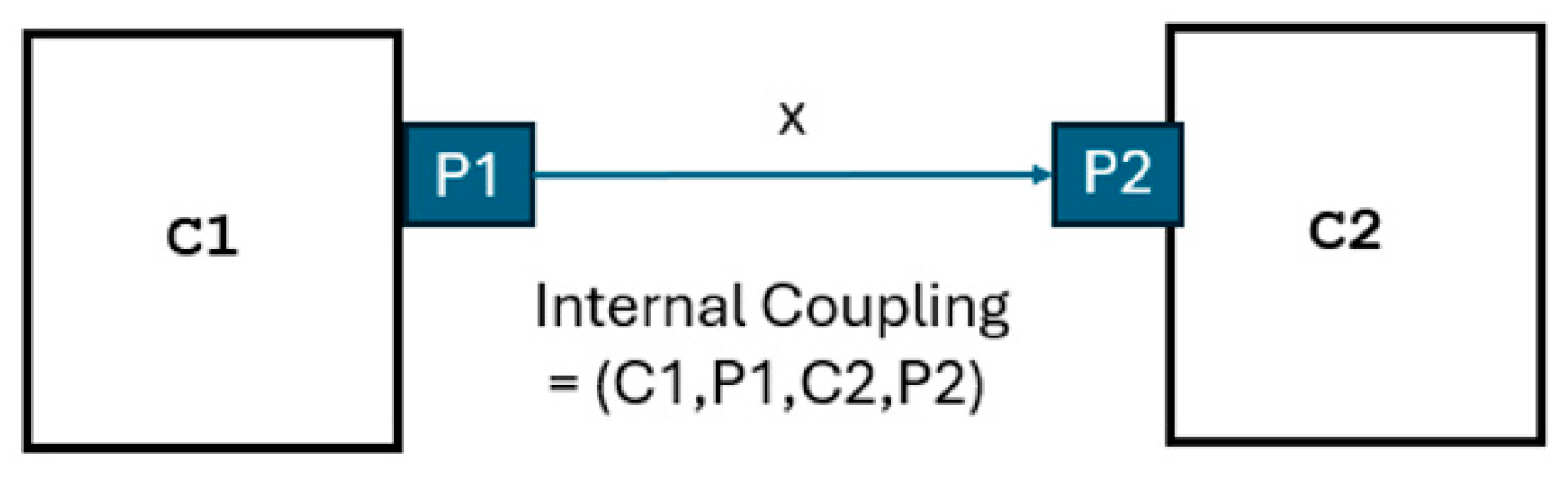
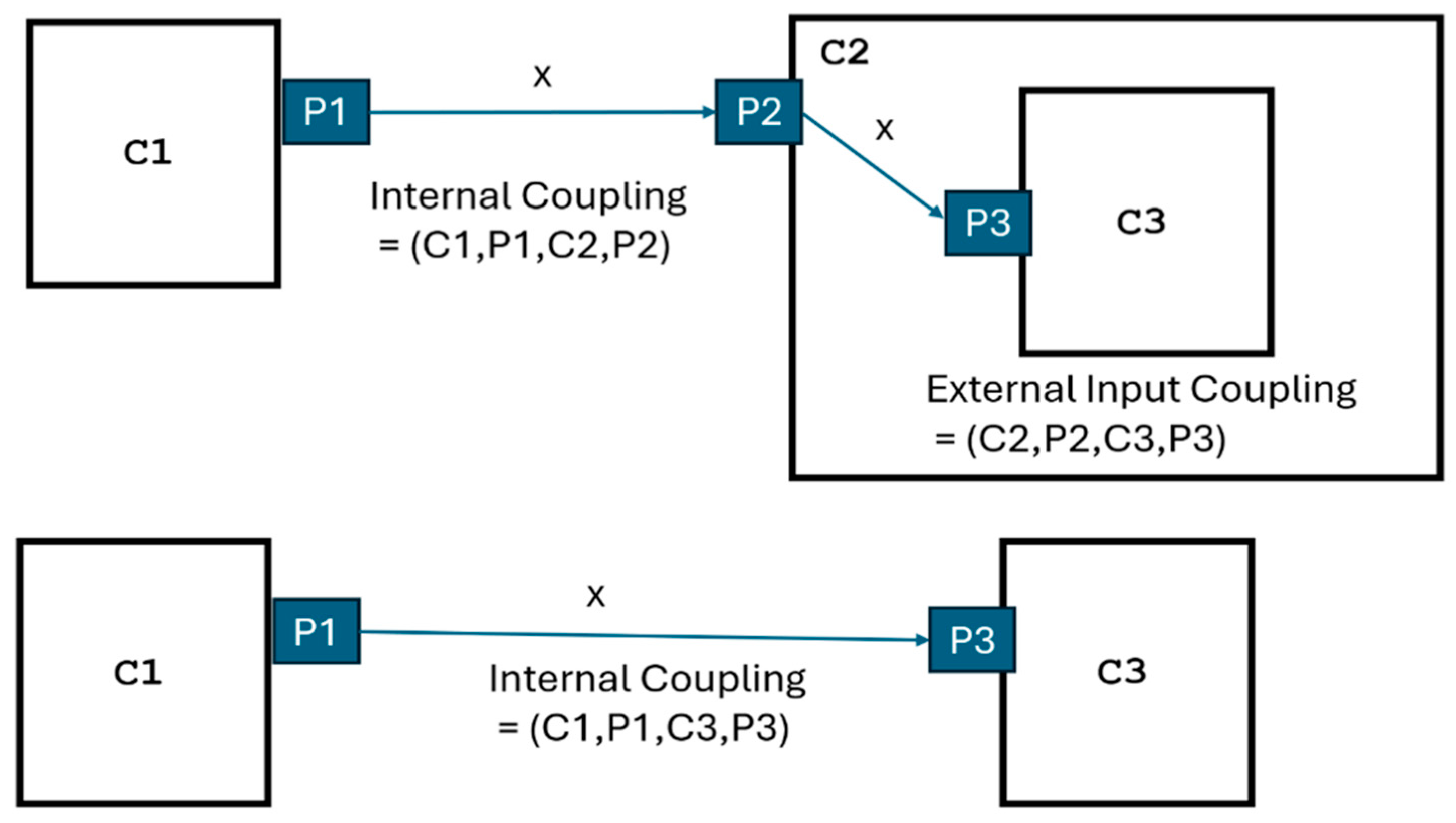
- Internal Coupling: Output of one component becomes input to another component.
- External Output Coupling: Output of a component becomes output of the entire coupled model.
- External Input Coupling: Input to the coupled model is routed to one or more components.
- Each imminent component produces an output via its output.
- The coupling map determines:
- ○
- Which components receive these outputs as inputs.
- ○
- Whether any outputs are sent to the environment.
- The receiving components then process these inputs via their external transition functions at the same simulation time.
Appendix C
Overview of the DEVS Simulation Protocol
- Assigned to atomic model.
- Responsible for the following:
- ○
- Managing the model’s state and time.
- ○
- Executing internal, external, and confluent transitions.
- ○
- Generating outputs.
- Assigned to each coupled model.
- Responsible for the following:
- ○
- Coordinating simulators and/or other coordinators.
- ○
- Routing messages between components.
- ○
- Managing time synchronization.
- Top-level controller.
- Starts and manages the global simulation loop.
| Message | Purpose |
| init(t) | Initialize model at time t |
| star(t) | Trigger internal transition at time t |
| x(t, value) | Deliver external input at time t |
| y(t, value) | Output message from a model |
| done(t, ta) | Report completion of transition and next scheduled time |
- Initialization:
- ○
- init(t0) messages are sent to all components.
- ○
- Each simulator replies with done(t0, ta) indicating its next event time.
- Time Advance:
- ○
- The coordinator determines the minimum next event time across all components.
- Internal Transition:
- ○
- For imminent components, star(t) is sent.
- ○
- They compute output (λ) and apply internal transition (δ_int).
- ○
- Output is sent via y(t, value) and routed to other components through the internal coupling to receiver components as x(t, value)
- 4.
- External Transition:
- ○
- δ_ext is used if it is not also an imminent component.
- 5.
- Confluent Transition:
- ○
- δ_con is used if it is also imminent.
- 6.
- Completion:
- ○
- Each component sends done(t, ta) to indicate its next scheduled event.
- 7.
- Repeat:
- ○
- The root coordinator advances time and repeats the cycle.
Appendix D
Code Sketch of Object-Oriented Implementation of DEVS Simulator
Appendix E
Examples: Empirical Applications and Validation of DEVS Support for Interoperability
Appendix F
Closure Under Coupling for Other DEVS-Related System Specifications
References
- Barros, F.J. Modular representation of asynchronous geometric integrators with support for dynamic topology. Simulation 2018, 94, 259–274. [Google Scholar] [CrossRef]
- Chow, A.C. Parallel DEVS: A parallel, hierarchical, modular modeling formalism and its distributed simulator. Trans. Soc. Comput. Simul. Int. 1996, 13, 55–67. [Google Scholar]
- Shiginah, F.A. Multi-Layer Cellular DEVS Formalism for Faster Model Development and Simulation Efficiency. Doctoral Dissertation, Electrical and Computer Engineering Department, University of Arizona, Tucson, AZ, USA, 2006. [Google Scholar]
- Zeigler, B.P.; Sarjoughian, H.S. Support for hierarchical modular component based model construction in DEVS/HLA. In Proceedings of the Simulation Interoperability Workshop, Orlando, FL, USA, 14–19 March 1999. [Google Scholar]
- Breunese, A.; Broenink, J.; Top, J.; Akkermans, J. Libraries of Reusable Models: Theory and Application. Simulation 1998, 71, 7–22. [Google Scholar] [CrossRef]
- Hamri, M.E.A.; Giambiasi, N.; Frydman, C. Min–Max-DEVS modeling and simulation. Simul. Model. Pract. Theory 2006, 14, 909–929. [Google Scholar] [CrossRef]
- Mama Diakité, M.; Traoré, M. Formal Approach to Digital Twin Specification. In Proceedings of the ANNSIM ‘23, Mohawk College, ON, Canada, 23–26 May 2023. [Google Scholar]
- Muzy, A.; Touraille, L.; Vangheluwe, H.; Michel, O.; Kaba Traoré, M.; Hill, D. Activity regions for the specification of discrete event systems. In Proceedings of the Spring Simulation Multi-Conference Symposium on Theory of Modeling and Simulation (DEVS), Orlando, FL, USA, 11–15 April 2010; pp. 176–182. [Google Scholar]
- Risco-Martín, J.L.; de la Cruz, J.M.; Mittal, S.; Zeigler, B.P. EUDEVS: Executable UML with DEVS theory of modeling and simulation. Simulation 2009, 85, 750–777. [Google Scholar] [CrossRef]
- Traoré, M.K.; Muzy, A. Capturing the Dual Relationship Between Simulation Models and Their Context. Simul. Model. Pract. Theory 2006, 14, 126–142. [Google Scholar] [CrossRef]
- Wach, P.; Krometis, J.; Sonanis, A.; Verma, D.; Panchal, J.; Freeman, L.; Beling, P. Pairing Bayesian Methods and Systems Theory to Enable Test and Evaluation of Learning-Based Systems. Insight 2022, 25, 65–70. [Google Scholar] [CrossRef]
- Zeigler, B.P. A methodology to characterize simulation models for discovery and composition: A system theory-based approach to model curation for integration and reuse. Int. J. Simul. Process Model. 2022, 19, 3–13. [Google Scholar] [CrossRef]
- Diouf, Y.; Maïga, O.Y.; Traore, M.K. A Theoretical approach to the computational complexity measure of abstract DEVS simulators. Int. J. Model. Simul. Sci. Comput. 2023, 14, 2350013. [Google Scholar] [CrossRef]
- Zeigler, B.P.; Muzy, A.; Kofman, E. Theory of Modeling and Simulation, 3rd ed.; Academic Press: Amsterdam, The Netherlands, 2018. [Google Scholar]
- USDOD. MOSA-Implementation-Guidebook. Available online: https://www.cto.mil/wp-content/uploads/2025/03/MOSA-Implementation-Guidebook-27Feb2025-Cleared.pdf (accessed on 1 November 2025).
- Balci, O. A Library of reusable Model Components for Visual Simulation of the NCSTRL System. In Proceedings of the 1998 Winter Simulation Conference, Washington, DC, USA, 13–16 December 1998; pp. 1451–1460. [Google Scholar]
- Bernardi, F.; de Gentili, E.; Santucci, J. Reusable Models Integration in a DEVS Based Modelling and Simulation Environment. In Proceedings of the ESS2001, Marseille, France, 18–20 October 2001; Volume 1, p. 644. [Google Scholar]
- Petty, M.D.; Eric, W. Weisel Model Composition and Reuse. In Model Engineering for Simulation; Zhang, L., Zeigler, B.P., LaiLi, Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Praehofer, H.; Sametinger, J.; Stritzinger, A. Building Reusable Simulation Components. In Proceedings of the WEBSIM2000, Web Based Modelling & Simulation, San Diego, CA, USA, 23–27 January 2000; Volume 1, pp. 1–7. [Google Scholar]
- Keller, N.; Zeigler, B.; Kim, D.; Anderson, C.; Ceney, J. Supporting the Reuse of Algorithmic Simulation Models. In Proceedings of the SummerSim’20: 2020 Summer Simulation Conference, Virtual Event, 20–22 July 2020. [Google Scholar]
- Barros, F.J. A formal representation of hybrid mobile components. Simulation 2005, 81, 381–393. [Google Scholar] [CrossRef]
- Wach, P.; Beling, P.; Salado, A. Formalizing the Representativeness of Verification Models using Morphisms. Insight 2023, 26, 27–32. [Google Scholar] [CrossRef]
- Alur, R.; Grosu, R.; Lee, I.; Sokolsky, O. Compositional Refinement for Hierarchical Hybrid Systems. In Hybrid Systems: Computation and Control, Proceedings of the 4th International Conference (HSCC’01), Lecture Notes in Computer Science, Rome, Italy, 28–30 March 2001; Springer: New York, NY, USA, 2001; Volume 2034, pp. 33–48. [Google Scholar]
- Zacharewicz, G.; Frydman, C.; Giambiasi, N. Lookahead computation in G-DEVS/HLA environment. SNE Simul News Europe 2006, 16, 15–24. [Google Scholar]
- Bae, J.W.; Shin, S.-J.; Moon, I.-C. Faster Flattening of Hierarchical DEVS Model for Accelerated Simulation. In Proceedings of the 2013 Winter Simulation Conference, Washington, DC, USA, 8–11 December 2013. [Google Scholar]
- Barros, F.J. Defining hybrid hierarchical models in pHYFLOW. Simulation 2024, 100, 643–655. [Google Scholar] [CrossRef]
- Bernardi, F.; Santucci, J.F. Model Design Using Hierarchical Web Based Libraries. In Proceedings of the 39th Conference on Design Automation, New Orleans, LA, USA, 9–14 June 2002; Volume 1, pp. 14–17. [Google Scholar]
- Ayadi, A.; Frydman, C.; Laddada, W.; Imbert, I.; Zanni-Merk, C.; Soualmia, L.F. Combining DEVS simulation and ontological modeling for hierarchical analysis of the SARS-CoV-2 replication. Simulation 2023, 99, 1011–1039. [Google Scholar] [CrossRef]
- Kim, K.H.; Kim, T.G.; Park, K.H. Hierarchical partitioning algorithm for optimistic distributed simulation of DEVS models. J. Syst. Archit. 1998, 44, 433–455. [Google Scholar] [CrossRef]
- Lee, J.-K.; Lim, Y.-H.; Chi, S.-D. Hierarchical modeling and simulation environment for intelligent transportation systems. Simulation 2004, 80, 61–76. [Google Scholar] [CrossRef]
- Chen, B.; Vangheluwe, H. Symbolic flattening of DEVS models. In Proceedings of the SCSC ‘10: Proceedings of the 2010 Summer Computer Simulation Conference, Ottawa, ON, Canada, 11–14 July 2010; pp. 209–218. [Google Scholar]
- Trabes, G.G.; Gil-Costa, V.; Wainer, G.A. Complexity analysis on flattened PDEVS simulations. In Proceedings of the 2021 Winter Simulation Conference (WSC), Phoenix, AZ, USA, 12–15 December 2021; pp. 1–12. [Google Scholar]
- Zacharewicz, G.; Hamri, M.E.-A.; Frydman, C.; Giambiasi, N. A generalized discrete event system (G-DEVS) flattened simulation structure: Application to high-level architecture (HLA) compliant simulation of workflow. Simulation 2010, 86, 181–197. [Google Scholar] [CrossRef]
- Chreyh, R.; Wainer, G. CD++ Repository: An Internet Based Searchable Database of DEVS Models and Their Experimental Frames. In Proceedings of the SpringSim’09, San Diego, CA, USA, 23–25 March 2009. [Google Scholar]
- Schmidt, A.; Durak, U.; Rasch, C.; Pawletta, T. Model-Based Testing Approach for MATLAB/Simulink Using System Entity Structure and Experimental Frames. In Proceedings of the Spring Simulation Multi-Conference (SpringSim), TMS-DEVS Track, Alexandria, VA, USA, 12–15 April 2015; Society for Modeling & Simulation International (SCS): San Diego, CA, USA, 2015. [Google Scholar]
- Zeigler, B. Closure under coupling: Concept, proofs, DEVS recent examples (wip). In Proceedings of the 4th ACM International Conference of Computing for Engineering and Sciences (ICCES’18), Kuala Lumpur, Malaysia, 6–8 July 2018; ACM: New York, NY, USA, 2018. [Google Scholar]
- Cardoen, B.; Manhaeve, S.; Van Tendeloo, Y.; Broeckhove, J. A PDEVS simulator supporting multiple synchronization protocols: Implementation and performance analysis. Simulation 2018, 94, 281–300. [Google Scholar] [CrossRef]
- Folkerts, H. An Architecture for Model Behavior Generation for Multiple Simulators. Ph.D. Thesis, University of Applied Sciences Wismar, Wismar, Germany, 2024. Available online: https://dokumente.ub.tu-clausthal.de/receive/clausthal_mods_00002606 (accessed on 1 June 2025).
- Kim, S.; Sarjoughian, H.S.; Elamvazhuthi, V. DEVS-suite: A simulator supporting visual experimentation design and behavior monitoring. SpringSim 2009, 9, 1–7. [Google Scholar]
- Muzy, A.; Nutaro, J.J. Algorithms for efficient implementations of the DEVS&DSDEVS abstract simulators. In Proceedings of the 1st Open International Conference on Modeling & Simulation, OICMS, Clermont-Ferrand, France, 13–15 June 2005; pp. 273–279. [Google Scholar]
- Van Tendeloo, Y.; Vangheluwe, H. Increasing the performance of a Discrete Event System Specification simulator by means of computational resource usage “activity” models. Simulation 2017, 93, 1045–1061. [Google Scholar] [CrossRef]
- Wutzler, T.; Sarjoughian, H.S. Interoperability among parallel DEVS simulators and models implemented in multiple programming languages. Simulation 2007, 83, 473–490. [Google Scholar] [CrossRef]
- Chen, Y.; Sarjoughian, H.S. A component-based simulator for MIPS32 processors. Simulation 2010, 86, 271–290. [Google Scholar] [CrossRef]
- Praehofer, H.; Sametinger, J.; Stritzinger, A. Discrete Event Simulation Using the JavaBeans Component Model. In Proceedings of the International Conference on Web Based Modeling & Simulation, San Francisco, CA, USA, 17–20 January 1999. [Google Scholar]
- Kim, Y.J.; Kim, J.H.; Kim, T.G. 2003 Heterogeneous simulation framework using DEVS BUS. Simulation 2003, 79, 3–18. [Google Scholar] [CrossRef]
- Tolk, A. Conceptual alignment for simulation interoperability: Lessons learned from 30 years of interoperability research. Simulation 2024, 100, 709–726. [Google Scholar] [CrossRef]
- Tolk, A. Simulation-Based Optimization: Implications of Complex Adaptive Systems and Deep Uncertainty. Information 2022, 13, 469. [Google Scholar] [CrossRef]
- Cao, Q. Research on co-simulation of multi-resolution models based on HLA. Simulation 2023, 99, 515–535. [Google Scholar] [CrossRef]
- Lee, J.-K.; Lee, M.-W.; Chi, S.-D. DEVS/HLA-Based Modeling and Simulation for Intelligent Transportation Systems. Simulation 2003, 79, 423–439. [Google Scholar] [CrossRef]
- Zacharewicz, G.; Frydman, C.; Giambiasi, N. G-DEVS/HLA environment for distributed simulations of workflows. Simulation 2008, 84, 197–213. [Google Scholar] [CrossRef]
- DIS IEEE Standard. Available online: https://standards.ieee.org/ieee/1278.1/4949/ (accessed on 1 January 2024).
- Kewley, R.; Kester, N.; McDonnell, J. DEVS Distributed Modeling Framework: A Parallel DEVS Implementation via Microservices. In Proceedings of the 2016 Symposium on Theory of Modeling and Simulation (TMS-DEVS), Pasadena, CA, USA, 3–6 April 2016; 6 April 2016. [Google Scholar]
- Kewley, R.; Zeigler, B.; Wainer, G. The Relationship Between DEVS Models and Real Systems. In Proceedings of the 2024-SIW-Presentation-021, Orlando, FL, USA, 26 February–1 March 2024. [Google Scholar]
- Paredis, R.; Denil, J.; Vangheluwe, H. Specifying and executing the combination of timed finite state automata and causal-block diagrams by mapping onto DEVS. In Proceedings of the Winter Simulation Conference, Phoenix, AZ, USA, 12-15 December 2021; pp. 1–12. [Google Scholar] [CrossRef]
- Gomes, C.; Thule, C.; Broman, D.; Larsen, P.G.; Vangheluwe, H. Co-simulation: A survey. ACM Comput. Surv. (CSUR) 2018, 51, 49. [Google Scholar]
- Lin, X. Co-simulation of Cyber-Physical Systems Using DEVS and Functional Mockup. Master’s Thesis, Arizona State University, Tempe, AZ, USA, 2021. Available online: https://xlin.io/publication/master-thesis/ (accessed on 1 June 2025).
- Mittal, S.; Risco-Martín, J.L.; Zeigler, B.P. DEVS/SOA: A cross-platform framework for net-centric modeling and simulation in DEVS unified process. Simulation 2009, 85, 419–450. [Google Scholar] [CrossRef]
- Risco-Martín, J.L.; Esteban, S.; Chacón, J.; Carazo-Barbero, G.; Besada-Portas, E.; López-Orozco, J.A. Simulation-driven engineering for the management of harmful algal and cyanobacterial blooms. Simulation 2023, 99, 1041–1055. [Google Scholar] [CrossRef]
- Camus, B.; Paris, T.; Vaubourg, J.; Presse, Y.; Bourjot, C.; Ciarletta, L.; Chevrier, V. Co-simulation of cyber-physical systems using a DEVS wrapping strategy in the MECSYCO middleware. Simulation 2018, 94, 1099–1127. [Google Scholar] [CrossRef]
- Risco-Martín, J.L.; Mittal, S.; Jiménez, J.C.F.; Zapater, M.; Correa, R.H. Reconsidering the performance of DEVS modeling and simulation environments using the DEVStone benchmark. Simulation 2017, 93, 459–476. [Google Scholar] [CrossRef]
- Risco-Martín, J.L.; Mittal, S.; Fabero, J.C.; Malagón, P.; Ayala, J.L. Real-time hardware/software co-design using devs-based transparent M&S framework. In Proceedings of the SCSC ’16 Summer Computer Simulation Conference, San Diego, CA, USA, 24–27 July 2016. [Google Scholar]
- Risco-Martín, J.L.; Mittal, S.; Henares, K.; Cardenas, R.; Arroba, P. xDEVS: A toolkit for interoperable modeling and simulation of formal discrete event systems. Softw. Pract. Exp. 2023, 53, 748–789. [Google Scholar] [CrossRef]
- Risco-Martín, J.L.; Prado-Rujas, I.-I.; Campoy, J.; Pérez, M.S.; Olcoz, K. Advanced simulation-based predictive modelling for solar irradiance sensor farms. J. Simul. 2024, 19, 265–282. [Google Scholar] [CrossRef]
- Ritvik, J. A Method for FMI and Devs for Co-Simulation. In Proceedings of the Winter Simulation Conference (WSC), Seattle, WA, USA, 7–10 December 2025. [Google Scholar]
- Vanommeslaeghe, Y.; Van Acker, B.; Vanherpen, K.; De Meulenaere, P. A co-simulation approach for the evaluation of multi-core embedded platforms in cyber-physical systems. In Proceedings of the 2020 Summer Simulation Conference; Virtual Event, 20–22 July 2020, ACM: New York, NY, USA, 2020; pp. 1–12. [Google Scholar]
- Zeigler, B.P. Embedding DEV&DESS in DEVS. In Proceedings of the DEVS Symposium, Huntsville, AL, USA, 2–6 April 2006. [Google Scholar]
- Functional Mockup Interface Standard. Modelica Association. Available online: https://fmi-standard.org/assets/releases/FMI_for_ModelExchange_and_CoSimulation_v2.0.pdf (accessed on 9 July 2024).
- Hatledal, L.I.; Zhang, H.; Styve, A.; Hovland, G. Fmi4j: A software package for working with functional mock-up units on the java virtual machine. In Proceedings of the 59th Conference on Simulation and Modelling (SIMS 59), Oslo, Norway, 26–28 September 2018. [Google Scholar]
- Müller, W.; Widl, E. Linking FMI-based components with discrete event systems. In Proceedings of the 2013 IEEE International Systems Conference (SysCon), Orlando, FL, USA, 15–18 April 2013; IEEE: New York, NY, USA, 2013; pp. 676–680. [Google Scholar]
- Tripakis, S. Bridging the semantic gap between heterogeneous modeling formalisms and FMI. In Proceedings of the 2015 International Conference on Embedded Computer Systems: Architectures, Modeling, and Simulation (SAMOS), Samos, Greece, 19–23 July 2015; IEEE: New York, NY, USA, 2015; pp. 60–69. [Google Scholar]
- Joshi, R.; Nutaro, J.; Zeigler, B.; Wainer, G.; Kim, D. Functional Mock-up Interface Based Simulation of Continuous Time System in CADMIUM. In Annual Simulation Conference (ANNSIM’24); American University: Washington, DC, USA, 2024. [Google Scholar]
- Nutaro, J.; Sarjoughian, H. Design of distributed simulation environments: A unified system-theoretic and logical processes approach. Simulation 2004, 80, 577–589. [Google Scholar] [CrossRef]
- MS4 Me. Available online: https://www.ms4systems.com/pages/ms4me.php (accessed on 1 June 2025).
- Cadmium V2: An Object-Oriented C++ M&S Platform for the PDEVS Formalism. Available online: https://github.com/SimulationEverywhere/cadmium_v2 (accessed on 24 August 2024).
- Earle, B.; Bjornson, K.; Ruiz-Martin, C.; Wainer, G. Development of A Real-Time DEVS Kernel: RT-Cadmium. In Proceedings of the 2020 Spring Simulation Conference (SpringSim), Virtual Event, 18–21 May 2020; pp. 1–12. [Google Scholar]
- Bisgambiglia, P.A. DecPDEVS: New simulation algorithms to improve message handling in PDEVS. Open J. Model. Simul. 2021, 9, 172–197. [Google Scholar] [CrossRef]
- Castro, R.; Marcosig, E.P.; Giribet, J.I. Simulation model continuity for efficient development of embedded controllers in cyber-physical systems. In Complexity Challenges in Cyber Physical Systems: Using Modeling and Simulation (M&S) to Support Intelligence, Adaptation and Autonomy; Springer: Cham, Switzerland, 2019; pp. 81–93. [Google Scholar]
- Ho, Y.-C. Discrete Event Dynamic Systems: Analyzing Complexity and Performance in the Modern World; IEEE Press: Piscataway, NJ, USA, 1992; p. 36. [Google Scholar]
- Thompson, J.S.; Hodson, D.D.; Grimaila, M.R.; Hanlon, N.; Dill, R. Toward a Simulation Model Complexity Measure. Information 2023, 14, 202. [Google Scholar] [CrossRef]
- Albrecht, R.F. On mathematical systems theory. In Systems: Theory and Practice; Springer: Vienna, Austria, 1998; pp. 33–86. [Google Scholar]
- Wach, P.; Zeigler, B.P.; Salado, A. Conjoining Wymore’s Systems Theoretic Framework and the DEVS Modeling Formalism: Toward Scientific Foundations for MBSE. Appl. Sci. 2021, 11, 4936. [Google Scholar] [CrossRef]
- Wymore, A. A Mathematical Theory of Systems Engineering: The Elements; Krieger: Huntington, NY, USA, 1967. [Google Scholar]
- Wymore, A.W. Model-Based Systems Engineering; CRC Press LLC: Boca Raton, FL, USA, 1993. [Google Scholar]
- Wiener, N. Cybernetics: Or Control and Communication in the Animal and the Machine; MIT Press: Cambridge, MA, USA, 1948. [Google Scholar]
- Ashby, W.R. An Introduction to Cybernetics; Chapman & Hall: Saddle River, NJ, USA, 1956. [Google Scholar]
- Sipser, M. Introduction to the Theory of Computation, 3rd ed.; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Milner, R. Communication and Concurrency; Prentice Hall: Hoboken, NJ, USA, 1989. [Google Scholar]
- Wing, J.M. FAQ on p-Calculus; Carnegie Mellon University: Pittsburgh, PA, USA, 2002. [Google Scholar]
- Cicirelli, F.; Furfaro, A.; Nigro, L. Using time stream Petri nets for workflow modelling analysis and enactment. Simulation 2013, 89, 68–86. [Google Scholar] [CrossRef]
- da Silva Fonseca, J.P.; de Sousa, A.R.; de Souza Tavares, J.J.P.Z. Modeling and controlling IoT-based devices’ behavior with high-level Petri nets. Procedia Comput. Sci. 2023, 217, 1462–1469. [Google Scholar] [CrossRef]
- Lechenne, S.; Eberhart, C.; Hasuo, I. A Compositional Framework for Petri Nets. In Coalgebraic Methods in Computer Science (LNCS 14617); Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Sobocinski, P. Compositional Model Checking of Concurrent Systems with Petri Nets. arXiv 2016, arXiv:1603.009. [Google Scholar] [CrossRef]
- Park, S.; Hunt, C.A.; Zeigler, B.P. Cost-based partitioning for distributed and parallel simulation of decomposable multiscale constructive models. Simulation 2006, 82, 809–826. [Google Scholar] [CrossRef]
- Sisti, A.F. Large-Scale Battlefield Simulation Using a Multi-Level Model Integration Methodology, DTIC Report. 1992. Available online: https://apps.dtic.mil/sti/html/tr/ADA251357/index.html (accessed on 1 November 2025).
- Baohong, L. A formal description specification for multi-resolution modeling based on DEVS formalism and its applications. J. Def. Model. Simul. Appl. Methodol. Technol. 2007, 4, 229–251. [Google Scholar] [CrossRef]
- Bouanan, Y.; Zacharewicz, G.; Ribault, J.; Vallespir, B. Discrete event system specification-based framework for modeling and simulation of propagation phenomena in social networks: Application to the information spreading in a multi-layer social network. Simulation 2019, 95, 411–427. [Google Scholar] [CrossRef]
- Djitog, I.; Aliyu, H.O.; Traoré, M.K. A model-driven framework for multi-paradigm modeling and holistic simulation of healthcare systems. Simulation 2018, 94, 235–257. [Google Scholar] [CrossRef]
- Goldstein, R.; Khan, A.; Dalle, O.; Wainer, G. Multiscale representation of simulated time. Simulation 2018, 94, 519–558. [Google Scholar] [CrossRef]
- Hardebolle, C.; Boulanger, F. Exploring multi-paradigm modeling techniques. Simulation 2009, 85, 688–708. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Kim, T.G. Specification of multi-resolution modeling space for multi-resolution system simulation. Simulation 2013, 89, 28–40. [Google Scholar] [CrossRef]
- Kim, S.; Cho, J.; Park, D. Accelerated DEVS Simulation Using Collaborative Computation on Multi-Cores and GPUs for Fire-Spreading IoT Sensing Applications. Appl. Sci. 2018, 8, 1466. [Google Scholar] [CrossRef]
- Liu, Q.; Wainer, G. Multicore acceleration of discrete event system specification systems. Simulation 2012, 88, 801–831. [Google Scholar] [CrossRef]
- Mosterman, P.J.; Vangheluwe, H. Computer automated multi-paradigm modeling: An introduction. Simulation 2004, 80, 433–450. [Google Scholar] [CrossRef]
- Pérez, E.; Ntaimo, L.; Ding, Y. Multi-component wind turbine modeling and simulation for wind farm operations and maintenance. Simulation 2015, 91, 360–382. [Google Scholar] [CrossRef]
- Steiniger, A.; Uhrmacher, A.M. Intensional coupling in variable structure models: An exploration based on multi-level DEVS. ACM Trans. Model. Comput. Simul. (TOMACS) 2016, 26, 9. [Google Scholar] [CrossRef]
- Vangheluwe, H. DEVS as a common denominator formulti-formalism hybrid systems modelling. In Proceedings of the IEEE International Symposium on Computer-Aided Control System Design, Anchorage, AK, USA, 25–27 September 2000; Varga, A., Ed.; IEEE: New York, NY, USA, 2000; pp. 129–134. [Google Scholar]
- Balci, O. Principles and techniques of simulation validation, verification, and testing. In Proceedings of the WSC ‘95 27th Conference on Winter Simulation, Arlington, VA, USA, 3–6 December 1995; pp. 147–154. [Google Scholar]
- Dacharry, H.; Giambiasi, N. Formal Verification with Timed Automata and DEVS Models: A Case Study. In Proceedings of the ASSE 2005 Simposio Argentino de Ingeniería de Software—34 JAAIO Jornadas Argentinas de Informática e Investigación Operativa, Rosario, Argentina, 29 August–2 September 2005; pp. 251–265. [Google Scholar]
- Hwang, M.H. Tutorial: Verification of real-time system based on schedule-preserved DEVS. In Proceedings of the 2005 DEVS Symposium, San Diego, CA, USA, 3–7 April 2005. [Google Scholar]
- Labiche, Y.; Wainer, G. Towards the verification and validation of DEVS models. In Proceedings of the 1st Open International Conference on Modeling & Simulation, Clermont-Ferrand, France, 28–30 September 2005; pp. 295–305. [Google Scholar]
- Saadawi, H.; Wainer, G. Principles of discrete event system specification model verification. Simulation 2013, 89, 41–67. [Google Scholar] [CrossRef]
- Samuel, K.G.; Bouare, N.-D.M.; Maïga, O.; Traoré, M.K. A DEVS-based pivotal modeling formalism and its verification and validation framework. Simulation 2020, 96, 969–992. [Google Scholar] [CrossRef]
- Aliyu, H.O.; Maïga, O.; Traoré, M.K. A framework for discrete event systems enactment. In Proceedings of the 29th European Simulation and Modeling Conference-ESM’15, EUROSIS-ETI, Leicester, UK, 26–28 October 2015; pp. 149–156. [Google Scholar]
- Sargent, R.G. Validation and verification of simulation models. In Proceedings of the WSC ‘04: Proceedings of the 36th Conference on Winter Simulation, Washington, DC, USA, 5–8 December 2004; pp. 17–28. [Google Scholar]
- Yacoub, A.; Hamri, M.E.A.; Frydman, C. DEv-PROMELA: Modeling, verification, and validation of a video game by combining model-checking and simulation. Simulation 2020, 96, 881–910. [Google Scholar] [CrossRef]
- Sung, C.H.; Moon, I.-C.; Kim, T.G. Collaborative Work in Domain-Specific Discrete Event Simulation Software Development: Fleet Anti-air Defense Simulation Software. In Proceedings of the 2010 19th IEEE International Workshops on Enabling Technologies: Infrastructures for Collaborative Enterprises, Larissa, Greece, 28–30 June 2010. [Google Scholar] [CrossRef]
- Seo, K.-M.; Choi, C.; Kim, T.G.; Kim, J.H. DEVS-based combat modeling for engagement-level simulation. Simulation 2014, 90, 759–781. [Google Scholar] [CrossRef]
- Kim, T.; Hwang, M.H.; Kim, D. DEVS/NS-2 Environment: An Integrated Tool for Efficient Networks Modeling and Simulation. J. Def. Model. Simul. Appl. Methodol. Technol. 2008, 5, 33–60. [Google Scholar] [CrossRef]
- Yu, T.; Lee, S. Evolving cellular automata to model fluid flow in porous media. In Proceedings of the EH’02: Proceedings of the 2002 NASA/DoD Conference on Evolvable Hardware (EH’02), Alexandria, VA, USA, 15–18 July 2002; p. 210. [Google Scholar]
- Aliyu, H.O.; Maïga, O.; Traoré, M.K. The high level language for system specification: A model-driven approach to systems engineering. Int. J. Model. Simul. Sci. Comput. 2016, 7, 1641003. [Google Scholar] [CrossRef]
- Alvarado, M.M.; Cotton, T.G.; Ntaimo, L.; Pérez, E.; Carpentier, W.R. Modeling and simulation of oncology clinic operations in discrete event system specification. Simulation 2018, 94, 105–121. [Google Scholar] [CrossRef]
- Barros, F.J. Dynamic structure discrete event system specification formalism. Trans. Soc. Comput. Simul. Int. 1996, 13, 35–46. [Google Scholar]
- Blas, M.J.; Gonnet, S.; Leone, H. Routing structure over discrete event system specification: A DEVS adaptation to develop smart routing in simulation models. In Proceedings of the 2017 Winter Simulation Conference, Las Vegas, NV, USA, 3–6 December 2017; Chan, W.K.V., D’Ambrogio, A., Zacharewicz, G., Mustafee, N., Wainer, G., Page, E., Eds.; IEEE: New York, NY, USA, 2017; pp. 774–785. [Google Scholar]
- Byon, E.; Pérez, E.; Ding, Y.; Ntaimo, L. Simulation of wind farm operations and maintenance using discrete event system specification. Simulation 2011, 87, 1093–1117. [Google Scholar] [CrossRef]
- Fonseca i Casas, P. Transforming classic discrete event system specification models to specification and description language. Simulation 2015, 91, 249–264. [Google Scholar] [CrossRef]
- Franceschini, R.; Bisgambiglia, P.-A.; Touraille, L.; Hill, D. A survey of modelling and software framework using discrete event system specification. In 2014 Imperial College Computing Student Workshop; OpenAccess Series in Informatics (OASIcs); Neykova, R., Ng, N., Eds.; Schloss Dagstuhl—Leibniz-Zentrum fuer Informatik, Dagstuhl: Wadern, Germany, 2014; pp. 40–49. [Google Scholar]
- Capocchi, L. DEVSimPy. Software Available on GitHub. 2024. Available online: https://github.com/capocchi/DEVSimPy (accessed on 11 June 2025).
- Capocchi, L.; Santucci, J.; Poggi, B.; Nicolai, C. DEVSimPy: A Collaborative Python Software for Modeling and Simulation of DEVS Systems. In Proceedings of the 2011 IEEE 20th International Workshops on Enabling Technologies: Infrastructure for Collaborative Enterprises, Paris, France, 27–29 June 2011; pp. 170–175. [Google Scholar]
- Capocchi, L.; Santucci, J.-F.; Tigli, J.-Y.; Gomnin, T.; Lavirotte, S.; Rocher, G. Actuation Conflict Management in Internet of Things Systems DevOps: A Discrete Event Modeling and Simulation Approach. In Proceedings of the Internet of Things; Rey, G., Tigli, J.Y., Franquet, E., Eds.; Springer: Cham, Switzerland, 2025; pp. 189–206. [Google Scholar]
- Dominici, A.; Capocchi, L.; De Gentili, E.; Santucci, J.F. Discrete Event Modeling and Simulation of Smart Parking Conflict Management. In Proceedings of the 24th International Congress on Modelling and Simulation, Sydney, Australia, 5–10 December 2021; pp. 246–252. [Google Scholar]
- Sehili, S.; Capocchi, L.; Santucci, J.F.; Lavirotte, S.; Tigli, J.Y. Discrete Event Modeling and Simulation for IoT Efficient Design Combining WComp and DEVSimPy Framework. In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications, Colmar, France, 21–23 July 2015; pp. 26–34. [Google Scholar]
- Wach, P.; Salado, A. The need for semantic extension of SysML to model the problem space. In Recent Trends and Advances in Model Based Systems Engineering; Springer International Publishing: Cham, Switzerland, 2022; pp. 279–289. [Google Scholar]
- Zeigler, B.P.; Sarjoughian, H.S.; Duboz, R.; Souli, J.-C. Guide to Modeling and Simulation of Systems of Systems; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Beltrame, T.; Cellier, F.E. Quantized state system simulation in Dymola/Modelica using the DEVS formalism. In Proceedings of the 5th International Modelica Conference, Vienna, Austria, 4–5 September 2006; pp. 73–82. [Google Scholar]
- Bergero, F.; Fernández, J.; Kofman, E.; Portapila, M. Time discretization versus state quantization in the simulation of a one-dimensional advection–diffusion–reaction equation. Simulation 2016, 92, 47–61. [Google Scholar] [CrossRef]
- Castro, R.; Bergonzi, M.; Pecker-Marcosig, E.; Fernández, J.; Kofman, E. Discrete-event simulation of continuous-time systems: Evolution and state of the art of quantized state system methods. Simulation 2024, 100, 613–638. [Google Scholar] [CrossRef]
- Di Pietro, F.; Migoni, G.; Kofman, E. Improving linearly implicit quantized state system methods. Simulation 2019, 95, 127–144. [Google Scholar] [CrossRef]
- Fernández, J.; Kofman, E. A stand-alone quantized state system solver for continuous system simulation. Simulation 2014, 90, 782–799. [Google Scholar] [CrossRef]
- Grinblat, G.L.; Ahumada, H.; Kofman, E. Quantized state simulation of spiking neural networks. Simulation 2012, 88, 299–313. [Google Scholar] [CrossRef]
- Kofman, E. Quantization-based simulation of differential algebraic equation systems. Simulation 2003, 79, 363–376. [Google Scholar] [CrossRef]
- Kofman, E.; Junco, S. Quantized-state systems: A DEVS Approach for continuous system simulation. Trans. Soc. Model. Simul. Int. 2001, 18, 123–132. [Google Scholar]
- Hong, K.J.; Kim, T.G. DEVSpecL: DEVS specification language for modeling, simulation, and analysis of discrete event systems. Inform. Software Technol. 2006, 48, 221–234. [Google Scholar] [CrossRef]
- Furfaro, A.; Nigro, L. A development methodology for embedded systems based on RT-DEVS. Innovat. Syst. Software Eng. 2009, 5, 117–127. [Google Scholar] [CrossRef]
- Migoni, G.; Kofman, E.; Bergero, F.; Fernández, J. Quantization-based simulation of switched mode power supplies. Simulation 2015, 91, 320–336. [Google Scholar] [CrossRef]
- Migoni, G.; Kofman, E.; Cellier, F. Quantization-based new integration methods for stiff ordinary differential equations. Simulation 2012, 88, 387–407. [Google Scholar] [CrossRef]
- Nutaro, J.; Kuruganti, P.T.; Protopopescu, V.; Shankar, M. The split system approach to managing time in simulations of hybrid systems having continuous and discrete event components. Simulation 2012, 88, 281–298. [Google Scholar] [CrossRef]
- Barros, F.J. Modeling and simulation of dynamic structure heterogeneous flow systems. Simulation 2002, 78, 18–27. [Google Scholar] [CrossRef]
- Kang, B.G.; Seo, K.-M.; Kim, T.G. Machine learning-based discrete event dynamic surrogate model of communication systems for simulating the command, control, and communication system of systems. Simulation 2019, 95, 673–691. [Google Scholar] [CrossRef]
- Pang, C.K.; Mathew, J. Dynamically reconfigurable command and control structure for network-centric warfare. Simulation 2015, 91, 417–431. [Google Scholar] [CrossRef]
- Sun, Y.; Hu, X. Performance measurement of dynamic structure DEVS for large-scale cellular space models. Simulation 2009, 85, 335–351. [Google Scholar] [CrossRef]
- Uhrmacher, A.M. Dynamic structures in modeling and simulation: A reflective approach. ACM Trans. Model. Comput. Simul. 2001, 11, 206–232. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Q.; Xu, X.; Li, W. Modeling and Simulation of Unmanned Swarm System Based on Dynamic Structure DEVS. J. Phys. Conf. Ser. 2024, 2755, 012021. [Google Scholar] [CrossRef]
- Adegoke, A.; Togo, H.; Traoré, M.K. A unifying framework for specifying DEVS parallel and distributed simulation architectures. Simulation 2013, 89, 1293–1309. [Google Scholar] [CrossRef]
- Bergero, F.; Kofman, E.; Cellier, F. A novel parallelization technique for DEVS simulation of continuous and hybrid systems. Simulation 2013, 89, 663–683. [Google Scholar] [CrossRef]
- Bergero, F.; Kofman, E. A vectorial DEVS extension for large scale system modeling and parallel simulation. Simulation 2014, 90, 522–546. [Google Scholar] [CrossRef]
- Bergero, F.; Kofman, E. A Vectorial DEVS Extension for Large Scale System Modeling and Parallel Simulation; Simulation University: Dresden, Germany; Linköping University Electronic Press: Linköping, Sweden, 2014; pp. 657–667. [Google Scholar]
- Nutaro, J.; Ozmen, O. Race conditions and data partitioning: Risks posed by common errors to reproducible parallel simulations. Simulation 2023, 99, 417–427. [Google Scholar] [CrossRef]
- Steinman, J.S. Discrete-event simulation and the event horizon part 2: Event list management. In Proceedings of the PADS ‘96: Proceedings of the Tenth Workshop on Parallel and Distributed Simulation, Philadelphia, PA, USA, 22–24 May 1996; pp. 170–178. [Google Scholar]
- Trabes, G.G.; Wainer, G.A.; Gil-Costa, V. A Parallel Algorithm to Accelerate DEVS Simulations in Shared Memory Architectures. Trans. Soc. Model. Simul. Int. 2023, 90, 522–546. [Google Scholar] [CrossRef]
- Van Mierlo, S.; Van Tendeloo, Y.; Vangheluwe, H. Debugging parallel DEVS. Simulation 2017, 93, 285–306. [Google Scholar] [CrossRef]
- Boukerche, A.; Zhang, M.; Shadid, A. DEVS approach to real-time RTI design for large-scale distributed simulation systems. Simulation 2008, 84, 231–238. [Google Scholar] [CrossRef]
- Cho, Y.K.; Hu, X.; Zeigler, B.P. The RTDEVS/CORBA environment for simulation-based design of distributed real-time systems. Simulation 2003, 79, 197–210. [Google Scholar] [CrossRef]
- Gianni, D.; D’AMbrogio, A.; Iazeolla, G. A software architecture to ease the development of distributed simulation systems. Simulation 2011, 87, 819–836. [Google Scholar] [CrossRef]
- Kim, T.G.; Kim, Y.J. A heterogeneous distributed simulation framework based on DEVS formalism. In Proceedings of the Sixth Annual Conference on Artificial Intelligence, Simulation and Planning in High Autonomy Systems; 1996; pp. 116–121. [Google Scholar]
- Lee, J.S.; Zeigler, B.P.; Venkatesan, S.M. Design and development of data distribution management environment. Simulation 2001, 77, 39–52. [Google Scholar] [CrossRef]
- Sarjoughian, H.S.; Hild, D.R.; Hu, X.; Strini, R.A. Simulation-based SW/HW architectural design configurations for distributed mission training systems. Simulation 2001, 77, 23–38. [Google Scholar] [CrossRef]
- Trabes, G.G. Efficient DEVS Simulations Design on Heterogeneous Platforms. Doctoral Dissertation, Universidad Nacional de San Luis, San Luis, Argentina, 2023. [Google Scholar]
- Foures, D.; Franceschini, R.; Bisgambiglia, P.-A.; Zeigler, B.P. multiPDEVS: A Parallel Multicomponent System Specification Formalism. Complexity 2018, 2018, 3751917. [Google Scholar] [CrossRef]
- Zeigler, B.P.; Mittal, S.; Traore, M.K. MBSE with/out Simulation: State of the Art and Way Forward. Systems 2018, 6, 40. [Google Scholar] [CrossRef]
- Mac Lane, S. Categories for the Working Mathematician, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1998; ISBN -13978-0387984032. [Google Scholar]
- Edwin, Z.C.; Daniel, D.E.; Falcone, A.; Garro, A.; Möller, B. Enabling Simulation Interoperability between International Standards in the Space Domain, DS_RT_2022; IEEE: New York, NY, USA, 2022. [Google Scholar]
- NATO Science and Technology Organization. Simulation Interoperability. STO Technical Report FR-MSG-086-Part-I. 2015. Available online: https://www.sto.nato.int/document/simulation-interoperability/ (accessed on 1 June 2025).
- NATO Science and Technology Organization. Allied Modelling and Simulation Publications. Available online: https://www.sto.nato.int/the-collaborative-programme-of-work-cpow/modeling-and-simulation/nato-modelling-simulation-group/nato-ms-standards-and-guidance/ (accessed on 28 October 2025).
- Simulation Interoperability Standards Organization. Standards Products. Available online: https://www.sisostandards.org/page/StandardsProducts. (accessed on 28 October 2025).
- Available online: https://www.navsea.navy.mil/Home/Warfare-Centers/NSWC-Dahlgren/Resources/Leading-Edge/I-I-Leading-Edge/Wallace-andCummings/#:~:text=OSM%20Overview,level%20model%20of%20many%20systems (accessed on 1 June 2025).
- Kim, Y.J.; Kim, T.G. A heterogeneous simulation framework based on the DEVS BUS and the high level architecture. In Proceedings of the 1998 Winter Simulation Conference. Proceedings (Cat. No.98CH36274), Washington, DC, USA, 13–16 December 1998; Volume 1, pp. 421–428. [Google Scholar] [CrossRef]
- NATO Modelling and Simulation Group—164. MSaaS in Action from a Customer Perspective. Presented at NATO CA2X2 Forum. Available online: https://www.mscoe.org/nato-ca2x2-forum-agenda/ (accessed on 23 September 2020).
- US Army Program Executive Office Simulation, Training, and Instrumentation (PEO STRI). Bifrost. 2024. Available online: https://www.peostri.army.mil/Portals/140/Documents/OneSAF/onesaf-bifrost-fact-sheet.pdf?ver=lxrXLPEO179xUC8Z9ddtiA%3D%3D (accessed on 1 December 2020).
- Orozco, J. Enabling Multi-Domain Operations through Simulation Services. In Proceedings of the 2023 Interservice/Industry Training, Simulation, and Education Conference (I/ITSEC), Orlando, FL, USA, 27 November–1 December 2023. [Google Scholar]
- Simlytics.cloud, LLC. DEVS Streaming Framework Introduction. Available online: https://github.com/simlytics-cloud/devs-streaming/blob/main/docs/import/DEVS%20Streaming%20Framework%20Introduction.md. (accessed on 28 October 2025).
| Component | Sequential State | Time Advance |
|---|---|---|
| Imm (imminent) | sendActivate | 1. |
| RecImm (receives input and is imminent) | sendActivate | 1. |
| RecNonImm (receives input and is not imminent) | waitForActivate | infinity |
| NonImm (nonimminent) | active | 10. |
| Source | Outport | Destination | Inport |
|---|---|---|---|
| Imm | Activate | RecImm | Activate |
| Imm | Activate | RecNonImm | Activate |
| RecImm | Activate | NonImm | Activate |
| Component | Sequential State | Time Advance |
|---|---|---|
| Imm (imminent) | passive | Infinity |
| RecImm (receives input and is imminent) | waitForActivate | Infinity |
| RecNonImm (receives input and is not Imminent) | passive | Infinity |
| NonImm (nonImminent) | active | 9 |
| The Wrapped Model Definition of the | Sketch of Its Definition |
|---|---|
| Internal transition function | (1) Get the next event time from the internal coordinator (2) Tell the internal coordinator to execute its next event at the given next event time |
| External transition function with arguments of elapsed time and input bag | (1) Get the last event time from the internal coordinator (2) Tell the internal coordinator to process the input bag with the time stamp of the given last event time plus the elapsed time |
| Output function | Tell the internal coordinator to compute the output and return this output bag |
| Time advance function | Tell the internal coordinator to get the next event time and the last event time and to return the second minus the first |
| Aspect | Drawbacks |
|---|---|
| Information Retention | Loss of critical design information from intermediate models; less intuitive for human analysis. |
| Verification & Validation (V&V) | Greater difficulty in gaining insight during V&V; harder to quickly identify errors. |
| Visualization | Less data available for visualizations unless extra logging is added, which may slow performance. |
| Computation for Flattening | Potentially computationally expensive flattening algorithms, especially for deep hierarchies. |
| Dynamic Structure Change | Complex-to-implement dynamic changes without original hierarchical location data. |
| Reusability | Reduced modularity making components harder to reuse across models. |
| Parallel/Distributed Simulation | Greater complexity in partitioning for parallel/distributed execution; reduced modular boundaries hindering load balancing. |
| Design Intent | Requirement of supplementary metadata/annotations to convey original design intent. |
| Scalability | Potential creation of combinatorially larger number of direct couplings, increasing memory and initialization costs. |
| Reconstruction of Hierarchy | An ability to uniquely recover original modular structure without comprehensive metadata. |
| Aspect | Benefits of Deepening | Drawbacks of Deepening |
|---|---|---|
| Abstraction and Clarity | Groups related components into a higher-level coupled model, improving conceptual clarity and modularity. | May obscure fine-grained details, making debugging or tracing individual component behavior harder. |
| Reusability | Facilitates reuse of coupled subsystems as encapsulated modules in other models. | Over-encapsulation can reduce flexibility if frequent modifications to internal components are needed. |
| Maintainability | Simplifies top-level model structure by reducing the number of visible components. | Adds complexity to the hierarchy, requiring careful documentation to avoid confusion. |
| Scalability | Supports scaling by organizing large systems into manageable subsystems. | Excessive nesting can lead to deep hierarchies that are difficult to navigate and maintain. |
| Behavior Preservation | Uses coupling amendments to ensure that the overall system behavior remains consistent after grouping. | Risk of introducing coupling errors or unintended side effects during restructuring. |
| Decision Support | Provides a structured view of system evolution, useful for teaching, analysis, and standards alignment. | May require additional reasoning steps to validate equivalence with the flattened version. |
| Type of Challenge | Description |
|---|---|
| Support for Experimental Frames | Support for specification of experimental frames is essential to facilitating the sharing, reuse, and management of DEVS models and simulation experiments within the modeling and simulation community, promoting collaboration and reducing redundant efforts. |
| Semantic Divergence | There are variations in lifecycle semantics and behavior across DEVS implementations and a lack of formal equivalence between DEVS variants (classic, parallel, etc.). |
| Platform & Language Interoperability | Diverse programming languages and environments complicate module exchange; middleware and adapter design must preserve DEVS semantics. |
| Tool Development & Infrastructure Gaps | Unified model formats, graphical editors, and debugging tools are absent, limiting usability and adoption across domains. |
| Testing & Certification | There is no standard benchmark suite or compliance criteria; distributed execution introduces synchronization and rollback complexities. |
| Community & Governance | Fragmented research communities and legacy systems resist change; balancing extensibility with strict interoperability is politically and technically complex. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeigler, B.P.; Kewley, R.; Wainer, G. DEVS Closure Under Coupling, Universality, and Uniqueness: Enabling Simulation and Software Interoperability from a System-Theoretic Foundation. Computers 2025, 14, 514. https://doi.org/10.3390/computers14120514
Zeigler BP, Kewley R, Wainer G. DEVS Closure Under Coupling, Universality, and Uniqueness: Enabling Simulation and Software Interoperability from a System-Theoretic Foundation. Computers. 2025; 14(12):514. https://doi.org/10.3390/computers14120514
Chicago/Turabian StyleZeigler, Bernard P., Robert Kewley, and Gabriel Wainer. 2025. "DEVS Closure Under Coupling, Universality, and Uniqueness: Enabling Simulation and Software Interoperability from a System-Theoretic Foundation" Computers 14, no. 12: 514. https://doi.org/10.3390/computers14120514
APA StyleZeigler, B. P., Kewley, R., & Wainer, G. (2025). DEVS Closure Under Coupling, Universality, and Uniqueness: Enabling Simulation and Software Interoperability from a System-Theoretic Foundation. Computers, 14(12), 514. https://doi.org/10.3390/computers14120514








