Waveform Design Method for Piezoelectric Print-Head Based on Iterative Learning and Equivalent Circuit Model
Abstract
1. Introduction
2. Model and Desired Volume Flow Rate
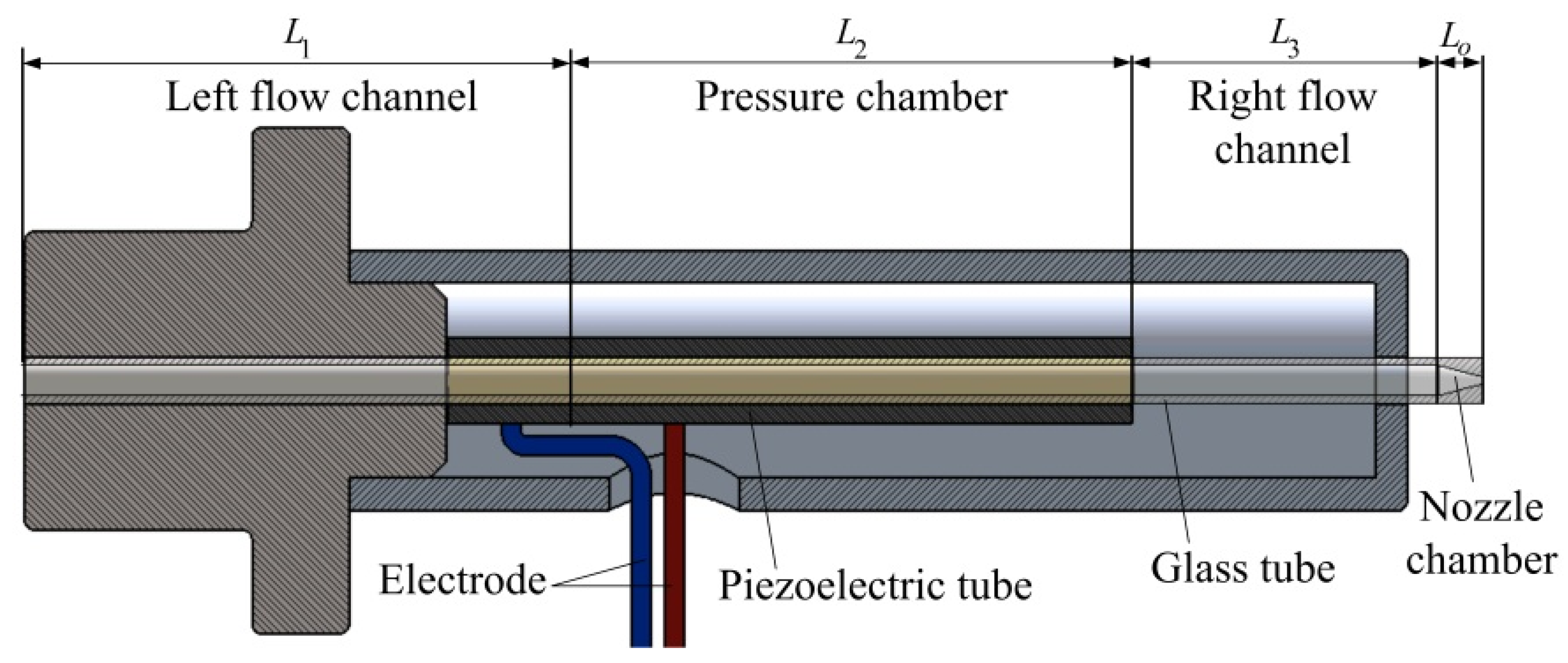
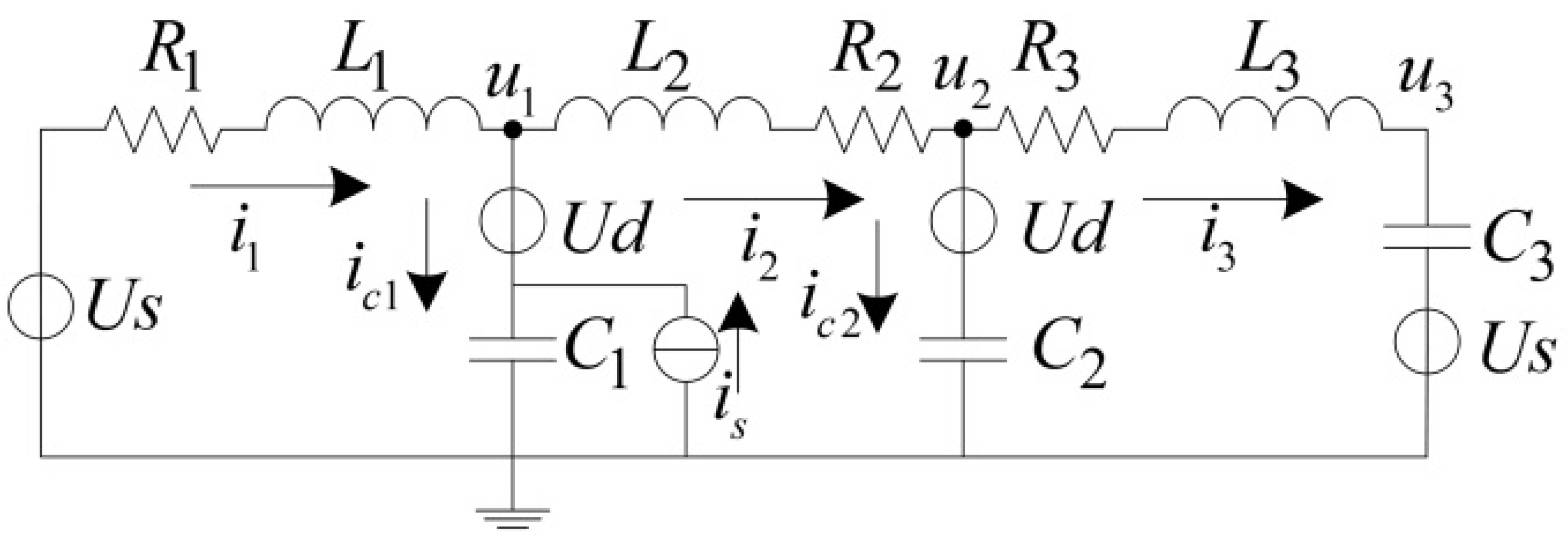
2.1. Equivalent Circuit Model
2.2. Parameter Estimation
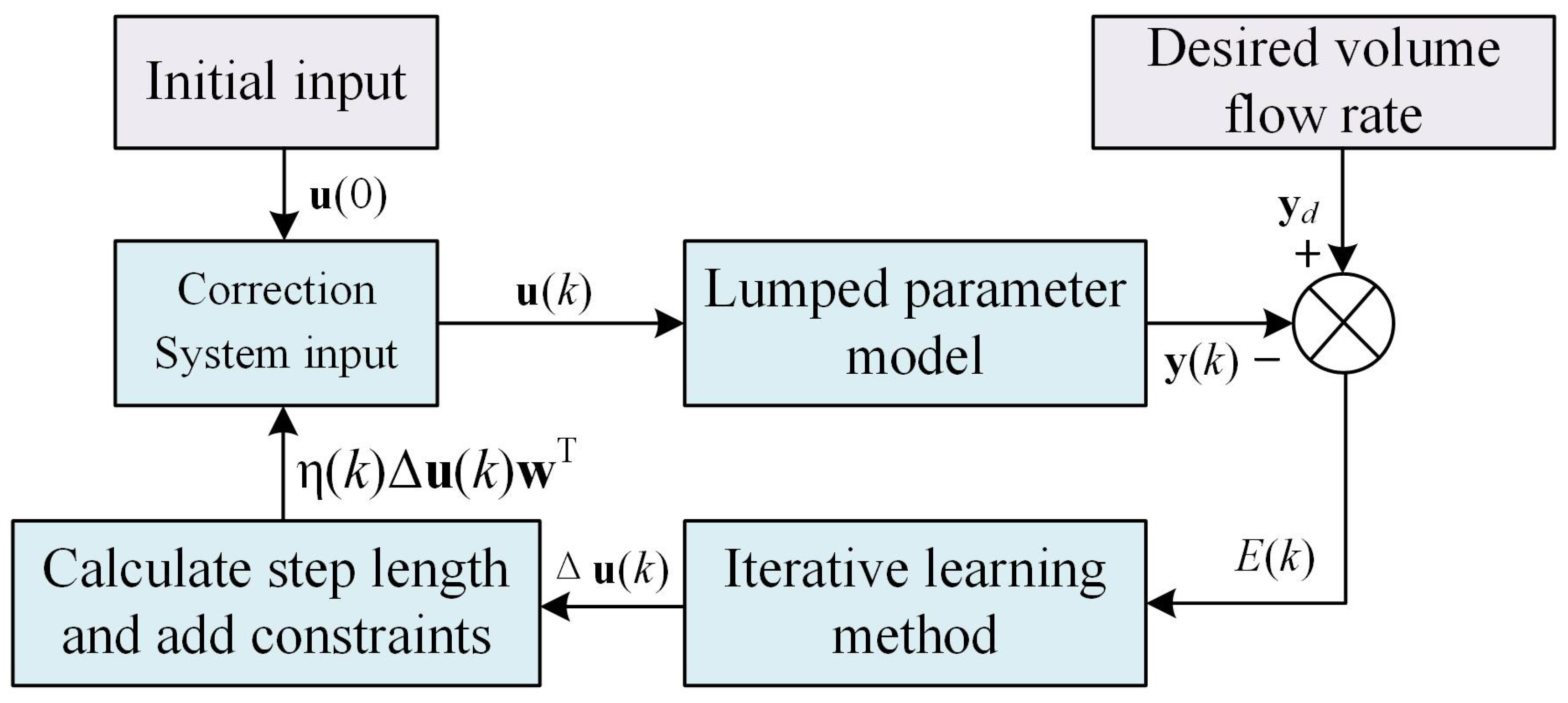
3. Iterative Learning Process
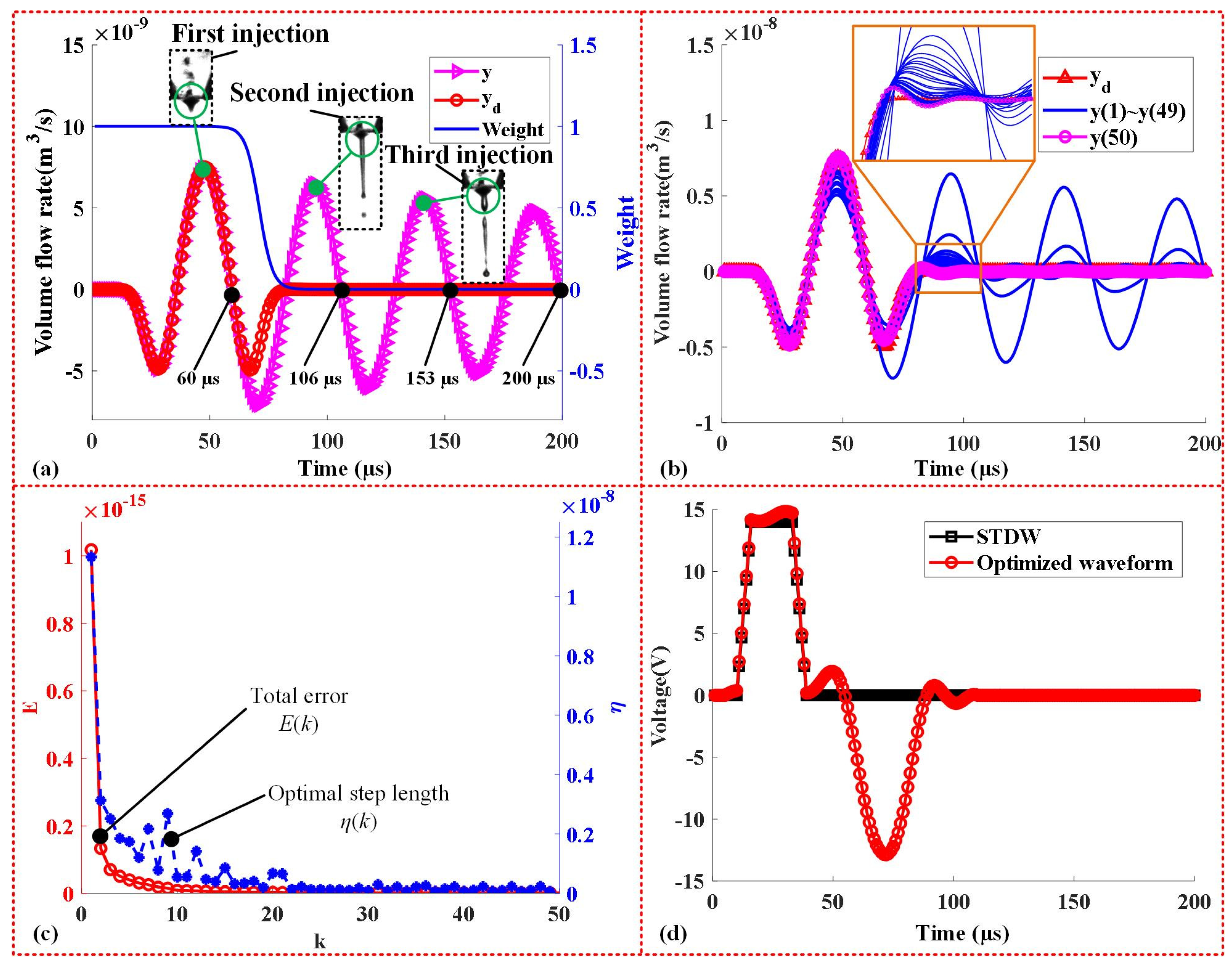
3.1. Iterative Learning Method
3.2. Optimal Iteration Step Length
3.3. Adding to Iterative Learning Constraint
3.4. Calculated Waveform with the Iterative Learning Method
4. Results and Discussion
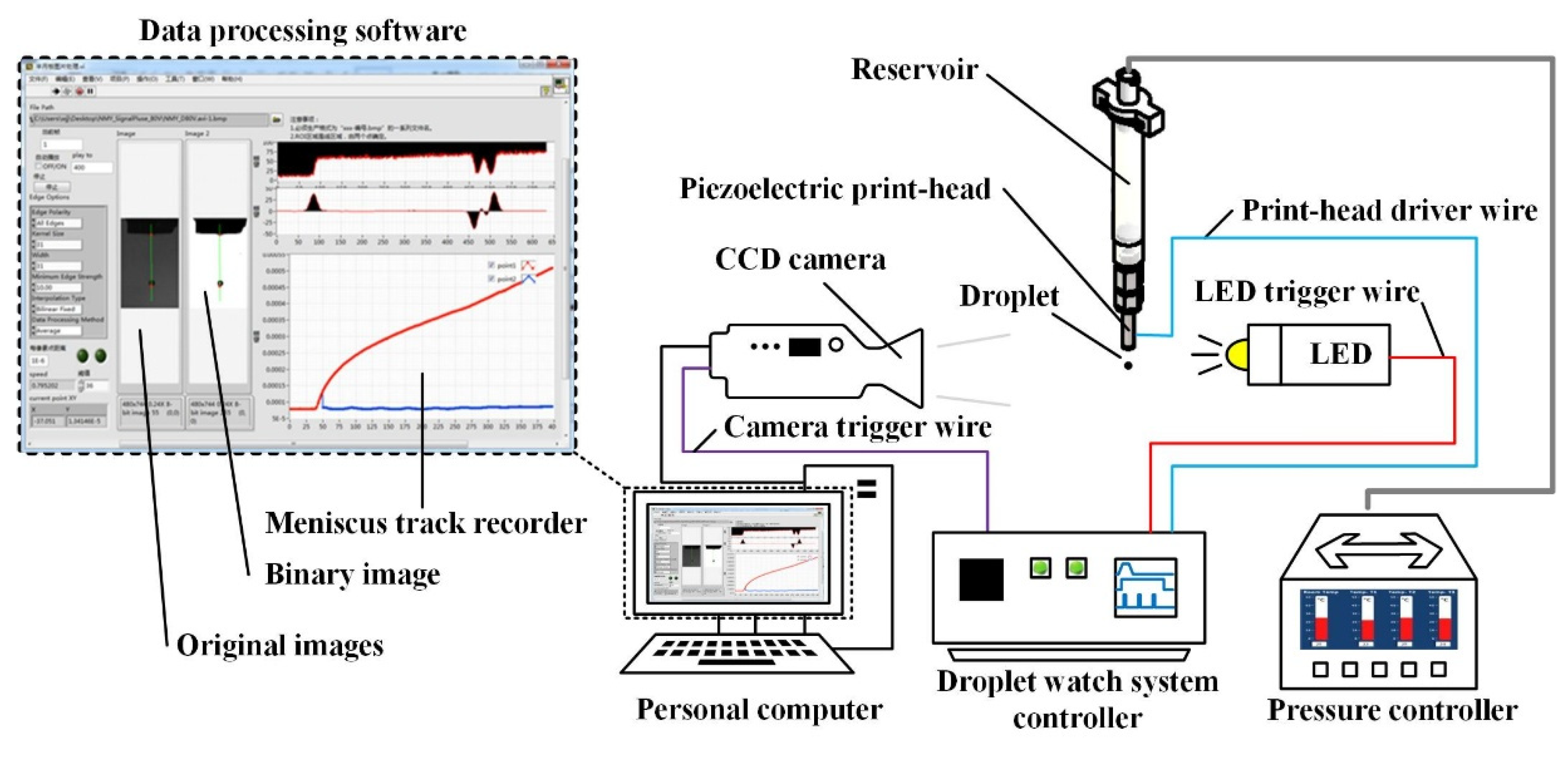
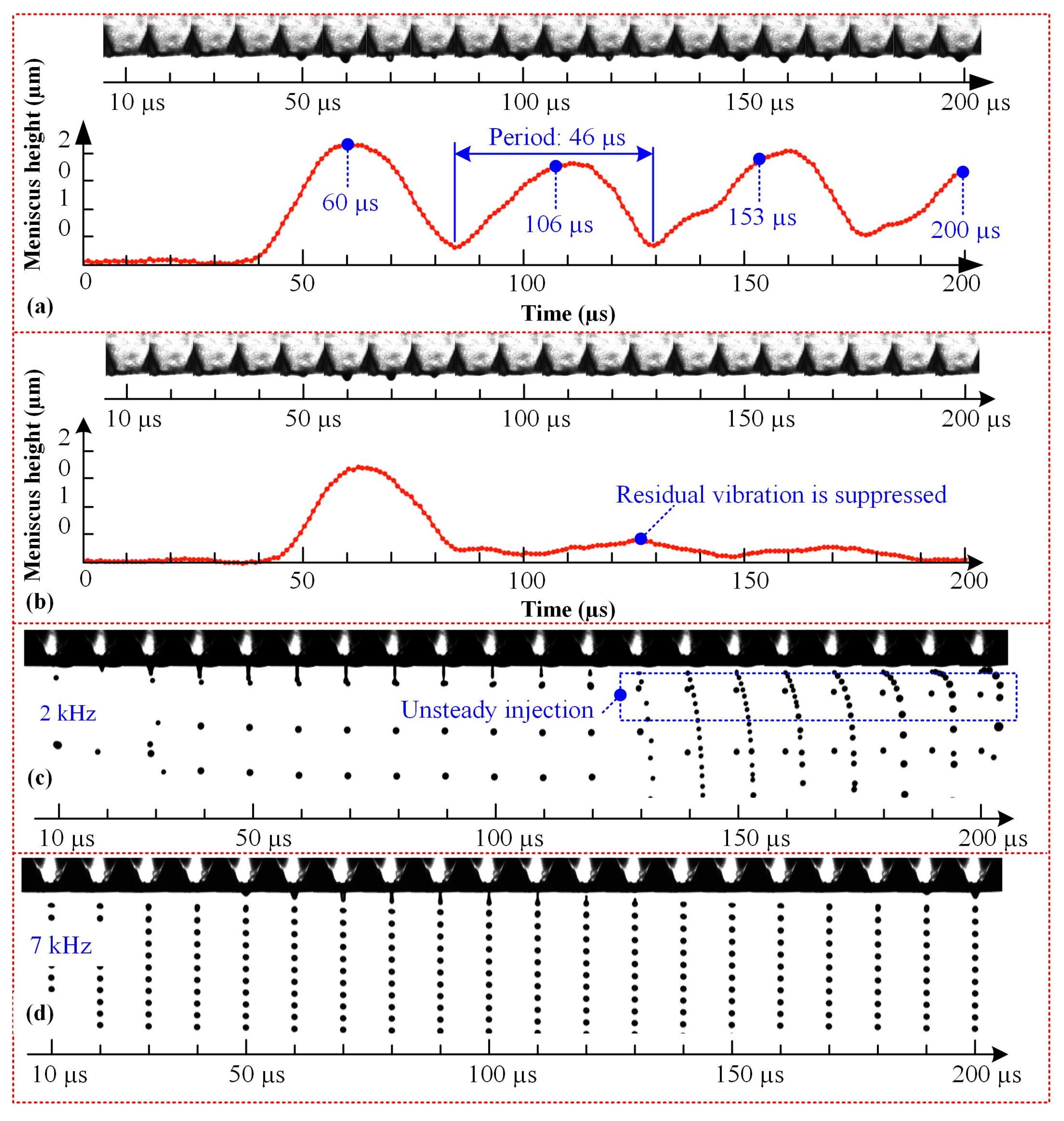
4.1. Experimental Setup
4.2. Suppressed Residual Vibration
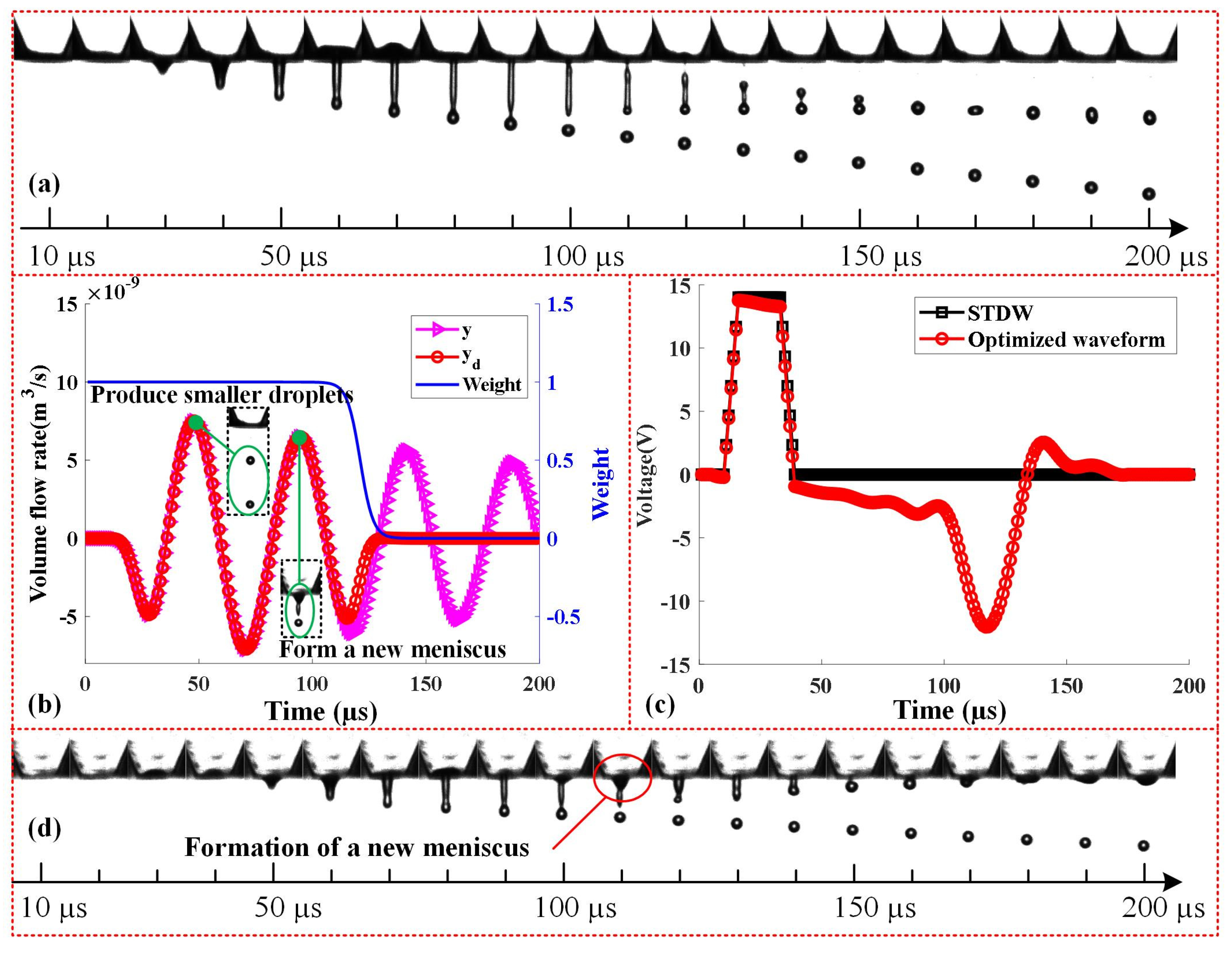
4.3. Production of Smaller Droplets
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Meaning |
| PPH | Piezoelectric print-heads |
| STDW | Single trapezoidal drive waveform |
| DTDW | Double trapezoidal drive waveform |
| DWS | Droplet watch system |
| KVL | Kirchhoff’s voltage law |
| KCL | Kirchhoff’s current law |
| PID | proportional integral derivative |
References
- Kyobula, M.; Adedeji, A.; Alexander, M.R.; Saleh, E.; Wildman, R.; Ashcroft, I.; Gellert, P.R.; Roberts, C.J. 3D inkjet printing of tablets exploiting bespoke complex geometries for controlled and tuneable drug release. J. Control Release 2017, 261, 207–215. [Google Scholar] [CrossRef] [PubMed]
- Roh, J.; Kim, H.; Park, M.; Kwak, J.; Lee, C. Improved electron injection in all-solution-processed n-type organic field-effect transistors with an inkjet-printed ZnO electron injection layer. Appl. Surf. Sci. 2017, 420, 100–104. [Google Scholar] [CrossRef]
- Bogy, D.B.; Talke, F.E. Experimental and Theoretical Study of Wave Propagation Phenomena in Drop-on-Demand Ink Jet Devices. IBM J. Res. Dev. 1984, 28, 314–321. [Google Scholar] [CrossRef]
- Liou, T.-M.; Chan, C.-Y.; Shih, K.-C. Effects of actuating waveform, ink property, and nozzle size on piezoelectrically driven inkjet droplets. Microfluid. Nanofluid. 2009, 8, 575–586. [Google Scholar] [CrossRef]
- Kwon, K.-S. Waveform Design Methods for Piezo Inkjet Dispensers Based on Measured Meniscus Motion. J. Microelectromech. Syst. 2009, 18, 1118–1125. [Google Scholar] [CrossRef]
- Kwon, K.-S. Experimental analysis of waveform effects on satellite and ligament behavior via in situ measurement of the drop-on-demand drop formation curve and the instantaneous jetting speed curve. J. Micromech. Microeng. 2010, 20, 115005. [Google Scholar] [CrossRef]
- Wu, C.-H.; Hwang, W.-S. The effect of the echo-time of a bipolar pulse waveform on molten metallic droplet formation by squeeze mode piezoelectric inkjet printing. Microelectron. Reliab. 2015, 55, 630–636. [Google Scholar] [CrossRef]
- Khalate, A.A.; Bombois, X.; Babuška, R.; Wijshoff, H.; Waarsing, R. Performance improvement of a drop-on-demand inkjet printhead using an optimization-based feedforward control method. Control Eng. Pract. 2011, 19, 771–781. [Google Scholar] [CrossRef]
- Khalate, A.A.; Bombois, X.; Scorletti, G.; Babuska, R.; Koekebakker, S.; de Zeeuw, W. A Waveform Design Method for a Piezo Inkjet Printhead Based on Robust Feedforward Control. J. Microelectromech. Syst. 2012, 21, 1365–1374. [Google Scholar] [CrossRef]
- He, M.-W.; Sun, L.-L.; Hu, K.-Y.; Zhu, Y.-L.; Chen, H.-N. Analysis of DoD inkjet printhead performance for printable electronics fabrication using dynamic lumped element modeling and swarm intelligence based optimal prediction. J. Central South Univ. 2015, 22, 3925–3934. [Google Scholar] [CrossRef]
- Rensch, C. Creation of Small Microdrops; MicroFab Technote; MicroFab Technologies: Plano, TX, USA, 2006. [Google Scholar]
- Chen, A.U.; Basaran, O.A. A new method for significantly reducing drop radius without reducing nozzle radius in drop-on-demand drop production. Phys. Fluids 2002, 14, L1–L4. [Google Scholar] [CrossRef]
- Wassink, M.G.; Bosch, N.J.M.; Bosgra, O.H.; Koekebakker, S. Enabling higher jet frequencies for an inkjet printhead using Iterative Learning Control. In Proceedings of the 2005 IEEE Conference on Control Applications, Toronto, ON, Canada, 28–31 August 2005. [Google Scholar]
- Kwon, K.-S.; Kim, W. A waveform design method for high-speed inkjet printing based on self-sensing measurement. Sens. Actuators A Phys. 2007, 140, 75–83. [Google Scholar] [CrossRef]
- Wang, J.; Huang, J.; Peng, J. Hydrodynamic response model of a piezoelectric inkjet print-head. Sens. Actuators A Phys. 2019, 285, 50–58. [Google Scholar] [CrossRef]
- Kwon, K.-S.; Jang, M.-H.; Park, H.Y.; Ko, H.-S. An inkjet vision measurement technique for high-frequency jetting. Rev. Sci. Instrum. 2014, 85, 065101. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.M.; Du, G.H.; Gong, X.F. Theory of Acoustics, 3rd ed.; Nanjing University Press: Nanjing, China, 2012. [Google Scholar]
- Kim, B.H.; Lee, H.S.; Kim, S.W.; Kang, P.; Park, Y.S. Hydrodynamic responses of a piezoelectric driven MEMS inkjet print-head. Sens. Actuators A Phys. 2014, 210, 131–140. [Google Scholar] [CrossRef]
- Poozesh, S.; Akafuah, N.; Saito, K. New criteria for filament breakup in droplet-on-demand inkjet printing using volume of fluid (VOF) method. Korean J. Chem. Eng. 2016, 33, 775–781. [Google Scholar] [CrossRef]
- Dijkstra, B.G. Iterative Learning Control with Applications to a Wafer Stage. Ph.D. Thesis, T.U. Delft, Delft, The Netherlands, September 2004. [Google Scholar]
- Owens, D.; Rogers, E.; Moore, K.L. Analysis of Linear Iterative Learning Control Schemes Using Repetitive Process Theory. Asian J. Control 2008, 4, 68–89. [Google Scholar] [CrossRef]
- Rogers, E.; Owens, D.H.; Werner, H.; Freeman, C.T.; Lewin, P.L.; Kichhoff, S.; Lichtenberg, G. Norm-Optimal It-erative Learning Control with Application to Problems in Accelerator-Based Free Electron Lasers and Rehabilitation Ro-botics. Eur. J. Control 2010, 16, 497–522. [Google Scholar] [CrossRef]

| Equivalent Circuit Components | Mapping Expressions | Parameters for MJ-AL-80 |
|---|---|---|
| Capacitance C1, C2, C3 | C1 = 1.4374 × 10−18 C2 = 8.2565 × 10−19 C3 = 1.1888 × 10−16 | |
| Voltage source Ud | Ud = 9.897216 × 108 | |
| Resistance R1, R2, R3 | R1 = 2.3018 × 1011 R2 = 1.5635 × 1011 R3 = 3.7675 × 1011 | |
| Inductance L1, L2, L3 | , | R1 = 5.8984 × 107 R2 = 4.0065 × 107 R3 = 3.4867 × 107 |
| Current source is |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Xiong, C.; Huang, J.; Peng, J.; Zhang, J.; Zhao, P. Waveform Design Method for Piezoelectric Print-Head Based on Iterative Learning and Equivalent Circuit Model. Micromachines 2023, 14, 768. https://doi.org/10.3390/mi14040768
Wang J, Xiong C, Huang J, Peng J, Zhang J, Zhao P. Waveform Design Method for Piezoelectric Print-Head Based on Iterative Learning and Equivalent Circuit Model. Micromachines. 2023; 14(4):768. https://doi.org/10.3390/mi14040768
Chicago/Turabian StyleWang, Jianjun, Chuqing Xiong, Jin Huang, Ju Peng, Jie Zhang, and Pengbing Zhao. 2023. "Waveform Design Method for Piezoelectric Print-Head Based on Iterative Learning and Equivalent Circuit Model" Micromachines 14, no. 4: 768. https://doi.org/10.3390/mi14040768
APA StyleWang, J., Xiong, C., Huang, J., Peng, J., Zhang, J., & Zhao, P. (2023). Waveform Design Method for Piezoelectric Print-Head Based on Iterative Learning and Equivalent Circuit Model. Micromachines, 14(4), 768. https://doi.org/10.3390/mi14040768






