Abstract
In this article, a Riga plate is exhibited with an electric magnetization actuator consisting of permanent magnets and electrodes assembled alternatively. This Riga plate creates an electric and magnetic field, where a transverse Lorentz force is generated that contributes to the flow along the plate. A new study field has been created by Sutterby nanofluid flows down the Riga plate, which is crucial to the creation of several industrial advancements, including thermal nuclear reactors, flow metres, and nuclear reactor design. This article addresses the second law analysis of MHD Sutter by nanofluid over a stretching sheet with the Riga plate. The Cattaneo–Christov Double Diffusion heat and mass flux have been created to examine the behaviour of relaxation time. The bioconvection of motile microorganisms and chemical reactions are taken into consideration. Similarity transformations are used to make the governing equations non-dimensional ordinary differential equations (ODE’s) that are subsequently solved through an efficient and powerful analytic technique, the homotopy analysis method (HAM). The effect of pertained variables on velocity, temperature, concentration, and motile microorganism distributions are elaborated through the plot in detail. Further, the velocity distribution enhances and reduces for greater value Deborah number and Reynold number for the two cases of pseudoplastic and dilatant flow. Microorganism distribution decreases with the augmented magnitude of Peclet number , Bioconvection Lewis number , and microorganism concentration difference number . The entropy production distribution is increased for the greater estimations of the Reynolds number and Brinkman parameter . Two sets of graphical outputs are presented for the Sutterby fluid parameter. Finally, for the justification of these outcomes, tables of comparison are made with various variables.
1. Introduction
The rate of heat transport characteristics is a subject of enduring interest for various researchers and scientists owing to its tremendous industrial applications, for example, in mechanical, optical, electrical, and cooling instruments. The rate of heat transport increment is very crucial in depositing energy. Thus, researchers are focused on the investigation of a new fluid substance that is a mixture of nanoparticles 100 nm in size and more thermophysical properties than ordinary fluid, known as nanoliquid. Nanoliquid is the colloidal suspension of the nanoparticles’ thermal behaviour of the ordinary fluid. The first endeavour was performed by Choi et al. [1] in 1995. They exposed the thermal conductivity of nanoliquid by adding nanosized particles. Later, Buongiorno [2] used this notation of nanofluid to make a mathematical form by adding terms known as Brownian and Thermophoretic. The mixed convection nanofluid flows with different surfaces and geometry were conducted by Hussain et al. [3,4], and Haq et al. [5] deliberated the second law analysis on a cross nanofluid. The impact of microorganisms on the Darcy flow of Sutterby nanofluid, taking into account microorganisms over movable cylinders, was examined by Aldabesh et al. [6]. Mankiw et al. [7] analysed the MHD time-dependent flow of nanofluid with variable properties due to an inclined stretching sheet under thermal radiation. Shahid [8] demonstrated the effect of upper convective flow of Maxwell liquid over a permeable surface near the stagnation point. Rafique et al. [9] addressed the stratified micropolar nanofluid flow past an exponentially stretchable plate with the Riga surface. The unsteady viscous flow of nanofluid over the Riga plate using a rotating plate was investigated by Parvine et al. [10]. Abbas et al. [11] deliberated the entropy production over the Riga plate and the suction case. Sannad et al. [12] using a non-homogeneous dynamic model, which is more accurate in physically describing nanofluids than homogeneous ones, wherein free convective flow in a cubical cavity filled with copper-water nanofluid was explored numerically. Some of the latest developments in nanofluids were obtained from references [13,14,15,16,17,18,19].
Different fluid forms, including polymer melts, colloidal suspensions, organic chain mixes, etc., are used in a wide range of industries and production processes. The rheological behaviour of these fluids cannot be well described by the Naiver–Stokes equation alone. Therefore, several nonlinear fluid models are proposed to represent the rheological characteristics of complicated fluids. One non-Newtonian fluid model used to examine key characteristics of pseudoplastic and dilatant fluids is the Sutterby fluid model. Numerous experts have extensively studied the flow of Sutterby liquid. Waqas et al. [20] inspected Sutterby nanofluid using two rotating disks. Yahya et al. [21] investigated Williamson Sutterby nanoparticles under the Cattaneo–Christov heat flux. The effect of MHD on Sutterby nanoparticles due to porous movable sheets was discovered by Fayydh et al. [22]. Gowda et al. [23] examined the Cattaneo–Christof theory of heat diffusion in Sutterby nanofluid. The impact of thermal radiation and heat source/sink on Sutterby nanofluid has been studied by Ali et al. [24]. Hayat et al. [25] investigated the Sutterby fluid with thermal radiation due to a rotating disk. Recently, Fujii et al. [26] addressed Sutterby fluid with natural convection flow due to a vertical plate. The Darcy surface with MHD flow of Sutterby fluid was reported by Bilal et al. [27]. The bioconvection flow of Sutterby nanofluid due to a rotating disk was described by Khan et al. [28]. Sohail et al. [29] designed the free convection flow of Sutterby fluid with heat under the Cattaneo–Christov theory. The heat generation/absorption in the thermally stratified flow of stagnant Sutterby fluid through a linearly stretched plate is analysed in this article by Saif et al. [30]. Usman et al. [31] investigated the two-dimensional stagnant flow of Sutterby nanofluid across a stretching wedge placed in a porous media. Song et al. [32] discussed the two-dimensional flow of Sutterby nanofluids over a stretching cylinder, scrutinized in the presence of bioconvection and swimming microorganisms. The influence of homogeneous heterogeneous reaction on Sutterby fluid flow by a disk with Cattaneo–Christov heat flux is studied by Khan et al. [33].
In the modern period, the research on bio-convection exists due to the motion of microorganisms upwards because microorganisms are denser than water. The upward surface of the fluid develops thickness as a result of the collection of the microorganism. For this reason, the upper surface becomes disturbed, and microorganisms sink, which develops bioconvection. Bio-convection continues to be the subject of research broadly due to its many applications in the clinical area, manufacturing process, and biofuel production. Bio-convection could be organised as consisting of the motion of direction with a vast number of microorganism species. In this way, gyrotactic microorganisms are among those whose swimming direction is based on viscous torque and gravitational force. Kuznetsov et al. [34,35] reported the early investigation of bio-convection in the mixed suspension of nanoparticles with gyrotactic microorganisms. Kotha et al. [36] examined the MHD flow of nanofluid with motile gyrotactic microorganisms over a vertical plate. Siddiq et al. [37] numerically analysed the bioconvection of micropolar nanofluid flow restricted through the stretchable disk using the bvp4c method. Bagh et al. [38] studied the effect of bioconvection and Cattaneo–Christov with a vertical stretching sheet. Azam et al. [39] investigated the effect of bioconvection flow for the Sutterby nanoliquid with nonlinear radiation. Khashi’ie et al. [40] tested a hybrid nanofluid that had bioconvection with gyrotactic microorganisms. Azam [41] explored the time-dependent flow of the chemically reactive Sutterby nanofluid and the influence of gyrotactic microorganisms. Hayat et al. [42] operated the bio-convection flow of nanomaterial subject to melting effect. They addressed thermal nonlinear radiation and Joule heating for heat distribution characteristics. Reddy et al. [43] analysed the time-dependent flow of Cross nanofluid comprising the gyrostatic microorganisms due to slip velocity. Sarkar et al. [44] defined Sutterby nanofluid flow as having motile gyrotactic microorganisms over the Riga plate. Shah et al. [45] described the heat transfer properties of a magnetohydrodynamic Prandtl hybrid nanofluid over a stretched surface in the presence of bioconvection and chemical reaction effects. Ali et al. [46] explored the fluctuating temperature with Cattaneo–Christov features and self-motivated bioconvective microbes immersed in the water-based nanofluid, observed with the excision/accretion of the leading edge.
Riga plate is an electromagnetic actuator, which is made by the combination of a span-wise aligned array of alternating electrodes and permanent magnets. This actuator is responsible for producing a Lorentz force that decreases exponentially. It is important to note that when an external magnetic field is applied to a fluid with high electrical conductivity, it has a provocative effect. However, this device has been used to reduce pressure drag by preventing boundary layer separation and reducing the generation of turbulence requirements. Riga plate was first introduced by Gailitis and Leilausis [47], and they generated a wall paralleled by Lorentz force to control the fluid flow. Further, in contrast to this, the Grinberg term was introduced with a most important feature that the boundary layer of the momentum equation is fully separate from the flow, and exponentially decreases in the direction of the normal to the plate. Subsequently, the Lorentz force was detected over a Riga plate, and then the researchers regained interest in the Gailitis–Lielausis actuator. Islam and Nasrin [48] described the one-dimensional unsteady micropolar fluid flow set in a porous medium along with an inclined infinite Riga plate. Nasrin et al. [49] explored the impulsively started horizontal Riga plate in two-dimensional unsteady Casson fluid flows with rotation. Anjum et al. [50] concentrated on thermal stratification in the flow of second-grade fluid past a Riga plate with linear stretching toward a stagnation region. Hayat et al. [51] investigated the convective heat transfer of electron magnetohydrodynamic squeezed flow past a Riga plate. Wahidunnisa et al. [52] stduied a mixed convective nanofluid flow along a heated Riga plate with viscous dissipation and heat source. Iqbal et al. [53,54] have found the stagnation point flow of the melting heat, thermal radiation, and viscous dissipation effects on the Riga plate using erratic thickness, and considered the Casson fluid stagnation point flow along with a Riga plate. Vishnu et al. [55] discussed the γ Al2O3–Water/Ethylene Glycol over a Gailitis and Lielausis device with an effective Prandtl number.
Newtonian fluids have been mostly discussed as base fluids in the prior work. We were motivated to examine Sutterby as a base fluid along with the Riga plate and chemical reaction effects with Cattaneo–Christove double diffusion for microorganism flow of nanofluids due to stretching surface because there have been so few studies on them. These facets of the issue, as far as the authors can tell, are not taken into consideration in the investigations that have already been done. The improvement of heat and mass transportation is the main goal of this extensive investigation. The current investigation was encouraged to express the Sutterby nanofluid inserted on a porous surface with Cattaneo–Christof double diffusion due to the Riga plate containing gyrotactic microorganisms. The chemical reaction and heat source-sink are considered worthy of attention. The leading aim of this work is an inclusive analysis of this flow problem. The coupled equations of the current flow problem are altered into the nonlinear system by applying suitable correspondence transformations. Further, the solution of ordinary differential equations is utilized via the Homotopy Analysis Method (HAM). The novel outcomes of the current work are obtained through different parameters and explained with the assistance of graphs and tables.
2. Description of the Physical Model
Consider the incompressible and steady flow of second law analysis in Sutterby nanofluid due to the Riga Plate containing gyrotactic microorganisms displayed in Figure 1. Cattaneo–Christov with heat and mass flux has also been pondering the temperature and concentration equation. The x-axis is considered along with the sheet and the y-axis is taken perpendicular to the sheet. Moreover, the sheet of velocity is . At the surface of the sheet, the temperature of the surface, the concentration of the surface, and the microorganisms of the surface are symbolized by , , . The swimming route and velocity of microorganisms do not alter when nanoparticles are present. However, if the volume percentage of nanoparticles exceeds 1%, the motility of microorganisms is impacted. As a result, the base liquid is blended with microorganisms and solid nanoparticles to provide the necessary bioconvection stability. Furthermore, it has been assumed that the fluid contains gyrotactic bacteria. The fluid microorganisms gravitate towards the light. Gyrotactic phenomena, or movement against gravity, are made possible by the “bottom heavy” bulk microorganism, which orients their bodies. The existence of microorganisms is advantageous for the suspension of the nanoparticles. The motion of microorganisms has been taken, irrespective of that of the nanoparticles, to ensure the stability of convection. The flow of a double-diffusive fluid across a stretching sheet containing gyrotactic microorganisms has not yet been investigated, and this study aims to fill that gap with the simplifying of boundary layer approximations of the leading expressions given by [23]:
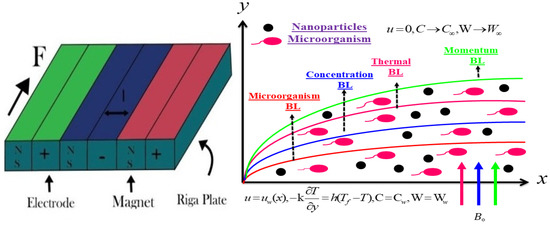
Figure 1.
Physical configuration of the flow problem.
3. Fluid Flow Problem
Cauchy Stress tensor for the Sutterby fluid [56,57]
Sutterby viscosity model is represented as
where n, , , are described as power law index, zero share rate viscosity, and time material constant.
Using Equation (2) in Equation (1), we have
The governing equation of the following form [23]
where u and v are velocity components in the x and y- directions. represents kinematic viscosity of the fluid, represents kinematic viscosity of the fluid, represents the density of the fluid, represents thermal diffusivity, is the concentration, represent Brownian diffusion and thermophoretic diffusion, denotes volumetric expansion, represents the microorganism coefficient, and fluid relaxation time,
In the above equations, the terms are stated as
The relevant boundary conditions are assumed to be the form
where can be expanded as follows:
Replacing Equation (12) into Equation (13),
Introducing the similarity variables [24]
Using Equation (15), Equations (4)–(6) become
The corresponding boundary conditions are
where is the Modified Hartmann number; is the Reynolds number; is the Deborah number; is the Radiation parameter; is the Prandtl number; is the Brownian motion parameter; is the Thermophoresis parameter; is the Schmidt number; is the Biot number; is the Peclet number; is the Bio convection Lewis number; is the Chemical reaction; is the Magnetic number.
The thermo-fluidic quantities of engineering interest in this study are skin friction , heat transfer rate , mass transfer rate , and motile density .
where surface shear stress, surface heat flux, surface mass flux, and motile density are given by the following expressions:
The dimensionless form of the above parameters is expressed as
Here, is the local Reynolds number.
4. Entropy Generation Analysis
Entropy generation with Sutterby fluid is communicated as [39]:
From Equation (23) the entropy production consists of some terms.
The first term represents heat transfer, the second-term fluid friction, and the third to sixth terms represent diffusive irreversibility. The significance of entropy production can be written as
Using Equation (15) the rate of entropy production with Sutter by Equation (23) can be converted
The Bejan number is defined as the ratio over the entropy generation with heat transport and the total entropy production , and it can be written as:
5. Homotopy Expression
HAM was used to investigate the explicit and analytic solutions of Equations (16)–(19) [51]. This analytical technique is quite effective and flexible in solving the parabolic-type boundary value problems of any order, is unconditionally stable, and attains remarkable accuracy. Taking the initial guesses and the linear operators as
with the property
in which are the constants.
6. The Zeroth Order Formulation
For and , the results are achieved
7. The mth Order Formulation
The order deformation can be presented in the following forms
Boundary conditions are
where
The general solutions are
in which are the special solution.
8. Convergence of Homotopy Solutions
These parameters are the converging control of the desired series solution. For the function to seek the permissible values to obtain the 25th and 30th order. Figure 1, Figure 2, Figure 3 and Figure 4 specify that the range of The series converges in the entire region of when . Table 1 indicates the convergence solution of HAM versus different order of approximations.
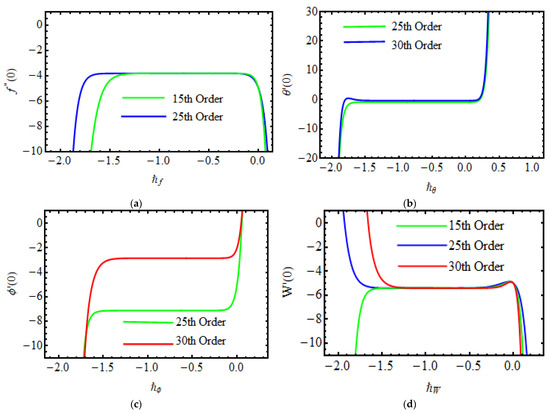
Figure 2.
Plots of (a) the curve of (b) the curve of (c) the curve of (d) the curve of .
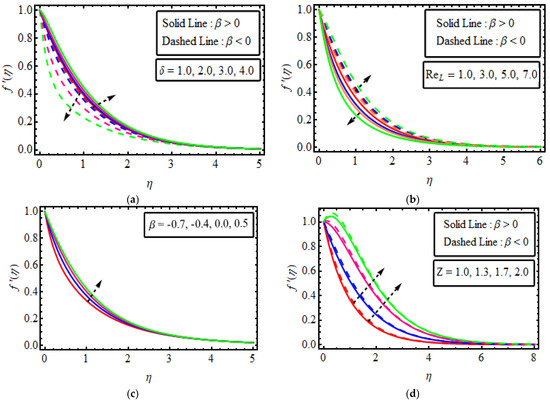
Figure 3.
(a–d). The impact of numerous variables (a) (b) (c) (d) .
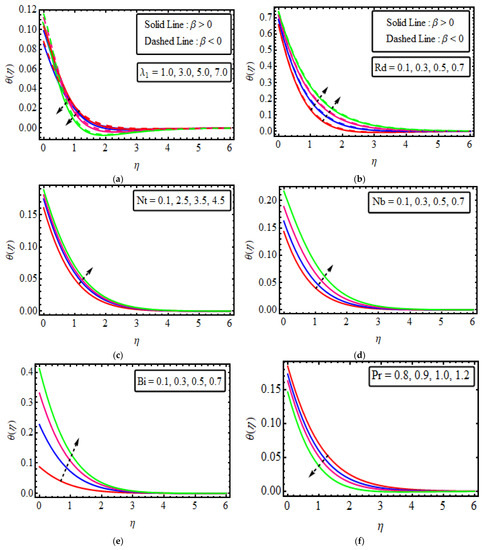
Figure 4.
(a–f). The impact of numerous variables (a) (b) (c) (d) (e) (f) .

Table 1.
Convergence solutions of HAM for different order of approximations when .
9. Results and Discussion
The system of Equations (16)–(19) subject to the boundary conditions (20) has been tackled through the analytical technique known as the Homotopy analysis method (HAM) for distinct parameters that emerged in the analytical simulation. To discuss the performance of physical significance against the velocity field , temperature distribution , concentration field , motile microorganism profile , entropy production, Bejan number, as well as skin friction, Nusselt number, Sherwood number and motile density microorganism, are delineated in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. Table 2 verifies with Ali and Zaib [55], and found a good agreement.
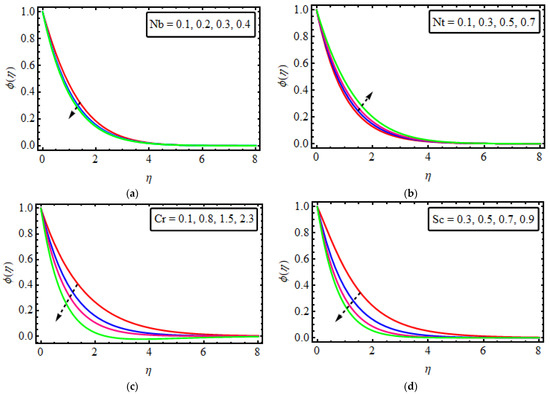
Figure 5.
(a–d) The impact of numerous variables (a) (b) (c) (d) .
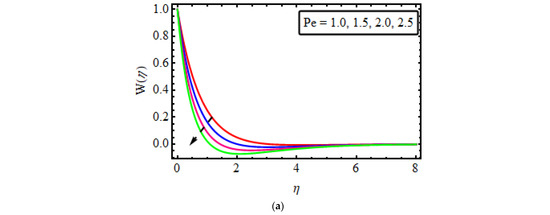
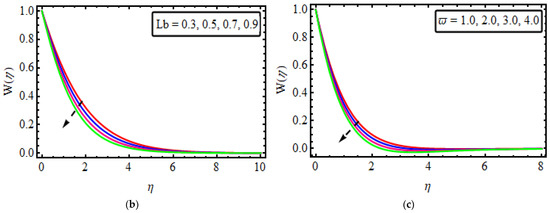
Figure 6.
(a–c) The impact of numerous variables (a) (b) (c) Cr (d) Sc.
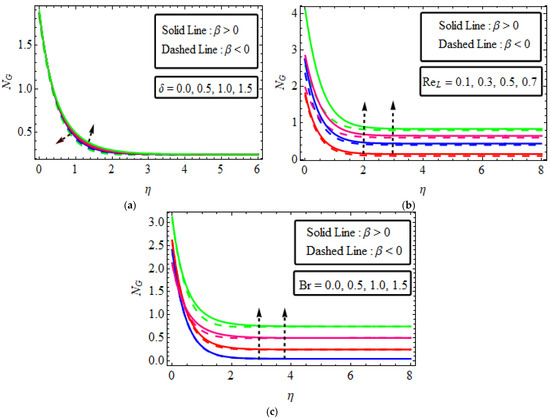
Figure 7.
(a–c) The impact of numerous variables (a) (b) (c) .
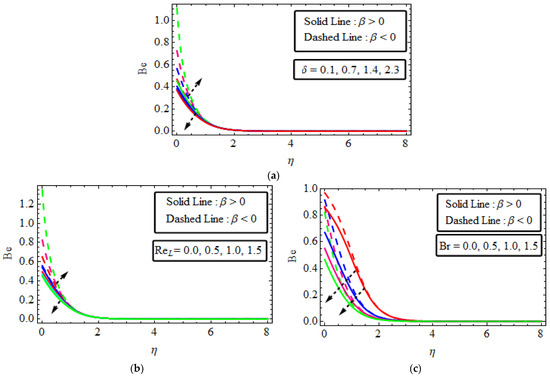
Figure 8.
(a–c) The impact of numerous variables (a) (b) (c) .
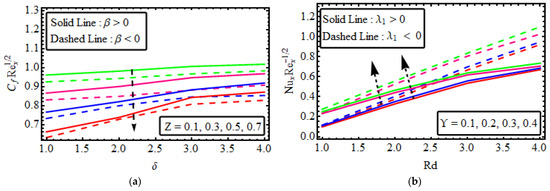
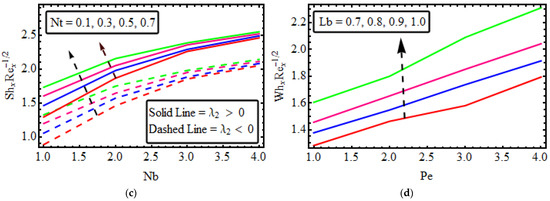
Figure 9.
(a–d) Variation in numerous variables (a) (b) (c) (d) .

Table 2.
Numerical outcomes of When Pr = Sc = 10, Bi = 0.1.
10. Results and Discussion
The system of Equations (16)–(19) subject to the boundary conditions (20) has been tackled through the analytical technique known as the Homotopy analysis method (HAM) for distinct parameters that emerged in the analytical simulation. To discuss the performance of physical significance against the velocity field , temperature distribution , concentration field , motile microorganism profile , entropy production, Bejan number, as well as skin friction, Nusselt number, Sherwood number and motile density microorganism, are displayed graphically and in tabular form. Table 2 verifies with Ali and Zaib [58], and found a good agreement.
11. Velocity Field
The effects of different numerous parameters on velocity distribution are discussed in Figure 3a–d. Figure 3a shows that for pseudoplastic, the velocity of fluid lessens with the larger value of Deborah number , and the velocity field is enhanced for the rising value of Deborah number for the two cases of when and . This result is shown to be the same as in F. Ali et al. [56]. Figure 3b shows that the velocity curve shortens with increasing values of the Reynold number in the case of ; a higher , the more diminished the viscous force and hence fluid depreciates for the pseudoplastic fluid. Thus, for shear thickening fluid, the velocity field enhances as increasing the impact of the values of in the two cases. As shown in the figure, the velocity for both values shows mixed behaviour with increasing fluid parameters. The Reynold number described the proportion of inertial to viscous forces due to this inertial force being prominent for the two cases of velocity magnitude when and increases when . Figure 3c manifests the effect of the enhanced power-law index parameter, resulting in a better velocity profile for shear thickening fluid. Figure 3d demonstrates the significance of the Hartmann number on velocity fluid field for the two cases of and . It has been revealed that with changes in the strength of the velocity of the fluid escalates in both cases. Physically, an increment in corresponds to enhancing the external electric field that constructs wall-parallel Lorentz force. Therefore rises. The velocity is more pronounced for pseudo-plastic fluid than a fluid dilatant fluid with increasing for the shear-thinning as well as shear-thickening fluid.
12. Temperature Field
Figure 4a–f plotted the consequences of temperature against different values of various involved parameters. The thermal relaxation time parameter causes are demonstrated in Figure 4a. The thermal relaxation parameter tends to decrease the temperature curve in both cases of dilatants and pseudoplastic. It impacts the strength of heat transfer. So, the dissimilar decayed impact of on the temperature field takes place away from the surface. Figure 4b reveals the inclination of for specific values of thermal radiation parameters fo and The temperature of the fluid increases due to the enlargement in the radiation parameter in both cases. Physically, by increasing the radiation parameter more energy is added to the system, which uplifts the kinetic energy of molecules and also causes a rise in the temperature profile. Figure 4c shows that temperature increases with the increments in the values of . Thermophoresis is a phenomenon where small particles diffuse under the effect of a temperature gradient. An increase in the value of the thermophoresis parameter sets the nanoparticle in motion, and thus on the hotter side, the momentum of the nanoparticles rises. Due to the rise in the momentum, nanoparticles transfer their kinetic energy in the direction of the cooler side, and thus the region gets warmed up quickly; i.e., the temperature of the fluid is increased. Figure 4d also suggests that the nanofluid temperature rises with the increasing value of the Brownian motion parameter , and the opposite effect is examined in the Figure 4e. The reason behind this is that Brownian motion is the irregular movement of the particles suspended in the fluid. The temperature of the fluid increases as a result of the random collision of particles suspended in the liquid, which further leads to an expected improvement in the temperature profile Figure 4e depicts the impact of the Biot number . These figures point out that the temperature field is boosted by enhancing the value of the Biot number. It seems that the value of the Biot number is directly proportional to the temperature, as the higher value of corresponds to greater convective heating along the sheet, which increases the temperature gradient on the sheet. Therefore, the thickness of the boundary layer and temperature are increasing functions of the Biot number. Figure 4f display variations of the Prandtl number against . Temperature is restrained against higher . Basically, the Prandtl number refers to thermal diffusivity. Larger indicates lower thermal diffusivity, which causes the temperature to decompose.
13. Concentration Field
The outcomes of different leading parameters are presented in Figure 5a–d. Figure 5a is designed to show the characteristics of on . The concentration distribution is depleted by rising . The reason behind the decrease in the concentration field is the relation of Brownian motion with the Brownian diffusion coefficient which is responsible for decreasing the concentration field. The influence of the thermophoresis variable is rendered in Figure 5b. It can be seen that increasing values of the thermophoresis parameter enhances mass concentration. This is because the increase in corresponds to the increase in thermophoretic diffusion coefficient enhancing mass concentration. The influence of chemical reaction on the profile of concentration is shown in Figure 5c. The enhanced values result in a fluid particle breakthrough near the surface, which reduces the concentration and the corresponding boundary layer thickness. The further rate of inclination is slower in the presence of the chemical reaction rate parameter. The Schmidt number outcomes for concentration are displayed in Figure 5d. A depreciation in concentration arises with greater due to the reduction of mass diffusion. In the physical phenomenon of sight, an increase in the lessens the molecular diffusivity and results in the declination of the concentration gradient.
14. Microorganism Field
The effect of different influential variables on the microorganism’s field is shown in Figure 6a–c. Variations in motile microorganisms against the Lewis number for various values are seen in Figure 6a. The reduces the density of microorganisms. Actually, have an opposite trend with thermal diffusivity, as an escalation in decreases the thermal diffusivity with regard to a decline in motile density. Figure 6b points out the behaviour of the Peclet number in the microorganism field. The motile density profile decreases with an increase in . Actually, the Peclet number is the quotient of heat transfer by fluid motion to the heat transfer through thermal conduction, and the microorganism’s diffusivity is in an inverse relationship with the Peclet number. That is why the motile density field is on the decline for large estimates of The relationship between the microorganisms’ difference parameter and the motile density is present in Figure 6c. It has been noticed that motile density shrinks for larger . In fact, improving the values escalates the concentration of microorganisms in the ambient concentration, and so declines.
15. Entropy Generation
Figure 7a–c examined the performance of numerous variable parameters and entropy production . Figure 7a sketched the effect of Deborah’s number versus the entropy generation number . This shows an enhancement in entropy production close to the wall for dilatant , and deduction close to the wall for pseudo-plastic fluid . The increasing influence of the Reynolds number in entropy generation studied for dilatant and pseudoplastic fluids is plotted in Figure 7b. The disparity has been plotted in Figure 7c. Entropy generation is boosted with increasing values of in both cases. Subsequently, attributes a proportion of the free heat through viscous heating to the molecular condition. Therefore, heat is created in the system for increased values of while the disorderliness of Re also rises in the system, which increases the entropy of the system.
16. Bejan Number
The performance with the variations in the variables , and , plotted in Figure 8a–c. Figure 8a,b signify the behaviour of the physical parameters Deborah’s number and the Reynold number on the Bejan number. It is shown that the Bejan number declines as the larger values of Deborah’s and the Reynold number for shear-thickening and upsurge in both numbers for shear-thinning fluid. Furthermore, Figure 8c shows that the influence of the Bejan number is reduced and with the growing values of Actually, the thermal conductivity of the fluid declines with the rise in , so that a greater amount of heat is transmitted through the fluid. The parameter characterizes the heat generated by viscous dissipation. So as a result, the Bejan number is reduced via the uplift value of the Brickman number .
17. Physical Entitles
Figure 9a shows that the skin friction coefficient is deformed in both cases for the larger values of the parameter when and . The influence of the non-Newtonian nanofluid parameter on the Nusselt against thermal radiation are highlighted in Figure 9b. The heat transport gradient upsurges with rises in the thermal radiation and heat source/sink parameters . The significance of and on the Sherwood number is intimated in Figure 9c. It is determined that there is an amplification in the Sherwood number for raised values of fluid parameters. Figure 9d elucidates the substantial rescaled density number of motile microorganisms. The rescaled density number of motile microorganisms is voluminous for higher variations of and . Figure 10a–d shows the 3D representation of the Skin, Nusselt, Sherwood and Motile density respectively.
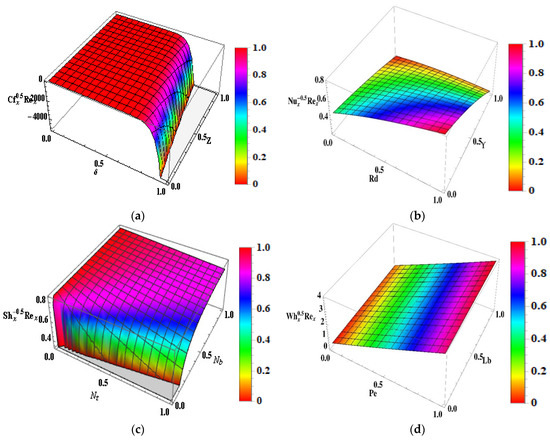
Figure 10.
(a–d) 3D graph (a) Skin friction for and (b) Nusselt number for and . (c) Sherwood number for and (d) Motile density for and .
The numerical estimation of drag friction has been given in Table 3. The larger the magnitude of , the lower the drag friction. Table 4 and Table 5 produce the data of heat and mass related to the diverse value of . Here it is illustrated that the magnitude of heat and mass transport is increased via a large value of for the Nusselt number and for the Sherwood number. Table 6 shows the variation of on the motile density profile. In Table 6, it is shown the motile density profile is the leading function .

Table 3.
Numerical outcomes for numerous values of .

Table 4.
Numerical outcomes of numerous values of .

Table 5.
Numerical outcomes f for numerous values of .

Table 6.
Numerical outcomes for numerous values of .
18. Streamline and Isotherm Line
Figure 11a,b exhibits the behaviour of the stream function for the current flow. The patterns show that the streamlines are more obscured and split into two sections pseudo-plastic and dilatant ; the shape is modest and fills the floe field. Figure 12a,b show the behaviour of the isotherm line for present flow for both cases.
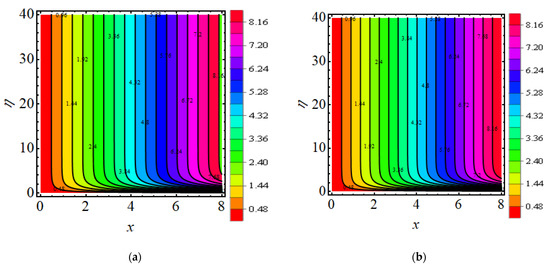
Figure 11.
(a,b) Streamline for (a) (b) .
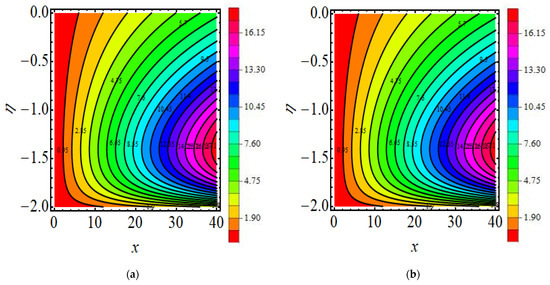
Figure 12.
(a,b) Isotherms lines (a) (b) .18. Major Outcomes.
This investigation examines MHD Sutterby nanofluid with Cattaneo–Christov Double Diffusion (CCDD) dual diffusion theory due to the Riga Plate, as well as the bioconvection of motile microorganisms; a chemical reaction is also analysed. Appropriately modified transformations are invoked to get a non-linear system of differential problems. The model under consideration consists of both gyrotactic microorganisms and nanoparticles. By using bio-convective flow, which is produced by the combined impacts of nanoparticles and buoyancy forces, microorganisms maintain the suspension of nanoparticles. Refs. [59,60,61,62,63] are extended in future with different flow assumptions. Along with Newtonian heating, the mechanics of Brownian motion and thermophoresis are also considered. The main findings of the current study are the following:
- The convergence of HAM solutions is ensured up to the 25th iteration.
- Deterioration and elevation behaviour in the momentum of fluid is manifested in relation to Deborah’s number and Reynold’s number when and .
- The velocity shows continuous improvement with increases in the Hartman number in cases of dilatant and pseudoplastic fluid.
- The growing estimate of the variable leads to increases in the dimensionless temperature field.
- Declining aptitude expressed in the concentration field against the Schmidt number and Prandtl number.
- A larger chemical reaction portrays a decline in the concentration, while the Biot number lead to the expansion in concentration.
- The microorganism field has deteriorated for the higher value of and microorganism difference parameter.
- The entropy generation number presented an increasing magnitude for large values of the Reynolds number and Brinkman number, for the case of pseudoplastic and dilatants fluid. Large values of the entropy generation number appear in the vicinity of the sheet due to high viscous effects.
- Enhancing the value of Deborah’s number and Reynold’s number results in Bejan’s profile decay in the case of dilatant fluid, while the opposite effect is observed in the case of shear-thinning.
- Skin fraction decelerated for the modified Hartman number but accelerated against the Nusselt number for the heat source/sink parameter and the Sherwood number for the Thermophoresis parameter .
- The density of motile microorganisms goes up with rising values of and
Author Contributions
Conceptualization, M.F.A. and A.Z.; methodology, M.F.A. and F.A.; software, A.Z.; validation, E.S.M.T.-E. and O.T.B.; formal analysis, K.G.; investigation, A.M.G.; resources, E.S.M.T.-E.; data curation, M.O.; writing—original draft preparation, A.Z.; writing—review and editing, M.O. and K.G.; visualization, A.M.G.; supervision, F.A. and N.B.K.; project administration, N.B.K. and M.F.A.; funding acquisition, E.S.M.T.-E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data available inside the research work.
Acknowledgments
The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4340474DSR08.
Conflicts of Interest
The authors declares no conflict of interest.
Abbreviations
| Constant | |
| Velocity components | |
| Similarity function for velocity | |
| Ambient temperature | |
| Wall constant temperature | |
| Fluid Temperature | |
| Microorganism concentration | |
| Dimensionless temperature | |
| Dimensionless concentration | |
| Ambient concentration | |
| Fluid concentration | |
| Power index number | |
| Deborah number | |
| Local Reynolds number | |
| Modified Hartmann number | |
| Magnetic Parameter | |
| Thermal Radiation | |
| Heat source/sink parameter | |
| Chemical reaction | |
| Thermal Relaxation parameter | |
| Concentration Relaxation parameter | |
| Thermophoresis parameter | |
| Brownian motion parameter | |
| Biot number | |
| Prandtl number | |
| Schmidt number | |
| Peclet number | |
| Lewis number | |
| Microorganism concentration difference parameter | |
| Mass diffusivity | |
| Thermophoresis diffusivity | |
| Current density | |
| Skin friction coefficient | |
| Nusselt number | |
| Sherwood number | |
| Microorganism density number | |
| Thermal conductivity of the fluid | |
| Brickman number | |
| Local volumetric entropy generation rate | |
| Entropy number | |
| Bejan number | |
| Ratio of the effective heat capacity | |
| Similarity variable | |
| Fluid Density | |
| Dynamic viscosity | |
| Ambient condition |
References
- Choi, S.U.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. in development and applications of non-Newtonian flow. ASME 1995, 66, 99–105. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmad, S.; Mehmod, K.; Sagheer, M. Effects of inclintion angle on mixed convetivenanofluid flow in a double lid-driven cavity with discrete heat sources. Int. J. Heat Mass Transf. 2017, 106, 847–860. [Google Scholar] [CrossRef]
- Hussain, S.; Ahmed, S.E.; Saleem, F. Impact of periodic magnetic field on entropy generation and mixed convection. J. Thermophys. Heat Transf. 2018, 32, 999–1012. [Google Scholar] [CrossRef]
- Haq, F.; Saleem, M.; Rahman, M.U. Investigation of natural bio-convective flow of cross nanofluid containing gyrotacticmicroorganisems subject to activation energy and magnetic field. Phys. Scr. 2020, 95, 105219. [Google Scholar] [CrossRef]
- Aldabesh, A.; Haredy, A.; Al-Khalid, K.; Khan, S.U.; Tlili, I. Darcy resistance flow of Sutterby nanofluid with microorganisms with applications of nano-biofuel cells. Sci. Rep. 2022, 12, 7514. [Google Scholar] [CrossRef]
- Mjankwi, M.A.; Masanja, V.G.; Mureithi, E.W.; James, M.N. Unsteady MHD flow of nanofluid with variable properties over a stretching sheet in the presence of thermal radiation and chemical reaction. Int. J. Math. Math. Sci. 2019, 2019, 7392459. [Google Scholar] [CrossRef]
- Shahid, A. The effectiveness of mass transfer in the MHD upper-convected Maxwell fluid flow on a stretched porous sheet near stagnation point: A numerical invstigation. Inventions 2020, 5, 64. [Google Scholar] [CrossRef]
- Rafique, K.; Alotaibi, H.; Ibrar, N.; Khan, I. Stratified flow of micropolarnanofluid over riga plate: Numerical analysis. Energies 2022, 15, 316. [Google Scholar] [CrossRef]
- Parvine, M.; Alam, M. Nnaofluid flow along the riga plate with electromagnetic field in a rotating system. AIP Conf. Proc. 2019, 2121, 070003. [Google Scholar]
- Abbas, T.; Ayub, M.; Bhatti, M.M.; Rashidi, M.M.; Ali, M.E.-S. Entropy Generation on Nanofluid Flow through a Horizontal Riga Plate. Entropy 2016, 18, 223. [Google Scholar] [CrossRef]
- Sannad, M.; Hussein, A.K.; Abidi, A.; Homod, R.Z.; Biswal, U.; Ali, B.; Kolsi, L.; Younis, O. Numeical study of MHD natural convection inside a cubical cavity loaded with copper-water nanofluid by using a non-homogeneous dynamic mathematical model. Mathematics 2022, 10, 2072. [Google Scholar] [CrossRef]
- Hayat, T.; Rashid, M.; Khan, M.I.; Alsaedi, A. Melting heat transferand induced magnetic field effects on flow of water based nanofluid over a rotating disk with variable thickness. Result Phys. 2018, 9, 1618–1630. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Waqas, M.; Alsaedi, A.; Khan, M.I. Radiative flow of micropolar nanofluid accounting thermophoresis and brownian moment. Int. J. Hydrogen Energy 2017, 42, 16821–16833. [Google Scholar] [CrossRef]
- Muhammad, R.; Khan, M.I.; Khan, N.B.; Jameel, M. Magnetohydrodynamics (MHD) radiated nanomaterial viscous material flow by a curved surface with second order slip and entropy generation. Comput. Methods Programs Biomed. 2020, 189, 105294. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Khan, M.I.; Hayat, T.; Khan, M.I.; Alsaedi, A. Entropy genertion optimization and unsteady squeezing flow of viscous fluid with five different shapes of nanoparticles. Colloids Surf. A Physicochem. Eng. Asp. 2018, 554, 197–210. [Google Scholar] [CrossRef]
- Reddy, S.R.R.; Reddy, B.A.P.; Rashed, A.M. Activation energy impact on chemically reacting Eyring-Powell Nanofluid flow over a stretching cylinder. Arab. J. Sci. Eng. 2020, 45, 5227–5242. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Liu, X.; Iqbal, T.; Zulqarnain, R.M.; Javid, M. A comparative study of unsteady MHD Falkner–Skan wedge flow for non-Newtonian nanofluids considering thermal radiation and activation energy. Chin. J. Phys. 2022, 77, 1625–1638. [Google Scholar] [CrossRef]
- Abbasi, A.; Farooq, W.; Tag-ElDin, E.S.M.; Khan, S.U.; Khan, M.I.; Guedri, K.; Elattar, S.; Waqas, M.; Galal, A.M. Heat Transport Exploration for Hybrid Nanoparticle (Cu, Fe3O4)-Based Blood Flow via Tapered Complex Wavy Curved Channel with Slip Features. Micromachines 2022, 13, 1415. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Muhammad, T.; Hussain, S.; Khan, I. Thermal effect on bioconvection flow of Sutterby nanofluid between two rotating disks with motile microorganisms. Case Stud. Therm. Eng. 2021, 26, 101136. [Google Scholar] [CrossRef]
- Yahya, A.U.; Salamat, N.; Habib, D.; Ali, B.; Hussain, S.; Abdal, S. Implication of Bio-convection and Cattaneo-Christov heat flux on Williamson Sutterby nanofluid transportation caused by a stretching surface with convective boundary. Chin. J. Phys. 2021, 73, 706–718. [Google Scholar] [CrossRef]
- Fayyadh, M.M.; Naganthran, K.; Basir, M.F.M.; Hashim, I.; Roslan, R. Radiative MHD Sutterby Nanofluid Flow Past a Moving Sheet: Scaling Group Analysis. Mathematics 2020, 8, 1430. [Google Scholar] [CrossRef]
- Gowda, J.P.R.; Kumar, R.N.; Rauf, A.; Prasannakumara, B.C.; Shehzad, S.A. Magnetized flow of sutterbynanofluid through cattneo-christov theory of heat diffusion and stefan blowing condition. Appl. Nanosci. 2021. [Google Scholar] [CrossRef]
- Ali, F.; Loganathan, K.; Prabu, E.; Eswaramoorthi, S.; Faizan, M.; Zaib, A.; Chaudhary, D.K. Entropy minimization o Sutterby nanofluid past a stretching surface with swimming of gyrtactic microorganisms and nanoparticles. Math. Probl. Eng. 2022, 2022, 5759671. [Google Scholar]
- Hayat, T.; Masood, F.; Qayyum, S.; Alsaedi, A. Sutterby fluid flow subject to homogeneous-heterogeneous reactions and nonlinear radiation. Phys. A Stat. Mech. Its Appl. 2019, 123439. [Google Scholar] [CrossRef]
- Fujii, T.; Miyatake, O.; Fujii, M.; Tanaka, H.; Murakami, K. Natural convective heat transfers from a vertical isothermal surface to a non-Newtonian Sutterby fluid. Int. J. Heat Mass Transf. 1973, 16, 2177–2187. [Google Scholar]
- Bilal, S.; Sohail, M.; Naz, R.; Malik, Y.M. Dynamical and optimal procedure to analyse the exhibition of physical attribute imparted by Sutterby magneto nano fluid in Darcy medium yield by axially stretched cylindr. Can. J. Phys. 2019, 98, 1–10. [Google Scholar] [CrossRef]
- Khan, I.M.; Waqas, H.; Farooq, U.; Khan, S.U.; Chu, Y.M.; Kadry, S. Assessment of bioconvection in magentizedSutterbynanofluid configured by a rotating disk: A numerical approach. Mod. Phys. Lett. B 2021, 35, 2150202. [Google Scholar] [CrossRef]
- Sohail, M.; Naz, R. Modified heat and mass transmission models in the magnetohydrodynamic flow of Sutterby fluid flow in stretching cylinder. Phys. A Stat. Mech. Its Appl. 2020, 549, 124088. [Google Scholar] [CrossRef]
- Saif-ur-Rehman; Mir, N.A.; Alqarni, M.S.; Farooq, M.; Malik, Y.M. Analysis of heat generation/absorption in thermally stratified Sutterby fluid flow with Cattaneo-Christov theory. Microsyst. Technol. 2019, 25, 3365–3373. [Google Scholar] [CrossRef]
- Usman; Lin, P.; Ghaffari, A. Heat and mass transfer in a steady flow of Sutterby nanofluid over the surface of a stretching wedge. Phys. Scr. 2021, 96, 065003. [Google Scholar] [CrossRef]
- Song, Y.-Q.; Waqas, H.; Al-Khaled, K.; Farooq, U.; Khan, S.U.; Khan, M.I.; Yu-Ming, C.; Qayyum, S. Bioconvection analysis for Sutterbynanofluid over an axially stretched cylinder with melting heat transfer and variable thermal features: A Marangoni and solutal model. Alex. Eng. J. 2021, 60, 4663–4675. [Google Scholar] [CrossRef]
- Khan, I.M.; Qayyum, S.; Hayat, T. Stratified flow of Sutterby fluid homogeneous-heterogeneous reaction and Cattaneo-Christov heat flux. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 2977–2992. [Google Scholar] [CrossRef]
- Kuznestov, V.A.; Nield, D.A. Natural convective boundary layer flow of a nanofluid past a verticle plate. Int. Therm. Sci. 2010, 49, 243–247. [Google Scholar]
- Kuznetsov, A.V. The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 2010, 37, 1421–1425. [Google Scholar] [CrossRef]
- Kotha, G.; Kolipaula, V.R.; Rao, V.S.M.; Penki, S.; Chamkha, J.A. Internal heat generation on bioconvection of an MHD nanofluid flow due to gyrotactic microorganisms. Eur. Phys. J. Plus 2020, 135, 135–600. [Google Scholar] [CrossRef]
- Siddiq, K.M.; Ashraf, M. Bioconvection of micropolar nanofluid with modified cattaneo-christov theories. Adv. Mech. Eng. 2020, 12, 1–11. [Google Scholar] [CrossRef]
- Bagh, A.; Sajjad, H.; Yufeng, N.; Liaqat, A.; Ul Shabih, H. Finite element simulation of bioconvection and cattaneo-Christov effects on micropolar based nanofluid flow over a vertically stretching sheet. Chin. J. Phys. 2020, 68, 654–670. [Google Scholar]
- Azam, M.; Mahbood, F.; Khan, M. Bioconvection and activation energy dynamisms on radiative sutterby melting nanomaterial with gyrotactic microorganism. Case Stud. Therm. Eng. 2022, 30, 101749. [Google Scholar] [CrossRef]
- Khashi’ie, N.S.; Arifin, N.M.; Pop, I.; Nazar, R. Dual solutions of bioconvection hybrid nanofluid flow due to gyrotactic microorganisms towards a vertical plate. Chin. J. Phys. 2021, 72, 461–474. [Google Scholar] [CrossRef]
- Azam, M. Bioconvection and nonlinear thermal extrusion in development of chemically reactive Sutterbynano-material due to gyrotactic microorganisms. Int. Commun. Heat Mass Transf. 2022, 130, 105820. [Google Scholar] [CrossRef]
- Hayat, T.; Inayatullah, A.; Alsaedi, A. Development of bioconvection flow of nano-material with melting effects. Chaos Solitons Fractals 2021, 148, 111015. [Google Scholar] [CrossRef]
- Reddy, C.S.; Ali, F.; Ahmed, M.F.A.F. Aspect on unsteady for MHD flow of cross nanofluid having gyrotactic motile microorganism due to convectively heated sheet. Int. J. Ambient. Energy 2021. [Google Scholar] [CrossRef]
- Sarkar, S.; Kumar, T.; Ali, A.; Das, S. Themo-bioconvection of gyrotactic microorganisms in a polymer solution near a perforated Riga plate immersed in a DF medium involving heat radiation, and Arrhenius kinetics. Chem. Phys. Lett. 2022, 797, 139557. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Ahammad, N.A.; Din, E.M.T.E.; Gamaoun, F.; Awan, A.U.; Ali, B. Bio-Convection effects on prandtl hybrid nanofluid flow with chemical reaction and motile microorganism over a stretching sheet. Natl. Libr. Med. 2022, 12, 2174. [Google Scholar] [CrossRef]
- Ali, L.; Ali, B.; Ghori, M.B. Melting effect on Cattaneo–Christov and thermal radiation features for aligned MHD nanofluid flow comprising microorganisms to leading edge: FEM approach. Comput. Math. Appl. 2022, 109, 260–269. [Google Scholar]
- Gailitis, A.; Leilausis, O. On a possibility to reduce the hydro dynamical resistance of a plate in an electrode. Appl. Magnetohydrodyn. 1961, 12, 143–146. [Google Scholar]
- Islam, M.R.; Nasrin, S. Micropolar fluid flow along with an inclined Riga plate through a porous medium. Int. J. Heat Technol. 2021, 39, 1123–1133. [Google Scholar] [CrossRef]
- Nasrin, S.; Mondal, R.N.; Alam, M.M. Impulsively started horizontal Riga plate embedded in unsteady Casson fluid flow with rotation. J. Appl. Math. Phys. 2020, 8, 1861–1876. [Google Scholar] [CrossRef]
- Anjum, A.; Mir, N.A.; Farooq, M.; Javed, M.; Ahmad, S.; Malik, M.Y.; Alshomrani, A.S. Physical aspects of heat generation/absorption in the second grade fluid flow due to Riga plate: Application of Cattaneo-Christov approach. Result Phys. 2018, 9, 955–960. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.; Imtiaz, M.; Alsaedi, A. Squeezing flow past a Riga plate with chemical reaction and convective conditions. J. Mol. Liq. 2016, 225, 569–576. [Google Scholar] [CrossRef]
- Wahidunnisa, L.; Subbarayudu, K.; Suneetha, S. Effect of viscous dissipation over a Riga plate in a nanofluid with heat source/sink: A numerical study. Int. J. Tech. Innov. Mod. Eng. Sci. 2016, 4, 1124. [Google Scholar]
- Iqbal, Z.; Azhar, E.; Mehmood, Z.; Maraj, E.N. Melting heat transport of nanofludic problem over a Riga plate with erratic thickness: Use of Kaller Box scheme. Result Phys. 2017, 7, 3648–3658. [Google Scholar] [CrossRef]
- Iqbal, Z.; Azhar, E.; Mehmood, Z.; Maraj, E.N. Unique outcomes of internal heat generation and thermal deposition on viscous dissipative transport of viscoplastic fluid over a Riga plate. Commun. Theor. Phys. 2018, 69, 68–76. [Google Scholar] [CrossRef]
- Ganesh, N.V.; Al-Mdallal, Q.M.; Al Fahel, S.; Dadoa, S. Riga—Plate flow of γ Al2O3-water/ethylene glycol with effective Prandtl number impact. Heliyon 2019, 5, E01651. [Google Scholar] [CrossRef]
- Ali, F.; Padmavathi, T.; Hemalatha, B. Entropy minimization in Darcy Forchheimer on Sutterby nanofluid past a stretching surface with the swimming of gyrotactic microorganisms. Waves Random Complex Media 2022. [Google Scholar] [CrossRef]
- Rana, S.; Nawaz, M. Investigation of enhancement of heat transfer in Sutterby nanofluid using Koo-Kleinstreuer and Li (KKL) correlations and Cattaneo-Christov heat flux model. Phys. Scr. 2019, 94, 115213. [Google Scholar] [CrossRef]
- Ali, F.; Zaib, A. Unsteady flow of an Eyring-Powell nanofluid near stagnation point past a convectively heated stretching sheet. Arab. J. Basic Appl. Sci. 2019, 26, 215–224. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, K.; Khan, M.I.; Alsaedi, A. Theoretical investigation of chemically reactive flow of water based carbon nanotubes with melting heat transfer. Pramana-J. Phys. 2019, 92, 57. [Google Scholar] [CrossRef]
- Khan, M.W.A.; Khan, M.I.; Hayat, T.; Alsaedi, A. Numerical solution of MHD flow of power law fluid subject to convective boundary conditions and entropy generation. Comput. Methods Programs Biomed. 2020, 188, 105262. [Google Scholar] [CrossRef]
- Khan, M.I.; Qayyum, S.; Kadry, S.; Khan, W.A.; Abbas, S.Z. Theoretical investigations of entropy optimization in electro-magneto nonlinear mixed convective second order slip flow. J. Magn. 2020, 25, 8–14. [Google Scholar] [CrossRef]
- Waqas, M.; Dogonchi, A.S.; Shehzad, S.A.; Khan, M.I.; Hayat, T.; Alsaedi, A. Nonlinear convection and joule heating impacts in magneto-thixotropic nanofluid stratified flow by convectively heated variable thicked surface. J. Mol. Liq. 2020, 300, 111945. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F. Transportation of heat through Cattaneo-Christov heat flux model in non-Newtonian fluid subject to internal resistance of particles. Appl. Math. Mech. (Engl. Ed.) 2020, 41, 1157–1166. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).