Positioning Error Analysis and Control of a Piezo-Driven 6-DOF Micro-Positioner
Abstract
1. Introduction
2. Positioning Error Analysis
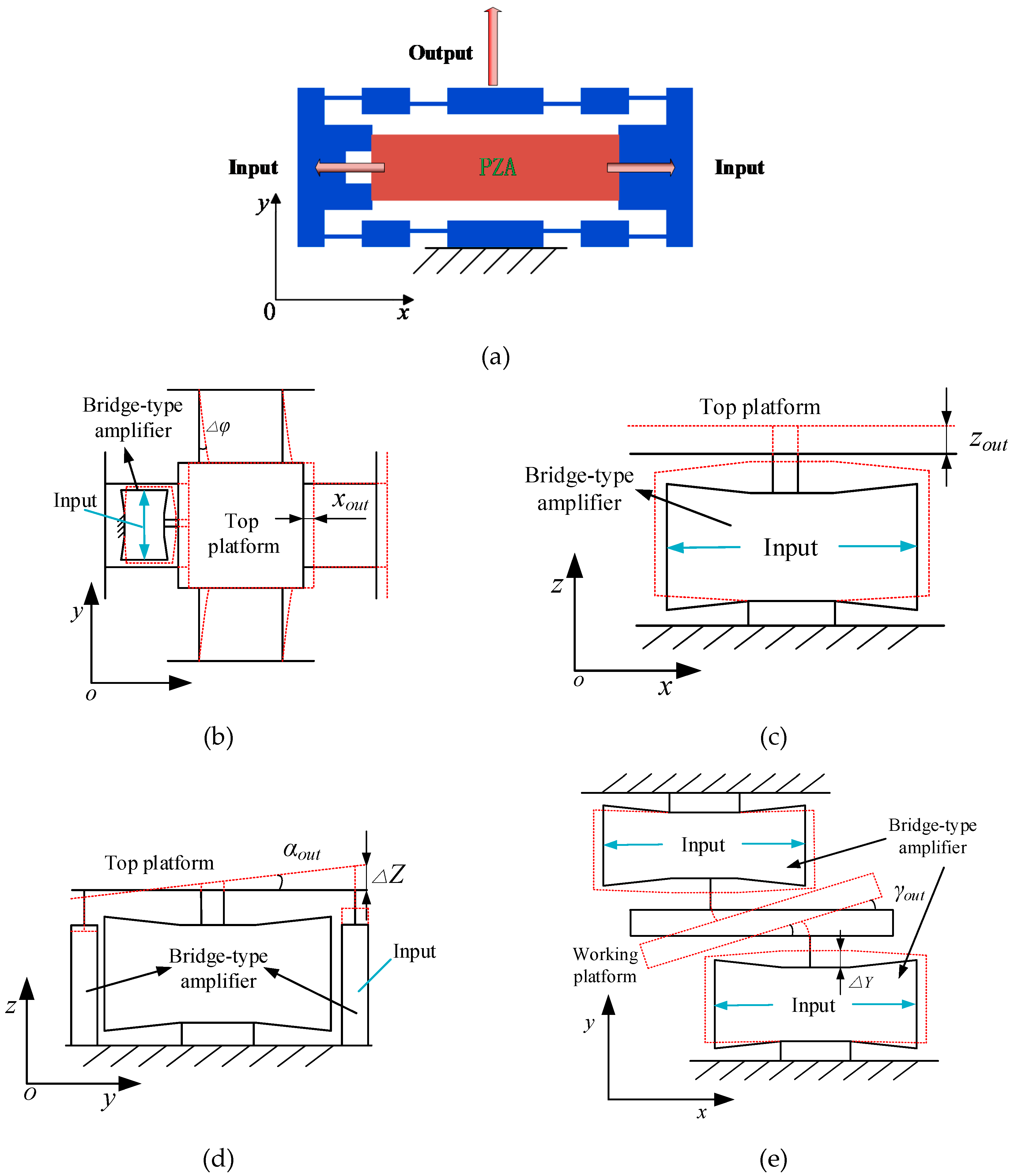
2.1. Mechanism Description
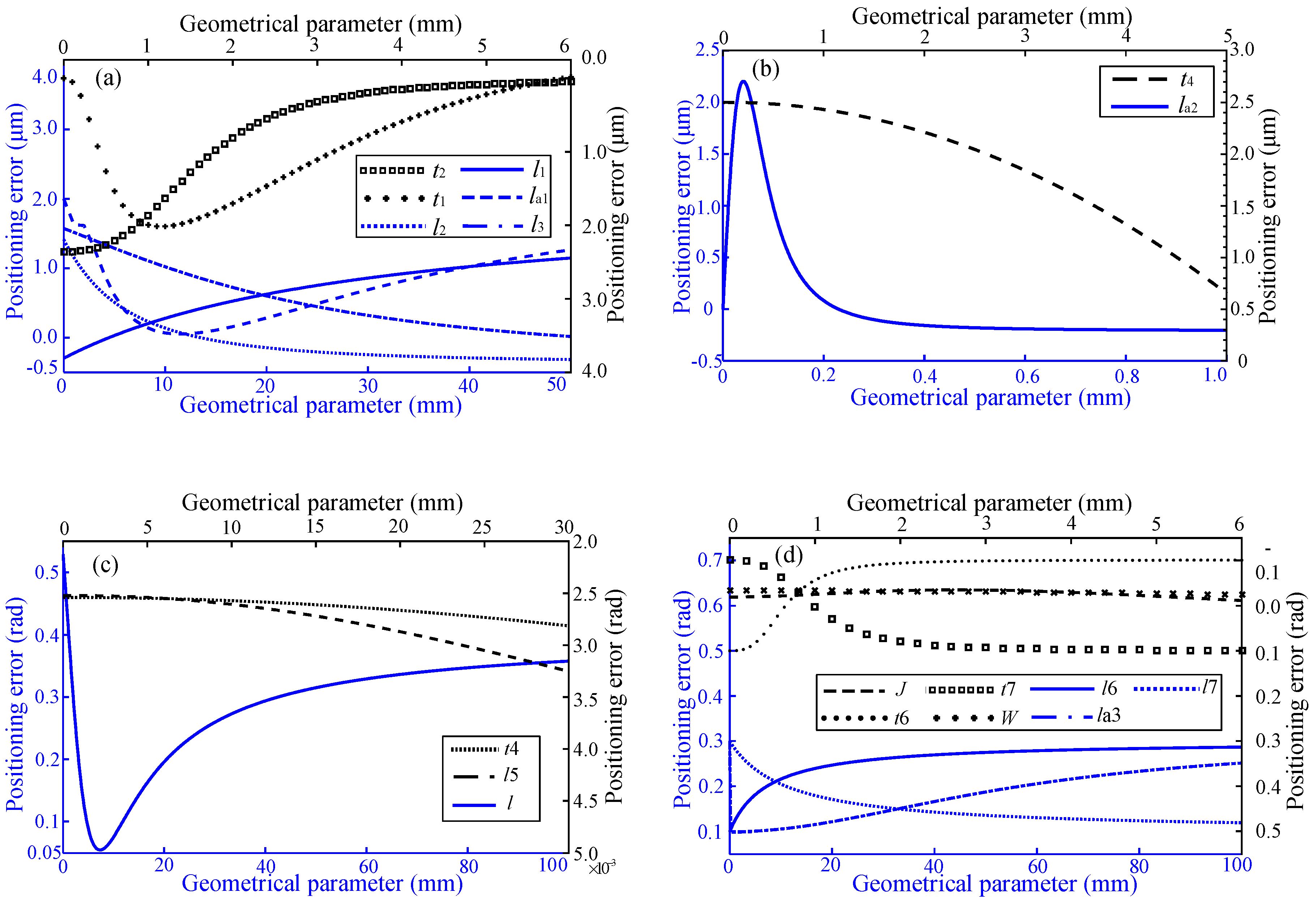
2.2. Modeling Positioning Error
3. Positioning Error Compensation Design
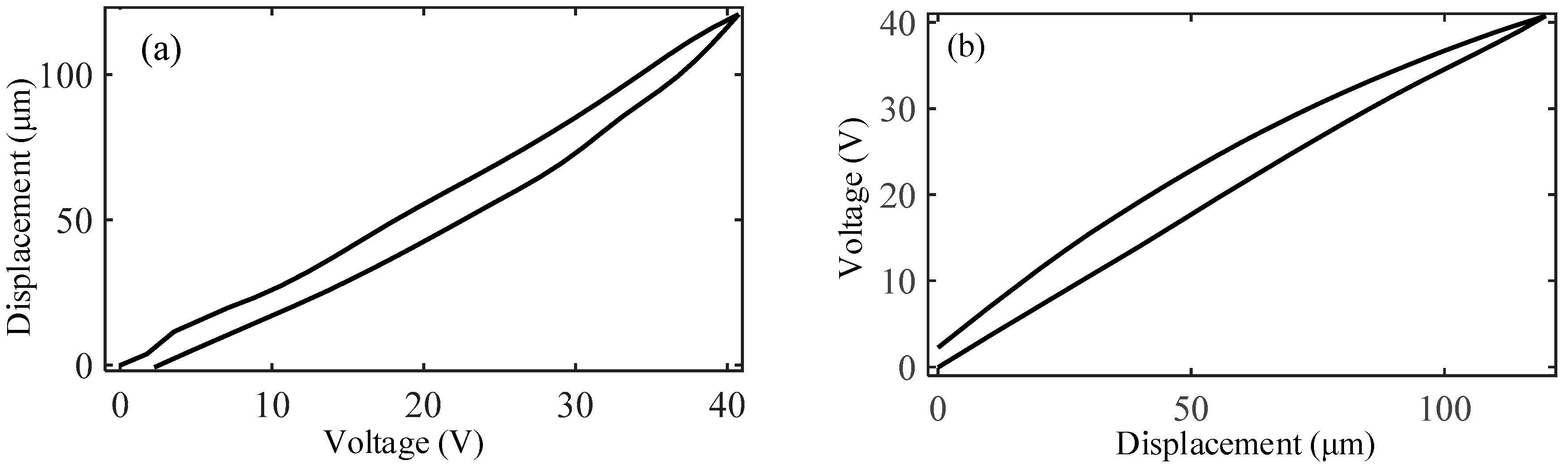
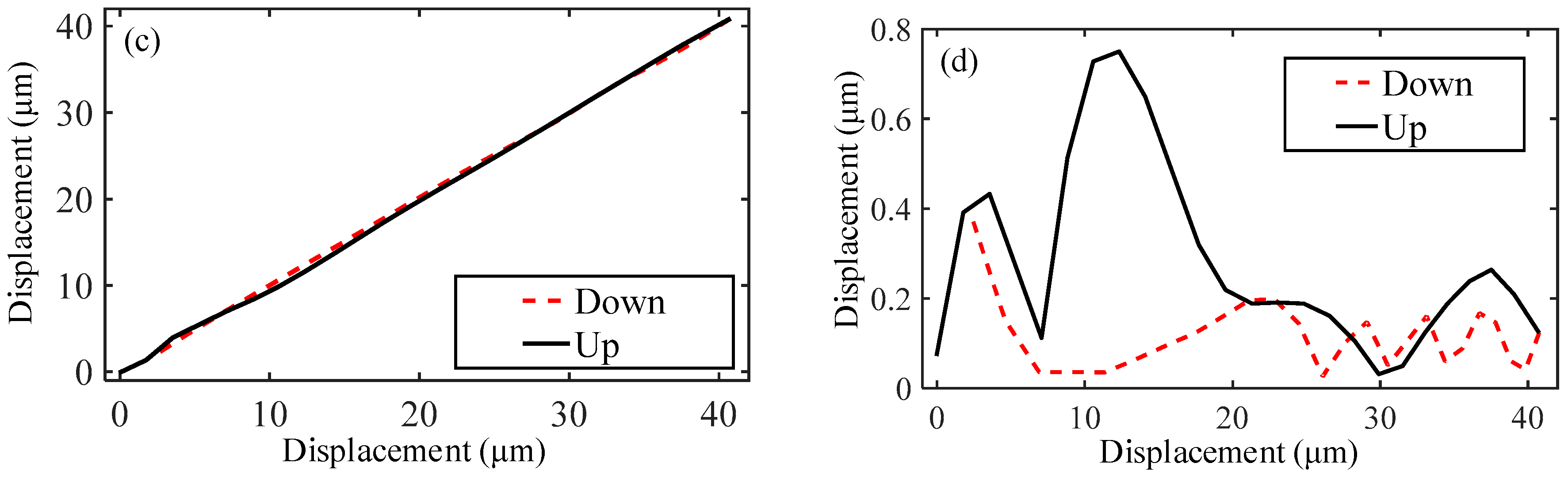
3.1. System Identification
3.2. Feedforward Compensation
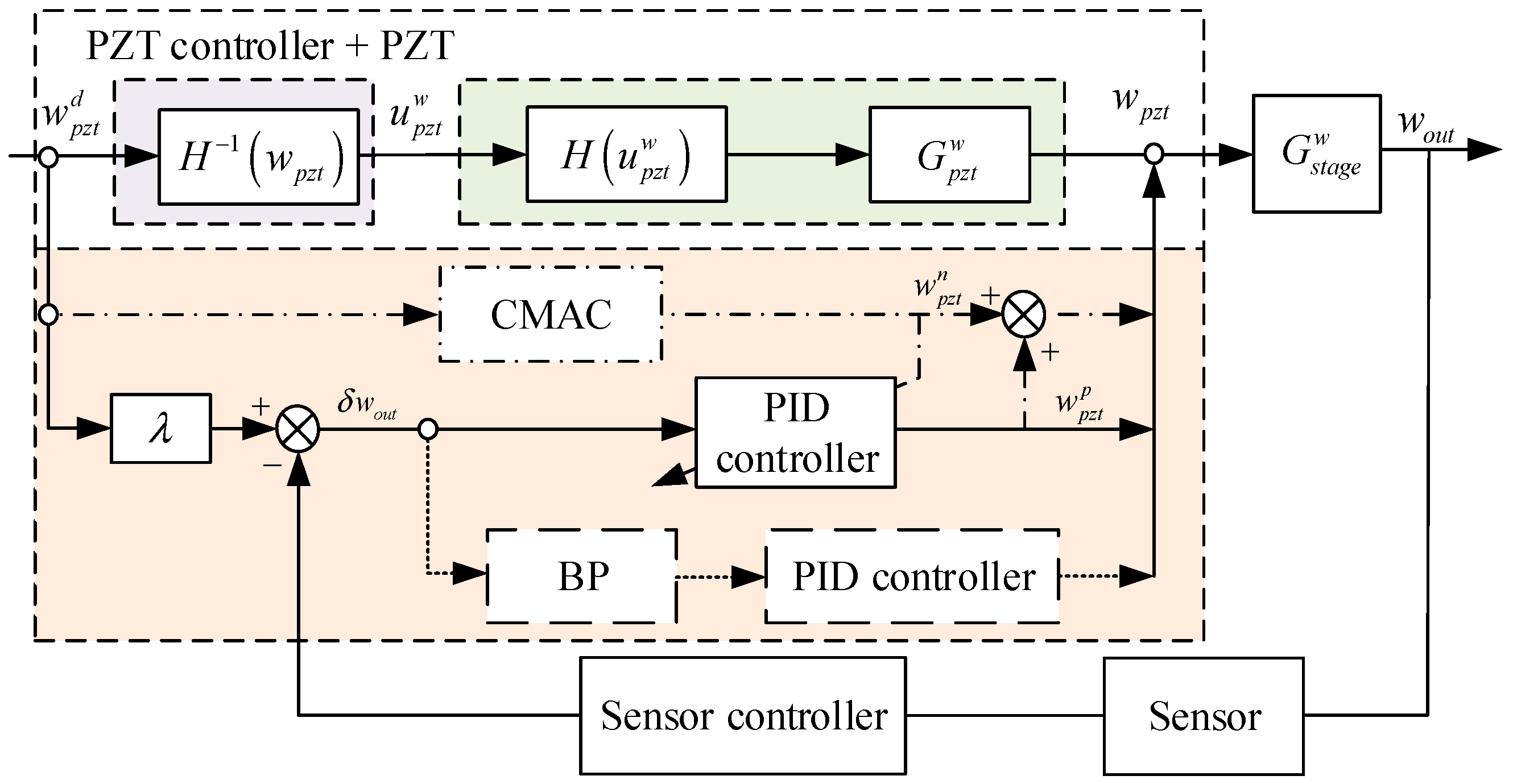
3.3. Feedforward Plus Feedback Compensation
4. Simulation, Experiment and Discussion
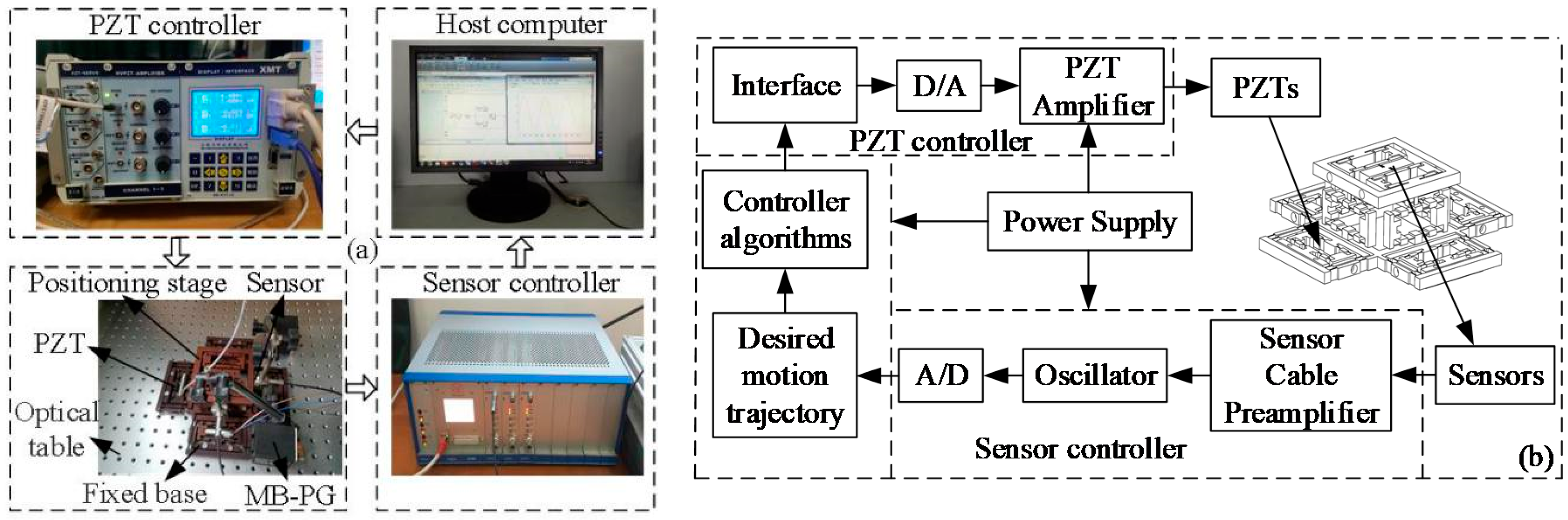
4.1. Experimental Setup
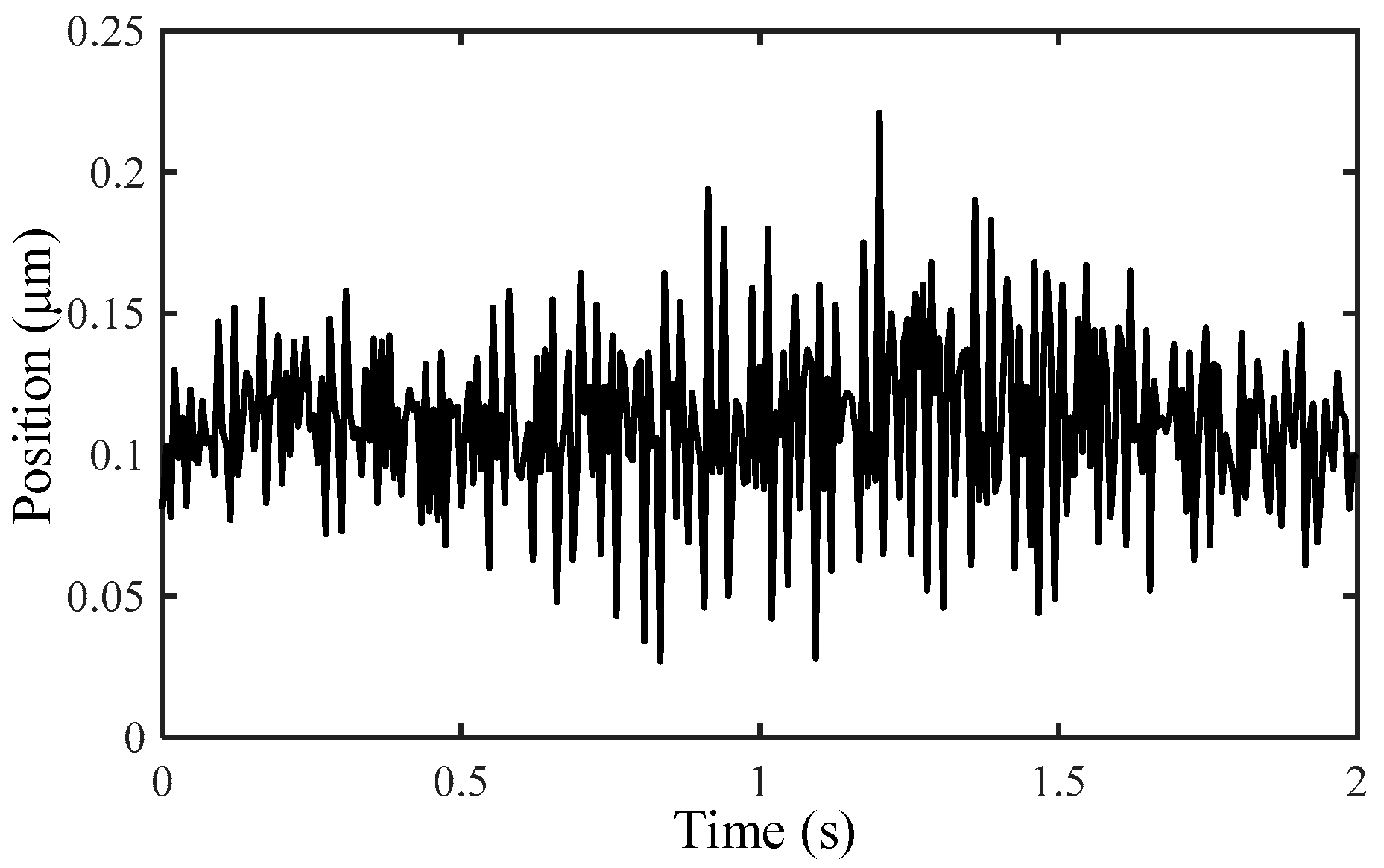
4.2. Experiments of Positioning Error
4.3. Simulated Testing of Error Compensation
4.4. Positioning Error Compensation Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Notations
| Notation | Explanation |
| Positioning error of the micro-positioner | |
| Positioning error of the driving stage | |
| Positioning error of the machining stage | |
| Positioning error of the measuring stage | |
| 6-DOF of the micro-positioner | |
| Top, middle and bottom platform of the compliant mechanism | |
| Implicit functions of motion | |
| Output displacement of micro-positioner | |
| Load output displacement of PZTs | |
| No-load output displacement of PZTs | |
| Driving error of PZTs | |
| Measuring error of the micro-positioner | |
| Positioning error of the micro-positioner | |
| Machining error of the geometric parameters | |
| Ideal linear ratio of the output displacement to the input voltage of PZTs | |
| Hysteresis nonlinear model of PZTs | |
| Preisach function | |
| Weighting function | |
| Hysteresis operator | |
| , | Up and down switching value of the input voltage |
| Input voltage of PZTs | |
| External voltage supply of PZT controller | |
| Equivalent mass of compliant mechanism | |
| Equivalent damping coefficient of compliant mechanism | |
| Equivalent stiffness of compliant mechanism | |
| Input stiffness of compliant mechanism | |
| Stiffness of PZT | |
| Driving force of PZTs | |
| Electric charge of PZTs | |
| Input driving force of compliant mechanism | |
| Number of piezoelectric ceramics of PZTs | |
| Amplification ratio of PZT controller | |
| Equivalent resistance of PZT controller | |
| Equivalent capacitance of PZT controller | |
| Transfer function of PZT | |
| Transfer function of the stage | |
| Transfer function of the entire system | |
| Expected output displacement | |
| Displacement amplification ratio of the compliant mechanism | |
| Load output displacement of PZTs of PID controller | |
| Time variable | |
| Proportional gain of PID controller | |
| Integral time of PID controller | |
| Derivative time of PID controller | |
| Input matrix of BP-PID controller | |
| Output matrix of BP-PID controller | |
| Weight matrix of the hidden layer | |
| Weight matrix of the output layer | |
| Threshold matrix of the hidden layer | |
| Threshold matrix of the output layer | |
| Activation functions of the hidden layer | |
| Activation functions of the output layer | |
| Binary selection vector of CMAC neural network | |
| Load output displacement of PZTs of CMAC neural network | |
| Generalization parameter of CMAC neural network | |
| Performance indicator function | |
| The maximum hysteresis error | |
| The maximum positioning error | |
| The root-mean-square error |
References
- Aktakka, E.E.; Woo, J.K.; Egert, D.; Gordenker, R.J.M.; Najafi, K. A microactuation and sensing platform with active lockdown for in situ calibration of scale factor drifts in dual-axis gyroscopes. IEEE/ASME Trans. Mechatron. 2014, 20, 934–943. [Google Scholar] [CrossRef]
- Thoma, F.; Goldschmidtböing, F.; Woias, P. A new concept of a drug delivery system with improved precision and patient safety features. Micromachines 2015, 6, 80–95. [Google Scholar] [CrossRef]
- Putra, A.S.; Huang, S.; Tan, K.K.; Panda, S.K.; Lee, T.H. Design, modeling, and control of piezoelectric actuators for intracytoplasmic sperm injection. IEEE Trans. Control Syst. Technol. 2007, 15, 879–890. [Google Scholar] [CrossRef]
- Habibullah, H.; Pota, H.R.; Petersen, I.R. A novel control approach for high-precision positioning of a piezoelectric tube scanner. IEEE Trans. Autom. Sci. Eng. 2017, 14, 325–336. [Google Scholar] [CrossRef]
- Linß, S.; Schorr, P.; Zentner, L. General design equations for the rotational stiffness, maximal angular deflection and rotational precision of various notch flexure hinges. Mech. Sci. 2017, 8, 29–49. [Google Scholar]
- Tseytlin, Y.M. Notch flexure hinges: An effective theory. Rev. Sci. Instrum. 2002, 73, 3363–3368. [Google Scholar] [CrossRef]
- Zelenika, S.; Munteanu, M.G.; De Bona, F. Optimized flexural hinge shapes for microsystems and high-precision applications. Mech. Mach. Theory 2009, 44, 1826–1839. [Google Scholar] [CrossRef]
- Valentini, P.P.; Pennestrì, E. Elasto-kinematic comparison of flexure hinges undergoing large displacement. Mech. Mach. Theory 2017, 110, 50–60. [Google Scholar] [CrossRef]
- Zhu, W.L.; Zhu, Z.; Guo, P.; Ju, B.F. A novel hybrid actuation mechanism based XY nanopositioning stage with totally decoupled kinematics. Mech. Syst. Sig. Process. 2018, 99, 747–759. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.; Ahn, D.; Gweon, D. Development of a nanoprecision 3-DOF vertical positioning system with a flexure hinge. IEEE Trans. Nanotechnol. 2013, 122, 234–245. [Google Scholar] [CrossRef]
- Cai, K.; Tian, Y.; Liu, X.; Fatikow, S.; Wang, F.; Cui, L.; Zhang, D. Shirinzadeh, B. Modeling and controller design of a 6-DOF precision positioning system. Mech. Syst. Sig. Process. 2018, 104, 536–555. [Google Scholar] [CrossRef]
- Lin, C.; Shen, Z.; Wu, Z.; Yu, J. Kinematic characteristic analysis of a micro-/nano positioning stage based on bridge-type amplifier. Sens. Actuators A 2018, 271, 230–242. [Google Scholar] [CrossRef]
- Shinno, H.; Yoshioka, H.; Taniguchi, K. A newly developed linear motor-driven aerostatic x-y planar motion table system for nano-machining. CIRP Ann. Manuf. Technol. 2007, 56, 369–372. [Google Scholar] [CrossRef]
- Zeng, Q.; Ehmann, K.F. Error modeling of a parallel wedge precision positioning stage. J. Manuf. Sci. Eng. 2012, 134, 061005. [Google Scholar] [CrossRef]
- Kang, R.; Sheng, X.; Wang, K. Volumetric error modelling, measurement, and compensation for an integrated measurement-processing machine tool. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 2477–2486. [Google Scholar]
- Cui, H.; Zhu, Z.; Gan, Z.; Brogardh, T. Kinematic analysis and error modeling of TAU parallel robot. Rob. Comput. Integr. Manuf. 2005, 21, 497–505. [Google Scholar] [CrossRef]
- Gatti, G.; Danieli, G. A practical approach to compensate for geometric errors in measuring arms: Application to a six-degree-of-freedom kinematic structure. Meas. Sci. Technol. 2007, 19, 015107. [Google Scholar] [CrossRef]
- Cui, C.; Feng, Q.; Kuang, C.; Cuifang, K.; Yusheng, Z.; Fenglin, Y. Development of a simple system for simultaneously measuring 6dof geometric motion errors of a linear guide. Opt. Express 2013, 21, 25805–25819. [Google Scholar]
- Zhang, B.; Cui, C.; Feng, Q.; Cui, C.; Chen, S.; Zhao, Y. Errors crosstalk analysis and compensation in the simultaneous measuring system for five-degree-of-freedom geometric error. Appl. Opt. 2015, 54, 458–466. [Google Scholar]
- Lee, J.I.; Huang, X.; Chu, P.B. Nanoprecision mems capacitive sensor for linear and rotational positioning. J. Microelectromech. Syst. 2009, 18, 660–670. [Google Scholar] [CrossRef]
- Ge, P.; Jouaneh, M. Generalized preisach model for hysteresis nonlinearity of piezoceramic actuators. Precis. Eng. 1997, 20, 99–111. [Google Scholar] [CrossRef]
- Oh, J.H.; Bernstein, D.S. Semilinear duhem model for rate-independent and rate-dependent hysteresis. IEEE Trans. Autom. Control 2005, 50, 631–645. [Google Scholar]
- Goldfarb, M.; Celanovic, N. Modeling piezoelectric stack actuators for control of micromanipulation. IEEE Control Syst. Mag. 1997, 17, 69–79. [Google Scholar]
- Xu, Q.; Li, Y. Dahl model-based hysteresis compensation and precise positioning control of an XY parallel micromanipulator with piezoelectric actuation. J. Dyn. Syst. Meas. Contr. 2010, 132, 558–564. [Google Scholar] [CrossRef]
- Gu, G.Y.; Yang, M.J.; Zhu, L.M. Real-time inverse hysteresis compensation of piezoelectric actuators with a modified prandtl-ishlinskii model. Rev. Sci. Instrum. 2012, 83, 65–83. [Google Scholar] [CrossRef]
- Wang, X.; Pommier-Budinger, V.; Reysset, A.; Gourinata, Y. Simultaneous compensation of hysteresis and creep in a single piezoelectric actuator by open-loop control for quasi-static space active optics applications. Control Eng. Pract. 2014, 33, 48–62. [Google Scholar] [CrossRef]
- Ru, C.; Sun, L. Hysteresis and creep compensation for piezoelectric actuator in open-loop operation. Sens. Actuators A 2005, 122, 124–130. [Google Scholar]
- Yen, P.L.; Yan, M.T.; Chen, Y. Hysteresis compensation and adaptive controller design for a piezoceramic actuator system in atomic force microscopy. Asian J. Control 2012, 14, 1012–1027. [Google Scholar] [CrossRef]
- Nguyen, P.B.; Sohn, J.W.; Choi, S.B. Position tracking control of a flexible beam using a piezoceramic actuator with a hysteretic compensator. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 2141–2153. [Google Scholar] [CrossRef]
- Sebastian, A.; Salapaka, S.M. Design methodologies for robust nano-positioning. IEEE Trans. Control Syst. Technol. 2005, 13, 868–876. [Google Scholar] [CrossRef]
- Rakotondrabe, M.; Haddab, Y.; Lutz, P. Quadrilateral modelling and robust control of a nonlinear piezoelectric cantilever. IEEE Trans. Control Syst. Technol. 2009, 17, 528–539. [Google Scholar] [CrossRef]
- Li, J.; Yang, L. Finite-time terminal sliding mode tracking control for piezoelectric actuators. Abst. Appl. Anal. 2014, 3, 760937. [Google Scholar] [CrossRef]
- Xu, Q. Enhanced discrete-time sliding mode strategy with application to piezoelectric actuator control. IET Control Theory Appl. 2013, 7, 2153–2163. [Google Scholar] [CrossRef]
- Gu, G.Y.; Zhu, L.M. An experimental comparison of proportional-integral, sliding mode, and robust adaptive control for piezo-actuated nanopositioning stages. Rev. Sci. Instrum. 2014, 85, 055112. [Google Scholar] [CrossRef]
- Qi, K.; Xiang, Y.; Fang, C.; Zhang, Y.; Yua, C. Analysis of the displacement amplification ratio of bridge-type mechanism. Mech. Mach. Theory 2015, 87, 45–56. [Google Scholar] [CrossRef]
- Wei, Y.; Tao, H. Preisach model research on hysteresis characteristics of piezoelectric actuators. Piezoelectrics Acorstooptics 2004, 5, 364–367. (In Chinese). Available online: http://www.cqvip.com/qk/92382x/200405/10536930.html (accessed on 10 August 2019).
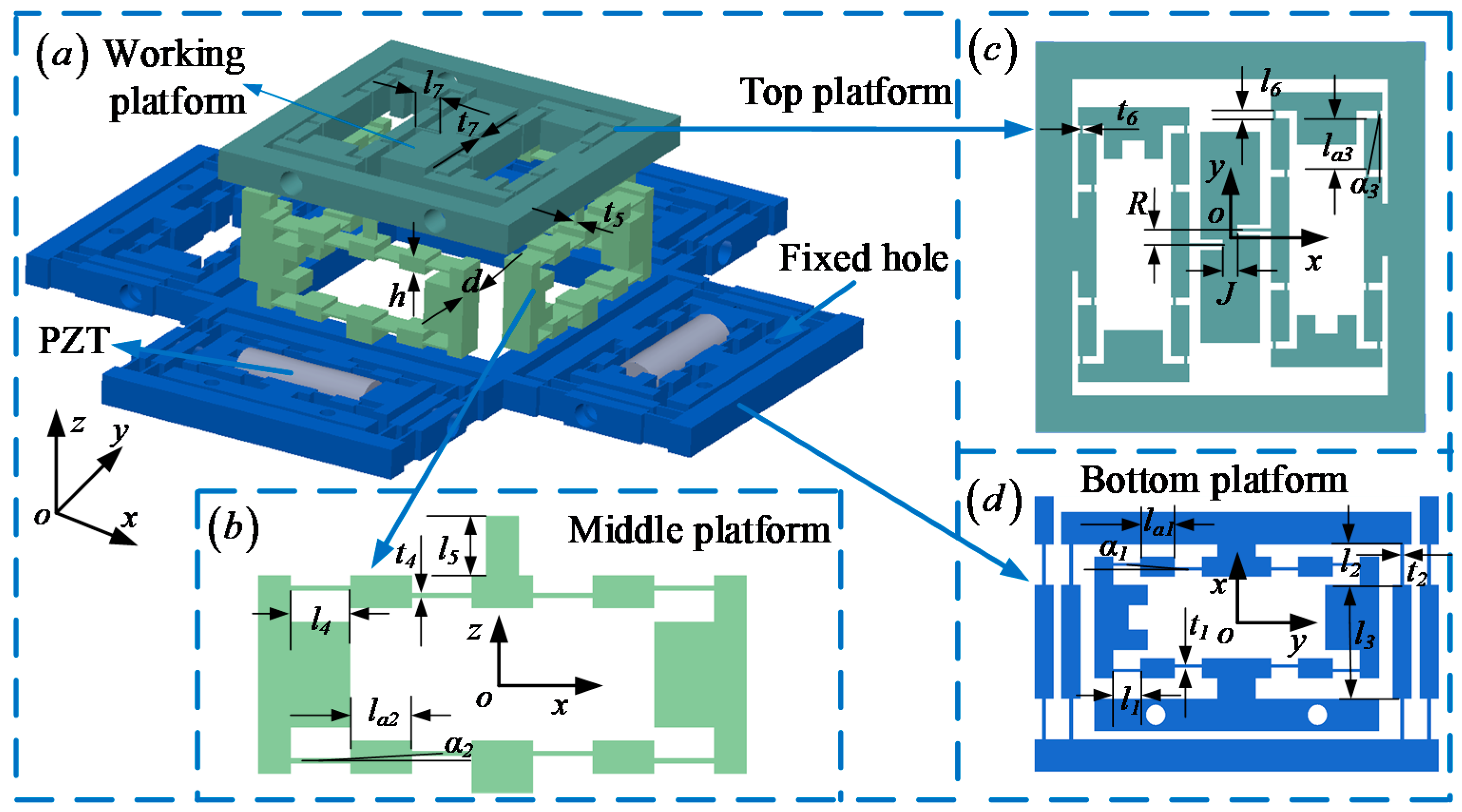


| Top Platform | Middle Platform | Bottom Platform | |||
|---|---|---|---|---|---|
| l6 (mm) | 2 | l4 (mm) | 9 | l1 (mm) | 7 |
| t6 (mm) | 0.8 | t4 (mm) | 0.8 | t1 (mm) | 0.8 |
| la3 (mm) | 14 | la2 (mm) | 9 | la1 (mm) | 9 |
| α3 (rad) | 0.185 | α2 (rad) | 0.061 | α1 (rad) | 0.068 |
| l7 (mm) | 2 | l5 (mm) | 9 | l2 (mm) | 10 |
| t7 (mm) | 0.8 | t5 (mm) | 0.8 | t2 (mm) | 1 |
| R (mm) | 4 | h (mm) | 5 | l3 (mm) | 28 |
| J (mm) | 4 | d (mm) | 10 | _ | |
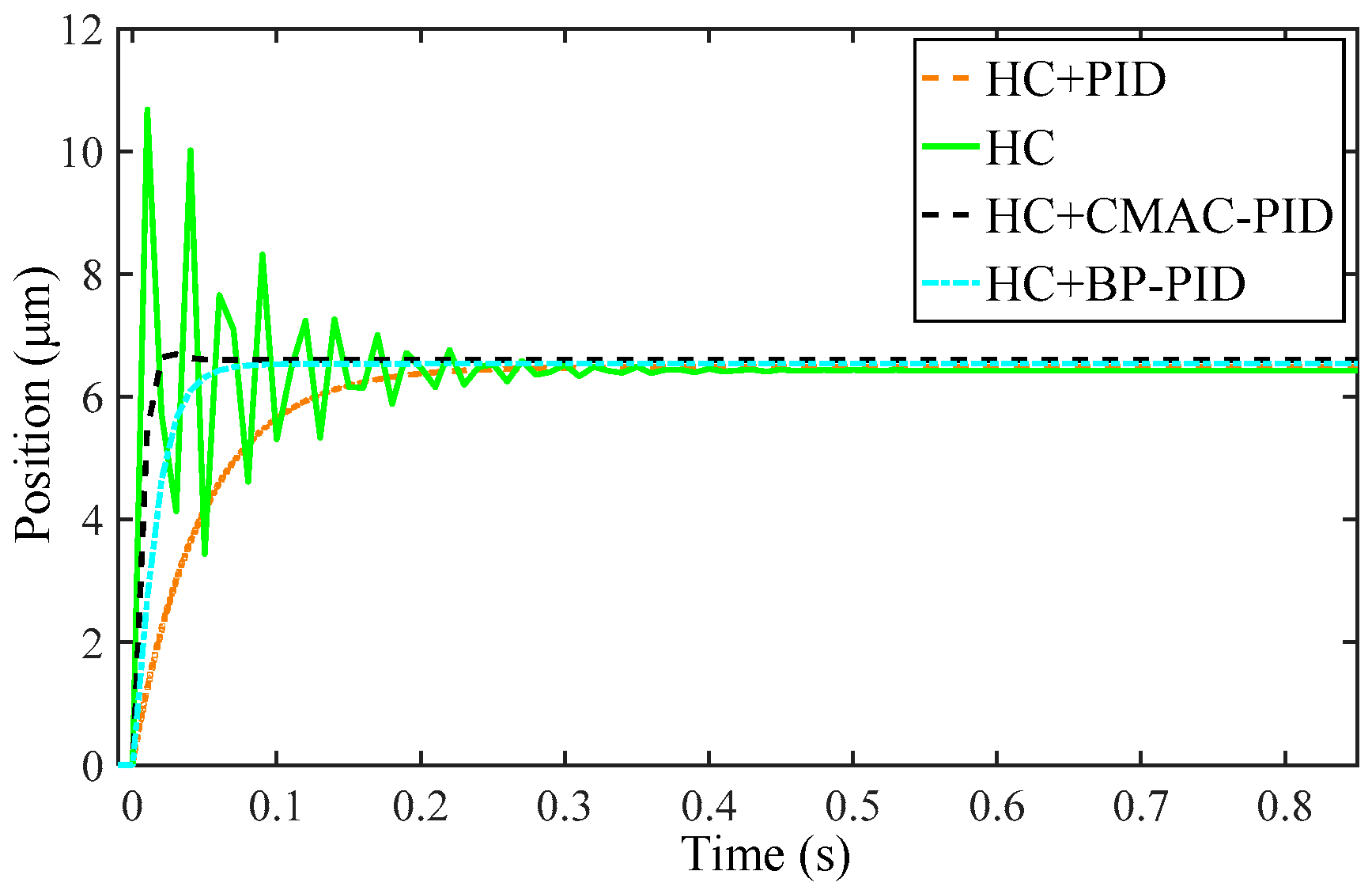
| Performance | HC | HC+PID | HC+BP-PID | HC+CMAC-PID |
|---|---|---|---|---|
| Settling time(sec) | 0.84 | 0.68 | 0.46 | 0.11 |
| Overshoot (%) | 66.12 | 0 | 0 | 1.39 |
| Settling value(μm) | 6.429 | 6.488 | 6.542 | 6.601 |
| Positioning error (%) | 2.78 | 1.89 | 1.07 | 0.18 |
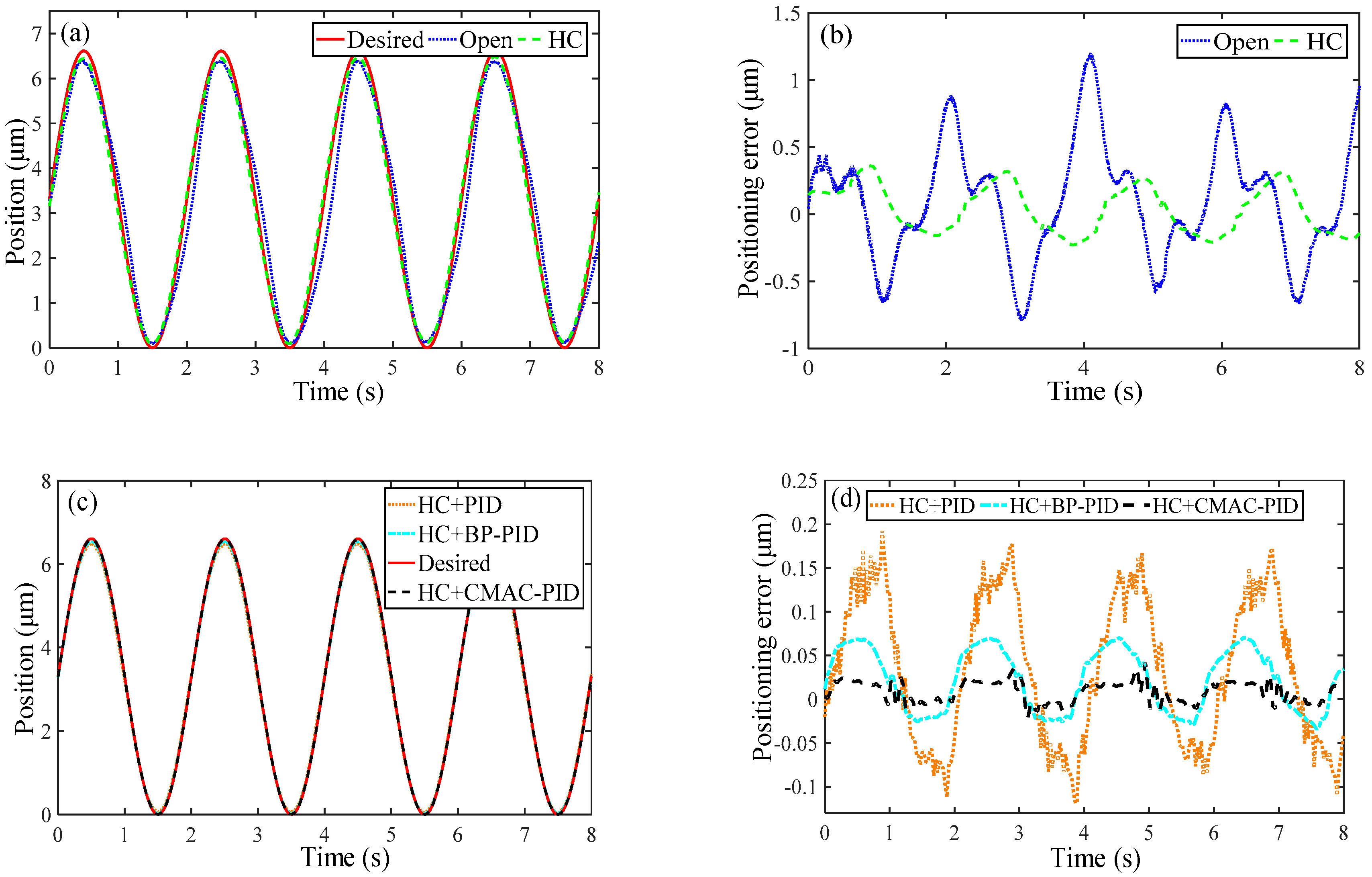
| Performance | OPEN | HC | HC+PID | HC+BP-PID | HC+CMAC-PID |
|---|---|---|---|---|---|
| (%) | 18.22 | 5.46 | 2.91 | 1.07 | 0.63 |
| (%) | 6.70 | 2.61 | 1.38 | 0.62 | 0.23 |
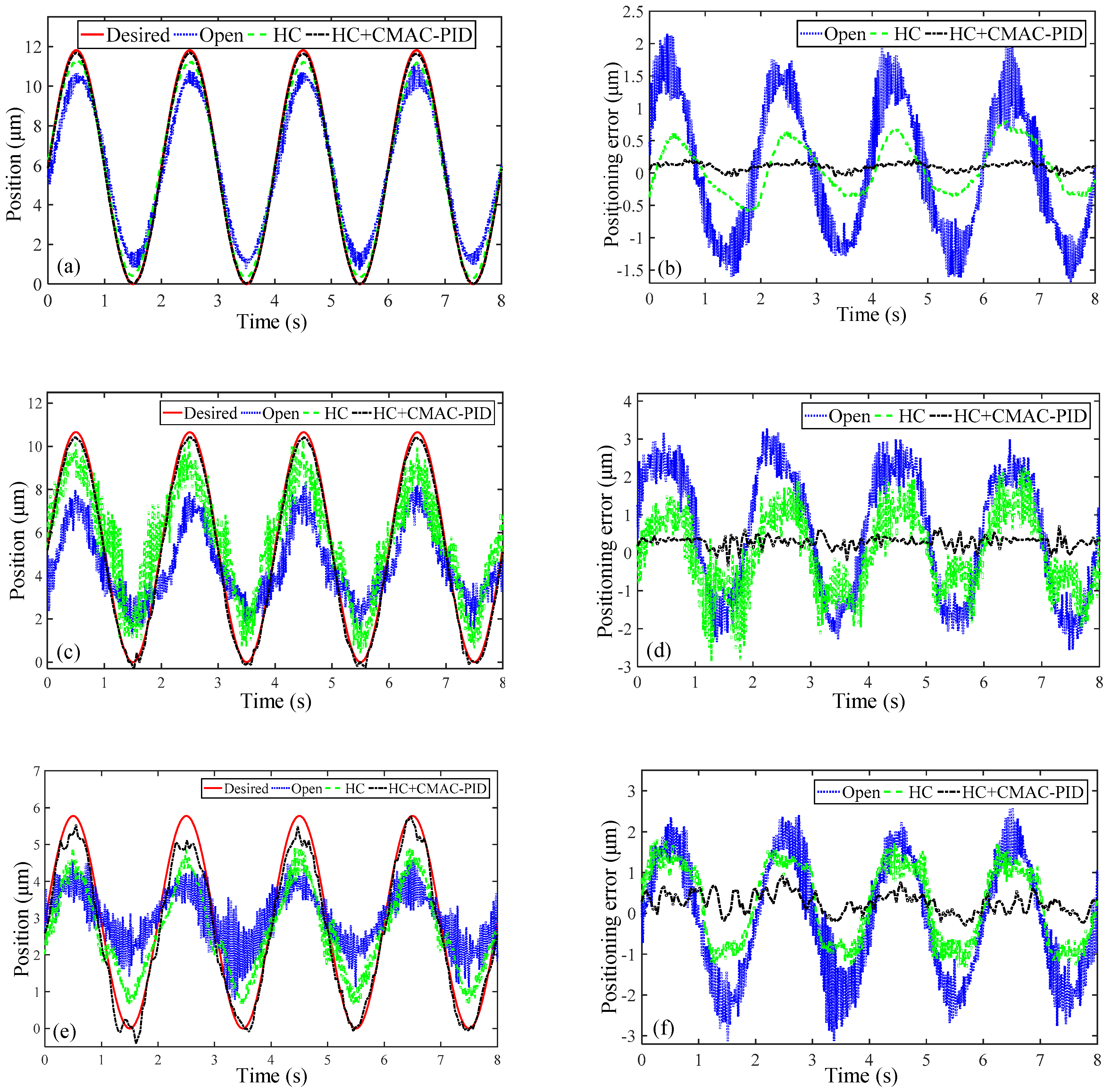
| Freedom | Translation Along Z Axis | Rotation Around X/Y Axis | Rotation Around Z Axis | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Performance | OPEN | HC | HC+CMAC-PID | OPEN | HC | HC+CMAC-PID | OPEN | HC | HC+CMAC-PID |
| emax (%) | 11.62 | 6.79 | 1.77 | 30.77 | 22.16 | 6.97 | 54.17 | 31.53 | 19.02 |
| erms (%) | 50 | 3.30 | 0.95 | 16.10 | 10.33 | 3.06 | 25.34 | 16.82 | 7.32 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.; Zheng, S.; Li, P.; Shen, Z.; Wang, S. Positioning Error Analysis and Control of a Piezo-Driven 6-DOF Micro-Positioner. Micromachines 2019, 10, 542. https://doi.org/10.3390/mi10080542
Lin C, Zheng S, Li P, Shen Z, Wang S. Positioning Error Analysis and Control of a Piezo-Driven 6-DOF Micro-Positioner. Micromachines. 2019; 10(8):542. https://doi.org/10.3390/mi10080542
Chicago/Turabian StyleLin, Chao, Shan Zheng, Pingyang Li, Zhonglei Shen, and Shuang Wang. 2019. "Positioning Error Analysis and Control of a Piezo-Driven 6-DOF Micro-Positioner" Micromachines 10, no. 8: 542. https://doi.org/10.3390/mi10080542
APA StyleLin, C., Zheng, S., Li, P., Shen, Z., & Wang, S. (2019). Positioning Error Analysis and Control of a Piezo-Driven 6-DOF Micro-Positioner. Micromachines, 10(8), 542. https://doi.org/10.3390/mi10080542





