Abstract
Multipurpose small reservoirs are important for livelihoods in rural semi-arid regions. To manage and plan these reservoirs and to assess their hydrological impact at a river basin scale, it is important to monitor their water storage dynamics. This paper introduces a Bayesian approach for monitoring small reservoirs with radar satellite images. The newly developed growing Bayesian classifier has a high degree of automation, can readily be extended with auxiliary information and reduces the confusion error to the land-water boundary pixels. A case study has been performed in the Upper East Region of Ghana, based on Radarsat-2 data from November 2012 until April 2013. Results show that the growing Bayesian classifier can deal with the spatial and temporal variability in synthetic aperture radar (SAR) backscatter intensities from small reservoirs. Due to its ability to incorporate auxiliary information, the algorithm is able to delineate open water from SAR imagery with a low land-water contrast in the case of wind-induced Bragg scattering or limited vegetation on the land surrounding a small reservoir.
1. Introduction
To overcome droughts and ensure water availability, the rural population in many semi-arid areas of the world relies on small reservoirs []. In this context, small reservoirs are defined as reservoirs with a surface area smaller than 100 hectares. Typically, these reservoirs are embanked streams that capture water in the wet season, to be made available during the dry season. Small reservoirs are used for year-round irrigation, fishery, cattle and domestic purposes.
Currently, the cumulative impact of small reservoirs on water resources at a river basin scale is still debated [], and the sustainability of small reservoirs under climate change is unknown []. In order to plan, manage and improve our understanding of small reservoirs, it is important to monitor the water storage dynamics. Ground-based surveys are both labor intensive and time consuming. Alternatively, small reservoir storage can be measured from space, based on remotely sensed surface area measurements in combination with regional area-volume equations, which can be derived from in situ bathymetric measurements [– ]. For large lakes and reservoirs, water stage measurements from space have recently become available [,], which enable the estimation of water storage changes using only remote sensing observations.
Water surface areas can be delineated through optical imagery (e.g., MODIS, SPOTand Landsat), as well as synthetic aperture radar (SAR) imagery (e.g., Envisat, ALOSand Radarsat). A common practice for optical-based water surface delineation is to put a threshold on a vegetation [] or water index [,] for decision making. For large water bodies, MODIS yields good results, but the spatial resolution is too low for small reservoirs. Instead Landsat imagery (30-m spatial resolution) has successfully been applied using various techniques in Ghana [], Zimbabwe [], India [] and Brazil []. A strong limitation of optical imagery is its dependence on cloud- and smoke-free day acquisitions, which makes its application for operational monitoring very limited. For the detection and the creation of a base map, optical imagery is, however, very suitable [].
The application of SAR imagery for small reservoir monitoring has recently been studied based on Envisat ASARimages [,]. Smooth open water acts as a specular reflector, reflecting most of the radar signal away from the sensor. Radar backscatter intensities from open water are therefore generally lower than backscatter intensities from the surrounding land, which enables the delineation of open water. The roughness of the water is very variable and influences backscatter intensities over time and space. Difficulties arise when wind-induced Bragg scattering enhances backscatter from the open water or when the contrast between land and water deteriorates, due to the absence of vegetation on the land surrounding a small reservoir at the end of the dry season []. Vegetation in the tail-end of small reservoirs has a different signature from open water, which may result in an error in the delineation []. Based on an earlier study [], SAR imagery is found to be suitable for the delineation of small reservoirs in the wet season, but to be affected by wind and a low land-water contrast in the dry season. To date, no weather-independent method that yields good year-round results has been developed for remotely sensed areal measurements of small reservoirs.
In this paper, we propose a new Bayesian algorithm to delineate small reservoirs. The algorithm can deal with a large variability in backscatter intensities from open water, exploits information contained in multi-polarized SAR imagery and readily allows for the input of auxiliary information, e.g., temporal information about the small reservoir area. For this study, Radarsat-2 SAR images of the Upper East Region (UER), Ghana, were acquired. The Radarsat-2 has an improved resolution compared to Envisat ASAR imagery and offers full polarimetric data.
2. Datasets
2.1. Ground Truth
The study area is located in the Upper East Region (UER) of Ghana; see Figure 1. The UER has a semi-arid climate, characterized by a five month, mono-modal wet season and an average rainfall of 1,044 mm/yr over the past 40 years.
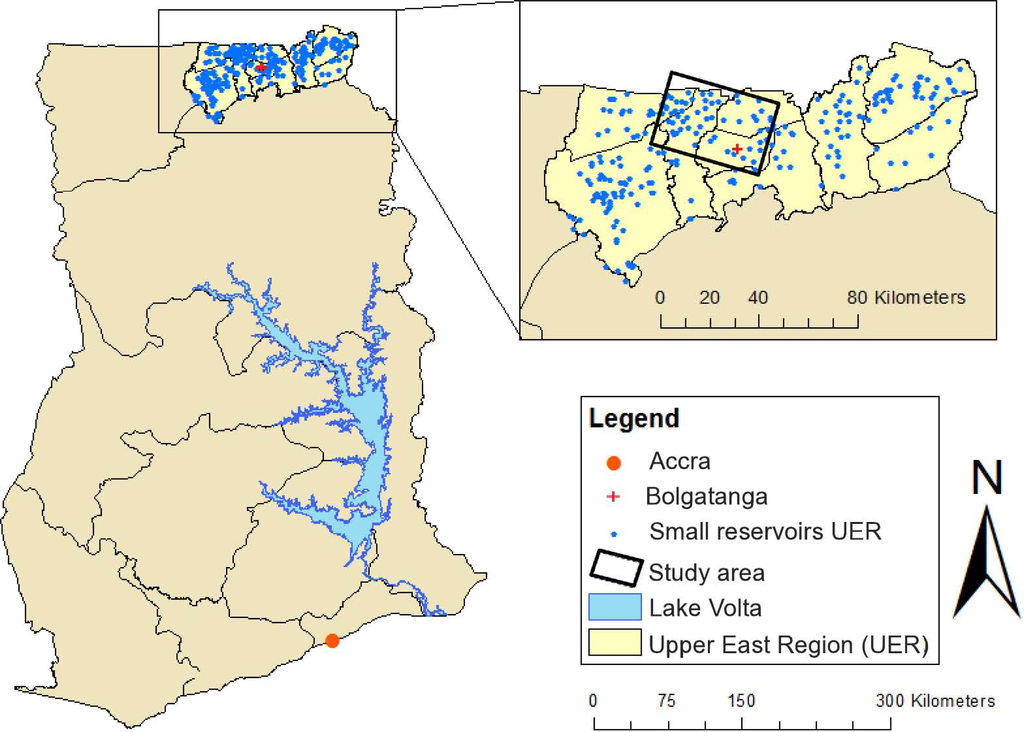
Figure 1.
The study area in the Upper East Region of Ghana, overlaid with a base map of small reservoirs in the region.
Fieldwork was conducted in November 2012. This period is at the start of the dry season, when the water levels in the small reservoirs are still around their upper limits. In total, 29 small reservoirs in the Kasena Nankana West, Kasena Nankana East, Bongo and Bolgatanga districts were visited, of which 26 are covered by all acquired images. All reservoirs were delineated in the field using a Garmin eTrex HCx handheld GPS, with an accuracy of 10 m (95% typical). With a simple walk around the reservoir, waypoints were taken at the land-water boundary in such a way that interpolating between the points yielded a good delineation of the reservoir. The boundary of the reservoir at the tail-end streams was defined as the point of a 10-m stream width. The area of the visited small reservoirs varied from 2.5 ha to 22.6 ha.
2.2. Precipitation Data
Rainfall series with a 15-min temporal resolution were obtained from a meteorological station in Navrongo (UER, Ghana) for the period from January until April 2013. The rainfall series were converted to daily rainfall and are presented in Section 4.3.
2.3. Radarsat-2 SAR Data
In this study, the small reservoir delineation is based on one or more polarizations from full polarimetric fine resolution Radarsat-2 data. First, two fine quad-pol images covering the study area were acquired at the start of the dry season in November 2012, followed by a time series of Wide fine quad-pol images from January until April 2013. The 2012 acquisitions allow for comparison with the ground truth data, while the time series allows for a temporal analysis and covers different dry season backscatter scenarios. Details about the acquired images are given in Table 1.

Table 1.
Radarsat-2 imagery acquired for this study.
3. Methods
3.1. Pre-Processing SAR Imagery
All images of one beam mode were co-registered and resampled to a grid of 5 m × 5 m using the open source Next ESA SAR Toolbox (NEST) software by the European Space Agency. Some additional dedicated effort in MATLAB was required to co-register the stacks from different beam modes. This was done in two steps. Firstly, absolute verification of image geolocation was carried out on the November acquisitions (FQ10 and FQ31), hereby referred to as the reference, which showed consistent agreement with the GPS ground-truth data. Secondly, the residual shifts between the FQ04W and FQ17W datasets and the reference acquisitions were retrieved by incoherent speckle correlation [] procedures between the reference images and the first image of each dataset. Cross-correlation of intensities performed block-wise throughout the image returned almost uniform patterns of a few pixel shifts, due also to the relatively small elevation dynamics (100 m) of the scene. The shifts were averaged and used to achieve stack co-registration. A simple moving average filter (3 × 3 pixels) was applied on backscatter intensities to remove speckle by increasing the number of looks.
From the literature [], it was found that the delineation is best performed within a reservoir mask in which the reservoir area and total area of the surrounding land are of a similar size. Here, the masks were created by manually selecting a rectangular area around a small reservoir at full capacity, in such a way that it contained a similar number of water and land pixels.
3.2. Growing Bayesian Classifier
The newly developed growing Bayesian classifier (gBC) [] is used for the delineation of small reservoirs. The gBC classifies a pixel based on the maximum a posteriori probability (MAP), which is calculated from a multivariate Gaussian likelihood function, multiplied by one or more conditional priors. The Gaussian model is justified by the application of the algorithm to logarithmic intensities. In previous work [], it was outlined that the Gamma distribution, typical of homogeneous areas of fully developed speckle, tends toward a log-normal behavior for an increasing number of looks. The multivariate likelihood function exploits information contained in multi-polarized SAR imagery, while the conditional priors update the likelihood with auxiliary information. The basic gBC makes use of one conditional prior, the so-called growing prior, which includes information about neighboring pixels in the classification. The gBC can readily be extended with auxiliary information, e.g., temporal information, in the form of a conditional prior, according to the principle of naive Bayesian image classification [,]. Contrary to traditional maximum likelihood, the gBC does not require a priori training data to calculate the classes’ signatures. Instead, signatures are developed during the iterative classification procedure based on the growing land and water seeds. The gBC flow scheme is given in Figure 2.
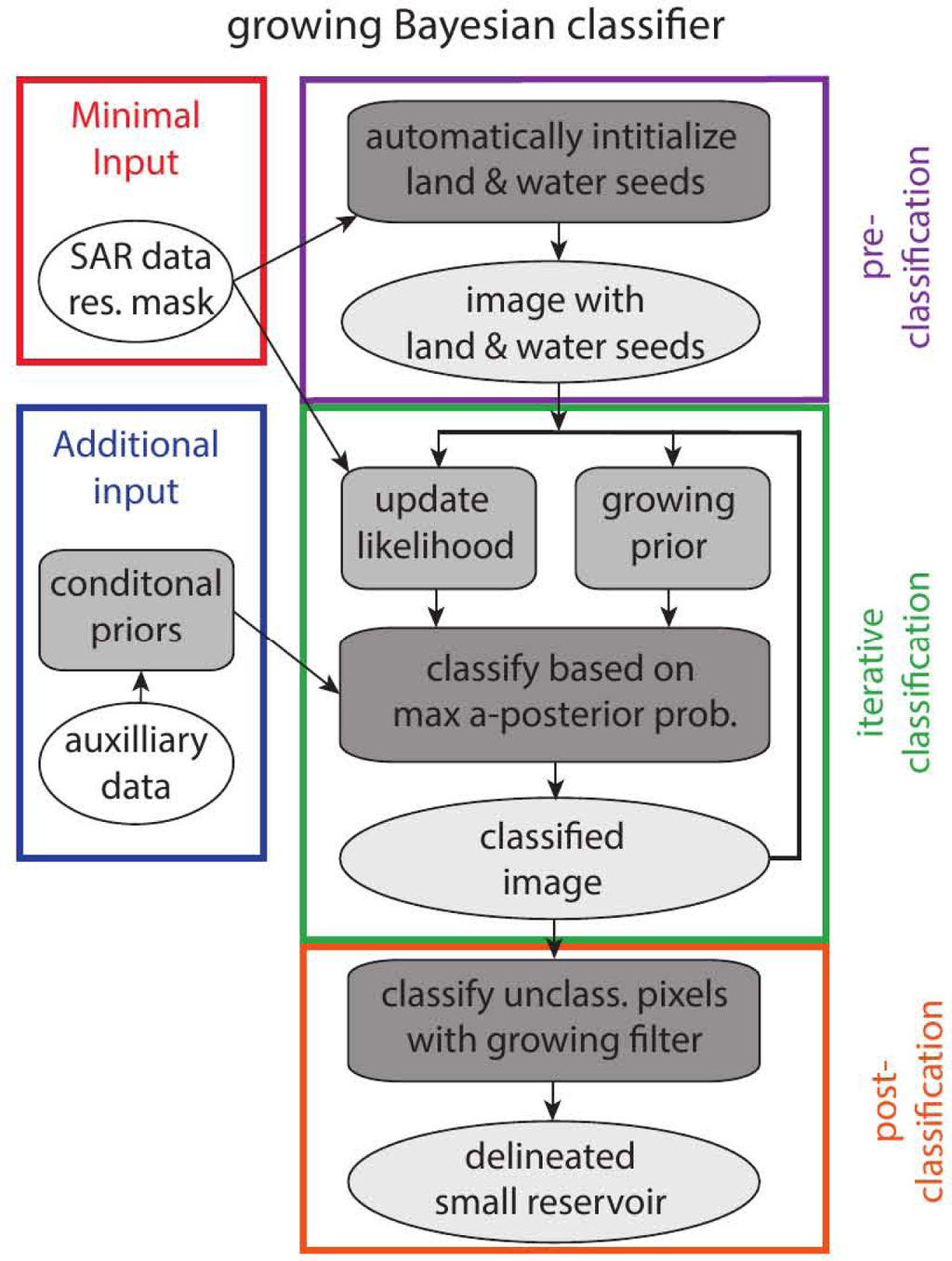
Figure 2.
Flow diagram for the growing Bayesian classifier: first, the seeds are initialized (top right) for which a SAR reservoir image is required (top left); then, the iterative Bayesian classification is performed (right middle); finally, a growing filter is applied (right bottom); the algorithm can readily be extended with additional information (left middle).
3.2.1. Basic Growing Bayesian Classifier
The gBC is automatically initiated within the reservoir mask. The land seed is initiated at the two outer rows and columns. The water seed at the area with the minimum average backscatter intensity, of a minimum of 3 × 3 pixels, is derived from a moving average filter. If a delineation at the previous time step is available, the potential water seed area is restricted to the small reservoir area from the previous time step. All other pixels are initially unclassified. The water seed and land seed are then iteratively grown, until both classes converge at the land-water boundary, according to the Bayesian decision rule:
where ωk is the class with k ∈ l, w, u for the land, water and unclassified classes, respectively, and
the likelihood, Φk(xi), based on the pixel intensity vector, xi, for pixel i multiplied with the growing prior, P(ωk|νj), which is proportional to the posterior probability, according to:
where νj is a conditional variable of the growing prior with state j, which is based on the classification of neighboring pixels; see Table 2. Here, the assumption is made that the likelihood function is independent of the state of the conditional variable, ν. Note that a pixel is only classified if its probability of being a member of a class is larger than the probability of remaining unclassified. The likelihood, Φu (xi), for a pixel to remain unclassified is defined as the minimum of the land and water likelihood for that pixel. The classification is therefore not governed by the priors alone, but based on the likelihood computed from the pixel intensity vector.

Table 2.
Growing conditional prior probabilities based on the classification of neighboring pixels.
The growing conditional variable, v (see Table 2), is based on the assumption that, within the reservoir mask, all water pixels are one connected area, i. e., the small reservoir. The state of the variable is defined according to the number of neighboring land and water pixels. The prior only allows for a new water pixel next to an already classified water pixel (the water seed) and for a new land pixel next to an already classified land pixel (the land seed). The growing prior reduces the confusion error (the error from incorrect classification of pixels within the spectral area of overlap between two classes) to the land water boundary, where both classes have an equal prior probability.
After the classification, a growing filter is applied to classify the pixels that remained unclassified after convergence of the land and water seeds. Starting from the seeds, all unclassified pixels connected to the water seed by water pixels are classified as water and all pixels connected to the land seed by land pixels are classified as land. Land and water pixels that are not connected to the seed are then reclassified using the same method.
3.2.2. Extended Growing Bayesian Classifier
The gBC can readily be extended with auxiliary information in the form of conditional priors according to the principle of naive Bayesian classification. In the general case that the basic gBC is extended with P prior probabilities, Equation (2) becomes:
where
is prior probability p with conditional variable
determined by its state, j.
For this study, an additional conditional variable based on temporal information was developed. The classification from a previous or subsequent time step is used to update the delineation at the current time step. This can be very useful information, especially when the land-water contrast deteriorates. Two temporal conditional variables,
and
, were developed based on the strong seasonal behavior of small reservoirs, i.e., small reservoirs are replenished in the wet season, and the water is released for use in the dry season. The states of the temporal variables are based on the classification of a pixel, i, in the previous and subsequent time step, respectively; see Tables 3 and 4. Equation (3) then becomes:

Table 3.
Temporal conditional prior probabilities based on the classification of a pixel in the previous time step.

Table 4.
Temporal conditional prior probabilities based on the classification of a pixel in the subsequent time step.
The temporal priors increase the posterior probability for a pixel of being a member of the same class as in the previous and/or subsequent time step. If the previous and subsequent classification of a pixel are equal, the pixel is given a relatively high prior probability of being a member of the same class. Similar prior probabilities are given for land and water if the class changes from the previous to the subsequent time step. One exception is formed by pixels classified as water in the subsequent time step during the dry season. Small reservoir areas do not increase, as long as there is no rain during the dry season. Based on this knowledge, a prior probability of being a member of the water class 1 is given to pixels that are classified as water in the subsequent time step. The temporal priors allow for the delineation of images with a very low land-water contrast if the previous and/or subsequent images are correctly classified.
In an operational setting, reservoirs at the current time step, t, can be delineated using prior
based on the classification from the previous time step. Then, the delineation at time step t-1 can be updated with temporal priors
and
based on the classified images at time step t and t-2 The classifications at time step t until t-3 could then further be updated with the same procedure. However, this only yields a small improvement and would allow for a classification error to propagate back in time.
4. Results and Discussion
4.1. Polarimetric SAR Remote Sensing of Small Reservoirs for Different Backscatter Scenarios
Four distinct backscatter scenarios for backscatter from small reservoirs are found within the acquired data series of SAR imagery, i.e., Smooth open water, water with vegetation, wind-induced Bragg scatter and backscatter during a rain-event. For every backscatter scenario, a sample of land and water pixels was taken from different reservoirs and its backscatter intensity distribution plotted (Figure 3). The backscatter intensities, as well as the contrast between land and water are different for every scenario. This calls for a flexible classification method (a method without fixed thresholds) and optimal use of the available polarizations.
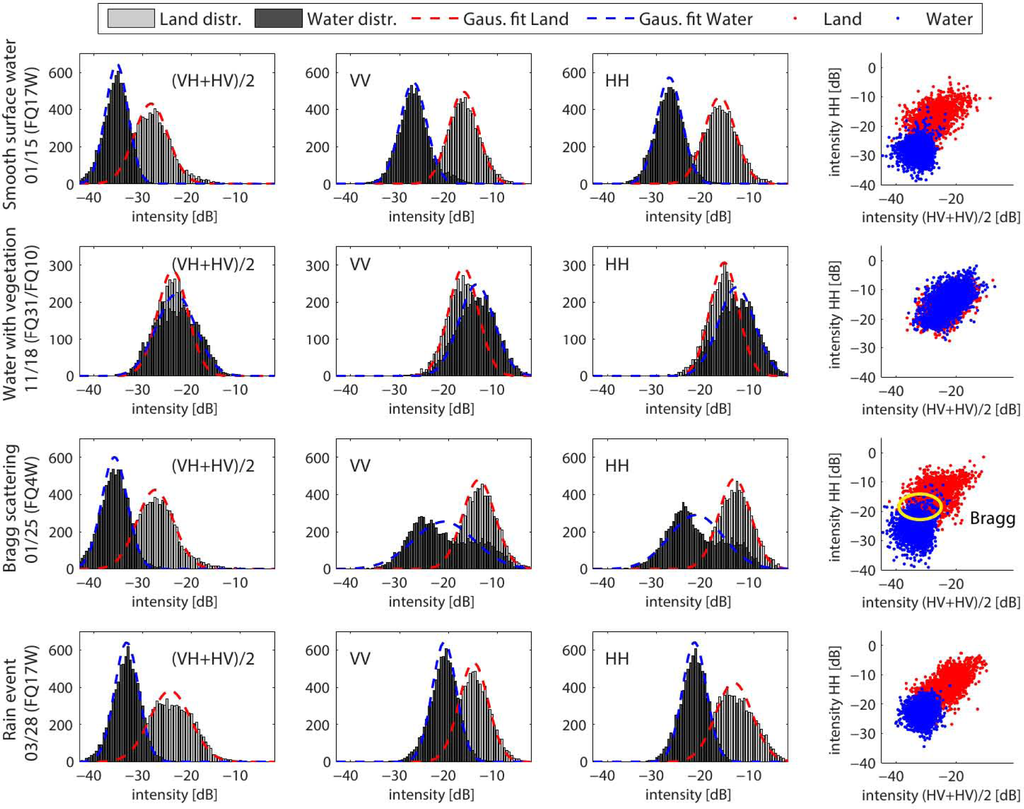
Figure 3.
Backscatter intensity distributions and scatter plots for the land and water classes from the samples of four distinct small reservoir backscatter scenarios, i. e., smooth open water, water with vegetation, Bragg scattering and backscatter during a rain event.
The optimal combinations of polarizations were evaluated based on the separability between the land and water class. The separability was calculated from the Jeffries-Matusita (JM) distance [], based on the land and water samples for the different scenarios. A JM distance of two indicates that there is no confusion area (i.e., the spectral area of overlap between two classes) and can thus perfectly be separated based on backscatter intensity alone. A JM distance of zero means that the backscatter distributions for both classes completely overlap. The presented combinations (see Figure 4) are chosen for comparability and based on operational considerations. Depending on the choice of SAR mission, single, dual or full polarimetric images can be acquired. In total, 12 combinations were presented: three single polarizations, eight combinations from dual polarization modes, of which five use polarization intensity ratios, and one full polarimetric combination, in which the average of the cross-polarizations is used to increase radiometric resolution. The presented tests were applied on indicators based on channel intensities or intensity ratios only. Further research should address the use of the coherent polarimetric information for decompositions, such as alpha-entropy [] and refined polarization synthesis [–], to achieve optimal contrast.
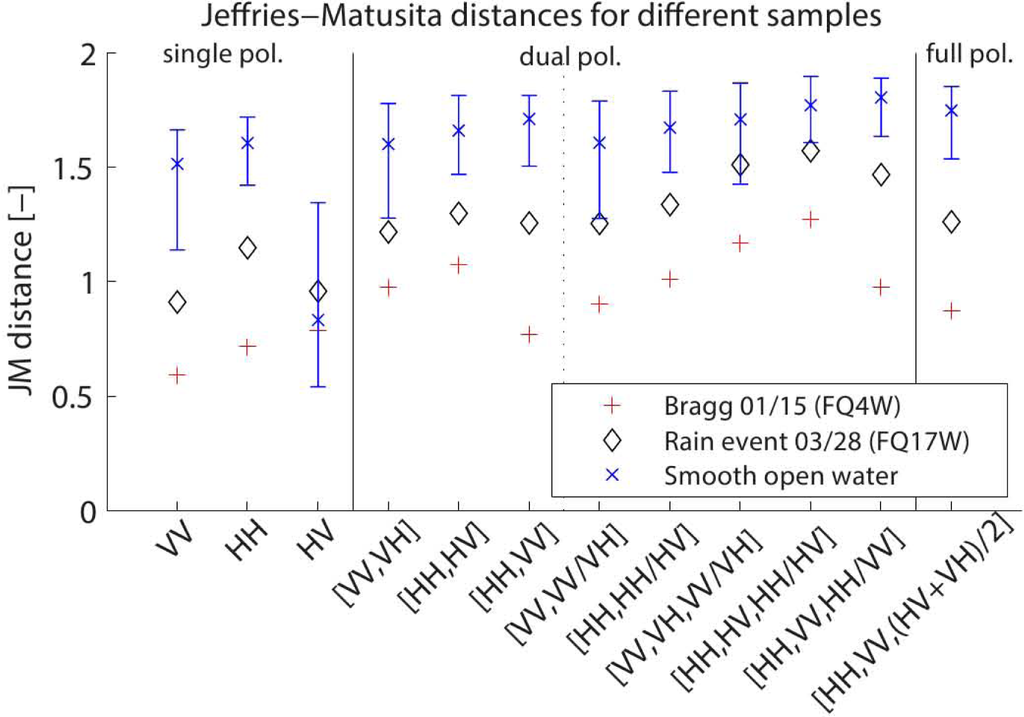
Figure 4.
Jeffries-Matusita (JM) distances for the samples of three distinct backscatter scenarios from small reservoirs, where the error bars show the mean, minimum and maximum JM distances from the different samples.
4.1.1. Smooth Open Water
Compared to land, smooth open water shows lower backscatter intensities, as it acts as a specular reflector, reflecting most of the radar signal away from the sensor. The high dielectric constant of water also decreases the penetration depth of the signal, which results in low volume scattering and, thus, predominantly co-polarized reflection []. The discrimination of smooth open water from land is therefore a simple task []. This is in agreement with the results presented here. The lowest backscatter intensities and smallest confusion area are found in the co-polarized ‘HH’polarization, while the cross-polarized ‘HV’shows the largest confusion area; see the top row in Figure 3. The JM distances for open water show that a high separability can be obtained from single co-polarized polarizations (1.6 on average in ‘HH’), and only a small improvement (up to 1.8 for ‘HH, VV, HH/VV’) is found from adding more polarizations; see also Figure 4. The contrast is optimal in the case of reeds on the water boundary and land with vegetation, which enhances the delineation accuracy [].
4.1.2. Water With Vegetation
This backscatter scenario refers to vegetation within the small reservoir, mainly at the tail-ends, where grasses and other weeds increase the local surface roughness. This results in higher backscatter intensities; see the second row in Figure 3. Depending on the type of the vegetation, the double bounce scattering can also be enhanced. The mean backscatter intensities from these areas are similar to land in the cross-polarized ‘HV’ and higher than land in the co-polarized ‘HH’ and ‘VV’. Water with vegetation is therefore difficult to include in the small reservoir delineation [].
4.1.3. Wind-Induced Bragg Scatter
Bragg scattering occurs when the position of scatterers are aligned parallel with the line of flight with regular spacing. In this case, the radar backscatter is coherently reinforced depending on the incidence angle, wavelength and spacing of the scatterers [,]. This type of scattering can be induced by wind waves on the surface of the water, depending on the wind direction and speed. According to [,], Bragg scattering from open water is significant with wind velocities over 9–10 km/h and in specific combinations of wind direction and polarization. Bragg scatter is most apparent in co-polarized polarizations and small in cross-polarized polarizations, which is in agreement with the histograms in the third row of Figure 3. Compared to smooth open water, the water distribution shows a long tail with high back scatter intensities and, thus, a larger confusion area between the land and water class. The scatterplot shows the decreased separability between the land and water class in the case of dual polarization, when the water surface shows patches with Bragg scattering. The separability in the single co-polarized ‘HH’ deteriorates compared to smooth open water (0.72). The separability for the cross-polarized polarization is similar to open water; see Figure 4. The value of a second polarization and polarization combinations becomes visible here, as a clear improvement in separability is found (up to 1.27 for ‘HH, HV, HH/HV’).
4.1.4. Rain Event
Backscatter intensities from the surface show a significant change during rain events, due to increased surface wetness. For bare soil, where the dominant backscatter mechanism is surface scattering, increased backscatter intensities are expected, due to the increased surface wetness. However, if pools of water start to form, backscatter intensities will decrease, as a larger portion of the signal will be scattered away. The effect of rainfall on vegetation is smaller, as vegetation already contains ‘a layer of water’, and there are different operating scattering mechanism on which rainfall has different effects. If volume scattering is the dominant mechanism, backscatter intensities can be reduced. Wetness of the top layer increases the portion scattered away from the sensor, and reduced power is available for the volume scattering mechanism. Areas where surface scattering is the dominant mechanism show an increase in backscatter intensities []. As surface scattering is the dominant mechanism in the land surrounding small reservoirs, a small increase in backscatter is observed. These effects are most significant during the rain event, when no evaporation has occurred yet. At the water surface, rain droplets can cause an increase in surface roughness, which results in increased backscatter intensities []. This is also observed in the sampled reservoirs; see the bottom row in Figure 3. Since no ground truth is available for the March 28 acquisition, the land sample is taken from the land outside the known maximum boundaries of the small reservoir, where vegetation is present. The bare soil surrounding the small reservoirs at this date is not included in the land sample. Larger confusion areas and, thus, lower JM distances for all polarization combinations are measured; see Figure 4. This is caused by a larger increase in backscatter intensities from open water compared to the land with vegetation. The separability between the open water and the surrounding bare land mainly depends on whether pools of water are formed, in which case, the contrast can strongly decrease.
4.2. Comparison with Ground Truth
All small reservoirs that were visited during the fieldwork are delineated from the ‘HH, HV’ polarization combination from two Radarsat-2 images, which were acquired within three days from the ground truth. Since substantial areas of grass and weed vegetation were found inside the small reservoirs during the fieldwork, the reservoirs were divided into three vegetation content classes: ‘low vegetation’, ‘tail-end vegetation’ and ‘all boundary vegetation’. This classification was based on photos of the small reservoirs taken during the fieldwork. The delineation (red line) and ground truth (yellow line) of two typical reservoirs from each category are projected on Pauli RGBcolor composite images (Figure 5). Open water (dark areas, low backscatter intensities) are very clear in the images and easily delineated from the surrounding land (blue and green areas, higher single bounce and volume scattering). Patches of Bragg scatter (dark blue areas, increased surface scattering) are also classified as small reservoir, because of the dual polarization combination. The second and third row show the reservoirs with vegetation in the tail-end and at all boundaries, respectively. The small reservoir areas with vegetation (red and bright areas, high backscatter intensities and double bounce scattering) are not classified as small reservoir, because of their very different polarimetric signature. In all the reservoir images, the open water areas are well delineated by the gBC based on visual inspection.
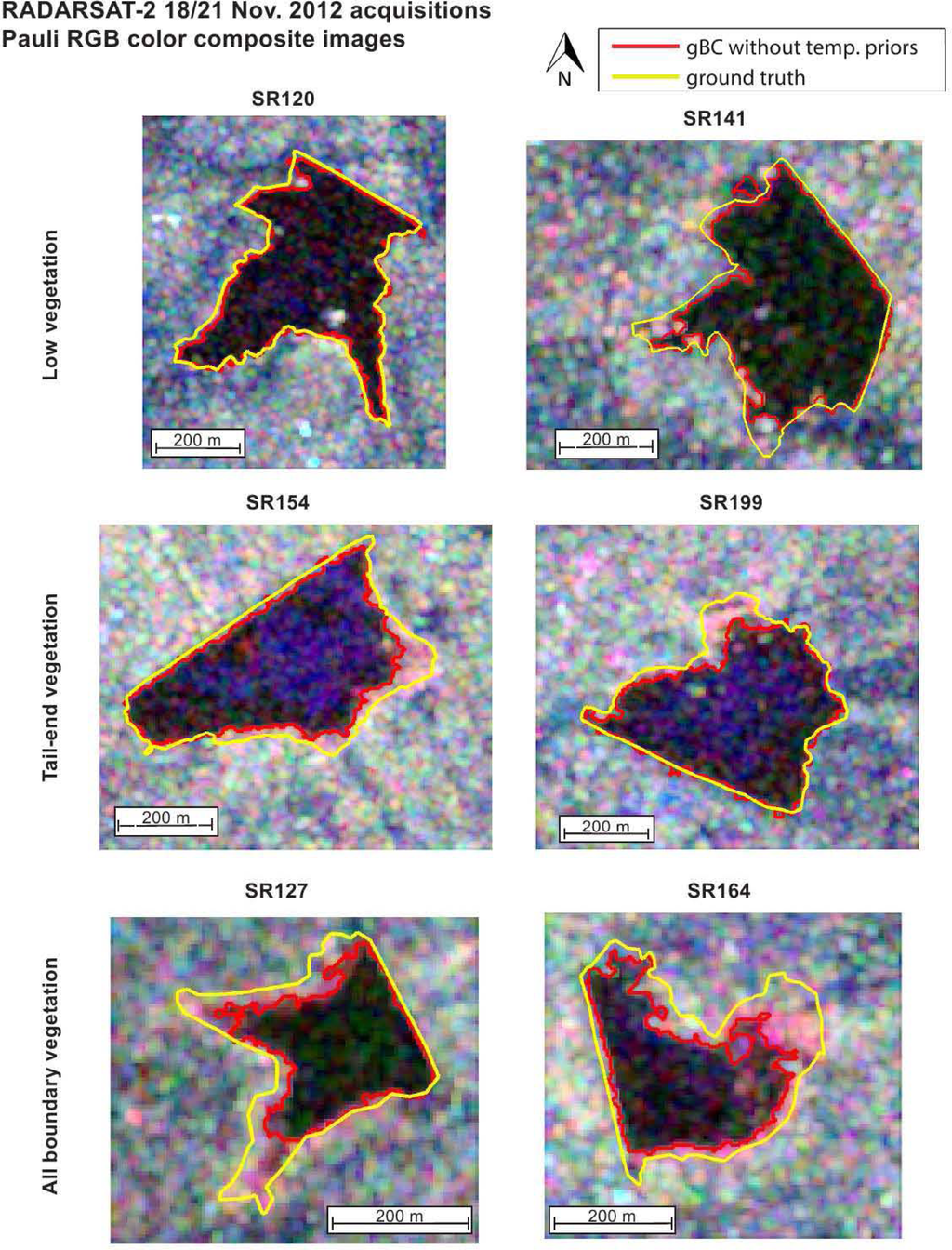
Figure 5.
Ground truth (yellow line) and delineation (red line) based on the ‘HH, HV’ polarization combination overlaid on Pauli RGB-images, with red colors for double bounce, green for volume scatter and blue for single bounce; note that the different color scales are used for the different Pauli components to enhance the image contrast.
The results are summarized in Figure 6 with the Differential Area Index (DAI), as used by [], and the JM distance based on the ground truth. The figure shows an overall underestimation of the classified small reservoir area. Compared to the ground truth, an underestimation of 12.8% to 14.8%, depending on the polarization combination, of the small reservoir area is found for small reservoirs with low vegetation. This underestimation is larger for the classes with more vegetation. The error made for delineating open water is expected to be smaller than suggested by these numbers, as the underestimation is due to different classification errors and a bias towards the land in the ground truth. First of all, there is an error due to vegetation in the small reservoirs, even in the reservoirs with ‘low vegetation’; see, e.g., SR141 in Figure 5, where some trees within the reservoir cause an incorrect classification at the tail-ends. A smaller error is due to the moving average filter, which reduces noise, but might also cause some boundary pixels to be classified as land instead of water. Furthermore, there is an error in the ground truth from the inaccuracy of the GPS device. The ground truth also shows a bias towards the land, due to the fact that the measurements were all taken while walking around the reservoir as close to the land-water boundary as possible, but on the land side. The JM distances show a clear trend between the increase in vegetation in the small reservoir and a decrease in separability. This is due to the increasing confusion area with an increasing vegetation area in the small reservoir.
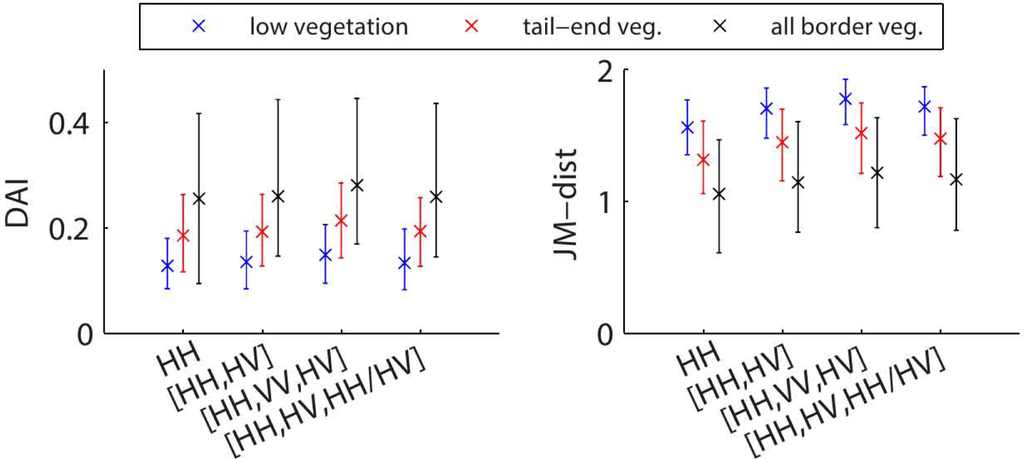
Figure 6.
Comparison between classified and ground truth areas of all 29 small reservoir from November 2012, based on the Differential Area Index (DAI) and the Jeffries Matusita (JM) distance.
4.3. Image Quality
The quality of the images is determined based on the contrast between the land and water class, which is calculated from the JM distance based on the classified images. This method for determining image quality is similar to the numbers of peaks in the backscatter intensity histogram of an image, as used by []. Two quality classes were used, with a threshold for high image quality images set to 1.5. This roughly corresponds to the minimum JM distance found for smooth open water for the ‘HH, HV’ polarization combination; see Figure 4. Within the time series, 170 reservoir images with high quality and 64 with low quality, of which 18 had substantial Bragg scatter, were found. Only two high quality images with substantial Bragg scatter were found. The images with Bragg scatter have an average JM distance of 1.22, while all other images have an average JM distance of 1.58. The acquisitions with Bragg scatter are 25 January, 14 March and 7 April, of which especially the last two have a significant amount of low quality reservoir images (Figure 7). The acquisitions with Bragg scatter show higher mean backscatter intensities, but also a larger variability in the ‘HH’ polarization and no significant change in the ‘HV’ polarization. A large variability in backscatter intensities from open water pixels within the same acquisition is typical for Bragg scattering. Most reservoir images from 28 March, the acquisition during a rain event (see the top graph), are of high quality. The delineations for this date are likely to be overestimated; see the next section. Part of the low backscatter area that is classified as small reservoir is from the bare soil with water pools surrounding the small reservoir. The presented JM distances are, therefore, also likely to overestimate the actual image quality. The rain event has a clear impact on the mean backscatter intensities. In both the ‘HH’ and ‘HV’ polarizations, the backscatter intensities are elevated, while the variation is similar. Acquisitions during a rainfall event can easily be detected based on its open water backscatter intensities alone. A substantial number of reservoir images on 21 April have a low quality, although no Bragg scatter is found in this date. Here, the contrast is low, due to reduced vegetation on the land surrounding the small reservoir at the end of the dry season. Visual inspection of the Pauli images from the time series in comparison to images from November indicated a strong decrease in vegetated area inside the small reservoir. Vegetation in the small reservoirs is therefore expected to have a smaller influence on the classification accuracy compared to the start of the dry season.
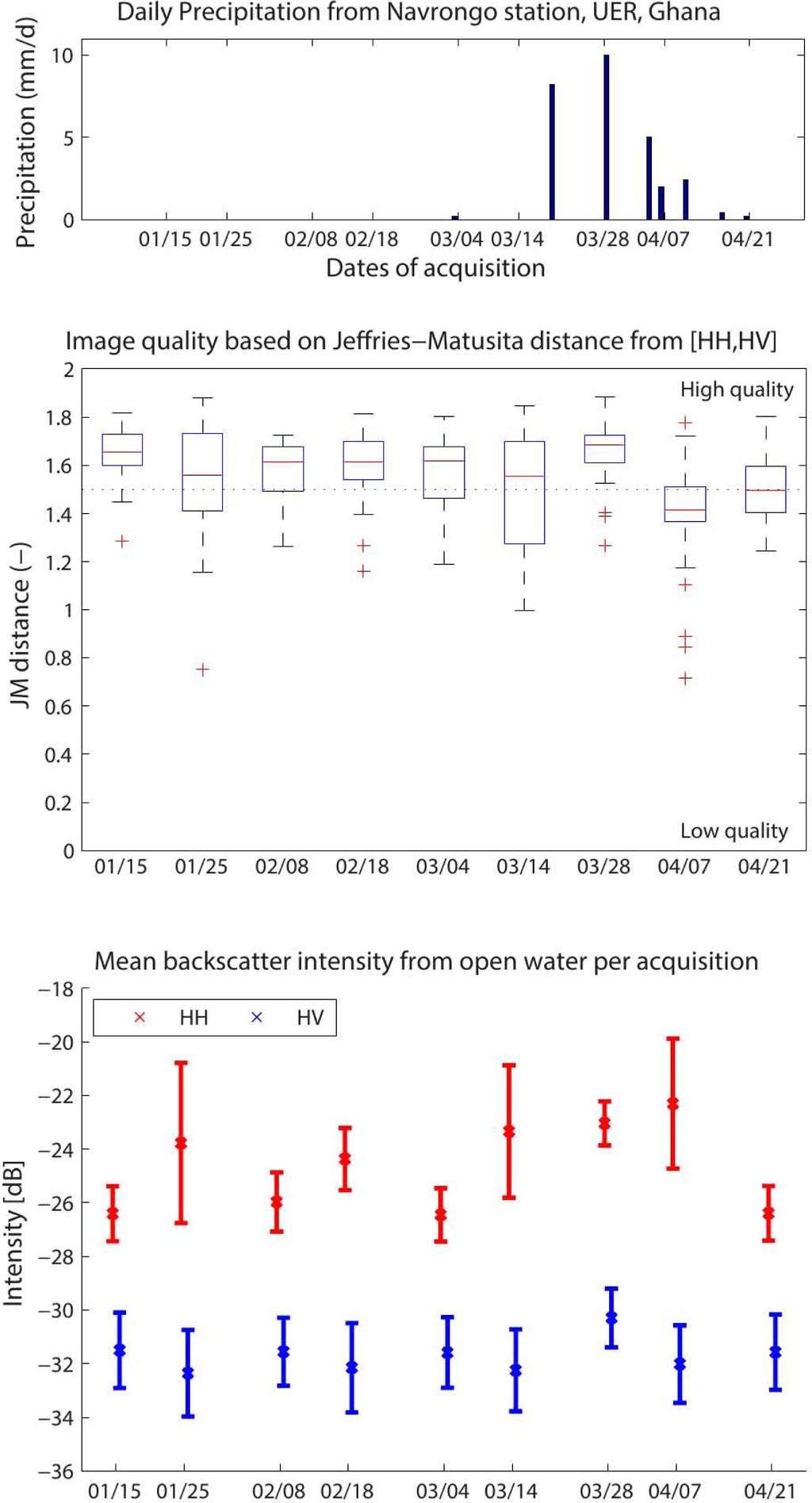
Figure 7.
Rainfall time senes (top), the quality of an acquisition based on the Jeffries Matusita (JM) distance (middle) and the mean backscatter intensity of the minimum delineated small reservoir area (bottom), where the boxplots show the median, first and second quartile boundaries and the red crosses are outliers; the error bars show the mean and one standard deviation boundaries.
4.4. Time Series Analysis
To demonstrate the Bayesian approach, two temporal priors were introduced. The priors update the classification at the current time step based on temporal information from the previous and subsequent classifications. Because of the rain event on 19 March (Figure 7), the temporal prior probabilities for prior Tt+1 change as well as from the 14 March acquisition; see Table 4.
Figure 8 shows the delineations based on the gBC with (blue and green lines) and without temporal priors (red line) for small reservoirs SR120 and SR154. From the delineations of both reservoirs, it can be seen that the classifications with and without temporal priors are similar for high quality images. Temporal priors improve the classification when the image has a low quality. A relative difference in the classified area between the delineations with and without temporal priors of more than 5% is found for 42 (55%) of the low quality reservoir images and only for 34 (22%) of the high quality reservoir images.
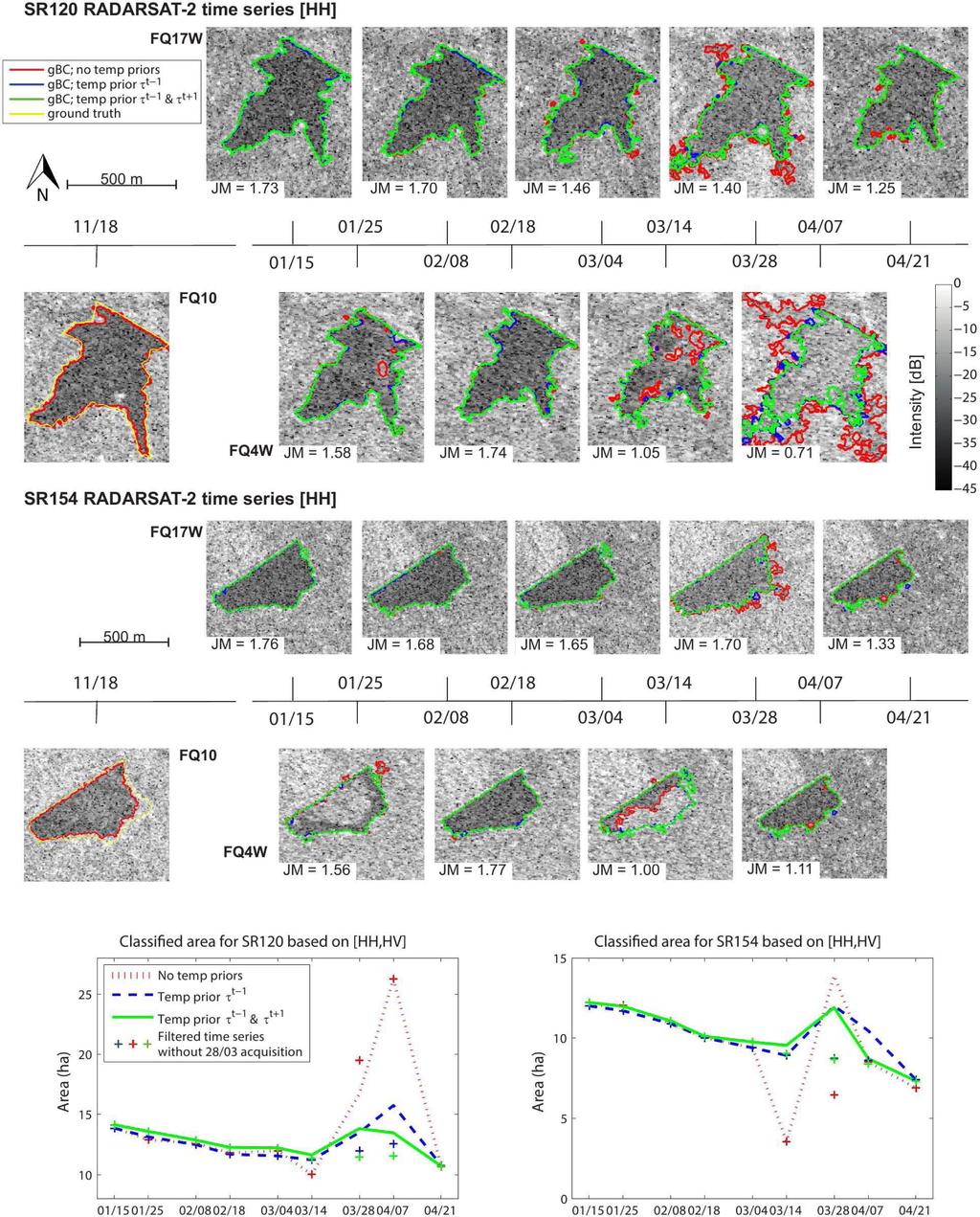
Figure 8.
Time series of small reservoir delineation based on the ‘HH, HV’ polarization combination and the basic gBC (red line), the gBC updated with temporal prior τt−1 (blue line) and the gBC updated with both priors τt−1 and τt+1 (green line) overlaid on HH backscatter intensity images; the bottom graphs show the areal variation in time for the same reservoirs, where the crosses show the filtered time series without the rain-affected March 28 acquisition.
Depending on the location within the small reservoir and the change of the polarimetric signature, some areas with Bragg scatter are classified as small reservoir, even without the temporal priors. This is because of the multi-polarized input data; see, e.g., SR154 on 25 January. The Bragg scatter at 14 March is not captured without the temporal priors in both reservoirs. The graphs in Figure 8 show that most of the water patches with Bragg scatter are delineated based on the classification at the previous time step (prior τt−1). Additional updating based on the subsequent classification (prior τt+1) only improves the classification in some cases. An extreme case of Bragg scatter is found in the 7 April image for SR120, where the full reservoir is affected and the contrast with the surrounding land significantly deteriorates. Here, the classification is mostly governed by the temporal priors, as can be seen from the large difference in the delineations with and without temporal priors. The classification at the previous time step is affected by rainfall; see the next paragraph. In the case that the delineation is updated with the classification from this time step, the small reservoir area is still overestimated. When updated with the classification from the subsequent time step, the overestimation is further limited. The discrepancy between the normal and the filtered time series (the 28 March acquisition is filtered out) of small reservoir areas for 7 April shows that the temporal priors are less effective when two low quality images follow each other (Figure 8).
The classified small reservoir areas from images acquired during a rain event are likely to be overestimated. The 28 March acquisition shows increased average backscatter intensities from the full images, but low backscatter intensities from land area within the maximum small reservoir boundary. This is probably because of the formation of water pools on the bare ground surrounding the small reservoirs. The delineation for both reservoirs on this date is not able to separate between the elevated backscatter intensities from the roughened water surface and the decreased backscatter intensities from the bare ground with water pools surrounding the small reservoir. This results in an overestimated small reservoir area. This hypothesis is strengthened by the total rainfall amount from these dates, which amounts to 18 mm (10 mm on 18 March and 8 mm on 19 March). Based on the regional area-volume equations [] and the classified small reservoir areas, this total rainfall causes an increase of the water level of 94 mm in SR154 and 76 mm in SR120. This increase in the water level is unlikely, given that the first rains after a long dry spell in the region do not create much runoff []. The most accurate estimation of the small reservoir area for this date is found through interpolating between the areas from subsequent and previous time steps in a time series, where 28 March is filtered out (Figure 8).
The results for the time series analysis of the gBC are summarized in Figure 9. The cumulative time series, as presented in the top graph in Figure 9, shows a strong decreasing trend of the total small reservoir area in the study area, which is expected during the dry season. The cumulative area on 28 March is a clear outlier, because of rainfall during the acquisition; see the previous paragraph. The filtered time series (the 28 March acquisition is filtered out) is in agreement with the expected trend. The largest influence of the temporal priors is, as expected, found for acquisitions with Bragg scatter (25 January, 14 March and 7 April) and the acquisition during a rain event (28 March). The bottom graph shows the effect of the chosen polarization combination on the delineated small reservoir areas. For acquisitions where most reservoir images are of good quality, the differences are minimal. The single polarization ‘HH’ tends to underestimate the small reservoir areas for all images with Bragg scatter. Multi-polarized combinations improve the delineation in some cases of Bragg scatter, e.g., the 25 January acquisition. The dual polarization combinations perform similar to the full polarized combination and are thus sufficient for small reservoir delineation. The combination with the backscatter intensity ratio in general results in the largest classified area for small reservoirs. During the 14 March, 28 March and 7 April acquisitions, which have the most low quality reservoir images, the temporal priors are needed to improve the delineations regardless of the polarization combination.
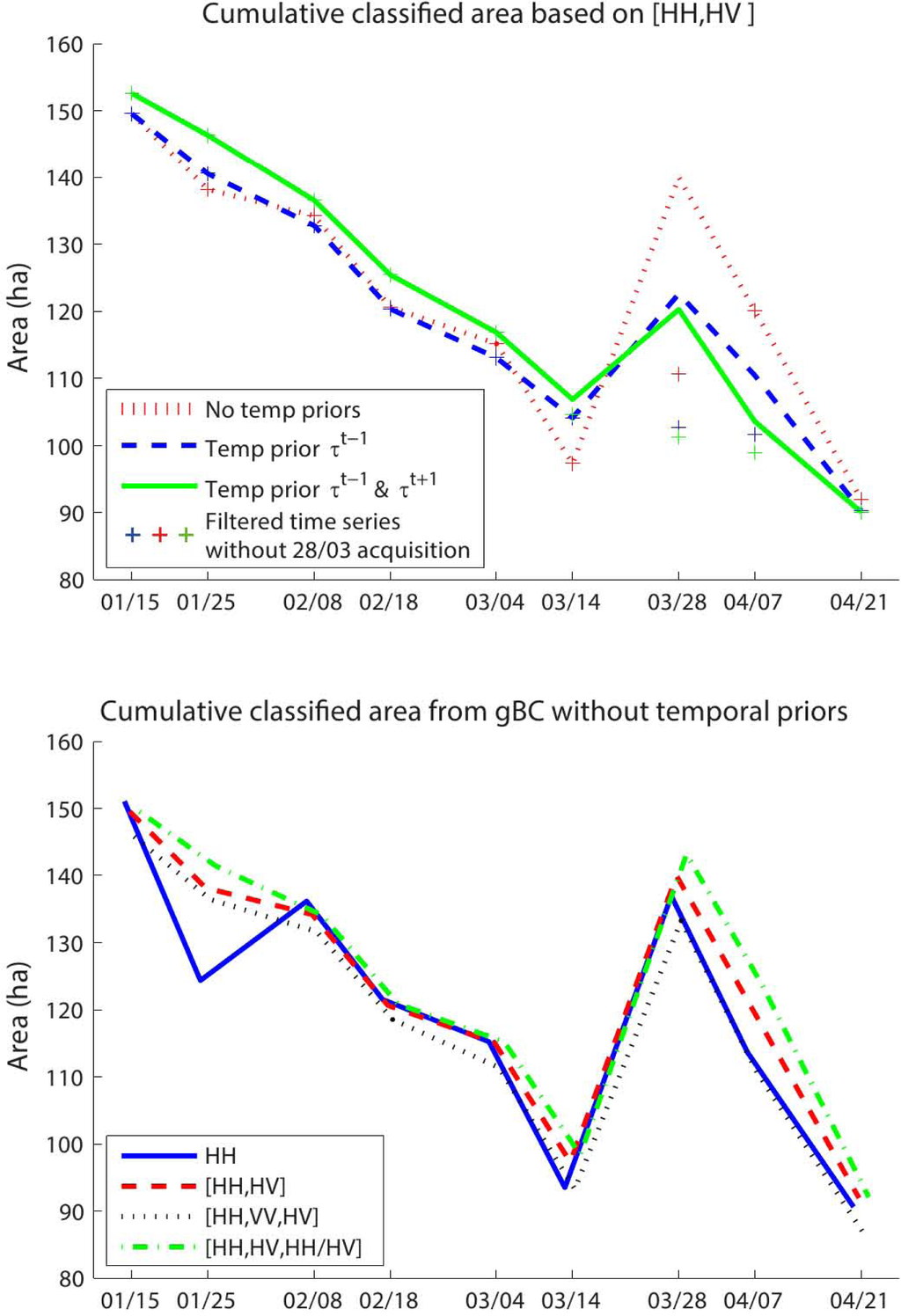
Figure 9.
Time series of the cumulative classified area for 26 small reservoirs, based on the growing Bayesian classifier (gBC) with and without temporal priors (top) and the gBC without temporal priors for different polarization combinations (bottom).
5. Conclusions
A Bayesian approach to monitoring small reservoirs was successfully applied. Despite temporal and spatial variation in backscatter intensities from small reservoirs, the newly developed algorithm is able to delineate open water throughout the dry season. The algorithm has a high accuracy, as the confusion area is restricted to the land-water boundary. Due to auxiliary temporal information, images with a low land-water contrast are resolved, even in the case of wind-induced Bragg scattering. One exception was the images acquired during a rain event, when water pools started forming on the bare ground surrounding the small reservoirs in the dry season and the land-water contrast deteriorates. In such cases, the use of time-series was able to mitigate the segmentation error, but not to completely resolve the land-water ambiguity.
The land-water contrast decreases with increasing roughness of the water surface or decreasing roughness of the surrounding land. The water surface roughness was found to increase due to wind-induced Bragg scattering and during rain events. The roughness of the land surrounding the small reservoir decreases towards the end of the dry season, when the water level in the small reservoirs is low and bare ground surrounds it. Areas with vegetation inside the small reservoir at the start of the dry season have a backscatter signature similar to land and were, therefore, not included in the delineation, causing an underestimation of the actual small reservoir area.
Single co-polarized backscatter intensities are sufficient in the case of high quality images. The dual polarization combinations ‘HH, HV’ and ‘HH, HV, HH/HV’ improve the land-water contrast significantly in the case of Bragg scattering and are, therefore, the preferred combinations of backscatter intensities for small reservoir monitoring. This is also relevant in the light of the European Space Agency’s (ESA) Sentinel 1 satellite, which does not produce full polarimetric images. Further research should address the exploitation of the coherent polarimetric information.
The overall conclusion of the paper is that, due to a Bayesian approach, the dynamics of small reservoirs can be monitored from SAR data with a high level of automation and without the restriction of cloud-free days. The suggested approach is to create a base map of small reservoirs first, after which small reservoir dynamics can be monitored with SAR data using a Bayesian time series approach. The base map is best created at the onset of the dry season, when the reservoirs are at full capacity and the reservoir masks can be determined.
Acknowledgments
The authors would like to acknowledge the support of the European Space Agency (ESA) ALCANTARAproject AO-1-7102 A11and TIGERproject No. 32, the RADARSAT-2 Science and Operational Applications Research and Development Program (“SOAR Program”) No. 5116 of the Canadian Space Agency, the Challenge Program for Water and Food (CPWF-Volta) and the Trans-African Hydro-Meteorological Observatory (TAHMO) for providing the meteorological data for this study.
Author Contributions
All authors contributed extensively to the work presented in this paper. Specific contributions include development of the concept, provision of data and data acquisition capacity (Nick van de Giesen, Frank O. Annor); SAR data pre-processing and signature interpretation (Lorenzo Iannini); fieldwork, development of algorithm, data analysis and preparation manuscript and figures (Dirk Eilander).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Venot, J.P.; Fraiture, C.D.; Nti Acheampong, E. Revisiting Dominant Notions: A Review of Costs, Performance and Institutions of Small Reservoirs in Sub-Saharan Africa; IWMI Research Report 144; International Water Management Institute: Colombo, Sri Lanka, 2012; p. 39. [Google Scholar]
- Leemhuis, C.; Jung, G.; Kasei, R.; Liebe, J. The Volta Basin Water Allocation System: Assessing the impact of small-scale reservoir development on the water resources of the Volta basin, West Africa. Adv. Geosci 2009, 21, 57–62. [Google Scholar]
- Krol, M.S.; de Vries, M.J; van Oel, P.R.; de Araújo, J.C. Sustainability of small reservoirs and large scale water availability under current conditions and climate change. Water Resour. Manag 2011, 25, 3017–3026. [Google Scholar]
- Annor, F.; van de Giesen, N.; Liebe, J; van de Zaag, P.; Tilmant, A.; Odai, S. Delineation of small reservoirs using radar imagery in a semi-arid environment: A case study in the Upper East Region of Ghana. Phys. Chem. Earth, Parts A/B/C 2009, 34, 309–315. [Google Scholar]
- Liebe, J; van de Giesen, N.; Andreini, M. Estimation of small reservoir storage capacities in a semi-arid environment: A case study in the Upper East Region of Ghana. Phys. Chem. Earth 2005, 30, 448–454. [Google Scholar]
- Sawunyama, T.; Senzanje, A.; Mhizha, A. Estimation of small reservoir storage capacities in Limpopo River Basin using geographical information systems (GIS) and remotely sensed surface areas: Case of Mzingwane catchment. Phys. Chem. Earth 2006, 31, 935–943. [Google Scholar]
- Crétaux, J.F.; Birkett, C. Lake studies from satellite radar altimetry. Comptes Rendus Geosci 2006, 338, 1098–1112. [Google Scholar]
- Gao, H.; Birkett, C.; Lettenmaier, D. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res 2012, 48, W09504. [Google Scholar]
- Islam, A.; Bala, S.; Haque, M. Flood inundation map of Bangladesh using MODIS time-series images. J. Flood Risk Manag 2010, 3, 210–222. [Google Scholar]
- McFeeters, S. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens 1996, 17, 1425–1432. [Google Scholar]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens 2006, 27, 3025–3033. [Google Scholar]
- Mialhe, F.; Gunnell, Y; Mering, C. Synoptic assessment of water resource variability in reservoirs by remote sensing: General approach and application to the runoff harvesting systems of south India. Water Resour. Res 2008, 44, W05411. [Google Scholar]
- Rodrigues, L.; Sano, E.; Steenhuis, T.; Passo, D. Estimation of small reservoir storage capacities with remote sensing in the Brazilian Savannah Region. Water Resour. Manag 2012, 26, 1–10. [Google Scholar]
- Liebe, J.; van de Giesen, N.; Andreini, M.; Steenhuis, T.; Walter, M. Suitability and limitations of ENVISAT ASAR for monitoring small reservoirs in a semiarid area. Geosci. Remote Sens 2009a, 47, 1536–1547. [Google Scholar]
- Bamler, R.; Eineder, M. Accuracy of differential shift estimation by correlation and split-bandwidth interferometry for wideband and delta-k SAR systems. IEEE Geosci. Remote Sens. Lett 2005, 2, 151–155. [Google Scholar]
- Van de Giesen, N. Characterization of West African Shallow Flood Plains with L-and C-Band Radar; Owe, M., Brubaker, K., Ritchie, J., Rango, A., Eds.; IAHS Publication: Wallingford, UK, 2001. [Google Scholar]
- Eilander, D.M. Remotely Sensed Small Reservoir Monitoring: A Bayesian Approach. Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- Hoekman, D.H.; Vissers, M.A. A new polarimetric classification approach evaluated for agricultural crops. IEEE Trans. Geosci. Remote Sens 2003, 41, 2881–2889. [Google Scholar]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math 1991, 43, 1–20. [Google Scholar]
- Strahler, A.H. The use of prior probabilities in maximum likelihood classification of remotely sensed data. Remote Sens. Environ 1980, 10, 135–163. [Google Scholar]
- Kailath, T. The divergence and Bhattacharyya distance measures in signal selection. IEEE Trans. Commun. Technol 1967, 15, 52–60. [Google Scholar]
- Cloude, S.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens 1997, 35, 68–78. [Google Scholar]
- Yang, J.; Yamaguchi, Y.; Yamada, H.; Sengoku, M.; Lin, S. Optimal problem for contrast enhancement in polarimetric radar remote sensing. IEICE Trans. Commun 1999, 82, 174–183. [Google Scholar]
- Yang, J.; Yamaguchi, Y.; Boerner, W.M.; Lin, S. Numerical methods for solving the optimal problem of contrast enhancement. IEEE Trans. Geosci. Remote Sens 2000, 38, 965–971. [Google Scholar]
- Yang, J.; Dong, G.; Peng, Y.; Yamaguchi, Y.; Yamada, H. Generalized optimization of polarimetric contrast enhancement. IEEE Geosci. Remote Sens. Lett 2004, 1, 171–174. [Google Scholar]
- Henderson, F. Environmental factors and the detection of open surface water areas with X-band radar imagery. Int. J. Remote Sens 1995, 16, 2423–2437. [Google Scholar]
- Henderson, F.; Lewis, A. Principles and Applications of Imaging Radar. Manual of Remote Sensing; John Wiley and Sons: New York, USA, 1998; Volume 2. [Google Scholar]
- Valenzuela, G.R. Theories for the interaction of electromagnetic and oceanic waves—A review. Bound.-Layer Meteorol 1978, 13, 61–85. [Google Scholar]
- Brisco, B.; Short, N.; van der Sanden, J.; Landry, R.; Raymond, D. A semi-automated tool for surface water mapping with RADARSAT-1. Can. J. Remote Sens 2009, 35, 336–344. [Google Scholar]
- Dubois, P.C.; van Zyl, J.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens 1995, 33, 915–926. [Google Scholar]
- Liebe, J.; van de Giesen, N.; Andreini, M.; Walter, M.; Steenhuis, T. Determining watershed response in data poor environments with remotely sensed small reservoirs as runoff gauges. Water Resour. Res 2009, 45, W07410. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).